Effect of Adding Hydrometeor Mixing Ratios Control Variables on Assimilating Radar Observations for the Analysis and Forecast of a Typhoon
Abstract
1. Introduction
2. Methodologies
2.1. Cost Function in WRFDA
2.2. The NMC Method
2.3. B Modeling in WRFDA-3DVar
2.4. Radar Observation Operators
3. Experiment Setup
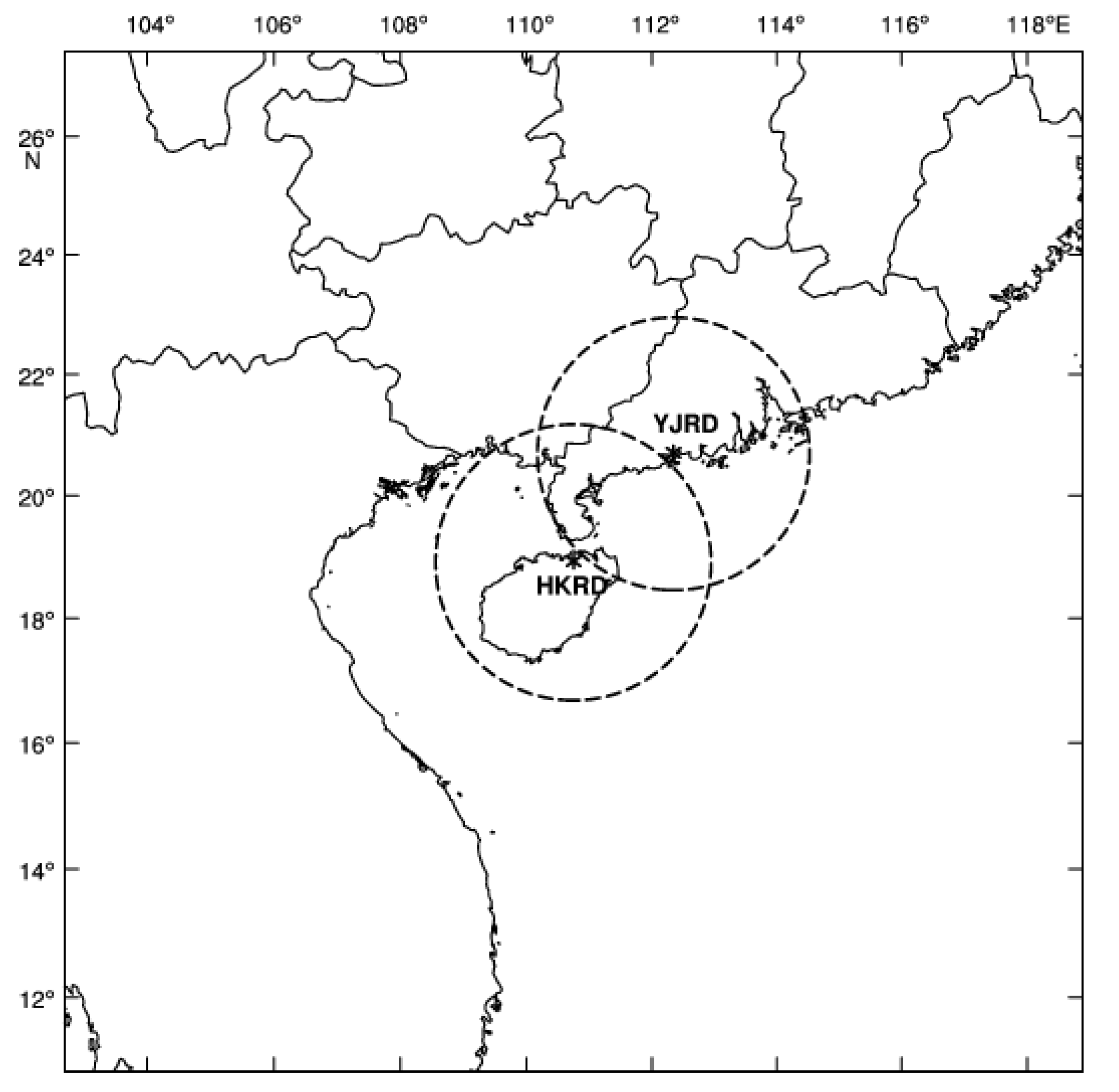
3.1. Radar Observation
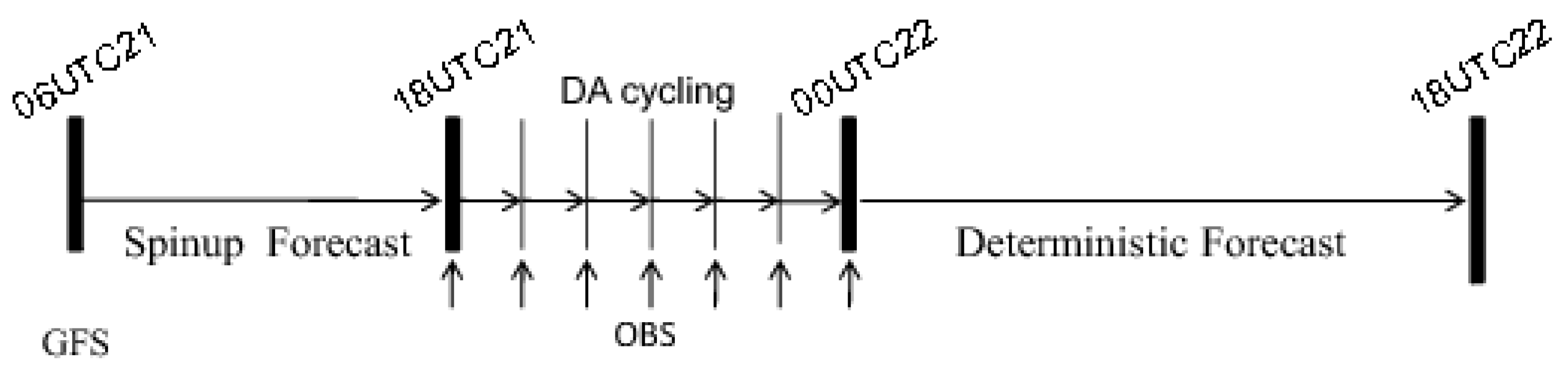
3.2. Model Configuration and Experimental Design
4. Results
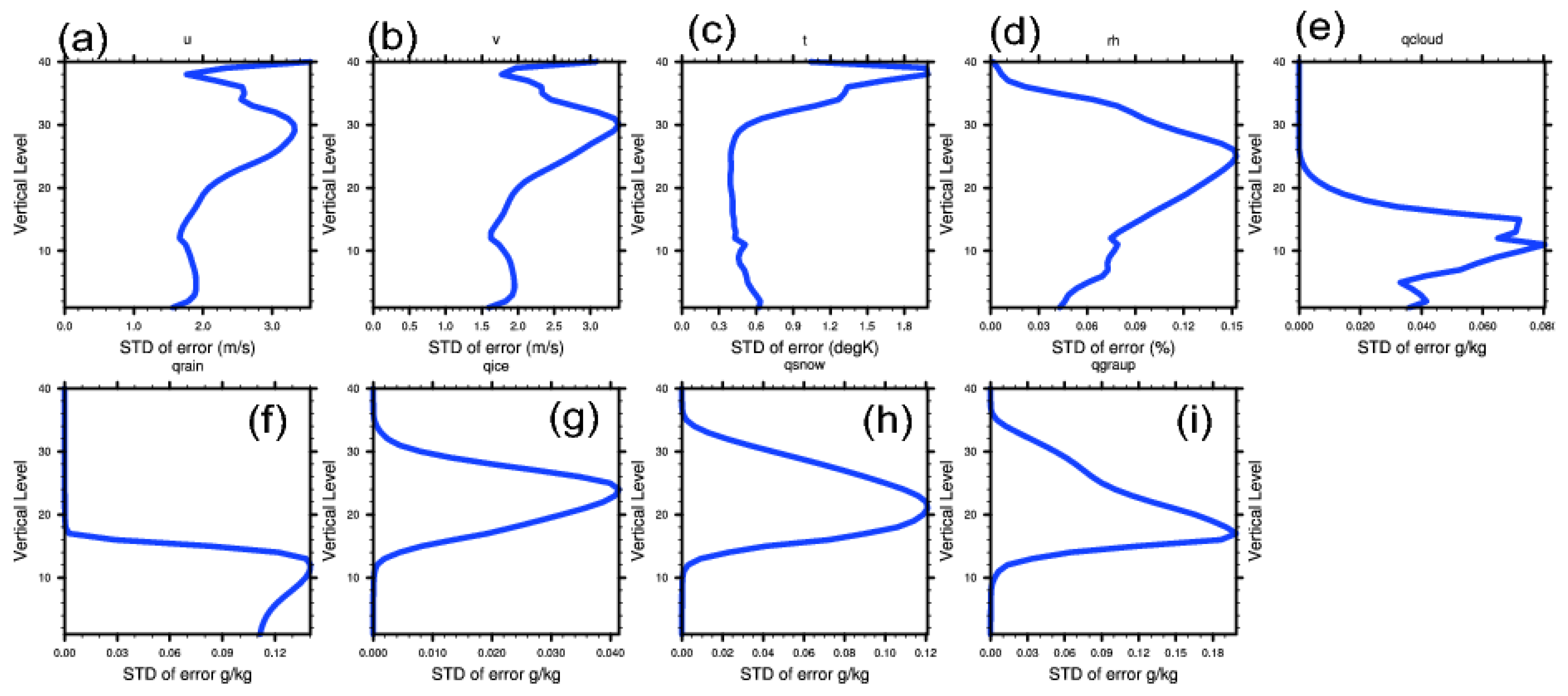
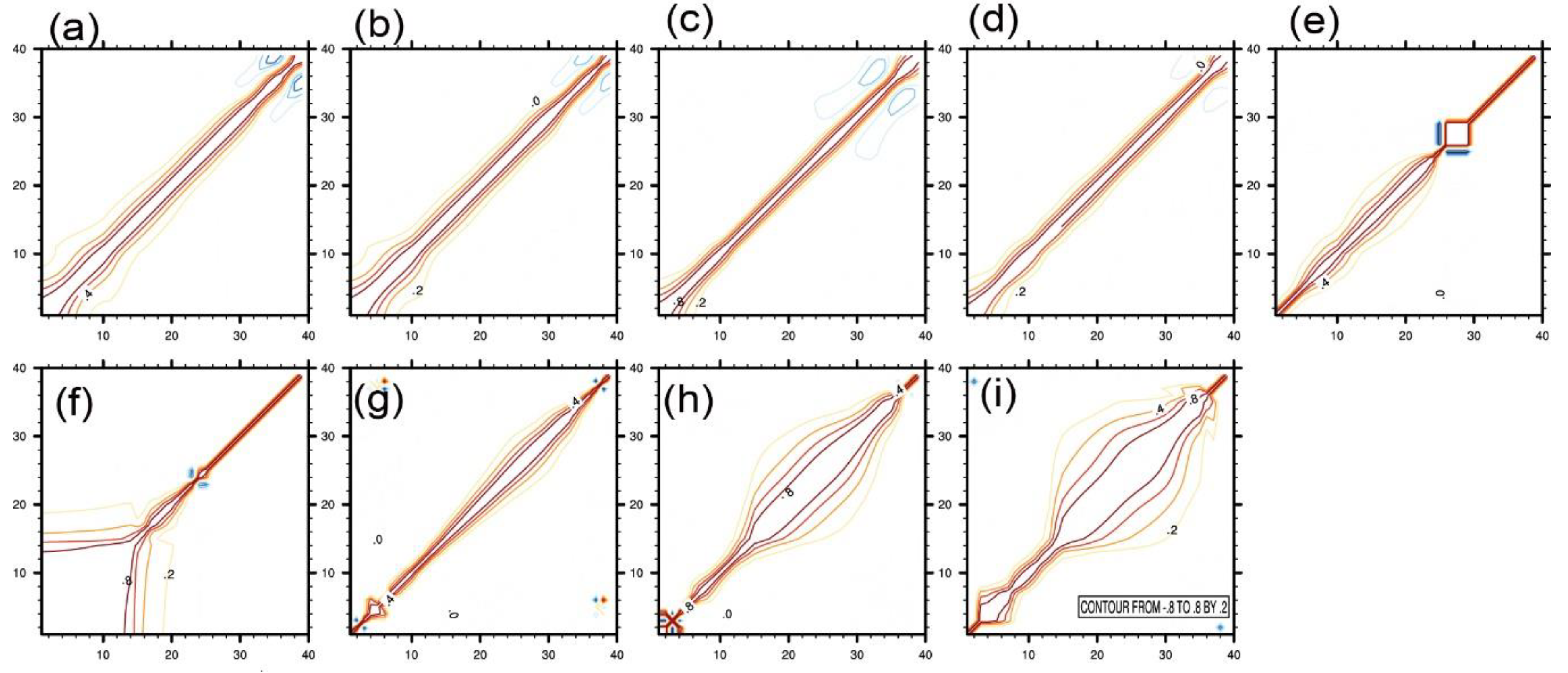
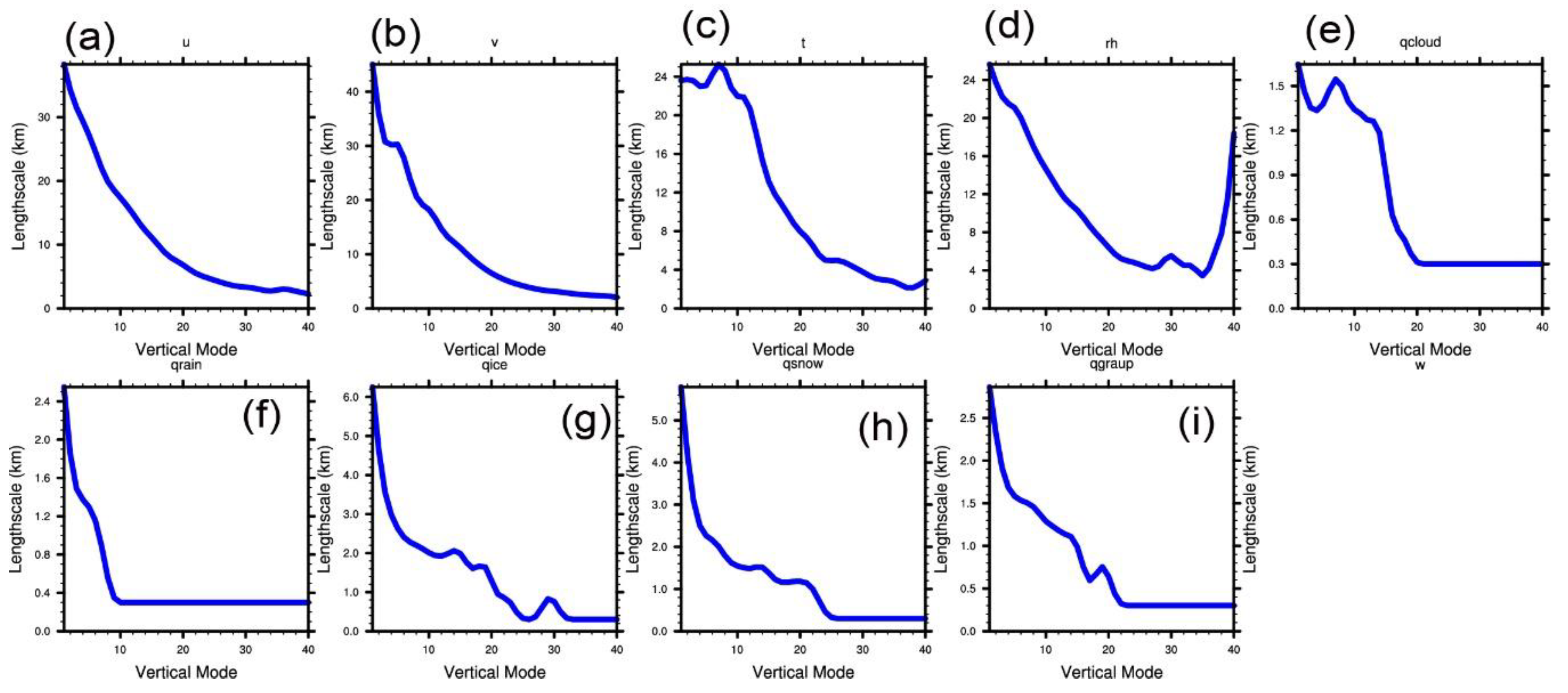
4.1. The Background Error Statistics
4.2. Analysis Increment
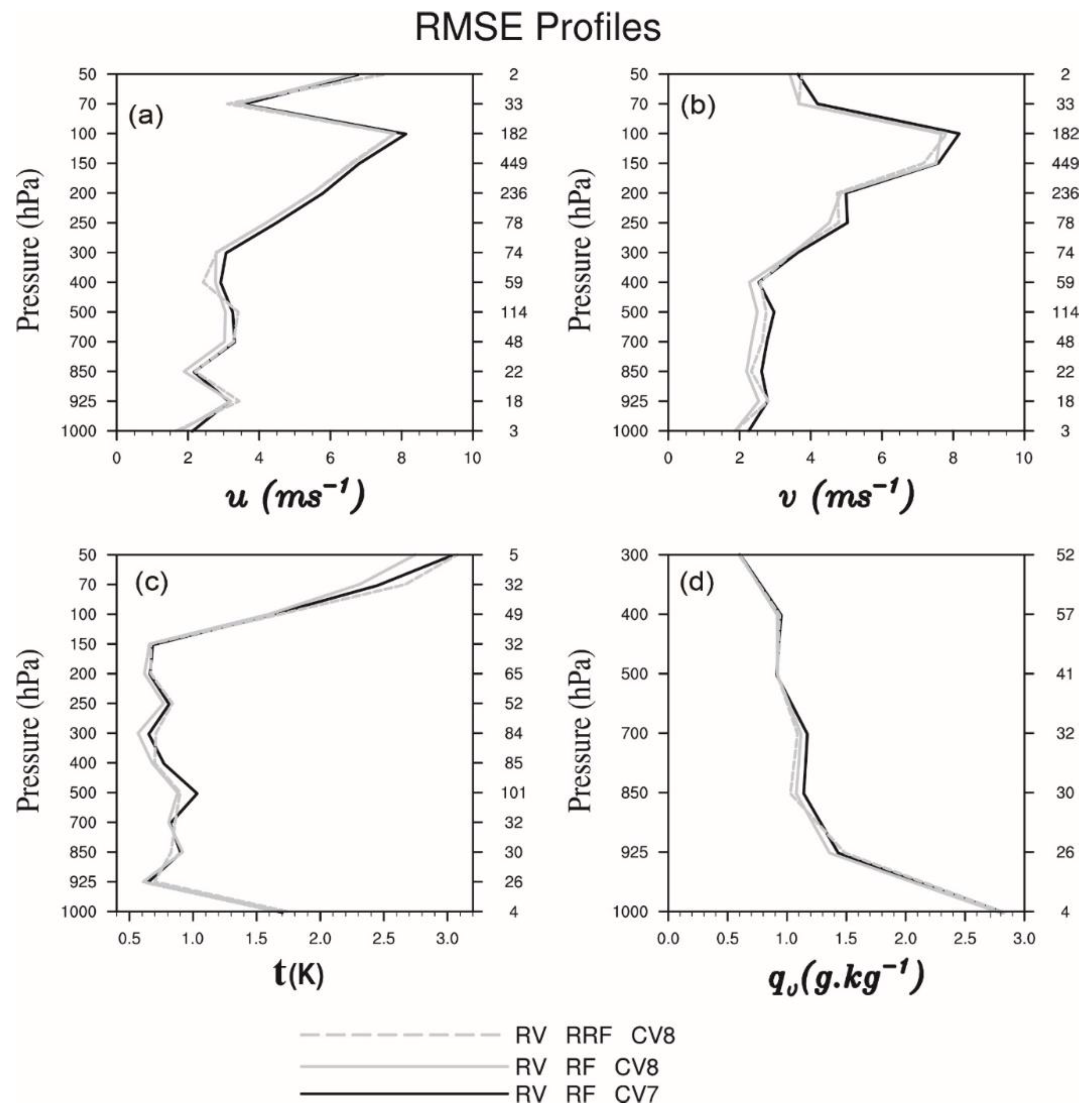
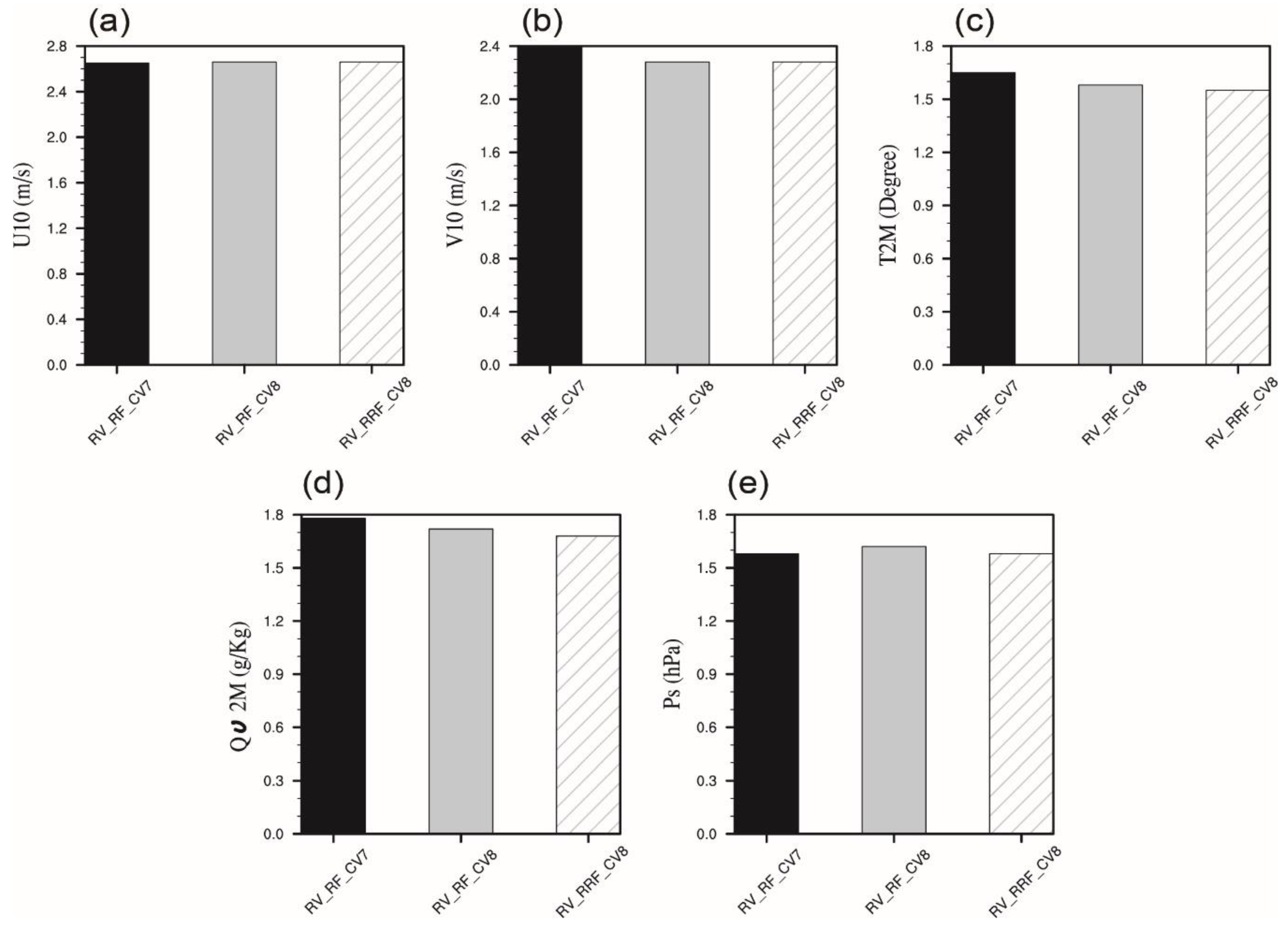
4.3. Verification against the Conventional Observations
4.4. Track, Intensity, and Precipitation Forecast
4.5. Precipitation Forecast
5. Conclusions and Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Desroziers, G.; Ivanov, S. Diagnosis and adaptive tuning of observation-error 629 parameters in a variational assimilation. Q. J. R. Meteorol. Soc. 2001, 127, 1433–1452. [Google Scholar] [CrossRef]
- Xie, Y.; MacDonals, A.E. Selection of momentum variables for a three-dimensional variational analysis. Pure Appl. Geophys. 2012, 169, 335–351. [Google Scholar] [CrossRef]
- Sun, J.; Wang, H.; Tong, W. Comparison of the impacts of momentum control variables on high-resolution variational data assimilation and precipitation forecasting. Mon. Weather Rev. 2016, 144, 149–169. [Google Scholar] [CrossRef]
- Michel, Y.; Auligné, T.; Montmerle, T. Heterogeneous convective-scale background error covariances with the inclusion of hydrometeor variables. Mon. Weather Rev. 2011, 139, 2994–3015. [Google Scholar] [CrossRef]
- Descombes, G.; Auligné, T.; Vandenberghe, F.; Barker, D.M.; Barré, J. Generalized background error covariance matrix model (GEN_BE v2.0). Geosci. Model Dev. 2015, 8, 669–696. [Google Scholar] [CrossRef]
- Sokol, Z. Effects of an assimilation of radar and satellite data on a very-short range forecast of heavy convective rainfalls. Atmos. Res. 2009, 93, 188–206. [Google Scholar] [CrossRef]
- Sokol, Z. Assimilation of extrapolated radar reflectivity into a NWP model and its impact on a precipitation forecast at high resolution. Atmos. Res. 2011, 100, 201–212. [Google Scholar] [CrossRef]
- Courtier, P. The ECMWF implementation of three dimensional variational assimilation (3D-Var). I: Formulation. Q. J. R. Meteorol. Soc. 1998, 124, 1783–1807. [Google Scholar] [CrossRef]
- Barker, D.M.; Huang, X.Y.; Liu, Z.; Auligné, T.; Zhang, X.; Rugg, S.; Ajjaji, R.; Bourgeois, A.; Bray, J.; Chen, Y.; et al. The Weather Research and Forecasting Model’s Community Variational/Ensemble Data Assimilation System: WRFDA. Bull. Am. Meteorol. Soc. 2012, 93, 831–843. [Google Scholar] [CrossRef]
- Ide, K.; Courtier, P.; Ghil, M.; Lorenc, A.C. Unified notation for data assimilation: Operational sequential and variational. J. Meteorol. Soc. 1997, 75, 181–189. [Google Scholar] [CrossRef]
- Parrish, D.F.; Derber, J.C. The national meteorological center’s spectral statistical-interpolation analysis system. Mon. Weather Rev. 1992, 120, 1747–1763. [Google Scholar] [CrossRef]
- Wang, H.; Huang, X.; Sun, J.; Xu, D.; Zhang, M.; Fan, S.; Zhong, J. Inhomogeneous background rrror modeling for WRF-Var using the NMC method. J. Appl. Meteor. Climatol. 2014, 53, 2287–2309. [Google Scholar] [CrossRef]
- Li, X.; Zeng, M.; Wang, Y.; Wang, W.; Wu, H.; Mei, H. Evaluation of two momentum control variable schemes and their impact on the variational assimilation of radar wind data: Case study of a squall line. Adv. Atmos. Sci. 2016, 33, 1143–1157. [Google Scholar] [CrossRef]
- Xiao, Q.; Kuo, Y.; Sun, J.; Lee, W.; Baker, D.M.; Lim, E. An Approach of Radar Reflectivity Data Assimilation and Its Assessment with the Inland QPF of Typhoon Rusa (2002) at Landfall. J. Appl. Meteor. Climatol. 2007, 46, 14–22. [Google Scholar] [CrossRef]
- Tong, M.; Xue, M. Ensemble Kalman filter assimilation of Doppler radar data with a compressible nonhydrostatic model: OSS experiments. Mon. Weather Rev. 2005, 133, 1789–1807. [Google Scholar] [CrossRef]
- Sun, J.; Crook, N.A. Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint. Part I: Model development and simulated data experiments. J. Atmos. Sci. 1997, 54, 1642–1661. [Google Scholar] [CrossRef]
- Wang, H.; Sun, J.; Zhang, X.; Huang, X.; Auligné, T. Radar data assimilation with WRF 4D-Var. Part I: System development and preliminary testing. Mon. Weather Rev. 2013, 141, 2224–2244. [Google Scholar] [CrossRef]
- Gao, J.; Stensrud, D.J. Assimilation of reflectivity data in a convective-scale, cycled 3DVAR framework with hydrometeor classification. J. Atmos. Sci. 2012, 69, 1054–1065. [Google Scholar] [CrossRef]
- Xue, M.; Wang, D.H.; Gao, J.D.; Brewster, K.; Droegemeier, K.K. The Advanced Regional Prediction System (ARPS), storm-scale numerical weather prediction and data assimilation. Meteorol. Atmos. Phys. 2003, 82, 139–170. [Google Scholar] [CrossRef]
- Brewster, K.; Hu, M.; Xue, M.; Gao, J. Efficient assimilation of radar data at high resolution for short-range numerical weather prediction. In Proceedings of the WWRP International Symposium on Nowcasting and Very Short Range Forecasting, Toulouse, France, 3 June 2005. [Google Scholar]
- Oye, R.; Mueller, C.; Smith, C. Software for radar data translation, visualization, editing and interpolation. In Proceedings of the 27th Conference on Radar Meteorology, Vail, CO, USA, 9–13 October 1995. [Google Scholar]
- Xiao, Q.; Zhang, X.Y.; Davis, C.; Tuttle, J.; Holland, G.; Fitzpatrick, P.J. Experiments of hurricane initialization with airborne Doppler radar data for the advanced research hurricane WRF (AHW) model. Mon. Weather Rev. 2009, 137, 2758–2777. [Google Scholar] [CrossRef]
- Shen, F.; Min, J. Assimilation of radar radial velocity data with the WRF hybrid ETKF-3DVAR system for the prediction of hurricane Ike (2008). Atmos. Res. 2016, 169, 127–138. [Google Scholar] [CrossRef]
- Shen, F.; Xu, D.; Xue, M.; Min, J. A comparison between EDA-EnVar and ETKF-EnVar data assimilation techniques using radar observations at convective scales through a case study of Hurricane Ike (2008). Meteorol. Atmos. Phys. 2017, 130, 1–18. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; NCAR Technical Note, NCAR/TN-4751STR; NCAR: Pod, CA, USA, 2008. [Google Scholar]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Hong, S.Y.; Dudhia, J.; Chen, S.H. A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation. Mon. Weather Rev. 2004, 132, 103–120. [Google Scholar] [CrossRef]
- Kain, J.S.; Fritsch, J.M. A one-dimensional entraining/detraining plume model and its application in convective parameterization. J. Atmos. Sci. 1990, 47, 2784–2802. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, F. E4DVar: Coupling an ensemble Kalman filter with four-dimensional variational data assimilation in a limited-area weather prediction model. Mon. Weather Rev. 2012, 140, 587–600. [Google Scholar] [CrossRef]
- Xie, Y.; Koch, S.; McGinley, J.; Albers, S.; Bieringer, P.E.; Wolfson, M.; Chan, M. A space–time multiscale analysis system: A sequential variational analysis approach. Mon. Weather Rev. 2011, 139, 1224–1240. [Google Scholar] [CrossRef]
- Tong, W.; Li, G.; Sun, J.; Tang, X.; Zhang, Y. Design Strategies of an Hourly Update 3DVAR Data Assimilation System for Improved Convective Forecasting. Weather Forecast. 2016, 31, 1673–1695. [Google Scholar] [CrossRef]
- Yu, H.; Hu, C.; Jiang, L. Comparison of three tropical cyclone intensity datasets. Acta Meteorol. Sin. 2007, 21, 121–128. [Google Scholar]
- Song, J.J.; Wang, Y.; Wu, L. Trend discrepancies among three best track data sets of western North Pacific tropical cyclones. J. Geophys. Res. 2010, 115, D12. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Schaefer, J.T. The critical success index as an indicator of warning skill. Weather Forecast. 1990, 5, 570–575. [Google Scholar] [CrossRef]
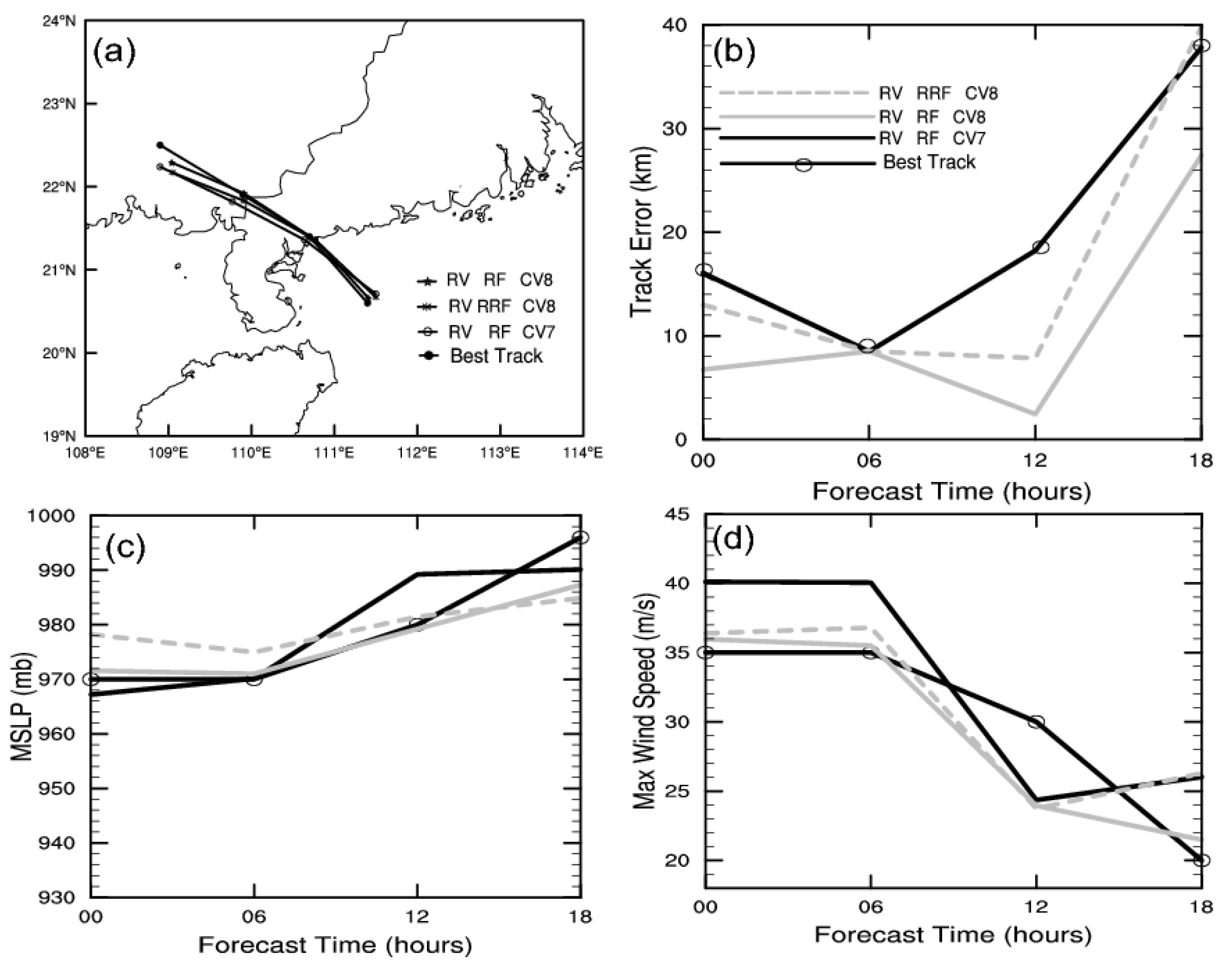
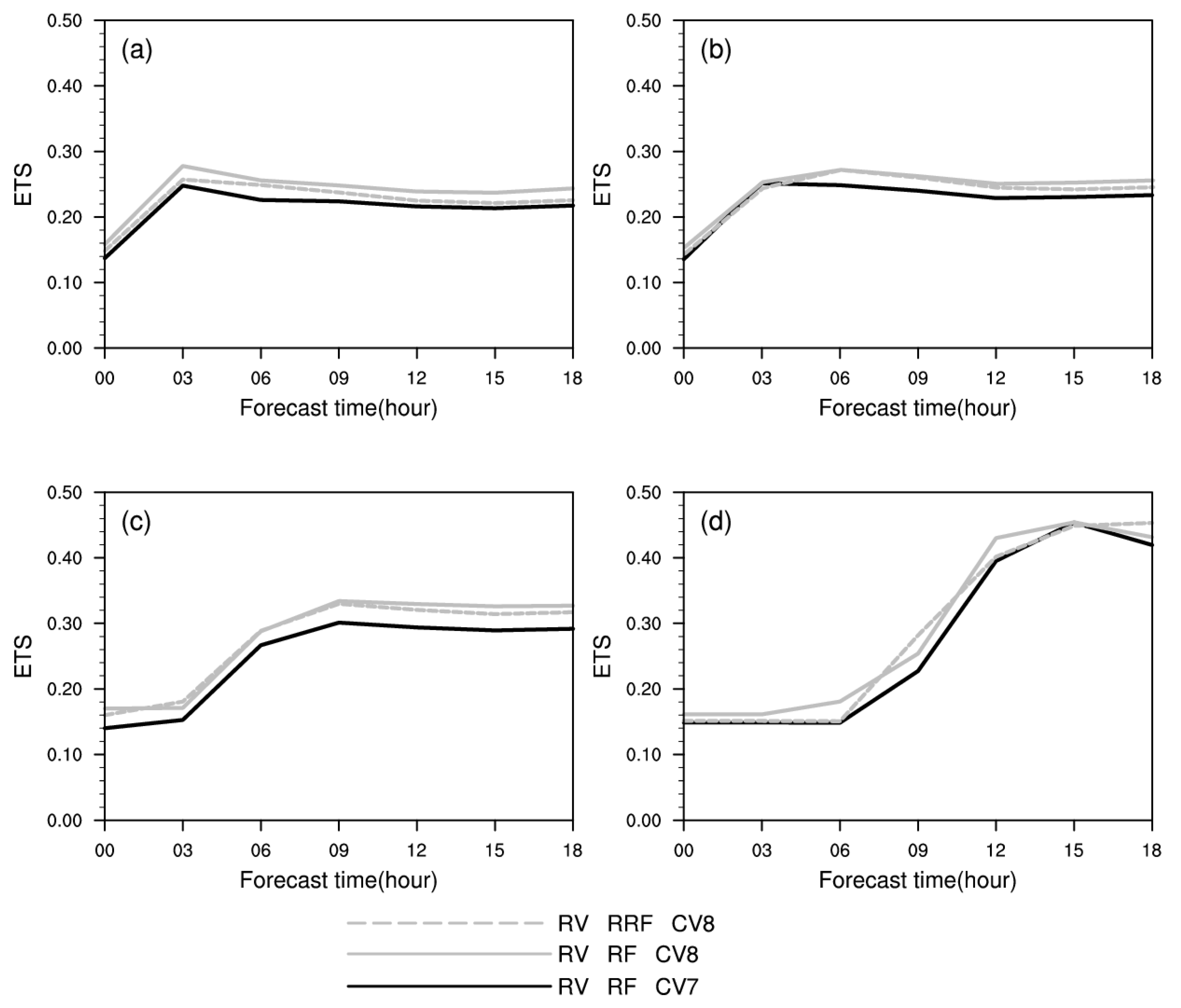
| Exp Name | Data | CV Type |
|---|---|---|
| RV_RF_CV7 | RV, RF | CV7 |
| RV_RF_CV8 | RV, RF | CV8 |
| RV_RRF_CV8 | RV, hydrometers from RF | CV8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, D.; Shen, F.; Min, J. Effect of Adding Hydrometeor Mixing Ratios Control Variables on Assimilating Radar Observations for the Analysis and Forecast of a Typhoon. Atmosphere 2019, 10, 415. https://doi.org/10.3390/atmos10070415
Xu D, Shen F, Min J. Effect of Adding Hydrometeor Mixing Ratios Control Variables on Assimilating Radar Observations for the Analysis and Forecast of a Typhoon. Atmosphere. 2019; 10(7):415. https://doi.org/10.3390/atmos10070415
Chicago/Turabian StyleXu, Dongmei, Feifei Shen, and Jinzhong Min. 2019. "Effect of Adding Hydrometeor Mixing Ratios Control Variables on Assimilating Radar Observations for the Analysis and Forecast of a Typhoon" Atmosphere 10, no. 7: 415. https://doi.org/10.3390/atmos10070415
APA StyleXu, D., Shen, F., & Min, J. (2019). Effect of Adding Hydrometeor Mixing Ratios Control Variables on Assimilating Radar Observations for the Analysis and Forecast of a Typhoon. Atmosphere, 10(7), 415. https://doi.org/10.3390/atmos10070415






