Parallelization Performances of PMSS Flow and Dispersion Modeling System over a Huge Urban Area
Abstract
1. Introduction
2. The PMSS Modeling System
2.1. Overview of the Modeling System
2.2. Parallel Algorithms
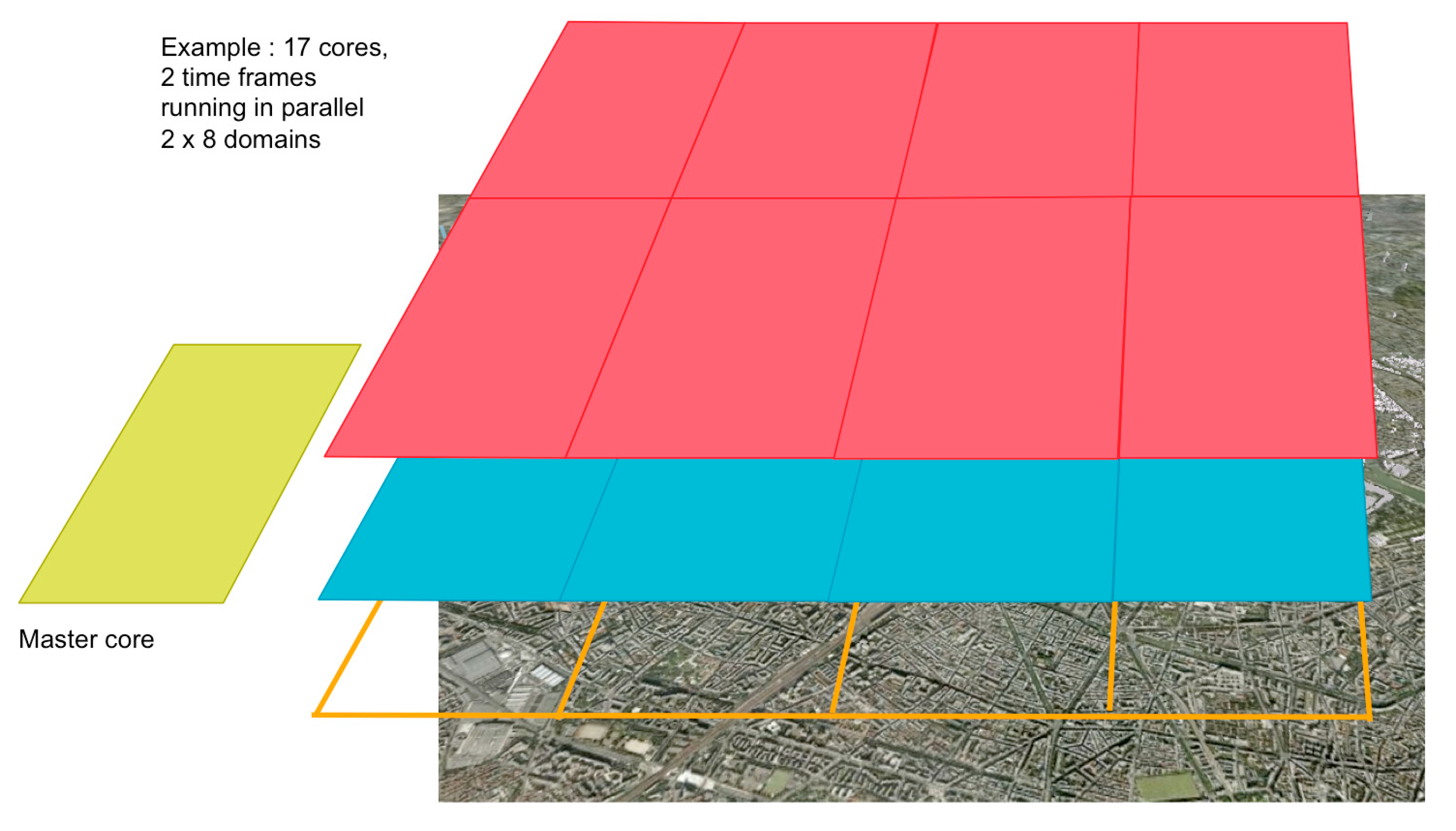
- Time Decomposition (TD): each individual timeframe of the calculation can be distributed to a calculation core. This is possible due to the diagnostic property of the model. In the case of a calculation using the RANS solver option, TD is still possible since a stationary calculation is done for each timeframe considered by the model, and each stationary calculation is independent.
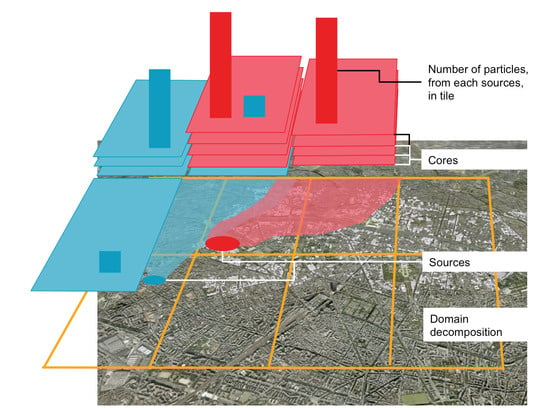
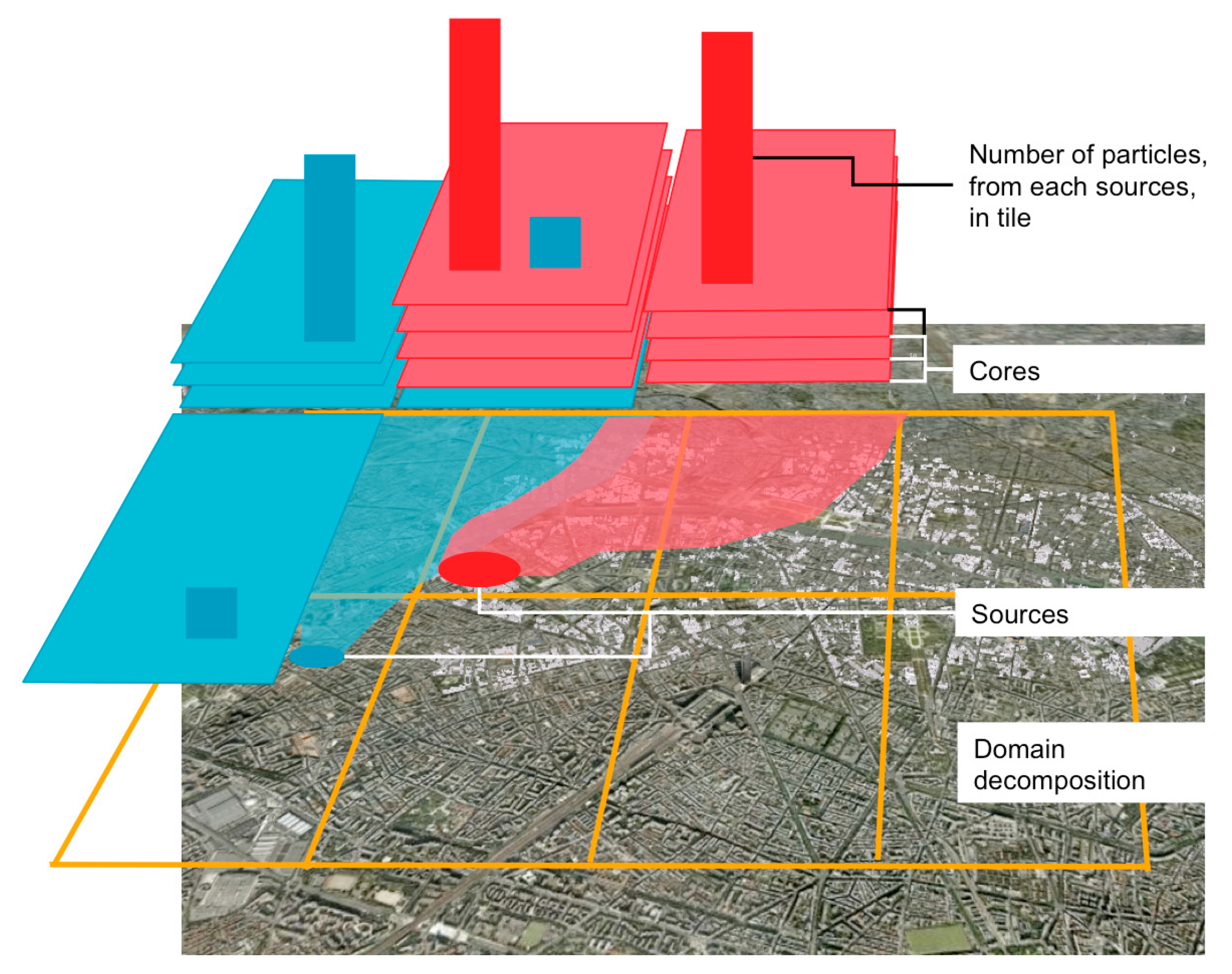
- Domain Decomposition (DD): the domain is horizontally sliced in multiple tiles distributed to available calculations cores.
- DD, essentially to handle weak scaling issues. DD is inherited from PSWIFT,
- Particle Decomposition (PD), essentially to handle strong scaling and reduce the computational time of a given calculation. PD uses the Lagrangian property of the code: each particle is independent, except for Eulerian processes.
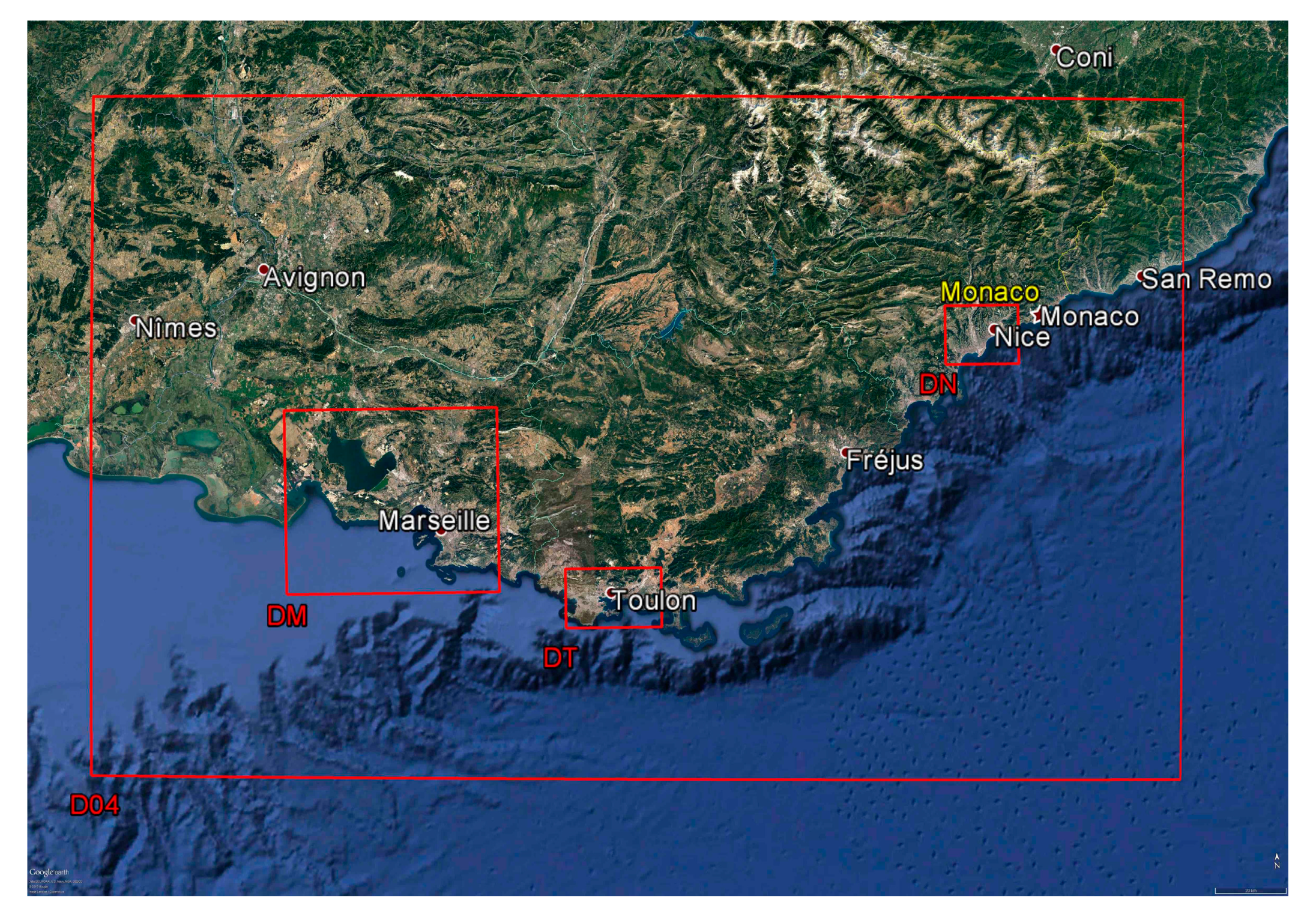
3. Model Setup for the EMED Project
3.1. The EMED Project
- Routine calculation using PSWIFT flow model on the nested domains with a horizontal grid step of 3 m, using WRF meteorological forecasts as input data. These calculations were performed for 24 h with timeframes of every 15 min. The WRF horizontal grid step was 1 km.
- On-demand calculations using PSPRAY dispersion model in case of accidental or malevolent releases and the PSWIFT flow predictions. In the project, we considered fictive releases.
3.2. Configurations of the Calculations and of the Computing Cluster
- Concentrations are calculated every minute using 12 samples taken every 5 s;
- 400,000 numerical particles are emitted every 5 s during the release periods. Hence 384 millions of numerical particles are emitted during the whole simulation. This number is very large and was chosen to allow for the computation of concentration each and every minute.
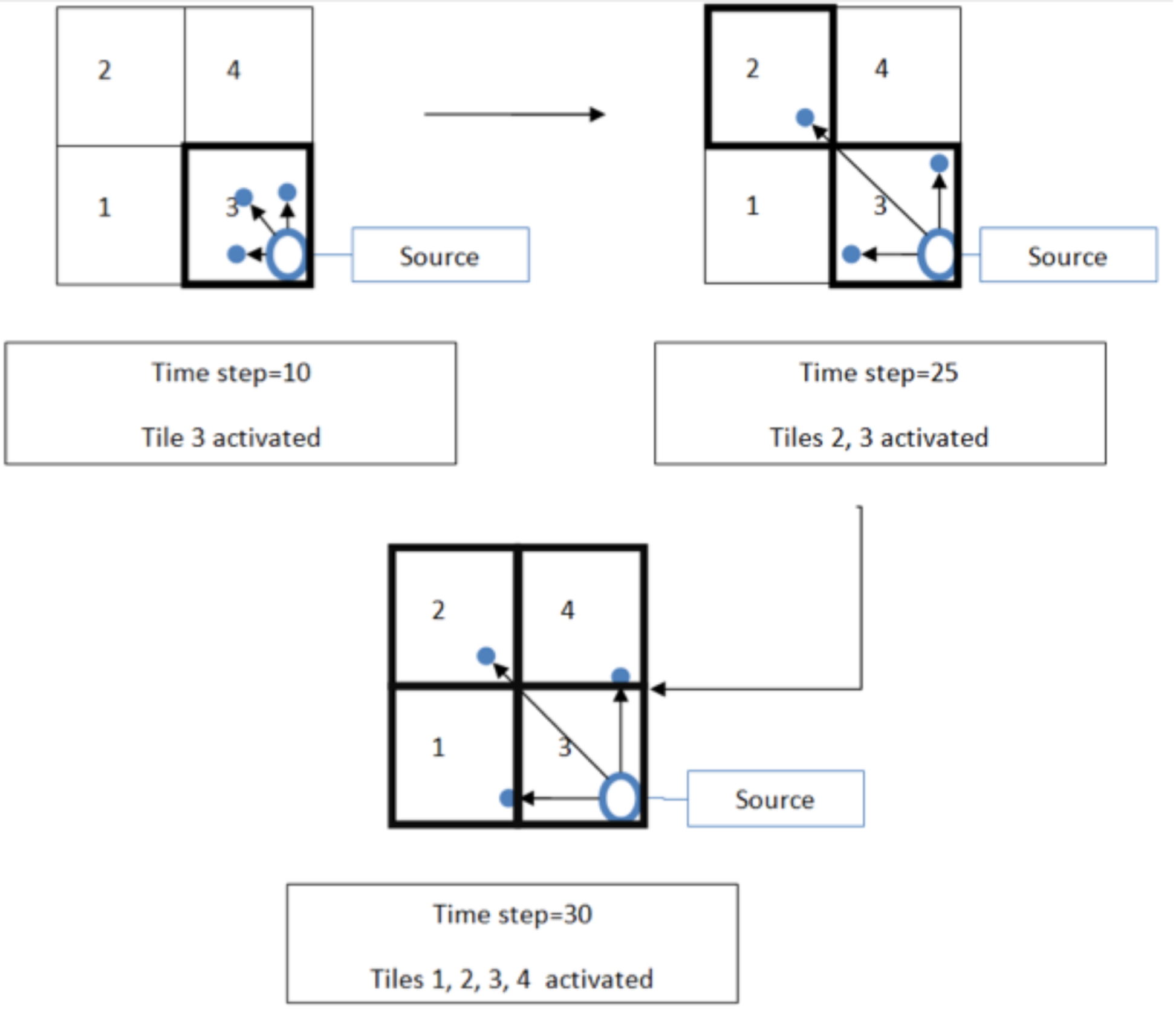
- Performing the LB too often, and getting too many LB additional computing costs implying notably loading and unloading flow data, sending and receiving particles;
- Not performing the LB, and having inefficient setup of cores on the domain, with respect to the locations of the particles.
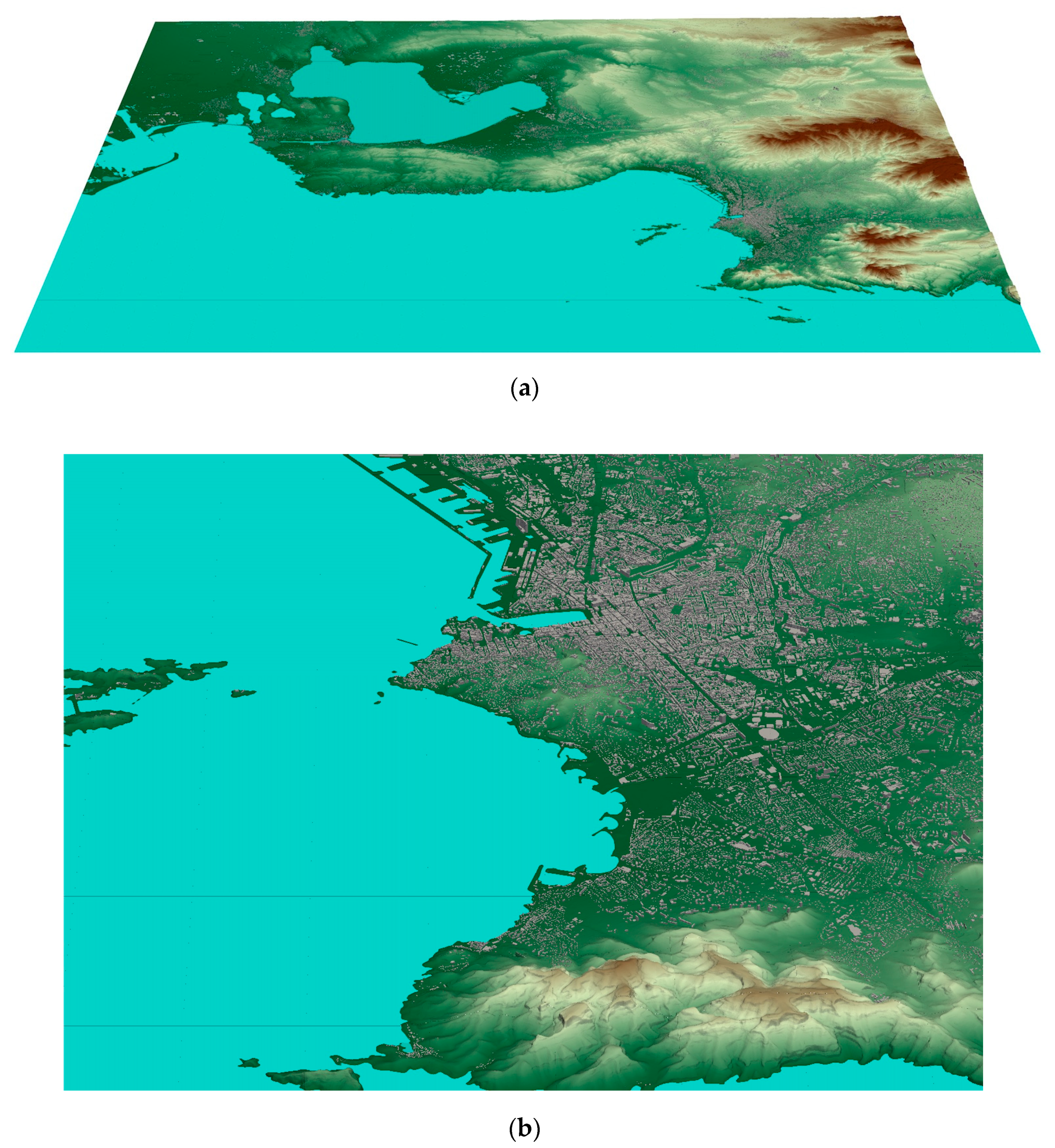
4. Domain Decomposition for the PMSS Modeling System on EMED Project
4.1. DD for the PSWIFT Flow Model
4.1.1. DD Setup
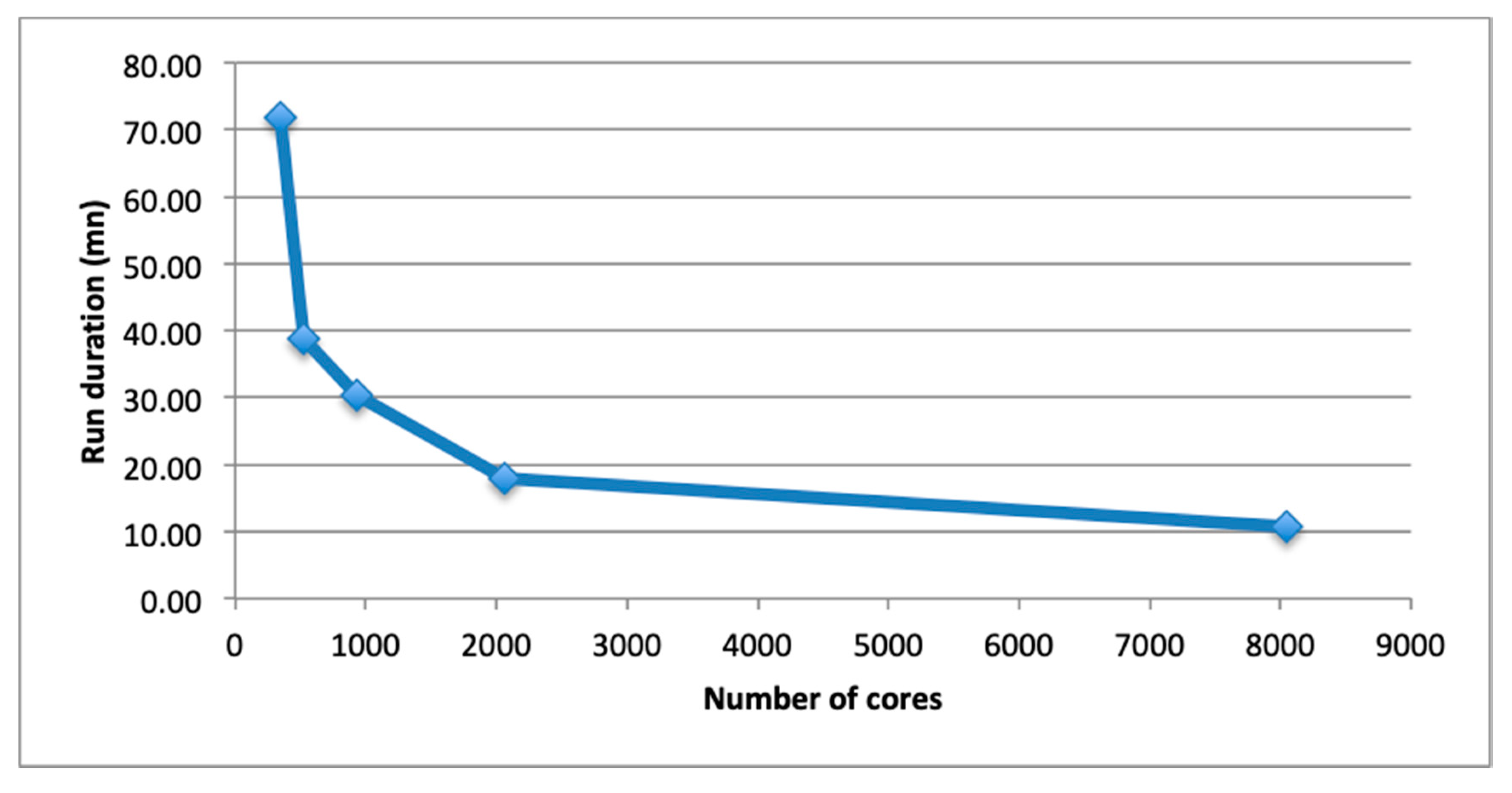
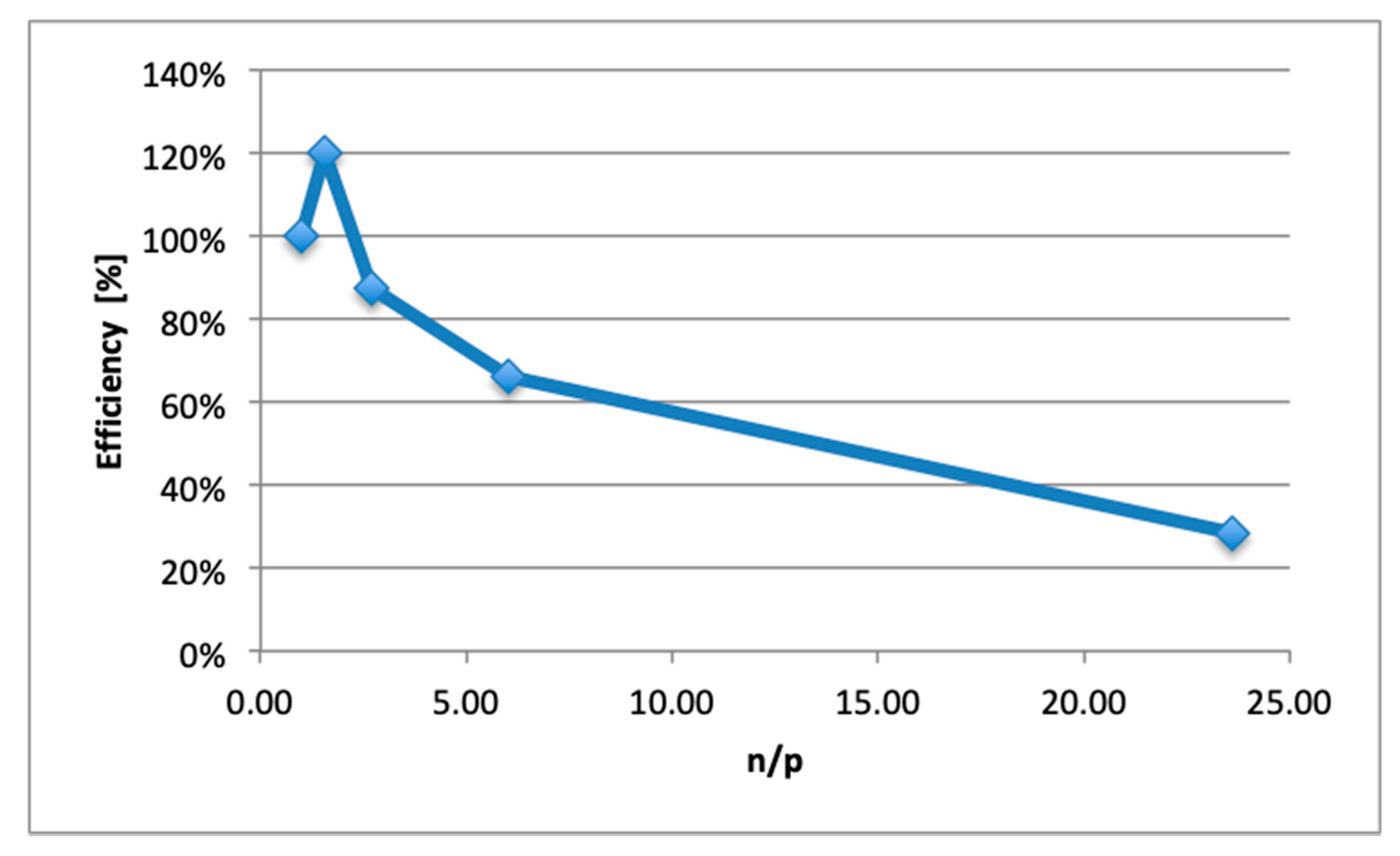
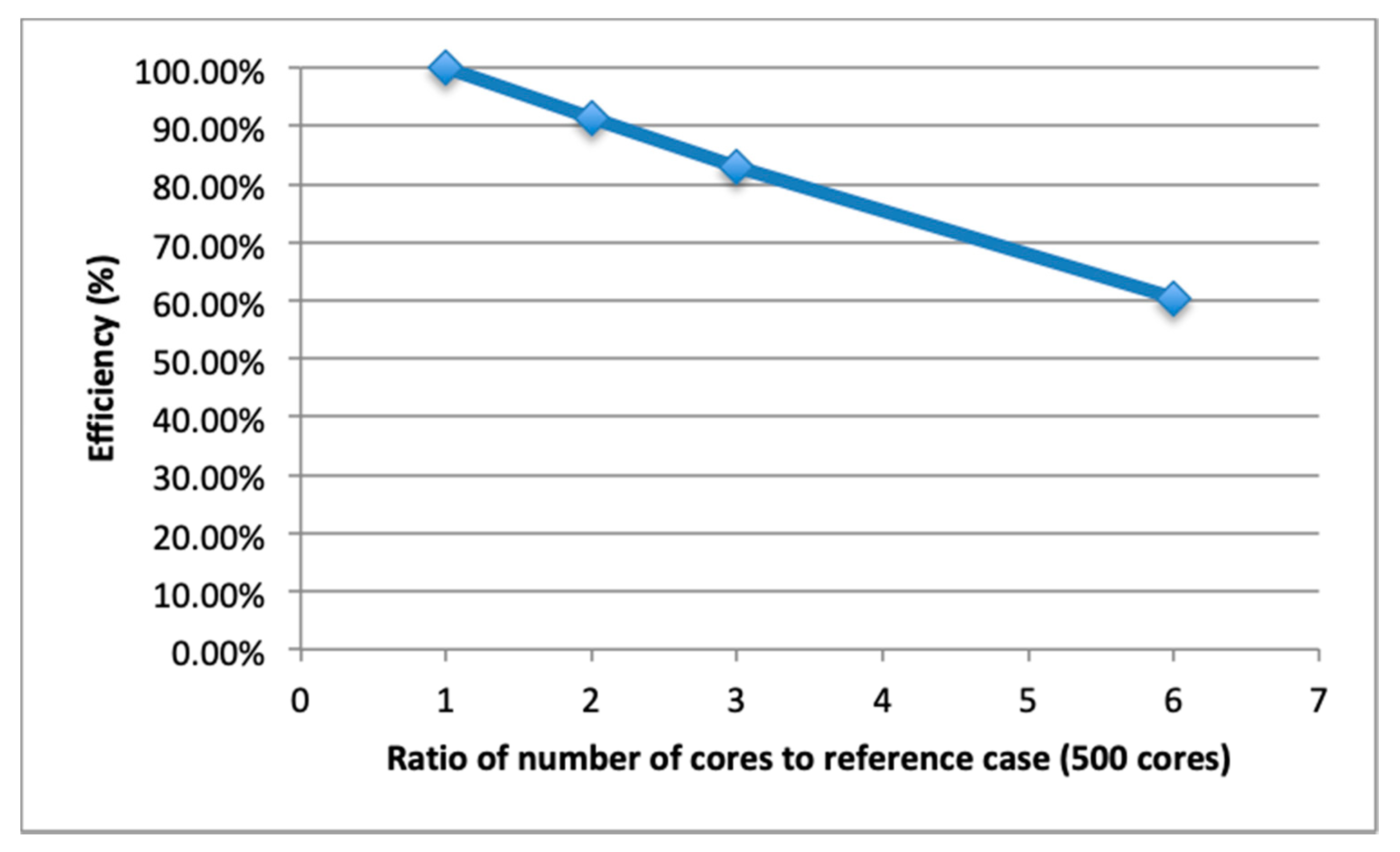
4.1.2. DD Results
4.1.3. Discussion
- The efficiency remained still above 50% of the minimal setup to be able to run the calculation on the supercomputer;
- The local scale flow simulation duration took less than 20 min for a timeframe calculation, allowing the prediction of the minimum 24 timeframes in around 7 h.
4.2. DD for the PSPRAY Dispersion Model
4.2.1. DD Setup
- On all the DD defined for PSWIFT: 340, 525, 924, 2058 and 8051 tiles,
- With a number of 500, 1000, 1500 and 3000 cores.
- The influence of the number of cores on a given DD,
- The influence of the DD on a given number of cores.
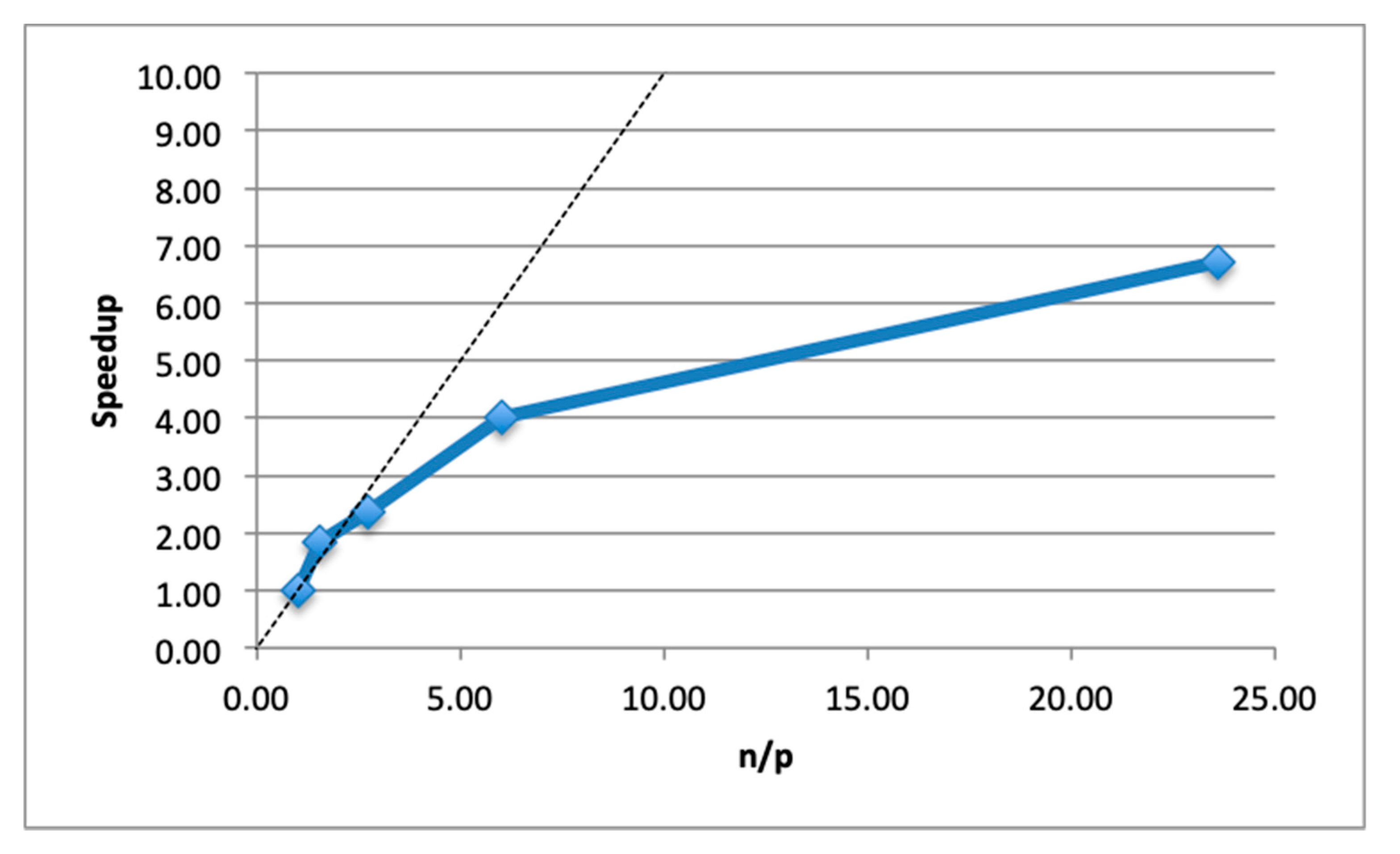
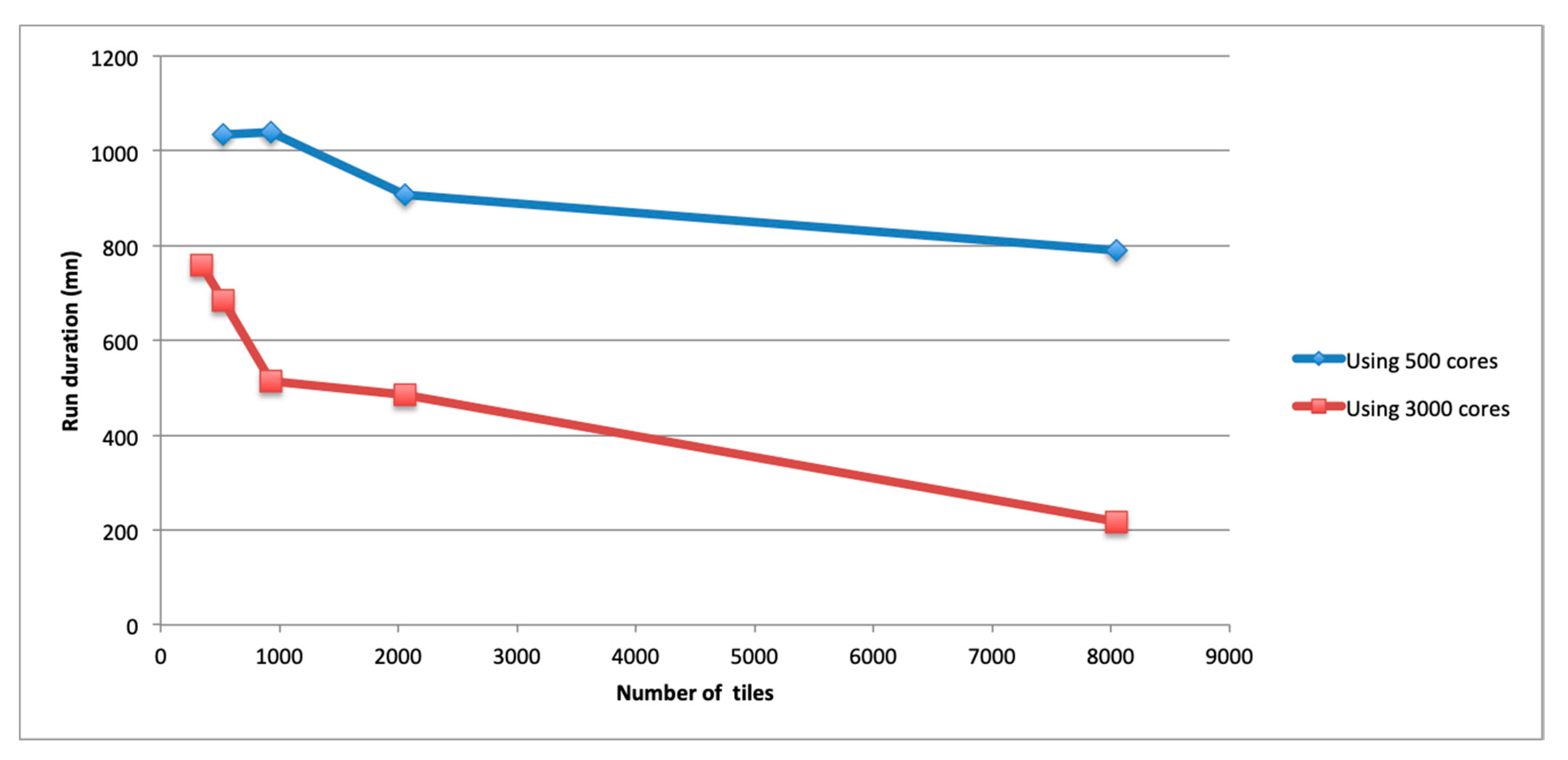
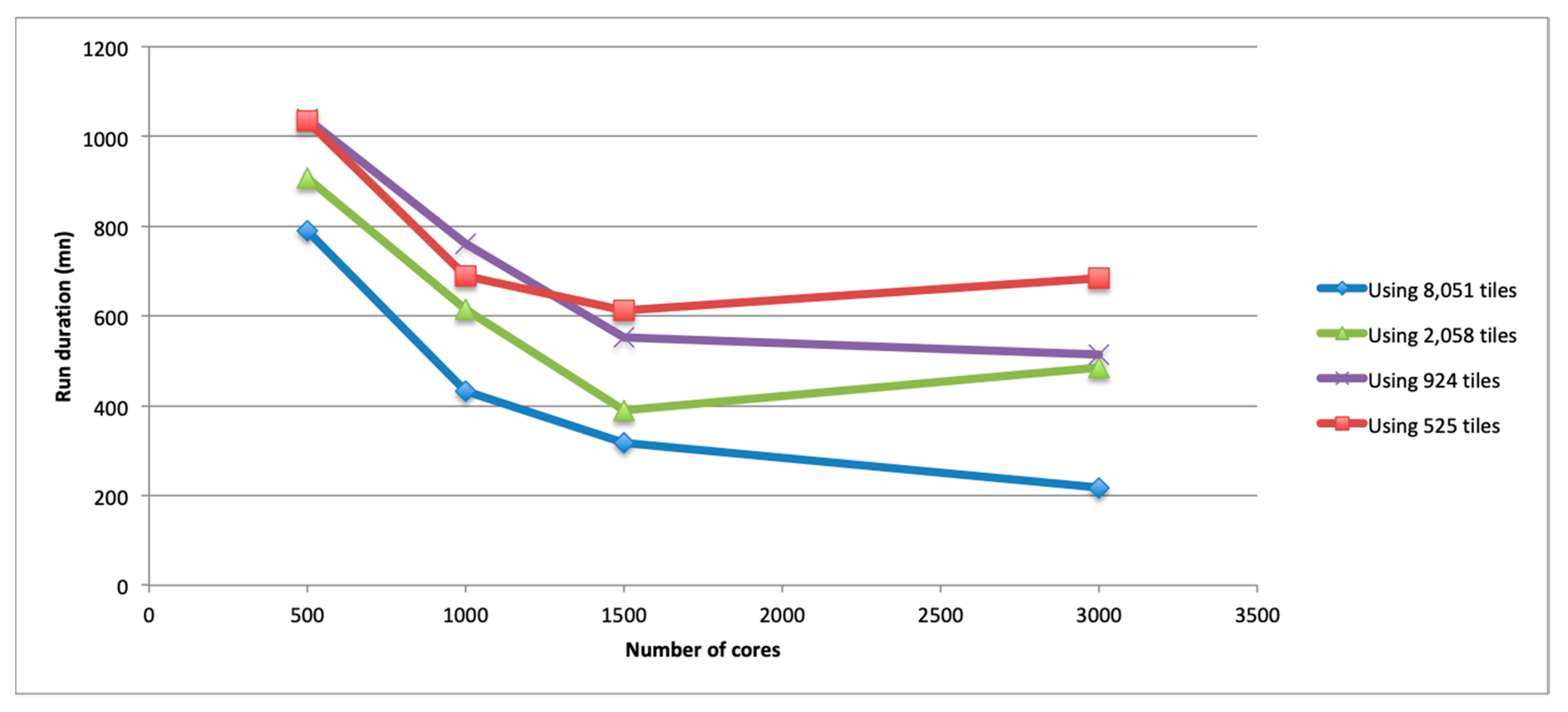
4.2.2. DD Results
4.2.3. Discussion on the Influence of the DD
- As expected, the run duration is the shortest when using 3000 cores;
- The finer the DD, the shorter the run duration is;
- Reducing the number of tiles in the DD decomposition reduces the impact of using more computing cores.
4.2.4. Discussion on the Influence of the Number of Cores
- Consistently with the previous section, a finer DD generally shortens the duration of the simulation.
- More computing cores reduce the simulation duration up to the point where the additional cost of LB more than compensate the gain in computing power.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Oldrini, O.; Armand, P.; Duchenne, C.; Olry, C.; Moussafir, J.; Tinarelli, G. Description and preliminary validation of the PMSS fast response parallel atmospheric flow and dispersion solver in complex built-up areas. Environ. Fluid Mech. 2017, 17, 997–1014. [Google Scholar] [CrossRef]
- Armand, P.; Bartzis, J.; Baumann-Stanzer, K.; Bemporad, E.; Evertz, S.; Gariazzo, C.; Gerbec, M.; Herring, S.; Karppinen, A.; Lacome, J.M.; et al. Best Practice Guidelines for the Use of the Atmospheric Dispersion Models in Emergency Response Tools at Local-Scale in Case of Hazmat Releases into the Air. Technical Report COST Action ES 1006. 2015. Available online: http://elizas.eu/images/Documents/Best%20Practice%20Guidelines_web.pdf (accessed on 6 July 2019).
- Oldrini, O.; Armand, P. Validation and Sensitivity Study of the PMSS Modelling System for Puff Releases in the Joint Urban 2003 Field Experiment. Bound. Layer Meteorol. 2019. [Google Scholar] [CrossRef]
- McHugh, C.A.; Carruthers, D.J.; Edmunds, H.A. ADMS-Urban: An air quality management system for traffic, domestic and industrial pollution. Int. J. Environ. Pollut. 1997, 8, 666–674. [Google Scholar]
- Schulman, L.L.; Strimaitis, D.G.; Scire, J.S. Development and evaluation of the PRIME plume rise and building downwash model. J. Air Waste Manag. Assoc. 2000, 5, 378–390. [Google Scholar] [CrossRef]
- Sykes, R.I.; Parker, S.F.; Henn, D.S.; Cerasoli, C.P.; Santos, L.P. PC-SCIPUFF Version 1.3—Technical Documentation. ARAP Report No. 725; Titan Corporation: San Diego, CA, USA, 2000. [Google Scholar]
- Hanna, S.; Baja, E. A simple urban dispersion model tested with tracer data from Oklahoma City and Manhattan. Atmos. Environ. 2009, 43, 778–786. [Google Scholar] [CrossRef]
- Soulhac, L.; Salizzoni, P.; Cierco, F.X.; Perkins, R. The model SIRANE for atmospheric urban pollutant dispersion—Part I: Presentation of the model. Atmos. Environ. 2011, 45, 7379–7395. [Google Scholar] [CrossRef]
- Carpentieri, M.; Salizzoni, P.; Robins, A.; Soulhac, L. Evaluation of a neighbourhood scale, street network dispersion model through comparison with wind tunnel data. Environ. Model. Softw. 2012, 37, 110–124. [Google Scholar] [CrossRef]
- Soulhac, L.; Lamaison, G.; Cierco, F.X.; Ben Salem, N.; Salizzoni, P.; Mejean, P.; Armand, P.; Patryl, L. SIR-ANERISK: Modelling dispersion of steady and unsteady pollutant releases in the urban canopy. Atmos. Environ. 2016, 140, 242–260. [Google Scholar] [CrossRef]
- Camelli, F.E.; Hanna, S.R.; Lohner, R. Simulation of the MUST field experiment using the FEFLO-urban CFD model. In Proceedings of the 5th Symposium on the Urban Environment, American Meteorological Society, Vancouver, BC, Canada, 23–26 August 2004. [Google Scholar]
- Gowardhan, A.A.; Pardyjak, E.R.; Senocak, I.; Brown, M.J. A CFD-based wind solver for an urban fast response transport and dispersion model. Environ. Fluid Mech. 2011, 11, 439–464. [Google Scholar] [CrossRef]
- Gowardhan, A.A.; Pardyjak, E.R.; Senocak, I.; Brown, M.J. Investigation of Reynolds stresses in a 3D idealized urban area using large eddy simulation. In Proceedings of the AMS Seventh Symposium on Urban Environment, San Diego, CA, USA, 26 April 2007. [Google Scholar]
- Kurppa, M.; Hellsten, A.; Auvinen, M.; Raasch, S.; Vesala, T.; Järvi, L. Ventilation and air quality in city blocks using Large Eddy Simulation–Urban planning perspective. Atmosphere 2018, 9, 65. [Google Scholar] [CrossRef]
- Kristóf, G.; Papp, B. Application of GPU-based Large Eddy Simulation in urban dispersion studies. Atmosphere 2018, 9, 442. [Google Scholar] [CrossRef]
- Röckle, R. Bestimmung der Strömungsverhältnisse im Bereich komplexer Bebauungsstrukturen. Ph.D. Thesis, Techn. Hochschule Darmstadt, Darmstadt, Germany, 1990. [Google Scholar]
- Kaplan, H.; Dinar, N. A Lagrangian dispersion model for calculating concentration distribution within a built-up domain. Atmos. Environ. 1996, 30, 4197–4207. [Google Scholar] [CrossRef]
- Hanna, S.; White, J.; Trolier, J.; Vernot, R.; Brown, M.; Gowardhan, A.; Kaplan, H.; Alexander, Y.; Moussafir, J.; Wang, Y.; et al. Comparisons of JU2003 observations with four diagnostic urban wind flow and Lagrangian particle dispersion models. Atmos. Environ. 2011, 45, 4073–4081. [Google Scholar] [CrossRef]
- Brown, M.J.; Gowardhan, A.A.; Nelson, M.A.; Williams, M.D.; Pardyjak, E.R. QUIC transport and dispersion modelling of two releases from the Joint Urban 2003 field experiment. Int. J. Environ. Pollut. 2013, 52, 263–287. [Google Scholar] [CrossRef]
- Singh, B.; Pardyjak, E.R.; Norgren, A.; Willemsen, P. Accelerating urban fast response Lagrangian dispersion simulations using inexpensive graphics processor parallelism. Environ. Model. Softw. 2011, 26, 739–750. [Google Scholar] [CrossRef]
- Pinheiro, A.; Desterro, F.; Santos, M.C.; Pereira, C.M.; Schirru, R. GPU-based implementation of a diagnostic wind field model used in real-time prediction of atmospheric dispersion of radionuclides. Prog. Nucl. Energy 2017, 100, 146–163. [Google Scholar] [CrossRef]
- Armand, P.; Duchenne, C.; Oldrini, O.; Perdriel, S. Emergencies Mediterranean—A Prospective High Resolution Modelling and Decision-Support System in Case of Adverse Atmospheric Releases Applied to the French Mediterranean Coast. In Proceedings of the 18th International conference on Harmonisation within Atmospheric Dispersion Modeling for Regulatory Purposes, Bologna, Italy, 9–12 October 2017. [Google Scholar]
- Oldrini, O.; Olry, C.; Moussafir, J.; Armand, P.; Duchenne, C. Development of PMSS, the parallel version of Micro-SWIFT-SPRAY. In Proceedings of the 14th International Conference on Harmonisation within Atmospheric Dispersion Modelling for Regulatory Purposes, Kos, Greece, 2–6 October 2011; pp. 443–447. [Google Scholar]
- Tinarelli, G.; Brusasca, G.; Oldrini, O.; Anfossi, D.; Trini Castelli, S.; Moussafir, J. Micro-Swift-Spray (MSS): A new modelling system for the simulation of dispersion at microscale–General description and validation. In Air Poll Modelling and Its Applications, 17th ed.; Borrego, C., Norman, A.N., Eds.; Springer: Dordrecht, The Netherlands, 2007; pp. 449–458. [Google Scholar]
- Oldrini, O.; Nibart, M.; Armand, P.; Olry, C.; Moussafir, J.; Albergel, A. Multi-scale build-up area integration in Parallel SWIFT. In Proceedings of the 15th International Conference on Harmonisation within Atmospheric Dispersion Modeling for Regulatory Purposes, Madrid, Spain, 6–9 May 2013. [Google Scholar]
- Oldrini, O.; Nibart, M.; Armand, P.; Moussafir, J.; Duchenne, C. Development of the parallel version of a CFD-RANS flow model adapted to the fast response in built-up environment. In Proceedings of the 17th International Conference on Harmonisation within Atmospheric Dispersion Modeling for Regulatory Purposes, Budapest, Hungary, 9–12 May 2016. [Google Scholar]
- Moussafir, J.; Oldrini, O.; Tinarelli, G.; Sontowski, J.; Dougherty, C. A new operational approach to deal with dispersion around obstacles: The MSS (Micro-Swift-Spray) software suite. In Proceedings of the 9th International Conference on Harmonisation within Atmospheric Dispersion Modeling for Regulatory Purposes, Garmisch, Germany, 1–4 June 2004. [Google Scholar]
- Oldrini, O.; Nibart, M.; Armand, P.; Olry, C.; Moussafir, J.; Albergel, A. Introduction of momentum equations in Micro-SWIFT. In Proceedings of the 16th International Conference on Harmonisation within Atmospheric Dispersion Modeling for Regulatory Purposes, Varna, Bulgaria, 8–11 September 2014. [Google Scholar]
- Anfossi, D.; Desiato, F.; Tinarelli, G.; Brusasca, G.; Ferrero, E.; Sacchetti, D. TRANSALP 1989 experimental campaign–II Simulation of a tracer experiment with Lagrangian particle models. Atmos. Environ. 1998, 32, 1157–1166. [Google Scholar] [CrossRef]
- Anfossi, D.; Tinarelli, G.; Trini Castelli, S.; Nibart, M.; Olry, C.; Commanay, J. A new Lagrangian particle model for the simulation of dense gas dispersion. Atmos. Environ. 2010, 44, 753–762. [Google Scholar] [CrossRef]
- Tinarelli, G.; Anfossi, D.; Brusasca, G.; Ferrero, E.; Giostra, U.; Morselli, M.G.; Tampieri, F. Lagrangian particle simulation of tracer dispersion in the lee of a schematic two-dimensional hill. J. Appl. Meteorol. 1994, 33, 744–756. [Google Scholar] [CrossRef]
- Tinarelli, G.; Mortarini, L.; Trini Castelli, S.; Carlino, G.; Moussafir, J.; Olry, C.; Armand, P.; Anfossi, D. Review and validation of Micro-Spray, a Lagrangian particle model of turbulent dispersion. Lagrangian Modeling Atmos. 2012, 200, 311–327. [Google Scholar]
- Rodean, H.C. Stochastic Lagrangian Models of Turbulent Diffusion; American Meteorological Society: Boston, MA, USA, 1996. [Google Scholar]
- Thomson, D.J. Criteria for the selection of stochastic models of particle trajectories in turbulent flows. J. Fluid Mech. 1987, 180, 529–556. [Google Scholar] [CrossRef]
- Moussafir, J.; Olry, C.; Nibart, M.; Albergel, A.; Armand, P.; Duchenne, C.; Oldrini, O. AIRCITY: A very high resolution atmospheric dispersion modelling system for Paris. In Proceedings of the ASME 2014 4th Joint US-European Fluids Engineering Division Summer Meeting Collocated with the ASME 2014 12th International Conference on Nanochannels, Microchannels, and Minichannels, Chicago, IL, USA, 3–7 August 2014; American Society of Mechanical Engineers: New York, NY, USA, 2014; p. V01DT28A010. [Google Scholar]
- Oldrini, O.; Perdriel, S.; Nibart, M.; Armand, P.; Duchenne, C.; Moussafir, J. EMERGENCIES–A modelling and decision-support project for the Great Paris in case of an accidental or malicious CBRN-E dispersion. In Proceedings of the 17th International Conference on Harmonisation within Atmospheric Dispersion Modeling for Regulatory Purposes, Budapest, Hungary, 9–12 May 2016. [Google Scholar]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 2 (No. NCAR/TN-468+ STR); National Center for Atmospheric Research: Boulder, CO, USA, 2005. [Google Scholar]
- Hill, M.D.; Marty, M.R. Amdahl’s law in the multicore era. Computer 2008, 41, 33–38. [Google Scholar] [CrossRef]

| Number of Points Per Side of Tile | Number of Tiles | Number of Computing Cores |
|---|---|---|
| 1001 | 20 × 17 = 340 | 341 |
| 801 | 25 × 21 = 525 | 526 |
| 601 | 33 × 28 = 924 | 925 |
| 401 | 49 × 42 = 2058 | 2059 |
| 201 | 97 × 83 = 8051 | 8052 |
| Number of Cores | Number of Points Per Side of Tile | Calculation Duration Single Timeframe (HH:mm:ss) | Calculation Duration 24 Timeframes (HH:mm:ss) |
|---|---|---|---|
| 341 | 1001 | 01:11:57 | 28:47 |
| 526 | 801 | 00:38:51 | 15:33 |
| 925 | 601 | 00:30:20 | 12:08 |
| 2059 | 401 | 00:18:00 | 07:12 |
| 8052 | 201 | 00:10:42 | 04:17 |
| Cores Tiles | 500 | 1000 | 1500 | 3000 |
|---|---|---|---|---|
| 340 | X | X | X | 12:38:44 |
| 525 | 17:14:23 | 11:29:14 | 10:11:26 | 11:25:20 |
| 924 | 17:18:43 | 12:41:57 | 09:13:32 | 08:33:25 |
| 2058 | 15:07:57 | 10:14:00 | 06:30:01 | 08:04:57 |
| 8051 | 13:10:13 | 07:11:53 | 05:17:13 | 03:37:54 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oldrini, O.; Armand, P.; Duchenne, C.; Perdriel, S. Parallelization Performances of PMSS Flow and Dispersion Modeling System over a Huge Urban Area. Atmosphere 2019, 10, 404. https://doi.org/10.3390/atmos10070404
Oldrini O, Armand P, Duchenne C, Perdriel S. Parallelization Performances of PMSS Flow and Dispersion Modeling System over a Huge Urban Area. Atmosphere. 2019; 10(7):404. https://doi.org/10.3390/atmos10070404
Chicago/Turabian StyleOldrini, Oliver, Patrick Armand, Christophe Duchenne, and Sylvie Perdriel. 2019. "Parallelization Performances of PMSS Flow and Dispersion Modeling System over a Huge Urban Area" Atmosphere 10, no. 7: 404. https://doi.org/10.3390/atmos10070404
APA StyleOldrini, O., Armand, P., Duchenne, C., & Perdriel, S. (2019). Parallelization Performances of PMSS Flow and Dispersion Modeling System over a Huge Urban Area. Atmosphere, 10(7), 404. https://doi.org/10.3390/atmos10070404