Objective Center-Finding Algorithm for Tropical Cyclones in Numerical Models
Abstract
1. Introduction
2. Description of the Objective Center-Finding Algorithm
- Step 1. Detection potential cyclonic vortexDetecting potential vortex is the fundamental step towards finding the location of centers in the existence of multiple cyclonic vortexes. Similar to the criteria used in previous research, the grid point whose smoothed pressure or geopotential height is lower than its eight surroundings is determined as a candidate for a potential cyclonic vortex center [41,42]. For simplicity, the field is smoothed by a nine-point averaged operator. Meanwhile, the radius of maximum azimuthal mean tangential wind (RMMTW) and maximum azimuthal tangential wind (MMTW) are calculated for each candidate. A candidate will be disqualified once if its MMTW is found lower than a prescribed value (for instance, category 1 vortex defined by the Saffir-Simpson hurricane wind scale was used in this manuscript). The precise center position of potential vortex will be detected by the following two steps, individually.
- Step 2. Removing small scale perturbationsVorticity in a square area centered at each candidate is selected, and it is on this area where a two-dimensional Fourier transformation is carried on. The domain size varies among different candidates as it is supposed to be relative to the estimated RMW of the target vortex. The Fourier coefficients are computed as follows:where F is the Fourier coefficients. M and N are domain sizes in direction x and y, respectively. As the domain is chosen as a square area, M equals to N. The wavenumber in x and y direction is represented by u and v. Besides, the space resolution is supposed to be equal in both directions. To remove smaller-scale perturbations, Fourier coefficients are set to be 0 where its wave length () is shorter than a prescribed scale (), where is defined as . The filtered coefficients are defined in Equation (2).The filtered vorticity field is obtained by applying an inverting Fourier transformation with the modified Fourier coefficients. The inverted Fourier transformation is described in Equation (3).
- Step 3. Determining the vortex centerA centroid algorithm is applied to the filtered vorticity filed to determine the final center of the vortex. The centroid algorithm is briefly illustrated in Equation (4),where and represent the location of center in x and y direction, respectively. R represents the searching radius, and with a subscript i represents vorticity at each grid within the searching radius. There are only two parameters (an initial guess center and a searching radius R) involved in a centroid algorithm. The guess center is chosen as the position of the candidate calculated in step 1. Meanwhile, the searching radius is objectively defined according to the scale of target vortex which will be illustrate in the Section 4.
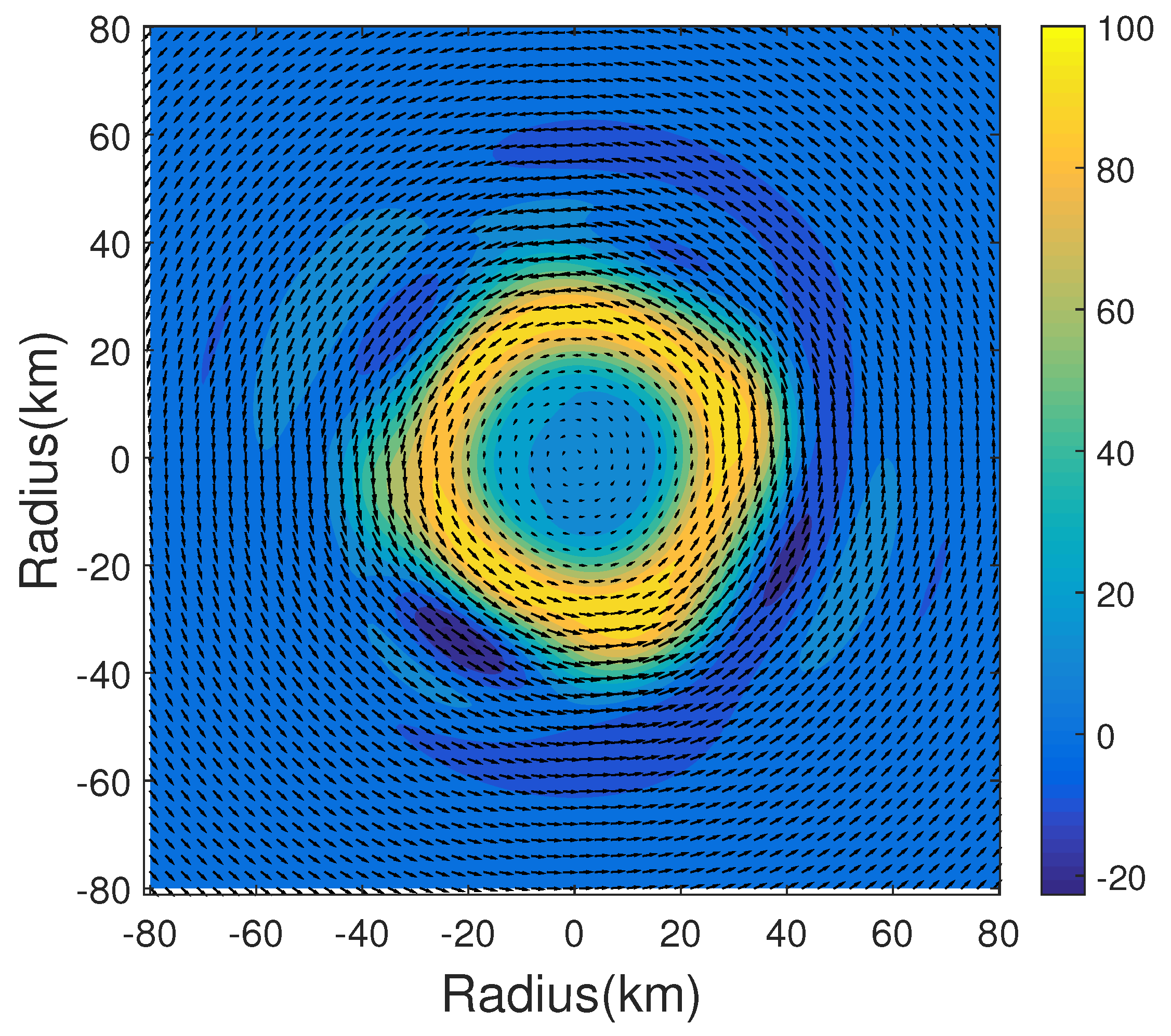
3. Construction of Idealized Vortexes
4. Algorithm Optimization and Validation
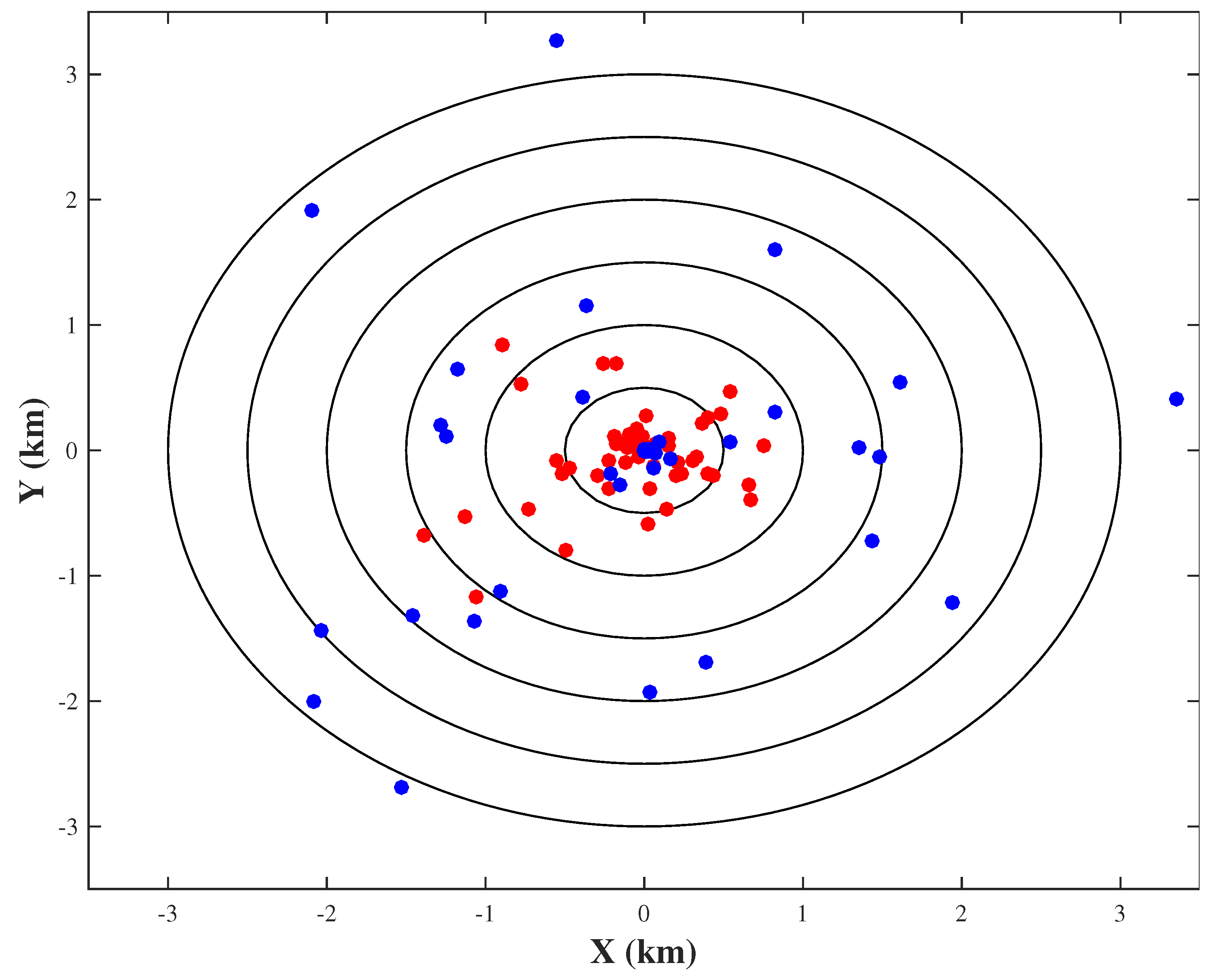
4.1. Method
4.2. Algorithm Optimization
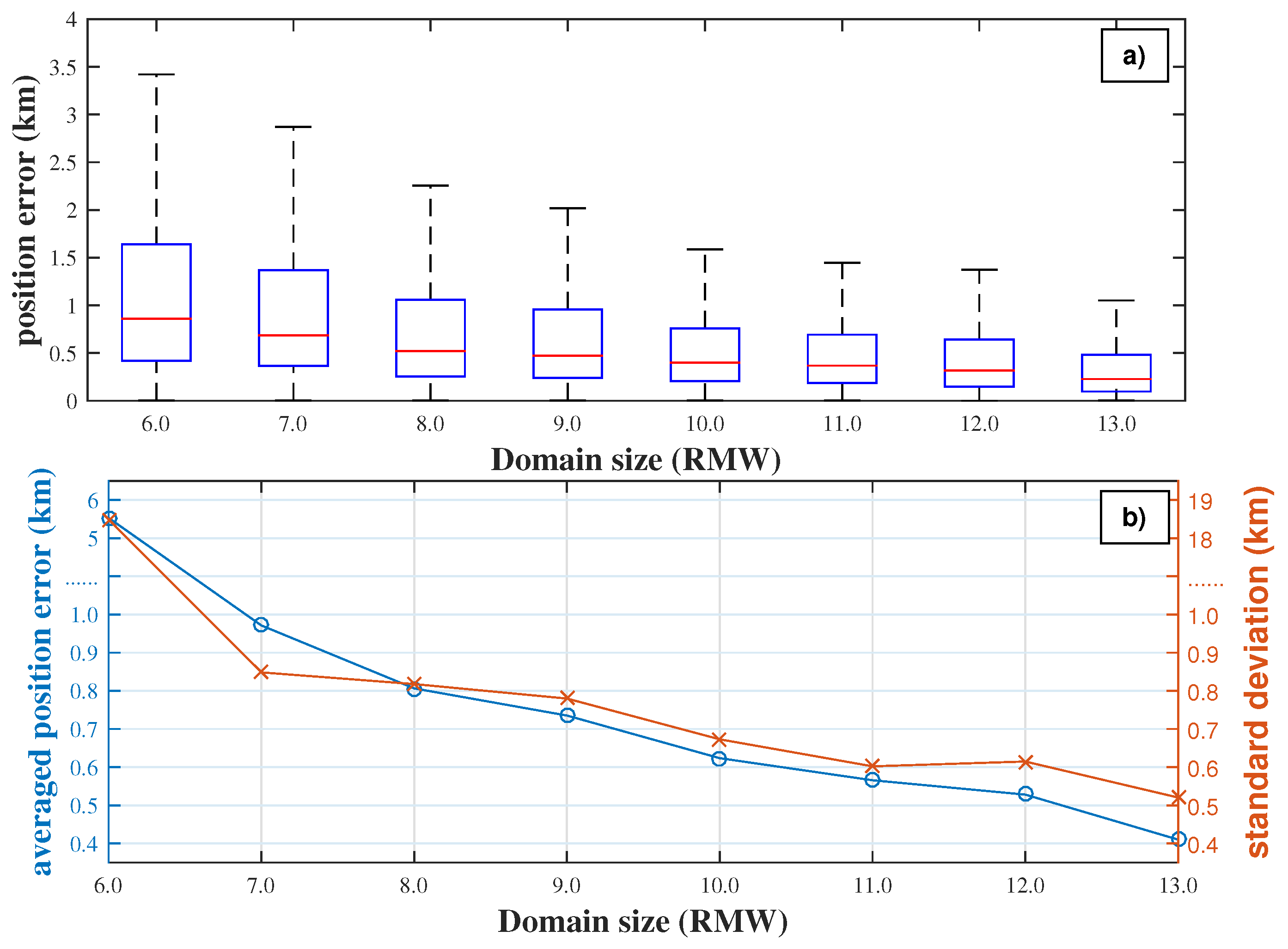
4.2.1. The Domain Size
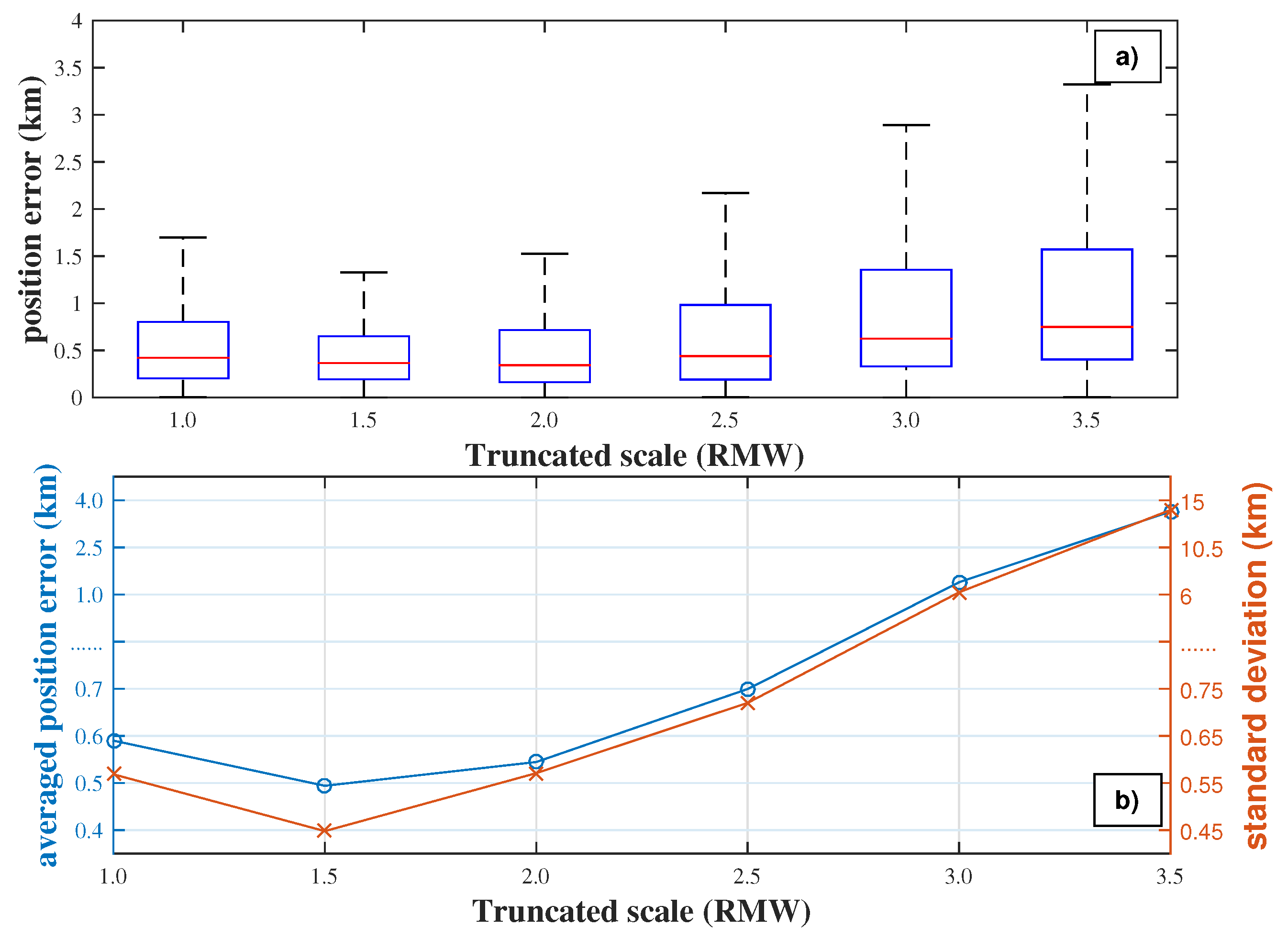
4.2.2. The Truncated Scale
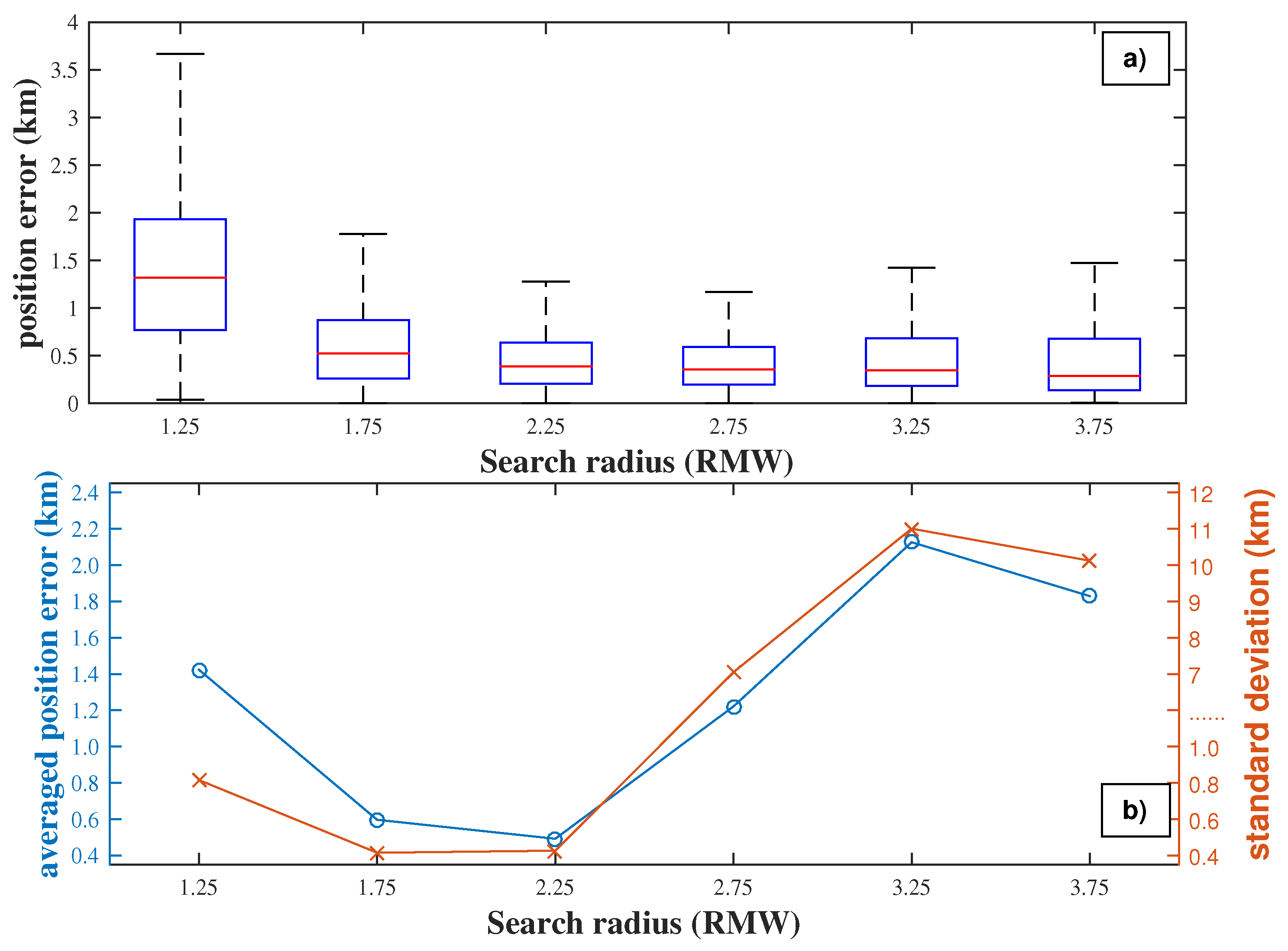
4.2.3. The Searching Radius
4.3. Algorithm Validation
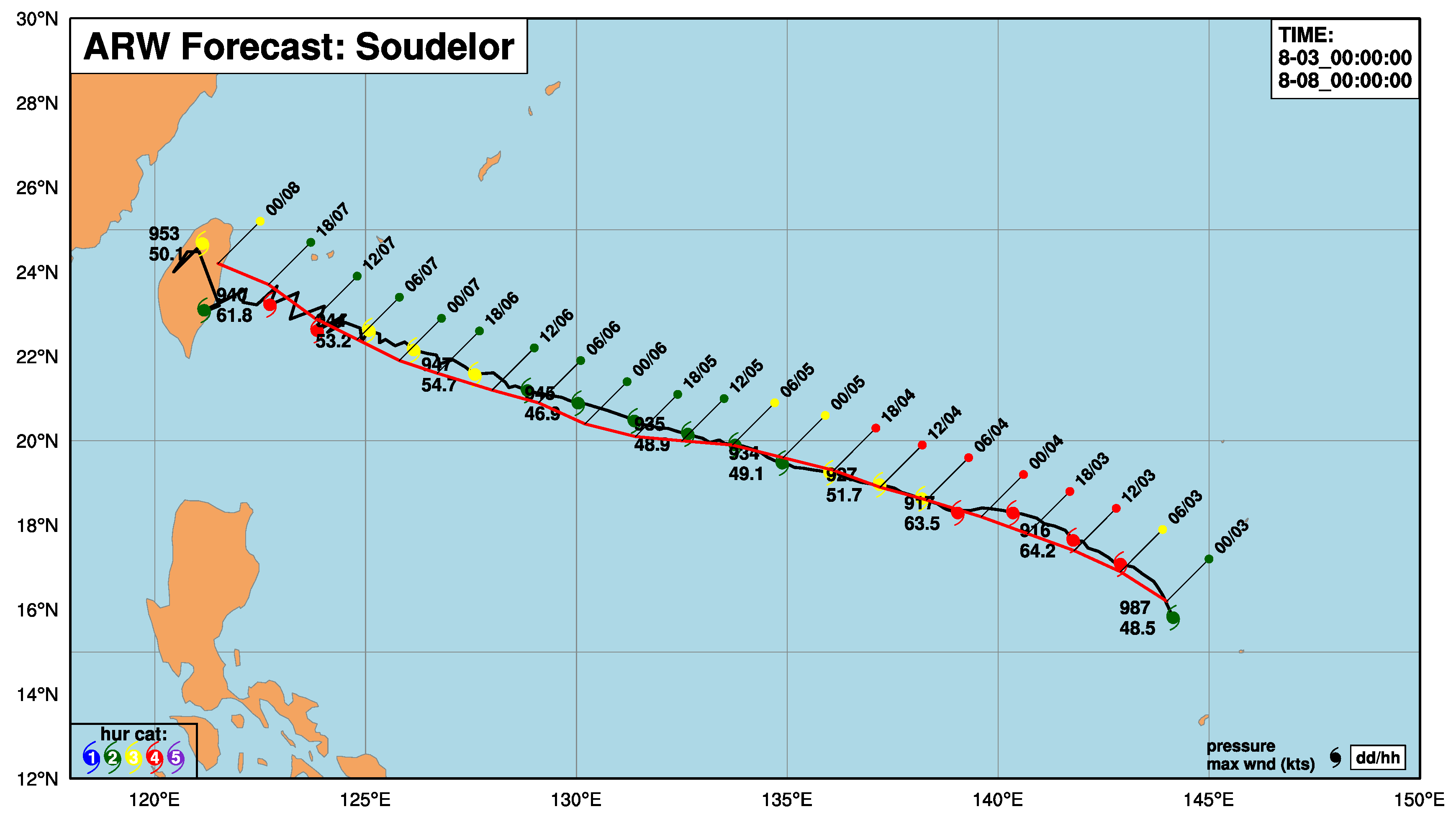
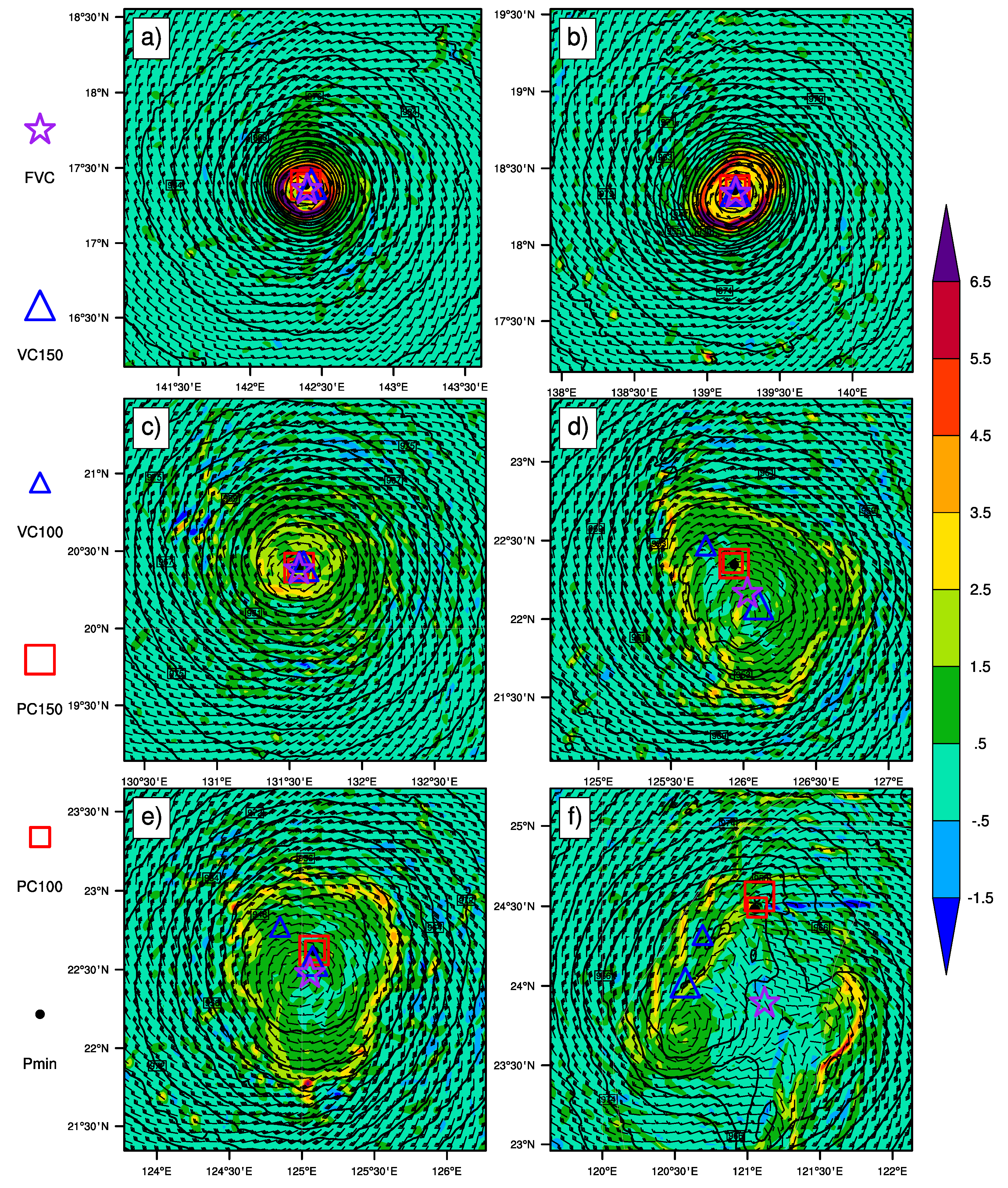
5. Application to High-Resolution Model Data
5.1. Model Setup
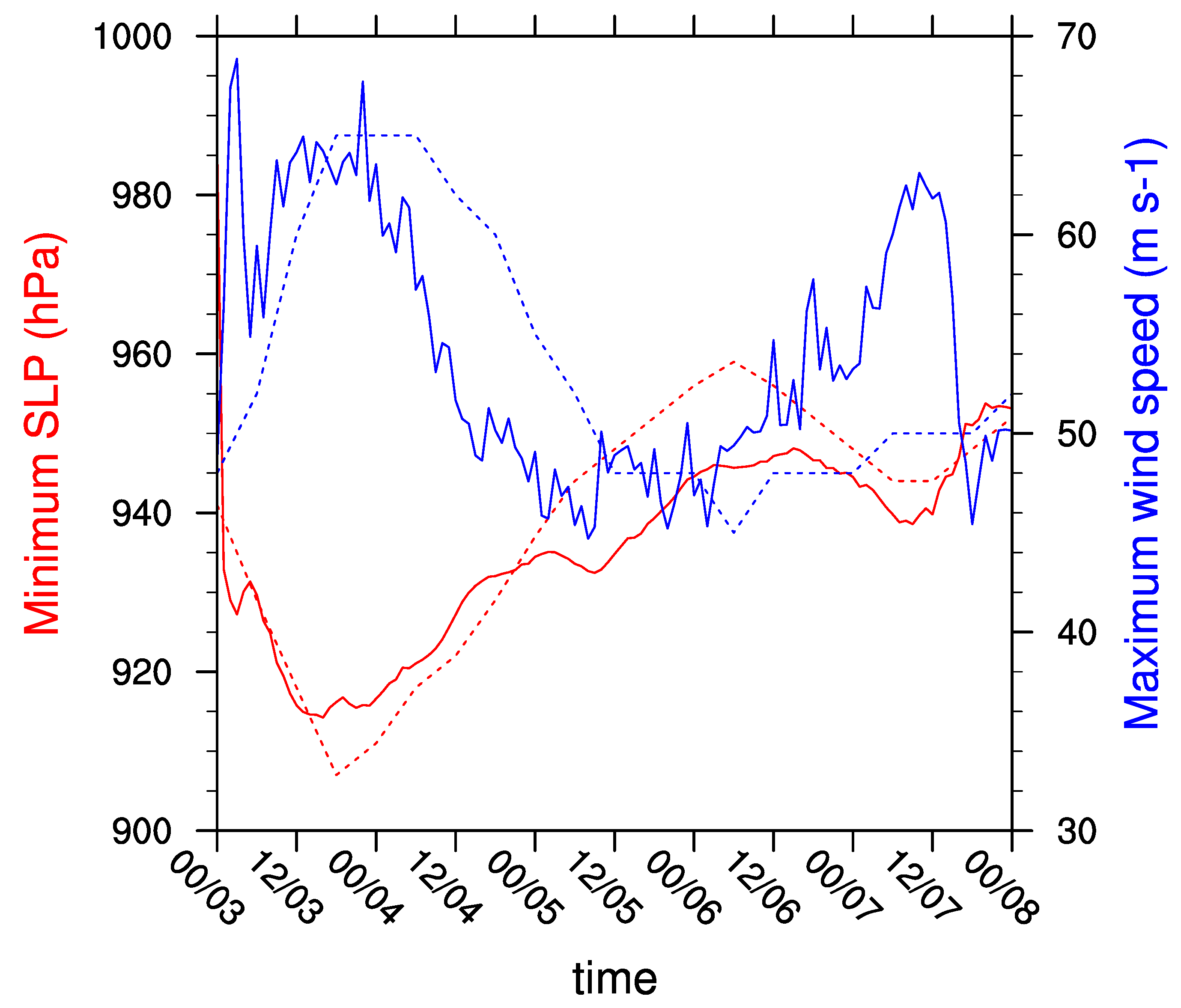
5.2. Verification of the Simulation
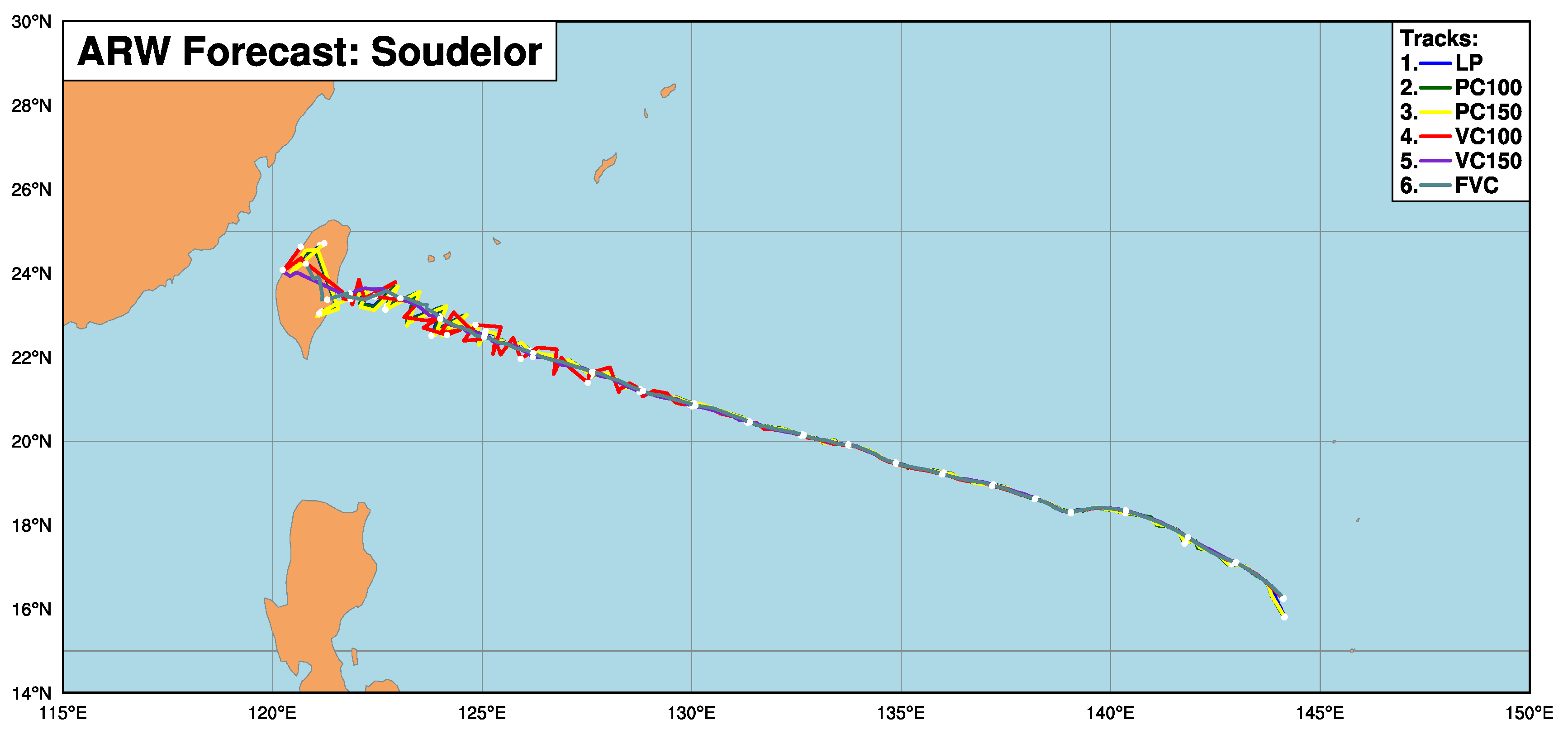
5.3. Performance of the Proposed Algorithm
6. Conclusions
- Pressure, winds and vorticity fields are involved in the new algorithm rather than using a single field in previous algorithms. The participating of multiple fields provides more physical factors of a TC.
- A two-dimensional Fourier filter is involved in the new algorithm to eliminate perturbations whose wave length are smaller than a certain threshold.
- Most importantly, the parameters involved in the new algorithm could automatically change their physical values according to the scale of target vortex.
Author Contributions
Funding
Conflicts of Interest
References
- Velden, C.; Harper, B.; Wells, F.; Beven, J.L.; Zehr, R.; Olander, T.; Mayfield, M.; Lander, M.; Edson, R.; Avila, L.; et al. The dvorak tropical cyclone intensity estimation technique a Satellite-Based Method that Has Endured for over 30 Years. Bull. Am. Meteorol. Soc. 2006, 87, 1195–1210. [Google Scholar] [CrossRef]
- Olander, T.L.; Velden, C.S. The Advanced Dvorak Technique: Continued Development of an Objective Scheme to Estimate Tropical Cyclone Intensity Using Geostationary Infrared Satellite Imagery. Weather Forecast. 2007, 22, 287–298. [Google Scholar] [CrossRef]
- Rozoff, C.M.; Velden, C.S.; Kaplan, J.; Kossin, J.P.; Wimmers, A.J. Improvements in the Probabilistic Prediction of Tropical Cyclone Rapid Intensification with Passive Microwave Observations. Weather Forecast. 2015, 30, 1016–1038. [Google Scholar] [CrossRef]
- Montgomery, M.T.; Zhang, J.A.; Smith, R.K. An Analysis of the Observed Low-level Structure of Rapidly Intensifying and Mature Hurricane Earl (2010). Q. J. R. Meteorol. Soc. 2014, 140, 2132–2146. [Google Scholar] [CrossRef]
- Abarca, S.F.; Montgomery, M.T. Are Eyewall Replacement Cycles Governed Largely by Axisymmetric Balance Dynamics. J. Atmos. Sci. 2015, 72, 82–87. [Google Scholar] [CrossRef]
- Flaounas, E.; Kelemen, F.D.; Wernli, H.; Gaertner, M.A.; Reale, M.; Sanchez-Gomez, E.; Lionello, P.; Calmanti, S.; Podrascanin, Z.; Somot, S.; et al. Assessment of an ensemble of ocean–atmosphere coupled and uncoupled regional climate models to reproduce the climatology of Mediterranean cyclones. Clim. Dyn. 2018, 51, 1023–1040. [Google Scholar] [CrossRef]
- Knapp, K.R.; Kruk, M.C.; Levinson, D.H.; Diamond, H.J.; Neumann, C.J. The International Best Track Archive for Climate Stewardship (IBTrACS): Unifying tropical cyclone data. Bull. Am. Meteorol. Soc. 2010, 91, 363–376. [Google Scholar] [CrossRef]
- Ulbrich, U.; Leckebusch, G.C.; Grieger, J.; Schuster, M.; Akperov, M.G.; Bardin, M.Y.; Feng, Y.; Gulev, S.; Inatsu, M.; Keay, K.; et al. Are greenhouse gas signals of Northern Hemisphere winter extra-tropical cyclone activity dependent on the identification and tracking algorithm? Meteorol. Z. 2013, 22, 61–68. [Google Scholar] [CrossRef]
- Neu, U.; Akperov, M.G.; Bellenbaum, N.; Benestad, R.S.; Blender, R.; Caballero, R.; Cocozza, A.; Dacre, H.F.; Feng, Y.; Fraedrich, K.; et al. IMILAST: A Community Effort to Intercompare Extratropical Cyclone Detection and Tracking Algorithms. Bull. Am. Meteorol. Soc. 2013, 94, 529–547. [Google Scholar] [CrossRef]
- Lionello, P.; Trigo, I.; Gil, V.; Liberato, M.; Nissen, K.M.; Pinto, J.; Raible, C.; Reale, M.; Tanzarella, A.; Trigo, R.; et al. Objective Climatology of Cyclones in the Mediterranean Region: A consensus view among methods with different system identification and tracking criteria. Tellus 2016, 68, 29391. [Google Scholar] [CrossRef]
- Reale, M.; Liberato, M.L.; Lionello, P.; Pinto, J.G.; Salon, S.; Ulbrich, S. A Global Climatology of Explosive Cyclones using a Multi-Tracking Approach. Tellus A Dyn. Meteorol. Oceanogr. 2019, 71, 1–19. [Google Scholar] [CrossRef]
- Song, J.; Wang, Y.; Wu, L. Trend discrepancies among three best track data sets of western North Pacific tropical cyclones. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Wimmers, A.J.; Velden, C.S. Advancements in Objective Multisatellite Tropical Cyclone Center Fixing. J. Appl. Meteorol. Climatol. 2016, 55, 197–212. [Google Scholar] [CrossRef]
- Lee, W.C.; Jou, B.J.D.; Chang, P.L.; Deng, S.M. Tropical Cyclone Kinematic Structure Retrieved from Single-Doppler Radar Observations. Part I: Interpretation of Doppler Velocity Patterns and the GBVTD Technique. Mon. Weather Rev. 1999, 127, 2419–2439. [Google Scholar] [CrossRef]
- Chaurasia, S.; Kishtawal, C.M.; Pal, P.K. An objective method of cyclone centre determination from geostationary satellite observations. J. Remote Sens. 2010, 31, 2429–2440. [Google Scholar] [CrossRef]
- Jaiswal, N.; Kishtawal, C.M. Automatic Determination of Center of Tropical Cyclone in Satellite-Generated IR Images. IEEE Geosci. Remote Sens. Lett. 2011, 8, 460–463. [Google Scholar] [CrossRef]
- Bell, M.M.; Lee, W.C. Objective Tropical Cyclone Center Tracking Using Single-Doppler Radar. J. Appl. Meteorol. Climatol. 2012, 51, 878–896. [Google Scholar] [CrossRef]
- Wimmers, A.J.; Velden, C.S. Objectively Determining the Rotational Center of Tropical Cyclones in Passive Microwave Satellite Imagery. J. Appl. Meteorol. Climatol. 2010, 49, 2013–2034. [Google Scholar] [CrossRef]
- Reppucci, A.; Lehner, S.; Schulz-Stellenfleth, J.; Brusch, S. Tropical Cyclone Intensity Estimated from Wide-Swath SAR Images. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1639–1649. [Google Scholar] [CrossRef]
- Li, X.; Yang, X.; Li, Z. Tropical Cyclone Morphology from Spaceborne Synthetic Aperture Radar. Bull. Am. Meteorol. Soc. 2013, 94, 215–230. [Google Scholar] [CrossRef]
- Wood, V.T. A Technique for Detecting a Tropical Cyclone Center Using a Doppler Radar. J. Atmos. Ocean. Technol. 1994, 11, 1207–1216. [Google Scholar] [CrossRef][Green Version]
- Potvin, C.K.; Shapiro, A.; Yu, T.Y.; Gao, J.; Xue, M. Using a Low-Order Model to Detect and Characterize Tornadoes in Multiple-Doppler Radar Data. Mon. Weather Rev. 2009, 137, 1230–1249. [Google Scholar] [CrossRef]
- Potvin, C.K. A Variational Method for Detecting and Characterizing Convective Vortices in Cartesian Wind Fields. Mon. Weather Rev. 2013, 141, 3102–3115. [Google Scholar] [CrossRef]
- Lee, W.C.; Marks, F.D.; Carbone, R.E. Velocity Track Display—A Technique to Extract Real-Time Tropical Cyclone Circulations Using a Single Airborne Doppler Radar. J. Atmos. Ocean. Technol. 1994, 11, 337–356. [Google Scholar] [CrossRef]
- Lee, W.C.; Marks, F.D. Tropical Cyclone Kinematic Structure Retrieved from Single-Doppler Radar Observations. Part II: The GBVTD-Simplex Center Finding Algorithm. Mon. Weather Rev. 2000, 128, 1925–1936. [Google Scholar] [CrossRef][Green Version]
- Gang, Z.; Yang, J.; Liu, A.K.; Li, X.; Pichel, W.G.; He, S. Comparison of Typhoon Centers From SAR and IR Images and Those From Best & Track Data Sets. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1000–1012. [Google Scholar]
- Ryglicki, D.R.; Hart, R.E. An Investigation of Center-Finding Techniques for Tropical Cyclones in Mesoscale Models. J. Appl. Meteorol. Climatol. 2015, 54, 825–846. [Google Scholar] [CrossRef]
- Jones, S.C. The evolution of vortices in vertical shear. I: Initially barotropic vortices. Q. J. R. Meteorol. Soc. 1995, 121, 821–851. [Google Scholar] [CrossRef]
- Hsiao, L.F.; Liou, C.S.; Yeh, T.C.; Guo, Y.R.; Chen, D.S.; Huang, K.N.; Terng, C.T.; Chen, J.H. A Vortex Relocation Scheme for Tropical Cyclone Initialization in Advanced Research WRF. Mon. Weather Rev. 2010, 138, 3298–3315. [Google Scholar] [CrossRef]
- Riemer, M.; Montgomery, M.T.; Nicholls, M.E. A new paradigm for intensity modification of tropical cyclones: Thermodynamic impact of vertical wind shear on the inflow layer. Atmos. Chem. Phys. 2009, 10, 3163–3188. [Google Scholar] [CrossRef]
- Reasor, P.D.; Montgomery, M.T. Three-Dimensional Alignment and Corotation of Weak, TC-like Vortices via Linear Vortex Rossby Waves. J. Atmos. Sci. 2001, 58, 2306–2330. [Google Scholar] [CrossRef]
- Braun, S.A. A Cloud-Resolving Simulation of Hurricane Bob (1991): Storm Structure and Eyewall Buoyancy. Mon. Weather Rev. 2002, 130, 1573–1592. [Google Scholar] [CrossRef]
- Nguyen, L.T.; Molinari, J.; Thomas, D. Evaluation of Tropical Cyclone Center Identification Methods in Numerical Models. Mon. Weather Rev. 2014, 142, 4326–4339. [Google Scholar] [CrossRef]
- Ryglicki, D.R.; Hodyss, D. A Deeper Analysis of Center-Finding Techniques for Tropical Cyclones in Mesoscale Models. Part I: Low-Wavenumber Analysis. J. Appl. Meteorol. Climatol. 2016, 55, 531–559. [Google Scholar] [CrossRef]
- Zhao, C.; Song, J.; Leng, H.; Zhao, J. Potential Uncertainties in the Analysis of Low-Wavenumber Asymmetries Caused by Aliasing Center in Tropical Cyclones. Atmosphere 2019, 6, 300. [Google Scholar] [CrossRef]
- Frank, W.M.; Ritchie, E.A. Effects of Environmental Flow upon Tropical Cyclone Structure. Mon. Weather Rev. 1999, 127, 2044–2061. [Google Scholar] [CrossRef]
- Zou, H.; Wu, S.; Yi, X.; Wu, N. The Application of Barnes Filter to Positioning the Center of Landed Tropical Cyclone in Numerical Models. Adv. Meteorol. 2018, 2018, 1747530. [Google Scholar] [CrossRef]
- Reasor, P.D.; Montgomery, M.T.; Grasso, L.D. A New Look at the Problem of Tropical Cyclones in Vertical Shear Flow: Vortex Resiliency. J. Atmos. Sci. 2004, 61, 3–22. [Google Scholar] [CrossRef]
- Stern, D.P.; Zhang, F. How Does the Eye Warm? Part II: Sensitivity to Vertical Wind Shear and a Trajectory Analysis. J. Atmos. Sci. 2013, 70, 1849–1873. [Google Scholar] [CrossRef]
- Davis, C.A.; Jones, S.C.; Riemer, M. Hurricane Vortex Dynamics during Atlantic Extratropical Transition. J. Atmos. Sci. 2008, 65, 714–736. [Google Scholar] [CrossRef][Green Version]
- Cavicchia, L.; von Storch, H.; Gualdi, S. A long-term climatology of medicanes. Clim. Dyn. 2014, 43, 1183–1195. [Google Scholar] [CrossRef]
- Lu, C. A Modified Algorithm for Identifying and Tracking Extratropical Cyclones. Adv. Atmos. Sci. 2017, 34, 909–924. [Google Scholar] [CrossRef]
- Nolan, D.S.; Montgomery, M.T. Nonhydrostatic, Three-Dimensional Perturbations to Balanced, Hurricane-like Vortices. Part I: Linearized Formulation, Stability, and Evolution. J. Atmos. Sci. 2002, 59, 2989–3020. [Google Scholar] [CrossRef]
- Nolan, D.S.; Moon, Y.; Stern, D.P. Tropical Cyclone Intensification from Asymmetric Convection: Energetics and Efficiency. J. Atmos. Sci. 2007, 64, 3377–3405. [Google Scholar] [CrossRef]
- Kampstra, P. Beanplot: A Boxplot Alternative for Visual Comparison of Distributions. J. Stat. Softw. 2008, 28, 1–9. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Y.; Xu, H. Improving simulation of a tropical cyclone using dynamical initialization and large-scale spectral nudging: A case study of Typhoon Megi (2010). Acta Meteorol. Sin. 2013, 27, 455–475. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Y. A Numerical Study of Typhoon Megi (2010). Part I: Rapid Intensification. Mon. Weather Rev. 2014, 142, 29–48. [Google Scholar] [CrossRef]
| r (km) | Numbers | Wavenumber | Amplitude (m s) | b (RMW) | c (km) | (degree) |
|---|---|---|---|---|---|---|
| 35–45 | 1–10 | 1–4 | – | – | 10–14 | 0–360 |
| Truncated Scale | Searching Radius | |
|---|---|---|
| 260–500 (40) | 50–150 (20) | 50–150 (20) |
| Min | Max | Mean | Median | Std dev | |
|---|---|---|---|---|---|
| VC | |||||
| FVC |
| Method | Abbreviation |
|---|---|
| Surface pressure minimum | Pmin |
| Pressure centroid, 100 km × 100 km weighting area, pressure min first guess, 1000 iterations | PC100 |
| Pressure centroid, 150 km × 150 km weighting area, pressure min first guess, 1000 iterations | PC150 |
| Vorticity centroid, 100 km × 100 km weighting area, pressure min first guess, 1000 iterations | VC100 |
| Vorticity centroid, 150 km × 150 km weighting area, pressure min first guess, 1000 iterations | VC150 |
| The proposed objective center-finding algorithm | FVC |
| Mesh 1 | Mesh 2 | Mesh 3 | |
|---|---|---|---|
| Time steps (s) | 45 | 15 | 5 |
| Cloud microphysics | WSM6 (Hong and Lim 2006) | WSM6 | WSM6 |
| Longwave radiation | RRTM (Hong and Lim 2006) | RRTM | RRTM |
| Shortwave radiation | Dudhia (Dudhia 1989) | Dudhia | Dudhia |
| Cumulus convection | Kain-Fritsch (Kain 2005) | No | No |
| PBL scheme | MYNN2.5 (Nakanishi and Niino 2004) | MYNN2.5 | MYNN2.5 |
| Land surface processes | Noah (Ek et al. 2003) | Noah | Noah |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Song, J.; Leng, H.; Zhao, J. Objective Center-Finding Algorithm for Tropical Cyclones in Numerical Models. Atmosphere 2019, 10, 376. https://doi.org/10.3390/atmos10070376
Zhao C, Song J, Leng H, Zhao J. Objective Center-Finding Algorithm for Tropical Cyclones in Numerical Models. Atmosphere. 2019; 10(7):376. https://doi.org/10.3390/atmos10070376
Chicago/Turabian StyleZhao, Chengwu, Junqiang Song, Hongze Leng, and Juan Zhao. 2019. "Objective Center-Finding Algorithm for Tropical Cyclones in Numerical Models" Atmosphere 10, no. 7: 376. https://doi.org/10.3390/atmos10070376
APA StyleZhao, C., Song, J., Leng, H., & Zhao, J. (2019). Objective Center-Finding Algorithm for Tropical Cyclones in Numerical Models. Atmosphere, 10(7), 376. https://doi.org/10.3390/atmos10070376




