Next Article in Journal
Spatiotemporal Variability of Actual Evapotranspiration and the Dominant Climatic Factors in the Pearl River Basin, China
Next Article in Special Issue
Analysis of Mountain Wave Effects on a Hard Landing Incident in Pico Aerodrome Using the AROME Model and Airborne Observations
Previous Article in Journal
Analysis of a Haze Event over Nanjing, China Based on Multi-Source Data
Previous Article in Special Issue
Diurnal Variations of Different Cloud Types and the Relationship between the Diurnal Variations of Clouds and Precipitation in Central and East China
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 10
Issue 6
10.3390/atmos10060339
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Hurricane Boundary Layer Height Relative to Storm Motion from GPS Dropsonde Composites

by
Yifang Ren
1,
Jun A. Zhang
2,3,*,
Stephen R. Guimond
4,5 and
Xiang Wang
6
1
The Center of Jiangsu Meteorological Service, Nanjing 21008, China
2
Cooperative Institute for Marine and Atmospheric Studies, University of Miami, Miami, FL 33149, USA
3
NOAA/AOML/Hurricane Research Division, Miami, FL 33149, USA
4
Joint Center for Earth Systems Technology, University of Maryland Baltimore County, Baltimore, MD 21250, USA
5
NASA Goddard Space Flight Center (GSFC), Greenbelt, MD 20771, USA
6
Centre of Data Assimilation for Research and Application, Nanjing University of Information Science & Technology, Nanjing 210044, China
*
Author to whom correspondence should be addressed.
Atmosphere 2019, 10(6), 339; https://doi.org/10.3390/atmos10060339
Submission received: 9 May 2019 / Revised: 3 June 2019 / Accepted: 10 June 2019 / Published: 21 June 2019
(This article belongs to the Special Issue Lower Atmosphere Meteorology)
Browse Figures
Versions Notes

Abstract

This study investigates the asymmetric distribution of hurricane boundary layer height scales in a storm-motion-relative framework using global positioning system (GPS) dropsonde observations. Data from a total of 1916 dropsondes collected within four times the radius of maximum wind speed of 37 named hurricanes over the Atlantic basin from 1998 to 2015 are analyzed in the composite framework. Motion-relative quadrant mean composite analyses show that both the kinematic and thermodynamic boundary layer height scales tend to increase with increasing radius in all four motion-relative quadrants. It is also found that the thermodynamic mixed layer depth and height of maximum tangential wind speed are within the inflow layer in all motion-relative quadrants. The inflow layer depth and height of the maximum tangential wind are both found to be deeper in the two front quadrants, and they are largest in the right-front quadrant. The difference in the thermodynamic mixed layer depth between the front and back quadrants is smaller than that in the kinematic boundary layer height. The thermodynamic mixed layer is shallowest in the right-rear quadrant, which may be due to the cold wake phenomena. The boundary layer height derived using the critical Richardson number ( R i c ) method shows a similar front-back asymmetry as the kinematic boundary layer height.

1. Introduction

The atmospheric boundary layer (ABL) is the turbulent layer close to the Earth’s surface that is influenced by surface friction. Physical processes in the ABL play an important role in regulating the atmosphere at both weather and climate scales, including hurricanes. The top of the ABL (i.e., the boundary layer height) is a key parameter that determines the vertical distribution of turbulent mixing in numerical models that require a boundary layer parameterization. In numerical models where turbulent fluxes are parameterized using a first-order K-profile method, the boundary layer height is usually defined as the height at which the bulk Richardson number (Ric) reaches a threshold (typically 0.25), where Ric is defined as the ratio of buoyancy to shear forcing [1,2,3]. Note that this Richardson number method was also previously used in observational studies to determine the boundary layer height in non-hurricane conditions [4,5,6,7,8].
Under non-hurricane conditions when vertical profiles of turbulent intensity and/or flux are measured, the boundary layer height is usually taken as the height where the magnitude of the turbulence parameter is much smaller (~95%) than that in the surface layer. Note that the surface layer height is usually taken as 10% of the ABL height [9]. Without turbulence data, the height of the temperature inversion layer is generally used to define the boundary layer height, in particular, under unstable conditions [9,10,11,12]. Since passive scalars are accumulated in the ABL, large gradients of temperature and water vapor occur at the inversion layer capping the ABL [13,14]. Above the inversion layer, a rising air parcel typically becomes neutrally buoyant.
The top of the stable or neutral boundary layer is more difficult to determine than the unstable convective boundary layer. The boundary layer height is typically defined using the vertical gradient of virtual potential temperature with a threshold [4,15,16,17], when flux data are not available. This method has been widely used when radiosonde data are available. The parcel method developed by Holzworth [18] was also used in previous studies to estimate the boundary layer height using radiosonde data [15,19,20]. Remote sensing data (e.g., lidars, radars, sodas, and wind profilers), although sometimes ambiguous, can also be used to determine the boundary layer height when other types of data are not available [21,22,23,24].
In hurricane conditions, it is even more difficult to acquire direct turbulence measurements due to safety issues and measurement constraints. Multi-level turbulent intensity and flux data that can be used to estimate the boundary layer height are scarce in hurricane conditions. The only in situ data of this kind was collected in regions either 100 km away from the hurricane eyewall or in weak tropical storms [25,26,27,28]. Note that a new airborne Doppler radar dataset from the Imaging Wind and Rain Airborne Profiler (IWRAP) is able to provide three-dimensional winds, deep into the hurricane boundary layer, at high resolution (~200 m horizontal and 30 m vertical), which will be useful for characterizing the boundary layer height using dynamical metrics [29,30].
Dropsonde data have been used to estimate the hurricane boundary layer height scales in previous studies [31]. Zhang et al. [31] pointed out differences between the kinematic boundary layer height denoted by the height of the maximum tangential wind speed (hvtmax) or inflow layer depth (hinflow), and the thermodynamic boundary layer height denoted by the mixed layer depth (zi). Of note, hinflow is taken as the height of strong inflow layer where the inflow strength is equal to 10% of the maximum inflow [32]. Furthermore, zi is taken as the height where the vertical gradient of the virtual potential temperature (theta-v) is equal to 3 K km−1, a widely used approach in non-hurricane ABL studies [4]. Ming et al. [33] confirmed the result of Zhang et al. [31] by analyzing a smaller number of dropsonde data in Pacific typhoons.
Previous modeling studies on air-sea coupling processes of individual tropical cyclones (TCs) showed an asymmetric distribution of the boundary layer structure relative to the storm motion, suggesting that the boundary layer is more stable in the right-rear quadrant [34,35]. Although a significant number of observational studies have documented the mean boundary layer structure of individual hurricanes [27,36,37,38,39,40,41], the variability of the ABL structure as a function of azimuth remains to be explored. The objective of the present study is to investigate the asymmetry of the boundary layer structure in a storm-motion-relative framework with a focus on the boundary layer height scales. This study is a first attempt to analyze the motion-induced asymmetry of the boundary layer heights in a climatological sense by compositing dropsonde data collected in multiple hurricanes. The results of this study will be useful for improving our understanding of the low-level structure of hurricanes and providing composite analyses that can be used for model evaluation and physics improvements [42].
This paper is organized as follows. Section 2 describes the dropsonde data and the composite analysis methodology. The dropsonde composites used to compute the boundary layer heights are shown in Section 3, which is followed by the discussion and conclusion in Section 4.

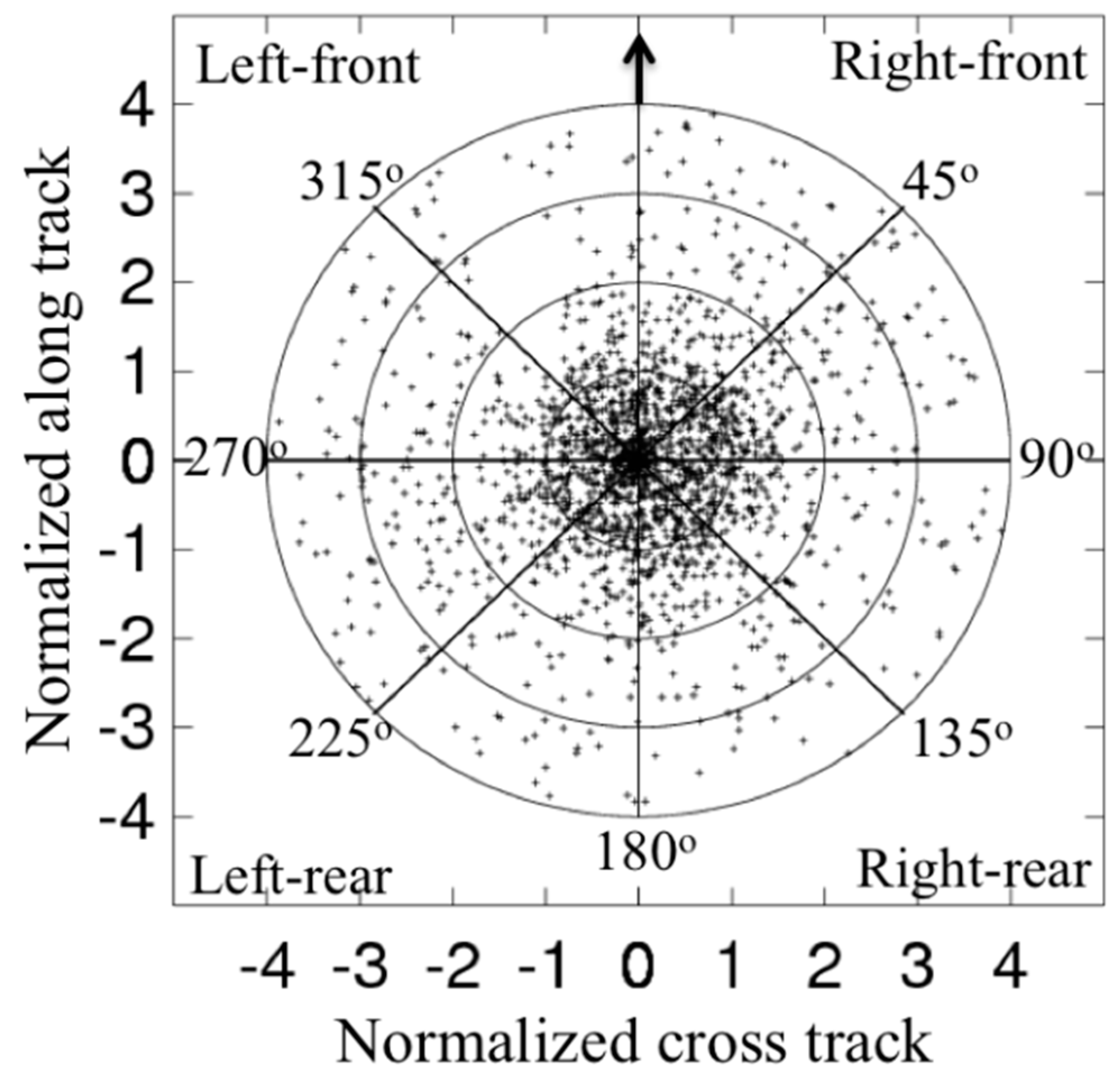
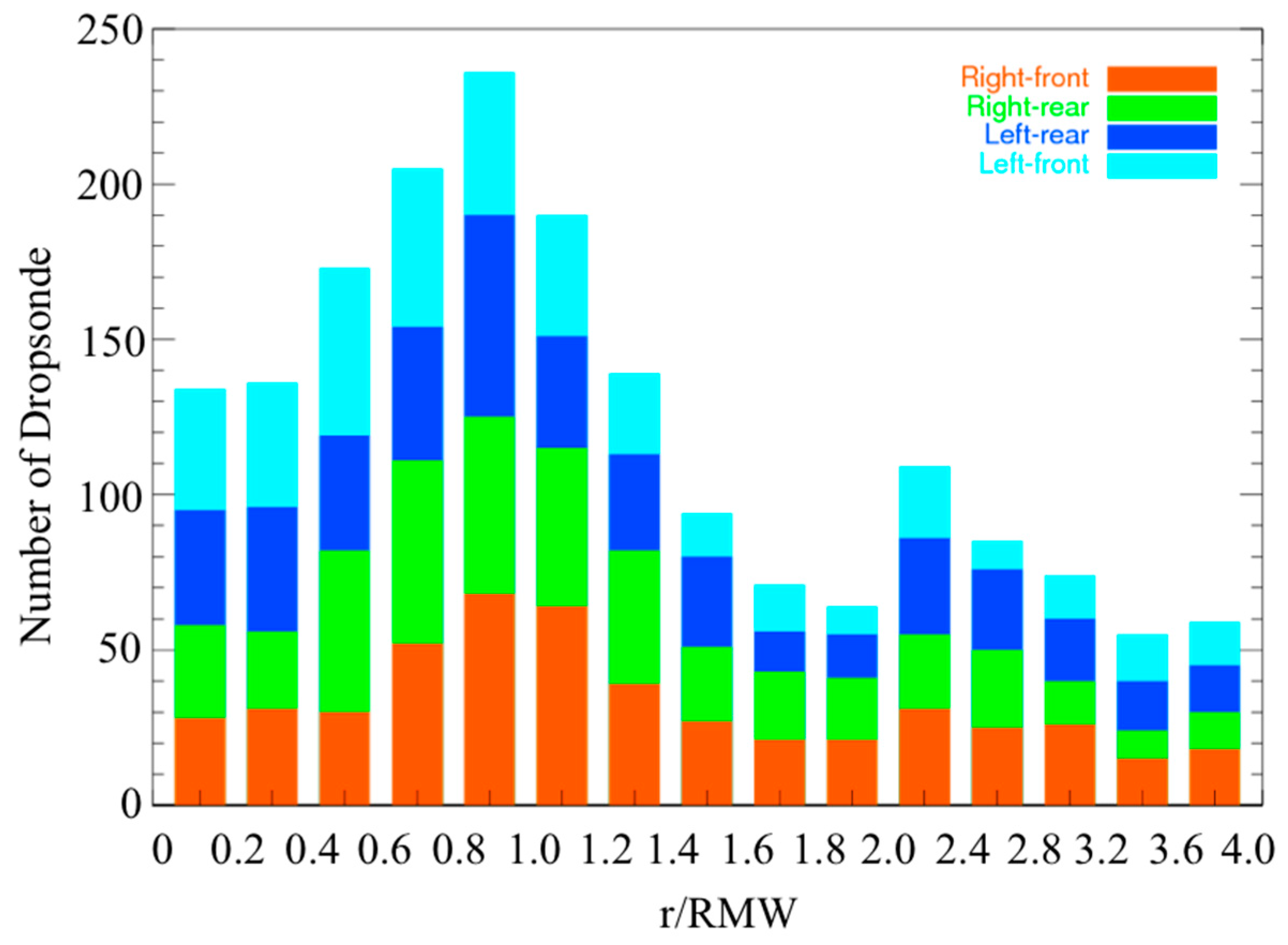
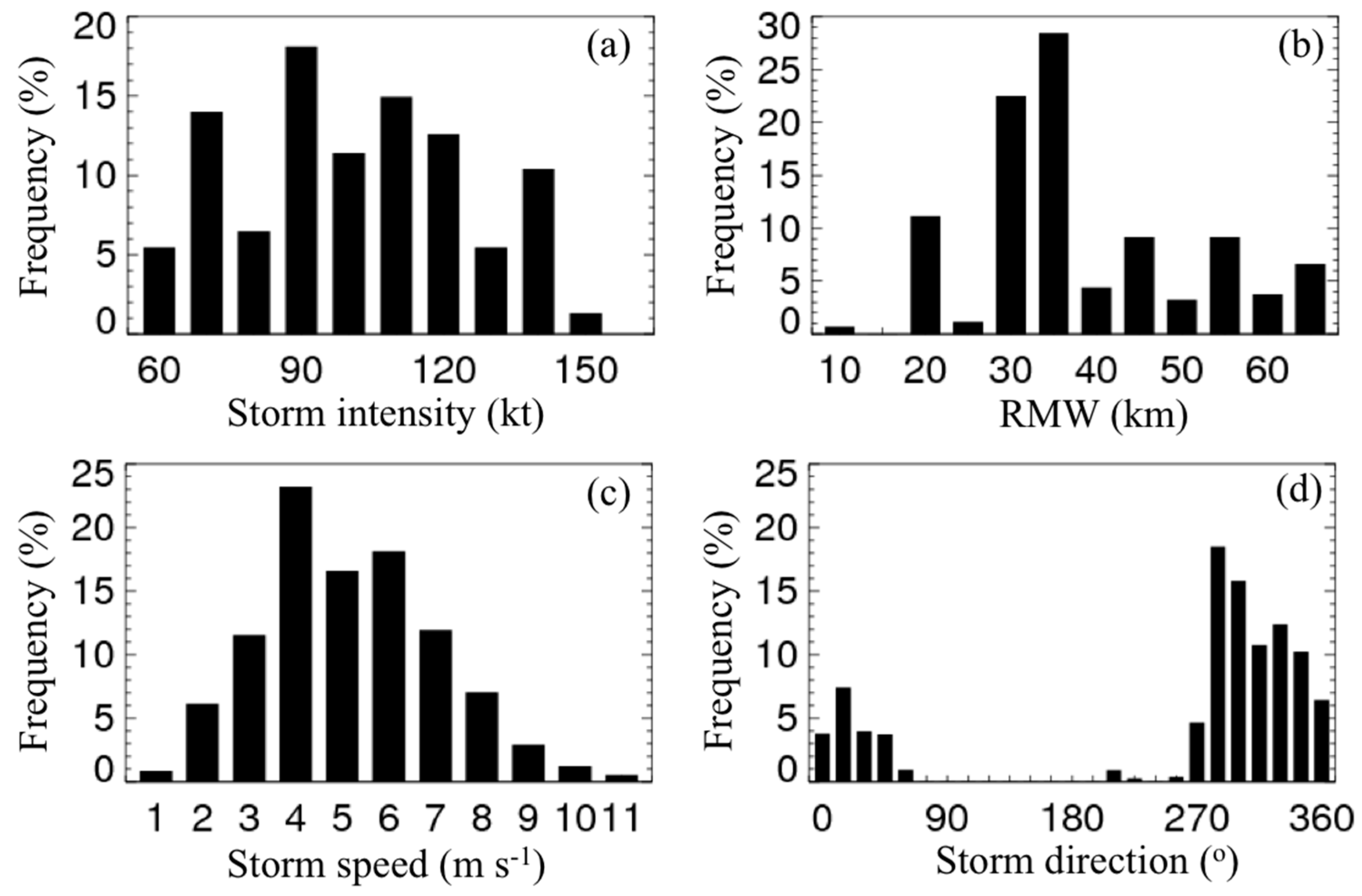
2. Data and Composite Methodology

Dropsondes are typically deployed from research or reconnaissance aircraft at a height of ~3 km (i.e., 700 hPa), with a descending rate of ~ 10 m s−1 and a vertical sampling resolution of ~7 m. During the process of descent, atmospheric profiles of pressure, temperature, relative humidity, and horizontal winds are collected by the dropsonde. The accuracy of pressure, temperature, relative humidity and horizontal wind speed are ±1.0 hPa, ±0.2 °C, ±5%, and ±0.5 ms−1, respectively [43]. The dropsonde data used in this study are from the Hurricane Research Division (HRD) archives and have been quality controlled using the Editsonde and/or ASPEN programs.
In this study, a total of 7326 GPS dropsonde profiles collected by research aircraft in 37 TCs from 1998 to 2015 are analyzed. The storm intensity is obtained from the hurricane best track database produced by the National Hurricane Center (NHC). The storm tracks processed by HRD, which combine the best track storm locations with aircraft center fixes, are used in the analysis. We linearly interpolate the storm intensity, center and motion from the track data to the dropsonde time. For the composite analysis of the inner-core structure, the dropsonde profiles must meet the following requirements: (i) They have measurements of wind speed, temperature, and humidity from flight-level all the way to the surface with no data gaps, (ii) the maximum sustained wind speed (i.e., storm intensity) from NHC’s best track is larger than 64 kt (Cat 1 strength), and (iii) the sondes are deployed within four times the radius of maximum wind speed (RMW). A total of 1916 dropsonde profiles are used in the final composite analysis after this screening. Note that the RMW data used in this study are calculated based on the flight-level data following [44]. Table 1 summarizes the storm information and numbers of dropsondes used in this work.
The dropsonde distribution relative to the storm center is shown in Figure 1, with observation locations rotated with respect to the storm motion direction to the top of the figure. Figure 1 shows nearly evenly distributed data at motion-relative azimuths at all radii, although more dropsonde data are located close to the RMW (i.e., r/RMW = 1). The dropsonde data are composited in four motion-relative quadrants defined clockwise from the storm motion direction, as right-front, right-rear, left-rear and left-front (Figure 2). The storm characteristics in terms of frequency distribution, including the storm intensity V m a x , RMW, storm translational direction, and storm speed are presented in Figure 3. Storm intensities range from 65–150 kt, sizes in terms of RMW range from 10–65 km, and translational speed ranges from 2–20 ms−1. The mean storm intensity for the whole sample is 105.5 kt, the mean RMW is 28.5 km, and the mean storm translational speed is 5.27 ms−1.
In this study, we use the same composite methodology as Zhang et al. [31] to construct the radial-vertical profiles of virtual temperature ( θ v ), tangential wind, radial wind, and Richardson number in four quadrants relative to the storm motion. When compositing the data, the radial bin width is 0.2 r * (r* = r/RMW) for the inner core ( r * < 2 ), and it is 0.4 r * for the outer part. The data are also bin averaged vertically at 10 m resolution. The final averaged data are also smoothed with three passes of a 1-2-1 filter, instead of five passes as in Zhang et al. [31]. The data sampling sizes for different quadrants are displayed in Figure 2 as a function of normalized radius and height. The largest sample size is located in the vicinity of the eyewall as expected. Figure 2 also indicates that the data samples for the four motion-relative quadrants are similar.

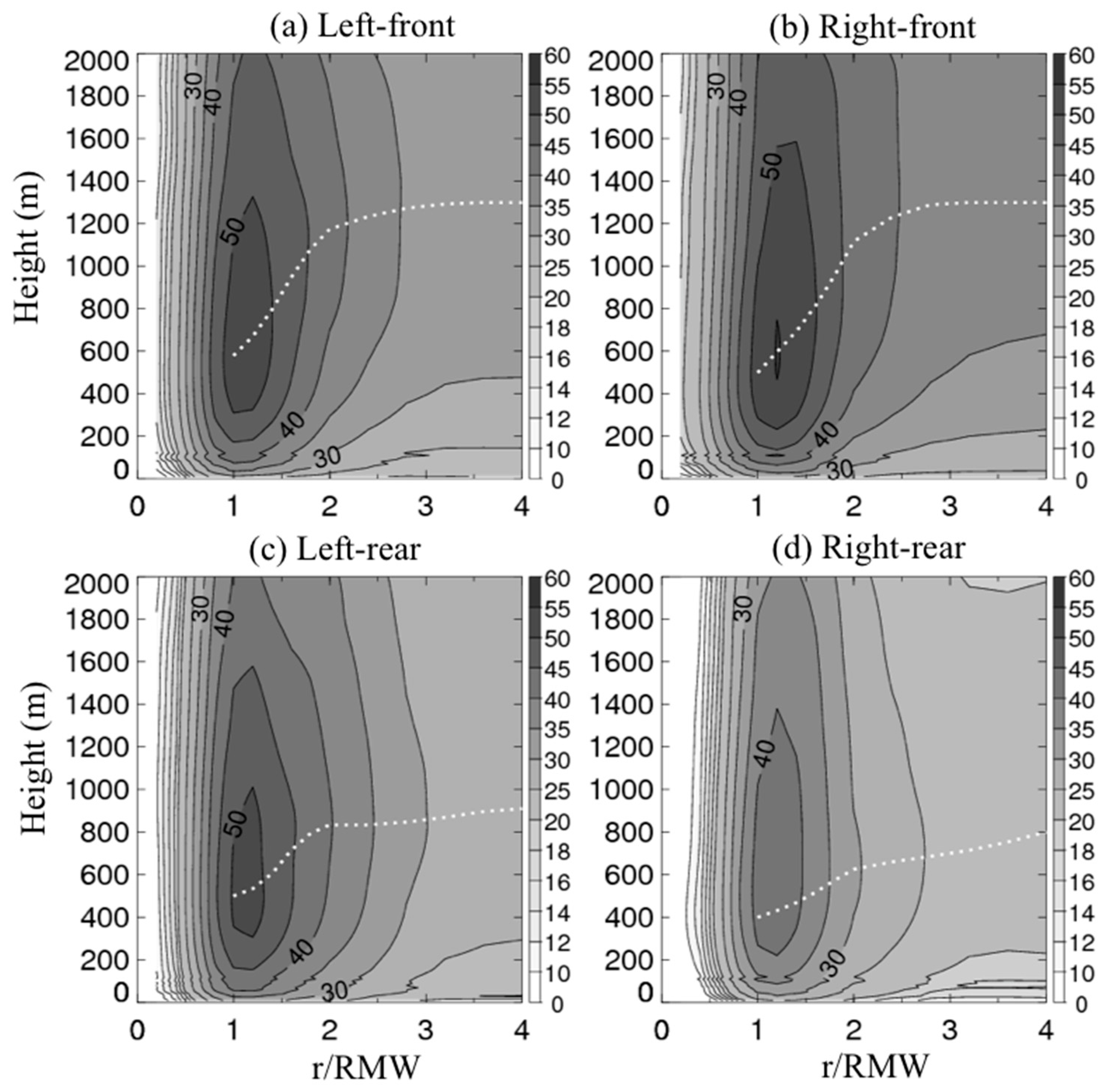
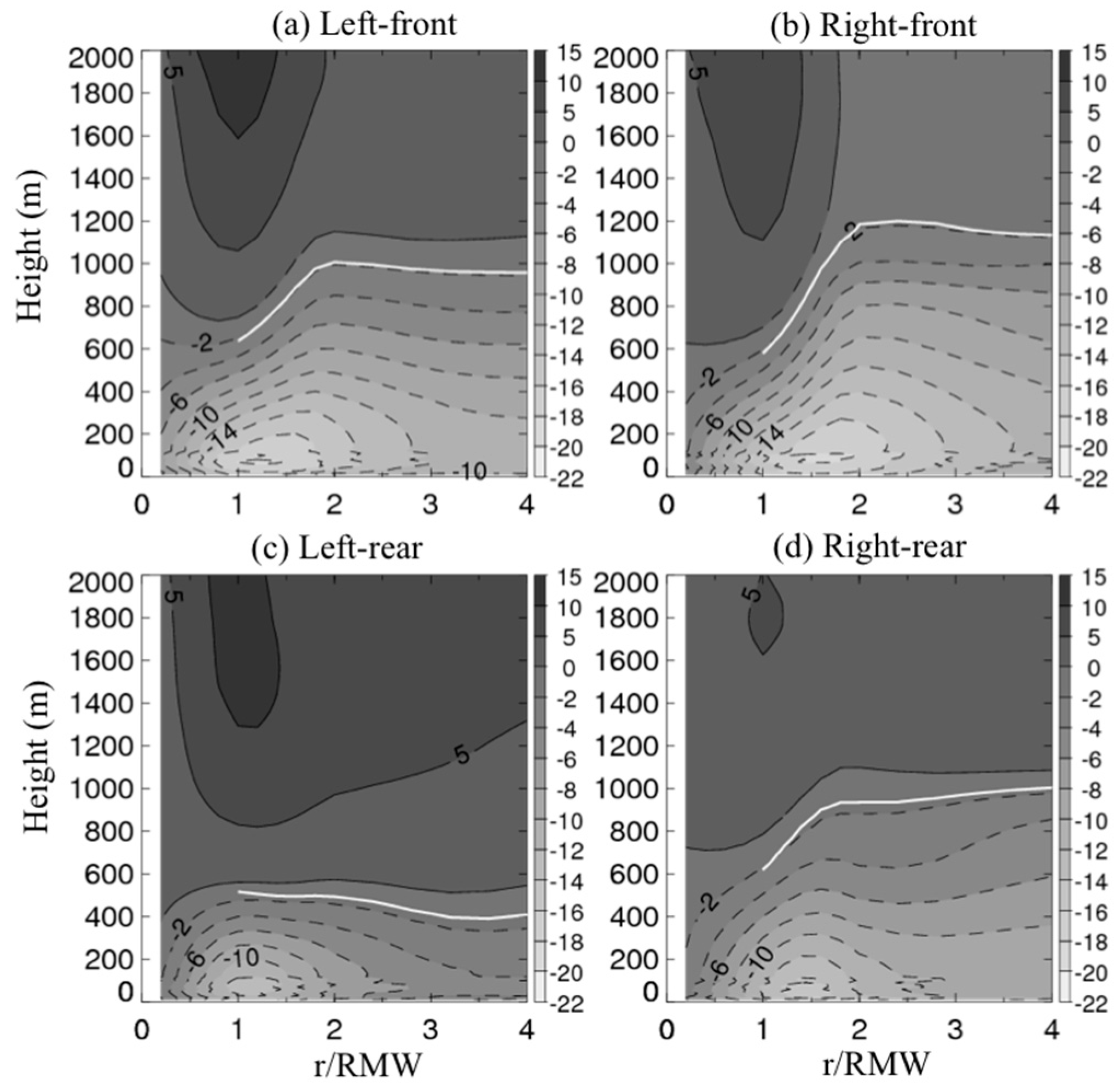
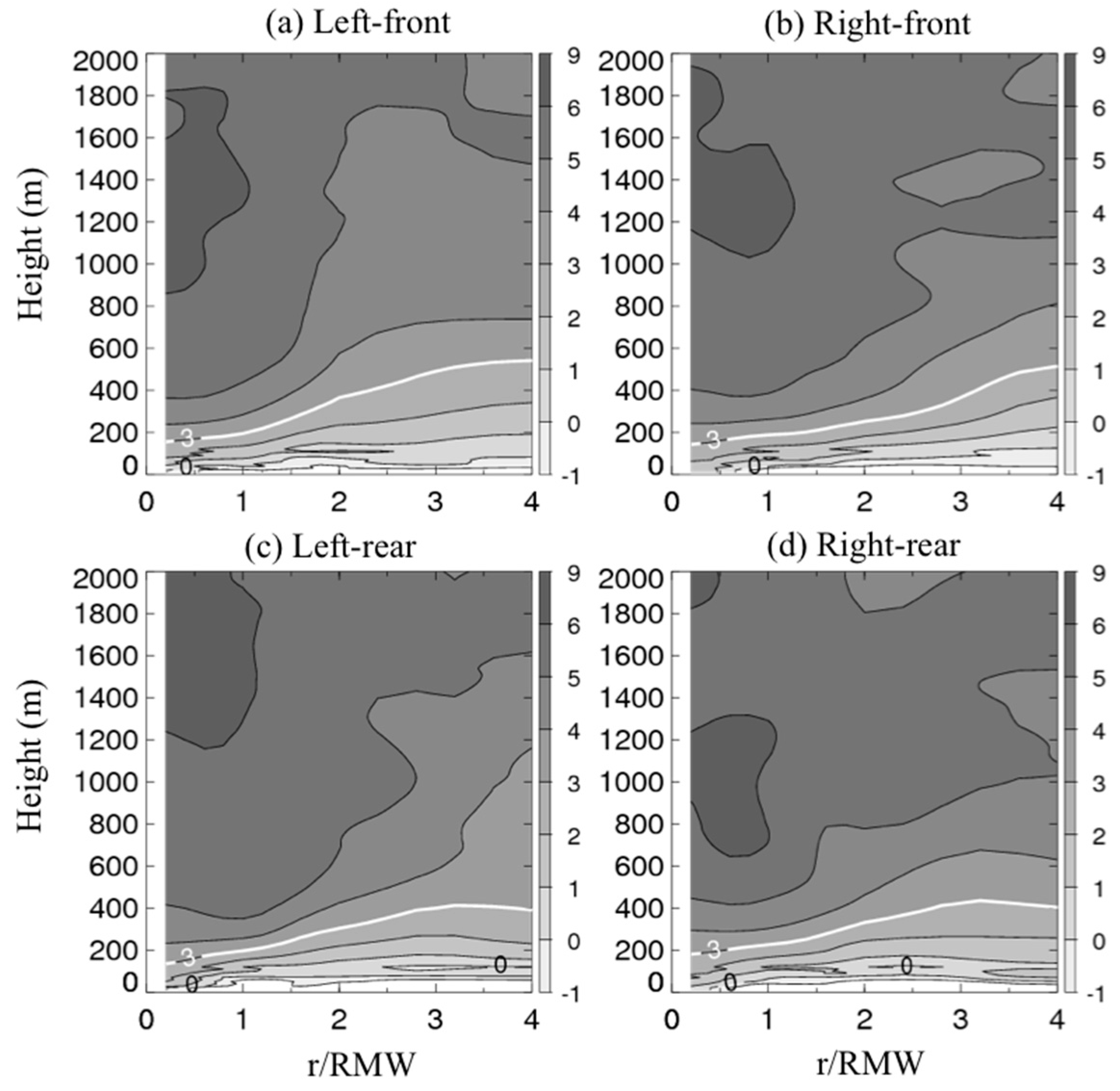
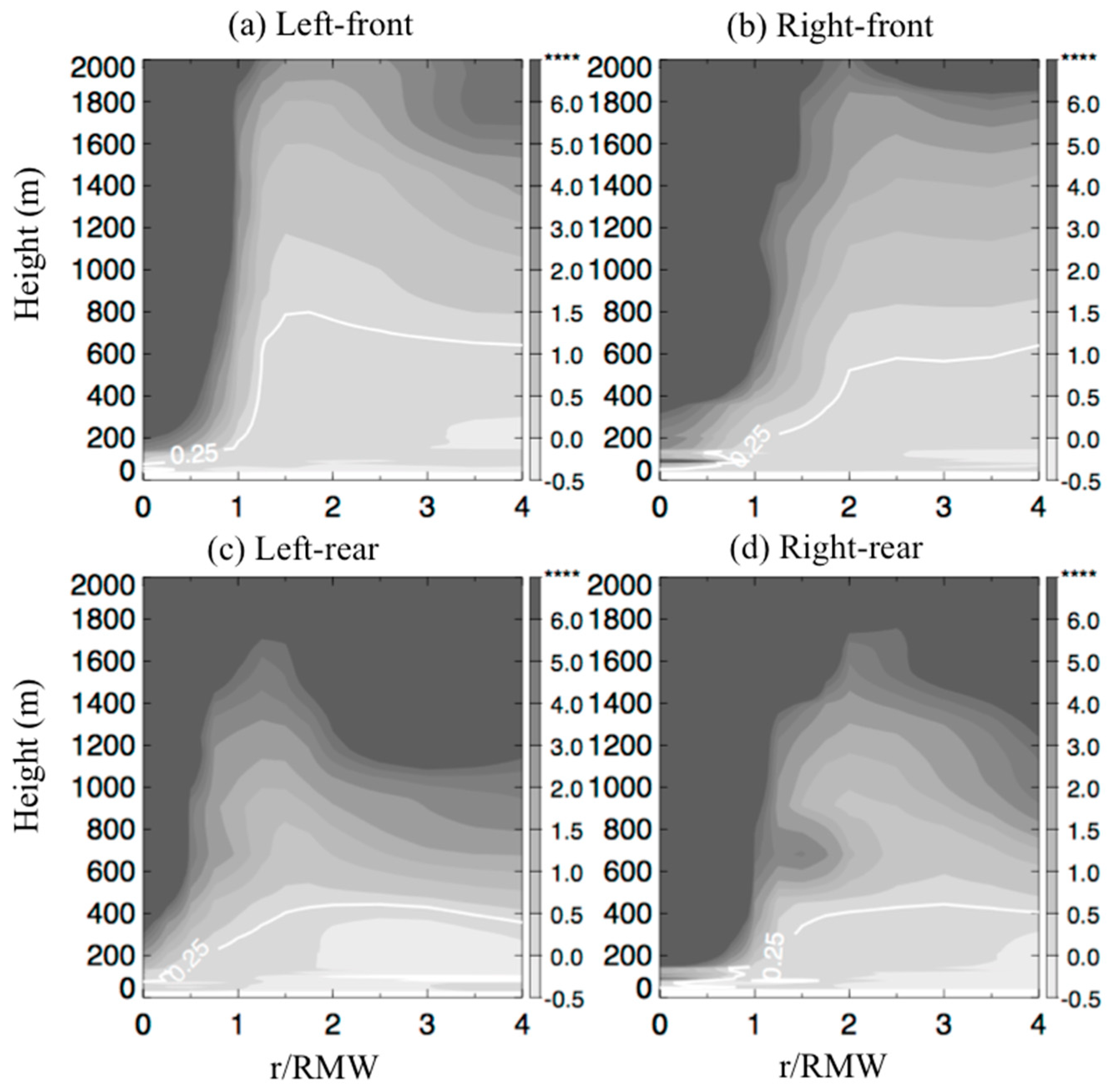
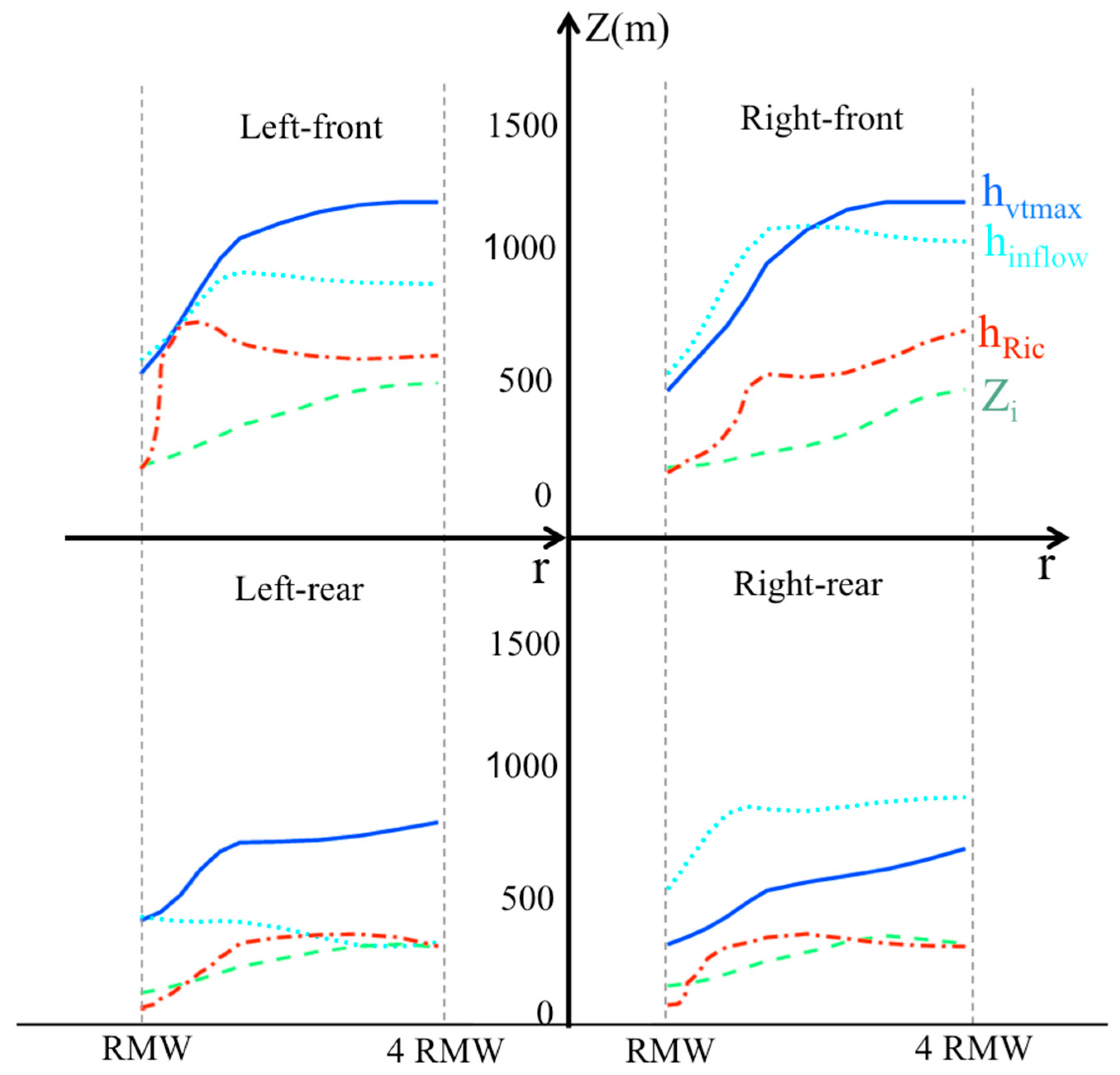
3. Results

The storm-motion-relative normalized radius-height representation of the tangential wind speed is displayed in Figure 4. The tangential wind first increases with height to a maximum value then decreases with height in all four motion-relative quadrants. This tangential wind maximum has been called the boundary layer jet [45,46]. The maximum tangential wind speed is largest in the right-front quadrant and it is smallest at the right-rear quadrant. Specifically, the peak values of the tangential wind speed are 53.5, 55.8, 52.6, and 44.3 ms−1 for left-front, right-front, left-rear and right-rear quadrant, respectively. The fact that the front quadrants have stronger tangential wind speeds than the rear quadrants in a storm-relative framework is consistent with previous theoretical studies [45,46,47,48].
It is also evident from Figure 4 that the jet height, hvtmax, has a trend of decreasing with smaller r* values in all four motion-relative quadrants. This result further supports the findings of Zhang et al. [31] in terms of the radial variation of the hurricane boundary layer height, which may be applied in the asymmetric sense. Interestingly, hvtmax is higher in the front quadrants than in the rear quadrants, which may be associated with the stronger tangential wind speed in the front quadrants. Specifically, hvtmax increases from ~600 m at a radius of r * = 1 to ~1200 m at a radius of r * = 2 , then slightly increases with increasing radius in the front two quadrants. In the left-rear quadrant, hvtmax is ~100 m smaller than in the front two quadrants at r* = 1, and increases with radius to ~800 m at r* = 2, then increases to ~900 m at r* = 4. In the right-rear quadrant, hvtmax is the lowest among all four quadrants, and it gradually increases from ~400 m at radius of r * = 1 to ~600 m at radius of r * = 2 , and increases to ~800 m at r* = 4.
The normalized radius-height representation of the radial velocity for the four motion-relative quadrants is displayed in Figure 5. The peak values of the radial wind speed are −18.5, −18.7, −13.5 and −15.4 ms−1 for left-front, right-front, left-rear and right-rear quadrant, respectively. These peak inflow values are located at ~100 m altitude between r* = 1 − 2 and closer to r* = 1, which is consistent with the axisymmetric structure documented by Zhang et al. [31]. In addition, a pronounced outflow of 5–10 m s−1 can be seen in all the four quadrants above the inflow layer. The inflow is stronger in the front quadrants compared to the rear quadrants, which is consistent with previous theoretical and numerical studies [46,47,48]. Observational studies of individual hurricanes also showed similar front-back wind asymmetry [37,38,49].
The inflow layer depth, hinflow, which is depicted by the white line in Figure 5, shows a decreasing trend with decreasing radius in all four motion-relative quadrants. It is also evident from Figure 5 that, hinflow is larger in the front two quadrants than in the rear two quadrants. Specifically, hinflow evolves similarly in left-front, right-front and right-rear quadrants from an altitude of ~600 m to an altitude of 900–1200 m with highest heights in the right-front quadrant and lowest heights in the right-rear quadrant. However, hinflow remains nearly constant (~500 m) with a slightly negative trend in the left-rear quadrant. This result suggests that the asymmetric distribution of hinflow follows that of hvtmax. From Figure 4 and Figure 5, the maximum tangential wind speed in the eyewall region is close to the top of the inflow layer in all quadrants.
The thermodynamic mixed layer depth, zi, is depicted by the white line in Figure 6 that shows the normalized radius-height representation of the vertical gradient of theta-v ( d θ v / d z ). In all quadrants, the boundary layer is unstable near the surface as indicated by the negative value of d θ v / d z . Above this very shallow unstable layer, the boundary layer becomes nearly neutral up to the mixed layer depth and then becomes stable. There is a strong stable layer inside the RMW above the mixed layer at heights of 600–2000 m with d θ v / d z > 5 K/km. This strong stable layer is shallowest at the right-rear quadrant among the four motion-relative quadrants, which may be tied to the cold wake phenomena observed in the sea surface temperature (SST) field [50,51,52]. On average when the storm motion of a hurricane is ~6 ms−1, which is the average value of our data, the typical SST close to the cold wake region at the right-rear quadrant is of the order of 1–2 K smaller than the front quadrants based on in-situ data [53]. The smaller SST in the right-rear quadrant would stabilize the low-level boundary layer due to a reduction in surface enthalpy fluxes.
In all four quadrants, zi decreases with distance toward the storm center, in a similar manner as the kinematic boundary layer heights. This result again supports that of Zhang et al. [31] and Zhang et al. [54]. From Figure 4, Figure 5 and Figure 6, it is clear that zi is much smaller than hinflow and hvtmax in all quadrants, the kinematic and thermodynamic boundary layer heights largely depart from each other, as noted by Zhang et al. [31]. This structure is different from that of the ABL in non-hurricane conditions. Close to the eyewall region (r* < 1.5), zi is nearly symmetric with a value of ~200 m. Outside the eyewall, the left-front quadrant has the largest zi while the other three quadrants have similar magnitudes of zi. In the outer radii (r* > 3), zi is largest in the left-front quadrant and is smallest in the right-rear quadrant. There is a weak front-back asymmetry in zi, which is similar to the asymmetric distribution of the kinematic boundary layer height, but the mixed layer depth difference is less than ~100 m.
The storm-motion-relative normalized radius-height representation of the bulk Richardson number is displayed in Figure 7. Here the height of R i c = 0.25 is taken as the top of the boundary layer (hRic), which is depicted by the solid white line in Figure 7. The front-back difference in hRic is clearly shown in Figure 7 with the front two quadrants displaying a deeper boundary layer, consistent with the other height scales investigated earlier. Combining Figure 4, Figure 5, Figure 6 and Figure 7, it appears that hRic lies between the thermodynamic mixed layer depth and the kinematic boundary layer height, which agrees with the axisymmetric structure documented by Zhang et al. [31]. The left-front quadrant has the deepest boundary layer while the right-rear quadrant has the shallowest boundary layer, in terms of hRic.

4. Discussion and Conclusions

The ABL plays an important role in the energy transport processes related to hurricane intensification and maximum intensity [32,55,56,57,58,59,60] and it is essential to understand the ABL structure. This paper analyzes a total of 1916 GPS dropsondes within four times the RMW distance from 37 hurricanes over the tropical Atlantic basin from 1998 to 2015 to study the characteristic height scales of the ABL with respect to the storm-motion direction. Figure 8 is a schematic diagram that summarizes the height scales investigated in this study based on the composite dropsonde analysis. The results show a clear departure between thermodynamic and kinematic boundary layer heights with the thermodynamic boundary layer height much shallower than the kinematic boundary layer height. Supporting the findings of Zhang et al. [31] based on the symmetric analysis of the dropsonde data, our results show that the hurricane boundary layer height increases with increasing radius in a storm-relative framework. This observed variation of boundary layer height with radius supports the theoretical scaling of a rotating boundary layer [46,59,61,62,63,64] in an axisymmetric framework. Our results indicate that this scaling also holds in a motion-relative asymmetric distribution of the boundary layer height.
In the eyewall region, all height scales show relatively small asymmetric distribution. The weak asymmetry is found in the kinematic boundary layer heights (hvtmax and hinflow) that are slightly smaller in the left-rear quadrant than in other quadrants. All height scales demonstrate similar front-back asymmetry outside the eyewall region, in that the two front motion-relative quadrants have a deeper boundary layer. The front-back difference in the thermodynamic boundary layer height is smaller than that in the kinematic boundary layer height. The mixed layer depth being smallest in the right-rear quadrant may be due to the SST cooling effect in this quadrant where the cold wake is located, following the argument of previous modeling studies [35,52].
The boundary layer height derived using the critical Richardson number ( R i c ) method shows a similar asymmetry as the kinematic boundary layer height, confirming that turbulence in the hurricane boundary layer is mainly shear driven. Consistent with Zhang et al. [31], our results suggest that the hurricane research community should use the kinematic height scales to represent the top of the boundary layer instead of the thermodynamic mixed layer depth typically used in non-hurricane conditions. Kepert [65] and Kepert et al. [66] discussed the limitation of using thermodynamic mixed layer depth to represent the boundary layer height in numerical models, which is in agreement with our observational findings here.
Our results in terms of the asymmetry of maximum tangential and radial wind speeds in the boundary layer generally agree with previous theoretical and numerical studies [46,47,48] Our result in terms of front-back asymmetry in the velocity fields also agrees with previous observational case studies such as the ABL structure in Hurricanes Mitch (1998), George (1998), Isabel (2003) and Daniel (2008) as shown by Kepert [37,38]. Although previous studies did not focus on the boundary layer height asymmetry, their results indicate a similar structure of the inflow and inflow layer depth as well as the height of the boundary layer jet. The surface wind asymmetry is consistent with Uhlhorn et al. [67] who analyzed stepped frequency microwave radiometer (SFMR) data, as well as Klotz and Jiang [68] who analyzed satellite data. The inflow asymmetry near the surface is consistent with the result of Zhang and Uhlhorn [69], who studied the characteristics of surface inflow angle in both axisymmetric and asymmetric framework.
Note that Zhang et al. [54] investigated the asymmetric structure of the hurricane boundary layer in relation to the environmental vertical wind shear. They focused on investigating how boundary layer thermodynamic structure is tied to the upper-level convection in an energy-cycling paradigm. They also studied the asymmetry of the boundary layer height scales relative to the environmental shear direction and found that the kinematic boundary layer height scales are larger in the downshear direction than in the upshear direction, while the thermodynamic boundary layer height scale is slightly larger left of the shear than right of the shear. The boundary layer being deeper in the downshear quadrants may be tied to the asymmetric distribution of convection that is usually initiated in the downshear-right quadrant and propagates to downshear-left quadrant [70]. The boundary layer is deeper in the quadrants where stronger convection occurs. Following this argument, storm-motion induced asymmetry of the boundary layer height scales may also be linked to asymmetric distribution of convective activity relative to storm motion, although storm motion and environmental wind shear are very different parameters.
The asymmetric structure above the boundary layer (i.e., convection) in tropical cyclones with respect to storm motion have been extensively studied using radar observations in both case studies and composite analysis studies. For instance, Jorgensen et al. [71] utilized flight-level data and found maximum upward mass transport in slow-moving storms occurred to the right of motion, with equal amounts occurring in the front and rear of the inner core. Our composite analysis supports strong convection occurs in the right-front quadrant, as both the maximum tangential wind speed and maximum inflow strength occur in this quadrant. Marks et al. [72] found that the maximum upward vertical velocities were in the left-front quadrant of Hurricane Norbert (1984). Marks [73] found that the maximum precipitation of Hurricane Allen (1980) in the eyewall region was in the left-front quadrant, while the maximum precipitation of Hurricane Elena (1985) was in the right-front quadrant. Through examining the patterns of reflectivity in the eyewall region of Hurricane Olivia (1994), Reasor et al. [74] found that the maximum radar reflectivity was located in the left quadrants relative to the motion direction, which was consistent with the structure in Hurricane Gloria (1985) documented by Franklin et al. [75]. Our composite analysis shows that the strongest inflow in the boundary layer is located in the front quadrants, which support large vertical motion and strong convection due to mass continuity. Overall, it is hypothesized that the asymmetry of boundary layer inflow and jet strength are tied to the asymmetry of convection and precipitation.
Furthermore, the composite analysis result showing the front-back asymmetry of the boundary layer heights supports the theoretical argument that the boundary-layer convergence is larger in the front quadrants relative to the storm motion direction [45,47]. The surface wind asymmetry related to storm-motion effect induces the asymmetry of surface drag forcing, which in turn affects the distribution of boundary layer convergence and convection. Larger wind speed observed in the front quadrants induces larger turbulent mixing in the boundary layer, which supports larger kinematic boundary layer height according to dynamic scaling [42,45].
Of note, the combined effects of storm motion and environmental wind shear on the asymmetry of the boundary layer structure remains to be understood due to the limitation of data sampling size at the current stage. Future studies will combine the dropsonde and Doppler radar data to investigate the linkage between the boundary layer and convective processes and their asymmetry relative to both the storm motion and environmental wind shear. The extent of asymmetry of the boundary layer structure to the storm motion speed will also be evaluated when more observational data are available than those used in the present study.

Author Contributions

Conceptualization, J.A.Z., X.W.; methodology, Y.R., J.A.Z.; software, X.W.; validation, Y.R., J.A.Z., S.R.G. and X.W.; formal analysis, Y.R., X.W.; resources, J.A.Z., X.W.; data curation, Y.R.; writing—original draft preparation, Y.R., J.A.Z., S.R.G., X.W.; writing—review and editing, J.A.Z., S.R.G., X.W.; visualization, X.W.; supervision, J.A.Z.; project administration, Y.R.; funding acquisition, J.A.Z., S.R.G., X.W.

Funding

This study was partially supported by NSF Grant AGS1822128, NOAA Grant NA14NWS4680030, NASA Grant NNX14AM69G, and NASA Weather and Atmospheric Dynamics program (Grant NNH16ZDA001N-WEATHER) directed by Ramesh Kakar.

Acknowledgments

The authors would like to thank all the scientists and crew members who have been involved in the hurricane field program and operational reconnaissance hurricane missions to help collect the dropsonde data used in this study. This paper is a follow-up work of the first author’s Master thesis and she would like to acknowledge Prof. Xiaolei Zou and Prof. Ming Cai for their helpful discussions. We also wish to thank the reviewers for their comments that led to improvement of the paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Troen, I.B.; Mahrt, L. A simple model of the atmospheric boundary layer; sensitivity to surface evaporation. Bound. Layer Meteorol. 1986, 37, 129–148. [Google Scholar] [CrossRef]
  2. Hong, S.-Y.; Pan, H.-L. Nonlocal Boundary Layer Vertical Diffusion in a Medium-Range Forecast Model. Mon. Weather Rev. 1996, 124, 2322–2339. [Google Scholar] [CrossRef]
  3. Hong, S.-Y.; Noh, Y.; Dudhia, J. A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
  4. Zeng, X.; Brunke, M.A.; Zhou, M.; Fairall, C.; Bond, N.A.; Lenschow, D.H. Marine Atmospheric Boundary Layer Height over the Eastern Pacific: Data Analysis and Model Evaluation. J. Clim. 2004, 17, 4159–4170. [Google Scholar] [CrossRef]
  5. Balsley, B.B.; Frehlich, R.G.; Jensen, M.L.; Meillier, Y. High-Resolution In Situ Profiling through the Stable Boundary Layer: Examination of the SBL Top in Terms of Minimum Shear, Maximum Stratification, and Turbulence Decrease. J. Atmos. Sci. 2006, 63, 1291–1307. [Google Scholar] [CrossRef]
  6. Hennemuth, B.; Lammert, A. Determination of the Atmospheric Boundary Layer Height from Radiosonde and Lidar Backscatter. Bound. Layer Meteorol. 2006, 120, 181–200. [Google Scholar] [CrossRef]
  7. Sicard, M.; Pérez, C.; Rocadenbosch, F.; Baldasano, J.M.; García-Vizcaino, D. Mixed-layer depth determination in the Barcelona coastal area from regular lidar measurements: methods, results and limitations. Bound. Layer Meteorol. 2006, 119, 135–157. [Google Scholar] [CrossRef]
  8. Georgoulias, A.K.; Papanastasiou, D.K.; Melas, D.; Amiridis, V.; Alexandri, G.; Georgoulias, A. Statistical analysis of boundary layer heights in a suburban environment. Theor. Appl. Clim. 2009, 104, 103–111. [Google Scholar] [CrossRef]
  9. Stull, R.B. An Introduction to Boundary-layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA; London, UK, 1988; 666p. [Google Scholar]
  10. Fetzer, E.J.; Teixeira, J.; Olsen, E.T.; Fishbein, E.F. Satellite remote sounding of atmospheric boundary layer temperature inversions over the subtropical eastern Pacific. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
  11. Wood, R.; Bretherton, C.S. Boundary Layer Depth, Entrainment, and Decoupling in the Cloud-Capped Subtropical and Tropical Marine Boundary Layer. J. Clim. 2004, 17, 3576–3588. [Google Scholar] [CrossRef]
  12. Medeiros, B.; Hall, A.; Stevens, B. What Controls the Mean Depth of the PBL? J. Clim. 2005, 18, 3157–3172. [Google Scholar] [CrossRef]
  13. Palm, S.P.; Spinhirne, J.; Benedetti, A. Validation of ECMWF global forecast model parameters using GLAS atmospheric channel measurements. Geophys. Res. Lett. 2005, 32, 109–127. [Google Scholar] [CrossRef]
  14. Sokolovskiy, S.; Röcken, C.; Hunt, D.; Schreiner, W.; Johnson, J.; Masters, D.; Esterhuizen, S. GPS profiling of the lower troposphere from space: Inversion and demodulation of the open-loop radio occultation signals. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
  15. Beyrich, F. Mixing height estimation from sodar data—A critical discussion. Atmos. Environ. 1997, 31, 3941–3953. [Google Scholar] [CrossRef]
  16. Dupont, E.; Menut, L.; Carissimo, B.; Pelon, J.; Flamant, P. Comparison between the atmospheric boundary layer in Paris and its rural suburbs during the ECLAP experiment. Atmos. Environ. 1999, 33, 979–994. [Google Scholar] [CrossRef]
  17. Bianco, L.; Wilczak, J.M. Convective Boundary Layer Depth: Improved Measurement by Doppler Radar Wind Profiler Using Fuzzy Logic Methods. J. Atmos. Ocean. Technol. 2002, 19, 1745–1758. [Google Scholar] [CrossRef]
  18. Holzworth, C.G. Estimates of mean maximum mixing depths in the contiguous United States. Mon. Weather Rev. 1964, 92, 235–242. [Google Scholar] [CrossRef]
  19. Coulter, R.L. A Comparison of Three Methods for Measuring Mixing-Layer Height. J. Appl. Meteorol. 1979, 18, 1495–1499. [Google Scholar] [CrossRef]
  20. Lokoshchenko, M.A. Long-Term Sodar Observations in Moscow and a New Approach to Potential Mixing Determination by Radiosonde Data. J. Atmos. Ocean. Technol. 2002, 19, 1151–1162. [Google Scholar] [CrossRef]
  21. Emeis, S.; Münkel, C.; Vogt, S.; Müller, W.J.; Schäfer, K. Atmospheric boundary-layer structure from simultaneous SODAR, RASS, and ceilometer measurements. Atmos. Environ. 2004, 38, 273–286. [Google Scholar] [CrossRef]
  22. Nielsen-Gammon, J.W.; Powell, C.L.; Mahoney, M.J.; Angevine, W.M.; Senff, C.; White, A.; Berkowitz, C.; Doran, C.; Knupp, K. Multisensor Estimation of Mixing Heights over a Coastal City. J. Appl. Meteorol. Clim. 2008, 47, 27–43. [Google Scholar] [CrossRef]
  23. Guo, P.; Kuo, Y.-H.; Sokolovskiy, S.V.; Lenschow, D. Estimating Atmospheric Boundary Layer Depth Using COSMIC Radio Occultation Data. J. Atmos. Sci. 2011, 68, 1703–1713. [Google Scholar] [CrossRef]
  24. Seidel, D.J.; Ao, C.O.; Li, K. Estimating climatological planetary boundary layer heights from radiosonde observations: Comparison of methods and uncertainty analysis. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef]
  25. Moss, M.S. Low-level turbulence structure in the vicinity of a hurricane. Mon. Weather Rev. 1978, 106, 841–849. [Google Scholar] [CrossRef]
  26. French, J.R.; Drennan, W.M.; Zhang, J.A.; Black, P.G. Turbulent fluxes in the hurricane boundary layer. Part I: Momentum flux. J. Atmos. Sci. 2007, 64, 1089–1102. [Google Scholar] [CrossRef]
  27. Zhang, J.A.; Drennan, W.M.; Black, P.G.; French, J.R. Turbulence Structure of the Hurricane Boundary Layer between the Outer Rainbands. J. Atmos. Sci. 2009, 66, 2455–2467. [Google Scholar] [CrossRef]
  28. Zhang, J.A.; Drennan, W.M. An Observational Study of Vertical Eddy Diffusivity in the Hurricane Boundary Layer. J. Atmos. Sci. 2012, 69, 3223–3236. [Google Scholar] [CrossRef]
  29. Guimond, S.R.; Tian, L.; Heymsfield, G.M.; Frasier, S.J. Wind Retrieval Algorithms for the IWRAP and HIWRAP Airborne Doppler Radars with Applications to Hurricanes. J. Atmos. Ocean. Technol. 2014, 31, 1189–1215. [Google Scholar] [CrossRef]
  30. Guimond, S.R.; Zhang, J.A.; Sapp, J.W.; Frasier, S.J. Coherent turbulence in the boundary layer of Hurricane Rita (2005) during an eyewall replacement cycle. J. Atmos. Sci. 2018, 75, 3071–3093. [Google Scholar] [CrossRef]
  31. Zhang, J.A.; Rogers, R.F.; Nolan, D.S.; Marks, F.D. On the Characteristic Height Scales of the Hurricane Boundary Layer. Mon. Weather Rev. 2011, 139, 2523–2535. [Google Scholar] [CrossRef]
  32. Smith, R.K.; Montgomery, M.T.; Nguyen, S.V. Tropical cyclone spinup revisited. Q. J. R. Meteor. Soc. 2009, 135, 1321–1335. [Google Scholar] [CrossRef]
  33. Ming, J.; Zhang, J.A.; Rogers, R.F. Typhoon kinematic and thermodynamic boundary layer structure from dropsonde composites. J. Geophys. Res. Atmos. 2015, 120, 3158–3172. [Google Scholar] [CrossRef]
  34. Lee, C.-Y.; Chen, S.S. Symmetric and Asymmetric Structures of Hurricane Boundary Layer in Coupled Atmosphere–Wave–Ocean Models and Observations. J. Atmos. Sci. 2012, 69, 3576–3594. [Google Scholar] [CrossRef]
  35. Wu, C.; Tu, W.; Pun, I.; Lin, I.; Peng, M.S. Tropical cyclone-ocean interaction in Typhoon Megi (2010)—A synergy study based on ITOP observations and atmosphere-ocean coupled model simulations. J. Geophys. Res. Atmos. 2016, 121, 153–167. [Google Scholar] [CrossRef]
  36. Powell, M.D. Boundary layer structure and dynamics in outer hurricane rainbands. Part II: Downdraft modification and mixed layer recovery. Mon. Weather Rev. 1990, 118, 918–938. [Google Scholar] [CrossRef]
  37. Kepert, J.D. Observed boundary layer wind structure and balance in the hurricane core. Part I: Hurricane Georges. J. Atmos. Sci. 2006, 63, 2169–2193. [Google Scholar] [CrossRef]
  38. Kepert, J.D. Observed boundary layer wind structure and balance in the hurricane core. Part II: Hurricane Mitch. J. Atmos. Sci. 2006, 63, 2194–2211. [Google Scholar] [CrossRef]
  39. Bell, M.M.; Montgomery, M.T. Observed structure, evolution, and potential intensity of category 5 Hurricane Isabel (2003) from 12 to 14 September. Mon. Weather Rev. 2008, 136, 2023–2046. [Google Scholar] [CrossRef]
  40. Barnes, G.M. Atypical Thermodynamic Profiles in Hurricanes. Mon. Weather Rev. 2008, 136, 631–643. [Google Scholar] [CrossRef]
  41. Lokoshchenko, M.T.; Zhang, J.A.; Smith, R.K. An analysis of the observed low-level structure of rapidly intensifying and mature hurricane Earl (2010). Q. J. R. Meteorol. Soc. 2014, 140, 2132–2146. [Google Scholar]
  42. Zhang, J.A.; Nolan, D.S.; Rogers, R.F.; Tallapragada, V. Evaluating the impact of improvements in the boundary layer parameterization on hurricane intensity and structure forecasts in HWRF. Mon. Weather Rev. 2015, 143, 3136–3155. [Google Scholar] [CrossRef]
  43. Hock, T.F.; Franklin, J.L. The NCAR GPS dropwindsonde. Bull. Am. Meteor. Soc. 1999, 80, 407–420. [Google Scholar] [CrossRef]
  44. Vigh, J.L.; Dorst, N.M.; Williams, C.L.; Uhlhorn, E.W.; Klotz, B.W.; Martinez, J.; Willoughby, H.E.; Marks, F.D., Jr.; Chavas, D.R. FLIGHT+: The Extended Flight Level Dataset for Tropical Cyclones (Version 1.0); Tropical Cyclone Data Project; National Center for Atmospheric Research, Research Applications Laboratory: Boulder, CO, USA, 2015; Available online: http://dx.doi.org/10.5065/D6WS8R93 (accessed on 21 January 2015).
  45. Kepert, J.D. The Dynamics of Boundary Layer Jets within the Tropical Cyclone Core. Part I: Linear Theory. J. Atmos. Sci. 2001, 58, 2485–2501. [Google Scholar] [CrossRef]
  46. Kepert, J.D.; Wang, Y. The dynamics of boundary layer jets within the tropical cyclone core. Part II: Nonlinear enhancement. J. Atmos. Sci. 2001, 58, 2485–2501. [Google Scholar] [CrossRef]
  47. Shapiro, L.J. The Asymmetric Boundary layer Flow Under a Translating Hurricane. J. Atmos. Sci. 1983, 40, 1984–1998. [Google Scholar] [CrossRef]
  48. Thomsen, G.L.; Smith, R.K.; Montgomery, M.T. Tropical cyclone flow asymmetries induced by a uniform flow revisited. J. Adv. Model. Earth Syst. 2015, 7, 1265–1284. [Google Scholar] [CrossRef]
  49. Schwendike, J.; Kepert, J.D. The boundary layer winds in hurricanes Danielle (1998) and Isabel (2003). Mon. Weather Rev. 2008, 136, 3168–3192. [Google Scholar] [CrossRef]
  50. Price, J.F. Upper Ocean Response to a Hurricane. J. Phys. Oceanogr. 1981, 11, 153–175. [Google Scholar] [CrossRef]
  51. Shay, L.K.; Black, P.G.; Mariano, A.J.; Hawkins, J.D.; Elsberry, R.L. Upper ocean response to Hurricane Gilbert. J. Geophys. Res. Space Phys. 1992, 97, 20227. [Google Scholar] [CrossRef]
  52. Lee, C.-Y.; Chen, S.S. Stable Boundary Layer and Its Impact on Tropical Cyclone Structure in a Coupled Atmosphere–Ocean Model. Mon. Weather Rev. 2014, 142, 1927–1944. [Google Scholar] [CrossRef]
  53. Cione, J.J.; Kalina, E.A.; Zhang, J.A.; Uhlhorn, E.W. Observations of Air–Sea Interaction and Intensity Change in Hurricanes. Mon. Weather Rev. 2013, 141, 2368–2382. [Google Scholar] [CrossRef]
  54. Zhang, J.A.; Rogers, R.F.; Reasor, P.D.; Uhlhorn, E.W.; Marks, F.D. Asymmetric Hurricane Boundary Layer Structure from Dropsonde Composites in Relation to the Environmental Vertical Wind Shear. Mon. Weather Rev. 2013, 141, 3968–3984. [Google Scholar] [CrossRef]
  55. Ooyama, K.V. Numerical simulation of the life cycle of tropical cyclones. J. Atmos. Sci. 1969, 26, 3–40. [Google Scholar] [CrossRef]
  56. Emanuel, K.A. An Air-Sea Interaction Theory for Tropical Cyclones. Part I: Steady-State Maintenance. J. Atmos. Sci. 1986, 43, 585–605. [Google Scholar] [CrossRef]
  57. Emanuel, K.A. Sensitivity of Tropical Cyclones to Surface Exchange Coefficients and a Revised Steady-State Model incorporating Eye Dynamics. J. Atmos. Sci. 1995, 52, 3969–3976. [Google Scholar] [CrossRef]
  58. Bryan, G.H.; Rotunno, R. The maximum intensity of tropical cyclones in axisymmetry numerical model simulations. Mon. Weather Rev. 2009, 137, 1770–1789. [Google Scholar] [CrossRef]
  59. Foster, R.C. Boundary-Layer Similarity Under an Axisymmetric, Gradient Wind Vortex. Bound. Layer Meteorol. 2009, 131, 321–344. [Google Scholar] [CrossRef]
  60. Montgomery, M.T.; Smith, R.K. Recent Developments in the Fluid Dynamics of Tropical Cyclones. Annu. Rev. Fluid Mech. 2017, 49, 541–574. [Google Scholar] [CrossRef]
  61. Eliassen, A. On the Ekman Layer in a circular Vortex. J. Meteorol. Soc. Jpn. 1971, 49, 784–789. [Google Scholar] [CrossRef]
  62. Carrier, G.F. Swirling flow boundary layers. J. Fluid Mech. 1971, 49, 133–144. [Google Scholar] [CrossRef]
  63. Montgomery, M.T.; Snell, H.D.; Yang, Z. Axisymmetric Spindown Dynamics of Hurricane-like Vortices. J. Atmos. Sci. 2001, 58, 421–435. [Google Scholar] [CrossRef]
  64. Nolan, D.S. Instabilities in hurricane-like boundary layers. Dyn. Atmos. Oceans 2005, 40, 209–236. [Google Scholar] [CrossRef]
  65. Kepert, J.D. Slab- and height-resolving models of the tropical cyclone boundary layer. Part I: Comparing the simulations. Q. J. R. Meteorol. Soc. 2010, 136, 1686–1699. [Google Scholar] [CrossRef]
  66. Kepert, J.D.; Schwendike, J.; Ramsay, H. Why is the tropical cyclone boundary layer not “well mixed”? J. Atmos. Sci. 2016, 73, 957–973. [Google Scholar] [CrossRef]
  67. Uhlhorn, E.W.; Klotz, B.W.; Vukićević, T.; Reasor, P.D.; Rogers, R.F. Observed Hurricane Wind Speed Asymmetries and Relationships to Motion and Environmental Shear. Mon. Weather Rev. 2014, 142, 1290–1311. [Google Scholar] [CrossRef]
  68. Klotz, B.W.; Jiang, H. Global composites of surface wind speeds in tropical cyclones based on a 12-year scatterometer database. Geophys. Res. Lett. 2016, 43, 10480–10488. [Google Scholar] [CrossRef]
  69. Zhang, J.A.; Uhlhorn, E.W. Hurricane Sea Surface Inflow Angle and an Observation-Based Parametric Model. Mon. Weather Rev. 2012, 140, 3587–3605. [Google Scholar] [CrossRef]
  70. Reasor, P.D.; Rogers, R.; Lorsolo, S. Environmental Flow Impacts on Tropical Cyclone Structure Diagnosed from Airborne Doppler Radar Composites. Mon. Weather Rev. 2013, 141, 2949–2969. [Google Scholar] [CrossRef]
  71. Jorgensen, D.P.; Zipser, E.J.; LeMone, M.A. Vertical Motions in Intense Hurricanes. J. Atmos. Sci. 1985, 42, 839–856. [Google Scholar] [CrossRef]
  72. Marks, F.D., Jr.; Houze, R.A., Jr.; Gamache, J.F. Dual-aircraft investigation of the inner core of Hurricane Norbert. Part I: Kinematic structure. J. Atmos. Sci. 1992, 49, 919–942. [Google Scholar] [CrossRef]
  73. Marks, F.D. Evolution of the Structure of Precipitation in Hurricane Allen (1980). Mon. Weather Rev. 1985, 113, 909–930. [Google Scholar] [CrossRef]
  74. Reasor, P.D.; Montgomery, M.T.; Marks, F.D.; Gamache, J.F. Low-Wavenumber Structure and Evolution of the Hurricane Inner Core Observed by Airborne Dual-Doppler Radar. Mon. Weather Rev. 2000, 128, 1653–1680. [Google Scholar] [CrossRef]
  75. Franklin, J.L.; Lord, S.J.; Feuer, S.E.; Marks, F.D. The Kinematic Structure of Hurricane Gloria (1985) Determined from Nested Analyses of Dropwindsonde and Doppler Radar Data. Mon. Weather Rev. 1993, 121, 2433–2451. [Google Scholar] [CrossRef]
Atmosphere 10 00339 g001
Figure 1. Storm-relative two-dimensional distribution of dropsonde surface observation locations. Cross- and along-track positions are normalized by the radius of maximum wind at the time of observation. The arrow indicates the storm motion direction.
Figure 1. Storm-relative two-dimensional distribution of dropsonde surface observation locations. Cross- and along-track positions are normalized by the radius of maximum wind at the time of observation. The arrow indicates the storm motion direction.
Atmosphere 10 00339 g001
Atmosphere 10 00339 g002
Figure 2. Radial distribution of dropsonde counts per bin as a function of normalized distance by radius of maximum wind speed (RMW).
Figure 2. Radial distribution of dropsonde counts per bin as a function of normalized distance by radius of maximum wind speed (RMW).
Atmosphere 10 00339 g002
Atmosphere 10 00339 g003
Figure 3. Frequency distribution of dropsondes according to the corresponding (a) storm intensity, (b) radius of maximum wind speed (RMW), (c) storm speed, and (d) storm direction rotated clockwise with 0° pointing to the north.
Figure 3. Frequency distribution of dropsondes according to the corresponding (a) storm intensity, (b) radius of maximum wind speed (RMW), (c) storm speed, and (d) storm direction rotated clockwise with 0° pointing to the north.
Atmosphere 10 00339 g003
Atmosphere 10 00339 g004
Figure 4. Composite analysis result of the relative tangential wind velocity as a function of altitude and the normalized radius to the storm center for the four quadrants relative to the motion direction. The panels show the left-front (a), right-front (b), left-rear (c) and right-rear (d) quadrants. The white dashed line in each panel depicts the height of the maximum tangential wind speed varying with radius.
Figure 4. Composite analysis result of the relative tangential wind velocity as a function of altitude and the normalized radius to the storm center for the four quadrants relative to the motion direction. The panels show the left-front (a), right-front (b), left-rear (c) and right-rear (d) quadrants. The white dashed line in each panel depicts the height of the maximum tangential wind speed varying with radius.
Atmosphere 10 00339 g004
Atmosphere 10 00339 g005
Figure 5. Same as in Figure 4 but the results are for the relative radial wind velocity as a function of altitude and the normalized radius to the storm center for the four quadrants relative to the shear direction. The panels show the left-front (a), right-front (b), left-rear (c) and right-rear (d) quadrants. The white line in each panel represents the height of 10% peak inflow.
Figure 5. Same as in Figure 4 but the results are for the relative radial wind velocity as a function of altitude and the normalized radius to the storm center for the four quadrants relative to the shear direction. The panels show the left-front (a), right-front (b), left-rear (c) and right-rear (d) quadrants. The white line in each panel represents the height of 10% peak inflow.
Atmosphere 10 00339 g005
Atmosphere 10 00339 g006
Figure 6. Same as in Figure 4 but the results show the lapse rate of the virtual potential temperature. The panels show the left-front (a), right-front (b), left-rear (c) and right-rear (d) quadrants. The thick white line denotes the contour. The contour denotes the constant contour of d θ v / d z = 3 K km−1.
Figure 6. Same as in Figure 4 but the results show the lapse rate of the virtual potential temperature. The panels show the left-front (a), right-front (b), left-rear (c) and right-rear (d) quadrants. The thick white line denotes the contour. The contour denotes the constant contour of d θ v / d z = 3 K km−1.
Atmosphere 10 00339 g006
Atmosphere 10 00339 g007
Figure 7. Same as in Figure 4 but the results are for the Richardson numbers as a function of altitude and the normalized radius to the storm center. The panels show the left-front (a), right-front (b), left-rear (c) and right-rear (d) quadrants. The white line shows the contour of 0.25.
Figure 7. Same as in Figure 4 but the results are for the Richardson numbers as a function of altitude and the normalized radius to the storm center. The panels show the left-front (a), right-front (b), left-rear (c) and right-rear (d) quadrants. The white line shows the contour of 0.25.
Atmosphere 10 00339 g007
Atmosphere 10 00339 g008
Figure 8. Schematic diagram of the characteristic height scales of the hurricane boundary layer for the four quadrants relative to the storm motion. The height scales are based on the composite analysis of the dropsonde data. hinflow is the inflow layer depth (cyan dotted line); zi is the mixed layer depth (green dashed line); hvtmax is the height of the maximum tangential wind speed (blue solid line) and; hRic is the height of the bulk Richardson number value of 0.25.
Figure 8. Schematic diagram of the characteristic height scales of the hurricane boundary layer for the four quadrants relative to the storm motion. The height scales are based on the composite analysis of the dropsonde data. hinflow is the inflow layer depth (cyan dotted line); zi is the mixed layer depth (green dashed line); hvtmax is the height of the maximum tangential wind speed (blue solid line) and; hRic is the height of the bulk Richardson number value of 0.25.
Atmosphere 10 00339 g008
Table 1. Storm information and number of dropsondes (1916).
Table 1. Storm information and number of dropsondes (1916).
IDStormIntensity Range (kt)No. of Sondes
0298BONNIE98.6–100.0101
0498DANIELLE65.0–73.143
0598EARL79.6–83.03
0798GEORGES65.0–131.1106
1398MITCH139.1–139.66
0399BRET101.9–111.49
0599DENNIS67.1–90.019
0899FLOYD81.3–122.523
1399IRENE65.04
1002ISIDORE66.1–110.014
1003FABIAN100.0–125.0154
1303ISABEL79.6–140.0271
0304CHARLEY64.1–120.449
0604FRANCES87.6–124.7128
0904IVAN105.0–145.0158
1104JEANNE85.0–105.011
0405DENNIS71.6–84.521
1205KATRINA100.0–150.060
1805RITA123.4–146.513
0906HELENE80.0–98.342
0708GUSTAV75.3–111.723
1708PALOMA79.1–125.020
0309BILL105.1–115.037
0710EARL71.8–121.141
1310KARL71.6–76.99
0911IRENE72.7–104.691
1811RINA81.8–100.07
0912ISAAC64.0–70.042
1812SANDY65.0–74.590
1013INGRID65.0–70.935
0114ARTHUR67.8–82.446
0314BERTHA64.6–70.023
0414CRISTOBAL65.0–67.028
0614EDOUARD72.5–101.573
0814GONZALO106.9–125.040
0415DANNY105.7–106.410
1115JOAQUIN75.0–120.066

Share and Cite

MDPI and ACS Style

Ren, Y.; Zhang, J.A.; Guimond, S.R.; Wang, X. Hurricane Boundary Layer Height Relative to Storm Motion from GPS Dropsonde Composites. Atmosphere 2019, 10, 339. https://doi.org/10.3390/atmos10060339

AMA Style

Ren Y, Zhang JA, Guimond SR, Wang X. Hurricane Boundary Layer Height Relative to Storm Motion from GPS Dropsonde Composites. Atmosphere. 2019; 10(6):339. https://doi.org/10.3390/atmos10060339

Chicago/Turabian Style

Ren, Yifang, Jun A. Zhang, Stephen R. Guimond, and Xiang Wang. 2019. "Hurricane Boundary Layer Height Relative to Storm Motion from GPS Dropsonde Composites" Atmosphere 10, no. 6: 339. https://doi.org/10.3390/atmos10060339

APA Style

Ren, Y., Zhang, J. A., Guimond, S. R., & Wang, X. (2019). Hurricane Boundary Layer Height Relative to Storm Motion from GPS Dropsonde Composites. Atmosphere, 10(6), 339. https://doi.org/10.3390/atmos10060339

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop