Optimal Design of Air Quality Monitoring Network for Pollution Detection and Source Identification in Industrial Parks
Abstract
1. Introduction
2. Methods
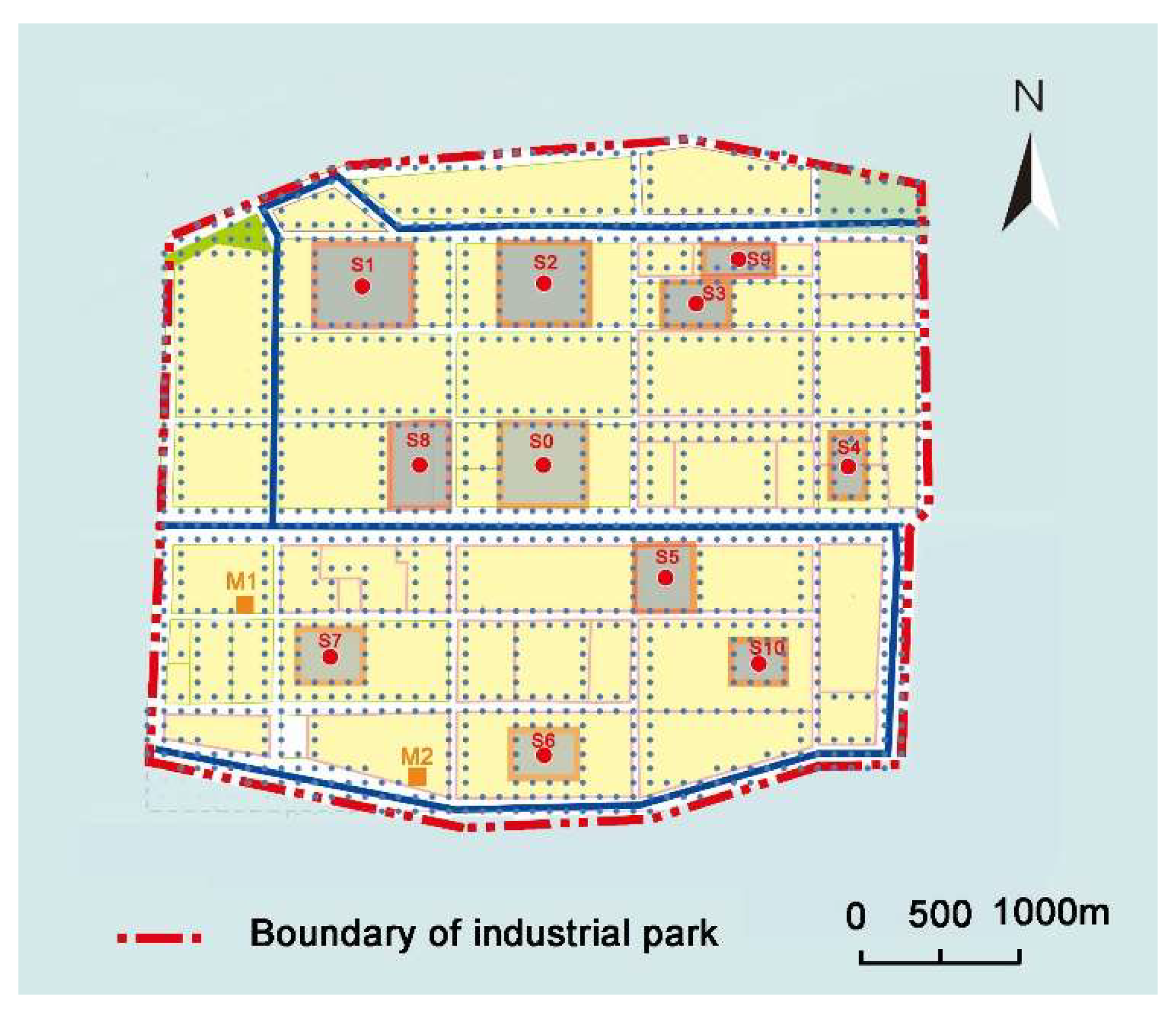
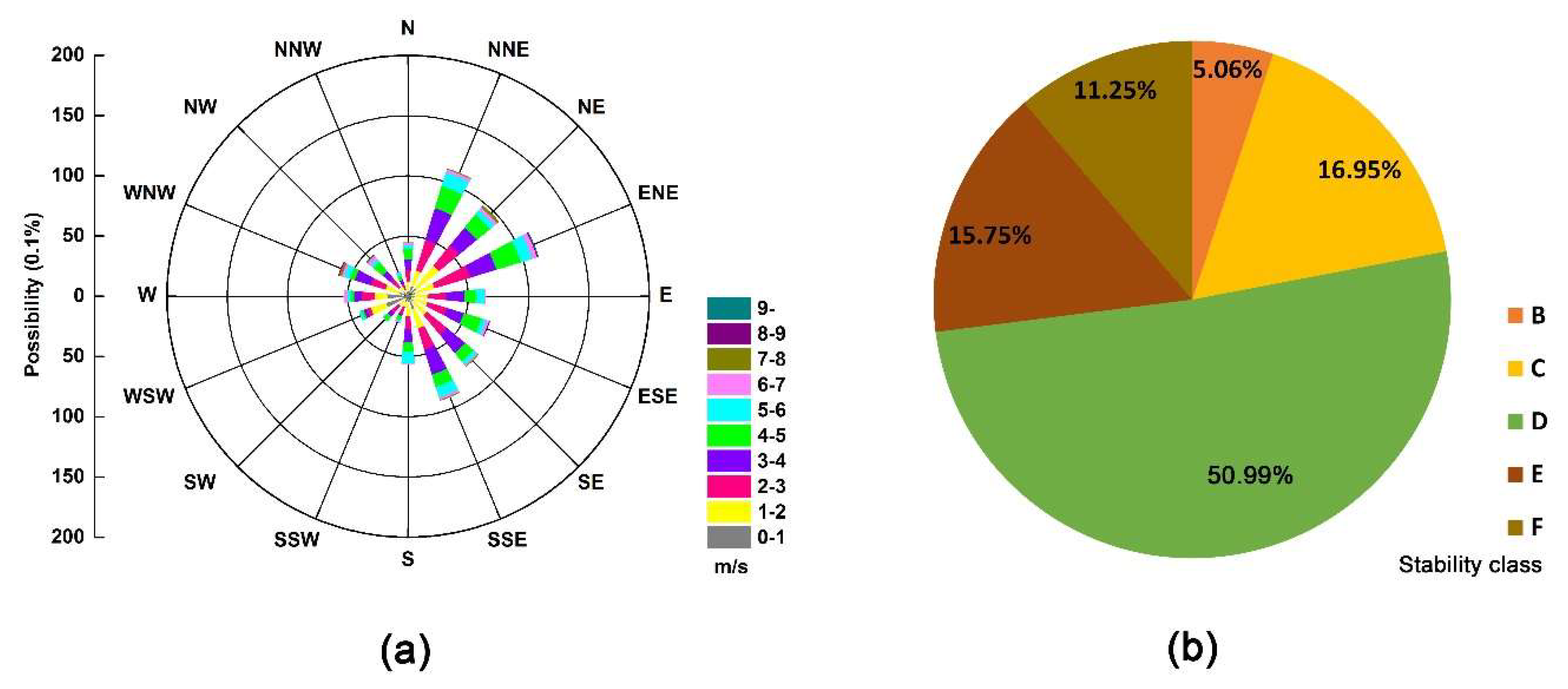
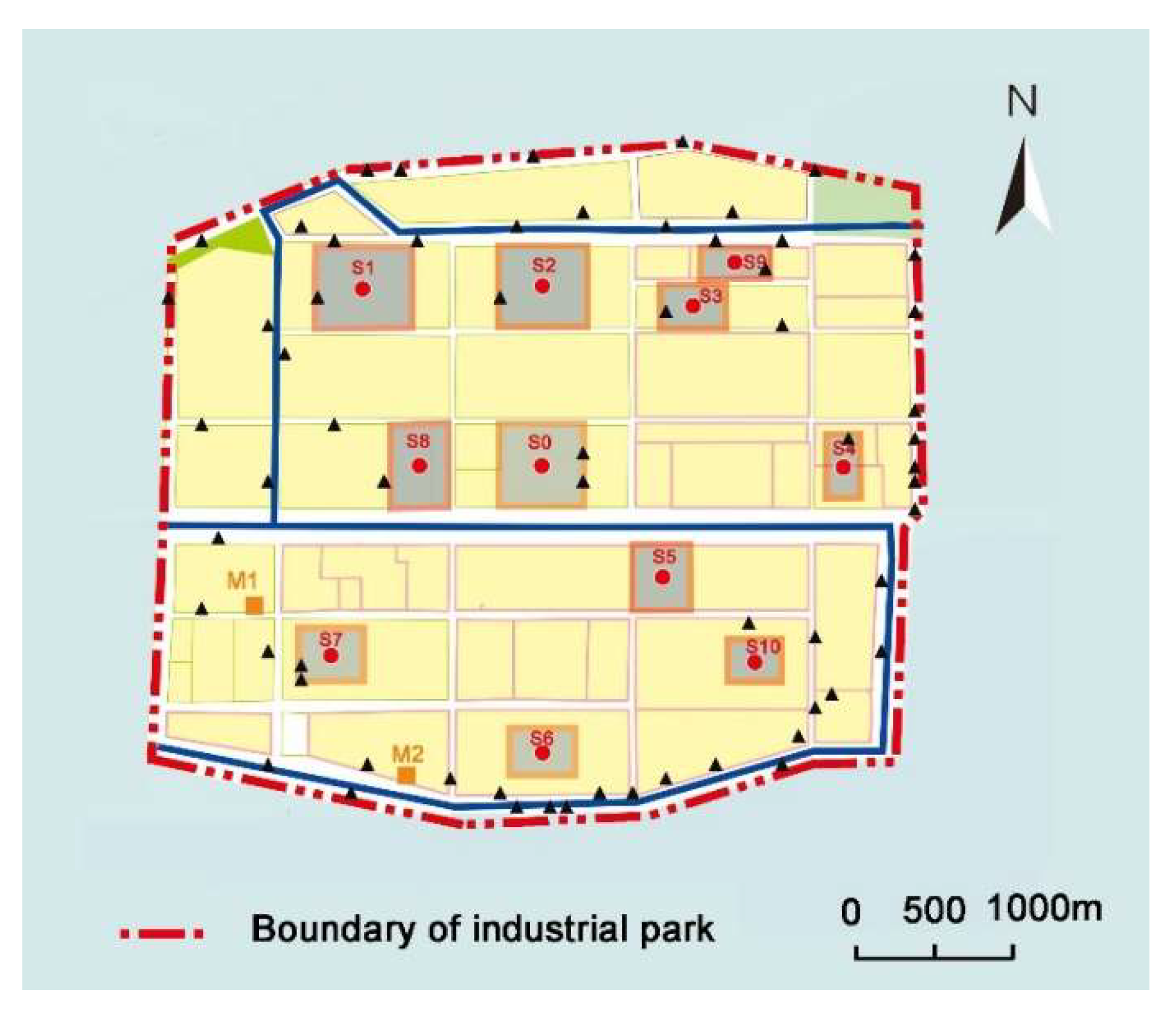
2.1. Data Configuration
2.2. Method
2.2.1. Gaussian Puff Model
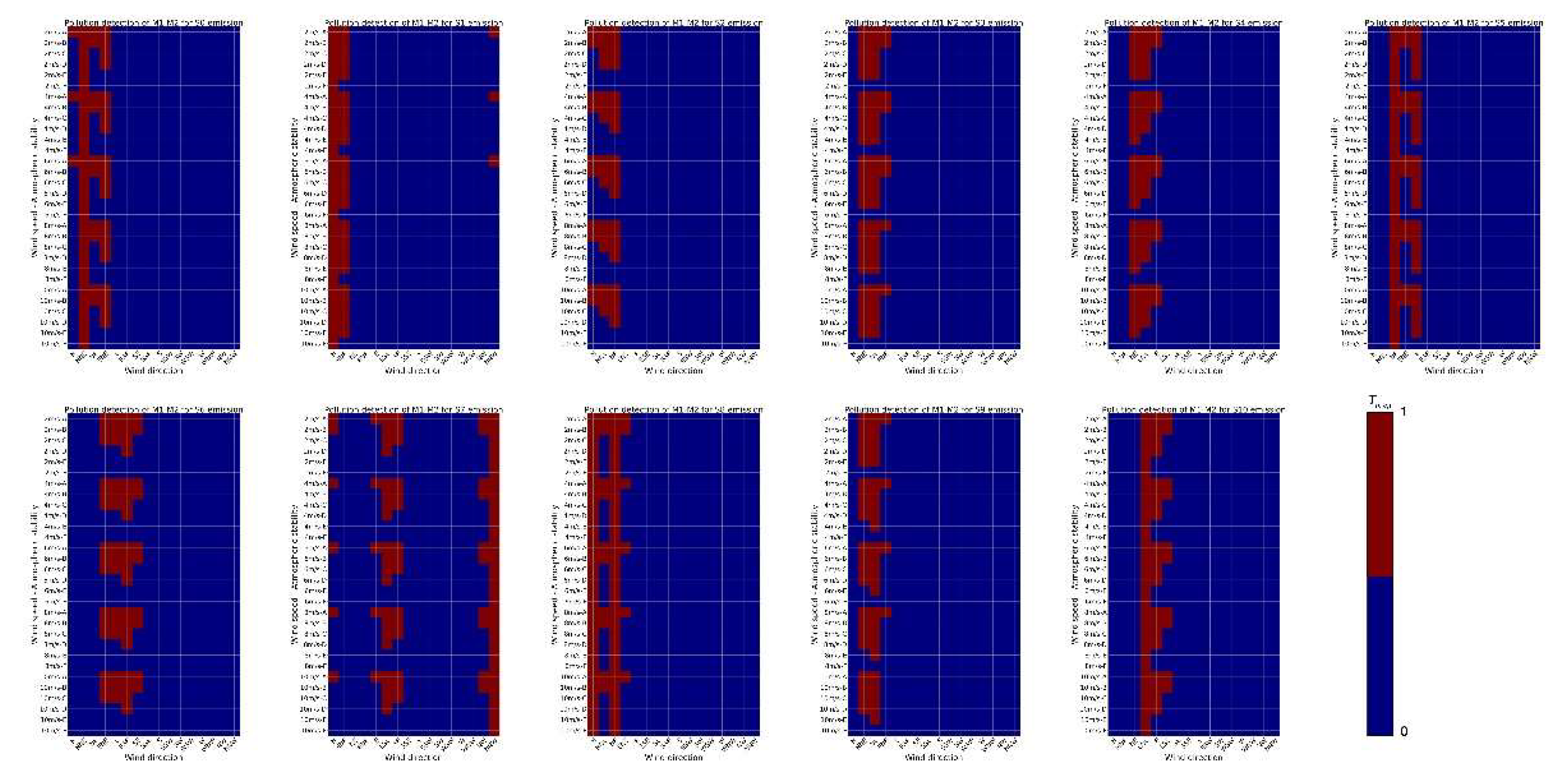
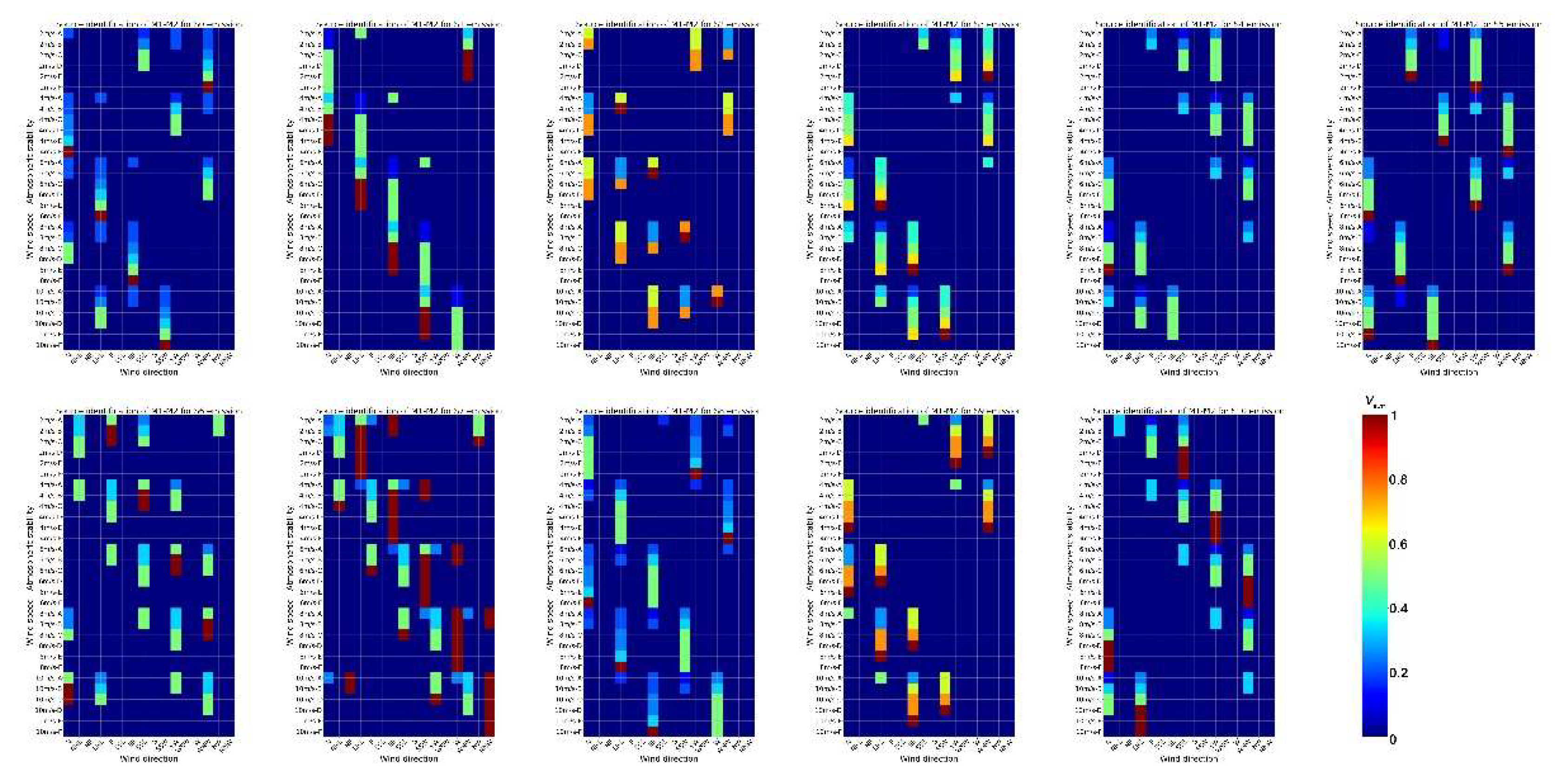
2.2.2. Source Area Analysis
2.2.3. The SE Indicator
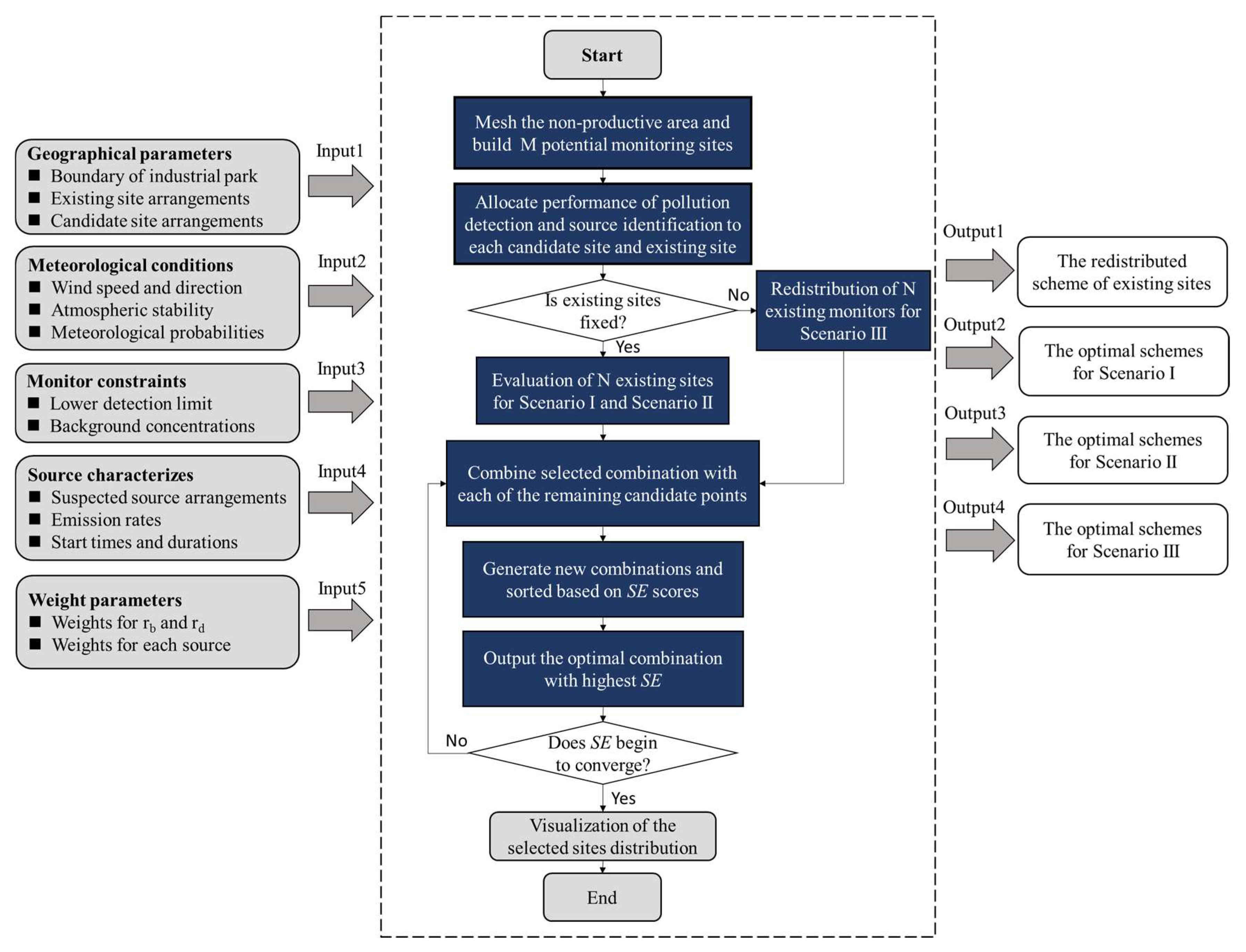
2.2.4. Optimal Design of the AQMN
- Scenario I: Existing sites are fixed and more sites with a known number are added based on the performance of existing sites;
- Scenario II: Existing sites are fixed and more sites with an unknown number are added based on the performance of existing sites;
- Scenario III: Existing sites are allowed to be relocated and more sites with an unknown number are added.
- Step 1. The industrial park is divided into M grids and the centroid of each grid cell is considered as a potential monitoring site;
- Step 2. Concentration results obtained by Gaussian puff dispersion and source area results back-calculated by source area analysis are allocated to corresponding grid cells for each meteorological condition when each source is considered as the real emission source;
- Step 3. The SE scores of integrated existing sites are evaluated. If existing AQMN with the N sites are fixed (Scenario I and Scenario II), continue the next step; while if existing N sites are allowed to be relocated (Scenario III), site combinations with the same number are generated from M candidate sites and evaluated. Then sorted based on their SE scores, and the combination with highest score is considered as the optimal redistribution scheme;
- Step 4. The selected existing or redistributed combination with N sites is further combined with each of the remaining candidate points. The new combinations with N + 1 are generated and evaluated, then sorted again based on their scores, and the N + 1 combination with highest score is considered as the optimal selection when one added monitor is available;
- Step 5. The optimal N + 1 selection is further combined with each of the remaining candidate points. The new combinations with N + 2 sites are generated and evaluated, then these combinations are sorted again based on their scores, and the N + 2 combination with highest score is considered as the optimal selection when two added monitors are available;
- Step 6. This process is continued until the number of selected sites is adequate (for Scenario I) or the surveillance efficiency begin to converge (for Scenario II and Scenario III).
3. Results
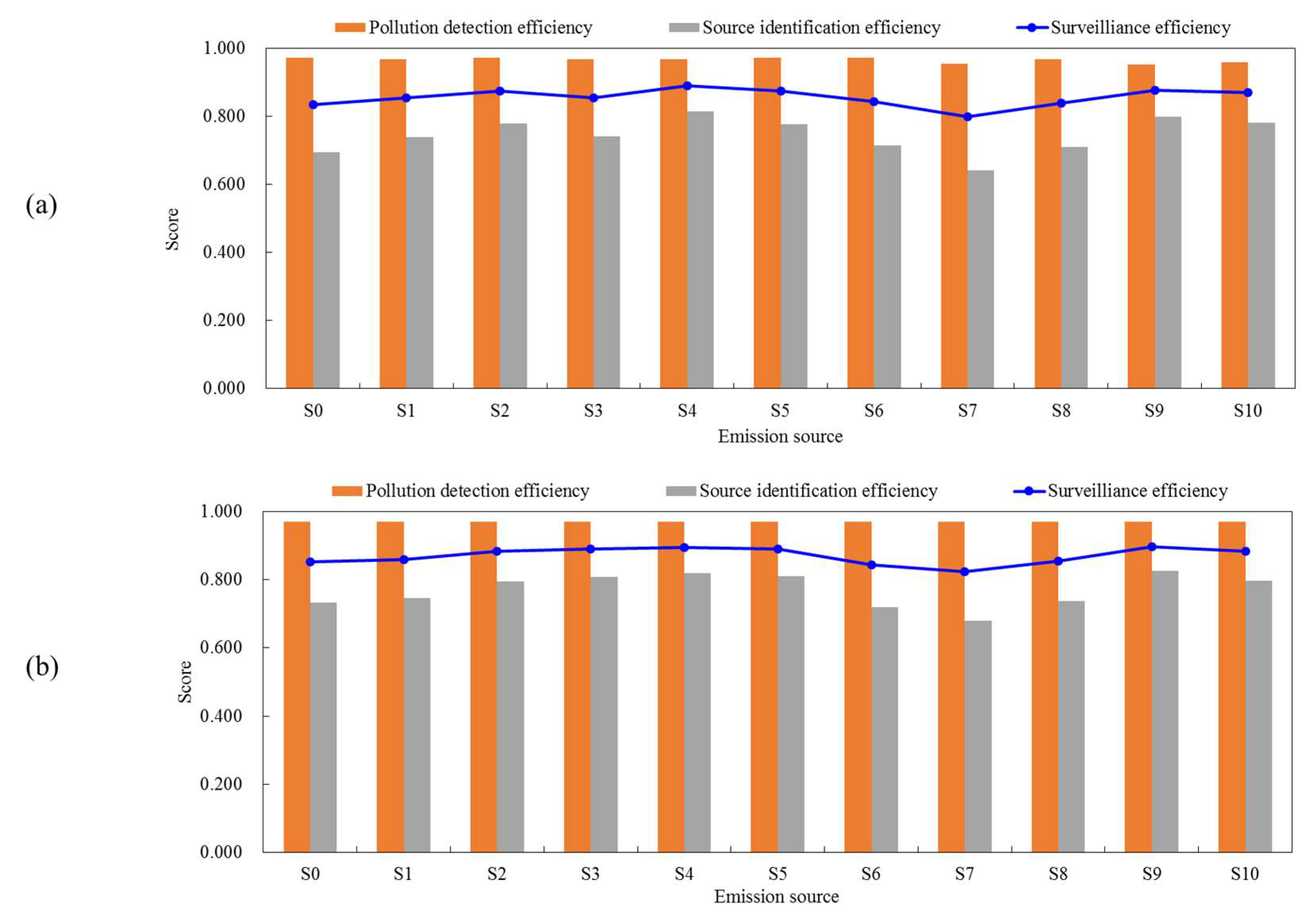
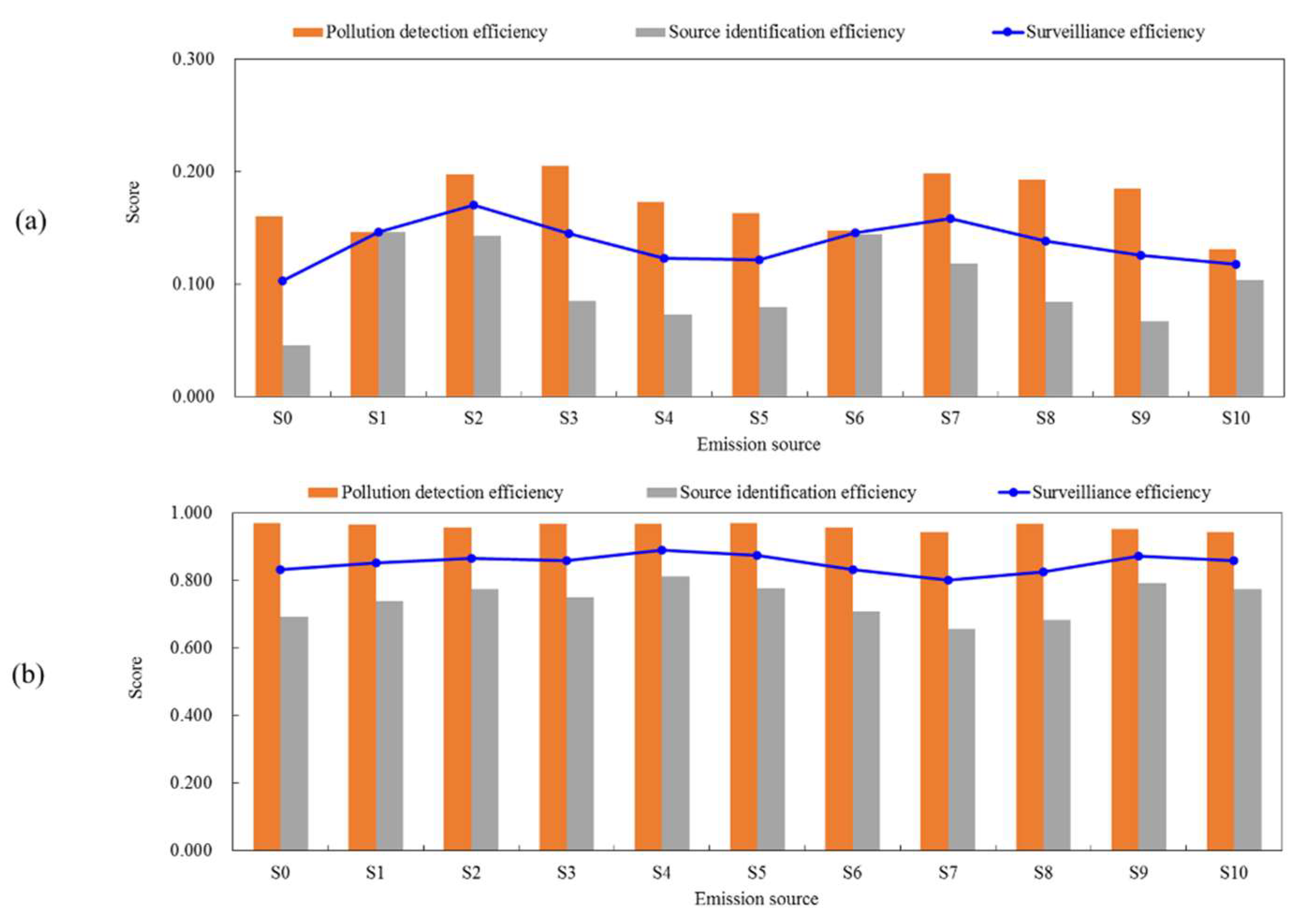
3.1. Evaluation of Existing Monitors
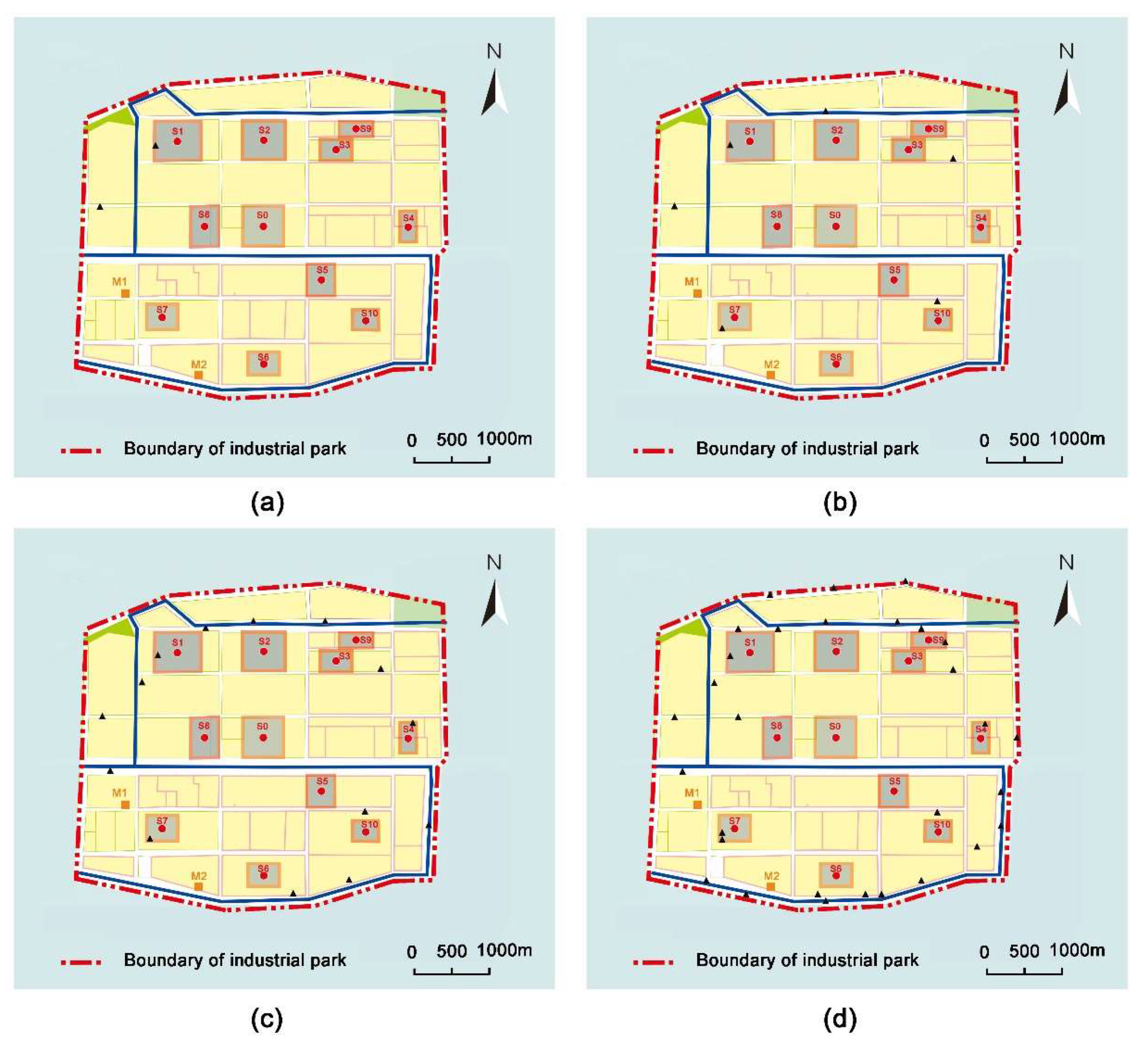
3.2. Optimal Schemes of AQMN for Different Scenarios
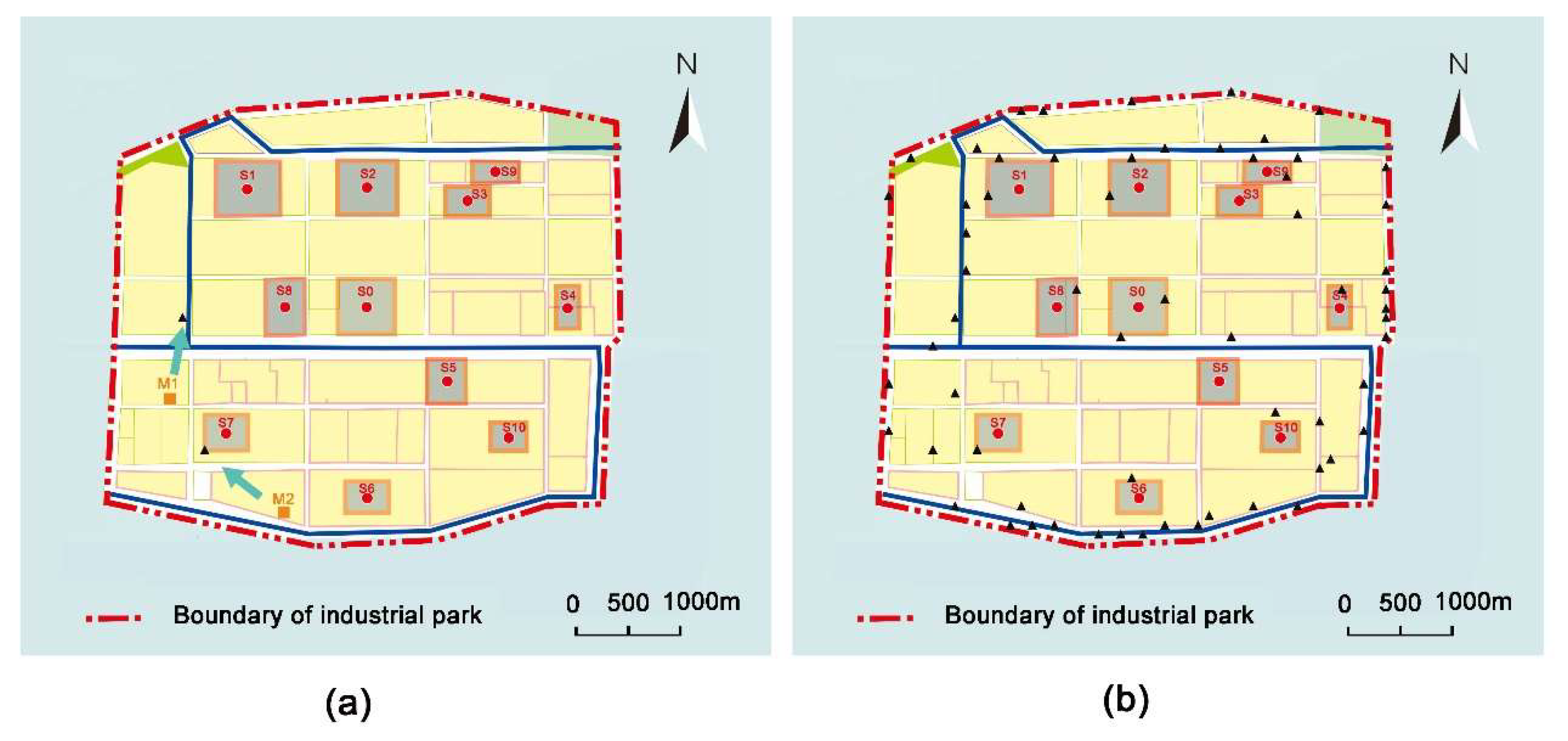
3.2.1. Scenario I
3.2.2. Scenario II
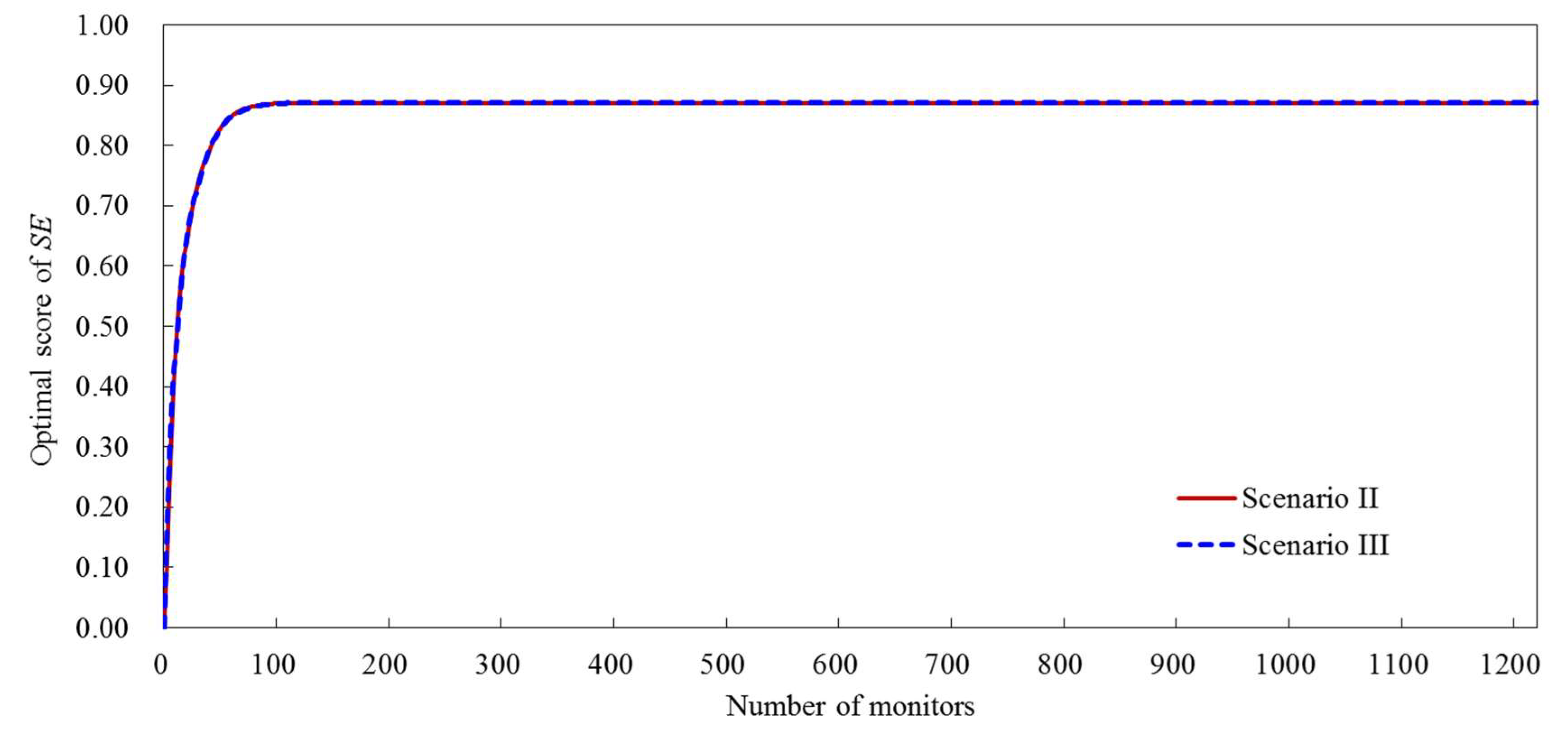
3.2.3. Scenario III
3.3. Discussion
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
References
- Lozano, A.; José, U.; Vanderlinden, E.; Raez, J.; Contreras, J.; Navarrete, B. Optimization of the design of air quality monitoring networks and its application to NO2 and O3 in Jaen, Spain. Microchem. J. 2010, 96, 406–411. [Google Scholar] [CrossRef]
- Zheng, J.; Feng, X.; Liu, P.; Zhong, L.; Lai, S. Site location optimization of regional air quality monitoring network in China: Methodology and case study. J. Environ. Monit. 2011, 13, 3185–3195. [Google Scholar] [CrossRef] [PubMed]
- Nejadkoorki, F.; Nicholson, K.; Hadad, K. The design of long-term air quality monitoring networks in urban areas using a spatiotemporal approach. Environ. Monit. Assess. 2011, 172, 215–223. [Google Scholar] [CrossRef] [PubMed]
- Pope, R.; Wu, J. A multi-objective assessment of an air quality monitoring network using environmental, economic, and social indicators and GIS-based models. J. Air Waste Manag. Assoc. 2014, 64, 721–737. [Google Scholar] [CrossRef] [PubMed]
- Al-Adwani, S.; Elkamel, A.; Duever, T.A.; Yetilmezsoy, K.; Abdul-Wahab, S.A. A surrogate-based optimization methodology for the optimal design of an air quality monitoring network. Can. J. Chem. Eng. 2015, 93, 1176–1187. [Google Scholar] [CrossRef]
- Araki, S.; Iwahashi, K.; NShimadera, H.; Yamamoto, K.; Kondo, A. Optimization of air monitoring networks using chemical transport model and search algorithm. Atmos. Environ. 2015, 122, 22–30. [Google Scholar] [CrossRef]
- Zhao, L.; Xie, Y.; Wang, J.; Xiang, X. A performance assessment and adjustment program for air quality monitoring networks in Shanghai. Atmos. Environ. 2015, 122, 382–392. [Google Scholar] [CrossRef]
- Benis, K.Z.; Fatehifar, E.; Shafiei, S.; Nahr, F.K.; Purfarhadi, Y. Design of a sensitive air quality monitoring network using an integrated optimization approach. Stoch. Environ. Res. Risk Assess. 2016, 30, 779–793. [Google Scholar] [CrossRef]
- Orłowski, A.; Marć, M.; Namieśnik, J.; Tobiszewski, M. Assessment and Optimization of Air Monitoring Network for Smart Cities with Multicriteria Decision Analysis. In Intelligent Information and Database Systems; Nguyen, N., Tojo, S., Nguyen, L., Trawiński, B., Eds.; Springer: Cham, Switzerland, 2011; Volume 10192. [Google Scholar]
- Mousavi, M.S.; Ashrafi, K.; Motlagh, M.S.P.; Niksokhan, M.H.; Vosoughifar, H.R. Design of a correlated validated CFD and genetic algorithm model for optimized sensors placement for indoor air quality monitoring. Heat Mass Transf. 2018, 54, 509–521. [Google Scholar] [CrossRef]
- Hao, Y.; Xie, S. Optimal redistribution of an urban air quality monitoring network using atmospheric dispersion model and genetic algorithm. Atmos. Environ. 2018, 177, 222–233. [Google Scholar] [CrossRef]
- Chen, C.H.; Liu, W.L.; Chen, C.H. Development of a multiple objective planning theory and system for sustainable air quality monitoring networks. Sci. Total Environ. 2006, 354, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Beaulant, A.L.; Perron, G.; Kleinpeter, J.; Weber, C.; Ranchin, T.; Wald, L. Adding virtual measuring stations to a network for urban air pollution mapping. Environ. Int. 2008, 34, 599–605. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Bocquet, M. Optimal redistribution of the background ozone monitoring stations over France. Atmos. Environ. 2011, 45, 772–783. [Google Scholar] [CrossRef]
- Henriquez, A.; Osses, A.; Gallardo, L.; Resquin, M.D. Analysis and optimal design of air quality monitoring networks using a variational approach. Tellus Ser. B Chem. Phys. Meteorol. 2015, 67. [Google Scholar] [CrossRef]
- Gupta, S.; Pebesma, E.; Mateu, J.; Degbelo, A. Air quality monitoring network design optimisation for robust land use regression models. Sustainability 2018, 10, 1442. [Google Scholar] [CrossRef]
- Sharan, M.; Singh, S.K.; Issartel, J.P. Least square data assimilation for identification of the point source emissions. Pure Appl. Geophys. 2012, 169, 483–497. [Google Scholar] [CrossRef]
- Turbelin, G.; Singh, S.K.; Issartel, J.P. Reconstructing source terms from atmospheric concentration measurements: Optimality analysis of an inversion technique. J. Adv. Model. Earth Syst. 2014, 6, 1244–1255. [Google Scholar] [CrossRef]
- Hosseini, B.; Stockie, J.M. Bayesian estimation of airborne fugitive emissions using a gaussian plume model. Atmos. Environ. 2016, 141, 122–138. [Google Scholar] [CrossRef]
- Efthimiou, G.C.; Kovalets, I.V.; Venetsanos, A.; Andronopoulos, S.; Argyropoulos, C.D.; Kakosimos, K. An optimized inverse modelling method for determining the location and strength of a point source releasing airborne material in urban environment. Atmos. Environ. 2017, 170, 118–129. [Google Scholar] [CrossRef]
- Huang, Z.; Qi, Y.; Ma, W.; Chen, L. Surveillance efficiency evaluation of air quality monitoring networks for air pollution episodes in industrial parks: Pollution detection and source identification. Atmos. Environ. 2019. Under Review. [Google Scholar]
- Flesch, T.K.; Wilson, J.D.; Harper, L.A. Deducing ground-to-air emissions from observed trace gas concentrations: A field trial with wind disturbance. J. Appl. Meteorol. 2005, 43, 487–502. [Google Scholar] [CrossRef]
- Chow, F.K.; Kosović, B.; Chan, S. Source inversion for contaminant plume dispersion in urban environments using building-resolving simulations. J. Appl. Meteorol. Climatol. 2008, 47, 1553–1572. [Google Scholar] [CrossRef]
- Long, K.J.; Haupt, S.E.; Young, G.S. Assessing sensitivity of source term estimation. Atmos. Environ. 2010, 44, 1558–1567. [Google Scholar] [CrossRef]
- Rodriguez, L.M.; Haupt, S.E.; Young, G.S. Impact of sensor characteristics on source characterization for dispersion modeling. Measurement 2011, 44, 802–814. [Google Scholar] [CrossRef]
- Kovalets, I.V.; Andronopoulos, S.; Venetsanos, A.G.; Bartzis, J.G. Identification of strength and location of stationary point source of atmospheric pollutant in urban conditions using computational fluid dynamics model. Math. Comput. Simul. 2011, 82, 244–257. [Google Scholar] [CrossRef]
- Ma, D.L.; Deng, J.Q.; Zhang, Z.X. Comparison and improvements of optimization methods for gas emission source identification. Atmos. Environ. 2013, 81, 188–198. [Google Scholar] [CrossRef]
- Ma, D.L.; Zhang, Z.X. Contaminant dispersion prediction and source estimation with integrated gaussian-machine learning network model for point source emission in atmosphere. J. Hazard. Mater. 2016, 311, 237–245. [Google Scholar] [CrossRef] [PubMed]
- Duyzer, J.; Dick, V.D.H.; Zandveld, P.; Van Ratingen, S. Representativeness of air quality monitoring networks. Atmos. Environ. 2015, 104, 88–101. [Google Scholar] [CrossRef]
- Kumar, P.; Feiz, A.A.; Ngae, P.; Singh, S.K.; Issartel, J.P. CFD simulation of short-range plume dispersion from a point release in an urban like environment. Atmos. Environ. 2015, 122, 645–656. [Google Scholar] [CrossRef]
- Kumar, P.; Singh, S.K.; Feiz, A.A.; Ngae, P. An urban scale inverse modelling for retrieving unknown elevated emissions with building-resolving simulations. Atmos. Environ. 2016, 140, 135–146. [Google Scholar] [CrossRef]
- Huang, Z.; Yuan, W.; Qi, Y.; Ma, W.; Yan, Z.; Chen, L. Source area identification with observation from limited monitor sites for air pollution episodes in industrial parks. Atmos. Environ. 2015, 122, 1–9. [Google Scholar] [CrossRef]
- MODEL T101 UV FLUORESCENCE23 H2S ANALYZER. 2016. Available online: http://www.teledyne-api.com/prod/Downloads/07266C%20-%20T101%20Manual.pdf#search=User%20MANUAL%20MODEL%20T101%20UV%20FLUORESCENCE (accessed on 11 May 2019).
- Arbeloa, F.J.S.; Caseiras, C.P.; Andrés, P.M.L. Air quality monitoring: Optimization of a network around a hypothetical potash plant in open countryside. Atmos. Environ. Part A Gen. Top. 1993, 27, 729–738. [Google Scholar] [CrossRef]
- Jiang, W. Air Pollution Meteorology; Nanjing University Press: Nanjing, China, 2003; pp. 124–125. [Google Scholar]
- MEEPRC (Ministry of Ecology and Environment of the People’s Republic of China). Technical Guidelines for Environmental Risk Assessment on Projects (HJ/T 169-2004). 2004. Available online: http://kjs.mee.gov.cn/hjbhbz/bzwb/other/pjjsdz/200412/W020110127329297430823.pdf (accessed on 11 May 2019).
- MEEPRC (Ministry of Ecology and Environment of the People’s Republic of China). Technical Methods for Making Local Emission Standards of Air Pollutants (GB/T3840-91). 1991. Available online: http://www.mee.gov.cn/image20010518/5332.pdf (accessed on 11 May 2019).
- Petty, G.W. A First Course in Atmospheric Thermodynamics; Sundog Pub.: Madison, WI, USA, 2008; p. 33. [Google Scholar]
- Venkatram, A.; Klewicki, J. Validation of Concentrations Estimated from Air Dispersion Modeling for Source-Receptor Distances of Less than 100 Meters; California Air Resources Board, Research Division: Sacramento, CA, USA, 2003. [Google Scholar]
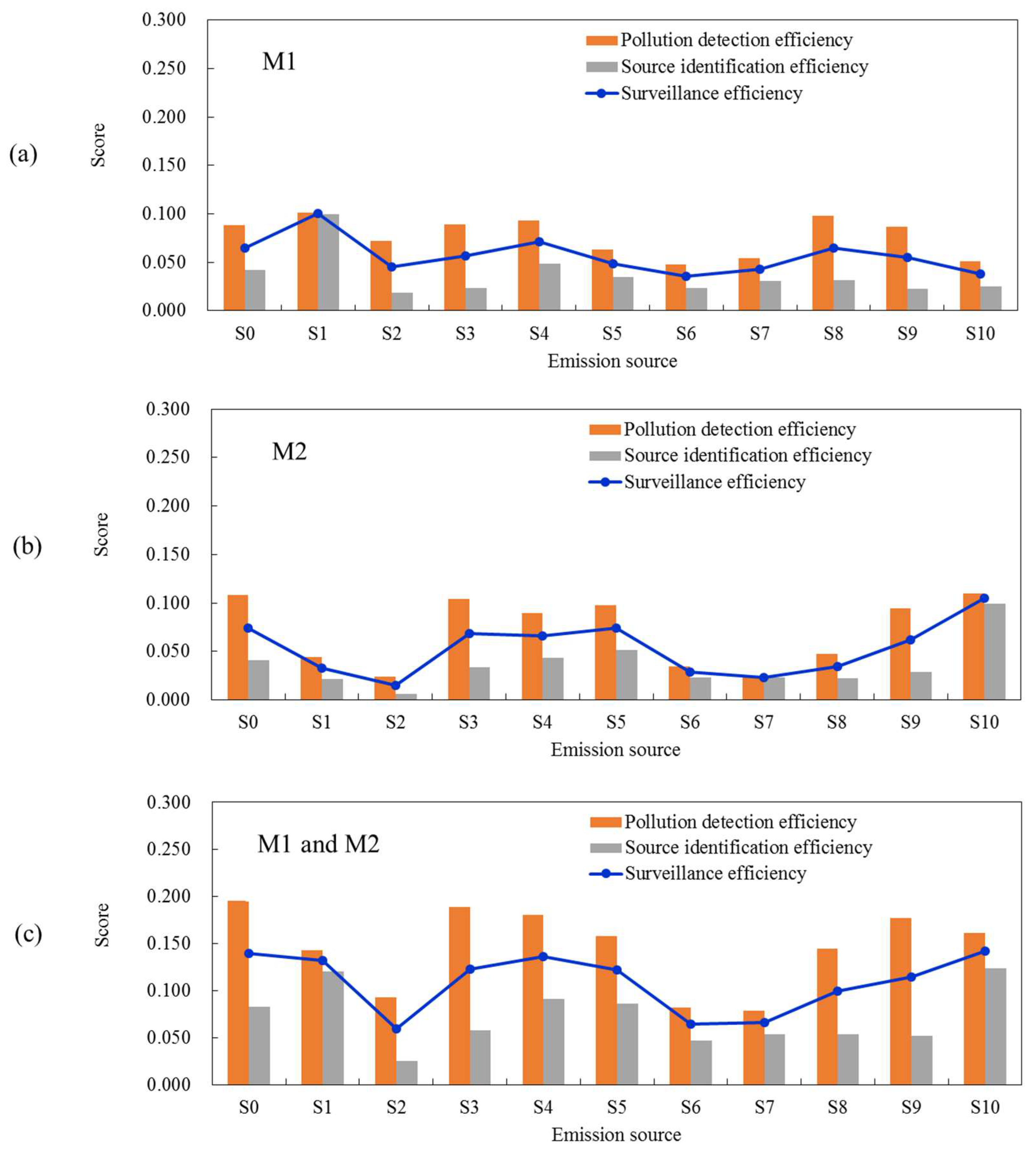
| Monitors | rd | rb | SE | SE/SEmax |
|---|---|---|---|---|
| M1 | 0.077 | 0.036 | 0.057 | 6.54% |
| M2 | 0.071 | 0.036 | 0.053 | 6.09% |
| M1 and M2 | 0.146 | 0.072 | 0.109 | 12.51% |
| Optimal AQMN with two monitors | 0.173 | 0.099 | 0.136 | 15.61% |
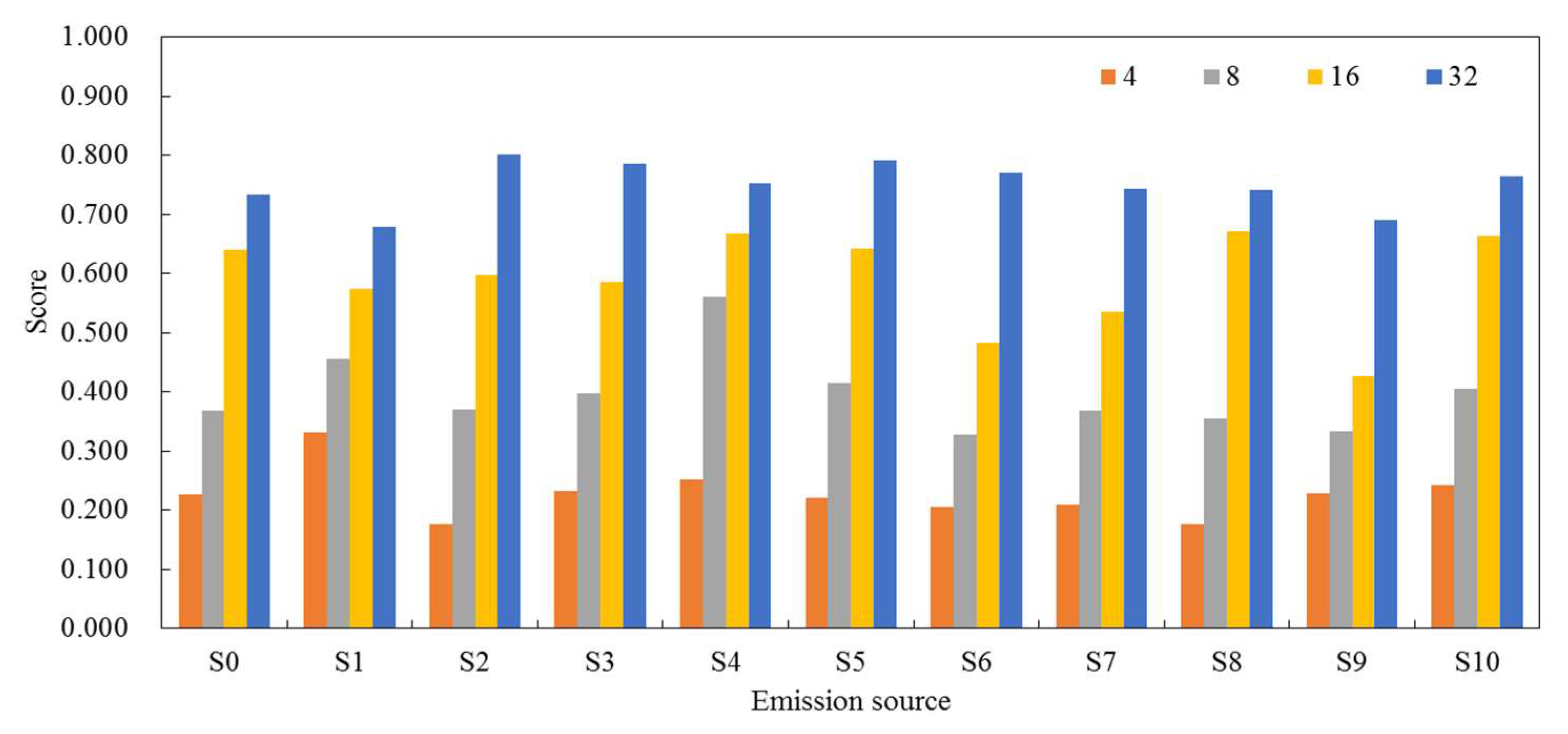
| Number of Monitors | rd | rb | SE | SE/SEmax |
|---|---|---|---|---|
| 4 | 0.296 | 0.158 | 0.227 | 26.06% |
| 8 | 0.492 | 0.299 | 0.396 | 45.47% |
| 16 | 0.688 | 0.491 | 0.590 | 67.74% |
| 32 | 0.863 | 0.638 | 0.750 | 86.11% |
| 64 | 0.965 | 0.744 | 0.854 | 98.05% |
| 110 | 0.971 | 0.771 | 0.871 | 100% |
| 1221 | 0.971 | 0.771 | 0.871 | 100% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Yu, Q.; Liu, Y.; Ma, W.; Chen, L. Optimal Design of Air Quality Monitoring Network for Pollution Detection and Source Identification in Industrial Parks. Atmosphere 2019, 10, 318. https://doi.org/10.3390/atmos10060318
Huang Z, Yu Q, Liu Y, Ma W, Chen L. Optimal Design of Air Quality Monitoring Network for Pollution Detection and Source Identification in Industrial Parks. Atmosphere. 2019; 10(6):318. https://doi.org/10.3390/atmos10060318
Chicago/Turabian StyleHuang, Zihan, Qi Yu, Yujie Liu, Weichun Ma, and Limin Chen. 2019. "Optimal Design of Air Quality Monitoring Network for Pollution Detection and Source Identification in Industrial Parks" Atmosphere 10, no. 6: 318. https://doi.org/10.3390/atmos10060318
APA StyleHuang, Z., Yu, Q., Liu, Y., Ma, W., & Chen, L. (2019). Optimal Design of Air Quality Monitoring Network for Pollution Detection and Source Identification in Industrial Parks. Atmosphere, 10(6), 318. https://doi.org/10.3390/atmos10060318




