Abstract
Rain microstructure parameters assessed by disdrometers are commonly used to classify rain into convective and stratiform. However, different types of disdrometer result in different values for these parameters. This in turn potentially deteriorates the quality of rain type classifications. Thies disdrometer measurements at two sites in Bavaria in southern Germany were combined with cloud observations to construct a set of clear convective and stratiform intervals. This reference dataset was used to study the performance of classification methods from the literature based on the rain microstructure. We also explored the possibility of improving the performance of these methods by tuning the decision boundary. We further identified highly discriminant rain microstructure parameters and used these parameters in five machine-learning classification models. Our results confirm the potential of achieving high classification performance by applying the concepts of machine learning compared to already available methods. Machine-learning classification methods provide a concrete and flexible procedure that is applicable regardless of the geographical location or the device. The suggested procedure for classifying rain types is recommended prior to studying rain microstructure variability or any attempts at improving radar estimations of rain intensity.
Keywords:
convective; stratiform; rain microstructure; Thies; disdrometer; classification; machine learning 1. Introduction
Different precipitation droplet growth mechanisms lead to the different properties of convective and stratiform rain [1,2,3]. This is due to the vertical development of convective clouds in contrast to the more horizontal development of stratiform clouds [4]. An accurate classification of rain types has the potential to improve radar estimations of the rain rate [5]. Equally importantly, it fosters the development of global climate and circulation models [1,6,7]. In addition, it is an important preliminary step to investigating variations of rain properties with general weather conditions [8].
A simple and widely used rain classification method was proposed by Bringi et al. [9], where a threshold of the rain intensity and its standard deviation over 10 successive minutes are used to separate convective and stratiform intervals. Llasat [10] also classified rain using a rain intensity threshold for different time intervals. Such methods are prone to misclassification [11]; however, they are applicable independent of the instrument type. Another classification approach is based on cloud observations [12,13,14]. Convective rain is expected when cumulus and cumulonimbus clouds are observed, while nimbus and nimbostratus clouds produce stratiform rain. Rulfová and Kyselý [15] used cloud types in combination with synoptic weather state reports for this purpose. Other methods rely on the availability of wind profiler [16] and radar [17,18,19] data, or satellite images [20,21,22]. These methods classify the rain type by identifying patterns in the vertical wind velocity, the spatial and temporal extension of the detected clouds, the reflectivity values and their variations, and the existence of a bright band and its thickness. Radars and satellites have the advantage of wide coverage, but usually assume specific drop size distribution (DSD) models derived by disdrometers.
Just two decades after Yuter and Houze [23] questioned the accuracy of rain microstructure techniques for rain type classification, Thurai et al. [24] concluded that “rain DSD classification is sound.” Within this period, many classification methods were proposed relying on rain DSDs as provided by different types of disdrometers. Each method provides a classification boundary based on a pair of parameters, such as the rain rate with the slope parameter (R–Λ), the rain rate with the intercept parameter (R–N0) [25], the slope with the shape parameter (Λ–μ) [26], the intercept with the slope parameter (N0–Λ) [27], or the median drop diameter with the log normalized concentration (N0–logNw) [28].
Despite the availability of all these methods, rain classification remains challenging, especially because these classes are not mutually exclusive [6]. The successful use of one classification method for one case study does not imply repetition in other cases where different climate conditions exist [26,29]. It might also be incorrect to apply a method that has been specifically developed for one type of disdrometer to the measurements of another type of disdrometer [11]. For example, You et al. [30] adjusted the method proposed by Bringi et al. [28] for a specific region (Korea) and a specific disdrometer device (PARSIVEL). To improve the classification accuracy, Bukovčić et al. [11] proposed using a Bayesian approach with four parameters. Such an approach requires the availability of vertical wind speed measurements or cloud type observations to construct a prior classification.
The German Meteorological Service DWD (Deutscher Wetterdienst) operates a large network of Thies disdrometers across Germany for radar calibration and precipitation classification [31]. To adequately investigate rain microstructure variation using Thies disdrometers, an accurate method for rain type classification is needed. However, no method exists that is specifically designed to classify the rain type based on Thies disdrometers because most available methods were developed using impact disdrometers or two-dimensional video disdrometers (2DVD). Thies disdrometers are low-cost easy-maintenance devices. They are well suited to construct long-term climatological radar algorithms with performances comparable to more accurate devices such as 2DVD [32]. Nevertheless, even laser disdrometers that use the same detection principle have different designs, minimum sensitivity thresholds, drop counting velocity and size ranges, and internal correction algorithms. Consequently, bulk precipitation parameters, such as rain intensity, radar reflectivity, and kinetic energy, are significantly different when measured by a Thies disdrometer compared to PARSIVEL [33]. These parameters are also used in the different rain type classification methods, and thus the following questions must be asked.
- How do classification methods designed for other disdrometer types perform when applied to Thies disdrometer measurements?
- Can we achieve better classification performance by tuning the decision boundary for each method?
- Which rain microstructure parameters are superior as rain type classifiers?
- Do machine-learning techniques support a better classification?
We aim to examine the performances of the available methods and their parameters. These parameters will then be used to construct a classification method that should be suitable for Thies disdrometers. The developed method will be needed in future studies to investigate the spatial and temporal rain microstructure variations across Bavaria and Germany.
2. Materials and Methods
2.1. Data Sources and Tools
We used cloud observations and measurements of rain DSDs by Thies disdrometers. Cloud observations were obtained from the DWD’s Climate Data Center [34]. Disdrometer data were provided upon request directly from the DWD for two locations: Fürstenzell at 48.545146° N 13.353054° E 476.4 m ASL (hereafter FUR) and Regensburg at 49.042357° N 12.102053° E 365.4 m ASL (hereafter REG). The availability of both cloud observations and DSD data limited the spatial and temporal extent of the study. Simultaneous measurements and observation records were available between July 2013 and August 2014 at FUR and between July 2013 and January 2014 at REG.
Data from FUR were used to test the performance of the existing classification methods and to re-adjust the decision boundaries of these methods and improve their performance. These data also served as a training set for constructing new predictive models. This included identifying the most important predictors of rain type, constructing and training the models, and then testing their performance by means of cross validation with 200 repetitions of stratified sampling.
The REG data were used for testing the newly suggested models. This included the adjusted models from the literature and the new predictive models, which were trained using the first dataset.
For data handling, calculations, feature selection, model training, performance estimation, and visual and statistical results, we used R [35], RStudio [36], and the reader [37], dplyr [38], reshape2 [39], lubridate [40], stringr [41], ggplot2 [42], cowplot [43], caret [44], e1071 [45], doSNOW [46], zoo [47], MASS [48], corrplot [49], and pROC [50] packages.
2.2. Cloud Observations
According to the World Meteorological Organization (WMO), clouds are classified into ten genera (hereafter types). These types can be further classified into species and varieties [51]. Cloud types have been used to classify precipitation type [12,13,14]. Hourly observations of the cloud types are available for both locations for up to four layers. Possible cloud types and the corresponding expected rain type are provided in Table 1. Convective rain is believed to correspond to convective cloud types (cumulus and cumulonimbus), while stratiform rain corresponds to stratiform cloud types (stratus and nimbostratus) [12]. It is possible for several cloud types to be observed at the same time. Such cases might produce mixed rain properties; therefore, these cases were discarded. All cloud data have been recorded by trained staff, which still leaves (although reduced) chances for human errors. However, DWD marks this data with the third quality level. This means that the data went through a completeness check, climatological consistency check, time consistency check, internal consistency check and spatial consistency check [52].

Table 1.
Cloud types and their associated expected rain type.
2.3. Thies Disdrometer and Extraction of Rain DSD
Thies disdrometers provide the current weather state in addition to a number of precipitation parameters such as the rain intensity and reflectivity with a high temporal resolution (1 min in our case). However, the most relevant output in our case is the raw representation of the particle size and velocity distribution. This is provided via the number of particles that fall within the limits of 22 particle size and 20 velocity ranges. The measurement principal is based on the reduction of the power of a light beam that is transmitted from one end of the disdrometer to the other. The magnitude and time of this reduction determine the size and velocity of the passing particle [53].
Specific filtering steps are needed prior to the calculation of the rain parameters. The process proposed by Friedrich et al. [54], and additional steps performed by Ghada et al. [8], were used to remove intervals with very high wind speed, snow, hail, frozen rain, graupel, intervals with very low rain intensity (R < 0.1 mm/h), margin fallers, unrealistically large drops, and the splashing effect. Consequently, the filtered rain data set contains 22,592 min at FUR and 4585 min at REG.
Table 2 provides a list of parameters that were calculated from the Thies measurements of the rain DSD and rain velocity distribution. This list is the result of a literature survey of the potential predictors of the rain type. Each reference contains either an equation to calculate the corresponding parameter or the motivation for the use of the corresponding parameter. All these parameters can be obtained from the rain DSD provided by a Thies disdrometer. Some parameters are acquired with different equations according to different references (e.g., Lambda_TS, Lambda_Ca06, and Lambda_Ca08). These are marked with the appropriate reference.

Table 2.
Drop size distribution parameters as potential rain type classifiers.
2.4. Prior Rain Type Classification
Clearly separated convective and stratiform samples of rain are needed to evaluate the performance of the classification methods. We relied in the first step on the simple and widely used method of Bringi et al. [9], where rain is considered to be convective when the standard deviation of rain intensity over five consecutive two-min intervals exceeds 1.5 mm/h or when the rain intensity exceeds 10 mm/h. There is a risk of misclassification for weak convective and strong stratiform events. Therefore, in a second step, we restricted the convective intervals to instances that corresponded to convective cloud types and the stratiform events to those corresponding to stratiform clouds. This step removed all intervals where a combination of convective and stratiform cloud types was observed, and intervals where none of the four relevant cloud types were observed (nimbostratus, stratus, cumulus, and cumulonimbus). Events were defined by a minimum inter-event time of 15 min where the rain intensity did not exceed 0.1 mm/h.
Figure 1 and Figure 2 display examples from the reference dataset. All events in Figure 1 occurred while a convective cloud type was observed. We are only interested in instances that show high rain intensities or sudden variations in the intensity. Therefore, intervals where the convective signal was weak were filtered out (blue points). In the case of stratiform clouds (Figure 2), when an event contained even one interval that was classified as convective rain by the classification method of Bringi et al. [9], the entire event was removed because it might be an indication of a convective cell embedded within a stratiform cloud. These events are marked with an asterisk in the top left corner of each panel. The filtered dataset with prior classification of rain type consisted of 7260 min (674 min) of stratiform (convective) rain at FUR and 406 min (83 min) of stratiform (convective) rain at REG.
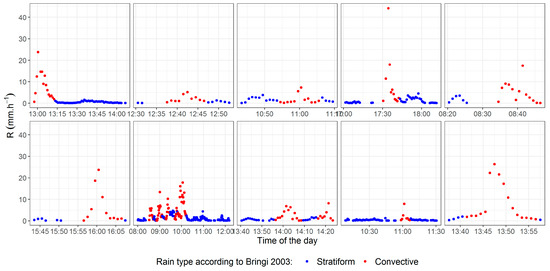
Figure 1.
Rain intensity variations for selected events with convective clouds at Fürstenzell. Rain intervals classified as stratiform by Bringi et al. [9] (blue points) were removed from the reference dataset.
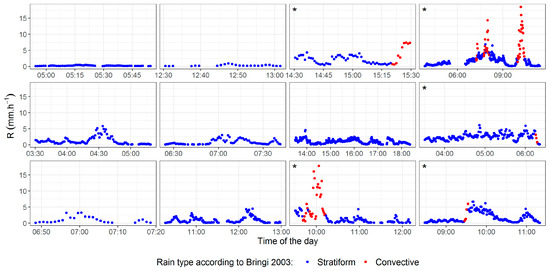
Figure 2.
Rain intensity variation for selected events with stratiform clouds at Fürstenzell. Rain events that are marked with an asterisk in the upper left corner of the panel were removed from the reference dataset due to sub-periods with convective rain type.
2.5. Rain Microstructure-Based Classification Methods
A list of rain type classification methods that rely on disdrometer measurements is provided in Table 3. This table refers to the parameters listed in Table 2 and the decision boundary that separates convective and stratiform rain intervals proposed by the corresponding references. The convective region explained in the decision boundary column assumes that the vertical axis represents the first parameter. Note that the You_16 method uses the same parameters as Br_09 but its decision boundary is different. The Bu_15 method uses four parameters in a Bayesian approach, and no decision boundary is applicable in this case.

Table 3.
Rain type classification methods from the literature.
2.6. Indicators of the Classification Performance
From a statistical point of view, this presented an imbalanced classification problem. The probability of observing a stratiform rain interval is much higher than the probability of observing a convective rain interval; therefore, any model that predicts all cases as stratiform will achieve a high accuracy. This rules out accuracy as a sole performance measure in this case. Other potential performance indicators are Kappa and the F-measure.
Kappa [60] is defined as:
where O is the observed accuracy and E is the expected accuracy.
Kappa can take values between −1 and 1. A perfect performance would be indicated by a Kappa value of 1. A Kappa value of zero means that no agreement was achieved between the observed and predicted classes and that the classification method is not performing better than a random classifier. A negative value indicates prediction performance that is worse than a random classifier [60].
The F-measure is the harmonic average between the recall and the precision (Equation (2)). It guarantees a higher score for classification methods that increase both recall and precision values compared to those that increase just one of the two [61].
where the recall and precision are given by Equations (3) and (4):
where TP, FN, and FP are explained in the confusion matrix in Table 4. In our case, the recall (also known as the sensitivity) is the number of the correctly detected convective rain intervals divided by the total number of actual convective rain intervals (according to the prior classification). Precision is the number of the correctly detected convective rain intervals divided by the total number of predicted convective rain intervals.

Table 4.
The confusion matrix.
2.7. Advanced Predictive Models
Machine learning (ML) aims to solve real-world problems while reducing human errors [62]. ML methods are used in different domains including weather forecasting and interpreting radar and satellite output. Classification is a huge domain of predictive modeling. However, we were unable to find studies where such models have already been used in combination with the rain microstructure for rain type classifications except for Bukovčić et al. [11]. The number of possible ML classification methods is huge. To maintain the appropriate length for this manuscript, we only tested five well-known types of ML classification methods. Note that the different rain parameters act as the features for the models. Therefore, these two terms are used interchangeably.
2.7.1. Linear Discriminate Analysis (LDA)
LDA creates linear combinations of the available features that enlarge the mean differences between the targeted classes while decreasing the mean differences within each class [63]. The rain type classification methods proposed in the literature define the decision boundary based on visual inspections of the relationships between two parameters for a limited number of events. LDA provides an objective and mathematically valid approach to identify the most suitable decision boundary that minimizes the error rate. This method was applied to optimize the decision boundary for each of the methods in the literature. It was also applied using combinations of the most predictive features after the process of feature selection.
2.7.2. K Nearest Neighbor (KNN)
KNN is one of the simplest models for classification. It assigns a class for each value in the predictor space by examining the classes of the nearest k available observations in the training set. The distance used in our case is the Euclidean distance, and the value of k is tuned automatically by the model to maximize the accuracy based on cross validation within the training set [60].
2.7.3. Naïve Bayes (NB)
This method was applied for rain type classification by Bukovčić et al. [11]. It is based on the strong assumption that the predictors are independent of each other. Despite the fact that this assumption is not realistic, this method reduces the complexity of the model [60], and often yields a high performance compared to advanced and more complex predictive methods [64].
2.7.4. Conditional Trees (Ctree)
This method tries to split the data into sub-datasets while maximizing homogeneity using a series of rules. The target is to minimize the classification error rate. This is done by partitioning the dataset based on the value of one predictor each time and trying to maximize the probability of having one class within one or more of the subsequent partitions [60]. This method is computationally fast and easy to understand and interpret. It handles irrelevant features automatically and eliminates the need for feature selection [65].
2.7.5. Random Forests (RF)
This method was introduced by Breiman [66]. It uses the concept of bagged trees (conditional trees with bootstrap aggregation). The random forest algorithm samples predictors during the training process so that the subsequent trees are not correlated. For each case, each tree casts a vote for the final class and the class with the highest number of votes is then assigned to this case [65].
2.8. Selecting Rain DSD Parameters
Thies disdrometers provide a rain DSD, which is used to calculate many features (see Table 2). These features serve as input for the predictive models. However, involving a large number of features in a predictive model has some disadvantages, including:
- High computational costs,
- The risk of overfitting the training set,
- Non-informative features that negatively affect some models [60], and
- Constructed models that are difficult to interpret.
Therefore, it is a common practice to reduce the number of features that are used in a model while keeping the performance of the model within accepted levels. Some automated feature selection methods such as forward or backward stepwise selection can be used [60]. However, we decided to follow a heuristic approach that consists of two steps:
- 1-
- The features are clustered into X groups (hierarchal clustering). Each group contains a few correlated features.
- 2-
- One feature is chosen out of each cluster. The chosen feature is the one with the highest AUC value, where AUC is the area under the receiver operating characteristic curve [67]. The AUC value is a measure of the capability of each feature to separate the classes.
The value of X in the first step needs to be high enough to insure that sufficient features are included in the classification models to capture the distinct properties of the two rain types. At the same time, choosing a very high value of X would result in high computational costs without important improvements in the classification performance. The value of X was set to seven, which resulted in seven clusters of features and ultimately seven parameters to be used in constructing the predictive models. Five different types of classification models were constructed: LDA, KNN, NB, Ctree, and RF. For each type of predictive model, seven models were constructed. The first (second, third, …, seventh) model used the most important feature (two features, three features, …, seven features). The resulting 35 models were evaluated and compared via cross validation on the FUR data with 200 repetitions of stratified sampling. A second evaluation was performed by training the models on the FUR data and testing them on the REG data.
3. Results
3.1. Performance of the Classification Methods from the Literature
The Ca_06 and Ca_08 models had the highest accuracy compared to the other methods. Br_09 recorded lower accuracy than its modified version You_16, while TS_b had the smallest accuracy of slightly more than 50% (see the colored columns in Figure 3). As pointed out in the methods, focusing on the accuracy as the sole performance indicator might lead to incorrect conclusions; Br_09 and You_16 had much better F-measure and Kappa values than Ca_06 and Ca_08 despite having lower accuracy. You_16 performed best considering all three performance indicators. It is important here to note that Ca_08 had a value of zero for the F-measure and Kappa because all intervals were classified as stratiform according to this method. The negative values of Kappa for TS_a and TS_b indicate that the detection of convective rain by these methods was worse than a random classifier.
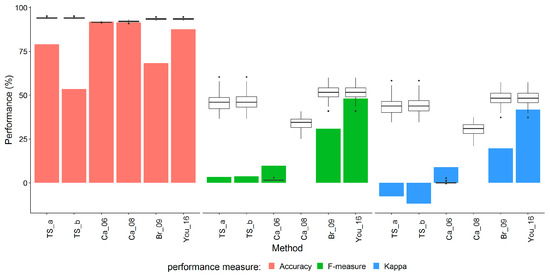
Figure 3.
Performance of the classification methods from the literature (columns) using different performance indicators. The box plots represent the performance of a linear discriminant model (LDA) using the same parameters suggested by each model and a cross validation with 200 repetitions of stratified sampling.
After adjusting the decision boundary of the methods in the literature using LDA, a better classification performance was achieved for all methods except Ca_06 (see the boxplots in Figure 3). In this case, LDA did not find a suitable decision boundary and ended up classifying all rain intervals as stratiform rain. This explains the corresponding zero values for the F-measure and Kappa. In all other cases, the new accuracy was above 90%, while the F-measure and Kappa increased clearly compared to the original methods. The modified decision boundary of Br_09 achieved again the highest values for both the F-measure and Kappa. Because You_16 differs from Br_09 only by the decision boundary, the same boxplot for the Br_09 performance indicators applies.
3.2. Feature Selection
A correlation matrix of the rain microstructure parameters (Figure 4) reveals that most features correlated. Only R and D0_Nt have low correlations with the other parameters. The parameters clustered into seven groups of highly correlated parameters (the black frames in Figure 4). For example, logLambda, mu_TS, and logN0 were highly correlated with each other.
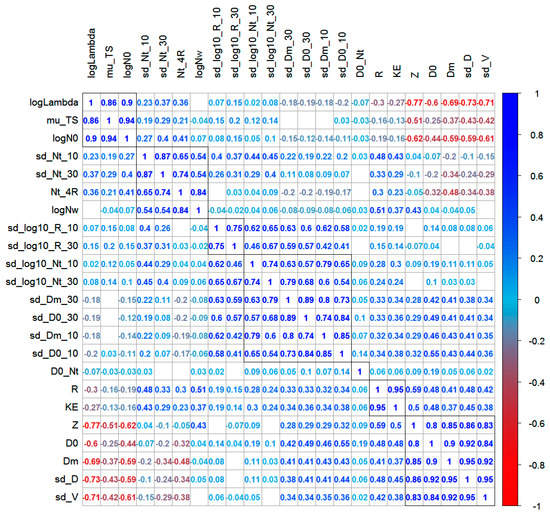
Figure 4.
Correlation matrix of the rain microstructure parameters. Blank cells represent insignificant correlation with confidence level of 0.95.
The capability of each feature to distinguish between the two classes is represented by the AUC (Figure 5). For each of the seven groups, which were determined from the correlation matrix, the feature with the highest AUC value was chosen and the remaining features were discarded. For example, out of logLambda, mu_TS, and logN0, only logLambda was chosen in the final list of features.
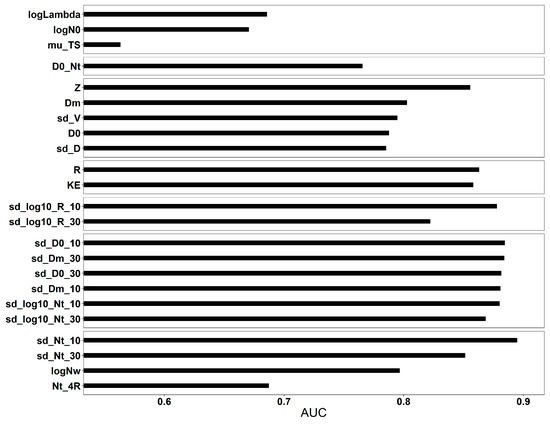
Figure 5.
Relative importance of the rain microstructure parameters expressed by the area under the receiver operating characteristic curve (AUC) [67].
The final selection of features, ordered by the AUC values, comprised of sd_Nt_10, sd_D0_10, sd_log10_R_10, R, Z, D0_Nt, and logLambda. The correlation matrix and AUC values of the selected features are provided in Figure 6.
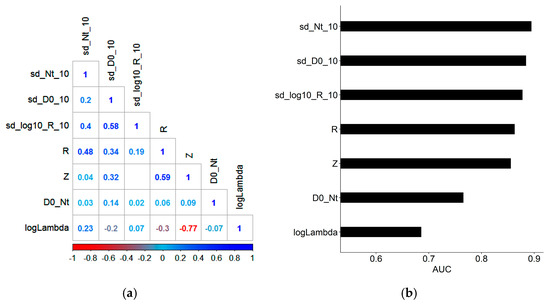
Figure 6.
(a) Correlation matrix where blank cells represent insignificant correlation with confidence level of 0.95. (b) AUC values of the final list of selected features.
3.3. Performance of the ML Methods
After applying the five different machine-learning classification methods on the FUR dataset, their performances were measured by means of cross validation. High accuracy values were achieved in all cases, while the F-measure and Kappa were near 0.8 in the best cases (Figure 7). Four appeared to be the optimum number of features to be used because the improvement beyond four parameters was marginal. The RF models performed the best in most cases, followed by KNN, NB, and Ctree. NB performed worse when the number of features exceeded four parameters. LDA performed the worst. The performance of the NB method when using the four parameters (Z, Nt_4R, sd_log10(Nt)_30, and sd_log10(R)_30) suggested in the Bu_15 method [11] (the red point in Figure 7) was lower than its performance when using the four optimal parameters identified by the correlation matrix and AUC (see Section 3.2).
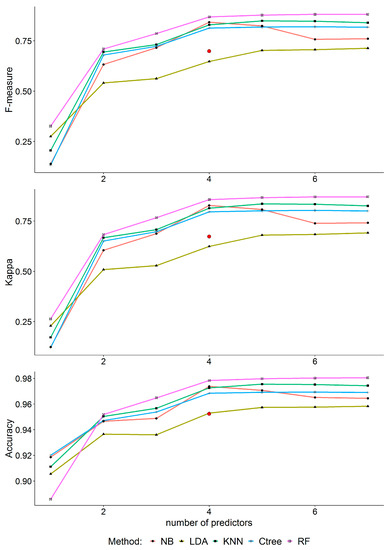
Figure 7.
Performance of the machine-learning classification methods with different numbers of features. Each point is produced by taking the mean value of 200 repetitions of stratified cross validation performed on the Fürstenzell dataset. The red point represents the performance of the Bu_15 method with four parameters.
When using the data from FUR to train the models and then testing them on the REG dataset, the patterns of the performance indicators (Figure 8) were similar to the cross validation on the FUR dataset (Figure 7); RF was still the best model, and four was again the optimum number of features. Using RF with four parameters resulted in an accuracy of 98% and an F-measure and Kappa of 80%. The NB performance dropped noticeably when using six parameters. It also dropped when using the four parameters suggested in the Bu_15 method [11] (the red point in Figure 8). Remarkably, Ctree achieved high performance indicators using only two parameters and its performance dropped when using more than two parameters.
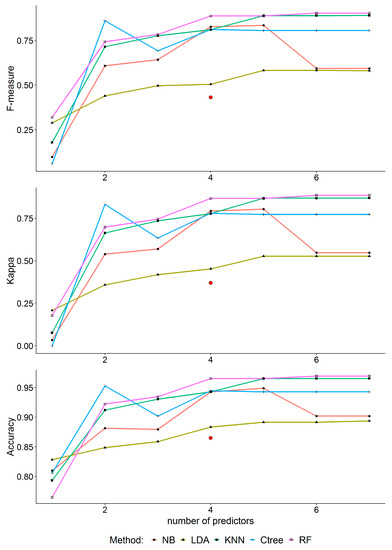
Figure 8.
Performance of the machine-learning classification methods with different numbers of features. Each model was trained on the Fürstenzell dataset and tested on the Regensburg dataset. The red point represents the performance of the Bu_15 method with four parameters.
4. Discussion
The low percentage of convective rain intervals in the reference dataset (8.5%) explains the high accuracy of most methods in the literature simply because they classify most intervals as stratiform rain. The F-measure and Kappa revealed clear differences in the performances of the different methods. The You_16, Ca_06, and Ca_08 methods have high accuracies. However, the Kappa and F-measure values for You_16 are much better than those of the other methods.
The performance of You_16 compared to Br_09 provides clear evidence that adjusting the decision boundary can considerably improve the performance. This was confirmed again by the improvement achieved when optimizing the decision boundary by using LDA in three other cases.
The performance of the modified Br_09 and You_16 methods indicates that using the combination of D0 and log10(Nw) to classify rain type is superior to any other combination suggested in the literature. This is in agreement with the findings of Thurai et al. [24] and explains the good performance reported in various papers despite the different geographical locations and use of different devices. However, after adjusting the decision boundary, TS_a and TS_b revealed very similar values for the three performance indicators, i.e., accuracy, F-measure, and Kappa. This strongly suggests that the parameters used in TS_a, TS_b, and Br_09 carry a sensitive signal that can successfully be used in classifying the rain type.
As pointed out by Bukovčić et al. [11], two parameters are not sufficient to clearly separate convective and stratiform rain. Many parameters have been suggested in the literature as potential classifiers for the rain type. Our results show that many of these parameters are intercorrelated; however, it is possible to limit the number of parameters to four while achieving a high performance. The choice of these parameters is affected by the training dataset, the disdrometer type, and the prior classification method. For example, Niu et al. [2] proposed using the spread of the measured velocities across the diameter sizes. Our results suggest that this spread is correlated with Z, which is a better classifier for the rain type. In addition, choosing the same parameters as Bukovčić et al. [11] resulted in lower performance indicators than using the same method (NB) with the four best parameters, as explained in Section 3.2. sd_R is also a very important parameter that can be used as a classifier. However, it was not included in the feature selection process because it was already used in the process of constructing the prior classification. In other cases (e.g., where the prior classification is done by other methods such as using a wind profiler, radar, or satellite data), sd_R should also be tested as a strong candidate among the classification parameters. We expect that other combinations of parameters will be able to achieve even higher performance depending on the location, device type, or the method of building the prior classification. However, we expect the improvement to be marginal. The features presenting the fluctuation of the rain microstructure parameters generally have the highest classification power, while fitted gamma distribution parameters have the lowest despite being used widely in the literature [25,26,27,28,30].
The rain type classification was considerably improved by the ML classification models. Using the seven most important features in the models revealed that RF performed the best in almost all cases, closely followed by KNN and Ctree, while LDA had the lowest performance. This means that achieving a better classification might also be possible by choosing different and more advanced predictive models with different combinations of rain microstructure parameters.
For most of the tested models, the performance stabilizes when using four parameters. The exceptions are LDA and NB. For LDA, five appears to be the critical number of parameters, which is obvious in both the cross validation and the testing on the REG dataset. For NB, the performance peaks and then drops again when further increasing the number of predictors. The likely reason for this is that, in NB, it is assumed that the predictors are independent of each other even though the fifth parameter Z has a high negative correlation with the fourth parameter R. In addition, note that this drop in the performance might be influenced by the small size of the REG dataset. This small size might also be the reason for the peak performance of Ctree with only two parameters when testing on the REG dataset.
The ML models, which are trained on the FUR dataset and tested on the REG dataset, performed well and with similar performance values when applying the cross validation. This indicates that it is appropriate to train ML models for classifying the rain type in one location and use these models in adjacent locations that have similar climate conditions. The spatial extent of the applicability of these models however requires further investigation.
The initial choice of methods to construct the prior classification is definitely prone to errors and inaccuracies. However, this choice was driven by the available data. Furthermore, observations of cloud types are generally scarce, and this limited the size of our dataset. However, based on enhanced prior classifications of cloud types, better classification models will be achievable. An improved assessment of the performance of such models will need to include all rain intervals for a long time period without discarding events with unclear or mixed cloud types. In the next step, we also suggest classifying rain events into clearly defined convective, stratiform, and mixed events based on the pattern of successive interval rain type classes produced by this method.
5. Conclusions
Thies measurements of the rain microstructure were combined with cloud observations at two sites in Bavaria in southern Germany to test the quality of rain type classification methods and suggest improvements. A subset of the dataset was used to construct a reference classification and test the classification models from the literature. Some machine-learning classification models were trained on the data from FUR and then tested on the data from REG.
The simple dual parameter classification methods that had been built for other disdrometer types performed poorly in their original form. However, the classification performance could be improved via an objective specification of the decision boundary. The modified Br_09 [28] performed better than the other methods.
The optimal features for classifying the rain type were those associated with the fluctuation of the rain microstructure parameters over 10 min. Conversely, the parameters of the fitted gamma distribution to the rain DSD were the least important.
Machine-learning rain type classification methods performed better than the simple dual parameter classification methods when applied to Thies disdrometer measurements. RF methods performed the best of the tested ML models, both via cross validation and when training the model in one location and testing it in another. Four parameters are sufficient to reach high performance levels for the classification model. The performance of the ML methods based on the rain microstructure features as measured by other types of disdrometers needs to be investigated in the future.
We suggest using the same procedure of feature selection and model testing for future studies after applying different methods for prior classification to build the training model, ideally using wind profilers collocated with disdrometers of different types. The variation of the rain microstructure in several locations in Bavaria will be investigated after classifying the rain type using this method. We expect that this procedure of rain type classification will foster better quantitative estimations of rain by remote sensors.
Author Contributions
Conceptualization, W.G. and A.M.; formal analysis, W.G.; supervision, A.M.; writing—original draft, W.G.; writing—review and editing, W.G., N.E., and A.M.
Funding
This work was supported by the German Research Foundation (DFG) and the Technical University of Munich (TUM) in the framework of the Open Access Publishing Program.
Acknowledgments
We thank the Deutscher Wetterdienst (German Meteorological Service DWD) for providing Thies measurements and cloud observations. We also thank Anna-Maria Tilg for her valuable comments. The first author thanks the Deutscher Akademischer Austauschdienst (DAAD) for financial support. We appreciate the valuable comments provided by two anonymous reviewers.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Steiner, M.; Smith, J.A. Convective versus stratiform rainfall: An ice-microphysical and kinematic conceptual model. Atmos. Res. 1998, 47–48, 317–326. [Google Scholar] [CrossRef]
- Niu, S.; Jia, X.; Sang, J.; Liu, X.; Lu, C.; Liu, Y. Distributions of raindrop sizes and fall velocities in a semiarid plateau climate: Convective versus stratiform rains. J. Appl. Meteorol. Climatol. 2010, 49, 632–645. [Google Scholar] [CrossRef]
- Islam, T.; Rico-Ramirez, M.A.; Thurai, M.; Han, D. Characteristics of raindrop spectra as normalized gamma distribution from a Joss–Waldvogel disdrometer. Atmos. Res. 2012, 108, 57–73. [Google Scholar] [CrossRef]
- World Meteorological Organization. International Meteorological Vocabulary, 2nd ed.; Secretariat of the World Meteorological Organization: Geneva, Switzerland, 1992; ISBN 9789263021823. [Google Scholar]
- Thompson, E.J.; Rutledge, S.A.; Dolan, B.; Thurai, M. Drop size distributions and radar observations of convective and stratiform rain over the equatorial Indian and West Pacific Oceans. J. Atmos. Sci. 2015, 72, 4091–4125. [Google Scholar] [CrossRef]
- Houze, R.A. Stratiform precipitation in regions of convection: A meteorological paradox? Bull. Am. Meteorol. Soc. 1997, 78, 2179–2196. [Google Scholar] [CrossRef]
- Ferrier, B.S.; Tao, W.-K.; Simpson, J. A double-moment multiple-phase four-class bulk ice scheme. Part II: Simulations of convective storms in different large-scale environments and comparisons with other bulk parameterizations. J. Atmos. Sci. 1995, 52, 1001–1033. [Google Scholar] [CrossRef]
- Ghada, W.; Buras, A.; Lüpke, M.; Schunk, C.; Menzel, A. Rain microstructure parameters vary with large-scale weather conditions in Lausanne, Switzerland. Remote Sens. 2018, 10, 811. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V.; Hubbert, J.; Gorgucci, E.; Randeu, W.L.; Schoenhuber, M. Raindrop size distribution in different climatic regimes from disdrometer and dual-polarized radar analysis. J. Atmos. Sci. 2003, 60, 354–365. [Google Scholar] [CrossRef]
- Llasat, M.-C. An objective classification of rainfall events on the basis of their convective features: Application to rainfall intensity in the northeast of Spain. Int. J. Climatol. 2001, 21, 1385–1400. [Google Scholar] [CrossRef]
- Bukovčić, P.; Zrnić, D.; Zhang, G. Convective–stratiform separation using video disdrometer observations in central Oklahoma—The Bayesian approach. Atmos. Res. 2015, 155, 176–191. [Google Scholar] [CrossRef]
- Berg, P.; Moseley, C.; Haerter, J.O. Strong increase in convective precipitation in response to higher temperatures. Nat. Geosci. 2013, 6, 181–185. [Google Scholar] [CrossRef]
- Langer, I.; Reimer, E. Separation of convective and stratiform precipitation for a precipitation analysis of the local model of the German weather service. Adv. Geosci. 2007, 10, 159–165. [Google Scholar] [CrossRef][Green Version]
- Houze, R.A. Cloud Dynamics, 2nd ed.; Elsevier: Amsterdam, NY, USA, 2014; ISBN 978-0-12-374266-7. [Google Scholar]
- Rulfová, Z.; Kyselý, J. Disaggregating convective and stratiform precipitation from station weather data. Atmos. Res. 2013, 134, 100–115. [Google Scholar] [CrossRef]
- Williams, C.R.; Ecklund, W.L.; Gage, K.S. Classification of precipitating clouds in the tropics using 915-MHz wind profilers. J. Atmos. Ocean. Technol. 1995, 12, 996–1012. [Google Scholar] [CrossRef]
- Steiner, M.; Houze, R.A.; Yuter, S.E. Climatological characterization of three-dimensional storm structure from operational radar and rain gauge data. J. Appl. Meteorol. 1995, 34, 1978–2007. [Google Scholar] [CrossRef]
- Churchill, D.D.; Houze, R.A. Development and structure of winter monsoon cloud clusters on 10 December 1978. J. Atmos. Sci. 1984, 41, 933–960. [Google Scholar] [CrossRef]
- Kummerow, C.; Hakkarinen, I.M.; Pierce, H.F.; Weinman, J.A. Determination of precipitation profiles from airborne passive microwave radiometric measurements. J. Atmos. Ocean. Technol. 1991, 8, 148–158. [Google Scholar] [CrossRef]
- Berendes, T.A.; Mecikalski, J.R.; MacKenzie, W.M.; Bedka, K.M.; Nair, U.S. Convective cloud identification and classification in daytime satellite imagery using standard deviation limited adaptive clustering. J. Geophys. Res. 2008, 113, 909. [Google Scholar] [CrossRef]
- Anagnostou, E.N.; Kummerow, C. Stratiform and Convective Classification of rainfall using SSM/I 85-GHz brightness temperature observations. J. Atmos. Ocean. Technol. 1997, 14, 570–575. [Google Scholar] [CrossRef]
- Adler, R.F.; Negri, A.J. A satellite infrared technique to estimate tropical convective and stratiform rainfall. J. Appl. Meteorol. 1988, 27, 30–51. [Google Scholar] [CrossRef]
- Yuter, S.E.; Houze, R.A. Measurements of raindrop size distributions over the pacific warm pool and implications for Z–R relations. J. Appl. Meteorol. 1997, 36, 847–867. [Google Scholar] [CrossRef]
- Thurai, M.; Gatlin, P.N.; Bringi, V.N. Separating stratiform and convective rain types based on the drop size distribution characteristics using 2D video disdrometer data. Atmos. Res. 2016, 169, 416–423. [Google Scholar] [CrossRef]
- Tokay, A.; Short, D.A. Evidence from tropical raindrop spectra of the origin of rain from stratiform versus convective clouds. J. Appl. Meteorol. 1996, 35, 355–371. [Google Scholar] [CrossRef]
- Caracciolo, C.; Prodi, F.; Battaglia, A.; Porcu, F. Analysis of the moments and parameters of a gamma DSD to infer precipitation properties: A convective stratiform discrimination algorithm. Atmos. Res. 2006, 80, 165–186. [Google Scholar] [CrossRef]
- Caracciolo, C.; Porcù, F.; Prodi, F. Precipitation classification at mid-latitudes in terms of drop size distribution parameters. Adv. Geosci. 2008, 16, 11–17. [Google Scholar] [CrossRef]
- Bringi, V.N.; Williams, C.R.; Thurai, M.; May, P.T. Using dual-polarized radar and dual-frequency profiler for DSD characterization: A case study from Darwin, Australia. J. Atmos. Ocean. Technol. 2009, 26, 2107–2122. [Google Scholar] [CrossRef]
- Uijlenhoet, R.; Steiner, M.; Smith, J.A. Variability of raindrop size distributions in a squall line and implications for radar rainfall estimation. J. Hydrometeorol. 2003, 4, 43–61. [Google Scholar] [CrossRef]
- You, C.-H.; Lee, D.-I.; Kang, M.-Y.; Kim, H.-J. Classification of rain types using drop size distributions and polarimetric radar: Case study of a 2014 flooding event in Korea. Atmos. Res. 2016, 181, 211–219. [Google Scholar] [CrossRef]
- Steinert, J.; Tracksdorf, P. On the Verification of DWD’s Polarimetric Hydrometeor Classification and Improved QPE. Available online: https://ams.confex.com/ams/37RADAR/webprogram/Handout/Paper275625/ams2015_poster22_steinert_verification.pdf (accessed on 29 April 2019).
- Adirosi, E.; Roberto, N.; Montopoli, M.; Gorgucci, E.; Baldini, L. Influence of disdrometer type on weather radar algorithms from measured DSD: Application to Italian climatology. Atmosphere 2018, 9, 360. [Google Scholar] [CrossRef]
- Angulo-Martínez, M.; Beguería, S.; Latorre, B.; Fernández-Raga, M. Comparison of precipitation measurements by OTT Parsivel2 and Thies LPM optical disdrometers. Hydrol. Earth Syst. Sci. 2018, 22, 2811–2837. [Google Scholar] [CrossRef]
- Historical Records of Cloud Type Observations in Germany. Available online: ftp://ftp-cdc.dwd.de/pub/CDC/observations_germany/climate/hourly/cloud_type/historical/ (accessed on 6 May 2019).
- R Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria, 2018. Available online: https://www.R-project.org/ (accessed on 6 May 2019).
- RStudio Team. RStudio: Integrated Development Environment for R. Boston, MA, USA, 2016. Available online: http://www.rstudio.com/ (accessed on 6 May 2019).
- Cooper, N. Reader: Suite of Functions to Flexibly Read Data from Files. 2017. Available online: https://CRAN.R-project.org/package=reader (accessed on 6 May 2019).
- Wickham, H.; François, R.; Henry, L.; Müller, K. dplyr: A Grammar of Data Manipulation. 2018. Available online: https://CRAN.R-project.org/package=dplyr (accessed on 6 May 2019).
- Wickham, H. Reshaping data with the reshape package. J. Stat. Soft. 2007, 21, 1–20. [Google Scholar] [CrossRef]
- Grolemund, G.; Wickham, H. Dates and times made easy with lubridate. J. Stat. Soft. 2011, 40, 1–25. [Google Scholar] [CrossRef]
- Wickham, H. Stringr: Simple, Consistent Wrappers for Common String Operations. 2018. Available online: https://CRAN.R-project.org/package=stringr (accessed on 6 May 2019).
- Wickham, H. Ggplot2. Elegant Graphics for Data Analysis, 2nd ed.; Springer: Cham, Switzerland, 2016; ISBN 978-3-319-24277-4. [Google Scholar]
- Wilke, C. Cowplot: Streamlined Plot Theme and Plot Annotations for ’ggplot2’. 2018. Available online: https://CRAN.R-project.org/package=cowplot (accessed on 6 May 2019).
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Soft. 2008, 28. [Google Scholar] [CrossRef]
- Meyer, D.; Dimitriadou, E.; Hornik, K.; Weingessel, A.; Leisch, F. e1071: Misc Functions of the Department of Statistics, Probability Theory Group (Formerly: E1071), TU Wien, 2018. Available online: https://CRAN.R-project.org/package=e1071 (accessed on 6 May 2019).
- Microsoft Corporation; Weston, S. doSNOW: For each Parallel Adaptor for the ’snow’ Package. 2017. Available online: https://CRAN.R-project.org/package=doSNOW (accessed on 6 May 2019).
- Zeileis, A.; Grothendieck, G. Zoo: S3 infrastructure for regular and irregular time series. J. Stat. Soft. 2005, 14, 1–27. [Google Scholar] [CrossRef]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2002; ISBN 0-387-95457-0. [Google Scholar]
- Taiyun, W.; Simko, V. R package “corrplot”: Visualization of a Correlation Matrix. 2017. Available online: https://github.com/taiyun/corrplot (accessed on 6 May 2019).
- Robin, X.; Turck, N.; Hainard, A.; Tiberti, N.; Lisacek, F.; Sanchez, J.-C.; Müller, M. pROC: An open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinform. 2011, 12, 77. [Google Scholar] [CrossRef] [PubMed]
- World Meteorological Organization. Principles of Cloud Classification. Available online: https://cloudatlas.wmo.int/principles-of-cloud-classification-genera.html (accessed on 2 May 2019).
- Deutscher Wetterdienst. Datenprüfung/Qualitatskontrolle. Available online: https://cdc.dwd.de/catalogue/Klimadaten_QC.htm (accessed on 2 May 2019).
- Thies Clima. Instructions for use. Laser Precipitation Monitor 5.4110. xx. x00 V2. 4x STD, 2007. Available online: https://www.biral.com/wp-content/uploads/2015/01/5.4110.xx_.xxx_.pdf (accessed on 6 February 2019).
- Friedrich, K.; Kalina, E.A.; Masters, F.J.; Lopez, C.R. Drop-size distributions in thunderstorms measured by optical disdrometers during VORTEX2. Mon. Weather Rev. 2013, 141, 1182–1203. [Google Scholar] [CrossRef]
- Marzuki, M.; Randeu, W.L.; Schönhuber, M.; Bringi, V.N.; Kozu, T.; Shimomai, T. Raindrop size distribution parameters of distrometer data with different bin sizes. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3075–3080. [Google Scholar] [CrossRef]
- Kanofsky, L.; Chilson, P. An analysis of errors in drop size distribution retrievals and rain bulk parameters with a UHF wind profiling radar and a two-dimensional video disdrometer. J. Atmos. Ocean. Technol. 2008, 25, 2282–2292. [Google Scholar] [CrossRef]
- Chen, B.; Wang, J.; Gong, D. Raindrop size distribution in a midlatitude continental squall line measured by Thies optical disdrometers over East China. J. Appl. Meteorol. Climatol. 2016, 55, 621–634. [Google Scholar] [CrossRef]
- Testud, J.; Oury, S.; Black, R.A.; Amayenc, P.; Dou, X. The concept of “normalized” distribution to describe raindrop spectra: A tool for cloud physics and cloud remote sensing. J. Appl. Meteorol. 2001, 40, 1118–1140. [Google Scholar] [CrossRef]
- Ochou, A.D.; Zahiri, E.-P.; Bamba, B.; Koffi, M. Understanding the variability of Z-R relationships caused by natural variations in raindrop size distributions (DSD): Implication of drop size and number. ACS 2011, 1, 147–164. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Corrected at 5th printing; Springer: New York, NY, USA, 2013; ISBN 1461468485. [Google Scholar]
- Chinchor, N. MUC-4 evaluation metrics. In Proceedings of the 4th Conference on Message understanding, McLean, Virginia, 16–18 June 1992; p. 22, ISBN 1558602739. [Google Scholar]
- Deepika, J.; Senthil, T.; Rajan, C.; Surendar, A. Machine learning algorithms: A background artifact. IJET 2017, 7, 143. [Google Scholar] [CrossRef][Green Version]
- Fisher, R.A. The statistical utilization of multiple measurements. Ann. Eugen. 1938, 8, 376–386. [Google Scholar] [CrossRef]
- Press, L.P.a.I.S. 605215, 2009, ISBN 1694-0784. Available online: http://www.ijcsi.org/issues.php (accessed on 6 May 2019).
- Burger, S.V. Introduction to Machine Learning with R. Rigorous Mathematical Analysis, 1st ed.; O’Reilly: Sebastopol, CA, USA, 2018; ISBN 1491976446. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
