1. Introduction
Extremely cold weather and climate events have occurred in many regions throughout the northern hemisphere over the past few decades, including the United States, China, and Europe. These events have been accompanied by strong storms, snowstorms, and record-breaking freezing rain and snow events. Two questions need to be addressed in relation to these extreme weather and climate events in midlatitudes: (1) Are these extremely cold midlatitude events during the northern hemisphere winter related to Arctic warming; (2) If a relationship does exist between these cold events and Arctic warming, then what are the weather and climate processes and dynamic mechanisms that cause these extreme cold events in midlatitudes?
There have been many studies of the relationship between recent Arctic warming and midlatitude atmospheric motion, including the interactive processes and mechanisms between them [
1,
2,
3,
4,
5,
6,
7]. It has been shown that the differences in temperature caused by warming of the Arctic and cooling of Eurasia will change the prevailing path of cyclones and block their eastward movement. As a result, the anticyclone along the coast of Siberia is strengthened, leading to the formation of a double-resistance block (i.e., dipole blocking over the Ural Mountains and Lake Baikal) during the cold period and a deepening of the trough over East Asia [
8]. This further favors the migration of cold air toward the southern region of East Asia and the formation and development of explosive cyclones over eastern Japan. However, few studies have been performed on the thermodynamic and dynamic mechanisms causing cooling in Eurasia as a result of warming in the Arctic.
A blocking structure can be regarded as an isolated, large-amplitude system with a relatively long life and a continuous, stable structure. Malguzzi and Malanotte-Rizzoli [
9] illustrated the formation, maintenance, and collapse of a blocking structure using the Korteweg–de Vries dynamic method (soliton waves). However, the blocking structures and cut-off lows observed in the atmosphere are not characterized by undulance; instead, they are characterized as isolated vortices [
10,
11]. Flierl [
11], McWilliams and Flierl [
12], and McWilliams [
13,
14] obtained a solution for these vortices using strong nonlinear effects in the barotropic mode. The streamline distribution of an isolated vortex forms a pair of antisymmetrical dipoles, where the interaction between the two poles causes the entire dipole to move either eastward or westward. However, such a solution for dipole-type isolated vortices only exists if the internal wavenumber of the first Bessel function falls within a narrow range, although no dispersive characteristic of isolated vortices can effectively reveal the long-term maintenance of blocking.
The nonlinear Schrӧdinger-type envelope theorem for Rossby solitary waves proposed by Luo and Ji [
15] not only reflects the solitary wave characteristics of dipole blocking but also signifies the attenuation mechanism. Thus, the problem of Arctic warming in winter affecting the westerly zone can be regarded as a nonlinear Schrӧdinger-type solitary wave with a thermal forcing term. We used the direct approach to perturbation theory of Grorshov and Ostrovsky [
16], Yan and Tang [
17], and Yan et al. [
18,
19] to analyze the effect of the thermal forcing term on solitary waves. We then combined these results with the topology of solitons to discuss the effect of Arctic warming on dipole blocking and its contribution to negative temperature anomalies over the mid-to-low-latitude regions of Eurasia in winter.
Coincident with the ongoing warming of the Arctic, research has increasingly shifted to focus on the correlation between cold air activity and extreme events at midlatitudes around the globe. Consequently, many innovative results have been obtained—for example, new insights and mechanisms have been proposed regarding the effect of Arctic warming on midlatitude weather and climate events. Recent studies have found that Arctic warming can cause a stronger meridional circulation and a weaker westerly jet. Under such circumstances, blocking can occur frequently in the northern hemisphere, including Europe and Asia, resulting in a higher frequency of cold air outbreaks. To explain this discovery theoretically, we developed this work based on the following three aspects. First, it was established that a barotropic channel model for thermal forcing contains temperature differences between the Arctic and midlatitude regions, which are separated by a nonhomogeneous boundary. Second, the barotropic channel model was simplified to the nonlinear Schrӧdinger equation with a perturbation term via multiscale transformation and the perturbation method. Third, the effect of Arctic warming on dipole blocking, which is conducive to the distribution of warm Arctic–cold Eurasian temperatures, was studied via a direct approach to the perturbation theory.
2. Schrӧdinger Equation in the Quasi-Geostrophic Model with Thermal Forcing
Blocking is a large-scale anomalous atmospheric circulation [
20] and large-scale dynamics are therefore used to study the impact of Arctic warming on blocking. The barotropic quasi-geostrophic mode was used here because the large-scale atmospheric circulation is quasi-geostrophic [
21,
22] and blocking has an equivalent barotropic structure [
23]. The effects of frictional dissipation and thermal forcing were discussed through Equation (1) by Charney and DeVore [
21] and Luo and Ma [
23]. However, we have omitted the dissipation due to friction and only analyzed thermal forcing in our exploration of the effect of variations in circulation due to Arctic warming on westerly air flows. The zonal flow motion is, therefore, governed by the barotropic quasi-geostrophic vorticity equation with only thermal forcing:
where
is the geostrophic stream function representing the westerly air flow,
,
is the Coriolis parameter,
,
,
and
are the boundary layer thickness and the height of a homogeneous atmosphere, respectively,
is the Coriolis parameter at 45° N, and
is the vorticity source of thermal wind driven by the radiation field.
As a result of the uneven distribution of solar radiation in the latitudinal direction, it is necessary to consider the temperature difference in the latitudinal direction when discussing thermal forcing. We assumed that the central position of the westerly air flow is
, where the average temperature is
, the average temperature at midlatitudes. Similarly, the northern boundary of the westerly air flow is
, where the average temperature is
. As a result of the
channel flow of the midtroposphere [
24], the side boundary conditions in Equation (1) are
We analyzed the effect of the temperature difference
between the Arctic and midlatitudes on the westerly air flow. The thermal vorticity
is expressed in terms of the temperature gradient:
where
is the average temperature in the mid- to high latitudes of the northern hemisphere in winter and
denotes the unit zonal thermal forcing.
Substituting Equation (3) into Equation (1), we obtained
The quasi-geostrophic stream function
and the stream function
driven by unit zonal thermal forcing was decomposed into a zonal average flow and its deviation:
By substituting Equation (5) into Equation (4) and ignoring the prime, we obtained an equation for the perturbation in the stream function
:
where
represents the mean zonal wind speed and
is the second derivative of
.
The following definition is provided:
where
and
are the characteristic horizontal scale and wind speed [
23,
25].
By substituting Equation (7) into Equation (6) and ignoring the prime, the dimensionless equation could be obtained:
Through an analysis of data, Tao and Ye [
26] noted that a warm center is located 15° longitude upstream of a dipole blocking center. The thermal distribution is similar to the perturbation stream field of the unforced form in Equation (8). We could therefore assume that
, which represent the perturbation terms in Equation (8), where
,
and
are the coefficients of thermal forcing and sea-level friction, respectively. The thermal distribution shown in
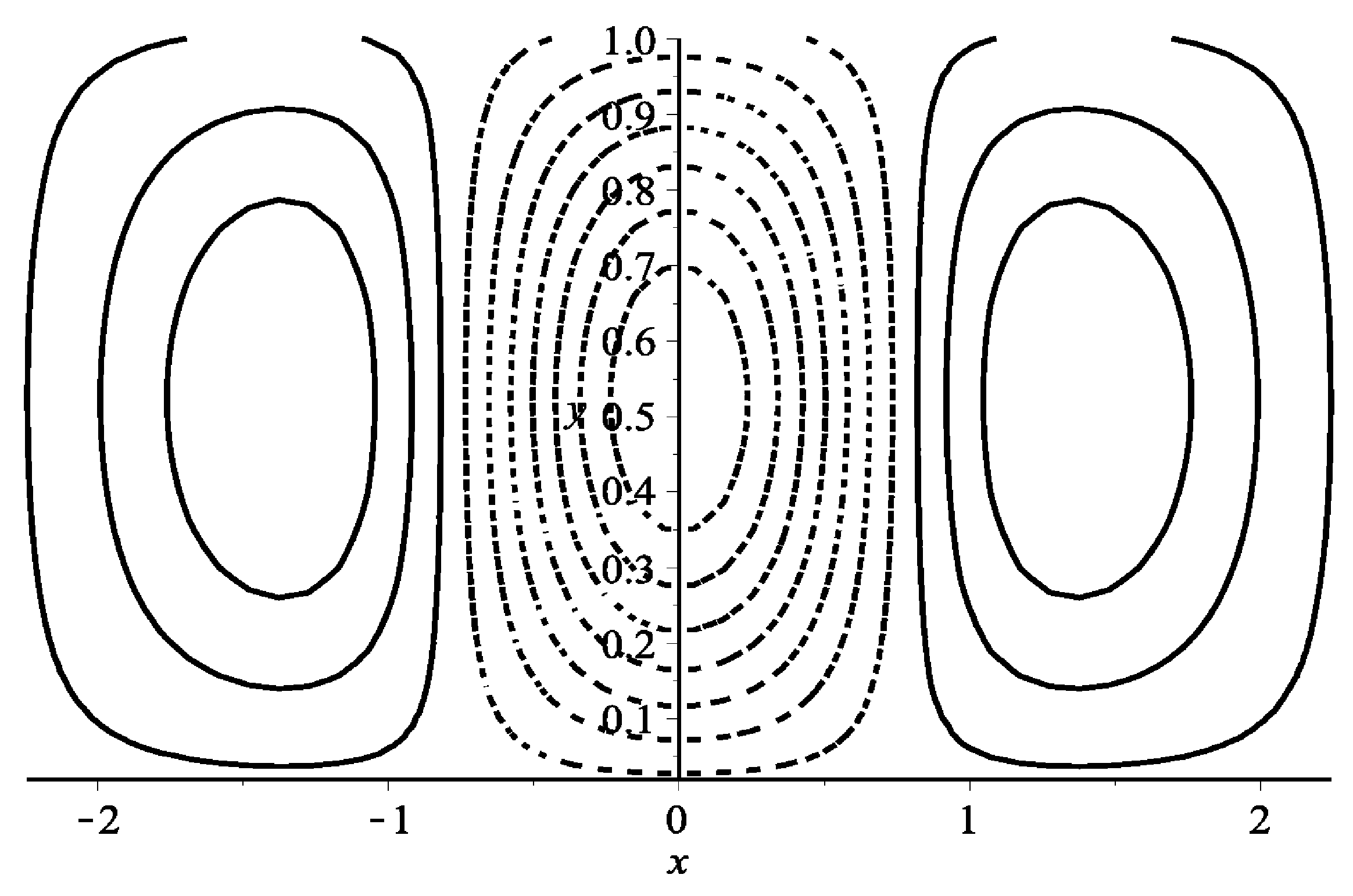
Figure 1 is based on this assumption. The center of thermal vorticity is located upstream of the blocking center and the distance between the two thermal vorticities is about 1500 km in the east–west direction, which is consistent with the results of previous data analyses [
26,
27].
If we let
and
, then
.
, which denotes weak heating in the mid- to high-latitude atmosphere [
28]. Thus, we obtained
Then,
and Equation (8) could be written in the following form:
Based on the multiscale transformation method [
20,
24,
29], we introduced the following slow coordinates:
Considering that
is a small parameter,
,
,
, and
are slow variables. According to the results of Ye and Chao [
30],
represents the large-scale characteristic time,
is the slow exogenous forced characteristic time,
is the longwave characteristic scale, and
is the ultra-longwave characteristic scale. A transformation was then performed [
24]:
The stream function could then be expanded into a series via the perturbation method [
29]:
where
is the approximation of the
th-order perturbation stream function
.
According to Equation (2), the boundary condition of the perturbation flow could be given as follows:
Substituting Equations (12) and (13) into Equation (10), all the order problems with respect to could be obtained by combining the like terms.
The
problem satisfies the equation based on the following linear partial differential equation:
where
K is a linear operator (similarly hereinafter). The solution of Equation (15) based on the boundary condition of Equation (14) is as follows:
where
is a complex amplitude,
and
represent the zonal wavenumber and zonal wave velocity, respectively, and
signifies the complex conjugate of the preceding term. The eigenvalue problem of
is governed by an ordinary differential equation with a homogeneous boundary:
The
problem satisfies the following equation:
Substituting Equation (16) into Equation (17), we obtained the following nonlinear partial differential equation:
Because the operator
contains a homogeneous solution of the form
, the right-hand side of Equation (18) cannot exhibit resonance forcing of the form
. Therefore, the condition for eliminating the secular term is as follows:
with
.
We could therefore rewrite Equation (17):
where
According to the boundary conditions of Equations (14) and (19), we could obtain the solution to Equation (19) in the following form:
By comparing Equations (19) and (20), we obtained the following relationship between
and
:
In this equation,
and
are functions of
, and
is proportional to
. Then,
could be written in the following form [
15,
31]:
Accordingly, the characteristic equation of
could be obtained:
The
problem satisfies the following equation:
For the
problem (Equation (22)), similar to the
problem, the condition of eliminating the secular term about
could be obtained by removing the resonance term. The equation about the amplitude
could be obtained from Equation (21) because the condition for eliminating the secular term contains the formula about
:
where
,
, and
In the following section, we discuss the geometric structure of the flow field of the dipole blocking and the influence of the anomalous thermal vorticity in the Arctic on its structure based on the amplitude of the perturbation (Equation (23)) in the quasi-geostrophic flow.
3. Dipole Blocking Structure without Thermal Forcing
Before discussing the effect of Arctic warming on the dipole blocking structure, we need to understand the topological structure of dipole blocking without thermal forcing. The following equation can be obtained after establishing
,
, and
:
Considering
as
, Equation (24) becomes
Without thermal forcing (i.e.,
), Equation (25) is a standard nonlinear Schrӧdinger equation, for which there is the following single-soliton case:
where
,
,
, and
are real parameters.
and
represent the amplitude and velocity of the soliton, respectively, whereas
and
represent the initial position and initial phase of the soliton, respectively. If
, then the corresponding stream function becomes
Because the initial phase
can only change the position of the soliton center, the amplitude and structure of the soliton cannot be changed. The initial position
can only alter the center position and amplitude of the soliton, not its structure. The flow structure for
and
is discussed without loss of generality. Given that
is in a conjugate form, Equation (27) can be written as:
where
and
. Given the relations of the stream function
with the zonal velocity
and meridional velocity
, the following vector equation can be obtained:
According to the characteristics of the average zonal wind velocity in Equations (29), (7), (9), and (11),
km was determined after establishing
km,
km,
m/s,
m/s, and
[
15]. The corresponding flow then followed the dipole blocking flow (
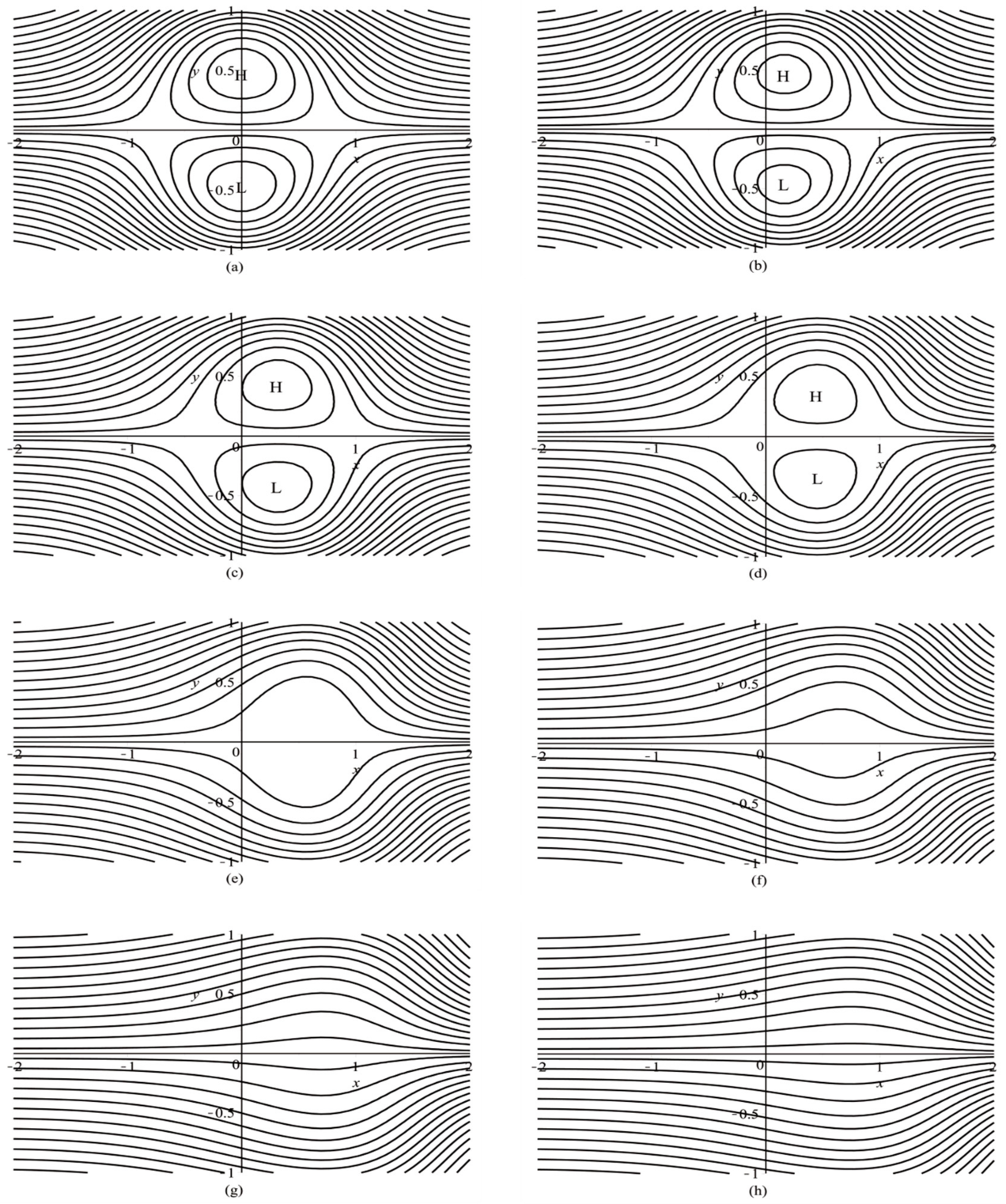
Figure 2).
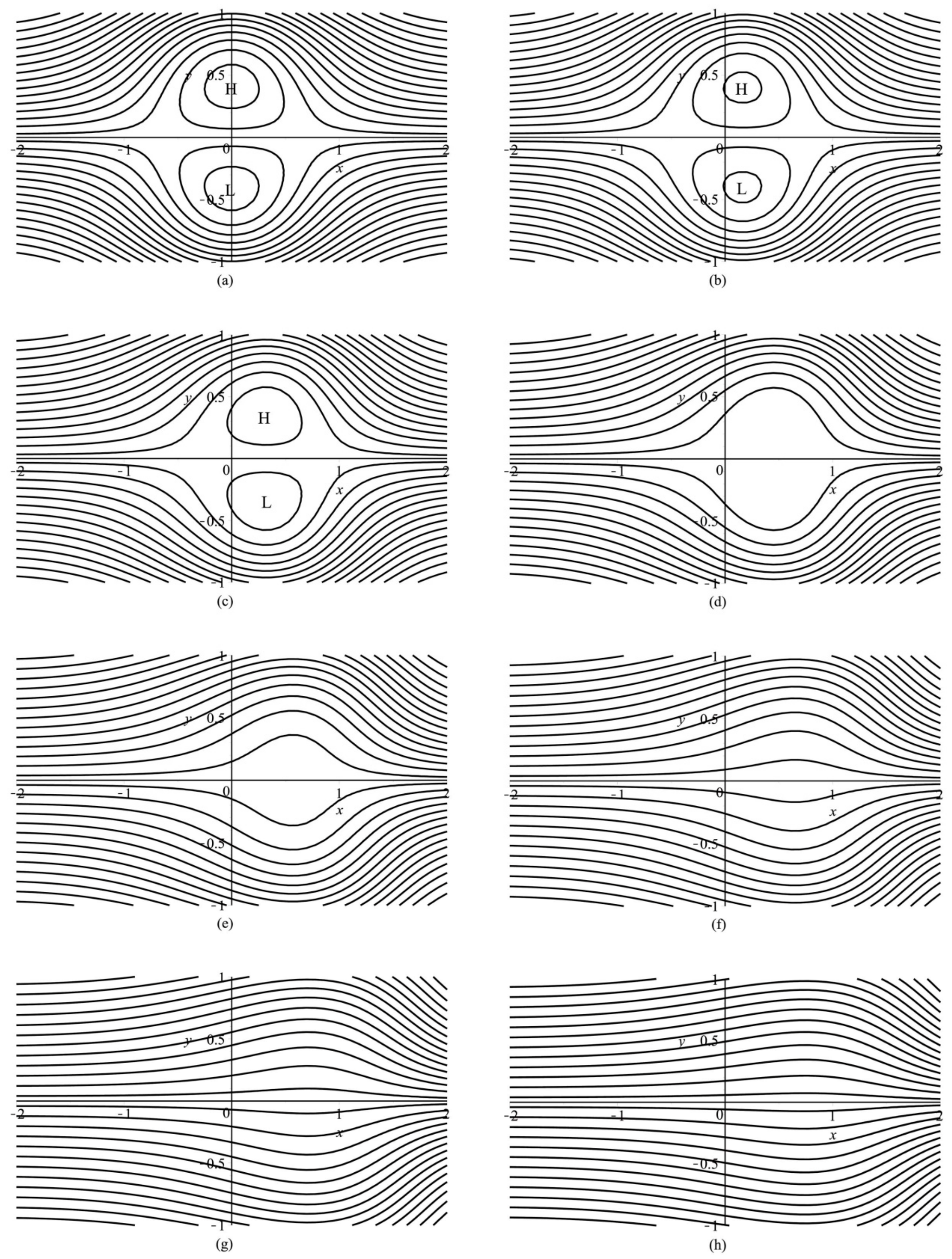
Because the wave amplitude of the dipole blocking flow increases monotonically with and , the dipole blocking flow is dispersive. From this analysis, the effect of the zonal wind velocity on the dipole blocking structure can explain why the development of planetary waves tends to be accompanied by low wind velocities when a meridional circulation prevails. Equation (29) shows that with a certain number of waves () and an average zonal velocity (), the amplitude of the soliton determines the type of flow field and is not related to the velocity of the soliton. From this analysis, a blocked flow field is formed under the nonlinear action of the atmosphere without thermal forcing. Under the effect of dipole blocking on the flow field, the movement of Arctic cold air toward the south is conducive to the formation of cold air or cold waves over Eurasia in winter. The Arctic has experienced significant warming in recent years and a warm Arctic–cold Eurasian temperature distribution often appears. To explain this phenomenon, we need to theoretically prove that Arctic warming in winter strengthens dipole blocking and contributes to the abnormal distribution of warm Arctic–cold Eurasian temperatures. Therefore, the effect of decreasing the absolute value of the difference in temperature () between the Arctic and midlatitudes on dipole blocking was studied through the influence of the thermal forcing terms on the Schrӧdinger soliton.
4. Impact of Thermal Forcing on the Schrӧdinger Equation for Solitons
Because
and
, the thermal forcing term in Equation (24) is of the
order of magnitude, namely,
, which can be considered as a small term. Therefore, we discuss the effect of thermal forcing on dipole blocking by analyzing the effect of a perturbation on the amplitude of the soliton. To use the direct approach to perturbation theory for solitons to analyze the effect of atmospheric thermal forcing on the nonlinear Schrӧdinger equation, we rewrote Equation (25) in the following form:
with
,
,
, and
.
For Equation (30), we sought a first-order approximate solution, as follows:
with the initial conditions
, where
represents the zero-order term and
represents the first-order term. Furthermore, to eliminate the so-called secular terms, we introduced a slow time variable:
The derivative with respect to
then became
By substituting Equations (31)–(33) into Equation (30), the first-order term
was linearized into the following equations (with appropriate initial conditions):
and
where an overbar signifies a complex conjugate. The zero-order approximation in Equation (34) is simply the standard nonlinear Schrӧdinger equation, which has a single-soliton solution that is formally the same as that for Equation (26):
with
The soliton parameters
, and
were hypothesized to be functions of the slow time variable
, but
and
are independent of
. It then follows from Equation (36) that
where
It was convenient to use the independent variable
. Therefore, substituting Equation (33) into Equation (35) and its complex conjugate equation led to the following:
The following forms were allowed:
Equation (38) could then be written as a matrix:
where
, which is called the third Pauli matrix;
and
are two-dimensional column matrices; and
represents a
matrix. They are defined as follows:
Because Equation (39) is a separable partial differential equation with a zero boundary, it can be solved by the Sturm–Liouville eigenvalue theory. According to the Sturm–Liouville eigenvalue theory of linear operator equations, the sequences of the real eigenvalues and eigenfunctions of the linear operator and its adjoint operator can be obtained. can then be constituted by the complete orthogonal basis functions spanned by these eigenfunctions.
To obtain the solution of the variable (
) in Equation (39), the key was to solve the following two eigenvalue problems:
where
is the adjoint operator of
,
and
are the eigenvalues of
and
, respectively,
is the eigenfunction of
with respect to
, and
is the eigenfunction of
, which is defined as
In addition, the operator
and its adjoint operator
have the same continuous spectrum [
32]. Given
, then
Therefore, the eigenvalues of operator
and its adjoint operator
can be obtained:
where
is a real number. Correspondingly, the orthogonal basis of Equation (40) is as follows:
with
Expanding
with the basis function
, we obtained the following equation:
where
,
, and
represent expansion coefficients.
By substituting Equation (41) into Equation (39), the coefficient of which is a function of only
after integration, Equation (39) could be separated into ordinary differential equations about the expansion coefficients
,
, and
[
33,
34].
According to Equations (42) and (37), the terms
,
, and
can be solved. The expression of
and
is then known. Substituting
into Equation (38) and differentiating Equation (38) to
, the formulas for the variations in the soliton amplitude (
) and velocity (
) with a slow time variable (
) can be obtained:
with
After obtaining Equation (43) for the effects of perturbations on solitons, we can now discuss the effect of Arctic warming on dipole blocking using Equation (43).
5. Impact of Arctic Warming on Dipole Blocking
To further discuss the impact of Arctic warming on dipole blocking, we substituted the thermal forcing term
into Equation (43) and used the following formula computed by the residue theorem [
35]:
We then further considered the following matrix-order power formula:
We could obtain the relation between the motion velocity of the soliton and the slow time variable
by solving Equation (43):
Equation (44) signifies that
is steady with respect to the slow time variable
. Therefore, we could obtain the variation in the amplitude
of the soliton with regard to the slow time variable
:
According to Equation (45),
increases monotonically about
.
In general, the temperature difference between the Arctic and midlatitudes at 500 hPa is less than zero (
). Equation (45) can then be rewritten as:
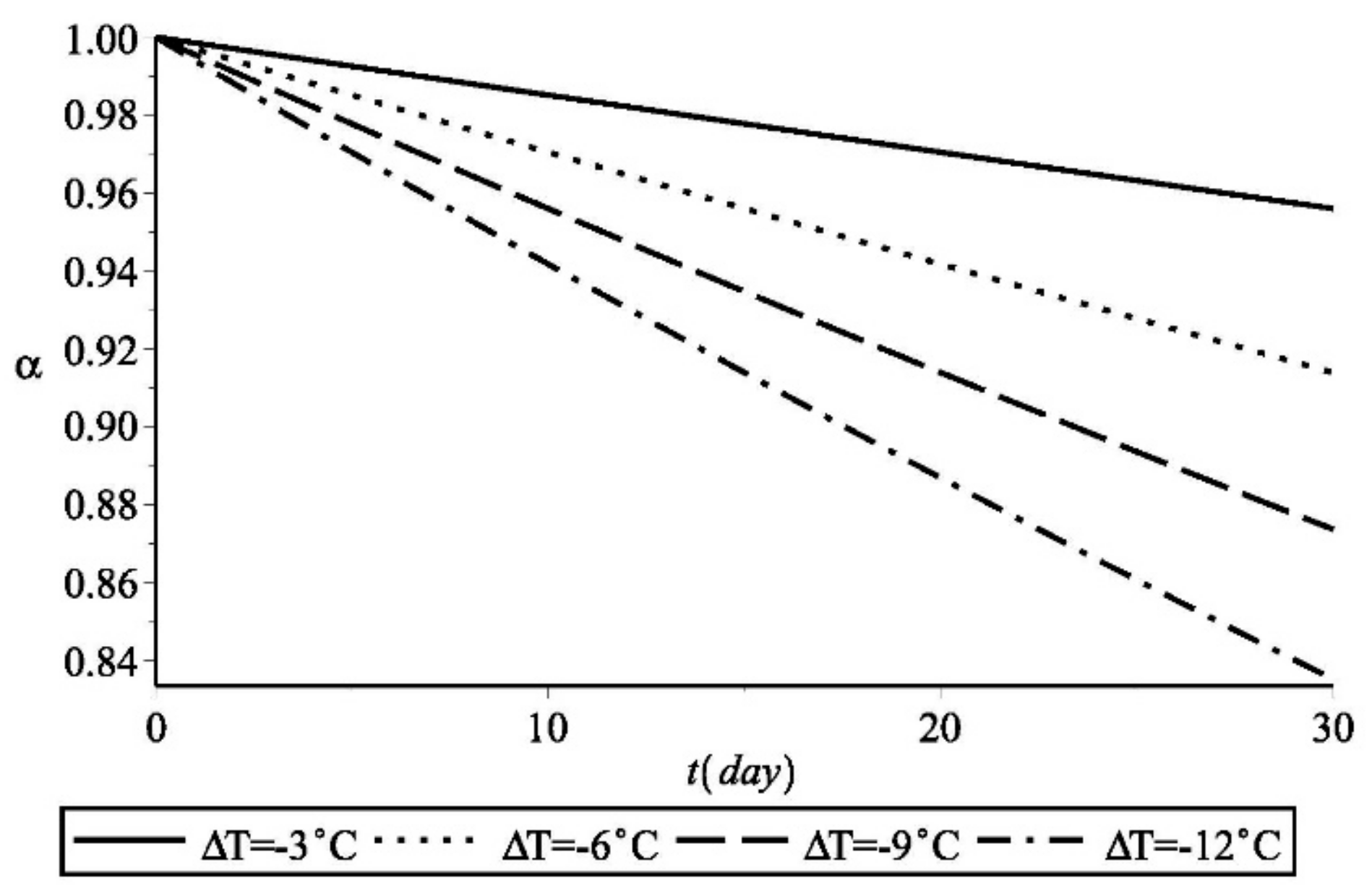
According to Equation (46), the soliton amplitude decays slowly with time under the action of thermal forcing. In other words, the temperature distribution of midlatitude warming and Arctic cooling has an inhibitory effect on the development of blocking during the maintenance phase of dipole blocking. Further analysis shows that the decay rate of the amplitude of the soliton is positively proportional to —that is, the greater the temperature difference , the faster the amplitude of the soliton will decrease. Based on this analysis, a decrease in the absolute difference in temperature between the Arctic and Eurasia—namely, —is conducive to the development of a blocking dipole.
Similar to the analysis in
Section 3,
km,
km,
m/s,
m/s, and
were established [
15]. Then,
,
,
and
,
°C, and Equations (7), (9), (11), and (32) were used to obtain the growth trend for the amplitude of the soliton (
Figure 3) when the temperature difference
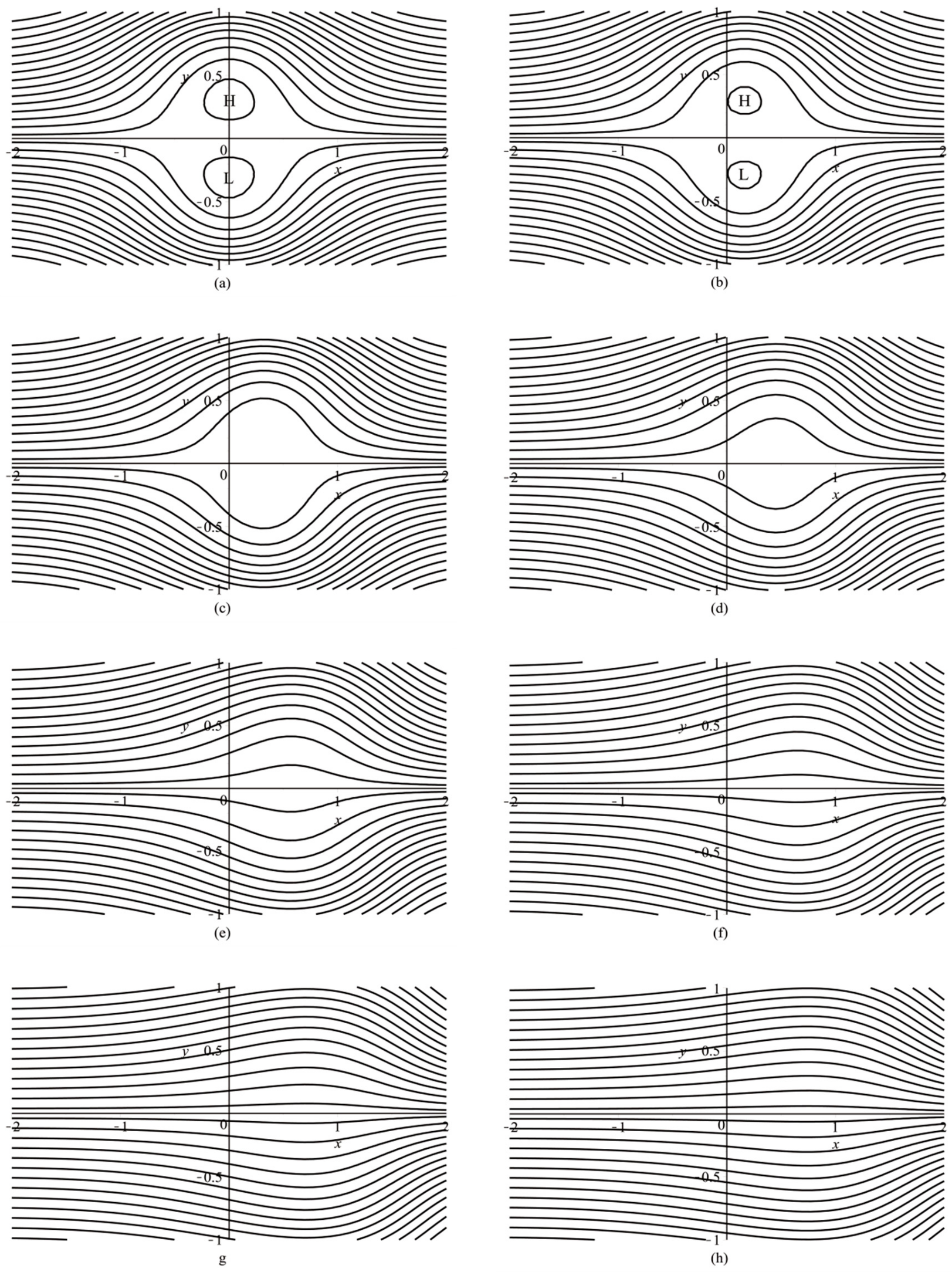
is −3, −6, −9, and −12 °C and to obtain the dipole blocking flow when
°C (
Figure 4) and
°C (
Figure 5).
This analysis shows that if there is a perturbation in the zonal flow, the nonlinear interactions between waves and flows within the westerly zone in the northern hemisphere probably induce dipole blocking of the Schrödinger solitons. In addition, the distribution of lower Arctic and higher midlatitude temperatures inhibits the development of solitons. The decrease in the absolute difference in temperature between the Arctic and Eurasia originating from Arctic warming weakens the inhibitory effect on dipole blocking—that is, dipole blocking becomes stronger and lasts for longer as the Arctic warms. It is easy to stimulate the generation of dipole blocking structures over the Ural Mountains, Lake Baikal, and the Okhotsk Sea [
15] due to the shear in the zonal base flow caused by the large-scale compulsive action of the Tibetan Plateau, which further strengthens dipole blocking over Eurasia as the Arctic warms.
In January 2008, for example, the Arctic temperature at a 2-m height over a wide area showed positive anomalies, particularly over the Barents–Kara Sea. This caused the westerlies in mid- to high latitudes to weaken [
36,
37] and formed an anomalous dipole consisting of a Ural blocking high and a low-pressure center over Eurasia, causing the northern branch of the circulation in the Urals to develop strongly toward the Arctic. The northern branch of the circulation then turned south from the Arctic, guiding the cold air of the Arctic in a southeasterly direction to invade East Asia (
Figure 6), causing the extremely cold event recorded over eastern China in January 2008.