A Combined Model Based on Feature Selection and WOA for PM2.5 Concentration Forecasting
Abstract
1. Introduction
2. Methods
2.1. Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (Ceemdan)
2.2. Variational Mode Decomposition (Vmd)
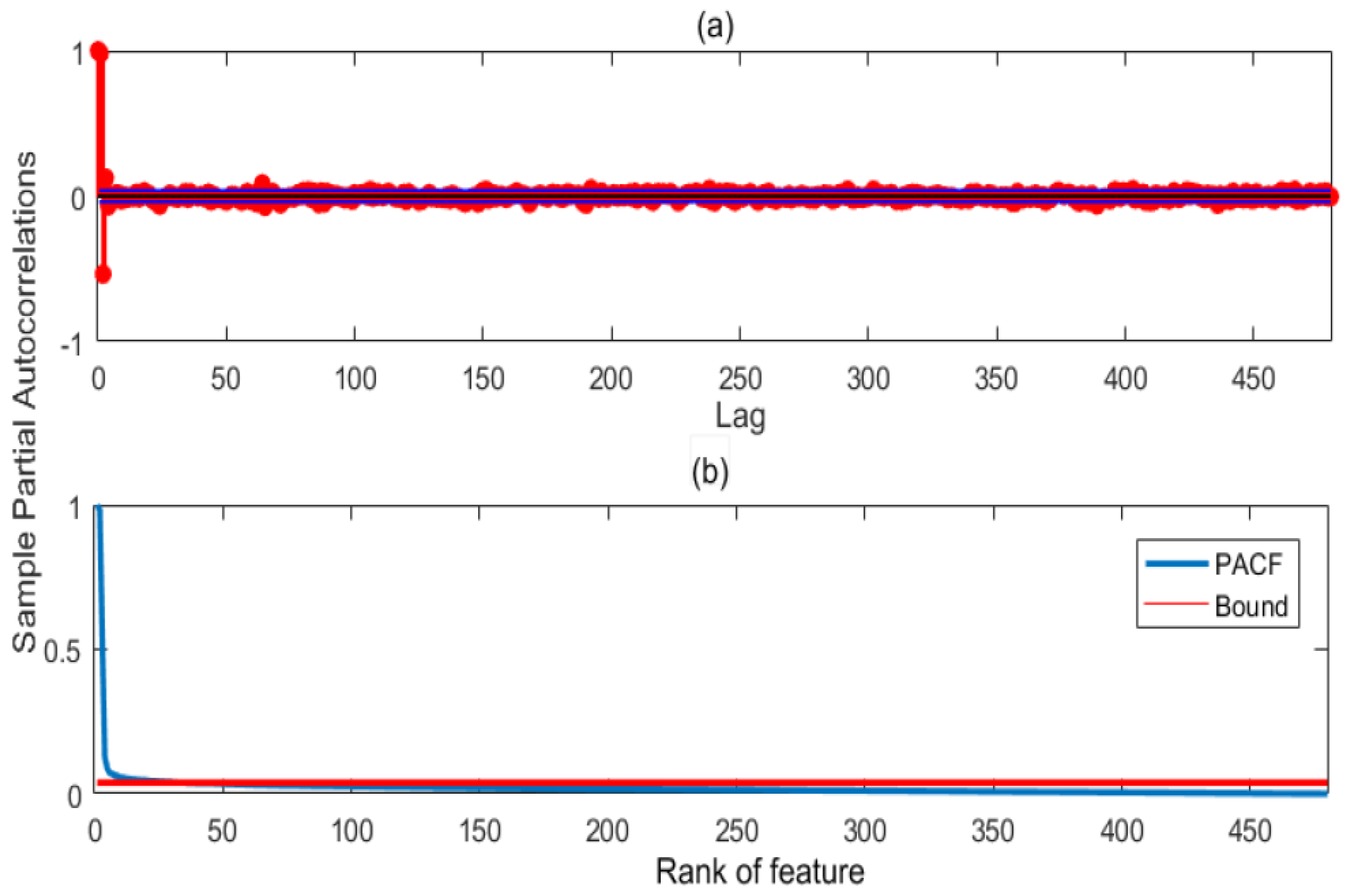
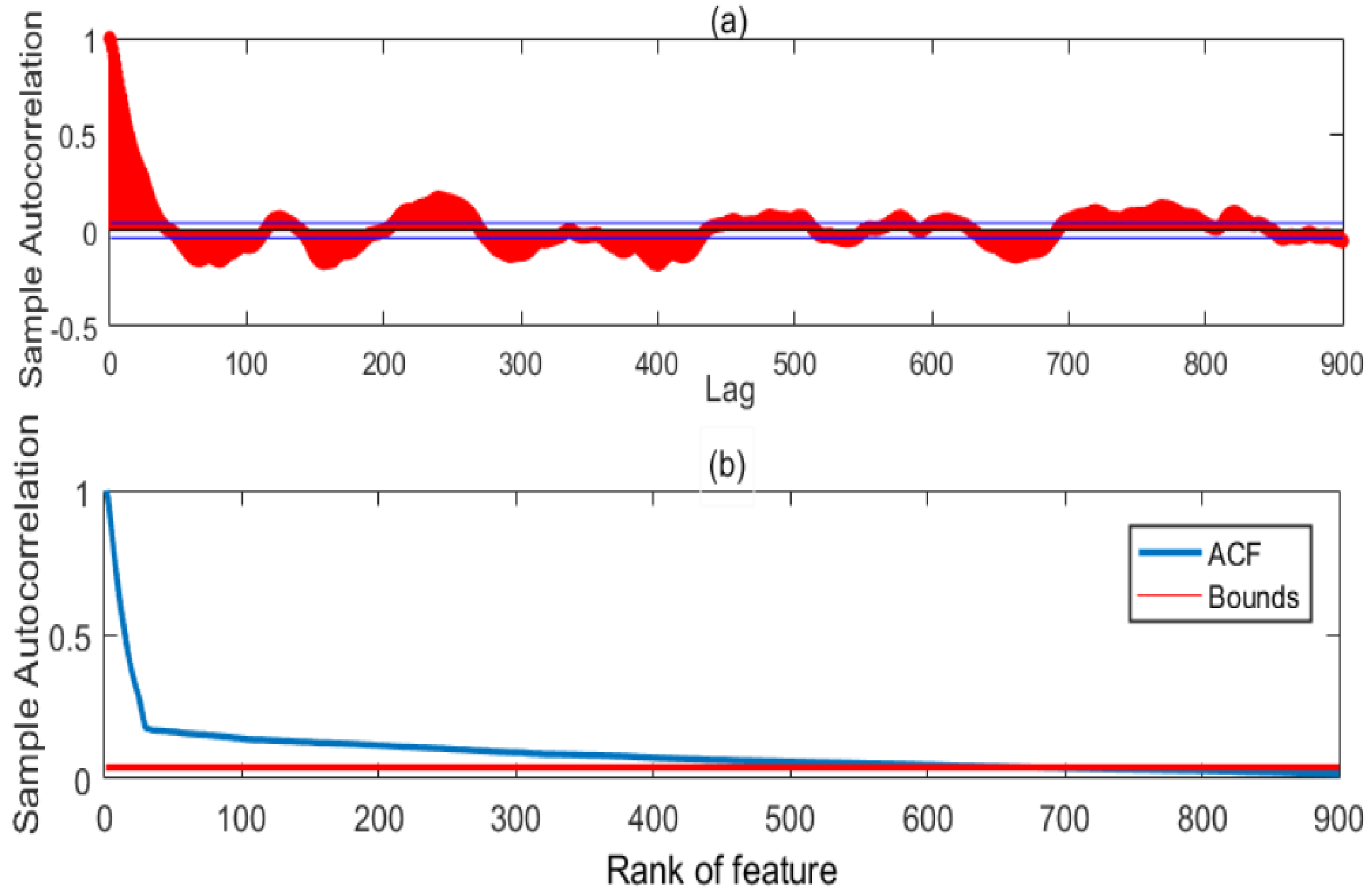
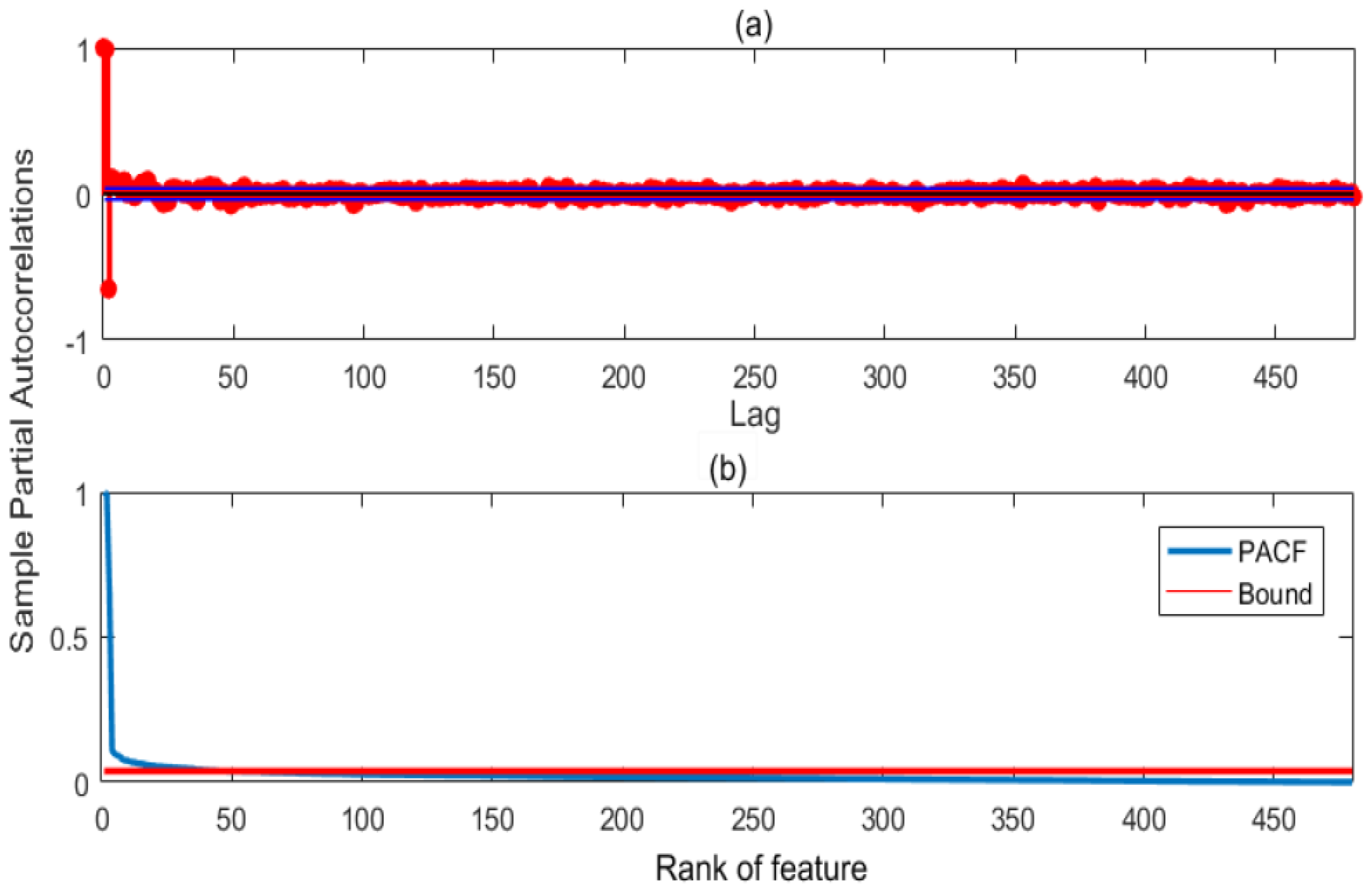
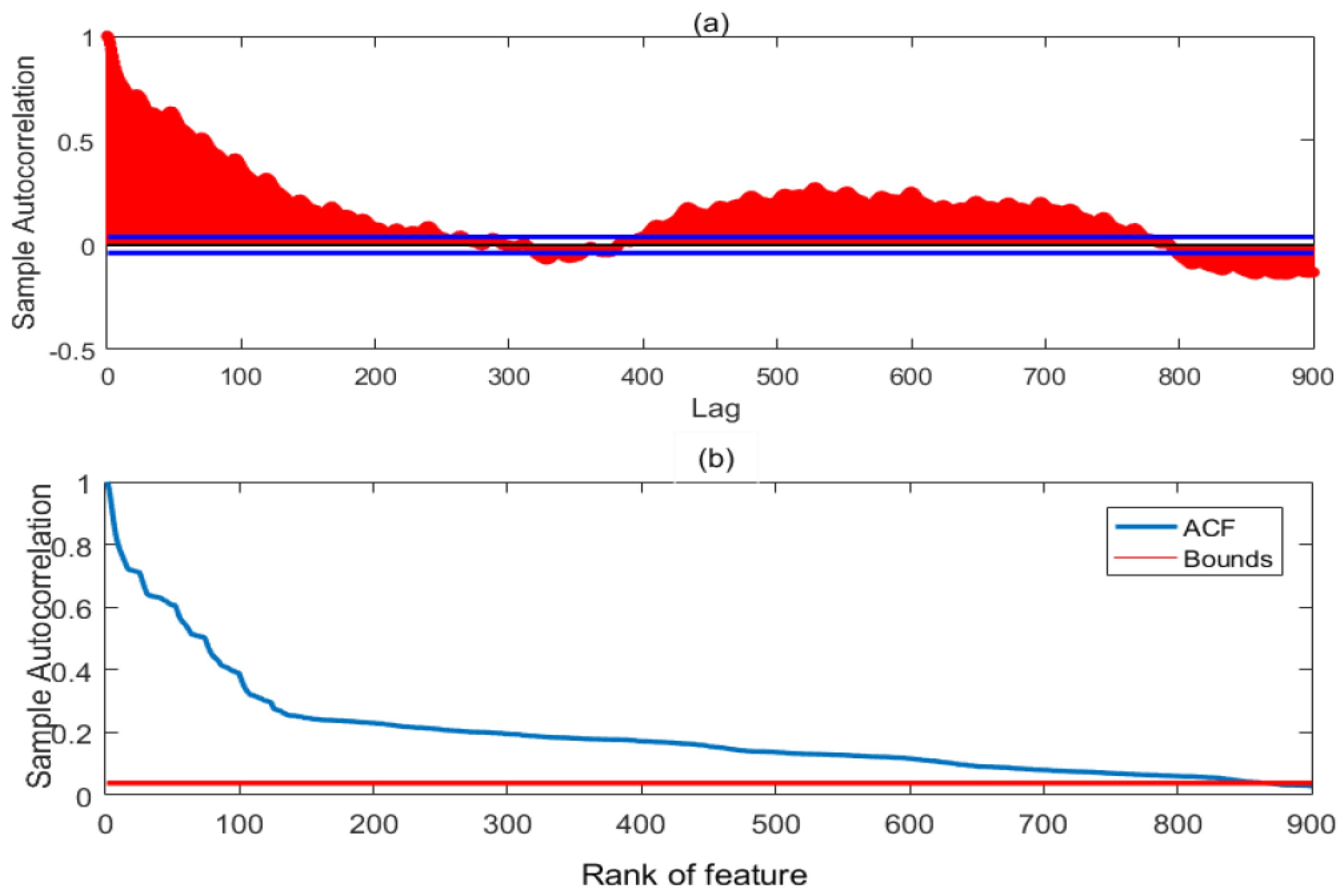
2.3. Autocorrelation Function (Acf)
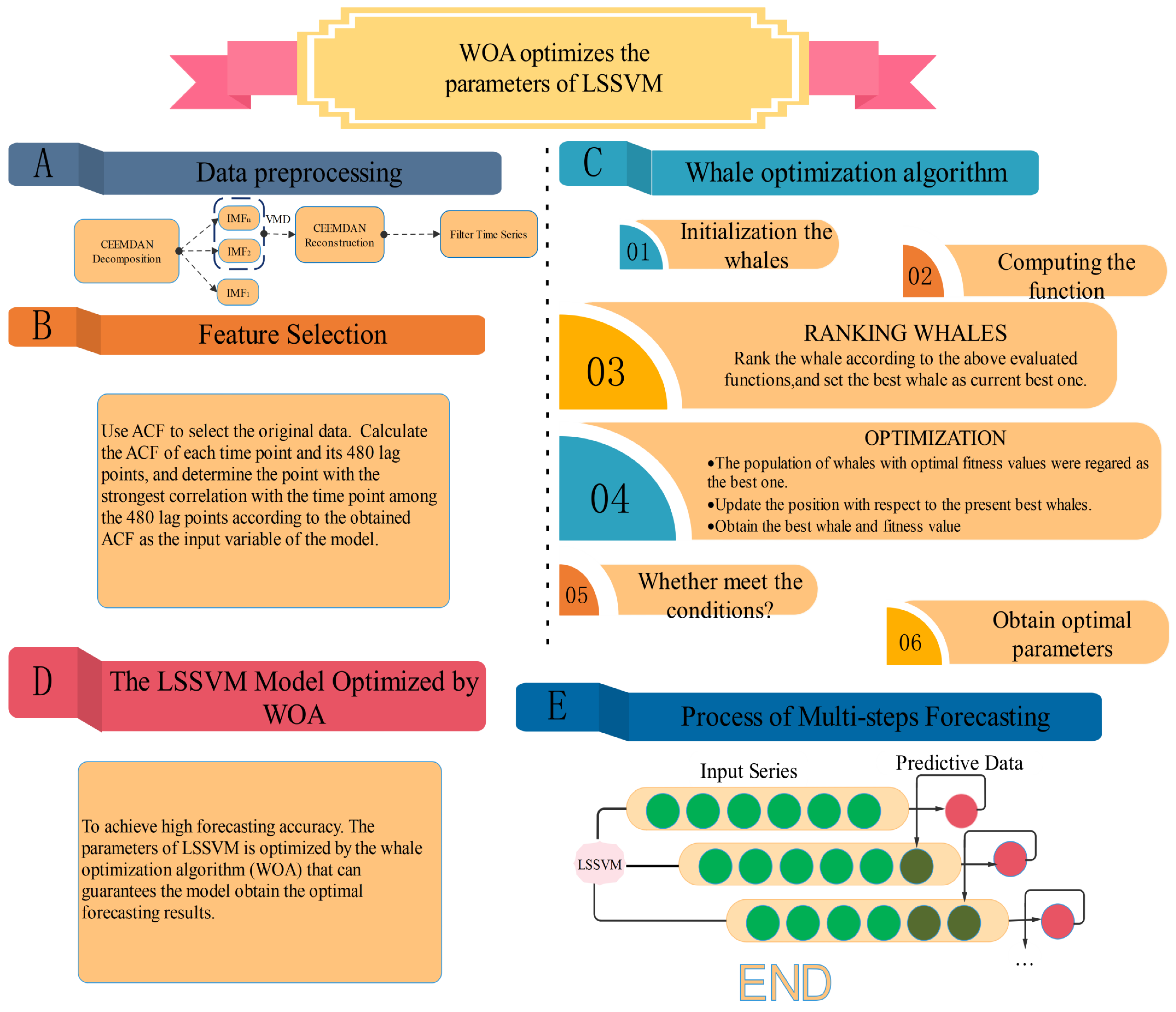
2.4. Whale Optimization Algorithm (Woa)
- Given a random number , if and , proceed to wandering for preyArtificial whales use random individual position in the population to navigate for food, and their spatial position is updated by Equation (2):where X is the position of the individual, t is the current number of iterations, and represents the length of the population to a random choosing individual before the position update. The parameter A is random number on the interval . Furthermore, C is the random number on the interval , which controls the influence of the random individual on the distance of the current individual X.
- If and , proceed to Encircling preyAfter the artificial whale finds the food, its spatial position is updated by Equation (3):where the position of the food is the position of the global optimal individual in the population .
- If , Spiral catching preyWhile the artificial whale swims to the optimal individual , it also follows the trajectory movement of the logarithmic spiral, and its spatial position is updated by Equation (4):where is the position of the artificial whale after the current iteration update, indicates the length of the individual of the individual X before the position update, and b is the constant for shaping the spiral trajectory, l is a random number on the interval .
- Substituting the optimized model parameters into the main model to calculate the fitness value.
2.5. Least Squares Support Vector Machines (Lssvm)
2.6. Lssvm Optimized by Woa
- Initialize the parameters of the WOA and determine the objective function Equation (5)where M is the number of samples, and are the observed and predictive values of , respectively.
- Using WOA to iteratively optimize the parameters of LSSVM;
- See if the maximum iteration or preset error is met. If yes, run 4; Otherwise, continue to run 2;
- Set the optimal value obtained by WOA to c and of LSSVM. Finally, the preprocessed data are used as the input of LSSVM to obtain the predicted value .
| Algorithm 1 WOA-LSSVM: optimize the parameters c and g of LSSVM with WOA. |
| Input: -the training time series -the testing time series Output: -the forecasting data LSSVM Parameters -the maximum number of iterations n-the number of whales -the fitness function of i-th whale -the position of i-th whale -current iteration number dim-the number of dimension. /*Set the parameters of WOA.*/ /*Initilize population of n whale randomly.*/ if then Evaluate the corresponding fitness function end if while do for each do for each do Update a,A,C,l and p if then if then /*Update the position of the current search agent.*/ else Select a random search agent() /*Update the position of the current search agent.*/ end if else /*Update the position of the current search agent.*/ end if end for end for /*Check if any search agent goes beyond the search space and amend it*/ for each do Calculate fitness values of each search agent end for /*Update the best search agent .*/ end while return Set parameters of LSSVM according to Use to train the LSSVM and update the parameters of the LSSVM Input the historical data into LSSVM to obtain the forecasting value . |
3. Data Collection and Experimental Analysis
3.1. Data Description
3.2. Performance Estimation
3.3. Testing Method
3.4. Experimental Setup
4. Results
4.1. Experimental I
4.1.1. Feature Selection
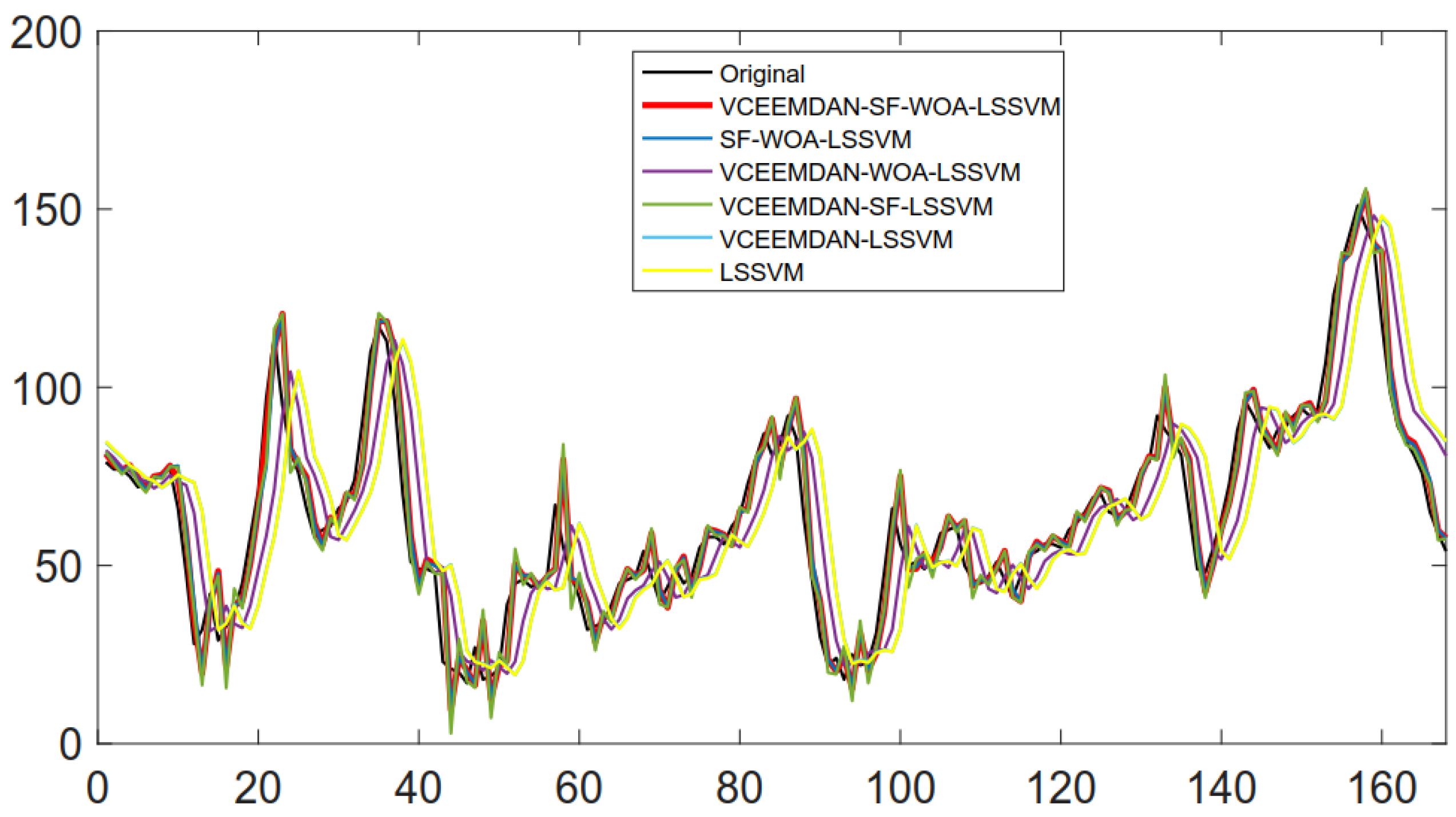
4.1.2. Forecast Results and Analysis
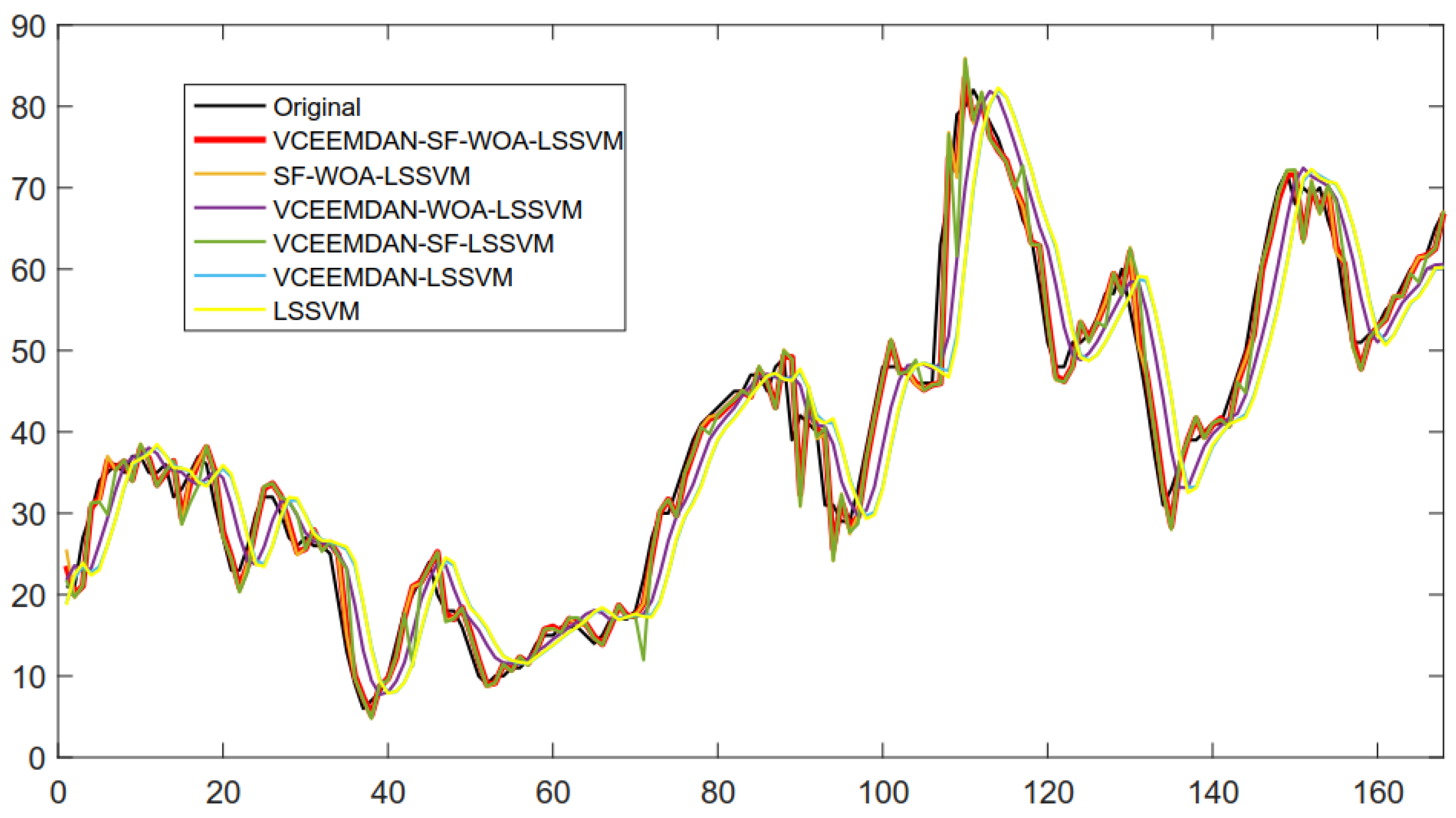
4.2. Experimental II
5. Conclusions and Future Study
Author Contributions
Funding
Conflicts of Interest
References
- Chen, W. Urban air quality evaluations under two versions of the national ambient air quality standards of China. Atmos. Pollut. Res. 2016, 7, 49–57. [Google Scholar] [CrossRef]
- Ye, W.F. Spatial-temporal patterns of PM2.5 concentrations for 338 Chinese cities. Sci. Total. Environ. 2018, 631–632, 524–533. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y. Air quality assessment by contingent valuation in Ji’nan, China. J. Environ. Manag. 2009, 90, 1022–1029. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Wang, S.; Hao, J. Air pollution and control action in Beijing. J. Clean. Prod. 2016, 112, 1519–1527. [Google Scholar] [CrossRef]
- Zheng, S. The impacts of provincial energy and environmental policies on air pollution control in China. Renew. Sustain. Energy Rev. 2015, 49, 386–394. [Google Scholar] [CrossRef]
- Chen, T.F. Modeling direct and indirect effect of long range transport on atmospheric PM2.5, levels. Atmos. Environ. 2014, 89, 1–9. [Google Scholar] [CrossRef]
- Fang, G.C.; Chang, C.N.; Wang, N.P. The study of TSP, PM2.5–10, and PM2.5, during Taiwan Chi-Chi Earthquake in the traffic site of central Taiwan, Taichung. Chemosphere 2000, 41, 1727–1731. [Google Scholar] [CrossRef]
- Chudnovsky, A.A.; Koutrakis, P.; Kloog, I. Fine particulate matter predictions using high resolution Aerosol Optical Depth(AOD) retrievals. Atmos. Environ. 2014, 89, 189–198. [Google Scholar] [CrossRef]
- Shen, F.; Ge, X.; Hu, J. Air pollution characteristics and health risks in Henan Province, China. Environ. Res. 2017, 156, 625–634. [Google Scholar] [CrossRef]
- You, W.; Zang, Z.; Pan, X. Estimating PM2.5 in Xi’an, China using aerosol optical depth: A comparison between the MODIS and MISR retrieval models. Sci. Total. Environ. 2015, 505, 1156–1165. [Google Scholar] [CrossRef] [PubMed]
- Scapellato, M.L.; Canova, C.; Simone, A.D. Personal PM10 exposure in asthmatic adults in Padova, Italy: seasonal variability and factors affecting individual concentrations of particulate matter. Int. J. Hyg. Environ. Health 2009, 212, 626–636. [Google Scholar] [CrossRef] [PubMed]
- Niu, M.; Wang, Y.; Sun, S. A novel hybrid decomposition-and-ensemble model based on CEEMD and GWO for short-term PM2.5, concentration forecasting. Atmos. Environ. 2016, 134. [Google Scholar] [CrossRef]
- Kukkonen, J.; Partanen, L.; Karppinen, A. Extensive evaluation of neural network models for the prediction of NO and PM10 concentrations, compared with a deterministic modelling system and measurements in central Helsinki. Atmos. Environ. 2003, 37, 4539–4550. [Google Scholar] [CrossRef]
- Turner, M.C.; Krewski, D.; Pope, C.A. Long-term ambient fine particulate matter air pollution and lung cancer in a large cohort of never-smokers. Am. J. Respir. Crit. Care Med. 2011, 184, 1374–1381. [Google Scholar] [CrossRef] [PubMed]
- Gu, K. Highly efficient picture-based prediction of PM2.5 concentration. IEEE Trans. Ind. Electron. 2018, 99, 1. [Google Scholar] [CrossRef]
- Zhai, B.; Chen, J. Development of a stacked ensemble model for forecasting and analyzing daily average PM2.5, concentrations in Beijing, China. Sci. Total. Environ. 2018, 635, 644–658. [Google Scholar] [CrossRef]
- Yufang, W.; Haiyan, W.; Shuhua, C. Prediction of daily PM2.5 concentration in China using partial differential equations. PLoS ONE 2018, 13, e0197666. [Google Scholar]
- Stella, M. A dynamic multiple equation approach for forecasting PM2.5 pollution in Santiago, Chile. Int. J. Forecast. 2018, 34, 566–581. [Google Scholar]
- Junxiong, H.; Qi, L.I.; Yajie, Z. Real-time forecasting system of PM2.5 concentration based on spark framework and random forest model. Sci. Surv. Mapp. 2017, 42, 1–6. [Google Scholar] [CrossRef]
- Yichao, L.; Lu, X.; Christakos, G. Forecasting concentrations of PM2.5 in main urban area of Hangzhou and mapping using SARIMA model and ordinary Kringing method. Acta Sci. Circumstantiae 2018, 38, 62–70. [Google Scholar] [CrossRef]
- Cobourn, W.G. An enhanced PM2.5 air quality forecast model based on nonlinear regression and back-trajectory concentrations. Atmos. Environ. 2010, 44, 3015–3023. [Google Scholar] [CrossRef]
- Bai, Y.; Li, Y.; Wang, X. Air pollutants concentrations forecasting using back propagation neural network based on wavelet decomposition with meteorological conditions. Atmos. Pollut. Res. 2016, 7, 557–566. [Google Scholar] [CrossRef]
- Biancofiore, F.; Busilacchio, M.; Verdecchia, M. Recursive neural network model for analysis and forecast of PM10 and PM2.5. Atmos. Pollut. Res. 2017, 8, 652–659. [Google Scholar] [CrossRef]
- Díaz-Robles, L.A.; Ortega, J.C.; Fu, J.S.; Reed, G.D.; Chow, J.C.; Watson, J.G.; Moncada-Herrera, J.A. A hybrid ARIMA and artificial neural networks model to forecast particulate matter in urban areas: The case of Temuco, Chile. Atmos. Environ. 2008, 42, 8331–8340. [Google Scholar] [CrossRef]
- Prakash, A.; Kumar, U.; Kumar, K. A Wavelet-based Neural Network Model to Predict Ambient Air Pollutants’ Concentration. Environ. Model. 2011, 16, 503–517. [Google Scholar] [CrossRef]
- Lv, B.; Cobourn, W.G.; Bai, Y. Development of nonlinear empirical models to forecast daily PM2.5, and ozone levels in three large Chinese cities. Atmos. Environ. 2016, 147, 209–223. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, H.; Palazoglu, A. Prediction of 24-Hour-Average PM2.5 Concentrations Using a Hidden Markov Model with Different Emission Distributions in Northern California. Sci. Total. Environ. 2012, 443, 93–103. [Google Scholar] [CrossRef]
- Shenru, X.; Binbin, Q.; Baohua, Y. Influence on Input Parameters of PM2.5 Concentration Prediction Model Based on LIBSVM. J. Luoyang Inst. Sci. Technol. 2017, 27, 9–12. [Google Scholar] [CrossRef]
- Zhu, S.; Lian, X.; Wei, L. PM2.5 forecasting using SVR with PSOGSA algorithm based on CEEMD, GRNN and GCA considering meteorological factors. Atmos. Environ. 2018, 183. [Google Scholar] [CrossRef]
- Paschalidou, A.K.; Karakitsios, S.; Kleanthous, S. Forecasting hourly PM10 concentration in Cyprus through artificial neural networks and multiple regression models: implications to local environmental management. Environ. Sci. Pollut. Res. 2011, 18, 316–327. [Google Scholar] [CrossRef]
- Feng, X.; Li, Q.; Zhu, Y. Artificial neural networks forecasting of PM2.5, pollution using air mass trajectory based geographic model and wavelet transformation. Atmos. Environ. 2015, 107, 118–128. [Google Scholar] [CrossRef]
- Feng, S.; Wengao, L.; Bo, Z. Neural network model for PM2.5 concentration prediction by grey wolf optimizer algorithm. J. Comput. Appl. 2017, 37, 2854–2860. [Google Scholar] [CrossRef]
- Yali, F.U.; Ya, H. Air Quality Forecasting Based on IPSO-ELM. Environ. Sci. Technol. 2017, 40, 324–328. [Google Scholar]
- Liming, W.; Xianghua, W.U.; Tianliang, Z. A scheme for rolling statistical forecasting of PM2.5 concentrations based on distance correlation coefficient and support vector regression. Acta Sci. Circumstantiae 2017, 37, 1268–1276. [Google Scholar] [CrossRef]
- Lijie, D.; Changjiang, Z.; Leiming, M.A. Dynamic forecasting model of short-term PM2.5 concentration based on machine learning. J. Comput. Appl. 2017, 37, 3057–3063. [Google Scholar] [CrossRef]
- Gan, K.; Sun, S.; Wang, S. A secondary-decomposition-ensemble learning paradigm for forecasting PM2.5, concentration. Atmos. Pollut. Res. 2018, 9, 989–999. [Google Scholar] [CrossRef]
- García Nieto, P.J.; Sánchez Lasheras, F.; Garcxixa-Gonzalo, E.; de Cos Juez, F.J. PM10, concentration forecasting in the metropolitan area of Oviedo (Northern Spain) using models based on SVM, MLP, VARMA and ARIMA: A case study. Sci. Total. Environ. 2018, 621, 753–761. [Google Scholar] [CrossRef]
- Gualtieri, G. Forecasting PM10, hourly concentrations in northern Italy: Insights on models performance and PM10, drivers through self-organizing maps. Atmos. Pollut. Res. 2018. [Google Scholar] [CrossRef]
- Zhou, Q.; Jiang, H.; Wang, J. A hybrid model for PM2.5, forecasting based on ensemble empirical mode decomposition and a general regression neural network. Sci. Total. Environ. 2014, 496, 264–274. [Google Scholar] [CrossRef]
- Weide, L.; Demeng, K.; Jinran, W. A New Hybrid Model FPA-SVM Considering Cointegration for Particular Matter Concentration Forecasting: A Case Study of Kunming and Yuxi, China. Comput. Intell. Neurosci. 2017, 366, 1–11. [Google Scholar] [CrossRef]
- Ping, J. A novel hybrid strategy for PM2.5, concentration analysis and prediction. J. Environ. Manag. 2017, 196, 443–457. [Google Scholar] [CrossRef]
- Liu, B. Forecasting PM2.5 concentration using spatio-temporal extreme learning machine. In Proceedings of the 2016 15th IEEE International Conference on Machine Learning and Applications (ICMLA), Anaheim, CA, USA, 18–20 December 2016. [Google Scholar]
- Li, X.; Peng, L.; Yao, X. Long short-term memory neural network for air pollutant concentration predictions: Method development and evaluation. Environ. Pollut. 2017, 231, 997–1004. [Google Scholar] [CrossRef]
- Huang, N.E. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z. Ensemble empirical mode decomposition. Adv. Adapt. Data Anal. 2009, 1, 1e41. [Google Scholar]
- María, E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Dragomiretskiy, K. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Du, P.; Wang, J.; Yang, W. Multi-step ahead forecasting in electrical power system using a hybrid forecasting system. Renew. Energy 2018, 122, 533–550. [Google Scholar] [CrossRef]
- Wang, J. A novel hybrid system based on a new proposed algorithm - Multi - Objective Whale Optimization Algorithm for wind speed forecasting. Appl. Energy 2017, 208, 344–360. [Google Scholar] [CrossRef]
- Dong, Y. A hybrid seasonal mechanism with a chaotic cuckoo search algorithm with a support vector regression model for electric load forecasting. Energies 2018, 11, 1009. [Google Scholar] [CrossRef]
- Fan, G.F. Short term load forecasting based on phase space reconstruction algorithm and bi-square kernel regression model. Appl. Energy 2018, 224, 13–33. [Google Scholar] [CrossRef]
- Sun, W. Daily PM2.5 concentration prediction based on principal component analysis and LSSVM optimized by cuckoo search algorithm. J. Environ. Manag. 2017, 188, 144–152. [Google Scholar] [CrossRef] [PubMed]
- Deyun, W.; Yanling, L.; Hongyuan, L. Day-ahead PM2.5 concentration forecasting using WT-VMD based decomposition method and back propagation neural network improved by differential evolution. Int. J. Environ. Res. Public Health 2017, 14, 764. [Google Scholar] [CrossRef]
- Mahajan, S.; Chen, L.J.; Tsai, T.C. Short-term PM2.5 forecasting using exponential smoothing method: A comparative analysis. Sensors 2018, 18, 3223. [Google Scholar] [CrossRef] [PubMed]
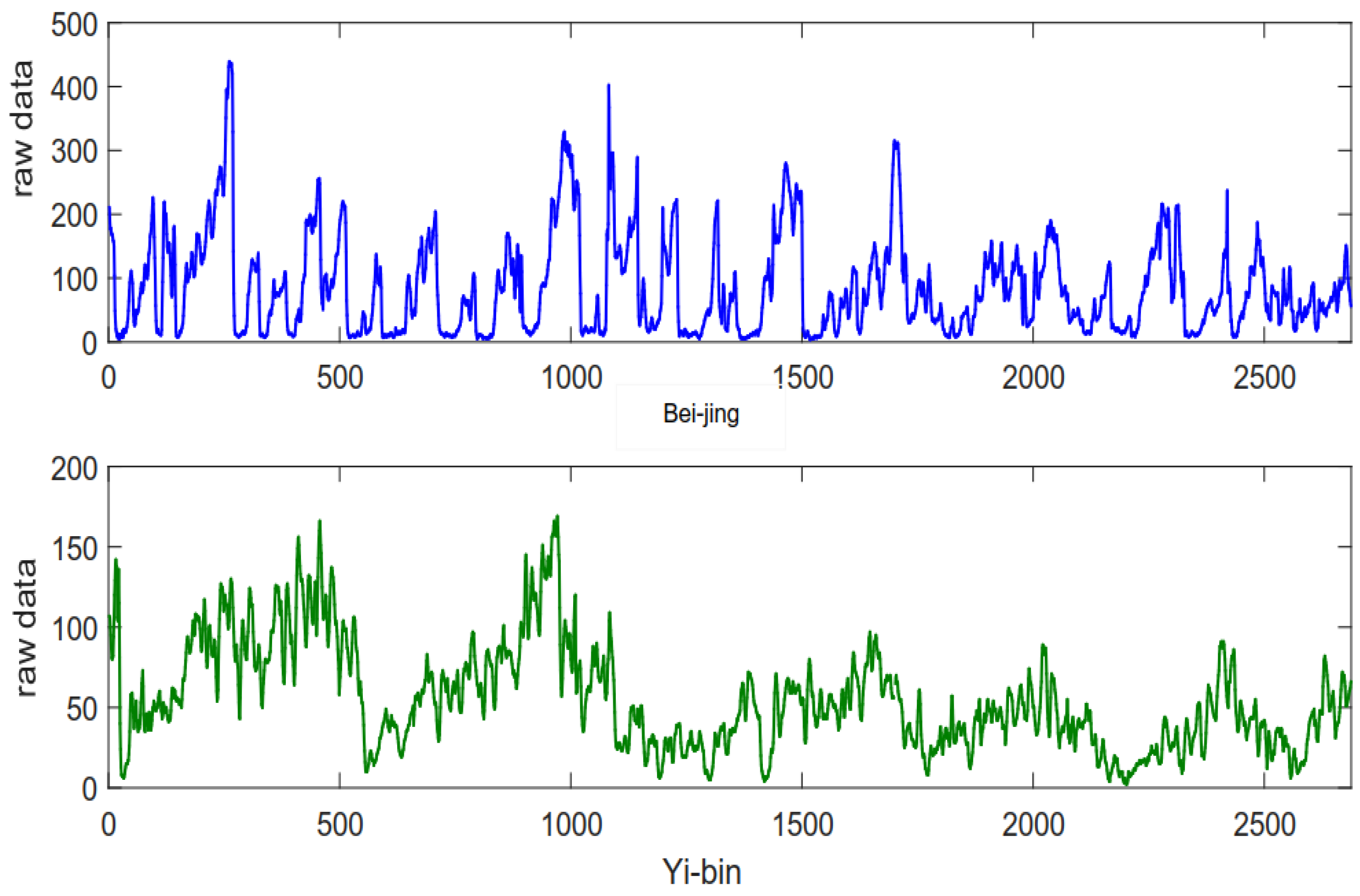
| Data Sets | Time | Training Days | Testing Days | Numbers | Means | min. | max. | std. |
|---|---|---|---|---|---|---|---|---|
| Beijing | 1 h | 5 January–19 April 2015 | 20 April–26 April 2015 | 2688 | 85.67 | 4 | 439 | 75.36 |
| Yibin | 1 h | 5 January–19 April 2015 | 20 April–26 April 2015 | 2688 | 55.23 | 2 | 169 | 32.22 |
| Metric | Definition | Equation |
|---|---|---|
| The index of agreement of forecasting results | ||
| The average forecasting error | ||
| The mean absolute forecasting error | ||
| Average of prediction error squares | ||
| Mean Absolute Percentage Error |
| Model | AE | MAE | MSE | MAPE (%) | IA |
|---|---|---|---|---|---|
| VCEEMDAN-SF-WOA-LSSVM | −0.9931 | 5.4957 | 57.7116 | 11.34 | 0.9803 |
| SF-WOA-LSSVM | −0.8994 | 5.6535 | 60.5557 | 11.65 | 0.9792 |
| VCEEMDAN-WOA-LSSVM | 0.1008 | 11.2102 | 226.1804 | 20.17 | 0.9151 |
| VCEEMDAN-SF-LSSVM | −0.4904 | 6.0393 | 67.2461 | 13.01 | 0.9774 |
| VCEEMDAN-LSSVM | −0.3252 | 15.1042 | 404.6517 | 27.73 | 0.8412 |
| LSSVM | −0.3110 | 15.1609 | 407.8657 | 27.78 | 0.8409 |
| Model | AE | MAE | MSE | MAPE (%) | IA |
|---|---|---|---|---|---|
| SF-WOA-LSSVM | 0.0784 | 2.0839 | 9.5472 | 6.40 | 0.9932 |
| VCEEMDAN-WOA-LSSVM | 0.08 | 4.1267 | 28.6088 | 13.34 | 0.9788 |
| VCEEMDAN-SF-LSSVM | 0.1905 | 2.5544 | 14.2633 | 7.85 | 0.9898 |
| VCEEMDAN-LSSVM | 0.2954 | 5.8399 | 56.9245 | 19.18 | 0.9570 |
| LSSVM | 0.3266 | 5.8170 | 56.3109 | 19.39 | 0.9575 |
| Compared Models | Beijing | Yibin | ||
|---|---|---|---|---|
| DM-Value | p-Value | DM-Value | p-Value | |
| VCEEMDAN-SF-WOA-LSSVM vs. SF-WOA-LSSVM | 2.984 | 0.000 ** | 5.714 | 0.000 ** |
| VCEEMDAN-SF-WOA-LSSVM vs. VCEEMDAN-WOA-LSSVM | 6.167 | 0.000 ** | 2.935 | 0.002 ** |
| VCEEMDAN-SF-WOA-LSSVM vs. VCEEMDAN-SF-LSSVM | 2.769 | 0.000 ** | 6.877 | 0.000 ** |
| VCEEMDAN-SF-WOA-LSSVM vs. VCEEMDAN-LSSVM | 7.248 | 0.000 ** | 5.659 | 0.000 ** |
| VCEEMDAN-SF-WOA-LSSVM vs. LSSVM | 7.246 | 0.000 ** | 7.354 | 0.000 ** |
| Model | AE | MAE | MSE | MAPE (%) | IA |
|---|---|---|---|---|---|
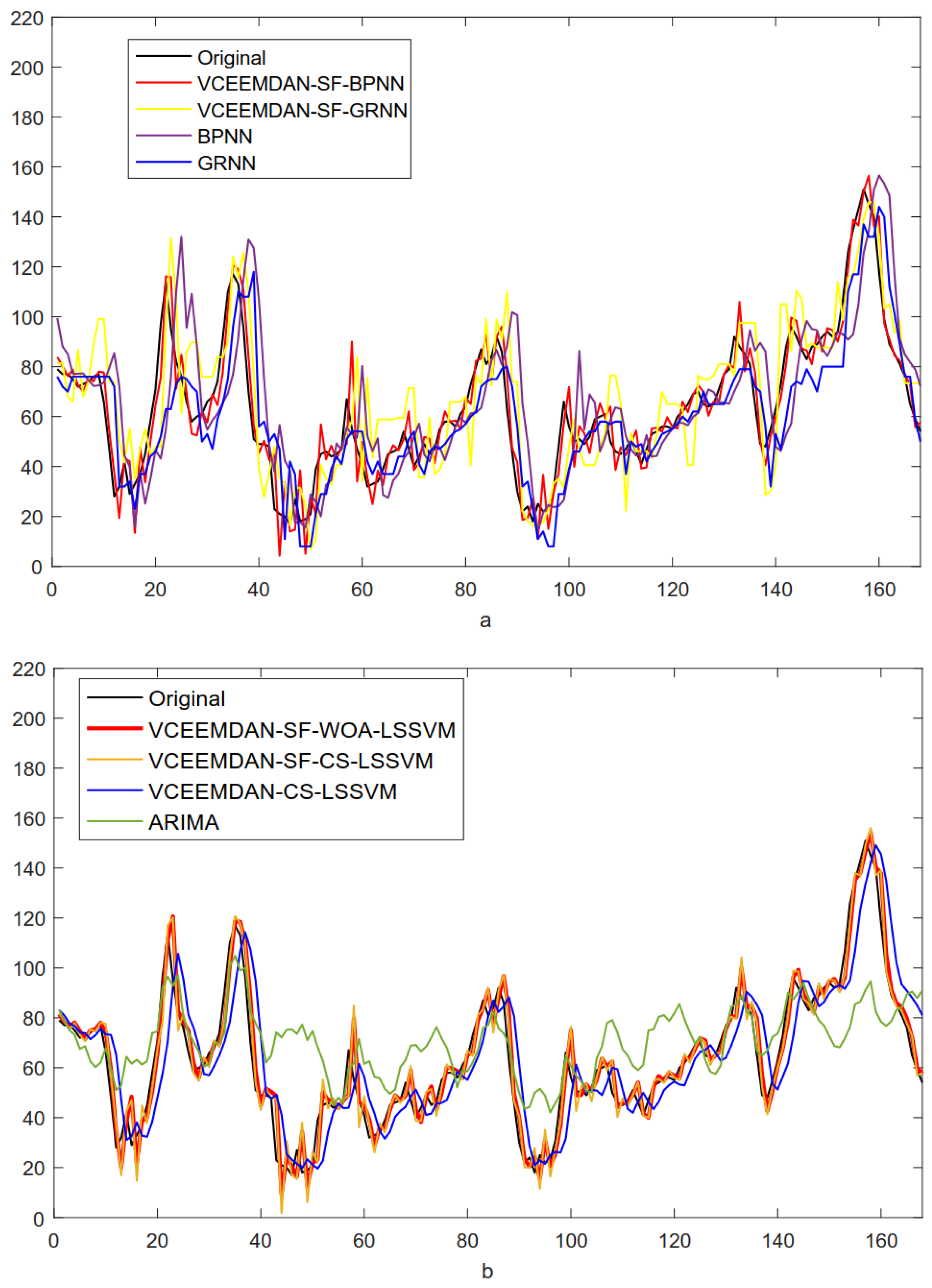
| VCEEMDAN-SF-WOA-LSSVM | −0.9931 | 5.4957 | 57.7116 | 11.34 | 0.9803 |
| VCEEMDAN-SF-CS-LSSVM | −0.6123 | 6.1817 | 69.5793 | 13.38 | 0.9766 |
| VCEEMDAN-SF-BPNN | −0.3991 | 6.6083 | 75.8084 | 14.24 | 0.9746 |
| VCEEMDAN-SF-GRNN | −4.1243 | 14.1117 | 313.2350 | 26.87 | 0.8962 |
| VCEEMDAN-CS-LSSVM | −0.1054 | 11.4278 | 234.7603 | 20.46 | 0.9125 |
| BPNN | −2.5047 | 17.2058 | 556.2312 | 32.46 | 0.7997 |
| GRNN | 3.3690 | 12.0000 | 258.2738 | 22.77 | 0.9012 |
| ARIMA | −6.9863 | 16.6792 | 490.1992 | 39.44 | 0.6893 |
| Model | AE | MAE | MSE | MAPE (%) | IA |
|---|---|---|---|---|---|
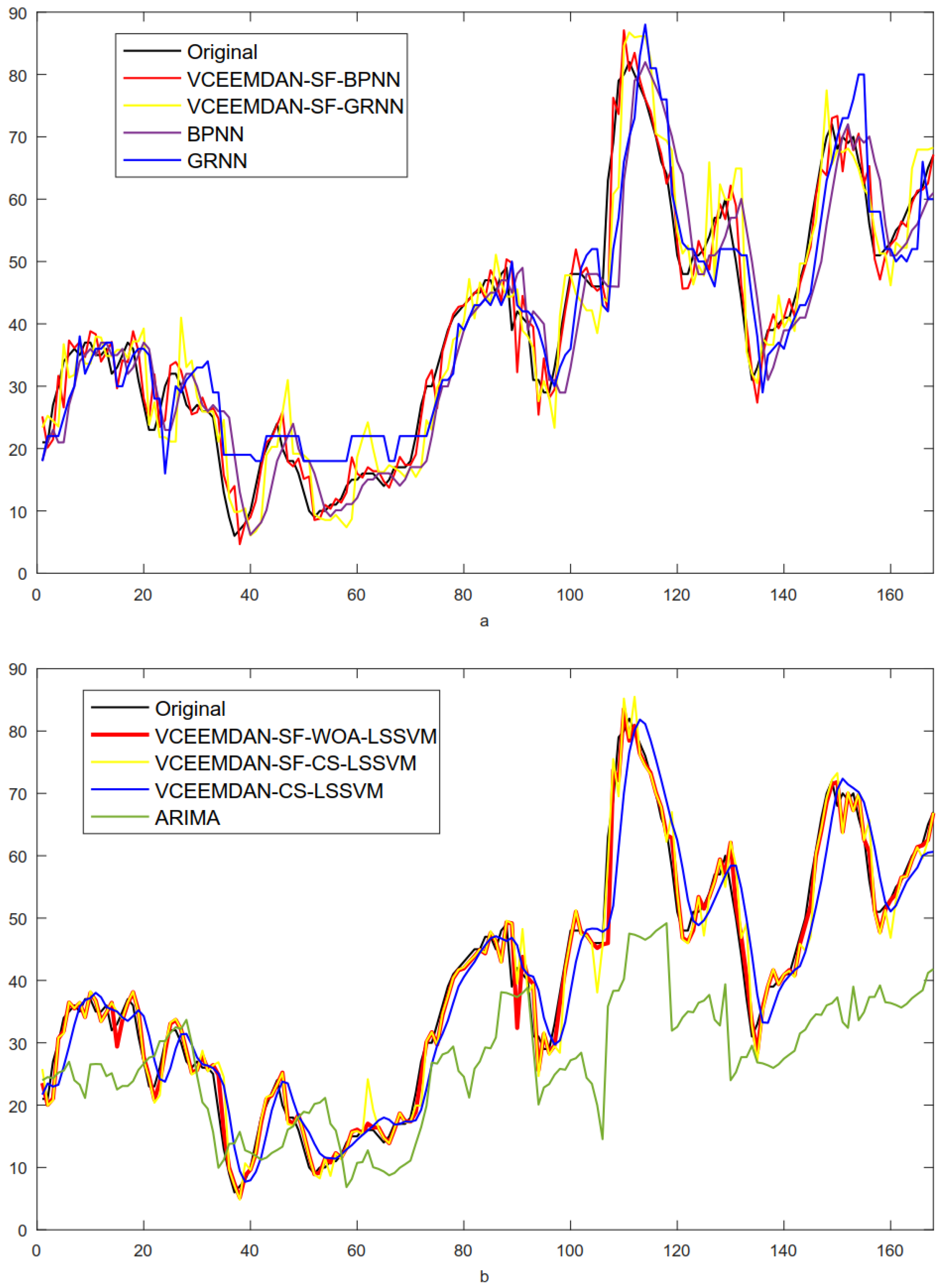
| VCEEMDAN-SF-WOA-LSSVM | 0.0844 | 1.9688 | 8.4035 | 6.15 | 0.9940 |
| VCEEMDAN-SF-CS-LSSVM | −0.0935 | 2.5581 | 13.2533 | 8.29 | 0.9905 |
| VCEEMDAN-SF-BPNN | −0.2707 | 2.4995 | 13.5391 | 8.48 | 0.9903 |
| VCEEMDAN-SF-GRNN | −0.1704 | 4.3682 | 32.0127 | 14.74 | 0.9778 |
| VCEEMDAN-CS-LSSVM | 0.0919 | 4.1194 | 28.4881 | 13.31 | 0.9789 |
| BPNN | 0.7761 | 6.0931 | 64.3302 | 20.06 | 0.9521 |
| GRNN | −0.5357 | 5.9405 | 50.7738 | 22.31 | 0.9594 |
| ARIMA | 12.0946 | 16.5594 | 276.9223 | 35.05 | 0.7300 |
| Compared Models | Beijing | Yibin | ||
|---|---|---|---|---|
| DM-Value | p-Value | DM-Value | p-Value | |
| VCEEMDAN-SF-WOA-LSSVM vs. VCEEMDAN-SF-CS-LSSVM | 3.034 | 0.000 ** | 3.636 | 0.009 ** |
| VCEEMDAN-SF-WOA-LSSVM vs. VCEEMDAN-SF-BPNN | 2.928 | 0.004 ** | 3.843 | 0.000 ** |
| VCEEMDAN-SF-WOA-LSSVM vs. VCEEMDAN-SF-GRNN | 7.697 | 0.000 ** | 5.719 | 0.000 ** |
| VCEEMDAN-SF-WOA-LSSVM vs. VCEEMDAN-CS-LSSVM | 6.246 | 0.000 ** | 5.952 | 0.000 ** |
| VCEEMDAN-SF-WOA-LSSVM vs. BPNN | 6.588 | 0.000 ** | 6.458 | 0.000 ** |
| VCEEMDAN-SF-WOA-LSSVM vs. GRNN | 5.167 | 0.000 ** | 8.839 | 0.000 ** |
| VCEEMDAN-SF-WOA-LSSVM vs. ARIMA | 7.097 | 0.000 ** | 9.992 | 0.000 ** |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, F.; Li, W. A Combined Model Based on Feature Selection and WOA for PM2.5 Concentration Forecasting. Atmosphere 2019, 10, 223. https://doi.org/10.3390/atmos10040223
Zhao F, Li W. A Combined Model Based on Feature Selection and WOA for PM2.5 Concentration Forecasting. Atmosphere. 2019; 10(4):223. https://doi.org/10.3390/atmos10040223
Chicago/Turabian StyleZhao, Fang, and Weide Li. 2019. "A Combined Model Based on Feature Selection and WOA for PM2.5 Concentration Forecasting" Atmosphere 10, no. 4: 223. https://doi.org/10.3390/atmos10040223
APA StyleZhao, F., & Li, W. (2019). A Combined Model Based on Feature Selection and WOA for PM2.5 Concentration Forecasting. Atmosphere, 10(4), 223. https://doi.org/10.3390/atmos10040223





