1. Introduction
During May and June (i.e., MJ, the so-called Meiyu season in Taiwan), one of the most frequently observed weather systems affecting rainfall formation in Taiwan is the frontal event [
1,
2]. In general, the Meiyu frontal systems can bring heavy rainfall formations in Taiwan, which have a high potential to cause severe property damage [
3]. For example, during the Meiyu season of 2017, three frontal rainfall events (
Figure 1) brought continuous heavy rainfall to Taiwan and led to severe crop damage and large economic losses. Among these three frontal rainfall events (named FR1~FR3;
Figure 1), the most intense rainfall occurred from June 2 to June 4 (i.e., FR2) of 2017. In this natural disaster, there were approximately 6,000 hectares of cropland destroyed, and local economic losses reached approximately
$9 million USD, according to the estimations of agricultural disaster reports from the Food Agency Council of Agriculture, Executive Yuan in Taiwan (
https://eng.coa.gov.tw). Therefore, understanding what might affect the formation of heavy Meiyu rainfall events, as well as what might affect the capability of models to predict the Meiyu rainfall formation, is one of the most important research subjects for the local community in Taiwan [
4,
5,
6,
7,
8,
9].
The weather systems occurring over the East Asian summer monsoon region during the warm seasons (May to October, MJJASO) are known to be under the modulation of atmospheric circulation changes related to the 30–60 day and 10–30 day boreal summer intra-seasonal oscillations (BSISOs) [
10,
11,
12,
13]. Lee et al. [
10] have proposed a specific metric for better characterizing the intra-seasonal variability of Asian summer monsoon circulation related to the 30–60 day ISO (named BSISO1) and 10–30 day ISO (named BSISO2) from observations. Using the index of BSISOs proposed by Lee et al. [
10], more recent observational studies have examined the impact of changes in atmospheric circulations related to BSISOs (hereafter refers to the impact of BSISOs) in affecting rainfall characteristics over various areas of the East Asian summer monsoon region [
13,
14,
15,
16,
17,
18,
19]. Among these studies, the impact of BSISOs in affecting the typhoon type of rainfall [
17] and the diurnal type of rainfall [
13] in Taiwan have been examined in detail. Chen et al. [
20] pointed out that the MJJASO rainfall in Taiwan is mainly modulated by different types of weather systems in different months. In MJ, the heavy rainfall in Taiwan is mainly contributed to the frontal type of rainfall, while the typhoon type of rainfall is the major contributor of heavy rainfall in Taiwan during JAS [
20]. However, compared to issues related to other types of rainfall, the issue of how the circulation changes associated with BSISOs can modulate the formation of frontal rainfall (or the heavy rainfall) in Taiwan during the Meiyu season has been rarely discussed. This will be examined in detail herein.
On the other hand, besides the observational studies, other studies have focused on the predictive skill of BSISOs in the models [
11] and have studied the sub-seasonal prediction of extreme precipitation over Asia using the perspective of BSISOs [
12]. Overall, it seems that the predictions of BSISOs are important for the predictions of heavy rainfall formation over Asia [
12,
21,
22]. However, whether or not this is also true for the prediction of local rainfall formation in Taiwan is still unknown and deserves research attention.
In summary of the above, underexplored issues, the main objective of this study is to examine the possible impacts of BSISOs in affecting the formation of heavy Meiyu rainfall events in Taiwan from the observational data. In addition, this study aims to understand whether the model’s capability in forecasting the BSISOs has some insight on its capability in forecasting the Meiyu rainfall formation in Taiwan. We mainly use the rainfall events during the 2017 Meiyu season as examples to examine the above scientific issues. For the models, we use the forecast data at lead times of 1 day to 16 days (i.e., LT1~16) obtained from the National Centers for the Environmental Prediction Global Forecast System (i.e., NCEPgfs) and the Taiwan Central Weather Bureau Global Forecast System (i.e., CWBgfs). Notably, the impact of BSISOs on various research subjects have been documented in many journal articles [
13,
15,
16,
17,
18,
23,
24,
25], but not in only the technical reports. The importance of this kind of study [
13,
15,
16,
17,
18,
23,
24,
25] is that they can provide useful information for understanding how the local weather can be affected by the intra-seasonal variability of large-scale atmospheric circulations. Since the current study is the first to document the relationship between the phases of BSISO2 and the occurrence frequency of heavy Meiyu rainfall in Taiwan (including the related circulation changes, explained later), we believe that the findings of this study can provide lots of useful information for the research communities interested in studying or in predicting the Meiyu rainfall formation in Taiwan.
The remainder of this paper is organized as follows. Details of the observational data and the forecast data used for the analyses are provided in
Section 2. Results of the observational evidence of BSISOs in modulating the rainfall formation in Taiwan are presented in
Section 3, which is followed by a discussion of the model forecasts in
Section 4. A conclusion is given in
Section 5.
3. Results
Various distinct features revealed from the observational data regarding the potential impact of BSISOs in modulating the rainfall formation over Taiwan are documented in this section, and discussed as follows.
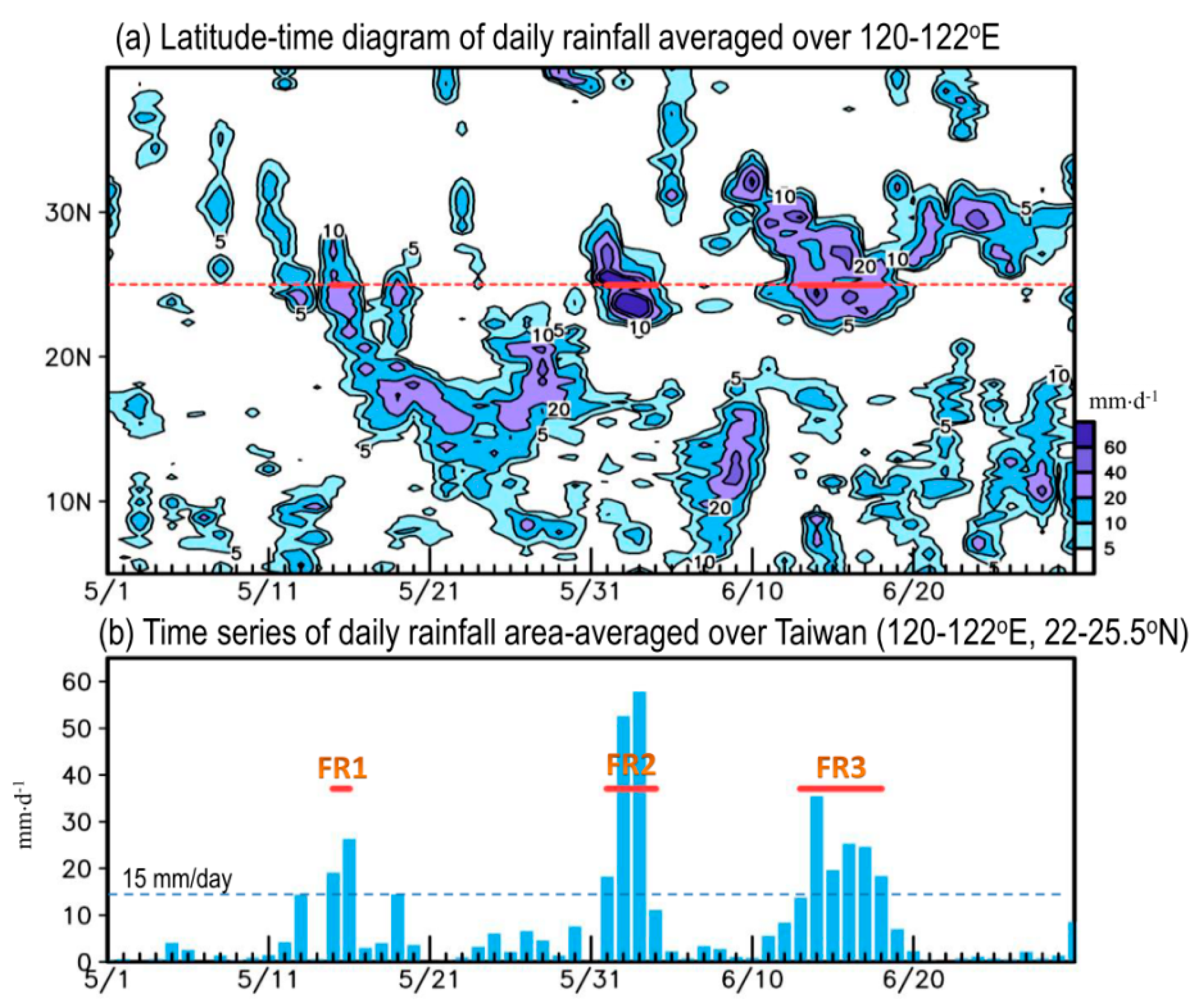
First, we examine the north-south propagating behavior of the rainfall formation over the longitudinal zone of Taiwan (120–122° E) during May and June 2017, based on the latitude-time diagram shown in
Figure 1a. According to
Figure 1a, Taiwan (located around 25° N, indicated by the dashed orange line) is mainly under the modulation of southward propagating rainfall systems from north of 25° N and northward propagating rainfall systems from south of 25° N during three different time periods: 15–16 May (FR1 in
Figure 1b), 1–3 June (FR2), and 14–18 June (FR3). In this case, the heavy rainfall events (FR1~FR3) are selected based on the criterion that the daily rainfall amount of >15 mm/day has continued for at least two days (see
Figure 1b). It can be seen from the synoptic weather maps provided by the Central Weather Bureau of Taiwan (
Figure 2a,c) that the rainfall formation over Taiwan during these three periods is caused by the passage of frontal events. By examining the daily mean fields of low-level atmospheric circulation changes at 850 hPa (
Figure 2d,f), it is further noted that each of these three heavy rainfall events are modulated by the enhanced southwesterly winds over the South China Sea. Previous studies have noted that the enhancement of southwesterly winds over the South China Sea is important in bringing the moisture supply from the lower latitude regions to the area of Taiwan to support the heavy rainfall formation in Taiwan [
1,
2]. Recently, Huang and Chang [
13] noted that, under the modulation of BSISOs, a northward propagation of moisture supply was revealed over the domain covering 115° E–130° E to 5° N–35° N to support the warm season diurnal rainfall formation in Taiwan. Focusing on
Figure 1a, it seems that the rainfall over the domain south of 25° N also consists of some northward propagation signals. As inferred from these documented features of
Figure 1 and
Figure 2 and the findings of Huang and Chang [
13], we hypothesize that the evolution of atmospheric conditions (including the movement of southwesterly wind and moisture supply) related to BSISOs, might be important in modulating the formation of the Meiyu rainfall in Taiwan. This hypothesis will be clarified in later examinations.
Also noted from
Figure 1 and
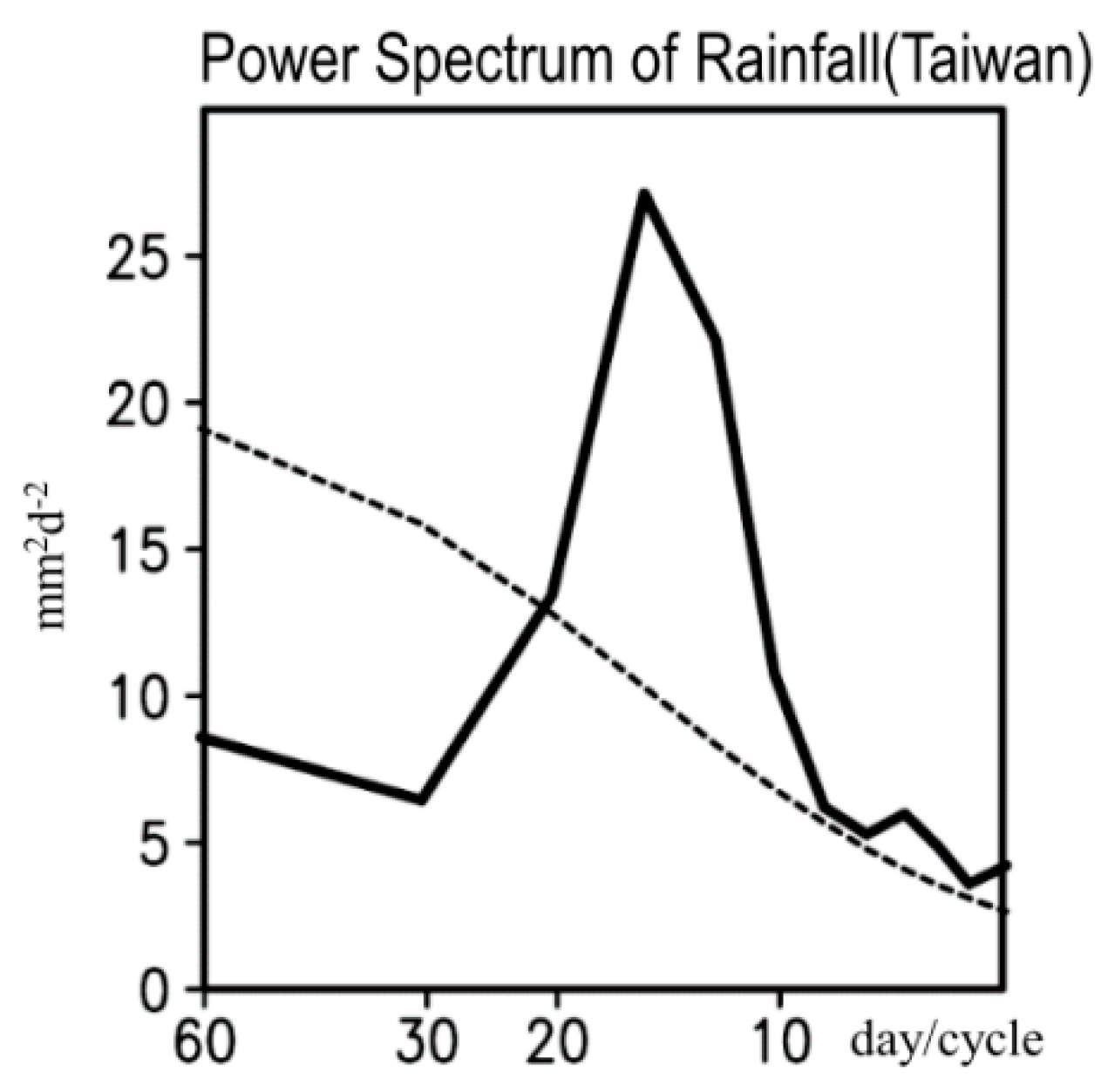
Figure 2, the difference between the appearance times of the three heavy rainfall events is approximately 12 to 17 days. This implies that the rainfall formation over Taiwan during the 2017 Meiyu season might be modulated by the BSISO2 (i.e., 10 to 30 day ISO) more than the BSISO1 (i.e., 30 to 60 day ISO). By applying a power spectrum analysis on daily rainfall over Taiwan during the 2017 Meiyu season, the result shown in
Figure 3 confirms that the variation of rainfall is mainly dominated by an ISO mode within the 10 to 30 day range. This suggests that the rainfall variation in
Figure 1b is mainly regulated by the evolution of BSISO2, and the influence of BSISO1 is less.
One might question that the lack of 30 to 60 day ISO mode in
Figure 3 is because only 61-day data is used for the analysis. To clarify this, we have tested
Figure 3 using a longer period (i.e., MJJASO) of 2017. The result also points out that the 10 to 30 day ISO mode is more important than the 30 to 60 day ISO mode (
Supplementary Figure S4). In addition, from our tests for other years, we note that although only 61-day rainfall data in Taiwan are used for the power spectrum analysis, we can find a clear signal of 30 to 60 day ISO mode in some years (e.g., 2008, 2009, 2012,
Supplementary Figure S5). In other words, the lack of 30 to 60 day ISO mode in
Figure 3 is not because a 61-day data is used. Regarding why a longer period is not focused on (e.g., MJJASO, as in MV-EOF analysis), but only on MJ, this is related to the fact that the rainfall in Taiwan is mainly contributed by different types of rainfall in different months [
20]. Because the focus of this study is to understand how the atmospheric circulation changes related to BSISOs can impact the heavy Meiyu rainfall in Taiwan, we only examine the changes in MJ, but not in other months.
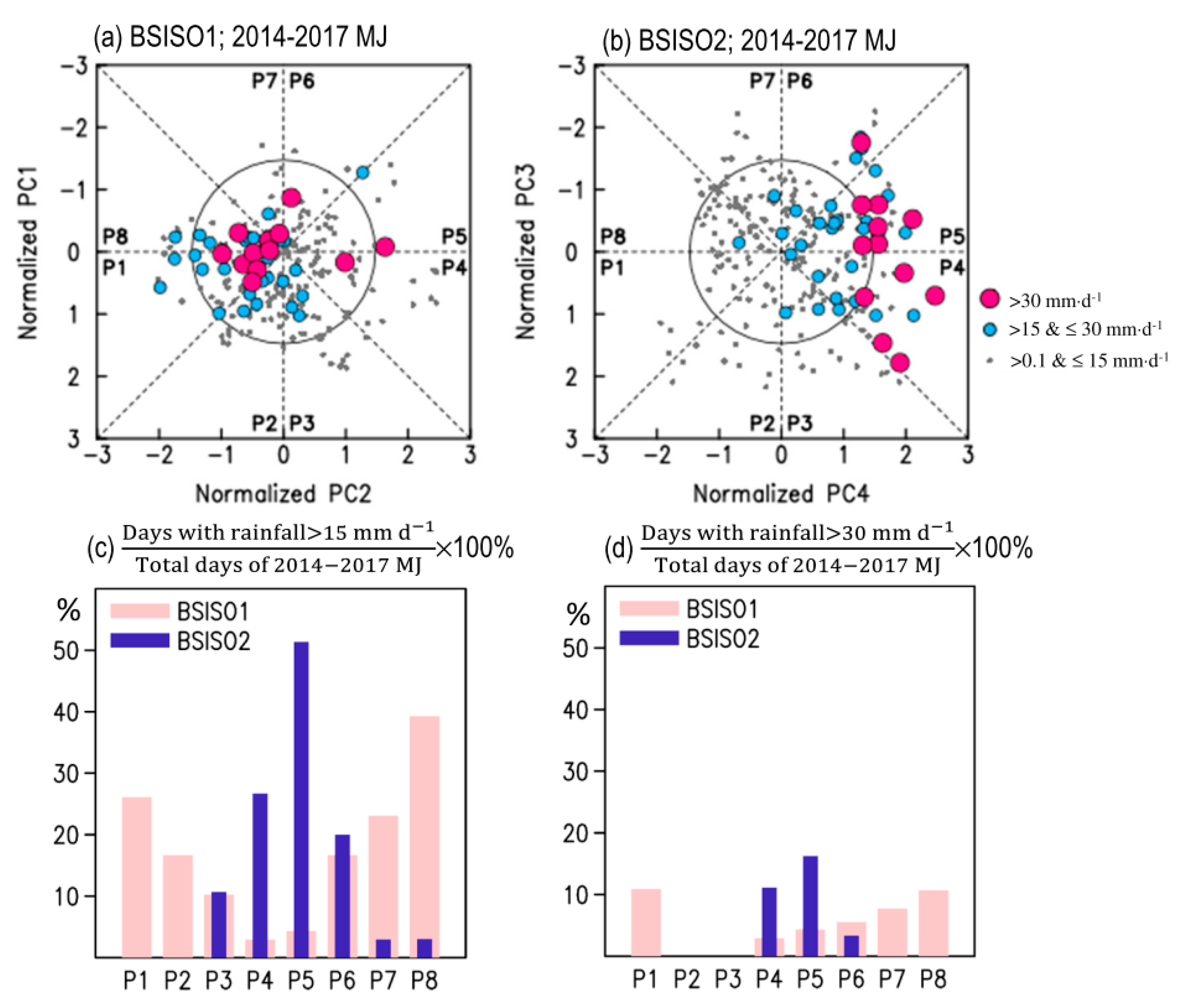
To further understand the potential linkage between the evolution of BSISOs and the occurrence of heavy rainfall events in Taiwan during the 2017 Meiyu season, we construct the phase diagram of BSISOs and mark the dates with daily rainfall amounts over Taiwan to be larger than 15 mm/day in the related phase of BSISOs. The method used to construct the phase diagram of
Figure 4a,b follows the procedure described in Lee et al. [
10]. As seen from
Figure 4b (
Figure 4a), most of the heavy rainfall days occurred when the BSISO2 (BSISO1) was in phases 4–6 (phase 8-1). In addition, it seems that, when the amplitude of BSISO2 is larger (i.e., >1.5; strong BSISO2 event), the rainfall amount in Taiwan is also larger (i.e., more chance to have daily rainfall amount >30 mm/day). In contrast, it is noted from
Figure 4a that all the heavy rainfall days occur when the amplitude of BSISO1 is smaller than 1.5 (i.e., weak BSISO1 event). Such a difference between the amplitude of BSISO1 (
Figure 4a) and BSISO2 (
Figure 4b), suggests that BSISO2 might have stronger influence than BSISO1 in modulating the heavy rainfall formation in Taiwan during the 2017 Meiyu season. By comparing several types of time series [including the anomalies (i.e., remove the mean of rainfall during May and June 2017) of daily rainfall (gray bars in
Figure 4c), 30 to 60 day band pass filtered daily rainfall (red line in
Figure 4c) and 10 to 30 day band pass filtered daily rainfall (green line in
Figure 4c)] in Taiwan, we clarify that the variation of rainfall is mainly dominated by BSISO2, rather than by BSISO1.
The question remains of whether the above documented features are only revealed in the Meiyu season of 2017. To clarify this, we further examine the rainfall events for the Meiyu seasons of 2014–2017. The selection of the starting year of 2014 is because GPM IMERG data are only available after March 2014. It is noted from
Figure 5a,c,d (pink bar) that most of the heavy rainfall events (>15 mm/day) occurred in phase 8 to 1 of BSISO1, with an amplitude of BSISO1 smaller than 1.5 (i.e., weak BSISO1 case). This is similar to what was revealed in
Figure 4a for the 2017 Meiyu season. In contrast, it is noted from
Figure 5b,c,d (blue bar) that most of the heavy rainfall events (>15 mm/day) occurred in phases 4-6 of BSISO2. Focusing on
Figure 5b, it is further noted that not all of the heavy rainfall events (>15 mm/day, blue and red dots) occur when the BSISO2 is strong (i.e., amplitude >1.5). However, when the BSISO2 is stronger, it has a higher chance to have a larger amount of Meiyu rainfall formed in Taiwan (i.e., red dots mostly occur when the amplitude of BSISO2 > 1.5). This is consistent with what was revealed in
Figure 4b.
In a summary of
Figure 4 and
Figure 5, we find that BSISO2 is more important than BSISO1 in determining the occurrence of heavy rainfall events in Taiwan during the 2014–2017 Meiyu seasons. Huang et al. [
28] have applied the power spectrum analysis on the Taiwan rainfall during the entire period of March 2014 to February 2017, and it can be seen in their result that the 30 to 60 day ISO mode is not as important as the 10 to 30 day ISO mode. This is consistent with our findings of
Figure 4 and
Figure 5. Therefore, the following analyses will be focused only on issues related to BSISO2.
It can be inferred from (1) the similarity between the EOF patterns used in the current study (
Supplementary Figure S1) and those used in Lee et al. [
10] and (2) the similarity between the time series of PCs used in the current study and those provided by APCC (
Supplementary Figure S2) that the phase-space patterns in
Figure 4a,b and
Figure 5a,b should correspond to those shown in Figure 8 of Lee et al. [
10]. This inference is confirmed by the figure provided in the
Supplementary Information (
Figure S6), which consists of northward moving signals. Further examinations and discussions for the northward propagating signals of atmospheric circulations related to BSISO2 are given next to help understand why the heavy rainfall events tend to occur in phases 4–6 of BSISO2.
First, we make composites of low-level wind circulation at 850 hPa superimposed with the related stream function for the 8 phases of BSISO2 during the Meiyu seasons of 2014 to 2017 (
Figure 6a). Notably, to help make a difference among the 8 phases of BSISO2 clearer,
Figure 6 is constructed using the daily anomalies. In addition, because only data of 2014–2017 MJ is used for the composites in
Figure 6, the daily anomalies are obtained by removing the mean value of 2014–2017 MJ, instead of the seasonal mean of the whole period used for the MV-EOF analysis (i.e., 2014–2017 MJJASO). By doing this, we can ensure that the average of 8 phases in
Figure 6 is close to zero, and the differences between phases can be more clearly represented. In contrast, if
Figure 6a is constructed by removing the mean value of 2014–2017 MJJASO (see
Supplementary Figure S7b), a high system pattern will be revealed over the western North Pacific region in all phases of BSISO2. This high system pattern is induced because of the difference between the MJ mean and the MJJASO mean of 2014–2017 (see
Supplementary Figure S8).
Notably, even though months and years used in this study for the composites of circulations are different to those used in Lee et al. [
10], we do find that our phase-space patterns for the composites of circulations in
Figure 6a are similar to those in Figure 10 of Lee et al. [
10], which both show the northward moving signal of atmospheric circulations. The propagating signal of
Figure 6a is described below. As seen from
Figure 6a, the low-pressure system (i.e., cyclonic flow) first appears over the Bay of Bengal in phases 1–2 and then propagates north and expands westward to cover the area of the South China Sea during phases 2–3. At phase 3, the low system is located south of Taiwan, and Taiwan is under the modulation of northerly wind anomalies, which implies a decrease in monsoon southwesterly wind. The low system over southern Taiwan keeps propagating northward during phases 4–6. During this period, Taiwan is mainly under the modulation of southwesterly wind anomalies (i.e., increase in the southwesterly monsoon). During phases 7-1 of BSISO2, the low system closes to Taiwan disappeared and Taiwan is under the modulation of a high system (i.e., anti-cyclonic flow).
Overall, the enhancement of monsoon southwesterly wind appears over Taiwan at phases 4–6 of BSISO2. Such enhancement of monsoon southwesterly wind can generally bring more moisture supply to support rainfall formation in Taiwan [
1,
2]. It can be seen in
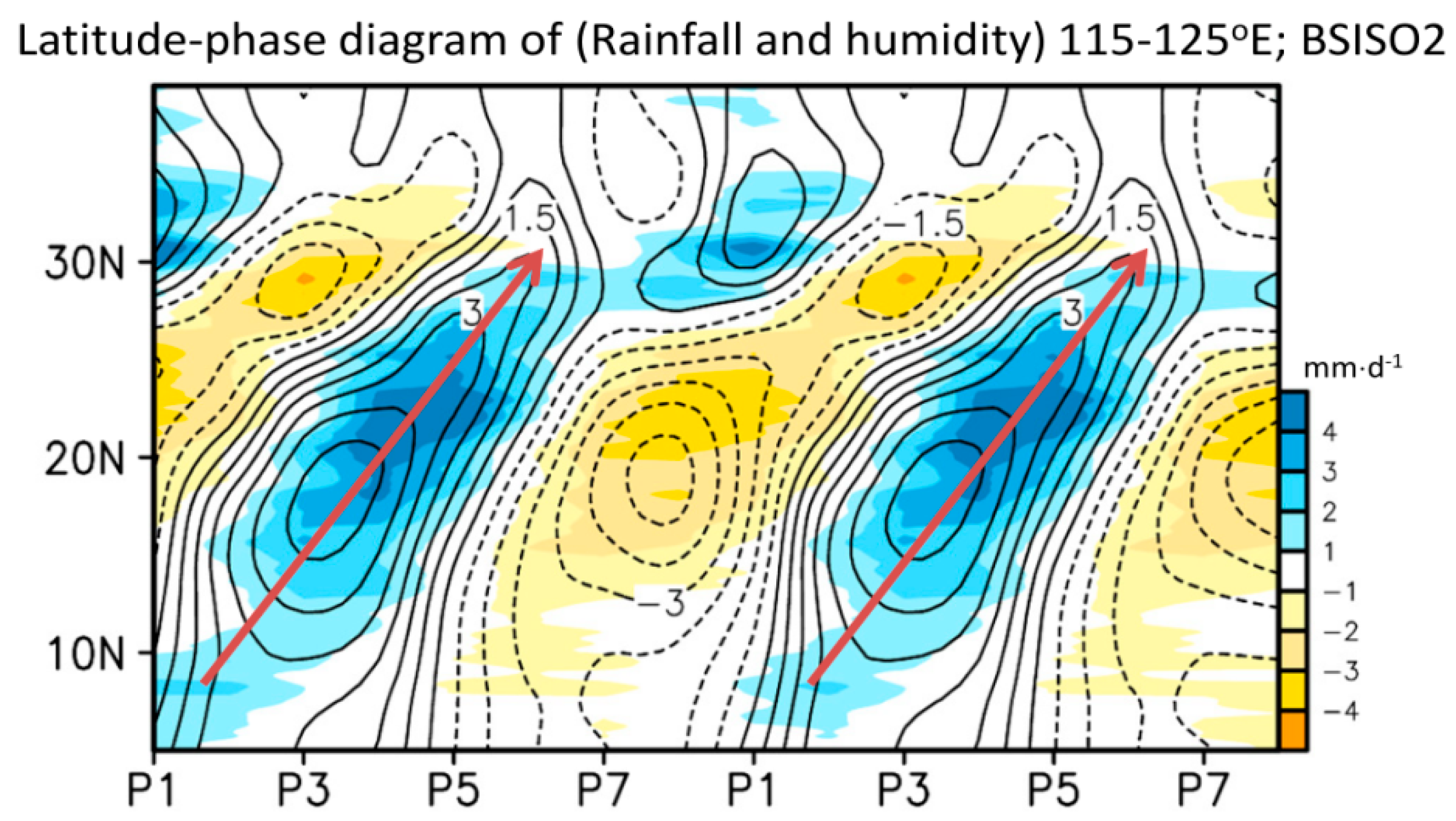
Figure 6b, which is the composite daily rainfall superimposed with the potential function of vertically integrated moisture flux convergence for the 8 phases of BSISO2, that the moisture flux convergence center is located over Taiwan during phases 4–6 of BSISO2. If we backtrack the movement of the moisture flux convergence center, it can be found that the convergence is actually propagating from the lower latitude regions to Taiwan. Such a feature can be further clarified by
Figure 7, which shows a good match between the northward propagation of rainfall (shaded) and vertically integrated specific humidity (contoured) averaged over 115–125° E under the modulation of 8 phases of BSISO2. Notably, the data used to construct
Figure 7 are extracted from the related composites for 8 phases of BSISO2 during the Meiyu seasons of 2014–2017 (e.g.,
Figure 6b).
On the other hand, focusing on 2017, it can be seen from the examinations of 10-to-30 day band pass filtered (i.e., related to BSISO2) low-level circulation and moisture flux convergence for cases FR1, FR2, and FR3, that Taiwan was under the modulation of enhanced monsoon southwesterly wind (
Figure 8a–c) and enhanced moisture flux convergence (
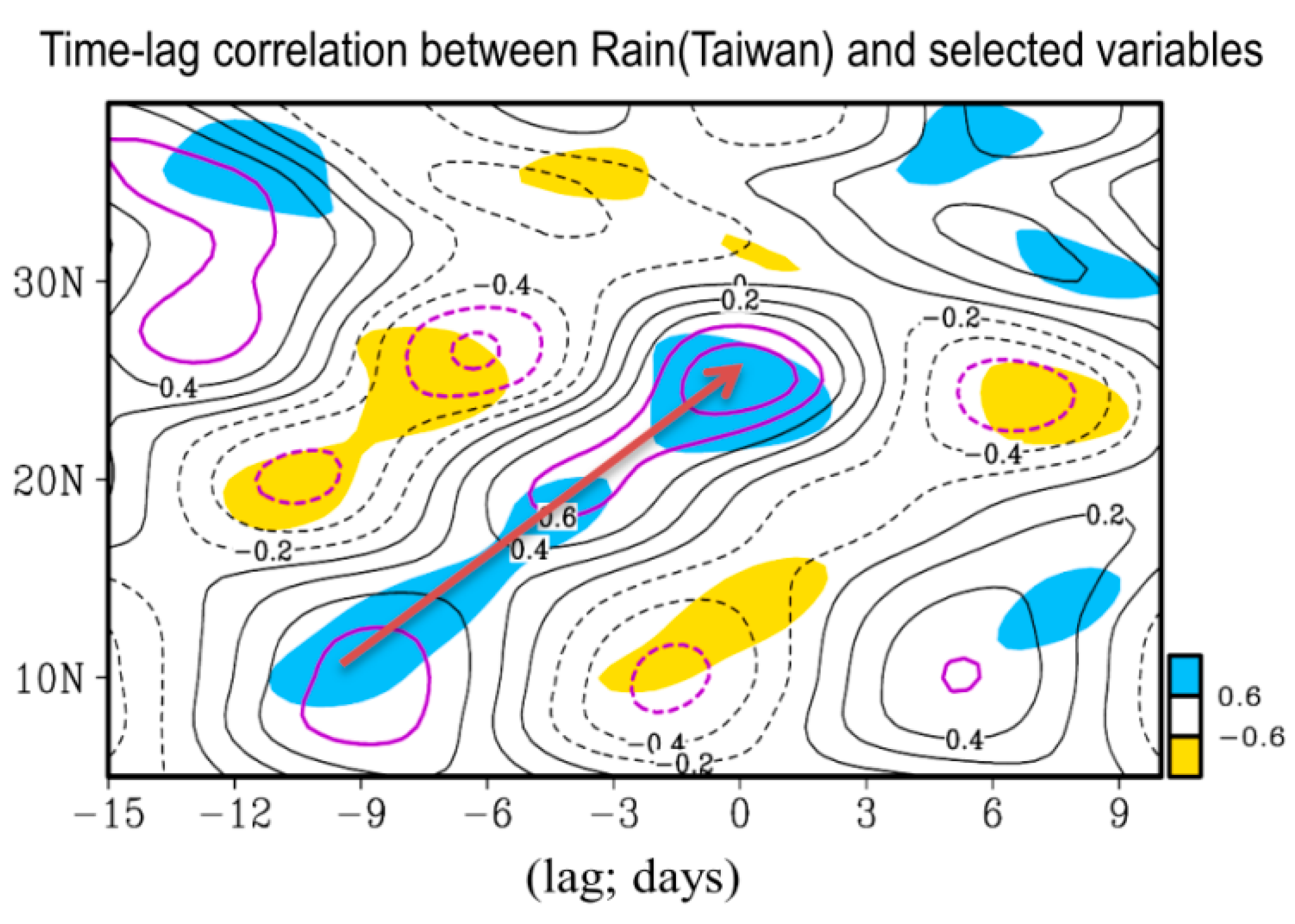
Figure 8d,f) when the heavy rainfall occurred. Moreover, to further clarify that, under the modulation of BSISO2 (i.e., 10 to 30 day ISO), the moisture supply propagates from the lower latitude regions to Taiwan to support the heavy rainfall formation in Taiwan during the 2017 Meiyu season, we construct a time lagged correlation between the 10 to 30 day bandpass filtered rainfall formation in Taiwan (green line in
Figure 4c), the related latitude time diagram of rainfall (shaded in
Figure 9), and the moisture supply (contoured in
Figure 9) for the 2017 Meiyu season. As seen from
Figure 9, a clear northward propagation feature is revealed for both the rainfall and moisture supply over 10–25° N. These features (
Figure 6,
Figure 7,
Figure 8 and
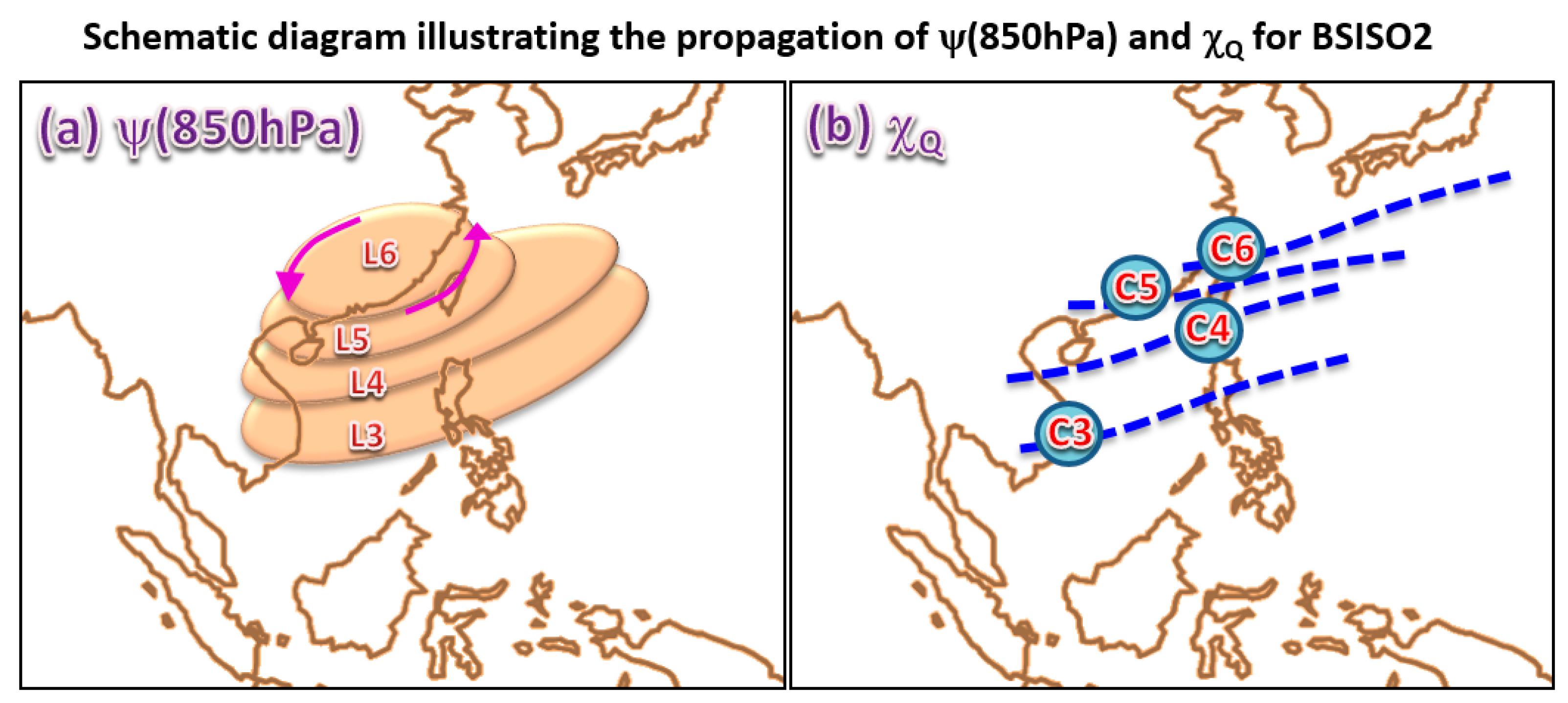
Figure 9), which are summarized by a schematic diagram given in
Figure 10, explain how the BSISO2 can impact the atmospheric conditions (including the enhancement of southwesterly winds and moisture flux convergence) that are favorable for the formation of heavy rainfall events in Taiwan during the Meiyu seasons of 2014 to 2017.
4. Discussion
Since the rainfall formation in Taiwan during the 2017 Meiyu season has been demonstrated to be greatly modulated by the atmospheric circulation and moisture flux convergence related to BSISO2 (see
Section 3), this section discusses whether a better performance of the model in predicting the index of BSISO2, is related to a better performance of the model in forecasting the timing of rainfall formation in Taiwan during the 2017 Meiyu season.
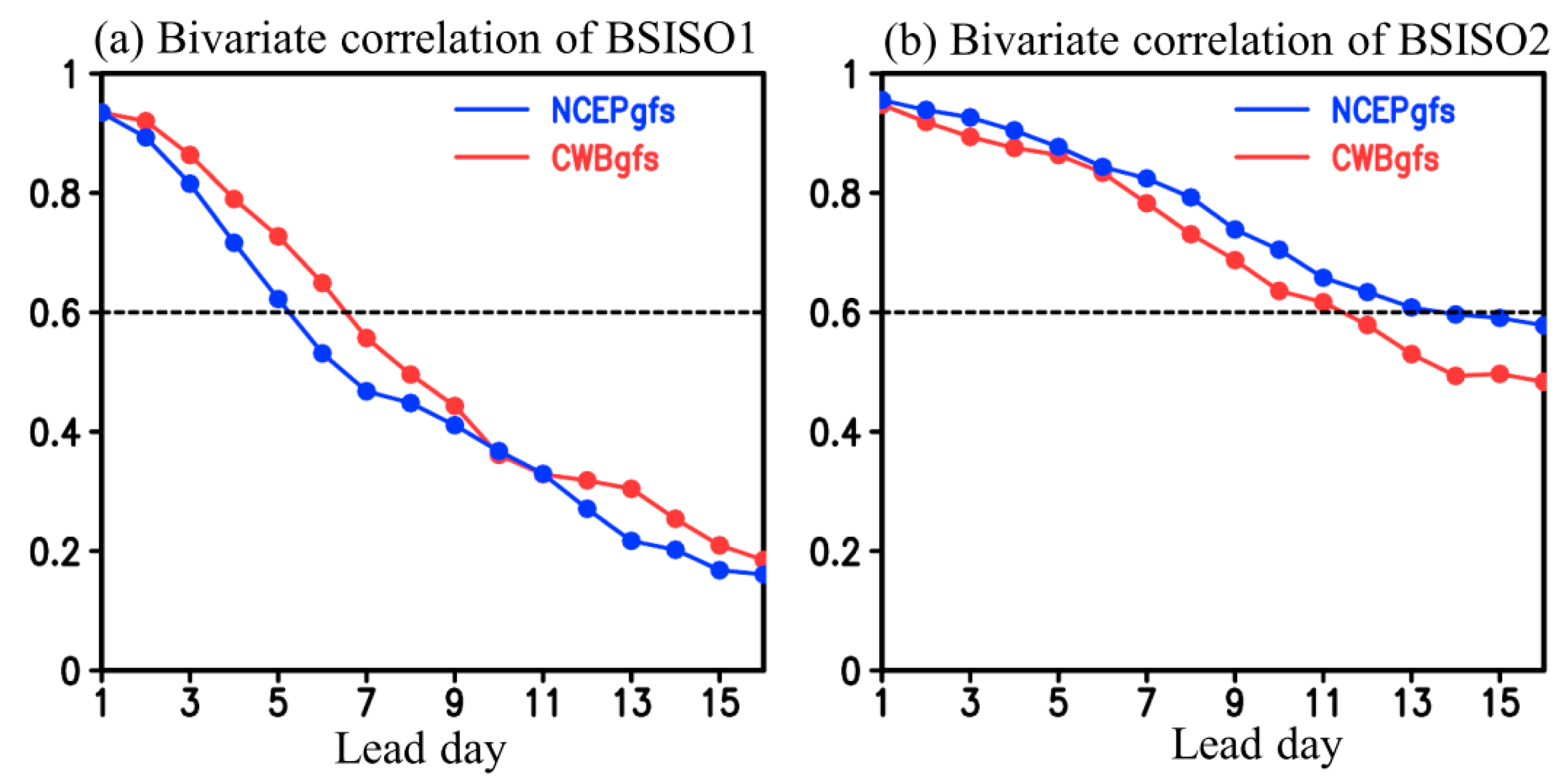
First, we evaluate the model’s performance in depicting the BSISO indices by examining the bivariate correlation coefficients following Lee et al. [
12].
Figure 11 shows the bivariate correlation coefficients for the index of BSISOs during the 2017 Meiyu season forecasted by NCEPgfs (blue line) and CWBgfs (red line) at lead times of 1 day to 16 days. The calculation of bivariate correlation coefficients is based on Equation (2) using the PCs from the two sets of forecasts, as documented in the
Supplementary Information (
Figure S3). Overall, it shows that both NCEPgfs and CWBgfs have better performance in evaluating the index of BSISO2 (
Figure 11b) than the index of BSISO1 (
Figure 11a). Using the value of 0.6 as the criterion of good forecast skill, the NCEPgfs has a good forecast skill of BSISO2 (BSISO1) at lead times of 1 day to 14 days (1 day to 5 days), while CWBgfs has a good forecast skill of BSISO2 (BSISO1) at lead times of 1 day to 11 day (1 day to 6 days).
Notably, by using the same criterion of 0.6, it can be inferred from
Figure 8 of Lee et al. [
12] that CFS (Climate Forecast System) and ECM (ECMWF Ensemble Prediction System) models also perform better in forecasting the index of BSISO2 than the index of BSISO1 in the months of May and June, but not in the months of July to October, during 2013 to 2015. In contrast, BOM (the model provided by the Australian Bureau of Meteorology) shows a better performance in predicting the index of BSISO1 than the index of BSISO2 for all months of May to October, during 2013 to 2015 [
12]. Based on above discussions, it is clear that the prediction skill for the index of BSISOs can vary by the selection of months and by the selection of models. However, because the focus of this study is on the Meiyu season (i.e., MJ), no further discussions are provided for the performance of NCEPgfs and CWBgfs in forecasting the index of BSISOs in the other months of 2017.
On the other hand, by comparing
Figure 11a with
Figure 11b, it seems that CWBgfs has a better skill than NCEPgfs in forecasting the BSISO1, and the reverse situation is true for the forecast of BSISO2 during the 2017 Meiyu season. Since the BSISO2 is more important than BSISO1 in affecting the rainfall formation in Taiwan during the 2017 Meiyu season (see
Section 3), it is important to understand if the NCEPgfs also performs better than CWBgfs in rainfall prediction over the areas near Taiwan during the 2017 Meiyu season. To clarify this question, we plot the point-to-point temporal correlation of daily rainfall between the observation (i.e., time series in
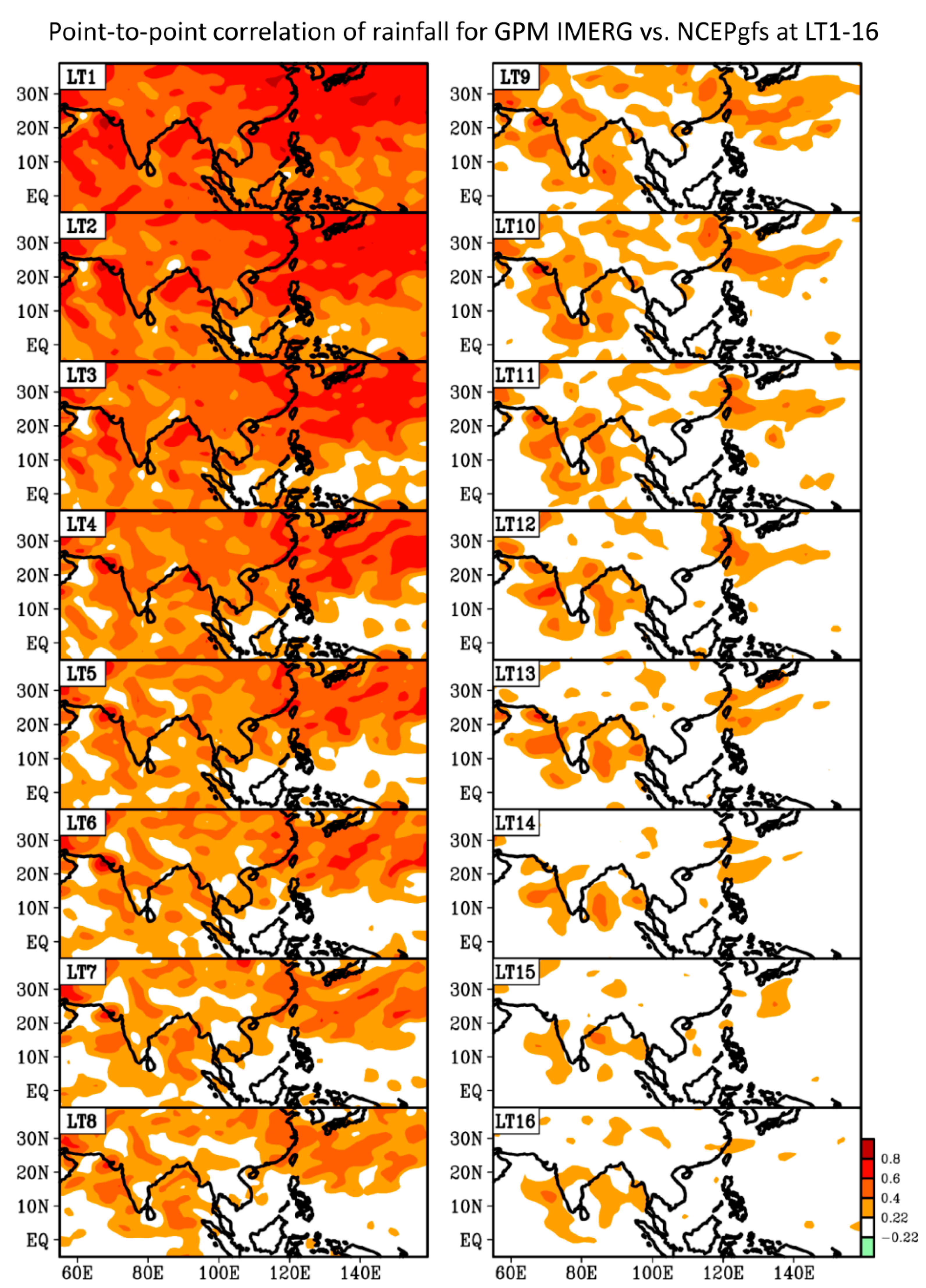
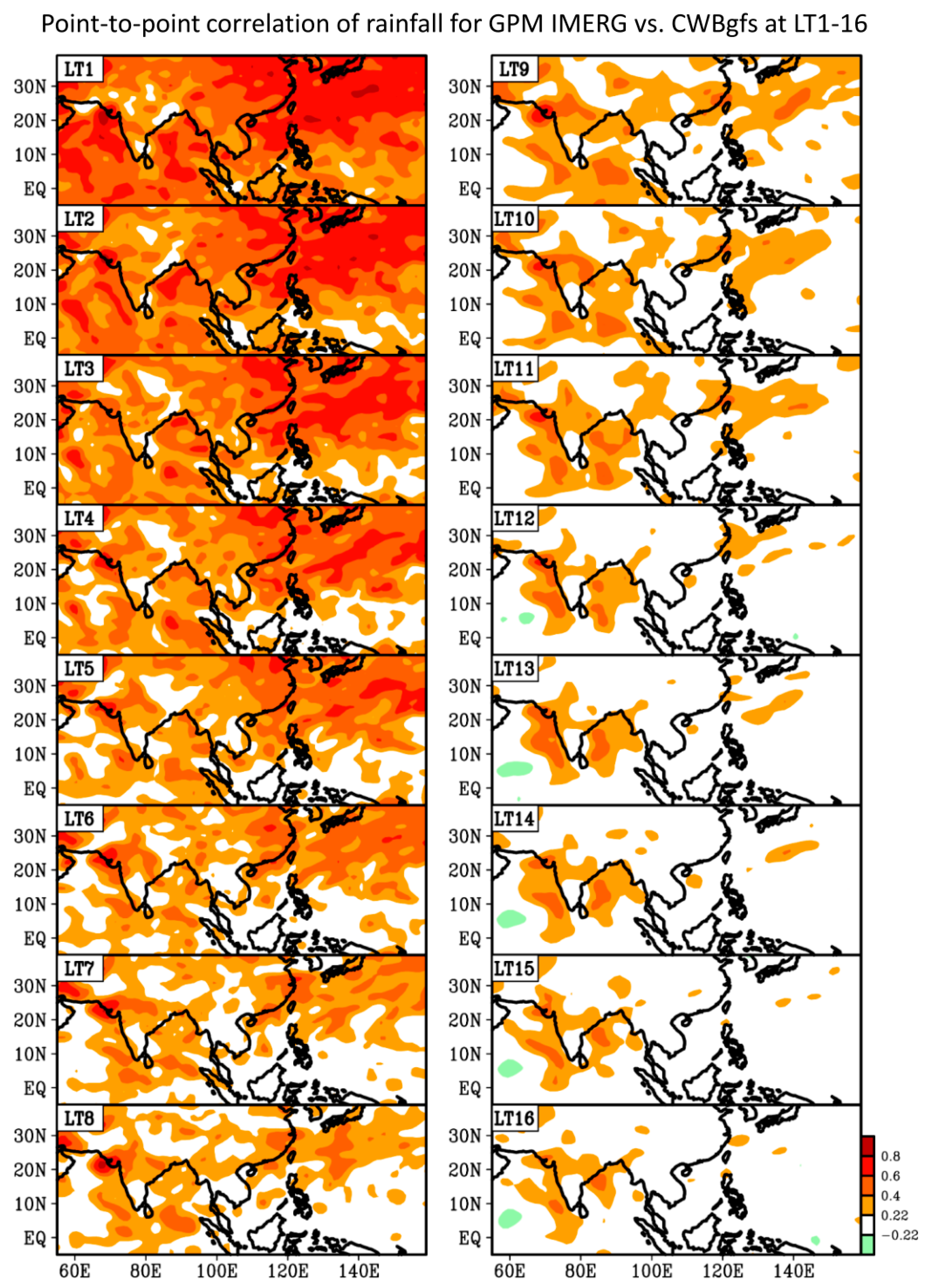
Figure 1b) and the model forecasts at each of the lead time up to 16 days (i.e., LT1~LT16) during the 2017 Meiyu season. Shown in
Figure 12 (
Figure 13) is the result for NCEPgfs (CWBgfs). In Figurs 12–13, only the areas with the correlation coefficients passing the significance test at the 90% confidence interval are shaded.
Overall, it can be seen from
Figure 12 and
Figure 13 that the model’s performance in predicting the temporal variation of rainfall during the 2017 Meiyu season is location-dependent. For the areas near Taiwan, the temporal correlation between the observation of GPM IMERG and the forecast of NCEPgfs has passed the significance test at lead times of 1 day to 14 days (see
Figure 12). This is better than the forecast of CWBgfs, which has passed the significance test at lead times of 1 day to approximately 12 days (see
Figure 13). Many studies have demonstrated that the higher the resolution of the model is, the better the predictive skill of the GFS forecast data is [
42,
43,
44]. Likely, the better the skill of NCEPgfs, compared to that of CWBgfs, in forecasting the timing of rainfall formation during the 2017 Meiyu season is, also partly attributed to a fact that both spatial and vertical resolutions of NCEPgfs are higher than those of CWBgfs (see
Table 1).
Most importantly, it can be seen from
Figure 12 and
Figure 13 that the model with better simulation of BSISO2 (i.e., NCEPgfs) has a better forecast skill in predicting the rainfall formation in Taiwan during the 2017 Meiyu season. This suggestion is consistent with the finding of Lee et al. [
12], which focuses on a larger domain of Asia but not specifically on Taiwan. However, we would like to mention that the discussion in this study only gives some insights for the possible relationship between the forecast skill of BSISOs and the forecast skill of rainfall variation in Taiwan during the 2017 Meiyu season. To clarify whether or not the above finding related to the relationship between the forecast skill of BSISOs and the forecast skill of rainfall formation in Taiwan is also true for other months and other years, a greater assessment for the model data in other months or in multiple years are planned in the near future.