Analysis of Two Dimensionality Reduction Techniques for Fast Simulation of the Spectral Radiances in the Hartley-Huggins Band
Abstract
:1. Introduction
- the approximate model is a two-stream radiative transfer model, while the accurate model is a multi-stream radiative transfer model;
- the PCA is used to reduce the dimensionality of the optical parameters of the atmospheric system;
- the dependency of the correction factor on the optical parameters is modeled by a second-order Taylor expansion about the mean value of the optical parameters.
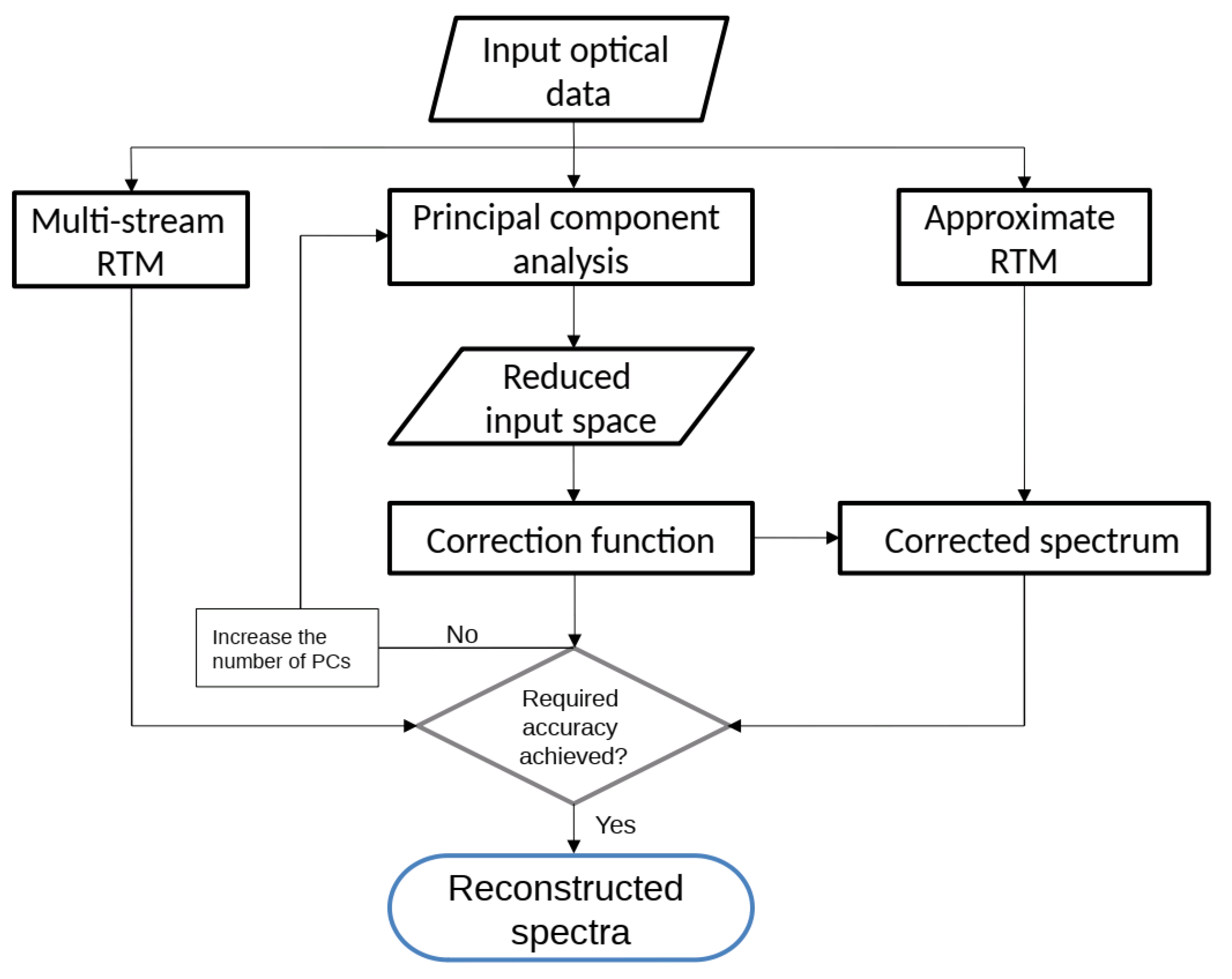
2. Input Space Reduction Technique
2.1. Radiative Transfer Models
2.2. Correction Function in the Reduced Input Space
3. Output Space Reduction Technique
3.1. PCA Description
3.2. Reconstruction of the Full Resolution Spectrum
3.3. Spectral Sampling
- the correlation coefficients are computed for the radiance values and then converted to vector angles by an arccosine function;
- the spectral data are rearranged according to the magnitudes of the correlation coefficients;
- the monochromatic radiances are selected with equal distances in the space of correlation coefficients.
4. Results
4.1. Dimensionality Reduction of the Optical Parameters in the Hartley-Huggins Band
- Case 1: considering the whole spectral range of 290–335 nm.
- Case 2: considering two intervals of 290–303 nm and 303–335 nm.
- Case 3: considering three intervals: 290–303 nm, 303–321 nm and 321–335 nm.
- the increase in the number of PC scores results in the increase of the computational time. However, this increase is not significant (0.05 s per PC score, i.e., ≈1% from the total computational time). Therefore, it is recommended to choose .
- the TS model is 40 times slower than the SS model for simulating the approximate spectra. However, the overall computational times differ by a factor of 2. Given that the TS model is more accurate than the SS model (as it has been shown in Table 1), it is recommended to use the TS model.
4.2. Principal Component Analysis of the Data Set of Spectral Radiances
4.3. Combined Use of Input and Output Space Reduction Techniques
- the number of preserved principal components is ,
- the correction function is expanded in Taylor series up to the second order,
- the two-stream model is used for computing the approximate solution; and for that, the two-stream model is called for each spectral point (i.e., times).
5. Summary
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DOME | Discrete Ordinate Method with Matrix Exponential |
| EOF | Empirical Orthogonal Function |
| PCA | Principal Component Analysis |
| PC | Principal Component |
| RTM | Radiative Transfer Model |
| SS | Single Scattering |
| TROPOMI | TROPospheric Ozone Monitoring Instrument |
| TS | Two-Stream |
References
- Natraj, V. A review of fast radiative transfer techniques. In Light Scattering Reviews 8; Springer: Berlin/Heidelberg, Germany, 2013; pp. 475–504. [Google Scholar] [CrossRef]
- Goody, R.; West, R.; Chen, L.; Crisp, D. The correlated-k method for radiation calculations in nonhomogeneous atmospheres. J. Quant. Spectrosc. Radiat. Transf. 1989, 42, 539–550. [Google Scholar] [CrossRef]
- Wiscombe, W. The delta-M method: Rapid yet accurate radiative flux calculations for strongly asymmetric phase functions. J. Atmos. Sci. 1977, 34, 1408–1422. [Google Scholar] [CrossRef]
- Tjemkes, S.A.; Schmetz, J. Synthetic satellite radiances using the radiance sampling method. J. Geophys. Res. Atmos. 1997, 102, 1807–1818. [Google Scholar] [CrossRef]
- West, R.; Crisp, D.; Chen, L. Mapping transformations for broadband atmospheric radiation calculations. J. Quant. Spectrosc. Radiat. Transf. 1990, 43, 191–199. [Google Scholar] [CrossRef]
- Natraj, V.; Jiang, X.; Shia, R.; Huang, X.; Margolis, J.; Yung, Y. Application of the principal component analysis to high spectral resolution radiative transfer: A case study of the O2A-band. J. Quantit. Spectrosc. Radiat. Transf. 2005, 95, 539–556. [Google Scholar] [CrossRef]
- Efremenko, D.S.; Loyola, D.G.; Doicu, A.; Spurr, R.J. Multi-core-CPU and GPU-accelerated radiative transfer models based on the discrete ordinate method. Comput. Phys. Commun. 2014, 185, 3079–3089. [Google Scholar] [CrossRef]
- Natraj, V.; Shia, R.; Yung, Y. On the use of principal component analysis to speed up radiative transfer calculations. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 810–816. [Google Scholar] [CrossRef]
- Somkuti, P.; Boesch, H.; Natraj, V.; Kopparla, P. Application of a PCA-Based Fast Radiative Transfer Model to XCO2 Retrievals in the Shortwave Infrared. J. Geophys. Res. Atmos. 2017, 122, 10477–10496. [Google Scholar] [CrossRef]
- Kopparla, P.; Natraj, V.; Spurr, R.; Shia, R.; Crisp, D.; Yung, Y. A fast and accurate PCA based radiative transfer model: Extension to the broadband shortwave region. J. Quant. Spectrosc. Radiat. Transf. 2016, 173, 65–71. [Google Scholar] [CrossRef]
- Liu, X.; Smith, W.; Zhou, D.; Larar, A. Principal component-based radiative transfer model for hyperspectral sensors: Theoretical concept. Appl. Opt. 2006, 45, 201–208. [Google Scholar] [CrossRef]
- Matricardi, M. A principal component based version of the RTTOV fast radiative transfer model. Q. J. R. Meteorol. Soc. 2010, 136, 1823–1835. [Google Scholar] [CrossRef]
- Hurley, P.D.; Oliver, S.; Farrah, D.; Wang, L.; Efstathiou, A. Principal component analysis and radiative transfer modelling of Spitzer Infrared Spectrograph spectra of ultraluminous infrared galaxies. Mon. Not. R. Astronom. Soc. 2012, 424, 2069–2078. [Google Scholar] [CrossRef]
- Hollstein, A.; Lindstrot, R. Fast reconstruction of hyperspectral radiative transfer simulations by using small spectral subsets: Application to the oxygen A band. Atmos. Meas. Tech. 2014, 7, 599–607. [Google Scholar] [CrossRef]
- Efremenko, D.S.; Loyola, D.G.; Hedelt, P.; Spurr, R.J.D. Volcanic SO2 plume height retrieval from UV sensors using a full-physics inverse learning machine algorithm. Int. J. Remote Sens. 2017, 38, 1–27. [Google Scholar] [CrossRef]
- Xu, J.; Schussler, O.; Rodriguez, D.L.; Romahn, F.; Doicu, A. A Novel Ozone Profile Shape Retrieval Using Full-Physics Inverse Learning Machine (FP-ILM). IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5442–5457. [Google Scholar] [CrossRef]
- Roozendael, V.; Spurr, R.; Loyola, D.; Lerot, C.; Balis, D.; Lambert, J.; Zimmer, W.; Gent, J.; Van Geffen, J.; Koukouli, M.; et al. Sixteen years of GOME/ERS2 total ozone data: The new direct-fitting GOME Data Processor (GDP) Version 5: I. algorithm description. J. Geophys. Res. Atmos. 2012, 117, D03305. [Google Scholar] [CrossRef]
- Stamnes, K.; Tsay, S.; Wiscombe, W.; Jayaweera, K. Numerically stable algorithm for discrete-ordinate-method radiative transfer in multiple scattering and emitting layered media. Appl. Opt. 1988, 12, 2502–2509. [Google Scholar] [CrossRef]
- Doicu, A.; Trautmann, T. Discrete-ordinate method with matrix exponential for a pseudo-spherical atmosphere: Scalar case. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 146–158. [Google Scholar] [CrossRef]
- Efremenko, D.S.; García, V.M.; García, S.G.; Doicu, A. A review of the matrix-exponential formalism in radiative transfer. J. Quant. Spectrosc. Radiat. Transf. 2017, 196, 17–45. [Google Scholar] [CrossRef]
- Molina García, V.; Sasi, S.; Efremenko, D.; Doicu, A.; Loyola, D. Radiative transfer models for retrieval of cloud parameters from EPIC/DSCOVR measurements. J. Quant. Spectrosc. Radiat. Transf. 2018, 213, 228–240. [Google Scholar] [CrossRef]
- Nakajima, T.; Tanaka, M. Algorithms for radiative intensity calculations in moderately thick atmos using a truncation approximation. J. Quant. Spectrosc. Radiat. Transf. 1988, 40, 51–69. [Google Scholar] [CrossRef]
- Kerschen, G.; Golinval, J. Non-linear generalization of principal component analysis: From a global to a local approach. J. Sound Vib. 2002, 254, 867–876. [Google Scholar] [CrossRef]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinburgh Dublin Philos. Mag J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- MacArthur, R.H. On the relative abundance of bird species. Proc. Natl. Acad. Sci. USA 1957, 43, 293–295. [Google Scholar] [CrossRef] [PubMed]
- Bodhaine, B.A.; Wood, N.B.; Dutton, E.G.; Slusser, J.R. On rayleigh optical depth calculations. J. Atmos. Ocean. Technol. 1999, 16, 1854–1861. [Google Scholar] [CrossRef]
- Coldewey-Egbers, M.; Weber, M.; Lamsal, L.N.; de Beek, R.; Buchwitz, M.; Burrows, J.P. Total ozone retrieval from GOME UV spectral data using the weighting function DOAS approach. Atmos. Chem. Phys. 2005, 5, 1015–1025. [Google Scholar] [CrossRef]
- Lerot, C.; Van Roozendael, M.; Lambert, J.C.; Granville, J.; van Gent, J.; Loyola, D.; Spurr, R. The GODFIT algorithm: A direct fitting approach to improve the accuracy of total ozone measurements from GOME. Int. J. Remote Sens. 2010, 31, 543–550. [Google Scholar] [CrossRef]
- Loyola, D.G.; Pedergnana, M.; Gimeno García, S. Smart sampling and incremental function learning for very large high dimensional data. Neural Netw. 2016, 78, 75–87. [Google Scholar] [CrossRef]
- Halton, J.H. Algorithm 247: Radical-inverse quasi-random point sequence. Commun. ACM 1964, 7, 701–702. [Google Scholar] [CrossRef]







| M | Expansion Order | Single-Scattering | Two-Stream | ||
|---|---|---|---|---|---|
| 303–321 nm | 321–335 nm | 303–321 nm | 321–335 nm | ||
| 1 | 1 | 3.02 | 1.19 | 0.67 | 0.088 |
| 2 | 1.43 | 1.07 | 0.19 | 0.081 | |
| 3 | 1.07 | 1.10 | 0.19 | 0.087 | |
| 4 | 1.11 | 1.06 | 0.18 | 0.068 | |
| 2 | 1 | 2.40 | 0.41 | 0.67 | 0.088 |
| 2 | 1.19 | 0.24 | 0.09 | 0.082 | |
| 3 | 1.09 | 0.25 | 0.10 | 0.087 | |
| 4 | 0.59 | 0.18 | 0.11 | 0.069 | |
| 3 | 1 | 2.35 | 0.33 | 0.67 | 0.042 |
| 2 | 1.03 | 0.15 | 0.09 | 0.036 | |
| 3 | 1.02 | 0.18 | 0.10 | 0.046 | |
| 4 | 0.46 | 0.14 | 0.10 | 0.038 | |
| 4 | 1 | 2.34 | 0.29 | 0.67 | 0.034 |
| 2 | 1.03 | 0.11 | 0.09 | 0.029 | |
| 3 | 1.02 | 0.13 | 0.10 | 0.039 | |
| 4 | 0.46 | 0.11 | 0.11 | 0.034 | |
| M | Order | Single-Scattering | Two-Stream | ||||||
|---|---|---|---|---|---|---|---|---|---|
| L | Total | Number of MS Calls | L | Total | Number of MS Calls | ||||
| 1 | 1 | 0.0043 | 0.227 | 0.231 | 3 | 0.175 | 0.268 | 0.434 | 6 |
| 2 | 0.0043 | 0.251 | 0.255 | 3 | 0.175 | 0.297 | 0.477 | 6 | |
| 3 | 0.0043 | 0.416 | 0.420 | 5 | 0.175 | 0.494 | 0.674 | 10 | |
| 4 | 0.0043 | 0.418 | 0.422 | 5 | 0.175 | 0.493 | 0.673 | 10 | |
| 2 | 1 | 0.0043 | 0.276 | 0.280 | 5 | 0.175 | 0.320 | 0.485 | 10 |
| 2 | 0.0043 | 0.306 | 0.310 | 5 | 0.175 | 0.354 | 0.533 | 10 | |
| 3 | 0.0043 | 0.526 | 0.531 | 9 | 0.175 | 0.605 | 0.784 | 18 | |
| 4 | 0.0043 | 0.514 | 0.519 | 9 | 0.175 | 0.595 | 0.775 | 18 | |
| 3 | 1 | 0.0043 | 0.325 | 0.329 | 7 | 0.175 | 0.370 | 0.536 | 14 |
| 2 | 0.0043 | 0.350 | 0.354 | 7 | 0.175 | 0.288 | 0.577 | 14 | |
| 3 | 0.0043 | 0.619 | 0.623 | 13 | 0.175 | 0.700 | 0.877 | 26 | |
| 4 | 0.0043 | 0.627 | 0.632 | 13 | 0.175 | 0.711 | 0.891 | 26 | |
| 4 | 1 | 0.0043 | 0.363 | 0.367 | 9 | 0.175 | 0.409 | 0.572 | 18 |
| 2 | 0.0043 | 0.401 | 0.406 | 9 | 0.175 | 0.452 | 0.629 | 18 | |
| 3 | 0.0043 | 0.711 | 0.715 | 17 | 0.175 | 0.794 | 0.970 | 34 | |
| 4 | 0.0043 | 0.726 | 0.730 | 17 | 0.175 | 0.813 | 0.991 | 34 | |
| Input Space Reduction | Output Space Reduction | Combined Use | |
|---|---|---|---|
| Acceleration factor | 13 | 12 | 18.2 |
| Mean error | 0.05 | 0.00023 | 0.05 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
del Águila, A.; Efremenko, D.S.; Molina García, V.; Xu, J. Analysis of Two Dimensionality Reduction Techniques for Fast Simulation of the Spectral Radiances in the Hartley-Huggins Band. Atmosphere 2019, 10, 142. https://doi.org/10.3390/atmos10030142
del Águila A, Efremenko DS, Molina García V, Xu J. Analysis of Two Dimensionality Reduction Techniques for Fast Simulation of the Spectral Radiances in the Hartley-Huggins Band. Atmosphere. 2019; 10(3):142. https://doi.org/10.3390/atmos10030142
Chicago/Turabian Styledel Águila, Ana, Dmitry S. Efremenko, Víctor Molina García, and Jian Xu. 2019. "Analysis of Two Dimensionality Reduction Techniques for Fast Simulation of the Spectral Radiances in the Hartley-Huggins Band" Atmosphere 10, no. 3: 142. https://doi.org/10.3390/atmos10030142
APA Styledel Águila, A., Efremenko, D. S., Molina García, V., & Xu, J. (2019). Analysis of Two Dimensionality Reduction Techniques for Fast Simulation of the Spectral Radiances in the Hartley-Huggins Band. Atmosphere, 10(3), 142. https://doi.org/10.3390/atmos10030142







