Abstract
In this study, we assessed the performance of 34 Coupled Model Intercomparison Project Phase 5 (CMIP5) general climate models (GCMs) for simulating the observed temperature over the Lower Mekong Basin (LMB) in 1961–2004. An improved score-based method was used to rank the performance of the GCMs over the LMB. Two methods of multi-model ensemble (MME), sub-ensemble from the top 25% ranked GCMs and full ensemble from the entire GCMs, were calculated using arithmetic mean (AM) method and downscaled using the Delta method to project future temperature change during two future time periods, the near future (2006–2049) and the far future (2050–2093), under representative concentration pathways (RCP2.6, RCP4.5, and RCP8.5 scenarios) over the LMB. The improved score-based method combining multiple criteria showed a robust assessment of the GCMs performance over the LMB, which can provide good information for projecting future temperature change. The results showed a significant increase in temperature over the LMB under the two ensembles. However, there were differences in the magnitudes of the future temperature increase between the two ensemble methods, with a higher mean annual temperature increase from full ensemble and sub-ensemble at 1.26 °C (1.09 °C), 1.90 °C (1.70 °C), and 2.97 °C (2.78 °C) during 2050–2093 under the RCP2.6, RCP4.5, and RCP8.5 scenarios compared to the values at 0.93 °C (0.87 °C), 0.99 °C (0.95 °C), and 1.09 °C (1.06 °C) during 2006–2049, respectively, relative to the reference time period of 1961–2004. In the future (2006–2093), the temperature is likely to increase at 0.06 °C, 0.18 °C, and 0.39 °C decade−1 under the RCP2.6, RCP4.5, and RCP8.5 scenarios by the sub-ensemble, while a higher temperature increase at 0.08 °C, 0.20 °C, and 0.42 °C was found by the full ensemble over the LMB, relative to the reference time period of 1961–2004. On the whole, the higher warming mainly occurred in the northern and central areas over the LMB, while the lower warming mainly occurred in the southeast and the southwest, especially under the RCP4.5 and RCP8.5 scenarios, with the warming increased with increasing RCP for both ensembles. Moreover, in order to reduce the uncertainty of temperature projection in further studies in the LMB, multiple methods of GCMs ensemble should be considered and compared.
1. Introduction
Climate change has become one of the most important topics to scientists, the public, and governments around the world. The past 30 years (1983–2012) were probably the hottest in the Northern Hemisphere in the last 1400 years, with the warmest being the first 10 years of the 21st century [1]. Regionally, mean temperature is expected to rise 0.79 °C by the year 2030 compared to 1951–2000 in the Mekong River Basin [2]. Observational evidence from mainland and oceans has shown that the regional climate change associated with the rise in temperature has significant impacts on the population and environment [3].
Recently, multiple criteria have been widely used for assessing the performance of the CMIP5 GCMs in climate variable simulation [4,5,6,7,8]. Rupp et al. [4] assessed 41 CMIP5 GCMs’ abilities in temperature and precipitation simulation of the Pacific Northwest, USA, based on observed metrics such as the correlation and variance of mean seasonal spatial patterns, amplitude of seasonal cycle, diurnal temperature range, annual-to decadal-scale variance, and other metrics. Miao et al. [5] assessed the performance of 24 CMIP5 GCMs in simulating intra-annual, annual, and decadal temperature over Northern Eurasia based on the criteria of correlation, the centered root-mean-square-error, and the amplitude of the standard deviations. Ahmadalipour et al. [6] used criteria such as mean, standard deviation, coefficient of variation, relative change (variability), Mann‒Kendall test, Kolmogorov‒Smirnov test (KS test), and other criteria to assess the performance of 20 CMIP5 GCMs for selecting suitable GCMs for climate change impact analysis over the Columbia River Basin in the Pacific Northwest, USA. Dong et al. [7] assessed the performance of 22 CMIP5 GCMs in simulating annual mean surface air temperature over the critical Belt and Road region using criteria of temporal, spatial, and trend analysis. Das et al. [8] assessed the performance of 34 CMIP5 GCMs in reproducing observed temperature statistics over the Western Himalayan Region of India using criteria including mean seasonal cycle, temporal trends, and spatial correlation. Furthermore, additional researches on the comparison of the ability to reproduce the observed climate variables between CMIP5 and CMIP3 have been done, and many of them showed that CMIP5 models showed improvements compared to CMIP3 models [9,10,11,12]. In addition, many studies have been conducted assessing the performance of the GCMs in reproducing patterns of large-scale climate variability, such as the North Atlantic Oscillation (NAO), Pacific/North America pattern (PNA), North Pacific Oscillation (NPO), and El Niño Modoki [13,14,15]. Lee and Black [13] found that the low-frequency mode structure from model biases has a significant effect on representing associated regional anomalies in surface air temperature and storm track behavior. Ning and Bradley [14] found that the winter temperature correlation changes over the eastern USA are usually highly affected by the NAO and PNA. Wang et al. [15] showed that future projections of El Niño Modoki of the multi-model simulations can be analyzed based on the changes in the warm wind‒evaporation‒SST (WES) feedback intensity and simulations of the NPO. Moreover, Hawkins and Sutton [16] suggested that model uncertainty was more important than internal variability for decadal time scales and regional spatial scales (~2000 km). Therefore, a GCM that can simulate observed temperature reasonably well should be selected before a climate change projection is made [5,17,18].
The fifth assessment report of IPCC put forward a new set of scenarios called representative concentration pathways (RCPs) for climate change projection. In detail, four typical pathways include the radiative forcing levels of 2.6 W/m2 (RCP2.6), 4.5 W/m2 (RCP4.5), 6.0 W/m2 (RCP6.0) and 8.5 W/m2 (RCP8.5) by the end of this century, which represent the low (RCP2.6), the low-medium (RCP4.5), the medium-high (RCP6.0), and the high (RCP8.5) greenhouse gas emissions [1]. However, because of the coarse spatial resolution of the GCMs, the outputs from the future projections of the GCMs are inadequate to project the regional climate scenarios in detail [19,20,21]. Thus, downscaling methods have been applied to transfer the coarse outputs of the GCMs to regional or local high-resolution climate change scenarios [21,22]. Currently there are three downscaling methods that are being applied: dynamic downscaling, statistical downscaling, and a combination of both. Statistical downscaling is advantageous in that it requires a small amount of calculation, simple to use and does not consider the effects of boundary conditions on the predicted results [23]. A statistical downscaling method called the Delta method, which is simple and easy to operate, has been widely used for projection of future climate change around the world [22,24,25,26,27,28,29].
Future climate change will affect water yield and rice cultivation in the tributary countries over the Lower Mekong Basin (LMB) [30]. Due to the population growth in the Lower Mekong Basin (LMB), the demands for agricultural products from the LMB is expected to increase by 20–50% in the next 30 years [31]. Additionally, it is likely that the demands for water for agriculture in 2010–2050 will increase as a result of the higher temperatures [32]. Therefore, assessing performance of the GCMs in temperature simulation is essential for projection of future temperature change and for policy-making over the LMB. In previous studies, performance of the GCMs and projection of future temperature change have been mainly focused on the watersheds in the Mekong River Basin [2,33,34,35]. However, fewer studies have focused on the LMB. Meanwhile, no research exits that assessing performance of the GCMs in simulating the observed temperature, based on an improved score-based method, using gauge-based data of the Asian Precipitation-Highly Resolved Observational Data Integration Towards Evaluation of Water Resources (APHRODITE) temperature data in the Lower Mekong Basin. Moreover, the multi-model ensemble projection can improve the temporal simulation relative to a single GCM in the Mekong River Basin [35]. Thus, in this study, we aim to assess the performance of the CMIP5 models in temperature simulation and use multi-model ensemble (MME) to project future temperature change during two periods of the near future (2006–2049) and the far future (2050–2093) under RCP2.6, RCP4.5, and RCP8.5 scenarios over the LMB.
2. Data and Methods
2.1. Data
2.1.1. GCM Data
Thirty-four GCM models from the CMIP5 [36] were used in this study. Table 1 provides a detailed description of the origin and their spatial resolution. More details can be found on the CMIP5 website (http://cmip-pcmdi.llnl.gov/cmip5/index.html). Meanwhile, detailed information for the future projection of 2006–2093 on the RCP2.6, RCP4.5, and RCP8.5 scenarios were also acquired from the website.

Table 1.
Basic information of the CMIP5 models used in this study.
2.1.2. Temperature Data
Gauge-based data from the Asian Precipitation-Highly Resolved Observational Data Integration Towards Evaluation of Water Resources (APHRODITE) temperature dataset were used as the observational data. APHRODITE temperature data have a high spatial resolution of 0.25° × 0.25° [37], which has been proven to be a better gridded temperature product for studies of climate changes in the Mekong River Basin [38]. APHRODITE temperature data are taken daily. Thus, we calculated them into monthly data before assessment.
Because of the different spatial resolutions of the GCMs and the observation, monthly temperature outputs for the 34 GCMs and APHRODITE temperature data were converted to 2.5° × 2.5° using bilinear interpolation, and 21 grids were selected for comparison (Figure 1). In this paper, we consider 1961–2004 as the reference time period. The LMB temperature data were calculated by taking the arithmetic mean of the 21 grids.

Figure 1.
Location of the Lower Mekong Basin (LMB) and the 21 selected grids (shade of yellow) over the LMB.
2.2. Methods
2.2.1. Assessment of the Performance for CMIP5 GCMs
A GCM that performs well for a specific statistic does not necessarily perform well for a different statistic; moreover, an individual assessment criterion can produce a biased assessment [39]. Thus, it is beneficial to use multiple criteria for comprehensively assessing the performance for CMIP5 GCMs. Thus, we used seven assessment criteria, including Mean value (M), Standard deviation (SD), Normalized Root mean square error (NRMSE), linear correlation coefficient (r) for spatial distribution, Mann‒Kendall test statistic Z, Sen’s slope, and Significance score (Sscore). Then we used an improved RS (Rank Score) method [39,40] to rank the GCMs to comprehensively assess the performance of GCMs for temperature simulation over the LMB.
- Mean valueThe mean value (M) is defined as follows:Here Ti represents the monthly temperature for the LMB at ith time step, and n represents the total number of the time steps.
- Standard deviationThe standard deviation (SD) is defined as follows:Here Ti represents the monthly temperature for the LMB at ith time step, represents the mean monthly temperature for the LMB, and n represents the total number of the time steps. A smaller value of SD indicates a better performance of a GCM.
- Normalized root mean square errorThe normalized root mean square error (NRMSE) is defined as follows:Here Tmi and Toi represent the monthly temperature for the GCM and the observed value for the LMB at ith time step, respectively. represents the mean value of the observed value for the LMB. n represents the total number of the time steps. A smaller value of NRMSE indicates a better performance of a GCM.
- Linear correlation coefficient (r) for spatial distributionThe correlation coefficient (r) was used to as a measure to compare spatial distribution of temperature between the observation and the GCMs. The sample size is 21, and r was calculated between the observation and the GCMs for long-term mean values of each grid. The formula is defined as follows:Tmi and Toi represent temperature for the GCM and the observation of the mean annual values at ith grid, respectively, and the and represent the corresponding mean values for temperature of the GCM and the observation of all grids, respectively. A larger value of the r indicates a better performance of a GCM.
- Mann‒Kendall test statistic Z and Sen’s slopeThe Mann‒Kendall test statistic Z and Sen’s slope were used to obtain the trends and their magnitudes for GCMs and observations. Thus, the ability of how well the GCMs represent the variation trend of the observations can be obtained. The statistics of the annual time series were used for analysis.The Mann‒Kendall test statistic Z is defined as follows [41,42,43]:andHere xk, xi are the sequential temperature values, n is the length (44) of the dataset, andandHere t is the extent of any given tie and ∑ denotes the summation over all ties.The Sen’s slope is defined as follows [44,45]:Here 1 < j < i < n, and the slope estimator β represents the median of the entire dataset.
- Probability density functions (PDF)The Significance score (Sscore) was used to assess the GCM’s probability density functions (PDF) for monthly temperature. The formula is defined as follows [46]:Here Bmi and Boi represent the probability of GCM and observed temperature values at the ith of bin, respectively.The n is the number of bins, and it was set to 100 according to the data range. The Sscore is a measurement of the degree of overlap between the simulated probability distribution and the observed value [46]. Thus, a larger Sscore value indicates a better performance of a GCM [39].
- Improved RS (Rank Score)The improved RS distinguishes between the relative error index and non-relative error index in comparison to the RS method, which could avoid inconsistent results [40]. For example, a smaller value of NRMSE of the relative error index indicates a better performance of a GCM, while a larger value of r of the non-error index indicates a better performance of a GCM. Thus, the improved RS can be used for different assessment criteria and climatic variables to comprehensively assess the performance of GCMs in the regions. The Rank Score of each assessment criterion can be calculated by its statistic [40]:Here RSi represents the score for GCM calculated by an assessment criterion i. For the relative error indexes of M, SD, Z and Sen’s slope, Ti represents absolute error that was calculated between a GCM and the observation (Equation (12)), and Tmin and Tmax represent the corresponding minimum and maximum among all GCMs. Moreover, for the relative error indexes of NRMSE, Ti represents the absolute value of statistic for a GCM, and Tmin and Tmax represent the corresponding minimum and maximum among all GCMs. For the non-relative error index of r and Sscore, Ti represents the absolute value of the statistic for a GCM, and Tmin and Tmax represent the corresponding minimum and maximum among all GCMs.Here Tsm and Tso represent the statistics of the GCM and the observation, respectively.Therefore, the overall RS for temperature can be calculated as follows:Here RST represents the overall RS of temperature for the GCM. Here n = 7 and i represents an assessment criterion, such as M, SD, NRMSE, Z, Sen’s slope, spatial distribution r, and Sscore. Wi represents the weight for an assessment criterion i, Ws represents the sum weight of all the assessment criteria. Since Z and Sen’s slope are part of trend analysis, we set 0.5 weight for Z, Sen’s slope, respectively, while 1.0 weight for M, SD, NRMSE, r, and Sscore, respectively.
2.2.2. Projection of Future Temperature Change
Based on the results of the performance for GCMs, we used two multi-model ensemble (MME) methods (sub-ensemble and full ensemble) to make comparison of future temperature projection under RCP2.6, RCP4.5, and RCP8.5 scenarios, which was calculated using arithmetic mean (AM) method. The formula can be defined as follows:
For the sub-ensemble method, j represents the GCM that ranked within the top 25% of all the GCMs, represents the future monthly temperature of GCM j at ith time step, and n represents the total number of the GCMs ranked within the top 25% of all the GCMs. For the full ensemble method, j represents the entire GCMs, which have outputs of three RCP scenarios, represents the future monthly temperature of GCM j at ith time step, and n represents the total number of the GCMs that has data of three RCP scenarios.
Subsequently, we applied the Delta method to calculate temperature changes between the historical MME outputs of temperature for the reference period 1961–2004 and projections of temperature under the same time duration of 44 years in the future, which can be defined as follows:
Here and represent mean temperature for month i of the projections of 44 years in the future and the historical MME outputs of the reference period of 1961–2004, respectively. We focused on two 44 years of 2006–2049 and 2050–2093 under RCP2.6, RCP4.5, and RCP8.5 scenarios for the projection of future temperature changes.
3. Results
3.1. Annual Cycle of Temperature
Temperature variation of the mean annual cycle for the observation and the 34 GCMs for the period 1961–2004 over the LMB is shown in Figure 2. Most of the GCMs had effectively reproduced the single-peak pattern of temperature in the mean annual cycle. The errors between the 34 GCMs and the observed temperature ranged from −3.02 °C to 1.06 °C, −2.68 °C to 3.08 °C, −3.21 °C to 1.30 °C, −3.19 °C to 0.09 °C, and −4.41 °C to 0.33 °C, with mean errors of −0.97°C, −0.02 °C, −0.58°C, −1.35 °C, and −1.94 °C for the mean temperature of annual, spring (March–April–May), summer (June–July–August), autumn (September–October–November), and winter (December–January–February), respectively (Figure 2). Moreover, the number of the negative errors showed by the 34 GCMs were 29, 18, 26, 32, and 32 for the mean temperature of annual, spring, summer, autumn, and winter, respectively. This indicated that most of the GCMs tended to underestimate temperature relative to the observation, especially during the winter.
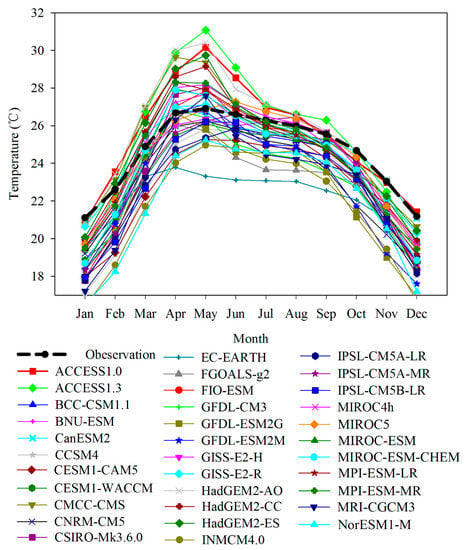
Figure 2.
Variation of the observed temperature and GCMs of the mean annual cycle during the reference period 1961–2004 over the LMB.
3.2. Characteristics of Statistics in Criteria
Table 2 shows the M, SD, NRMSE, r, Mann‒Kendall test statistic Z, Sen’s slope, and Sscore of the temperature for the 34 GCMs. The M for the temperature of the GCMs ranged from 21.60 °C to 25.68 °C, with mean and median values at 23.65 °C and 23.67 °C, respectively. A smaller absolute error indicates a better correspondence with the observed temperature for the GCM. CanESM2, HadGEM2-ES, and HadGEM2-CC had the smallest absolute errors (0.14 °C, 0.17 °C, and 0.20 °C, respectively), while INMCM4.0, NorESM1-M, and EC-EARTH had the largest absolute errors (3.02 °C, 2.62 °C, and 2.49 °C, respectively).

Table 2.
Statistics of assessment criteria of the GCMs over the LMB. “Obs” represents the observation, the ID numbers represent the GCMs, which the same as the ID in Table 1.
The SD values of the GCMs range from 1.57 to 3.77, with mean and median values of 2.96 and 3.05, respectively. CanESM2, GISS-E2-R, and FGOALS-g2 had the lowest absolute errors at 0.01, 0.33, and 0.40, respectively, indicating good simulation of the observed temperature. However, ACCESS1.3, CSIRO-Mk3.6.0, FIO-ESM had the highest absolute errors at 1.64, 1.42, and 1.23, respectively, indicating poor simulation of the observed temperature.
The NRMSE values of the GCMs ranged from 0.52 to 1.57, with mean and median values at 0.86 and 0.92, respectively. CanESM2, GISS-E2-R, and MIROC5 had the smallest NRMSE values (0.52, 0.54, and 0.60, respectively), while INMCM4.0, NorESM1-M, and GFDL-ESM2G showed the largest values (1.57, 1.41, and 1.32, respectively).
Most of the GCMs showed relatively high r, with minimum and mean r values of 0.83 and 0.92, respectively, and 26 of the 34 GCMs had higher r (r > 0.9), indicating good reproducibility of characteristics of time series and spatial distributions of the observed temperature. ACCESS1.3, GFDL-CM3, and GFDL-ESM2M had the highest spatial r at 0.972, 0.972, and 0.959, respectively, but the lowest values for INMCM4.0, CanESM2, and FGOALS-g2 were at 0.829, 0.874, and 0.883, respectively.
The observed temperature showed a significantly positive trend, with a Z statistic of 2.80, at the 0.01 significance level and a Sen’s slope of 0.01 °C/year. The Z statistics and Sen’s slope of the 34 GCMs ranged from 0.31 to 5.27, 0.0026 to 0.0233, respectively. Out of the 34 GCMs, all were able to reproduce the positive trend of the observed temperature, and 30 (28) GCMs showed a significantly positive trend of observed temperature at the significance level of 0.05 (0.01) compared to that at 0.01 significance level for the observed temperature. Moreover, only six GCMs showed statistics of Sen’s slope smaller than the observed temperature, indicating that most of the GCMs simulate higher temperature increase during 1961–2004 compared to the observed temperature. The results indicated that more than 80 percent of the GCMs showed relatively good reproducibility of the positive trend of the observed temperature. FIO-ESM, GFDL-ESM2M, and NorESM1-M had Z statistic values of 2.78, 2.78, and 2.84 closest to the observed temperature. CESM1(WACCM), CSIRO-Mk3.6.0, and GISS-E2-H had Sen’s slope values of 0.0101, 0.0098, and 0.0096, which are in near agreement with the observed temperature.
The Sscore of the GCMs ranged from 0.51 to 0.70, with mean and median values at 0.61 and 0.62, respectively. Out of the 34 GCMs, 21 showed the Sscore values of more than 0.6. This indicated that more than half of the GCMs models had relatively good ability in reproducing the characteristics of the probability distribution function of the observed temperature.
3.3. Comparison of the Performance of the GCMs
Ranking scores of the seven criteria of the GCMs are shown in Figure 3, which were calculated based on the criteria statistics. Overall ranking scores of the GCMs are shown in Figure 4, which were calculated based on the ranking scores of the eight criteria. For a set of different criteria, a GCM may perform well for one criterion but badly for another. For example, CanESM2 had the highest ranking score value of 1 based on the M but the low ranking score value at 0.14 for the Sen’s slope. Although GFDL-ESM2M had the lowest ranking score value at 0 by Sscore, it had the highest ranking score value at 1 by Z. For the overall ranking scores of the GCMs, a GCM may perform well for one or two criteria but badly for the overall result. For example, ACCESS1.3 had the highest ranking score value at 1 by r but low overall ranking scores at 0.51. Although INMCM4.0 had high ranking score value at 0.92 by Z, it had the lowest ranking score value at 0.21 for the overall result. This indicated that the results of GCMs performance relied mainly on the assessment of the criterion. Thus, using multiple criteria to comprehensively assess the performance of GCMs is essential.
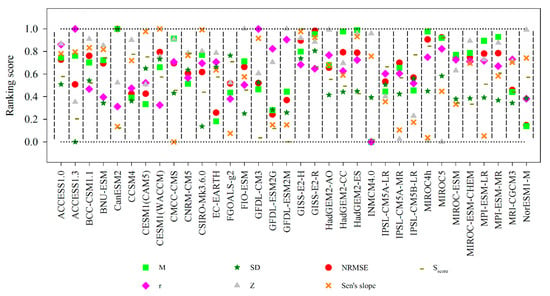
Figure 3.
Ranking scores of criteria of the GCMs over the LMB.
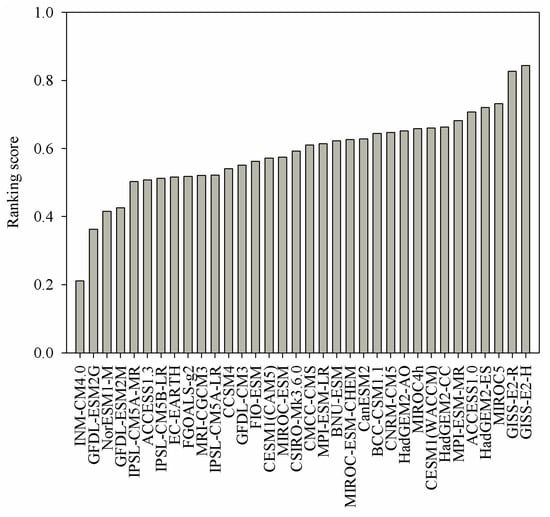
Figure 4.
Ascending order of ranking scores for the performance of the GCMs over the LMB.
3.4. Sensitivity Analysis of the GCMs Performance
The sensitivity analysis of the GCMs performance were made in two ways. First, the overall ranking scores were compared to the ranking scores after removing one criterion (Figure 5). The results showed overall ranking score had not been changed as a whole after removing each criterion individually, indicating that improved score-based method combining multiple criteria showed a robust assessment of the GCMs performance. Second, the temporal changes of the overall ranking scores were evaluated by comparing the results of two different reference time periods. In this paper, we selected the longest time series of 1961–2004 as the reference time period. Thus we selected a relatively short time series of 1975–2004 as another reference time period for comparison. As shown in Figure 6a, as a whole, the ranking scores of the GCMs had not changed much as the reference time periods changed. Moreover, the top 25% ranked GCMs were listed separately for making comparison under the two reference time periods (Figure 6b,c). Although the ranking scores of the top 25% ranked GCMs were different under the two reference time periods, ACCESS1.0, GISS-E2-H, GISS-E2-R, HadGEM2-ES, HadGEM2-CC, MIROC5, and MIROC4h were all ranked within the top 25% under the two reference time periods, except CanESM2 and CNRM-CM5 (red bar in Figure 6b) ranked within the top 25% for the reference time period of 1975–2004 and CESM1(WACCM) and MPI-ESM-MR (red bar in Figure 6c) ranked within the top 25% for the reference time period of 1961–2004. These indicated that the results of performance of the GCMs based on the improved score-based method are reliable and can be used as a reference for projecting temperature change in the future over the LMB.
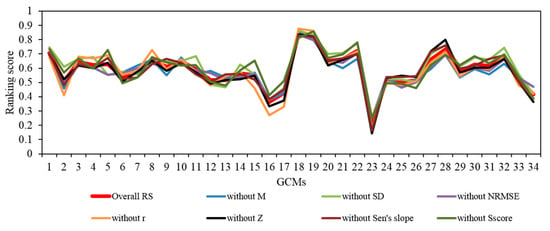
Figure 5.
Comparison of overall RS (ranking scores) and RS after removing one criterion. The numbers in the X axis represent the ID numbers in Table 1.
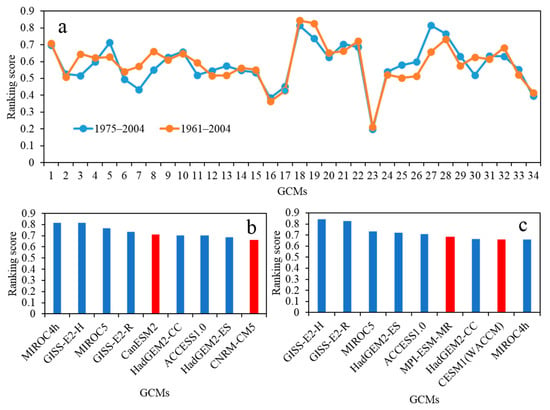
Figure 6.
Comparison of overall ranking scores of GCMs under reference periods of 1975–2004 and 1961–2004 (a) and top 25% ranking scores of GCMs under reference period of 1975–2004 (b) and 1961–2004 (c), respectively. The numbers on the x-axis (a) represent the ID numbers in Table 1.
3.5. Future Temperature Projection
The top 25% ranked GCMs (except the ACCESS1.0, HadGEM2-CC, and MIROC4h because of not having the outputs under the RCP 2.6 scenario) and the entire GCMs (except the ACCESS1.0, ACCESS1.3, CMCC-CMS, HadGEM2-CC, MIROC4h, INMCM4.0, and IPSL-CM5B-LR because of not having the outputs under the RCP 2.6 scenario) were used for calculating projections from the sub-ensemble and the full ensemble by arithmetic mean (AM) method, respectively. Then, we assessed the future temperature change under two periods of the near future (2006–2049) and the far future (2050–2093) under RCP 2.6, RCP 4.5, and RCP 8.5 scenarios based on the Delta method.
Table 3 shows that the LMB had higher mean annual temperature increase during 2050–2093 under RCP2.6, RCP4.5, and RCP8.5 scenarios compared to the period of 2006–2049, respectively, relative to the reference period of 1961–2004. Moreover, the projection by the full ensemble showed higher mean annual temperature increase compared to the sub-ensemble, with mean temperature increase at 1.26 °C (1.09 °C), 1.90 °C (1.70 °C), and 2.97 °C (2.78 °C) during 2050–2093 under RCP2.6, RCP4.5, and RCP8.5 scenarios, and at 0.93 °C (0.87 °C), 0.99 °C (0.95 °C), and 1.09 °C (1.06 °C) for the period 2006–2049. Additionally, the projection by the sub-ensemble showed that MAM (March–April–May) had the highest mean temperature increase during 2006–2049 under RCP4.5, and RCP8.5 scenarios and during 2050–2093 under RCP2.6 scenario, while DJF (December–January–February) showed the highest mean temperature increase during 2050–2093 under RCP4.5 and RCP8.5 scenarios. However, the projection by the full ensemble showed the highest mean temperature increase for the MAM for the RCP2.6, RCP4.5, and RCP8.5 scenarios during 2006–2049 and 2050–2093. Overall, the projected annual temperature change in future time period of 2006–2093 relative to the reference period of 1961–2004 showed highest warming for RCP8.5 scenario, followed by RCP4.5 scenario, with the RCP2.6 scenario showing the lowest warming, which is likely to increase at 0.06 °C, 0.18 °C, and 0.39 °C decade−1 under RCP2.6, RCP4.5, and RCP8.5 scenarios by the sub-ensemble, while higher temperature increase at 0.08 °C, 0.20 °C, and 0.42 °C by the full ensemble, with Z statistics of annual temperature increase series at 5.6(8.6), 10.7(12.1), and 12.5(13.2) for the sub-ensemble and full ensemble, respectively (Figure 7), indicating significant temperature increase over the LMB in the future.

Table 3.
Changes in mean annual and seasonal temperature (°C) over the LMB under RCP2.6, RCP4.5, and RCP8.5 relative to the period of 1961–2004 under two ensemble methods. Values in parentheses represent the results of the full ensemble.
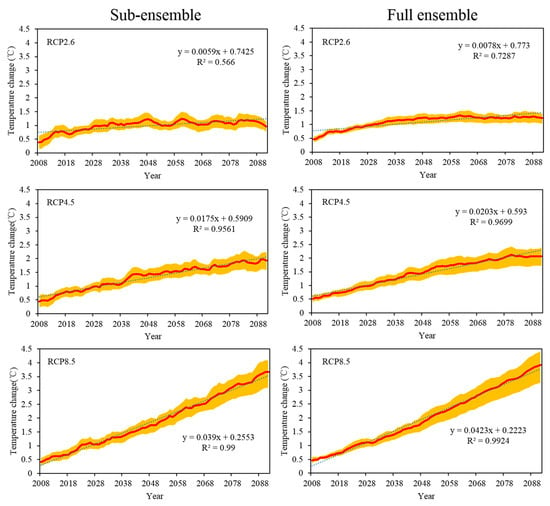
Figure 7.
Future temperature changes for RCP2.6, RCP4.5, and RCP8.5 scenarios relative to the period of 1961–2004 over the LMB under two ways of multi-model ensemble after smoothing with five years moving average. The red lines represent the mean values of all the grids. The shaded areas represent the values of variation range of all the grids. The dotted line represents the linear regression. The degrees of freedom (DOF) are all 83 for the RCP2.6, RCP4.5, and RCP8.5 scenarios.
Future temperature change under RCP2.6, RCP4.5, and RCP8.5 scenarios of all 21 grids over the LMB are shown in Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12. It is projected that the temperature will increase over the LMB. The projected mean annual temperature increase from the far future (2050–2093) showed significantly higher than the near future (2006–2049), and the projection by the full ensemble showed higher temperature increase than the sub-ensemble, with the values range from 1.06 °C to 1.39 °C, 1.55 °C to 2.14 °C, and 2.46 °C to 3.33 °C for the far future (2050–2093) and 0.81 °C to 1.00 °C, 0.83 °C to 1.10 °C, 0.92 °C to 1.20 °C for the near future (2006–2049) by the full ensemble, while range from 0.92 °C to 1.21 °C, 1.45 °C to 1.86 °C, and 2.36 °C to 3.03 °C for the far future (2050–2093) and 0.77 °C to 0.99 °C, 0.82 °C to 1.06 °C, and 0.93 °C to 1.15 °C for the near future (2006–2049) by the sub-ensemble, relative to the reference period of 1961–2004 under RCP2.6, RCP4.5, and RCP8.5 scenarios, respectively. On the whole, the distributions of the mean annual temperature change showed relatively similar spatial distributions between the near future (2006–2049) and the far future (2050–2093) under projections from the sub-ensemble and the full ensemble, showing that the higher warming mainly occurred in the northern and central areas of the LMB, while the lower warming mainly occurred in the southeast and the southwest, especially under the RCP4.5 and RCP8.5 scenarios. Moreover, the warming for individual grid increased as the RCP increased for the sub-ensemble and the full ensemble. For the seasonal change, the similar spatial patterns of temperature changes were also found in the MAM, JJA (June–July–August), SON (September–October–November), and DJF, but the MAM warming showed relatively higher in comparison with other seasonal warming.
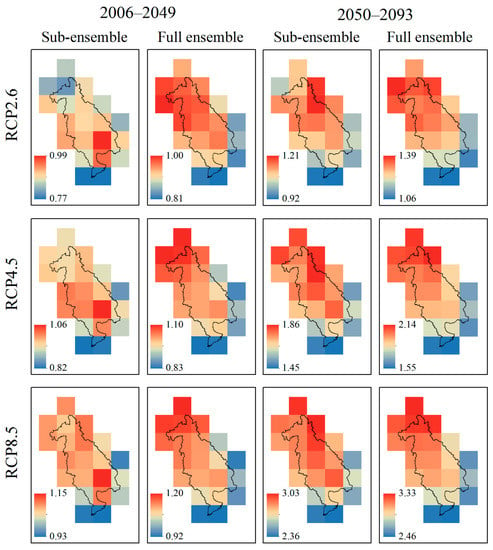
Figure 8.
Changes in mean annual temperature (°C) over the LMB during 2006–2049 and 2050–2093 relative to the reference period of 1961–2004 under RCP2.6, RCP4.5, and RCP8.5 scenarios from two ensemble methods.

Figure 9.
Changes in mean MAM temperature (°C) over the LMB during 2006–2049 and 2050–2093 relative to the reference period of 1961–2004 RCP2.6, RCP4.5, and RCP8.5 scenarios from two ensemble methods.
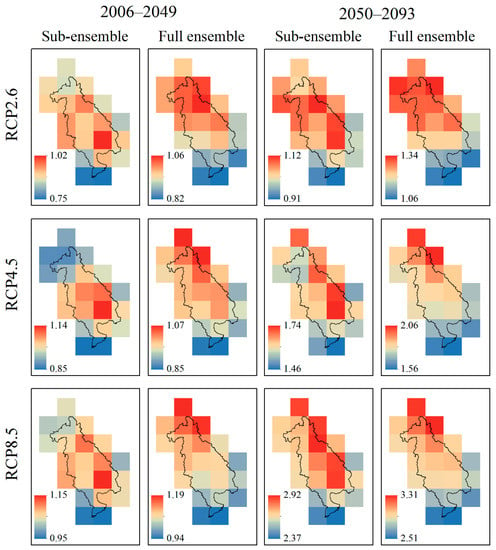
Figure 10.
Changes in mean JJA temperature (°C) over the LMB during 2006–2049 and 2050–2093 relative to the reference period of 1961–2004 RCP2.6, RCP4.5, and RCP8.5 scenarios from two ensemble methods.

Figure 11.
Changes in mean SON temperature (°C) over the LMB during 2006–2049 and 2050–2093 relative to the reference period of 1961‒2004 RCP2.6, RCP4.5, and RCP8.5 scenarios from two ensemble methods.
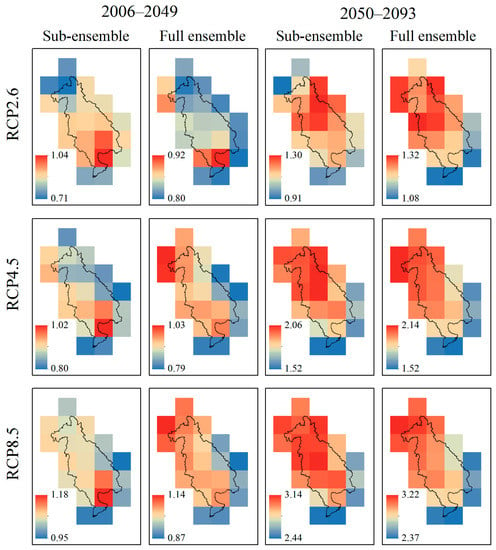
Figure 12.
Changes in mean DJF temperature (°C) over the LMB during 2006–2049 and 2050–2093 relative to the reference period of 1961–2004 RCP2.6, RCP4.5, and RCP8.5 scenarios from two ensemble methods.
4. Discussion
In this paper, most of the CMIP5 GCMs leaned towards underestimating the temperature relative to the observation, with mean annual bias at −3.02 °C for winter over the LMB. Similar results also been shown by Huang et al. [35] that the CMIP5 GCMs underestimated the annual mean surface air temperature relative to the Climate Research Unit temperature data (CRU TS 3.21) in Mekong River Basin. Other study in monsoon region of Sichuan Basin conducted by Bannister et al. [17] showed that mean temperature was underestimated by CMIP5 GCMs, especially during the winter, with bias exceeding −3 °C. Furthermore, another study in the Qinghai–Tibetan Plateau also showed that CMIP5 GCMs underestimated annual and seasonal temperatures, with bias at −2.3 °C for the annual mean, and larger cold biases for autumn and winter [47]. However, a study by Miao et al. [5] showed that most of the CMIP5 GCMs overestimated the annual mean surface air temperature in Northern Eurasia, especially during the winter. In addition, Zazulie et al. [48] also found that most of the GCMs overestimated the monthly mean temperature compared to ERA-Interim over the complex orographic region of the subtropical central Andes. Thus, the uncertainty of CMIP5 GCMs should be considered when applying them to regional scale. Additionally, there remains a need to understand why most of the GCMs underestimated the observed temperature over the LMB.
We used an improved score-based method to assess the performance of the GCMs in reproducing the observed temperature from 1961 to 2004. The improved score-based method combining not only the relative error index but also the non-relative error index, which have been proven to be effectively for the assessment [39,40]. Based on the method, multiple criteria were selected in this study, including Mean value (M), Standard deviation (SD), Normalized Root mean square error (NRMSE), linear correlation coefficient (r) for spatial distribution, Mann‒Kendall test statistic Z, Sen’s slope, and Significance score (Sscore). The results of sensitivity analysis showed that the improved score-based method combining multiple criteria showed a robust assessment of the GCMs performance. Thus, the methods can also be used for other study regions for assessing the GCMs performance for reproducing the climatic variables. After that, reliable information about the GCMs performance can be obtained for exploring future climate change.
Based on the results of the performance of the CMIP5 GCMs, the top 25% ranked GCMs were GISS-E2-H, GISS-E2-R, MIROC5, HadGEM2-ES, ACCESS1.0, MPI-ESM-MR, HadGEM2-CC, CESM1(WACCM), and MIROC4h. Study by Huang et al. 2014 [35] found that GISS-E2-H and MRI-CGCM3 was the best GCMs to simulate the annual surface temperature in the Mekong River Basin. A study by Das et al. [8] showed that CMCC-CM, GISS-E2-H, MIROC5, MPI-ESM-LR, MIROC4th, and CCSM4 were top-ranked models in reproducing the observed temperature over the Western Himalayan Region of India. Although different GCMs were likely to rank differently depending on the region [49], we highlighted the similar good performance of GISS-E2-H, MPI-ESM-LR, MIROC5, and MIROC4h over the LMB, which is in close proximity to the Western Himalayan Region of India, and is a part of the Mekong River Basin, both of which are affected by the southwest monsoon.
We used the top 25% ranked GCMs and the entire GCMs to build the multi-model ensemble (MME) for temperature projection over the LMB, respectively. A previous study by Huang et al. [35] also showed that it can improve the temporal simulation compared to a single GCM when assessing the performance of CMIP5 GCMs by MME of Bayesian moving average (BMA) in the Mekong River Basin. Miao et al. [5] also found that the performances of the MMEs by simple model averaging (SMA), reliability ensemble averaging (REA) and Bayesian model averaging (BMA) methods are superior to any single GCM output in simulating temperature over Northern Eurasia. Venkataraman et al. [50] showed that the ensemble mean based on the arithmetic mean (AM) method had advantages in performance of temperature and precipitation simulation compared to a single model. Similar results were also found by Ahmadalipour et al. [51] that the Bayesian model averaging (BMA) ensemble have advantages in simulating precipitation, maximum temperature, and minimum temperature than individual GCMs over the Columbia River Basin. These indicate that MME is superior to that of the single GCM, which can improve the skill scores for projecting future temperature. In this paper, our results showed that the sub-ensemble by the top 25% ranked GCMs and full ensemble by the entire GCMs have similar spatial distributions of temperature projection over the LMB. However, there existed differences about the magnitudes of the future temperature change between the two ensembles. In addition, previous studies also found that projection uncertainty varied as the model ensemble methods changed [5,52]. Moreover, Ahmadalipour et al. [51] found that model uncertainty is the major source of uncertainty in precipitation projection and near-future temperature simulations over the Columbia River Basin. Therefore, in order to reduce the uncertainty of temperature projection in further studies in the LMB, multiple methods of GCMs ensemble should be considered and compared.
5. Conclusions
This study focused mainly on the assessment of the performance of 34 CMIP5 GCMs in simulating the observed temperature using an improved score-based method and the projection of future temperature change over the LMB. The performance was assessed using seven criteria including the M, SD, NRMSE, r, Z, Sen’s slope, and Sscore over the LMB. Then, based on the results of the performance for these GCMs, two ways of the multi-model ensemble (MME), sub-ensemble from the top 25% ranked GCMs, full ensemble from the entire GCMs were calculated using arithmetic mean (AM) method and downscaled using the Delta method to project future temperature during two future time periods, the near future (2006–2049) and the far future (2050–2093) under RCP2.6, RCP4.5, and RCP8.5 scenarios, respectively. The major findings of this study are summarized below:
The results of the GCMs assessment varied as the criterion changed. It is essential to comprehensively assess the GCMs by multiple criteria rather than using single criterion. Based on the overall ranking scores, the top 25% ranked GCMs were GISS-E2-H, GISS-E2-R, MIROC5, HadGEM2-ES, ACCESS1.0, MPI-ESM-MR, HadGEM2-CC, CESM1(WACCM), and MIROC4h, which can be used to build the multi-model ensemble (MME) for future temperature projection over the LMB. Meanwhile, the improved score-based method combining multiple criteria showed a robust assessment of the GCMs performance, which can provide good information related to the studies of future temperature change.
The results showed significant temperature increase in the future over the LMB, with higher mean annual temperature increase from full ensemble and sub-ensemble at 1.26 °C (1.09 °C), 1.90 °C (1.70 °C), and 2.97 °C (2.78 °C) during 2050–2093 under RCP2.6, RCP4.5, and RCP8.5 scenarios compared to the values at 0.93 °C (0.87 °C), 0.99 °C (0.95 °C), and 1.09 °C (1.06 °C) during 2006–2049, respectively, relative to the reference time period of 1961–2004. Moreover, the projected seasonal temperature increase from the far future (2050–2093) also showed significantly higher than the near future (2006–2049). In addition, the projection by the full ensemble showed higher temperature increase than the sub-ensemble. The two ensembles showed similar spatial distributions of temperature change, with the higher warming mainly occurred in the northern and central areas of the LMB, while the lower warming mainly occurred in the southeast and the southwest, especially under the RCP4.5 and RCP8.5 scenarios. Moreover, the warming for individual grid increased as the RCP increased for the two ensembles.
The results provided an application of an improved score-based method in the GCMs assessment and the multi-model ensemble (MME) to project future temperature change over the LMB under three scenarios, which can be useful for GCMs assessment and policy making in this region. However, there remains a need to understand why most of the GCMs underestimated the observed temperature over the LMB, and a need to establish more meteorological stations for long-term observation over the LMB as well as a need to extend temperature projection to a larger region such as the entire Mekong Basin or the Southeast Asia for better understanding regional climate change impacts. Moreover, there existed differences about the magnitudes of the future temperature change between the two ways of ensemble. Therefore, in order to reduce the uncertainty of temperature projection in further studies in the LMB, multiple methods of GCMs ensemble should be taken into considered and compared.
Author Contributions
Y.R. wrote the manuscript text and contributed to the graphics. Z.L., R.W., and Z.Y. contributed to the methods, results, analysis, discussion, and revision of the manuscript.
Funding
The authors gratefully acknowledge the financial support provided by the National Natural Science Foundation of China (No. 41561144012 and 41661144030).
Conflicts of Interest
The authors declare no conflict of interest.
References
- IPCC. Climate Change 2013—The Physical Science Basis by Intergovernmental Panel on Climate Change; Cambridge University Press (CUP): Cambridge, UK, 2009. [Google Scholar]
- Eastham, J.; Mpelasoka, F.; Mainuddin, M.; Ticehurst, C.; Dyce, P.; Hodgson, G.; Ali, R.; Kirby, M. Mekong River Basin Water Resources Assessment: Impacts of Climate Change; Water for a Healthy Country National Research Flagship Report; CSIRO: Canberra, Australia, 2008. [Google Scholar]
- Qin, D.H.; Luo, Y.; Chen, Z.L.; Ren, J.W.; Shen, Y.P. Latest advances in climate change sciences: Interpretation of the synthesis report of the IPCC fourth assessment report. Adv. Climate. Change. Res. 2007, 3, 311–314. (In Chinese) [Google Scholar]
- Rupp, D.E.; Abatzoglou, J.T.; Hegewisch, K.C.; Mote, P.W. Evaluation of CMIP5 20th century climate simulations for the Pacific Northwest USA. J. Geophys. Res. Atmos. 2013, 118, 10884–10906. [Google Scholar] [CrossRef]
- Miao, C.Y.; Duan, Q.Y.; Sun, Q.H.; Huang, Y.; Kong, D.X.; Yang, T.T.; Ye, A.Z.; Di, Z.H.; Gong, W. Assessment of CMIP5 climate models and projected temperature changes over Northern Eurasia. Environ. Res. Lett. 2014, 9, 055007. [Google Scholar] [CrossRef]
- Ahmadalipour, A.; Rana, A.; Moradkhani, H.; Sharma, A. Multi-criteria evaluation of CMIP5 GCMs for climate change impact analysis. Theor. Appl. Climatol. 2015, 128, 71–87. [Google Scholar] [CrossRef]
- Dong, T.Y.; Dong, W.J.; Guo, Y.; Chou, J.M.; Yang, S.L.; Tian, D.; Yan, D.D. Future temperature changes over the critical Belt and Road region based on CMIP5 models. Adv. Climate Change Res. 2018, 9, 57–65. [Google Scholar] [CrossRef]
- Das, L.; Dutta, M.; Mezghani, A.; Benestad, R.E. Use of observed temperature statistics in ranking CMIP5 model performance over the Western Himalayan Region of India. Int. J. Climatol. 2017, 38, 554–570. [Google Scholar] [CrossRef]
- Sun, Q.H.; Miao, C.Y.; Duan, Q.Y. Comparative analysis of CMIP3 and CMIP5 global climate models for simulating the daily mean, maximum, and minimum temperatures and daily precipitation over China. J. Geophys. Res. Atmos. 2015, 120, 4806–4824. [Google Scholar] [CrossRef]
- Koutroulis, A.G.; Grillakis, M.G.; Tsanis, I.K.; Papadimitriou, L. Evaluation of precipitation and temperature simulation performance of the CMIP3 and CMIP5 historical experiments. Clim. Dyn. 2015, 47, 1881–1898. [Google Scholar] [CrossRef]
- Guo, Y.; Dong, W.J.; Ren, F.M.; Zhao, Z.C.; Huang, J.B. Surface Air Temperature Simulations over China with CMIP5 and CMIP3. Adv. Climate Change Res. 2013, 4, 145–152. [Google Scholar]
- Sonali, P.; Kumar, D.N.; Nanjundiah, R.S. Intercomparison of CMIP5 and CMIP3 simulations of the 20th century maximum and minimum temperatures over India and detection of climatic trends. Meteorol. Atmos. Phys. 2016, 128, 465–489. [Google Scholar] [CrossRef]
- Lee, Y.-Y.; Black, R.X. Boreal winter low-frequency variability in CMIP5 models. J. Geophys. Res. Atmos. 2013, 118, 6891–6904. [Google Scholar] [CrossRef]
- Ning, L.; Bradley, R.S. NAO and PNA influences on winter temperature and precipitation over the eastern United States in CMIP5 GCMs. Clim. Dyn. 2015, 46, 1257–1276. [Google Scholar] [CrossRef]
- Wang, X.; Chen, M.; Wang, C.; Yeh, S.-W.; Tan, W. Evaluation of performance of CMIP5 models in simulating the North Pacific Oscillation and El Niño Modoki. Clim. Dyn. 2018, 1–12. [Google Scholar] [CrossRef]
- Hawkins, E.; Sutton, R. The Potential to Narrow Uncertainty in Regional Climate Predictions. Bull. Amer. Meteor. Soc. 2009, 90, 1095–1108. [Google Scholar] [CrossRef]
- Bannister, D.; Herzog, M.; Graf, H.-F.; Hosking, J.S.; Short, C.A. An Assessment of Recent and Future Temperature Change over the Sichuan Basin, China, Using CMIP5 Climate Models. J. Clim. 2017, 30, 6701–6722. [Google Scholar] [CrossRef]
- Abbasian, M.; Moghim, S.; Abrishamchi, A. Performance of the general circulation models in simulating temperature and precipitation over Iran. Meteorol. Atmos. Phys. 2018, 1–19. [Google Scholar] [CrossRef]
- Robock, A.; Turco, R.P.; Harwell, M.A.; Ackerman, T.P.; Andressen, R.; Chang, H.-S.; Sivakumar, M.V.K. Use of general circulation model output in the creation of climate change scenarios for impact analysis. Climatic Change 1993, 23, 293–335. [Google Scholar] [CrossRef]
- Risbey, J.S.; Stone, P.H. A Case Study of the Adequacy of GCM Simulations for Input to Regional Climate Change Assessments. J. Clim. 1996, 9, 1441–1467. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, C.; Gao, X.; Luo, Y. Projected changes in temperature and precipitation extremes over the Yangtze River Basin of China in the 21st century. Quat. Int. 2009, 208, 44–52. [Google Scholar] [CrossRef]
- Luo, M.; Liu, T.; Frankl, A.; Duan, Y.; Meng, F.; Bao, A.; Kurban, A.; De Maeyer, P. Defining spatiotemporal characteristics of climate change trends from downscaled GCMs ensembles: How climate change reacts in Xinjiang, China. Int. J. Climatol. 2018, 38, 2538–2553. [Google Scholar] [CrossRef]
- Fan, L.J.; Fu, C.B.; Chen, D.L. Review on creating future climate change scenarios by statistical downscaling techniques. Adv. Earth. Sci. 2008, 20, 320–329. (In Chinese) [Google Scholar]
- Choi, W.; Rasmussen, P.F.; Moore, A.R.; Kim, S.J. Simulating streamflow response to climate scenarios in central Canada using a simple statistical downscaling method. Clim. Res. 2009, 40, 89–102. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Z.; Ren, X.; Fischer, T.; Xu, Y. Hydrological impacts of climate change in the Yellow River Basin for the 21st century using hydrological model and statistical downscaling model. Quat. Int. 2011, 244, 211–220. [Google Scholar] [CrossRef]
- Horton, R.M.; Gornitz, V.; Bader, D.A.; Goldberg, R.; Ruane, A.C.; Rosenzweig, C. Climate Hazard Assessment for Stakeholder Adaptation Planning in New York City. J. Appl. Meteor. Climatol. 2011, 50, 2247–2266. [Google Scholar] [CrossRef]
- Rahimi, J.; Ebrahimpour, M.; Khalili, A. Spatial changes of Extended De Martonne climatic zones affected by climate change in Iran. Theor. Appl. Climatol. 2012, 112, 409–418. [Google Scholar] [CrossRef]
- Wang, T.; Hamann, A.; Spittlehouse, D.; Carroll, C. Locally Downscaled and Spatially Customizable Climate Data for Historical and Future Periods for North America. PLoS ONE 2016, 11, 0156720. [Google Scholar] [CrossRef] [PubMed]
- Walsh, J.E.; Bhatt, U.S.; Littell, J.S.; Leonawicz, M.; Lindgren, M.; Kurkowski, T.A.; Bieniek, P.A.; Thoman, R.; Gray, S.; Rupp, T.S. Downscaling of climate model output for Alaskan stakeholders. Environ. Model. Software 2018, 110, 38–51. [Google Scholar] [CrossRef]
- Trisurat, Y.; Aekakkararungroj, A.; Ma, H.-O.; Johnston, J.M. Basin-wide impacts of climate change on ecosystem services in the Lower Mekong Basin. Ecol. Res. 2017, 33, 73–86. [Google Scholar] [CrossRef] [PubMed]
- Mekong River Commission; ICEM. MRC: Vulnerability Report Volume 2: Basin-Wide Climate Change Impact and Vulnerability Assessment for Wetland Dependent Livelihoods and Eco-Services; Mekong River Commission: Vientiane, Laos; ICEM: Melbourne, Australia, 2015. [Google Scholar]
- Hoanh, C.T.; Jirayoot, K.; Lacombe, G.; Srinetr, V. Impacts of Climate Change and Development on Mekong Flow Regimes. First Assessment—2009; International Water Management Institute: Colombo, Sri Lanka, 2010. [Google Scholar]
- Yoshimura, C.; Zhou, M.; Kiem, A.S.; Fukami, K.; Prasantha, H.H.; Ishidaira, H.; Takeuchi, K. 2020s scenario analysis of nutrient load in the Mekong River Basin using a distributed hydrological model. Sci. Total Environ. 2009, 407, 5356–5366. [Google Scholar] [CrossRef]
- Kingston, D.G.; Thompson, J.R.; Kite, G. Uncertainty in climate change projections of discharge for the Mekong River Basin. Hydrol. Earth Syst. Sci. 2011, 15, 1459–1471. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, F.; Li, Y.; Cai, T. Multi-model ensemble simulation and projection in the climate change in the Mekong River Basin. Part I: Temperature. Environ. Monit. Assess. 2014, 186, 7513–7523. [Google Scholar] [CrossRef] [PubMed]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of CMIP5 and the Experiment Design. Bull. Amer. Meteor. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Yasutomi, N.; Hamada, A.; Yatagai, A. Development of a long-term daily gridded temperature dataset and its application to rain/snow discrimination of daily precipitation. Global. Environ. Res. 2011, 15, 165–172. [Google Scholar]
- Lutz, A.; Terink, W.; Droogers, P.; Immerzeel, W.; Piman, T. Development of Baseline Climate Data Set and Trend Analysis in the Mekong Basin; Mekong River Commission: Vientiane, Laos, 2014; pp. 1–127. [Google Scholar]
- Fu, G.; Liu, Z.; Charles, S.P.; Xu, Z.; Yao, Z. A score-based method for assessing the performance of GCMs: A case study of southeastern Australia. J. Geophys. Res. Atmos. 2013, 118, 4154–4167. [Google Scholar] [CrossRef]
- Liu, Z.F.; Wang, R.; Yao, Z.J. Air temperature and precipitation over the Mongolian Plateau and assessment of CMIP5 climate models. Resour. Sci. 2016, 38, 956–969. (In Chinese) [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Charles Griffin: London, UK, 1975. [Google Scholar]
- Hirsch, R.M.; Alexander, R.B.; Smith, R.A. Selection of methods for the detection and estimation of trends in water quality. Water Resour. Res. 1991, 27, 803–813. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Hirsch, R.M.; Slack, J.R.; Smith, R.A. Techniques of trend analysis for monthly water quality data. Water Resour. Res. 1982, 18, 107–121. [Google Scholar] [CrossRef]
- Perkins, S.E.; Pitman, A.; Holbrook, N.J.; McAneney, J. Evaluation of the AR4 Climate Models’ Simulated Daily Maximum Temperature, Minimum Temperature, and Precipitation over Australia Using Probability Density Functions. J. Clim. 2007, 20, 4356–4376. [Google Scholar] [CrossRef]
- Hu, Q.; Jiang, D.B.; Fan, G.Z. Evaluation of CMIP5 models over the Qinghai-Tibetan Plateau. Chin. J. Atmosph. Sci. 2014, 38, 924–938. (In Chinese) [Google Scholar]
- Zazulie, N.; Rusticucci, M.; Raga, G.B. Regional climate of the subtropical central Andes using high-resolution CMIP5 models—Part I: Past performance (1980–2005). Clim. Dyn. 2017, 49, 3937–3957. [Google Scholar] [CrossRef]
- Kumar, D.; Kodra, E.; Ganguly, A.R. Regional and seasonal intercomparison of CMIP3 and CMIP5 climate model ensembles for temperature and precipitation. Clim. Dyn. 2014, 43, 2491–2518. [Google Scholar] [CrossRef]
- Venkataraman, K.; Tummuri, S.; Medina, A.; Perry, J. 21st century drought outlook for major climate divisions of Texas based on CMIP5 multimodel ensemble: Implications for water resource management. J. Hydrol. 2016, 534, 300–316. [Google Scholar] [CrossRef]
- Ahmadalipour, A.; Moradkhani, H.; Rana, A. Accounting for downscaling and model uncertainty in fine-resolution seasonal climate projections over the Columbia River Basin. Clim. Dyn. 2017, 50, 717–733. [Google Scholar] [CrossRef]
- Wang, X.; Yang, T.; Li, X.; Shi, P.; Zhou, X. Spatio-temporal changes of precipitation and temperature over the Pearl River basin based on CMIP5 multi-model ensemble. Stoch. Environ. Res. Risk Assess. 2016, 31, 1077–1089. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).