Convective Shower Characteristics Simulated with the Convection-Permitting Climate Model COSMO-CLM
Abstract
1. Introduction
2. Data and Methods
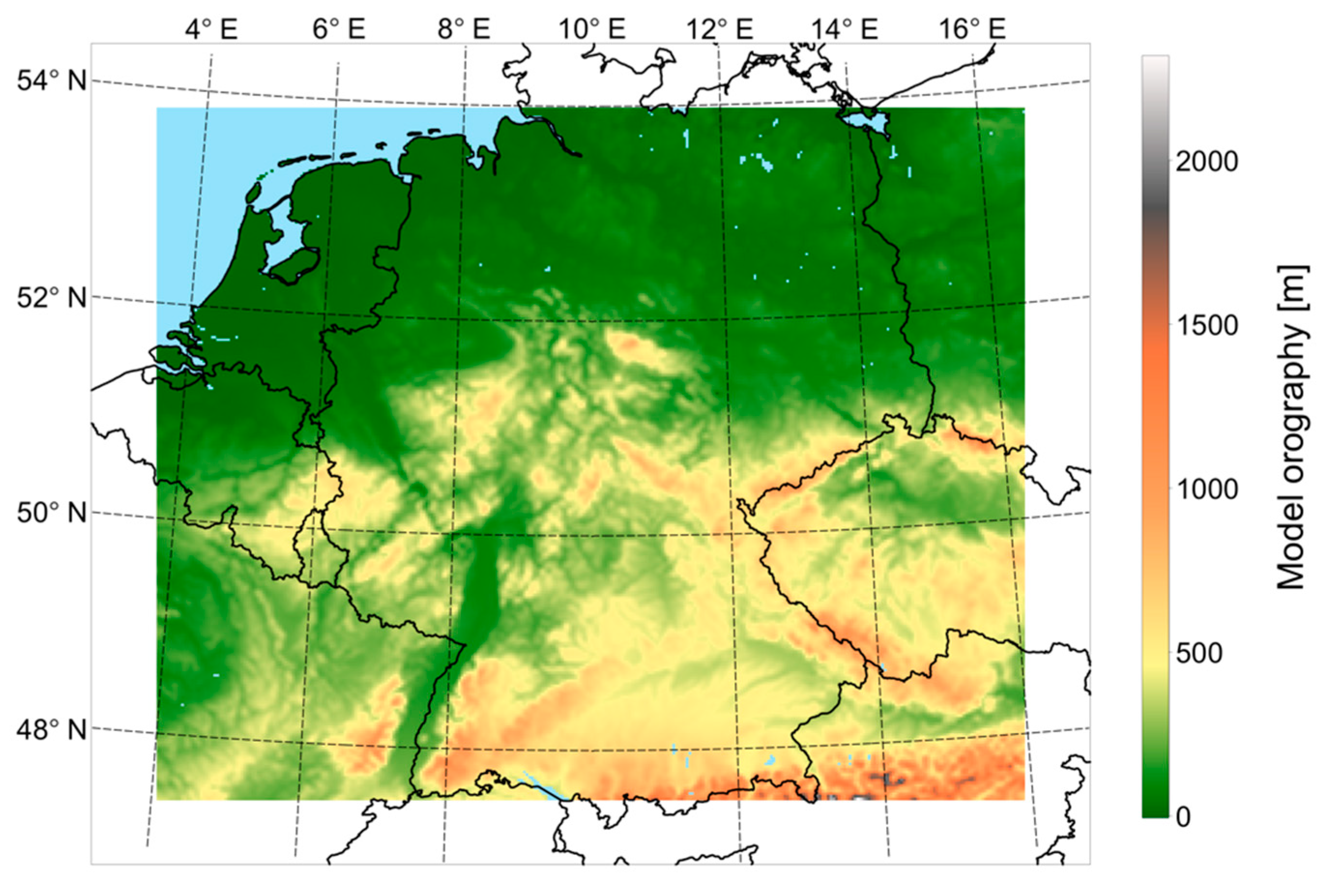
2.1. Model Setup
2.2. Radar Data
2.3. Tracking Algorithm
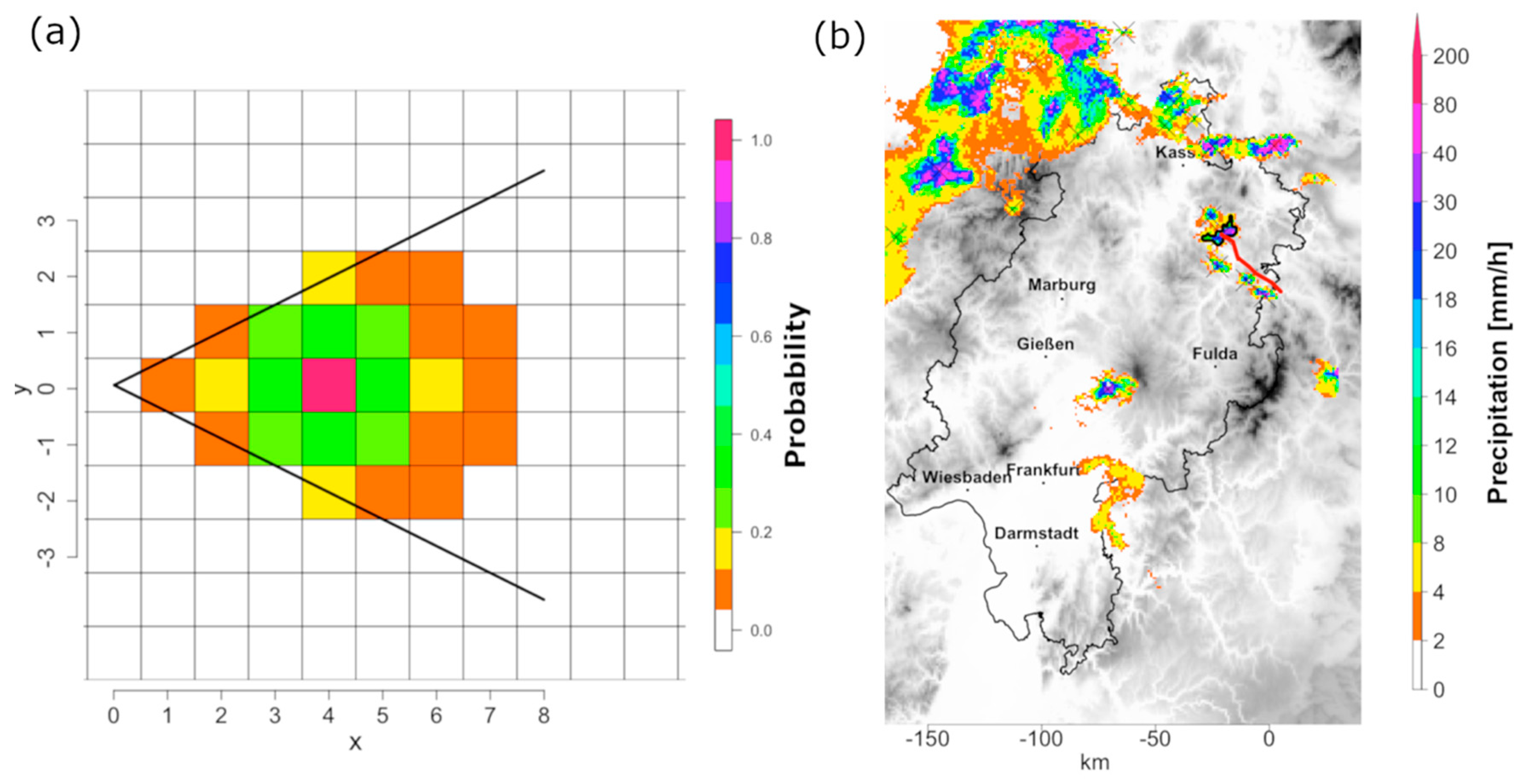
- Contiguous precipitation areas with precipitation intensity above a threshold of 8.5 mm/h (within 5 min), potential convective objects, are identified in the current and the subsequent time step. Contiguous areas are defined as pixels that share a common edge.
- Wind information is used to predict the position of the object at the subsequent time step. To this end, a “cone of detection” is set up for each pixel of every object, and the cone is swept for precipitation objects from the subsequent time step. The axis of the cone is defined by the wind direction; the length of the cone is calculated as twice the wind speed. The opening angle of the cone is 45°. If a new cell is present in the cone, a probability value is assigned to the origin pixel of the cone, which links this pixel to the new cell. The probability value is highest in the center of the cone and drops off exponentially in all directions. As an example, Figure 2a shows the probability values for a single pixel in the case of purely westward wind. In this case, the probability is calculated according to the following formula:where x and y are the indices in x and y direction starting at the original pixel (0,0). The parameter Ycent denotes the centerline of the cone, and Xmax is the length of the cone, as determined by the wind data. This procedure is repeated for wind information in three height levels (500, 700, and 850 hPa). Afterward, the height dependent probability values are averaged to obtain the final probability value.
- In the next step, the probabilities of all pixels are summed up for each cell. If one single object is present in the cone, the corresponding objects from the current and the subsequent time step are connected. If multiple cells are present, the current cell is associated with the cell with the highest probability in the subsequent time step.
3. Results and Discussion
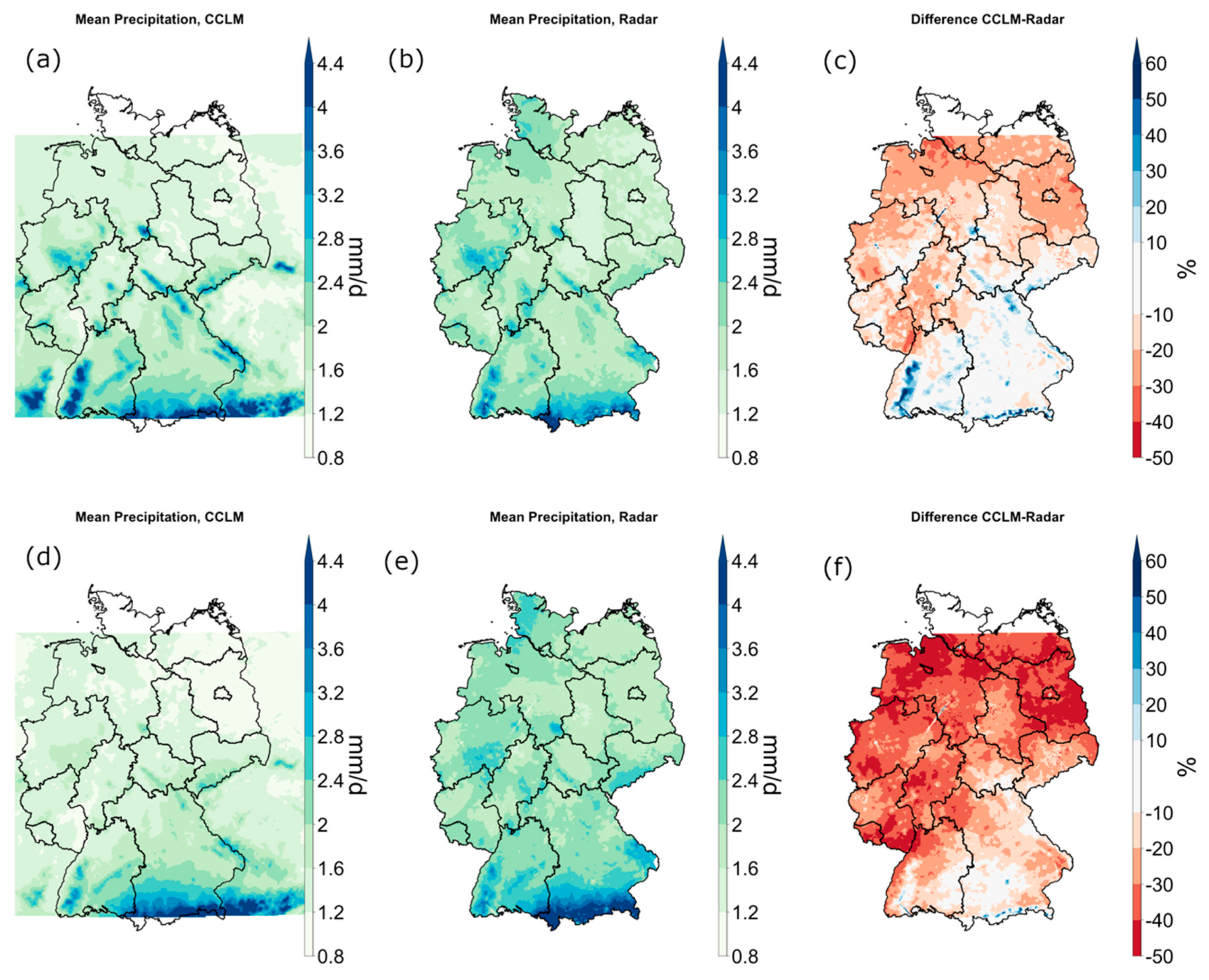
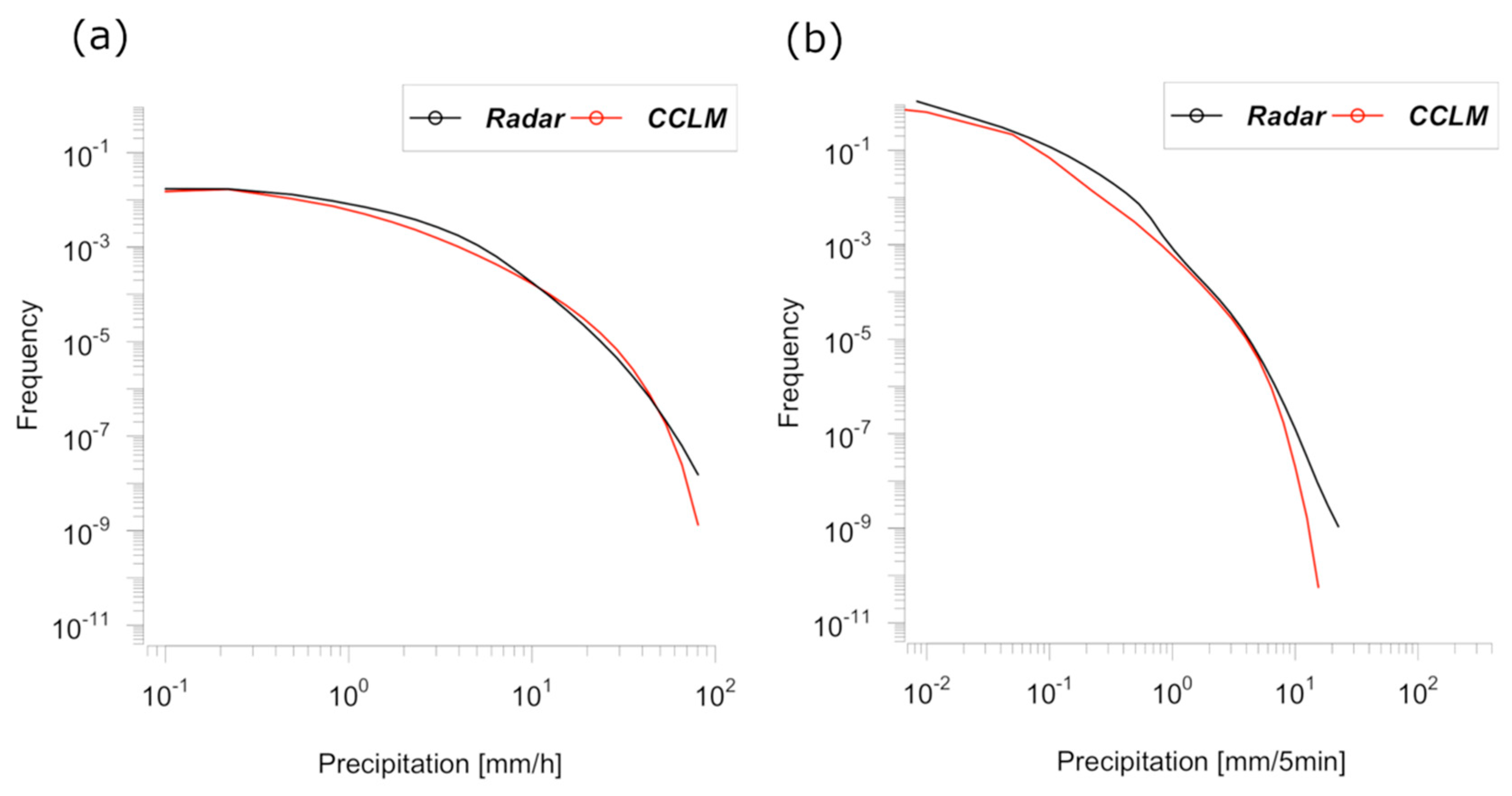
3.1. Precipitation Statistics
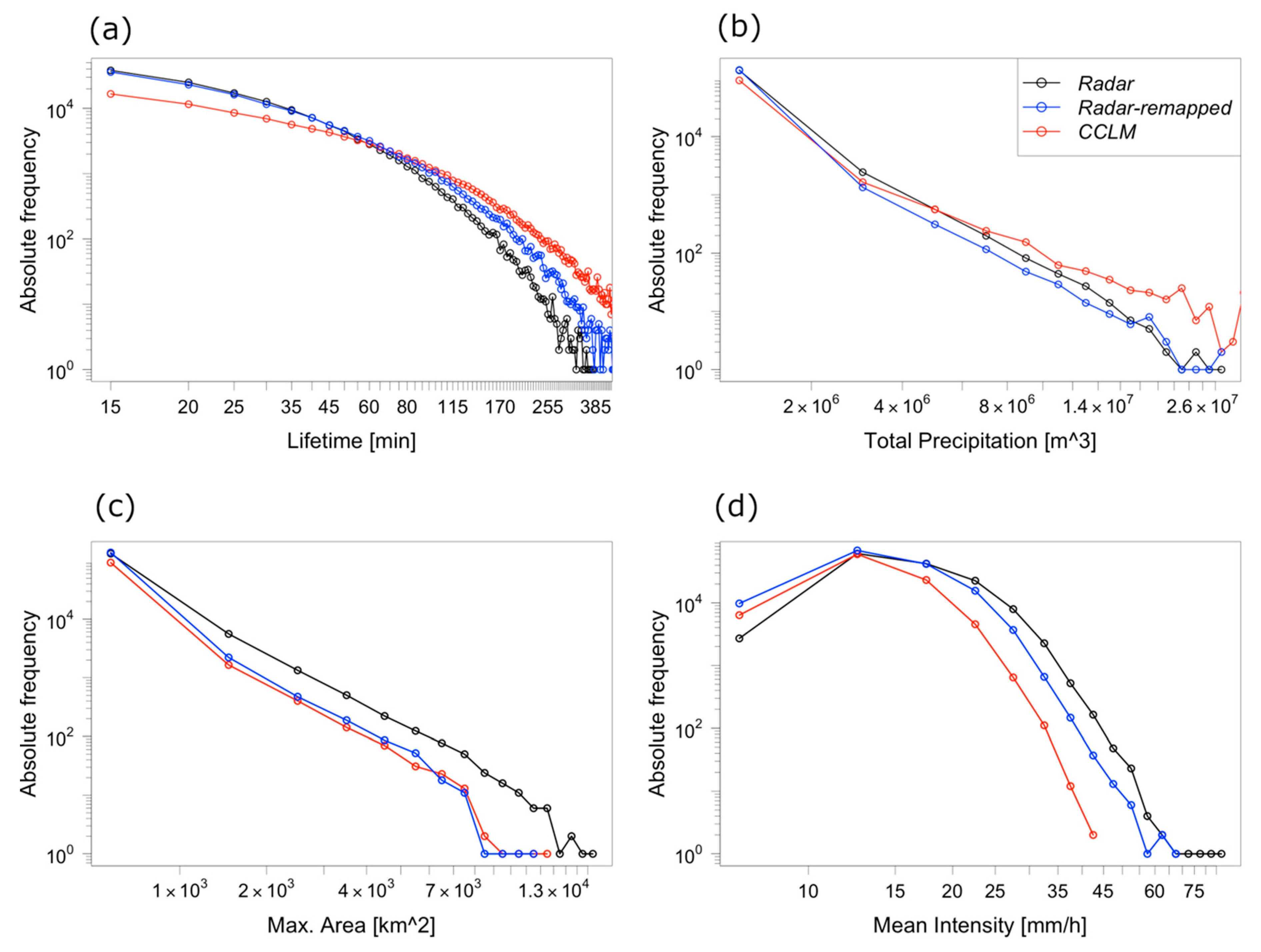
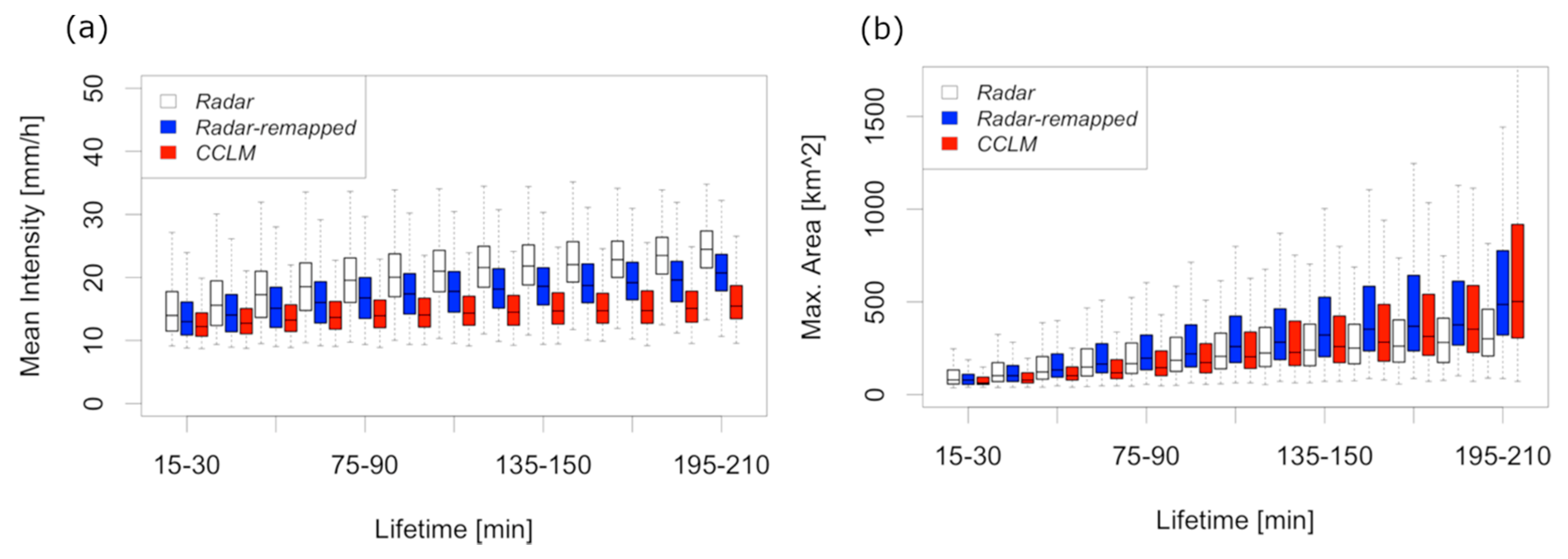
3.2. Frequency and Characteristics of Convective Cells
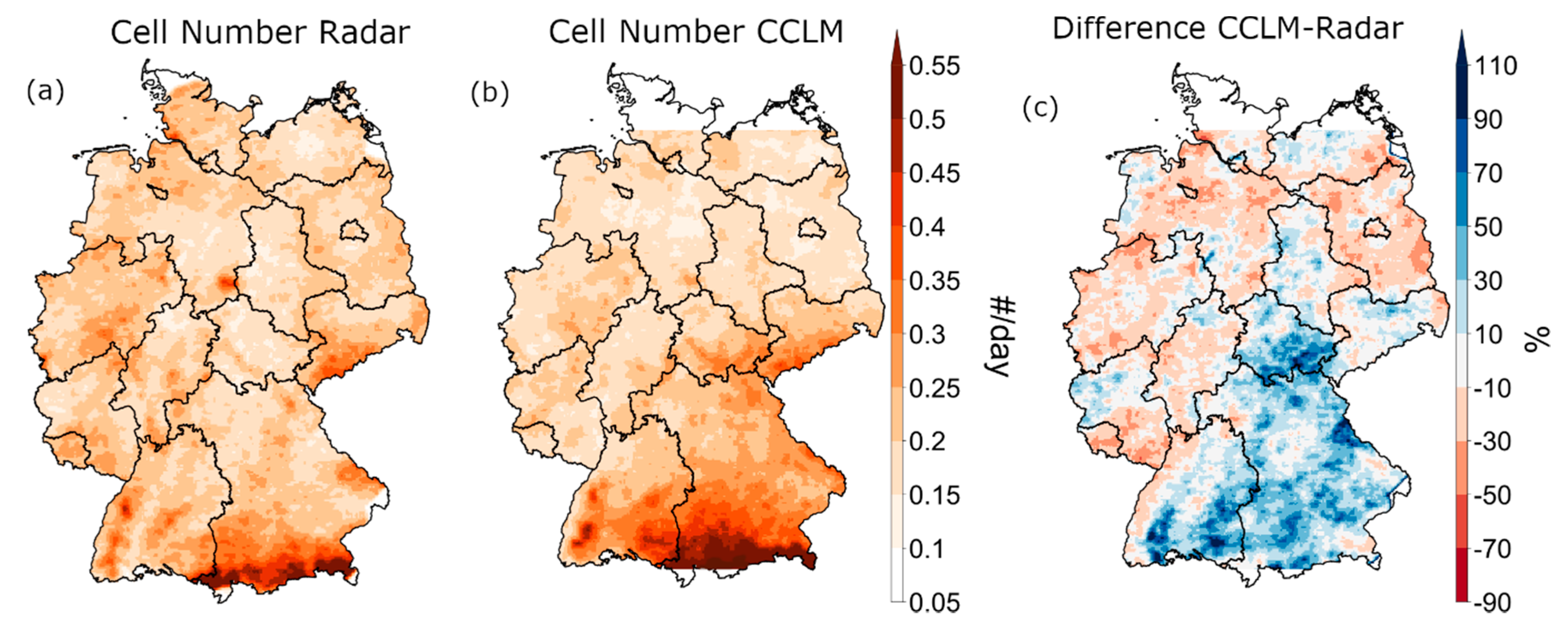
3.3. Spatial Distribution of Cell Characteristics
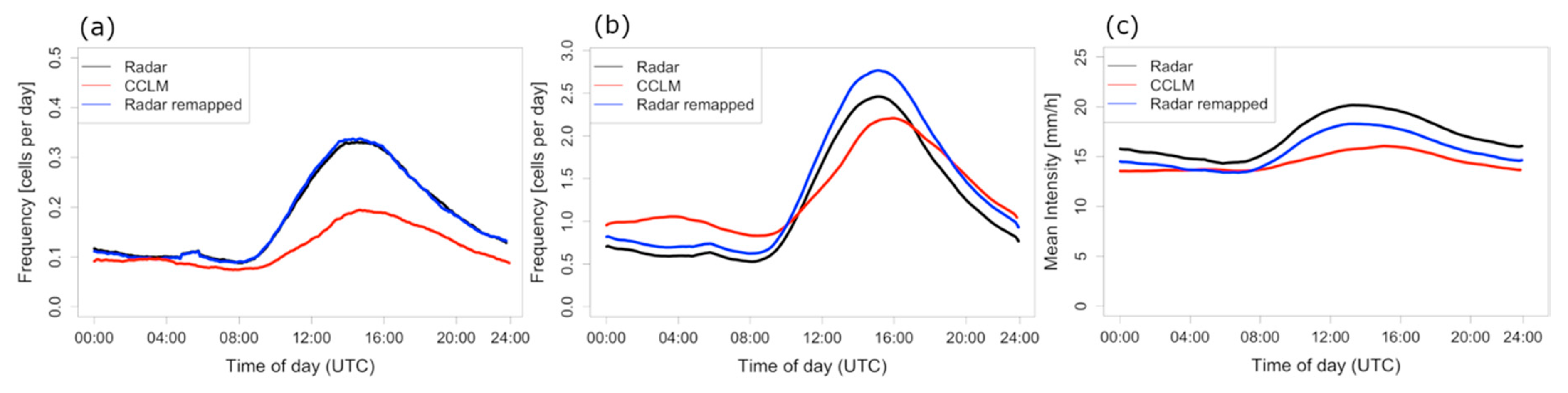
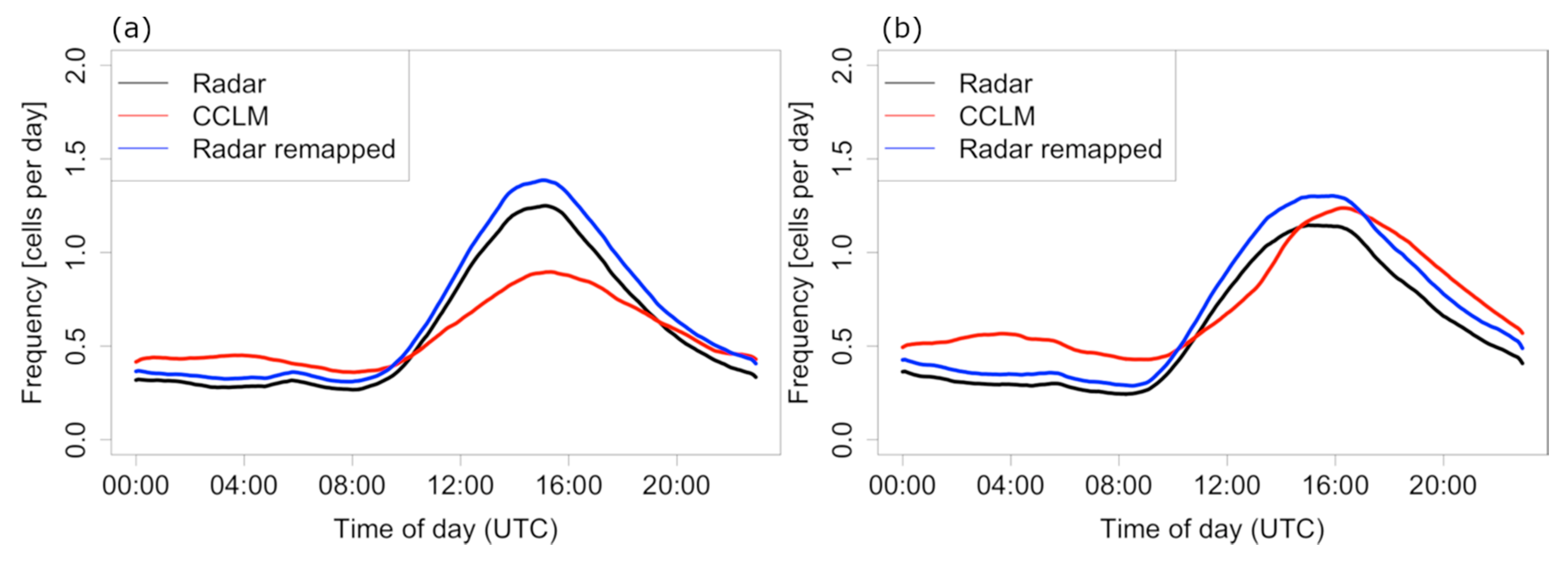
3.4. Diurnal Cycle
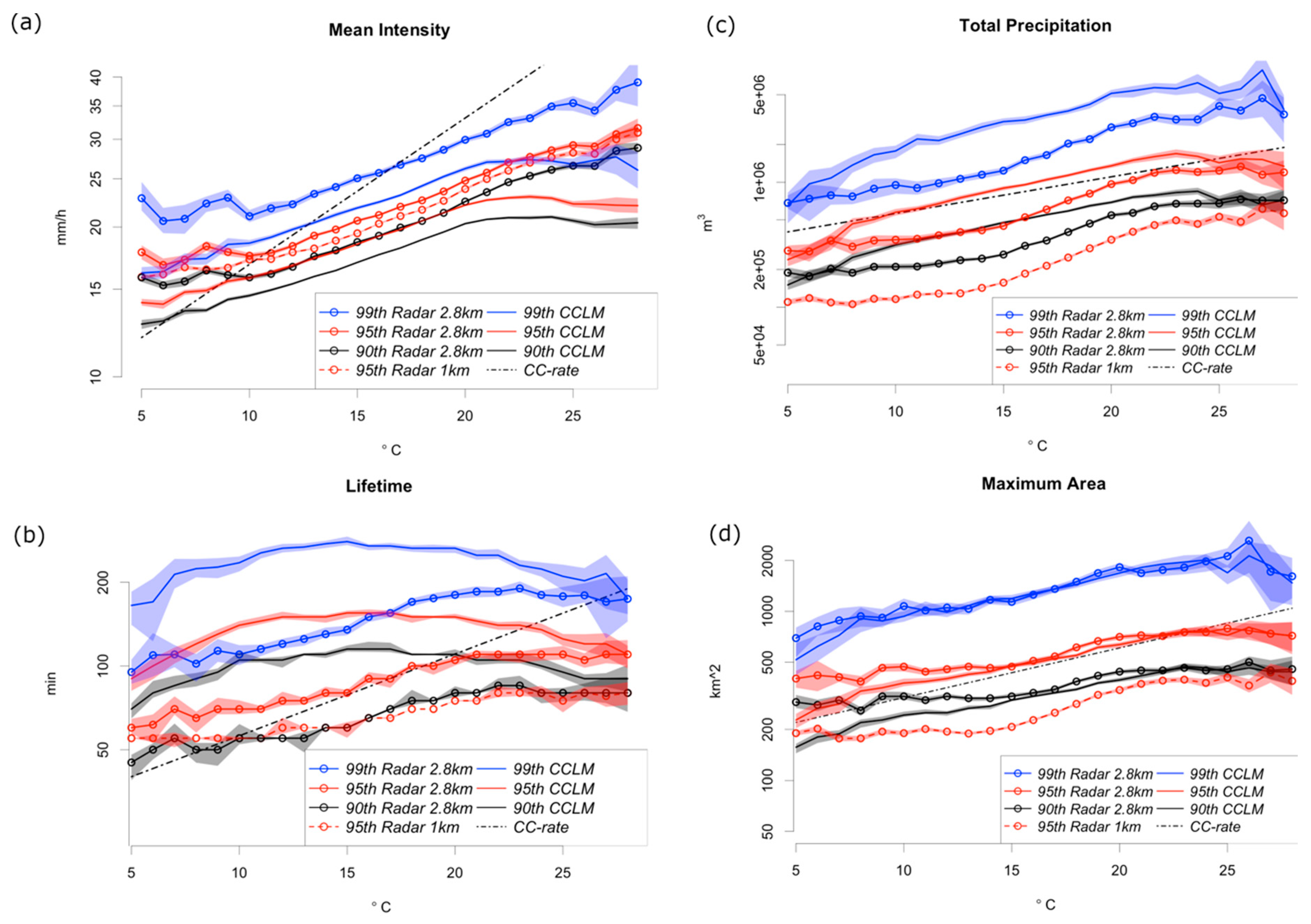
3.5. Temperature Scaling of Cell Characteristics
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ban, N.; Schmidli, J.; Schär, C. Evaluation of the convection-resolving regional climate modeling approach in decade-long simulations. J. Geophys. Res. Atmos. 2014, 119, 7889–7907. [Google Scholar] [CrossRef]
- Kendon, E.J.; Roberts, N.M.; Fowler, H.J.; Roberts, M.J.; Chan, S.C.; Senior, C.A. Heavier summer downpours with climate change revealed by weather forecast resolution model. Nat. Clim. Chang. 2014, 4, 570–576. [Google Scholar] [CrossRef]
- Prein, A.F.; Langhans, W.; Fosser, G.; Ferrone, A.; Ban, N.; Görgen, K.; Keller, M.; Tölle, M.; Gutjahr, O.; Feser, F.; et al. A review on regional convection-permitting climate modeling: Demonstrations, prospects, and challenges. Rev. Geophys. 2015, 53, 323–361. [Google Scholar] [CrossRef] [PubMed]
- Brisson, E.; van Weverberg, K.; Demuzere, M.; Devis, A.; Saeed, S.; Stengel, M.; van Lipzig, N.P.M. How well can a convection-permitting climate model reproduce decadal statistics of precipitation, temperature and cloud characteristics? Clim. Dyn. 2016, 47, 3043–3061. [Google Scholar] [CrossRef]
- Schroeer, K.; Kirchengast, G.; Sungmin, O. Strong dependence of extreme convective precipitation intensities on gauge network density. Geophys. Res. Lett. 2018, 45, 8253–8263. [Google Scholar] [CrossRef]
- Lochbihler, K.; Lenderink, G.; Siebesma, A.P. The spatial extent of rainfall events and its relation to precipitation scaling. Geophys. Res. Lett. 2017. [Google Scholar] [CrossRef]
- Moseley, C.; Berg, P.; Haerter, J.O. Probing the precipitation life cycle by iterative rain cell tracking. J. Geophys. Res. Atmos. 2013, 118, 13361–13370. [Google Scholar] [CrossRef]
- Brisson, E.; Brendel, C.; Herzog, S.; Ahrens, B. Lagrangian evaluation of convective shower characteristics in a convection-permitting model. Met. Z. 2017. [Google Scholar] [CrossRef]
- Prein, A.F.; Liu, C.; Ikeda, K.; Bullock, R.; Rasmussen, R.M.; Holland, G.J.; Clark, M. Simulating North American mesoscale convective systems with a convection-permitting climate model. Clim. Dyn. 2017. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Dai, A.; Rasmussen, R.M.; Parsons, D.B. The changing character of precipitation. Bull. Am. Meteorol. Soc. 2003, 84, 1205–12017. [Google Scholar] [CrossRef]
- Lenderink, G.; van Meijgaard, E. Increase in hourly precipitation extremes beyond expectations from temperature changes. Nat. Geosci. 2008, 1, 511–514. [Google Scholar] [CrossRef]
- Berg, P.; Moseley, C.; Haerter, J.O. Strong increase in convective precipitation in response to higher temperatures. Nat. Geosci. 2013, 6, 181–185. [Google Scholar] [CrossRef]
- Lenderink, G.; Barbero, R.; Loriaux, J.M.; Fowler, H.J. Super-Clausius-Clapeyron scaling of extreme hourly convective precipitation and its relation to large-scale atmospheric conditions. J. Clim. 2017, 30, 6037–6052. [Google Scholar] [CrossRef]
- Davies, H.C. A lateral boundary formulation for multi-level prediction models. Q. J. R. Meteorol. Soc. 1976, 102, 405–418. [Google Scholar] [CrossRef]
- Steppeler, J.; Doms, G.; Schaettler, U.; Bitzer, H.W.; Gassmann, A.; Damrath, U.; Gregoric, G. Meso-gamma scale forecasts using the nonhydrostatic model LM. Meteorol. Atmos. Phys. 2003, 82, 75–96. [Google Scholar] [CrossRef]
- Böhm, U.; Kücken, M.; Ahrens, W.; Block, A.; Hauffe, D.; Keuler, K.; Rockel, B.; Will, A. CLM—The Climate Version of LM: Brief Description and Long-Term Applications. COSMO Newsl. 2003, 6, 225–235. [Google Scholar]
- Rockel, B.; Will, A.; Hense, A. The Regional Climate Model COSMO-CLM (CCLM). Met. Z. 2008, 17, 347–348. [Google Scholar] [CrossRef]
- Ritter, B.; Geleyn, J.F. A comprehensive radiation scheme for numerical weather prediction models with potential applications in climate simulations. Mon. Weather Rev. 1992, 120, 303–325. [Google Scholar] [CrossRef]
- Brisson, E.; Demuzere, M.; van Lipzig, N.P.M. Modelling strategies for performing convective permitting climate simulations. Met. Z. 2015, 25, 149–163. [Google Scholar] [CrossRef]
- Tiedtke, M. A Comprehensive Mass Flux Scheme for Cumulus Parameterization in Large-Scale Models. Mon. Weather Rev. 1989, 117, 1779–1800. [Google Scholar] [CrossRef]
- Winterrath, T.; Brendel, C.; Hafer, M.; Junghänel, T.; Klameth, A.; Lengfeld, K.; Walawender, E.; Weigl, E.; Becker, A. Erstellung einer radargestützten Niederschlagsklimatologie. Ber. des Deutsch. Wetterd. 2017, 251. Available online: http://nbn-resolving.de/urn:nbn:de:101:1-20170908911 (accessed on 9 October 2019).
- Winterrath, T.; Brendel, C.; Hafer, M.; Junghänel, T.; Klameth, A.; Lengfeld, K.; Walawender, E.; Weigl, E.; Becker, A. RADKLIM Version 2017.002: Reprocessed quasi gauge-adjusted radar data, 5-minute precipitation sums (YW). Sci. Tech. Data 2018. [Google Scholar] [CrossRef]
- Winterrath, T.; Brendel, C.; Hafer, M.; Junghänel, T.; Klameth, A.; Lengfeld, K.; Walawender, E.; Weigl, E.; Becker, A. RADKLIM Version 2017.002: Reprocessed gauge-adjusted radar data, one-hour precipitation sums (RW). Sci. Tech. Data 2018. [Google Scholar] [CrossRef]
- Dobler, A.; Ahrens, B. Precipitation by a regional climate model and bias correction in Europe and South Asia. Met. Z. 2008, 17, 499–509. [Google Scholar] [CrossRef]
- Prein, A.F.; Gobiet, A. Impacts of uncertainties in European gridded precipitation observations on regional climate analysis. Int. J. Climatol. 2017, 37, 305–327. [Google Scholar] [CrossRef] [PubMed]
- Cornes, R.; van der Schrier, G.; van den Besselaar, E.J.M.; Jones, P.D. An Ensemble Version of the E-OBS Temperature and Precipitation Datasets. J. Geophys. Res. Atmos. 2018. [Google Scholar] [CrossRef]
- Perkins, S.E.; Pitman, A.J.; Holbrook, N.J.; McAneney, J. Evaluation of the AR4 Climate Models’ Simulated Daily Maximum Temperature, Minimum Temperature, and Precipitation over Australia Using Probability Density Functions. J. Climate 2007, 20, 4356–4376. [Google Scholar] [CrossRef]
- Kirshbaum, D.J.; Adler, B.; Kalthoff, N.; Barthlott, C.; Serafin, S. Moist Orographic Convection: Physical Mechanisms and Links to Surface-Exchange Processes. Atmos 2018, 9, 80. [Google Scholar] [CrossRef]
- Wapler, K.; James, P. High-resolution climatology of lightning characteristics within Central Europe. Meteorol. Atmos. Phys. 2013, 122, 175–184. [Google Scholar] [CrossRef]
- Knist, S.; Goergen, K.; Simmer, C. Evaluation and projected changes of precipitation statistics in convection-permitting WRF climate simulations over Central Europe. Clim. Dyn. 2018. [Google Scholar] [CrossRef]
- Pfeifroth, U.; Hollmann, R.; Ahrens, B. Cloud Cover Diurnal Cycles in Satellite Data and Regional Climate Model Simulations. Met. Z. 2012, 21, 551–560. [Google Scholar] [CrossRef]
- Barbero, R.; Westra, S.; Lenderink, G.; Fowler, H.J. Temperature-extreme precipitation scaling: A two-way causality? Int. J. Climatol. 2018, 38, e1274–e1279. [Google Scholar] [CrossRef]
- Hardwick Jones, R.; Westra, S.; Sharma, A. Observed relationships between extreme sub-daily precipitation, surface temperature, and relative humidity. Geophys. Res. Lett. 2010, 37, 1–5. [Google Scholar] [CrossRef]
- Chan, S.C.; Kendon, E.J.; Roberts, N.M.; Fowler, H.J.; Blenkinskop, S. Downturn in scaling of UK extreme rainfall with temperature for future hottest days. Nat. Geosci. 2016, 9, 24–28. [Google Scholar] [CrossRef]
- Brune, S.; Kapp, F.; Friederichs, P. A wavelet-based analysis of convective organization in ICON large-eddy simulations. Q. J. R. Meteorol. Soc. 2018, 144, 2812–2829. [Google Scholar] [CrossRef]
- Wapler, K.; James, P. Thunderstorm occurence and characteristics in Central Europe under different synoptic conditions. Atmos. Res. 2015, 158–159, 231–244. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Purr, C.; Brisson, E.; Ahrens, B. Convective Shower Characteristics Simulated with the Convection-Permitting Climate Model COSMO-CLM. Atmosphere 2019, 10, 810. https://doi.org/10.3390/atmos10120810
Purr C, Brisson E, Ahrens B. Convective Shower Characteristics Simulated with the Convection-Permitting Climate Model COSMO-CLM. Atmosphere. 2019; 10(12):810. https://doi.org/10.3390/atmos10120810
Chicago/Turabian StylePurr, Christopher, Erwan Brisson, and Bodo Ahrens. 2019. "Convective Shower Characteristics Simulated with the Convection-Permitting Climate Model COSMO-CLM" Atmosphere 10, no. 12: 810. https://doi.org/10.3390/atmos10120810
APA StylePurr, C., Brisson, E., & Ahrens, B. (2019). Convective Shower Characteristics Simulated with the Convection-Permitting Climate Model COSMO-CLM. Atmosphere, 10(12), 810. https://doi.org/10.3390/atmos10120810




