Next Article in Journal
Petrochemical and Industrial Sources of Volatile Organic Compounds Analyzed via Regional Wind-Driven Network in Shanghai
Previous Article in Journal
Source Apportionment of PM2.5 and of its Oxidative Potential in an Industrial Suburban Site in South Italy
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 10
Issue 12
10.3390/atmos10120759
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Response of Near-Surface Meteorological Conditions to Advection under Impact of the Green Roof

by
Haochen Tan
1,*,
Pallav Ray
1,
Mukul Tewari
2,
James Brownlee
1 and
Ajaya Ravindran
3
1
Meteorology, Florida Institute of Technology, Melbourne, FL 32901, USA
2
IBM, Thomas J. Watson Research Center, Yorktown Heights, NY 10598, USA
3
Center for Prototype Climate Modelling, The New York University Abu Dhabi, Abu Dhabi 129188, UAE
*
Author to whom correspondence should be addressed.
Atmosphere 2019, 10(12), 759; https://doi.org/10.3390/atmos10120759
Submission received: 6 November 2019 / Revised: 25 November 2019 / Accepted: 27 November 2019 / Published: 29 November 2019
(This article belongs to the Section Meteorology)
Browse Figures
Versions Notes

Abstract

:
Due to rapid urbanization, the near-surface meteorological conditions over urban areas are greatly modulated. To capture such modulations, sophisticated urban parameterizations with enhanced hydrological processes have been developed. In this study, we use the single-layer urban canopy model (SLUCM) available within the Weather Research and Forecasting (WRF) model to assess the response of near-surface temperature, wind, and moisture to advection under the impact of the green roof. An ensemble of simulations with different planetary boundary layer (PBL) schemes is conducted in the presence (green roof (GR)) and absence (control (CTL)) of green roof systems. Our results indicate that the near-surface temperature is found to be driven primarily by the surface heat flux with a minor influence from the zonal advection of temperature. The momentum budget analysis shows that both zonal and meridional momentum advection during the evening and early nighttime plays an important role in modulating winds over urban areas. The near-surface humidity remains nearly unchanged in GR compared to CTL, although the physical processes that determine the changes in humidity were different, in particular during the evening when the GR tends to have less moisture advection due to the reduced temperature gradient between the urban areas and the surroundings. Implications of our results are discussed.

1. Introduction

The modern urbanization over the past several decades has significantly modified the types of land-use around the globe [1]. The changes in the surface thermal and hydrological processes due to urbanization have led to elevated temperature [2,3], changes in soil cover [4,5,6], variation in precipitation patterns [7], and modification of surface roughness [8,9]. The reduction of natural surfaces and vegetation due to urbanization causes the re-distribution of surface heat flux components: a greater loss of sensible heat but less loss of latent heat [4]. The higher surface and air temperature in urban areas when compared with rural areas, known as the urban heat island (UHI) effect [10,11], leads to a greater need for cooling energy by the urban population [12,13,14,15].
To respond to the potential threat of UHI, there are two major strategies that involve the construction of green infrastructure (e.g., urban lawn, tree, green roof) and the use of reflective materials (e.g., cool pavement, white roof) [16,17,18,19,20,21,22,23,24,25]. Roofs that constitute a high fraction of the exposed area can provide an excellent space to apply mitigation techniques in the urban area. Akbari and Rose [26] explored four cities in America and found that the roof areas range from 20% to 25%. The advantage of green roofs in the presence of plants on the top of a building is regarded as environmentally friendly and contributes positively to the building’s energy efficiency. Green roofs have been shown to significantly mitigate the UHI effect by reducing near-surface temperature [27] and enhancing air quality [28] by increasing the evapotranspiration in urban areas and converting the available energy to latent heat. This mitigation mechanism over an urban area can be understood by looking at the surface heat flux components:
R n e t = S H + L H + G
where Rnet represents the net radiation at the surface, SH is the surface sensible heat flux, LH is the surface latent heat flux, and G is the storage heat flux. The net radiation is expressed as
R n e t = S W i n − S W o u t + L W i n − L W o u t
where SWin and SWout are the incoming and outgoing shortwave radiation, and LWin and LWout are the incoming and outgoing longwave radiation. Unlike other strategies that change the albedo and thus reduce the net radiation, the nature of the green roof strategy is to enhance latent heat for given net radiation, thereby reducing the sensible heat flux and resulting in a reduction in atmospheric heating and heat storage over urban areas.
Many new urban parameterization developments and improvements have been made for the Advanced Research Weather Research and Forecasting (WRF-ARW) model [29], including the single-layer urban canopy model (SLUCM) [30,31,32]. However, because of the poor representation of urban hydrological processes, the SLUCM has a larger bias in simulating the latent heat flux compared with other heat flux components [33,34,35]. Numerous efforts have been made to advance the performance of SLUCM in the WRF model by embedding five new urban hydrological processes [3,31,35,36,37]: anthropogenic latent heat flux, the urban oasis effect, urban irrigation, evaporation from paved surfaces, and multi-layer roofs. A notable improvement of latent heat flux was found over cities after incorporating hydrological processes [3]. Li et al. [38] examined the effectiveness of green roofs with white roofs over the Princeton urban canopy model into WRF, although the impact of urban hydrological processes was not explored in their study.
The objective of this study is to explore the response of near-surface meteorological conditions to advection under the impact of green roof systems using high-resolution simulations of the WRF model with sophisticated urban parameterizations over Houston, Texas. Metropolitan Houston has developed tremendously over the past decades and has experienced a strong UHI effect [3,39,40]. Therefore, Houston seems to be an ideal place to quantify the impacts of green roofs on certain physical processes such as advection that may play an important role in modulating near-surface atmospheric conditions. We believe that our study and its approach have three major novelties:
1. The most significant novelty in this study is the estimation of the impact of green roofs in modulating the advection of heat, momentum, and moisture that influences the temperature, wind, and humidity over Houston. To the best of our knowledge, the impact of green roofs on advection—in particular, on momentum advection—has not been quantified before.
2. The impact of green roofs has typically been assessed using a single simulation (deterministic approach) in most studies [41,42,43,44,45,46]. To the best of our knowledge, physics-based ensemble simulations using green roofs have not been performed previously to study the role of advection in the urban environment, although Munck et al. [46] used three simulations which differ in the initialization of the drainage layer in the green roof setup. Ensemble members were obtained by the combination of two drainage layer parameter values with all the other substrate-drainage characteristic values (see Table 4 of [46]), which resulted in a total of 32 simulations per ensemble. Given that near-surface conditions over an urban area critically depend on the planetary boundary layer (PBL) schemes [47,48,49], we have used four different popular PBL schemes to construct our ensemble for the control (CTL) and green roof (GR) experiments which is a different approach than that of [46].
3. Previous studies on the impact of the green roof using the SLUCM have mostly ignored hydrological processes within an urban area. This has led to a poor simulation of surface latent heat flux [33,34,35]. The performance of SLUCM has been advanced by embedding five new urban hydrological processes [3,31,43,50] that were included in our simulations.
The rest of the sections are constructed as follows. Section 2 describes the model, data, and methods, followed by the discussion of the results in Section 3. A summary and conclusions are presented in Section 4.

2. Methodology

2.1. Model

We use the SLUCM [3,31,32,51] available within the WRF model (version 3.7) with terrain-following coordinates [51]. The WRF model uses a fully compressible, non-hydrostatic modeling system that can be used at different spatial resolutions. The model domains are shown in Figure 1a with grid-spacings of 9 km (104 × 106), 3 km (190 × 196) and 1 km (280 × 262). The outermost domain is designed to be large enough to simulate any synoptic activity within the domain boundaries for the duration of the simulations. The innermost domain, DO3 (Figure 1b), includes the urban part of Houston and the observational stations. The model has 35 vertical levels from the surface to 50 hPa. The time step was 30 s for the outermost domain. The model output was taken every 10 min to capture the diurnal evolution of the urban atmosphere. All the simulations were integrated from 0000 UTC 24 August to 1800 UTC 26 August 2000. This period was chosen because August 25 was a day described by a stable air mass with weak convection [51,52]. This helps to avoid complexities associated with moist convection since our primary goal here is to evaluate the role of green roof systems on advection and how advection may influence near-surface meteorological conditions.
The parameterization schemes used in this study are (1) the Yonsei University (YSU) PBL scheme [53], Mellor–Yamada Janjic (MYJ) PBL scheme [54], Mellor–Yamada–Nakanishi–Niino (MYNN2.5) scheme [55] and Boujeault–Lacarrere (BouLac) scheme [56], (2) the WRF–Single Moment 3 [57] microphysics scheme, (3) the NOAH-LSM (Land Surface Model) [58], and (4) the Rapid Radiative Transfer Model (RRTM) [59] for longwave radiation and Dudhia (1989) [60] for shortwave radiation. For the parent domain, Kain–Fritsch (KF) cumulus parameterization [61] was used. Because the innermost domains were run at 3 km and 1 km horizontal resolutions, no cumulus parameterization was used. All other relevant parameters for the model are listed in Table 1.

2.2. Simulations

We use four different PBL schemes available in the WRF model to construct an ensemble (Table 2 and Table 3) since the simulations are arguably dependent on the PBL schemes used over the near-surface urban areas [47,48,49,62]. Further details about these PBL schemes can be found in [49,63], among others. To explore the mitigation effects of green roofs, we use multi-layer green roofs with 50% of the roof as green roof in the urban grid cell. The choice of 50% coverage is arguably more realistic than 100% coverage, which is too optimistic. Unless otherwise mentioned, the control (CTL) and green roof (GR) simulations are referred to as the ensemble mean of simulations without and with green roofs, respectively (Table 2). A comparison of CTL and GR is expected to provide a quantitative idea of the response of near-surface meteorological conditions to advection due to the use of green roofs.

2.3. Data and Method

The 2 m temperature (T2) and 10 m wind (W10) observations were taken from the 12 Texas Commission on Environmental Quality (TCEQ) stations (Table 4). The model output was hourly averaged to match the frequency of TCEQ observations. The urban land use data was taken from the 2001 National Land Cover Database (NLCD, 30 m resolution). The initial and boundary conditions were taken from the National Centers for Environmental Prediction (NCEP) final analysis (NCEP_fnl).

2.4. Green Roof Modeling

Figure 2 exhibits the schematic urban grid cell with both impervious and pervious fractions. The impervious fraction over the urban area has buildings, tar roads, and pavements. The conventional roofs can transfer most of the incoming energy to sensible heat flux, thereby enhancing the air temperature near the surface and above. On the other hand, green roofs can mitigate the surface temperature through evapotranspiration. Net cooling will occur when the sensible heat is reduced, with an increase in latent heat if the net radiation remains unchanged.
The green roofs in WRF for this study have four layers with a total depth of 50 cm, which consists of 15 cm soil layer of vegetation, 15 cm of growing layer, and 20 cm of concrete roof layer. For the pervious surface, the green surface is also part of an urban grid cell. The surface temperature over an urban cell can be calculated by area-averaged temperature, which is based on the surface temperature over the impervious and the vegetated area:
T s = f i m p e r v i o u s × T s ( i m p e r v i o u s ) + ( 1 − f i m p e r v i o u s ) × T s ( v e g )
The impervious surface temperature is calculated as the area-averaged temperature from the roof and street canyon:
T s ( i m p e r v i o u s ) = f r o o f × T r + f c a n y o n × T c a n y o n
The sensible heat flux over the urban grid cell is calculated in a similar way to surface temperature. The T2 is determined by the urban surface temperature and the total sensible heat flux (Htotal) from the impervious surface and the vegetated surface:
T 2 = T s − H t o t a l ρ C h 2 U 2
where ρ is the air density, U2 is the 2-m wind speed, and Ch2 is the turbulent transfer coefficient. The calculation of T2 can be used as a representative temperature that human beings can feel [64]. In the WRF, the grid cells where the major land use category is one of the three urban categories (low-intensity residential, LIR; high-intensity residential, HIR; and commercial/industrial, COI) are considered as the urban grid cells.

3. Results

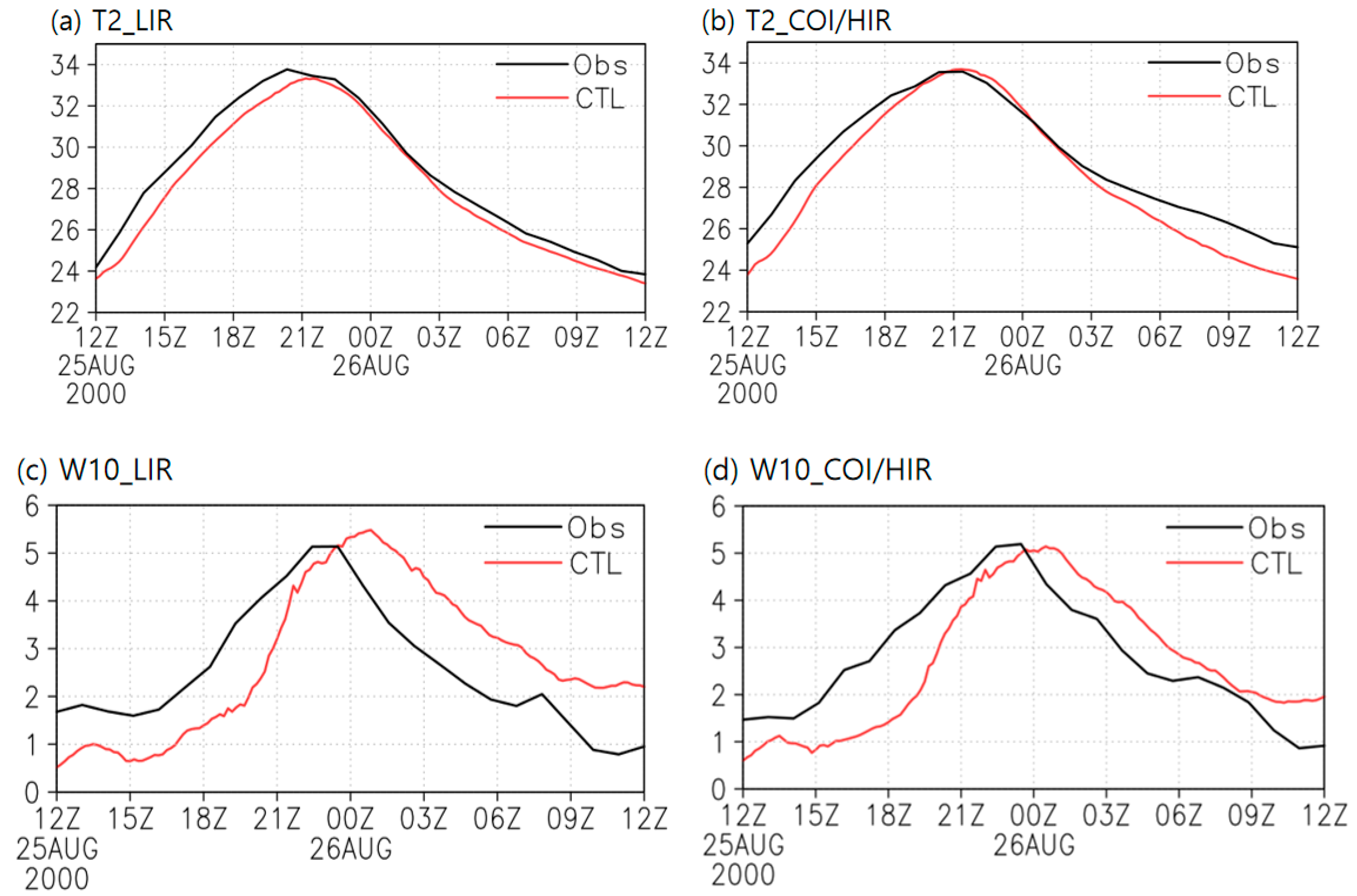
3.1. Near-Surface Temperature and Winds

The model performance is assessed for the model ensemble mean against observations from TCEQ urban stations for T2 and W10 (Figure 3). In the LIR (Figure 3a), the observed T2 is higher than the CTL during the daytime, but the CTL follows the observation well at night. In the COI/HIR area (Figure 3b), the T2 in the CTL shows a larger discrepancy during the night compared with the LIR area (Figure 3a). The performance of the simulations concerning mean error and the root mean squared error (RMSE) for different PBL schemes along with their ensemble mean is given in Table 3. The CTL winds, in general, are lower than that in the observation during the morning hours (Figure 3c,d). However, for the early evening and overnight periods, they remain higher than the observations. The peak W10 in CTL appears later than the observations, leading to a phase lag between the model and the observation. This phase lag is likely due to the use of SLUCM, with hydrological options that lead to the over-moistening of the urban surfaces. As a result, during the morning hours, solar radiation is used to evaporate the moisture (i.e., increased latent heat flux), leading to a smaller sensible heat flux. As the surface moisture reduces, sensible heat flux increases, leading to an increase in near-surface temperature which lags behind that from the observation. The lag in near-surface temperature causes a lag in mixing in the planetary boundary layer and near-surface winds in the simulations. A previous study by Brownlee et al. [37] also found this lag in temperature and winds using the MYJ PBL scheme when they used SLUCM with hydrological options; however, without the hydrological options, they found the lag to be smaller. Thus, there may be a systematic bias in surface wind speed in the WRF model [65], which may have been enhanced in our simulations due to the use of hydrological options. Over the 24 h period, all four PBL schemes produced stronger winds in LIR and weaker winds in COI/HIR than the observation, except for MYJ, which has little to no bias in W10 over LIR, and YSU, which has a positive bias in W10 (Table 3).
Figure 4 shows the difference between the GR and CTL simulations concerning the surface skin temperature (TSK, Figure 4, left) and T2 (Figure 4, right) over urban areas. The mitigation of heat stress by the green roofs is clear, with the maximum amplitude of TSK decreasing by 1.1 °C in LIR to 1.9 °C in COI/HIR. The decrease in TSK in GR compared to CTL is due to a larger loss in surface latent heat flux (Figure 5c). The change in the T2 (Figure 4, right) is much smaller due to green roofs compared to that in the TSK (Figure 4, left). The reduction in T2 (see Equation (5)) due to GR (Figure 4b) is due to the smaller sensible heat loss (Figure 5f). With green roof systems, there is an increase in the soil layer on the top of each building (see Figure 2) which can retain more energy than traditional roofs [43,66]. It is well known that, compared with the nighttime average (Figure 4, bottom), the green roof can have a larger effect over urban areas during daytime (Figure 4, middle). To explain the changes in temperature in GR compared to CTL, we present an analysis of the surface heat flux components that are a dominant factor in controlling the near-surface conditions.

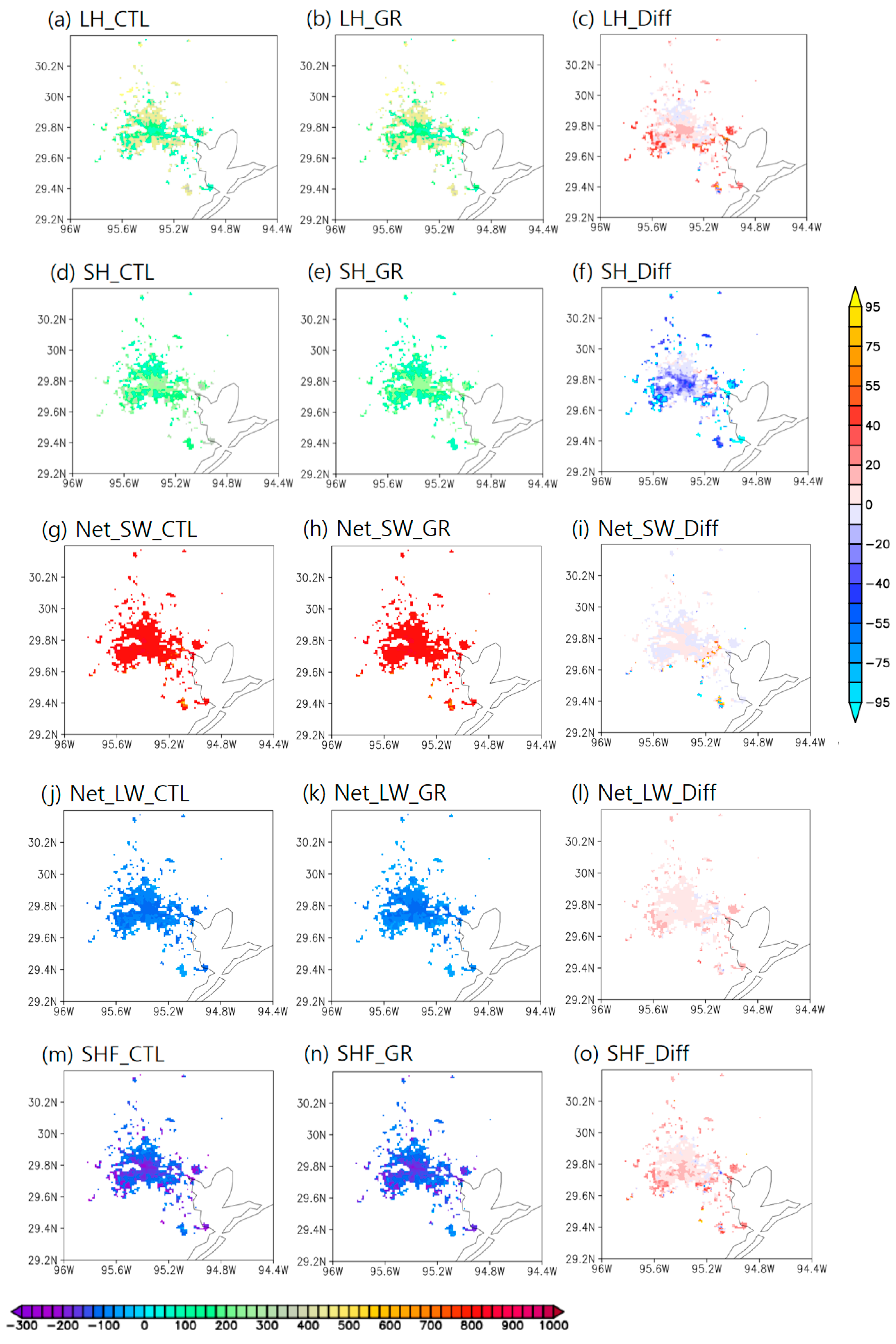
3.2. Surface Heat Flux

Figure 5 shows the surface latent heat flux (LH), sensible heat flux (SH), net shortwave radiation (Net_SW), net longwave radiation (Net_LW) and storage heat flux (SHF) from the CTL and GR and their differences. The LH is much smaller in the COI/HIR (green in Figure 5a) than LIR (yellow in Figure 5a) due to there being less surface moisture over the COI/HIR area. The addition of green roofs in urban areas increases surface moisture and hence the LH, particularly during the daytime (Figure 5c). This leads to a much cooler TSK in the GR simulation (Figure 4a). The opposite happens for SH (Figure 5f), where SH is larger over COI/HIR than LIR. As expected, the change in the SH from CTL to GR is the opposite of the change in LH; i.e., as the SH decreases, the LH increases. Overall, the net turbulent flux (LH + SH) in GR is lower than that in CTL over urban areas (Table 5). The range of values of LH, SH, and TSK shows the sensitivity of the results due to the use of different PBL schemes. The reduction in TSK in GR is much larger over HIR than over LIR. The implementation of a green roof leads to increased net shortwave radiation (Figure 5i). For net surface longwave radiation, there is also a moderate increase in GR compared to CTL (Figure 5l). The difference in storage heat flux (Figure 5m–o, [67]) between the CTL and GR varies (−20 to 20 W m−2) over the day and nighttime, with larger storage heat flux in GR during the daytime. Apart from the analysis of surface heat flux components, the extent to which the temperature advection modulates the near-surface temperature is examined in the next section.

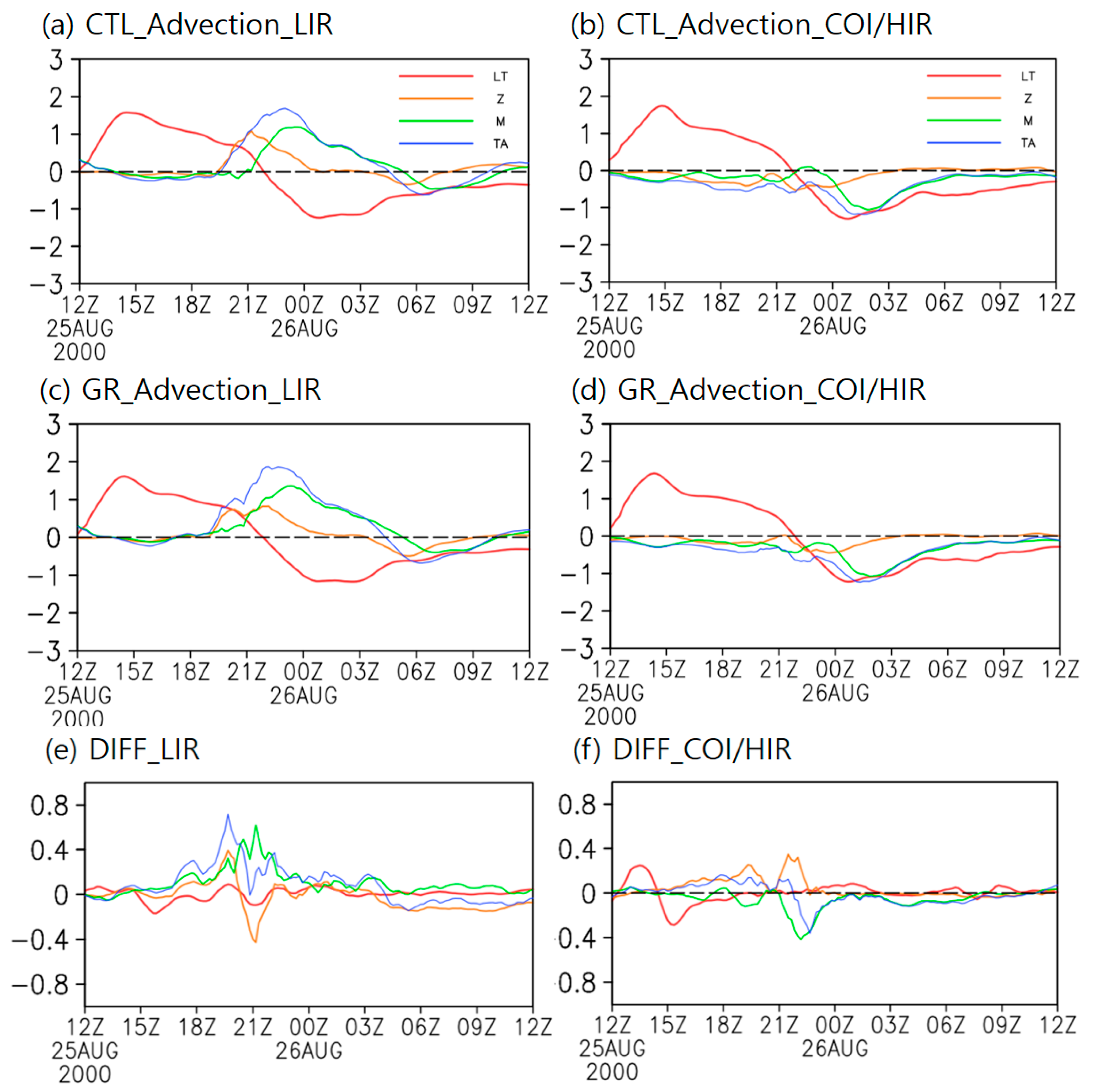
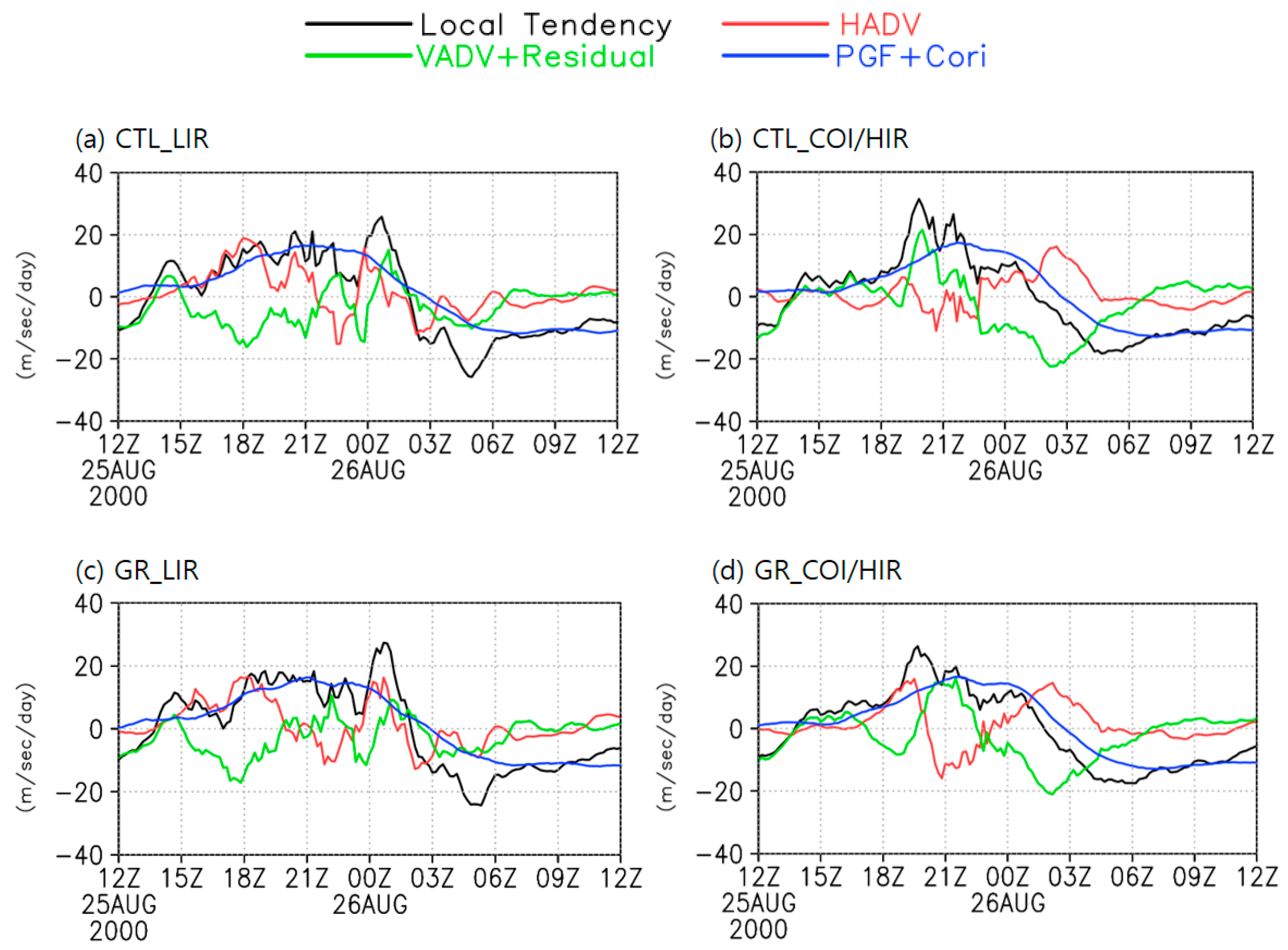
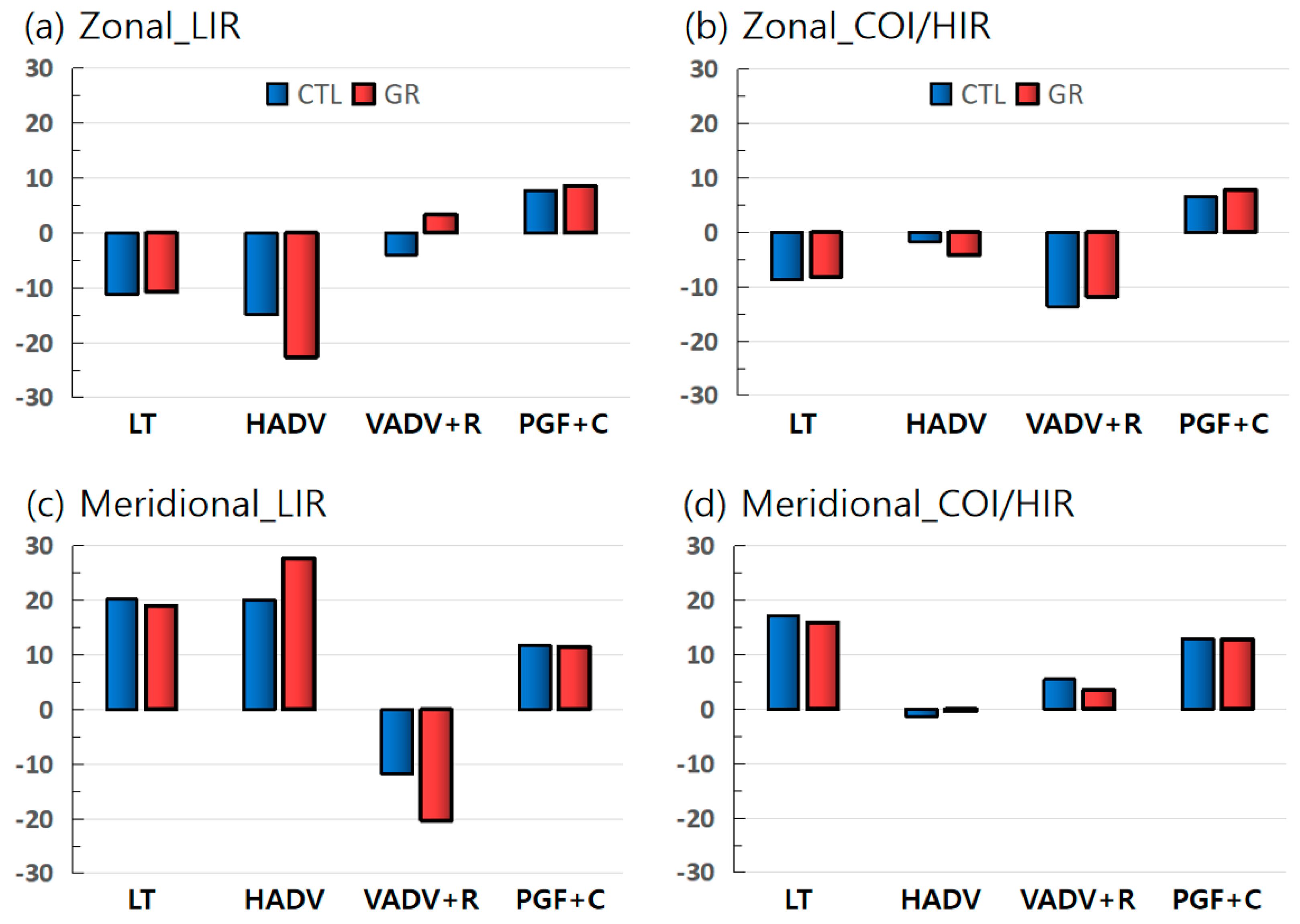
3.3. Role of Advection

3.3.1. Temperature Advection

Previous studies have demonstrated the importance of the surface heat fluxes on the near-surface temperature and winds, but they have not presented any quantitative estimates of heat advection over an urban area. The higher temperature in the urban areas compared to rural areas leads to a temperature and pressure gradient [68] which can initiate the advection of heat and momentum. Nevertheless, it is not well known how this advection alters temperature evolution over the city. Ignoring the material derivative and vertical advection of temperature, the local tendency in temperature is given by
∂ T ∂ t = − u   ∂ T ∂ x − v   ∂ T ∂ y
where −u(∂T/∂x) is zonal temperature advection and −v(∂T/∂y) represents meridional temperature advection. The horizontal temperature advection is the sum of zonal and meridional temperature advection. Figure 6 shows the influence of each term in CTL and GR and their difference. In the LIR area, the horizontal temperature advection reaches peaks before 00Z August 26 in both CTL (Figure 6a) and GR (Figure 6c) simulations. The GR has higher temperature advection (Figure 6e) which is mostly from meridional temperature advection due to onshore winds. Over the COI/HIR area, temperature advection becomes negative and appears after 00Z August 26 indicating that temperature advection plays a cooling role in GR compared with CTL in COI/HIR (Figure 6f). Overall, the meridional advection of temperature dominates over zonal advection, and the total horizontal advection plays some role between 1700 and 2200. For the rest of the time, it seems that the near-surface temperature is driven primarily by the surface heat flux.

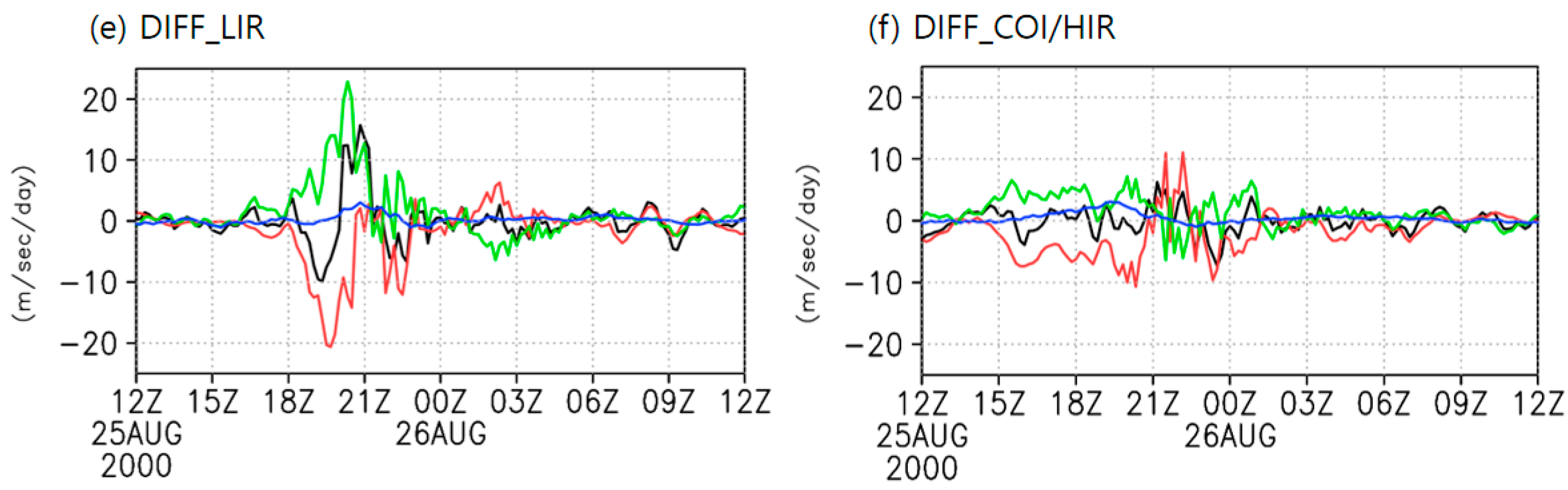
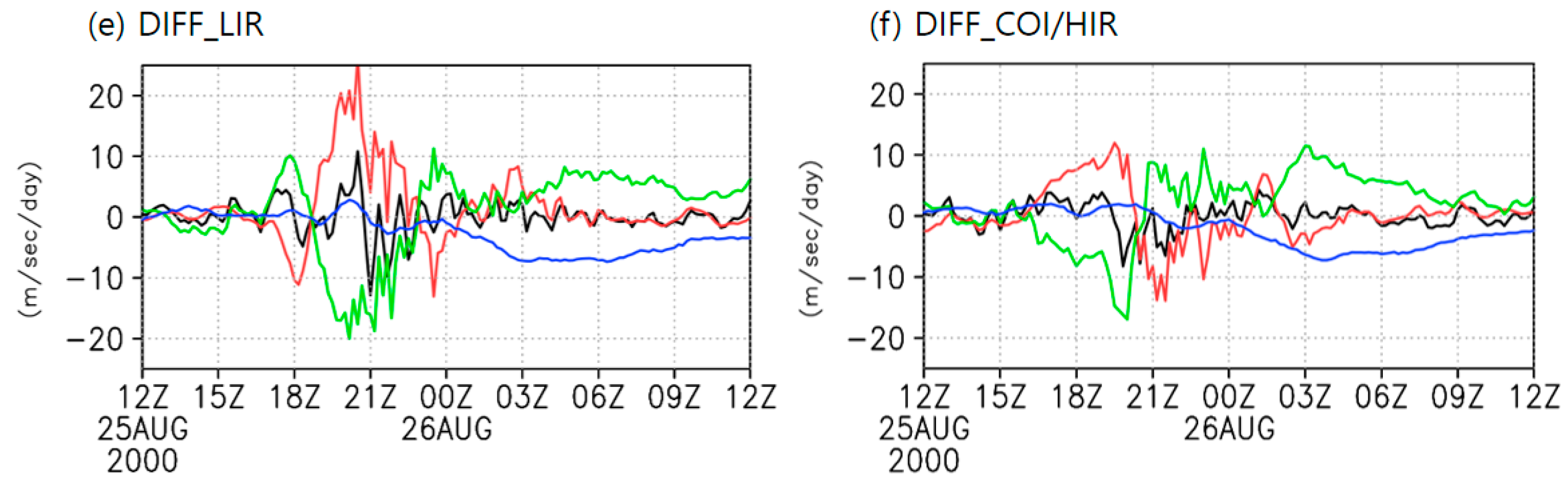
3.3.2. Momentum Advection

The momentum budget analysis has been extensively used [69,70,71,72,73] to understand the evolution of winds in a variety of meteorological conditions. However, such an analysis, to the best of our knowledge, has not been performed to understand the role of green roof systems on advection. The zonal and meridional momentum budgets are given by
∂ u ∂ t = − u ∂ u ∂ x − v ∂ u ∂ y − ω ∂ u ∂ p − ∂ ϕ ∂ x + f v + R
∂ v ∂ t = − u ∂ v ∂ x − v ∂ v ∂ y − ω ∂ v ∂ p − ∂ ϕ ∂ y − f u + R
where (u, v, ω) are three-dimensional wind vectors, φ is the geopotential height, f is the Coriolis parameter, and R stands for residual, which includes friction and errors in the calculation. The term on the left-hand side represents the local tendency, whereas the first three terms on the right-hand side represent zonal, meridional and vertical advection (VADV), respectively. The combined zonal and meridional advection is referred to as horizontal advection (HADV, red in Figure 7 and Figure 8). The last three terms represent the pressure gradient, the Coriolis, and the residual. We merge the vertical advection and the residual into one term (green in Figure 7 and Figure 8), and the pressure gradient and Coriolis into another term (blue in Figure 7 and Figure 8) to focus on any possible influence from HADV. For the zonal momentum budget (Figure 7), the local tendency peaks are similar in both urban areas and experiments (~0200Z, 26 August, Figure 7, top two panels). The increase in HADV from 2100Z, 25 August to 0300Z, 26 August is also similar to the increase in local tendency indicating that the winds were influenced by the HADV. Over LIR areas, the combined VADV and residual is positive during 1900Z–2200Z 25 August and then becomes negative, whereas over COI/HIR areas, the VADV + R remains mostly negative. The difference between CTL and GR is most prominent from 1800Z, 25 August to 0000Z, 26 August (Figure 7, bottom). The meridional momentum budget analysis.
Figure 8 shows a similar relationship between local tendency and HADV, but stronger association over COI/HIR area in CTL (Figure 8b). Compared with LIR areas in CTL (Figure 8a), the local tendency and HADV in GR have a higher correlation (Figure 8c). The peak of local tendency is different in GR over LIR (~0000Z, 26 August, Figure 8c) and COI/HIR (~2000Z, 25 August, Figure 8d). Notice that the magnitude of several terms during the period from 1800Z, 25 August–0000Z, 26 August is larger than other times, and hence is further illustrated in Figure 9. Although the local tendency of zonal (Figure 9, top) and meridional (Figure 9, bottom) momentum advection is similar, the HADV terms are quite different in CTL and GR over LIR areas.

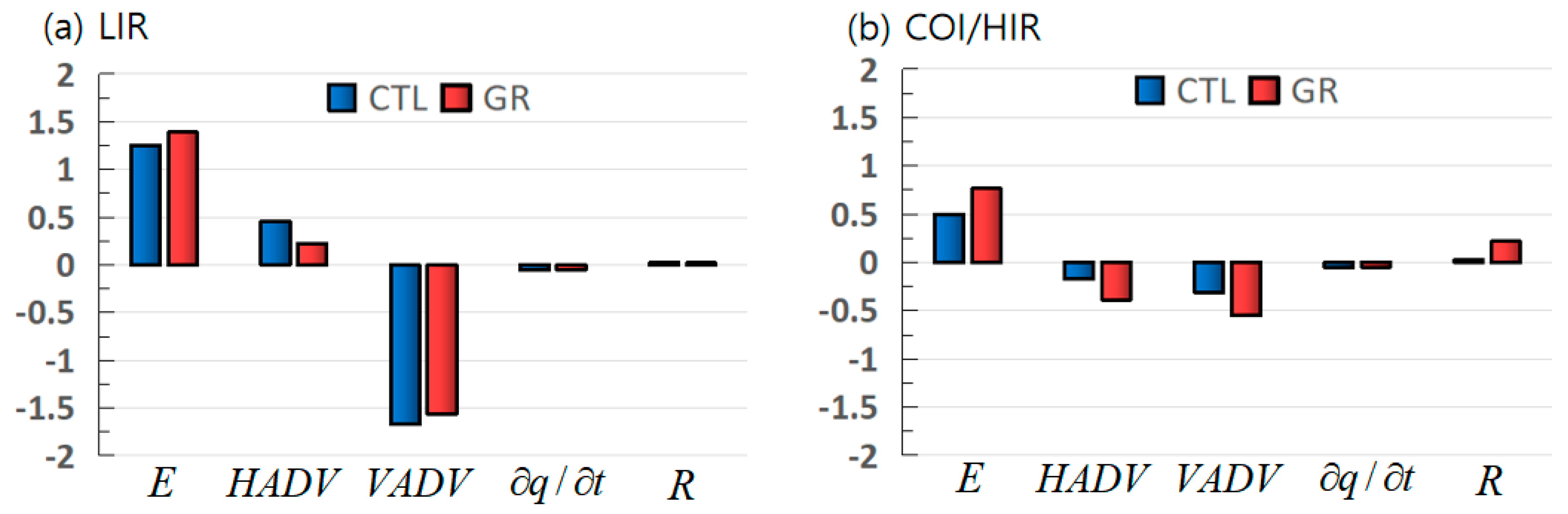
3.3.3. Moisture Advection

The atmospheric moisture budget is given by (e.g., [74,75])
< ∂ q ∂ t > = − < v h ⋅ ∇ q > − < ω ∂ q ∂ p > + E − P + R
where q is the specific humidity, vh is the horizontal wind vector, ω is the vertical velocity, E means the evaporation, P represents the precipitation, and R is the residual. The symbols < > stand for the mass-weighted vertical integral from 1000 hPa to 100 hPa. The term on the left-hand side is the moisture tendency. The first two terms on the right-hand side are the horizontal (HADV) and vertical (VADV) moisture advection. This equation is used extensively to understand the variability of atmospheric moisture and precipitation [76] that is important for water–climate–society research [77]. Figure 10 presents the terms in the moisture budget with a small residual that provides confidence regarding the estimates of the terms and their interpretations. Since there was no precipitation, we have not shown this in Figure 10. Over the LIR, the evaporation is compensated mostly by VADV in both experiments. In the COI/HIR area, the increase in evaporation in the presence of GR (see Figure 6) is compensated by an increase in HADV and VADV.

4. Discussion

The response of near-surface meteorological conditions (temperature, winds, and moisture) to advection under the impact of green roofs is evaluated over Houston using the WRF model. An ensemble mean of four simulations based on four widely used planetary boundary layer schemes was used for the control simulation (CTL) and the simulation with green roofs (GR). The main results are the following.
Models (CTL) T2 and W10 were found to be in good agreement when evaluated against available observations, although with a lag in time. With the inclusion of green roof systems (GR), the near-surface temperature and winds decrease. During the daytime, the LH (SH) increases (decreases) in GR compared to CTL leading to a cooling effect when the temperature decreased by 1–2 °C. Yang et al. [3] found that by using a 50% fraction of green roof, there is a reduction in surface temperature ranging from 2–4 °K at four different locations (Beijing, Vancouver, Phoenix, and Montreal). Our results also indicate that the green roofs can also cause cooling over the night, which is in contrast to Yang et al. [43] who found that the temperature was 1 °C higher during the nighttime. This discrepancy may be due to our short simulation period, the seasonal dependence of the impact of green roofs, and the differences in model horizontal resolutions, among other reasons.
Our results indicate that, in the CTL over LIR areas, a stronger temperature gradient leads to a stronger advection of temperature in the presence of onshore winds. Over COI/HIR, the temperature advection in GR plays a cooling role compared with CTL in COI/HIR. The temperature advection shows that it does not play a significant role, suggesting that the near-surface temperature is driven by the surface heat flux. The timing of peak temperature advection, however, should be treated with caution, given that there was a lag in model peak temperature and wind compared with the observations (Figure 3).
The analysis of the momentum budget shows that the differences between CTL and GR occur from 1800Z, 25 August to 0000Z, 26 August (Figure 7, Figure 8 and Figure 9). The variation of local tendency follows the variation of HADV over both LIR and COI/HIR in both zonal and meridional momentum budget analysis. Similar to temperature advection, the timing of peak momentum advection (Figure 7, Figure 8) in the model may be different from observations since the timing of peak T2 and W10 was different in model and observations. However, when the momentum advection is averaged over time, the lag in temperature and winds has expected to have less influence on our estimations of different advection quantities.
The moisture budget analysis suggests that, over the LIR area, the evaporation is mostly compensated by VADV in both CTL and GR experiments (Figure 10). In the COI/HIR area, the increase in evaporation in the presence of GR (see Figure 6) is compensated by an increase in HADV and VADV.
Our results imply that, even with a small change in temperature over cities due to green roofs, advective processes that influence near-surface temperature, winds, and humidity can have a large difference compared to control. The differences were most prominent during the evening when the temperature gradient between the urban areas and surroundings was small due to the cooling of the urban areas because of green roofs.

5. Conclusions

In summary, we have estimated the impact of green roofs in modulating the advection of heat, momentum, and moisture that influences the temperature, wind, and humidity using urban-aware simulations. Such an impact of the green roof, especially on momentum advection, has not been quantified before. We have accomplished this by employing physics-based simulations using different PBL schemes, whereas earlier studies were based on a single simulation (i.e., a deterministic approach). Unfortunately, because of the lack of observational data of heat flux components at the surface and other meteorological parameters in the PBL, our study lacks rigorous validation. However, since the model was able to capture the near-surface temperature and winds, the model simulations were likely realistic. A logical extension of our work would be to quantify the impact of the green roofs on advective processes under different green roof fractions and determine how this impact may change in a future climate.

Author Contributions

Conceptualization, H.T. and P.R.; Data curation, J.B.; Formal analysis, H.T., P.R. and A.R.; Investigation, M.T.; Methodology, M.T.; Visualization, H.T.; Writing—original draft, H.T. and P.R.; Writing—review & editing, All authors.

Funding

This research was supported by the grants from the ONR (N00014-16-1-3091) to PR.

Acknowledgments

The simulations were conducted at Florida Tech using the high-performance computing cluster ‘Blueshark’, which was funded by the National Science Foundation (NSF). This work was partially supported by ONR grant N00014-1601-3091 to PR. The publication cost for this paper was graciously provided by the Open Access Fund of the Florida Tech Library.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Seto, K.C.; Fragkias, M.; Guneralp, B.; Reilly, M.K. A meta-analysis of global urban land expansion. PLoS ONE 2011, 6, e23777. [Google Scholar] [CrossRef] [PubMed]
  2. Arnfield, A.J. Two decades of urban climate research: A review of turbulence, exchanges of energy and water, and the urban heat island. Int. J. Climatol. 2003, 23, 1–26. [Google Scholar] [CrossRef]
  3. Yang, J.; Wang, Z.H.; Chen, F.; Miao, S.; Tewari, M.; Voogt, J.; Myint, S. Enhancing hydrologic modelling in the coupled Weather Research and Forecasting-urban modelling system. Bound. Layer Meteorol. 2015, 155, 87–109. [Google Scholar] [CrossRef]
  4. Burian, S.J.; Shepherd, J.M. Effect of urbanization on the diurnal rainfall pattern in Houston. Hydrol. Process. 2005, 19, 1089–1103. [Google Scholar] [CrossRef]
  5. Oleson, K.W.; Bonan, G.B.; Feddema, J.; Jackson, T. An examination of urban heat island characteristics in a global climate model. Int. J. Climatol. 2011, 31, 1848–1865. [Google Scholar] [CrossRef]
  6. Unkasevic, M.; Jovanovic, O.; Popovic, T. Urban-suburban/rural vapour pressure and relative humidity differences at fixed hours over the area of Belgrade city. Theor. Appl. Climatol. 2001, 68, 67–73. [Google Scholar] [CrossRef]
  7. Georgescu, M.; Mahalov, A.; Moustaoui, M. Seasonal hydroclimatic impacts of Sun Corridor expansion. Environ. Res. Lett. 2012, 7, 034026. [Google Scholar] [CrossRef]
  8. Bornstein, R.D.; Johnson, D.S. Urban-rural wind velocity differences. Atmos. Environ. 1977, 11, 597–604. [Google Scholar] [CrossRef]
  9. Fernando, H.J.S. Fluid dynamics of urban atmospheres in complex terrain. Annu. Rev. Fluid Mech. 2010, 42, 365–389. [Google Scholar] [CrossRef]
  10. Landsberg, H.E. The Urban Climate; Academic Press: New York, NY, USA, 1981; 275p. [Google Scholar]
  11. Oke, T.R. The energetic basis of the urban heat island. Q. J. R. Meteorol. Soc. 1982, 108, 1–24. [Google Scholar] [CrossRef]
  12. Hassid, S.; Santamouris, M.; Papanikolaou, N.; Linardi, A.; Klitsikas, N.; Georgakis, C.; Assimakopoulos, D.N. The effect of the Athens heat island on air conditioning load. Energy Build. 2000, 32, 131–141. [Google Scholar] [CrossRef]
  13. Cartalis, C.; Synodinou, A.; Proedrou, M.; Tsangrasoulis, A.; Santamouris, M. Modification in energy demand in urban areas as a result of climate changes: An assessment for the Southeast Mediterranean region. Energy Convers. Manag. 2001, 42, 1647–1656. [Google Scholar] [CrossRef]
  14. Santamouris, M.; Papanikolaou, N.; Livada, I.; Koronakis, I.; Georgakis, C.; Argiriou, A.; Assimakopoulos, D.N. On the impact of urban climate to the energy consumption of buildings. Sol. Energy 2001, 70, 201–216. [Google Scholar] [CrossRef]
  15. Grimmond, S. Urbanization and global environmental change: Local effects of urban warming. Cities Glob. Environ. Chang. 2007, 173, 83–88. [Google Scholar] [CrossRef]
  16. Rosenfeld, A.H.; Akbari, H.; Bretz, S.; Fishman, B.L.; Kurn, D.M.; Sailor, D.; Taha, H. Mitigation of urban heat islands: Material, utility programs, updates. Energy Build. 1995, 22, 255–265. [Google Scholar] [CrossRef]
  17. Akbari, H.; Pomerantz, M.; Taha, H. Cool surfaces and shade trees to reduce energy use and improve air quality in urban areas. Sol. Energy 2001, 70, 295–310. [Google Scholar] [CrossRef]
  18. Akbari, H.; Levinson, R. Evolution of cool-roof standards in the U.S. Adv. Build. Energy Res. 2008, 2, 1–32. [Google Scholar] [CrossRef]
  19. Theodosiou, T. Green roofs in buildings: Thermal and environmental behavior. Adv. Build. Energy Res. 2009, 3, 271–288. [Google Scholar] [CrossRef]
  20. Sfakianaki, A.; Pagalou, E.; Pavlou, K.; Santamouris, M.; Assimakopoulos, M. Theoretical and experimental analysis of the thermal behavior of a green roof system installed in two residential buildings in Athens, Greece. Int. J. Energy Res. 2009, 33, 1059–1069. [Google Scholar] [CrossRef]
  21. Zinzi, M. Cool materials and cool roofs: Potentialities in Mediterranean buildings. Adv. Build. Energy Res. 2010, 4, 201–266. [Google Scholar] [CrossRef]
  22. Gaitani, N.; Spanou, A.; Saliari, M.; Synnefa, A.; Vassilakopoulou, K.; Papadopoulou, K.; Pavlou, K.; Santamouris, M.; Papaioannou, M.; Lagoudaki, A. Improving the microclimate in urban areas: A case study in the centre of Athens. J. Build. Serv. Eng. 2011, 32, 53–71. [Google Scholar] [CrossRef]
  23. Chow, W.T.L.; Chuang, W.C.; Gober, P. Vulnerability to extreme heat in metropolitan Phoenix: Spatial, temporal, and demographic dimensions. Prof. Geogr. 2012, 64, 286–302. [Google Scholar] [CrossRef]
  24. Takebayashi, H.; Moriyama, M. Study of a simple evaluation method of urban heat island mitigation technology using upper-air data. J. Heat Isl. Inst. Int. 2012, 7, 102–110. [Google Scholar]
  25. Santamouris, M. On the energy impact of urban heat island and global warming on buildings. Energy Build. 2014, 82, 100–113. [Google Scholar] [CrossRef]
  26. Akbari, H.; Rose, L.S. Urban surfaces and heat island mitigation potential. J. Hum. Environ. Syst. 2007, 11, 85–101. [Google Scholar] [CrossRef]
  27. Georgescu, M. Challenges associated with adaptation to future urban expansion. J. Clim. 2015, 28, 2544–2563. [Google Scholar] [CrossRef]
  28. Yang, J.; Yu, Q.; Gong, P. Quantifying air pollution removal by green roofs in Chicago. Atmos. Environ. 2008, 42, 7266–7273. [Google Scholar] [CrossRef]
  29. Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3. NCAR Technical Note NCAR/TN-475+STR. NCAR Tech. Notes 2008. [Google Scholar] [CrossRef]
  30. Kusaka, H.; Kondo, H.; Kikegawa, Y.; Kimura, F. A simple single-layer urban canopy model for atmospheric models: Comparison with multilayer and slab models. Bound. Layer Meteorol. 2001, 101, 329–358. [Google Scholar] [CrossRef]
  31. Wang, Z.H.; Bou-Zeid, E.; Au, S.K.; Smith, J.A. Analyzing the sensitivity of WRF’s single-layer urban canopy model to parameter uncertainty using advanced Monte Carlo simulation. J. Appl. Meteorol. Climatol. 2011, 50, 1795–1814. [Google Scholar] [CrossRef]
  32. Wang, Z.H.; Smith, J.A. A spatially-analytical scheme for surface temperatures and conductive heat fluxes in urban canopy models. Bound. Layer Meteorol. 2011, 138, 171–193. [Google Scholar] [CrossRef]
  33. Grimmond, C.S.B.; Blacketta, M.; Bestb, M.J.; Barlowc, J.; Baikd, J.-J.; Belcherc, S.E.; Bohnenstengelc, S.I.; Calmete, I.; Chenf, F.; Dandoug, A.; et al. The International Urban Energy Balance Models Comparison Project: First results from phase 1. J. Appl. Meteorol. Climatol. 2010, 49, 1268–1292. [Google Scholar] [CrossRef]
  34. Lee, S.H.; Kim, S.W.; Angevine, W.M.; Bianco, L.; McKeen, S.A.; Senff, C.J.; Trainer, M.; Tucker, S.C.; Zamora, R.J. Evaluation of urban surface parameterization in WRF model using measurements during the Texas Air Quality Study 2006 field campaign. Atmos. Chem. Phys. 2011, 11, 2127–2143. [Google Scholar] [CrossRef] [Green Version]
  35. Wang, Z.H.; Bou-Zeid, E.; Smith, J.A. A coupled energy transport and hydrological model for urban canopies evaluated using a wireless sensor network. Q. J. Meteorol. Soc. 2013, 139, 1643–1657. [Google Scholar] [CrossRef]
  36. Miao, S.; Chen, F. Formation of horizontal convective rolls in urban areas. Atmos. Res. 2008, 89, 298–304. [Google Scholar] [CrossRef]
  37. Brownlee, J.; Ray, P.; Tewari, M.; Tan, H. Relative role of turbulent and radiative flux on the near-surface temperature in a single-layer urban canopy model over Houston. J. Appl. Meteorol. Climatol. 2017, 56, 2173–2187. [Google Scholar] [CrossRef]
  38. Li, D.; Bou-Zeid, E. Synergistic interactions between urban heat islands and heat waves: The impact in cities is larger than the sum of its parts. J. Appl. Meteorol. Climatol. 2013, 52, 2051–2064. [Google Scholar] [CrossRef] [Green Version]
  39. Streutker, D.R. Satellite-measured growth of the urban heat island of Houston, Texas. Remote Sens. Environ. 2003, 85, 282–289. [Google Scholar] [CrossRef]
  40. Salamanca, F.; Martilli, A.; Tewari, M.; Chen, F. A study of the urban boundary layer using different urban parameterizations and high-resolution urban canopy parameters with WRF. J. Appl. Meteorol. Climatol. 2011, 50, 1107–1128. [Google Scholar] [CrossRef]
  41. Smith, K.R.; Roebber, P. Green roof mitigation potential for a proxy future climate scenario in Chicago, Illinois. J. Appl. Meteorol. Climatol. 2011, 50, 507–522. [Google Scholar] [CrossRef]
  42. Sun, T.; Grimmond, C.S.B.; Ni, G.H. How do green roofs mitigate urban thermal stress under heat waves? J. Geophy. Res. Atmos. 2016, 121, 5320–5335. [Google Scholar] [CrossRef]
  43. Yang, J.; Wang, Z.H.; Georgescu, M.; Chen, F.; Tewari, M. Assessing the impact of enhanced hydrological processes on urban hydrometeorology with application to two cities in contrasting climates. J. Hydrometeorol. 2016, 17, 1031–1047. [Google Scholar] [CrossRef]
  44. Sharma, A.; Conry, P.; Fernando, H.J.S.; Hamlet, A.F.; Hellmann, J.J.; Chen, F. Green and cool roofs to mitigate urban heat island effects in the Chicago metropolitan area: Evaluation with a regional climate model. Environ. Res. Lett. 2016, 11, 064004. [Google Scholar] [CrossRef]
  45. Tewari, M.; Yang, J.; Kusaka, H.; Salamanca, F.; Watson, C.; Treinish, L. Interaction of urban heat islands and heat waves under current and future climate conditions and their mitigation using green and cool roofs in New York City and Phoenix, Arizona. Environ. Res. Lett. 2019, 14, 034002. [Google Scholar] [CrossRef]
  46. De Munck, C.; Lemonsu, A.; Bouzouidja, R.; Masson, V.; Claverie, R. The GREENROOF module (v7.3) for modelling green roof hydrological and performances within TED. Geosci. Model Dev. 2013, 6, 1941–1960. [Google Scholar] [CrossRef] [Green Version]
  47. Xie, X.M.; Nielsen-Gammon, J.W.; Zhang, F. Evaluation of three planetary boundary layer schemes in the WRF model. J. Appl. Meteorol. Climatol. 2010, 49, 1831–1844. [Google Scholar]
  48. Xie, B.; Fung, J.C.H.; Chan, A.; Lau, A. Evaluation of nonlocal and local planetary boundary layer schemes in the WRF model. J. Geophys. Res. 2012, 117, D12103. [Google Scholar] [CrossRef]
  49. Cohen, A.E.; Cavallo, S.M.; Coniglio, M.C.; Brooks, H.E. A review of planetary boundary layer parameterization schemes and their sensitivity in simulating southeastern U.S. cold season severe weather environments. Weather Forecast. 2015, 30, 591–612. [Google Scholar] [CrossRef]
  50. Miao, S.; Chen, F. Enhanced modeling of latent heat flux from urbansurfaces in the Noah/single-layer urban canopy coupled model. Sci. China Earth Sci. 2014, 57, 2408–2416. [Google Scholar] [CrossRef]
  51. Nielsen-Gammon, J.W. Evaluation and Comparison of Preliminary Meteorological Modeling for the August 2000 Houston–Galveston Ozone Episode. TNRCC Report. 2002. Available online: https://www.tceq.texas.gov/assets/public/implementation/air/am/contracts/reports/mm/EvalComp_Preliminary_MM5_Modeling_2000Aug.pdf (accessed on 5 February 2002).
  52. Cheng, F.Y.; Byun, D.W. Application of high resolution land use and land cover data for atmospheric modeling in the Houston–Galveston metropolitan area, part I: Meteorological simulation results. Atmos. Environ. 2008, 42, 7795–7811. [Google Scholar] [CrossRef]
  53. Hong, S.-Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef] [Green Version]
  54. Janjic, Z.I. The step-mountain eta coordinate model: Further developments of the convection, viscous sub layer, and turbulence closure schemes. Mon. Weather Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef] [Green Version]
  55. Nakanishi, M.; Niino, H. An improved Mellor–Yamada level 3 model: Its numerical stability and application to a regional prediction of advecting fog. Bound. Layer Meteorol. 2006, 119, 397–407. [Google Scholar] [CrossRef]
  56. Bougeault, P.; Lacarrere, P. Parameterization of Orography–Induced Turbulence in a Mesobeta––Scale Model. Mon. Weather Rev. 1989, 117, 1872–1890. [Google Scholar] [CrossRef]
  57. Hong, S.Y.; Dudhia, J.; Chen, S.H. A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation. Mon. Weather Rev. 2004, 132, 103–120. [Google Scholar] [CrossRef]
  58. Chen, F.; Dudhia, J. Coupling an advanced land surface—Hydrology model with the Penn State–NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef] [Green Version]
  59. Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophy. Res. 1992, 102, 16663–16682. [Google Scholar] [CrossRef] [Green Version]
  60. Dudhia, J. Numerical study of convection observed during the Winter Monsoon Experiment using a mesoscale two—Dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
  61. Kain, J.S. The Kain—Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef] [Green Version]
  62. Berg, L.K.; Zhong, S. Sensitivity of MM5-simulated boundary layer characteristics to turbulence parameterizations. J. Appl. Meteorol. 2005, 44, 1467–1483. [Google Scholar] [CrossRef]
  63. Banks, R.F.; Baldasano, J.M. Impact of WRF model PBL schemes on air quality simulations over Catalonia, Spain. Sci. Total Environ. 2016, 572, 98–113. [Google Scholar] [CrossRef] [Green Version]
  64. Li, D.; Bou-Zeid, E. Quality and sensitivity of high-resolution numerical simulation of urban heat islands. Environ. Res. Lett. 2014, 9, 055001. [Google Scholar] [CrossRef]
  65. Shimada, S.; Ohsawa, T.; Chikaoka, S.; Kozai, K. Accuracy of the wind speed profile in the lower PBL as simulated by the WRF model. SOLA 2011, 7, 109–112. [Google Scholar] [CrossRef] [Green Version]
  66. Niachou, A.; Papakonstantinou, K.; Santamouris, M.; Tsangrassoulis, A.; Mihalakakou, G. Analysis of the green roof thermal properties and investigation of its energy performance. Energy Build. 2001, 33, 719–729. [Google Scholar] [CrossRef]
  67. Moriwaki, R.; Kanda, M. Seasonal and diurnal fluxes of radiation, heat, water vapor, and carbon dioxide over a suburban area. J. Appl. Meteorol. 2004, 43, 1700–1710. [Google Scholar] [CrossRef]
  68. Oke, T.R.; Maxwell, G.B. Urban heat island dybamics in Montreal and Vancouver. Atmos. Environ. 1975, 9, 191–200. [Google Scholar] [CrossRef]
  69. Large, W.G.; Pond, S. Open Ocean Momentum Flux Measurements in Moderate to Strong Winds. J. Phys. Oceanogr. 1981, 11, 324–336. [Google Scholar] [CrossRef] [Green Version]
  70. Gregory, D.; Kershaw, R.; Inness, P.M. Parametrization of momentum transport by convection. II: Tests in single-column and general circulation models. Q. J. R. Meteorol. Soc. 1997, 123, 1153–1183. [Google Scholar] [CrossRef]
  71. Carr, M.T.; Bretherton, C.S. Convective momentum transport over the tropical Pacific: Budget estimates. J. Atmos. Sci. 2001, 58, 1673–1693. [Google Scholar] [CrossRef]
  72. Richter, J.H.; Rasch, P.J. Effects of Convective Momentum Transport on the Atmospheric Circulation in the Community Atmosphere Model, Version 3. J. Clim. 2008, 21, 1487–1499. [Google Scholar] [CrossRef]
  73. Ray, P.; Zhang, C. A case study of the mechanics of extratropical influence on the initiation of the Madden-Julian oscillation. J. Atmos. Sci. 2010, 67, 515–528. [Google Scholar] [CrossRef]
  74. Ray, P.; Li, T. Relative roles of the circumnavigating waves and the extratropics on the MJO and its relationship with the mean state. J. Atmos. Sci. 2013, 70, 876–893. [Google Scholar] [CrossRef]
  75. Tan, H.; Ray, P.; Barrett, B.S.; Tewari, M.; Moncrieff, M.W. Role of topography on the MJO in the Maritime Continent: A numerical case study. Clim. Dyn. 2018. [Google Scholar] [CrossRef]
  76. Ray, P.; Zhang, C.; Dudhia, J.; Li, T.; Moncrieff, M.W. Tropical Channel Model. In Climate Models; Druyan, L.M., Ed.; InTech Open Access Publisher: Rijeka, Croatia, 2012; pp. 3–18. ISBN 978-953-308-181-6. [Google Scholar]
  77. McNeely, S.; Tessendorf, A.S.; Lazrus, H.; Heikkila, T.; Ferguson, M.I.; Arrigo, S.J.; Attari, A.Z.; Cianfrani, C.M.; Dilling, L.; Gurdak, J.J.; et al. Catalyzing frontiers in water-climate-society research: A view from early career scientists and junior faculty. Bull. Am. Meterol. Soc. 2012, 93, 477–484. [Google Scholar] [CrossRef]
Atmosphere 10 00759 g001 550
Figure 1. (a) Weather Research and Forecasting (WRF) domain configuration. The outer domain (DO3), the middle domain (DO2) and the inner domain (DO3) have 9 km, 3 km, and 1 km horizontal resolutions, respectively. (b) Urban land use categories (shaded) indicating low-intensity residential (LIR, yellow), high-intensity residential (HIR, red), commercial/industrial urban land use (COI, green), rural (white) and water (blue).
Figure 1. (a) Weather Research and Forecasting (WRF) domain configuration. The outer domain (DO3), the middle domain (DO2) and the inner domain (DO3) have 9 km, 3 km, and 1 km horizontal resolutions, respectively. (b) Urban land use categories (shaded) indicating low-intensity residential (LIR, yellow), high-intensity residential (HIR, red), commercial/industrial urban land use (COI, green), rural (white) and water (blue).
Atmosphere 10 00759 g001
Atmosphere 10 00759 g002 550
Figure 2. Schematic representation of urban grid cell used in WRF for green roof modeling. The grid cell has two parts: the impervious fraction and the pervious fraction. Ha is the height of the first level in the atmospheric model, Hr is the height of the building roof-top, and Hc is the street canyon height. In our simulations, there are conventional roofs and green roofs. The ground surface is composed of tar road, concrete and grass (50%, 30%, and 20%). The SH and LH are the sensible and latent heat flux. The subscript (g) stands for ground, (veg) for vegetated fraction, (w) for building wall, (r) for roof, (CR) for conventional roof, and (GR) for green roof. Gg is the storage heat flux. Ta, Tc, and Tveg denote the temperatures at the first level of an atmospheric model, at the street canyon, and at the vegetated fraction, respectively. Out of the total roof area, 50% of the roof was considered as GR, and the other 50% was the conventional roof.
Figure 2. Schematic representation of urban grid cell used in WRF for green roof modeling. The grid cell has two parts: the impervious fraction and the pervious fraction. Ha is the height of the first level in the atmospheric model, Hr is the height of the building roof-top, and Hc is the street canyon height. In our simulations, there are conventional roofs and green roofs. The ground surface is composed of tar road, concrete and grass (50%, 30%, and 20%). The SH and LH are the sensible and latent heat flux. The subscript (g) stands for ground, (veg) for vegetated fraction, (w) for building wall, (r) for roof, (CR) for conventional roof, and (GR) for green roof. Gg is the storage heat flux. Ta, Tc, and Tveg denote the temperatures at the first level of an atmospheric model, at the street canyon, and at the vegetated fraction, respectively. Out of the total roof area, 50% of the roof was considered as GR, and the other 50% was the conventional roof.
Atmosphere 10 00759 g002
Atmosphere 10 00759 g003 550
Figure 3. (top) The 2m temperature (°C) from observations (black) and CTL (red) averaged across all stations for (a) LIR and (b) COI/HIR. The bottom panels are for 10 m winds (m s−1). The X-axis is the UTC from 1200Z, 25 August to 1200Z, 26 August 2000.
Figure 3. (top) The 2m temperature (°C) from observations (black) and CTL (red) averaged across all stations for (a) LIR and (b) COI/HIR. The bottom panels are for 10 m winds (m s−1). The X-axis is the UTC from 1200Z, 25 August to 1200Z, 26 August 2000.
Atmosphere 10 00759 g003
Atmosphere 10 00759 g004 550
Figure 4. (left) Surface skin temperature (TSK), and (right) 2 m temperature (T2) for GR minus CTL (a,b) at 2000 UTC (1400 Local Standard Time, hereby LST) when the difference between the GR and CTL is maximum, (c,d) during the daytime (averaged between 0700 LST to 1900 LST, 25 August), and (e,f) nighttime (averaged between 1900Z, 25 August to 0700Z, 26 August 2000). Unit: °C.
Figure 4. (left) Surface skin temperature (TSK), and (right) 2 m temperature (T2) for GR minus CTL (a,b) at 2000 UTC (1400 Local Standard Time, hereby LST) when the difference between the GR and CTL is maximum, (c,d) during the daytime (averaged between 0700 LST to 1900 LST, 25 August), and (e,f) nighttime (averaged between 1900Z, 25 August to 0700Z, 26 August 2000). Unit: °C.
Atmosphere 10 00759 g004
Atmosphere 10 00759 g005 550
Figure 5. (a–c) Latent heat flux, (d–f) sensible heat flux, (g–i), net shortwave radiation, (j–l), net longwave radiation and (m–o) storage heat flux for (left) CTL, (middle) GR, and (right) GR minus CTL at 1900 UTC (1400 LST). The color bar on the right is for the difference plots. Unit: W m−2.
Figure 5. (a–c) Latent heat flux, (d–f) sensible heat flux, (g–i), net shortwave radiation, (j–l), net longwave radiation and (m–o) storage heat flux for (left) CTL, (middle) GR, and (right) GR minus CTL at 1900 UTC (1400 LST). The color bar on the right is for the difference plots. Unit: W m−2.
Atmosphere 10 00759 g005
Atmosphere 10 00759 g006 550
Figure 6. (left) The local tendency of temperature (LT, red), zonal advection (Z, orange), meridional advection (M, green) and horizontal advection (TA, blue) over LIR from (a) CTL, (c) GR, and (e) GR minus CTL. The right panels are for COI/HIR areas ((b) CTL, (d) GR, and (e) GR minus CTL). Unit in K hr−1.
Figure 6. (left) The local tendency of temperature (LT, red), zonal advection (Z, orange), meridional advection (M, green) and horizontal advection (TA, blue) over LIR from (a) CTL, (c) GR, and (e) GR minus CTL. The right panels are for COI/HIR areas ((b) CTL, (d) GR, and (e) GR minus CTL). Unit in K hr−1.
Atmosphere 10 00759 g006
Atmosphere 10 00759 g007a 550Atmosphere 10 00759 g007b 550
Figure 7. The terms of the zonal momentum budget from ((a) and (b)) the CTL, ((c) and (d)) the GR and ((e) and (f)) GR minus CTL for local tendency (first term on LHS in Equation (6)), horizontal advection or HADV (sum of the first two terms on the RHS in Equation (6)). The VADV + Residual (vertical advection plus residual; i.e., the sum of the third and sixth terms on the RHS in Equation (6)) and the pressure gradient and Coriolis (PGF + Cori; i.e., the sum of the fourth and fifth terms on RHS in Equation (6)). Unit m s−1 day−1.
Figure 7. The terms of the zonal momentum budget from ((a) and (b)) the CTL, ((c) and (d)) the GR and ((e) and (f)) GR minus CTL for local tendency (first term on LHS in Equation (6)), horizontal advection or HADV (sum of the first two terms on the RHS in Equation (6)). The VADV + Residual (vertical advection plus residual; i.e., the sum of the third and sixth terms on the RHS in Equation (6)) and the pressure gradient and Coriolis (PGF + Cori; i.e., the sum of the fourth and fifth terms on RHS in Equation (6)). Unit m s−1 day−1.
Atmosphere 10 00759 g007aAtmosphere 10 00759 g007b
Atmosphere 10 00759 g008a 550Atmosphere 10 00759 g008b 550
Figure 8. Same as Figure 7, but for the meridional momentum budget from ((a) and (b)) the CTL, ((c) and (d)) the GR and ((e) and (f)) GR minus CTL.
Figure 8. Same as Figure 7, but for the meridional momentum budget from ((a) and (b)) the CTL, ((c) and (d)) the GR and ((e) and (f)) GR minus CTL.
Atmosphere 10 00759 g008aAtmosphere 10 00759 g008b
Atmosphere 10 00759 g009 550
Figure 9. Time-averaged (1800Z, 25 August–2200Z, 25 August) terms in ((a) and (b)) zonal and ((c) and (d)) meridional momentum budgets for CTL (blue) and GR (red) over LIR and COI/HIR. Unit in mm sec−1 day−1.
Figure 9. Time-averaged (1800Z, 25 August–2200Z, 25 August) terms in ((a) and (b)) zonal and ((c) and (d)) meridional momentum budgets for CTL (blue) and GR (red) over LIR and COI/HIR. Unit in mm sec−1 day−1.
Atmosphere 10 00759 g009
Atmosphere 10 00759 g010 550
Figure 10. The moisture budget terms (averaged over 1800Z–2200Z, 25 August) over the (a) LIR and (b) COI/HIR areas from the CTL (blue) and GR (red) simulations. E is the evaporation, HADV is the horizontal moisture advection, VADV is the vertical moisture advection, ∂q/∂t is the local tendency of moisture, and R is the residual. unit in mm day−1.
Figure 10. The moisture budget terms (averaged over 1800Z–2200Z, 25 August) over the (a) LIR and (b) COI/HIR areas from the CTL (blue) and GR (red) simulations. E is the evaporation, HADV is the horizontal moisture advection, VADV is the vertical moisture advection, ∂q/∂t is the local tendency of moisture, and R is the residual. unit in mm day−1.
Atmosphere 10 00759 g010
Table
Table 1. Parameter values used in the simulations for three different urban categories (low-intensity residential, LIR; high-intensity residential, HIR; and commercial/industrial, COI).
Table 1. Parameter values used in the simulations for three different urban categories (low-intensity residential, LIR; high-intensity residential, HIR; and commercial/industrial, COI).
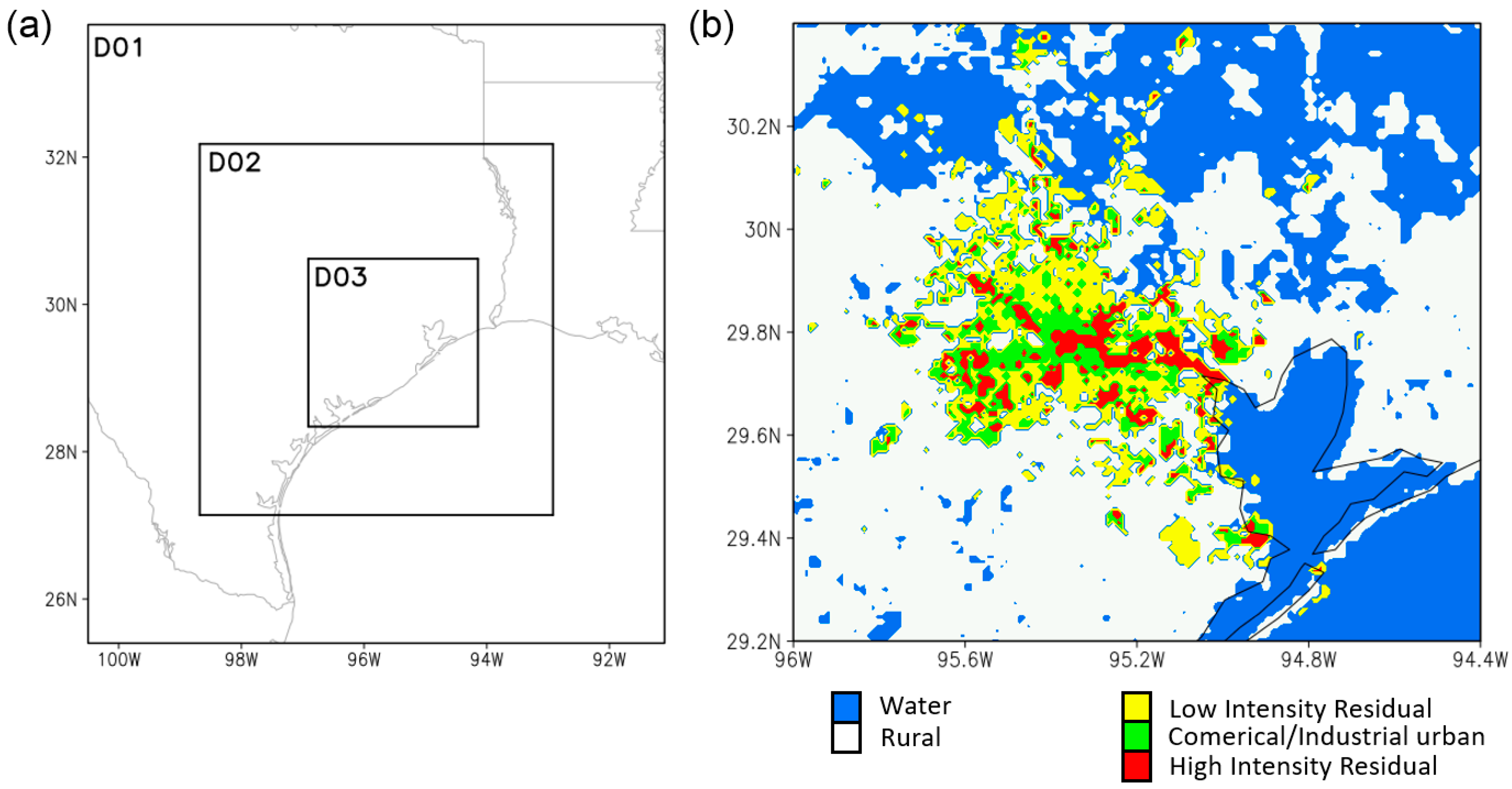
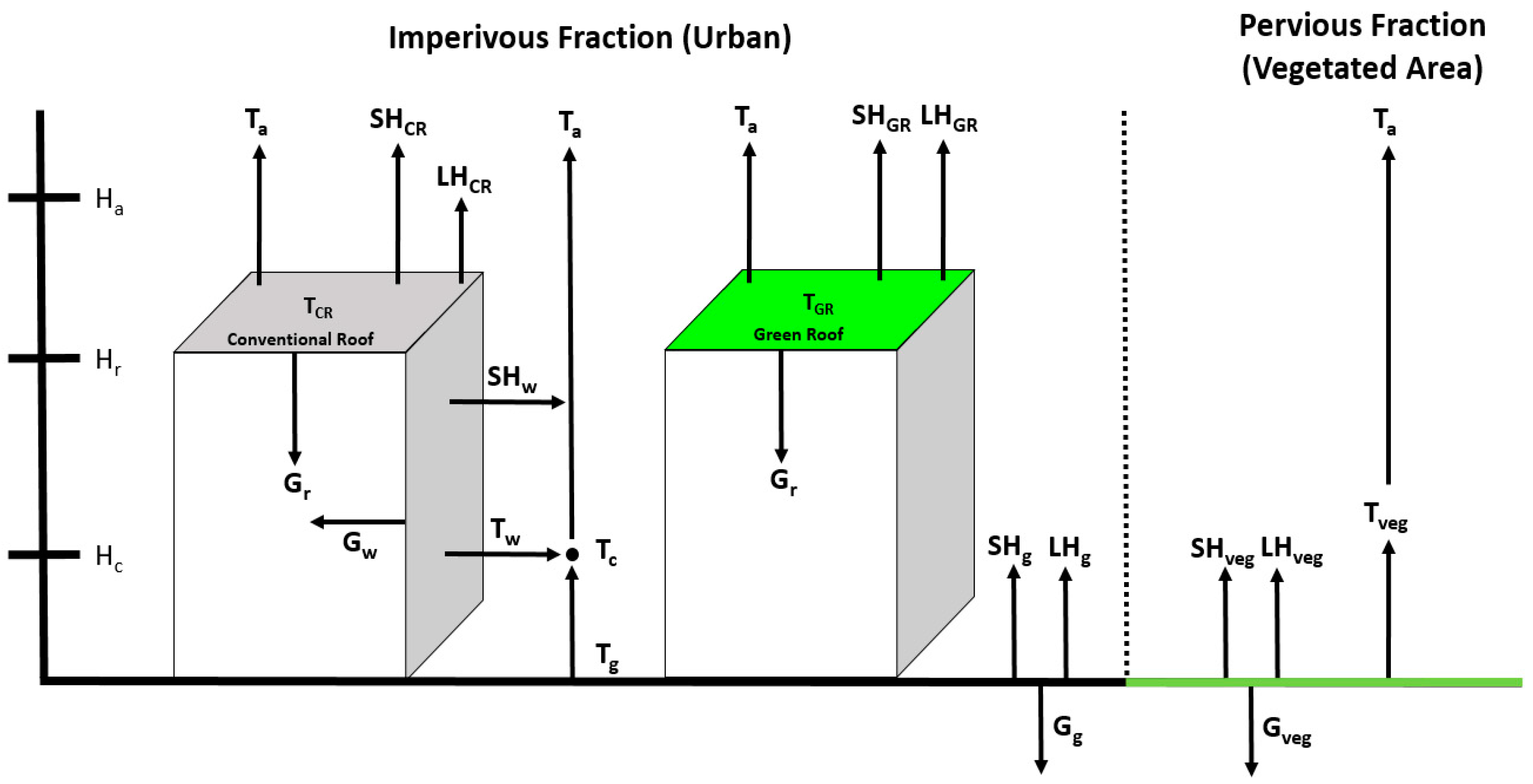
COIHIRLIRUnit
Mean building height (h)107.55m
Roof width (R)109.48.3m
Road width (Rd)109.48.3m
Impervious surface fraction (fimpervious)959050%
Roof fraction of the impervious part (froof = R/(R + Rd))505050%
Canyon fraction of the impervious part (fcanuon = 1 − froof)505050%
Roof fraction in the whole urban grid (froof × fimpervious)47.54525%
Table
Table 2. Summary of the model configurations. The references for the planetary boundary layer (PBL) schemes can be found in the text.
Table 2. Summary of the model configurations. The references for the planetary boundary layer (PBL) schemes can be found in the text.
ExperimentUrban Parameterization & Hydrological OptionsPurposePlanetary Boundary Layer Schemes
Control
(CTL)		Single-layer urban canopy model (SLUCM) with the following hydrological options: anthropogenic heat, urban oasis, urban irrigation, and evaporation.Use as a benchmark for SLUCM with urban hydrological processesYonsei University (YSU) scheme
Mellor–Yamada–Janjia (MYJ) scheme
Mellor–Yamada–Nakanishi–Niino (MYNN2.5) scheme
Boujeault–Lacarrere (BouLac) scheme
Green Roof
(GR)		Same as control (CTL), but with multi-layer green roof systemsTo explore the extent to which the multi-layer green roof can influence the advective processes
Table
Table 3. Mean bias and RMSE of 2 m temperature (°C) and 10 m winds (m s−1) for LIR and COI/HIR stations for simulations using different PBL schemes. The ensemble refers to the average of all 4 simulations using different PBL schemes. The period for the calculation is 1200Z, 25 August to 1200Z, 26 August 2000.
Table 3. Mean bias and RMSE of 2 m temperature (°C) and 10 m winds (m s−1) for LIR and COI/HIR stations for simulations using different PBL schemes. The ensemble refers to the average of all 4 simulations using different PBL schemes. The period for the calculation is 1200Z, 25 August to 1200Z, 26 August 2000.
CTLPBL SchemeT2 Mean BiasT2 RMSEW10 Mean BiasW10 RMSE
LIRYSU−0.620.720.380.65
MYJ−0.550.660.000.49
MYNN2.5−0.760.960.060.7
BouLac−0.320.480.020.6
Ensemble−0.560.590.120.53
COI/HIRYSU−1.011.330.211.33
MYJ−0.831.01−0.181.01
MYNN2.5−0.991.2−0.171.2
BouLac−0.570.87−0.210.87
Ensemble−0.851.01−0.090.88
Table
Table 4. Texas Commission on Environmental Quality (TCEQ) stations: low-intensity residential (LIR), high-intensity residential (HIR) and commercial/industrial (COI). CAMS: Continuous Ambient Monitoring Station.
Table 4. Texas Commission on Environmental Quality (TCEQ) stations: low-intensity residential (LIR), high-intensity residential (HIR) and commercial/industrial (COI). CAMS: Continuous Ambient Monitoring Station.
Station IDLatitude (°)Longitude (°)Land Category
CAMS 129.7681−95.2206LIR
CAMS 1529.8025−95.1256LIR
CAMS 8129.7335−95.3156HIR
CAMS 10029.3900−94.9194COI
CAMS 10829.9010−95.3261LIR
CAMS 14629.6957−95.4992HIR
CAMS 16729.7342−95.2383COI
CAMS 16929.7062−95.2611LIR
CAMS 40329.7336−95.2575COI
CAMS 40429.8069−95.2847COI
CAMS 40929.6239−95.4742LIR
CAMS 60329.7633−95.1811COI
Table
Table 5. Latent heat flux, sensible heat flux and surface skin temperature associated with 4 PBL schemes during daytime (averaged over 1200-0000Z, 25 August 2000), nighttime (averaged over 0000-1200Z, 26 August 2000) and daytime plus nighttime over LIR and COI/HIR areas.
Table 5. Latent heat flux, sensible heat flux and surface skin temperature associated with 4 PBL schemes during daytime (averaged over 1200-0000Z, 25 August 2000), nighttime (averaged over 0000-1200Z, 26 August 2000) and daytime plus nighttime over LIR and COI/HIR areas.
LIRDaytimeNighttimeDay+Night
Latent heat flux
(W m−2)		266–273 (CTL)
273–278 (GR)		5–7 (CTL)
6–8 (GR)		137–140 (CTL)
141–143 (GR)
Sensible heat flux
(W m−2)		60–70 (CTL)
44–53 (GR)		−3– −1 (CTL)
–2– −3 (GR)		29–34 (CTL)
21–25 (GR)
Surface skin
temperature (°C)		32–34 (CTL)
31–33 (GR)		26–27 (CTL)
26–27 (GR)		29–30 (CTL)
29–30 (GR)
COIHIR
Latent heat flux
(W m−2)		54–56 (CTL)
72–77 (GR)		16–16 (CTL)
17–19 (GR)		35–36 (CTL)
44–47 (GR)
Sensible heat flux
(W m−2)		172–179 (CTL)
135–139 (GR)		18–19 (CTL)
16–16 (GR)		95–98 (CTL)
76–78 (GR)
Surface skin
temperature (°C)		35–39 (CTL)
31–33 (GR)		27–28 (CTL)
26–27 (GR)		31–33 (CTL)
29–30 (GR)

Share and Cite

MDPI and ACS Style

Tan, H.; Ray, P.; Tewari, M.; Brownlee, J.; Ravindran, A. Response of Near-Surface Meteorological Conditions to Advection under Impact of the Green Roof. Atmosphere 2019, 10, 759. https://doi.org/10.3390/atmos10120759

AMA Style

Tan H, Ray P, Tewari M, Brownlee J, Ravindran A. Response of Near-Surface Meteorological Conditions to Advection under Impact of the Green Roof. Atmosphere. 2019; 10(12):759. https://doi.org/10.3390/atmos10120759

Chicago/Turabian Style

Tan, Haochen, Pallav Ray, Mukul Tewari, James Brownlee, and Ajaya Ravindran. 2019. "Response of Near-Surface Meteorological Conditions to Advection under Impact of the Green Roof" Atmosphere 10, no. 12: 759. https://doi.org/10.3390/atmos10120759

APA Style

Tan, H., Ray, P., Tewari, M., Brownlee, J., & Ravindran, A. (2019). Response of Near-Surface Meteorological Conditions to Advection under Impact of the Green Roof. Atmosphere, 10(12), 759. https://doi.org/10.3390/atmos10120759

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop