Precipitation Atlas for Germany (GePrA)
Abstract
:1. Introduction
2. Material and Methods
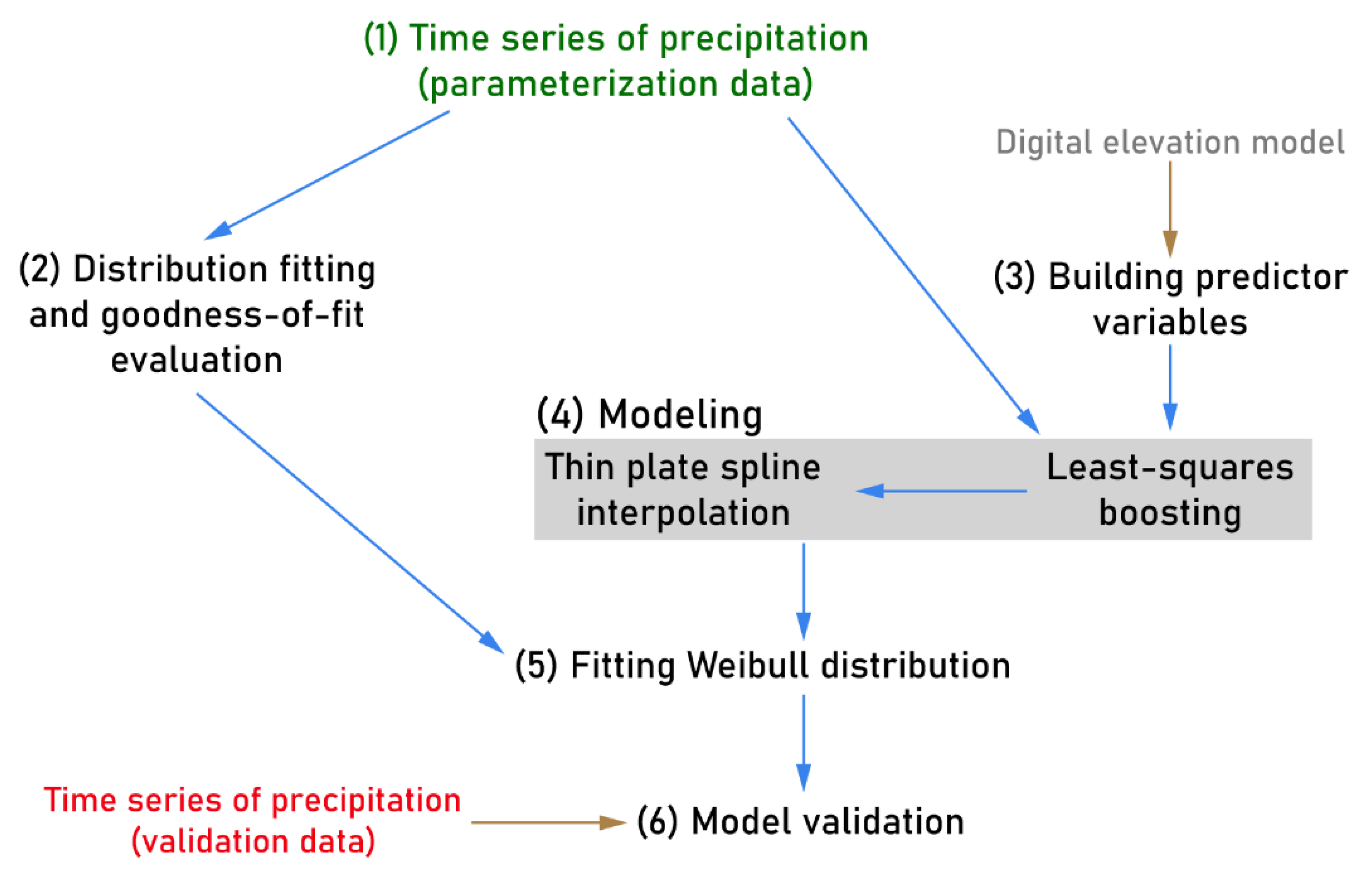
2.1. Overview
2.2. Study Area and Precipitation Data
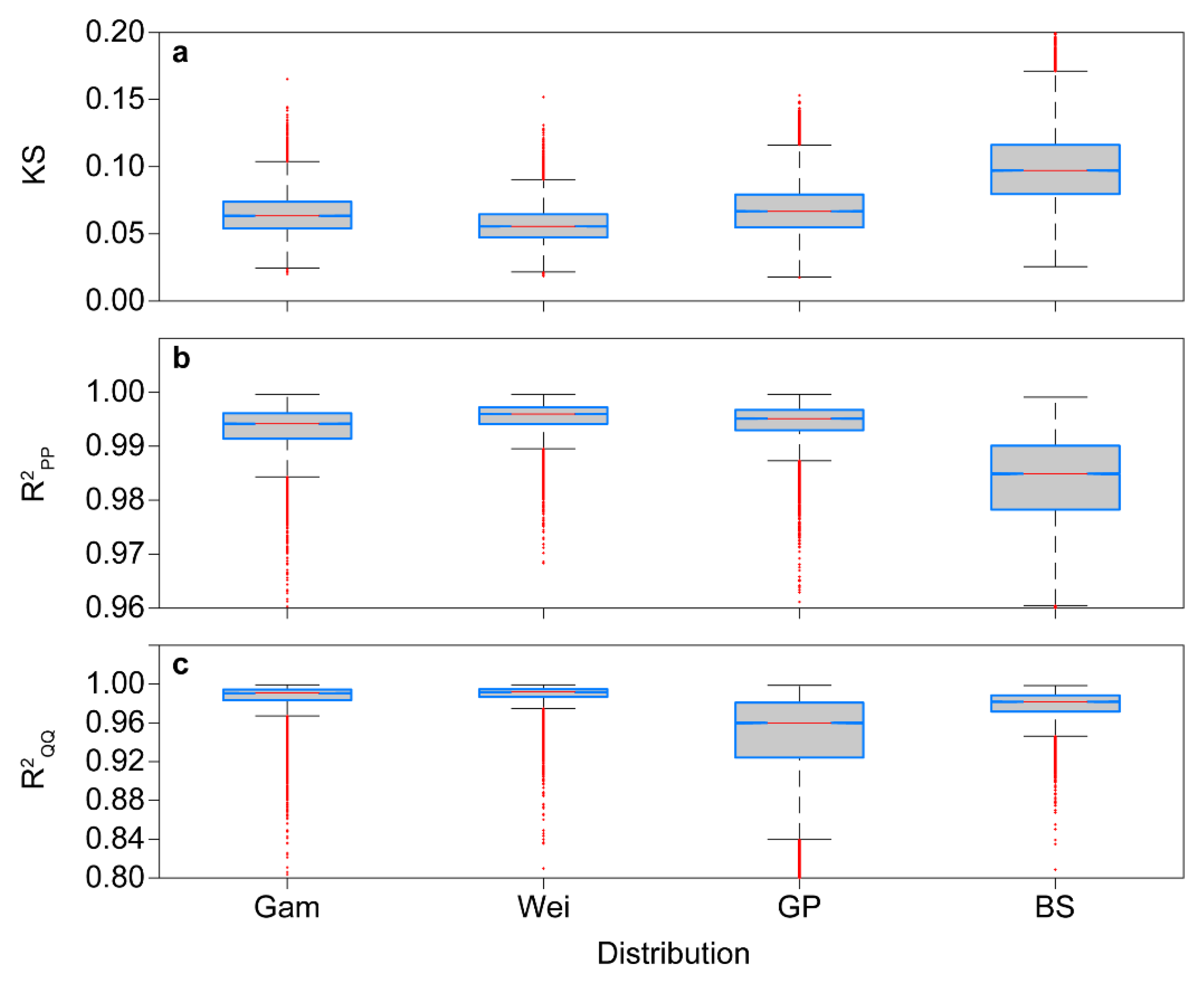
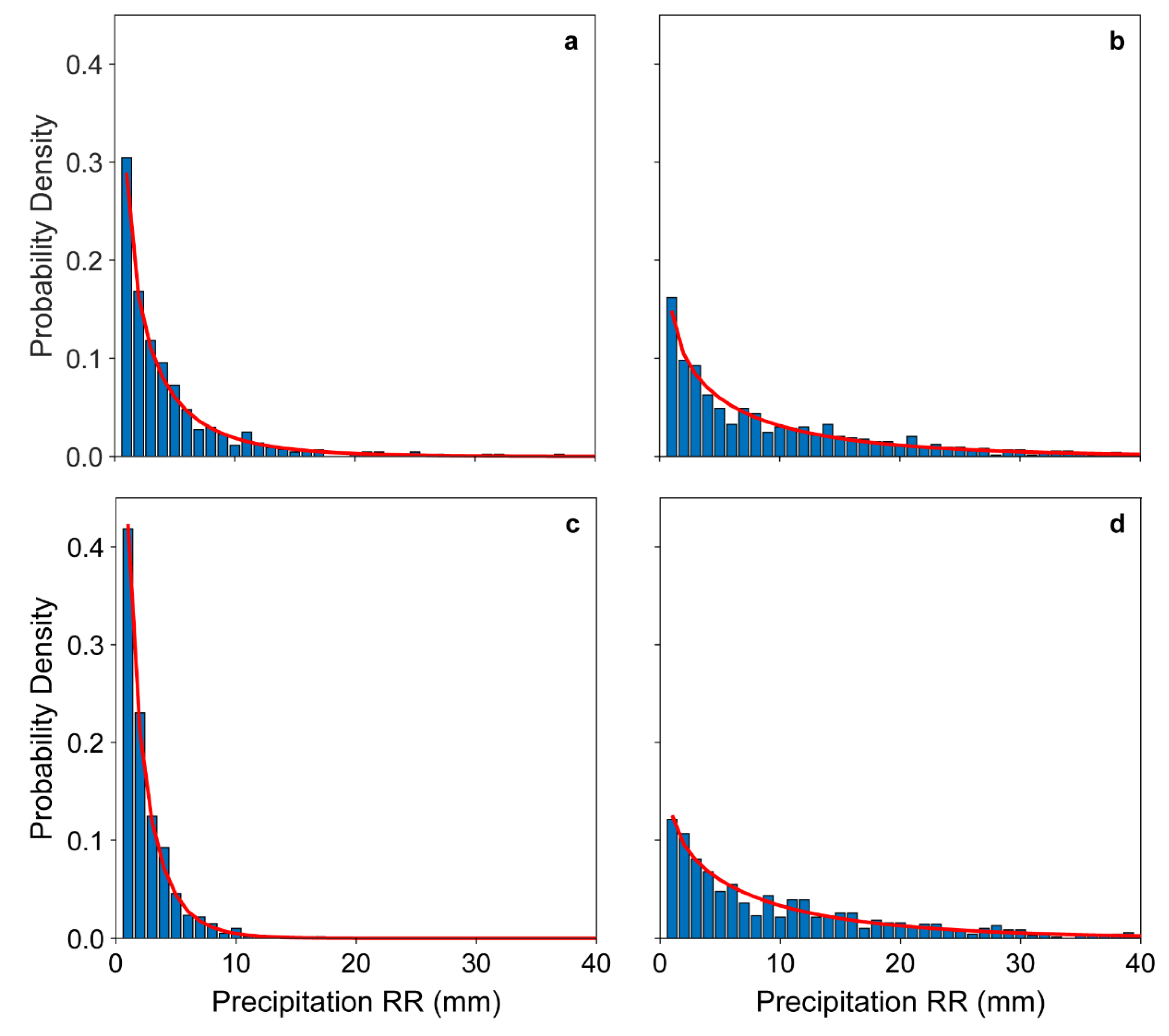
2.3. Distribution Fitting
2.4. Predictor Variables
2.5. LS-Boost Modeling (LSBoost) and Thin Plate Spline Interpolation (TPS)
2.6. Inter-Area Variability
3. Results and Discussion
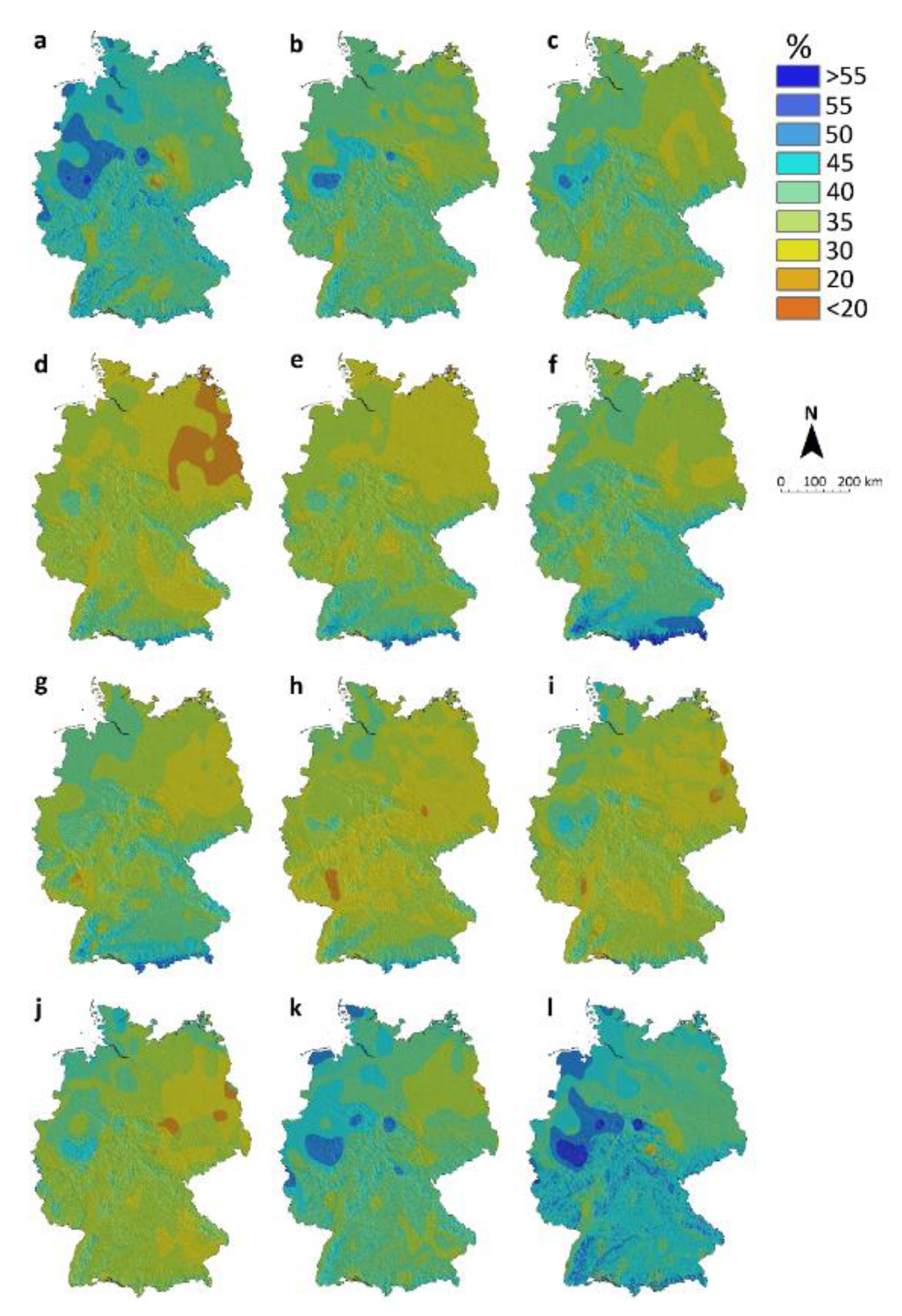
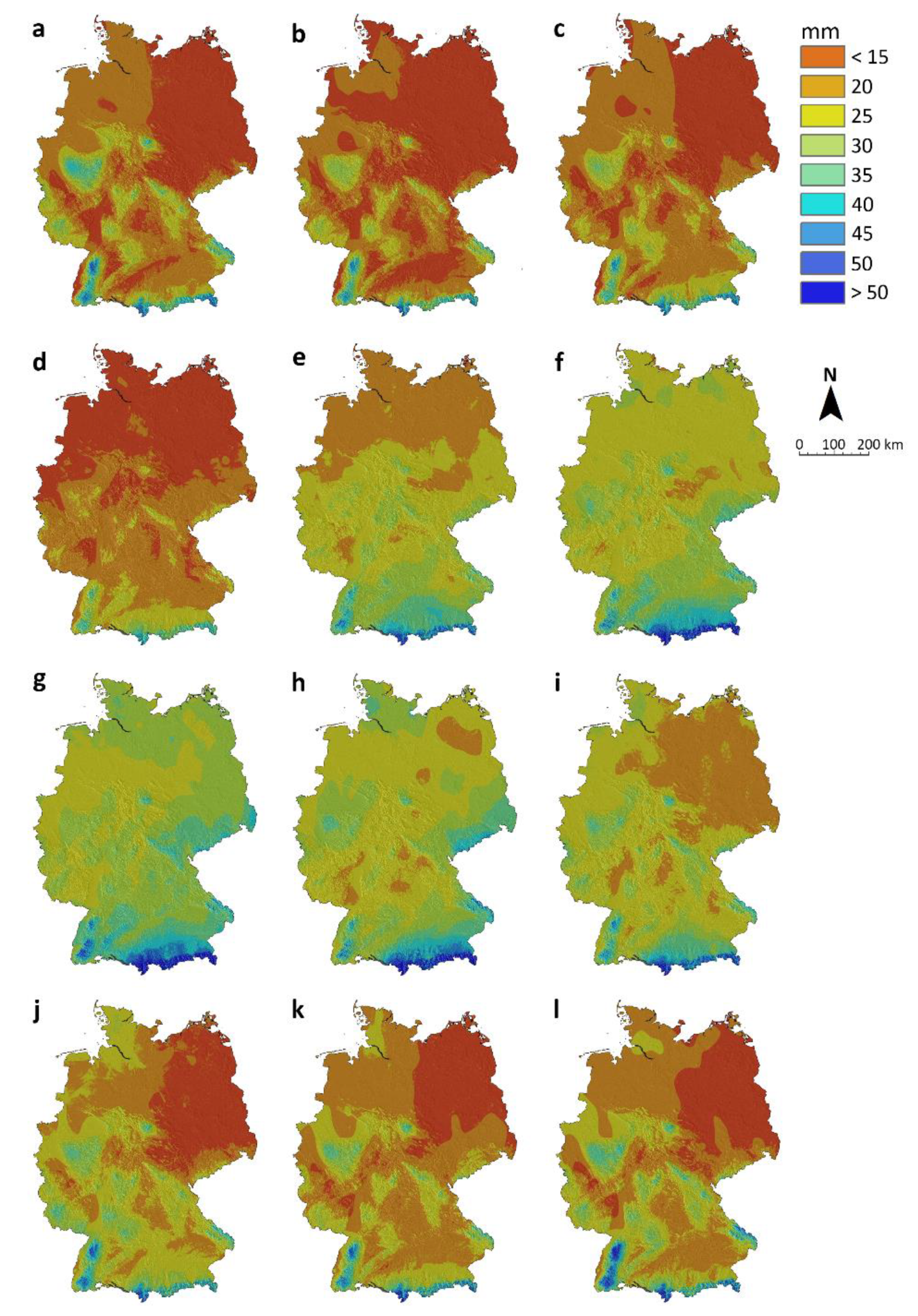
3.1. Proportion of Wet Days (PRwet)
3.2. Distribution Fitting
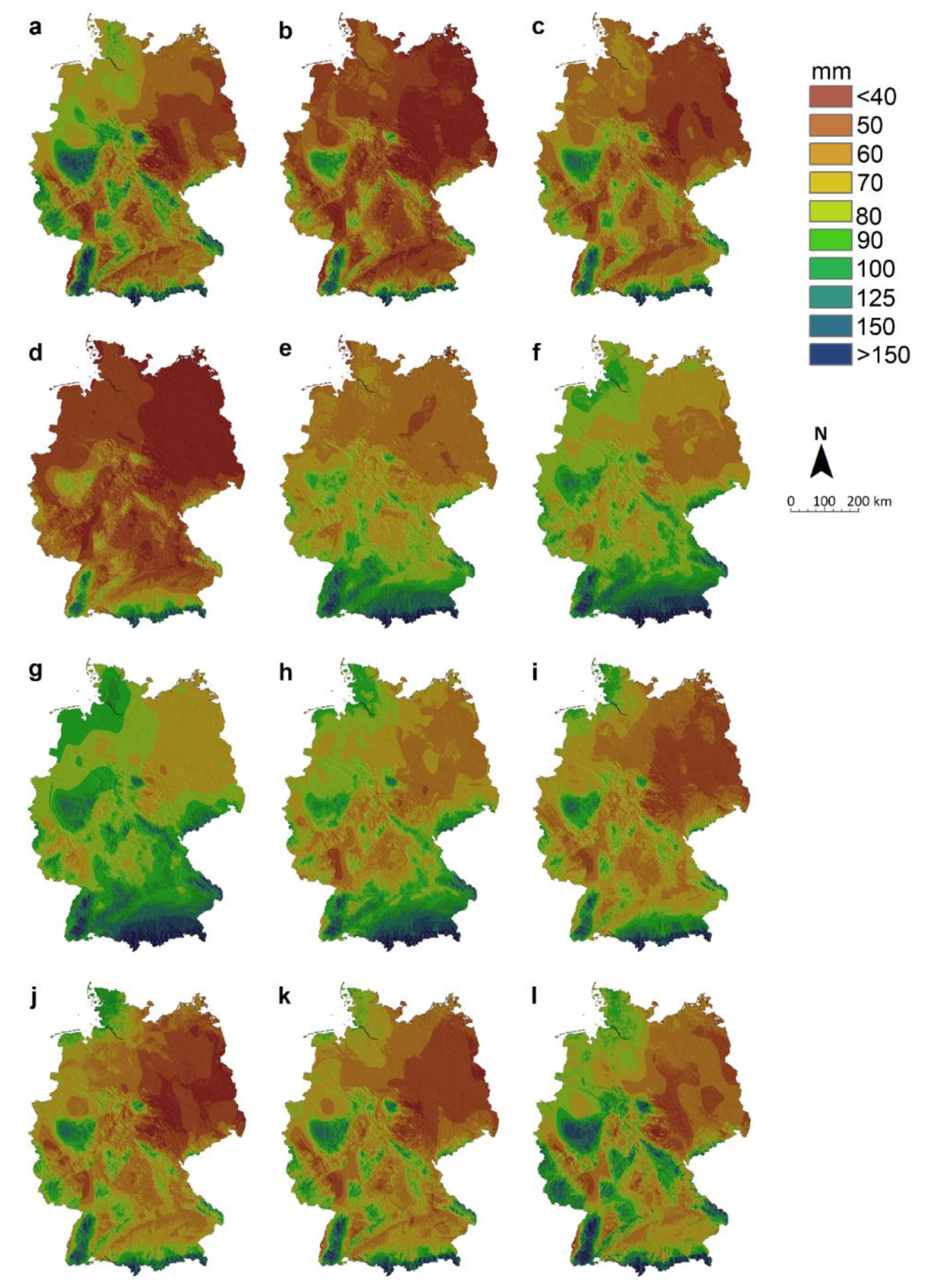
3.3. Heavy Precipitation
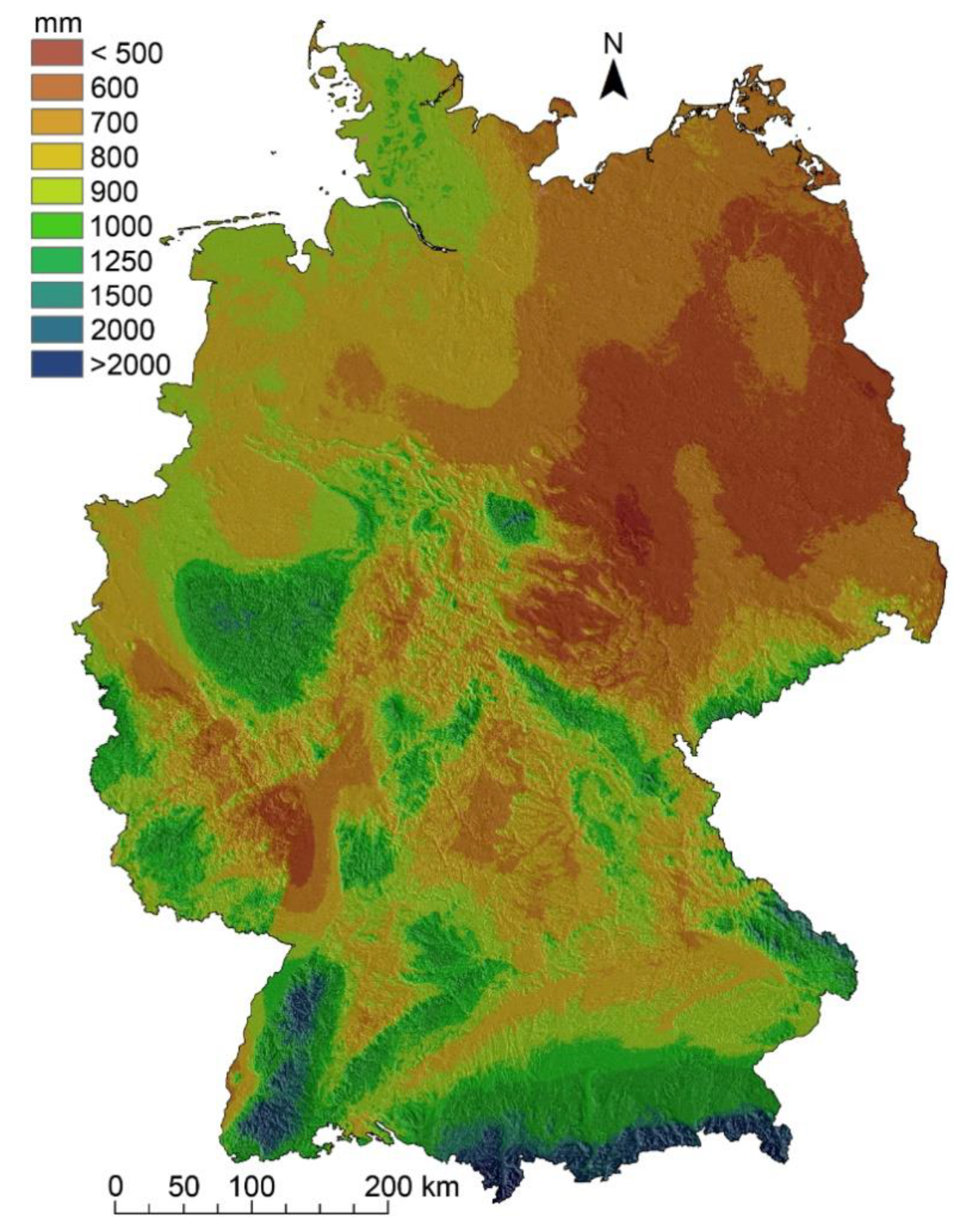
3.4. Monthly and Annual Precipitation Sums
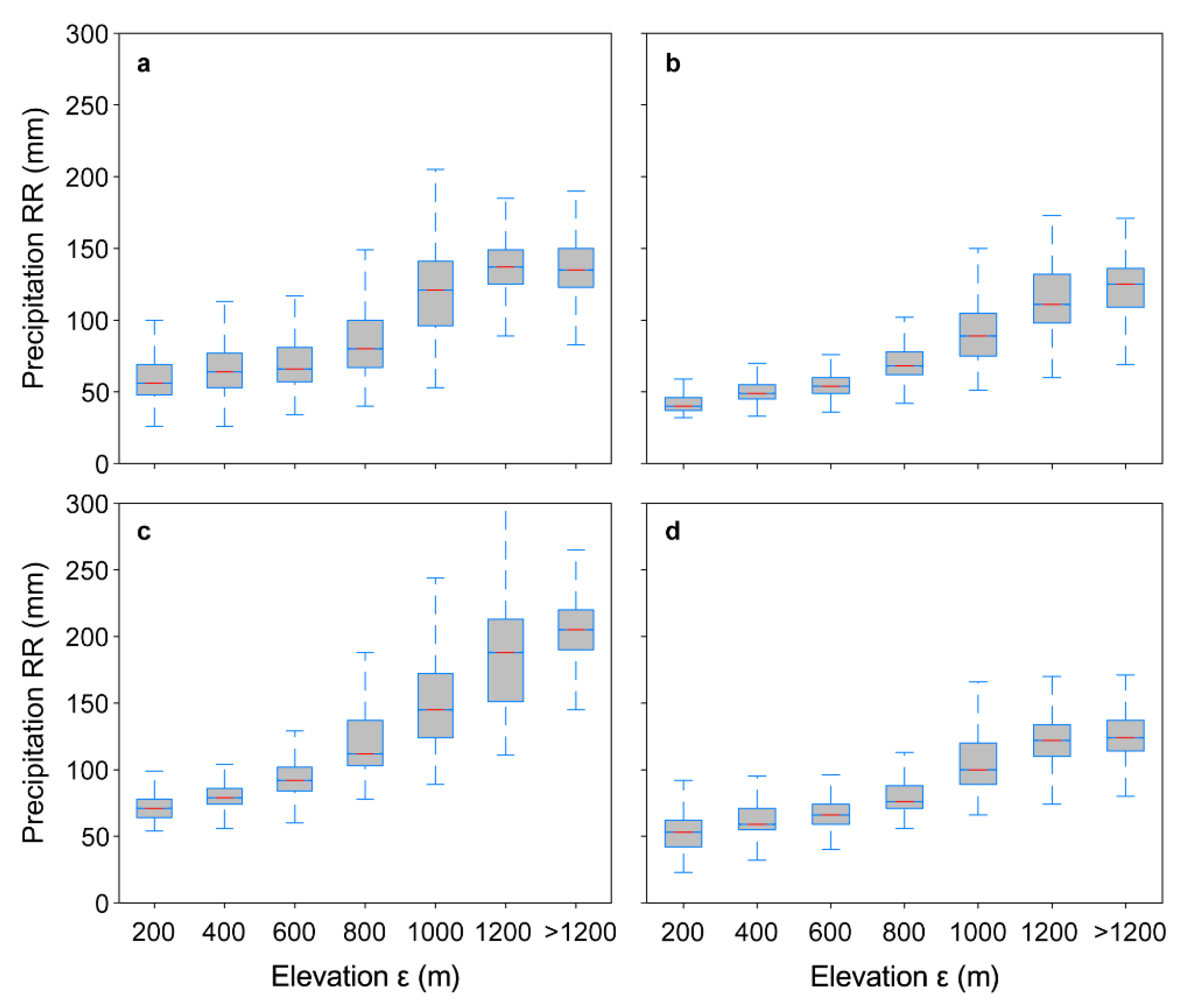
3.5. Orographic Influence on Precipitation Sums
3.6. Model Validation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Iqbal, M.F.; Athar, H. Validation of satellite based precipitation over diverse topography of Pakistan. Atmos. Res. 2018, 201, 247–260. [Google Scholar] [CrossRef]
- Zuo, J.; Xu, J.; Chen, Y.; Wang, C. Downscaling Precipitation in the Data-Scarce Inland River Basin of Northwest China Based on Earth System Data Products. Atmosphere 2019, 10, 613. [Google Scholar] [CrossRef]
- Yang, T.; Shao, Q.; Hao, Z.C.; Chen, X.; Zhang, Z.; Xu, C.Y.; Sun, L. Regional frequency analysis and spatio-temporal pattern characterization of rainfall extremes in the Pearl River Basin, China. J. Hydrol. 2010, 380, 386–405. [Google Scholar] [CrossRef]
- Putniković, S.; Tošić, I. Relationship between atmospheric circulation weather types and seasonal precipitation in Serbia. Meteorol. Atmos. Phys. 2018, 130, 393–403. [Google Scholar] [CrossRef]
- Hiebl, J.; Frei, C. Daily precipitation grids for Austria since 1961—Development and evaluation of a spatial dataset for hydroclimatic monitoring and modelling. Theor. Appl. Climatol. 2018, 132, 327–345. [Google Scholar] [CrossRef]
- Henn, B.; Newman, A.J.; Livneh, B.; Daly, C.; Lundquist, J.D. An assessment of differences in gridded precipitation datasets in complex terrain. J. Hydrol. 2018, 556, 1205–1219. [Google Scholar] [CrossRef]
- Herrnegger, M.; Senoner, T.; Nachtnebel, H.P. Adjustment of spatio-temporal precipitation patterns in a high Alpine environment. J. Hydrol. 2018, 556, 913–921. [Google Scholar] [CrossRef]
- Basist, A.; Bell, G.D.; Meentemeyer, V. Statistical relationships between topography and precipitation patterns. J. Climate 1994, 7, 1305–1315. [Google Scholar] [CrossRef]
- Yu, H.; Wang, L.; Yang, R.; Yang, M.; Gao, R. Temporal and spatial variation of precipitation in the Hengduan Mountains region in China and its relationship with elevation and latitude. Atmos. Res. 2018, 213, 1–16. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.L. A review of global precipitation data sets: Data sources, estimation, and intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Perugini, L; Caporaso, L.; Marconi, S.; Cescatti, A.; Quesada, B.; de Noblet-Ducoudre, N.; House, J.I.; Arneth, A. Biophysical effects on temperature and precipitation due to land cover change. Environ. Res. Lett. 2017, 12, 053002. [Google Scholar] [CrossRef]
- López-Espinoza, E.; Ruiz-Angulo, A.; Zavala-Hidalgo, J.; Romero-Centeno, R.; Escamilla-Salazar, J. Impacts of the Desiccated Lake System on Precipitation in the Basin of Mexico City. Atmosphere 2019, 10, 628. [Google Scholar] [CrossRef]
- Ghada, W.; Yuan, Y.; Wastl, C.; Estrella, N.; Menzel, A. Precipitation Diurnal Cycle in Germany Linked to Large-Scale Weather Circulations. Atmosphere 2019, 10, 545. [Google Scholar] [CrossRef]
- Long, Q.; Chen, Q.; Gui, K.; Zhang, Y. A Case Study of a Heavy Rain over the Southeastern Tibetan Plateau. Atmosphere 2016, 7, 118. [Google Scholar] [CrossRef]
- Tang, G.; Behrangi, A.; Long, D.; Li, C.; Hong, Y. Accounting for spatiotemporal errors of gauges: A critical step to evaluate gridded precipitation products. J. Hydrol. 2018, 559, 294–306. [Google Scholar] [CrossRef]
- Faiz, M.A.; Liu, D.; Fu, Q.; Sun, Q.; Li, M.; Baig, F.; Li, T.; Cui, S. How accurate are the performances of gridded precipitation data products over Northeast China? Atmos. Res. 2018, 211, 12–20. [Google Scholar] [CrossRef]
- Baker, L.H.; Shaffrey, L.C.; Scaife, A.A. Improved seasonal prediction of UK regional precipitation using atmospheric circulation. Int. J. Climatol. 2018, 38, 437–453. [Google Scholar] [CrossRef]
- Ehmele, F.; Kunz, M. Flood-related extreme precipitation in southwestern Germany: development of a two-dimensional stochastic precipitation model. Hydrol. Earth Syst. Sc. 2019, 23, 1083–1102. [Google Scholar] [CrossRef]
- Zhang, T.; Li, B.; Yuan, M.; Gao, X.; Sun, Q.; Xu, L.; Jiang, Y. Spatial downscaling of TRMM precipitation data considering the impacts of macro-geographical factors and local elevation in the Three-River Headwaters Region. Remote Sens. Environ. 2018, 215, 109–127. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D. Development of a statistical bivariate wind speed-wind shear model (WSWS) to quantify the height-dependent wind resource. Energy Convers. Manage. 2017, 149, 303–317. [Google Scholar] [CrossRef]
- CDC (Climate Data Center). Available online: https://cdc.dwd.de/portal/ (accessed on 28 May 2019).
- Martinez-Villalobos, C.; Neelin, J.D. Why do precipitation intensities tend to follow Gamma distributions? J. Atmos. Sci. 2019, 76, 3611–3631. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Koutsoyiannis, D. A global survey on the seasonal variation of the marginal distribution of daily precipitation. Adv. Water Resour. 2016, 94, 131–145. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D. Sensitivity analysis of the system of wind speed distributions. Energy Convers. Manag. 2018, 177, 376–384. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D. Global comparison of the goodness-of-fit of wind speed distributions. Energy Convers. Manage. 2017, 133, 216–234. [Google Scholar] [CrossRef]
- EU DEM. Available online: https://land.copernicus.eu/imagery-in-situ/eu-dem (accessed on 28 May 2019).
- Jung, C.; Schindler, D. Historical Winter Storm Atlas for Germany (GeWiSA). Atmosphere 2019, 10, 387. [Google Scholar] [CrossRef]
- Marra, F.; Nikolopoulos, E.I.; Anagnostou, E.N.; Morin, E. Metastatistical Extreme Value analysis of hourly rainfall from short records: Estimation of high quantiles and impact of measurement errors. Adv. Water Resour. 2018, 117, 27–39. [Google Scholar] [CrossRef]
- Friedman, J. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Van Heijst, D.; Potharst, R.; van Wezel, M. A support system for predicting eBay end prices. Decis. Support Syst. 2008, 44, 970–982. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D. 3D statistical mapping of Germany’s wind resource using WSWS. Energy Convers. Manaeg. 2018, 159, 96–108. [Google Scholar] [CrossRef]
- Wood, S.N. Thin-plate regression splines. J. R. Stat. Soc. Ser. B 2003, 65, 95–114. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D.; Laible, J.; Buchholz, A. Introducing a system of wind speed distributions for modeling properties of wind speed regimes around the world. Energy Convers. Manag. 2017, 144, 181–192. [Google Scholar] [CrossRef]
- Giorgi, F.; Torma, C.; Coppola, E.; Ban, N.; Schär, C.; Somot, S. Enhanced summer convective rainfall at Alpine high elevations in response to climate warming. Nat. Geosci. 2016, 9, 584. [Google Scholar] [CrossRef]
- Kyselý, J.; Rulfová, Z.; Farda, A.; Hanel, M. Convective and stratiform precipitation characteristics in an ensemble of regional climate model simulations. Clim. Dynam. 2016, 46, 227–243. [Google Scholar] [CrossRef]

| Distribution | Abbreviation | Parameters |
|---|---|---|
| Beta | Be | shape, shape |
| Birnbaum-Saunders | BS | shape, scale |
| Burr | Bu | shape, shape, scale |
| Epsilon Skew Normal | ESN | scale, location, skewness |
| Extreme Value | EV | location, scale |
| Gamma | Gam | shape, scale |
| Generalized Extreme Value | GEV | shape, scale, location |
| Generalized Pareto | GP | shape, scale, location |
| Inverse Gaussian | IG | scale, shape |
| Logistic | L | mean, scale |
| Log-logistic | LL | mean, scale (of logarithmic values) |
| Lognormal | LN | mean, standard deviation (of logarithmic values) |
| Nakagami | Na | shape, scale |
| Normal | N | mean, standard deviation |
| Poisson | P | mean |
| Rician | R | non-centrality, scale |
| t-Location Scale | tLS | location, scale, shape |
| Weibull | Wei | shape, scale |
| Symbol | Name | Sector (°) | Distance (m) | Data Source |
|---|---|---|---|---|
| lon | longitude | - | - | - |
| lat | latitude | - | - | - |
| ε | elevation | - | - | EU-DEM v.1 |
| η1000 | relative elevation | 1–360 | 1000 | EU-DEM v.1 |
| η3000 | relative elevation | 1–360 | 3000 | EU-DEM v.1 |
| η5000 | relative elevation | 1–360 | 5000 | EU-DEM v.1 |
| η7500 | relative elevation | 1–360 | 7500 | EU-DEM v.1 |
| ηn | relative elevation | 337.5–22.4 | 3000 | EU-DEM v.1 |
| ηne | relative elevation | 22.5–67.4 | 3000 | EU-DEM v.1 |
| ηe | relative elevation | 67.5–112.4 | 3000 | EU-DEM v.1 |
| ηse | relative elevation | 112.5–157.4 | 3000 | EU-DEM v.1 |
| ηs | relative elevation | 157.5–202.4 | 3000 | EU-DEM v.1 |
| ηsw | relative elevation | 202.5–247.4 | 3000 | EU-DEM v.1 |
| ηw | relative elevation | 247.5–292.4 | 3000 | EU-DEM v.1 |
| ηnw | relative elevation | 292.5–337.4 | 3000 | EU-DEM v.1 |
| σn | sheltering | 337.5–22.4 | 1000 | EU-DEM v.1 |
| σne | sheltering | 22.5–67.4 | 1000 | EU-DEM v.1 |
| σe | sheltering | 67.5–112.4 | 1000 | EU-DEM v.1 |
| σse | sheltering | 112.5–157.4 | 1000 | EU-DEM v.1 |
| σs | sheltering | 157.5–202.4 | 1000 | EU-DEM v.1 |
| σsw | sheltering | 202.5–247.4 | 1000 | EU-DEM v.1 |
| σw | sheltering | 247.5–292.4 | 1000 | EU-DEM v.1 |
| σnw | sheltering | 292.5–337.4 | 1000 | EU-DEM v.1 |
| σsum | sheltering | 1–360 | 1000 | EU-DEM v.1 |
| Month | R2 | MAE (mm) | ME (mm) |
|---|---|---|---|
| January | 0.78 | 9 | 1 |
| February | 0.70 | 8 | 1 |
| March | 0.76 | 9 | 1 |
| April | 0.75 | 7 | 1 |
| May | 0.83 | 8 | 0 |
| June | 0.87 | 8 | 0 |
| July | 0.87 | 9 | 0 |
| August | 0.85 | 8 | 0 |
| September | 0.80 | 8 | 0 |
| October | 0.79 | 8 | 1 |
| November | 0.75 | 8 | 0 |
| December | 0.78 | 9 | 0 |
| Year | 0.91 | 9 | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, C.; Schindler, D. Precipitation Atlas for Germany (GePrA). Atmosphere 2019, 10, 737. https://doi.org/10.3390/atmos10120737
Jung C, Schindler D. Precipitation Atlas for Germany (GePrA). Atmosphere. 2019; 10(12):737. https://doi.org/10.3390/atmos10120737
Chicago/Turabian StyleJung, Christopher, and Dirk Schindler. 2019. "Precipitation Atlas for Germany (GePrA)" Atmosphere 10, no. 12: 737. https://doi.org/10.3390/atmos10120737
APA StyleJung, C., & Schindler, D. (2019). Precipitation Atlas for Germany (GePrA). Atmosphere, 10(12), 737. https://doi.org/10.3390/atmos10120737





