Next Article in Journal
Observing and Modeling the Response of Placentia Bay to an Extratropical Cyclone
Previous Article in Journal
Impact of Sea Breeze Circulation on the Transport of Ship Emissions in Tangshan Port, China
Previous Article in Special Issue
Assessment of the Environmental and Societal Impacts of the Category-3 Typhoon Hato
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 10
Issue 11
10.3390/atmos10110725
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effect of Human-Induced Land Disturbance on Subseasonal Predictability of Near-Surface Variables Using an Atmospheric General Circulation Model

by
Tomohito J. Yamada
1,* and
Yadu Pokhrel
2
1
Faculty of Engineering, Hokkaido University, N13 W8, Kita-ku, Sapporo, Hokkaido 060-8628, Japan
2
Department of Civil and Environmental Engineering, Michigan State University, East Lansing, MI 48824, USA
*
Author to whom correspondence should be addressed.
Atmosphere 2019, 10(11), 725; https://doi.org/10.3390/atmos10110725
Submission received: 17 October 2019 / Revised: 11 November 2019 / Accepted: 13 November 2019 / Published: 19 November 2019
(This article belongs to the Special Issue Modeling and Monitoring Climate Extremes and Impacts on Natural-Human Systems)
Browse Figures
Versions Notes

Abstract

:
Irrigation can affect climate and weather patterns from regional to global scales through the alteration of surface water and energy balances. Here, we couple a land-surface model (LSM) that includes various human land-water management activities including irrigation with an atmospheric general circulation model (AGCM) to examine the impacts of irrigation-induced land disturbance on the subseasonal predictability of near-surface variables. Results indicate that the simulated global irrigation and groundwater withdrawals (circa 2000) are ~3600 and ~370 km3/year, respectively, which are in good agreement with previous estimates from country statistics and offline–LSMs. Subseasonal predictions for boreal summers during the 1986–1995 period suggest that the spread among ensemble simulations of air temperature can be substantially reduced by using realistic land initializations considering irrigation-induced changes in soil moisture. Additionally, it is found that the subseasonal forecast skill for near-surface temperature and sea level pressure significantly improves when human-induced land disturbance is accounted for in the AGCM. These results underscore the need to incorporate irrigation into weather forecast models, such as the global forecast system.

1. Introduction

Interactions between land and atmosphere are important drivers of the Earth’s climate and weather systems [1,2]. At local to regional scales, the land–atmospheric interactions are predominantly controlled by the changes in land-surface conditions [3,4,5], which have been profoundly altered in recent times by human management of land–water systems [6]. Agricultural land management and irrigation are by far the most important anthropogenic factors that affect land-surface conditions and the terrestrial water cycle. These anthropogenic factors can alter the biophysical properties of the land surface, such as its albedo, roughness, leaf area index, and rooting depth, consequently affecting various hydroclimatic processes, such as evaporation from land, transpiration from leaf stomata, and regional precipitation patterns [7,8,9,10,11]. Fundamentally, these alterations produce land disturbances through the changes in partitioning of sensible and latent heat fluxes at the land surface, which consequently, affect land–atmosphere interactions over a spread of spatio-temporal scales [12,13,14,15,16,17,18,19], potentially altering the long-term climate, as well as subseasonal weather patterns.
A number of studies have examined the impacts of land use change due to agricultural activities and irrigation on regional and global climates using observational data and/or climate model simulations [8,11,14,19,20,21,22,23,24,25,26,27,28,29,30,31]. Using atmospheric general circulation models (AGCMs) or observational data, these studies have consistently shown that while irrigation can significantly alter regional climate, the global impacts are relatively negligible [23]. However, how irrigation affects subseasonal weather forecasts still remains largely unexplored as most studies have focused on climate impacts [32].
Irrigation primarily affects weather forecasts through changes in soil moisture. In principle, for land-surface initialization to affect subseasonal forecasts, (1) the initialized soil moisture anomaly must persist throughout the forecast period and (2) the atmosphere must respond in a predictable way to the soil moisture anomaly. The timescale of soil moisture memory is typically 1 or 2 months [33], which is long compared to that of the atmosphere. The latter of the two aforementioned processes has been thoroughly examined by analyzing the response of a modeled atmosphere to soil moisture anomalies by employing a similarity diagnostic, using a dozen AGCMs [2,34,35,36]. These results suggested a strong land–atmosphere coupling over regions such as central parts of North America, Western India, Northern China, and the Sahel in Africa, all of which are located in transition zones of regions with dry and wet land-surface conditions. Using multi-AGCM ensemble results, a subsequent study [32] showed that soil moisture initialization can improve the subseasonal forecast skills of the near-surface temperature during boreal summer in regions such as Central North America, where a strong land–atmosphere coupling was found by [2].
Some of these dry–wet transition regions characterized by strong land–atmosphere coupling, including the Central US and Northern India, are among the world’s most intensively managed agricultural systems, where soil moisture is profoundly altered by irrigation using groundwater [37,38,39]. Our driving hypothesis in this study is that, in these highly irrigated regions, the changes in land-surface conditions due to irrigation alter the soil moisture memory and land–atmosphere coupling strength, significantly affecting the subseasonal forecast skills of the AGCM, which was not explored in the aforementioned land–atmosphere coupling studies.
Another ongoing issue is that the estimation of the irrigation amount itself suffers from large uncertainties arising from inaccurate representation of irrigation processes in climate models [40]. Sorooshian et al. [40] noted that due to the lack of observations and realistic irrigation schemes employed in climate models, most previous studies fall under the category of sensitivity test, with a focus on changes in the surface temperature at different levels of irrigation. Indeed, most of the early studies account for irrigation in a relatively crude manner, for example, by commonly fixing the annual volume of irrigation at a mean value based on available data or setting the soil moisture level in irrigated areas at saturation throughout the year without considering the crop growing season, consequently ignoring the spatio-temporal dynamics of crop growth and irrigation water use [20,21,23]. In addition, many studies do not take into account the source of irrigation water withdrawals, which is important to accurately simulate the coupled climate impacts and the changes in terrestrial water balance. Specifically, groundwater withdrawals, which account for the majority of irrigation water use in many regions, have been largely ignored in most studies. More recent studies have addressed some of these issues by employing improved irrigation schemes and datasets [19,29,30,40,41]; however, significant challenges and opportunities remain for better representing irrigation, especially by accounting for the source of irrigation water withdrawals and using these improved schemes to examine irrigation impacts not only on the regional climate but also on the forecast skills.
To fill this research gap, here we couple a land-surface model (LSM) that includes a detailed irrigation and groundwater pumping schemes into an AGCM and examine the effects of irrigation-induced changes in land initializations on subseasonal forecast skills. Our objectives are two-fold: (1) incorporate irrigation and groundwater pumping schemes into an AGCM and evaluate its performance in realistically simulating human water use and (2) employ the newly coupled model to examine the impacts of human land disturbance on the subseasonal predictability of near-surface atmospheric variables simulated by the AGCM. The central scientific question that drives the study is how does land disturbance due to human activities, such as irrigation, affect the subseasonal predictability of near-surface atmospheric variables, and what are the potential impacts on land–atmosphere coupling in transitional wet–dry regions? Various schemes representing human land-water management activities, including irrigation, are consistently coupled within the AGCM by fully taking into account the terrestrial water balance, which is an important advancement over previous studies on irrigation using AGCMs. The model also takes into account the water use from surface and groundwater resources, which is critical for simulating climate impacts in regions with intensive irrigation using groundwater. Simulations are conducted globally but results are discussed at varying spatial scales. The effects of irrigation on subseasonal forecast are discussed for the continental United States (US). For model evaluation, we use the region overlying the High Plains Aquifer (~450,000 km2) in the Central US, which is one of the most intensively irrigated regions in the world. The region is monitored by the US Geological Survey (USGS) on a regular basis and, therefore, ground-truth datasets are available for the analysis period. The remainder of the paper is structured as follows. Section 2 describes the methodology and the details of the model. Section 3 provides the results and discussion. Finally, we provide a summary in Section 4.

2. The Model and Experimental Designs

The AGCM we use is Version 3.2 of the Model for Interdisciplinary Research on Climate (MIROC) [42]. The land-surface component of MIROC is the Minimal Advanced Treatment of Surface Interaction and RunOff model (MATSIRO; [43]), which has recently been enhanced by incorporating various human impact modules, such as crop growth and irrigation, water withdrawal, reservoir operation, and environmental flow requirements [44], as well as a dynamic groundwater scheme [45] and a groundwater pumping scheme [38]. These advancements have led to a new version of MATSIRO termed as Human Impacts and Groundwater representation in MATSIRO (HiGW-MAT) [38], which we couple with MIROC in the present study.
A detailed description of human water management schemes can be found in our previous studies; here, for completeness, we provide a brief overview. In the crop growth and irrigation scheme, described in detail in [44], the subgrid variability of vegetation is represented by partitioning each grid cell into two tiles: natural vegetation and irrigated cropland. Taking into account the cropping period that is necessary to obtain mature and optimal total plant biomass for 18 different crop types, the scheme estimates irrigation water requirements based on the soil moisture deficit during the cropping period [44]. Irrigation water is obtained from surface or sub-surface sources as necessary and is added to the top-soil layer, the ultimate fate of which is determined by land-surface water and energy balances and land–atmosphere coupling. Runoff generated from the land-surface model is routed through the digital river network of the Total Runoff Integrating Pathways (TRIP) [46], which has been integrated within MIROC. The reservoir operation module, which was based on [47], releases water to meet the agricultural, domestic, and industrial demand in the downstream area. The withdrawal module obtains water from river channels, reservoirs, and groundwater to fulfill the domestic, industrial, and agricultural needs.
In this study, a series of numerical experiments are conducted by turning human impact schemes on and off, which are summarized in Table 1. First, we conduct offline simulations (Offline–Human) at 1° grids using the HiGW-MAT model to generate realistic land initializations for the coupled simulations. Then, we carry out two online climatological simulations (Table 1): one without considering human impacts (AGCM–ORG) and the other with human impacts (AGCM–Human). Then, following the simulation protocol of the GLACE-2 project [32], we conduct three sets of 10-ensemble forecast simulations (Table 1) using: (1) realistic land initialization but without considering human impacts (AGCM–ORG–ReLI); (2) realistic land initializations considering human impacts (AGCM–Human–ReLI); and (3) randomly chosen land initializations with human impacts (AGCM–Human–RaLI).
For climatological analysis and model evaluation, one long-term simulation each is performed using AGCM-ORG and AGCM-Human settings. The NCEP/NCAR-1 reanalysis data is used for atmospheric initializations. We use land initializations after conducting a 10-year spin-up run. For model evaluation we use the results from 1998 to 2010.
All forecast simulations (AGCM-ORG-ReLI, AGCM-Human-ReLI, and AGCM-Human-LaLI) begin on July 15 over the years from 1986 to 1995 and last for 60 days. The land initializations for each of the 10-ensemble simulations were produced by an offline LSM simulation. All online simulations are conducted at T42 spatial resolution. Simulations are conducted as follows. For the three sets of forecast simulations, we follow the framework of GLACE-2 [32]. Land initializations are produced by using offline LSM simulations, with a scaling technique [48] applied to adjust the climatology between the offline LSM and the AGCM. The human impacts schemes are incorporated both in the LSM and the AGCM; therefore, land initializations for AGCM-ORG and AGCM-Human are prepared separately. The anomaly that persisted in sea surface temperature (SST) data, which was applied in GLACE-2, is also adopted in this study. We use 10 sets of atmospheric initializations, in which 3-h perturbations are added to the NCEP/NCAR-1 reanalysis [49] data at each target date.

3. Results

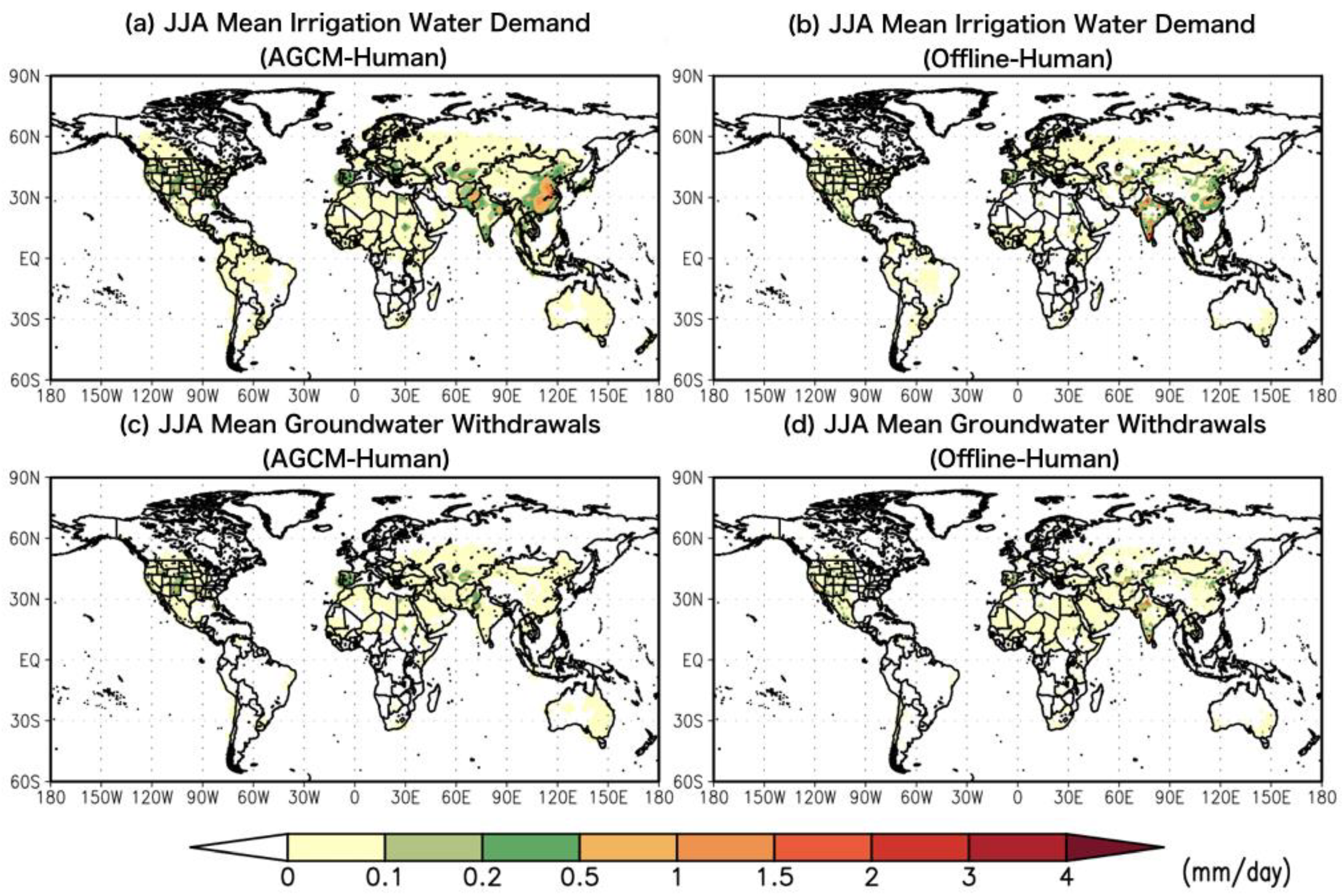
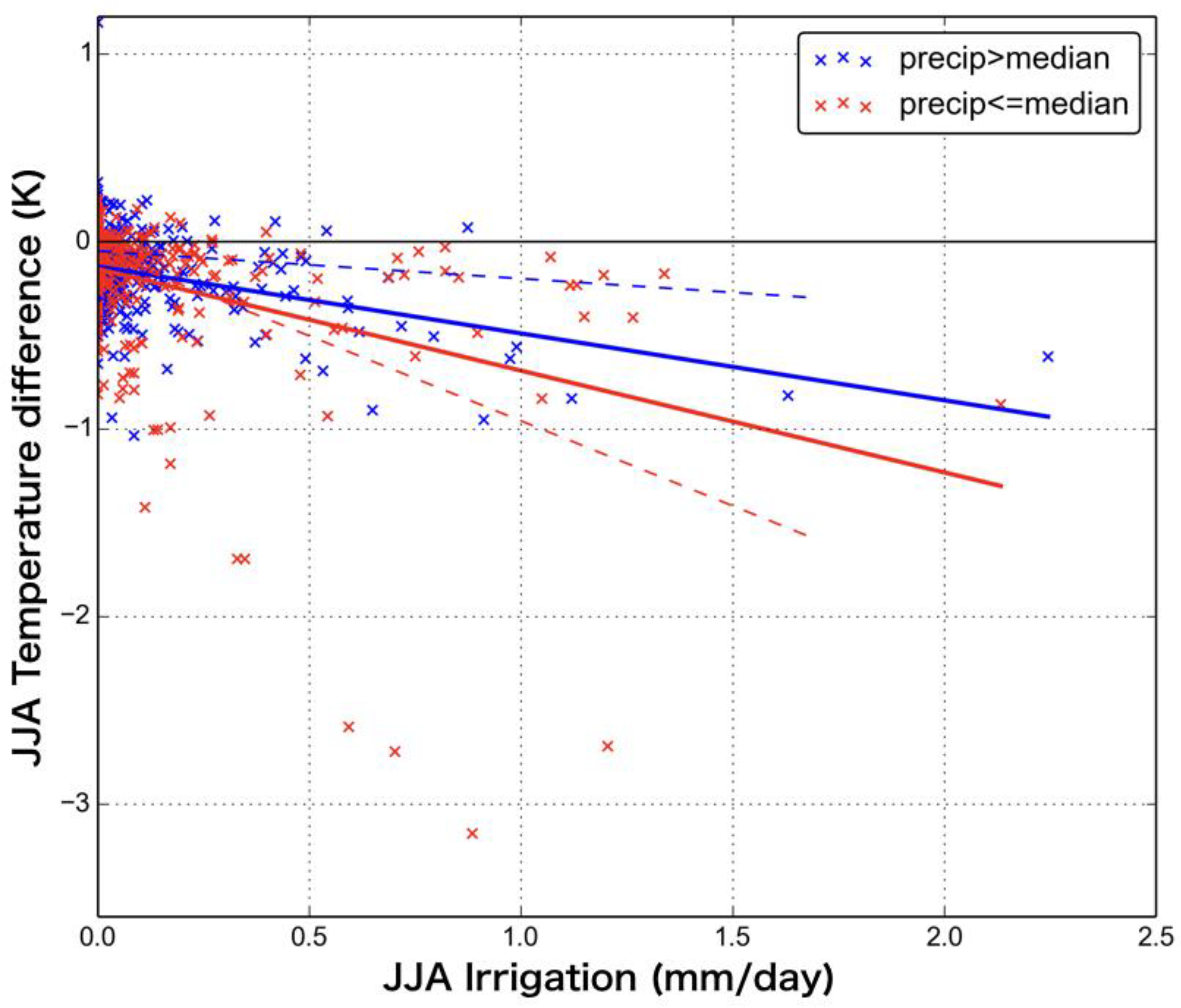
3.1. Climatology of Irrigation Water Use and Groundwater Withdrawal

The land-surface model, groundwater scheme, and the water use and pumping modules have been extensively used in an offline mode and results have been validated using ground- and satellite-based observations of various hydrologic fluxes and stores [39,44,45,50]. Here, we evaluate the simulated irrigation water requirements and groundwater withdrawals from the coupled AGCM–Human experiment against reported global volumes and the results from various offline hydrological models, including our own results from the Offline–Human experiment. We note that the objective of this evaluation is not to provide an extensive validation of the model results but, rather, to ensure that the results from the AGCM–Human setting—which has different climatology of precipitation and temperature—do not depart significantly from the offline model results due to climatological bias and are in general agreement with the reported statistics. Therefore, we focus on the spatial patters of long-term mean irrigation water use and groundwater withdrawal and their total global volumes.
Figure 1a,b present the geographical distribution of the irrigation water demand from AGCM–Human and Offline–Human experiments, respectively, averaged for the boreal summer (June–August: JJA) during 1998–2010, a reasonably long period for such a comparison. It is evident from the figures that the broad spatial patters of irrigation water use in the offline simulation are captured in the AGCM–Human experiment. Similarly, Figure 1c,d presents the spatial distribution of groundwater withdrawals from the two simulations, which are also in good agreement in terms of the broad spatial patterns in regions with intensive irrigation using groundwater (e.g., the High Plains, Northwest India). The global total irrigation water demand (i.e., the net water requirement) and withdrawal (i.e., water withdrawn from the source) from the AGCM–Human experiment are within the limits of reported estimates from the Food and Agricultural Organization (FAO) and the offline model results from various previous studies (Table 2). Note that the withdrawal is estimated by taking into account the irrigation efficiency that represents conveyance and other losses (see [44] for details). Despite a slight overestimation, we consider these results to be generally satisfactory as the objective of the present study is to examine the impacts of irrigation-induced soil moisture changes on subseasonal forecasts rather than an accurate estimation of water resources availability and use. Table 3 compares the results of global groundwater withdrawals. It is evident here that different estimates differ significantly and the AGCM–Human experiment underestimates global groundwater withdrawals compared to all other estimates. We attribute this underestimation to the increased availability of surface water in larger AGCM grids (T42) compared to the 1° grids in the offline experiment. While it is important to further improve the groundwater scheme for a realistic estimation of groundwater withdrawals, this does not affect the results presented here as the irrigation demand is fulfilled by using either surface water or groundwater. That is, surface water use could be overestimated and groundwater underestimated in the AGCM–Human experiment.
Next, we evaluate the simulated terrestrial water storage (TWS: the vertically integrated total surface and sub-surface water storage) to ensure that the coupled model simulates the trends of long-term TWS changes over highly irrigated regions within plausible limits. We perform this comparison over the High Plains region in the Central US because this is a relatively data-rich region and also the subseasonal forecast skill is examined over the continental US. Figure 2 presents the comparison of simulated TWS anomalies—averaged over the regions overlying the High Plains aquifer—from the AGCM–Human simulation with the observations of groundwater storage changes by USGS between 2003 to 2010. It is evident from the figure that the decreasing trend in TWS, which is primarily due to unsustainable groundwater use [38], is captured by the coupled model, with certain overestimation of the depletion compared to both USGS observations and offline model. Differences in inter-annual and seasonal variations between the coupled and offline model can also be seen, which can be attributed primarily to the difference in the meteorological input to the land-surface model, which is based on observations in the offline experiment. We note that the perfect match between simulations and USGS observations cannot be expected because the observations do not include surface water storages, which account for a small portion of the total TWS changes [38]. Despite some disagreements, these comparisons add further confidence to our coupled simulations, confirming that the results of TWS variations are not greatly affected due to model bias in simulating the long-term climate as compared to observations.
Finally, we compare the sensitivity of near surface temperature due the incorporation of irrigation modules using the results from a previous study that examined irrigation impacts on near-surface climate [23]. Figure 3 shows a scatter diagram of near surface air temperatures simulated by AGCM-Human and AGCM-ORG, grouped into two categories based on precipitation intensity, following the approach adopted by Sacks et al. [23] using an AGCM and prescribed water levels and heat fluxes, including irrigation activities, at the national level. In Figure 3, the red and blue solid lines indicate the linear regressions for the respective cases and the results from Sacks et al. [23] are plotted as dashed lines. In both our study and Sacks et al. [23], irrigation exerted a larger influence on near surface temperature in rather drier regions including semi-arid areas where strong land–atmosphere coupling strength is detected [2]. This result indicates that the prescription of surface wetness due to irrigation activities could decrease the spread among ensemble forecast simulations.

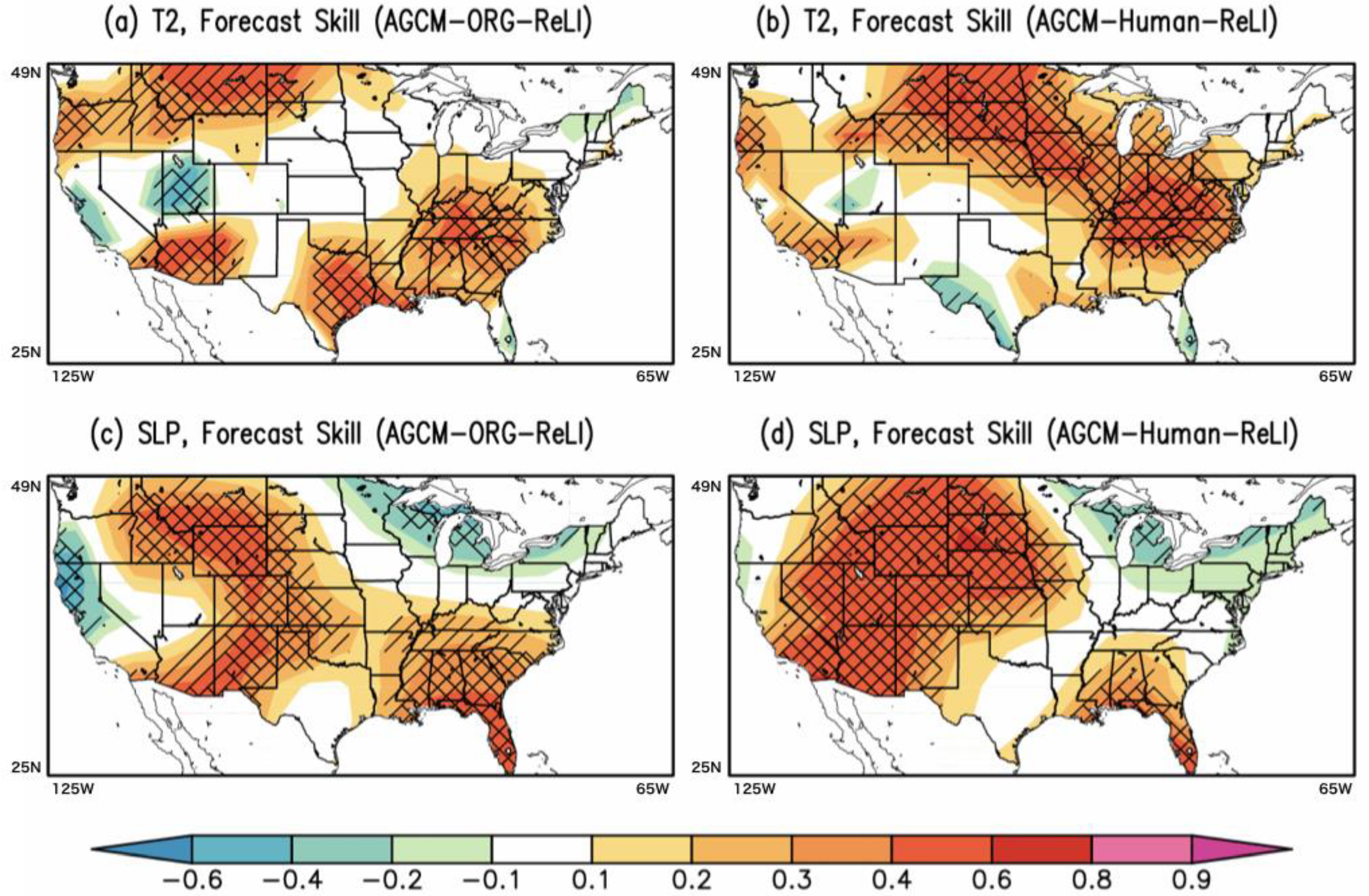
3.2. Subseasonal Predictability

Figure 4 shows the spatial distributions of the spread of air temperatures (K) among 10 ensemble members at the subseasonal scale (Day 16–39) for (a) AGCM–Human–RaLI, (b) AGCM–ORG–ReLI, and (c) AGCM–Human–ReLI (see Table 1 for experimental settings). Fifteen-day average states are examined at the subseasonal scale. In both the spread and the forecast skill, 10 sets of periods between Day 16–39 among the 10 years are used. The spread indicates the similarity among 10 ensemble members in each forecast simulation (the average value of all samples). The correlation coefficient between the forecast results and observations is a measure of the forecast skill. For each period, the anomaly was calculated for each year both for the forecast result and observations. The anomalies are applied to calculate the correlation coefficient among the all samples between 1986 and 1995.
In this figure, warmer colors indicate a large spread of values among the ensemble members; similar results for soil moisture are shown as overlaid contour lines. These results suggest that both the inclusion of human activities, especially irrigation, and realistic land initializations significantly contributed to a decreased spread among the ensemble members for air temperature. The spread of soil moisture over the three hatched boxes (west, middle, and east, from left to right) was investigated for the three forecast simulations. The central hatched boxes in Figure 4, which includes the center of the Mississippi River Basin, indicate large differences in the spread of soil moisture among different experiments, with AGCM–Human–ReLI showing the smallest spread (~10%) compared to the other two experiments. This evidently suggests that the variation in soil moisture levels is strongly influenced by the land disturbance due to human activities in addition to realistic land initializations, resulting in a smaller spread of air temperatures over the Central US.
Finally, the forecast skills of near-surface variables, such as air temperature (K) and sea level pressure (hPa), are investigated using the AGCM–ORG and AGCM–Human simulations in association with realistic land initializations (ReLI). AGCM–ORG–RaLI is not considered here because the GLACE-2 project has already reported that land initializations can contribute to the subseasonal forecast skill in air temperature [32]. Figure 5a,b show the forecast skill of air temperature for (a) AGCM–ORG–ReLI and (b) AGCM–Human–ReLI. The forecast skill is estimated by calculating the year-to-year correlation coefficients between forecasts and observations. In this analysis, the Japan Meteorological Agency Climate Data Assimilation System (JCDAS) [58] and National Centers for Environmental Prediction/National Center for Atmospheric Research (NCEP/NCAR-1) reanalysis data [49] are treated as observations for near-surface temperature and sea level pressure, respectively. As shown in Figure 5a,b, AGCM–ORG–ReLI shows improved skills over the Eastern US, as well as the southwestern and northwestern regions. This demonstrates that the incorporation of human land disturbance due to irrigation in an AGCM can substantially improve the subseasonal forecast skill. In particular, the regions with improved forecast skills expand over the central region by connecting the southeastern and northwestern regions. A similar characteristic can be seen for the sea level pressure in Figure 5c,d. A higher forecast skill can be seen in the Southeastern, Southwestern, and Northwestern US (Figure 5c). In Figure 5d, for AGCM–Human–ReLI, a higher forecast skill is apparent in western to northern mid-regions, despite the slightly weaker forecast skill in the Southeastern US. In both forecast simulations, there were negative correlation coefficients for the Northeastern US, and no improvements in forecast skills due to the incorporation of irrigation are found.

4. Discussion and Conclusions

In this study, we couple a land-surface model (LSM) with the representation of various human land-water management activities, including irrigation, with an atmospheric general circulation model (AGCM) to examine the impacts of irrigation-induced land disturbance on the subseasonal predictability of near-surface variables. The newly integrated modeling framework offers a major advancement over past efforts in the examination of irrigation-induced climate impacts as it dynamically simulates human–natural interactions by fully accounting for the terrestrial water balance within the AGCM framework. The results of irrigation and groundwater withdrawals from the coupled AGCM–Human experiment are found to be satisfactory in terms of their spatial patterns over the highly managed agroecosystems and their total global volumes are also found to be within plausible limits of previously reported values.
It has been reported in previous studies of global land–atmosphere coupling that the Central US, Northeastern China, and Western India and Pakistan are the hotspots where soil moisture anomalies affect the variations of air temperature and precipitation during the boreal summer. Since these regions are characterized by a semi-arid climate and host vast agricultural regions irrigated by using groundwater, the strength of the land–atmosphere coupling can be largely influenced by these human activities that affect soil wetness during the growing season. We hypothesized that the irrigation-induced soil wetness can be treated as the predictive diagnostic for subseasonal predictability, which generally requires variables with a longer memory, such as SSTs. Results suggest that the incorporation of irrigation into the AGCM, in addition to realistic land initializations, not only reduces the spread of near-surface air temperature forecast among ensemble members but also improves the forecast skill for near-surface air temperature and sea level pressure. These findings highlight the need to incorporate human land–water management, especially irrigation, in numerical weather prediction models, such as the global forecast system (GFS) of the National Oceanic and Atmospheric Administration (NOAA).

Author Contributions

T.J.Y. designed the research; T.J.Y. and Y.P. performed the analyses and wrote the paper.

Funding

This study was partially supported by MEXT/ SI-CAT, ADAP-T(SATREPS)/JICA-JST, ArCS, KAKENHI (19H02241), and a research grant (Award #1752729) from the National Science Foundation of the US.

Acknowledgments

We thank two anonymous reviewers for the comments that helped improve the quality of the paper substantially.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Shukla, J.; Mintz, Y. Influence of Land-Surface Evapotranspiration on the Earth’s Climate. Science 1982, 215, 1498–1501. [Google Scholar] [CrossRef]
  2. Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.T.; Kanae, S.; Kowalczyk, E.; Lawrence, D.; et al. Regions of Strong Coupling Between Soil Moisture and Precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef]
  3. Pielke, R.A.; Marland, G.; Betts, R.A.; Chase, T.N.; Eastman, J.L.; Niles, J.O.; Niyogi, D.D.; Running, S.W. The influence of land-use change and landscape dynamics on the climate system: Relevance to climate-change policy beyond the radiative effect of greenhouse gases. Philos. Trans. R. Soc. Lond. Math. Phys. Eng. Sci. 2002, 360, 1705–1719. [Google Scholar] [CrossRef]
  4. Pielke, R.A.; Pitman, A.; Niyogi, D.; Mahmood, R.; McAlpine, C.; Hossain, F.; Goldewijk, K.K.; Nair, U.; Betts, R.; Fall, S.; et al. Land use/land cover changes and climate: Modeling analysis and observational evidence. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 828–850. [Google Scholar] [CrossRef]
  5. Feddema, J.J.; Oleson, K.W.; Bonan, G.B.; Mearns, L.O.; Buja, L.E.; Meehl, G.A.; Washington, W.M. The Importance of Land-Cover Change in Simulating Future Climates. Science 2005, 310, 1674–1678. [Google Scholar] [CrossRef]
  6. Nazemi, A.; Wheater, H.S. On inclusion of water resource management in earth system models—Part 1: Problem definition and representation of water demand. Hydrol. Earth Syst. Sci. 2015, 19, 33–61. [Google Scholar] [CrossRef]
  7. Pielke, R.A., Sr.; Adegoke, J.O.; Chase, T.N.; Marshall, C.H.; Matsui, T.; Niyogi, D. A new paradigm for assessing the role of agriculture in the climate system and in climate change. Agric. For. Meteorol. 2007, 142, 234–254. [Google Scholar] [CrossRef]
  8. DeAngelis, A.; Dominguez, F.; Fan, Y.; Robock, A.; Kustu, M.D.; Robinson, D. Evidence of enhanced precipitation due to irrigation over the Great Plains of the United States. J. Geophys. Res. Atmos. 2010, 115, D15. [Google Scholar] [CrossRef]
  9. Levis, S. Modeling vegetation and land use in models of the Earth System. Wiley Interdiscip. Rev. Clim. Chang. 2010, 1, 840–856. [Google Scholar] [CrossRef]
  10. Oki, T.; Blyth, E.M.; Berbery, E.H.; Alcaraz-Segura, D. Land Use and Land Cover Changes and Their Impacts on Hydroclimate, Ecosystems and Society. In Climate Science for Serving Society; Asrar, G.R., Hurrell, J.W., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 185–203. [Google Scholar]
  11. Alter, R.E.; Fan, Y.; Lintner, B.R.; Weaver, C.P. Observational Evidence that Great Plains Irrigation Has Enhanced Summer Precipitation Intensity and Totals in the Midwestern United States. J. Hydrometeorol. 2015, 16, 1717–1735. [Google Scholar] [CrossRef]
  12. Segal, M.; Pan, Z.; Turner, R.W.; Takle, E.S. On the Potential Impact of Irrigated Areas in North America on Summer Rainfall Caused by Large-Scale Systems. J. Appl. Meteorol. 1998, 37, 325–331. [Google Scholar] [CrossRef]
  13. Pitman, A.J.; Zhao, M. The relative impact of observed change in land cover and carbon dioxide as simulated by a climate model. Geophys. Res. Lett. 2000, 27, 1267–1270. [Google Scholar] [CrossRef]
  14. Adegoke, J.O.; Pielke, R.A.; Eastman, J.; Mahmood, R.; Hubbard, K.G. Impact of Irrigation on Midsummer Surface Fluxes and Temperature under Dry Synoptic Conditions: A Regional Atmospheric Model Study of the U.S. High Plains. Mon. Weather Rev. 2003, 131, 556–564. [Google Scholar] [CrossRef]
  15. De Rosnay, P.; Polcher, J.; Laval, K.; Sabre, M. Integrated parameterization of irrigation in the land surface model orchidee. Validation over indian peninsula. Geophys. Res. Lett. 2003, 30, 1986. [Google Scholar] [CrossRef]
  16. Oleson, K.W.; Bonan, G.B.; Levis, S.; Vertenstein, M. Effects of land use change on North American climate: Impact of surface datasets and model biogeophysics. Clim. Dyn. 2004, 23, 117–132. [Google Scholar] [CrossRef]
  17. Findell, K.L.; Shevliakova, E.; Milly, P.C.D.; Stouffer, R.J. Modeled Impact of Anthropogenic Land Cover Change on Climate. J. Clim. 2007, 20, 3621–3634. [Google Scholar] [CrossRef]
  18. Mahmood, R.; Pielke, R.A., Sr.; Hubbard, K.G.; Niyogi, D.; Bonan, G.; Lawrence, P.; McNider, R.; McAlpine, C.; Etter, A.; Gameda, S.; et al. Impacts of Land Use/Land Cover Change on Climate and Future Research Priorities. Bull. Am. Meteorol. Soc. 2010, 91, 37–46. [Google Scholar] [CrossRef]
  19. Lawston, P.M.; Santanello, J.A.; Zaitchik, B.F.; Rodell, M. Impact of Irrigation Methods on Land Surface Model Spinup and Initialization of WRF Forecasts. J. Hydrometeorol. 2015, 16, 1135–1154. [Google Scholar] [CrossRef]
  20. Boucher, O.; Myhre, G.; Myhre, A. Direct human influence of irrigation on atmospheric water vapour and climate. Clim. Dyn. 2004, 22, 597–603. [Google Scholar] [CrossRef]
  21. Lobell, D.B.; Bala, G.; Duffy, P.B. Biogeophysical impacts of cropland management changes on climate. Geophys. Res. Lett. 2006, 33, L06708. [Google Scholar] [CrossRef]
  22. Kueppers, L.M.; Snyder, M.A.; Sloan, L.C.; Cayan, D.; Jin, J.; Kanamaru, H.; Kanamitsu, M.; Miller, N.L.; Tyree, M.; Du, H.; et al. Seasonal temperature responses to land-use change in the western United States. Glob. Planet. Chang. 2008, 60, 250–264. [Google Scholar] [CrossRef]
  23. Sacks, W.J.; Cook, B.I.; Buenning, N.; Levis, S.; Helkowski, J.H. Effects of global irrigation on the near-surface climate. Clim. Dyn. 2009, 33, 159–175. [Google Scholar] [CrossRef]
  24. Puma, M.J.; Cook, B.I. Effects of irrigation on global climate during the 20th century. J. Geophys. Res. Atmos. 2010, 115, D16120. [Google Scholar] [CrossRef]
  25. Kustu, M.D.; Fan, Y.; Rodell, M. Possible link between irrigation in the U.S. High Plains and increased summer streamflow in the Midwest. Water Resour. Res. 2011, 47, W03522. [Google Scholar] [CrossRef]
  26. Guimberteau, M.; Laval, K.; Perrier, A.; Polcher, J. Global effect of irrigation and its impact on the onset of the Indian summer monsoon. Clim. Dyn. 2012, 39, 1329–1348. [Google Scholar] [CrossRef]
  27. Wei, J.; Dirmeyer, P.A.; Wisser, D.; Bosilovich, M.G.; Mocko, D.M. Where Does the Irrigation Water Go? An Estimate of the Contribution of Irrigation to Precipitation Using MERRA. J. Hydrometeorol. 2012, 14, 275–289. [Google Scholar] [CrossRef]
  28. Lo, M.-H.; Famiglietti, J.S. Irrigation in California’s Central Valley strengthens the southwestern U.S. water cycle. Geophys. Res. Lett. 2013, 40, 301–306. [Google Scholar] [CrossRef]
  29. Sorooshian, S.; AghaKouchak, A.; Li, J. Influence of irrigation on land hydrological processes over California. J. Geophys. Res. Atmos. 2014, 119, 13137–13152. [Google Scholar] [CrossRef]
  30. Pei, L.; Moore, N.; Zhong, S.; Kendall, A.D.; Gao, Z.; Hyndman, D.W. Effects of Irrigation on Summer Precipitation over the United States. J. Clim. 2016, 29, 3541–3558. [Google Scholar] [CrossRef]
  31. Pokhrel, Y.N.; Felfelani, F.; Shin, S.; Yamada, T.J.; Satoh, Y. Modeling large-scale human alteration of land surface hydrology and climate. Geosci. Lett. 2017, 4, 1–13. [Google Scholar] [CrossRef]
  32. Koster, R.D.; Mahanama, S.P.P.; Yamada, T.J.; Balsamo, G.; Berg, A.A.; Boisserie, M.; Dirmeyer, P.A.; Doblas-Reyes, F.J.; Drewitt, G.; Gordon, C.T.; et al. Contribution of land surface initialization to subseasonal forecast skill: First results from a multi-model experiment. Geophys. Res. Lett. 2010, 37, L02402. [Google Scholar] [CrossRef] [Green Version]
  33. Vinnikov, K.Y.; Yeserkepova, I.B. Soil Moisture: Empirical Data and Model Results. J. Clim. 1991, 4, 66–79. [Google Scholar] [CrossRef] [Green Version]
  34. Koster, R.D.; Sud, Y.C.; Guo, Z.; Dirmeyer, P.A.; Bonan, G.; Oleson, K.W.; Chan, E.; Verseghy, D.; Cox, P.; Davies, H.; et al. GLACE: The Global Land–Atmosphere Coupling Experiment. Part I: Overview. J. Hydrometeorol. 2006, 7, 590–610. [Google Scholar] [CrossRef]
  35. Guo, Z.; Dirmeyer, P.A.; Koster, R.D.; Sud, Y.C.; Bonan, G.; Oleson, K.W.; Chan, E.; Verseghy, D.; Cox, P.; Gordon, C.T.; et al. GLACE: The Global Land–Atmosphere Coupling Experiment. Part II: Analysis. J. Hydrometeorol. 2006, 7, 611–625. [Google Scholar] [CrossRef]
  36. Yamada, T.J.; Koster, R.D.; Kanae, S.; Oki, T. Estimation of Predictability with a Newly Derived Index to Quantify Similarity among Ensemble Members. Mon. Weather Rev. 2007, 135, 2674–2687. [Google Scholar] [CrossRef] [Green Version]
  37. Wada, Y.; van Beek, L.P.H.; van Kempen, C.M.; Reckman, J.W.T.M.; Vasak, S.; Bierkens, M.F.P. Global depletion of groundwater resources. Geophys. Res. Lett. 2010, 37, L20402. [Google Scholar] [CrossRef] [Green Version]
  38. Pokhrel, Y.N.; Koirala, S.; Yeh, P.J.-F.; Hanasaki, N.; Longuevergne, L.; Kanae, S.; Oki, T. Incorporation of groundwater pumping in a global Land Surface Model with the representation of human impacts. Water Resour. Res. 2015, 51, 78–96. [Google Scholar] [CrossRef] [Green Version]
  39. Pokhrel, Y.N.; Hanasaki, N.; Wada, Y.; Kim, H. Recent progresses in incorporating human land–water management into global land surface models toward their integration into Earth system models. Wiley Interdiscip. Rev. Water 2016, 3, 548–574. [Google Scholar] [CrossRef] [Green Version]
  40. Sorooshian, S.; Li, J.; Hsu, K.; Gao, X. Influence of irrigation schemes used in regional climate models on evapotranspiration estimation: Results and comparative studies from California’s Central Valley agricultural regions. J. Geophys. Res. Atmos. 2012, 117, D06107. [Google Scholar] [CrossRef]
  41. Felfelani, F.; Pokhrel, Y.; Guan, K.; Lawrence, D.M. Utilizing SMAP soil moisture data to constrain irrigation in the Community Land Model. Geophys. Res. Lett. 2018, 45, 12892–12902. [Google Scholar] [CrossRef]
  42. K-1 Model Developers. K-1 Coupled Model (MIROC) K-1 Techical Report No.1, Center for Climate System Research (Univ. of Tokyo), National Institute for Environmental Studies, and Frontier Research Center for Global Change. Available online: https://ccsr.aori.u-tokyo.ac.jp/~hasumi/miroc_description.pdf (accessed on 23 September 2019).
  43. Takata, K.; Emori, S.; Watanabe, T. Development of the minimal advanced treatments of surface interaction and runoff. Glob. Planet. Chang. 2003, 38, 209–222. [Google Scholar] [CrossRef]
  44. Pokhrel, Y.; Hanasaki, N.; Koirala, S.; Cho, J.; Yeh, P.J.-F.; Kim, H.; Kanae, S.; Oki, T. Incorporating Anthropogenic Water Regulation Modules into a Land Surface Model. J. Hydrometeorol. 2012, 13, 255–269. [Google Scholar] [CrossRef] [Green Version]
  45. Koirala, S.; Yeh, P.J.-F.; Hirabayashi, Y.; Kanae, S.; Oki, T. Global-scale land surface hydrologic modeling with the representation of water table dynamics. J. Geophys. Res. Atmos. 2014, 119, 75–89. [Google Scholar] [CrossRef]
  46. Oki, T.; Sud, Y.C. Design of Total Runoff Integrating Pathways (TRIP)—A Global River Channel Network. Earth Interact. 1998, 2, 1–37. [Google Scholar] [CrossRef]
  47. Hanasaki, N.; Kanae, S.; Oki, T. A reservoir operation scheme for global river routing models. J. Hydrol. 2006, 327, 22–41. [Google Scholar] [CrossRef]
  48. Koster, R.D.; Suarez, M.J. Impact of land surface initialization on seasonal precipitation and temperature prediction. J. Hydrometeorol. 2003, 4, 408–423. [Google Scholar] [CrossRef]
  49. Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-Year Reanalysis Project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef] [Green Version]
  50. Pokhrel, Y.N.; Hanasaki, N.; Yeh, P.J.-F.; Yamada, T.J.; Kanae, S.; Oki, T. Model estimates of sea-level change due to anthropogenic impacts on terrestrial water storage. Nat. Geosci. 2012, 5, 389–392. [Google Scholar] [CrossRef]
  51. Döll, P.; Siebert, S. Global modeling of irrigation water requirements. Water Resour. Res. 2002, 38, 8-1–8-10. [Google Scholar] [CrossRef]
  52. Hanasaki, N.; Inuzuka, T.; Kanae, S.; Oki, T. An estimation of global virtual water flow and sources of water withdrawal for major crops and livestock products using a global hydrological model. J. Hydrol. 2010, 384, 232–244. [Google Scholar] [CrossRef]
  53. Siebert, S.; Burke, J.; Faures, J.M.; Frenken, K.; Hoogeveen, J.; Döll, P.; Portmann, F.T. Groundwater use for irrigation—A global inventory. Hydrol. Earth Syst. Sci. 2010, 14, 1863–1880. [Google Scholar] [CrossRef] [Green Version]
  54. Wisser, D.; Fekete, B.M.; Vörösmarty, C.J.; Schumann, A.H. Reconstructing 20th century global hydrography: A contribution to the Global Terrestrial Network-Hydrology (GTN-H). Hydrol. Earth Syst. Sci. 2010, 14, 1–24. [Google Scholar] [CrossRef] [Green Version]
  55. Döll, P.; Hoffmann-Dobrev, H.; Portmann, F.T.; Siebert, S.; Eicker, A.; Rodell, M.; Strassberg, G.; Scanlon, B.R. Impact of water withdrawals from groundwater and surface water on continental water storage variations. J. Geodyn. 2012, 59–60, 143–156. [Google Scholar] [CrossRef]
  56. Shah, T.; Model, D.; Sakthivadivel, D.; Seckler, D. The Global Groundwater Situation: Overview of Opportunities and Challenges; International Water Management Institute: Colombo, Sri Lanka, 2000. [Google Scholar]
  57. Giordano, M. Global Groundwater? Issues and Solutions. Annu. Rev. Environ. Resour. 2009, 34, 153–178. [Google Scholar] [CrossRef]
  58. Onogi, K.; Tsutsui, J.; Koide, H.; Sakamoto, M.; Kobayashi, S.; Hatsushika, H.; Matsumoto, T.; Yamazaki, N.; Kamahori, H.; Takahashi, K.; et al. The JRA-25 Reanalysis. J. Meteorol. Soc. Jpn. Ser. II 2007, 85, 369–432. [Google Scholar] [CrossRef] [Green Version]
Atmosphere 10 00725 g001 550
Figure 1. Spatial distribution of the irrigation water demand and groundwater withdrawals from AGCM–Human (a and c) and Offline–Human (b and d) simulations, respectively. Results are shown in mm/day and are averaged over the boreal summer (June–August: JJA) during the years 1998 to 2010.
Figure 1. Spatial distribution of the irrigation water demand and groundwater withdrawals from AGCM–Human (a and c) and Offline–Human (b and d) simulations, respectively. Results are shown in mm/day and are averaged over the boreal summer (June–August: JJA) during the years 1998 to 2010.
Atmosphere 10 00725 g001
Atmosphere 10 00725 g002 550
Figure 2. Comparison of simulated monthly terrestrial water storage anomalies (mm) averaged over the region overlying the High Plains aquifer with the observations from the United States Geological Survey (USGS). Blue and red lines represent the Offline–Human and AGCM–Human simulations, respectively. The USGS observations (stars), which are reported once every year in spring, are plotted in the month of February. The gray shading denotes ±1 standard deviation from the mean for ten ensemble simulations.
Figure 2. Comparison of simulated monthly terrestrial water storage anomalies (mm) averaged over the region overlying the High Plains aquifer with the observations from the United States Geological Survey (USGS). Blue and red lines represent the Offline–Human and AGCM–Human simulations, respectively. The USGS observations (stars), which are reported once every year in spring, are plotted in the month of February. The gray shading denotes ±1 standard deviation from the mean for ten ensemble simulations.
Atmosphere 10 00725 g002
Atmosphere 10 00725 g003 550
Figure 3. Differences in JJA near surface air temperature between AGCM-Human and AGCM-ORG simulations as a function of JJA irrigation amount. The relationship is separated into points with precipitation greater than the median (blue crosses) and with precipitation less than the median (red crosses) following Sacks et al. [23]. Blue and red solid lines denote regression lines for large (blue crosses) and small (red crosses) precipitation grid cells, respectively; the dashed lines with the same colors show the results from Sacks et al. [23].
Figure 3. Differences in JJA near surface air temperature between AGCM-Human and AGCM-ORG simulations as a function of JJA irrigation amount. The relationship is separated into points with precipitation greater than the median (blue crosses) and with precipitation less than the median (red crosses) following Sacks et al. [23]. Blue and red solid lines denote regression lines for large (blue crosses) and small (red crosses) precipitation grid cells, respectively; the dashed lines with the same colors show the results from Sacks et al. [23].
Atmosphere 10 00725 g003
Atmosphere 10 00725 g004 550
Figure 4. The spread of near-surface air temperatures (K) among 10 ensemble members for the periods from Days 16–39 from the initial date of the forecast simulations. The same as near-surface air temperature but for surface soil moisture (mm) is plotted by contour lines. The spread was averaged between 1986 and 1995. (a) AGCM–Human–RaLI, (b) AGCM–ORG–ReLI, and (c) AGCM–Human–ReLI. The three areas with black solid lines were used to discuss the spread of surface soil moisture.
Figure 4. The spread of near-surface air temperatures (K) among 10 ensemble members for the periods from Days 16–39 from the initial date of the forecast simulations. The same as near-surface air temperature but for surface soil moisture (mm) is plotted by contour lines. The spread was averaged between 1986 and 1995. (a) AGCM–Human–RaLI, (b) AGCM–ORG–ReLI, and (c) AGCM–Human–ReLI. The three areas with black solid lines were used to discuss the spread of surface soil moisture.
Atmosphere 10 00725 g004
Atmosphere 10 00725 g005 550
Figure 5. Forecast skill of near-surface air temperature and sea level pressure during the period from Days 16–39 from the initial date of the forecast simulations for (a), (c) AGCM–ORG–ReLI and (b), (d) AGCM–Human–ReLI between 1986 and 1995. Areas with single (double) diagonal lines were statistically significant at the 95% (99%) level upon performing a Student’s t-test.
Figure 5. Forecast skill of near-surface air temperature and sea level pressure during the period from Days 16–39 from the initial date of the forecast simulations for (a), (c) AGCM–ORG–ReLI and (b), (d) AGCM–Human–ReLI between 1986 and 1995. Areas with single (double) diagonal lines were statistically significant at the 95% (99%) level upon performing a Student’s t-test.
Atmosphere 10 00725 g005
Table
Table 1. Summary of experimental design. (HiGW-MAT: Human Impacts and Groundwater representation in the Minimal Advanced Treatment of Surface Interaction and RunOff model; MIROC: Model for Interdisciplinary Research on Climate; AGCM-ORG: Atmospheric General Circulation Model - Original).
Table 1. Summary of experimental design. (HiGW-MAT: Human Impacts and Groundwater representation in the Minimal Advanced Treatment of Surface Interaction and RunOff model; MIROC: Model for Interdisciplinary Research on Climate; AGCM-ORG: Atmospheric General Circulation Model - Original).
Experiment NameModelHuman ImpactsInitialization
Climatology simulations
Offline-HumanHiGW-MATONN/A
AGCM-ORGMIROCOFFACGM Climatology
AGCM-HumanMIROC-HiGW-MATONAGCM Climatology
Forecast simulations
AGCM-ORG-ReLIMIROCOFFOffline-Human
AGCM-Human-ReLIMIROC-HiGW-MATONOffline-Human
AGCM-Human-RaLIMIROC-HiGW-MATONRandom
Table
Table 2. Comparison of AGCM–Human simulated total irrigation water demand (actual use) and withdrawal (water withdrawn from source) with various previous estimates, including reported statistics and offline model results.
Table 2. Comparison of AGCM–Human simulated total irrigation water demand (actual use) and withdrawal (water withdrawn from source) with various previous estimates, including reported statistics and offline model results.
ReferenceYearIrrigation Water Demand (km3/year)Irrigation Water Withdrawal (km3/year)
This study1998–2010
1998–2002		1504 ± 14
1513 ± 22		3595 ± 36
3611 ± 57
FAO2000-2660
Döll and Siebert [51]1971–200012573256
Hanasaki et al. [52]200015983755
Siebert et al. [53]20001277-
Wisser et al. [54]2002-2997
Döll et al. [55]1998–200212313185
Pokhrel et al. [44]1998–20021021 ± 552462 ± 130
Wada et al. [37]200010982572
Pokhrel et al. [38]1998–20021238 ± 673028 ± 171
Table
Table 3. Same as Table 2 but for groundwater pumping.
Table 3. Same as Table 2 but for groundwater pumping.
ReferenceYearGroundwater Withdrawal (km3/year)
This study1998–2010
1998–2002		364 ± 13
373 ± 33
Shah et al. [56]Contemporary750–800
Giordano [57]-658
Döll et al. [51]1998–2002571
Pokhrel et al. [38]1998–2002570 ± 61

Share and Cite

MDPI and ACS Style

Yamada, T.J.; Pokhrel, Y. Effect of Human-Induced Land Disturbance on Subseasonal Predictability of Near-Surface Variables Using an Atmospheric General Circulation Model. Atmosphere 2019, 10, 725. https://doi.org/10.3390/atmos10110725

AMA Style

Yamada TJ, Pokhrel Y. Effect of Human-Induced Land Disturbance on Subseasonal Predictability of Near-Surface Variables Using an Atmospheric General Circulation Model. Atmosphere. 2019; 10(11):725. https://doi.org/10.3390/atmos10110725

Chicago/Turabian Style

Yamada, Tomohito J., and Yadu Pokhrel. 2019. "Effect of Human-Induced Land Disturbance on Subseasonal Predictability of Near-Surface Variables Using an Atmospheric General Circulation Model" Atmosphere 10, no. 11: 725. https://doi.org/10.3390/atmos10110725

APA Style

Yamada, T. J., & Pokhrel, Y. (2019). Effect of Human-Induced Land Disturbance on Subseasonal Predictability of Near-Surface Variables Using an Atmospheric General Circulation Model. Atmosphere, 10(11), 725. https://doi.org/10.3390/atmos10110725

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop