Comparison of NMC and Ensemble-Based Climatological Background-Error Covariances in an Operational Limited-Area Data Assimilation System
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model
2.2. Methods
2.2.1. NMC Method
2.2.2. Ensemble Method
3. Results
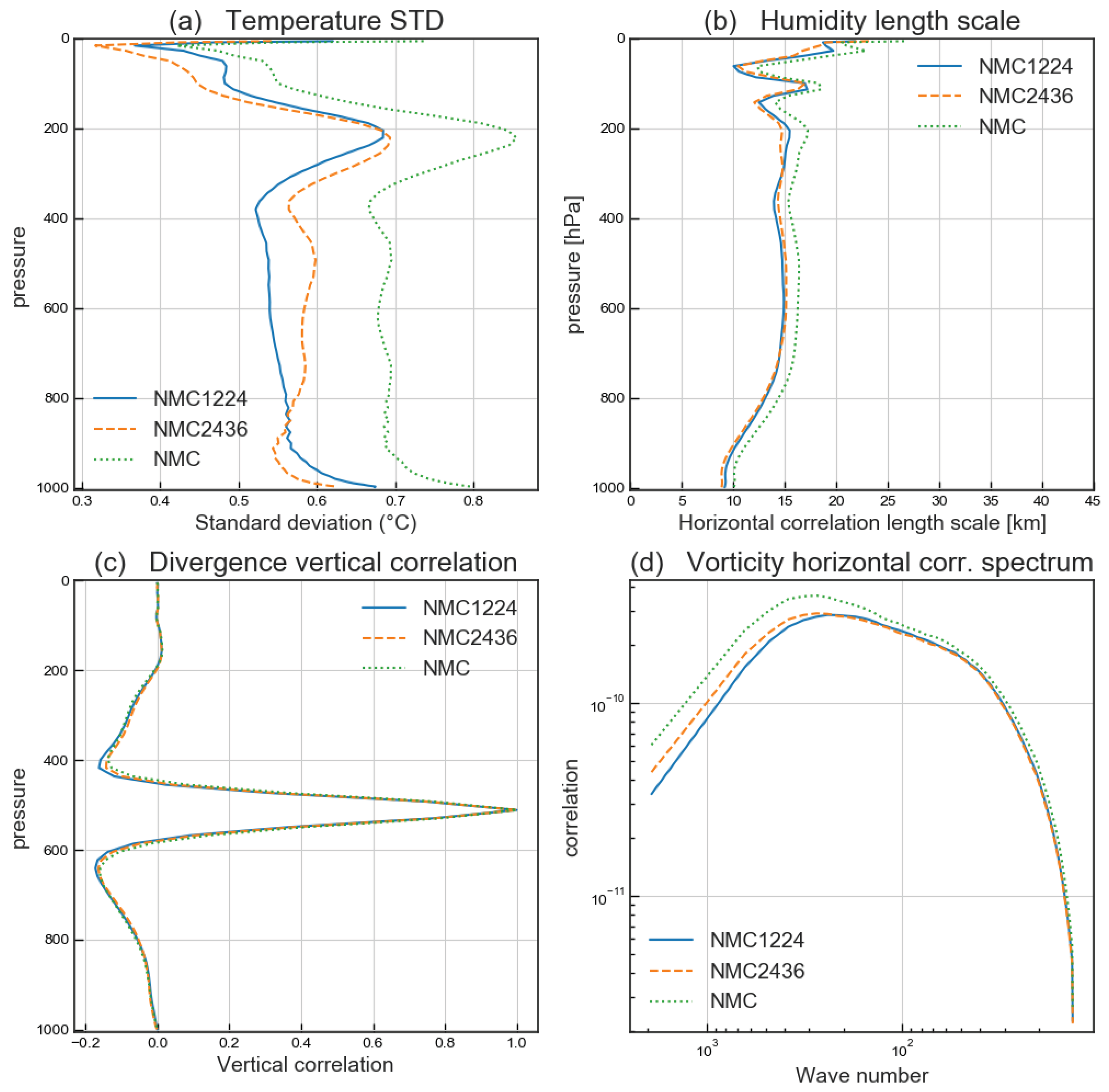
3.1. Diagnostic Comparison
3.1.1. Geographical Distribution of the Standard Deviations
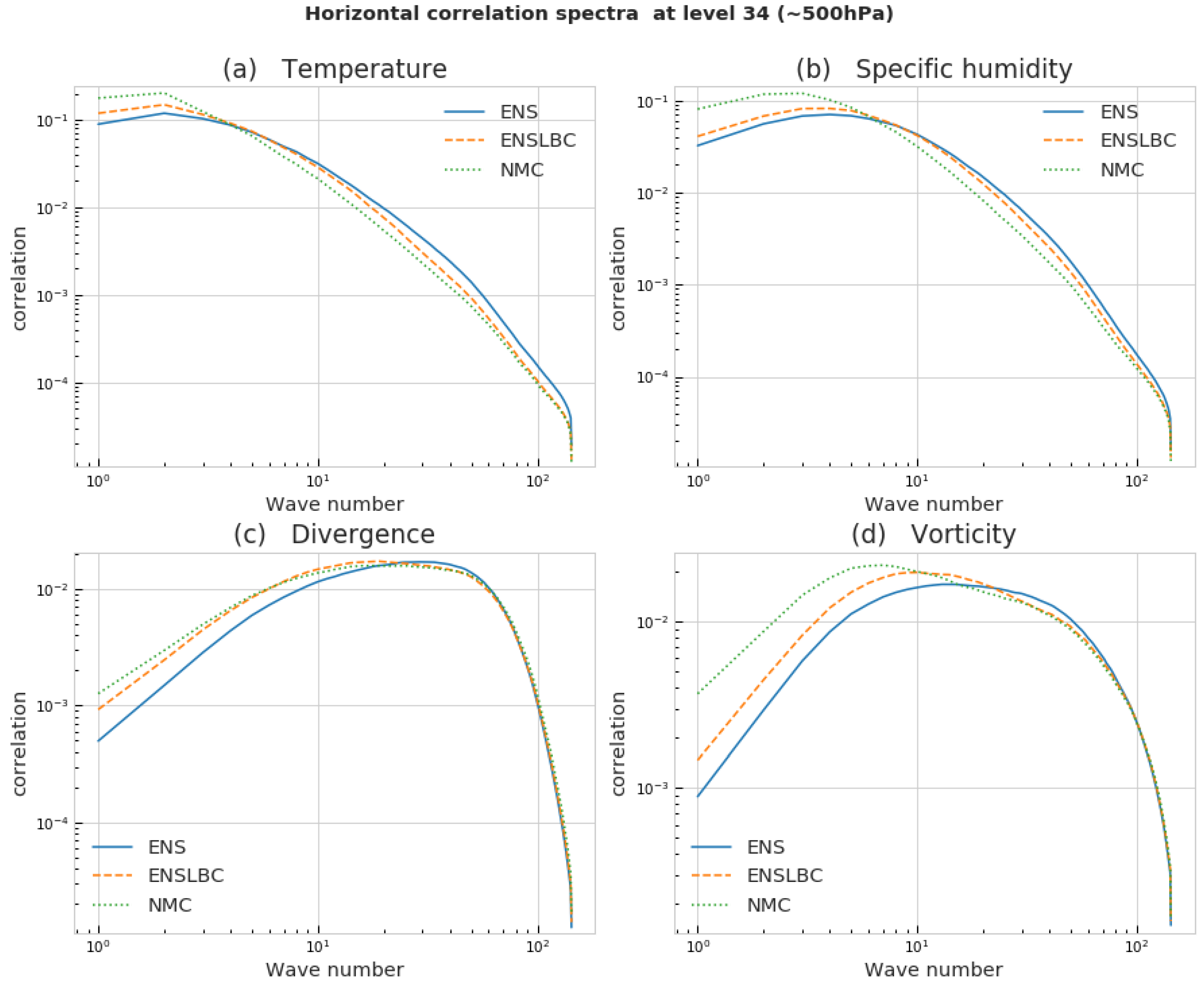
3.1.2. Horizontal Spectral Densities
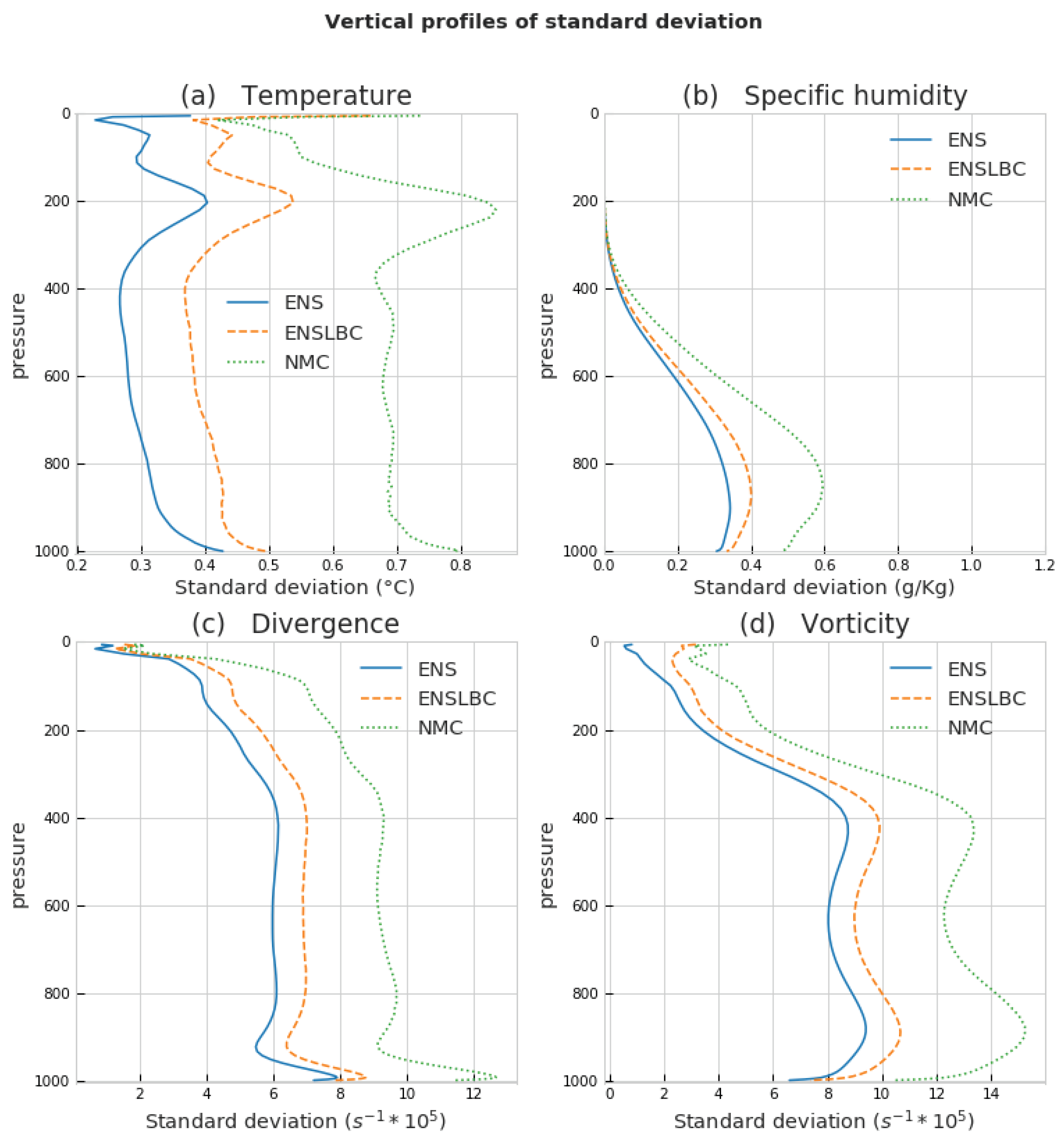
3.1.3. Standard Deviation
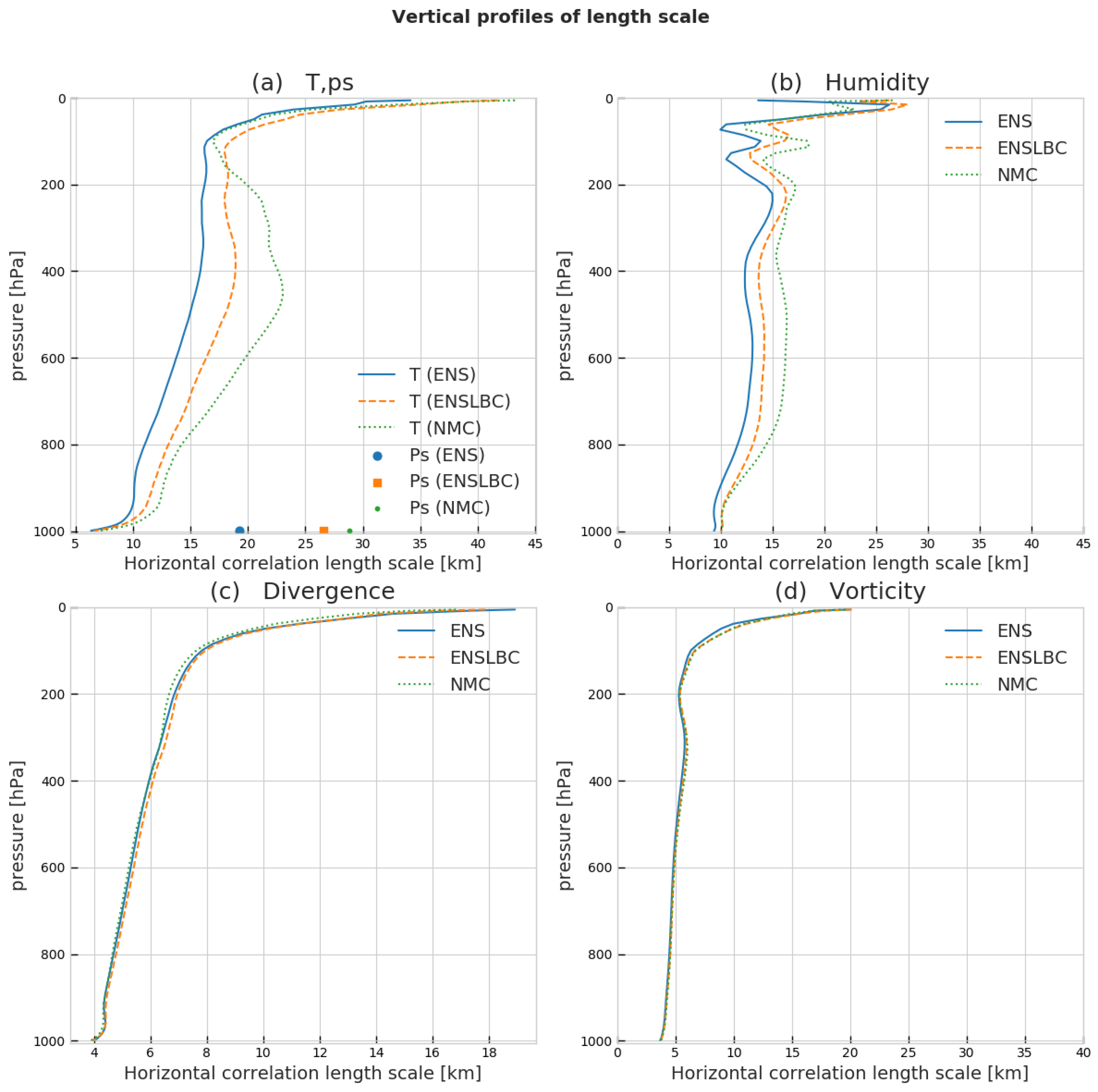
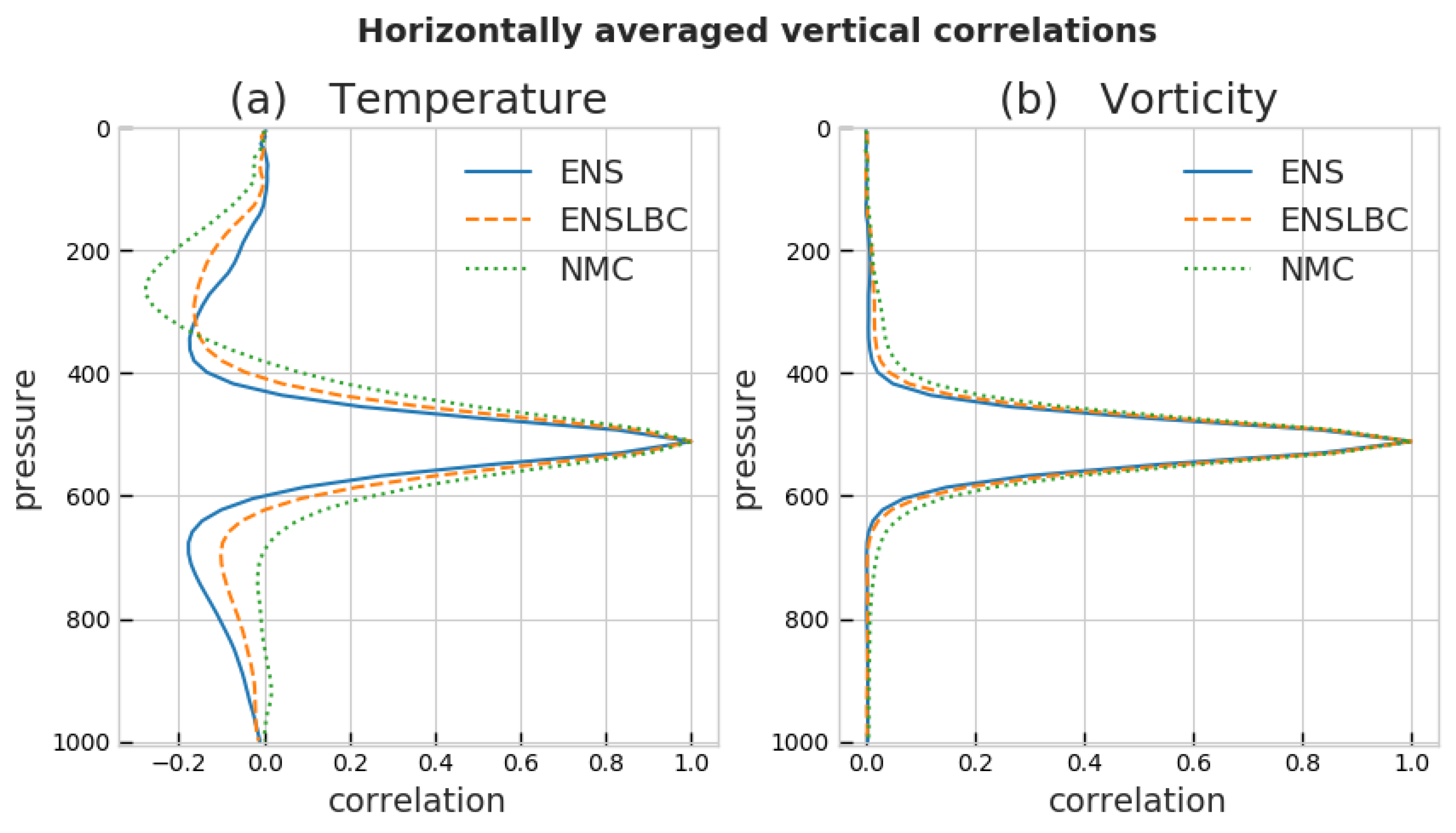
3.1.4. Horizontal and Vertical Correlations
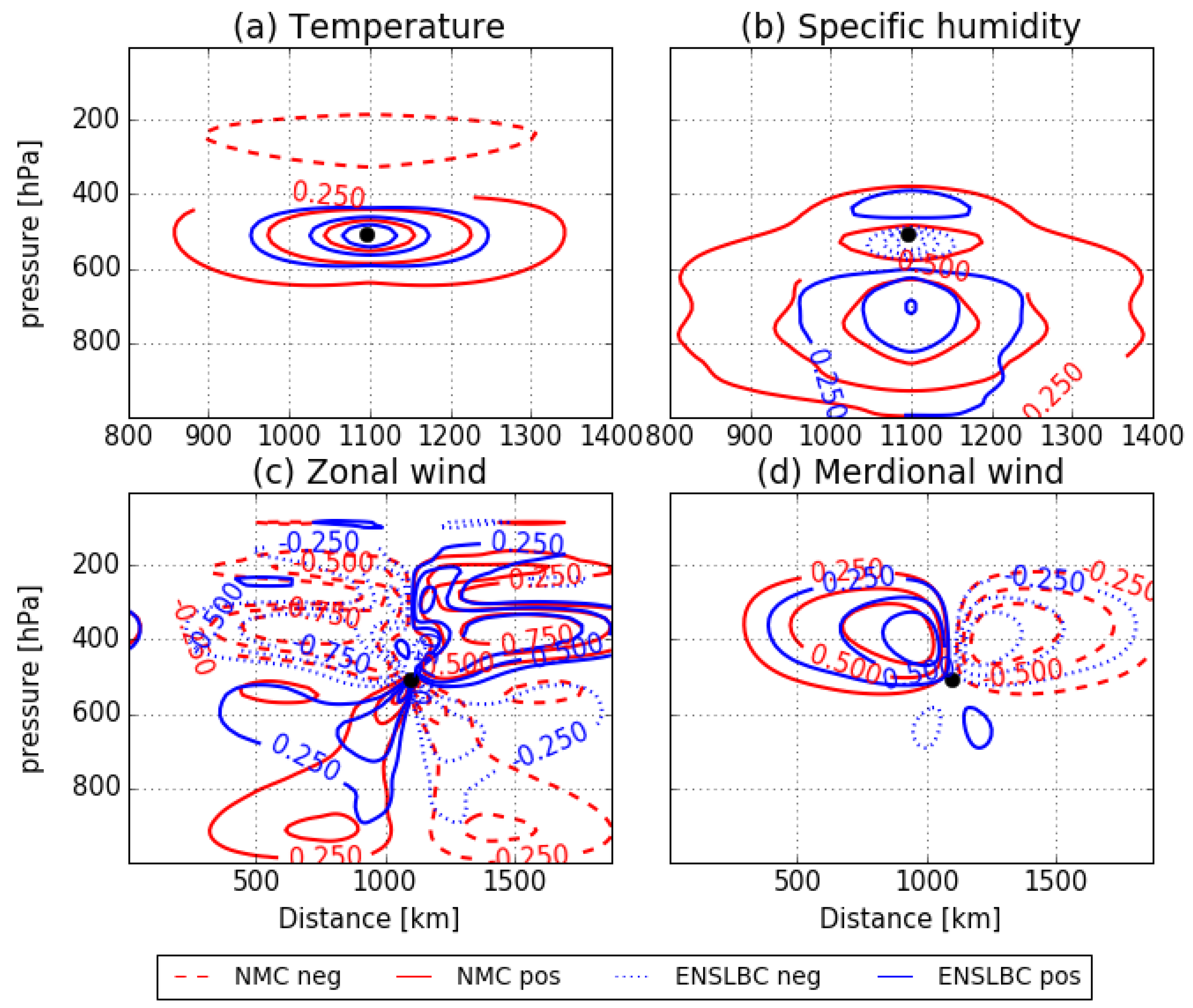
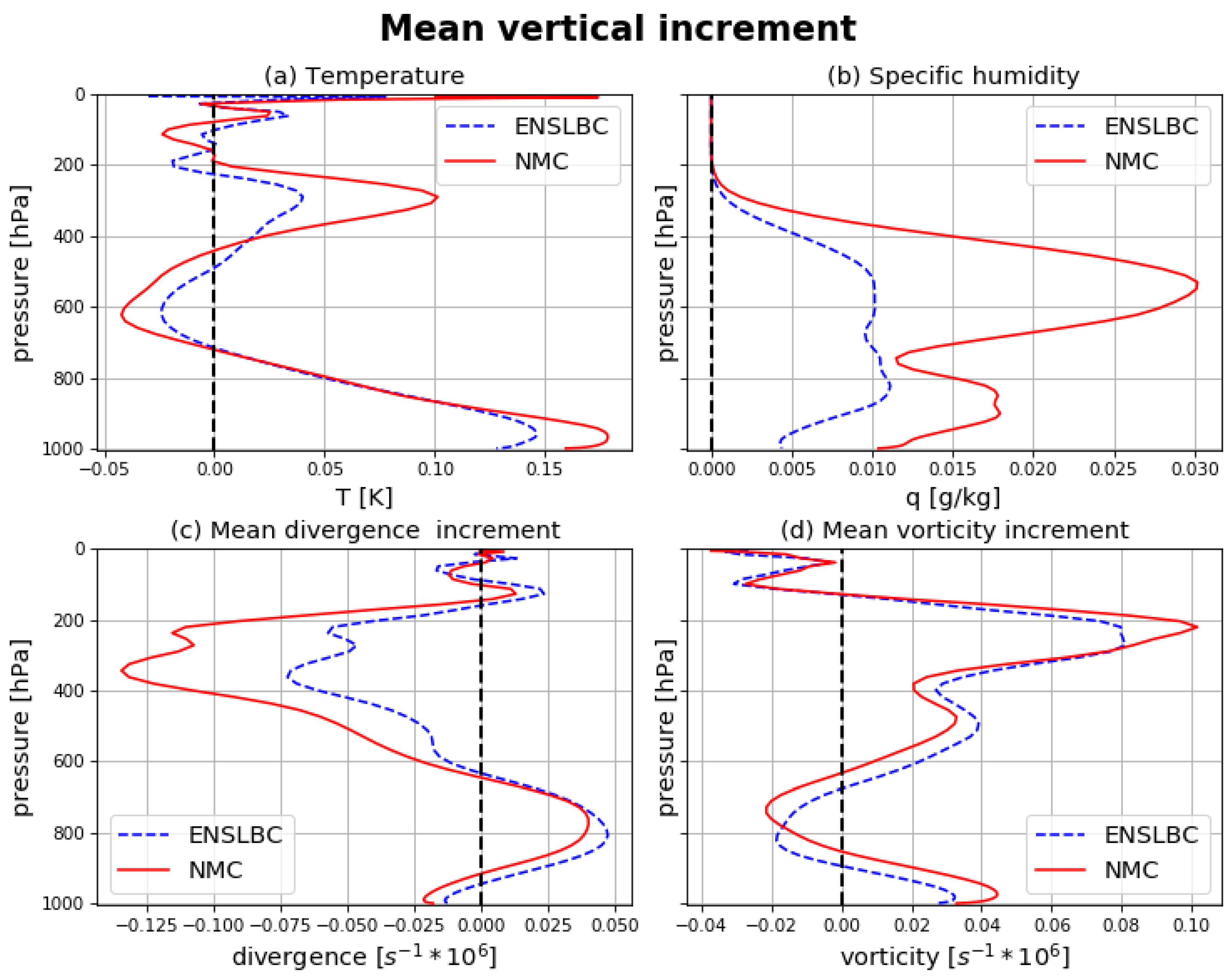
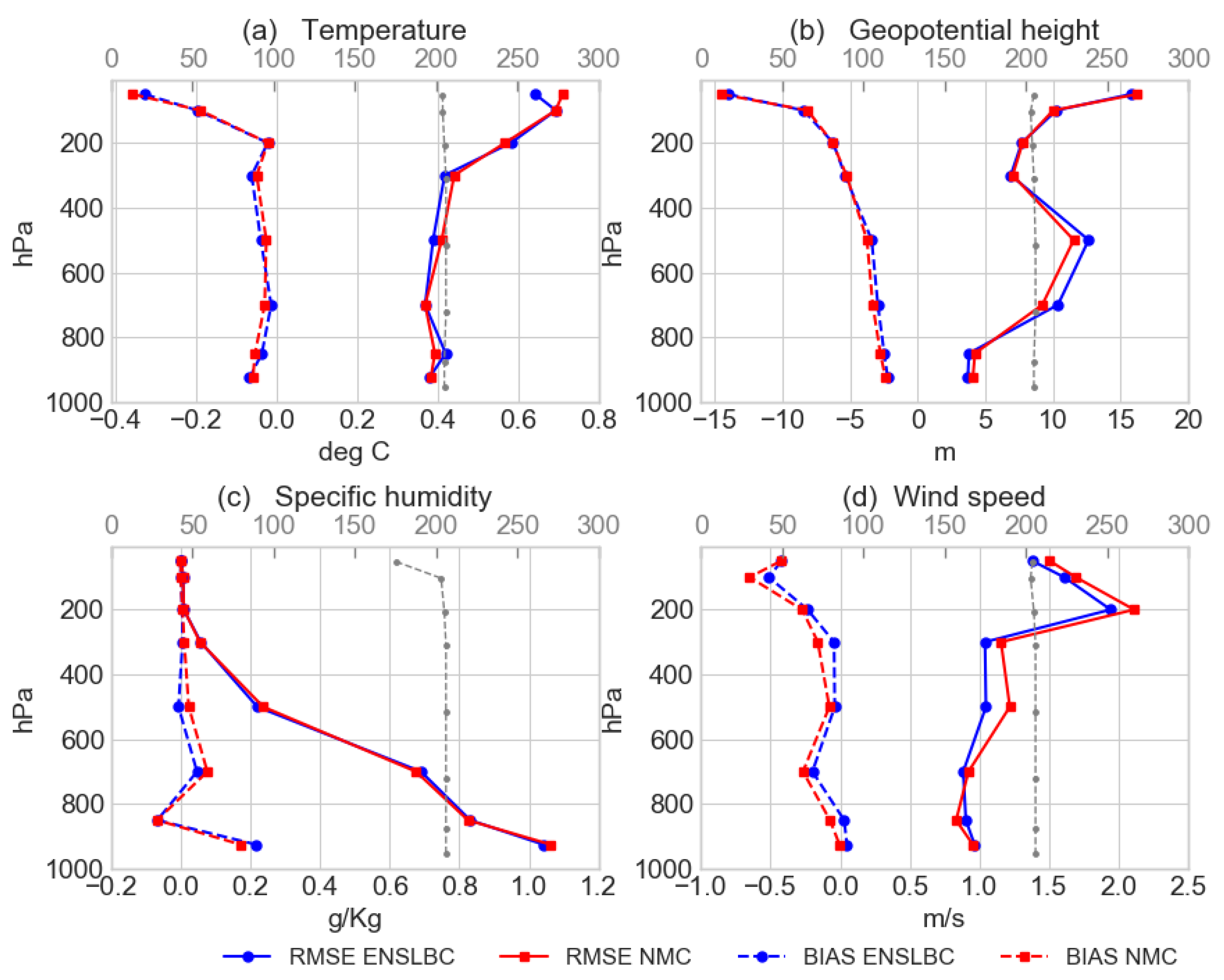
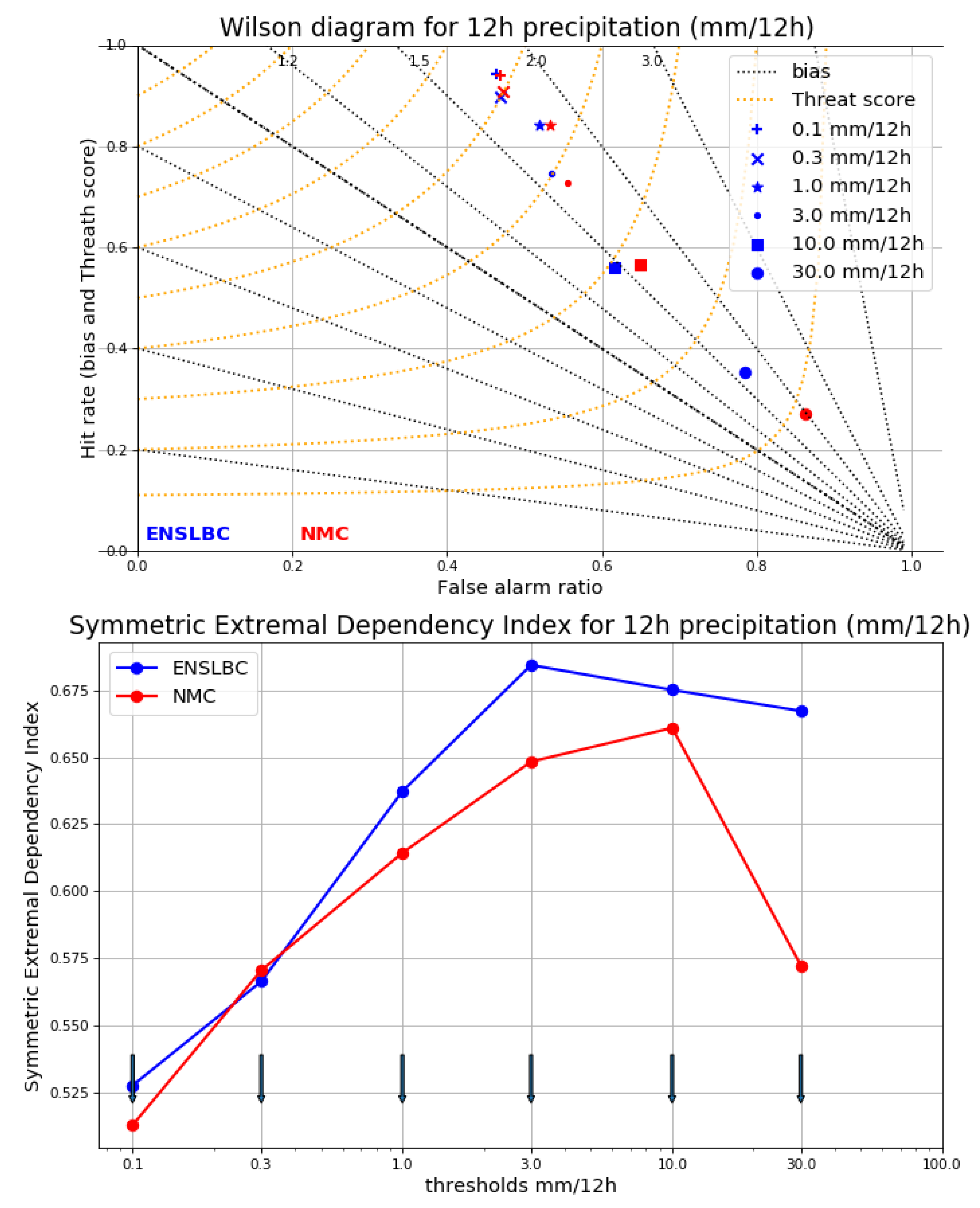
3.2. Impact on the Analysis and Forecast
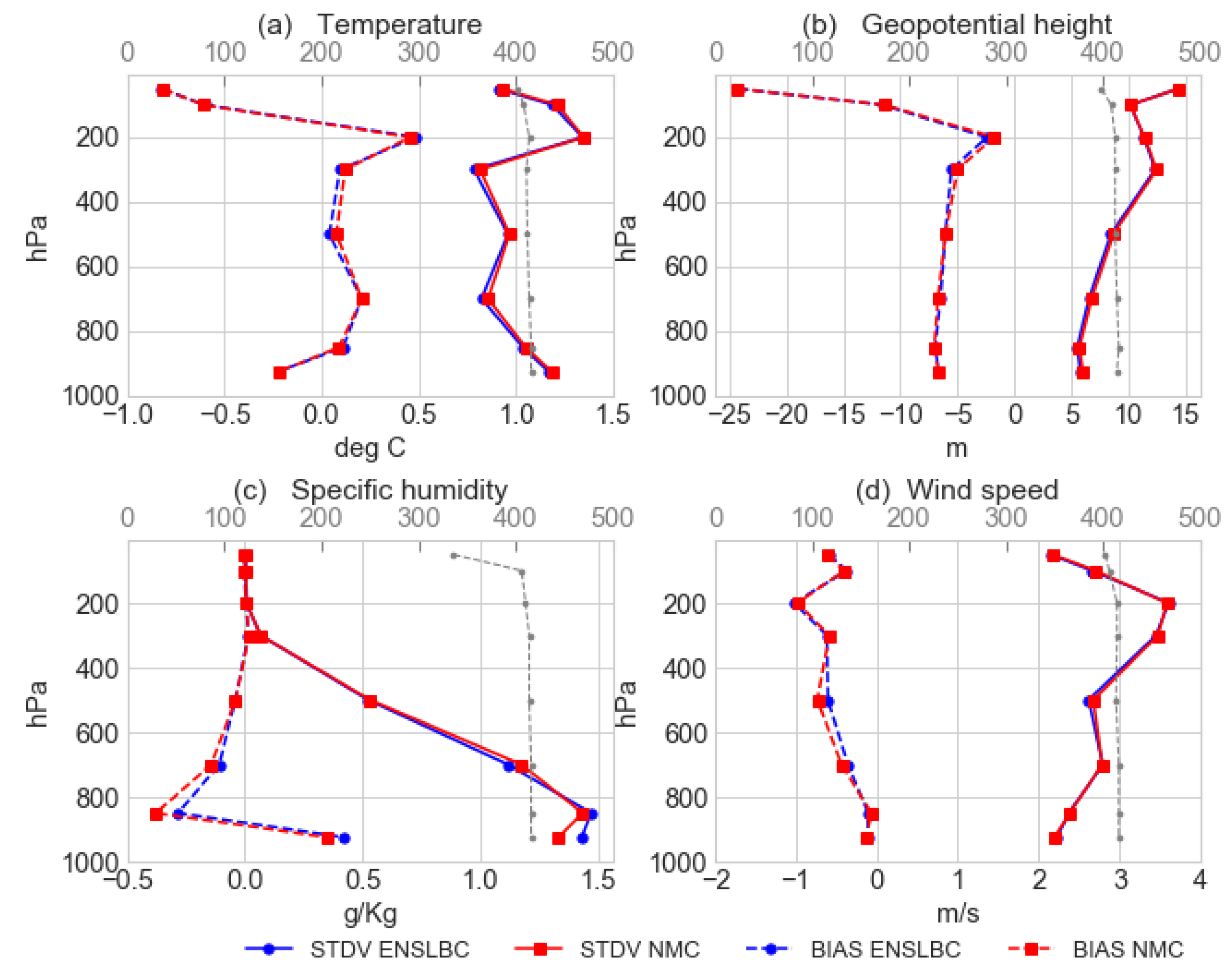
3.2.1. Impact on the Analysis
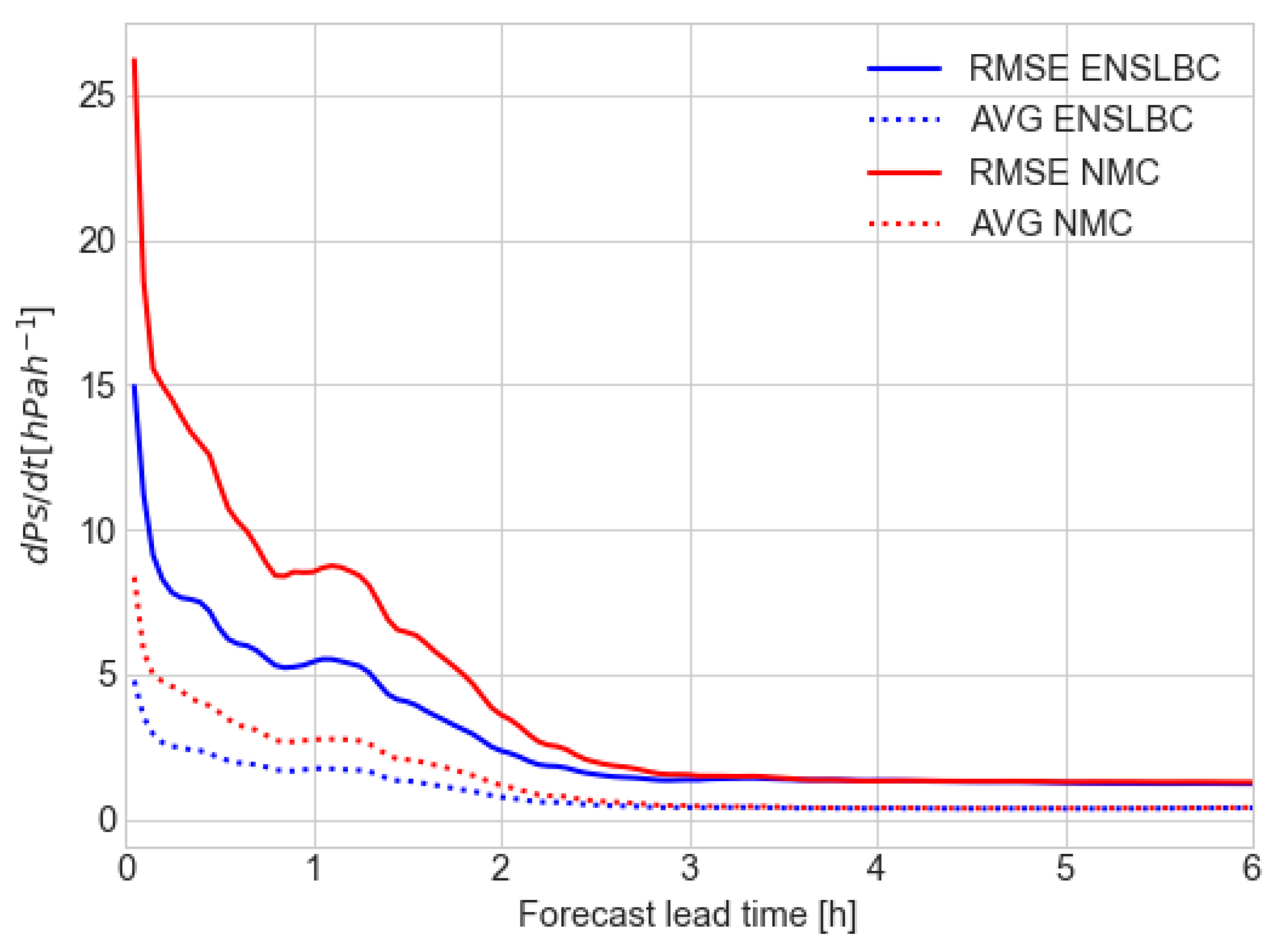
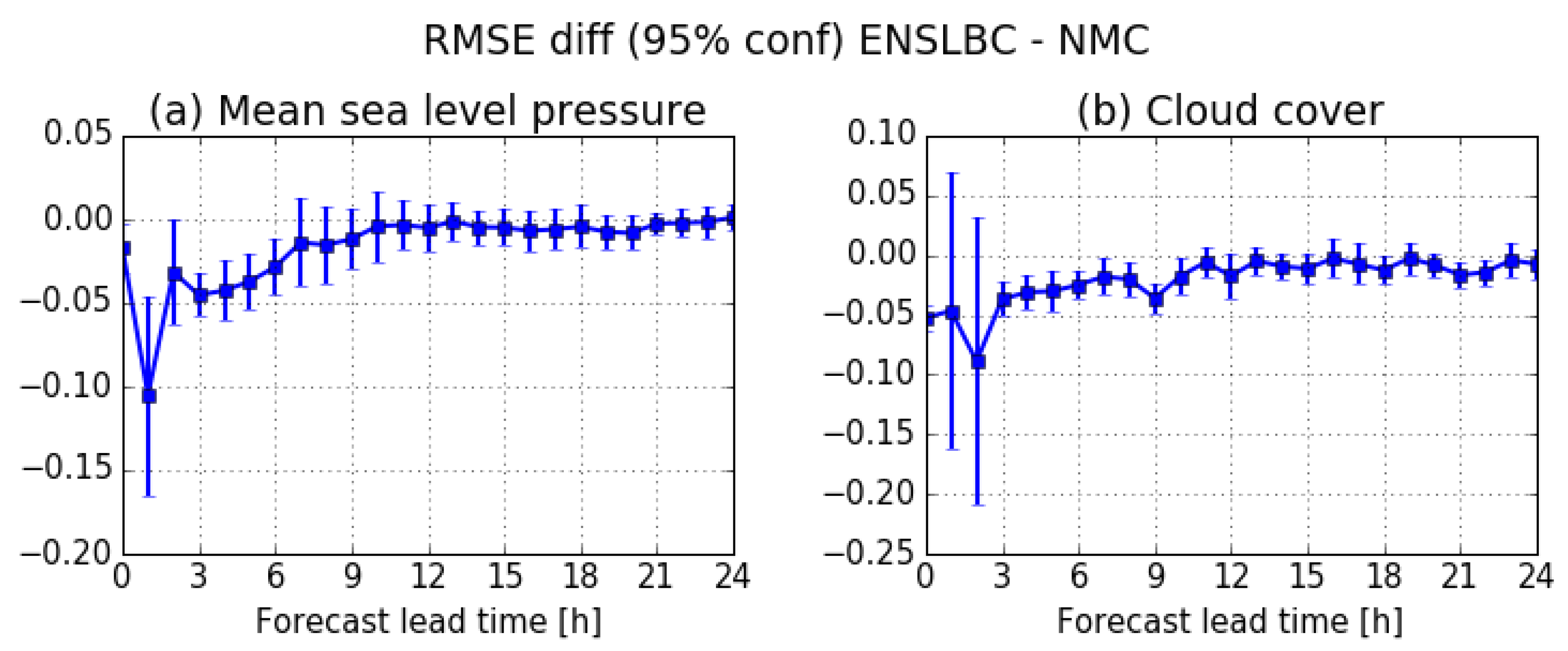
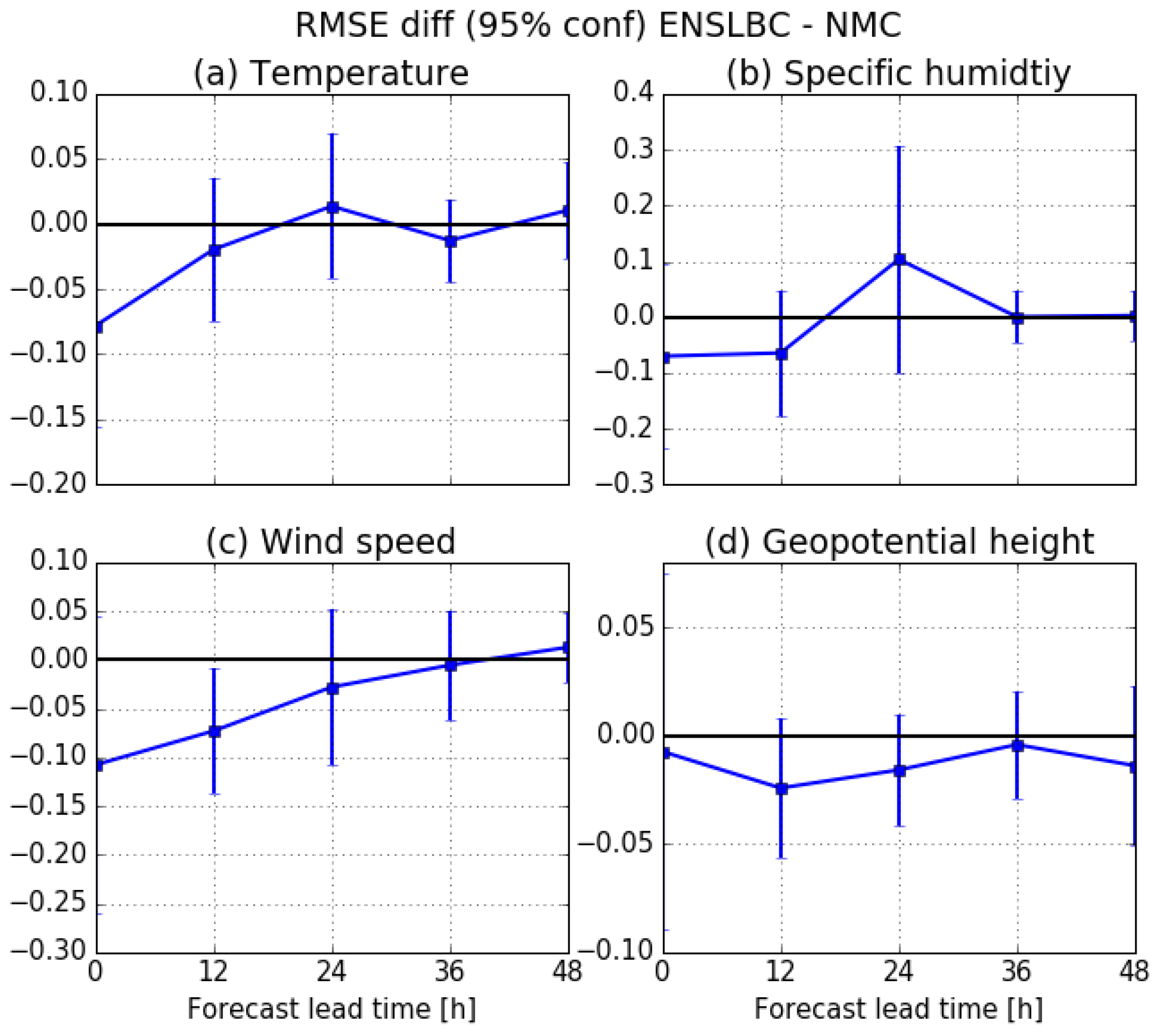
3.2.2. Impact on The Forecast Quality
4. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kalnay, E. Atmospheric Modeling, Data Assimilation and Predictability; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Bannister, R. A review of operational methods of variational and ensemble-variational data assimilation. Q. J. R. Meteorol. Soc. 2017, 143, 607–633. [Google Scholar] [CrossRef]
- Gustafsson, N.; Janjić, T.; Schraff, C.; Leuenberger, D.; Weissmann, M.; Reich, H.; Brousseau, P.; Montmerle, T.; Wattrelot, E.; Bučánek, A.; et al. Survey of data assimilation methods for convective-scale numerical weather prediction at operational centres. Q. J. R. Meteorol. Soc. 2018, 144, 1218–1256. [Google Scholar] [CrossRef]
- Parrish, D.F.; Derber, J.C. The National Meteorological Center’s spectral statistical-interpolation analysis system. Mon. Weather Rev. 1992, 120, 1747–1763. [Google Scholar] [CrossRef]
- Fisher, M. Background error covariance modelling. In Proceedings of the Seminar on Recent Development in Data Assimilation for Atmosphere and Ocean, Reading, UK, 8–12 September 2003; pp. 45–63. [Google Scholar]
- Errico, R.M.; Privé, N.C.; Gu, W. Use of an OSSE to evaluate background-error covariances estimated by the NMC method. Q. J. R. Meteorol. Soc. 2015, 141, 611–618. [Google Scholar] [CrossRef]
- Sun, J.; Wang, H.; Tong, W.; Zhang, Y.; Lin, C.Y.; Xu, D. Comparison of the impacts of momentum control variables on high-resolution variational data assimilation and precipitation forecasting. Mon. Weather Rev. 2016, 144, 149–169. [Google Scholar] [CrossRef]
- Xu, D.; Shen, F.; Min, J. Effect of Adding Hydrometeor Mixing Ratios Control Variables on Assimilating Radar Observations for the Analysis and Forecast of a Typhoon. Atmosphere 2019, 10, 415. [Google Scholar] [CrossRef]
- Široká, M.; Fischer, C.; Cassé, V.; Brožkova, R.; Geleyn, J.F. The definition of mesoscale selective forecast error covariances for a limited area variational analysis. Meteorol. Atmos. Phys. 2003, 82, 227–244. [Google Scholar] [CrossRef]
- Pereira, M.B.; Berre, L. The use of an ensemble approach to study the background error covariances in a global NWP model. Mon. Weather Rev. 2006, 134, 2466–2489. [Google Scholar] [CrossRef]
- Buehner, M. Ensemble-derived stationary and flow-dependent background-error covariances: Evaluation in a quasi-operational NWP setting. Q. J. R. Meteorol. Soc. 2005, 131, 1013–1043. [Google Scholar] [CrossRef]
- Ştefănescu, S.E.; Berre, L.; Pereira, M.B. The evolution of dispersion spectra and the evaluation of model differences in an ensemble estimation of error statistics for a limited-area analysis. Mon. Weather Rev. 2006, 134, 3456–3478. [Google Scholar] [CrossRef]
- Berre, L.; Ecaterina Ştefănescu, S.; Belo Pereira, M. The representation of the analysis effect in three error simulation techniques. Tellus A 2006, 58, 196–209. [Google Scholar] [CrossRef]
- Storto, A.; Randriamampianina, R. Ensemble variational assimilation for the representation of background error covariances in a high-latitude regional model. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Fischer, C.; Montmerle, T.; Berre, L.; Auger, L.; Ştefănescu, S.E. An overview of the variational assimilation in the ALADIN/France numerical weather-prediction system. Q. J. R. Meteorol. Soc. 2005, 131, 3477–3492. [Google Scholar] [CrossRef]
- Brousseau, P.; Berre, L.; Bouttier, F.; Desroziers, G. Background-error covariances for a convective-scale data-assimilation system: AROME–France 3D-Var. Q. J. R. Meteorol. Soc. 2011, 137, 409–422. [Google Scholar] [CrossRef]
- Berre, L.; Monteiro, M.; Pires, C. An impact study of updating background error covariances in the ALADIN-France data assimilation system. J. Geophys. Res. Atmos. 2013, 118, 11–075. [Google Scholar] [CrossRef]
- Bučánek, A.; Brožková, R. Background error covariances for a BlendVar assimilation system. Tellus A Dyn. Meteorol. Oceanogr. 2017, 69, 1355718. [Google Scholar] [CrossRef]
- Monteiro, M.; Berre, L. A diagnostic study of time variations of regionally averaged background error covariances. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Ménétrier, B.; Montmerle, T.; Berre, L.; Michel, Y. Estimation and diagnosis of heterogeneous flow-dependent background-error covariances at the convective scale using either large or small ensembles. Q. J. R. Meteorol. Soc. 2014, 140, 2050–2061. [Google Scholar] [CrossRef]
- Buehner, M.; Gauthier, P.; Liu, Z. Evaluation of new estimates of background-and observation-error covariances for variational assimilation. Q. J. R. Meteorol. Soc. 2005, 131, 3373–3383. [Google Scholar] [CrossRef]
- Hacker, J.; Draper, C.; Madaus, L. Challenges and Opportunities for Data Assimilation in Mountainous Environments. Atmosphere 2018, 9, 127. [Google Scholar] [CrossRef]
- ALADIN International Team. The ALADIN project: Mesoscale modelling seen as a basic tool for weather forecasting and atmospheric research. WMO Bull. 1997, 46, 317–324. [Google Scholar]
- Termonia, P.; Fischer, C.; Bazile, E.; Bouyssel, F.; Brožková, R.; Bénard, P.; Bochenek, B.; Degrauwe, D.; Derkova, M.; El Khatib, R.; et al. The ALADIN System and its Canonical Model Configurations AROME CY41T1 and ALARO CY40T1. Geosci. Model Dev. Discuss. 2017, 2017, 1–45. [Google Scholar] [CrossRef]
- Gerard, L.; Piriou, J.M.; Brožková, R.; Geleyn, J.F.; Banciu, D. Cloud and precipitation parameterization in a meso-gamma-scale operational weather prediction model. Mon. Weather Rev. 2009, 137, 3960–3977. [Google Scholar] [CrossRef]
- Geleyn, J. Use of a modified Richardson number for parameterizing the effect of shallow convection. J. Meteorol. Soc. Jpn. Ser. II 1986, 64, 141–149. [Google Scholar] [CrossRef]
- Tudor, M.; Ivatek-Šahdan, S.; Stanešić, A.; Horvath, K.; Hrastinski, M.; Odak Plenković, I.; Bajić, A.; Kovačić, T. Changes in the ALADIN operational suite in Croatia in the period 2011-2015. Hrvatski Meteorološki Časopis 2016, 50, 71–89. [Google Scholar]
- Stanešić, A. Assimilation system at DHMZ: Development and first verification results. Hrvatski Meteorološki Časopis 2011, 44, 3–17. [Google Scholar]
- Donlon, C.J.; Martin, M.; Stark, J.; Roberts-Jones, J.; Fiedler, E.; Wimmer, W. The operational sea surface temperature and sea ice analysis (OSTIA) system. Remote Sens. Environ. 2012, 116, 140–158. [Google Scholar] [CrossRef]
- Ivatek-Šahdan, S.; Stanešić, A.; Tudor, M.; Plenković, I.O.; Janeković, I. Impact of SST on heavy rainfall events on eastern Adriatic during SOP1 of HyMeX. Atmos. Res. 2018, 200, 36–59. [Google Scholar] [CrossRef]
- Bouttier, F.; Courtier, P. Data Assimilation Concepts and Methods March 1999; Meteorological Training Course Lecture Series; ECMWF: Reading, UK, 2002; p. 59. [Google Scholar]
- Berre, L. Estimation of synoptic and mesoscale forecast error covariances in a limited-area model. Mon. Weather Rev. 2000, 128, 644–667. [Google Scholar] [CrossRef]
- Buizza, R.; Leutbecher, M.; Isaksen, L. Potential use of an ensemble of analyses in the ECMWF Ensemble Prediction System. Q. J. R. Meteorol. Soc. 2008, 134, 2051–2066. [Google Scholar] [CrossRef]
- Hoskins, B.J.; McIntyre, M.; Robertson, A.W. On the use and significance of isentropic potential vorticity maps. Q. J. R. Meteorol. Soc. 1985, 111, 877–946. [Google Scholar] [CrossRef]
- Bölöni, G.; Horvath, K. Diagnosis and tuning of the background error statistics in a variational data assimilation system. Q. J. Hung. Meteorol. Serv. 2010, 114, 1–19. [Google Scholar]
- Desroziers, G.; Berre, L.; Chapnik, B.; Poli, P. Diagnosis of observation, background and analysis-error statistics in observation space. Q. J. R. Meteorol. Soc. 2005, 131, 3385–3396. [Google Scholar] [CrossRef]
- Roebber, P.J. Visualizing multiple measures of forecast quality. Weather Forecast. 2009, 24, 601–608. [Google Scholar] [CrossRef]
- Ferro, C.A.; Stephenson, D.B. Extremal dependence indices: Improved verification measures for deterministic forecasts of rare binary events. Weather Forecast. 2011, 26, 699–713. [Google Scholar] [CrossRef]
- Saltikoff, E.; Haase, G.; Delobbe, L.; Gaussiat, N.; Martet, M.; Idziorek, D.; Leijnse, H.; Novák, P.; Lukach, M.; Stephan, K. OPERA the Radar Project. Atmosphere 2019, 10, 320. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stanesic, A.; Horvath, K.; Keresturi, E. Comparison of NMC and Ensemble-Based Climatological Background-Error Covariances in an Operational Limited-Area Data Assimilation System. Atmosphere 2019, 10, 570. https://doi.org/10.3390/atmos10100570
Stanesic A, Horvath K, Keresturi E. Comparison of NMC and Ensemble-Based Climatological Background-Error Covariances in an Operational Limited-Area Data Assimilation System. Atmosphere. 2019; 10(10):570. https://doi.org/10.3390/atmos10100570
Chicago/Turabian StyleStanesic, Antonio, Kristian Horvath, and Endi Keresturi. 2019. "Comparison of NMC and Ensemble-Based Climatological Background-Error Covariances in an Operational Limited-Area Data Assimilation System" Atmosphere 10, no. 10: 570. https://doi.org/10.3390/atmos10100570
APA StyleStanesic, A., Horvath, K., & Keresturi, E. (2019). Comparison of NMC and Ensemble-Based Climatological Background-Error Covariances in an Operational Limited-Area Data Assimilation System. Atmosphere, 10(10), 570. https://doi.org/10.3390/atmos10100570




