Validation of HOAPS Rain Retrievals against OceanRAIN In-Situ Measurements over the Atlantic Ocean
Abstract
1. Introduction
2. Data
2.1. HOAPS
2.2. OceanRAIN
3. Methods
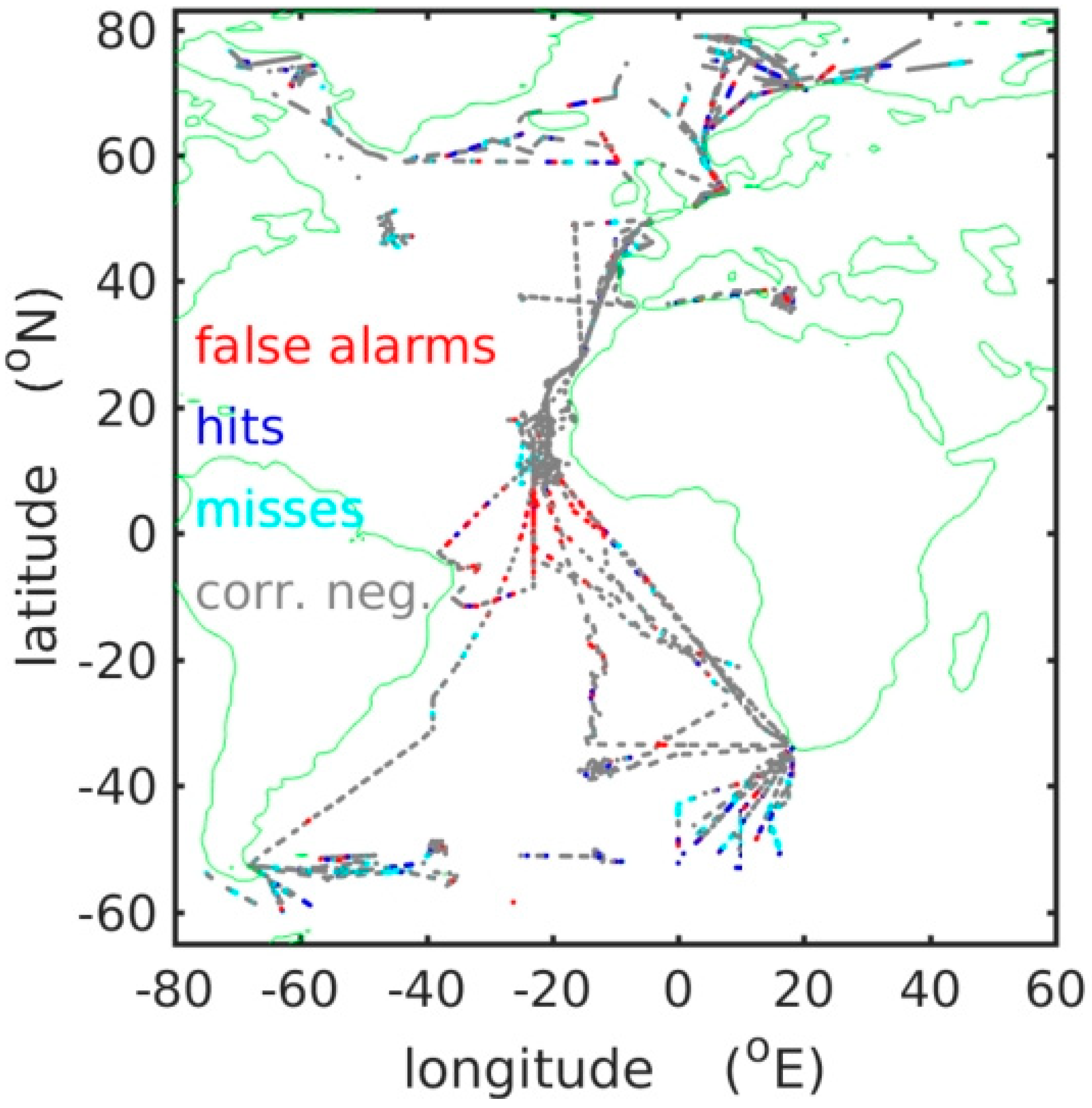
3.1. Collocation
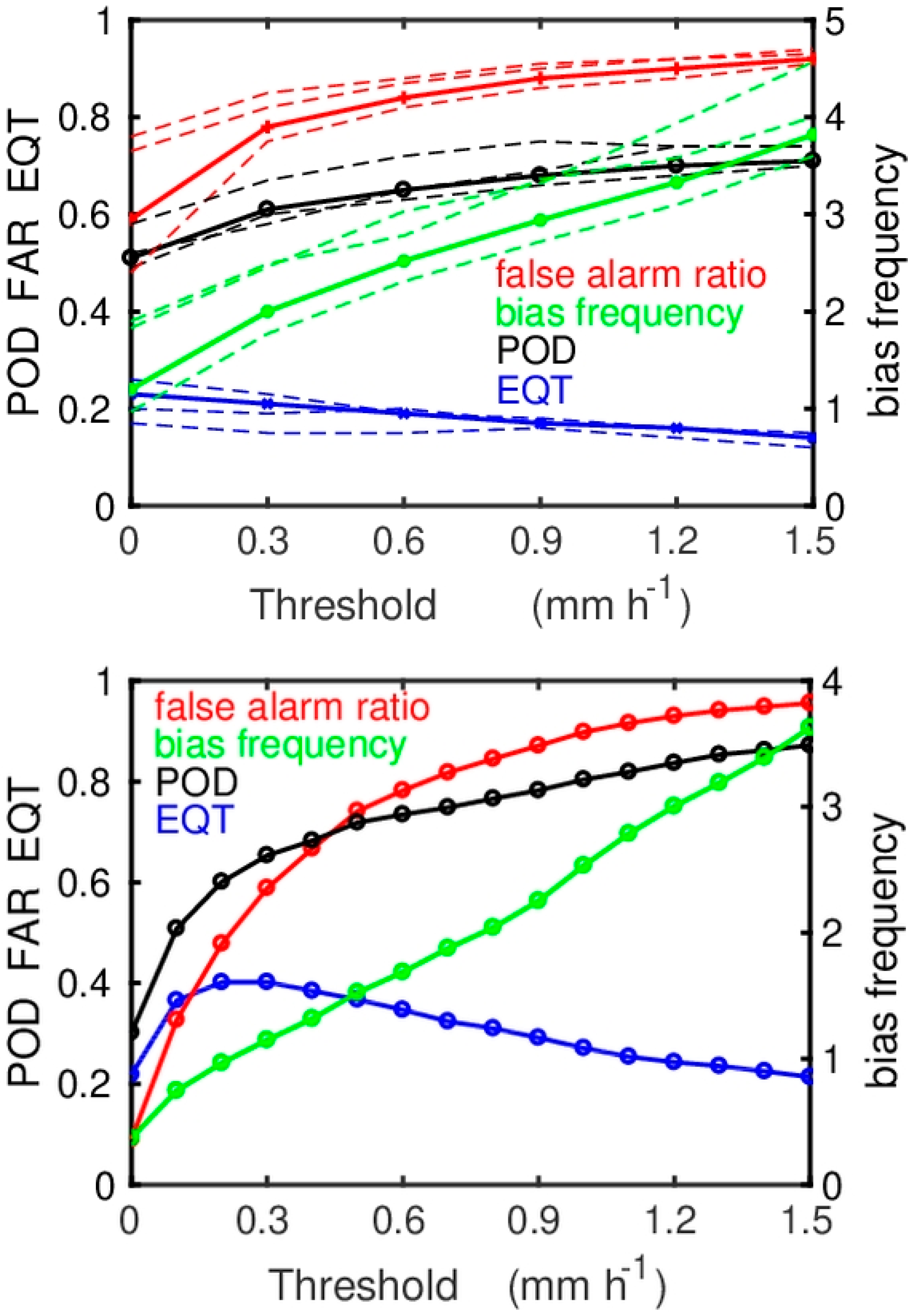
3.2. Statistical Analysis
3.3. Simulated Precipitation Fields
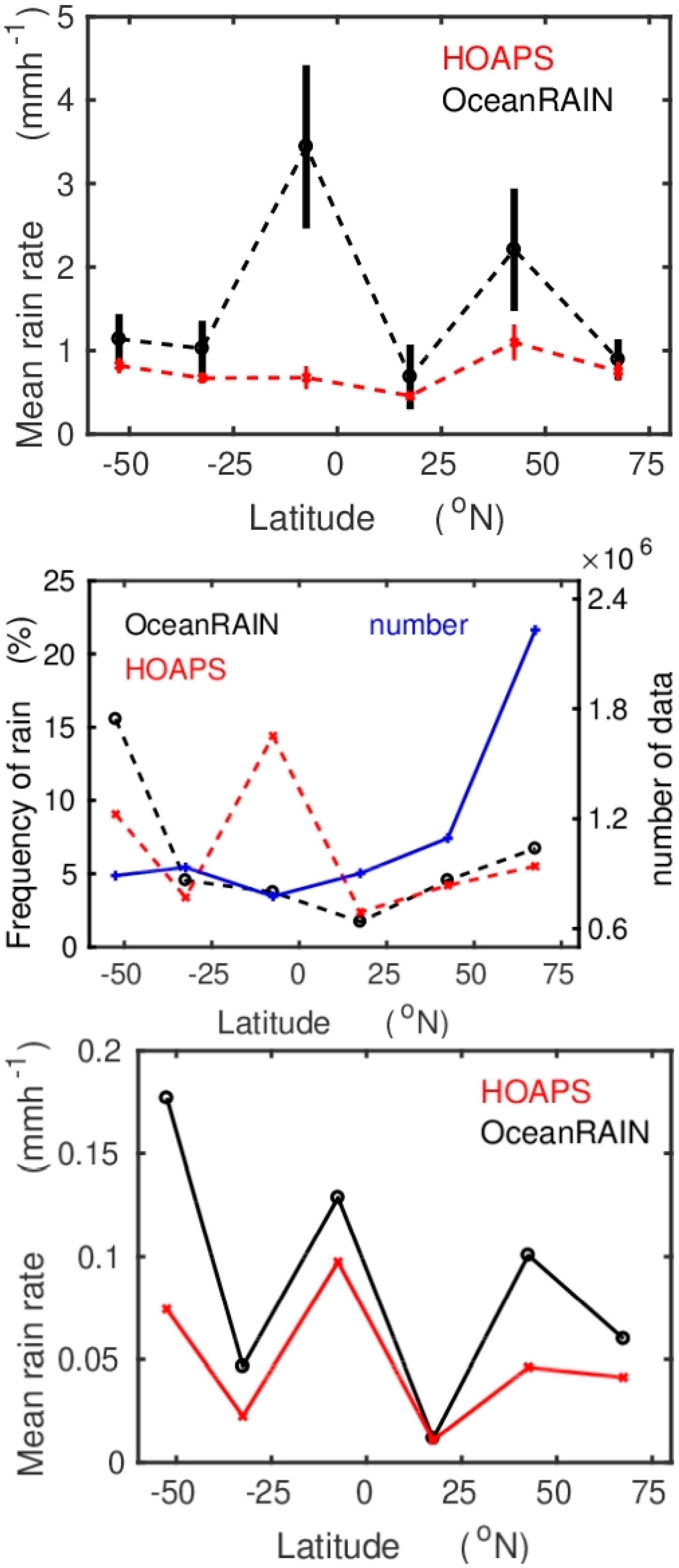
4. Results
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schmitt, R.W. Salinity and the global water cycle. Oceanography 2008, 21, 12–19. [Google Scholar] [CrossRef]
- Rhein, M.; Rintoul, S.R.; Aoki, S.; Campos, E.; Chambers, D.; Feely, R.A.; Gulev, S.; Johnson, G.C.; Josey, S.A.; Kostianoy, A.; et al. Observations: Ocean. In Climate Change 2013: The Physical Science Basis, Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 659–740. [Google Scholar] [CrossRef]
- Andersson, A.; Graw, K.; Schröder, M.; Fennig, K.; Liman, J.; Bakan, S.; Hollmann, R.; Klepp, C. Hamburg Ocean Atmosphere Parameters and Fluxes from Satellite Data—HOAPS 4.0. 2017. Available online: https://wui.cmsaf.eu/safira/action/viewDoiDetails?acronym=HOAPS_V002 (accessed on 8 November 2018).
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM Multi-satellite Precipitation Analysis: Quasi-Global, Multi-Year, Combined-Sensor Precipitation Estimates at Fine Scale. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- HOAPS. Available online: http://www.hoaps.org (accessed on 11 December 2018).
- NASA. Available online: https://pmm.nasa.gov/data-access/downloads/trmm (accessed on 11 December 2018).
- NASA. Available online: https://pmm.nasa.gov/data-access/downloads/gpm (accessed on 11 December 2018).
- Sanò, P.; Panegrossi, G.; Casella, D.; Marra, A.C.; Di Paola, F.; Dietrich, S. The new Passive microwave Neural network Precipitation Retrieval (PNPR) algorithm for the cross-track scanning ATMS radiometer: Description and verification study over Europe and Africa using GPM and TRMM spaceborne radars. Atmos. Meas. Tech. 2016, 9, 5441–5460. [Google Scholar] [CrossRef]
- Andersson, A.; Klepp, C.; Fennig, K.; Bakan, S.; Graßl, H.; Schulz, J. Evaluation of HOAPS-3 ocean surface freshwater flux components. J. Appl. Meteorol. Climatol. 2011, 50, 379–398. [Google Scholar] [CrossRef]
- Pfeifroth, U.; Mueller, R.; Ahrens, B. Evaluation of Satellite-Based and Reanalysis Precipitation Data in the Tropical Pacific. J. Appl. Meteorol. Climatol. 2013, 52, 634–644. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G. Improving the Global Precipitation Record: GPCP Version 2.1. Geophys. Res. Lett. 2009, 36, L17808. [Google Scholar] [CrossRef]
- Schlosser, C.A.; Houser, P.R. Assessing a Satellite-era Perspective of the Global Water Cycle. J. Clim. 2007, 20, 1316–1338. [Google Scholar] [CrossRef]
- Prakash, S.; Gairola, R.M. Validation of Trmm-3b42 Precipitation Product Over the Tropical Indian Ocean Using Rain Gauge Data from the Rama Buoy Array. Theor. Appl. Climatol. 2014, 115, 451–460. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Nelkin, E.J. The TRMM Multi-satellite Precipitation Analysis (TMPA). In Satellite Applications for Surface Hydrology; Hossain, F., Gebremichael, M., Eds.; Springer: Berlin, Germany, 2010; pp. 3–22. ISBN 978-90-481-2914-0. [Google Scholar]
- Neiman, P.J.; Gaggini, N.; Fairall, C.W.; Aikins, J.; Spackman, J.R.; Leung, L.R.; Fan, J.; Hardin, J.; Nalli, N.R.; White, A.B. An analysis of coordinated observations from NOAA’s Ronald H. Brown Ship and G-IV aircraft in a landfalling atmospheric river over the North Pacific, during CalWater-2015. Mon. Weather Rev. 2017, 145, 3647–3669. [Google Scholar] [CrossRef]
- Klepp, C. The oceanic shipboard precipitation measurement network for surface validation–OceanRAIN. Atmos. Res. 2015, 163, 74–90. [Google Scholar] [CrossRef]
- Klepp, C.; Michel, S.; Protat, A.; Burdanowitz, J.; Albern, N.; Dahl, A.; Kähnert, M.; Louf, V.; Bakan, S.; Buehler, S.A. OceanRAIN, a new in-situ shipboard global ocean surface-reference dataset of all water cycle components. Sci. Data 2018, 5. [Google Scholar] [CrossRef] [PubMed]
- Großklaus, M.; Uhlig, K.; Hasse, L. An optical disdrometer for use in high wind speeds. J. Atmos. Ocean. Technol. 1998, 15, 1051–1059. [Google Scholar] [CrossRef]
- Klepp, C.; Michel, S.; Protat, A.; Burdanowitz, J.; Albern, N.; Louf, V.; Bakan, S.; Dahl, A.; Thiele, T. Ocean Rainfall and Ice-Phase Precipitation Measurement Network—OceanRAIN-W; World Data Center for Climate (WDCC) at DKRZ: Hamburg, Germany, 2017. [Google Scholar]
- Burdanowitz, J.; Klepp, C.; Bakan, S.; Buehler, S.A. Simulation of Ship-Track versus Satellite-Sensor Differences in Oceanic Precipitation Using an Island-Based Radar. Remote Sens. 2017, 9, 593. [Google Scholar] [CrossRef]
- DWD. Available online: https://www.dwd.de/DE/fachnutzer/forschung_lehre/numerische_wettervorhersage/nwv_aenderungen/_functions/DownloadBox_modellaenderungen/cosmo_d2/pdf_2018_2020/pdf_cosmo_d2_15_05_2018.html?nn=346850 (accessed on 11 December 2018).
- Andersson, A.; Fennig, K.; Klepp, C.; Bakan, S.; Graßl, H.; Schulz, J. The Hamburg Ocean Atmosphere Parameters and Fluxes from Satellite Data—HOAPS-3. Earth Syst. Sci. Data 2010, 2, 215–234. [Google Scholar] [CrossRef]
- Fennig, K.; Andersson, A.; Bakan, S.; Klepp, C.P.; Schröder, M. Hamburg Ocean Atmosphere Parameters and Fluxes from Satellite Data—HOAPS 3.2—Monthly Means/6-Hourly Composites; Satellite Application Facility on Climate Monitoring (CM SAF): Geneva, Switzerland, 2012. [Google Scholar] [CrossRef]
- Bauer, P.; Lopez, P.; Benedetti, A.; Salmond, D.; Moreau, E. Implementation of 1D+4D-var assimilation of precipitation-affected microwave radiances at ECMWF: 1D-var. Q. J. R. Meteorol. Soc. 2006, 132, 2277–2306. [Google Scholar] [CrossRef]
- Bauer, P.; Moreau, E.; Chevallier, F.; O’Keeffe, U. Multiplescattering microwave radiative transfer for data assimilation applications. Q. J. R. Meteorol. Soc. 2006, 132, 1259–1281. [Google Scholar] [CrossRef]
- Froidurot, S.; Zin, I.; Hingray, B.; Gautheron, A. Sensitivity of Precipitation Phase over the Swiss Alps to Different Meteorological Variables. J. Hydrometeorol. 2014, 15, 685–696. [Google Scholar] [CrossRef]
- Hasse, L.; Großklaus, M.; Uhlig, K.; Timm, P. A ship rain gauge for use under high wind speeds. J. Atmos. Ocean. Technol. 1998, 15, 380–386. [Google Scholar] [CrossRef]
- Bundesamt für Seeschifffahrt und Hydrographie (BSH), DOD Data Centre. 2015. Available online: http://www.bsh.de/en/Marine_data/Observations/DOD_Data_Centre/ (accessed on 8 November 2018).
- Bumke, K.; König-Langlo, G.; Kinzel, J.; Schröder, M. HOAPS and ERA-Interim precipitation over the sea: Validation against shipboard in situ measurements. Atmos. Meas. Tech. 2016, 9, 1–15. [Google Scholar] [CrossRef]
- Clemens, M.; Bumke, K. Precipitation fields over the Baltic Sea derived from ship rain gauge measurements on merchant ships. Boreal Environ. Res. 2002, 7, 425–436. [Google Scholar]
- Klepp, C.; Bumke, K.; Bakan, S.; Bauer, P. Ground validation of oceanic snowfall detection in satellite climatologies during LOFZY. Tellus A Dyn. Meteorol. Oceanogr. 2010, 62, 469–480. [Google Scholar] [CrossRef]
- WWRP/WGNE. Methods for Dichotomous Forecasts. Joint Working Group on Verification Sponsored by the WMO, Forecast Verification, Issues, Methods and FAQ. Available online: www.cawcr.gov.au/projects/verification/#Methods_for_dichotomous_forecasts (accessed on 11 September 2018).
- Bumke, K.; Karger, U.; Hasse, L.; Niekamp, K.-P. Evaporation over the Baltic Sea as an example of a semi-enclosed sea. Contrib. Atmos. Phys. 1998, 71, 249–261. [Google Scholar]
- Efron, B. Bootstrap Methods: Another Look at the Jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]



| 3 | 2 | 1 | 2 | 3 |
| 4 | 3 | 2 | 3 | 4 |
| 5 | 4 | 3 | 4 | 5 |
| 6 | 5 | 4 | 5 | 6 |
| 7 | 6 | 5 | 6 | 7 |
| Latitude | <45° S | 45° S–20° S | 20° S–5° N | 5° N–30° N | 30° N–55° N | >55° N |
|---|---|---|---|---|---|---|
| Polarstern | ||||||
| Number | 1606 | 1159 | 716 | 736 | 936 | 2612 |
| POD | 0.51 | 0.43 | 0.64 | 0.73 | 0.50 | 0.47 |
| Bias frequ. | 0.71 | 0.71 | 3.29 | 4.91 | 1.30 | 0.83 |
| FAR | 0.29 | 0.33 | 0.88 | 0.94 | 0.62 | 0.41 |
| EQT | 0.32 | 0.28 | 0.11 | 0.13 | 0.22 | 0.27 |
| M.S.Merian | ||||||
| Number | 673 | 428 | 343 | 235 | 340 | |
| POD | 0.65 | - | - | - | 0.56 | |
| Bias frequ. | 1.70 | - | - | - | 1.34 | |
| FAR | 0.75 | - | - | - | 0.64 | |
| EQT | 0.28 | - | - | - | 0.22 | |
| Meteor | ||||||
| Number | 421 | 920 | 1666 | |||
| POD | 0.92 | - | 0.70 | |||
| Bias frequ. | 4.42 | - | 1.68 | |||
| FAR | 0.98 | - | 0.77 | |||
| EQT | 0.10 | - | 0.31 | |||
| All ships | ||||||
| Number | 1606 | 1832 | 1565 | 1999 | 2837 | 2952 |
| POD | 0.51 | 0.47 | 0.77 | 0.24 | 0.54 | 0.48 |
| Bias frequ. | 0.71 | 0.91 | 3.85 | 1.63 | 1.33 | 0.89 |
| FAR | 0.29 | 0.45 | 0.93 | 0.65 | 0.63 | 0.44 |
| EQT | 0.32 | 0.28 | 0.12 | 0.07 | 0.25 | 0.26 |
| All Ships, All Latitudes | Events | Collocated Pairs of Data | |
|---|---|---|---|
| Δx < 55 km, Δt < 45 min | Δx < 55 km, Δt < 45 min | Δx < 25 km, Δt < 15 min | |
| Number | 12,791 | 6,828,198 | 446,980 |
| POD | 0.51 | 0.40 | 0.47 |
| Bias frequency | 1.20 | 0.97 | 1.01 |
| FAR | 0.59 | 0.49 | 0.51 |
| EQT | 0.23 | 0.23 | 0.27 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bumke, K.; Pilch Kedzierski, R.; Schröder, M.; Klepp, C.; Fennig, K. Validation of HOAPS Rain Retrievals against OceanRAIN In-Situ Measurements over the Atlantic Ocean. Atmosphere 2019, 10, 15. https://doi.org/10.3390/atmos10010015
Bumke K, Pilch Kedzierski R, Schröder M, Klepp C, Fennig K. Validation of HOAPS Rain Retrievals against OceanRAIN In-Situ Measurements over the Atlantic Ocean. Atmosphere. 2019; 10(1):15. https://doi.org/10.3390/atmos10010015
Chicago/Turabian StyleBumke, Karl, Robin Pilch Kedzierski, Marc Schröder, Christian Klepp, and Karsten Fennig. 2019. "Validation of HOAPS Rain Retrievals against OceanRAIN In-Situ Measurements over the Atlantic Ocean" Atmosphere 10, no. 1: 15. https://doi.org/10.3390/atmos10010015
APA StyleBumke, K., Pilch Kedzierski, R., Schröder, M., Klepp, C., & Fennig, K. (2019). Validation of HOAPS Rain Retrievals against OceanRAIN In-Situ Measurements over the Atlantic Ocean. Atmosphere, 10(1), 15. https://doi.org/10.3390/atmos10010015





