An Improved Bayesian Shrinkage Regression Algorithm for Genomic Selection
Abstract
1. Introduction
2. Materials and Methods
2.1. Genetic Model
2.2. The Improved EM Algorithm for BayesA (emBayesAI) Algorithm
2.2.1. The Polygenic and Residual Noise Whitening Stage
2.2.2. EM Algorithm for BayesA Stage
- 1.
- E-step: is estimated as shown in (7).
- 2.
- M-step: updated and are given according to (9), (10) and (11).
2.3. Comparison Methods
2.4. Experimental Materials
2.4.1. The Simulation Data
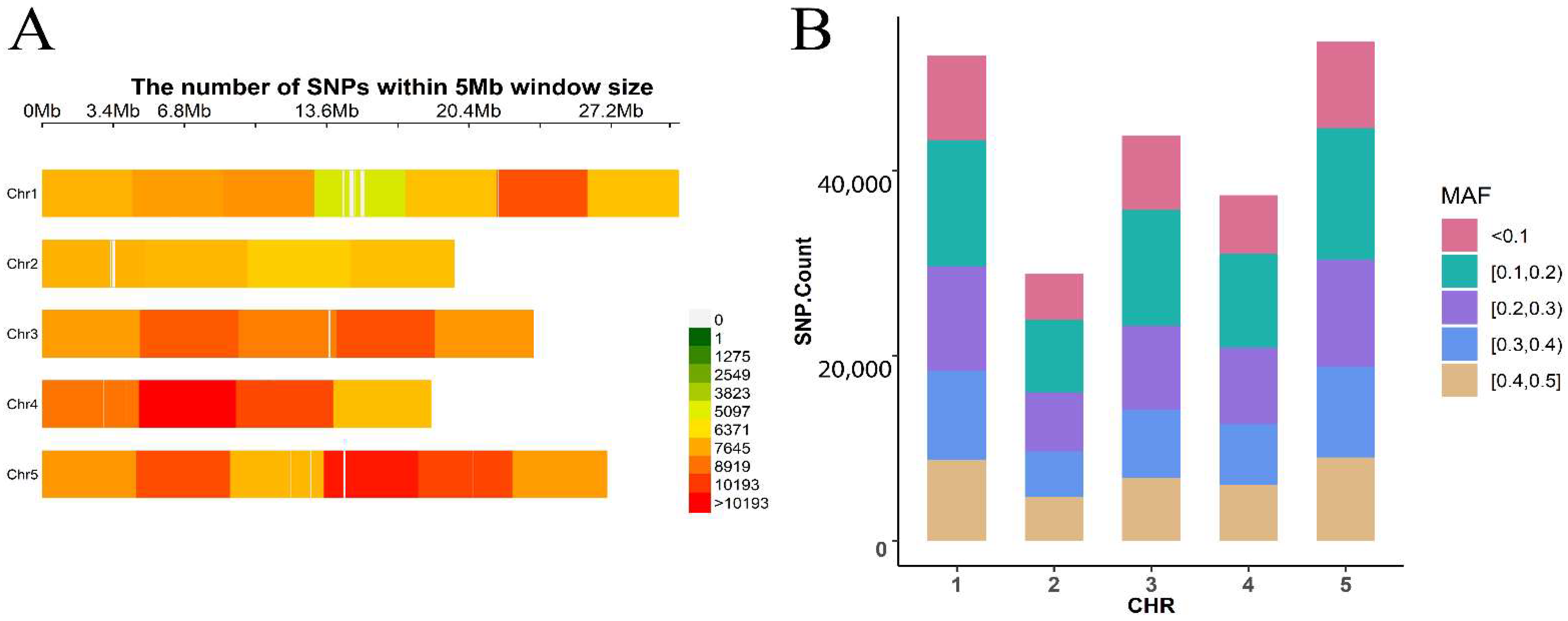
2.4.2. The Arabidopsis Data
2.4.3. Evaluation Indicators
3. Results
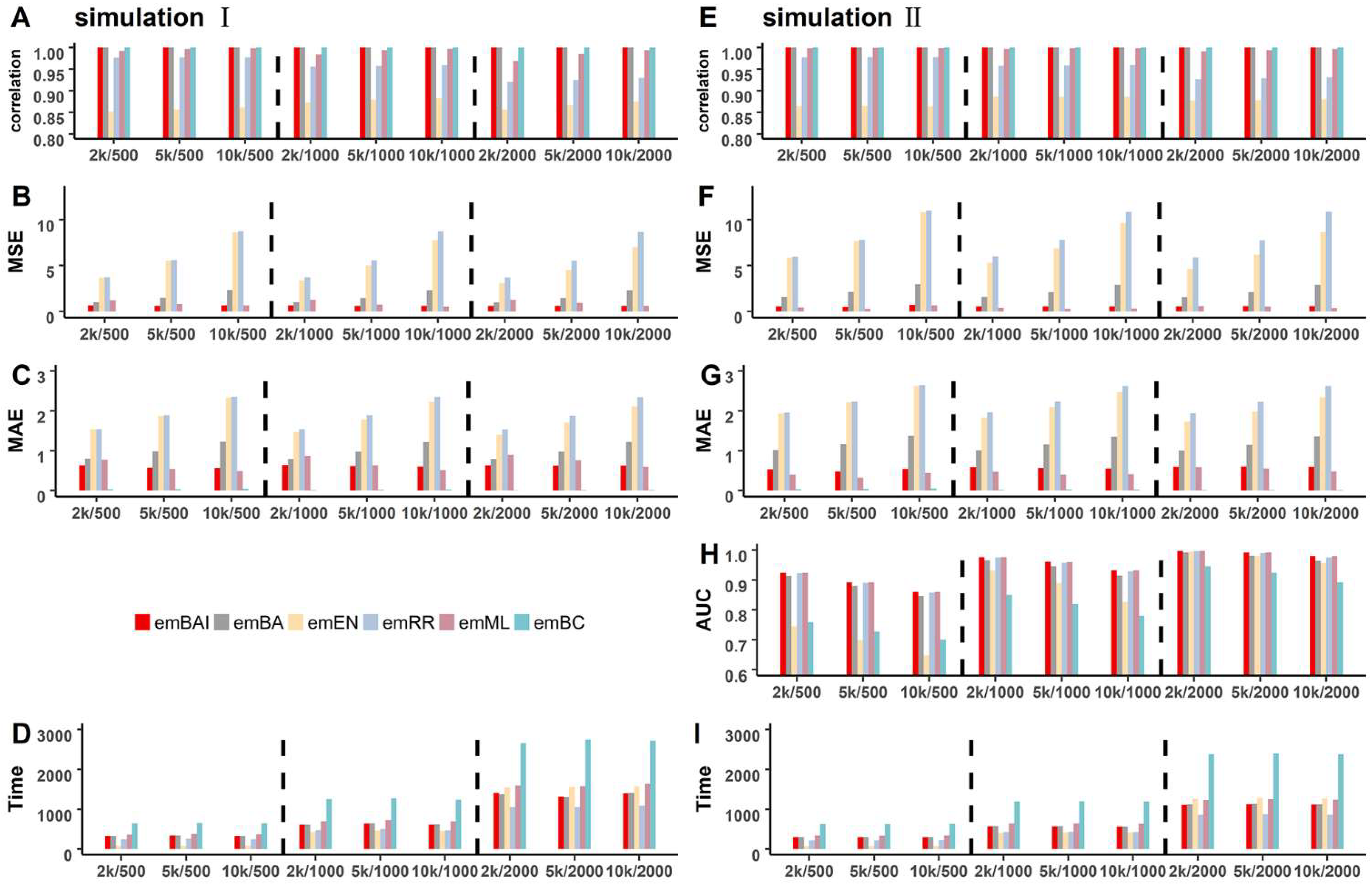
3.1. Simulation Studies
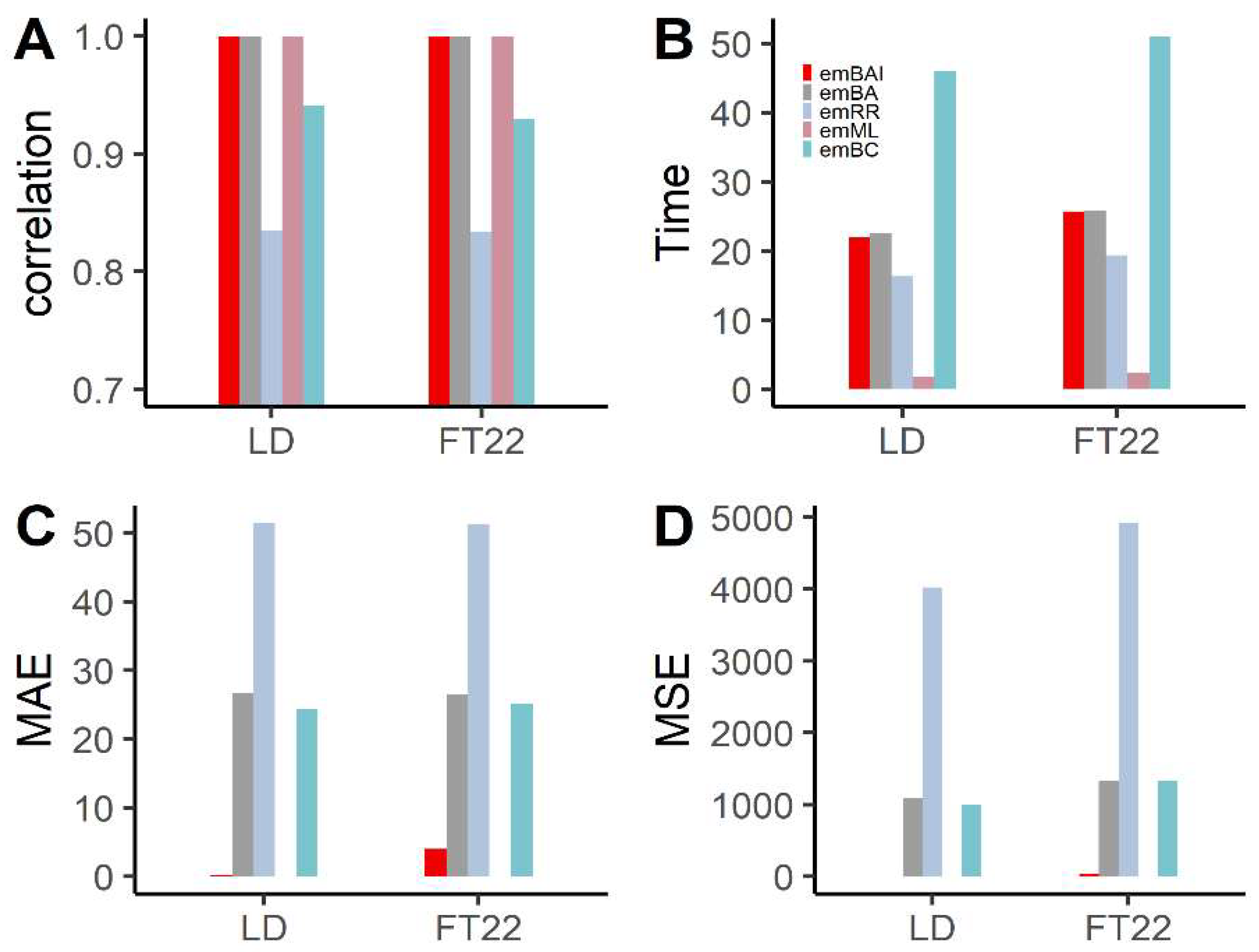
3.2. The Arabidopsis Data Analysis
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
References
- Pokharel, B.B.; Pandey, M. Genomic selection in Plant Breeding: Recent advances. In Proceedings of the National Conference on Biotechnology: Policies and Applications, Bharatpur, Nepal, 28–29 June 2017. [Google Scholar]
- Xu, Y.; Ma, K.X.; Zhao, Y.; Wang, X.; Zhou, K.; Yu, G.N.; Li, C.; Li, P.C.; Yang, Z.F.; Xu, C.W.; et al. Genomic selection: A breakthrough technology in rice breeding. Crop J. 2021, 9, 669–677. [Google Scholar] [CrossRef]
- Hayes, B.J.; Bowman, P.J.; Chamberlain, A.J.; Goddard, M.E. Invited review: Genomic selection in dairy cattle: Progress and challenges. J. Dairy Sci. 2009, 92, 433–443. [Google Scholar] [CrossRef] [PubMed]
- Crossa, J.; Perez-Rodriguez, P.; Cuevas, J.; Montesinos-Lopez, O.; Jarquin, D.; de los Campos, G.; Burgueno, J.; Gonzalez-Camacho, J.M.; Perez-Elizalde, S.; Beyene, Y.; et al. Genomic Selection in Plant Breeding: Methods, Models, and Perspectives. Trends Plant Sci. 2017, 22, 961–975. [Google Scholar] [CrossRef]
- VanRaden, P.M. Efficient Methods to Compute Genomic Predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef] [PubMed]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R Stat. Soc. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Meuwissen, T.H.E.; Hayes, B.J.; Goddard, M.E. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef]
- Habier, D.; Fernando, R.L.; Kizilkaya, K.; Garrick, D.J. Extension of the bayesian alphabet for genomic selection. BMC Bioinform. 2011, 12, 186. [Google Scholar] [CrossRef]
- Erbe, M.; Hayes, B.J.; Matukumalli, L.K.; Goswami, S.; Bowman, P.J.; Reich, C.M.; Mason, B.A.; Goddard, M.E. Improving accuracy of genomic predictions within and between dairy cattle breeds with imputed high-density single nucleotide polymorphism panels. J. Dairy Sci. 2012, 95, 4114–4129. [Google Scholar] [CrossRef]
- Meuwissen, T.H.E.; Solberg, T.R.; Shepherd, R.; Woolliams, J.A. A fast algorithm for BayesB type of prediction of genome-wide estimates of genetic value. Genet. Sel. Evol. 2009, 41, 2. [Google Scholar] [CrossRef]
- Wang, T.T.; Chen, Y.P.P.; Goddard, M.E.; Meuwissen, T.H.E.; Kemper, K.E.; Hayes, B.J. A computationally efficient algorithm for genomic prediction using a Bayesian model. Genet. Sel. Evol. 2015, 47, 34. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Shepherd, R.K.; Meuwissen, T.H.E.; Woolliams, J.A. Genomic selection and complex trait prediction using a fast EM algorithm applied to genome-wide markers. Bmc Bioinform. 2010, 11, 529. [Google Scholar] [CrossRef] [PubMed]
- Gianola, D. Priors in Whole-Genome Regression: The Bayesian Alphabet Returns. Genetics 2013, 194, 573–596. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, T.; Iwata, H. EM algorithm for Bayesian estimation of genomic breeding values. BMC Genet. 2010, 11, 3. [Google Scholar] [CrossRef]
- Zhao, T.; Fernando, R.L.; Garrick, D.J.; Cheng, H. Fast parallelized sampling of Bayesian regression models for whole-genome prediction. Genet. Sel. Evol. GSE 2020, 52, 16. [Google Scholar] [CrossRef]
- Breen, E.J.; MacLeod, I.M.; Ho, P.N.; Haile-Mariam, M.; Pryce, J.E.; Thomas, C.D.; Daetwyler, H.D.; Goddard, M.E. BayesR3 enables fast MCMC blocked processing for largescale multi-trait genomic prediction and QTN mapping analysis. Commun. Biol. 2022, 5, 661. [Google Scholar] [CrossRef]
- Yu, J.; Pressoir, G.; Briggs, W.H.; Vroh Bi, I.; Yamasaki, M.; Doebley, J.F.; McMullen, M.D.; Gaut, B.S.; Nielsen, D.M.; Holland, J.B.; et al. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat. Genet. 2006, 38, 203–208. [Google Scholar] [CrossRef]
- Zhang, Z.; Ersoz, E.; Lai, C.Q.; Todhunter, R.J.; Tiwari, H.K.; Gore, M.A.; Bradbury, P.J.; Yu, J.; Arnett, D.K.; Ordovas, J.M.; et al. Mixed linear model approach adapted for genome-wide association studies. Nat. Genet. 2010, 42, 355–360. [Google Scholar] [CrossRef]
- Zhou, X.; Stephens, M. Genome-wide efficient mixed-model analysis for association studies. Nat. Genet. 2012, 44, 821–824. [Google Scholar] [CrossRef]
- Zhou, X.; Carbonetto, P.; Stephens, M. Polygenic modeling with bayesian sparse linear mixed models. PLoS Genet. 2013, 9, e1003264. [Google Scholar] [CrossRef]
- Xu, W.; Liu, X.; Liao, M.; Xiao, S.; Zheng, M.; Yao, T.; Chen, Z.; Huang, L.; Zhang, Z. FMixFN: A Fast Big Data-Oriented Genomic Selection Model Based on an Iterative Conditional Expectation algorithm. Front. Genet. 2021, 12, 721600. [Google Scholar] [CrossRef] [PubMed]
- Goddard, M.E.; Wray, N.R.; Verbyla, K.; Visscher, P.M. Estimating Effects and Making Predictions from Genome-Wide Marker Data. Stat. Sci. 2009, 24, P.517–P.529. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, J.Y.; Ni, Y.L.; Wen, Y.J.; Niu, Y.; Tamba, C.L.; Yue, C.; Song, Q.; Zhang, Y.M. pLARmEB: Integration of least angle regression with empirical Bayes for multilocus genome-wide association studies. Heredity 2017, 118, 517–524. [Google Scholar] [CrossRef] [PubMed]
- Wen, Y.J.; Zhang, H.; Ni, Y.L.; Huang, B.; Zhang, J.; Feng, J.Y.; Wang, S.B.; Dunwell, J.M.; Zhang, Y.M.; Wu, R. Methodological implementation of mixed linear models in multi-locus genome-wide association studies. Brief Bioinform. 2018, 19, 700–712. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, M.; Wen, Y.J.; Zhang, Y.; Lu, Y.N.; Wang, S.M.; Chen, J.C. A Fast Multi-Locus Ridge Regression Algorithm for High-Dimensional Genome-Wide Association Studies. Front. Genet. 2021, 12, 649196. [Google Scholar] [CrossRef]
- Xavier, A.; Muir, W.M.; Rainey, K.M. bWGR: Bayesian whole-genome regression. Bioinformatics 2020, 36, 1957–1959. [Google Scholar] [CrossRef]
- Wen, Y.; Zhang, Y.; Zhang, J.; Feng, J.; Zhang, Y. The improved FASTmr EMMA and GCIM algorithms for genome-wide association and linkage studies in large mapping populations. Crop J. 2020, 8, 723–732. [Google Scholar] [CrossRef]
- Li, Q.; Lin, N. The Bayesian elastic net. Bayesian Anal. 2010, 5, 151–170. [Google Scholar] [CrossRef]
- Swallow, W.H.; Monahan, J.F. Monte Carlo Comparison of ANOVA, MIVQUE, REML, and ML Estimators of Variance Components. Technometrics 1984, 26, 47–57. [Google Scholar] [CrossRef]
- Da Silva, F.A.; Viana, A.P.; Correa, C.C.G.; Santos, E.A.; de Oliveira, J.; Andrade, J.D.G.; Ribeiro, R.M.; Glória, L.S. Bayesian ridge regression shows the best fit for SSR markers in Psidium guajava among Bayesian models. Sci. Rep. 2021, 11, 13639. [Google Scholar] [CrossRef]
- Atwell, S.; Huang, Y.S.; Vilhjálmsson, B.J.; Willems, G.; Horton, M.; Li, Y.; Meng, D.; Platt, A.; Tarone, A.M.; Hu, T.T.; et al. Genome-wide association study of 107 phenotypes in Arabidopsis thaliana inbred lines. Nature 2010, 465, 627–631. [Google Scholar] [CrossRef] [PubMed]
| Trait | Chr. | Position | Gene | Method |
|---|---|---|---|---|
| LD | 1 | 3760729 | AT1G11190, BFN1, ENDO1 | emBA |
| 1 | 3765344 | AT1G11190, BFN1, ENDO1 | emBAI, emML | |
| 2 | 13869948 | AT2G32700, LUH, MUM1 | emRR | |
| 2 | 16020457 | AT2G38185, APD1 | emBAI | |
| AT2G38195, APD4 | emBAI | |||
| AT2G38220, APD3 | emBAI | |||
| 4 | 14001595 | AT4G28190, ULT, ULT1 | emBC, emRR | |
| 5 | 18614010 | AT5G45890, ATSAG12, SAG12 | emBC | |
| FT22 | 1 | 9072307 | AT1G26260, CIB5 | emML |
| 2 | 16020457 | AT2G38185, APD1 | emBAI, emBC | |
| AT2G38195, APD4 | emBAI, emBC | |||
| AT2G38220, APD3 | emBAI, emBC | |||
| 2 | 13869948 | AT2G32700, LUH, MUM1 | emRR | |
| 4 | 17263477 | AT4G36620, GATA19, HANL2 | emBC, emRR | |
| 5 | 22328009 | AT5G55020, ATMYB120, MYB120 | emBAI | |
| 5 | 6844104 | AT5G20240, PI, PISTILLATA | emBAI | |
| 5 | AT5G20280, ATSPS1F, SPS1F, SPSA1 | emBAI | ||
| 5 | 13923880 13923160 13931089 13930569 13927017 | AT5G35750, AHK2, HK2 | emBA | |
| 5 | 17219669 | AT5G42900, COR27 | emBA | |
| 5 | 9808482 | AT5G27650, PDP1 | emBA | |
| 5 | 17463517 17478636 | AT5G43510, ATLURE1.2, CRP810_1.2, LURE 1.2 | emBA |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Li, L.; Lv, M.; Wang, Y.; Qiu, W.; An, Y.; Zhang, Y.; Wan, Y.; Xu, Y.; Chen, J. An Improved Bayesian Shrinkage Regression Algorithm for Genomic Selection. Genes 2022, 13, 2193. https://doi.org/10.3390/genes13122193
Zhang J, Li L, Lv M, Wang Y, Qiu W, An Y, Zhang Y, Wan Y, Xu Y, Chen J. An Improved Bayesian Shrinkage Regression Algorithm for Genomic Selection. Genes. 2022; 13(12):2193. https://doi.org/10.3390/genes13122193
Chicago/Turabian StyleZhang, Jin, Ling Li, Mingming Lv, Yidi Wang, Wenzhe Qiu, Yuan An, Ye Zhang, Yuxuan Wan, Yu Xu, and Juncong Chen. 2022. "An Improved Bayesian Shrinkage Regression Algorithm for Genomic Selection" Genes 13, no. 12: 2193. https://doi.org/10.3390/genes13122193
APA StyleZhang, J., Li, L., Lv, M., Wang, Y., Qiu, W., An, Y., Zhang, Y., Wan, Y., Xu, Y., & Chen, J. (2022). An Improved Bayesian Shrinkage Regression Algorithm for Genomic Selection. Genes, 13(12), 2193. https://doi.org/10.3390/genes13122193





