Evaluation of Genome-Enabled Prediction for Carcass Primal Cut Yields Using Single-Step Genomic Best Linear Unbiased Prediction in Hanwoo Cattle
Abstract
1. Introduction
2. Materials and Methods
2.1. Animals and Phenotypes
2.2. Genotypes and Quality Control
2.3. Statistical Analyses
2.3.1. Variance Components Estimation
2.3.2. Methods
2.4. Validation and Method Comparison
3. Results
3.1. Descriptive Analysis and Estimation of Variance Components
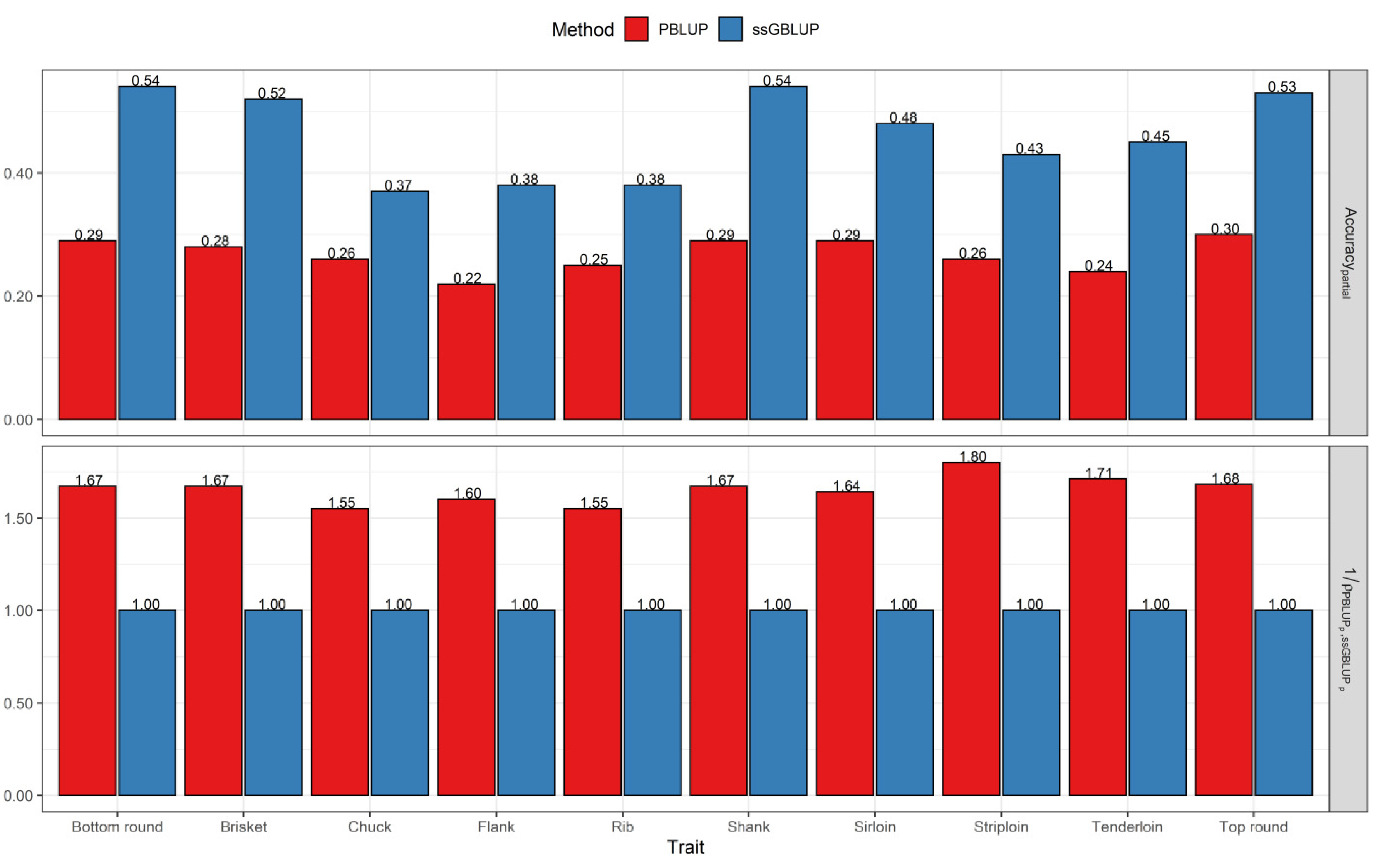
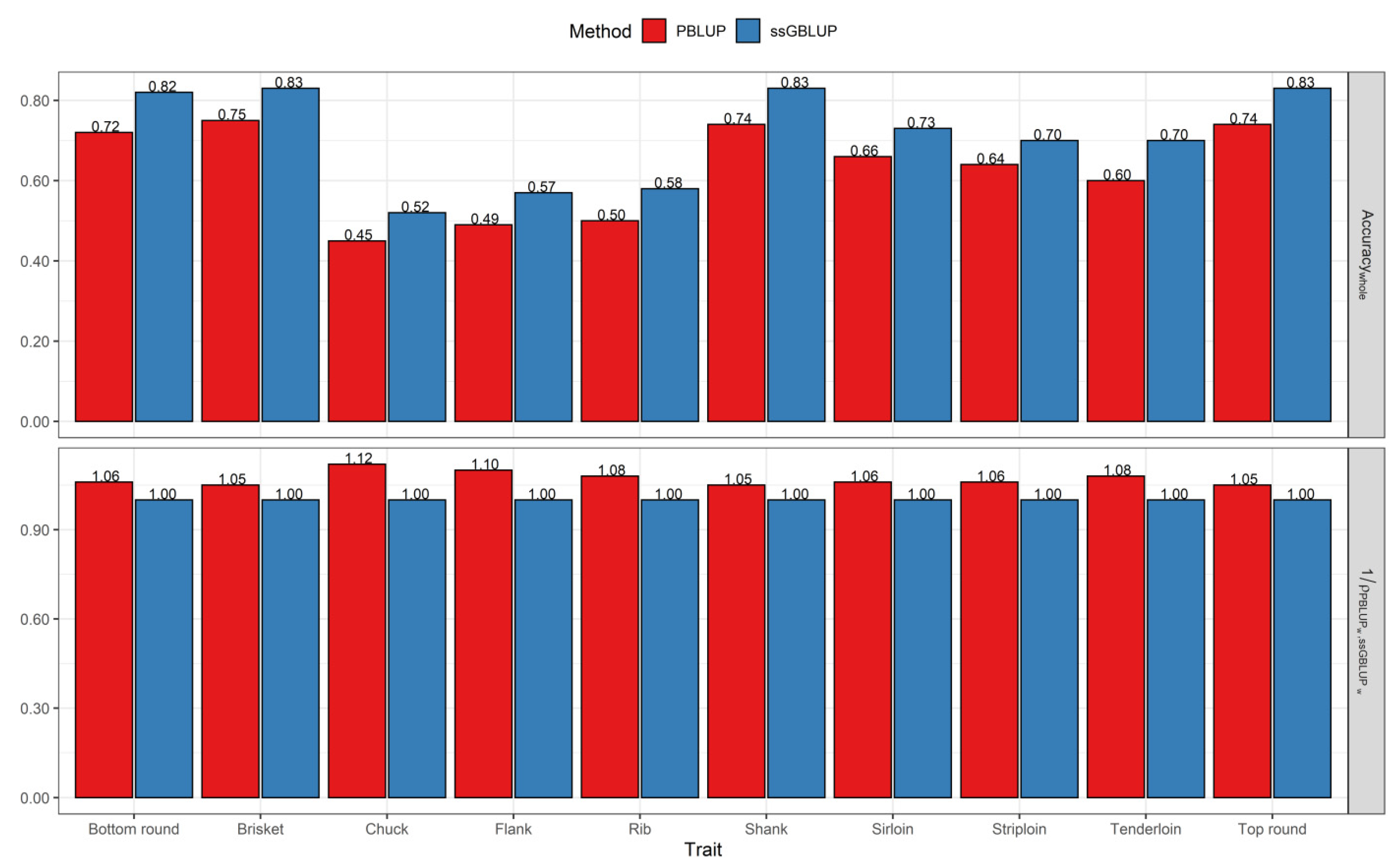
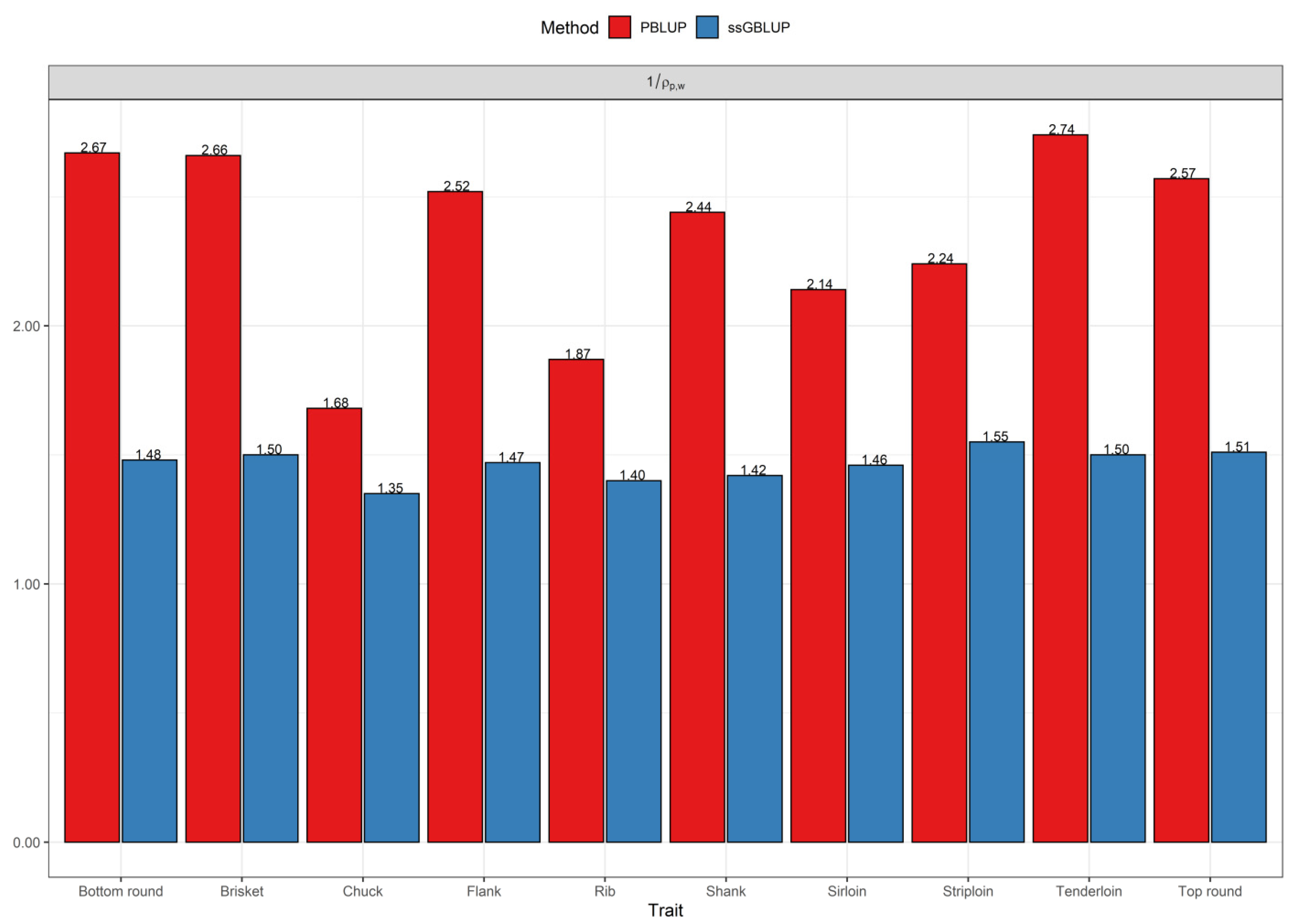
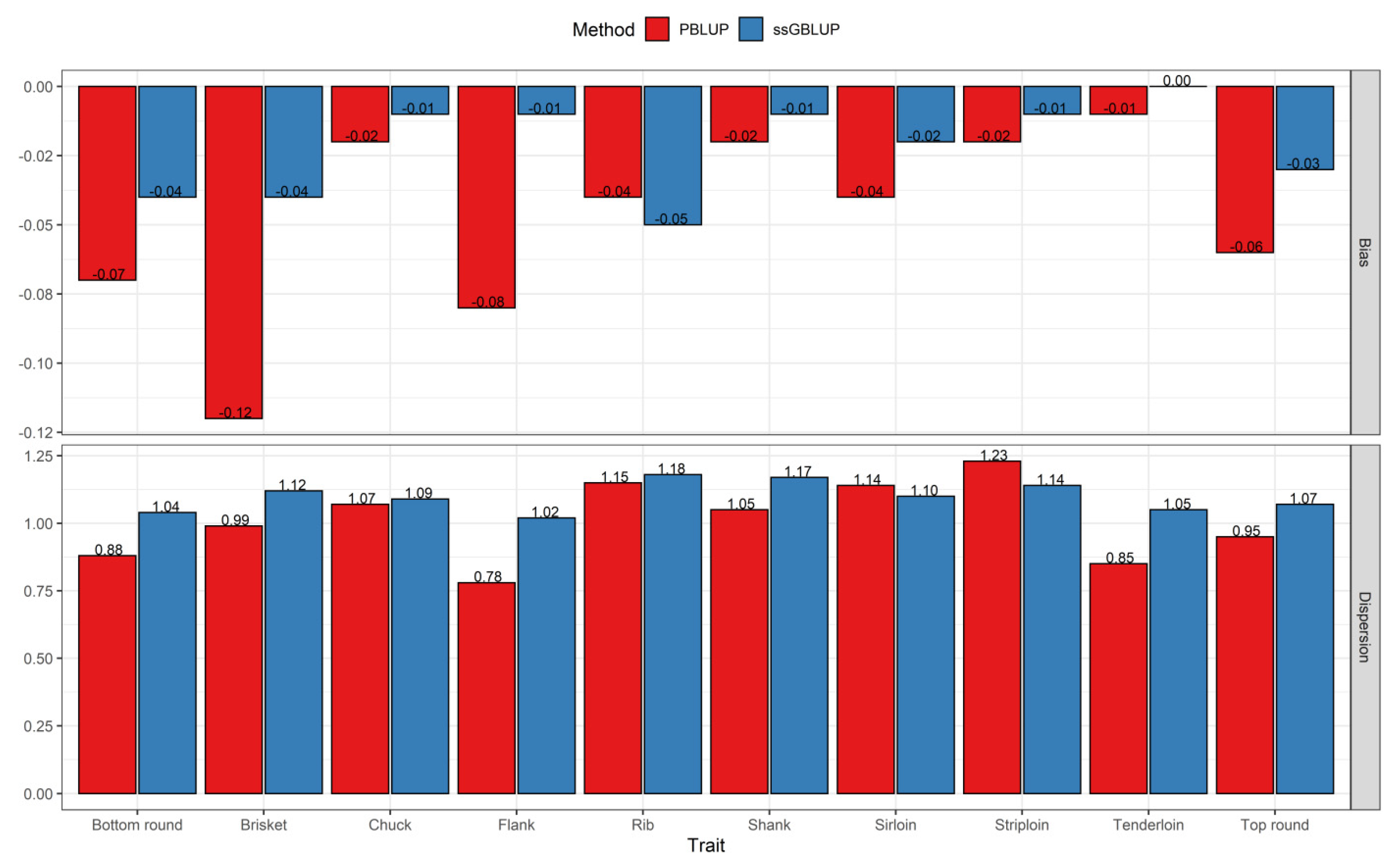
3.2. Comparisons of Prediction Accuracy, Bias, and Dispersion between Pedigree-Based BLUP and ssGBLUP
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gill, J.L.; Bishop, S.C.; McCorquodale, C.; Williams, J.L.; Wiener, P. Associations between single nucleotide polymorphisms in multiple candidate genes and carcass and meat quality traits in a commercial Angus-cross population. Meat Sci. 2010, 86, 985–993. [Google Scholar] [CrossRef] [PubMed]
- Jo, C.; Cho, S.; Chang, J.; Nam, K. Keys to production and processing of Hanwoo beef: A perspective of tradition and science. Anim. Front. 2012, 2, 32–38. [Google Scholar] [CrossRef]
- Kim, S.; Alam, M.; Park, M.N. Breeding initiatives for Hanwoo cattle to thrive as a beef industry–A review study. J. Anim. Breed. Genom. Vol 2017, 1, 103. [Google Scholar]
- Berry, D.P.; Pabiou, T.; Fanning, R.; Evans, R.D.; Judge, M.M. Linear classification scores in beef cattle as predictors of genetic merit for individual carcass primal cut yields. J. Anim. Sci. 2019, 97, 2329–2341. [Google Scholar] [CrossRef] [PubMed]
- Choi, T.; Alam, M.; Cho, C.; Lee, J.; Park, B.; Kim, S.; Koo, Y.; Roh, S. Genetic parameters for yearling weight, carcass traits, and primal-cut yields of Hanwoo cattle. J. Anim. Sci. 2015, 93, 1511–1521. [Google Scholar] [CrossRef]
- Judge, M.M.; Pabiou, T.; Murphy, J.; Conroy, S.B.; Hegarty, P.; Berry, D.P. Potential exists to change, through breeding, the yield of individual primal carcass cuts in cattle without increasing overall carcass weight. J. Anim. Sci. 2019, 97, 2769–2779. [Google Scholar] [CrossRef]
- Aguilar, I.; Misztal, I.; Johnson, D.; Legarra, A.; Tsuruta, S.; Lawlor, T. Hot topic: A unified approach to utilize phenotypic, full pedigree, and genomic information for genetic evaluation of Holstein final score. J. Dairy Sci. 2010, 93, 743–752. [Google Scholar] [CrossRef]
- Christensen, O.F.; Lund, M.S. Genomic prediction when some animals are not genotyped. Genet. Sel. Evol. 2010, 42, 1–8. [Google Scholar] [CrossRef]
- Legarra, A.; Aguilar, I.; Misztal, I. A relationship matrix including full pedigree and genomic information. J. Dairy Sci. 2009, 92, 4656–4663. [Google Scholar] [CrossRef]
- Misztal, I.; Legarra, A.; Aguilar, I. Computing procedures for genetic evaluation including phenotypic, full pedigree, and genomic information. J. Dairy Sci. 2009, 92, 4648–4655. [Google Scholar] [CrossRef]
- Lee, J.; Cheng, H.; Garrick, D.; Golden, B.; Dekkers, J.; Park, K.; Lee, D.; Fernando, R. Comparison of alternative approaches to single-trait genomic prediction using genotyped and non-genotyped Hanwoo beef cattle. Genet. Sel. Evol. 2017, 49, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Lopez, B.I.; Lee, S.-H.; Shin, D.-H.; Oh, J.-D.; Chai, H.-H.; Park, W.; Park, J.-E.; Lim, D. Accuracy of genomic evaluation using imputed high-density genotypes for carcass traits in commercial Hanwoo population. Livest. Sci. 2020, 241, 104256. [Google Scholar] [CrossRef]
- Mehrban, H.; Lee, D.H.; Naserkheil, M.; Moradi, M.H.; Ibáñez-Escriche, N. Comparison of conventional BLUP and single-step genomic BLUP evaluations for yearling weight and carcass traits in Hanwoo beef cattle using single trait and multi-trait models. PLoS ONE 2019, 14, e0223352. [Google Scholar] [CrossRef]
- Mehrban, H.; Naserkheil, M.; Lee, D.; Ibáñez-Escriche, N. Multi-Trait Single-Step GBLUP Improves Accuracy of Genomic Prediction for Carcass Traits Using Yearling Weight and Ultrasound Traits in Hanwoo. Front. Genet. 2021, 12, 692356. [Google Scholar] [CrossRef] [PubMed]
- Park, M.N.; Alam, M.; Kim, S.; Park, B.; Lee, S.H.; Lee, S.S. Genomic selection through single-step genomic best linear unbiased prediction improves the accuracy of evaluation in Hanwoo cattle. Asian-Australas. J. Anim. Sci. 2020, 33, 1544. [Google Scholar] [CrossRef]
- Naserkheil, M.; Lee, D.H.; Mehrban, H. Improving the accuracy of genomic evaluation for linear body measurement traits using single-step genomic best linear unbiased prediction in Hanwoo beef cattle. BMC Genet. 2020, 21, 1–9. [Google Scholar] [CrossRef]
- Elzo, M.; Mateescu, R.; Johnson, D.; Scheffler, T.; Scheffler, J.; Carr, C.; Rae, D.; Wasdin, J.; Driver, M.; Driver, J. Genomic-polygenic and polygenic predictions for nine ultrasound and carcass traits in Angus-Brahman multibreed cattle using three sets of genotypes. Livest. Sci. 2017, 202, 58–66. [Google Scholar] [CrossRef]
- Lourenco, D.; Tsuruta, S.; Fragomeni, B.; Masuda, Y.; Aguilar, I.; Legarra, A.; Bertrand, J.; Amen, T.; Wang, L.; Moser, D. Genetic evaluation using single-step genomic best linear unbiased predictor in American Angus. J. Anim. Sci. 2015, 93, 2653–2662. [Google Scholar] [CrossRef]
- Onogi, A.; Ogino, A.; Komatsu, T.; Shoji, N.; Simizu, K.; Kurogi, K.; Yasumori, T.; Togashi, K.; Iwata, H. Genomic prediction in Japanese Black cattle: Application of a single-step approach to beef cattle. J. Anim. Sci. 2014, 92, 1931–1938. [Google Scholar] [CrossRef]
- Legarra, A.; Reverter, A. Semi-parametric estimates of population accuracy and bias of predictions of breeding values and future phenotypes using the LR method. Genet. Sel. Evol. 2018, 50, 1–18. [Google Scholar] [CrossRef]
- Sargolzaei, M.; Chesnais, J.P.; Schenkel, F.S. A new approach for efficient genotype imputation using information from relatives. BMC Genom. 2014, 15, 1–12. [Google Scholar] [CrossRef]
- Misztal, I.; Tsuruta, S.; Lourenco, D.; Masuda, Y.; Aguilar, I.; Legarra, A.; Vitezica, Z. Manual for BLUPF90 Family of Programs; University of Georgia: Athens, GA, USA, 2018; p. 199. [Google Scholar]
- Houle, D. Comparing evolvability and variability of quantitative traits. Genetics 1992, 130, 195–204. [Google Scholar] [CrossRef]
- VanRaden, P.M. Efficient methods to compute genomic predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef]
- Aguilar, I.; Misztal, I.; Tsuruta, S.; Legarra, A.; Wang, H. PREGSF90–POSTGSF90: Computational tools for the implementation of single-step genomic selection and genome-wide association with ungenotyped individuals in BLUPF90 programs. In Proceedings of the 10 World Congress on Genetics Applied to Livestock Production (WCGALP), Vancouver, BC, Canada, 16–21 August 2014. [Google Scholar]
- Sorensen, D.; Fernando, R.; Gianola, D. Inferring the trajectory of genetic variance in the course of artificial selection. Genet. Res. 2001, 77, 83–94. [Google Scholar] [CrossRef] [PubMed]
- Zhu, B.; Guo, P.; Wang, Z.; Zhang, W.; Chen, Y.; Zhang, L.; Gao, H.; Wang, Z.; Gao, X.; Xu, L. Accuracies of genomic prediction for twenty economically important traits in Chinese Simmental beef cattle. Anim. Genet. 2019, 50, 634–643. [Google Scholar] [CrossRef] [PubMed]
- Sarti, F.; Pieramati, C.; Lubricchio, E.; Giontella, A.; Lasagna, E.; Panella, F. Genetic parameters for the weights and yields of carcass cuts in Chianina cattle. J. Anim. Sci. 2013, 91, 4099–4103. [Google Scholar] [CrossRef]
- Moore, K.; Mrode, R.; Coffey, M. Genetic parameters of Visual Image Analysis primal cut carcass traits of commercial prime beef slaughter animals. Animal 2017, 11, 1653–1659. [Google Scholar] [CrossRef] [PubMed]
- Naserkheil, M.; Lee, D.; Chung, K.; Park, M.N.; Mehrban, H. Estimation of Genetic Correlations of Primal Cut Yields with Carcass Traits in Hanwoo Beef Cattle. Animals 2021, 11, 3102. [Google Scholar] [CrossRef]
- Pabiou, T.; Fikse, W.; Amer, P.; Cromie, A.; Näsholm, A.; Berry, D.P. Genetic variation in wholesale carcass cuts predicted from digital images in cattle. Animal 2011, 5, 1720–1727. [Google Scholar] [CrossRef]
- Christensen, O.; Madsen, P.; Nielsen, B.; Ostersen, T.; Su, G. Single-step methods for genomic evaluation in pigs. Animal 2012, 6, 1565–1571. [Google Scholar] [CrossRef]
- Guo, X.; Christensen, O.F.; Ostersen, T.; Wang, Y.; Lund, M.; Su, G. Improving genetic evaluation of litter size and piglet mortality for both genotyped and nongenotyped individuals using a single-step method. J. Anim. Sci. 2015, 93, 503–512. [Google Scholar] [CrossRef] [PubMed]
- Campos, G.S.; Reimann, F.A.; Cardoso, L.L.; Ferreira, C.E.R.; Junqueira, V.S.; Schmidt, P.I.; Braccini Neto, J.; Yokoo, M.J.I.; Sollero, B.P.; Boligon, A.A. Genomic prediction using different estimation methodology, blending and cross-validation techniques for growth traits and visual scores in Hereford and Braford cattle. J. Anim. Sci. 2018, 96, 2579–2595. [Google Scholar] [CrossRef]
- Hayes, B.J.; Visscher, P.M.; Goddard, M.E. Increased accuracy of artificial selection by using the realized relationship matrix. Genet. Res. 2009, 91, 47–60. [Google Scholar] [CrossRef]
- Van Eenennaam, A.; Van Der Werf, J.; Goddard, M. The value of using DNA markers for beef bull selection in the seedstock sector. J. Anim. Sci. 2011, 89, 307–320. [Google Scholar] [CrossRef][Green Version]
- Bolormaa, S.; Pryce, J.; Kemper, K.; Savin, K.; Hayes, B.; Barendse, W.; Zhang, Y.; Reich, C.; Mason, B.; Bunch, R. Accuracy of prediction of genomic breeding values for residual feed intake and carcass and meat quality traits in Bos taurus, Bos indicus, and composite beef cattle. J. Anim. Sci. 2013, 91, 3088–3104. [Google Scholar] [CrossRef] [PubMed]
- Silva, R.; Fragomeni, B.; Lourenco, D.; Magalhães, A.; Irano, N.; Carvalheiro, R.; Canesin, R.; Mercadante, M.; Boligon, A.; Baldi, F. Accuracies of genomic prediction of feed efficiency traits using different prediction and validation methods in an experimental Nelore cattle population. J. Anim. Sci. 2016, 94, 3613–3623. [Google Scholar] [CrossRef]
- Bermann, M.; Legarra, A.; Hollifield, M.K.; Masuda, Y.; Lourenco, D.; Misztal, I. Validation of single-step GBLUP genomic predictions from threshold models using the linear regression method: An application in chicken mortality. J. Anim. Breed. Genet. 2021, 138, 4–13. [Google Scholar] [CrossRef] [PubMed]
- Granado-Tajada, I.; Legarra, A.; Ugarte, E. Exploring the inclusion of genomic information and metafounders in Latxa dairy sheep genetic evaluations. J. Dairy Sci. 2020, 103, 6346–6353. [Google Scholar] [CrossRef]
- Macedo, F.L.; Christensen, O.F.; Astruc, J.-M.; Aguilar, I.; Masuda, Y.; Legarra, A. Bias and accuracy of dairy sheep evaluations using BLUP and SSGBLUP with metafounders and unknown parent groups. Genet. Sel. Evol. 2020, 52, 1–10. [Google Scholar] [CrossRef]
- Aguilar, I.; Misztal, I.; Legarra, A.; Tsuruta, S. Efficient computation of the genomic relationship matrix and other matrices used in single-step evaluation. J. Anim. Breed. Genet. 2011, 128, 422–428. [Google Scholar] [CrossRef]
- Baloche, G.; Legarra, A.; Sallé, G.; Larroque, H.; Astruc, J.-M.; Robert-Granié, C.; Barillet, F. Assessment of accuracy of genomic prediction for French Lacaune dairy sheep. J. Dairy Sci. 2014, 97, 1107–1116. [Google Scholar] [CrossRef]
- Carillier, C.; Larroque, H.; Robert-Granié, C. Comparison of joint versus purebred genomic evaluation in the French multi-breed dairy goat population. Genet. Sel. Evol. 2014, 46, 1–10. [Google Scholar] [CrossRef]
- Heidaritabar, M.; Wolc, A.; Arango, J.; Zeng, J.; Settar, P.; Fulton, J.E.; O’Sullivan, N.P.; Bastiaansen, J.W.; Fernando, R.L.; Garrick, D.J. Impact of fitting dominance and additive effects on accuracy of genomic prediction of breeding values in layers. J. Anim. Breed. Genet. 2016, 133, 334–346. [Google Scholar] [CrossRef]
- Koivula, M.; Strandén, I.; Pösö, J.; Aamand, G.; Mäntysaari, E. Single-step genomic evaluation using multitrait random regression model and test-day data. J. Dairy Sci. 2015, 98, 2775–2784. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wang, S.; Huang, J.; Li, L.; Zhang, Q.; Ding, X. Improving the accuracy of genomic prediction in Chinese Holstein cattle by using one-step blending. Genet. Sel. Evol. 2014, 46, 1–5. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Su, G.; Madsen, P.; Nielsen, U.; Mäntysaari, E.A.; Aamand, G.; Christensen, O.; Lund, M. Genomic prediction for Nordic Red Cattle using one-step and selection index blending. J. Dairy Sci. 2012, 95, 909–917. [Google Scholar] [CrossRef] [PubMed]
- Tsuruta, S.; Misztal, I.; Aguilar, I.; Lawlor, T. Multiple-trait genomic evaluation of linear type traits using genomic and phenotypic data in US Holsteins. J. Dairy Sci. 2011, 94, 4198–4204. [Google Scholar] [CrossRef]
- Xiang, T.; Nielsen, B.; Su, G.; Legarra, A.; Christensen, O. Application of single-step genomic evaluation for crossbred performance in pig. J. Anim. Sci. 2016, 94, 936–948. [Google Scholar] [CrossRef]
- Mehrban, H.; Naserkheil, M.; Lee, D.H.; Cho, C.; Choi, T.; Park, M.; Ibáñez-Escriche, N. Genomic Prediction Using Alternative Strategies of Weighted Single-Step Genomic BLUP for Yearling Weight and Carcass Traits in Hanwoo Beef Cattle. Genes 2021, 12, 266. [Google Scholar] [CrossRef]
- Legarra, A.; Christensen, O.F.; Aguilar, I.; Misztal, I. Single Step, a general approach for genomic selection. Livest. Sci. 2014, 166, 54–65. [Google Scholar] [CrossRef]
- Vitezica, Z.-G.; Aguilar, I.; Misztal, I.; Legarra, A. Bias in genomic predictions for populations under selection. Genet. Res. 2011, 93, 357–366. [Google Scholar] [CrossRef] [PubMed]
- Henderson, C.R.; Kempthorne, O.; Searle, S.R.; Von Krosigk, C. The estimation of environmental and genetic trends from records subject to culling. Biometrics 1959, 15, 192–218. [Google Scholar] [CrossRef]
- Misztal, I.; Lourenco, D.; Legarra, A. Current status of genomic evaluation. J. Anim. Sci. 2020, 98, skaa101. [Google Scholar] [CrossRef] [PubMed]
| Trait (Unit) | No. of Records | Mean (SE) | Min. | Max. | SD | CV (%) |
|---|---|---|---|---|---|---|
| Bottom round (Kg) | 3467 | 32.99 (0.07) | 16.6 | 49.6 | 3.92 | 11.89 |
| Brisket (Kg) | 3466 | 23.76 (0.05) | 12.6 | 38.6 | 3.01 | 12.67 |
| Chuck (Kg) | 3463 | 14.61 (0.06) | 6.7 | 34.8 | 3.76 | 25.72 |
| Flank (Kg) | 3465 | 28.29 (0.08) | 12.5 | 50.3 | 4.83 | 17.08 |
| Rib (Kg) | 3467 | 57.55 (0.13) | 21.7 | 89.3 | 7.53 | 13.09 |
| Shank (Kg) | 3466 | 14.66 (0.03) | 9 | 21.7 | 1.77 | 12.09 |
| Sirloin (Kg) | 3465 | 34.23 (0.07) | 16.8 | 50.7 | 4.11 | 12.02 |
| Striploin (Kg) | 3465 | 7.85 (0.02) | 4.3 | 12.4 | 1.17 | 14.96 |
| Tenderloin (Kg) | 3466 | 6.04 (0.01) | 3 | 9 | 0.76 | 12.65 |
| Top round (Kg) | 3467 | 20.22 (0.04) | 10.5 | 30.2 | 2.43 | 12 |
| Trait | h2 | σ2a | σ2e | σ2p | CVg(%) |
|---|---|---|---|---|---|
| Bottom round | 0.50 (0.06) | 5.47 (0.73) | 5.41 (0.59) | 10.87 (0.30) | 7.09 |
| Brisket | 0.51 (0.06) | 3.17 (0.42) | 3.08 (0.34) | 6.25 (0.18) | 7.49 |
| Chuck | 0.21 (0.04) | 1.82 (0.38) | 6.64 (0.36) | 8.46 (0.22) | 9.23 |
| Flank | 0.29 (0.05) | 4.61 (0.86) | 11.58 (0.77) | 16.18 (0.42) | 7.59 |
| Rib | 0.27 (0.05) | 9.58 (1.93) | 27.18 (1.75) | 37.04 (0.96) | 5.38 |
| Shank | 0.50 (0.06) | 1.10 (0.15) | 1.11 (0.12) | 2.20 (0.06) | 7.15 |
| Sirloin | 0.42 (0.06) | 5.26 (0.78) | 7.20 (0.65) | 12.46 (0.34) | 6.70 |
| Striploin | 0.39 (0.06) | 0.31 (0.05) | 0.50 (0.04) | 0.81 (0.02) | 7.09 |
| Tenderloin | 0.34 (0.05) | 0.14 (0.02) | 0.27 (0.02) | 0.42 (0.01) | 6.19 |
| Top round | 0.52 (0.06) | 2.22 (0.29) | 2.07 (0.23) | 4.29 (0.12) | 7.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naserkheil, M.; Mehrban, H.; Lee, D.; Park, M.N. Evaluation of Genome-Enabled Prediction for Carcass Primal Cut Yields Using Single-Step Genomic Best Linear Unbiased Prediction in Hanwoo Cattle. Genes 2021, 12, 1886. https://doi.org/10.3390/genes12121886
Naserkheil M, Mehrban H, Lee D, Park MN. Evaluation of Genome-Enabled Prediction for Carcass Primal Cut Yields Using Single-Step Genomic Best Linear Unbiased Prediction in Hanwoo Cattle. Genes. 2021; 12(12):1886. https://doi.org/10.3390/genes12121886
Chicago/Turabian StyleNaserkheil, Masoumeh, Hossein Mehrban, Deukmin Lee, and Mi Na Park. 2021. "Evaluation of Genome-Enabled Prediction for Carcass Primal Cut Yields Using Single-Step Genomic Best Linear Unbiased Prediction in Hanwoo Cattle" Genes 12, no. 12: 1886. https://doi.org/10.3390/genes12121886
APA StyleNaserkheil, M., Mehrban, H., Lee, D., & Park, M. N. (2021). Evaluation of Genome-Enabled Prediction for Carcass Primal Cut Yields Using Single-Step Genomic Best Linear Unbiased Prediction in Hanwoo Cattle. Genes, 12(12), 1886. https://doi.org/10.3390/genes12121886






