Comparative Analysis of the Minimum Number of Replication Origins in Trypanosomatids and Yeasts
Abstract
1. Introduction
2. Materials and Methods
2.1. Trypanosomatids Culture, Growth Curves, and Morphological Patterns
2.2. EdU Incorporation Assays and ‘Click’ Chemistry Reaction
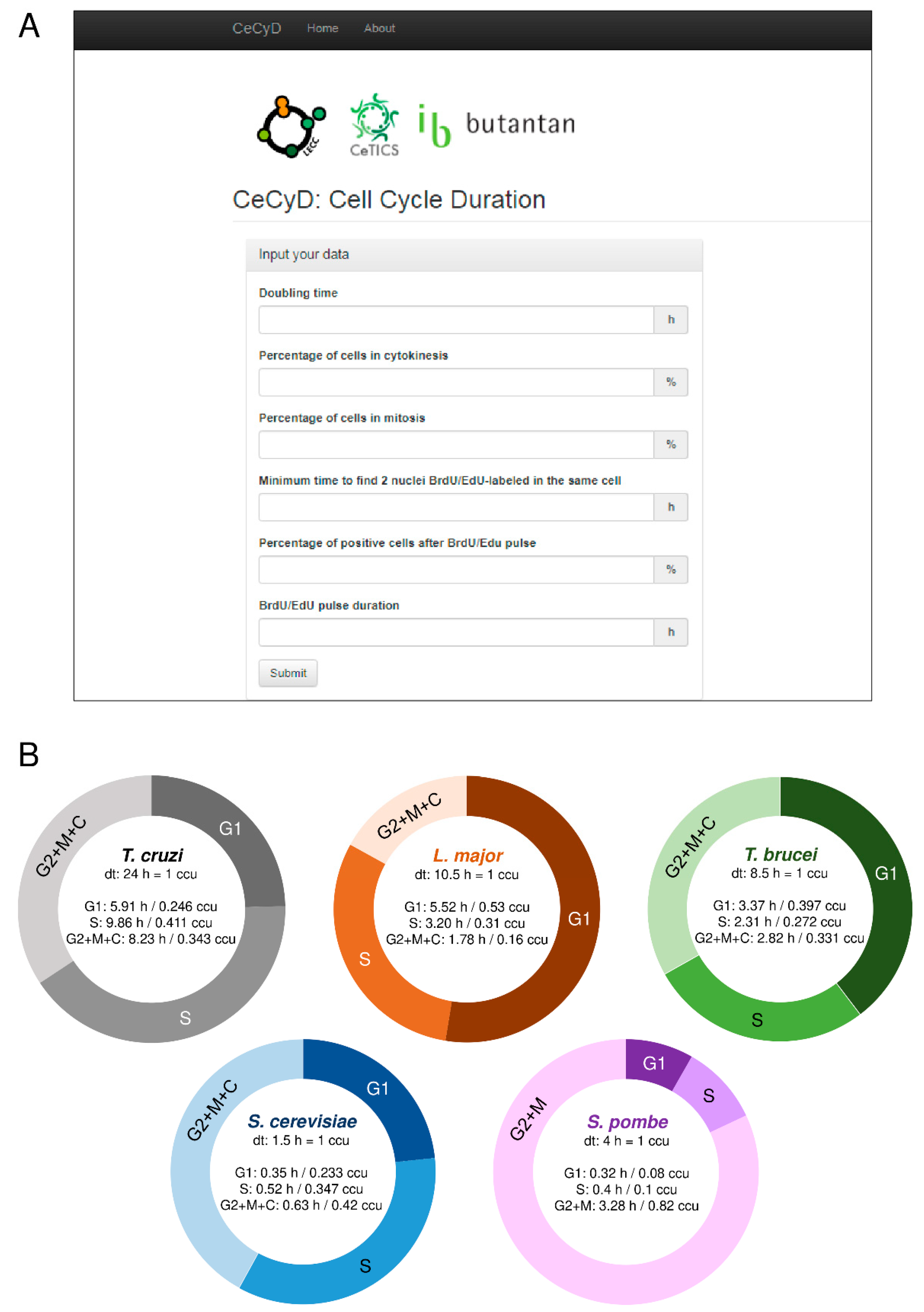
2.3. Development of the CeCyD Website and Analysis of the Cell Cycle
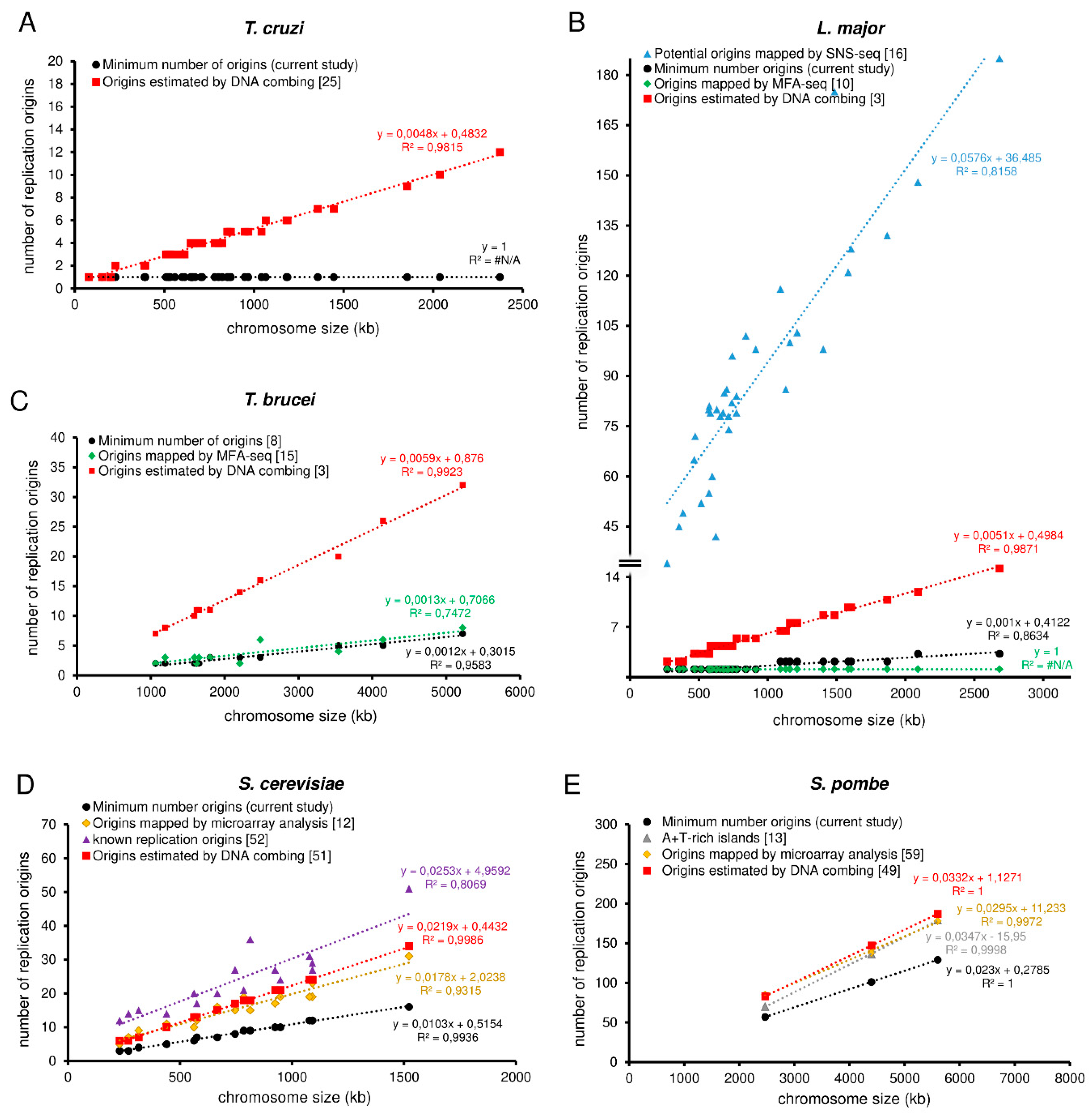
2.4. Estimation of the Minimum Number of Replication Origins (MO)
2.5. Origins Estimated by DNA Combing
3. Results and Discussion
3.1. The CeCyD Website Allows a Quick Estimation of the Cell Cycle Phases Duration
3.2. The Parameters Chromosome Size, S-Phase Duration, and Replication Rate Allow Estimating the MO per Chromosome in Any Organism
3.3. In the Presence of Hypothetical Replication Stress, the MO Increase to Maintain Robustness in S-Phase Duration
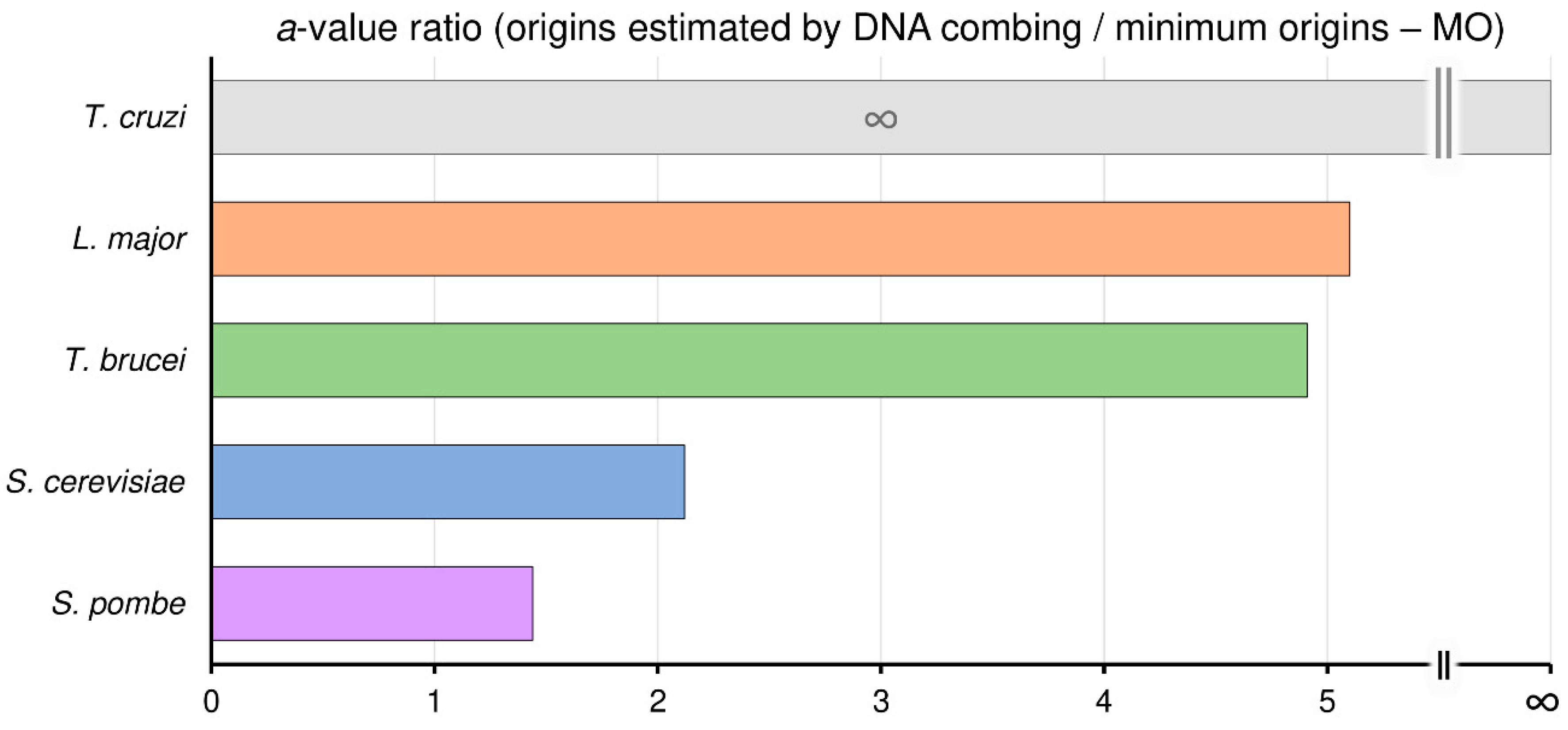
3.4. The MO Allows the Establishment of a Threshold That Can Serve as a Parameter by Other Methods That Detect Origins
3.5. Trypanosomatids Can Use Around Fivefold More Origins than the Minimum Required to Complete Replication within the S-Phase Duration
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Leonard, A.C.; Méchali, M. DNA replication origins. Cold Spring Harb. Perspect. Biol. 2013, 5, a010116. [Google Scholar] [CrossRef] [PubMed]
- Myllykallio, H.; Lopez, P.; López-García, P.; Heilig, R.; Saurin, W.; Zivanovic, Y.; Philippe, H.; Forterre, P. Bacterial mode of replication with eukaryotic-like machinery in a hyperthermophilic archaeon. Science 2000, 288, 2212–2215. [Google Scholar] [CrossRef] [PubMed]
- Stanojcic, S.; Sollelis, L.; Kuk, N.; Crobu, L.; Balard, Y.; Schwob, E.; Bastien, P.; Pagès, M.; Sterkers, Y. Single-molecule analysis of DNA replication reveals novel features in the divergent eukaryotes Leishmania and Trypanosoma brucei versus mammalian cells. Sci. Rep. 2016, 6, 23142. [Google Scholar] [CrossRef] [PubMed]
- Turrero García, M.; Chang, Y.; Arai, Y.; Huttner, W.B. S-phase duration is the main target of cell cycle regulation in neural progenitors of developing ferret neocortex. J. Comp. Neurol. 2016, 524, 456–470. [Google Scholar] [CrossRef]
- Günesdogan, U.; Jäckle, H.; Herzig, A. Histone supply regulates S phase timing and cell cycle progression. Elife 2014, 3, e02443. [Google Scholar] [CrossRef]
- Gindin, Y.; Valenzuela, M.S.; Aladjem, M.I.; Meltzer, P.S.; Bilke, S. A chromatin structure-based model accurately predicts DNA replication timing in human cells. Mol. Syst. Biol. 2014, 10, 722. [Google Scholar] [CrossRef]
- Zhang, Q.; Bassetti, F.; Gherardi, M.; Lagomarsino, M.C. Cell-to-cell variability and robustness in S-phase duration from genome replication kinetics. Nucleic Acids Res. 2017, 45, 8190–8198. [Google Scholar] [CrossRef]
- da Silva, M.S.; Cayres-Silva, G.R.; Vitarelli, M.O.; Marin, P.A.; Hiraiwa, P.M.; Araújo, C.B.; Scholl, B.B.; Ávila, A.R.; McCulloch, R.; Reis, M.S.; et al. Transcription activity contributes to the firing of non-constitutive origins in African trypanosomes helping to maintain robustness in S-phase duration. Sci. Rep. 2019, 9, 18512. [Google Scholar] [CrossRef]
- Robinson, N.P.; Bell, S.D. Origins of DNA replication in the three domains of life. FEBS J. 2005, 272, 3757–3766. [Google Scholar] [CrossRef]
- Marques, C.A.; Dickens, N.J.; Paape, D.; Campbell, S.J.; McCulloch, R. Genome-wide mapping reveals single-origin chromosome replication in Leishmania, a eukaryotic microbe. Genome Biol. 2015, 16, 230. [Google Scholar] [CrossRef]
- Sekedat, M.D.; Fenyö, D.; Rogers, R.S.; Tackett, A.J.; Aitchison, J.D.; Chait, B.T. GINS motion reveals replication fork progression is remarkably uniform throughout the yeast genome. Mol. Syst. Biol. 2010, 6, 353. [Google Scholar] [CrossRef] [PubMed]
- Yabuki, N.; Terashima, H.; Kitada, K. Mapping of early firing origins on a replication profile of budding yeast. Genes Cells 2002, 7, 781–789. [Google Scholar] [CrossRef] [PubMed]
- Segurado, M.; de Luis, A.; Antequera, F. Genome-wide distribution of DNA replication origins at A+T-rich islands in Schizosaccharomyces pombe. EMBO Rep. 2003, 4, 1048–1053. [Google Scholar] [CrossRef] [PubMed]
- Parker, M.W.; Botchan, M.R.; Berger, J.M. Mechanisms and regulation of DNA replication initiation in eukaryotes. Crit. Rev. Biochem. Mol. Biol. 2017, 52, 107–144. [Google Scholar] [CrossRef] [PubMed]
- Tiengwe, C.; Marcello, L.; Farr, H.; Dickens, N.; Kelly, S.; Swiderski, M.; Vaughan, D.; Gull, K.; Barry, J.D.; Bell, S.D.; et al. Genome-wide Analysis Reveals Extensive Functional Interaction between DNA Replication Initiation and Transcription in the Genome of Trypanosoma brucei. Cell Rep. 2012, 2, 185–197. [Google Scholar] [CrossRef] [PubMed]
- Lombraña, R.; Álvarez, A.; Fernández-Justel, J.M.; Almeida, R.; Poza-Carrión, C.; Gomes, F.; Calzada, A.; Requena, J.M.; Gómez, M. Transcriptionally Driven DNA Replication Program of the Human Parasite Leishmania major. Cell Rep. 2016, 16, 1774–1786. [Google Scholar] [CrossRef]
- Wang, X.; Lesterlin, C.; Reyes-Lamothe, R.; Ball, G.; Sherratt, D.J. Replication and segregation of an Escherichia coli chromosome with two replication origins. Proc. Natl. Acad. Sci. USA 2011, 108, 243–250. [Google Scholar] [CrossRef]
- Gao, F. Bacteria may have multiple replication origins. Front. Microbiol. 2015, 6, 324. [Google Scholar] [CrossRef]
- Müller, C.A.; Hawkins, M.; Retkute, R.; Malla, S.; Wilson, R.; Blythe, M.J.; Nakato, R.; Komata, M.; Shirahige, K.; De Moura, A.P.S.; et al. The dynamics of genome replication using deep sequencing. Nucleic Acids Res. 2013, 42, e3. [Google Scholar] [CrossRef]
- Salic, A.; Mitchison, T.J. A chemical method for fast and sensitive detection of DNA synthesis in vivo. Proc. Natl. Acad. Sci. USA 2008, 105, 2415–2420. [Google Scholar] [CrossRef]
- Williams, F.M. Dynamics of microbial populations. In Systems Analysis and Simulation in Ecology; Patten, B.C., Ed.; Academic Press Inc.: New York, NY, USA, 1971; pp. 198–268. [Google Scholar]
- Stanners, C.P.; Till, J.E. DNA synthesis in individual L-strain mouse cells. Biochim. Biophys. Acta 1960, 37, 406–419. [Google Scholar] [CrossRef]
- de Araujo, C.B.; Calderano, S.G.; Elias, M.C. The Dynamics of Replication in Trypanosoma cruzi Parasites by Single-Molecule Analysis. J. Eukaryot. Microbiol. 2019, 66, 514–518. [Google Scholar] [CrossRef] [PubMed]
- Iyer, D.R.; Rhind, N. The intra-S checkpoint responses to DNA damage. Genes 2017, 8, 74. [Google Scholar] [CrossRef] [PubMed]
- Nasmyth, K.; Nurse, P.; Fraser, R.S.S. The effect of cell mass on the cell cycle timing and duration of S-phase in fission yeast. J. Cell Sci. 1979, 39, 215–233. [Google Scholar]
- Carlson, C.R.; Grallert, B.; Stokke, T.; Boye, E. Regulation of the start of DNA replication in Schizosaccharomyces pombe. J. Cell Sci. 1999, 112, 939–946. [Google Scholar]
- Woodward, R.; Gull, K. Timing of nuclear and kinetoplast DNA replication and early morphological events in the cell cycle of Trypanosoma brucei. J. Cell Sci. 1990, 95 Pt 1, 49–57. [Google Scholar]
- Ploubidou, A.; Robinson, D.R.; Docherty, R.C.; Ogbadoyi, E.O.; Gull, K. Evidence for novel cell cycle checkpoints in trypanosomes: Kinetoplast segregation and cytokinesis in the absence of mitosis. J. Cell Sci. 1999, 112, 4641–4650. [Google Scholar]
- da Silva, M.S.; Monteiro, J.P.; Nunes, V.S.; Vasconcelos, E.J.; Perez, A.M.; Freitas-Júnior, L.d.H.; Elias, M.C.; Cano, M.I.N. Leishmania amazonensis Promastigotes Present Two Distinct Modes of Nucleus and Kinetoplast Segregation during Cell Cycle. PLoS ONE 2013, 8, e81397. [Google Scholar] [CrossRef]
- da Silva, M.S.; Muñoz, P.A.M.; Armelin, H.A.; Elias, M.C. Differences in the Detection of BrdU/EdU Incorporation Assays Alter the Calculation for G1, S, and G2 Phases of the Cell Cycle in Trypanosomatids. J. Eukaryot. Microbiol. 2017, 64, 756–770. [Google Scholar] [CrossRef]
- Tavernelli, L.E.; Motta, M.C.M.; Gonçalves, C.S.; da Silva, M.S.; Elias, M.C.; Alonso, V.L.; Serra, E.; Cribb, P. Overexpression of Trypanosoma cruzi High Mobility Group B protein (TcHMGB) alters the nuclear structure, impairs cytokinesis and reduces the parasite infectivity. Sci. Rep. 2019, 9, 192. [Google Scholar] [CrossRef]
- Ambit, A.; Woods, K.L.; Cull, B.; Coombs, G.H.; Mottram, J.C. Morphological events during the cell cycle of leishmania major. Eukaryot. Cell 2011, 10, 1429–1438. [Google Scholar] [CrossRef] [PubMed]
- Elias, M.C.; da Cunha, J.P.C.; de Faria, F.P.; Mortara, R.A.; Freymüller, E.; Schenkman, S. Morphological events during the Trypanosoma cruzi cell cycle. Protist 2007, 158, 147–157. [Google Scholar] [CrossRef] [PubMed]
- Brewer, B.J.; Chlebowicz-Sledziewska, E.; Fangman, W.L. Cell cycle phases in the unequal mother/daughter cell cycles of Saccharomyces cerevisiae. Mol. Cell. Biol. 1984, 4, 2529–2531. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ivanova, T.; Maier, M.; Missarova, A.; Ziegler-Birling, C.; Carey, L.B.; Mendoza, M. Budding yeast complete DNA replication after chromosome segregation begins. bioRxiv 2018, 407957. [Google Scholar]
- Berriman, M.; Ghedin, E.; Hertz-Fowler, C.; Blandin, G.; Renauld, H.; Bartholomeu, D.C.; Lennard, N.J.; Caler, E.; Hamlin, N.E.; Haas, B.; et al. The Genome of the African Trypanosome Trypanosoma brucei. Science 2005, 309, 416–422. [Google Scholar] [CrossRef]
- Saxena, S.; Somyajit, K.; Nagaraju, G. XRCC2 Regulates Replication Fork Progression during dNTP Alterations. Cell Rep. 2018, 25, 3273–3282.e6. [Google Scholar] [CrossRef]
- Wilhelm, T.; Magdalou, I.; Barascu, A.; Techer, H.; Debatisse, M.; Lopez, B.S. Spontaneous slow replication fork progression elicits mitosis alterations in homologous recombination-deficient mammalian cells. Proc. Natl. Acad. Sci. USA 2014, 111, 763–768. [Google Scholar] [CrossRef]
- Azvolinsky, A.; Giresi, P.G.; Lieb, J.D.; Zakian, V.A. Highly Transcribed RNA Polymerase II Genes Are Impediments to Replication Fork Progression in Saccharomyces cerevisiae. Mol. Cell 2009, 34, 722–734. [Google Scholar] [CrossRef]
- Deshpande, A.M.; Newlon, C.S. DNA replication fork pause sites dependent on transcription. Science 1996, 272, 1030–1033. [Google Scholar] [CrossRef]
- Dulev, S.; De Renty, C.; Mehta, R.; Minkov, I.; Schwob, E.; Strunnikov, A. Essential global role of CDC14 in DNA synthesis revealed by chromosome underreplication unrecognized by checkpoints in cdc14 mutants. Proc. Natl. Acad. Sci. USA 2009, 106, 14466–14471. [Google Scholar] [CrossRef]
- Branzei, D.; Foiani, M. Regulation of DNA repair throughout the cell cycle. Nat. Rev. Mol. Cell Biol. 2008, 9, 297–308. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Acebes, S.; Mourón, S.; Méndez, J. Uncoupling fork speed and origin activity to identify the primary cause of replicative stress phenotypes. J. Biol. Chem. 2018, 293, 12855–12861. [Google Scholar] [CrossRef] [PubMed]
- Zeman, M.K.; Cimprich, K.A. Causes and consequences of replication stress. Nat. Cell Biol. 2014, 16, 2–9. [Google Scholar] [CrossRef] [PubMed]
- Ge, X.Q.; Blow, J.J. Chk1 inhibits replication factory activation but allows dormant origin firing in existing factories. J. Cell Biol. 2010, 191, 1285–1297. [Google Scholar] [CrossRef] [PubMed]
- McIntosh, D.; Blow, J.J. Dormant Origins, the Licensing Checkpoint, and the Response to Replicative Stresses. Cold Spring Harb. Perspect. Biol. 2012, 4, a012955. [Google Scholar] [CrossRef]
- Chen, Y.-H.; Jones, M.J.K.; Yin, Y.; Crist, S.B.; Colnaghi, L.; Sims, R.J.; Rothenberg, E.; Jallepalli, P.V.; Huang, T.T. ATR-mediated phosphorylation of FANCI regulates dormant origin firing in response to replication stress. Mol. Cell 2015, 58, 323–338. [Google Scholar] [CrossRef]
- Courtot, L.; Hoffmann, J.S.; Bergoglio, V. The Protective Role of Dormant Origins in Response to Replicative Stress. Int. J. Mol. Sci. 2018, 19, 3569. [Google Scholar] [CrossRef]
- Poli, J.; Tsaponina, O.; Crabbé, L.; Keszthelyi, A.; Pantesco, V.; Chabes, A.; Lengronne, A.; Pasero, P. dNTP pools determine fork progression and origin usage under replication stress. EMBO J. 2012, 31, 883–894. [Google Scholar] [CrossRef]
- Patel, P.K.; Arcangioli, B.; Baker, S.P.; Bensimon, A.; Rhind, N. DNA replication origins fire stochastically in fission yeast. Mol. Biol. Cell 2006, 17, 308–316. [Google Scholar] [CrossRef]
- Oliva, A.; Rosebrock, A.; Ferrezuelo, F.; Pyne, S.; Chen, H.; Skiena, S.; Futcher, B.; Leatherwood, J. The cell cycle-regulated genes of Schizosaccharomyces pombe. PLoS Biol. 2005, 3, 1239–1260. [Google Scholar] [CrossRef]
- Fragkos, M.; Ganier, O.; Coulombe, P.; Méchali, M. DNA replication origin activation in space and time. Nat. Rev. Mol. Cell Biol. 2015, 16, 360–374. [Google Scholar] [CrossRef] [PubMed]
- Lengronne, A. Monitoring S phase progression globally and locally using BrdU incorporation in TK+ yeast strains. Nucleic Acids Res. 2001, 29, 1433–1442. [Google Scholar] [CrossRef] [PubMed]
- Nieduszynski, C.A.; Knox, Y.; Donaldson, A.D. Genome-wide identification of replication origins in yeast by comparative genomics. Genes Dev. 2006, 20, 1874–1879. [Google Scholar] [CrossRef]
- Broach, J.R.; Li, Y.Y.; Feldman, J.; Jayaram, M.; Abraham, J.; Nasmyth, K.A.; Hicks, J.B. Localization and sequence analysis of yeast origins of DNA replication. Cold Spring Harb. Symp. Quant. Biol. 1982, 47, 1165–1173. [Google Scholar] [CrossRef] [PubMed]
- Stinchcomb, D.T.; Struhl, K.; Davis, R.W. Isolation and characterisation of a yeast chromosomal replicator. Nature 1979, 282, 39–43. [Google Scholar] [CrossRef] [PubMed]
- Dershowitz, A.; Newlon, C.S. The effect on chromosome stability of deleting replication origins. Mol. Cell. Biol. 1993, 13, 391–398. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Raghuraman, M.K.; Winzeler, E.A.; Collingwood, D.; Hunt, S.; Wodicka, L.; Conway, A.; Lockhart, D.J.; Davis, R.W.; Brewer, B.J.; Fangman, W.L. Replication dynamics of the yeast genome. Science 2001, 294, 115–121. [Google Scholar] [CrossRef]
- Wyrick, J.J.; Aparicio, J.G.; Chen, T.; Barnett, J.D.; Jennings, E.G.; Young, R.A.; Bell, S.P.; Aparicio, O.M. Genome-wide distribution of ORC and MCM proteins in S. cerevisae: High-resolution mapping of replication origins. Science 2001, 294, 2357–2360. [Google Scholar] [CrossRef]
- Pasero, P.; Bensimon, A.; Schwob, E. Single-molecule analysis reveals clustering and epigenetic regulation of replication origins at the yeast rDNA locus. Genes Dev. 2002, 16, 2479–2484. [Google Scholar] [CrossRef]
- Heichinger, C.; Penkett, C.J.; Bähler, J.; Nurse, P. Genome-wide characterization of fission yeast DNA replication origins. EMBO J. 2006, 25, 5171–5179. [Google Scholar] [CrossRef]
- Yekezare, M.; Gómez-González, B.; Diffley, J.F.X. Controlling DNA replication origins in response to DNA damage—Inhibit globally, activate locally. J. Cell Sci. 2013, 126, 1297–1306. [Google Scholar] [CrossRef] [PubMed]
| Chrom. | T. cruzi1 | L. major2 | T. brucei3 | S. cerevisiae4 | S. pombe5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Size (bp) | MO | Size (bp) | MO | Size (bp) | MO | Size (bp) | MO | Size (bp) | MO | |
| I | 77,958 | 1 | 268,988 | 1 | 1,064,672 | 2 | 230,19 | 3 | 5,598,923 | 129 |
| II | 151,740 | 1 | 355,712 | 1 | 1,193,948 | 2 | 813,14 | 9 | 4,397,795 | 101 |
| III | 196,644 | 1 | 384,502 | 1 | 1,653,225 | 2 | 315,34 | 4 | 2,465,919 | 57 |
| IV | 200,401 | 1 | 472,852 | 1 | 1,590,432 | 2 | 1,522,19 | 16 | - | - |
| V | 227,319 | 1 | 465,823 | 1 | 1,802,303 | 2 | 574,86 | 7 | - | - |
| VI | 389,024 | 1 | 516,869 | 1 | 1,618,915 | 2 | 270,15 | 3 | - | - |
| VII | 391,095 | 1 | 596,352 | 1 | 2,205,233 | 3 | 1,090,94 | 12 | - | - |
| VIII | 393,423 | 1 | 574,960 | 1 | 2,481,190 | 3 | 562,64 | 6 | - | - |
| IX | 509,634 | 1 | 573,434 | 1 | 3,542,885 | 4 | 439,88 | 5 | - | - |
| X | 518,846 | 1 | 570,865 | 1 | 4,144,375 | 5 | 745,44 | 8 | - | - |
| XI | 526,141 | 1 | 582,573 | 1 | 5,223,313 | 6 | 666,45 | 7 | - | - |
| XII | 533,093 | 1 | 675,346 | 1 | - | - | 1,078,17 | 12 | - | - |
| XIII | 558,364 | 1 | 654,595 | 1 | - | - | 924,43 | 10 | - | - |
| XIV | 598,625 | 1 | 622,644 | 1 | - | - | 784,33 | 9 | - | - |
| XV | 612,853 | 1 | 629,517 | 1 | - | - | 1,091,28 | 12 | - | - |
| XVI | 646,207 | 1 | 714,651 | 1 | - | - | 948,06 | 10 | - | - |
| XVII | 648,584 | 1 | 684,829 | 1 | - | - | - | - | - | - |
| XVIII | 655,081 | 1 | 739,748 | 1 | - | - | - | - | - | - |
| XIX | 671,453 | 1 | 702,208 | 1 | - | - | - | - | - | - |
| XX | 656,799 | 1 | 742,537 | 1 | - | - | - | - | - | - |
| XXI | 704,149 | 1 | 772,972 | 1 | - | - | - | - | - | - |
| XXII | 710,778 | 1 | 716,602 | 1 | - | - | - | - | - | - |
| XXIII | 655,477 | 1 | 772,565 | 1 | - | - | - | - | - | - |
| XXIV | 779,922 | 1 | 840,950 | 1 | - | - | - | - | - | - |
| XXV | 822,374 | 2 | 912,845 | 1 | - | - | - | - | - | - |
| XXVI | 801,422 | 1 | 1,091,540 | 2 | - | - | - | - | - | - |
| XXVII | 850,241 | 2 | 1,130,424 | 2 | - | - | - | - | - | - |
| XXVIII | 853,233 | 1 | 1,160,104 | 2 | - | - | - | - | - | |
| XXIX | 870,934 | 1 | 1,212,663 | 2 | - | - | - | - | - | - |
| XXX | 863,882 | 1 | 1,403,434 | 2 | - | - | - | - | - | - |
| XXXI | 947,473 | 1 | 1,484,328 | 2 | - | - | - | - | - | - |
| XXXII | 968,069 | 1 | 1,604,637 | 2 | - | - | - | - | - | - |
| XXXIII | 1,041,172 | 1 | 1,583,653 | 2 | - | - | - | - | - | - |
| XXXIV | 1,065,764 | 1 | 1,866,748 | 2 | - | - | - | - | - | - |
| XXXV | 1,186,946 | 1 | 2,090,474 | 3 | - | - | - | - | - | - |
| XXXVI | 1,180,744 | 1 | 2,682,151 | 3 | - | - | - | - | - | - |
| XXXVII | 1,355,803 | 1 | - | - | - | - | - | - | - | - |
| XXXVIII | 1,444,805 | 1 | - | - | - | - | - | - | - | - |
| XXXIX | 1,854,104 | 1 | - | - | - | - | - | - | - | - |
| XL | 2,036,760 | 1 | - | - | - | - | - | - | - | - |
| XLI | 2,371,736 | 1 | - | - | - | - | - | - | - | - |
| Chrom. | T. cruzi1 | L. major2 | T. brucei3 | S. cerevisiae4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MO | MOMR | MOHR | MO | MOMR | MOHR | MO | MOMR | MOHR | MO | MOMR | MOHR | |
| I | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 4 | 3 | 4 | 8 |
| II | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 3 | 5 | 9 | 13 | 26 |
| III | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 3 | 6 | 4 | 5 | 10 |
| IV | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 3 | 6 | 16 | 24 | 48 |
| V | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 4 | 7 | 7 | 10 | 19 |
| VI | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 3 | 6 | 3 | 5 | 9 |
| VII | 1 | 1 | 1 | 1 | 1 | 2 | 3 | 4 | 8 | 12 | 18 | 35 |
| VIII | 1 | 1 | 1 | 1 | 1 | 2 | 3 | 5 | 9 | 6 | 9 | 18 |
| IX | 1 | 1 | 1 | 1 | 1 | 2 | 4 | 7 | 13 | 5 | 7 | 14 |
| X | 1 | 1 | 1 | 1 | 1 | 2 | 5 | 8 | 15 | 8 | 12 | 24 |
| XI | 1 | 1 | 1 | 1 | 1 | 2 | 6 | 10 | 19 | 7 | 11 | 21 |
| XII | 1 | 1 | 1 | 1 | 2 | 3 | - | - | - | 12 | 17 | 34 |
| XIII | 1 | 1 | 1 | 1 | 2 | 3 | - | - | - | 10 | 15 | 30 |
| XIV | 1 | 1 | 1 | 1 | 1 | 3 | - | - | - | 9 | 13 | 25 |
| XV | 1 | 1 | 1 | 1 | 2 | 3 | - | - | - | 12 | 18 | 35 |
| XVI | 1 | 1 | 1 | 1 | 2 | 3 | - | - | - | 10 | 15 | 30 |
| XVII | 1 | 1 | 1 | 1 | 2 | 3 | - | - | - | - | - | - |
| XVIII | 1 | 1 | 1 | 1 | 2 | 3 | - | - | - | - | - | - |
| XIX | 1 | 1 | 1 | 1 | 2 | 3 | - | - | - | - | - | - |
| XX | 1 | 1 | 1 | 1 | 2 | 3 | - | - | - | - | - | - |
| XXI | 1 | 1 | 1 | 1 | 2 | 3 | - | - | - | - | - | - |
| XXII | 1 | 1 | 1 | 1 | 2 | 3 | - | - | - | - | - | - |
| XXIII | 1 | 1 | 1 | 1 | 2 | 3 | - | - | - | - | - | - |
| XXIV | 1 | 1 | 1 | 1 | 2 | 3 | - | - | - | - | - | - |
| XXV | 1 | 1 | 2 | 1 | 2 | 3 | - | - | - | - | - | - |
| XXVI | 1 | 1 | 1 | 2 | 2 | 4 | - | - | - | - | - | - |
| XXVII | 1 | 1 | 2 | 2 | 2 | 4 | - | - | - | - | - | - |
| XXVIII | 1 | 1 | 2 | 2 | 2 | 4 | - | - | - | - | - | |
| XXIX | 1 | 1 | 2 | 2 | 2 | 4 | - | - | - | - | - | - |
| XXX | 1 | 1 | 2 | 2 | 3 | 5 | - | - | - | - | - | - |
| XXXI | 1 | 1 | 2 | 2 | 3 | 5 | - | - | - | - | - | - |
| XXXII | 1 | 1 | 2 | 2 | 3 | 6 | - | - | - | - | - | - |
| XXXIII | 1 | 1 | 2 | 2 | 3 | 6 | - | - | - | - | - | - |
| XXXIV | 1 | 1 | 2 | 2 | 3 | 6 | - | - | - | - | - | - |
| XXXV | 1 | 1 | 2 | 3 | 4 | 7 | - | - | - | - | - | - |
| XXXVI | 1 | 1 | 2 | 3 | 5 | 9 | - | - | - | - | - | - |
| XXXVII | 1 | 1 | 2 | - | - | - | - | - | - | - | - | - |
| XXXVIII | 1 | 1 | 2 | - | - | - | - | - | - | - | - | - |
| XXXIX | 1 | 2 | 2 | - | - | - | - | - | - | - | - | - |
| XL | 1 | 2 | 2 | - | - | - | - | - | - | - | - | - |
| XLI | 1 | 2 | 2 | - | - | - | - | - | - | - | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
da Silva, M.S.; O. Vitarelli, M.; F. Souza, B.; Elias, M.C. Comparative Analysis of the Minimum Number of Replication Origins in Trypanosomatids and Yeasts. Genes 2020, 11, 523. https://doi.org/10.3390/genes11050523
da Silva MS, O. Vitarelli M, F. Souza B, Elias MC. Comparative Analysis of the Minimum Number of Replication Origins in Trypanosomatids and Yeasts. Genes. 2020; 11(5):523. https://doi.org/10.3390/genes11050523
Chicago/Turabian Styleda Silva, Marcelo S., Marcela O. Vitarelli, Bruno F. Souza, and Maria Carolina Elias. 2020. "Comparative Analysis of the Minimum Number of Replication Origins in Trypanosomatids and Yeasts" Genes 11, no. 5: 523. https://doi.org/10.3390/genes11050523
APA Styleda Silva, M. S., O. Vitarelli, M., F. Souza, B., & Elias, M. C. (2020). Comparative Analysis of the Minimum Number of Replication Origins in Trypanosomatids and Yeasts. Genes, 11(5), 523. https://doi.org/10.3390/genes11050523