Size-Regulated Symmetry Breaking in Reaction-Diffusion Models of Developmental Transitions
Abstract
1. Introduction
2. Reaction–Diffusion as a Framework to Understand Size-Regulated Symmetry-Breaking
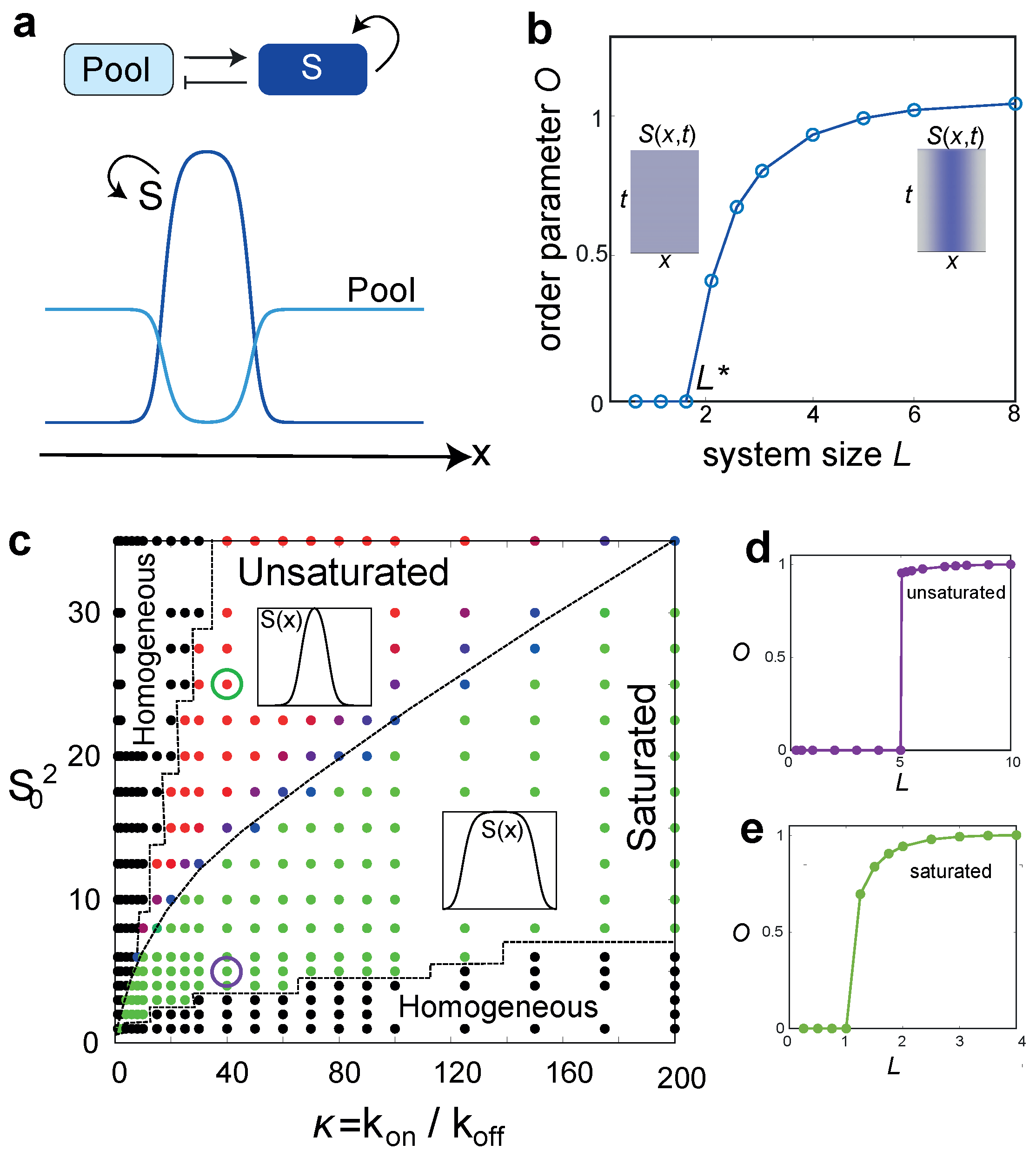
3. A Minimal Model for Size-Regulated Symmetry-Breaking
4. Critical Size for Polarisation Can Be Utilised to Enact Cell State Transitions
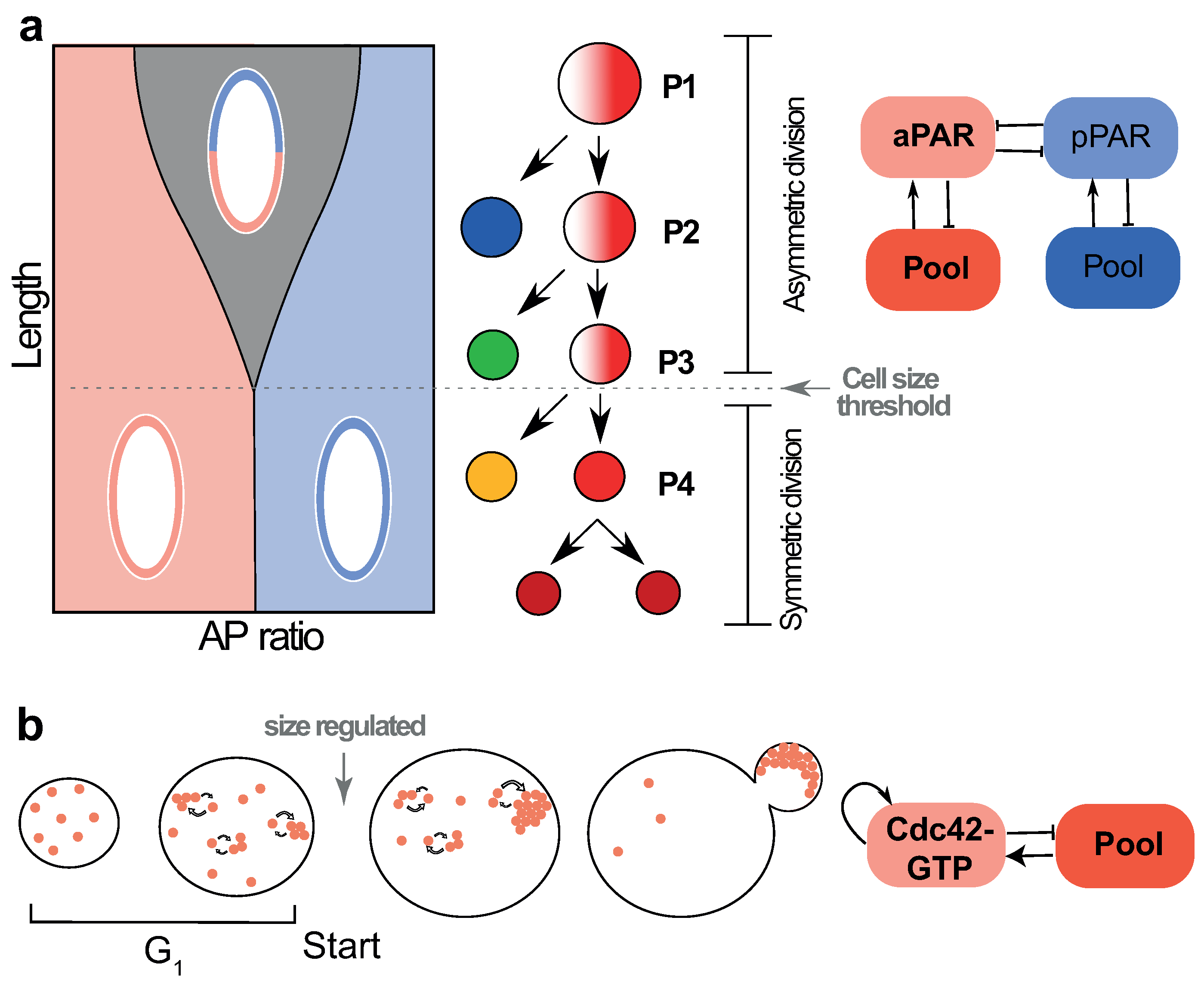
4.1. Cell Size Dependent Transition from Asymmetric to Symmetric Division in the Early C. elegans Embryo
4.2. Size-Dependent Polarity Establishment in Budding Yeast
5. Sequential Pattern Formation and Polarisation Can Be Coordinated by a Growing Domain
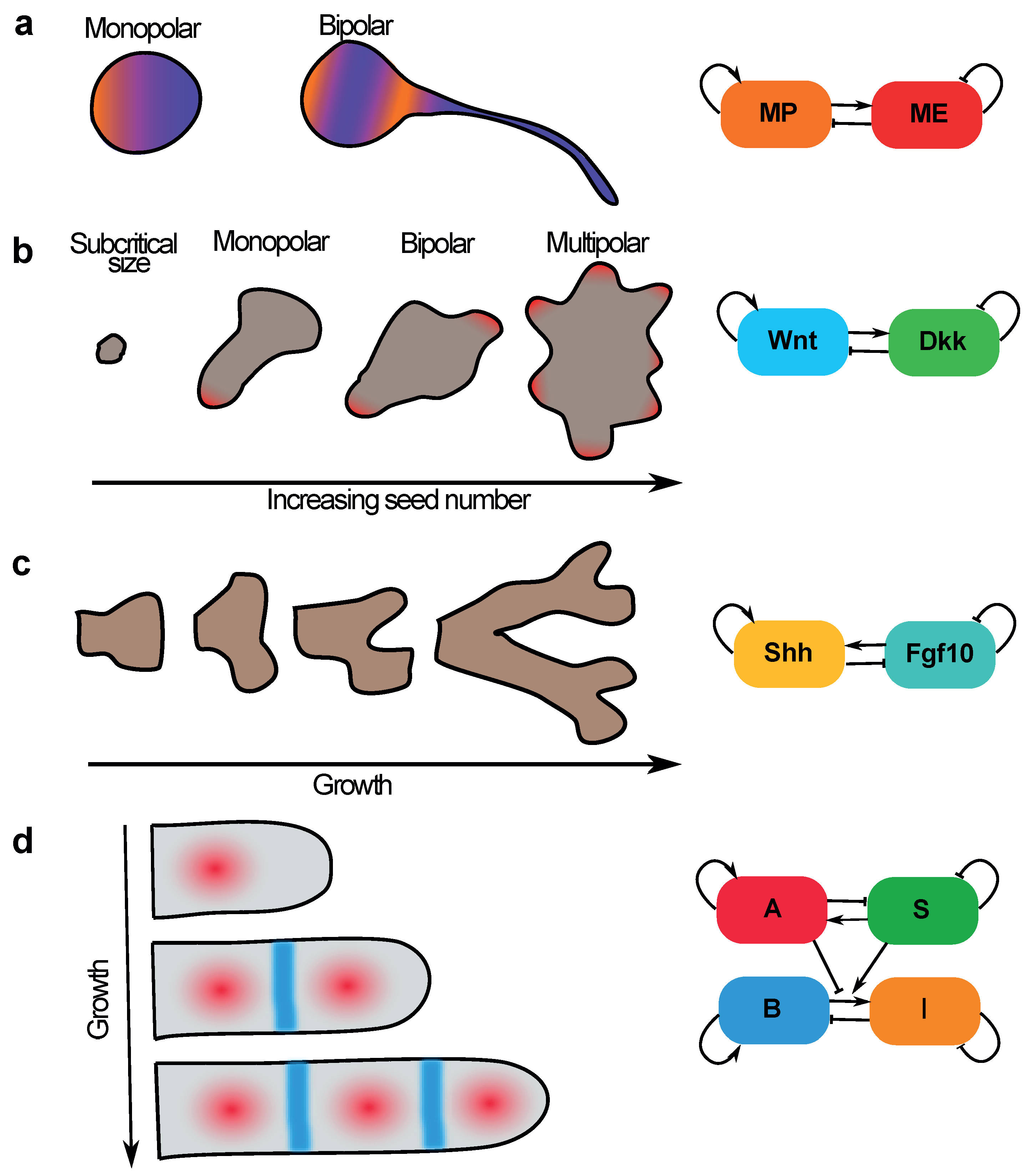
5.1. Neuronal Sequential Bipolarisation Coordinated by Membrane Growth
5.2. Size-Dependent Sequential Patterning in Mammalian Development—Insights from Gastruloids
5.3. Sequential Patterning of Phalanges in Developing Digits Is Coordinated by Coupling Patterning to Growth
6. Regulating Pattern Size and Lifetime in Growing Systems
6.1. Case 1: Transient Polarity Pattern Due to Growth-Induced Dilution
6.2. Case 2: Pattern Scaling Due to Proportional Growth of System Size and the Subunit Pool
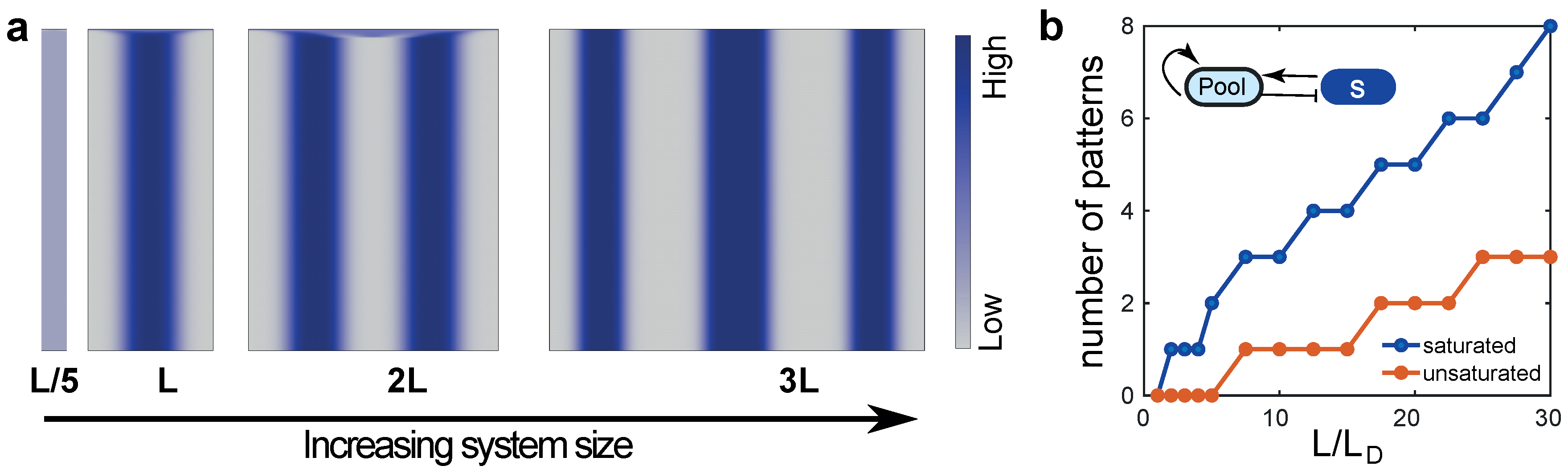
6.3. Case 3: Pattern Splitting
7. Using Growth as a Timer: Transient Symmetry Breaking at Intermediate Size
8. Overcoming Size Constraints: Scaling Patterns in Growing Systems
8.1. Autocatalysis as a Mechanism to Preserve Patterns in the Face of Growth
8.2. Expander-Coupled Systems Can Scale Patterns to Domain Size Irrespective of History
9. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Meinhardt, H. Models of biological pattern formation: From elementary steps to the organization of embryonic axes. Curr. Top. Dev. Biol. 2008, 81, 1–63. [Google Scholar] [PubMed]
- Green, J.B.; Sharpe, J. Positional information and reaction-diffusion: Two big ideas in developmental biology combine. Development 2015, 142, 1203–1211. [Google Scholar] [CrossRef] [PubMed]
- Saiz-Lopez, P.; Chinnaiya, K.; Campa, V.M.; Delgado, I.; Ros, M.A.; Towers, M. An intrinsic timer specifies distal structures of the vertebrate limb. Nat. Commun. 2015, 6, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Briscoe, J.; Small, S. Morphogen rules: Design principles of gradient-mediated embryo patterning. Development 2015, 142, 3996–4009. [Google Scholar] [CrossRef] [PubMed]
- Waters, C.M.; Bassler, B.L. Quorum sensing: Cell-to-cell communication in bacteria. Annu. Rev. Cell Dev. Biol. 2005, 21, 319–346. [Google Scholar] [CrossRef] [PubMed]
- Jörg, D.J.; Kitadate, Y.; Yoshida, S.; Simons, B.D. Competition for Stem Cell Fate Determinants as a Mechanism for Tissue Homeostasis. arXiv 2019, arXiv:1901.03903. [Google Scholar]
- Altschuler, S.J.; Angenent, S.B.; Wang, Y.; Wu, L.F. On the spontaneous emergence of cell polarity. Nature 2008, 454, 886–889. [Google Scholar] [CrossRef]
- Chara, O.; Tanaka, E.M.; Brusch, L. Mathematical modeling of regenerative processes. In Current Topics in Developmental Biology; Elsevier: Amsterdam, The Netherlands, 2014; Volume 108, pp. 283–317. [Google Scholar]
- Ebisuya, M.; Briscoe, J. What does time mean in development? Development 2018, 145, dev164368. [Google Scholar] [CrossRef] [PubMed]
- Turing, A.M. The chemical basis of morphogenesis. Phil. Trans. R. Soc. Lond. 1952, 237, 37–72. [Google Scholar]
- Kondo, S.; Miura, T. Reaction-Diffusion Model as a Framework for Understanding Biological Pattern Formation. Science 1999, 329, 1616–1620. [Google Scholar] [CrossRef]
- Butty, A.; Perrinjaquet, N.; Petit, A.; Jaquenoud, M.; Segall, J.; Hofmann, K.; Zwahlen, C.; Peter, M. A positive feedback loop stabilizes the guanine-nucleotide exchange factor Cdc24 at sites of polarization. EMBO J. 2002, 21, 1565–1576. [Google Scholar] [CrossRef]
- Kauffman, S.A. Pattern formation in the Drosophila embryo. Phil. Trans. R. Soc. Lond. B 1981, 295, 567–594. [Google Scholar]
- Meinhardt, A.; Gierer, J. Applications of a theory of biological pattern formation based on lateral inhibition. J. Cell Sci. 1974, 15, 321–346. [Google Scholar] [PubMed]
- Sick, S.; Reinker, S.; Timmer, J.; Schlake, T. WNT and DKK determine hair follicle spacing through a reaction-diffusion mechanism. Science 2006, 314, 1447–1450. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, T.; Mine, N.; Nakaguchi, E.; Mochizuki, A.; Yamamoto, M.; Yashiro, K.; Meno, C.; Hamada, H. Generation of robust left-right asymmetry in the mouse embryo requires a self-enhancement and lateral-inhibition system. Dev. Cell 2006, 11, 495–504. [Google Scholar] [CrossRef] [PubMed]
- Newman, S.A.; Frisch, H.L. Dynamics of skeletal pattern formation in developing chick limb. Science 1979, 205, 662–668. [Google Scholar] [CrossRef] [PubMed]
- Miura, T.; Shiota, K. TGFbeta2 acts as an “activator” molecule in reaction-diffusion model and is involved in cell sorting phenomenon in mouse limb micromass culture. Dev. Dyn. 2000, 217, 241–249. [Google Scholar] [CrossRef]
- Raspopovic, J.; Marcon, L.; Russo, L.; Sharpe, J. Digit patterning is controlled by a Bmp-Sox9-Wnt Turing network modulated by morphogen gradients. Science 2014, 345, 566–570. [Google Scholar] [CrossRef]
- Meinhardt, H.; de Boer, P.A.J. Pattern formation in Escherichia coli: A model for the pole-to-pole oscillations of Min proteins and the localization of the division site. Proc. Natl. Acad. Sci. USA 2001, 98, 14202–14207. [Google Scholar] [CrossRef] [PubMed]
- Bement, W.M.; Leda, M.; Moe, A.M.; Kita, A.M.; Larson, M.E.; Golding, A.E.; Pfeuti, C.; Su, K.C.; Miller, A.L.; Goryachev, A.B.; et al. Activator–inhibitor coupling between Rho signalling and actin assembly makes the cell cortex an excitable medium. Nat. Cell Biol. 2015, 17, 1471–1483. [Google Scholar] [CrossRef]
- Michaux, J.B.; Robin, F.B.; McFadden, W.M.; Munro, E.M. Excitable RhoA dynamics drive pulsed contractions in the early C. elegans embryo. J. Cell Biol. 2018, 217, 4230–4252. [Google Scholar] [CrossRef] [PubMed]
- Koch, A.; Meinhardt, H. Biological pattern formation: From basic mechanisms to complex structures. Rev. Mod. Phys. 1994, 66, 1481. [Google Scholar] [CrossRef]
- Marcon, L.; Sharpe, J. Turing patterns in development: What about the horse part? Curr. Opin. Genet. Dev. 2012, 22, 578–584. [Google Scholar] [CrossRef] [PubMed]
- Menshykau, D.; Kraemer, C.; Iber, D. Branch mode selection during early lung development. PLoS Comput. Biol. 2012, 8, e1002377. [Google Scholar] [CrossRef] [PubMed]
- Mori, Y.; Jilkine, A.; Edelstein-Keshet, A. Wave-Pinning and Cell Polarity from a Bistable Reaction-Diffusion System. Biophys. J. 2008, 94, 3684–3697. [Google Scholar] [CrossRef] [PubMed]
- Halatek, J.; Brauns, F.; Frey, E. Self-organization principles of intracellular pattern formation. Phil. Trans. R. Soc. Lond B 2018, 373, 20170107. [Google Scholar] [CrossRef]
- Munro, E.; Nance, J.; Priess, J.R. Cortical flows powered by asymmetrical contraction transport PAR proteins to establish and maintain anterior-posterior polarity in the early C. elegans embryo. Dev. Cell 2004, 7, 413–424. [Google Scholar] [CrossRef]
- Goehring, N.W.; Trong, P.K.; Bois, J.S.; Chowdhury, D.; Nicola, E.M.; Hyman, A.A.; Grill, S.W. Polarization of PAR proteins by advective triggering of a pattern-forming system. Science 2011, 334, 1137–1141. [Google Scholar] [CrossRef]
- Tostevin, F.; Howard, M. Modeling the establishment of PAR protein polarity in the one-cell C. elegans embryo. Biophys. J. 2008, 95, 4512–4522. [Google Scholar] [CrossRef]
- Goryachev, A.B.; Pokhilko, A.V. Dynamics of Cdc42 network embodies a Turing-type mechanism of yeast cell polarity. FEBS Lett. 2008, 582, 1437–1443. [Google Scholar] [CrossRef]
- Savage, N.S.; Layton, A.T.; Lew, D.J. Mechanistic mathematical model of polarity in yeast. Mol. Biol. Cell 2012, 23, 1998–2013. [Google Scholar] [CrossRef] [PubMed]
- Goryachev, A.B.; Leda, M. Many roads to symmetry breaking: Molecular mechanisms and theoretical models of yeast cell polarity. Mol. Biol. Cell 2017, 28, 370–380. [Google Scholar] [CrossRef] [PubMed]
- Howard, M.; Rutenberg, A.D.; de Vet, S. Dynamic compartmentalization of bacteria: Accurate division in E. coli. Phys. Rev. Lett. 2001, 87, 278102. [Google Scholar] [CrossRef] [PubMed]
- Kruse, K. A dynamic model for determining the middle of Escherichia coli. Biophys. J. 2002, 82, 618–627. [Google Scholar] [CrossRef]
- Huang, K.C.; Meir, Y.; Wingreen, N.S. Dynamic structures in Escherichia coli: Spontaneous formation of MinE rings and MinD polar zones. Proc. Natl. Acad. Sci. USA 2003, 100, 12724–12728. [Google Scholar] [CrossRef] [PubMed]
- Gierer, A.; Meinhardt, H. A theory of biological pattern formation. Kybernetik 1972, 12, 30–39. [Google Scholar] [CrossRef] [PubMed]
- Hiscock, T.W.; Megason, S.G. Mathematically guided approaches to distinguish models of periodic patterning. Development 2015, 142, 409–419. [Google Scholar] [CrossRef]
- Frohnhöfer, H.G.; Krauss, J.; Maischein, H.M.; Nüsslein-Volhard, C. Iridophores and their interactions with other chromatophores are required for stripe formation in zebrafish. Development 2013, 140, 2997–3007. [Google Scholar] [CrossRef]
- Murray, J.; Oster, G. Cell traction models for generating pattern and form in morphogenesis. J. Math. Biol. 1984, 19, 265–279. [Google Scholar] [CrossRef]
- Howard, J.; Grill, S.W.; Bois, J.S. Turing’s next steps: The mechanochemical basis of morphogenesis. Nat. Rev. Mol. Cell Biol. 2011, 12, 392–398. [Google Scholar] [CrossRef]
- Granero, M.; Porati, A.; Zanacca, D. A bifurcation analysis of pattern formation in a diffusion governed morphogenetic field. J. Math. Biol. 1977, 4, 21–27. [Google Scholar] [CrossRef] [PubMed]
- Zadorin, A.S.; Rondelez, Y.; Gines, G.; Dilhas, V.; Urtel, G.; Zambrano, A.; Galas, J.C.; Estevez-Torres, A. Synthesis and materialization of a reaction–diffusion French flag pattern. Nat. Chem. 2017, 9, 990–996. [Google Scholar] [CrossRef] [PubMed]
- Chiou, J.G.; Ramirez, S.A.; Elston, T.C.; Witelski, T.P.; Schaeffer, D.G.; Lew, D.J. Principles that govern competition or co-existence in Rho-GTPase driven polarization. PLoS Comput. Biol. 2018, 14, e1006095. [Google Scholar] [CrossRef] [PubMed]
- Otsuji, M.; Ishihara, S.; Co, C.; Kaibuchi, K.; Mochizuki, A.; Kuroda, S. A mass conserved reaction–diffusion system captures properties of cell polarity. PLoS Comput. Biol. 2007, 3, e108. [Google Scholar] [CrossRef]
- Banerjee, D.S.; Banerjee, S. Size regulation of multiple organelles competing for a shared subunit pool. bioRxiv 2020, bioRxiv:902783. [Google Scholar] [CrossRef]
- Brauns, F.; Halatek, J.; Frey, E. Phase-space geometry of reaction–diffusion dynamics. arXiv 2018, arXiv:1812.08684. [Google Scholar]
- Goehring, N.W.; Hyman, A.A. Organelle growth control through limiting pools of cytoplasmic components. Curr. Biol. 2012, 22, R330–R339. [Google Scholar] [CrossRef]
- Hoege, C.; Hyman, A.A. Principles of PAR polarity in Caenorhabditis elegans embryos. Nat. Rev. Mol. Cell Biol. 2013, 14, 315–322. [Google Scholar] [CrossRef]
- Kemphues, K.J.; Priess, J.R.; Morton, D.G.; Cheng, N. Identification of genes required for cytoplasmic localization in early C. elegans embryos. Cell 1988, 52, 311–320. [Google Scholar] [CrossRef]
- Goldstein, B.; Hird, S.N. Specification of the anteroposterior axis in Caenorhabditis elegans. Development 1996, 122, 1467–1474. [Google Scholar]
- Nguyen-Ngoc, T.; Afshar, K.; Gönczy, P. Coupling of cortical dynein and Gα proteins mediates spindle positioning in Caenorhabditis elegans. Nat. Cell Biol. 2007, 9, 1294–1302. [Google Scholar] [CrossRef] [PubMed]
- Gönczy, P. Mechanisms of asymmetric cell division: Flies and worms pave the way. Nat. Rev. Mol. Cell Biol. 2008, 9, 355–366. [Google Scholar] [CrossRef] [PubMed]
- Motegi, F.; Zonies, S.; Hao, Y.; Cuenca, A.A.; Griffin, E.; Seydoux, G. Microtubules induce self-organization of polarized PAR domains in Caenorhabditis elegans zygotes. Nat. Cell Biol. 2011, 13, 1361–1367. [Google Scholar] [CrossRef] [PubMed]
- Sailer, A.; Anneken, A.; Li, Y.; Lee, S.; Munro, E. Dynamic opposition of clustered proteins stabilizes cortical polarity in the C. elegans zygote. Dev. Cell 2015, 35, 131–142. [Google Scholar] [CrossRef] [PubMed]
- Hubatsch, L.; Peglion, F.; Reich, J.D.; Rodrigues, N.T.; Hirani, N.; Illukkumbura, R.; Goehring, N.W. A cell-size threshold limits cell polarity and asymmetric division potential. Nat. Phys. 2019, 15, 1078–1085. [Google Scholar] [CrossRef] [PubMed]
- Sulston, J.E.; Schierenberg, E.; White, J.G.; Thomson, J. The embryonic cell lineage of the nematode Caenorhabditis elegans. Dev. Biol. 1983, 100, 64–119. [Google Scholar] [CrossRef]
- Chiou, J.g.; Balasubramanian, M.K.; Lew, D.J. Cell polarity in yeast. Annu. Rev. Cell Dev. Biol. 2017, 33, 77–101. [Google Scholar] [CrossRef] [PubMed]
- Di Talia, S.; Skotheim, J.M.; Bean, J.M.; Siggia, E.D.; Cross, F.R. The effects of molecular noise and size control on variability in the budding yeast cell cycle. Nature 2007, 448, 947–951. [Google Scholar] [CrossRef] [PubMed]
- Ozbudak, E.M.; Becskei, A.; Oudenaarden, A. A system of counteracting feedback loops regulates Cdc42p activity during spontaneous cell polarization. Dev. Cell 2005, 9, 565–571. [Google Scholar] [CrossRef] [PubMed]
- Okada, S.; Leda, M.; Hanna, J.; Savage, N.S.; Bi, E.; Goryachev, A.B. Daughter Cell Identity Emerges from the Interplay of Cdc42, Septins, and Exocytosis. Dev. Cell 2013, 26, 148–161. [Google Scholar] [CrossRef]
- Turner, J.J.; Ewald, J.C.; Skotheim, J.M. Cell size control in yeast. Curr. Biol. 2012, 22, R350–R359. [Google Scholar] [CrossRef] [PubMed]
- Howell, A.S.; Savage, N.S.; Johnson, S.A.; Bose, I.; Wagner, A.W.; Zyla, T.R.; Nijhout, H.F.; Reed, M.C.; Goryachev, A.B.; Lew, D.J. Singularity in Polarization: Rewiring Yeast Cells to Make Two Buds. Cell 2009, 139, 731–743. [Google Scholar] [CrossRef] [PubMed]
- Maroto, M.; Bone, R.A.; Dale, J.K. Somitogenesis. Development 2012, 139, 2453–2456. [Google Scholar] [CrossRef] [PubMed]
- Sarrazin, A.F.; Peel, A.D.; Averof, M. A segmentation clock with two-segment periodicity in insects. Science 2012, 336, 338–341. [Google Scholar] [CrossRef]
- LoTurco, J.J.; Bai, J. The multipolar stage and disruptions in neuronal migration. Trends Neurosci. 2006, 29, 407–413. [Google Scholar] [CrossRef]
- Noctor, S.C.; Martínez-Cerdeño, V.; Ivic, L.; Kriegstein, A.R. Cortical neurons arise in symmetric and asymmetric division zones and migrate through specific phases. Nat. Neurosci. 2004, 7, 136–144. [Google Scholar] [CrossRef]
- De Anda, F.C.; Gärtner, A.; Tsai, L.H.; Dotti, C.G. Pyramidal neuron polarity axis is defined at the bipolar stage. J. Cell Sci. 2008, 121, 178–185. [Google Scholar] [CrossRef]
- Menchón, S.A.; Gärtner, A.; Román, P.; Dotti, C.G. Neuronal (bi) polarity as a self-organized process enhanced by growing membrane. PLoS ONE 2011, 6, e24190. [Google Scholar] [CrossRef] [PubMed]
- Van den Brink, S.C.; Baillie-Johnson, P.; Balayo, T.; Hadjantonakis, A.K.; Nowotschin, S.; Turner, D.A.; Arias, A.M. Symmetry breaking, germ layer specification and axial organisation in aggregates of mouse embryonic stem cells. Development 2014, 141, 4231–4242. [Google Scholar] [CrossRef] [PubMed]
- Arnold, S.J.; Robertson, E.J. Making a commitment: Cell lineage allocation and axis patterning in the early mouse embryo. Nat. Rev. Mol. Cell Biol. 2009, 10, 91–103. [Google Scholar] [CrossRef] [PubMed]
- Harrison, S.E.; Sozen, B.; Christodoulou, N.; Kyprianou, C.; Zernicka-Goetz, M. Assembly of embryonic and extraembryonic stem cells to mimic embryogenesis in vitro. Science 2017, 356, eaal1810. [Google Scholar] [CrossRef] [PubMed]
- Warmflash, A.; Sorre, B.; Etoc, F.; Siggia, E.D.; Brivanlou, A.H. A method to recapitulate early embryonic spatial patterning in human embryonic stem cells. Nat. Methods 2014, 11, 847. [Google Scholar] [CrossRef] [PubMed]
- Ten Berge, D.; Koole, W.; Fuerer, C.; Fish, M.; Eroglu, E.; Nusse, R. Wnt signaling mediates self-organization and axis formation in embryoid bodies. Cell Stem Cell 2008, 3, 508–518. [Google Scholar] [CrossRef] [PubMed]
- Sagy, N.; Slovin, S.; Allalouf, M.; Pour, M.; Savyon, G.; Boxman, J.; Nachman, I. Prediction and control of symmetry breaking in embryoid bodies by environment and signal integration. Development 2019, 146, dev181917. [Google Scholar] [CrossRef]
- Turner, D.A.; Girgin, M.; Alonso-Crisostomo, L.; Trivedi, V.; Baillie-Johnson, P.; Glodowski, C.R.; Hayward, P.C.; Collignon, J.; Gustavsen, C.; Serup, P.; et al. Anteroposterior polarity and elongation in the absence of extra-embryonic tissues and of spatially localised signalling in gastruloids: Mammalian embryonic organoids. Development 2017, 144, 3894–3906. [Google Scholar] [CrossRef] [PubMed]
- Morgani, S.M.; Hadjantonakis, A.K. Signaling regulation during gastrulation: Insights from mouse embryos and in vitro systems. eLife 2019, 137, 391–431. [Google Scholar]
- Juan, H.; Hamada, H. Roles of nodal-lefty regulatory loops in embryonic patterning of vertebrates. Genes Cells 2001, 6, 923–930. [Google Scholar] [CrossRef]
- Shahbazi, M.N.; Siggia, E.D.; Zernicka-Goetz, M. Self-organization of stem cells into embryos: A window on early mammalian development. Science 2019, 364, 948–951. [Google Scholar] [CrossRef]
- Cornwall Scoones, J.; Hiscock, T.W. A dot-stripe Turing model of joint patterning in the tetrapod limb. Development 2020, 147, dev183699. [Google Scholar] [CrossRef]
- Crampin, E.J.; Gaffney, E.A.; Maini, P.K. Reaction and diffusion on growing domains: Scenarios for robust pattern formation. Bull. Math. Biol. 1999, 61, 1093–1120. [Google Scholar] [CrossRef]
- Postma, M.; Roelofs, J.; Goedhart, J.; Gadella, T.W.; Visser, A.J.; Van Haastert, P.J. Uniform cAMP stimulation of Dictyostelium cells induces localized patches of signal transduction and pseudopodia. Mol. Biol. Cell 2003, 14, 5019–5027. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Erzurumlu, R.S.; Jhaveri, S.; Benowitz, L.I. Transient patterns of GAP-43 expression during the formation of barrels in the rat somatosensory cortex. J. Comp. Neurol. 1990, 292, 443–456. [Google Scholar] [CrossRef] [PubMed]
- Hecht, I.; Kessler, D.A.; Levine, H. Transient localized patterns in noise-driven reaction-diffusion systems. Phys. Rev. Lett. 2010, 104, 158301. [Google Scholar] [CrossRef] [PubMed]
- Ben-Zvi, D.; Shilo, B.Z.; Barkai, N. Scaling of morphogen gradients. Curr. Opin. Genet. Dev. 2011, 21, 704–710. [Google Scholar] [CrossRef] [PubMed]
- Wolpert, L. Positional information and the spatial pattern of cellular differentiation. J. Theor. Biol. 1969, 25, 1–47. [Google Scholar] [CrossRef]
- Kinney, J.B.; Atwal, G.S. Equitability, mutual information, and the maximal information coefficient. Proc. Natl. Acad. Sci. USA 2014, 111, 3354–3359. [Google Scholar] [CrossRef]
- Werner, S.; Stückemann, T.; Amigo, M.B.; Rink, J.C.; Jülicher, F.; Friedrich, B.M. Scaling and regeneration of self-organized patterns. Phys. Rev. Lett. 2015, 114, 138101. [Google Scholar] [CrossRef] [PubMed]
- Mark, S.; Shlomovitz, R.; Gov, N.S.; Poujade, M.; Grasland-Mongrain, E.; Silberzan, P. Physical model of the dynamic instability in an expanding cell culture. Biophys. J. 2010, 98, 361–370. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, S.; Utuje, K.J.; Marchetti, M.C. Propagating stress waves during epithelial expansion. Phys. Rev. Lett. 2015, 114, 228101. [Google Scholar] [CrossRef] [PubMed]
- Ravasio, A.; Le, A.P.; Saw, T.B.; Tarle, V.; Ong, H.T.; Bertocchi, C.; Mège, R.M.; Lim, C.T.; Gov, N.S.; Ladoux, B. Regulation of epithelial cell organization by tuning cell–substrate adhesion. Integr. Biol. 2015, 7, 1228–1241. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cornwall Scoones, J.; Banerjee, D.S.; Banerjee, S. Size-Regulated Symmetry Breaking in Reaction-Diffusion Models of Developmental Transitions. Cells 2020, 9, 1646. https://doi.org/10.3390/cells9071646
Cornwall Scoones J, Banerjee DS, Banerjee S. Size-Regulated Symmetry Breaking in Reaction-Diffusion Models of Developmental Transitions. Cells. 2020; 9(7):1646. https://doi.org/10.3390/cells9071646
Chicago/Turabian StyleCornwall Scoones, Jake, Deb Sankar Banerjee, and Shiladitya Banerjee. 2020. "Size-Regulated Symmetry Breaking in Reaction-Diffusion Models of Developmental Transitions" Cells 9, no. 7: 1646. https://doi.org/10.3390/cells9071646
APA StyleCornwall Scoones, J., Banerjee, D. S., & Banerjee, S. (2020). Size-Regulated Symmetry Breaking in Reaction-Diffusion Models of Developmental Transitions. Cells, 9(7), 1646. https://doi.org/10.3390/cells9071646




