Characterizing Human Cell Types and Tissue Origin Using the Benford Law
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets
2.2. Analysis of Benford Distribution
2.3. Lists of Genes
2.4. Statistical Analysis
2.5. Clustering and Machine Learning
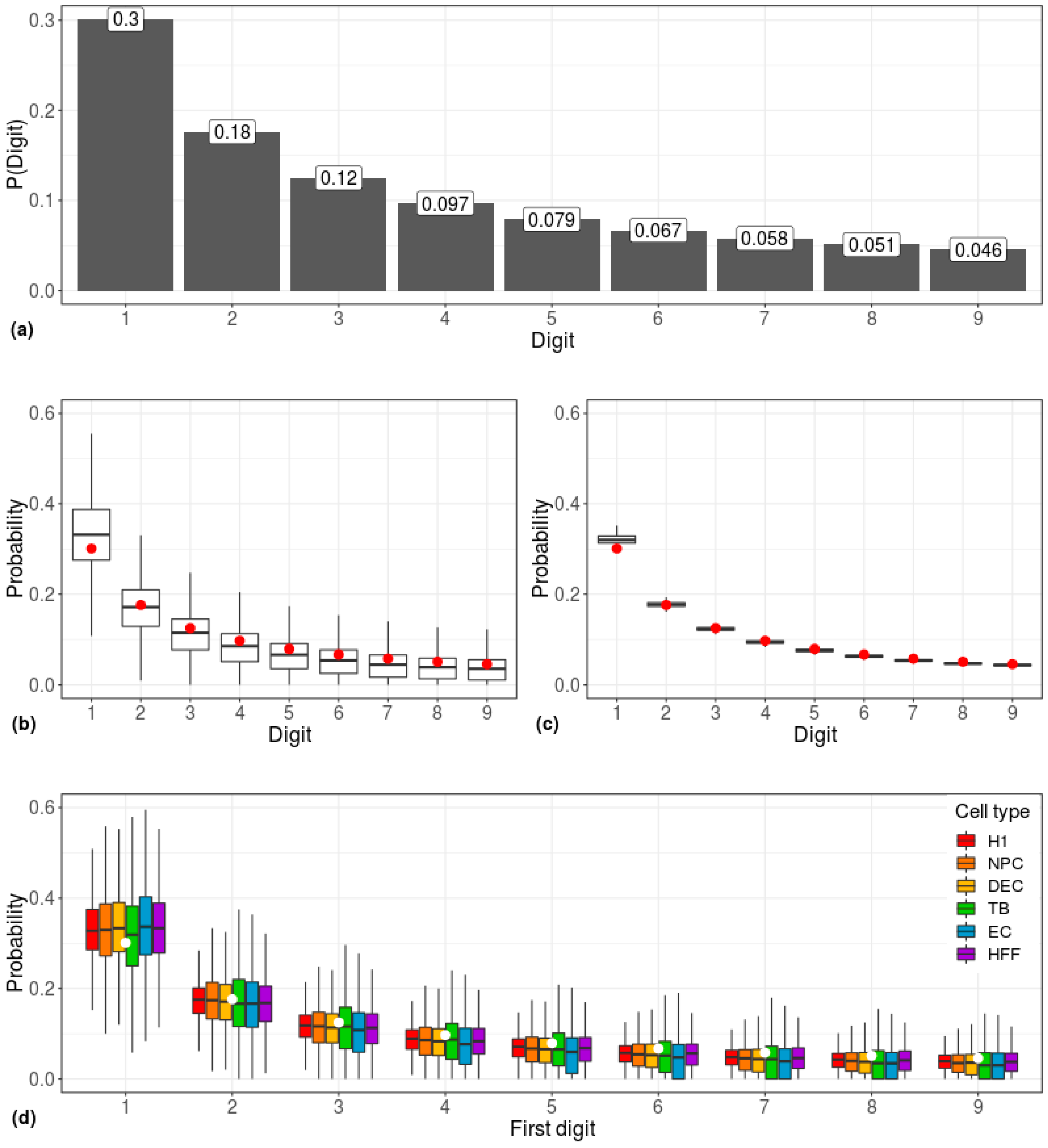
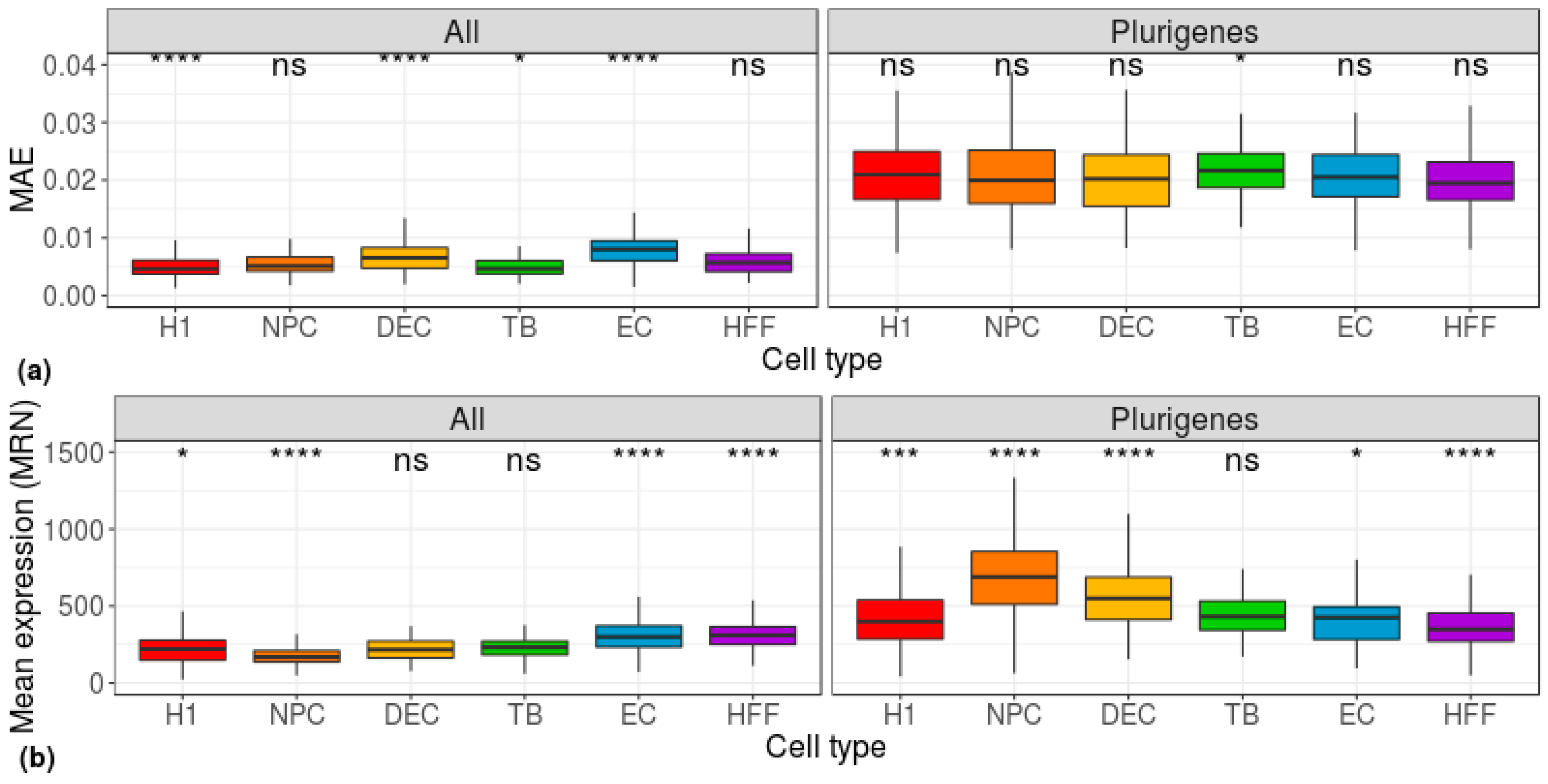
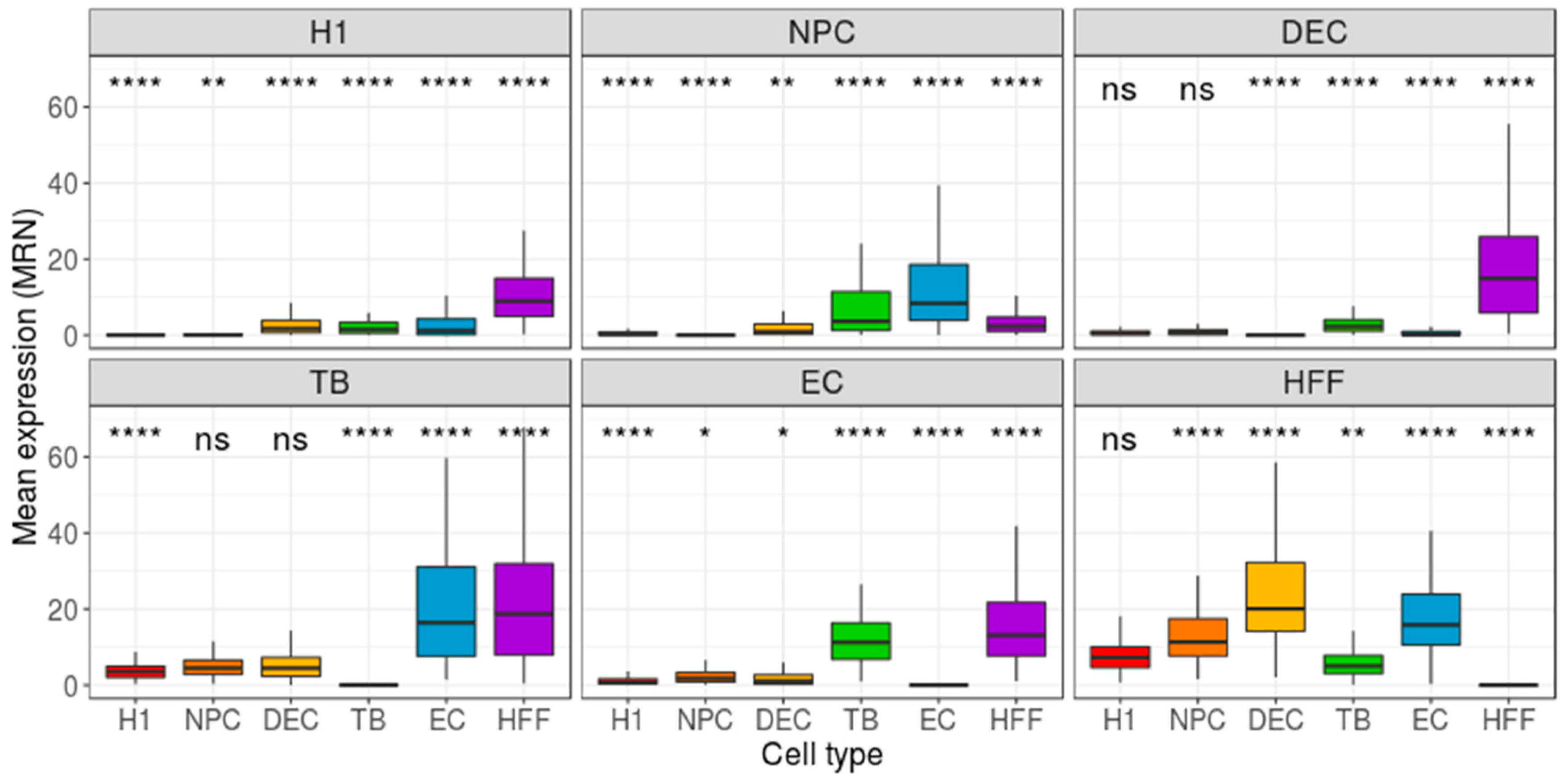
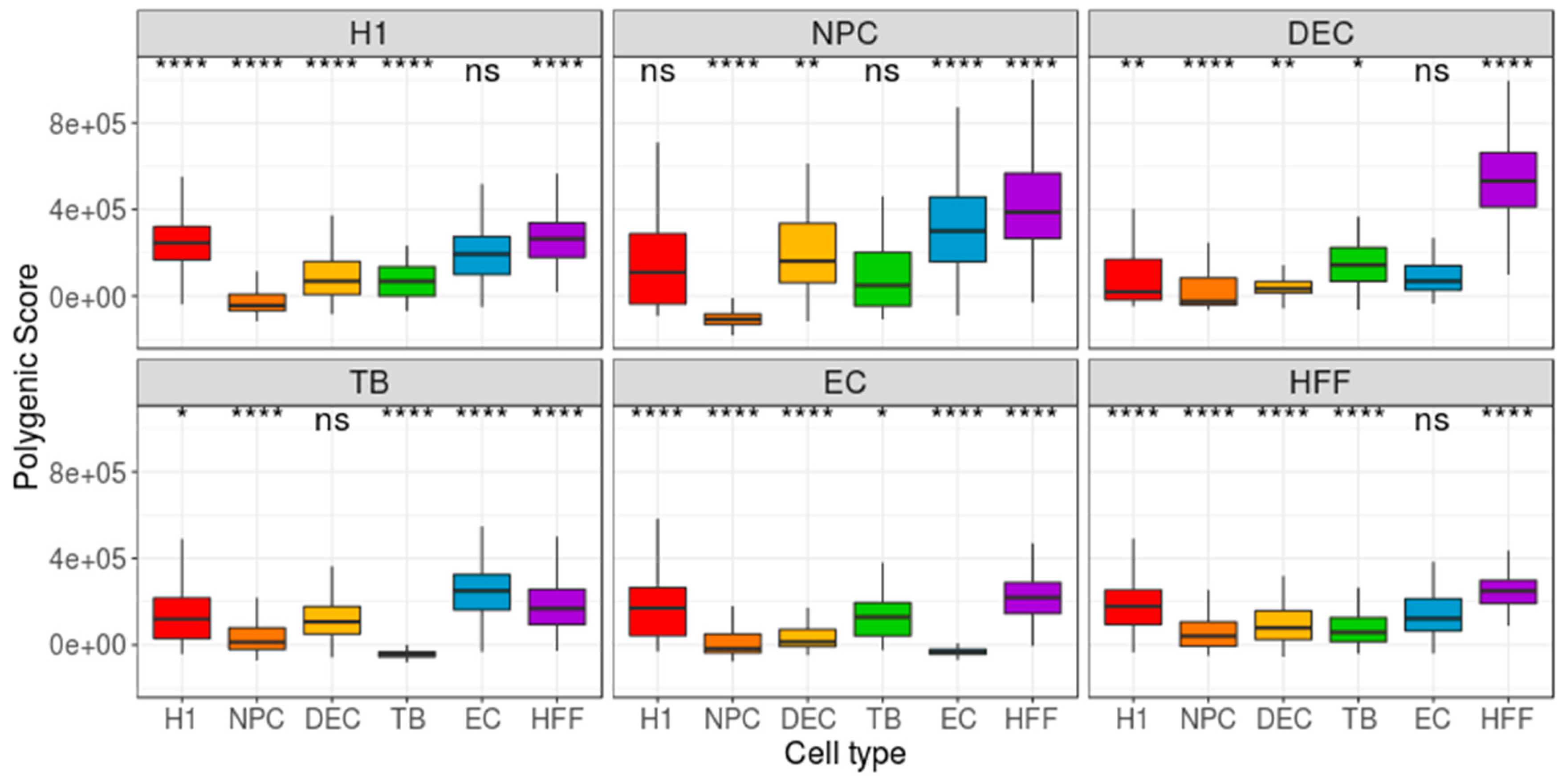
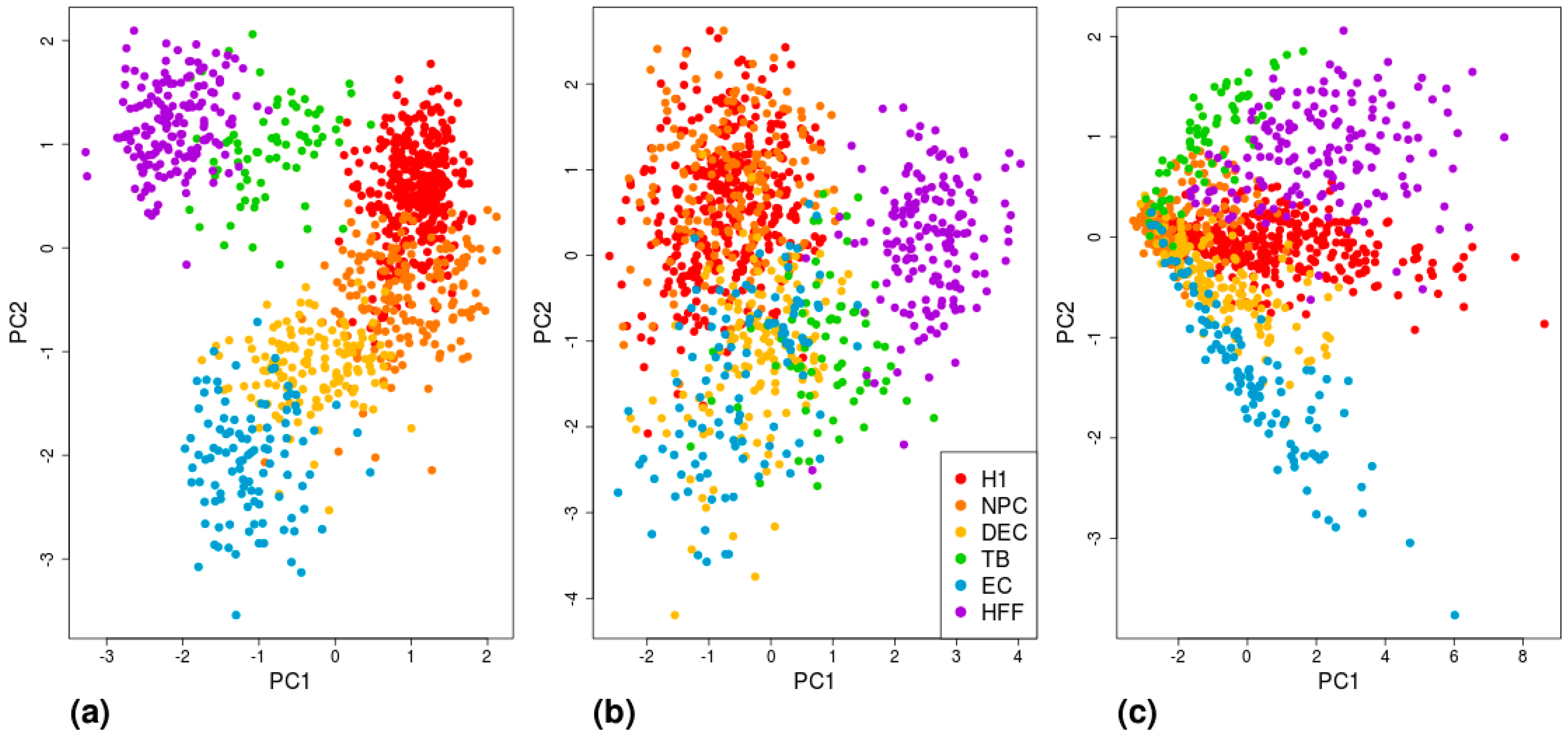
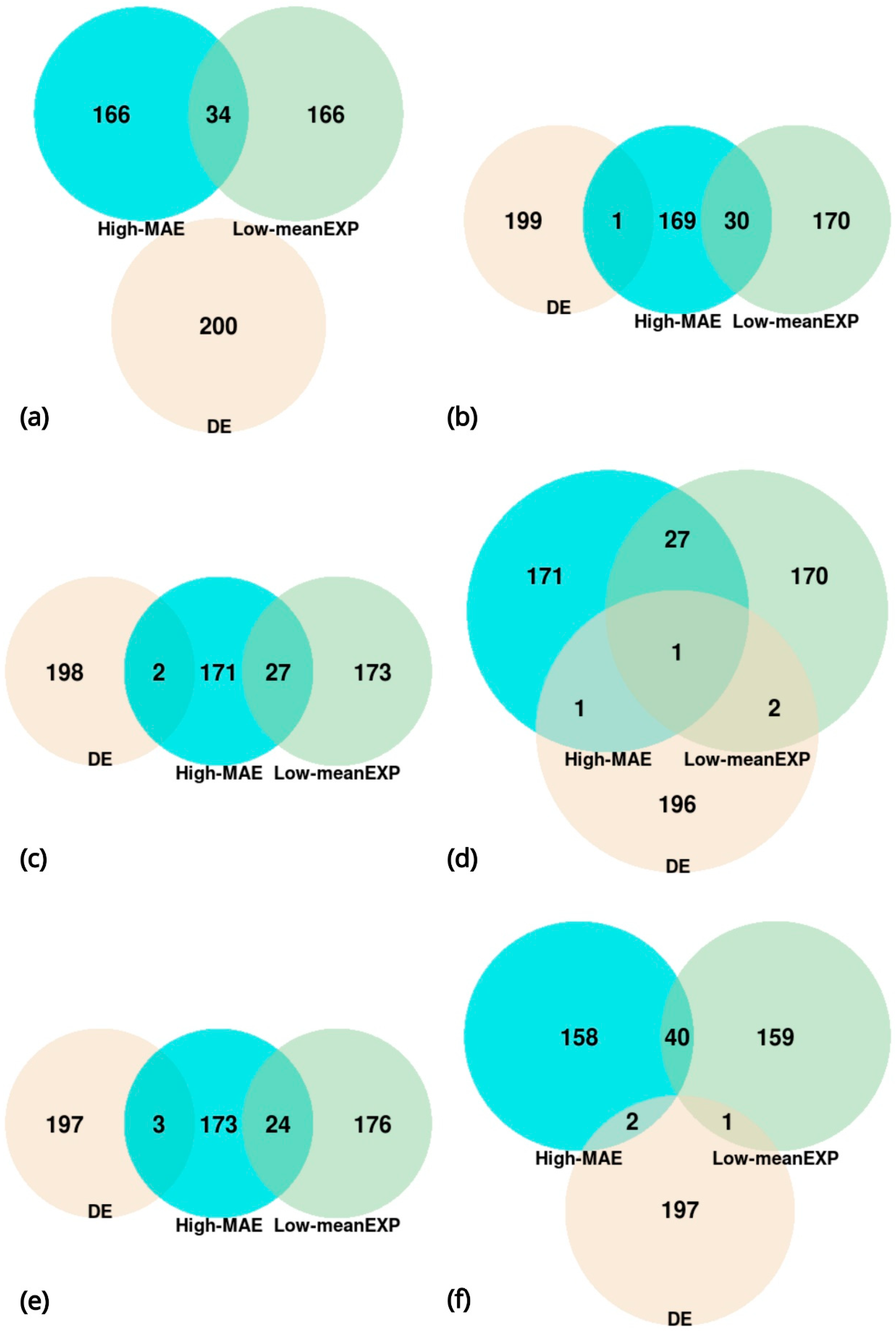
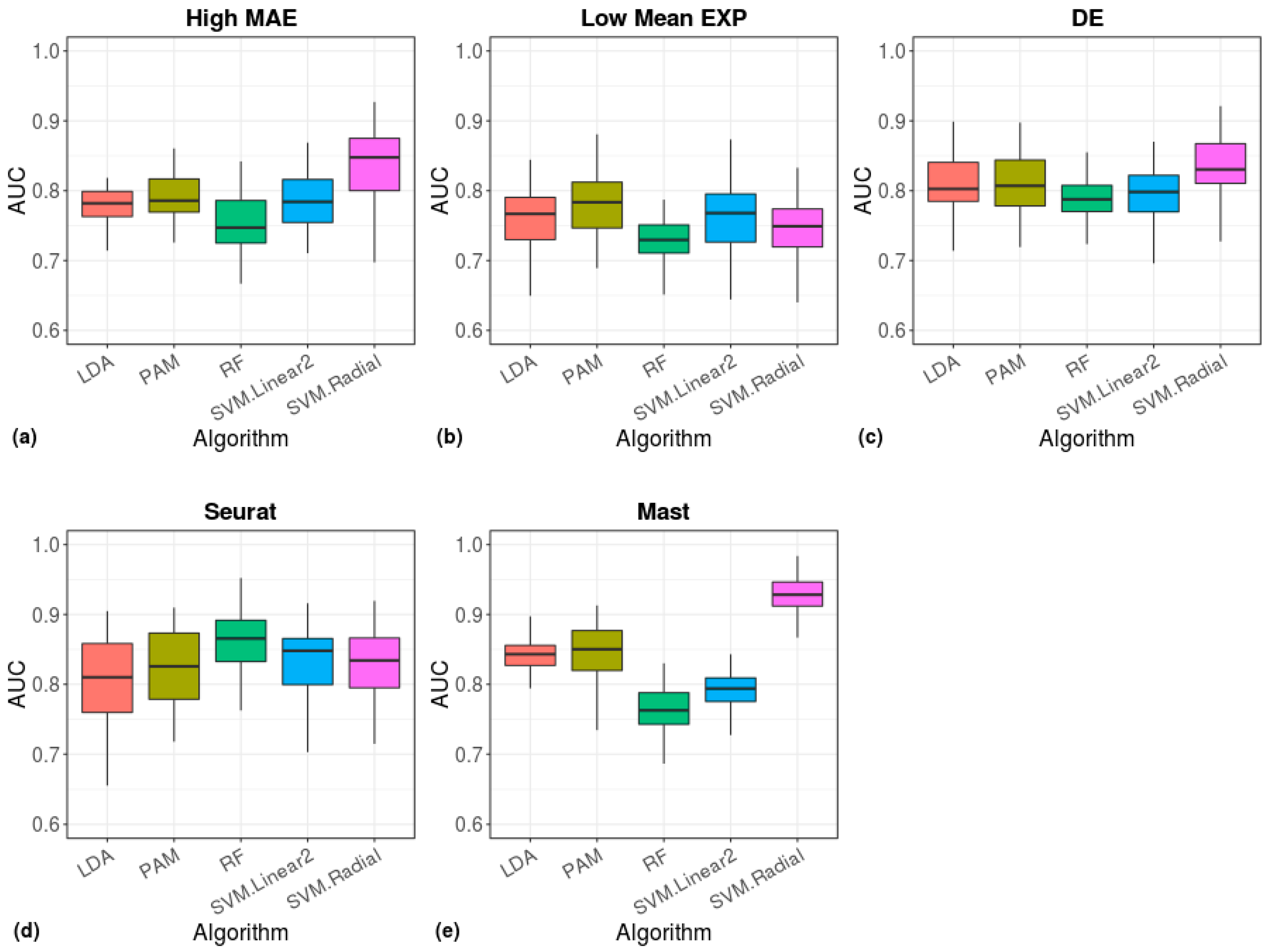
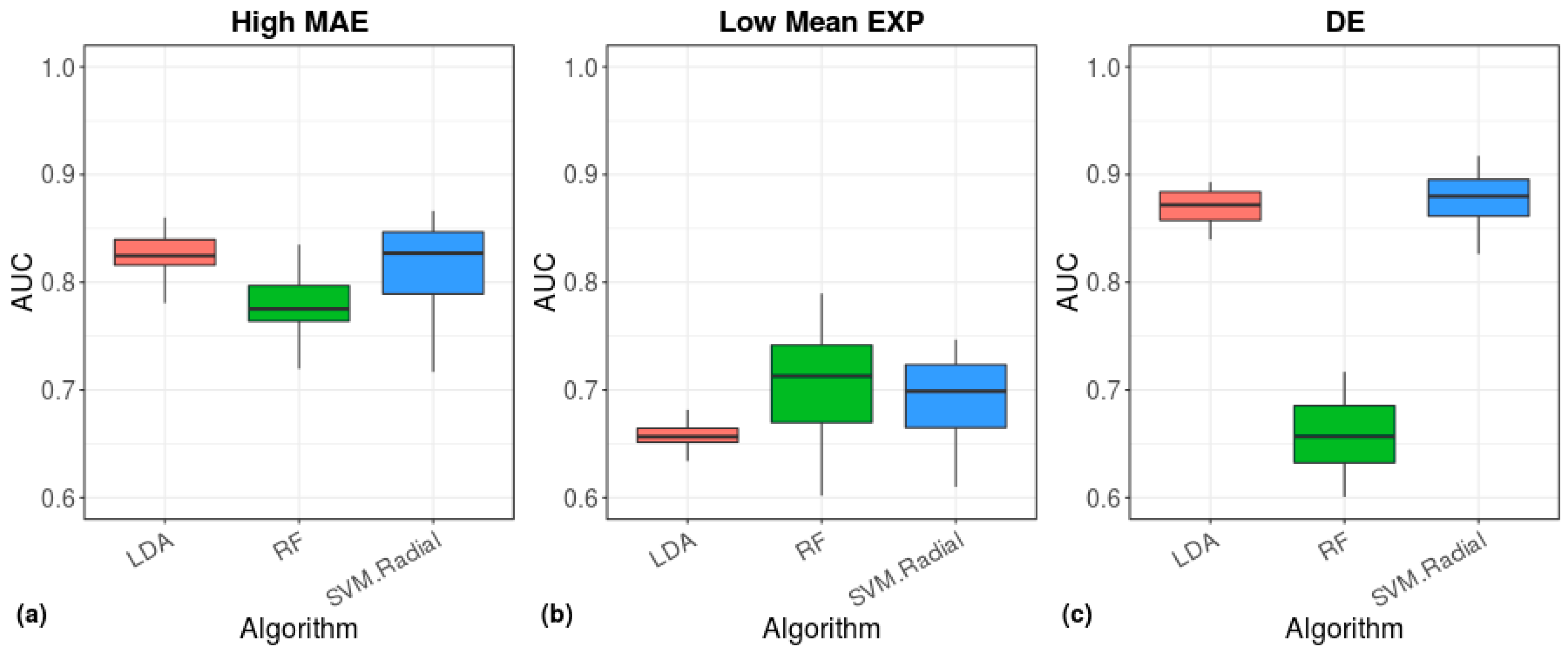
3. Results
4. Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Newcomb, S. Note on the Frequency of Use of the Different Digits in Natural Numbers. Am. J. Math. 1881, 4, 39–40. [Google Scholar] [CrossRef]
- Benford, F. The Law of Anomalous Numbers. Proc. Am. Philos. Soc. 1938, 78, 551–572. [Google Scholar]
- Nigrini, M.J. I’ve got your number. J. Account. 1999, 187, 79–83. [Google Scholar]
- Nigrini, M.J. Benford’s Law: Applications for Forensic Accounting, Auditing, and Fraud Detection; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Kreuzer, M.; Jordan, D.; Antkowiak, B.; Drexler, B.; Kochs, E.F.; Schneider, G. Brain Electrical Activity Obeys Benford’s Law. Anesth. Analg. 2014, 118, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Friar, J.L.; Goldman, T.; Pérez–Mercader, J. Genome Sizes and the Benford Distribution. PLoS ONE 2012. [Google Scholar] [CrossRef]
- Hoyle, D.C.; Rattray, M.; Jupp, R.; Brass, A. Making sense of microarray data distributions. Bioinformatics 2002, 18, 576–584. [Google Scholar] [CrossRef]
- Sandron, F.; Hayford, S.R. Do Populations Conform to the Law of Anomalous Numbers? Popululation 2002, 57, 753–761. [Google Scholar] [CrossRef]
- Costas, E.; López-Rodasa, V.; Toro, J.F.; Flores-Moya, A. The number of cells in colonies of the cyanobacterium Microcystis aeruginosa satisfies Benford’s law. Aquat. Bot. 2008, 89, 341–343. [Google Scholar] [CrossRef]
- Whyman, G.; Shulzinger, E.; Bormashenko, E. Intuitive considerations clarifying the origin and applicability of the Benford law. Results Phys. 2016, 6, 3–6. [Google Scholar] [CrossRef]
- Pericchi, L.; Torres, D.; Student, P.D. Quick Anomaly Detection by the Newcomb-Benford Law, with Applications to Electoral Processes Data from the USA, Puerto Rico and Venezuela. Stat. Sci. 2011, 26, 502–516. [Google Scholar] [CrossRef]
- Cerioli, A.; Barabesi, L.; Cerasa, A.; Menegatti, M.; Perrotta, D. Newcomb–Benford law and the detection of frauds in international trade. Proc. Natl. Acad. Sci. USA 2019, 116, 106–115. [Google Scholar] [CrossRef] [PubMed]
- Karthik, D.; Stelzer, G.; Gershanov, S.; Baranes, D.; Salmon-Divon, M. Elucidating tissue specific genes using the Benford distribution. BMC Genom. 2016. [Google Scholar] [CrossRef]
- Lun, A.T.L.; McCarthy, D.J.; Marioni, J.C. A step-by-step workflow for low-level analysis of single-cell RNA-seq data with Bioconductor. F1000Research 2016. [Google Scholar] [CrossRef]
- Stuart, T.; Butler, A.; Hoffman, P.; Hafemeister, C.; Papalexi, E.; Mauck, W.M.; Hao, Y.; Stoeckius, M.; Smibert, P.; Satija, R. Comprehensive Integration of Single-Cell Data. Cell 2019, 177, 1888–1902. [Google Scholar] [CrossRef] [PubMed]
- Wagner, F.; Yanai, I. Moana: A robust and scalable cell type classification framework for single-cell RNA-Seq data. bioRxiv 2018. [Google Scholar] [CrossRef]
- Alavi, A.; Ruffalo, M.; Parvangada, A.; Huang, Z.; Bar-Joseph, Z. A web server for comparative analysis of single-cell RNA-seq data. Nat. Commun. 2018. [Google Scholar] [CrossRef] [PubMed]
- Pollen, A.A.; Nowakowski, T.J.; Shuga, J.; Wang, X.; Leyrat, A.A.; Lui, J.H.; Li, N.; Szpankowski, L.; Fowler, B.; Chen, P.; et al. Low-coverage single-cell mRNA sequencing reveals cellular heterogeneity and activated signaling pathways in developing cerebral cortex. Nat. Biotechnol. 2014, 32, 1053–1058. [Google Scholar] [CrossRef] [PubMed]
- Rizzetto, S.; Eltahla, A.A.; Lin, P.; Bull, R.; Lloyd, A.R.; Ho, J.W.K.; Venturi, V.; Luciani, F. Impact of sequencing depth and read length on single cell RNA sequencing data of T cells. Sci. Rep. 2017. [Google Scholar] [CrossRef] [PubMed]
- Chu, L.F.; Leng, N.; Zhang, J.; Hou, Z.; Mamott, D.; Vereide, D.T.; Choi, J.; Kendziorski, C.; Stewart, R.; Thomson, J.A. Single-cell RNA-seq reveals novel regulators of human embryonic stem cell differentiation to definitive endoderm. Genome Biol. 2016. [Google Scholar] [CrossRef]
- Dobin, A.; Davis, C.A.; Schlesinger, F.; Drenkow, J.; Zaleski, C.; Jha, S.; Batut, P.; Chaisson, M.; Gingeras, T.R. STAR: Ultrafast universal RNA-seq aligner. Bioinformatics 2013, 29, 15–21. [Google Scholar] [CrossRef]
- Liao, Y.; Smyth, G.K.; Shi, W. featureCounts: An efficient general purpose program for assigning sequence reads to genomic features. Bioinformatics 2014, 30, 923–930. [Google Scholar] [CrossRef] [PubMed]
- GTEx Portal. Available online: https://gtexportal.org/home/ (accessed on 23 August 2019).
- R Development Core Team R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018.
- Joenssen, D.W. Statistical Tests for Evaluating Conformity to Benford’s Law. Available online: https://rdrr.io/cran/BenfordTests/ (accessed on 27 August 2019).
- Palmer, N.P.; Schmid, P.R.; Berger, B.; Kohane, I.S. A gene expression profile of stem cell pluripotentiality and differentiation is conserved across diverse solid and hematopoietic cancers. Genome Biol. 2012. [Google Scholar] [CrossRef] [PubMed]
- Satija, R.; Farrell, J.A.; Gennert, D.; Schier, A.F.; Regev, A. Spatial reconstruction of single-cell gene expression data. Nat. Biotechnol. 2015, 33, 495–502. [Google Scholar] [CrossRef] [PubMed]
- Finak, G.; McDavid, A.; Yajima, M.; Deng, J.; Gersuk, V.; Shalek, A.K.; Slichter, C.K.; Miller, H.W.; McElrath, M.J.; Prlic, M.; et al. MAST: A flexible statistical framework for assessing transcriptional changes and characterizing heterogeneity in single-cell RNA sequencing data. Genome Biol. 2015. [Google Scholar] [CrossRef] [PubMed]
- Sonnenblick, A.; Brohée, S.; Fumagalli, D.; Vincent, D.; Venet, D.; Ignatiadis, M.; Salgado, R.; Van den Eynden, G.; Rothé, F.; Desmedt, C.; et al. Constitutive phosphorylated STAT3-associated gene signature is predictive for trastuzumab resistance in primary HER2-positive breast cancer. BMC Med. 2015. [Google Scholar] [CrossRef] [PubMed]
- Van Der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Kuhn, M. Building Predictive Models in R Using the caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Robin, X.; Turck, N.; Hainard, A.; Tiberti, N.; Lisacek, F.; Sanchez, J.-C.; Müller, M. pROC: An open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinform. 2011. [Google Scholar] [CrossRef]
- Kafri, O. Cornell (Unversity Ithaca, NY, USA) Entropy Principle in Direct Derivation of Benford’s Law. 2009. Unpublished work. [Google Scholar]
- Shekhar, K.; Lapan, S.W.; Whitney, I.E.; Tran, N.M.; Macosko, E.Z.; Kowalczyk, M.; Adiconis, X.; Levin, J.Z.; Nemesh, J.; Goldman, M.; et al. Comprehensive Classification of Retinal Bipolar Neurons by Single-Cell Transcriptomics. Cell 2016, 166, 1308–1323. [Google Scholar] [CrossRef]
- Chen, H.-I.H.; Jin, Y.; Huang, Y.; Chen, Y. Detection of high variability in gene expression from single-cell RNA-seq profiling. BMC Genomics 2016. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Usoskin, D.; Furlan, A.; Islam, S.; Abdo, H.; Lönnerberg, P.; Lou, D.; Hjerling-Leffler, J.; Haeggström, J.; Kharchenko, O.; Kharchenko, P.V.; et al. Unbiased classification of sensory neuron types by large-scale single-cell RNA sequencing. Nat. Neurosci. 2015, 18, 145–153. [Google Scholar] [CrossRef]
- Wu, B. Differential gene expression detection and sample classification using penalized linear regression models. Bioinformatics 2006, 22, 472–476. [Google Scholar] [CrossRef] [PubMed]
- Luecken, M.D.; Theis, F.J. Current best practices in single-cell RNA-seq analysis: A tutorial. Mol. Syst. Biol. 2019. [Google Scholar] [CrossRef] [PubMed]


| Cell Type | Potency | Number of Cells |
|---|---|---|
| Human embryonic stem cells (hESC) | Pluripotent | 374 |
| Neural progenitor cells (NPC) | Multipotent | 173 |
| Definitive endoderm progenitors (DEP) | 138 | |
| Endothelial cells (EC) | 105 | |
| Trophoblasts (TB) | 69 | |
| Human foreskin fibroblasts (HFF) | Differentiated | 159 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morag, S.; Salmon-Divon, M. Characterizing Human Cell Types and Tissue Origin Using the Benford Law. Cells 2019, 8, 1004. https://doi.org/10.3390/cells8091004
Morag S, Salmon-Divon M. Characterizing Human Cell Types and Tissue Origin Using the Benford Law. Cells. 2019; 8(9):1004. https://doi.org/10.3390/cells8091004
Chicago/Turabian StyleMorag, Sne, and Mali Salmon-Divon. 2019. "Characterizing Human Cell Types and Tissue Origin Using the Benford Law" Cells 8, no. 9: 1004. https://doi.org/10.3390/cells8091004
APA StyleMorag, S., & Salmon-Divon, M. (2019). Characterizing Human Cell Types and Tissue Origin Using the Benford Law. Cells, 8(9), 1004. https://doi.org/10.3390/cells8091004





