2.1. Cell Preparation Methods
To prepare cells for microscopic examination of the lamins within the NL, we need to consider several factors for optimal imaging. Because the nucleus is typically not located near the surface of the cell attached to a glass coverslip, there are potential depth of field problems. Additionally, axial resolution in most light microscopy techniques is typically worse than the lateral resolution by a factor of two to three. This means that there are obvious advantages in using flatter cells to obtain larger in-focus areas of the nucleus. Further optimization is achieved by growing cells on glass coverslips for SIM imaging rather than glass slides.
Even though the lamina is a very thin layer, it is nonetheless a three-dimensional structure. Therefore, techniques need to be employed where volumetric imaging is possible and steps are taken to preserve the 3-D structure. We have found that methanol fixation of cells is particularly useful for single focal plane imaging of the NL because it is the ideal fixative for preserving intermediate filament proteins in general, and lamins in particular [
10,
11]. Moreover, this fixative dehydrates the cell and brings the nucleus closer to the coverglass. The small distance between the nucleus and the coverglass reduces issues with spherical aberration. In addition, to obtain optimal resolution we use Prolong Glass (ThermoFisher, Carlsbad, CA, USA) as a mounting medium, since this glycerol-based and hard-setting medium has a refractive index (RI) of 1.52, which closely mimics the RI of glass coverslips, and thereby provides optimal resolution due to the decrease in spherical aberration.
For this study, mouse embryonic fibroblasts (MEFs), courtesy of Yixian Zheng (Carnegie Institute), were seeded on round 12 mm coverslips (12-545-80, Thermo Fisher Scientific, Waltham, MA) and fixed and permeabilized with methanol for 10 min at −20 °C, followed by permeabilization with 0.1% Triton X-100 for 10 min at RT [
10]. Cells were then stained for 1 h at RT with a rabbit polyclonal antibody to lamin A (1:500, Dechat et al.) in phosphate buffered saline (PBS, Gibco, Life Technologies, Carlsbad, CA, USA) containing 5% normal goat serum (Jackson ImmunoResearch Laboratories, West Grove, PA, USA), washed in PBS, followed by 1 h at RT with goat anti-mouse IgG-Alexa Fluor 488 (1:400, Life Technologies, Carlsbad, CA, USA). DNA was stained with Hoechst 33,258 for 1 h at RT (1:10000, Thermo Fisher Scientific). TetraSpeck beads (0.1µm, Life Technologies) were diluted 1:20 in the mounting medium. Finally, coverslips were mounted on slides in ProLong Glass (Life Technologies, Carlsbad, CA, USA).
Human dermal fibroblasts from a healthy donor (previously described in West, Gullmets et al., 2016 [
12]) were seeded on glass bottom 35 mm dishes (MatTek, Ashland, MA, USA), fixed, and permeabilized with methanol for 10 min at −20 °C. Methanol fixation was used, since the flattening effect, as mentioned above, is helpful for Total Interference Reflection Fluorescence (TIRF), which is required for axial resolution with 2D-STORM. Cells were blocked for 30 min with 5% normal goat serum, stained for 1 h at RT with a rabbit polyclonal antibody to lamin A (1:500, 323; Dechat et al.), rinsed in phosphate buffered saline (Gibco, Life Technologies, Carlsbad, CA, USA), and then stained for 1 h at RT with goat anti-rabbit IgG-Alexa Fluor 647 (1:200, Life Technologies, Carlsbad, CA, USA). Cells on glass bottom dishes were kept in 1xPBS overnight at +4 °C and imaged the next day.
2.6. Analysis of Structured Illumination Microscopy Images
The reconstruction of SIM images is conducted in the frequency domain of the image, as described above. Before applying detailed analysis of the fine structure in these images, it is critical to verify that the reconstructions are of high quality. The resulting images can be evaluated manually and with open source tools to assess the quality of the reconstruction.
Two initial manual qualitative assessments involve constructing the widefield image and assessing the two-dimensional Fourier transform of the reconstructed image. These are typically obtained by using the acquisition software provided by commercial vendors as part of the SIM reconstruction package, but can also be done by open source tools.
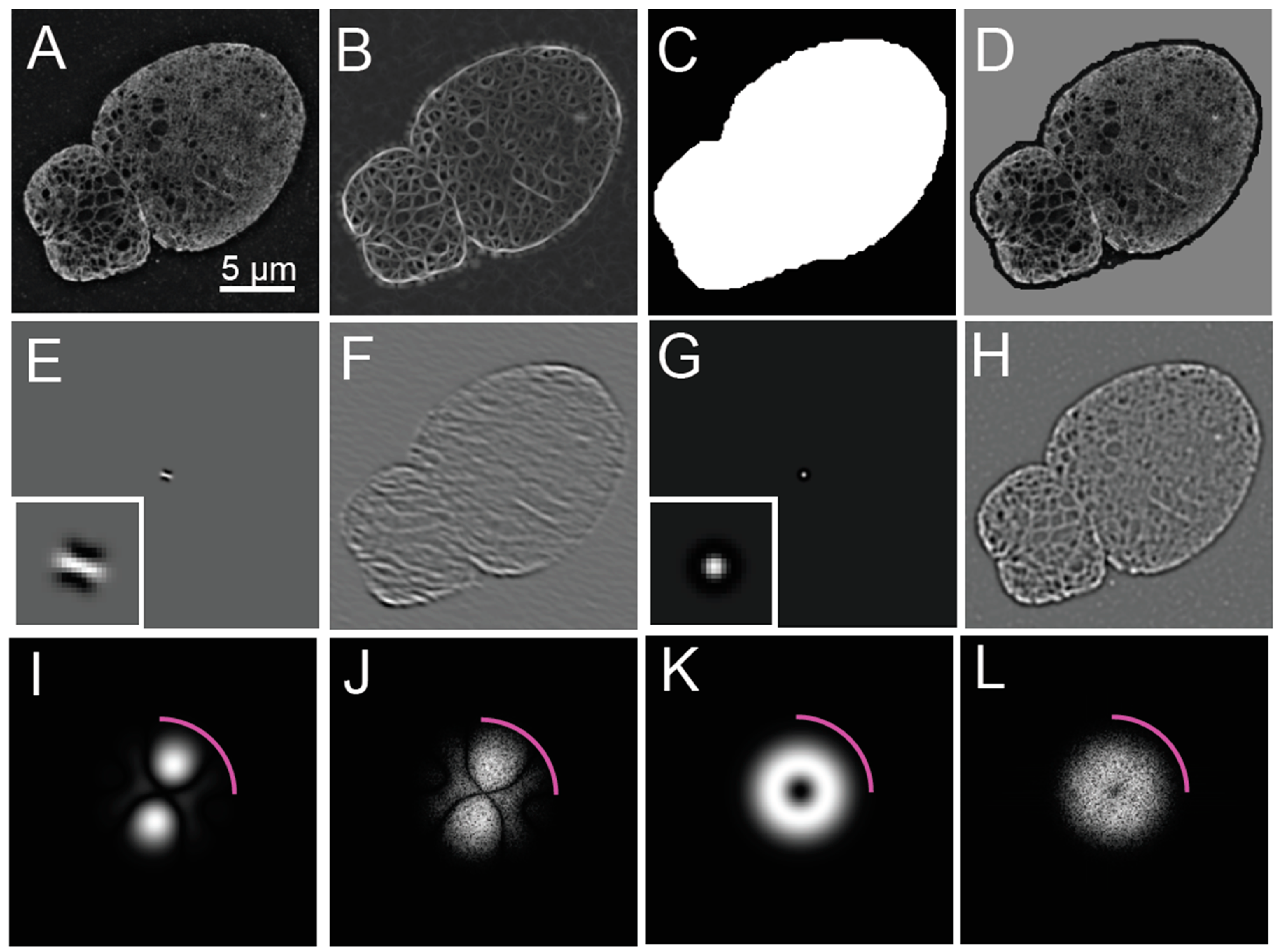
The widefield image is synthesized from the primary acquisition images by averaging the images across the distinct phases of each illumination angle (
Figure 1A). The average across the phases for each angle should resemble a similar widefield image. The reconstruction of the widefield image is possible since the illumination intensity patterns are modeled as phase shifted sinusoidal patterns of the form
, where x is the coordinate along the variation of the structured illumination pattern and
for
P phase shifts, where usually P = 3 for 2-D SIM. Since the phase shifts are evenly distributed, averaging them results in a constant illumination pattern across the field of view for P > 1:
The principle is similar for 3D-SIM, where five phases are collected with variations over two dimensions. The synthesized widefield images for each angle should look nearly identical, since differences between them will violate the assumption that the same object is being imaged at each angle, which is required for accurate reconstruction.
The Fourier domain of the acquired (
Figure 1B) and reconstructed images (
Figure 1C,D) should also be assessed for their signal-to-noise ratio necessary for contrast and the presence of calibration features in the form of bright spots corresponding to the frequency of the illumination pattern. For visualization, the magnitudes of the Fourier coefficients are displayed using a log contrast lookup table. Equivalently, evaluating the log of the magnitude of the Fourier transform using a linear lookup table can be accomplished by calculating the log transform, according to the following equation as used in this manuscript:
where
is the log-transformed magnitude of the Fourier transform,
is either an individual acquired image at a particular phase and angle or a reconstructed image. From the Fourier domain, the resolution of the reconstructed image can be evaluated from a circularly averaged power spectral density.
Quantitative assessment of images acquired by SIM can be evaluated using open source tools. SIMCheck is available as a plugin for ImageJ [
20]. SIMCheck provides a quantitative evaluation of the qualitative checks given above, as well as additional measures of reconstruction quality.
SIM images typically have a resolution improvement that is not fully isotropic due to the finite number of oriented illumination patterns used. Details are more resolvable along the angle of the illumination patterns used in SIM over the intervening angles, which is evident from the flower-like shape of the magnitude of the Fourier transform (
Figure 1D). If the resolution improvement were isotropic, the Fourier transform would be circular. This has important implications for the analysis of reconstructed SIM images, as detailed in the next section.
To evaluate the resolution enhancement of the SIM reconstruction over the widefield image, a ratio can be taken of the SIM reconstructed image and either a widefield fluorescence image or a resolution reduced version of the reconstructed image (
Figure 1E,F). This ratio will be used in later steps to help assess candidate features of the steerable filter, as described below.
2.7. Analysis of Lamin Fibers Using SIM and Steerable Filters
Steerable filters provide a way to detect curvilinear patterns within an image based on a particular scale and aspect ratio. These filters are used to detect the local orientation of structures in an image, which in turn is used to segment filaments.
Steerable filters are a type of linear filter, which in terms of image processing, process an input image and output a response image; where each pixel in the output is a linear combination of pixels in a neighborhood around the corresponding input pixel. Linear filters can be applied to an image using convolution in the spatial image domain or by pointwise multiplication in the Fourier domain due to the Fourier Convolution Theorem. A steerable filter can be represented either in the image domain (
Figure 2E) or in the Fourier domain (
Figure 2I). The image domain representation allows us to see the neighborhood around each pixel used by the filter via convolution (
Figure 2E). In convolution, the filter is first centered at a pixel, multiplied pointwise across an area around the pixel, and then the products are summed together to find the response value at that pixel. This process is repeated for each pixel in the image resulting in the filter response image (
Figure 2F). The Fourier domain representation makes the resolution and orientation selectivity of the filter apparent (
Figure 2I). In the Fourier domain, the filter is applied by pointwise multiplication to the complex field of the image (
Figure 2J). To obtain the filtered image from the pointwise product, the inverse two-dimensional Fourier transform is applied. The application of this filter to the reconstructed image (
Figure 1C,D) is seen as a response image in the spatial (
Figure 2F) and Fourier domains (
Figure 2J).
Because both steerable filters and SIM reconstruction act upon the Fourier domain of images, the relationship of the orientation and resolution selectivity of the filter to the respective properties of the reconstruction process need to be considered. Since the resolution of a reconstructed SIM image is not isotropically uniform in the lateral dimensions (
Figure 1D), orientation should not be assessed at the highest resolution available. Orientation measurements made at high resolution where information is not available equally in all directions would be biased towards the orientation of the structured illumination patterns used to acquire the images. Rather, spatial resolution should be selected at a scale where resolution is laterally isotropic. The spatial resolution selectivity of a steerable filter bank is assessed by calculating the mean filter across orientations, creating a Laplacian-like filter, which appears as a bright positive spot surrounded by a negative moat (
Figure 2G). The scale selected by the steerable filters is proportional to the size of the positive spot. The Fourier domain representation of the mean filter typically resembles an annulus, since steerable filters are usually designed as bandpass filters (
Figure 2K). Bandpass filters retain information around a certain spatial frequency, while attenuating or blocking smaller and larger frequencies (
Figure 2L). When this mean filter is applied to the image, ridge features that match the scale selected have a higher response and are brighter (
Figure 2H). While this would seem to negate the extended resolution of structured illumination, SIM does increase the magnitude of the Fourier coefficients within the low-resolution frequencies observable by widefield microscopy, and not just the higher frequencies contributing to extended resolution. Additionally, the original pixel intensities from the SIM reconstruction can be used to analyze the results of the steerable filter process, as outlined below.
Steerable filters can be used to either detect “ridges” (bright lines) or “edges” (lines of contrast between bright and dark areas). “Edge” detection by steerable filters are not considered further here, but may be useful in evaluating the width of lamin fibers in future studies. To clarify the terminology, the “ridges” detected here will be later referred to as edges of the lamin meshwork.
For the labeling of lamins by immunofluorescence for the detection of lamin fibers, ridge detection allows for the localization of the center of lamin fibers. This works in a two-step process by (1) determining the local orientation of a neighborhood around a pixel and (2) evaluating if that pixel has a value larger than its neighbors in the direction perpendicular to that orientation.
Steerable filters allow a response at any orientation to be interpolated from a finite set of oriented filter responses, as per the Nyquist-Shannon Sampling Theorem [
21,
22]. First, a set of steerable filters, called a filter bank, is used in combination to obtain a set of response images at distinct orientations (
Figure 2E). A finite set of orientations are initially compared to an area centered at each pixel by convolving an oriented filter with the image as above. Effectively, this returns a score of how well the neighborhood around the pixel matches the oriented filter. This score is termed an orientation response for a particular angle (
Figure 2B).
The orientation response can be interpolated from a finite sampling of orientations to form a continuous periodic function in terms of orientation angle. It is this property which makes these filters “steerable”, in that the filter orientation can be turned in any direction. From another perspective, a finite Fourier series in terms of orientation describes the periodic orientation response curves, meaning that the orientation response curves are band limited. The result is that steerable filters allow for the computation of a continuous response curve with respect to orientation. This property also means that steerable filters have limited orientation resolution, meaning that two orientations of equal intensity can only be distinguished if separated by a certain number of degrees.
Steerable filters first determine the best orientation for a neighborhood around each pixel (
Figure 3A). The orientation angle assigned to a pixel is the angle where the orientation response function reaches an absolute maximum (
Figure 3B). There are analytical and numerical methods for solving directly for the best orientation, so direct interpolation is not necessary. An orientation map can be generated by storing the best orientation angle as the value for each pixel (
Figure 3A). The response for the filter oriented at that angle can also be stored for each pixel generating an orientation response map (
Figure 2B and
Figure 3A,B).
The center of a ridge is determined by scanning along a line in the space of the orientation response map perpendicular to the orientation to find the position where the orientation response reaches a maximum (
Figure 3B). To encode this position in an image, a procedure called non-maximum suppression (NMS) is used. In NMS, pixels of the orientation response map that are not found to be the maximum in space along the perpendicular line are assigned a value of zero (
Figure 3C). The resulting NMS image (
Figure 3C), thus, contains non-zero pixels at the center of ridges in the image. The non-zero pixels have a value of the response corresponding to how well the neighborhood around them matches the filter steered to that orientation. The centers of these ridges then represent potential lamin fibers localized to the pixel grid.
To detect lamin fibers, the NMS image is processed by assessing the remaining non-zero pixels and the corresponding fluorescence values in the original image. The goal here is to compare the orientation response and fluorescence intensity values with the background values to separate true lamin fibers from false detections.
To evaluate the fluorescence intensity of immunostained lamins and the corresponding filtered response values, these intensities and their derivatives are compared to the statistical distribution of the background fluorescence intensity outside of the nucleus. While acquiring images, it is important to capture a sufficient amount of background for this purpose. To separate foreground, the nucleus, background, cytoplasm, and extracellular space, an initial rough segmentation of the nucleus is required.
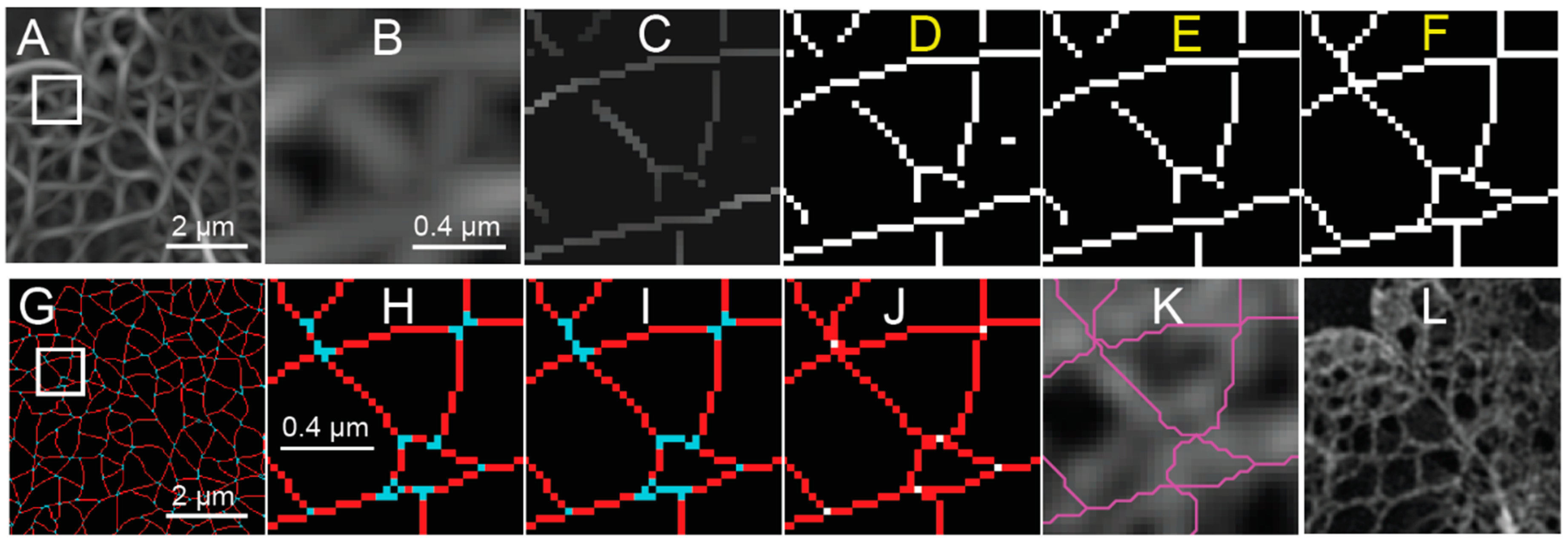
The nucleus is initially segmented as a whole by thresholding the orientation response map (
Figure 2B) and filling in enclosed areas of the binary outline. The objective here is to create a binary mask (
Figure 2C) to identify the location of the nucleus by detecting an area enclosed by lamin fibers. For this enclosure to be detected, a continuous border of lamin fibers must be inferred. This initial threshold is determined by knowing the approximate size of the nucleus relative to the field of view of the image and then selecting a percentile from a distribution of orientation responses.
With a single threshold there may still be gaps in the detected structure. Some of these gaps are filled by including pixels near the already validated structure that are above a low threshold that is less selective than the original. In hysteresis thresholding, connected pixels that are higher than the low threshold are identified as connected components [
23]. Only the connected components that also contain pixels that are above the high threshold are retained. Effectively, hysteresis thresholding identifies connected pixels likely to be lamin fibers that also contain pixels which are confidently lamin fibers.
The scheme we have employed is to select the 95th and 70th percentiles of the distribution of non-zero response values from the NMS map, and then use the two thresholds as high and low thresholds in the hysteresis thresholding process. The high threshold percentile should be adjusted to select pixels whose orientation response has a high confidence of selecting true lamin fibers. Here, we have heuristically assumed that the top 5% of steerable filter responses correspond to true detections of lamin fibers. The low threshold percentile should be selected by choosing an orientation response level that includes more lamin fibers but is less selective and may contain some false detections. Our selection assumes that the top 30% of steerable filter response intensities likely correspond to true detections. The idea is that for the purpose of identifying a rough mask of the nucleus, some false pixel detections may be acceptable as long as the nucleus is contained with the mask (
Figure 2D). Morphological closing and opening are applied to close small gaps in the boundaries of the nucleus, and then the area enclosed by the white pixels in the processed NMS are filled in to produce a rough mask for the nucleus. This mask is then expanded slightly by morphological dilation (
Figure 2C). The reconstructed image within the nuclear mask is shown in
Figure 2D for comparison.
The coarse detection of the nucleus allows for determination of thresholds through the separation of foreground and background areas by statistical analysis. For example, the probability of a filter response within the nucleus being a true detection is evaluated by determining the probability that it belongs to a statistical distribution of responses outside of the nucleus (
Figure 2C).
With the coarse mask, a threshold is determined by finding the response value that maximizes the difference between the statistical distributions of the response inside and outside the mask of the nucleus. This threshold is applied to produce a binary image (
Figure 4D) from the NMS (
Figure 4C), which still contains the non-suppressed values from the response (
Figure 4A,B). Isolated segments containing less than five pixels are removed (
Figure 4E), since the focus of this analysis is the meshwork structure, and short segments may correspond to false detections in the background.
A significant challenge occurs when lamin fibers intersect in an image. This may be because the lamin fibers are truly forming a junction or merely because they are crossing over or under each other in the z-dimension within the depth of focus of the 2D-image. For a steerable ridge filter, as outlined above, only a single orientation is detected, and thus only one lamin fiber is segmented at a time near an intersection (
Figure 3B,C). Several algorithms are available to directly detect junctions with multiple orientations but are based on having prescribed templates.
One method to resolve the area around the junctions is to extend endpoints based on their orientation. In the case of the lamin meshwork, we extend lines according to the local orientation of the lines leading up to the endpoints until they become connected with another segmented pixel (
Figure 4F). The extensions are then evaluated in a fashion similar to the calculation used to create the non-maximum suppression map (e.g., thresholding) during the later meshwork auditing process.
The next task is to analyze meshwork structure by classifying connected pixels as belonging to junctions (nodes) or edges in a graph theoretical sense. Again, to clarify, the graph edges discussed subsequently correspond with the computer vision “ridges” detected by the steerable filter. Junctions are initially identified by finding morphological branch points [
24]. In a binarized skeleton made up of white pixels, morphological branchpoints are white pixels surrounded by three or more white pixels in their 8-connected neighborhood, where the intervening black pixels are not 4-connected (
Figure 4G,H). Short segments of two pixels or less connecting the branchpoints are marked as being a part of the junction structure, as this indicates the convergence of many edges in close proximity. The pixels marked as being part of a junction are separated into connected components, and the location of the junction is then determined as being at the centroid of the connected components and reduced to a single pixel (white pixels,
Figure 4J). Next, edges connected to the previous junction pixels are extended to those junctions (red pixels,
Figure 4J). The endpoints of edges are either at a junction, where they connect to other edges, or they are freestanding and not connected to any other edges. Each edge is defined as an ordered set of pixels from one endpoint to the next. Pixels near junctions may be associated with more than one edge as the edges converge towards a junction. Once pixels have been assigned to edges and the location of junctions have been marked, the pixel-based representation of the meshwork is converted to an object-based representation, so that we can refine the meshwork further in terms of edges and junctions (
Figure 4K). This means we will no longer be manipulating single pixels but rather we will be operating on entire edges at a time.
The object-based representation (
Figure 5A) is further refined by removing edges based on the value of the pixels in either the reconstructed fluorescence image (
Figure 5B), the ratio image between the reconstructed image and the low resolution image (
Figure 5C), and the consistency of the fluorescence intensity along the edge (
Figure 5D). The remaining edges with free standing endpoints are then also removed (
Figure 5E). To perform these audits various thresholds are applied, including the mask-based threshold determined above. The other thresholds are automatically determined using Otsu’s method or Rosin’s method [
25]. The exact procedure was detailed previously [
10]. This results in the refined meshwork (
Figure 5F,G). An overlay of the refined meshwork in magenta over the fluorescence in green is seen in
Figure 5H, which is juxtaposed to the fluorescence image (
Figure 5I) for comparison. The two-dimensional areas enclosed by the edges are regarded as faces.
Upon segmenting the lamin fibers, the distribution of junctions, edges which connect them, and faces surrounded by edges could be analyzed and quantified (
Figure 5J). The quantitative evaluation of meshworks in this way could then provide insight into the effects of biological perturbations. For example, we previously used this to evaluate the effect of knocking out particular lamin subtypes and for characterizing individual lamin subtypes (
Figure 5K–P).
The use of steerable filters in this fashion has limitations with regard to orientation and scale. In the scheme described above, only a single orientation is detected at each pixel and gaps are closed by extension of line segments. Junctions, however, could be detected through specialized filters or a method that can resolve and detect multiple discrete orientations. The scale of structures being imaged and analyzed may be variable when applied to other filamentous systems. In this case a steerable filter bank capable of evaluating multiple scales may be more appropriate than one optimized for a single scale.
2.8. Analysis of Single Molecule Localization Microscopy Images with Steerable Filters and Graph Theory
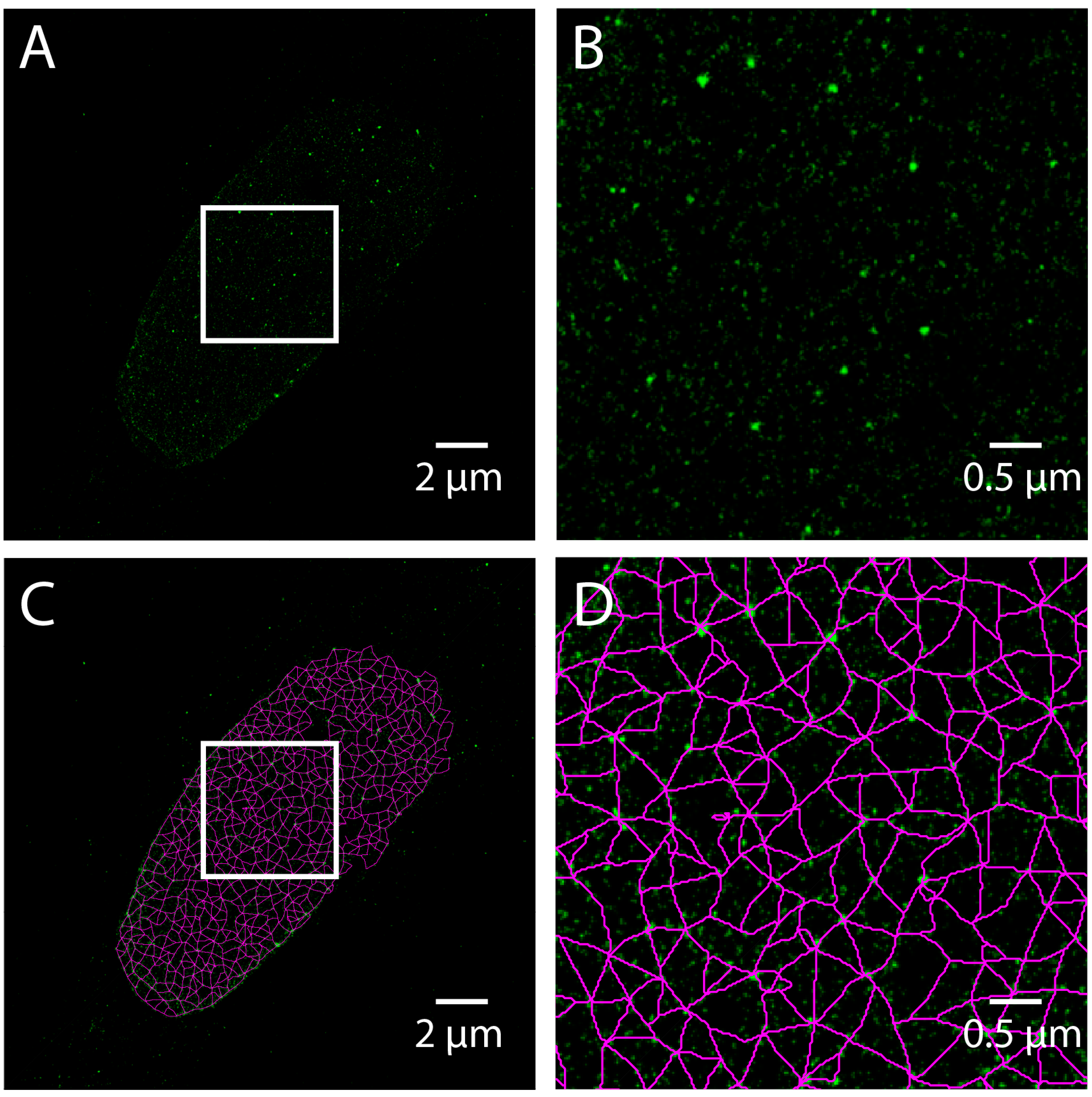
Single molecule localization microscopy (SMLM) techniques, such as STORM, do not produce an image directly, but rather result in a coordinate list of detected fluorophores generated from time-lapse series. Care must be taken to process the coordinate list to compensate for drift, thermal expansion, and multiple detections. To demonstrate the use of SMLM to study lamins, we have included a STORM image acquired using Total Internal Reflection Fluoresence (TIRF) microscopy of a human skin fibroblast labeled with Lamin A. A pixel-based image is made by accumulating the value of 2D Gaussian functions centered at each detected coordinate into a pixel grid (
Figure 6A,B) and analyzing the resulting image as above (
Figure 6C,D). This is equivalent to convolving the coordinate list with a 2D Gaussian. The width of the Gaussian determines the grid size by the Nyquist-Shannon sampling theorem. However, this approach is costly in time, and therefore a binning approach with a fine grid is often used for computational expediency [
26]. For commercial microscopes, these operations are included in the vendor supplied software. ThunderSTORM, an open-source software package for ImageJ, also performs these processing and visualization steps [
27].
SMLM detections can also be used to directly calculate a Fourier representation without the need for binning. Only the Fourier coefficients within the bandpass of the steerable filter bank (
Figure 2K) would need to be calculated. The convolution method above provides a method for doing so but the choice of method is independent of the result. Steerable filters could then be directly applied to the Fourier representation, as above.
SMLM data of nuclear lamins has been collected by advanced microscopy techniques, but has not always been subjected to further analysis [
28,
29]. Where analysis has been done, graph theoretical methods on the coordinates directly have been used primarily for the purpose of visualization and limited quantification.
One class of graph-based methods operate by linking the localizations together via computational geometry (
Figure 7). For example, a Delaunay triangulation links the localized fluorophores (
Figure 7A) together to form triangles (
Figure 7D, magenta). The triangles are chosen such that a circle drawn through the three localizations of the prospective triangle contains no other localizations. This is used to describe the space between fluorophores by examining either the edges of the triangles or the areas of the resulting triangles themselves [
30]. Another method in this class is the Euclidean minimum spanning tree (EMST). The EMST contains the shortest total length of edges in the Delaunay triangulation required to connect fully all the localizations (
Figure 7B, cyan). This method has been applied to segment the structure of nuclear lamins [
9,
31]. However, it is not clear how accurately the EMST as an abstract graph represents a physical structure and why this might be preferred over the Delaunay triangulation to describe lamin filaments.
A subgraph of the EMST is the nearest neighbor graph (NNG), where each localization is connected to the next nearest localization. Unlike the EMST, the NNG is not fully connected into a single graph, since the NNG only contains edges linking nearest neighbors and not the additional links needed to connect all the points into a single graph (
Figure 7B, gold). The NNG is used to measure the nearest neighbor distances, and thus provide a measure of density and clustering. The nearest neighbor distances were used as a measure in a study that compensated for chromatic aberration by using activator-reporter dye pairs to show that A-type lamins formed denser meshworks than B-type lamins, and that lamin B1 was more proximal to the inner nuclear membrane than the A-type lamins [
32].
The Voronoi tessellation falls in another class of graph-based methods, since this method partitions the space around localizations rather than between them [
33,
34,
35]. The Voronoi diagram consists of edges that are equidistant between the two nearest fluorophore localizations (
Figure 7C). The vertices of the localizations correspond to the centers of the circles drawn around the triangles of the Delaunay triangulation, making the Voronoi diagram the graph dual of Delaunay triangulation (
Figure 7C,D).
A method relying on the fluorophore coordinate list directly has been developed to perform a similar operation to how steerable filters are processed [
36]. The method proceeds by using an angular version of Ripley K’s function to determine orientation and traces fibers by assigning subsequent localizations to the fiber based on localized density and orientation [
36]. The localized density is based on the area of the polygons contained within the Voronoi tessellation. This technique, however, has not been applied to the study of the nuclear lamina as of this publication.
Overall, both steerable filters and graph-based methods are used to segment and analyze SMLM microscopy data of filamentous structures, as formed by nuclear lamins. However, only the EMST technique has been directly applied to segment lamin fibers from SMLM data [
9,
31]. Steerable filters are applied to SMLM data either by creating an image via binning or by computing a Fourier transform as the initial step and proceeding as with a SIM image. Alternatively, the coordinates of individual fluorophore detections are processed directly through graph theoretical methods to evaluate clustering and density [
32]. The advantages and disadvantages of these approaches are not clear, as a direct comparison of the methods and their utility in analysis has not been done.