Unlocking Cellular Memory and Gene Regulatory Networks: Pioneering the Future of Therapeutic Innovations
Abstract
1. Introduction
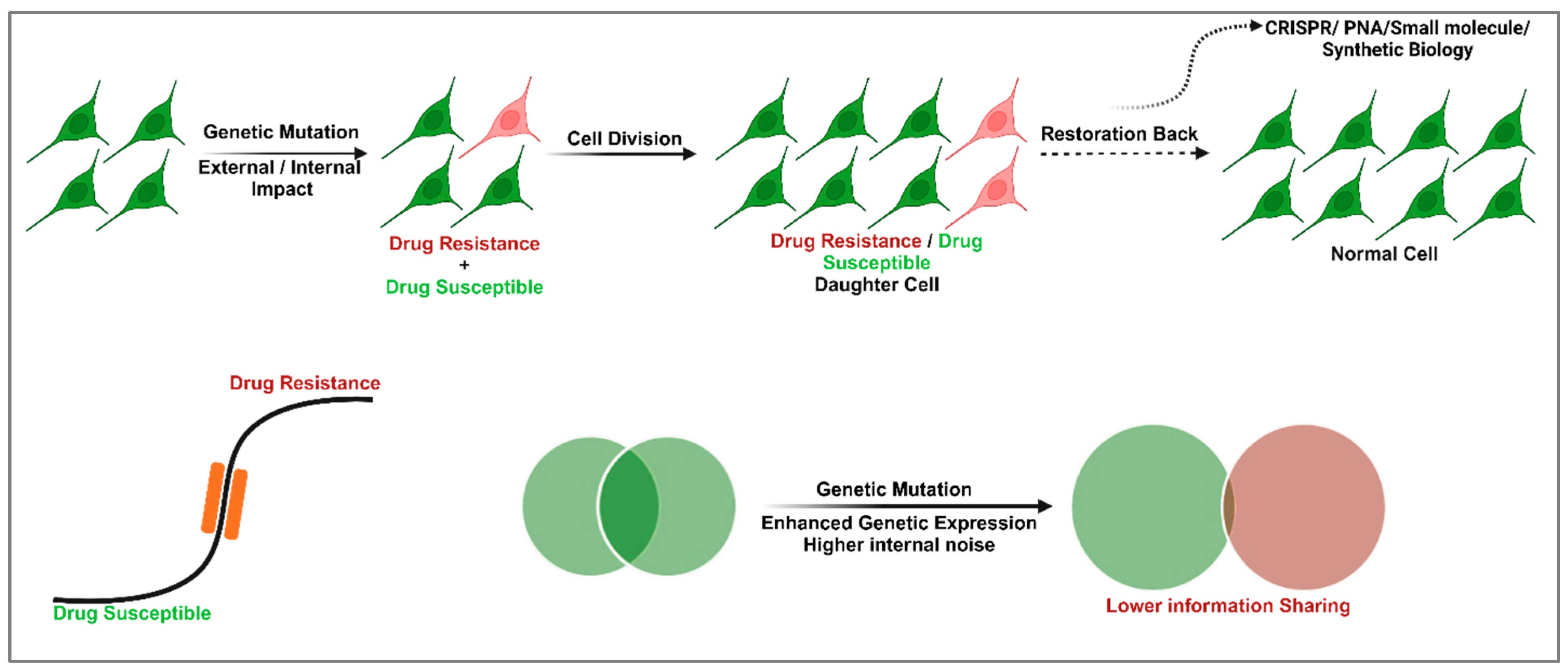
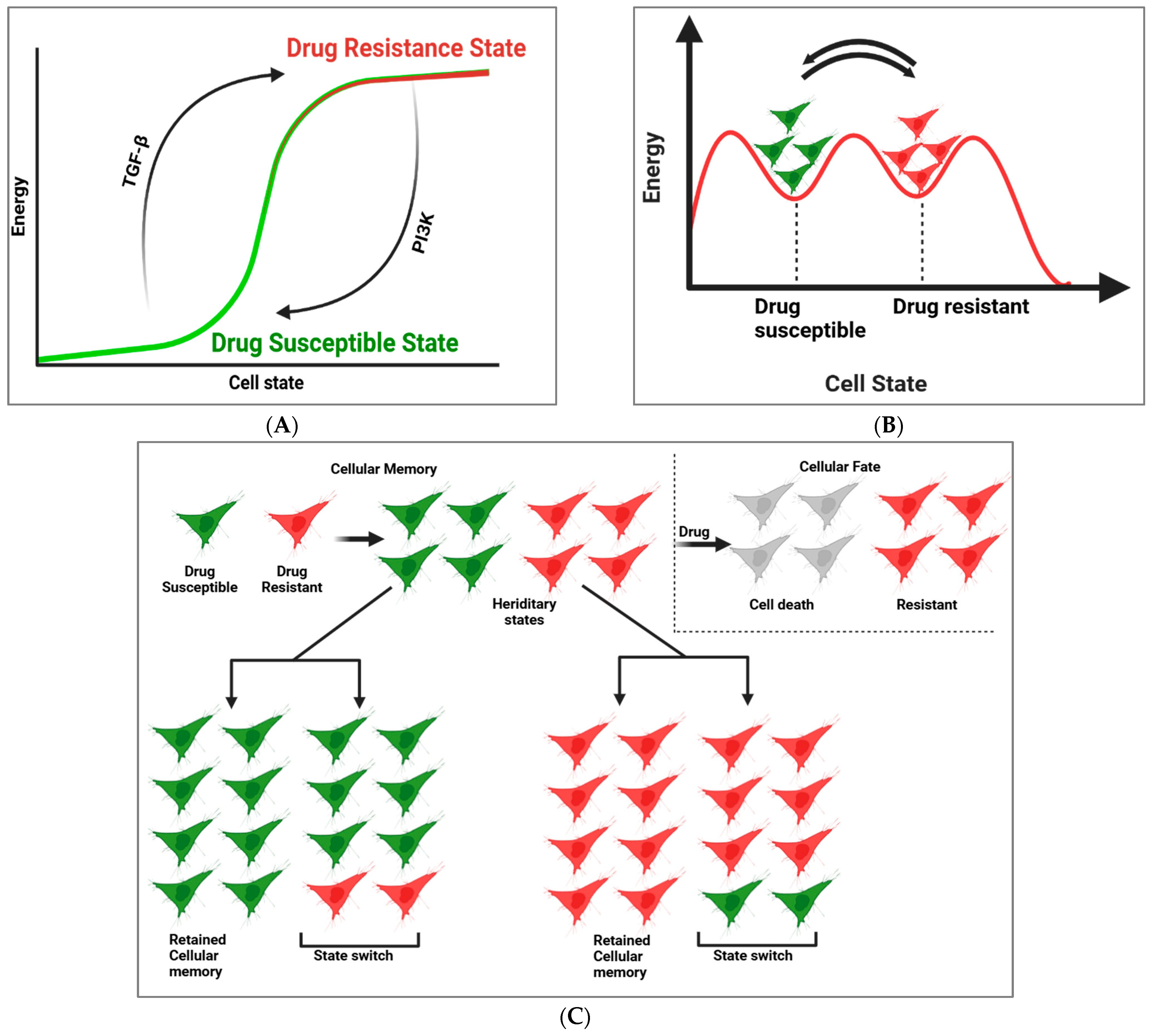
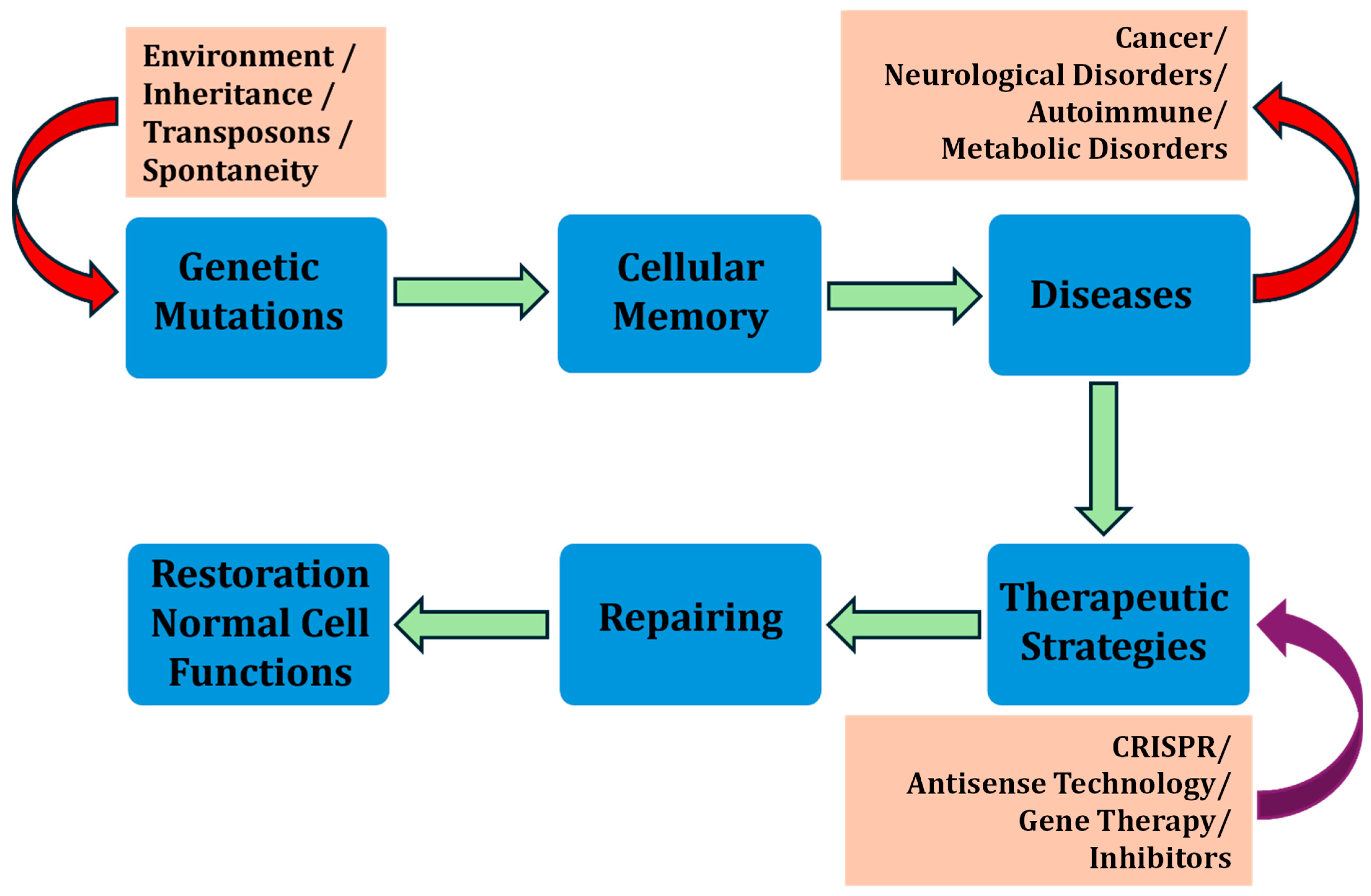
2. Cellular Memory and GRNs in Drug Resistance and Susceptibility
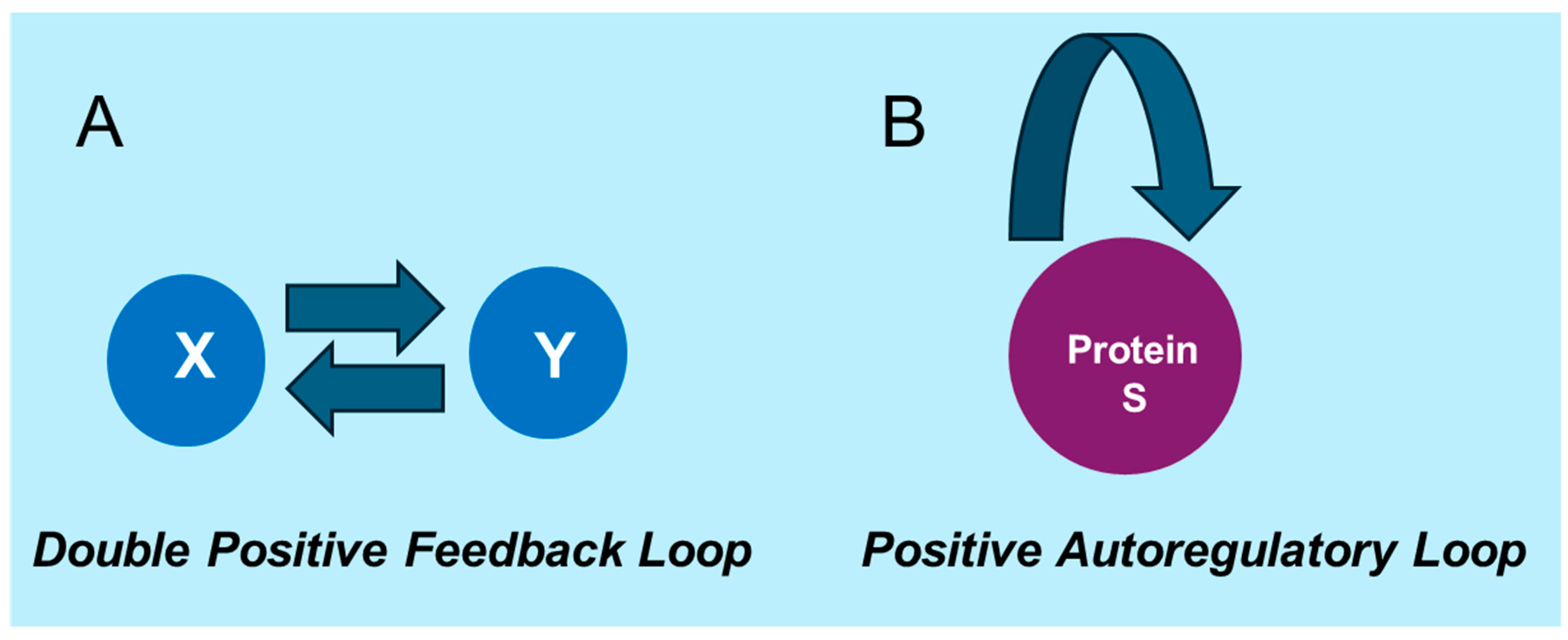
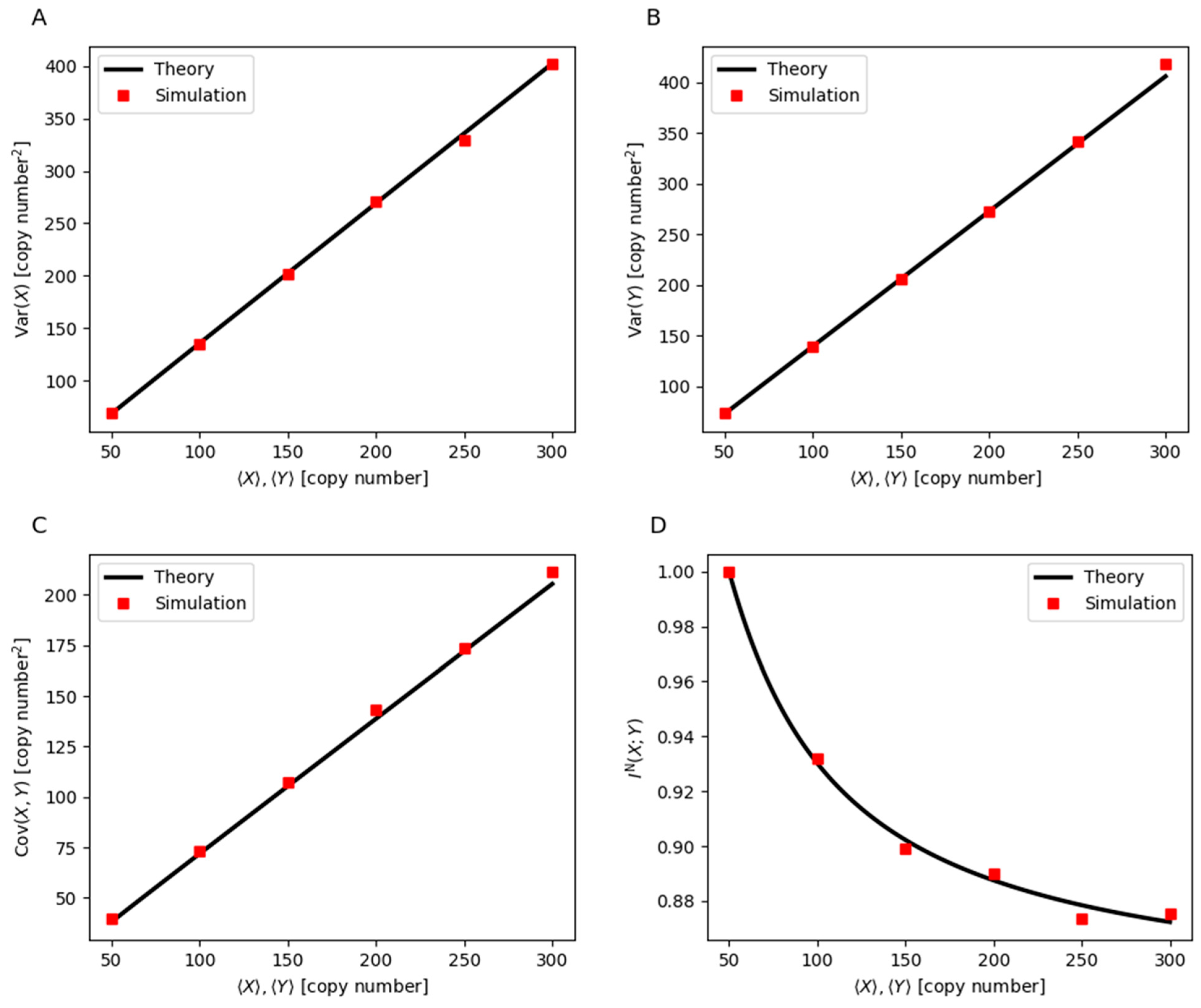
3. Mathematical Modeling of Noise Dynamics and Mutual Information in Gene Regulation
4. Inhibition of Cellular Memory with Selective Inhibitor
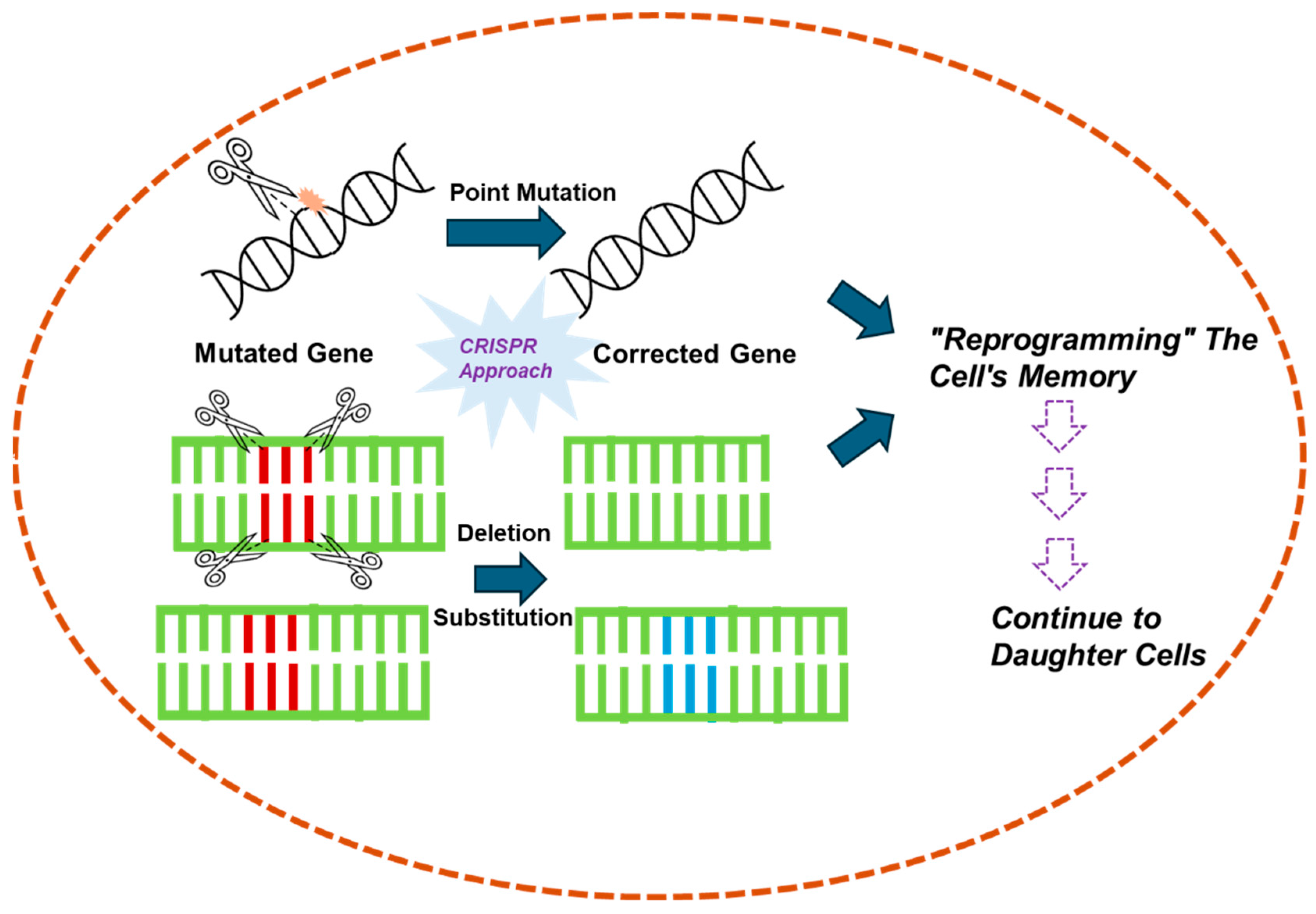
5. CRISPR’s Role in “Reverse Drug Resistance”
6. Cellular Memory for Next-Generation Therapeutic Breakthroughs
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shaffer, S.M.; Emert, B.L.; Hueros, R.A.R.; Cote, C.; Harmange, G.; Schaff, D.L.; Sizemore, A.E.; Gupte, R.; Torre, E.; Singh, A. Memory sequencing reveals heritable single-cell gene expression programs associated with distinct cellular behaviors. Cell 2020, 182, 947–959.e917. [Google Scholar] [CrossRef] [PubMed]
- Biehl, J.K.; Russell, B. Introduction to stem cell therapy. J. Cardiovasc. Nurs. 2009, 24, 98–103. [Google Scholar] [CrossRef] [PubMed]
- Monod, J.; Jacob, F. General conclusions: Teleonomic mechanisms in cellular metabolism, growth, and differentiation. In Cold Spring Harbor Symposia on Quantitative Biology; Cold Spring Harbor Laboratory Press: Long Island, NY, USA, 1961; Volume 26, pp. 389–401. [Google Scholar]
- Elowitz, M.B.; Levine, A.J.; Siggia, E.D.; Swain, P.S. Stochastic gene expression in a single cell. Science 2002, 297, 1183–1186. [Google Scholar] [CrossRef]
- Burrill, D.R.; Silver, P.A. Making cellular memories. Cell 2010, 140, 13–18. [Google Scholar] [CrossRef]
- Spencer, S.L.; Gaudet, S.; Albeck, J.G.; Burke, J.M.; Sorger, P.K. Non-genetic origins of cell-to-cell variability in TRAIL-induced apoptosis. Nature 2009, 459, 428–432. [Google Scholar] [CrossRef]
- Sharma, S.V.; Lee, D.Y.; Li, B.; Quinlan, M.P.; Takahashi, F.; Maheswaran, S.; McDermott, U.; Azizian, N.; Zou, L.; Fischbach, M.A. A chromatin-mediated reversible drug-tolerant state in cancer cell subpopulations. Cell 2010, 141, 69–80. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.; Cao, E.Y.; Kumar, V.; Zhang, X.; Leong, H.S.; Wong, A.M.L.; Ramakrishnan, N.; Hakimullah, M.; Teo, H.M.V.; Chong, F.T. Longitudinal single-cell RNA sequencing of patient-derived primary cells reveals drug-induced infidelity in stem cell hierarchy. Nat. Commun. 2018, 9, 4931. [Google Scholar] [CrossRef]
- Gupta, P.B.; Fillmore, C.M.; Jiang, G.; Shapira, S.D.; Tao, K.; Kuperwasser, C.; Lander, E.S. Stochastic state transitions give rise to phenotypic equilibrium in populations of cancer cells. Cell 2011, 146, 633–644. [Google Scholar] [CrossRef]
- Pisco, A.O.; Huang, S. Non-genetic cancer cell plasticity and therapy-induced stemness in tumour relapse: ‘What does not kill me strengthens me’. Br. J. Cancer 2015, 112, 1725–1732. [Google Scholar] [CrossRef]
- Fallahi-Sichani, M.; Becker, V.; Izar, B.; Baker, G.J.; Lin, J.R.; Boswell, S.A.; Shah, P.; Rotem, A.; Garraway, L.A.; Sorger, P.K. Adaptive resistance of melanoma cells to RAF inhibition via reversible induction of a slowly dividing de-differentiated state. Mol. Syst. Biol. 2017, 13, 905. [Google Scholar] [CrossRef]
- Su, Y.; Wei, W.; Robert, L.; Xue, M.; Tsoi, J.; Garcia-Diaz, A.; Homet Moreno, B.; Kim, J.; Ng, R.H.; Lee, J.W. Single-cell analysis resolves the cell state transition and signaling dynamics associated with melanoma drug-induced resistance. Proc. Natl. Acad. Sci. USA 2017, 114, 13679–13684. [Google Scholar] [CrossRef] [PubMed]
- Shaffer, S.M.; Dunagin, M.C.; Torborg, S.R.; Torre, E.A.; Emert, B.; Krepler, C.; Beqiri, M.; Sproesser, K.; Brafford, P.A.; Xiao, M. Rare cell variability and drug-induced reprogramming as a mode of cancer drug resistance. Nature 2017, 546, 431–435. [Google Scholar] [CrossRef] [PubMed]
- Schuh, L.; Saint-Antoine, M.; Sanford, E.M.; Emert, B.L.; Singh, A.; Marr, C.; Raj, A.; Goyal, Y. Gene networks with transcriptional bursting recapitulate rare transient coordinated high expression states in cancer. Cell Syst. 2020, 10, 363–378.e312. [Google Scholar] [CrossRef]
- Harmange, G.; Hueros, R.A.R.; Schaff, D.L.; Emert, B.; Saint-Antoine, M.; Kim, L.C.; Niu, Z.; Nellore, S.; Fane, M.E.; Alicea, G.M. Disrupting cellular memory to overcome drug resistance. Nat. Commun. 2023, 14, 7130. [Google Scholar] [CrossRef] [PubMed]
- Davidson, E.; Levin, M. Gene regulatory networks. Proc. Natl. Acad. Sci. USA 2005, 102, 4935. [Google Scholar] [CrossRef]
- De, N.; Nandi, M.; Banik, S.; Roy, S. Bi-stability of the master gene regulatory network of the common dendritic precursor cell: Implications for cell differentiation. IUBMB Life 2020, 72, 2225–2232. [Google Scholar] [CrossRef]
- Bonasio, R.; Tu, S.; Reinberg, D. Molecular signals of epigenetic states. Science 2010, 330, 612–616. [Google Scholar] [CrossRef]
- Huang, S. Multistability and multicellularity: Cell fates as high-dimensional attractors of gene regulatory networks. In Computational Systems Biology; Elsevier: Amsterdam, The Netherlands, 2006; pp. 293–326. [Google Scholar]
- Amir, A.; Kobiler, O.; Rokney, A.; Oppenheim, A.B.; Stavans, J. Noise in timing and precision of gene activities in a genetic cascade. Mol. Syst. Biol. 2007, 3, 71. [Google Scholar] [CrossRef]
- Raser, J.M.; O'shea, E.K. Noise in gene expression: Origins, consequences, and control. Science 2005, 309, 2010–2013. [Google Scholar] [CrossRef]
- Dong, D.; Shao, X.; Deng, N.; Zhang, Z. Gene expression variations are predictive for stochastic noise. Nucleic Acids Res. 2011, 39, 403–413. [Google Scholar] [CrossRef]
- Biswas, S.; Manicka, S.; Hoel, E.; Levin, M. Gene regulatory networks exhibit several kinds of memory: Quantification of memory in biological and random transcriptional networks. Iscience 2021, 24, 102131. [Google Scholar] [CrossRef]
- Liu, G.; David, B.T.; Trawczynski, M.; Fessler, R.G. Advances in pluripotent stem cells: History, mechanisms, technologies, and applications. Stem Cell Rev. Rep. 2020, 16, 3–32. [Google Scholar] [CrossRef]
- Nojadeh, J.N.; Eryilmaz, N.S.B.; Ergüder, B.İ. CRISPR/Cas9 genome editing for neurodegenerative diseases. EXCLI J. 2023, 22, 567. [Google Scholar]
- Waldo, J.J.; Halmai, J.A.; Fink, K.D. Epigenetic editing for autosomal dominant neurological disorders. Front. Genome Ed. 2024, 6, 1304110. [Google Scholar] [CrossRef]
- Burgos-Morales, O.; Gueye, M.; Lacombe, L.; Nowak, C.; Schmachtenberg, R.; Hörner, M.; Jerez-Longres, C.; Mohsenin, H.; Wagner, H.J.; Weber, W. Synthetic biology as driver for the biologization of materials sciences. Mater. Today Bio 2021, 11, 100115. [Google Scholar] [CrossRef]
- Chiang, A.J.; Hasty, J. Design of synthetic bacterial biosensors. Curr. Opin. Microbiol. 2023, 76, 102380. [Google Scholar] [CrossRef]
- Hicks, M.; Bachmann, T.T.; Wang, B. Synthetic biology enables programmable cell-based biosensors. ChemPhysChem 2020, 21, 132–144. [Google Scholar] [CrossRef] [PubMed]
- Arboleda-García, A.; Alarcon-Ruiz, I.; Boada-Acosta, L.; Boada, Y.; Vignoni, A.; Jantus-Lewintre, E. Advancements in synthetic biology-based bacterial cancer therapy: A modular design approach. Crit. Rev. Oncol./Hematol. 2023, 190, 104088. [Google Scholar] [CrossRef] [PubMed]
- Sannigrahi, A.; De, N.; Bhunia, D.; Bhadra, J. Peptide nucleic acids: Recent advancements and future opportunities in biomedical applications. Bioorg. Chem. 2025, 155, 108146. [Google Scholar] [CrossRef] [PubMed]
- Blake, W.J.; Kærn, M.; Cantor, C.R.; Collins, J.J. Noise in eukaryotic gene expression. Nature 2003, 422, 633–637. [Google Scholar] [CrossRef]
- Swain, P.S.; Elowitz, M.B.; Siggia, E.D. Intrinsic and extrinsic contributions to stochasticity in gene expression. Proc. Natl. Acad. Sci. USA 2002, 99, 12795–12800. [Google Scholar] [CrossRef] [PubMed]
- McAdams, H.H.; Arkin, A. Stochastic mechanisms in gene expression. Proc. Natl. Acad. Sci. USA 1997, 94, 814–819. [Google Scholar] [CrossRef]
- Pal, S.; Dhar, R. Living in a noisy world—Origins of gene expression noise and its impact on cellular decision-making. FEBS Lett. 2024, 598, 1673–1691. [Google Scholar] [CrossRef]
- Jovic, D.; Liang, X.; Zeng, H.; Lin, L.; Xu, F.; Luo, Y. Single-cell RNA sequencing technologies and applications: A brief overview. Clin. Transl. Med. 2022, 12, e694. [Google Scholar] [CrossRef]
- Haque, A.; Engel, J.; Teichmann, S.A.; Lönnberg, T. A practical guide to single-cell RNA-sequencing for biomedical research and clinical applications. Genome Med. 2017, 9, 75. [Google Scholar] [CrossRef]
- Bai, X.; Fisher, D.E.; Flaherty, K.T. Cell-state dynamics and therapeutic resistance in melanoma from the perspective of MITF and IFNγ pathways. Nat. Rev. Clin. Oncol. 2019, 16, 549–562. [Google Scholar] [CrossRef]
- Emert, B.L.; Cote, C.J.; Torre, E.A.; Dardani, I.P.; Jiang, C.L.; Jain, N.; Shaffer, S.M.; Raj, A. Variability within rare cell states enables multiple paths toward drug resistance. Nat. Biotechnol. 2021, 39, 865–876. [Google Scholar] [CrossRef]
- Gupta, A.; Ma, S.; Che, K.; Pobbati, A.V.; Rubin, B.P. Inhibition of PI3K and MAPK pathways along with KIT inhibitors as a strategy to overcome drug resistance in gastrointestinal stromal tumors. PLoS ONE 2021, 16, e0252689. [Google Scholar] [CrossRef]
- Martinez, E.; Vazquez, N.; Lopez, A.; Fanniel, V.; Sanchez, L.; Marks, R.; Hinojosa, L.; Cuello, V.; Cuevas, M.; Rodriguez, A. The PI3K pathway impacts stem gene expression in a set of glioblastoma cell lines. J. Cancer Res. Clin. Oncol. 2020, 146, 593–604. [Google Scholar] [CrossRef]
- Lange, M.; Piran, Z.; Klein, M.; Spanjaard, B.; Klein, D.; Junker, J.P.; Theis, F.J.; Nitzan, M. Mapping lineage-traced cells across time points with moslin. Genome Biol. 2024, 25, 277. [Google Scholar] [CrossRef]
- Guadarrama-Orozco, J.; Ortega-Gómez, A.; Ruiz-García, E.; Astudillo-de la Vega, H.; Meneses-García, A.; Lopez-Camarillo, C. Braf V600E mutation in melanoma: Translational current scenario. Clin. Transl. Oncol. 2016, 18, 863–871. [Google Scholar] [CrossRef]
- Frantz, W.T.; Ceol, C.J. From tank to treatment: Modeling melanoma in zebrafish. Cells 2020, 9, 1289. [Google Scholar] [CrossRef]
- Goyal, Y.; Busch, G.T.; Pillai, M.; Li, J.; Boe, R.H.; Grody, E.I.; Chelvanambi, M.; Dardani, I.P.; Emert, B.; Bodkin, N. Diverse clonal fates emerge upon drug treatment of homogeneous cancer cells. Nature 2023, 620, 651–659. [Google Scholar] [CrossRef]
- Madsen, R.R. PI3K in stemness regulation: From development to cancer. Biochem. Soc. Trans. 2020, 48, 301–315. [Google Scholar] [CrossRef]
- Bhat, G.R.; Sethi, I.; Sadida, H.Q.; Rah, B.; Mir, R.; Algehainy, N.; Albalawi, I.A.; Masoodi, T.; Subbaraj, G.K.; Jamal, F. Cancer cell plasticity: From cellular, molecular, and genetic mechanisms to tumor heterogeneity and drug resistance. Cancer Metastasis Rev. 2024, 43, 197–228. [Google Scholar] [CrossRef]
- Guo, W.; Wang, H.; Li, C. Signal pathways of melanoma and targeted therapy. Signal Transduct. Target. Ther. 2021, 6, 424. [Google Scholar] [CrossRef] [PubMed]
- Gray, R.; Cameron, D.A.; Early Breast Cancer Trialists’ Collaborative Group. Trastuzumab for HER2-positive early stage breast cancer: A meta-analysis of individual patient data from 13,864 women from seven randomised trials. Lancet Oncol. 2021, 22, 1139–1150. [Google Scholar] [CrossRef]
- García-Foncillas, J.; Sunakawa, Y.; Aderka, D.; Wainberg, Z.; Ronga, P.; Witzler, P.; Stintzing, S. Distinguishing features of cetuximab and panitumumab in colorectal cancer and other solid tumors. Front. Oncol. 2019, 9, 849. [Google Scholar] [CrossRef] [PubMed]
- Napolitano, A.; Thway, K.; Smith, M.J.; Huang, P.H.; Jones, R.L. KIT exon 9-mutated gastrointestinal stromal tumours: Biology and treatment. Chemotherapy 2022, 67, 81–90. [Google Scholar] [CrossRef] [PubMed]
- Stone, R.M.; Mandrekar, S.J.; Sanford, B.L.; Laumann, K.; Geyer, S.; Bloomfield, C.D.; Thiede, C.; Prior, T.W.; Döhner, K.; Marcucci, G. Midostaurin plus chemotherapy for acute myeloid leukemia with a FLT3 mutation. N. Engl. J. Med. 2017, 377, 454–464. [Google Scholar] [CrossRef]
- Royce, M.E.; Osman, D. Everolimus in the treatment of metastatic breast cancer. Breast Cancer Basic Clin. Res. 2015, 9, BCBCR-S29268. [Google Scholar] [CrossRef]
- Grinshpun, A.; Tolaney, S.M.; Burstein, H.J.; Jeselsohn, R.; Mayer, E.L. The dilemma of selecting a first line CDK4/6 inhibitor for hormone receptor-positive/HER2-negative metastatic breast cancer. NPJ Breast Cancer 2023, 9, 15. [Google Scholar] [CrossRef]
- González-Martín, A.; Pothuri, B.; Vergote, I.; DePont Christensen, R.; Graybill, W.; Mirza, M.R.; McCormick, C.; Lorusso, D.; Hoskins, P.; Freyer, G. Niraparib in patients with newly diagnosed advanced ovarian cancer. N. Engl. J. Med. 2019, 381, 2391–2402. [Google Scholar] [CrossRef] [PubMed]
- Verstovsek, S.; Mesa, R.A.; Gotlib, J.; Levy, R.S.; Gupta, V.; DiPersio, J.F.; Catalano, J.V.; Deininger, M.; Miller, C.; Silver, R.T. A double-blind, placebo-controlled trial of ruxolitinib for myelofibrosis. N. Engl. J. Med. 2012, 366, 799–807. [Google Scholar] [CrossRef]
- Gardner, T.S.; Cantor, C.R.; Collins, J.J. Construction of a genetic toggle switch in Escherichia coli. Nature 2000, 403, 339–342. [Google Scholar] [CrossRef]
- Ferrell, J.E., Jr. Self-perpetuating states in signal transduction: Positive feedback, double-negative feedback and bistability. Curr. Opin. Cell Biol. 2002, 14, 140–148. [Google Scholar] [CrossRef]
- Tkačik, G.; Walczak, A.M. Information transmission in genetic regulatory networks: A review. J. Phys. Condens. Matter 2011, 23, 153102. [Google Scholar] [CrossRef]
- Ziv, E.; Nemenman, I.; Wiggins, C.H. Optimal signal processing in small stochastic biochemical networks. PLoS ONE 2007, 2, e1077. [Google Scholar] [CrossRef][Green Version]
- Brock, A.; Chang, H.; Huang, S. Non-genetic heterogeneity—A mutation-independent driving force for the somatic evolution of tumours. Nat. Rev. Genet. 2009, 10, 336–342. [Google Scholar] [CrossRef] [PubMed]
- Momin, M.S.A.; Biswas, A.; Banik, S.K. Coherent feed-forward loop acts as an efficient information transmitting motif. Phys. Rev. E 2020, 101, 022407. [Google Scholar] [CrossRef] [PubMed]
- Bialek, W. Biophysics: Searching for Principles; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Momin, M.S.A.; Biswas, A. Extrinsic noise of the target gene governs abundance pattern of feed-forward loop motifs. Phys. Rev. E 2020, 101, 052411. [Google Scholar] [CrossRef]
- Momin, M.S.A.; Biswas, A. The role of gene regulation in redundant and synergistic information transfers in coherent feed-forward loop. J. Stat. Mech. Theory Exp. 2023, 2023, 023501. [Google Scholar] [CrossRef]
- Bintu, L.; Buchler, N.E.; Garcia, H.G.; Gerland, U.; Hwa, T.; Kondev, J.; Phillips, R. Transcriptional regulation by the numbers: Models. Curr. Opin. Genet. Dev. 2005, 15, 116–124. [Google Scholar] [CrossRef]
- Alon, U. An Introduction to Systems Biology: Design Principles of Biological Circuits; Chapman and Hall/CRC: Boca Raton, FL, USA, 2019. [Google Scholar]
- Tostevin, F.; Ten Wolde, P.R. Mutual information in time-varying biochemical systems. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2010, 81, 061917. [Google Scholar] [CrossRef]
- Keizer, J. Statistical Thermodynamics of Nonequilibrium Processes; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Elf, J.; Ehrenberg, M. Fast evaluation of fluctuations in biochemical networks with the linear noise approximation. Genome Res. 2003, 13, 2475–2484. [Google Scholar] [CrossRef] [PubMed]
- Van Kampen, N.G. Stochastic Processes in Physics and Chemistry; Elsevier: Amsterdam, The Netherlands, 1992; Volume 1. [Google Scholar]
- Paulsson, J. Summing up the noise in gene networks. Nature 2004, 427, 415–418. [Google Scholar] [CrossRef]
- Paulsson, J. Models of stochastic gene expression. Phys. Life Rev. 2005, 2, 157–175. [Google Scholar] [CrossRef]
- Barrett, A.B. Exploration of synergistic and redundant information sharing in static and dynamical Gaussian systems. Phys. Rev. E 2015, 91, 052802. [Google Scholar] [CrossRef]
- Gillespie, D.T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 1976, 22, 403–434. [Google Scholar] [CrossRef]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Raj, A.; Van Oudenaarden, A. Nature, nurture, or chance: Stochastic gene expression and its consequences. Cell 2008, 135, 216–226. [Google Scholar] [CrossRef]
- Morton, R.A.; Kim, T.N. Viscocohesive hyaluronan gel enhances stability of intravital multiphoton imaging with subcellular resolution. Neurophotonics 2025, 12, S14602. [Google Scholar] [CrossRef] [PubMed]
- Dar, R.D.; Razooky, B.S.; Singh, A.; Trimeloni, T.V.; McCollum, J.M.; Cox, C.D.; Simpson, M.L.; Weinberger, L.S. Transcriptional burst frequency and burst size are equally modulated across the human genome. Proc. Natl. Acad. Sci. USA 2012, 109, 17454–17459. [Google Scholar] [CrossRef]
- Junttila, M.R.; De Sauvage, F.J. Influence of tumour micro-environment heterogeneity on therapeutic response. Nature 2013, 501, 346–354. [Google Scholar] [CrossRef]
- Uddin, F.; Rudin, C.M.; Sen, T. CRISPR gene therapy: Applications, limitations, and implications for the future. Front. Oncol. 2020, 10, 1387. [Google Scholar] [CrossRef]
- Adli, M. The CRISPR tool kit for genome editing and beyond. Nat. Commun. 2018, 9, 1911. [Google Scholar] [CrossRef]
- Vaghari-Tabari, M.; Hassanpour, P.; Sadeghsoltani, F.; Malakoti, F.; Alemi, F.; Qujeq, D.; Asemi, Z.; Yousefi, B. CRISPR/Cas9 gene editing: A new approach for overcoming drug resistance in cancer. Cell. Mol. Biol. Lett. 2022, 27, 49. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Y. Application of the CRISPR/Cas9 system to drug resistance in breast cancer. Adv. Sci. 2018, 5, 1700964. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Z.; Unver, T.; Zhang, B. CRISPR/Cas: A powerful tool for gene function study and crop improvement. J. Adv. Res. 2021, 29, 207–221. [Google Scholar] [CrossRef] [PubMed]
- Akinci, E.; Hamilton, M.C.; Khowpinitchai, B.; Sherwood, R.I. Using CRISPR to understand and manipulate gene regulation. Development 2021, 148, dev182667. [Google Scholar] [CrossRef] [PubMed]
- Tao, S.; Chen, H.; Li, N.; Liang, W. The application of the CRISPR-Cas system in antibiotic resistance. Infect. Drug Resist. 2022, 15, 4155–4168. [Google Scholar] [CrossRef]
- Struhl, G.; Adachi, A. Nuclear access and action of notch in vivo. Cell 1998, 93, 649–660. [Google Scholar] [CrossRef]
- Sprinzak, D.; Lakhanpal, A.; LeBon, L.; Santat, L.A.; Fontes, M.E.; Anderson, G.A.; Garcia-Ojalvo, J.; Elowitz, M.B. Cis-interactions between Notch and Delta generate mutually exclusive signalling states. Nature 2010, 465, 86–90. [Google Scholar] [CrossRef]
- Tanase-Nicola, S.; Warren, P.B.; ten Wolde, P.R. Signal detection, modularity, and the correlation between extrinsic and intrinsic noise in biochemical networks. Phys. Rev. Lett. 2006, 97, 068102. [Google Scholar] [CrossRef]
- Warren, P.B.; Tanase-Nicola, S.; Wolde, P.R.T. Exact results for noise power spectra in linear biochemical reaction networks. J. Chem. Phys. 2006, 125, 144904. [Google Scholar] [CrossRef]
- Biswas, A.; Banik, S.K. Redundancy in information transmission in a two-step cascade. Phys. Rev. E 2016, 93, 052422. [Google Scholar] [CrossRef]
- de Ronde, W.H.; Tostevin, F.; Wolde, P.R.T. Feed-forward loops and diamond motifs lead to tunable transmission of information in the frequency domain. Phys. Rev. E 2012, 86, 021913. [Google Scholar] [CrossRef]
- Biswas, A.; Banik, S.K. Interplay of synergy and redundancy in diamond motif. Chaos 2018, 28, 103102. [Google Scholar] [CrossRef]
- Biswas, A. Multivariate information processing characterizes fitness of a cascaded gene-transcription machinery. Chaos 2019, 29, 063108. [Google Scholar] [CrossRef] [PubMed]
- Keizer, J. Statistical Thermodynamics of Nonequilibrium Processes; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Grima, R. Linear-noise approximation and the chemical master equation agree up to second-order moments for a class of chemical systems. Phys. Rev. E 2015, 92, 042124. [Google Scholar] [CrossRef] [PubMed]
| Signaling Pathways | Inhibitors | Chemical Structure of Inhibitors |
|---|---|---|
| TGF-β and PI3K signaling pathways are key regulators of melanoma cell survival, proliferation, and metastasis; targeting them may disrupt cancer adaptation and resistance. | BRAFi (e.g., Vemurafenib) and MEKi (e.g., Trametinib) target the MAPK pathway, commonly mutated in melanoma, and work synergistically to inhibit tumor-promoting signaling [48]. | 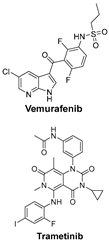 |
| The HER2 signaling pathway, often overexpressed in breast cancer, promotes cell proliferation. Targeted HER2 inhibitors block this signaling, thereby reducing tumor growth. | Trastuzumab is a monoclonal antibody that targets the extracellular domain of HER2. It is widely used to treat HER2-positive breast cancer and has significantly improved outcomes for patients with this aggressive subtype [49]. | Trastuzumab is a monoclonal antibody (148 kDa) of the IgG1 subclass, it consists of two heavy chains (~50 kDa each) and two light chains (~25 kDa each). |
| The Epidermal Growth Factor Receptor (EGFR) signaling pathway promotes cell proliferation, migration, and survival. Its inhibition can effectively suppress the growth of various cancers. | Cetuximab is a chimeric monoclonal antibody (IgG1) that targets EGFR and is primarily used to treat colorectal cancer and head and neck squamous cell carcinoma (HNSCC) [50]. | Cetuximab (152 kDa) is a chimeric monoclonal antibody made up of human and mouse components. |
| The KIT Pathway is a receptor tyrosine kinase that, when mutated, leads to unregulated cell growth in gastrointestinal stromal tumors (GISTs). | Imatinib is a tyrosine kinase inhibitor that specifically targets KIT mutations, especially KIT exon 9 mutations in gastrointestinal stromal tumors (GISTs) [51]. | 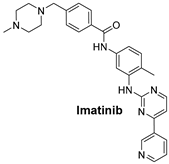 |
| FLT3 is a receptor tyrosine kinase whose mutations drive early-stage acute myeloid leukemia (AML). FLT3 inhibitors reduce leukemic cell proliferation by targeting these mutations. | Midostaurin is a first-generation, multi-targeted kinase inhibitor that blocks FLT3. It is primarily used in acute myeloid leukemia (AML) with FLT3 mutations and systemic mastocytosis (SM) [52]. | 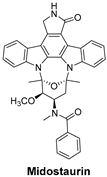 |
| The mechanistic target of rapamycin (mTOR) signaling pathway regulates cell growth, survival, and metabolism. The inhibition of mTOR can slow down cancer progression. | Everolimus is an mTOR inhibitor used to block the mTOR pathway, which is often dysregulated in cancers, including breast cancer [53]. | 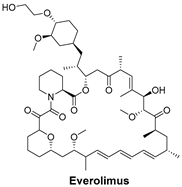 |
| The cyclin-dependent kinases (CDK4/6) pathway regulates the cell cycle and promotes cell division. Inhibiting CDK4/6 can halt cell cycle progression, leading to cancer cell death. | Ribociclib is a selective CDK4/6 inhibitor that prevents cell cycle progression from the G1 to S phase, thereby halting cancer cell proliferation and particularly effective for Triple-Positive Breast Cancer [54]. | 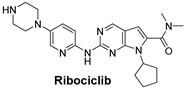 |
| The Poly (ADP-ribose) polymerase (PARP) pathway plays a key role in DNA repair. PARP inhibitors block this repair process, causing cancer cell death—especially effective in cancers with BRCA mutations. | Niraparib is a potent inhibitor of PARP, particularly useful in ovarian cancers, where defective DNA repair mechanisms are common [55]. | 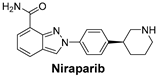 |
| The JAK (Janus Kinase) signaling Pathway regulates the immune response and hematopoiesis. In myelofibrosis, abnormal JAK activity drives excessive cell proliferation. | Ruxolitinib is a JAK1/2 inhibitor used to treat myelofibrosis by blocking the JAK–STAT signaling pathway, reducing cytokine production [56]. |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Momin, M.S.A.; Bhadra, J.; Bhunia, D.; Sannigrahi, A.; De, N. Unlocking Cellular Memory and Gene Regulatory Networks: Pioneering the Future of Therapeutic Innovations. Cells 2025, 14, 903. https://doi.org/10.3390/cells14120903
Momin MSA, Bhadra J, Bhunia D, Sannigrahi A, De N. Unlocking Cellular Memory and Gene Regulatory Networks: Pioneering the Future of Therapeutic Innovations. Cells. 2025; 14(12):903. https://doi.org/10.3390/cells14120903
Chicago/Turabian StyleMomin, Md Sorique Aziz, Jhuma Bhadra, Debmalya Bhunia, Achinta Sannigrahi, and Nayan De. 2025. "Unlocking Cellular Memory and Gene Regulatory Networks: Pioneering the Future of Therapeutic Innovations" Cells 14, no. 12: 903. https://doi.org/10.3390/cells14120903
APA StyleMomin, M. S. A., Bhadra, J., Bhunia, D., Sannigrahi, A., & De, N. (2025). Unlocking Cellular Memory and Gene Regulatory Networks: Pioneering the Future of Therapeutic Innovations. Cells, 14(12), 903. https://doi.org/10.3390/cells14120903






