Structure-Function Relationship of the Ryanodine Receptor Cluster Network in Sinoatrial Node Cells
Abstract
1. Introduction
2. Materials and Methods
2.1. Enzymatic Isolation of Individual SANC
2.2. Immunolabeling of RyRs
2.3. Structured Illumination Microscopy (SIM)
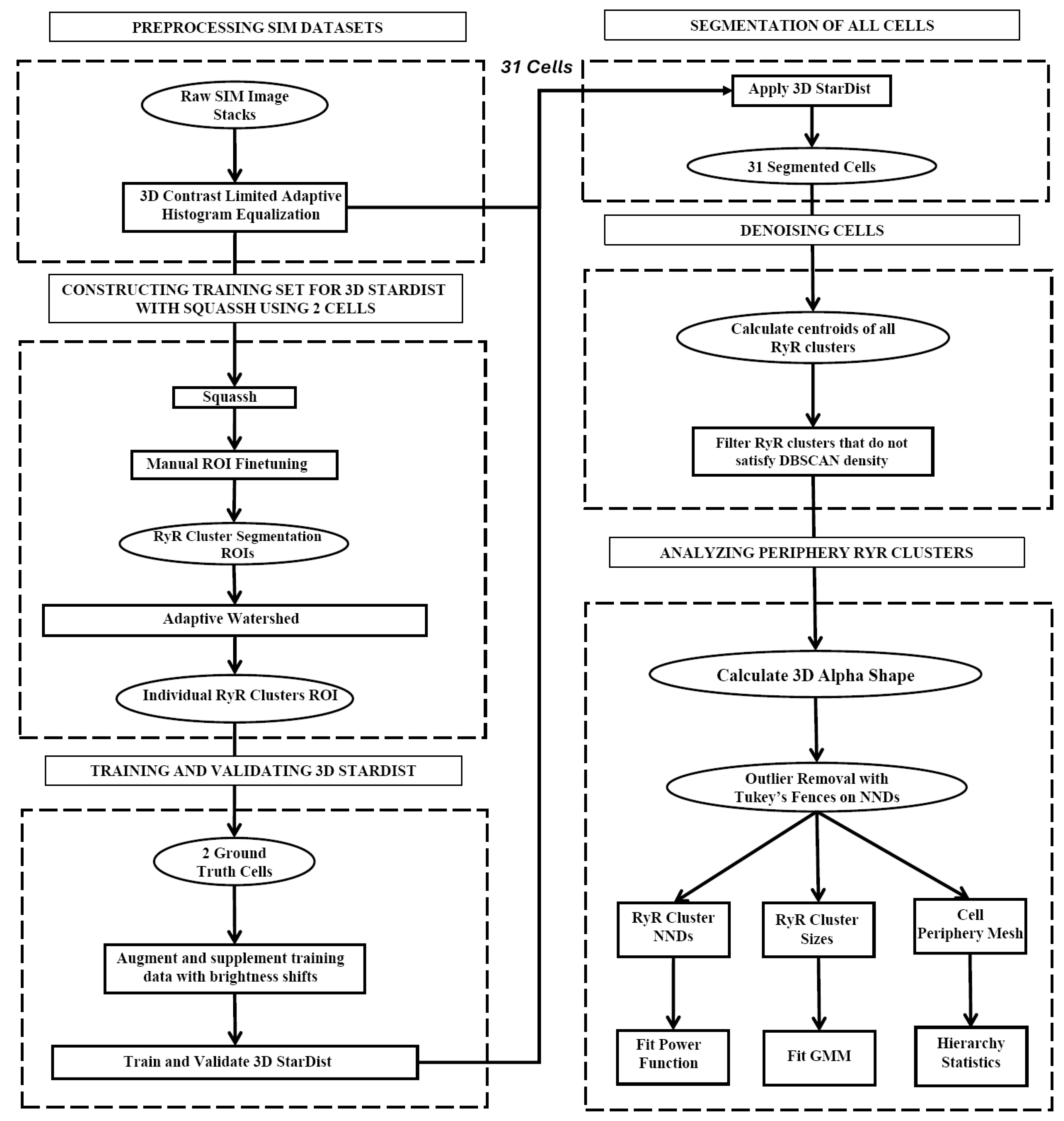
2.4. Segmentation of Peripheral RyR Clusters in 3D
3. Results
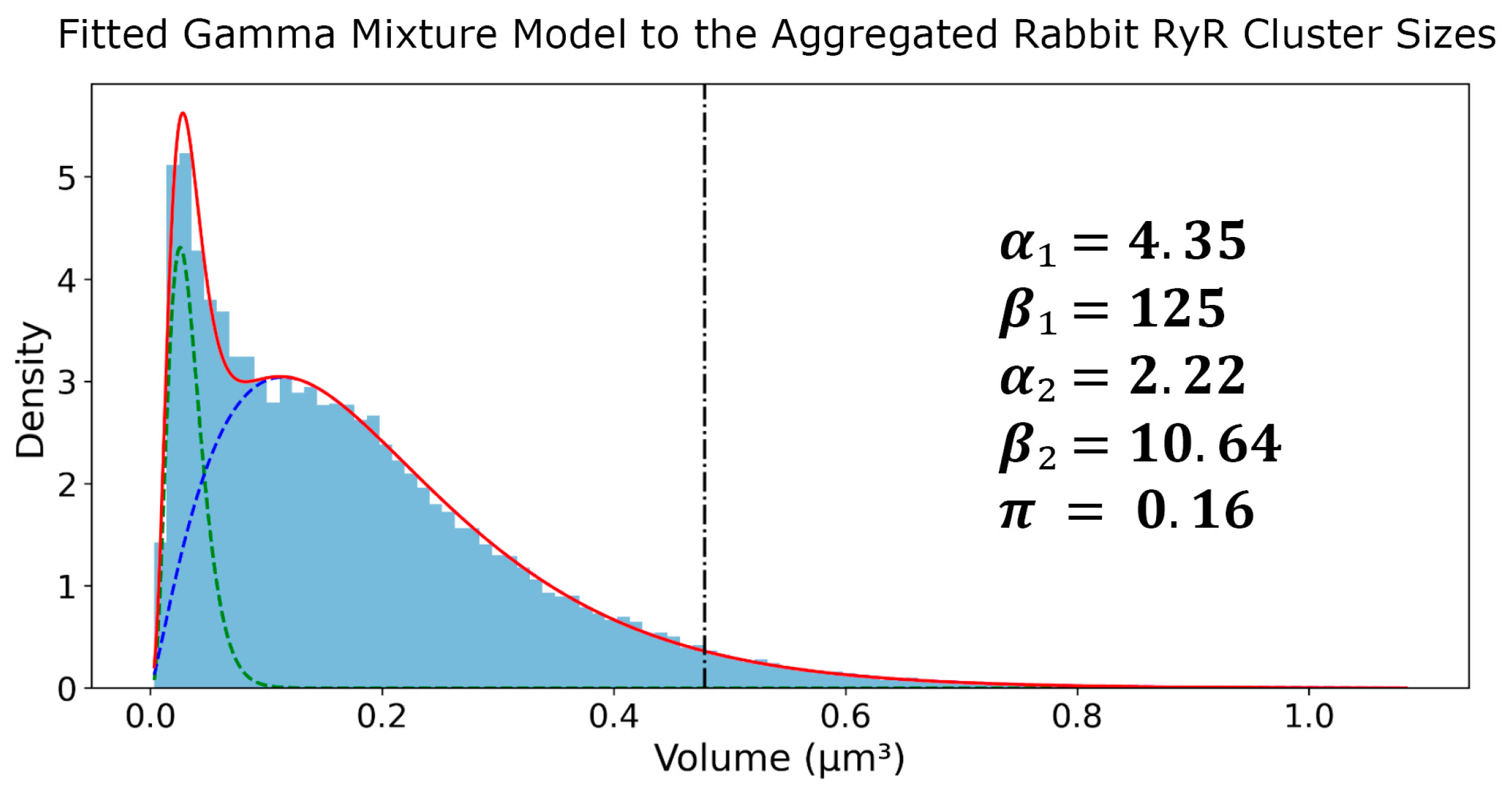
3.1. Two Subpopulations of RyR Cluster Sizes
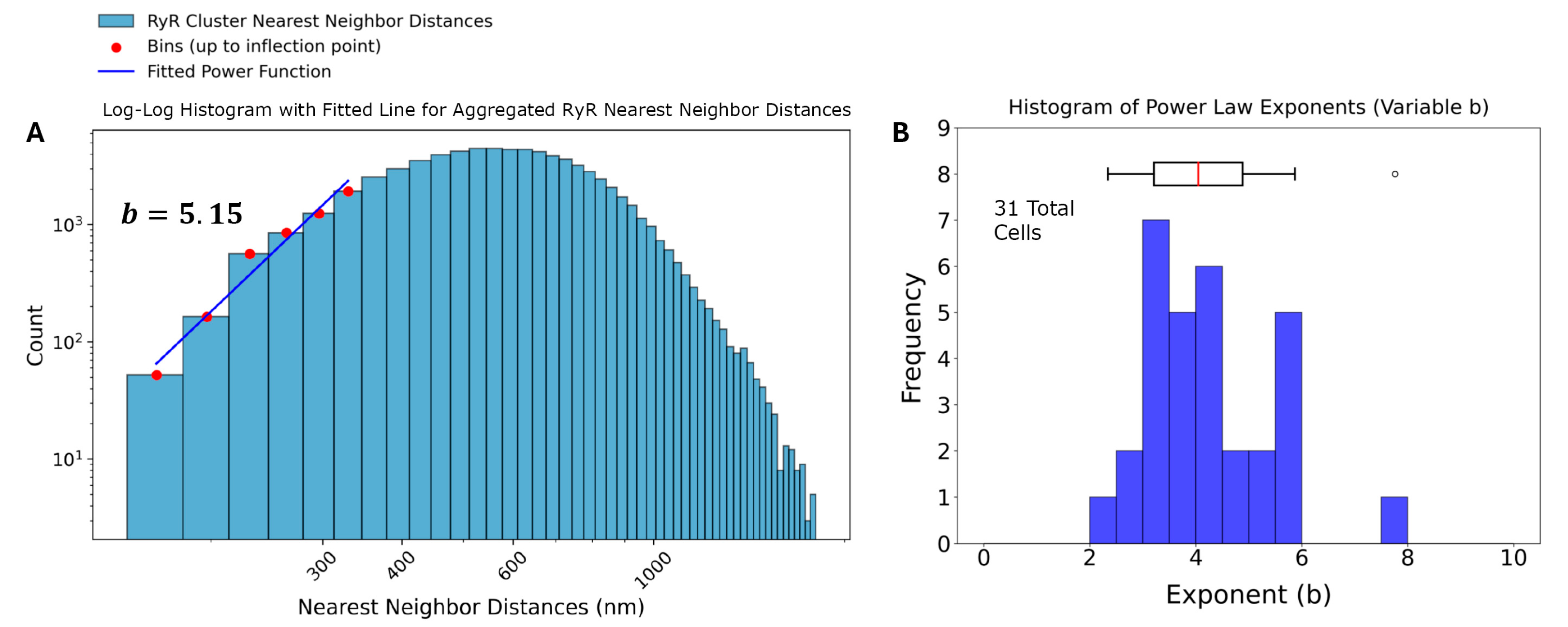
3.2. Repulsive Behavior of RyR Clusters in Spatial Distribution
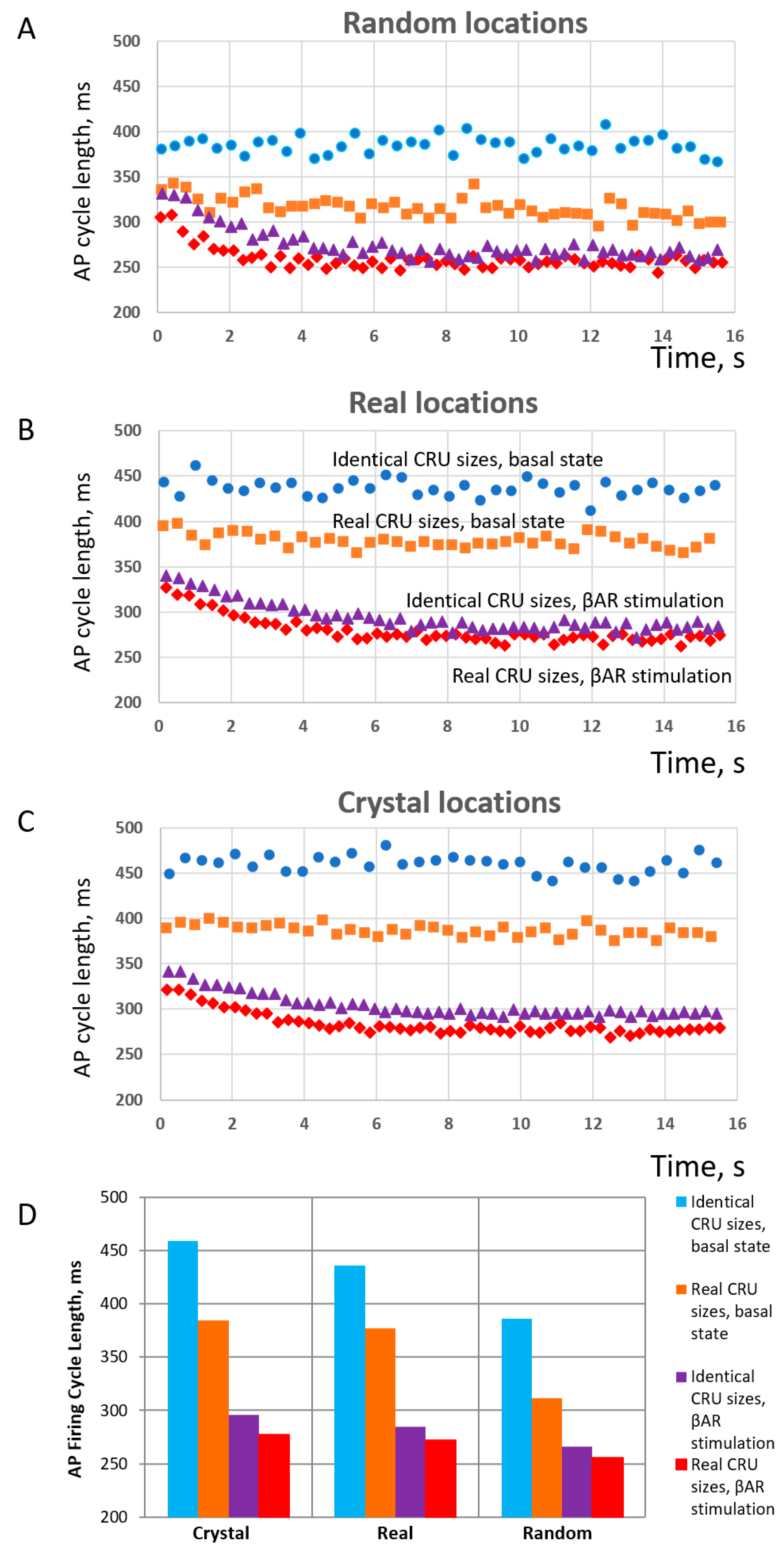
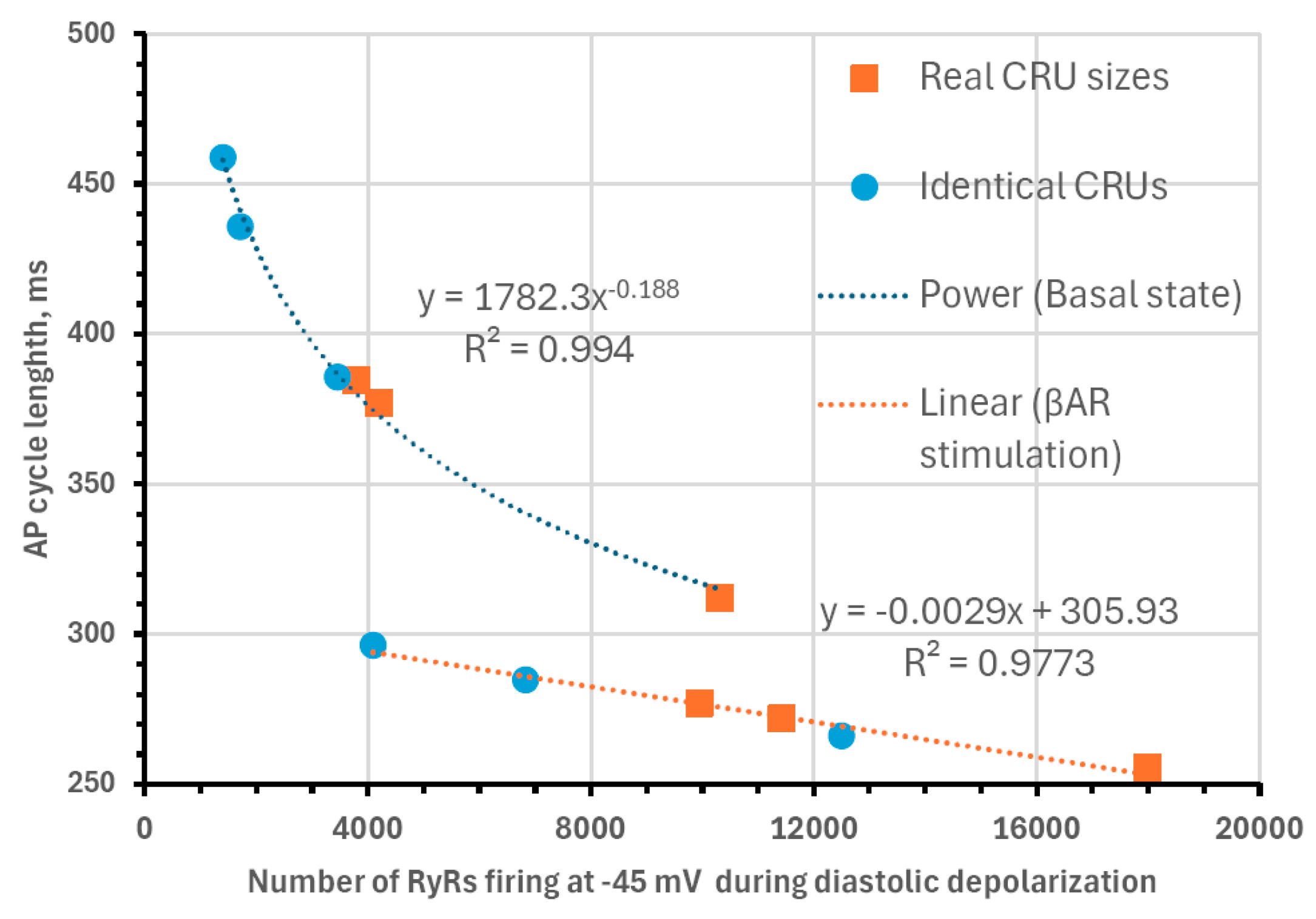
3.3. Structure–Function Relationship of CRU Network in Numerical Simulations of SANC Function
4. Discussion
4.1. Result Summary: Major Findings
- (1)
- Two distinct RyR cluster subpopulations with sizes adhering to a Gamma mixture distribution.
- (2)
- Notable repulsion between neighboring RyR clusters.
- (3)
- Model simulations showed that heterogeneities in both CRU sizes and locations facilitate CICR and increase AP firing rate in a cooperative manner, but decrease the effects of βAR stimulation. However, the highest possible absolute rate during βAR stimulation is reached with heterogeneities in both CRU sizes and locations.
4.2. New Image Analysis Methods and Numerical Models
4.3. Structure–Function Relations of RyR Network in SANC
4.4. Limitations and Future Studies
4.5. Implications for Clinical and Aging Research
4.6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SANC = sinoatrial node cell; |
| AP = action potential; |
| LCR = local Ca2+ release; |
| βAR = β-adrenergic receptor; |
| RyR = ryanodine receptor; |
| SERCA= sarco/endoplasmic reticulum Ca-ATPase; |
| Cycle length = action potential cycle length; |
| CRU = Ca2+ release unit; |
| SR = sarcoplasmic reticulum; |
| JSR = the junctional SR; |
| CICR = Ca-induced Ca release; |
| SIM = structured illumination microscopy; |
| NND = nearest-neighbor distances; |
| PBS = phosphate-buffered saline; |
| CLAHE = contrast-limited adaptive histogram equalization; |
| IoU = Intersection over Union; |
| DBSCAN = Density-Based Spatial Clustering of Applications with Noise; |
| MAD = median absolute deviation; |
| GMM = Gamma Mixture Model; |
| CDF = cumulative distribution function. |
Appendix A. Details of a Novel Numerical Model of SANC
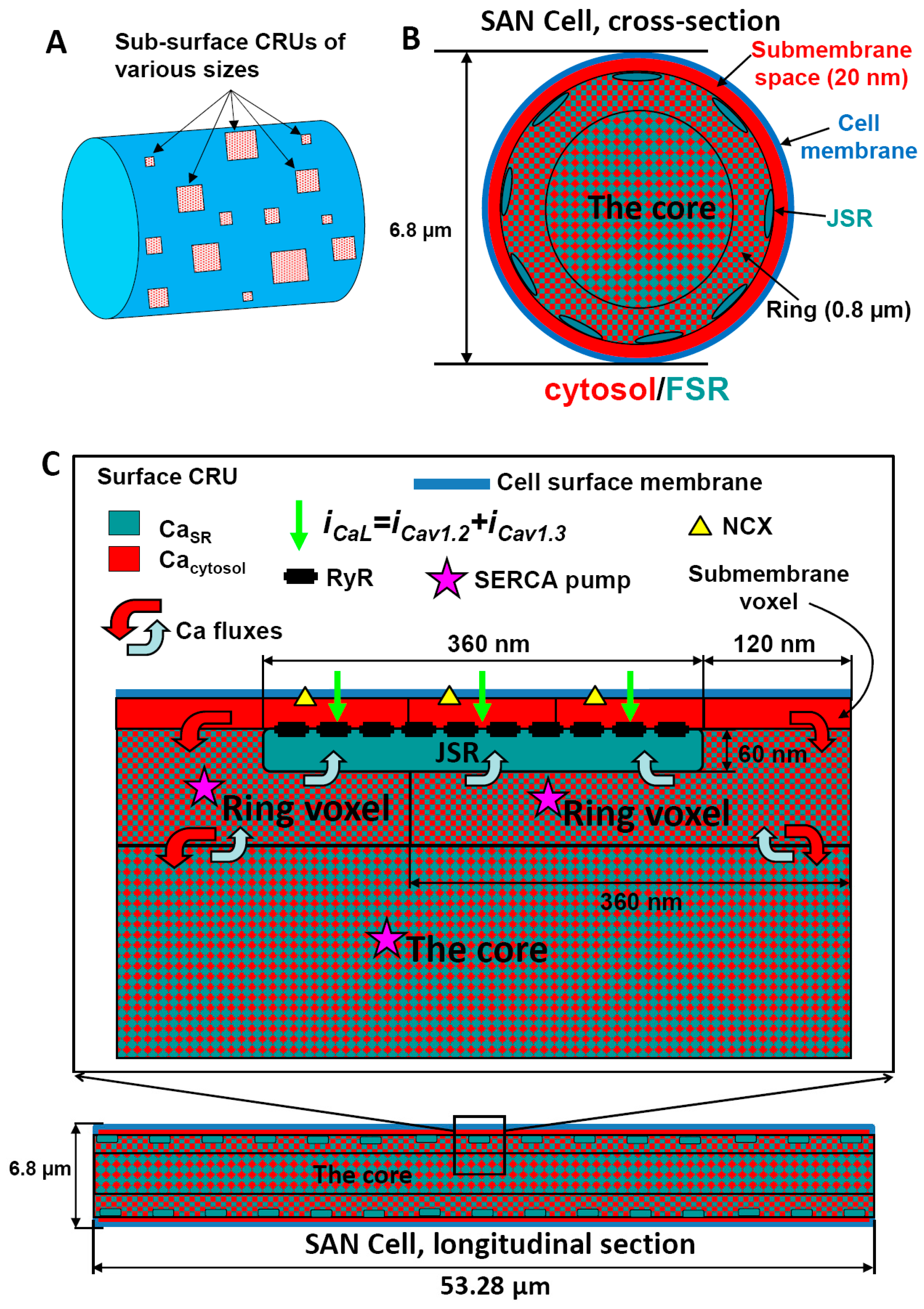
Appendix A.1. Cell Geometry, Compartments, Voxels, and Membrane Patches
Appendix A.1.1. Submembrane Voxels
Appendix A.1.2. JSR Level Voxels (“Ring” Voxels)
Appendix A.1.3. The Core
Appendix A.1.4. JSR
Appendix A.2. Ca2+ Cycling
Appendix A.2.1. Free SR (FSR)
Appendix A.2.2. SR Ca2+ Pump
Appendix A.2.3. Ca2+ Diffusion Within and Among Cell Compartments
Appendix A.2.4. Junctional SR (JSR) and Ca2+ Diffusion Between JSR and FSR
Appendix A.2.5. Spark Activation and Inactivation
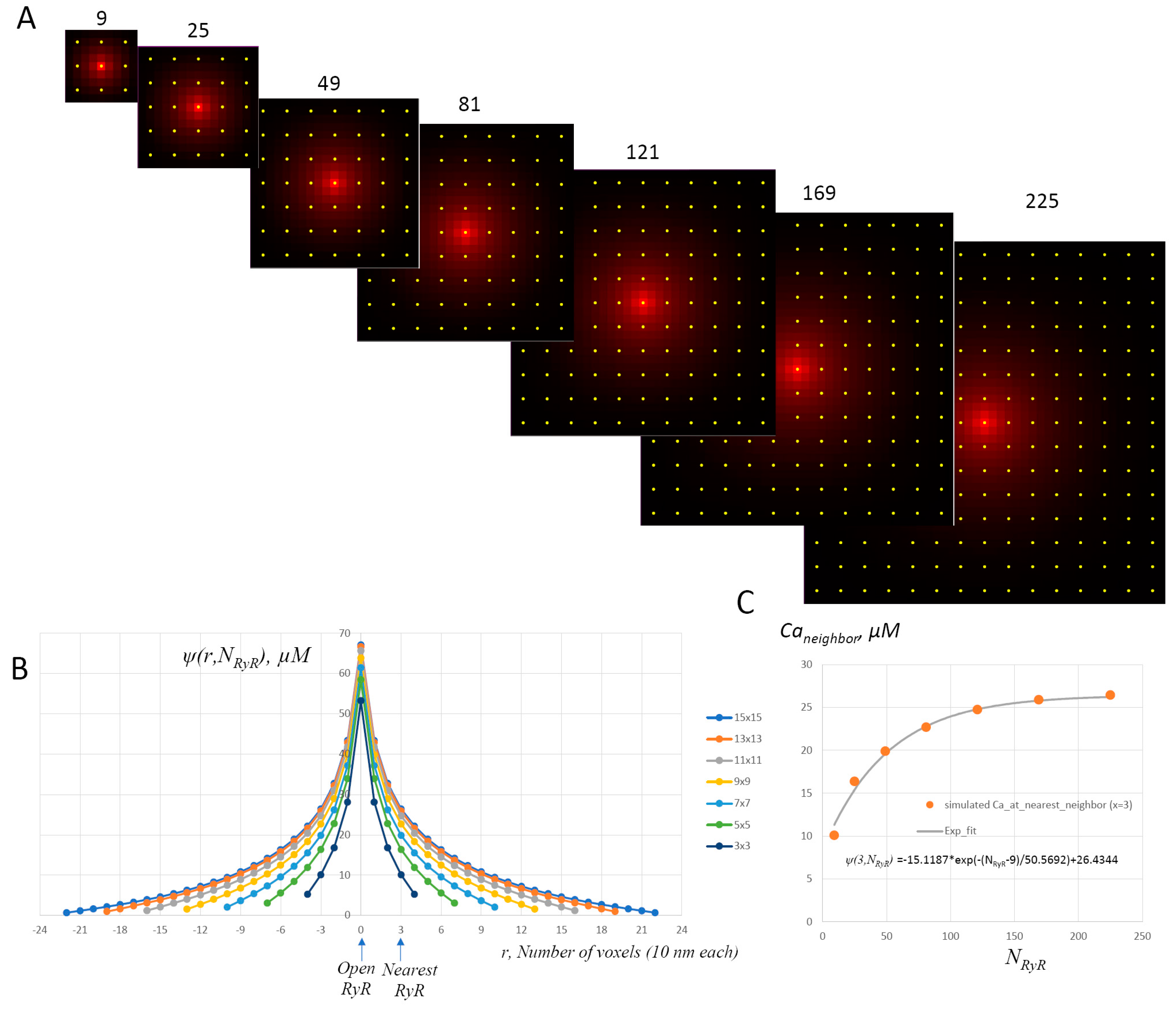
Appendix A.2.6. Spark Termination Mechanism
Appendix A.2.7. Ca2+ Buffering
Appendix A.2.8. Summary of Equations of Local Ca2+ Dynamics
Appendix A.3. Electrophysiology
Appendix A.3.1. Fixed Ion Concentrations, mM
Appendix A.3.2. The Nernst Equation and Electric Potentials, mV
Appendix A.3.3. Membrane Potential, Vm
Appendix A.3.4. Formulation of Cell Membrane Ion Currents
Appendix A.4. Initial Values
Appendix A.4.1. Electrophysiology
| −57.96393469 | Vm | Membrane potential, mV |
| 0.000584546 | dL | ICaL voltage-dependent activation |
| 0.86238125 | fL | ICaL voltage-dependent inactivation |
| 0.71139592 | fCa | ICaL Ca-dependent inactivation (local) |
| 0.144755091 | paF | IKr fast activation |
| 0.453100577 | paS | IKr slow activation |
| 0.849409822 | pi_ | IKr inactivation |
| 0.026460041 | n | IKs activation |
| 0.113643187 | y | If activation |
| 0.005043934 | dT | ICaT activation |
| 0.420757825 | fT | ICaT inactivation |
| 0.694241314 | q | Ito inactivation |
| 0.005581317 | r | Ito and Isus activation |
Appendix A.4.2. Ca2+ Dynamics
| 200 nM | [Ca] in cytosol |
| 1 mM | [Ca] in FSR |
| 0.8 mM | Ca concentration in JSR |
| 0.0787 | Fractional occupancy of calmodulin by Ca2+ in cytoplasm |
| 0.6 | Fractional occupancy of calsequestrin by Ca2+ in JSR |
Appendix A.5. Simulations of βAR Stimulation Effect
Appendix A.6. Model Integration
Appendix A.7. Appendix Glossary and Parameters’ Values
References
- Boyett, M.R.; Honjo, H.; Kodama, I. The sinoatrial node, a heterogeneous pacemaker structure. Cardiovasc. Res. 2000, 47, 658–687. [Google Scholar] [CrossRef] [PubMed]
- Mangoni, M.E.; Nargeot, J. Genesis and regulation of the heart automaticity. Physiol. Rev. 2008, 88, 919–982. [Google Scholar] [CrossRef] [PubMed]
- Dobrzynski, H.; Boyett, M.R.; Anderson, R.H. New insights into pacemaker activity: Promoting understanding of sick sinus syndrome. Circulation 2007, 115, 1921–1932. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, Y.; Tse, G.; Bazoukis, G.; Letsas, K.; Goudis, C.; Korantzopoulos, P.; Li, G.; Liu, T. Association between sick sinus syndrome and atrial fibrillation: A systematic review and meta-analysis. Int. J. Cardiol. 2023, 381, 20–36. [Google Scholar] [CrossRef]
- Lang, D.; Glukhov, A.V. Cellular and Molecular Mechanisms of Functional Hierarchy of Pacemaker Clusters in the Sinoatrial Node: New Insights into Sick Sinus Syndrome. J. Cardiovasc. Dev. Dis. 2021, 8, 43. [Google Scholar] [CrossRef]
- Jensen, P.N.; Gronroos, N.N.; Chen, L.Y.; Folsom, A.R.; deFilippi, C.; Heckbert, S.R.; Alonso, A. Incidence of and risk factors for sick sinus syndrome in the general population. J. Am. Coll. Cardiol. 2014, 64, 531–538. [Google Scholar] [CrossRef]
- Lakatta, E.G.; Maltsev, V.A.; Vinogradova, T.M. A coupled SYSTEM of intracellular Ca2+ clocks and surface membrane voltage clocks controls the timekeeping mechanism of the heart’s pacemaker. Circ. Res. 2010, 106, 659–673. [Google Scholar] [CrossRef] [PubMed]
- Inui, M.; Saito, A.; Fleischer, S. Isolation of the ryanodine receptor from cardiac sarcoplasmic reticulum and identity with the feet structures. J. Biol. Chem. 1987, 262, 15637–15642. [Google Scholar] [CrossRef]
- Franzini-Armstrong, C.; Protasi, F.; Ramesh, V. Shape, size, and distribution of Ca2+ release units and couplons in skeletal and cardiac muscles. Biophys. J. 1999, 77, 1528–1539. [Google Scholar] [CrossRef]
- Fabiato, A. Calcium-induced release of calcium from the cardiac sarcoplasmic reticulum. Am. J. Physiol. 1983, 245, C1–C14. [Google Scholar] [CrossRef]
- Cheng, H.; Lederer, W.J.; Cannell, M.B. Calcium sparks: Elementary events underlying excitation-contraction coupling in heart muscle. Science 1993, 262, 740–744. [Google Scholar] [CrossRef]
- Cheng, H.; Lederer, W.J. Calcium sparks. Physiol. Rev. 2008, 88, 1491–1545. [Google Scholar] [CrossRef] [PubMed]
- Rubenstein, D.S.; Lipsius, S.L. Mechanisms of automaticity in subsidiary pacemakers from cat right atrium. Circ. Res. 1989, 64, 648–657. [Google Scholar] [CrossRef] [PubMed]
- Huser, J.; Blatter, L.A.; Lipsius, S.L. Intracellular Ca2+ release contributes to automaticity in cat atrial pacemaker cells. J. Physiol. 2000, 524 Pt 2, 415–422. [Google Scholar] [CrossRef]
- Groenke, S.; Larson, E.D.; Alber, S.; Zhang, R.; Lamp, S.T.; Ren, X.; Nakano, H.; Jordan, M.C.; Karagueuzian, H.S.; Roos, K.P.; et al. Complete atrial-specific knockout of sodium-calcium exchange eliminates sinoatrial node pacemaker activity. PLoS ONE 2013, 8, e81633. [Google Scholar] [CrossRef] [PubMed]
- Lyashkov, A.E.; Behar, J.; Lakatta, E.G.; Yaniv, Y.; Maltsev, V.A. Positive Feedback Mechanisms among Local Ca Releases, NCX, and ICaL Ignite Pacemaker Action Potentials. Biophys. J. 2018, 114, 1176–1189. [Google Scholar] [CrossRef]
- Rigg, L.; Heath, B.M.; Cui, Y.; Terrar, D.A. Localisation and functional significance of ryanodine receptors during beta-adrenoceptor stimulation in the guinea-pig sino-atrial node. Cardiovasc. Res. 2000, 48, 254–264. [Google Scholar] [CrossRef]
- Musa, H.; Lei, M.; Honjo, H.; Jones, S.A.; Dobrzynski, H.; Lancaster, M.K.; Takagishi, Y.; Henderson, Z.; Kodama, I.; Boyett, M.R. Heterogeneous expression of Ca2+ handling proteins in rabbit sinoatrial node. J. Histochem. Cytochem. 2002, 50, 311–324. [Google Scholar] [CrossRef]
- Maltsev, A.V.; Maltsev, V.A.; Mikheev, M.; Maltseva, L.A.; Sirenko, S.G.; Lakatta, E.G.; Stern, M.D. Synchronization of stochastic Ca2+ release units creates a rhythmic Ca2+ clock in cardiac pacemaker cells. Biophys. J. 2011, 100, 271–283. [Google Scholar] [CrossRef]
- Maltsev, A.V.; Yaniv, Y.; Stern, M.D.; Lakatta, E.G.; Maltsev, V.A. RyR-NCX-SERCA local crosstalk ensures pacemaker cell function at rest and during the fight-or-flight reflex. Circ. Res. 2013, 113, e94–e100. [Google Scholar] [CrossRef]
- Stern, M.D.; Maltseva, L.A.; Juhaszova, M.; Sollott, S.J.; Lakatta, E.G.; Maltsev, V.A. Hierarchical clustering of ryanodine receptors enables emergence of a calcium clock in sinoatrial node cells. J. Gen. Physiol. 2014, 143, 577–604. [Google Scholar] [CrossRef] [PubMed]
- Maltsev, A.V.; Stern, M.D.; Maltsev, V.A. Disorder in Ca2+ release unit locations confers robustness but cuts flexibility of heart pacemaking. J. Gen. Physiol. 2022, 154, e202113061. [Google Scholar] [CrossRef]
- Weiss, J.N.; Qu, Z. The Sinus Node: Still Mysterious After All These Years. JACC Clin. Electrophysiol. 2020, 6, 1841–1843. [Google Scholar] [CrossRef]
- Clancy, C.E.; Santana, L.F. Evolving Discovery of the Origin of the Heartbeat: A New Perspective on Sinus Rhythm. JACC Clin. Electrophysiol. 2020, 6, 932–934. [Google Scholar] [CrossRef]
- Gustafsson, M.G. Surpassing the lateral resolution limit by a factor of two using structured illumination microscopy. J. Microsc. 2000, 198, 82–87. [Google Scholar] [CrossRef]
- Vinogradova, T.M.; Zhou, Y.Y.; Bogdanov, K.Y.; Yang, D.; Kuschel, M.; Cheng, H.; Xiao, R.P. Sinoatrial node pacemaker activity requires Ca2+/calmodulin-dependent protein kinase II activation. Circ. Res. 2000, 87, 760–767. [Google Scholar] [CrossRef]
- Wu, Y.; Shroff, H. Faster, sharper, and deeper: Structured illumination microscopy for biological imaging. Nat. Methods 2018, 15, 1011–1019. [Google Scholar] [CrossRef]
- York, A.G.; Chandris, P.; Nogare, D.D.; Head, J.; Wawrzusin, P.; Fischer, R.S.; Chitnis, A.; Shroff, H. Instant super-resolution imaging in live cells and embryos via analog image processing. Nat. Methods 2013, 10, 1122–1126. [Google Scholar] [CrossRef]
- Curd, A.; Cleasby, A.; Makowska, K.; York, A.; Shroff, H.; Peckham, M. Construction of an instant structured illumination microscope. Methods 2015, 88, 37–47. [Google Scholar] [CrossRef] [PubMed]
- Stimper, V.; Bauer, S.; Ernstorfer, R.; Schölkopf, B.; Xian, R.P. Multidimensional Contrast Limited Adaptive Histogram Equalization. IEEE Access 2019, 7, 165437–165447. [Google Scholar] [CrossRef]
- Schmidt, U.; Weigert, M.; Broaddus, C.; Myers, G. Cell Detection with Star-Convex Polygons. In Lecture Notes in Computer Science, Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2018, Granada, Spain, 16–20 September 2018; Frangi, A., Schnabel, J., Davatzikos, C., Alberola-López, C., Fichtinger, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; Volume 11071, pp. 265–273. [Google Scholar]
- Rizk, A.; Paul, G.; Incardona, P.; Bugarski, M.; Mansouri, M.; Niemann, A.; Ziegler, U.; Berger, P.; Sbalzarini, I.F. Segmentation and quantification of subcellular structures in fluorescence microscopy images using Squassh. Nat. Protoc. 2014, 9, 586–596. [Google Scholar] [CrossRef] [PubMed]
- Paul, G.; Cardinale, J.; Sbalzarini, I.F. Coupling Image Restoration and Segmentation: A Generalized Linear Model/Bregman Perspective. Int. J. Comput. Vis. 2013, 104, 69–93. [Google Scholar] [CrossRef]
- Helmuth, J.A.; Sbalzarini, I.F. Deconvolving active contours for fluorescence microscopy images. In Advances in Visual Computing, Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Las Vegas, NV, USA, 30 November–2 December 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 544–551. [Google Scholar]
- Helmuth, J.A.; Paul, G.; Sbalzarini, I.F. Beyond co-localization: Inferring spatial interactions between sub-cellular structures from microscopy images. BMC Bioinform. 2010, 11, 372. [Google Scholar] [CrossRef] [PubMed]
- Roerdink, J.B.; Meijster, A. The watershed transform: Definitions, algorithms and parallelization strategies. Fundam. Informaticae 2000, 41, 187–228. [Google Scholar] [CrossRef]
- Fill, M.; Gillespie, D. Simulating cardiac Ca2+ release units: Effects of RyR cluster size and Ca2+ buffers on diastolic Ca2+ leak. Pflug. Arch. 2021, 473, 435–446. [Google Scholar] [CrossRef]
- Xie, Y.; Yang, Y.; Galice, S.; Bers, D.M.; Sato, D. Size Matters: Ryanodine Receptor Cluster Size Heterogeneity Potentiates Calcium Waves. Biophys. J. 2019, 116, 530–539. [Google Scholar] [CrossRef]
- Veron, G.; Maltsev, V.A.; Stern, M.D.; Maltsev, A.V. Elementary intracellular Ca signals approximated as a transition of release channel system from a metastable state. J. Appl. Phys. 2023, 134, 124701. [Google Scholar] [CrossRef]
- Scriven, D.R.L.; Johnsen, A.B.; Asghari, P.; Chou, K.C.; Moore, E.D.W. Cardiomyocyte ryanodine receptor clusters expand and coalesce after application of isoproterenol. J. Gen. Physiol. 2023, 155, e202213109. [Google Scholar] [CrossRef]
- Greiser, M.; Joca, H.C.; Lederer, W.J. Pacemaker organization at the nanoscale: Imaging of ryanodine receptors as clusters in single sinoatrial nodal cells. Biophys. J. 2019, 116, 380A. [Google Scholar] [CrossRef]
- Yasin, S.; Kaplan, A.D.; Joca, H.C.; Lederer, W.J.; Greiser, M. ‘Calcium Clock’ at the Nanoscale in the RAT SA Node: 3D Ryanodine Receptor Cluster Organization and Intracellular Ca2+ Signaling. Biophys. J. 2020, 118, 173A. [Google Scholar] [CrossRef]
- Jensen, E.; Crossman, D.J. Technical review: Types of imaging-direct STORM. Anat. Rec. 2014, 297, 2227–2231. [Google Scholar] [CrossRef] [PubMed]
- Ren, L.; Gopireddy, R.R.; Perkins, G.; Zhang, H.; Timofeyev, V.; Lyu, Y.; Diloretto, D.A.; Trinh, P.; Sirish, P.; Overton, J.L.; et al. Disruption of mitochondria-sarcoplasmic reticulum microdomain connectomics contributes to sinus node dysfunction in heart failure. Proc. Natl. Acad. Sci. USA 2022, 119, e2206708119. [Google Scholar] [CrossRef] [PubMed]
- Louradour, J.; Bortolotti, O.; Torre, E.; Bidaud, I.; Lamb, N.; Fernandez, A.; Le Guennec, J.Y.; Mangoni, M.E.; Mesirca, P. L-Type Cav1.3 Calcium Channels Are Required for Beta-Adrenergic Triggered Automaticity in Dormant Mouse Sinoatrial Pacemaker Cells. Cells 2022, 11, 1114. [Google Scholar] [CrossRef] [PubMed]
- Torrente, A.G.; Mesirca, P.; Neco, P.; Rizzetto, R.; Dubel, S.; Barrere, C.; Sinegger-Brauns, M.; Striessnig, J.; Richard, S.; Nargeot, J.; et al. L-type Cav1.3 channels regulate ryanodine receptor-dependent Ca2+ release during sino-atrial node pacemaker activity. Cardiovasc. Res. 2016, 109, 451–461. [Google Scholar] [CrossRef]
- Mesirca, P.; Torrente, A.G.; Mangoni, M.E. Functional role of voltage gated Ca2+ channels in heart automaticity. Front. Physiol. 2015, 6, 19. [Google Scholar] [CrossRef] [PubMed]
- Masumiya, H.; Yamamoto, H.; Hemberger, M.; Tanaka, H.; Shigenobu, K.; Chen, S.R.; Furukawa, T. The mouse sino-atrial node expresses both the type 2 and type 3 Ca2+ release channels/ryanodine receptors. FEBS Lett. 2003, 553, 141–144. [Google Scholar] [CrossRef]
- Tellez, J.O.; Dobrzynski, H.; Greener, I.D.; Graham, G.M.; Laing, E.; Honjo, H.; Hubbard, S.J.; Boyett, M.R.; Billeter, R. Differential expression of ion channel transcripts in atrial muscle and sinoatrial node in rabbit. Circ. Res. 2006, 99, 1384–1393. [Google Scholar] [CrossRef]
- Cingolani, E.; Goldhaber, J.I.; Marban, E. Next-generation pacemakers: From small devices to biological pacemakers. Nat. Rev. Cardiol. 2018, 15, 139–150. [Google Scholar] [CrossRef]
- Qu, Z.; Garfinkel, A.; Weiss, J.N.; Nivala, M. Multi-scale modeling in biology: How to bridge the gaps between scales? Prog. Biophys. Mol. Biol. 2011, 107, 21–31. [Google Scholar] [CrossRef]
- Stern, M.D.; Rios, E.; Maltsev, V.A. Life and death of a cardiac calcium spark. J. Gen. Physiol. 2013, 142, 257–274. [Google Scholar] [CrossRef]
- Zhang, H.; Holden, A.V.; Kodama, I.; Honjo, H.; Lei, M.; Varghese, T.; Boyett, M.R. Mathematical models of action potentials in the periphery and center of the rabbit sinoatrial node. Am. J. Physiol. 2000, 279, H397–H421. [Google Scholar] [CrossRef] [PubMed]
- Shannon, T.R.; Wang, F.; Puglisi, J.; Weber, C.; Bers, D.M. A mathematical treatment of integrated Ca dynamics within the ventricular myocyte. Biophys. J. 2004, 87, 3351–3371. [Google Scholar] [CrossRef]
- Kurata, Y.; Hisatome, I.; Imanishi, S.; Shibamoto, T. Dynamical description of sinoatrial node pacemaking: Improved mathematical model for primary pacemaker cell. Am. J. Physiol. 2002, 283, H2074–H2101. [Google Scholar] [CrossRef]
- Zima, A.V.; Bovo, E.; Bers, D.M.; Blatter, L.A. Ca2+ spark-dependent and -independent sarcoplasmic reticulum Ca2+ leak in normal and failing rabbit ventricular myocytes. J. Physiol. 2010, 588, 4743–4757. [Google Scholar] [CrossRef]
- Maltsev, A.V.; Maltsev, V.A.; Stern, M.D. Clusters of calcium release channels harness the Ising phase transition to confine their elementary intracellular signals. Proc. Natl. Acad. Sci. USA 2017, 114, 7525–7530. [Google Scholar] [CrossRef] [PubMed]
- Laver, D.R.; Kong, C.H.; Imtiaz, M.S.; Cannell, M.B. Termination of calcium-induced calcium release by induction decay: An emergent property of stochastic channel gating and molecular scale architecture. J. Mol. Cell. Cardiol. 2013, 54, 98–100. [Google Scholar] [CrossRef]
- Christel, C.J.; Cardona, N.; Mesirca, P.; Herrmann, S.; Hofmann, F.; Striessnig, J.; Ludwig, A.; Mangoni, M.E.; Lee, A. Distinct localization and modulation of Cav1.2 and Cav1.3 L-type Ca2+ channels in mouse sinoatrial node. J. Physiol. 2012, 590, 6327–6342. [Google Scholar] [CrossRef] [PubMed]
- Mangoni, M.E.; Couette, B.; Bourinet, E.; Platzer, J.; Reimer, D.; Striessnig, J.; Nargeot, J. Functional role of L-type Cav1.3 Ca2+ channels in cardiac pacemaker activity. Proc. Natl. Acad. Sci. USA 2003, 100, 5543–5548. [Google Scholar] [CrossRef] [PubMed]
- Wilders, R.; Jongsma, H.J.; van Ginneken, A.C. Pacemaker activity of the rabbit sinoatrial node. A comparison of mathematical models. Biophys. J. 1991, 60, 1202–1216. [Google Scholar] [CrossRef]
- Dokos, S.; Celler, B.; Lovell, N. Ion currents underlying sinoatrial node pacemaker activity: A new single cell mathematical model. J. Theor. Biol. 1996, 181, 245–272. [Google Scholar] [CrossRef]
- Demir, S.S.; Clark, J.W.; Murphey, C.R.; Giles, W.R. A mathematical model of a rabbit sinoatrial node cell. Am. J. Physiol. 1994, 266, C832–C852. [Google Scholar] [CrossRef] [PubMed]
- Sakai, R.; Hagiwara, N.; Matsuda, N.; Kassanuki, H.; Hosoda, S. Sodium--potassium pump current in rabbit sino-atrial node cells. J. Physiol. 1996, 490 Pt 1, 51–62. [Google Scholar] [CrossRef] [PubMed]

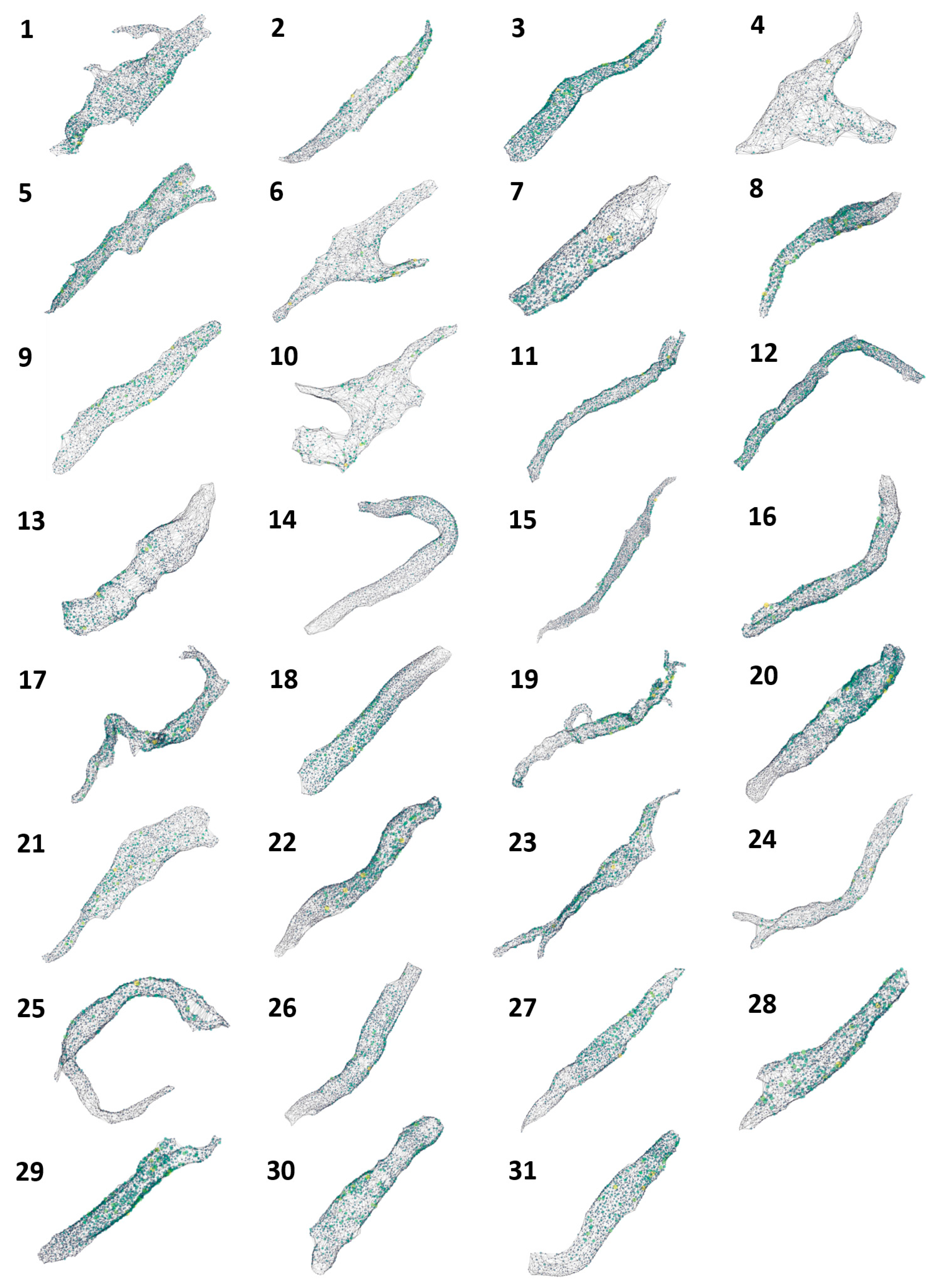
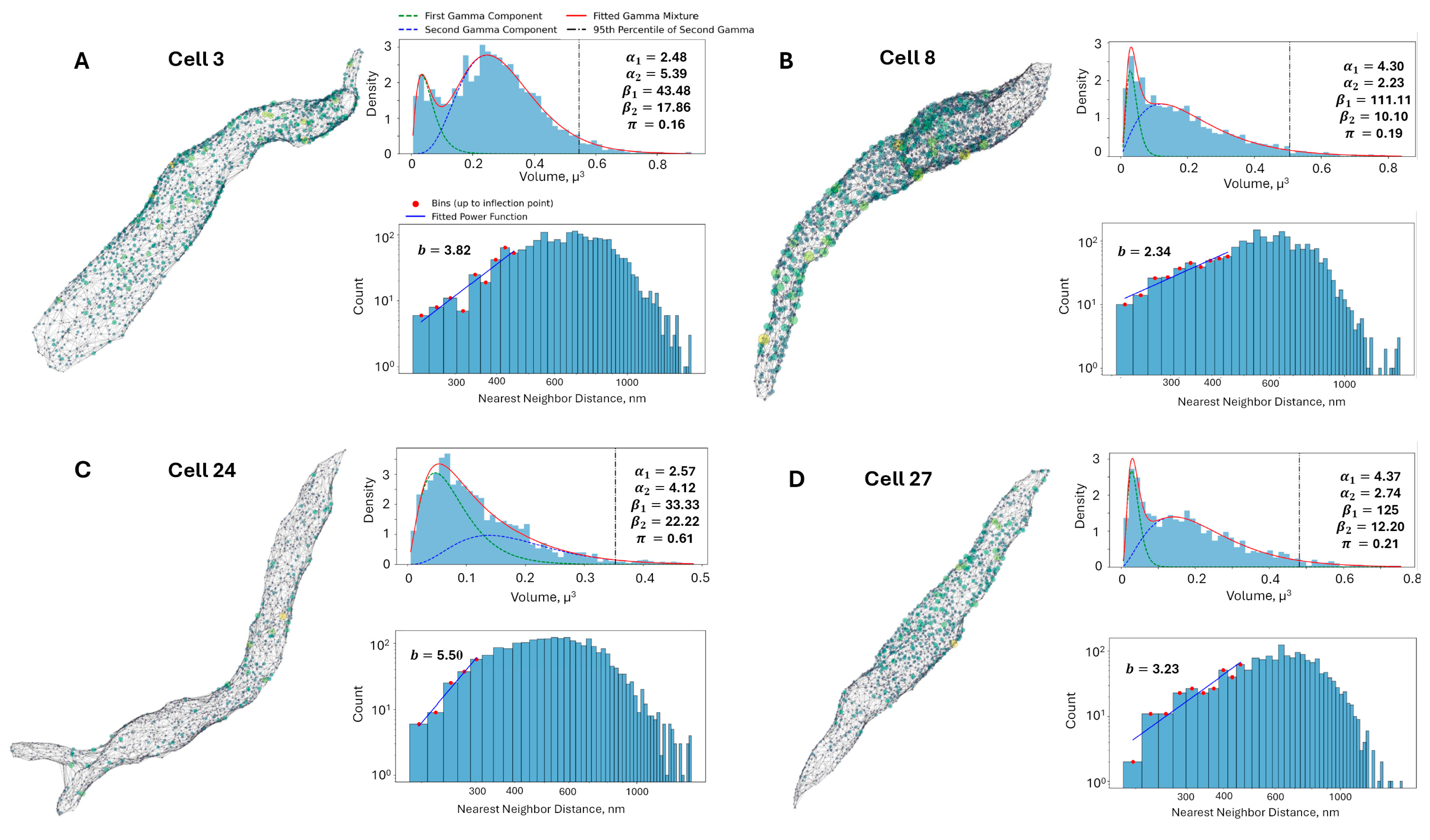

| Cell Statistics | RyR Cluster Distances | RyR Cluster Sizes | |||||
|---|---|---|---|---|---|---|---|
| Cell # | Surface Area (μm²) | Volume (μm³) | #RYR Clusters | Mean (nm) | SD (nm) | Mean (μm³) | SD (μm³) |
| 1 | 2494 | 2886 | 2775 | 586.78 | 191.25 | 0.21 | 0.17 |
| 2 | 2166 | 3050 | 1871 | 633.27 | 210.61 | 0.16 | 0.12 |
| 3 | 2698 | 5234 | 2035 | 722.19 | 218.38 | 0.26 | 0.15 |
| 4 | 2177 | 3695 | 1359 | 657.48 | 239.13 | 0.13 | 0.09 |
| 5 | 3182 | 4777 | 3341 | 579.93 | 212.91 | 0.17 | 0.17 |
| 6 | 2708 | 3868 | 1901 | 647.02 | 233.15 | 0.12 | 0.08 |
| 7 | 2435 | 6409 | 1566 | 695.58 | 243.85 | 0.19 | 0.14 |
| 8 | 1923 | 3119 | 2085 | 627.35 | 185.29 | 0.19 | 0.15 |
| 9 | 1583 | 1992 | 1573 | 617.39 | 209.54 | 0.19 | 0.16 |
| 10 | 2879 | 5088 | 1675 | 705.36 | 268.41 | 0.12 | 0.09 |
| 11 | 2300 | 2722 | 3046 | 555.98 | 174.95 | 0.20 | 0.18 |
| 12 | 3175 | 4822 | 3603 | 600.26 | 179.40 | 0.20 | 0.13 |
| 13 | 3097 | 8328 | 1976 | 702.53 | 229.66 | 0.14 | 0.09 |
| 14 | 2841 | 4579 | 2648 | 669.51 | 196.30 | 0.17 | 0.11 |
| 15 | 2129 | 2150 | 3243 | 530.22 | 164.79 | 0.16 | 0.13 |
| 16 | 2240 | 3431 | 2470 | 587.66 | 204.89 | 0.18 | 0.16 |
| 17 | 2139 | 2238 | 2577 | 570.93 | 185.03 | 0.19 | 0.16 |
| 18 | 2457 | 4984 | 2074 | 704.40 | 207.67 | 0.18 | 0.12 |
| 19 | 2688 | 2813 | 2575 | 606.69 | 196.25 | 0.17 | 0.15 |
| 20 | 2457 | 3735 | 2201 | 648.78 | 203.09 | 0.19 | 0.15 |
| 21 | 5256 | 15899 | 3364 | 736.34 | 253.06 | 0.20 | 0.14 |
| 22 | 2195 | 3898 | 2548 | 557.56 | 181.65 | 0.16 | 0.13 |
| 23 | 2318 | 2772 | 2292 | 633.41 | 194.55 | 0.23 | 0.18 |
| 24 | 2474 | 3655 | 2328 | 605.15 | 212.17 | 0.12 | 0.09 |
| 25 | 1983 | 2200 | 2205 | 596.14 | 191.90 | 0.18 | 0.14 |
| 26 | 2908 | 6224 | 2370 | 692.24 | 210.53 | 0.18 | 0.12 |
| 27 | 1877 | 3121 | 1639 | 676.19 | 209.62 | 0.18 | 0.14 |
| 28 | 1567 | 2278 | 1633 | 596.97 | 195.09 | 0.17 | 0.13 |
| 29 | 2564 | 4668 | 1987 | 694.89 | 212.81 | 0.19 | 0.12 |
| 30 | 3117 | 8181 | 2406 | 671.59 | 238.41 | 0.20 | 0.15 |
| 31 | 1640 | 2553 | 1483 | 687.51 | 198.09 | 0.22 | 0.14 |
| AVERAGE | 2505 | 4367 | 2285 | 638.62 | 208.14 | 0.18 | 0.13 |
| Repulsion | Gamma Mixture Model (GMM) | |||||
|---|---|---|---|---|---|---|
| Cell # | π | |||||
| 1 | 2.59 | 4.20 | 142.86 | 2.43 | 9.52 | 0.19 |
| 2 | 5.87 | 4.05 | 142.86 | 2.28 | 12.99 | 0.12 |
| 3 | 3.82 | 2.48 | 43.48 | 5.39 | 17.86 | 0.16 |
| 4 | 2.51 | 4.79 | 111.11 | 2.42 | 16.67 | 0.17 |
| 5 | 7.76 | 4.51 | 142.86 | 2.12 | 8.55 | 0.34 |
| 6 | 4.65 | 5.20 | 125.00 | 2.77 | 20.83 | 0.13 |
| 7 | 3.01 | 3.47 | 100.00 | 3.04 | 13.51 | 0.20 |
| 8 | 2.34 | 4.30 | 111.11 | 2.23 | 10.10 | 0.19 |
| 9 | 4.05 | 3.93 | 125.00 | 2.19 | 9.17 | 0.23 |
| 10 | 3.13 | 5.05 | 111.11 | 2.62 | 18.87 | 0.18 |
| 11 | 3.79 | 4.57 | 142.86 | 1.99 | 7.87 | 0.22 |
| 12 | 5.76 | 2.03 | 35.71 | 3.36 | 14.29 | 0.23 |
| 13 | 4.2 | 4.45 | 125.00 | 2.99 | 19.61 | 0.10 |
| 14 | 4.07 | 1.94 | 12.99 | 8.03 | 35.71 | 0.74 |
| 15 | 5.71 | 4.38 | 111.11 | 2.18 | 11.90 | 0.14 |
| 16 | 5.12 | 4.67 | 142.86 | 1.80 | 8.13 | 0.20 |
| 17 | 3.21 | 4.18 | 125.00 | 2.14 | 9.17 | 0.22 |
| 18 | 3.9 | 1.65 | 10.53 | 8.60 | 34.48 | 0.69 |
| 19 | 3.81 | 4.15 | 111.11 | 2.10 | 9.90 | 0.21 |
| 20 | 3.2 | 4.55 | 142.86 | 2.24 | 10.42 | 0.12 |
| 21 | 4.1 | 4.21 | 111.11 | 2.99 | 12.66 | 0.18 |
| 22 | 5.35 | 3.64 | 100.00 | 2.21 | 11.63 | 0.22 |
| 23 | 3.96 | 3.86 | 90.91 | 2.60 | 9.43 | 0.18 |
| 24 | 5.5 | 2.57 | 33.33 | 4.12 | 22.22 | 0.61 |
| 25 | 3.21 | 8.62 | 333.33 | 1.91 | 9.71 | 0.12 |
| 26 | 5.74 | 1.83 | 11.90 | 7.22 | 29.41 | 0.72 |
| 27 | 3.23 | 4.37 | 125.00 | 2.74 | 12.20 | 0.21 |
| 28 | 4.45 | 2.69 | 55.56 | 2.79 | 12.66 | 0.30 |
| 29 | 4.59 | 1.89 | 11.24 | 9.14 | 37.04 | 0.69 |
| 30 | 4.19 | 3.96 | 125.00 | 2.89 | 11.76 | 0.22 |
| 31 | 3.03 | 1.52 | 8.26 | 8.11 | 29.41 | 0.62 |
| AVERAGE | 4.19 | 3.80 | 100.68 | 3.54 | 16.05 | 0.29 |
| AGGREGATED | 5.15 | 4.35 | 125.00 | 2.22 | 10.64 | 0.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maltsev, A.V.; Ventura Subirachs, V.; Monfredi, O.; Juhaszova, M.; Ajay Warrier, P.; Rakshit, S.; Tagirova, S.; Maltsev, A.V.; Stern, M.D.; Lakatta, E.G.; et al. Structure-Function Relationship of the Ryanodine Receptor Cluster Network in Sinoatrial Node Cells. Cells 2024, 13, 1885. https://doi.org/10.3390/cells13221885
Maltsev AV, Ventura Subirachs V, Monfredi O, Juhaszova M, Ajay Warrier P, Rakshit S, Tagirova S, Maltsev AV, Stern MD, Lakatta EG, et al. Structure-Function Relationship of the Ryanodine Receptor Cluster Network in Sinoatrial Node Cells. Cells. 2024; 13(22):1885. https://doi.org/10.3390/cells13221885
Chicago/Turabian StyleMaltsev, Alexander V., Valeria Ventura Subirachs, Oliver Monfredi, Magdalena Juhaszova, Pooja Ajay Warrier, Shardul Rakshit, Syevda Tagirova, Anna V. Maltsev, Michael D. Stern, Edward G. Lakatta, and et al. 2024. "Structure-Function Relationship of the Ryanodine Receptor Cluster Network in Sinoatrial Node Cells" Cells 13, no. 22: 1885. https://doi.org/10.3390/cells13221885
APA StyleMaltsev, A. V., Ventura Subirachs, V., Monfredi, O., Juhaszova, M., Ajay Warrier, P., Rakshit, S., Tagirova, S., Maltsev, A. V., Stern, M. D., Lakatta, E. G., & Maltsev, V. A. (2024). Structure-Function Relationship of the Ryanodine Receptor Cluster Network in Sinoatrial Node Cells. Cells, 13(22), 1885. https://doi.org/10.3390/cells13221885






