PPSW–SHAP: Towards Interpretable Cell Classification Using Tree-Based SHAP Image Decomposition and Restoration for High-Throughput Bright-Field Imaging
Abstract
1. Introduction
2. Materials and Methods
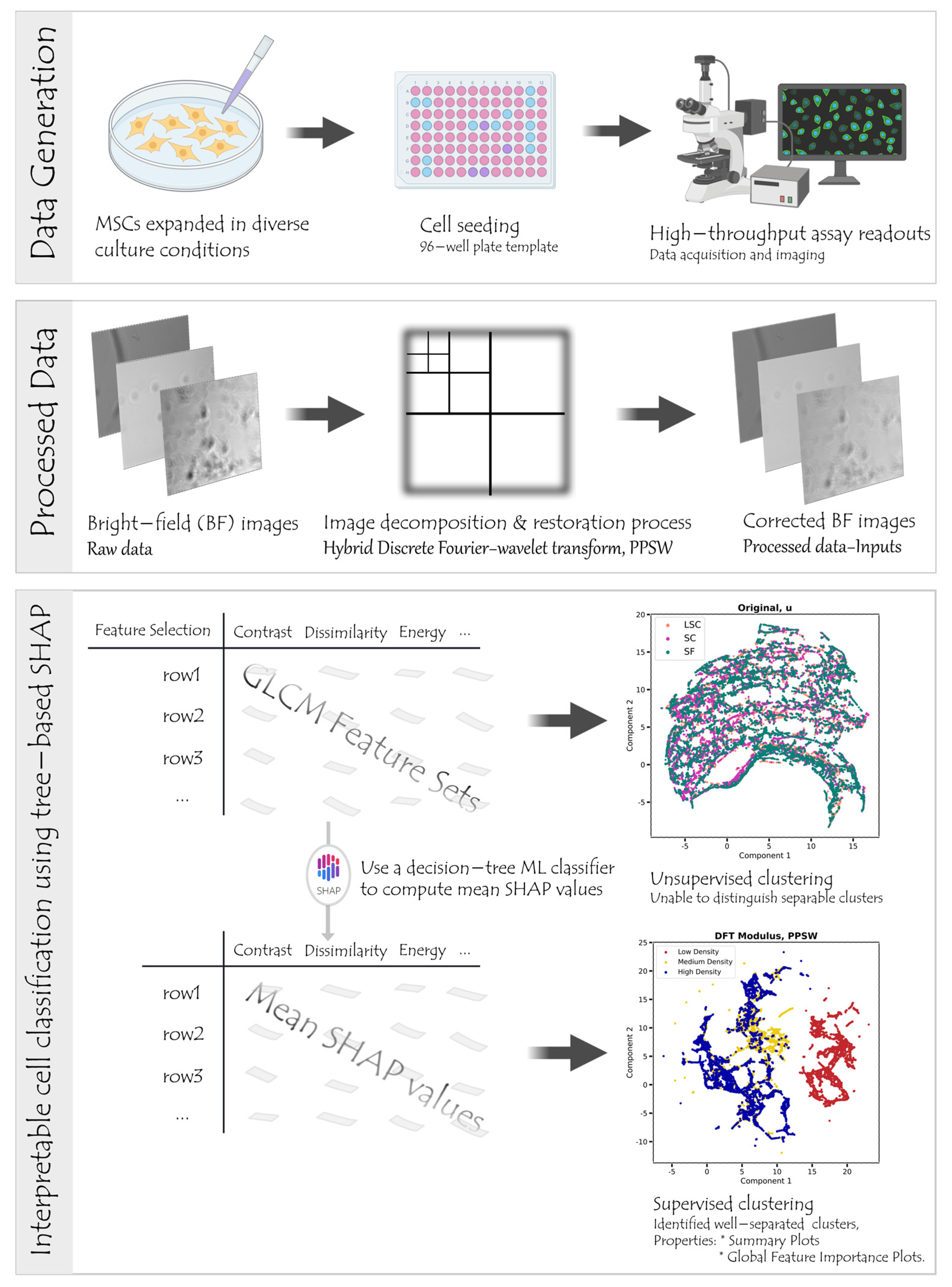
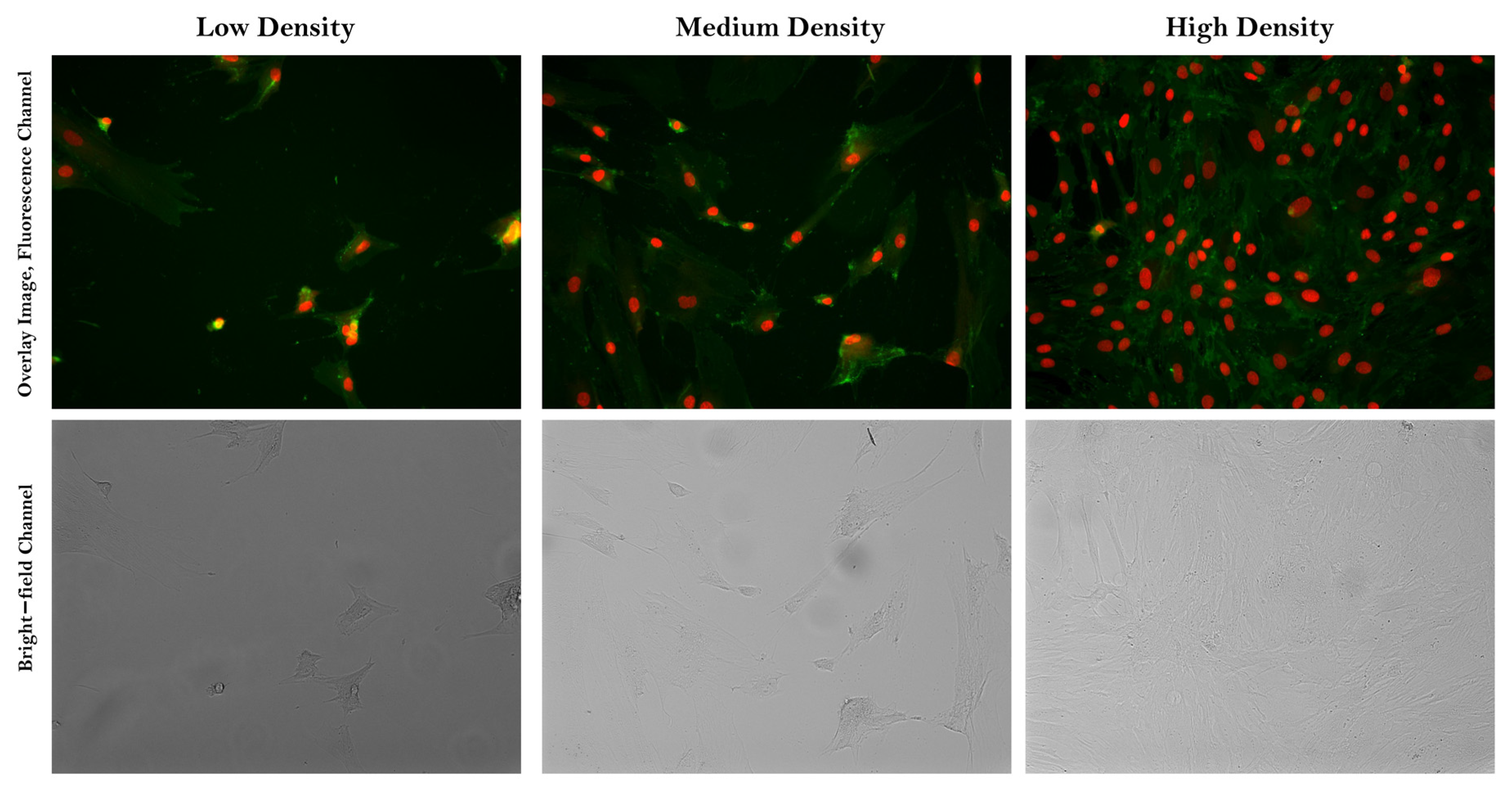
2.1. Data Collection
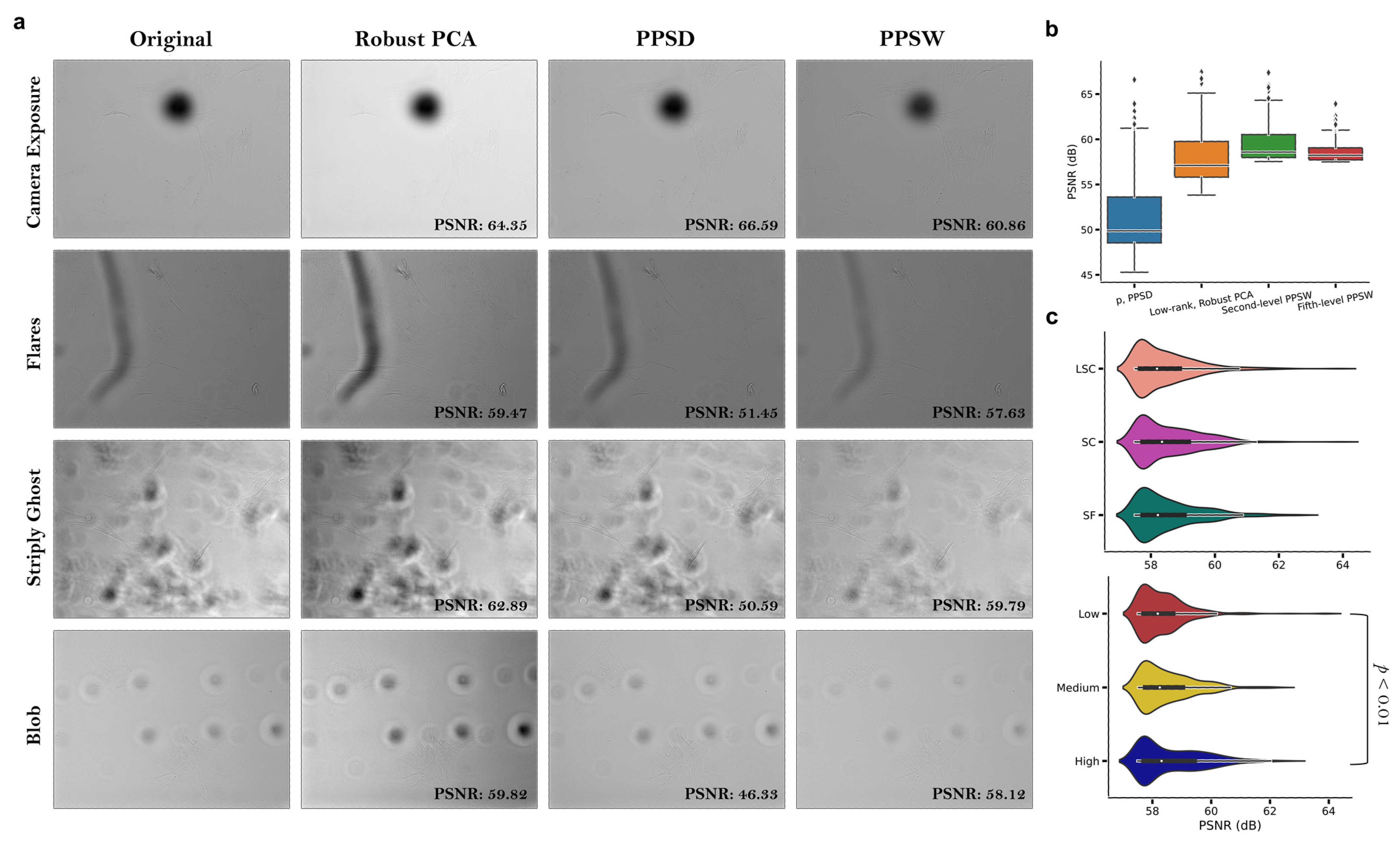
2.2. Image Decomposition and/or Restoration Techniques
2.3. Feature Engineering
2.4. Building and Evaluating Machine Learning Classification Models
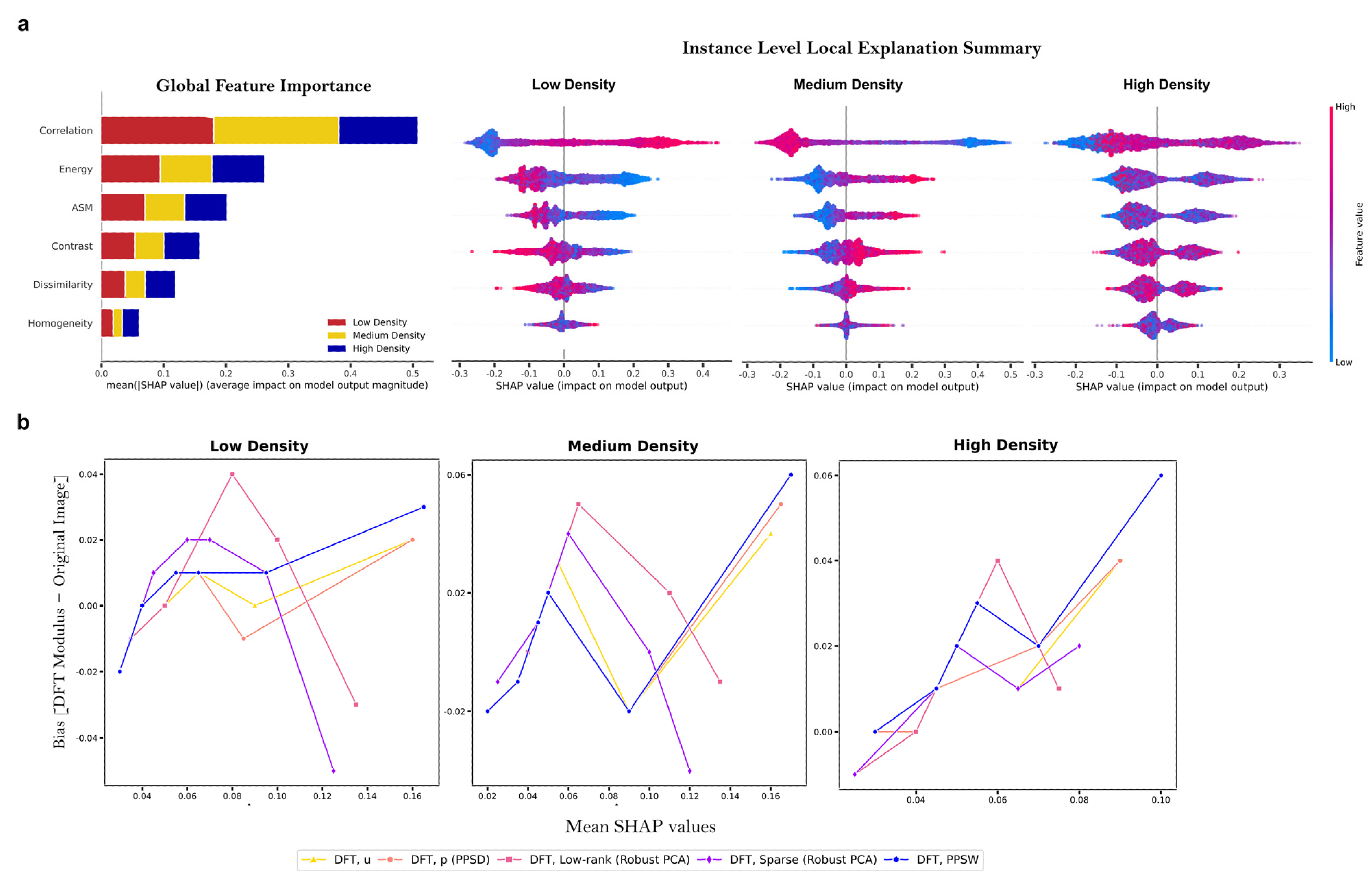
2.5. Feature Importance Measures
2.6. Dimensionality Reduction Based on SHAP Analysis
2.7. Statistics
3. Results
3.1. Computing a Hybrid Discrete Fourier–Wavelet Transform Approach and Assessing Anomalies
3.2. Achievement of a High Classification Accuracy with ‘DFT Modulus’
3.3. Supervised Clustering Based on SHAP Values Leads to More Accurate Cluster Analysis
4. Discussion
- Introduction of the Periodic Plus Smooth Wavelet Transform (PPSW) technique for image decomposition and restoration, minimizing the potential adverse impact of artifact structures on the ML classification accuracy. This technique allows for better feature extraction and representation, leading to higher performance in classification tasks.
- Utilization of a variety of tree–based ML models, specifically Random forest classifiers, for accurate stem cell classification based on label–free cell images. These models offer a fast and efficient way to extract rich biological insights from the images without the need for extensive pre–processing or data augmentation.
- Application of supervised clustering using Shapley Additive exPlanations (SHAP) values, offering both local and global interpretations, to enhance the understanding of CT bioprocesses. We demonstrated that supervised clustering using average SHAP values, obtained from the ‘DFT Modulus’ of the PPSW and of the periodic component, i.e., PPSD techniques applied to original BF images, in the tree–based ML model produced highly distinct clusters of human Mesenchymal Stem Cells (MSCs) corresponding to diverse cell culture conditions. This approach provides a clear understanding of the relationships between different features and their importance in the classification process, making it easier for researchers and practitioners to optimize their workflows.
- Reduction of noise and improved feature properties, allowing models to achieve encouraging accuracy with a limited dataset of approximately 1000 images. This advantage suggests that our proposed workflow can be effective even with relatively small datasets, lowering the barrier to entry for researchers and companies looking to adopt these techniques.
- Demonstration of reasonable computational burden and time for our PPSW technique across different hardware configurations, highlighting the efficiency of our approach. Our PPSW technique showcases reasonable computational burden and time across different hardware configurations, with the GPU server taking 0.115 s for the original image and 0.33 s for the bior2.4 mother wavelet type, while the laptop computer we used took 0.23 s and 0.75 s, respectively, for processing a single image and extracting the six Haralick texture feature sets with noise reduction. This efficiency enables our workflow to be applied in various settings, from high–end research facilities to smaller labs with limited computational resources.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chilima, T.D.P.; Moncaubeig, F.; Farid, S.S. Impact of allogeneic stem cell manufacturing decisions on cost of goods, process robustness and reimbursement. Biochem. Eng. J. 2018, 137, 132–151. [Google Scholar] [CrossRef]
- Wright, A.; Arthaud-Day, M.L.; Weiss, M.L. Therapeutic Use of Mesenchymal Stromal Cells: The Need for Inclusive Characterization Guidelines to Accommodate All Tissue Sources and Species. Front. Cell Dev. Biol. 2021, 9, 632717. [Google Scholar] [CrossRef] [PubMed]
- Friedenstein, A.J.; Chailakhjan, R.K.; Lalykina, K.S. The development of fibroblast colonies in monolayer cultures of guinea-pig bone marrow and spleen cells. Cell Tissue Kinet. 1970, 3, 393–403. [Google Scholar] [CrossRef] [PubMed]
- Galipeau, J.; Sensebe, L. Mesenchymal Stromal Cells: Clinical Challenges and Therapeutic Opportunities. Cell Stem Cell 2018, 22, 824–833. [Google Scholar] [CrossRef]
- Shi, Y.F.; Wang, Y.; Li, Q.; Liu, K.L.; Hou, J.Q.; Shao, C.S.; Wang, Y. Immunoregulatory mechanisms of mesenchymal stem and stromal cells in inflammatory diseases. Nat. Rev. Nephrol. 2018, 14, 493–507. [Google Scholar] [CrossRef] [PubMed]
- Ratcliffe, E.; Thomas, R.J.; Williams, D.J. Current understanding and challenges in bioprocessing of stem cell-based therapies for regenerative medicine. Brit. Med. Bull. 2011, 100, 137–155. [Google Scholar] [CrossRef]
- Mount, N.M.; Ward, S.J.; Kefalas, P.; Hyllner, J. Cell-based therapy technology classifications and translational challenges. Philos. T. R. Soc. B 2015, 370, 20150017. [Google Scholar] [CrossRef]
- Teixeira, F.G.; Salgado, A.J. Mesenchymal stem cells secretome: Current trends and future challenges. Neural Regen. Res. 2020, 15, 75–77. [Google Scholar] [CrossRef]
- Imboden, S.; Liu, X.Q.; Lee, B.S.; Payne, M.C.; Hsieh, C.J.; Lin, N.Y.C. Investigating heterogeneities of live mesenchymal stromal cells using AI-based label-free imaging. Sci. Rep. UK 2021, 11, 1–11. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Leong, K.W.; Van Vliet, K.; Barbastathis, G.; Ravasio, A. Deep learning for label-free nuclei detection from implicit phase information of mesenchymal stem cells. Biomed. Opt. Express 2021, 12, 1683–1706. [Google Scholar] [CrossRef]
- Kim, G.; Jeon, J.H.; Park, K.; Kim, S.W.; Kim, D.; Lee, S. High throughput screening of mesenchymal stem cell lines using deep learning. Sci. Rep. UK 2022, 12, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.L.; Mahjoubfar, A.; Tai, L.-C.; Blaby, I.K.; Huang, A.; Niazi, K.R.; Jalali, B. Deep learning in label-free cell classification. Sci. Rep. UK 2016, 6, 21471. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How transferable are features in deep neural networks? Adv. Neural Inf. Process. Syst. 2014, 27, 3320–3328. [Google Scholar]
- Olah, C.; Satyanarayan, A.; Johnson, I.; Carter, S.; Schubert, L.; Ye, K.; Mordvintsev, A. The building blocks of interpretability. Distill 2018, 3, e10. [Google Scholar] [CrossRef]
- Ruff, L.; Kauffmann, J.R.; Vandermeulen, R.A.; Montavon, G.; Samek, W.; Kloft, M.; Dietterich, T.G.; Muller, K.R. A Unifying Review of Deep and Shallow Anomaly Detection. P. IEEE 2021, 109, 756–795. [Google Scholar] [CrossRef]
- Goldman, D.B. Vignette and Exposure Calibration and Compensation. IEEE T. Pattern Anal. 2010, 32, 2276–2288. [Google Scholar] [CrossRef]
- Tomazevic, D.; Likar, B.; Pernus, F. Comparative evaluation of retrospective shading correction methods. J. Microsc. Oxf. 2002, 208, 212–223. [Google Scholar] [CrossRef]
- Piccinini, F.; Lucarelli, E.; Gherardi, A.; Bevilacqua, A. Multi-image based method to correct vignetting effect in light microscopy images. J. Microsc. 2012, 248, 6–22. [Google Scholar] [CrossRef]
- Ray, S.F. Applied Photographic Optics: Lenses and Optical Systems for Photography, Film, Video, Electronic and Digital Imaging; Routledge: Abingdon, UK, 2002. [Google Scholar]
- Leong, F.J.; Brady, M.; McGee, J.O. Correction of uneven illumination (vignetting) in digital microscopy images. J. Clin. Pathol. 2003, 56, 619–621. [Google Scholar] [CrossRef]
- Smith, K.; Li, Y.P.; Piccinini, F.; Csucs, G.; Balazs, C.; Bevilacqua, A.; Horvath, P. CIDRE: An illumination-correction method for optical microscopy. Nat. Methods 2015, 12, 404. [Google Scholar] [CrossRef]
- Singh, S.; Bray, M.A.; Jones, T.R.; Carpenter, A.E. Pipeline for illumination correction of images for high-throughput microscopy. J. Microsc. 2014, 256, 231–236. [Google Scholar] [CrossRef]
- Khaw, I.; Croop, B.; Tang, J.L.; Mohl, A.; Fuchs, U.; Han, K.Y. Flat-field illumination for quantitative fluorescence imaging. Opt. Express 2018, 26, 15276–15288. [Google Scholar] [CrossRef] [PubMed]
- Todorov, H.; Saeys, Y. Computational approaches for high-throughput single-cell data analysis. Febs. J. 2019, 286, 1451–1467. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE T. Syst. Man. Cyb. 1973, Smc3, 610–621. [Google Scholar] [CrossRef]
- Albregtsen, F.; Nielsen, B.; Danielsen, H.E. Adaptive gray level run length features from class distance matrices. In Proceedings of the 15th International Conference on Pattern Recognition, ICPR-2000, Barcelona, Spain, 3–7 September 2000; pp. 738–741. [Google Scholar]
- Gipp, M.; Marcus, G.; Harder, N.; Suratanee, A.; Rohr, K.; König, R.; Männer, R. Haralick’s Texture Features Computed by GPUs for Biological Applications. IAENG Int. J. Comput. Sci. 2009, 36, 1–10. [Google Scholar]
- Weiss, M.L.; Rao, M.S.; Deans, R.; Czermak, P. Manufacturing Cells for Clinical Use. Stem Cells Int. 2016, 2016, 1750697. [Google Scholar] [CrossRef]
- Chase, L.G.; Yang, S.F.; Zachar, V.; Yang, Z.; Lakshmipathy, U.; Bradford, J.; Boucher, S.E.; Vemuri, M.C. Development and Characterization of a Clinically Compliant Xeno-Free Culture Medium in Good Manufacturing Practice for Human Multipotent Mesenchymal Stem Cells. Stem Cell Transl. Med. 2012, 1, 750–758. [Google Scholar] [CrossRef] [PubMed]
- Oikonomopoulos, A.; van Deen, W.K.; Manansala, A.R.; Lacey, P.N.; Tomakili, T.A.; Ziman, A.; Hommes, D.W. Optimization of human mesenchymal stem cell manufacturing: The effects of animal/xeno-free media. Sci. Rep. UK 2015, 5, 1–11. [Google Scholar] [CrossRef]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM 2011, 58, 1–37. [Google Scholar] [CrossRef]
- Clausi, D.A. An analysis of co-occurrence texture statistics as a function of grey level quantization. Can. J. Remote Sens. 2002, 28, 45–62. [Google Scholar] [CrossRef]
- Mohanaiah, P.; Sathyanarayana, P.; GuruKumar, L. Image texture feature extraction using GLCM approach. Int. J. Sci. Res. Publ. 2013, 3, 1–5. [Google Scholar]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Routledge: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hastie, T.; Rosset, S.; Zhu, J.; Zou, H. Multi-class adaboost. Stat. Its Interface 2009, 2, 349–360. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Scikit-Learn. HistGradientBoostingClassifier. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.HistGradientBoostingClassifier.html (accessed on 26 April 2023).
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3149–3157. [Google Scholar]
- Fisher, A.; Rudin, C.; Dominici, F. All Models are Wrong, but Many are Useful: Learning a Variable’s Importance by Studying an Entire Class of Prediction Models Simultaneously. J. Mach. Learn. Res. 2019, 20, 1–81. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426, preprint. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Massey, F.J., Jr. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Kruskal, W.H.; Wallis, W.A. Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Moisan, L. Periodic plus smooth image decomposition. J. Math Imaging Vis. 2011, 39, 161–179. [Google Scholar] [CrossRef]
- Vogelstein, J.T.; Bridgeford, E.W.; Tang, M.; Zheng, D.; Douville, C.; Burns, R.; Maggioni, M. Supervised dimensionality reduction for big data. Nat. Commun. 2021, 12, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. Adv. Neur. 2017, 30, 4765–4774. [Google Scholar]



| Media | Variables | Gradient Density Spectra | p Value+ | ||
|---|---|---|---|---|---|
| Low | Medium | Hight | |||
| LSC | Homogeneity | 0.741 (0.022) α | 0.715 (0.695–0.735) | 0.695 (0.674–0.720) | <0.001 |
| Contrast | 0.727 (0.617–0.851) β | 0.943 (0.755–1.152) | 1.119 (0.848–1.322) | ||
| Correlation | 0.616 (0.456–0.766) | 0.580 (0.408–0.738) | 0.571 (0.387–0.715) | ||
| Dissimilarity | 0.549 (0.512–0.592) | 0.626 (0.563–0.687) | 0.685 (0.604–0.748) | ||
| Energy | 0.345 (0.308–0.382) | 0.326 (0.296–0.362) | 0.312 (0.278–0.341) | ||
| ASM | 0.118 (0.095–0.146) | 0.106 (0.087–0.131) | 0.098 (0.077–0.116) | ||
| SC | Homogeneity | 0.748 (0.738–0.759) | 0.718 (0.698–0.736) | 0.675 (0.648–0.701) | <0.001 |
| Contrast | 0.711 (0.615–0.824) | 1.007 (0.781–1.248) | 1.339 (0.981–1.927) | ||
| Correlation | 0.622 (0.461–0.803) | 0.568 (0.385–0.734) | 0.557 (0.342–0.703) | ||
| Dissimilarity | 0.532 (0.504–0.565) | 0.628 (0.565–0.691) | 0.748 (0.650–0.836) | ||
| Energy | 0.339 (0.306–0.393) | 0.330 (0.287–0.369) | 0.294 (0.258–0.328) | ||
| ASM | 0.115 (0.093–0.155) | 0.109 (0.082–0.136) | 0.087 (0.067–0.107) | ||
| SF | Homogeneity | 0.744 (0.731–0.755) | 0.709 (0.684–0.733) | 0.671 (0.644–0.701) | <0.001 |
| Contrast | 0.718 (0.616–0.859) | 0.942 (0.736–1.126) | 1.212 (0.882–1.469) | ||
| Correlation | 0.652 (0.505–0.806) | 0.567 (0.392–0.734) | 0.582 (0.376–0.721) | ||
| Dissimilarity | 0.542 (0.509–0.582) | 0.636 (0.567–0.705) | 0.742 (0.633–0.826) | ||
| Energy | 0.337 (0.295–0.376) | 0.322 (0.278–0.354) | 0.293 (0.257–0.326) | ||
| ASM | 0.114 (0.087–0.141) | 0.104 (0.078–0.126) | 0.086 (0.066–0.106) | ||
| Variables | Model | Percentage Split | |||
|---|---|---|---|---|---|
| Accuracy | Precision | Recall | F1–Score | ||
| Original, u Baseline | LightGBM | 73.945 | 73.155 | 73.770 | 73.928 |
| XGBoost | 74.796 | 74.177 | 74.635 | 74.314 | |
| Random Forest | 80.129 | 79.797 | 80.100 | 79.887 | |
| DFT modulus, u | XGBoost | 87.268 | 87.404 | 87.202 | 87.295 |
| Decision Tree | 88.727 | 88.694 | 88.702 | 88.696 | |
| Random Forest | 92.826 | 92.875 | 92.792 | 92.832 | |
| DFT modulus, ulow–rank | XGBoost | 87.216 | 87.363 | 87.168 | 87.247 |
| Decision Tree | 90.116 | 90.099 | 90.172 | 90.125 | |
| Random Forest | 92.322 | 92.308 | 92.335 | 92.321 | |
| DFT modulus, usparse | XGBoost | 86.625 | 86.784 | 86.360 | 86.526 |
| Decision Tree | 88.848 | 88.786 | 88.763 | 88.770 | |
| Random Forest | 93.556 | 93.569 | 93.452 | 93.505 | |
| DFT modulus, p | LightGBM | 88.154 | 88.173 | 88.078 | 88.117 |
| Decision Tree | 91.489 | 91.443 | 91.426 | 91.432 | |
| Random Forest | 94.511 | 94.499 | 94.442 | 94.476 | |
| DFT modulus, PPSW | XGBoost | 88.917 | 89.042 | 88.839 | 88.932 |
| Decision Tree | 90.846 | 90.775 | 90.821 | 90.797 | |
| Random Forest | 94.754 | 94.744 | 94.729 | 94.734 | |
| Variables | Model | Percentage Split | |||
|---|---|---|---|---|---|
| Accuracy | Precision | Recall | F1–Score | ||
| Original, u Baseline | Decision Tree | 71.947 | 71.777 | 71.782 | 71.767 |
| XGBoost | 72.295 | 72.204 | 72.210 | 72.217 | |
| Random Forest | 80.146 | 80.041 | 80.085 | 80.058 | |
| DFT modulus, u | XGBoost | 80.684 | 80.727 | 80.625 | 80.649 |
| Decision Tree | 85.861 | 85.863 | 85.874 | 85.868 | |
| Random Forest | 90.290 | 90.318 | 90.294 | 90.306 | |
| DFT modulus, ulow–rank | XGBoost | 78.426 | 78.555 | 78.320 | 78.402 |
| Decision Tree | 83.933 | 83.926 | 83.858 | 83.889 | |
| Random Forest | 89.196 | 89.219 | 89.153 | 89.182 | |
| DFT modulus, usparse | XGBoost | 85.948 | 86.306 | 85.532 | 85.721 |
| Decision Tree | 89.387 | 89.344 | 89.355 | 89.312 | |
| Random Forest | 93.677 | 93.705 | 93.564 | 93.625 | |
| DFT modulus, p | Decision Tree | 90.099 | 90.386 | 90.377 | 90.381 |
| XGBoost | 90.603 | 90.886 | 90.976 | 90.898 | |
| Random Forest | 93.260 | 93.440 | 93.518 | 93.466 | |
| DFT modulus, PPSW | XGBoost | 81.414 | 81.468 | 81.276 | 81.351 |
| Decision Tree | 86.434 | 86.394 | 86.468 | 86.425 | |
| Random Forest | 91.437 | 91.403 | 91.436 | 91.419 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goktas, P.; Simon Carbajo, R. PPSW–SHAP: Towards Interpretable Cell Classification Using Tree-Based SHAP Image Decomposition and Restoration for High-Throughput Bright-Field Imaging. Cells 2023, 12, 1384. https://doi.org/10.3390/cells12101384
Goktas P, Simon Carbajo R. PPSW–SHAP: Towards Interpretable Cell Classification Using Tree-Based SHAP Image Decomposition and Restoration for High-Throughput Bright-Field Imaging. Cells. 2023; 12(10):1384. https://doi.org/10.3390/cells12101384
Chicago/Turabian StyleGoktas, Polat, and Ricardo Simon Carbajo. 2023. "PPSW–SHAP: Towards Interpretable Cell Classification Using Tree-Based SHAP Image Decomposition and Restoration for High-Throughput Bright-Field Imaging" Cells 12, no. 10: 1384. https://doi.org/10.3390/cells12101384
APA StyleGoktas, P., & Simon Carbajo, R. (2023). PPSW–SHAP: Towards Interpretable Cell Classification Using Tree-Based SHAP Image Decomposition and Restoration for High-Throughput Bright-Field Imaging. Cells, 12(10), 1384. https://doi.org/10.3390/cells12101384






