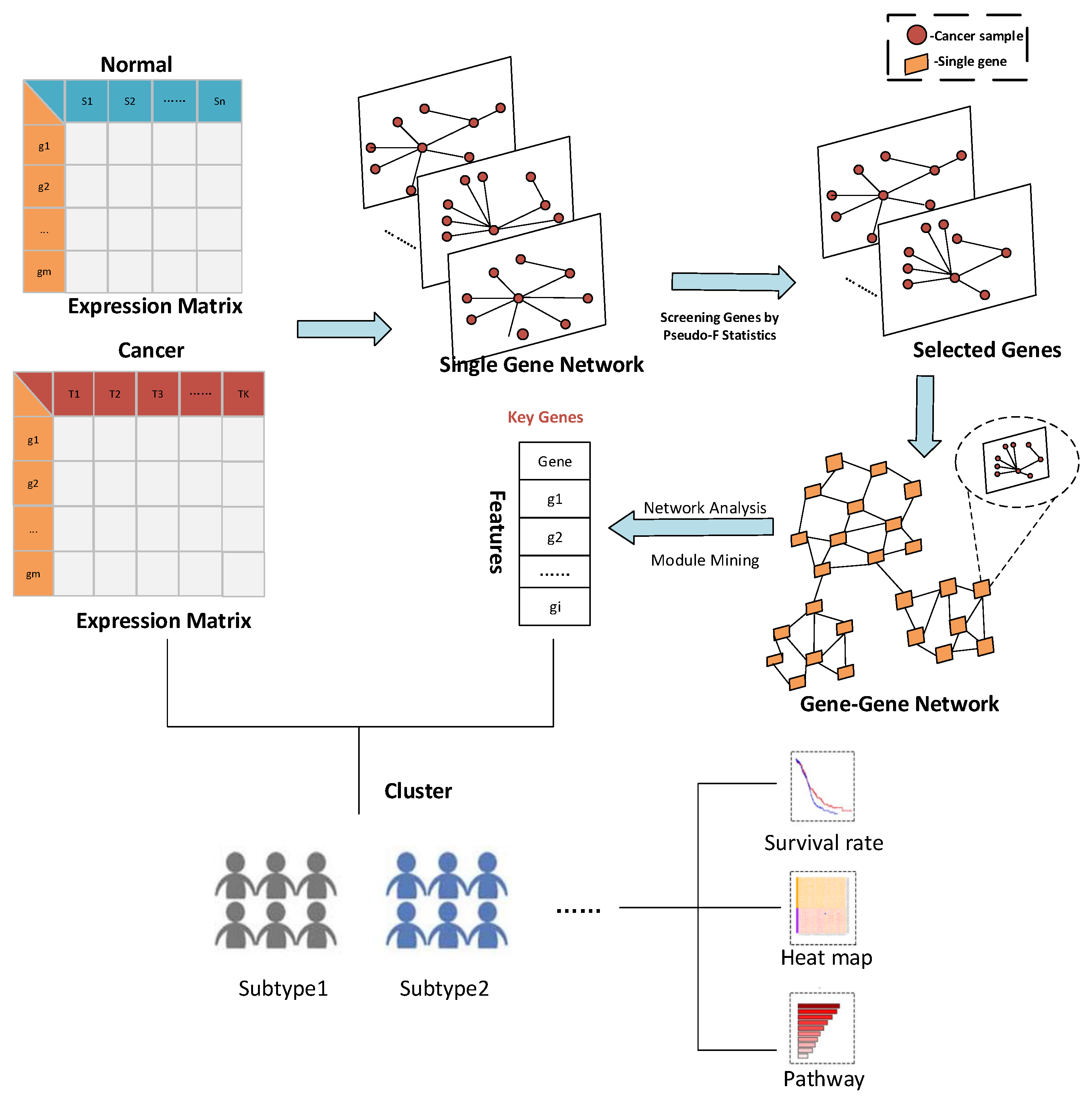
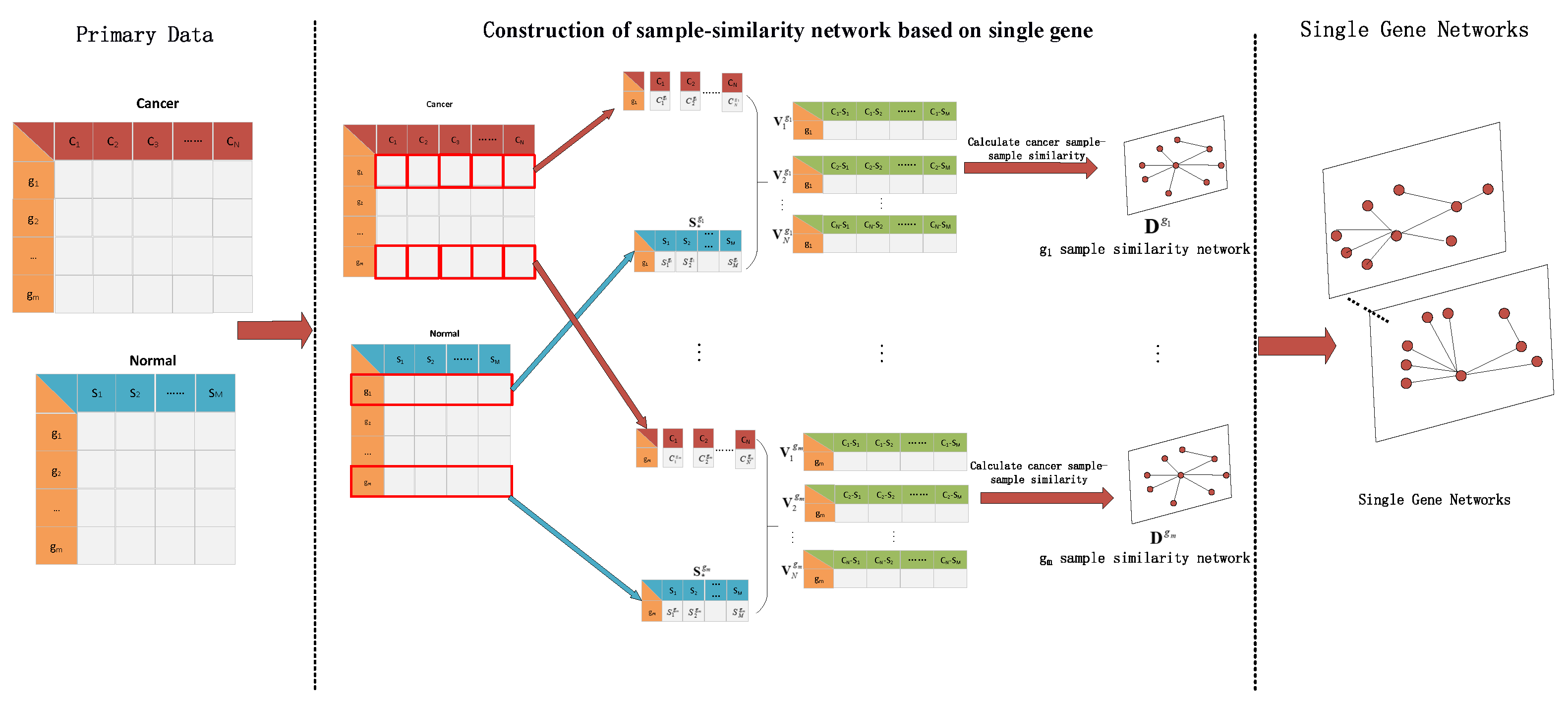
3.1.1. Result of Identifying Two Cancer Subtypes
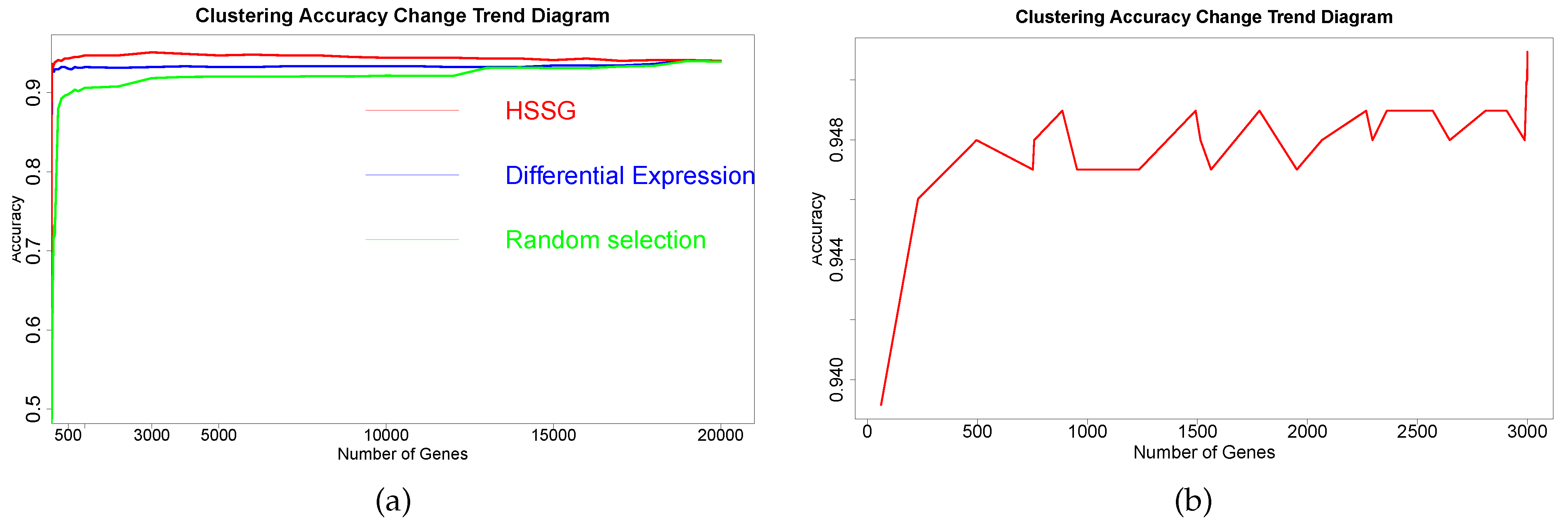
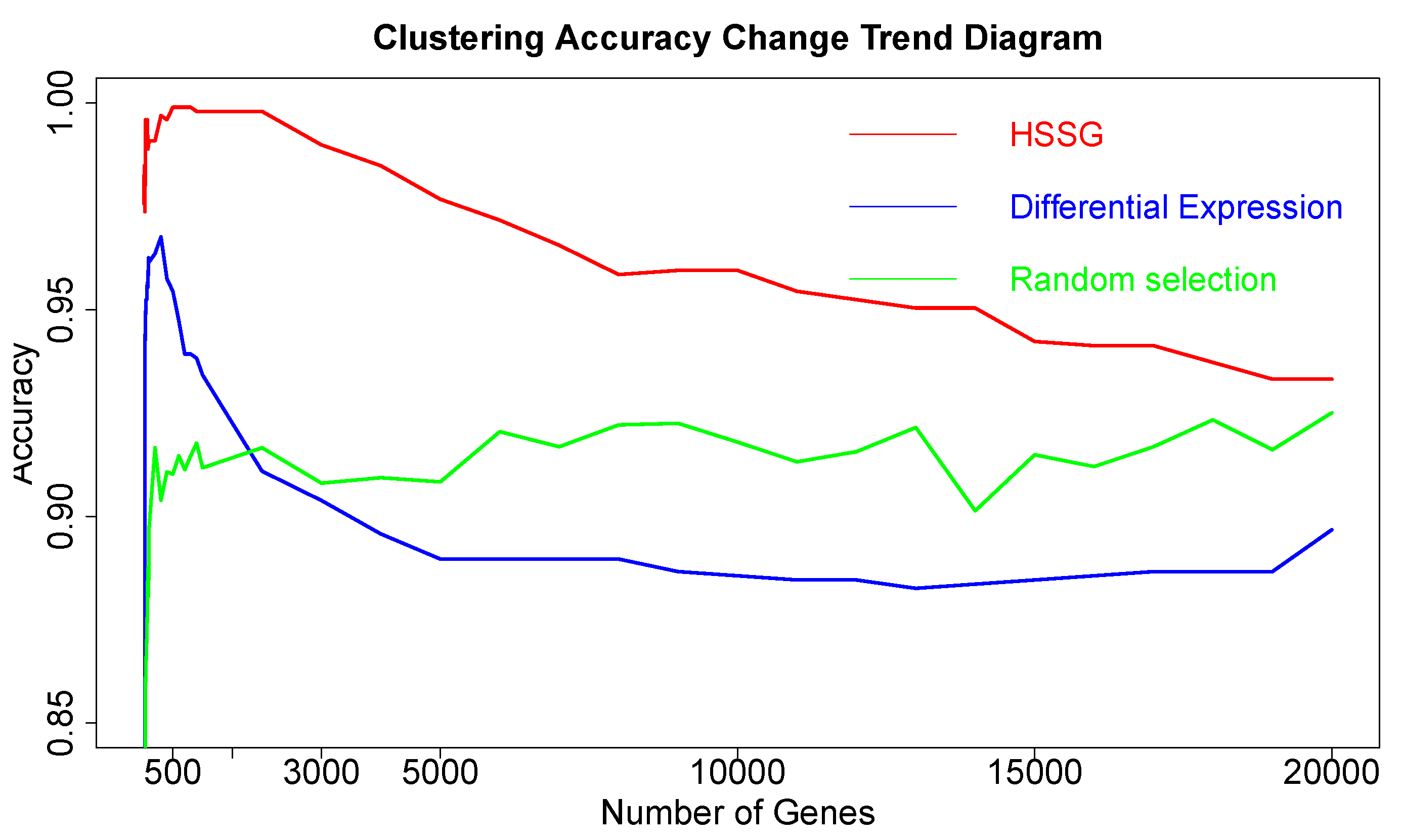
The RNA-seq data of lung cancer, including LUAD and LUSC, was involved in this experiment (the data includes 517 samples of lung adenocarcinoma and 502 samples of lung squamous cell carcinoma). By the above method, the heterogeneity score of each gene for the identification of cancer subtypes was calculated, and the genes were sorted according to the value of pseudo-F statistics. By adding genes as features to theorderfor clustering, the curve of clustering accuracy with the number of genes is shown by the red line in
Figure 3a. The red line in
Figure 3a shows the clustering accuracy curve with the number of genes added, based on the ranking of each gene’s contribution (pseudo-F statistic value), with the constant addition of genes. When the number of added genes reaches 3000, the accuracy rate is the highest (95.1%). At the same time, to highlight the effectiveness of HSSG in screening essential genes that can identify cancer subtypes, we compared three different methods for screening genes. The curve of clustering accuracy of the three methods with the rank of gene addition is shown in
Figure 3a. The genes selected based on the differential expression method were analyzed using the limma differential expression analysis method. The limma package in R language (R package limma 3.46.0) was used to conduct differential expression analysis on sample data of two cancer subtypes, and the obtained results were ranked according to logFC. LogFC represented the ratio of expression levels between two samples (groups). In general, the absolute value of logFC could be used as the screening criterion for differential genes. The clustering accuracy rate of random selection averaged the clustering accuracy rates of the corresponding number of genes after 50 random selections. The figure shows that the accuracy rate of gene clustering sorted by HSSG screening is higher than that of the other two methods.
Then, the first 3000 genes were used to construct a gene-gene network using the methods described above. After obtaining the gene-gene network, the weighted adjacency matrix of the network was normalized, and the threshold was set to 0.7 to remove the edges where the two genes were far apart. On the one hand, through the analysis of the largest network degrees, the largest 67 network nodes were obtained (the degree of these nodes is 2999). On the other hand, module mining also was used on the network. By setting the random walk step size to 7 in module mining, 28 gene modules could be obtained. The proposed method for rankingthe gene modules to cluster shows the precision curve in
Figure 3b. And
Figure 3b shows the clustering accuracy curve with module genes accessions after constructing a gene-gene network, based on network mining of functional modules and ranking modules by average module contribution. It is not difficult to see that with adding a module, the accuracy of clustering does not continuously increase, but there is continuous fluctuation after adding specific module genes. To accurately mine the key gene modules for cancer subtype identification, the Matthews correlation coefficient (MCC) was used to measure the clustering effect. Matthews correlation coefficient is one of the practical evaluation indexes to measure the result of the two-classification model. In the end, six gene modules were retained for 644 genes. The 67 genes were mined by performing a degree analysis on the constructed gene-gene network to find the gene nodes with the maximum degree. In addition, the 644 genes were mined for the more important gene modules by performing module mining of the constructed gene-gene network. Finally, through the above gene–gene network analysis and module mining, we obtained 67 key genes and 644 key genes.
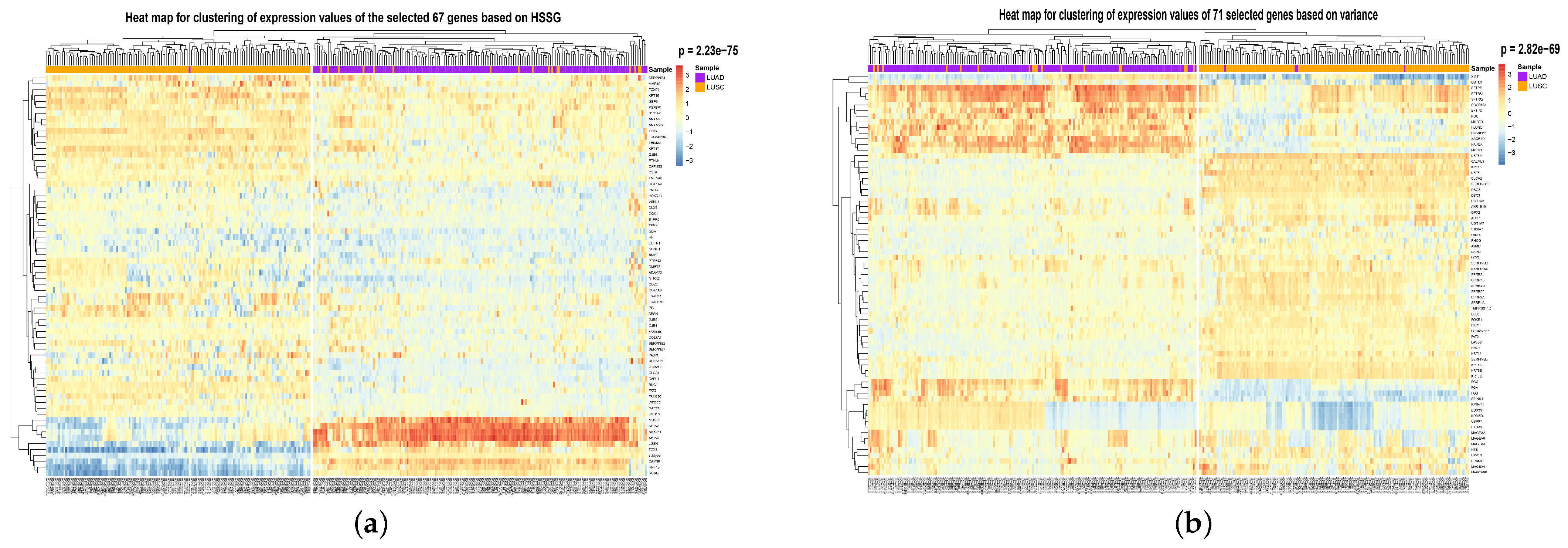
To visualize the global expression changes of the selected genes in all cancer samples, the simple heat maps of the expression values in two different cancer samples of the screened 67 genes and 644 genes found by module mining were drawn, as shown in
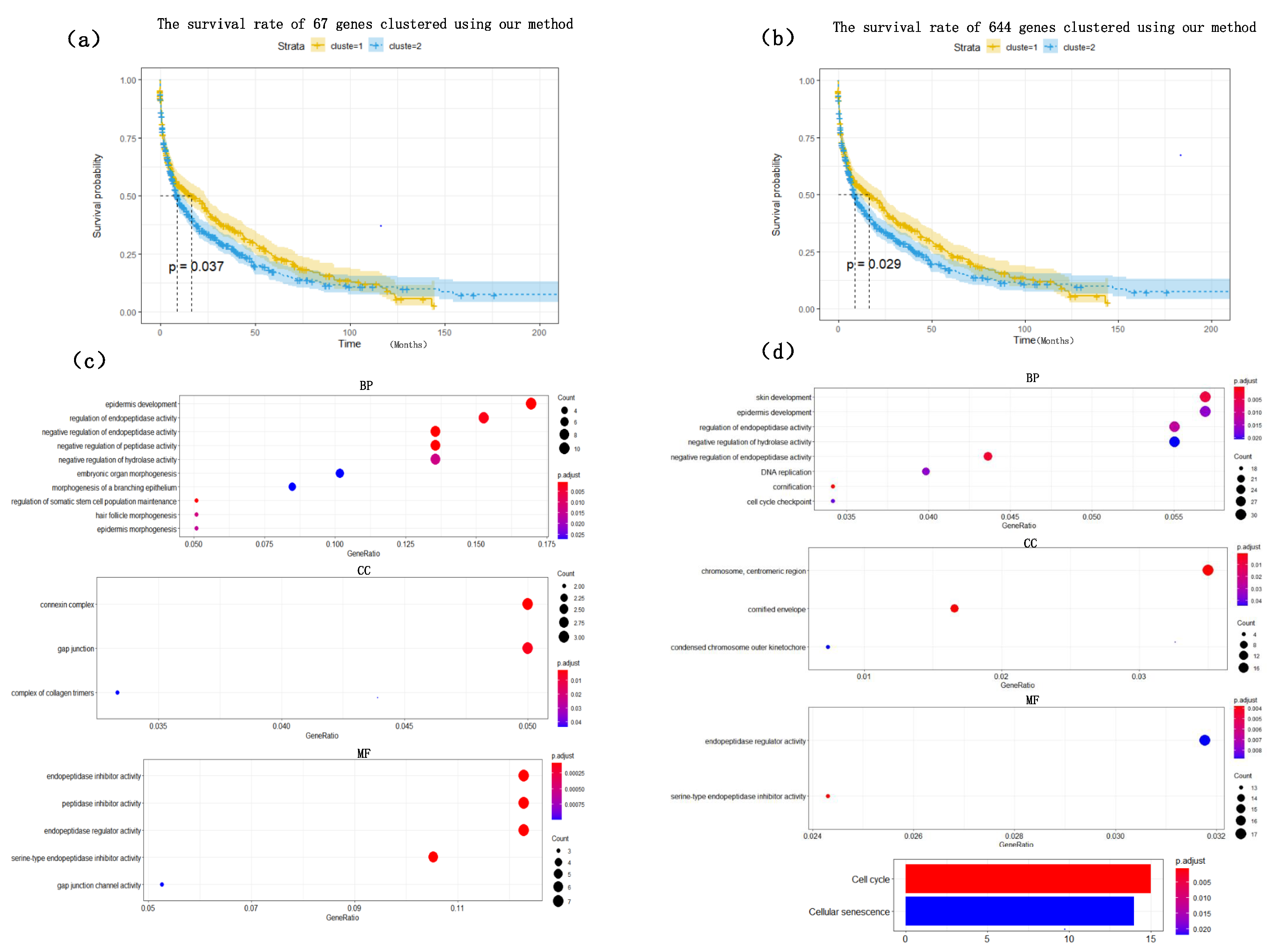
Figure 4. The heat map clearly shows that the expression values of most of the genes based on the HSSG screen are more significantly different between the LUAD and LUSC subtypes. Finally, the clinical information of the samples was used to analyze the survival rate of the clustering results. As shown in
Figure 5a, it was the graph showing the change in sample survival rate after clustering the 67 genes. The
p-value of the survival rate in the schematic diagram is 0.037 < 0.05, which indicates that there are significant differences between the two groups. As shown in
Figure 5b, the graph shows the change in sample survival rate after clustering the 644 genes. The
p-value of the survival rate in the schematic diagram is 0.029 < 0.05, indicating significant differences between the two groups. They demonstrated the superior performance of HSSG.
To find out whether the genes we found have biological significance, 67 genes and 644 genes were enriched and analyzed, and the results showed in
Figure 5c,d. The result of GO enrichment analysis on 67 genes showed that these genes were mainly related to epidermis development, regulation of endopeptidase activity, negative regulation of endopeptidase in biological processes; They were related to connexin complex and gap junction in cell composition; they were related to endopeptidase inhibitor activity, peptidase inhibitor activity, endopeptidase regulator activity in molecular function; From the go enrichment analysis of the above 67 genes, these 67 genes were related to the development of epithelial cells. However, it is well known that the most significant difference between lung adenocarcinoma and lung squamous cell carcinoma is that lung squamous cell carcinoma is mainly caused by chronic irritation and injury of columnar epithelial cells of the bronchial mucosa, cilia loss, squamous metaplasia of basal cells, atypical hyperplasia and hypoplasia [
33]. They showed, in some ways, the correctness of the screening genes of HSSG. Similarly, the GO enrichment analysis on 644 genes was also performed. Furthermore, the results were similar to those of the 67 genes enrichment analysis, mainly related to the development of epithelial cells.
To show the effectiveness of the proposed method, we compared its performance with the other six popular feature/gene scoring methods, which used Random selection, Differential Expression selection, Variance-based score, Kruskal–Wallis Test [
34], Entropy-based score, and Random Forest as the gene importance evaluation criterion. Random selection and differential expression selection methods are consistent with the beginning of this experiment. The effects of the above methods in selecting 67 genes and 644 genes are shown in
Table 2 and
Table 3. It can be seen from the Table that HSSG is slightly better than other feature/gene scoring methods. To compare the performance of HSSG with other popular feature scoring methods and the degree of overlap between the features selected by the different methods, we set thresholds for the five popular methods to make them select the best features. The number of features selected, the accuracy rate, the number of overlaps between each method and the features selected by HSSG, and the overlap rate are shown in
Table 4 (the Random selection method is the average number of feature overlaps taken 50 times at random). As can be seen from
Table 4, HSSG can select relatively few genes while achieving the final performance. Then, the clustering heatmaps of gene expression values for the genes screened by the different methods were drawn to visually compare the effects of the different methods of gene screening, as shown in
Figure 6 (the clustering heatmaps for random selection are not drawn here because the random selection method was averaged 50 times at random and the features selected at random were not consistent each time). In
Figure 6, the cancer subtype samples were clustered hierarchically with genes based on the expression values of the screened genes, respectively, and the clustering results were subjected to the fisher test. As can be seen from the figure, the HSSG test with the smallest
p-value (
p = 2.23 × 10
−75) obtained the best results.
In addition, 79 genes selected by Differential Expression were enriched for analysis to explore how the biological significance of the genes selected by the HSSG differs from the commonly used differential expression-based approach. The differential expression-based gene enrichment analysis is shown in
Figure 7 and the HSSG screened genes enrichment analysis is shown in
Figure 5. As can be seen from the figure, the results of the GO enrichment analysis based on HSSG screening genes and the results of the conventional differential expression-based GO enrichment analysis are in agreement for a large part. There are also some inconsistencies, such as embryonic organ morphogenesis in Biological Process, complex trimers in Cellular Component; gap junction in Molecular Function channel activity in Molecular Function, etc. Finally, the HSSG KEGG pathway enrichment analysis and differential expression-based KEGG pathway enrichment analysis were completed. We found that the HSSG-selected gene pathways were mainly related to Cell cycle and Cellular senescence, while the differential expression-based pathways were mainly related to the estrogen signaling pathway and
Staphylococcus aureus infection.
3.1.2. Result of Identifying Multiple Cancer Subtypes
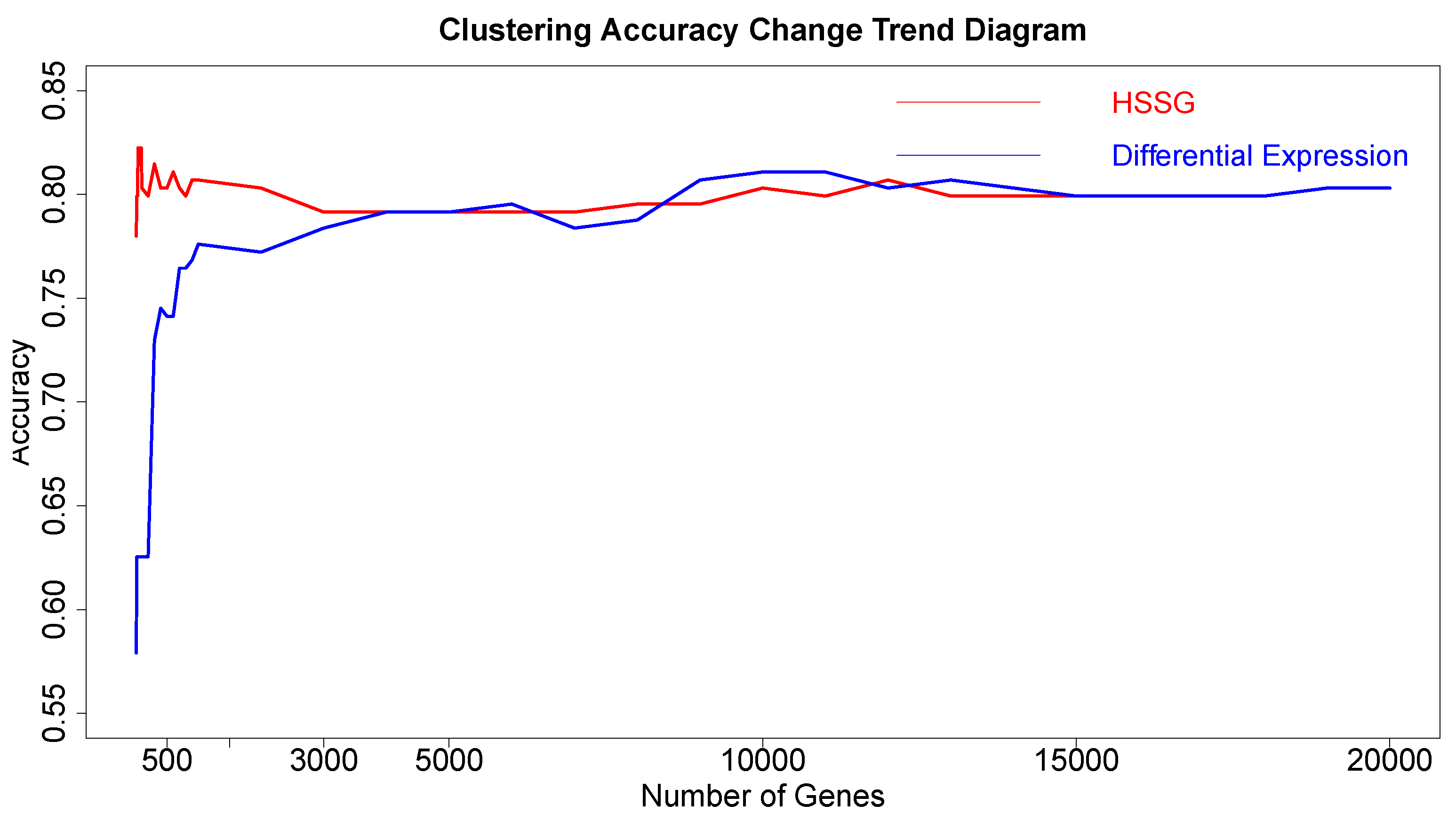
After proving the effectiveness of HSSG in the identification of two cancer subtypes, another experiment was done to verify the recognition effect of HSSG in three or more cancer subtypes. However, due to the uncertainty of cancer subtypes, it was difficult to find definite three or more subtypes data of the same cancer. In this experiment, the samples of three different cancers (350 gastric cancer, 288 colon cancer, and 350 thyroid cancer) were mixed, and HSSG was used to verify whether different cancer samples could be effectively distinguished. As the above method, the heterogeneity score of each gene could be calculated, and the genes were sorted with the score. Then, genes were added in order as features, and K-means clustering was adopted (clustering into three classes). The change curve of clustering accuracy is shown in the red line in
Figure 8. The meaning of the other two curves shown in
Figure 8 is consistent with that of the above experiment. From the figure, the accuracy fluctuates first rose to the highest and then decreased with different numbers of genes added. When the number of genes was added to 500, i.e., When the top 500 genes in pseudo-F statistics were added, the accuracy reached 99.89%. To further enhance the bio-interpretability of the method and improve the gene-gene relationship, the first 500 genes were selected to construct a gene–gene network.
On the one hand, through analyzing the degree distribution of the network, the nodes with the largest degrees in the network were selected, with 90 full-degree nodes selected. And the clustering accuracy was 89.3% when the samples were clustered based on these genes as a feature. (Results from the degrees distribution analysis for the network in this experiment were not very effective, and these genes were not studied in depth later). On the other hand, module mining was performed on the network. We got six gene communities using the cluster_walktrap function and setting the step size to 7. The communities are sorted according to the average pseudo-F statistic. Then, the Rand Index (RI) was used to measure the effectiveness of clustering when joining different communities. In the end, 196 community genes could be gained with a cluster accuracy of 99.89% and RI of 0.9986. Then, the selected genes were compared with the corresponding numbers of genes from the other six different methodsselected, with the accuracy shown in
Table 5. From
Table 5, it is not hard to see that the effect of screening practical features of HSSG is better than the other methods.
At the same time, the simple heat maps of the expression values in three different cancer samples of the 500 genes and the 196 genes screened were shown in
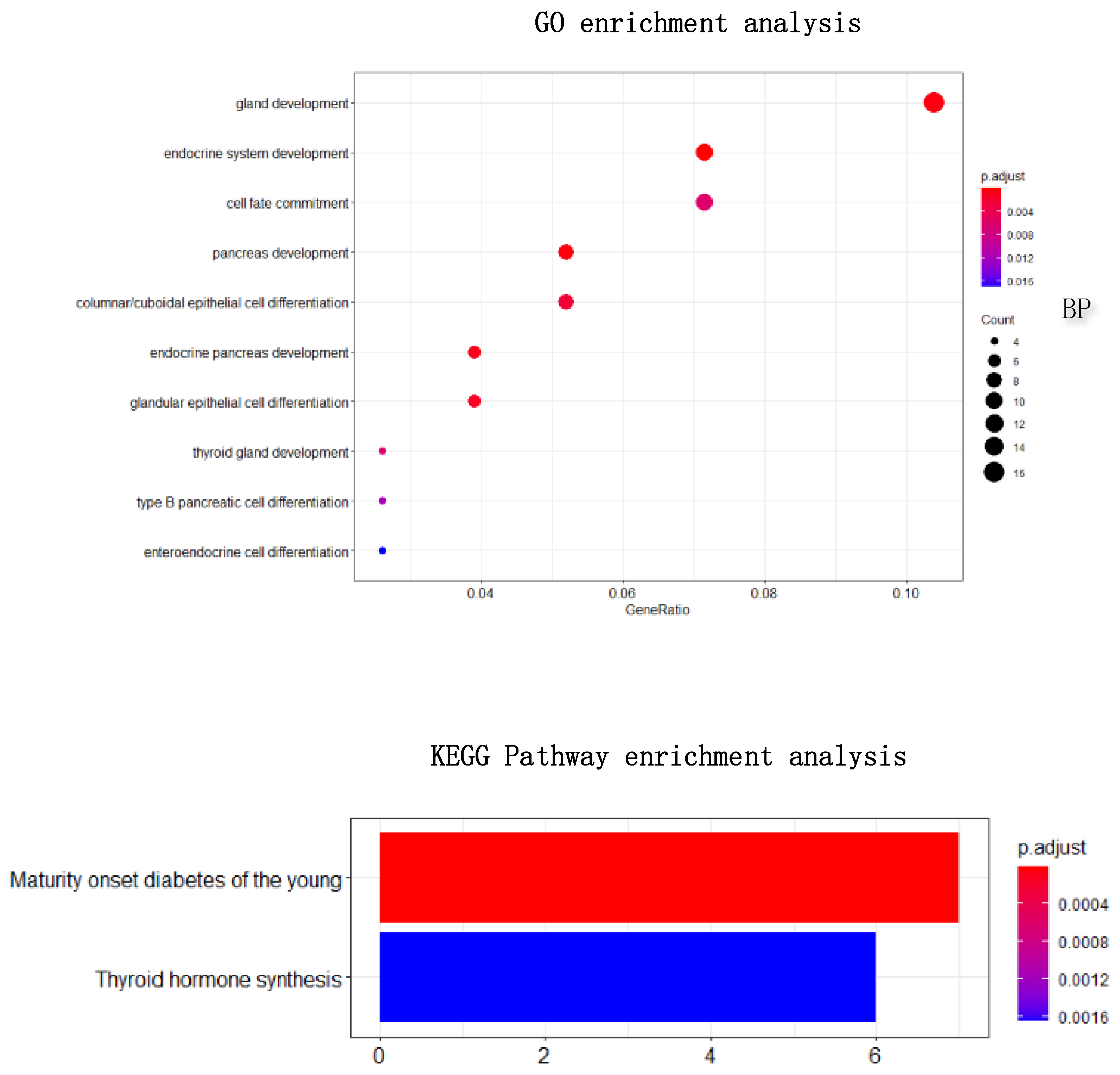
Figure 9. Through the heat maps, it is not difficult to see a significant difference in the expression of genes screened by HSSG in the samples of three cancer subtypes. Finally, the enrichment analysis of 196 genes is shown in
Figure 10. Through enrichment analysis, it could find that most of our selected genes were related to gland development, and the KEGG pathway was also related to thyroid hormone synthesis.