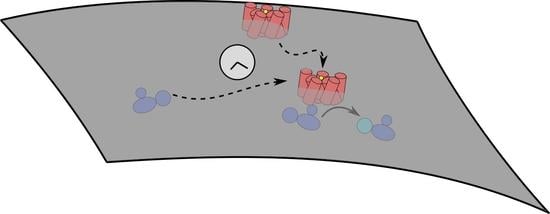
The Impact of Membrane Protein Diffusion on GPCR Signaling
Abstract
1. Introduction
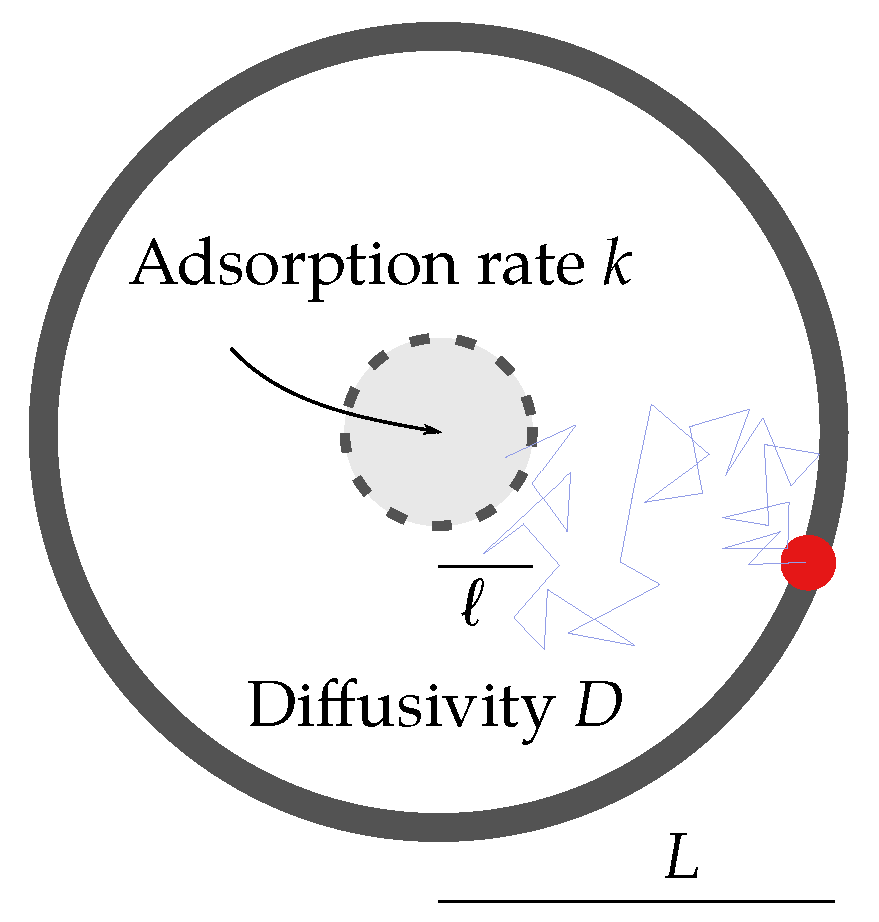
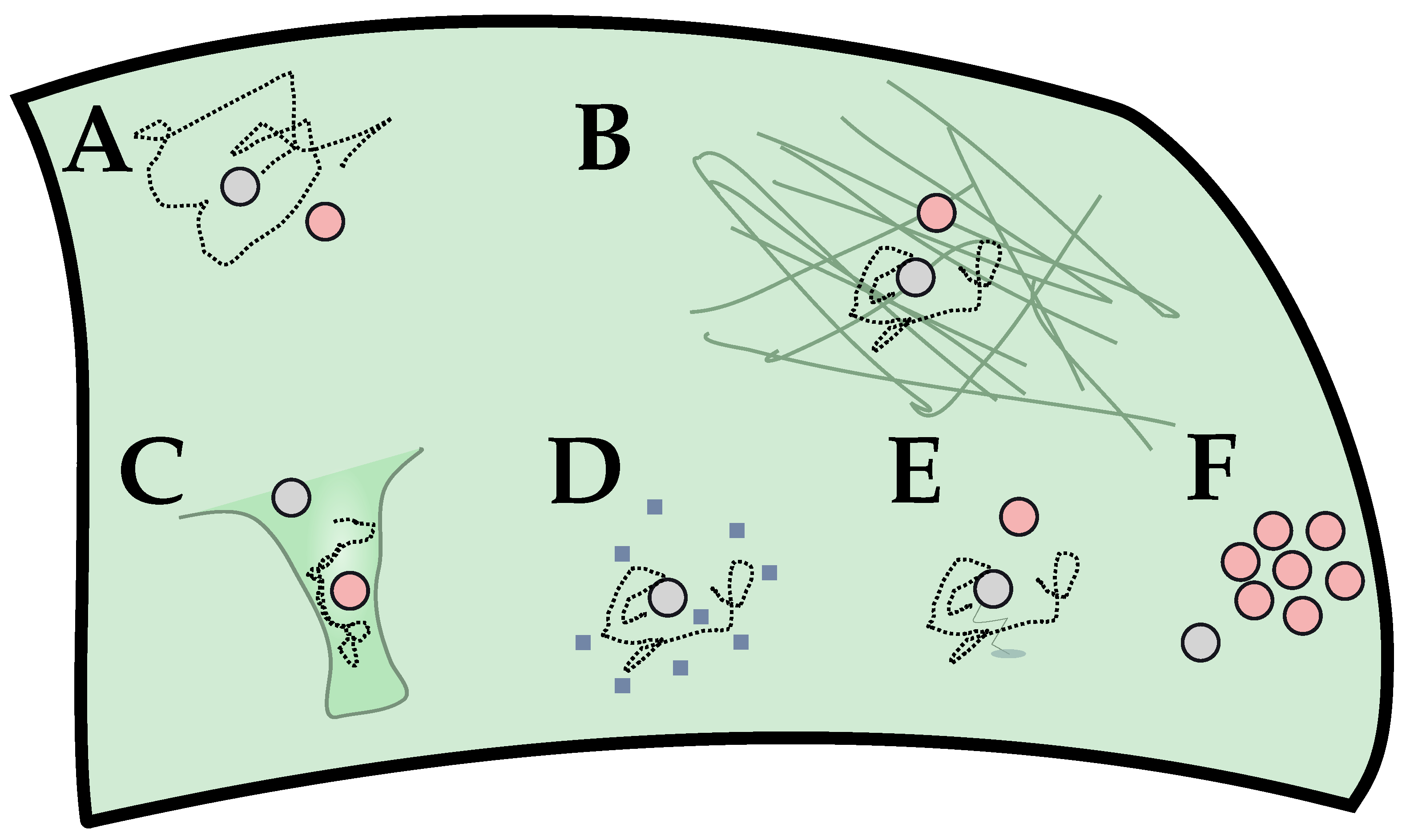
2. Diffusion Limitation in GPCR-G Protein Binding
2.1. Reduced Diffusional Model
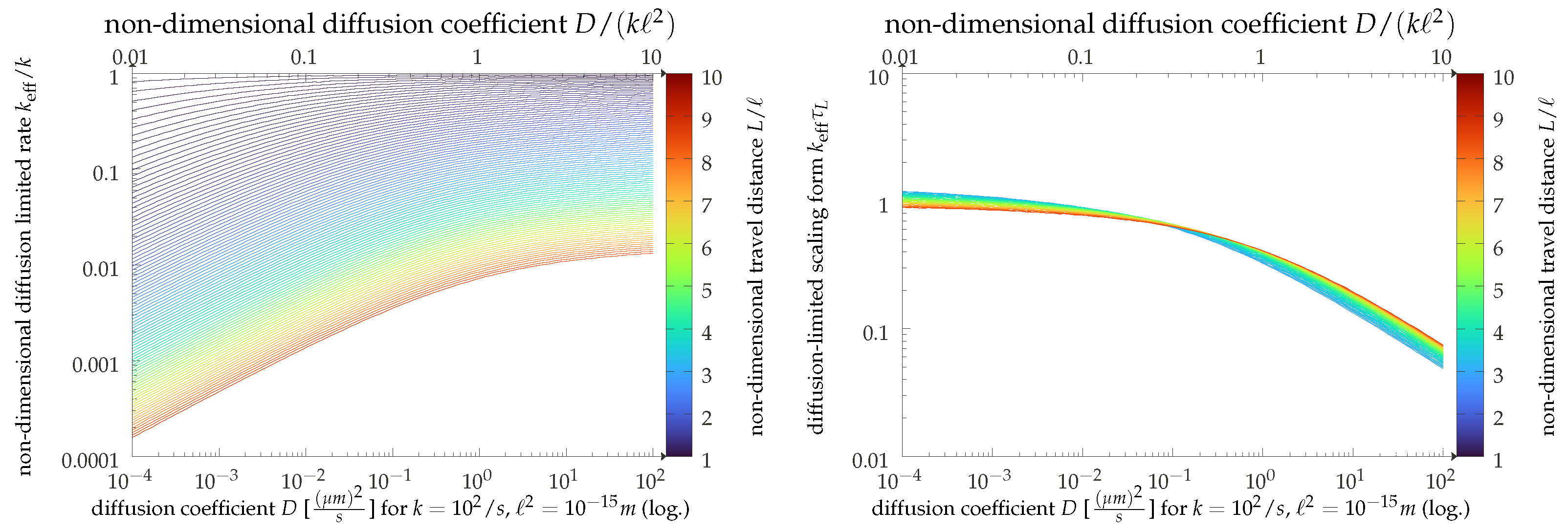
2.2. Scaling Analysis
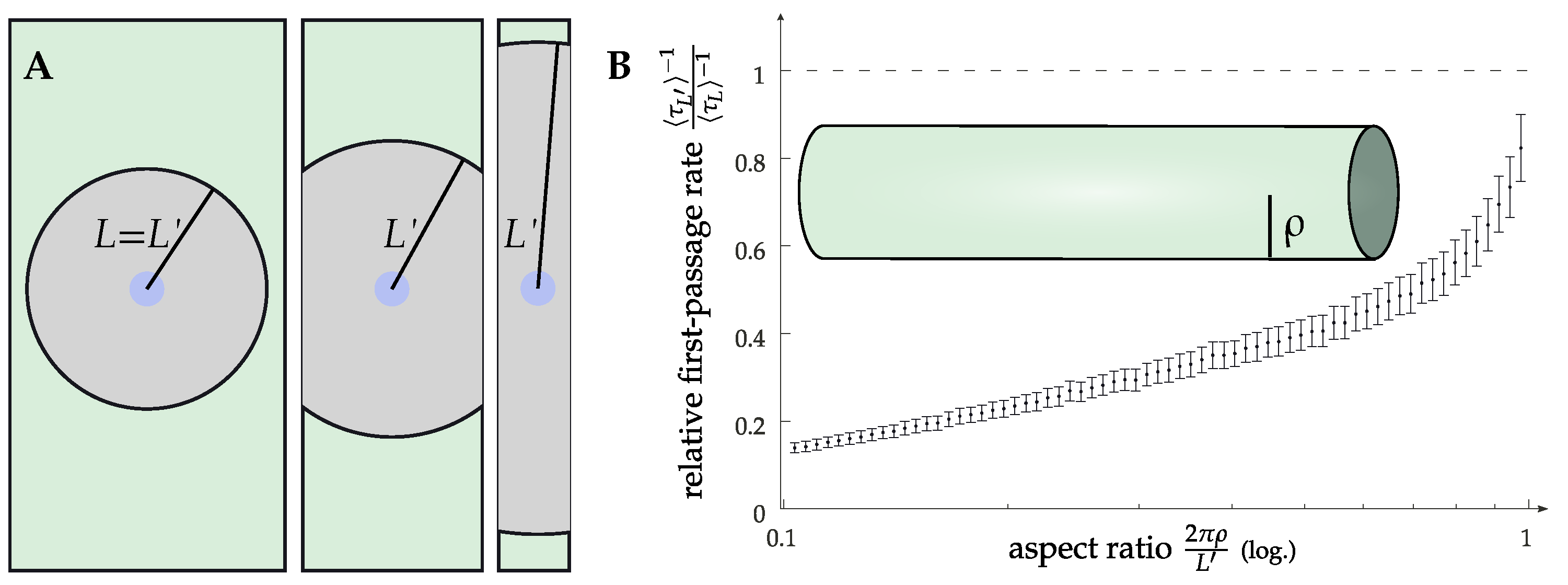
2.3. More Complicated Scenarios: Clustering and Geometries Other Than Planar
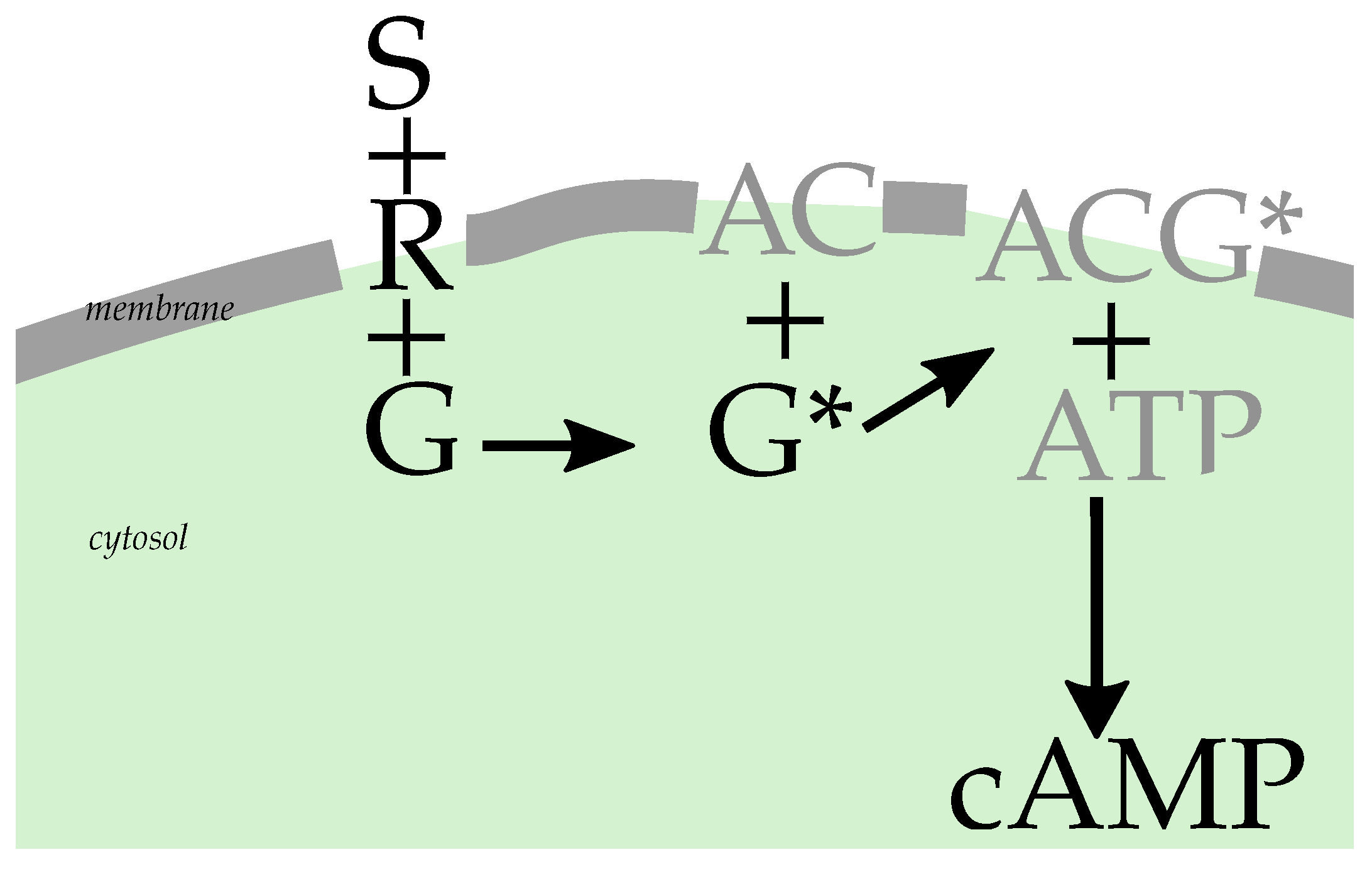
3. Measuring the Second Messenger Concentration: The Reaction Network
3.1. The Signaling Network
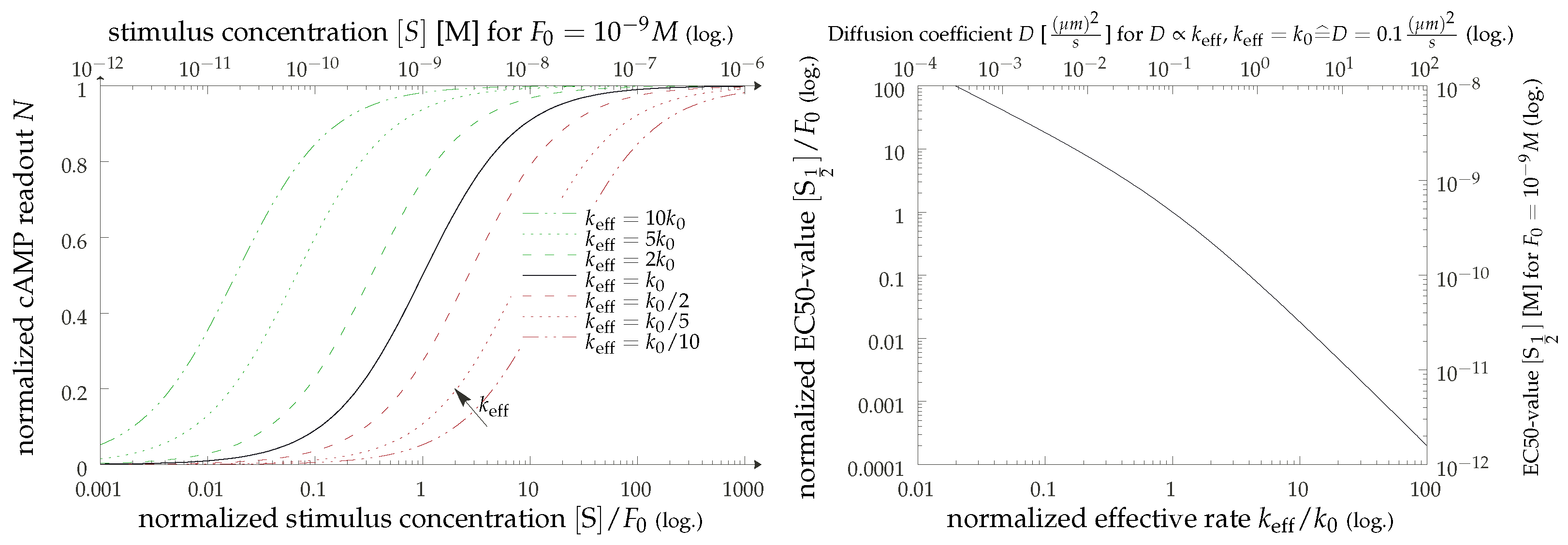
3.2. Concentration of Activated G Protein
3.3. cAMP Production
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PBRD | particle-based reaction-diffusion |
| GPCR | G protein-coupled receptor |
| cAMP | cyclic adenosine monophosphate |
| GTP | guanosine triphosphate |
| GDP | guanosine diphosphate |
| AC | adenolyate cyclase |
| ATP | adenosine triphosphate |
| LatB | Latrunculin B |
| AR | adrenergic receptor |
| concentration of X (in cell or membrane, depending on context) | |
| G | unactivated G protein |
| activaced G protein | |
| R | receptor |
| S | stimulus, agonistic ligand |
| complex of molecules X and Y |
Appendix A. Simulation Details
References
- Hauser, A.S.; Attwood, M.M.; Rask-Andersen, M.; Schiöth, H.B.; Gloriam, D.E. Trends in GPCR drug discovery: New agents, targets and indications. Nat. Rev. Drug Discov. 2017, 16, 829–842. [Google Scholar] [CrossRef] [PubMed]
- Bers, D.M.; Ziolo, M.T. When is cAMP not cAMP? Circ. Res. 2001, 89, 373–375. [Google Scholar] [CrossRef] [PubMed]
- Calebiro, D.; Koszegi, Z. The subcellular dynamics of GPCR signaling. Mol. Cell. Endocrinol. 2019, 483, 24–30. [Google Scholar] [CrossRef]
- Bock, A.; Annibale, P.; Konrad, C.; Hannawacker, A.; Anton, S.E.; Maiellaro, I.; Zabel, U.; Sivaramakrishnan, S.; Falcke, M.; Lohse, M.J. Optical mapping of cAMP signaling at the nanometer scale. Cell 2020, 182, 1519–1530. [Google Scholar] [CrossRef]
- Maudsley, S.; Martin, B.; Luttrell, L.M. The origins of diversity and specificity in G protein-coupled receptor signaling. J. Pharmacol. Exp. Ther. 2005, 314, 485–494. [Google Scholar] [CrossRef]
- Wacker, D.; Stevens, R.C.; Roth, B.L. How Ligands Illuminate GPCR Molecular Pharmacology. Cell 2017, 170, 414–427. [Google Scholar] [CrossRef]
- Zaccolo, M.; Pozzan, T. Discrete microdomains with high concentration of cAMP in stimulated rat neonatal cardiac myocytes. Science 2002, 295, 1711–1715. [Google Scholar] [CrossRef]
- De Lean, A.; Stadel, J.; Lefkowitz, R. A ternary complex model explains the agonist-specific binding properties of the adenylate cyclase-coupled beta-adrenergic receptor. J. Biol. Chem. 1980, 255, 7108–7117. [Google Scholar] [CrossRef]
- Sutherland, E.W.; Wosilatt, W.D. Inactivation and activation of liver phosphorylase. Nature 1955, 175, 169–170. [Google Scholar] [CrossRef]
- Neves, S.R.; Ram, P.T.; Iyengar, R. G protein pathways. Science 2002, 296, 1636–1639. [Google Scholar] [CrossRef]
- Fay, S.P.; Posner, R.G.; Swann, W.N.; Sklar, L.A. Real-Time Analysis of the Assembly of Ligand, Receptor, and G Protein by Quantitative Fluorescence Flow Cytometry. Biochemistry 1991, 30, 5066–5075. [Google Scholar] [CrossRef] [PubMed]
- Shea, L.D.; Neubig, R.R.; Linderman, J.J. Timing is everything: The role of kinetics in G protein activation. Life Sci. 2000, 68, 647–658. [Google Scholar] [CrossRef]
- Sungkaworn, T.; Jobin, M.L.; Burnecki, K.; Weron, A.; Lohse, M.J.; Calebiro, D. Single-molecule imaging reveals receptor–G protein interactions at cell surface hot spots. Nature 2017, 550, 543–547. [Google Scholar] [CrossRef] [PubMed]
- Alhadeff, R.; Vorobyov, I.; Yoon, H.W.; Warshel, A. Exploring the free-energy landscape of GPCR activation. Proc. Natl. Acad. Sci. USA 2018, 115, 10327–10332. [Google Scholar] [CrossRef] [PubMed]
- Lamb, T.D. Stochastic simulation of activation in the G-protein cascade of phototransduction. Biophys. J. 1994, 67, 1439–1454. [Google Scholar] [CrossRef]
- Linderman, J.J.; Mahama, P.A.; Forsten, K.E.; Lauffenburger, D.A. Diffusion and probability in receptor binding and signaling. Adv. Chem. Eng. 1994, 19, 51–127. [Google Scholar] [CrossRef]
- Melo, E.; Martins, J. Kinetics of bimolecular reactions in model bilayers and biological membranes. A critical review. Biophys. Chem. 2006, 123, 77–94. [Google Scholar] [CrossRef]
- Goldstein, B.; Levine, H.; Torney, D. Diffusion limited reactions. SIAM J. Appl. Math. 2007, 67, 1147–1165. [Google Scholar] [CrossRef]
- Kenakin, T. Drug efficacy at G protein–coupled receptors. Annu. Rev. Pharmacol. Toxicol. 2002, 42, 349–379. [Google Scholar] [CrossRef]
- Bornheimer, S.J.; Maurya, M.R.; Farquhar, M.G.; Subramaniam, S. Computational modeling reveals how interplay between components of a GTPase-cycle module regulates signal transduction. Proc. Natl. Acad. Sci. USA 2004, 101, 15899–15904. [Google Scholar] [CrossRef]
- Jaeger, J.C.; Carslaw, H.S. XVIII.—Heat Flow in the Region bounded Internally by a Circular Cylinder. Proc. R. Soc. Edinburgh. Sect. Math. Phys. Sci. 1943, 61, 223–228. [Google Scholar] [CrossRef]
- Waite, T.R. Theoretical treatment of the kinetics of diffusion-limited reactions. Phys. Rev. 1957, 107, 463–470. [Google Scholar] [CrossRef]
- Szabo, A.; Schulten, K.; Schulten, Z. First passage time approach to diffusion controlled reactions. J. Chem. Phys. 1980, 72, 4350–4357. [Google Scholar] [CrossRef]
- Torney, D.C.; McConnell, H.M. Diffusion-limited reaction rate theory for two-dimensional systems. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1983, 387, 147–170. [Google Scholar] [CrossRef]
- Molski, A. A Model of Diffusion-Influenced Enzyme Activation. J. Phys. Chem. 2000, 104, 4532–4536. [Google Scholar] [CrossRef]
- Mahama, P.A.; Linderman, J.J. A Monte Carlo study of the dynamics of G-protein activation. Biophys. J. 1994, 67, 1345–1357. [Google Scholar] [CrossRef][Green Version]
- Lauffenburger, D.A.; Linderman, J. Receptors: Models for Binding, Trafficking, and Signaling; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Doi, M. Stochastic theory of diffusion-controlled reaction. J. Phys. A Math. Theor. 1976, 9, 1479. [Google Scholar] [CrossRef]
- Calebiro, D.; Rieken, F.; Wagner, J.; Sungkaworn, T.; Zabel, U.; Borzi, A.; Cocucci, E.; Zurn, A.; Lohse, M.J. Single-molecule analysis of fluorescently labeled G-protein-coupled receptors reveals complexes with distinct dynamics and organization. Proc. Natl. Acad. Sci. USA 2013, 110, 743–748. [Google Scholar] [CrossRef]
- Scarselli, M.; Annibale, P.; McCormick, P.J.; Kolachalam, S.; Aringhieri, S.; Radenovic, A.; Corsini, G.U.; Maggio, R. Revealing G-protein-coupled receptor oligomerization at the single-molecule level through a nanoscopic lens: Methods, dynamics and biological function. FEBS J. 2016, 283, 1197–1217. [Google Scholar] [CrossRef]
- Boltz, H.H.; Sirbu, A.; Stelzer, N.; Lohse, M.J.; Schütte, C.; Annibale, P. Quantitative spectroscopy of single molecule interaction times. Opt. Lett. 2021, 46, 1538–1541. [Google Scholar] [CrossRef]
- Bathe-Peters, M.; Gmach, P.; Boltz, H.-H.; Einsiedel, J.; Gotthardt, M.; Hübner, H.; Gmeiner, P.; Lohse, M.J.; Annibale, P. Visualization of β-adrenergic receptor dynamics and differential localization in cardiomyocytes. Proc. Natl. Acad. Sci. USA 2021, 118, e2101119118. [Google Scholar] [CrossRef] [PubMed]
- Bakardjieva, A.; Galla, H.J.; Helmreich, E.J. Modulation of the β-Receptor Adenylate Cyclase Interactions in Cultured Chang Liver Cells by Phospholipid Enrichment. Biochemistry 1979, 18, 3016–3023. [Google Scholar] [CrossRef] [PubMed]
- Heron, D.S.; Shinitzky, M.; Hershkowitz, M.; Samuel, D. Lipid fluidity markedly modulates the binding of serotonin to mouse brain membranes. Proc. Natl. Acad. Sci. USA 1980, 77, 7463–7467. [Google Scholar] [CrossRef] [PubMed]
- Bockaert, J.; Fagni, L.; Dumuis, A.; Marin, P. GPCR interacting proteins (GIP). Pharmacol. Ther. 2004, 103, 203–221. [Google Scholar] [CrossRef] [PubMed]
- Stelzer, N. Investigating How Cortical Actin Modulates GPCR Dynamics and Signaling. Master’s Thesis, TU Berlin, Berlin, Germany, 2021. [Google Scholar]
- Bockaert, J.; Marin, P.; Dumuis, A.; Fagni, L. The ’magic tail’ of G protein-coupled receptors: An anchorage for functional protein networks. FEBS Lett. 2003, 546, 65–72. [Google Scholar] [CrossRef]
- Di Rienzo, C.; Gratton, E.; Beltram, F.; Cardarelli, F. Fast spatiotemporal correlation spectroscopy to determine protein lateral diffusion laws in live cell membranes. Proc. Natl. Acad. Sci. USA 2013, 110, 12307–12312. [Google Scholar] [CrossRef]
- Posern, G.; Sotiropoulos, A.; Treisman, R. Mutant actins demonstrate a role for unpolymerized actin in control of transcription by serum response factor. Mol. Biol. Cell 2002, 13, 4167–4178. [Google Scholar] [CrossRef]
- Gronewold, T.M.A.; Sasse, F.; Lünsdorf, H.; Reichenbach, H. Effects of rhizopodin and latrunculin B on the morphology and on the actin cytoskeleton of mammalian cells. Cell Tissue Res. 1999, 295, 121–129. [Google Scholar] [CrossRef]
- Bornancin, F.; Pfister, C.; Chabre, M. The transitory complex between photoexcited rhodopsin and transducin. Eur. J. Biochem. 1989, 184, 687–698. [Google Scholar] [CrossRef]
- Taylor, C.W. The role of G proteins in transmembrane signalling. Biochem. J. 1990, 272, 1–13. [Google Scholar] [CrossRef]
- Gregorio, G.G.; Masureel, M.; Hilger, D.; Terry, D.S.; Juette, M.; Zhao, H.; Zhou, Z.; Perez-Aguilar, J.M.; Hauge, M.; Mathiasen, S.; et al. Single-molecule analysis of ligand efficacy in β2AR–G-protein activation. Nature 2017, 547, 68–73. [Google Scholar] [CrossRef] [PubMed]
- Guo, C.; Levine, H. A thermodynamic model for receptor clustering. Biophys. J. 1999, 77, 2358–2365. [Google Scholar] [CrossRef]
- Broday, D.M. Diffusion of clusters of transmembrane proteins as a model of focal adhesion remodeling. Bull. Math. Biol. 2000, 62, 891–924. [Google Scholar] [CrossRef][Green Version]
- Cairo, C.W. Signaling by Committee: Receptor Clusters Determine Pathways of Cellular Activation. ACS Chem. Biol. 2007, 2, 652–655. [Google Scholar] [CrossRef]
- Caré, B.R.; Soula, H.A. Impact of receptor clustering on ligand binding. BMC Syst. Biol. 2011, 5, 48. [Google Scholar] [CrossRef] [PubMed]
- Caré, B.R.; Soula, H.A. Receptor clustering affects signal transduction at the membrane level in the reaction-limited regime. Phys. Rev. -Stat. Nonlinear Soft Matter Phys. 2013, 87, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Watabe, M.; Yoshimura, H.; Arjunan, S.N.; Kaizu, K.; Takahashi, K. Signaling activations through G-protein-coupled-receptor aggregations. Phys. Rev. E 2020, 102, 32413. [Google Scholar] [CrossRef]
- Woolf, P.J.; Linderman, J.J. An algebra of dimerization and its implications for G-protein coupled receptor signaling. J. Theor. Biol. 2004, 229, 157–168. [Google Scholar] [CrossRef]
- Rosholm, K.R.; Leijnse, N.; Mantsiou, A.; Tkach, V.; Pedersen, S.L.; Wirth, V.F.; Oddershede, L.B.; Jensen, K.J.; Martinez, K.L.; Hatzakis, N.S.; et al. Membrane curvature regulates ligand-specific membrane sorting of GPCRs in living cells. Nat. Chem. Biol. 2017, 13, 724–729. [Google Scholar] [CrossRef]
- Nikolaev, V.O.; Moshkov, A.; Lyon, A.R.; Miragoli, M.; Novak, P.; Paur, H.; Lohse, M.J.; Korchev, Y.E.; Harding, S.E.; Gorelik, J. β 2-adrenergic receptor redistribution in heart failure changes cAMP compartmentation. Science 2010, 327, 1653–1657. [Google Scholar] [CrossRef]
- Daniels, D.R. Receptor-ligand diffusion-limited reaction rates on curved membranes. Chem. Phys. Lett. 2022, 795, 139516. [Google Scholar] [CrossRef]
- Dorsaz, N.; De Michele, C.; Piazza, F.; De Los Rios, P.; Foffi, G. Diffusion-limited reactions in crowded environments. Phys. Rev. Lett. 2010, 105, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Schütz, G.J.; Schindler, H.; Schmidt, T. Single-molecule microscopy on model membranes reveals anomalous diffusion. Biophys. J. 1997, 73, 1073–1080. [Google Scholar] [CrossRef]
- Wawrezinieck, L.; Rigneault, H.; Marguet, D.; Lenne, P.F. Fluorescence correlation spectroscopy diffusion laws to probe the submicron cell membrane organization. Biophys. J. 2005, 89, 4029–4042. [Google Scholar] [CrossRef]
- Haugh, J.M. Analysis of reaction-diffusion systems with anomalous subdiffusion. Biophys. J. 2009, 97, 435–442. [Google Scholar] [CrossRef]
- Debnath, T.; Ghosh, P.K.; Li, Y.; Marchesoni, F.; Nori, F. Active diffusion limited reactions. J. Chem. Phys. 2019, 150. [Google Scholar] [CrossRef]
- Di Rienzo, C.; Annibale, P. Visualizing the molecular mode of motion from a correlative analysis of localization microscopy datasets. Opt. Lett. 2016, 41, 4503. [Google Scholar] [CrossRef]
- Sarkar, S. Concentration Dependence of Diffusion-Limited Reaction Rates and Its Consequences. Phys. Rev. X 2020, 10, 41032. [Google Scholar] [CrossRef]
- Irannejad, R.; von Zastrow, M. GPCR signaling along the endocytic pathway. Curr. Opin. Cell Biol. 2014, 27, 109–116. [Google Scholar] [CrossRef]
- Yu, J.Z.; Rasenick, M.M. Real-Time Visualization of a Fluorescent Gαs: Dissociation of the Activated G Protein from Plasma Membrane. Mol. Pharmacol. 2002, 61, 352–359. [Google Scholar] [CrossRef]
- Gillespie, D.T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 1976, 22, 403–434. [Google Scholar] [CrossRef]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boltz, H.-H.; Sirbu, A.; Stelzer, N.; de Lanerolle, P.; Winkelmann, S.; Annibale, P. The Impact of Membrane Protein Diffusion on GPCR Signaling. Cells 2022, 11, 1660. https://doi.org/10.3390/cells11101660
Boltz H-H, Sirbu A, Stelzer N, de Lanerolle P, Winkelmann S, Annibale P. The Impact of Membrane Protein Diffusion on GPCR Signaling. Cells. 2022; 11(10):1660. https://doi.org/10.3390/cells11101660
Chicago/Turabian StyleBoltz, Horst-Holger, Alexei Sirbu, Nina Stelzer, Primal de Lanerolle, Stefanie Winkelmann, and Paolo Annibale. 2022. "The Impact of Membrane Protein Diffusion on GPCR Signaling" Cells 11, no. 10: 1660. https://doi.org/10.3390/cells11101660
APA StyleBoltz, H.-H., Sirbu, A., Stelzer, N., de Lanerolle, P., Winkelmann, S., & Annibale, P. (2022). The Impact of Membrane Protein Diffusion on GPCR Signaling. Cells, 11(10), 1660. https://doi.org/10.3390/cells11101660