Quantitative Evaluation of Cardiac Cell Interactions and Responses to Cyclic Strain
Abstract
1. Introduction
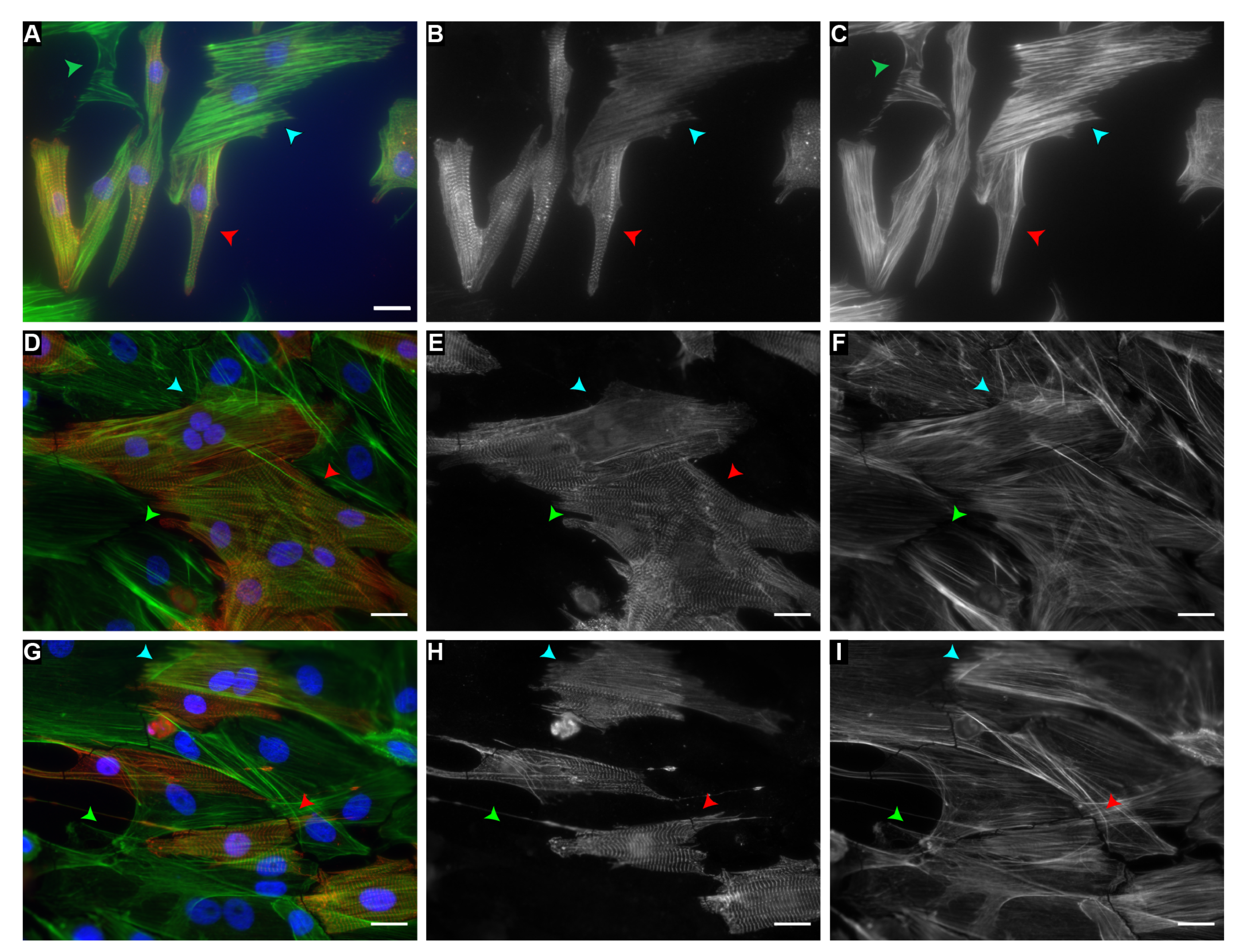
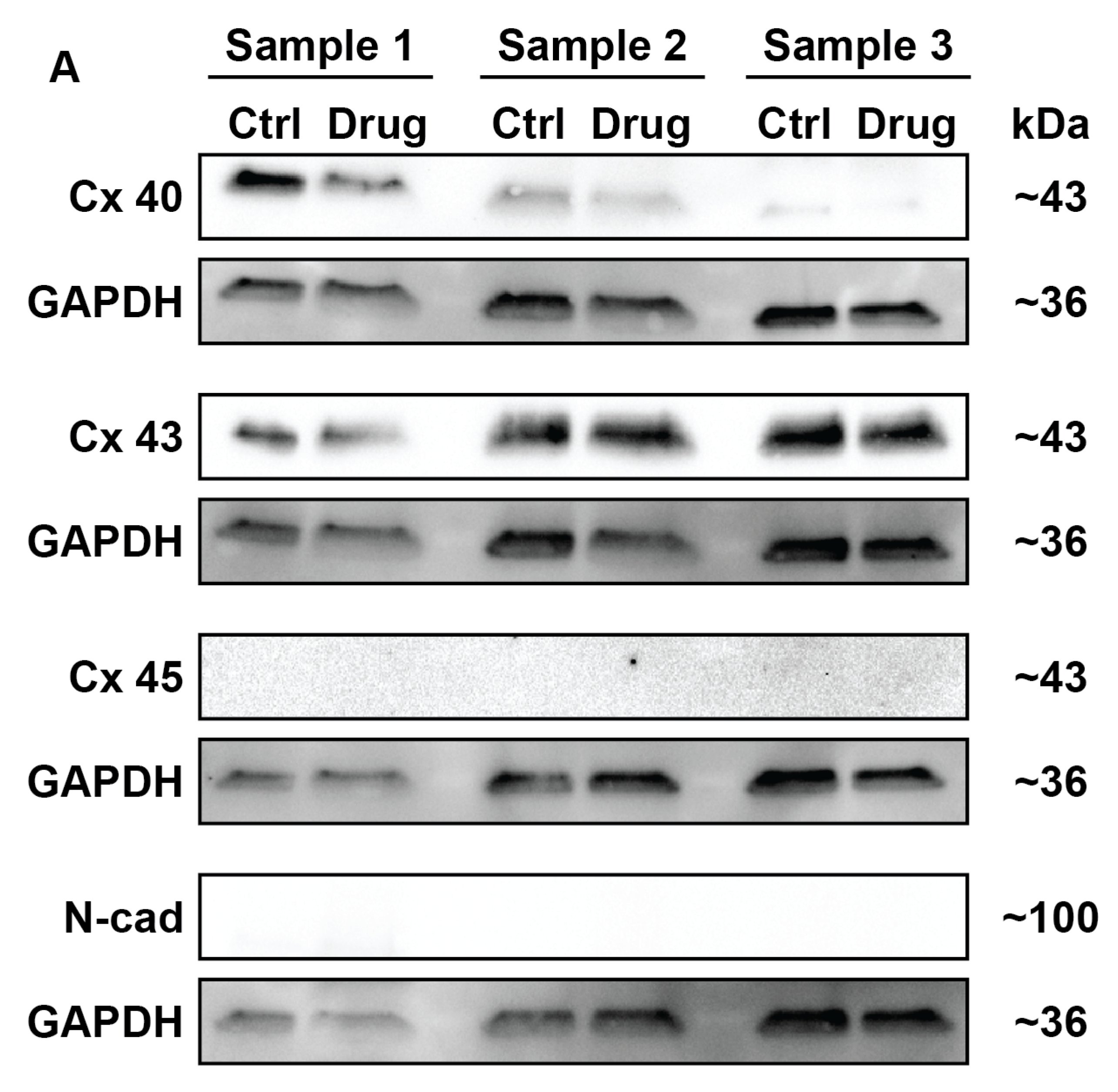
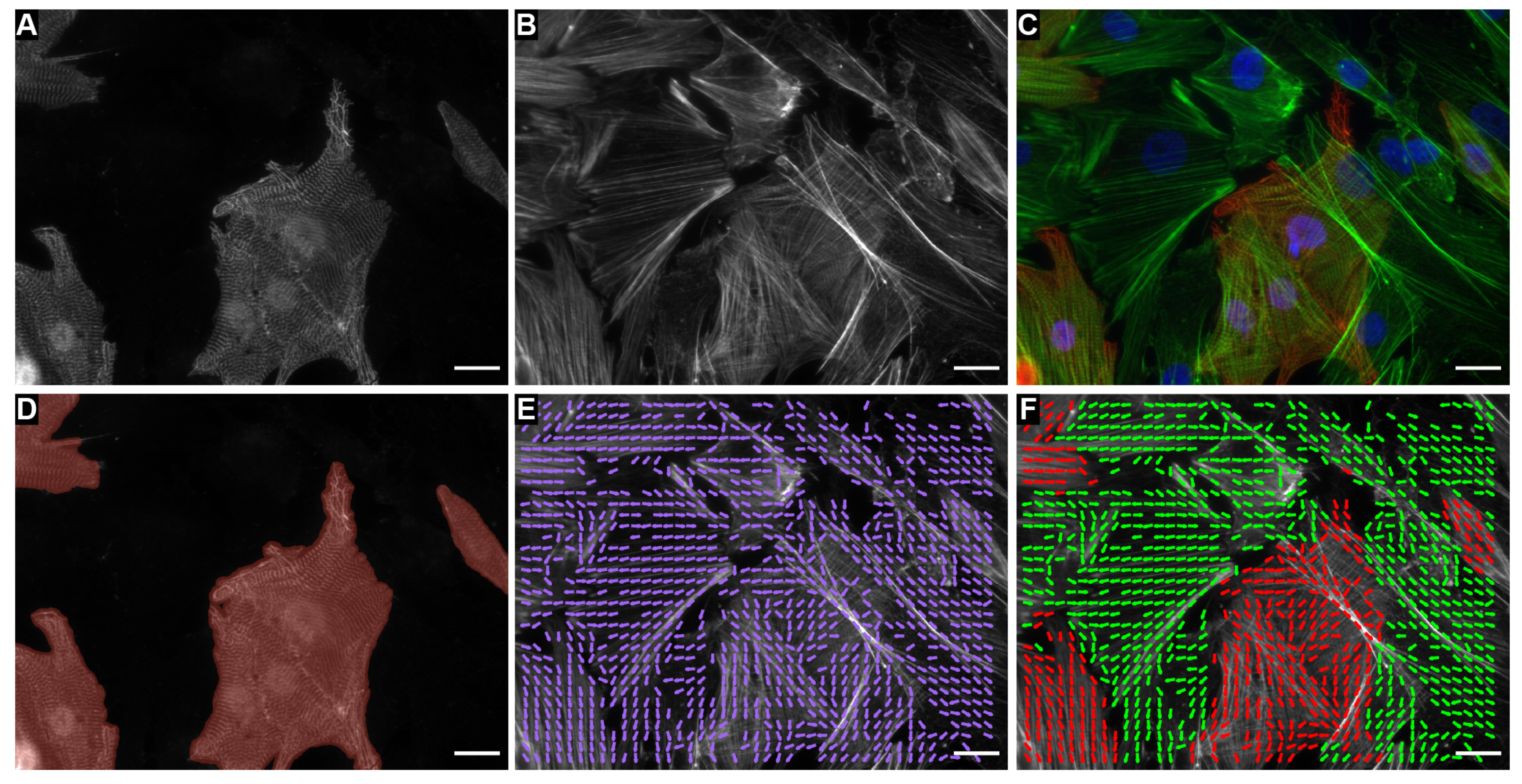
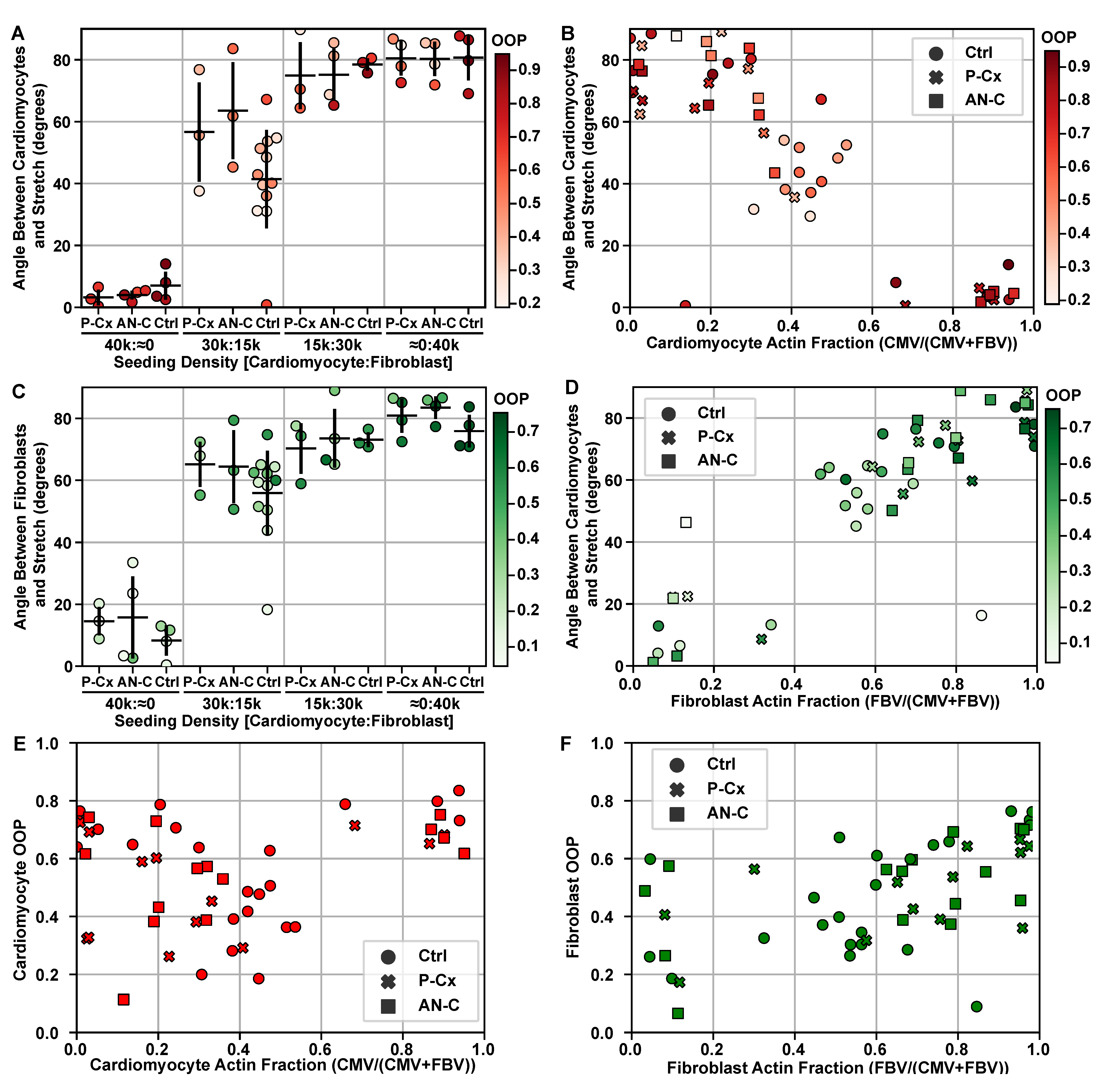
2. Results
3. Discussion
4. Materials and Methods
4.1. Cardiomyocyte and Fibroblast Harvest
4.2. Stretcher Experiments
4.3. Inhibiting Intercellular Junctions
4.4. Fixing and Immunofluorescent Staining
4.5. Imaging and Data Acquisition
4.6. Western Blotting
4.7. Statistical Analysis
4.8. Log-Normal Fit
4.9. Image Classification
4.10. Nuclei Segmentation and Cell Type Classification
4.11. Cell Type Orientation Analysis
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| CM:FB Seeding Density | Drug Condition | Sample Size |
|---|---|---|
| 40k:≈0 | P-Cx | 3 |
| 40k:≈0 | AN-C | 4 |
| 40k:≈0 | Ctrl | 4 |
| 40k:10k | Ctrl | 8 |
| 30k:15k | P-Cx | 3 |
| 30k:15k | AN-C | 3 |
| 30k:15k | Ctrl | 12 |
| 15k:30k | P-Cx | 3 |
| 15k:30k | AN-C | 4 |
| 15k:30k | Ctrl | 3 |
| ≈0:40k | P-Cx | 4 |
| ≈0:40k | AN-C | 4 |
| ≈0:40k | Ctrl | 4 |
References
- Knight, M.B.; Grosberg, A.; McCain, M.L. In Vitro Tools for Quantifying Structure—Function Relationships in Cardiac Myocyte Cells and Tissues. In Cardiac Cytoarchitecture; Springer: Berlin, Germany, 2015; pp. 15–39. [Google Scholar]
- Vliegen, H.; Van der Laarse, A.; Cornelisse, C.; Eulderink, F. Myocardial changes in pressure overload-induced left ventricular hypertrophy: A study on tissue composition, polyploidization and multinucleation. Eur. Heart J. 1991, 12, 488–494. [Google Scholar] [CrossRef]
- Banerjee, I.; Fuseler, J.W.; Price, R.L.; Borg, T.K.; Baudino, T.A. Determination of cell types and numbers during cardiac development in the neonatal and adult rat and mouse. Am. J. Physiol.-Heart Circ. Physiol. 2007, 293, H1883–H1891. [Google Scholar] [CrossRef]
- Souders, C.A.; Bowers, S.L.K.; Baudino, T.A. Cardiac Fibroblast The Renaissance Cell. Circ. Res. 2009, 105, 1164–1176. [Google Scholar] [CrossRef] [PubMed]
- Kohl, P.; Camelliti, P. Fibroblast–myocyte connections in the heart. Heart Rhythm. 2012, 9, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Camelliti, P.; Borg, T.K.; Kohl, P. Structural and functional characterisation of cardiac fibroblasts. Cardiovasc. Res. 2005, 65, 40–51. [Google Scholar] [CrossRef]
- Lasher, R.A.; Pahnke, A.Q.; Johnson, J.M.; Sachse, F.B.; Hitchcock, R.W. Electrical stimulation directs engineered cardiac tissue to an age-matched native phenotype. J. Tissue Eng. 2012, 3, 2041731412455354. [Google Scholar] [CrossRef]
- Kohl, P.; Gourdie, R.G. Fibroblast—Myocyte electrotonic coupling: Does it occur in native cardiac tissue? J. Mol. Cell. Cardiol. 2014, 70, 37–46. [Google Scholar] [CrossRef] [PubMed]
- Santos, A.R.M.; Jang, Y.; Son, I.; Kim, J.; Park, Y. Recapitulating cardiac structure and function in vitro from simple to complex engineering. Micromachines 2021, 12, 386. [Google Scholar] [CrossRef]
- Beltrami, C.A.; Finato, N.; Rocco, M.; Feruglio, G.A.; Puricelli, C.; Cigola, E.; Sonnenblick, E.H.; Olivetti, G.; Anversa, P. The cellular basis of dilated cardiomyopathy in humans. J. Mol. Cell. Cardiol. 1995, 27, 291–305. [Google Scholar] [CrossRef]
- Camelliti, P.; Devlin, G.P.; Matthews, K.G.; Kohl, P.; Green, C.R. Spatially and temporally distinct expression of fibroblast connexins after sheep ventricular infarction. Cardiovasc. Res. 2004, 62, 415–425. [Google Scholar] [CrossRef]
- Humeres, C.; Frangogiannis, N.G. Fibroblasts in the infarcted, remodeling, and failing heart. JACC Basic Transl. Sci. 2019, 4, 449–467. [Google Scholar] [CrossRef]
- Chen, W.; Frangogiannis, N.G. Fibroblasts in post-infarction inflammation and cardiac repair. Biochim. Biophys. Acta (BBA)-Mol. Cell Res. 2013, 1833, 945–953. [Google Scholar] [CrossRef]
- Driesen, R.B.; Verheyen, F.K.; Dijkstra, P.; Thoné, F.; Cleutjens, J.P.; Lenders, M.H.; Ramaekers, F.C.; Borgers, M. Structural remodelling of cardiomyocytes in the border zone of infarcted rabbit heart. Mol. Cell. Biochem. 2007, 302. [Google Scholar] [CrossRef]
- Palojoki, E.; Saraste, A.; Eriksson, A.; Pulkki, K.; Kallajoki, M.; Voipio-Pulkki, L.M.; Tikkanen, I. Cardiomyocyte apoptosis and ventricular remodeling after myocardial infarction in rats. Am. J. Physiol.-Heart Circ. Physiol. 2001, 280. [Google Scholar] [CrossRef] [PubMed]
- Noorden, S.V.; Olsen, E.G.; Pearse, A.G. Hypertrophic obstructive cardiomyopathy, a histological, histochemical, and ultrastructural study of biopsy material. Cardiovasc. Res. 1971, 5. [Google Scholar] [CrossRef] [PubMed]
- Ferrans, V.J.; Morrow, A.G.; Roberts, W.C. Myocardial ultrastructure in idiopathic hypertrophic subaortic stenosis. A study of operatively excised left ventricular outflow tract muscle in 14 patients. Circulation 1972, 45. [Google Scholar] [CrossRef]
- Maron, B.J.; Anan, T.J.; Roberts, W.C. Quantitative analysis of the distribution of cardiac muscle cell disorganization in the left ventricular wall of patients with hypertonic cardiomyopathy. Circulation 1981, 63. [Google Scholar] [CrossRef] [PubMed]
- McMahan, S.; Taylor, A.; Copeland, K.M.; Pan, Z.; Liao, J.; Hong, Y. Current advances in biodegradable synthetic polymer based cardiac patches. J. Biomed. Mater. Res. Part A 2020, 108, 972–983. [Google Scholar] [CrossRef] [PubMed]
- Noor, N.; Shapira, A.; Edri, R.; Gal, I.; Wertheim, L.; Dvir, T. 3D Printing of Personalized Thick and Perfusable Cardiac Patches and Hearts. Adv. Sci. 2019, 6. [Google Scholar] [CrossRef] [PubMed]
- Lakshmanan, R.; Krishnan, U.M.; Sethuraman, S. Living cardiac patch: The elixir for cardiac regeneration. Expert Opin. Biol. Ther. 2012, 12, 1623–1640. [Google Scholar] [CrossRef] [PubMed]
- Grosberg, A.; Alford, P.W.; McCain, M.L.; Parker, K.K. Ensembles of engineered cardiac tissues for physiological and pharmacological study: Heart on a chip. Lab Chip 2011, 11, 4165–4173. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Rafatian, N.; Wang, E.Y.; Feric, N.T.; Lai, B.F.; Knee-Walden, E.J.; Backx, P.H.; Radisic, M. Engineering microenvironment for human cardiac tissue assembly in heart-on-a-chip platform. Matrix Biol. 2020, 85–86, 189–204. [Google Scholar] [CrossRef]
- Tran, R.D.; Siemens, M.; Nguyen, C.H.; Ochs, A.R.; Zaragoza, M.V.; Grosberg, A. The Effect of Cyclic Strain on Human Fibroblasts With Lamin A/C Mutations and Its Relation to Heart Disease. J. Biomech. Eng. 2020, 142, 061002. [Google Scholar] [CrossRef] [PubMed]
- Matsuda, T.; Takahashi, K.; Nariai, T.; Ito, T.; Takatani, T.; Fujio, Y.; Azuma, J. N-cadherin-mediated cell adhesion determines the plasticity for cell alignment in response to mechanical stretch in cultured cardiomyocytes. Biochem. Biophys. Res. Commun. 2005, 326, 228–232. [Google Scholar] [CrossRef] [PubMed]
- Salameh, A.; Wustmann, A.; Karl, S.; Blanke, K.; Apel, D.; Rojas-Gomez, D.; Franke, H.; Mohr, F.W.; Janousek, J.; Dhein, S. Cyclic Mechanical Stretch Induces Cardiomyocyte Orientation and Polarization of the Gap Junction Protein Connexin43. Circ. Res. 2010, 106, 1592–1602. [Google Scholar] [CrossRef] [PubMed]
- Greiner, A.M.; Chen, H.; Spatz, J.P.; Kemkemer, R. Cyclic tensile strain controls cell shape and directs actin stress fiber formation and focal adhesion alignment in spreading cells. PLoS ONE 2013, 8, e77328. [Google Scholar]
- Faust, U.; Hampe, N.; Rubner, W.; Kirchgeßner, N.; Safran, S.; Hoffmann, B.; Merkel, R. Cyclic stress at mHz frequencies aligns fibroblasts in direction of zero strain. PLoS ONE 2011, 6. [Google Scholar] [CrossRef]
- Schwarz, U.S.; Safran, S.A. Physics of adherent cells. Rev. Mod. Phys. 2013, 85. [Google Scholar] [CrossRef]
- De, R.; Zemel, A.; Safran, S.A. Do cells sense stress or strain? Measurement of cellular orientation can provide a clue. Biophys. J. 2008, 94, L29–L31. [Google Scholar] [CrossRef]
- De, R.; Safran, S.A. Dynamical theory of active cellular response to external stress. Rev. Mod. Phys 2008, 78. [Google Scholar] [CrossRef]
- Dhein, S.; Schreiber, A.; Steinbach, S.; Apel, D.; Salameh, A.; Schlegel, F.; Kostelka, M.; Dohmen, P.M.; Mohr, F.W. Mechanical control of cell biology. Effects of cyclic mechanical stretch on cardiomyocyte cellular organization. Prog. Biophys. Mol. Biol. 2014, 115, 93–102. [Google Scholar] [CrossRef]
- Zhang, P.; Su, J.; Mende, U. Cross talk between cardiac myocytes and fibroblasts: From multiscale investigative approaches to mechanisms and functional consequences. Am. J. Physiol. Heart Circ. Physiol. 2012, 303, H1385–H1396. [Google Scholar] [CrossRef] [PubMed]
- Vasquez, C.; Mohandas, P.; Louie, K.L.; Benamer, N.; Bapat, A.C.; Morley, G.E. Enhanced fibroblast-myocyte interactions in response to cardiac injury. Circ. Res. 2010, 107. [Google Scholar] [CrossRef] [PubMed]
- Desplantez, T.; Dupont, E.; Severs, N.J.; Weingart, R. Gap junction channels and cardiac impulse propagation. J. Membr. Biol. 2007, 218, 13–28. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Merkel, C.D.; Zeng, X.; Heier, J.A.; Cantrell, P.S.; Sun, M.; Stolz, D.B.; Watkins, S.C.; Yates, N.A.; Kwiatkowski, A.V. The N-cadherin interactome in primary cardiomyocytes as defined using quantitative proximity proteomics. J. Cell Sci. 2019, 132. [Google Scholar] [CrossRef]
- Wu, J.C.; Tsai, R.Y.; Chung, T.H. Role of catenins in the development of gap junctions in rat cardiomyocytes. J. Cell. Biochem. 2003, 88, 823–835. [Google Scholar] [CrossRef] [PubMed]
- Baudino, T.A.; McFadden, A.; Fix, C.; Hastings, J.; Price, R.; Borg, T.K. Cell patterning: Interaction of cardiac myocytes and fibroblasts in three-dimensional culture. Microsc. Microanal. 2008, 14, 117–125. [Google Scholar] [CrossRef]
- Pellman, J.; Zhang, J.; Sheikh, F. Myocyte-fibroblast communication in cardiac fibrosis and arrhythmias: Mechanisms and model systems. J. Mol. Cell. Cardiol. 2016, 94, 22–31. [Google Scholar] [CrossRef]
- Sorensen, C.M.; Salomonsson, M.; Braunstein, T.H.; Nielsen, M.S.; Holstein-Rathlou, N.H. Connexin mimetic peptides fail to inhibit vascular conducted calcium responses in renal arterioles. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2008, 295. [Google Scholar] [CrossRef][Green Version]
- Schajnovitz, A.; Itkin, T.; D’Uva, G.; Kalinkovich, A.; Golan, K.; Ludin, A.; Cohen, D.; Shulman, Z.; Avigdor, A.; Nagler, A.; et al. CXCL12 secretion by bone marrow stromal cells is dependent on cell contact and mediated by connexin-43 and connexin-45 gap junctions. Nat. Immunol. 2011, 12. [Google Scholar] [CrossRef]
- Bray, M.A.; Singh, S.; Han, H.; Davis, C.T.; Borgeson, B.; Hartland, C.; Kost-Alimova, M.; Gustafsdottir, S.M.; Gibson, C.C.; Carpenter, A.E. Cell Painting, a high-content image-based assay for morphological profiling using multiplexed fluorescent dyes. Nat. Protoc. 2016, 11, 1757. [Google Scholar] [CrossRef]
- Held, M.; Schmitz, M.H.; Fischer, B.; Walter, T.; Neumann, B.; Olma, M.H.; Peter, M.; Ellenberg, J.; Gerlich, D.W. CellCognition: Time-resolved phenotype annotation in high-throughput live cell imaging. Nat. Methods 2010, 7, 747. [Google Scholar] [CrossRef]
- Chessel, A. An overview of data science uses in bioimage informatics. Methods 2017, 115, 110–118. [Google Scholar] [CrossRef]
- Sommer, C.; Gerlich, D.W. Machine learning in cell biology—Teaching computers to recognize phenotypes. J. Cell Sci. 2013, 126, 5529–5539. [Google Scholar] [CrossRef]
- Rajaram, S.; Pavie, B.; Wu, L.F.; Altschuler, S.J. PhenoRipper: Software for rapidly profiling microscopy images. Nat. Methods 2012, 9, 635–637. [Google Scholar] [CrossRef] [PubMed]
- Sommer, C.; Straehle, C.N.; Koethe, U.; Hamprecht, F.A. Ilastik: INTERACTIVE Learning and Segmentation Toolkit. In Proceedings of the 2011 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Chicago, IL, USA, 30 March–2 April 2011; pp. 230–233. [Google Scholar] [CrossRef]
- Berg, S.; Kutra, D.; Kroeger, T.; Straehle, C.N.; Kausler, B.X.; Haubold, C.; Schiegg, M.; Ales, J.; Beier, T.; Rudy, M.; et al. Ilastik: Interactive machine learning for (bio) image analysis. Nat. Methods 2019, 16, 1226–1232. [Google Scholar] [CrossRef] [PubMed]
- Grys, B.T.; Lo, D.S.; Sahin, N.; Kraus, O.Z.; Morris, Q.; Boone, C.; Andrews, B.J. Machine learning and computer vision approaches for phenotypic profiling. J. Cell Biol. 2017, 216, 65–71. [Google Scholar] [CrossRef] [PubMed]
- Caicedo, J.C.; Cooper, S.; Heigwer, F.; Warchal, S.; Qiu, P.; Molnar, C.; Vasilevich, A.S.; Barry, J.D.; Bansal, H.S.; Kraus, O.; et al. Data-analysis strategies for image-based cell profiling. Nat. Methods 2017, 14, 849–863. [Google Scholar] [CrossRef]
- Zhou, J.; Lamichhane, S.; Sterne, G.; Ye, B.; Peng, H. BIOCAT: A pattern recognition platform for customizable biological image classification and annotation. BMC Bioinform. 2013, 14, 1–14. [Google Scholar] [CrossRef]
- Sanger, J.W.; Ayoob, J.C.; Chowrashi, P.; Zurawski, D.; Sanger, J.M. Assembly of myofibrils in cardiac muscle cells. In Elastic Filaments of the Cell; Springer: Berlin, Germany, 2000; pp. 89–110. [Google Scholar]
- Morris, T.A.; Naik, J.; Fibben, K.S.; Kong, X.; Kiyono, T.; Yokomori, K.; Grosberg, A. Striated myocyte structural integrity: Automated analysis of sarcomeric z-discs. PLoS Comput. Biol. 2020, 16, e1007676. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef]
- Zhou, P.; Pu, W.T. Recounting cardiac cellular composition. Circ. Res. 2016, 118, 368–370. [Google Scholar] [CrossRef] [PubMed]
- LeGrice, I.J.; Smaill, B.H.; Chai, L.Z.; Edgar, S.G.; Gavin, J.B.; Hunter, P.J. Laminar structure of the heart: Ventricular myocyte arrangement and connective tissue architecture in the dog. Am. J. Physiol.-Heart Circ. Physiol. 1995, 269. [Google Scholar] [CrossRef] [PubMed]
- LeGrice, I.J.; Hunter, P.J.; Smaill, B.H. Laminar structure of the heart: A mathematical model. Am. J. Physiol.-Heart Circ. Physiol. 1997, 272. [Google Scholar] [CrossRef] [PubMed]
- Robinson, T.F.; Geraci, M.A.; Sonnenblick, E.H.; Factor, S.M. Coiled perimysial fibers of papillary muscle in rat heart: Morphology, distribution, and changes in configuration. Circ. Res. 1988, 63. [Google Scholar] [CrossRef]
- Anderson, R.H.; Razavi, R.; Taylor, A.M. Cardiac anatomy revisited. J. Anat. 2004, 205, 159–177. [Google Scholar] [CrossRef]
- Shinde, A.V.; Frangogiannis, N.G. Fibroblasts in myocardial infarction: A role in inflammation and repair. J. Mol. Cell. Cardiol. 2014, 70, 74–82. [Google Scholar] [CrossRef]
- Lin, X.; Gemel, J.; Glass, A.; Zemlin, C.W.; Beyer, E.C.; Veenstra, R.D. Connexin40 and connexin43 determine gating properties of atrial gap junction channels. J. Mol. Cell. Cardiol. 2010, 48. [Google Scholar] [CrossRef]
- Salameh, A.; Blanke, K.; Daehnert, I. Role of connexins in human congenital heart disease: The chicken and egg problem. Front. Pharmacol. 2013, 4, 70. [Google Scholar] [CrossRef]
- Li, C.; Meng, Q.; Yu, X.; Jing, X.; Xu, P.; Luo, D. Regulatory effect of connexin 43 on basal Ca2+ signaling in rat ventricular myocytes. PLoS ONE 2012, 7. [Google Scholar] [CrossRef]
- Faniku, C.; O’Shaughnessy, E.; Lorraine, C.; Johnstone, S.R.; Graham, A.; Greenhough, S.; Martin, P.E. The connexin mimetic peptide Gap27 and Cx43-knockdown reveal differential roles for connexin43 in wound closure events in skin model systems. Int. J. Mol. Sci. 2018, 19, 604. [Google Scholar] [CrossRef] [PubMed]
- Hurlburt, H.M.; Aurigemma, G.P.; Hill, J.C.; Narayanan, A.; Gaasch, W.H.; Vinch, C.S.; Meyer, T.E.; Tighe, D.A. Direct ultrasound measurement of longitudinal, circumferential, and radial strain using 2-dimensional strain imaging in normal adults. Echocardiography 2007, 24, 723–731. [Google Scholar] [CrossRef] [PubMed]
- Ng, A.C.; Delgado, V.; Bertini, M.; van der Meer, R.W.; Rijzewijk, L.J.; Shanks, M.; Nucifora, G.; Smit, J.W.; Diamant, M.; Romijn, J.A.; et al. Findings from left ventricular strain and strain rate imaging in asymptomatic patients with type 2 diabetes mellitus. Am. J. Cardiol. 2009, 104, 1398–1401. [Google Scholar] [CrossRef]
- Gjesdal, O.; Hopp, E.; Vartdal, T.; Lunde, K.; Helle-Valle, T.; Aakhus, S.; Smith, H.J.; Ihlen, H.; Edvardsen, T. Global longitudinal strain measured by two-dimensional speckle tracking echocardiography is closely related to myocardial infarct size in chronic ischaemic heart disease. Clin. Sci. 2007, 113, 287–296. [Google Scholar] [CrossRef]
- Kouzu, H.; Yuda, S.; Muranaka, A.; Doi, T.; Yamamoto, H.; Shimoshige, S.; Hase, M.; Hashimoto, A.; Saitoh, S.; Tsuchihashi, K.; et al. Left ventricular hypertrophy causes different changes in longitudinal, radial, and circumferential mechanics in patients with hypertension: A two-dimensional speckle tracking study. J. Am. Soc. Echocardiogr. 2011, 24, 192–199. [Google Scholar] [CrossRef] [PubMed]
- Serri, K.; Reant, P.; Lafitte, M.; Berhouet, M.; Le Bouffos, V.; Roudaut, R.; Lafitte, S. Global and regional myocardial function quantification by two-dimensional strain: Application in hypertrophic cardiomyopathy. J. Am. Coll. Cardiol. 2006, 47, 1175–1181. [Google Scholar] [CrossRef]
- Wang, J.; Khoury, D.S.; Yue, Y.; Torre-Amione, G.; Nagueh, S.F. Preserved left ventricular twist and circumferential deformation, but depressed longitudinal and radial deformation in patients with diastolic heart failure. Eur. Heart J. 2008, 29, 1283–1289. [Google Scholar] [CrossRef]
- Waldman, L.K.; Fung, Y.; Covell, J.W. Transmural myocardial deformation in the canine left ventricle. Normal in vivo three-dimensional finite strains. Circ. Res. 1985, 57, 152–163. [Google Scholar] [CrossRef]
- Kasner, M.; Gaub, R.; Sinning, D.; Westermann, D.; Steendijk, P.; Hoffmann, W.; Schultheiss, H.P.; Tschöpe, C. Global strain rate imaging for the estimation of diastolic function in HFNEF compared with pressure–volume loop analysis. Eur. J. Echocardiogr. 2010, 11, 743–751. [Google Scholar] [CrossRef][Green Version]
- Leitman, M.; Lysyansky, P.; Sidenko, S.; Shir, V.; Peleg, E.; Binenbaum, M.; Kaluski, E.; Krakover, R.; Vered, Z. Two-dimensional strain—A novel software for real-time quantitative echocardiographic assessment of myocardial function. J. Am. Soc. Echocardiogr. 2004, 17, 1021–1029. [Google Scholar] [CrossRef]
- Grosberg, A.; Kuo, P.L.; Guo, C.L.; Geisse, N.A.; Bray, M.A.; Adams, W.J.; Sheehy, S.P.; Parker, K.K. Self-organization of muscle cell structure and function. PLoS Comput. Biol. 2011, 7, e1001088. [Google Scholar] [CrossRef] [PubMed]
- Drew, N.K.; Eagleson, M.A.; Baldo, D.B., Jr.; Parker, K.K.; Grosberg, A. Metrics for assessing cytoskeletal orientational correlations and consistency. PLoS Comput. Biol. 2015, 11, e1004190. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Drew, N.K.; Johnsen, N.E.; Core, J.Q.; Grosberg, A. Multiscale Characterization of Engineered Cardiac Tissue Architecture. J. Biomech. Eng. 2016, 138, 111003. [Google Scholar] [CrossRef] [PubMed]
- Knight, M.B.; Drew, N.K.; McCarthy, L.A.; Grosberg, A. Emergent global contractile force in cardiac tissues. Biophys. J. 2016, 110, 1615–1624. [Google Scholar] [CrossRef]
- Meli, V.S.; Atcha, H.; Veerasubramanian, P.K.; Nagalla, R.R.; Luu, T.U.; Chen, E.Y.; Guerrero-Juarez, C.F.; Yamaga, K.; Pandori, W.; Hsieh, J.Y.; et al. YAP-mediated mechanotransduction tunes the macrophage inflammatory response. Sci. Adv. 2020, 6. [Google Scholar] [CrossRef] [PubMed]
- Atcha, H.; Jairaman, A.; Holt, J.R.; Meli, V.S.; Nagalla, R.R.; Veerasubramanian, P.K.; Brumm, K.T.; Lim, H.E.; Othy, S.; Cahalan, M.D.; et al. Mechanically activated ion channel Piezo1 modulates macrophage polarization and stiffness sensing. Nat. Commun. 2021, 12. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC superpixels compared to state-of-the-art superpixel methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef] [PubMed]
- Persson, N.E.; McBride, M.A.; Grover, M.A.; Reichmanis, E. Automated analysis of orientational order in images of fibrillar materials. Chem. Mater. 2016, 29, 3–14. [Google Scholar] [CrossRef]
- Weickert, J. Coherence-enhancing diffusion filtering. Int. J. Comput. Vis. 1999, 31, 111–127. [Google Scholar] [CrossRef]
- Perona, P.; Malik, J. Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 629–639. [Google Scholar] [CrossRef]
- Kroon, D.; Slump, C.H. Coherence filtering to enhance the mandibular canal in cone-beam CT data. In Proceedings of the IEEE-EMBS Benelux Chapter Symposium, Leuven, Belgium, 28–29 November 2009; Volume 11, pp. 40–41. [Google Scholar]
- Schmidt, U.; Weigert, M.; Broaddus, C.; Myers, G. Cell detection with star-convex polygons. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin, Germany, 2018; pp. 265–273. [Google Scholar]
- Feinberg, A.W.; Alford, P.W.; Jin, H.; Ripplinger, C.M.; Werdich, A.A.; Sheehy, S.P.; Grosberg, A.; Parker, K.K. Controlling the contractile strength of engineered cardiac muscle by hierarchal tissue architecture. Biomaterials 2012, 33, 5732–5741. [Google Scholar] [CrossRef] [PubMed]
- Kovesi, P.D. MATLAB and Octave Functions for Computer Vision and Image Processing. 2000. Available online: http://www.peterkovesi.com/matlabfns/ (accessed on 31 January 2021).
- Hong, L.; Wan, Y.; Jain, A. Fingerprint image enhancement: Algorithm and performance evaluation. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 777–789. [Google Scholar] [CrossRef]
- Umeno, A.; Kotani, H.; Iwasaka, M.; Ueno, S. Quantification of adherent cell orientation and morphology under strong magnetic fields. IEEE Trans. Magn. 2001, 37, 2909–2911. [Google Scholar] [CrossRef]
- Meier, G.; Saupe, A. Dielectric relaxation in nematic liquid crystals. Mol. Cryst. Liq. Cryst. 1966, 1, 515–525. [Google Scholar] [CrossRef]
- Chaikin, P.M.; Lubensky, T.C.; Witten, T.A. Principles of Condensed Matter Physics; Cambridge University Press: Cambridge, UK, 1995; Volume 10. [Google Scholar]


| Class | α-Actinin Description | Actin Description |
|---|---|---|
| Fibroblast | no α-actinin | actin fibrils |
| Striated Myocyte | α-actinin sarcomere striations | actin fibrils |
| Other | α-actinin, but no sarcomere striations | actin fibrils |
| Background | no α-actinin | no actin fibrils |
| CM:FB Seeding Ratio | Description | Relevance |
|---|---|---|
| ≈0:1 | Fibroblast dominant | Recapitulate published results |
| 1:2 | Fibroblast dominant | Intermediate; beginning of injury/inflammation |
| 2:1 | Cardiomyocyte dominant | Physiologically relevant |
| 4:1 | Cardiomyocyte dominant | Rare fibroblast |
| 1:≈0 | Cardiomyocyte dominant | Recapitulate published results |
| Variable | Description or Coefficient | Significance |
|---|---|---|
| x | Cardiomyocyte actin fraction | N/A |
| y | Cardiomyocyte OOP | N/A |
| a | −0.1605 | <0.0001 |
| b | 0.3504 | 0.0006 |
| 0.4334 | <0.0001 | |
| 0.7437 | <0.0001 | |
| 0.5554 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, R.D.H.; Morris, T.A.; Gonzalez, D.; Hetta, A.H.S.H.A.; Grosberg, A. Quantitative Evaluation of Cardiac Cell Interactions and Responses to Cyclic Strain. Cells 2021, 10, 3199. https://doi.org/10.3390/cells10113199
Tran RDH, Morris TA, Gonzalez D, Hetta AHSHA, Grosberg A. Quantitative Evaluation of Cardiac Cell Interactions and Responses to Cyclic Strain. Cells. 2021; 10(11):3199. https://doi.org/10.3390/cells10113199
Chicago/Turabian StyleTran, Richard Duc Hien, Tessa Altair Morris, Daniela Gonzalez, Ali Hatem Salaheldin Hassan Ahmed Hetta, and Anna Grosberg. 2021. "Quantitative Evaluation of Cardiac Cell Interactions and Responses to Cyclic Strain" Cells 10, no. 11: 3199. https://doi.org/10.3390/cells10113199
APA StyleTran, R. D. H., Morris, T. A., Gonzalez, D., Hetta, A. H. S. H. A., & Grosberg, A. (2021). Quantitative Evaluation of Cardiac Cell Interactions and Responses to Cyclic Strain. Cells, 10(11), 3199. https://doi.org/10.3390/cells10113199





