Effects of Quantitative Ordinal Scale Design on the Accuracy of Estimates of Mean Disease Severity

Abstract

Estimates of plant disease severity are crucial to various practical and research-related needs in agriculture. Ordinal scales are used for categorizing severity into ordered classes. Certain characteristics of quantitative ordinal scale design may affect the accuracy of the specimen estimates and, consequently, affect the accuracy of the resulting mean disease severity for the sample. The aim of this study was to compare mean estimates based on various quantitative ordinal scale designs to the nearest percent estimates, and to investigate the effect of the number of classes in an ordinal scale on the accuracy of that mean. A simulation method was employed. The criterion for comparison was the mean squared error of the mean disease severity for each of the different scale designs used. The results indicate that scales with seven or more classes are preferable when actual mean disease severities of 50% or less are involved. Moreover, use of an amended 10% quantitative ordinal scale with additional classes at low severities resulted in a more accurate mean severity compared to most other scale designs at most mean disease severities. To further verify the simulation results, estimates of mean severity of pear scab on samples of leaves from orchards in Taiwan demonstrated similar results. These observations contribute to the development of plant disease assessment scales to improve the accuracy of estimates of mean disease severities.

1. Introduction

In agricultural research, estimates of disease severity are needed to understand and predict yield loss due to disease, for monitoring and forecasting epidemics, for comparing treatments or genotypes for disease resistance, and so on. Accuracy of the mean disease severity is critical in these studies to ensure there is no failure of analysis [1]. Here, accuracy refers to the deviation between the true value of a quantity (in this case, the actual mean disease severity) and estimates of that value based on the sampling process [2]. The reliability (or precision) of this mean estimate is the extent of the deviations occurring when the mean severity is repeatedly estimated using the same sampling process. The definition of the mean accuracy should not be confused with the definition of accuracy used in measurement science and as applied to estimates of disease severity on individual specimens—where accuracy can be defined as the degree of closeness of estimated or measured severity to a recognized actual value [2,3].

When estimated visually, plant disease severity can be defined as the proportion of symptoms and/or signs of the disease at the scale of a plant organ, a plant, a field plot, or more rarely a field [2]. During visual severity estimation, an individual will assign a disease severity score to a specimen using one of several rating scales [4]. A special type of ordinal scale, a quantitative ordinal scale, which comprises a number of intervals of known numeric ranges, is commonly used when estimating plant disease severity. The intervals are most often based on the percent area with symptoms. The most widely used quantitative ordinal scale is the Horsfall-Barratt (HB) scale which divides the percent scale into 12 consecutive, logarithmically increasing (from 0 to 50% severity), and then decreasing intervals (from 50% to 100% severity) numbered 1 to 12, where 1 = 0, 2 = 0⁺–3, 3 = 3⁺–6, 4 = 6⁺–12, 5 = 12⁺–25, 6 = 25⁺–50, 7 = 50⁺–75, 8 = 75⁺–88, 9 = 88⁺–94, 10 = 94⁺–97, 11 = 97⁺–100, and 12 = 100% disease [5]. Several other similar scales have been developed that subdivide the percent scale into different numbers of intervals and interval sizes [6,7,8,9,10,11,12,13]. For subsequent data analysis, it is recommended that the mid-point of the scale interval be used if applying parametric methods [2,14], although the ordinal ratings may be analyzed directly if non-parametric methods are used [14].

Nutter and Esker [15] demonstrated the barely noticeable difference in the ability to differentiate two severities between 25 and 50%. Due to the resolution of many ordinal scales in this range, accurate estimates of severity using the 0–100% ratio scale (i.e., nearest percent estimate, NPE) are almost always going to be more informative compared with those from an ordinal scale [16], but the latter has the perceived advantage of being easier for raters to learn, and quicker and cheaper to implement. However, due to the structure of some ordinal scales, additional variability may be added into the samples [17]. This is because certain characteristics of quantitative ordinal scale design might cause the information to be distorted in the process of transforming NPE data into ordinal disease severity scores. To what extent is the information distorted, and what impact does it have on the accuracy of the mean value and variance of the sample mean? If the distortion is severe, it will result in inaccurate mean estimates. The consequence of inaccurate estimates of mean disease severity could be misleading when the estimates are used as predictors of crop loss, or for other decision-making purposes [2]. This issue must be understood before steps can be taken for practitioners in plant pathology to optimize the designs of ordinal scales in situations where the scales are preferred. Furthermore, an incorrect scale rating for a specimen estimate can exacerbate the inaccuracy [18].

The number of classes in an ordinal scale has been discussed by Kranz [19,20] and Hau et al. [21] in relation to scales with unequal-sized categories. Kranz [19] suggested that about seven classes were optimal. Furthermore, the underlying distribution of severities may have ramifications for the number of classes needed on a scale to accurately estimate the mean disease severity [21]. Kranz [22] believed that the maximum likely severity to be encountered should be considered, and the scale set accordingly. However, these studies neither compared these interval-scale estimates to nearest percent estimates (NPEs), nor did they investigate the effects of sample size on the accuracy of the resulting mean estimate of severity.

Several studies have compared different scales for their accuracy, precision, agreement, and reliability of disease severity estimates [23,24,25,26]. The studies demonstrate that estimates of disease severity using the HB scale are less precise compared to NPEs using the 0–100% ratio scale. Nita et al. [26] reported that estimates using a 5% increment scale were closer to NPE estimates compared to those estimates using the HB scale. They recommended using an equal-interval scale for estimating disease severity rather than the unequal-interval HB scale, at least where the use of a disease scale is preferred. Madden et al. [2] and Nutter and Esker [15] contend that equal-increment scales may be preferable to the HB scale. An advantage of equal-sized ordinal scales is that they can be treated as continuous data. However, to ensure accuracy of estimates of specimens with severity <10%, Bock et al. [4] suggested that even equal-interval ordinal scales should be designed to accommodate severities at the low end of the spectrum to minimize overestimation of low mean severities.

Several studies have used simulation modeling to compare ordinal and other scale types to study aspects of disease assessment. Hartung and Piepho [16] evaluated three different rating scales regarding the accuracy, precision, and time needed for scoring. Chiang et al. [27] explored issue related to the use of the disease severity index (DSI) on accuracy. The objective of these studies was to determine which assessment method was most accurate. Besides investigating the accuracy and precision of disease severity estimates, some studies have explored the impact of the relative values resulting from different rating scales using hypothesis testing [14,17,28,29,30]. The criteria used to compare rating scales was the power of the hypothesis test for comparing treatment means using simulated rater estimates relative to the means based on actual data. Chiang et al. [17] showed that linear quantitative ordinal scales with 5%–10% intervals and additional classes at lower severity appear to be equivalent to NPEs for hypothesis testing. Also, intervals in the mid-range not exceeding 10% was recommended. Furthermore, if there are too many classes, the assumed advantages of speed and simplicity offered by the scale will be lost. Thus, it was suggested that a 10% (not 5%) linear quantitative ordinal scale with sensitivity to low disease severity is preferable to a non-linear ordinal scales (e.g., HB scale) for assessing disease severity.

Few studies have determined scale characteristics that maximize the accuracy of estimates of mean disease severity. The purpose of this study is to compare various ordinal scales to the 0 to 100% ratio scale and explore the effect of the number of classes in an ordinal scale on the accuracy of the mean estimate. To determine the accuracy of the mean, we used the mean squared error (MSE) of the mean disease severity estimates for each scales type, applying a simulation approach as described by Hartung and Piepho [16] and Chiang et al. [27]. To validate these results, we assessed the severity of pear scab (caused by Venturia nashicola Tanaka & Yamamoto) in 6 pear orchards in Taiwan. Pear scab is a particularly destructive disease of pear in Taiwan and elsewhere [31,32,33,34]. Specifically, we asked the following questions, (i) What is the effect of equal or unequal intervals on the mean estimate? (ii) How does interval width affect the mean estimate? (iii) What is the optimal number of classes in a quantitative ordinal scale to maximize the accuracy of the mean? Finally, we used these results to develop a more accurate assessment scale for assessing the severity of pear scab.

2. Materials and Methods

2.1. Assessment Methods

We adopted a two-stage approach to explore the effects of ordinal scale structure (linear or non-linear) and class number on accuracy and imprecision. The scales used in the first stage to explore scale structure are as follows:

1. NPE: disease severity estimated by the raters to the nearest 1%.

2. HB: non-linear, unequal intervals with 12 categories: 0, 0⁺–3, 3⁺–6, 6⁺–12, 12⁺–25, 25⁺–50, 50⁺–75, 75⁺–88, 88⁺–94, 94⁺–97, 97⁺–99% and 100% [5].

3. EI10: a linear, 10-class 10% interval scale with equal intervals from 0% to 100%.

4. AM10: an amended linear 10% interval scale with 10 classes emphasizing low severities: 0, 0⁺–1, 1⁺–4, 4⁺–10, 10⁺–20, 20⁺–30, 30⁺–40, 40⁺–50, 50⁺–70, 70⁺–100% disease) [17]. Here, only severities <50% were emphasized because leaves often abscise if the disease becomes too severe, making it difficult to obtain samples with severity >50% [22]. Thus, only two classes (50⁺–70, 70⁺–100% disease) account for severities ≥50% for assessment in methods 4 through 7.

The scales used in the second stage to explore the effect number of classes are as follows:

5. AM20: AM10 but with 20% linear intervals for disease severities 10% to 50% (with 8 classes: 0, 0⁺–1, 1⁺–4, 4⁺–10, 10⁺–30, 30⁺–50, 50⁺–70, 70⁺–100% disease).

6. AM5: AM10 but with 5% intervals for disease severities 10% to 50% with 14 classes: 0, 0⁺–1, 1⁺–4, 4⁺–10, 10⁺–15, 15⁺–20, 20⁺–25, 25⁺–30, 30⁺–35, 35⁺–40, 40⁺–45, 45⁺–50, 50⁺–70, 70⁺–100% disease).

7. AM10f: AM10 but finer intervals at ≤10% disease with 11 classes: 0, 0⁺–1, 1⁺–3, 3⁺–6, 6⁺–10, 10⁺–20, 20⁺–30, 30⁺–40, 40⁺–50, 50⁺–70, 70⁺–100% disease).

2.2. Simulation Method

To obtain specimen estimates of disease severity, the simulation was performed according to a positively skewed beta-distribution. A beta-distribution, defining the distribution of a random variable on the closed unit interval 0–1 is commonly used for a proportion and can be made very flexible by choosing different shape parameters (α and β) [35,36,37]. In this study, the means (α/(α + β)) of the random variables of the beta-distributions (given the two chosen parameters: α and β) were set at 1%, 5%, 10%, 20%, 30%, and 40% severities to demonstrate a range of possible “actual” mean disease severities (%). Furthermore, we selected three different variance parameter settings (representing situations of large, medium, and small sample variation) for the fixed means to illustrate the effects of the variance between estimates with the different assessment methods (Figure 1).

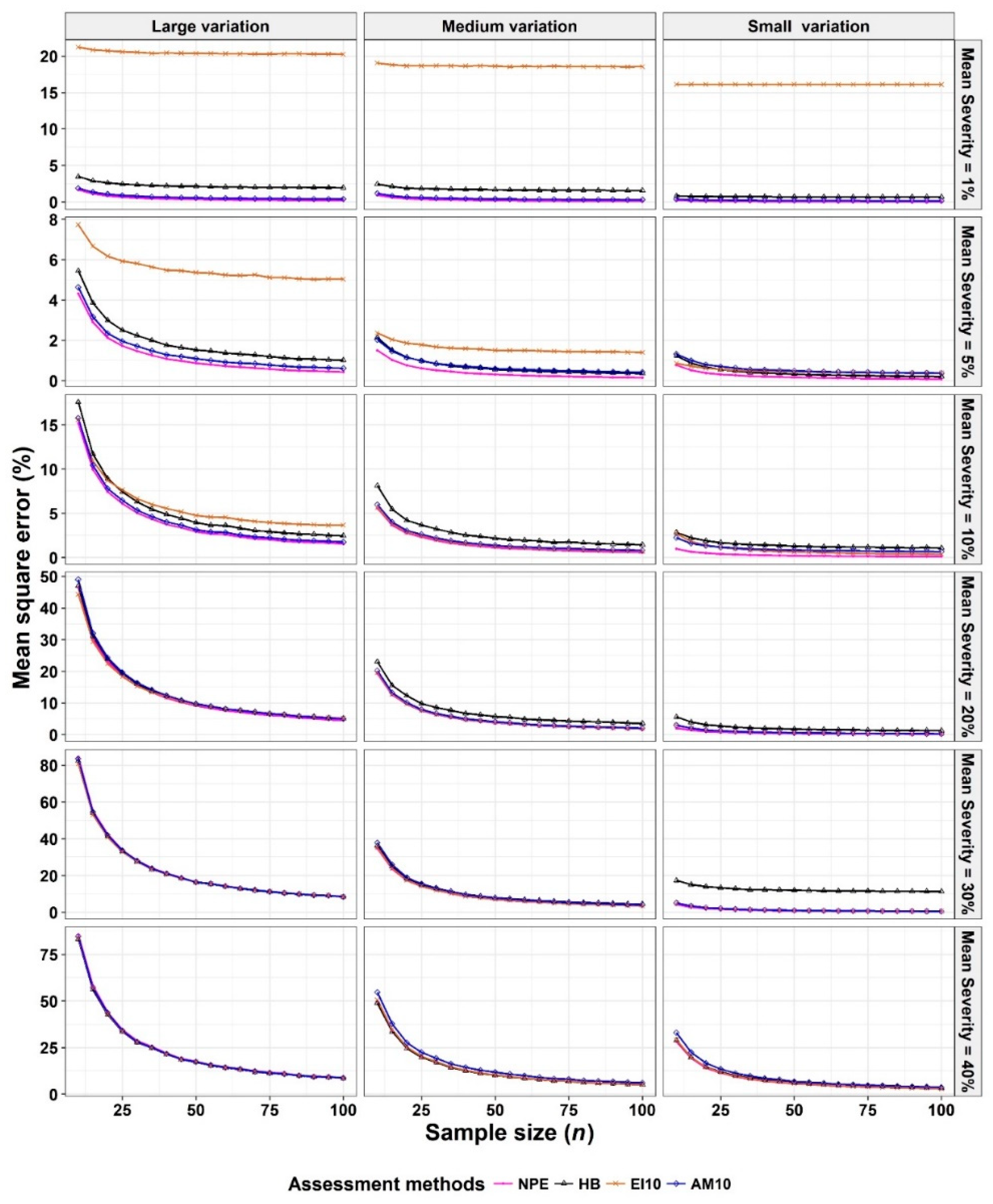
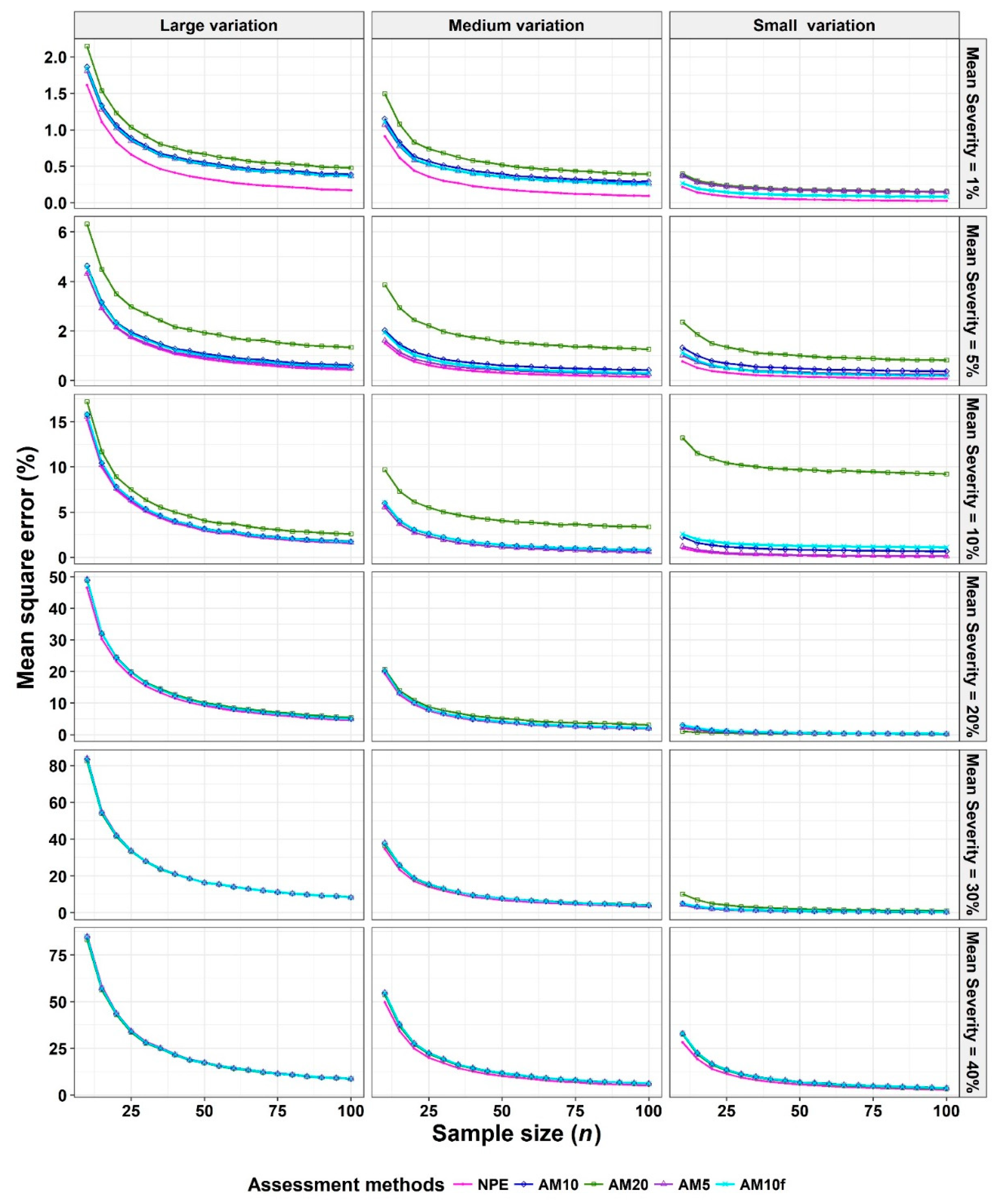
2.3. Criterion for Comparison: Mean Squared Error (MSE)

The MSE takes into account both the variance (precision) and the bias (accuracy) of a mean severity, so it provides a useful method for comparing several assessment scales [38]. The MSE is calculated as follows:

$$\mathrm{MSE}\left(\overline{X}\right)=E{\left(\overline{X}-\mu \right)}^2=\mathrm{Variance}\left(\overline{X}\right)+{\left[\mathrm{Bias}\left(\overline{X}\right)\right]}^2$$

(1)

where μ is a population mean; E is, an average, a mathematical EXPECTATION (each amount is multiplied by the corresponding probability). $\overline{X}$ represents the average disease severity of the specimens.

$$\mathrm{Variance}\left(\overline{X}\right)=\frac{\mathrm{Variance}\left(X\right)}{n}$$

(2)

where $\mathrm{Variance}\left(\overline{X}\right)$ is the variance of the sampling distribution of $\overline{X}$; and its square root is the standard error of the mean severity. Here, $\mathrm{Bias}\left(\overline{X}\right)$ was used to investigate the effects of bias (over and underestimates) in estimates of the mean disease severities.

$$\mathrm{Bias}\left(\overline{X}\right)=E\left(\overline{X}\right)-\mu$$

(3)

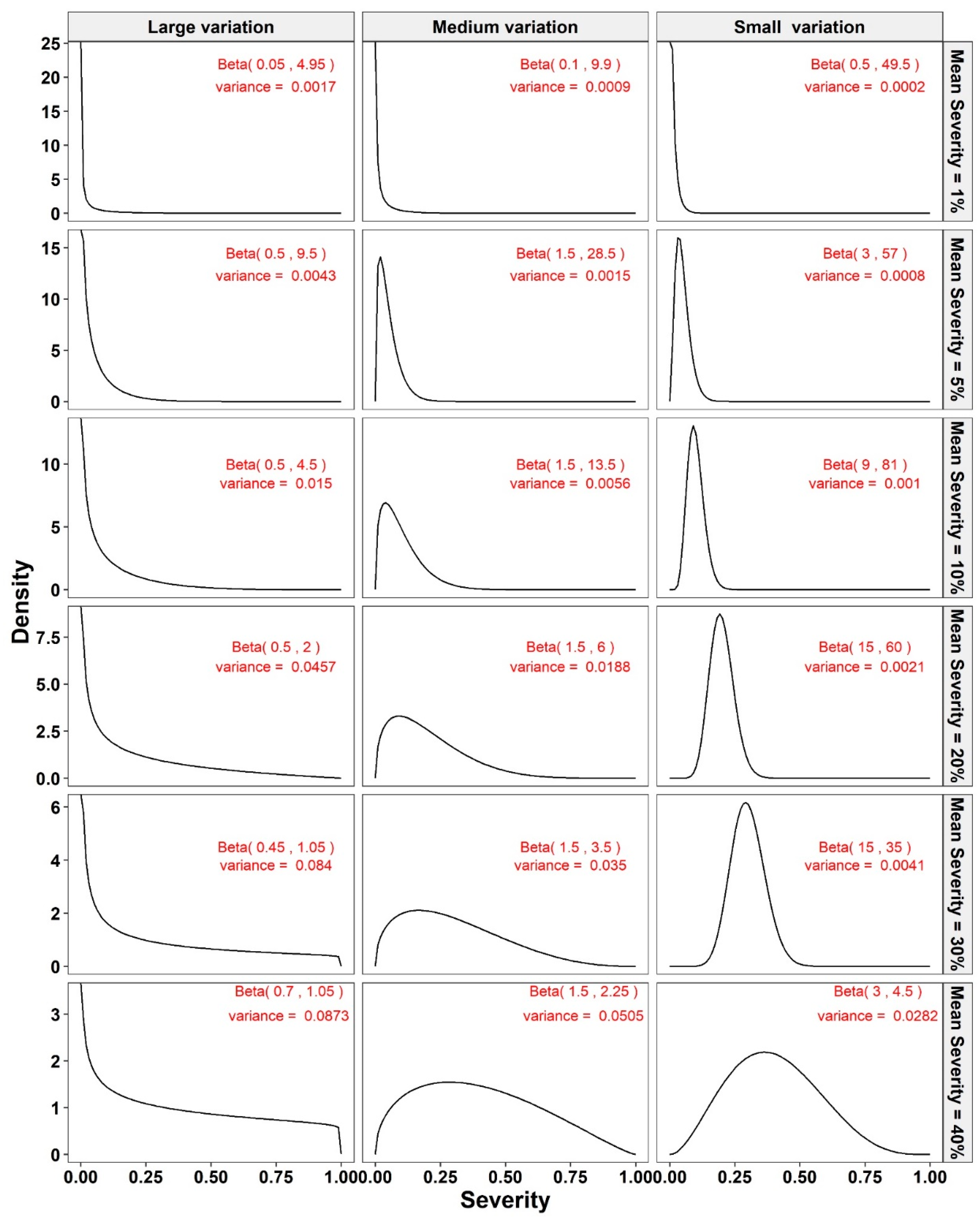
2.4. Simulation Framework

The simulation steps are as follows:

• We simulated n sample size values (from 10 to 100 in increments of 5) from a beta-distribution with the preselected specific mean severity and variance for that sample (which might represent a plot in a field). These n simulated values on the continuous percentage scale, defined by the beta distribution of a random variable on the closed unit interval 0–1, represent the NPEs.
• The resulting NPEs were converted to the appropriate classes for assessment methods 2–7. These scale data were subsequently converted to the appropriate midpoint value of each class for subsequent analysis [2].
• The MSEs of mean disease severity estimates for each of the different scales were calculated (Equation (1)).
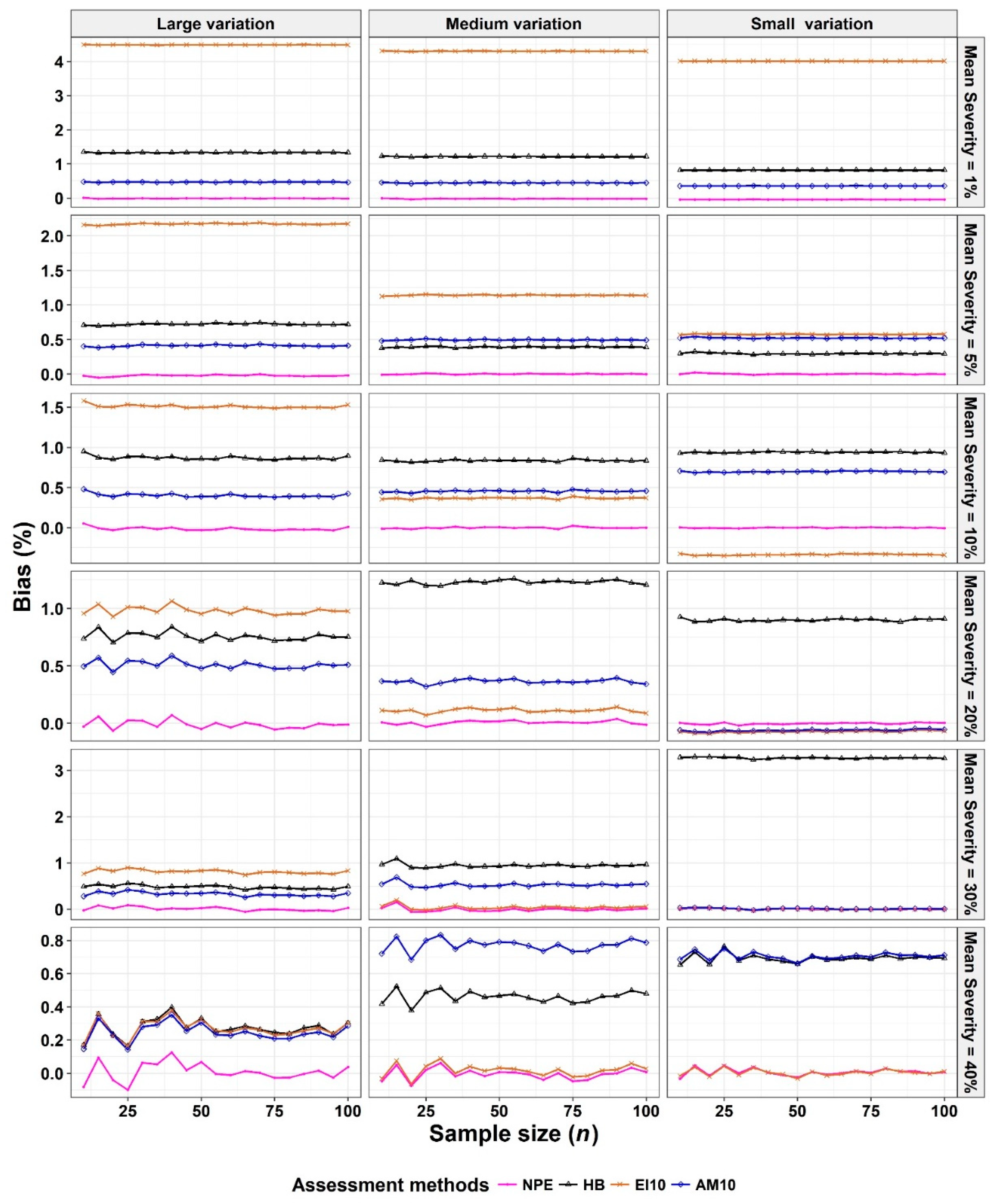
• The corresponding variances and biases were calculated (equations 2 and 3, respectively).
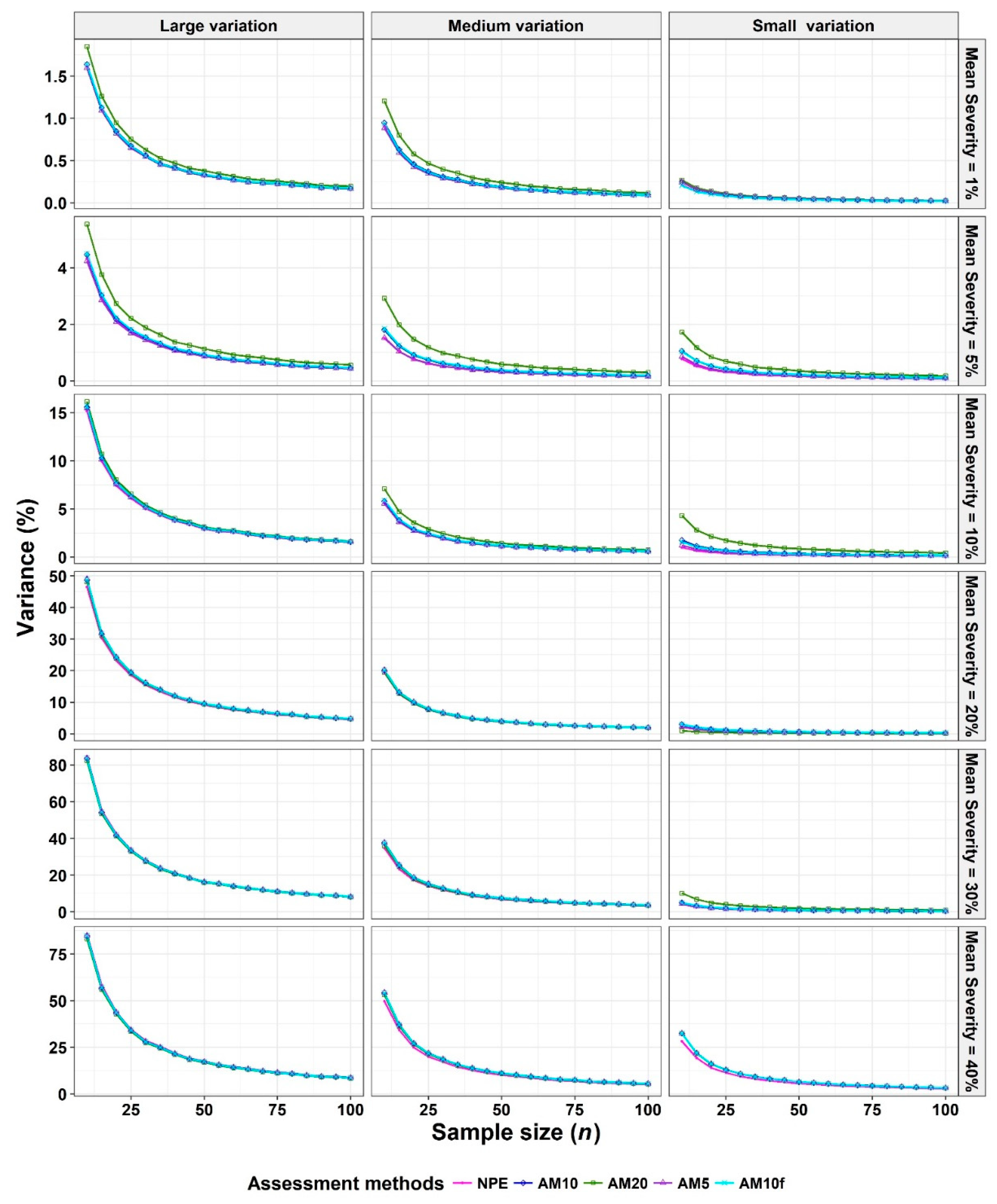
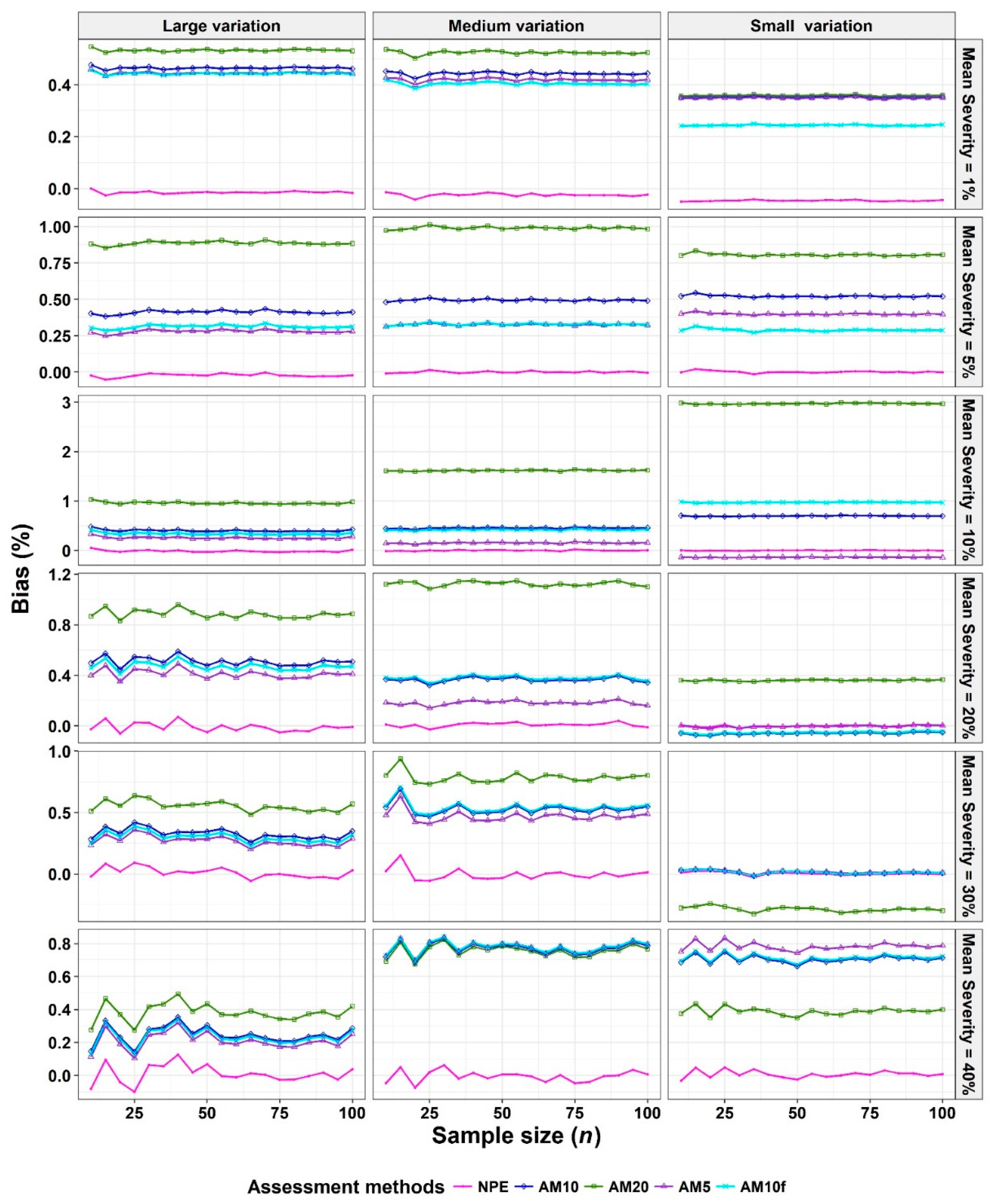
• The Monte Carlo simulation process was repeated 10,000 times. To present the results comparing assessment methods, we plot MSEs (or variance or bias) on the y-axis against sample size values (from n = 10 to 100 in n = 5 increments) on the x-axis at each of a range of “actual” mean disease severities (1%, 5%, 10%, 20%, 30%, and 40% [6 mean disease severities]) and disease severity variances (representing large, medium, and small variation [3 variances]). Thus, the results are presented in a montage (a 6 × 3 array of figures). For example, R1C2 (chart in row 1, column 2) indicates the chart in the second column in the first row, and presents the relationships between the MSE, variance, or bias of the mean disease severity estimates and sample size (n) for each of the different scales used, at an “actual” mean disease severity of 1%, and the medium variation.

2.5. Pear scab Assessment

Leaves of pear with scab were collected from six orchards in Dongshi District, Taichung County in Taiwan from September–November 2018. The data sets consist of 658, 389, 269, 453, 209, and 244 diseased leaves. Images of the leaves were captured with a digital camera (Sony CyberShot DSC-F717, 5.0 megapixels; SONY Corporation, Tokyo, Japan), and the area with symptoms of scab on each leaf was measured using Assess© V2.0 (APS Press, Image Analysis Software for Plant Disease Quantification) [39] to obtain “actual” values of the disease severities. Subsequently, we used the data sets to gauge the performance of the different quantitative ordinal scales described in order to assess the accuracy of estimates of mean disease severity. The procedures used were the same as described for the previous simulation steps. Briefly, simulations were undertaken using the estimated severity data to replace the values sampled from beta-distributions in step 1 of the simulation framework.

All statistical analyses, simulations, and graphics were performed in R [40]. We used the cloud for data storage. The data can be found at the following link: https://drive.google.com/drive/folders/1tqM7ZPyiCxETfsDrTRKgGgVzQ_ASs5jZ?usp=sharing

3. Results

3.1. Comparison to Determine the Effect of Scale Structure

Most MSEs decreased significantly as sample size (n) increased (Figure 2). Moreover, the decrease in magnitude was rapid as variation increases with the fixed mean severity (e.g., R2C1, R3C1, and R4C1 of Figure 2). NPEs most often had the smallest MSE, although, at higher mean severities (≥20%), there was little difference between the methods. Thus, overall, the performance of the 0% to 100% ratio scale was superior to all other scales tested when the MSE was used as the criterion for comparison. This is unsurprising because the process of simulating NPEs did not include any bias factor, so the mean of the NPEs would always be close to the “actual” severities. That is, using the NPE scale did not distort any information.

Comparing the four quantitative ordinal scales (Figure 2), MSEs were increased at lower severities (≤10%) when assessments were made using the EI10 scale (equal intervals of 10%). A sharp contrast exists between the effect of using the EI10 and the other assessment methods; e.g., R1C1, R1C2, R1C3, and R2C1 of Figure 2. Differences among MSEs using the other assessment methods (HB and AM10 scales) were minor at low severities (≤10%), but MSEs using the HB scale were larger at severities of 20% and 30%, especially when variation in the sample was small (e.g., R5C3 of Figure 2). The likely reason for this is that the HB scale intervals of 12⁺ to 25% and 25⁺ to 50% are so wide (13% and 25%, respectively) that when mid-points are taken for analysis they more often result in less accurate specimen estimates compared with what is achieved based on NPEs, the EI10 or the AM10 scales.

The results show that variance decreased as the sample size increased, with the initial decline being steep (Figure 3). There were no noticeable differences in variances among the different assessment methods. The decrease is inversely proportional to the square root of the sample size, and the pattern of change in relation to sample size is most often similar to those for the MSEs (Figure 2). Thus most of the differences in magnitudes of the MSEs can be ascribed to the variance (or precision) of the sample estimates, with the exception of the ordinal scale with large intervals (EI10) at severities of 1% or 5% which resulted in grossly inflated MSEs. These inflated MSEs when using the EI10 scale were due to biases that were greatest at severities of 1% and 5% as compared to the other scales (e.g., R1C1, R1C2, and R2C1 of Figure 4). Use of the HB scale resulted in large biases at severities of 20% and 30% (e.g., R4C3 and R5C3 of Figure 4). With the AM10 scale, biases occurred at a severity of 40%, but as with the other assessment scales at 40% severity, the bias was relatively small (<1%) (e.g., R6C2 and R6C3 of Figure 4).

3.2. Comparison to Determine the Effect of Number of Classes

The first stage determined that the AM10 scale (10% quantitative ordinal scale with additional classes to accommodate low disease severities) is the optimal ordinal scale type (Figure 2, Figure 3 and Figure 4). In the second stage, we investigated the effect of the number of classes (and therefore resulting interval widths). MSEs were greater when the interval width was 20% (AM20 scale) at mean severities of 10% or less (see R2C1, R2C2, R3C2, and R3C3 of Figure 5). However, at severities of 20% or more, the differences in MSEs between the scales with different class numbers are small (Figure 5). Both the scale with 5% intervals at ≥10% severity (AM5 scale) and the scale with 10% intervals at ≥10% severity (AM10 scale) had equivalent MSEs. Furthermore, MSEs were similar when using the scale that incorporated finer interval classes at <10% severity (AM10f scale) compared to when using the AM10 scale.

The relationship between variance and sample size at all levels of variation (large, medium, and small) was similar for all scale types and also similar to that for the MSE, regardless of class number (Figure 6). Only in some cases, for very small sample sizes, was the variance of the AM20 scale slightly greater compared to the other scales. Moreover, as noted above, most differences in the magnitude of the MSE can be attributed to the contribution made by its variance, or lack of precision, rather than bias.

Sample size had little or no effect on the bias, regardless of variation (large, medium, and small) (Figure 7). Using the AM20 scale at severities ≤30% resulted in the largest biases. Biases when using the AM10 scale were similar or only slightly higher when compared to those obtained when using the AM5 or AM10f scales.

Based on the MSE, variance, and bias, the performance of the AM10 scale is not inferior to that of the AM5 or AM10f scales. A linear structure is preferred. Too many classes in an ordinal scale could negate the assumed advantages of speed and simplicity offered by these scales. Based on these results and criteria, we recommend the AM10 scale structure as an optimal ordinal scale structure for estimating plant disease severity. Furthermore, the results indicate that scales with ≥7 classes are preferable, where severity ≤50% disease is emphasized.

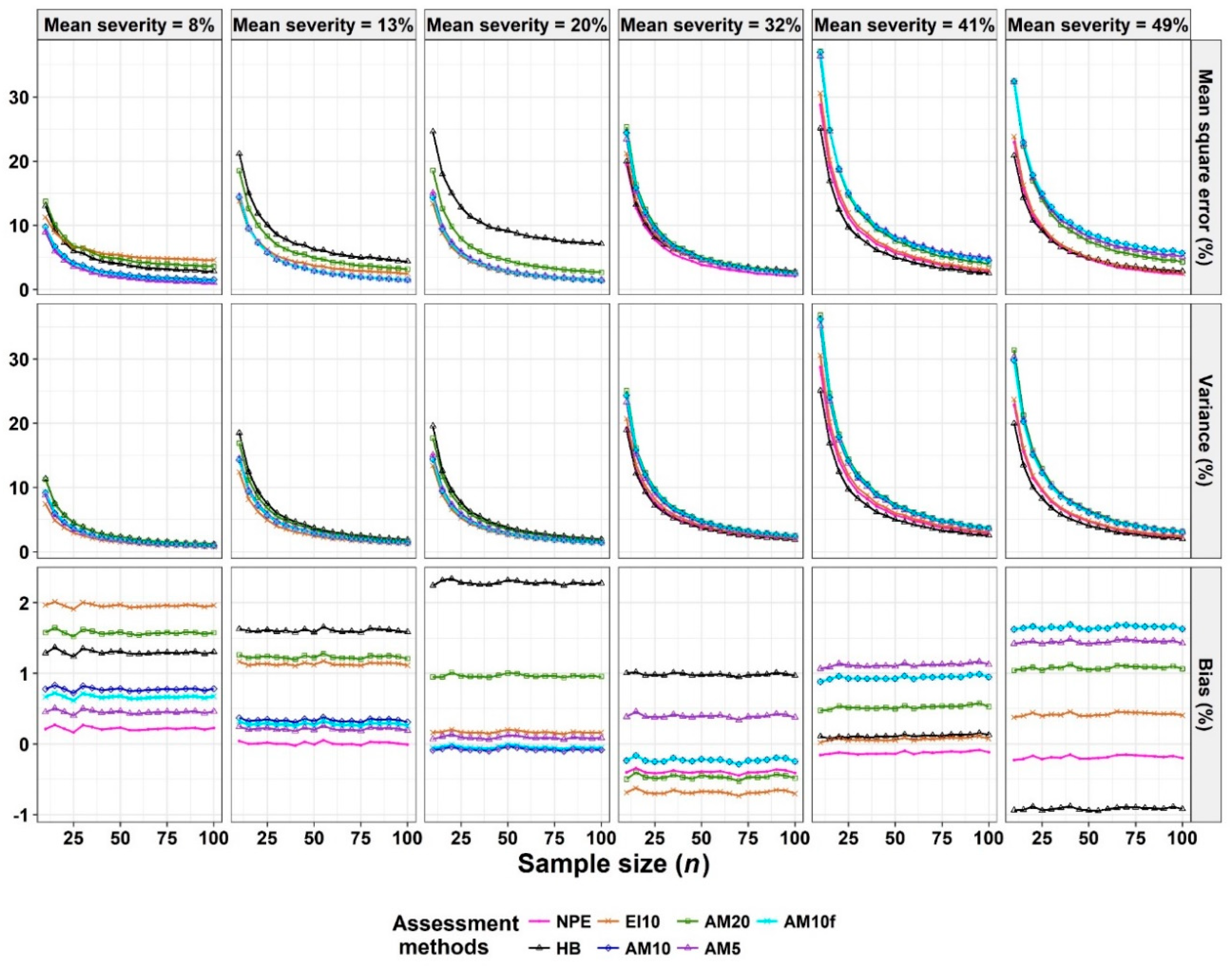
3.3. Analysis of Severity of Pear Scab Data

Based on the image analysis measurements, the six plots had actual mean disease severities of 8%, 13%, 20%, 32%, 41%, and 49% with corresponding variances of 0.0091%, 0.0146%, 0.0146%, 0.0192%, 0.0287%, and 0.0231%, respectively (Figure 8).

The pattern of MSE, variance, and bias for a mean scab severity of 8% were similar to that for a mean severity of 10% with large variation in the simulated studies (i.e., R3C1 of Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7); the EI10 and AM20 scales did not perform well. Moreover, the overall patterns for a mean scab severity of 13% are similar to that for a mean disease severity of 10% with medium variation in the simulated studies (R3C2 of Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7); in this case, the HB and AM20 scales did not perform well. The pattern of MSE, variance, and bias for a mean scab severity of 20% is similar to that of a mean severity of 20% with medium variation in the simulated studies (R4C2 of Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7); in this case the performance of the HB scale was particularly poor, with the greatest MSE and bias compared to other scales. The mean scab severity of 32% presented a similar pattern to those of a mean severity of 30% with medium variation in the simulated studies (R5C2 of Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7); again, the HB scale had the greatest bias. With a mean scab severity of 41% or 49%, the performance of the AM5, AM10 and AM10f scales were all slightly inferior to the other scales based on all three criteria, but this is unlikely to be an issue as the mean scab severity was close to 50% and is usually in a range of less interest. Based on MSE, variance, and bias, the AM5, AM10, and AM10f scales all performed well at mean scab severities <41%. NPEs performed well at all mean disease severities. Thus, the trends for both simulated and empirical data are consistent.

We developed a ranking system using the simulated data and the pear scab assessment data to support the claim that NPEs, the AM5, AM10f, and AM10 scales had the lowest MSEs compared to the other methods (

Table 1. The mean square error (MSE) for the seven assessment methods summed from n = 10 to 100 in n = 5 increments for each specific mean severity and variance (large, medium, and small) for the simulated data sets and the estimated pear scab severity data. The sums of the MSEs for all the mean disease severities were calculated (“Overall”), and a ranking (1 to 7) assigned for each assessment method, where 1 = lowest MSE.

Data Set	Assessment Method 1	Mean Disease Severities						Overall	Rank
		0.01	0.05	0.10	0.20	0.30	0.40
Simulation study (large variance)	NPE	8.54	22.55	78.35	239.49	437.87	451.96	1238.75	1
	HB	42.39	35.98	100.32	250.65	429.65	438.37	1297.36	6
	EI10	388.52	105.69	111.06	241.90	427.15	442.51	1716.84	7
	AM10	12.78	26.60	83.61	255.08	434.88	445.73	1258.68	4
	AM20	15.15	43.92	101.50	261.36	432.26	439.79	1293.98	5
	AM5	12.19	23.62	81.04	254.71	435.83	447.02	1254.41	2
	AM10f	12.38	25.47	83.28	255.18	435.43	446.17	1257.90	3
Simulation study (medium variance)	NPE	4.71	7.98	29.17	98.64	181.68	262.46	584.63	1
	HB	32.69	13.50	51.56	139.14	201.28	259.75	697.92	5
	EI10	354.06	30.54	31.62	100.54	184.71	265.91	967.38	7
	AM10	8.61	14.12	34.26	105.27	202.16	296.57	661.00	4
	AM20	11.40	34.03	86.93	123.69	200.86	290.04	746.96	6
	AM5	7.91	10.08	29.40	104.11	202.57	297.94	652.01	2
	AM10f	7.91	11.77	34.21	105.50	202.25	296.62	658.27	3
Simulation study (small variance)	NPE	1.12	4.08	5.18	10.96	21.54	147.22	190.10	1
	HB	13.31	7.73	27.22	40.17	236.39	157.86	482.68	6
	EI10	306.01	9.16	15.50	15.94	25.77	151.53	523.92	7
	AM10	3.65	10.66	18.19	15.74	26.04	177.88	252.16	3
	AM20	3.84	21.35	189.88	7.44	54.30	170.53	447.35	5
	AM5	3.57	7.48	6.59	12.05	22.91	180.01	232.61	2
	AM10f	2.19	7.09	26.22	15.65	26.04	177.82	255.02	4
		Mean disease severities
		0.08	0.13	0.20	0.32	0.41	0.49
Based on estimates of pear scab	NPE	48.74	77.60	77.90	103.34	151.03	122.66	581.27	1
	HB	91.44	146.95	199.68	115.86	132.38	122.26	808.58	6
	EI10	111.89	89.24	70.20	116.81	160.47	129.65	678.25	2
	AM10	59.36	77.02	74.96	127.37	206.95	211.12	756.80	5
	AM20	106.09	117.79	110.30	133.63	199.47	189.06	856.32	7
	AM5	49.55	76.98	77.99	123.25	208.75	201.55	738.07	3
	AM10f	57.02	77.07	74.62	127.37	206.95	211.12	754.16	4

¹ Assessment methods: NPE (nearest percentage estimate); HB (Horsfall-Barratt scale); EI10 (equal interval 10% linear scale); AM10 (10% linear scale emphasizing severities ≤50% disease, and with additional intervals at severities <10%); AM20: Similar to the structure of AM10 (both scales have the same structure at ≤10%), this scale has wider ordinal scale intervals for disease severities 10 through 50% based on a 20% linear scale; AM5: Similar to the structure of AM10 (both scales have the same structure at ≤10%), this scale has narrower ordinal scale intervals for disease severities 10 through 50% based on a 5% linear scale; AM10f: Similar to the structure of AM10, this scale has 10% linear intervals at >10%, but has finer intervals at ≤10% disease.

). For the seven assessment methods, we calculated the sum of MSEs from n = 10 to 100 in n = 5 increments at the specific mean severities and variances for the simulated and real data, resulting in aggregate MSEs at each mean severity for each variance, and for the pear scab assessment data. Subsequently, we summed these aggregate MSEs for each of the mean disease severities as an “overall” measure of accuracy. Based on the magnitude of these overall MSE data, we assigned a rank from 1 to 7 for each of the assessment methods, where 1 indicated the smallest MSE, and therefore the most accurate assessment method.

As expected, the smallest MSE (ranked #1) is observed when assessments are made using NPEs. Although the AM10 scale was consistently ranked as 3, 4 or 5, there is only a slight difference in the overall MSE values compared with the AM5 and AM10f methods (ranked #2, 3 or 4). However, too many divisions in an ordinal scale might negate the assumed advantages of speed and simplicity offered by an ordinal scale. The AM5 or AM10f scales both have more classes to differentiate (14 and 11 classes, respectively). Thus, the AM10 scale (10 classes) is recommended as the most appropriate ordinal scale design to use for disease severity assessment. In future studies where severity estimates of pear scab (or other diseases) are needed using a quantitative ordinal scale, the scale is recommended to conform to that described for the AM10 scale.

4. Discussion

Plant pathologists often obtain data on disease severity using visual assessments made by individuals who assign a disease severity score to each specimen in a sample using one of several rating scales [4]. Quantitative ordinal scales are usually preferred for convenience and speed of rating [2]. However, due to their structure, certain quantitative ordinal scales might introduce additional variability into the samples [17]. Thus, the objective of this study was to build on previous research [14,17] and to seek the “optimal” design for this scale type (i.e., equal or unequal classes, the width of intervals, and numbers of classes) so as to maximize the accuracy of estimates of mean disease severity.

4.1. “Optimal” Design for an Ordinal Scale

Our results indicate that an amended 10% interval ordinal scale (AM10) was the most appropriate ordinal scale design for researchers who desired to base disease severity estimation on an ordinal scale; the AM10 scale yielded a high level of accuracy in estimates of mean disease severity, while minimizing the number of classes (10 classes). In particular, the additional low classes included in the AM10 scale were more sensitive to the ranges of severity at which many diseases frequently occur and at which they needed to be estimated. The HB scale (and other lower resolution, non-linear ordinal scales), the EI10 scale (10 equal 10% intervals) scale, and the AM20 scale (20% linear intervals at severity ≥10%) generally had larger MSEs (disease severity estimates were not reliable and/or accurate as NPEs and the AM10 scale). Furthermore, when the AM5 scale (5% linear intervals at severity ≥10%) or the AM10f scale (an additional interval at severity ≤10%) were included for comparison, neither the MSE, variance, or bias indicated they had an advantage over the AM10 scale. Both the AM5 and AM10f scales would further negate the assumed advantages of simplicity (fewer classes) offered by ordinal scales. Additional findings of this study indicate that, when preparing quantitative ordinal scales for rating disease severity, scales with ≥7 classes were preferable where severities ≤50% disease was emphasized. Additional classes will be needed at severities >50%. These should be at equal 10% intervals based on the ability of raters to detect a just noticeable difference [15]. In contrast, Kranz [19] and Hau et al. [21] had previously conjectured that a minimum of 7 and 8 classes should be recommended for the 0% to 100% scale. The pear scab severity estimates we collected from the pear plots further support the simulation results.

4.2. Effects of Statistical Distributions of Diseased Leaves

There is generally a positively skewed distribution for the disease at low severities. Bock et al. [4] states that as estimates cannot be <0%; all estimates at low disease severities (<10%) are subject to a “barrier” at the low end (i.e., 0%). As disease approaches mid-range severity, it resembles a normal distribution. For example, the data set used to compare the severity of Septoria leaf blotch (SLB) in Chiang et al. [28] exhibit these characteristics. In our study, the “actual” mean disease severities had specified statistical distributions of diseased leaves (Figure 1). The different statistical distributions affected the MSE of mean disease severity estimates for each of the different scales used for estimation (Figure 2 and Figure 5). Thus, our results support the statement of Hau et al. [21] that the characteristics of the distribution of diseased leaves in the population and the number of classes in a disease scale affect the accuracy of the estimate of mean disease severity; very skewed populations rated using a scale with few categories (<7) result in inaccurate mean estimates. After 30 years, we tested and provided strong support for these claims using both simulation studies and empirical data sets.

4.3. Properties of the AM10 Quantitative Ordinal Scale

The AM10 scale is based on a 10% linear scale emphasizing severities ≤50% disease and had additional classes at low severities ≤10%. AM10 could be regarded as a linear ordinal scale with sensitivity emphasized at low disease severity (<10%). Although it is technically a non-linear scale, at severities ≥10%, it resembles a linear scale. So in this regard, the AM10 scale can be considered a hybrid scale, part linear, and part non-linear. The conclusions here are consistent with those of a previous study based on estimates of the severity of citrus canker by different raters [14]. Whereas the present study explored the issue of the accuracy of the mean disease severity, the earlier study compared the relative differences due to scale type when comparing treatments using a hypothesis test based on the probability of a type II error.

One thing to note is that when using the AM10 scale, larger biases may occur at severities of 40% because only two classes (50⁺–70, 70⁺–100% disease) account for severities ≥50%. Thus, as some diseases can exceed 50% severity, maintaining a linear 10% interval from 10% to 100% will help avoid undesirable bias in the upper range (but increasing the number of classes).

4.4. Mean Squared Error (MSE), Variance, and Bias

The criterion for comparison of the scales was the MSE of the mean disease severity estimates ($\overline{X}$). The MSE ($\overline{X}$) is separated into variance ($\overline{X}$) (precision) and square of the bias ($\overline{X}$). We found that most differences in the magnitudes of the MSE could be ascribed to its variance. Although biases due to scale type accounted for only a small portion of the MSE, it played a crucial role in comparison among assessment methods, especially at low disease severities (≤10%). Biases resulting from the use of ordinal disease assessment scales almost invariably resulted in overestimation (Equation (3) $\mathrm{Bias}\left(\overline{X}\right)=E\left(\overline{X}\right)-\mu$ > 0) compared to the actual disease severity. On the other hand, bias was not observed for NPEs. Disease estimates at low actual severities usually have a positively skewed distribution, and estimates of mean disease severity are inflated by one or a few very large values. When using EI10, the MSEs of the mean disease severity estimates were particularly high at severities of 1% and 5%. The critical factor here was the bias. When NPEs were transformed into values on a 10% equal-interval scale, the mean of individual units sampled was greater than that of the original NPEs. The result was the data were distorted after the transformation and could not represent the “actual” mean disease severity (%) in a population at low severities (1% or 5%) due to the positively skewed distribution noted above. Although the distribution of severities resembled a normal distribution as mean severity approaches 50%, there were only two classes (50⁺–70, 70⁺–100%) which include severities ≥50% for assessment methods 4 through 7; this resulted from the use of a coarse measurement scale at the right as opposed to a finer scale at the left side of a normal distribution.

Thus, for the fixed numbers of classes (10 classes) in the disease scales tested, the AM10 scale is recommended, despite slight bias at actual severities close to 40%, which seldom need to be considered for practical use [22]. Thus, the results presented here are of great value with regard to that range of disease most often observed in the field for many pathosystems. Thus, as noted in the previous section, where greater resolution is needed at severities >50%, a continued linear 10% scale is recommended.

4.5. Rationale for Simulation Studies

In this study, a two-stage approach was performed to firstly compare the scale structure (linear or non-linear), and secondly the number of classes (interval size) in a scale. We wanted to determine which scales minimized inaccuracy and imprecision. It is rational to explore the two factors in turn. We found that there was little variation among biases based on sample size, allowing us to conclude that biases are stable regardless of sample size (n). The reason for this phenomenon is that the simulation process was repeated 10,000 times, making it possible to average the 10,000 means of each individual sample size for each situation. If the simulation process was repeated fewer times, there would be extreme fluctuations in the biases (K-S Chiang, unpublished data). Therefore, more repetitions (in these cases 10,000 times) are required in order to compare various NPE and ordinal scale estimates.

4.6. Direction for Future Studies

In this study, the process of simulating the estimates did not take rater biases into account; only the effects of biases due to assessment method were studied. Although the effects of rater bias (over and underestimates) on estimates of disease severity of individual specimens on hypothesis testing using different assessment methods was previously explored [28,29], in this study, we were investigating the effect of the scale per se, on MSE, variance, and bias of the sample mean. Thus we focused on the issue of absolute values to provide information regarding which assessment method is preferable to use to provide the most accurate estimates of the mean disease severity. Taking rater biases into account for mean disease severity estimates will be an area for future studies.

5. Conclusions

We believe that the results of this study will contribute to the development of improved disease assessment quantitative ordinal scales. Use of better-designed ordinal scales will be helpful in improving the accuracy of disease severity estimates in plant disease epidemiology and related areas of research. The recommendations are general and applicable across most or many plant disease assessment situations.