1. Introduction
Understanding boundary layer and land surface feedbacks on canopy transpiration is essential for developing simpler and realistic climate change models and for improving the prediction of ecosystem-level water fluxes in response to climatic variables [
1,
2]. Canopy stomatal conductance (G
S), a key physiological factor controlling transpiration from plant stands, is an important component of land surface feedbacks because it regulates evapotranspiration and surface temperature changes in response to incident radiation, CO
2 concentration, and vapor pressure deficit (VPD). This regulatory function is reflected in canopy temperature, which in turn, determines the magnitude and direction of sensible heat exchange between the vegetation and its environment. At regional scales, stomata exert little control, and daily transpiration of well-watered vegetation is predominantly controlled by radiation and temperature [
3,
4,
5], in part due to feedbacks that cannot be predicted from single leaf measurements alone [
3]. Since canopy-scale transpiration is determined by the ratio between canopy aerodynamic conductance (g
A) and G
S [
4,
6,
7], improved methods for measuring g
A, as well as measuring responses of G
S to environmental variables (e.g., light, CO
2, VPD, soil moisture, and temperature), are needed for studying the processes controlling feedback and stomatal control of evaporation from regional land surfaces.
In the field, g
A is often approximated by the conductance to momentum transfer determined using the log-wind profile approximation, which requires at least 100 m of fetch and thus cannot be used in controlled-environment chambers [
8]. In controlled environments, leaf boundary conductance has been estimated from measurements with wet filter paper analogs [
9], from cooling curves of metal models of leaves [
10], or from combined energy balance and temperature measurements using metal leaf models [
11,
12]. However, Jarvis and McNaughton [
3] argue that leaf level measurements of stomatal control of transpiration may not be applicable to plant canopies in the field because the amount of ventilation in leaf cuvettes and plant chambers typically prevents feedback between transpiration and VPD observed in the field.
G
S can be derived using energy balance approaches from canopy surface conductance to water vapor (G
SFC), latent heat flux (LE), and the VPD at the leaf surface (Ds). Similarly, the single-layer or “big leaf” G
S may be computed from G
SFC, provided the boundary layer conductance to water vapor (i.e., g
A) and the mean aerodynamic canopy temperature (T
Aero) are known [
13,
14]. In the field, G
SFC is calculated from canopy-level LE obtained using lysimeters, Bowen ratio, and eddy correlation systems [
15], or by inverting the Penman–Monteith equation [
13]. However, these approaches for measuring canopy-level LE do not permit partitioning of transpiration among individual species and often cannot distinguish between transpiration and evaporation from the soil or from wet leaf surfaces. Thus, G
SFC is not always related to estimates of canopy G
S derived from single leaf measurements because it often includes significant contributions from soil evaporation [
13].
Smith et al. [
16] used canopy-level energy balance measurements to estimate sensible heat flux (H) of a wheat field from radiometric canopy temperature when canopy g
A and LE were known. Their approach produced accurate estimates of hourly LE, which suggests that g
A could be estimated if H and the canopy-to-air temperature difference are measured accurately. However, canopy g
A determined from changes in radiometric canopy temperature differs from g
A determined using the log-wind profile approximation because it includes the conductance to heat and water vapor across leaf boundary layers, as well as the turbulent conductance caused by the movement of air eddies between the canopy and the atmosphere [
17,
18].
Canopy G
S obtained from energy balance approaches may contain considerable errors because Ds and LE are estimated using measurements of canopy radiometric temperature (T
R) to approximate the aerodynamic canopy temperature [
19,
20,
21]. In the field, estimating T
Aero from infrared measurements is complicated because radiometric measurements depend on the view angle of the sensor, sun angle, degree of crop cover, spatial variability of canopy emissivity, and atmospheric attenuation, and they often include significant temperature contributions from soil surfaces [
20,
22,
23,
24,
25]. A systematic difference of −1 °C was measured between radiometric and aerodynamic temperatures by Huband and Monteith [
26], although differences ranging from 2 to 6 °C have also been observed [
13]. The difference between T
Aero and T
R can be very small in dense canopies, but it can exceed 10 °C in sparse vegetation because of contributions from soil temperature ([
18,
27]. These differences are significant because small errors of −1 °C in the surface-to-air temperature difference can represent an uncertainty in latent heat fluxes of ~40 W m
−2 [
13]. Many complicating factors that affect infrared measurements of canopy temperature in field settings can be minimized in controlled environments by using high planting density canopies grown under constant lighting. In dense canopies, canopy brightness temperature measured with infrared sensors approximates canopy radiometric temperature [
28], but errors due to radiation reflected into the sensor and artifacts caused by fluctuating sensor body temperatures remain [
29].
The purpose of this study was to develop a radiometric method for measuring canopy G
S of well-watered plant canopies in controlled environments. The hypothesis tested was that a radiometric method utilizing canopy-level energy balance measurements provides more accurate estimates of canopy stomatal conductance than bottom-up methods scaling leaf-level to canopy-level conductance or top-down methods that estimate canopy surface conductance from field data. Bottom-up methods require that leaf area index be known and must integrate the responses of leaf stomatal conductance to vertical gradients in radiation, temperature, and humidity. Conductances from top-down methods using field data typically include significant contributions of soil evaporation, and field radiometric data include soil surface temperatures that cause significant differences between radiometric and aerodynamic temperatures [
13].
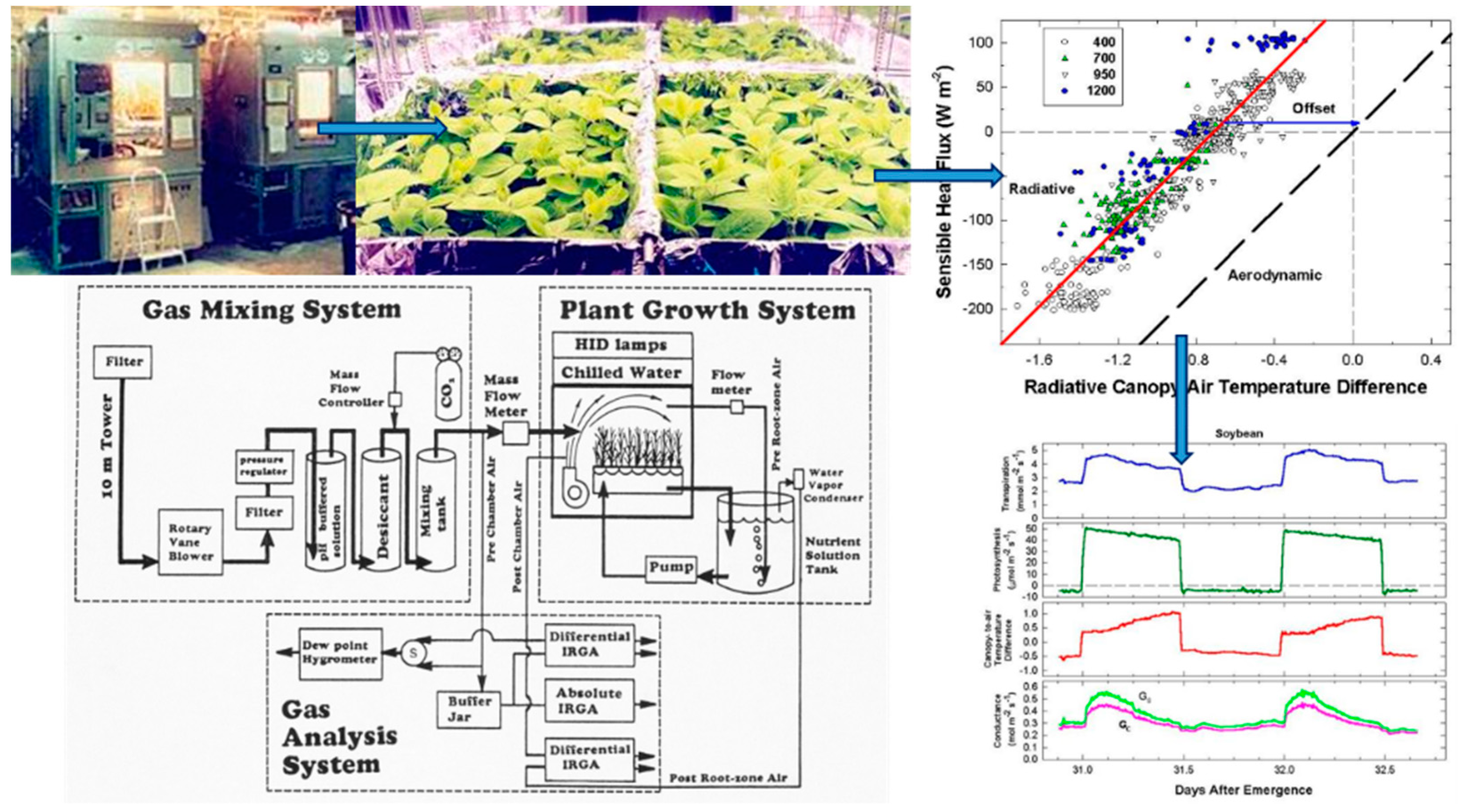
Simultaneous measurements of energy balance, gas fluxes, and canopy temperature at constant environmental conditions were used to compute canopy G
S from surface G
SFC and canopy g
A (
Figure 1). The relation between radiometric and aerodynamic temperatures was studied by varying incident radiation and wind speed. Canopy G
S and g
A of high planting density wheat (
Triticum aestivum L. cv. USU Apogee) and soybean (
Glycine max L. cv. Hoyt) canopies were measured at 400 umol mol
−1 CO
2. The radiometric method was used to explore the effects of rising CO
2 concentration on canopy G
S and to describe stomatal feedbacks to transpiration using the canopy-scale decoupling coefficient.
2. Materials and Methods
2.1. Chamber System
In this study, 18–35-day-old, closed wheat and soybean canopies were used to examine various aspects of the method—energy balance responses to changes in radiation forcing, responses of vertical gradients in canopy-to-air temperature to fan speed or light level, responses in canopy-to-air temperature and sensible heat flux to CO2 concentration, etc. Each test took several days to conduct, and plant canopies of different ages were used because the logistics of growing canopies to the same age for each test was impractical. Thus, conductances observed in a vegetative 20-day-old wheat canopy may not be the same as in a reproductive 35-day-old canopy due to ontogenetic changes in canopy structure (i.e., the presence of heads). However, overall the method is robust as long as energy balance components and canopy-to-air temperature differences are measured accurately and simultaneously.
2.2. Cultural and Environmental Conditions
Wheat and soybean canopies were grown in sealed, water-cooled, controlled-environment chambers (Model EGC-13, Environmental Growth Chambers, Chagrin Falls, OH, USA). Two canopies of the same species were grown simultaneously in adjacent chambers. Wheat was seeded into lids containing a 10 mm layer of inert media (Isolite, size CG-2, Sumitomo Corp., Denver, CO, USA) at a density of 1100 plants m
−2. Soybean seedlings were transplanted into closed cell foam plugs in a Styrofoam lid at a planting density of 60 plants m
−2. The seedling roots grew into a recirculating hydroponic solution after germination. The hydroponic system is described in Monje and Bugbee [
30].
Inside each chamber, a polished aluminum, reflective side-wall was built around the perimeter of the ~1 m2 canopy to minimize edge effects and side lighting. The incident photosynthetic photon flux (PPFo) was 1600 µmol m−2 s−1 for wheat and 750 µmol m−2 s−1 for soybean. Lighting was provided by four, 1000 W high-pressure sodium (HPS) lamps, which were adjusted with neutral density filters to achieve ±5% PPFo uniformity over the crop surface. PPFo was measured at the top of the canopy with a quantum sensor (Model LI-190SB, LI-COR, Lincoln, NE, USA), and was adjusted daily throughout the life cycle by lowering the canopy platform as the plants grew taller. Longwave radiation emitted by the lamps was removed by a 10 cm deep water filter. The filter consisted of a glass box filled with recirculating, chilled water located below the lamps. The water filter under the lamps was removed over the course of several days during tests that change surface radiation forcing by increasing incident PPFo and longwave radiation impinging on the canopy. Advective conditions existed in the chamber because the temperature control system heated the air to maintain the chamber temperature setpoint, and the canopy was exposed to a continuous flow of warm air.
Air temperature was 21.0 ± 0.3 °C, the barometric pressure was 86 ± 0.1 kPa, and chamber CO2 varied between 400 and 1400 µmol mol−1 to manipulate canopy temperature, LE and H. Relative humidity at night was 50% ± 5%. During the day, transpiration humidified the 1300 L of chamber air and daytime relative humidity was 70 ± 5%. Wheat was grown under a 20 h light/4 h dark photoperiod and soybean under a 12 h light/12 h dark photoperiod. The canopies grew in a chamber supplied with a constant temperature (TAir) and VPD of bulk air surrounding the vegetation (DBulk) as well as a constant wind speed. Thus, boundary layer forcing (TAir and DBulk) and surface layer feedbacks (chamber wind speed) were held constant, but in nature they are dictated by diurnal changes in local climate (TAir, DBulk, and wind speed).
2.3. Gas Exchange System
Each chamber used an open gas exchange system to measure canopy photosynthesis [
30,
31]. The open flow system ensured that humid air (~50% relative humidity) of a constant CO
2 concentration (setpoint ±10 µmol mol
−1) fed the chambers at flow rates between 500 and 1100 L min
−1. Air mass flow (MF; mol s
−1) into the chambers was measured with mass flow meters (Model 730, Sierra Instruments, Monterey, CA, USA). The gas exchange systems were modified to use a dew point hygrometer to measure the water vapor concentration of pre- and post-chamber air from which evapotranspiration was calculated. Two solid-state multiplexers (Model AM-25T, Campbell Scientific, Logan, UT, USA), each referenced to a 100 Ohm platinum resistance thermometer, were used for precision thermocouple measurements. Data acquisition and control were performed with a datalogger (Model CR-10T, Campbell Scientific, Logan, UT, USA).
Gas exchange fluxes in each chamber were measured continuously and averaged for 2 min every 8 min. Net photosynthesis, P
net, and dark respiration rates were calculated from the difference between pre- and post-chamber CO
2 concentrations (ΔCO
2), multiplied by MF of air into the chambers. ΔCO
2 was measured with a differential infrared gas analyzer (Model LI-6251, LI-COR, Lincoln, NE, USA). The temperature, water vapor band broadening, and dilution corrections used for the C fluxes are described in Monje and Bugbee [
30]. Chamber evapotranspiration (ET) was determined from the difference in mole fraction of water vapor between pre- and post-chamber air (ΔX
h20), multiplied by mass flow rate entering the chamber (ET = ΔX
h20 × MF). ΔΧ
h20 was determined from sequential measurements of pre- and post-chamber air dewpoint made with a dewpoint hygrometer (Model Dew-10, General Eastern, Watertown, MA, USA). Air flow was changed to increase ΔCO
2 and ΔΧ
h20 in the chamber. The flow rate of air entering the chamber was not corrected for the amount of water vapor added by canopy transpiration (a maximum of ~15 L/day) because this correction was negligible, which would not be the case in smaller leaf gas exchange systems [
32]. Water use efficiency (μmol mmol
−1) was calculated from the ratio of P
net to ET.
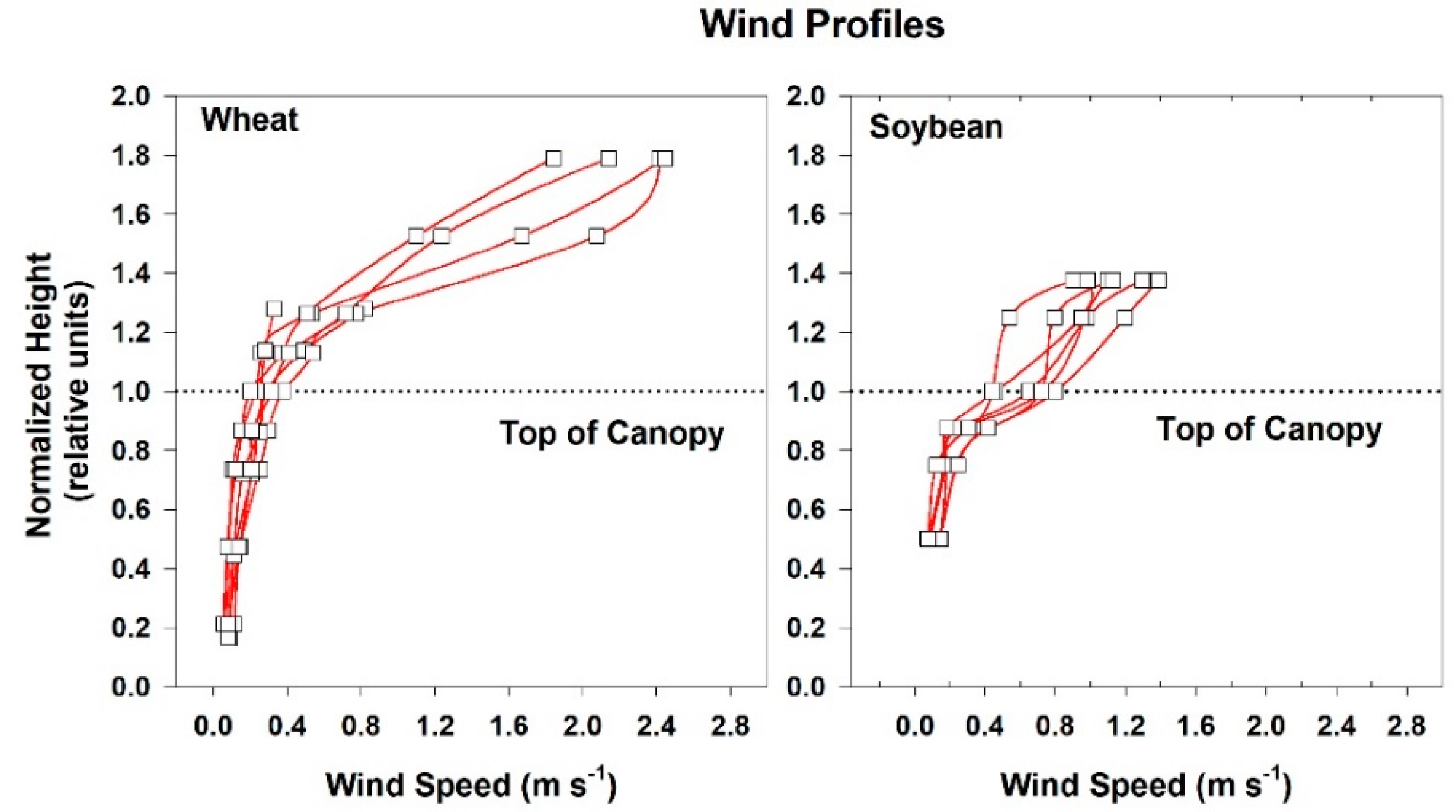
2.4. Chamber Wind Speed
Wind speed above and within the canopies was measured with heat transfer needle anemometers (Model AN-27, Soiltronics, Burlington, WA, USA). These anemometers were well-suited for making wind measurements within canopies because they are small, have fast response times (half-life t
1/2 = 1 s), and are omnidirectional. The anemometers were calibrated in a wind tunnel for windspeeds between 0.05 and 5 m s
−1 [
33]. Vertical gradients in mean wind speed above and within the canopies were measured with anemometers spaced between 4 and 6 cm apart. Each chamber was modified to include variable speed centrifugal blowers so that wind speed above the vegetation could be controlled over a wide range. Three wind speed settings (high: 2.3 m s
−1; medium: 1.7 m s
−1, and low: 0.8 m s
−1) were used in the chambers, but the majority of the measurements were made at the medium setting.
2.5. Temperature Measurements
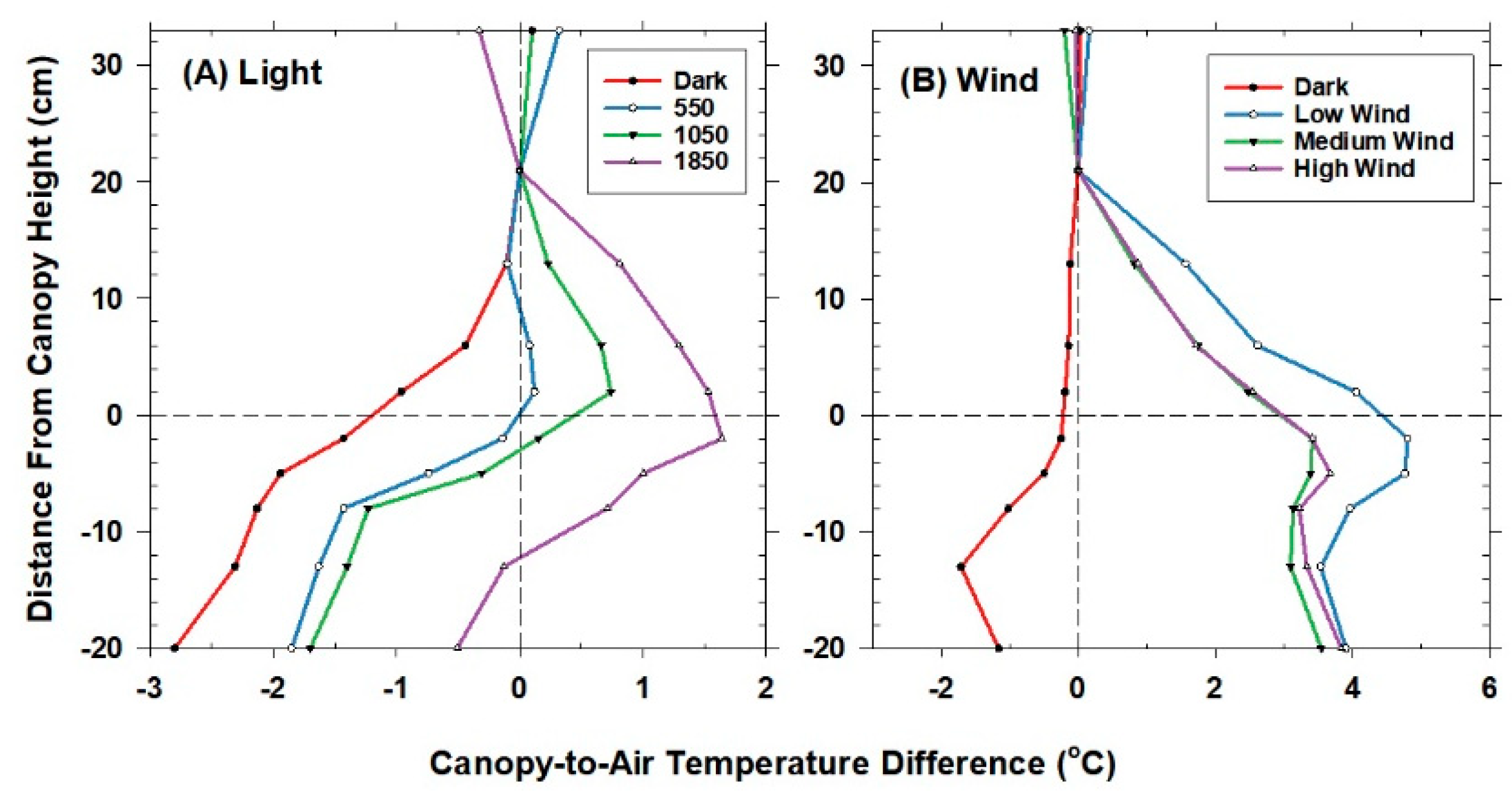
The temperature sensor used to control chamber air temperature was situated 20 cm above the canopy and 10 cm below the lamps. This reference location was chosen because the lamps were found to heat the air in the top 5 cm of the chamber near the water filter. Mean air temperature (Tair) at the reference location was measured using a shielded and aspirated thermocouple (Type-E, 30 gauge). Vertical profiles of air temperature within the canopies were measured with an aspirated thermocouple manifold. The thermocouples were arranged in parallel within a manifold that held the thermocouples evenly spaced (10 cm apart) and were ventilated at about 1–2 m s−1 by a single aspirator (a vacuum cleaner). The aspirated thermocouples were shielded from incident radiation by plastic tubing wrapped in aluminum foil. The vertical profiles in temperature were expressed as an air temperature difference from the reference air temperature above the canopy.
Canopy temperature measurements made using infrared temperature sensors are described using the nomenclature and definitions of Norman and Becker [
28]. Two nadir-viewing (e.g., perpendicular to the canopy) infrared sensors in each chamber (Model IRTS-P, Apogee Instruments, Logan, UT, USA) were used to measure canopy brightness temperature (T
canopy,IR), which is a directional temperature that depends on the angle of observation, the wavelength band of the infrared sensor, the sensor body temperature, and sensor position above the top of the canopy. The IRTS-P infrared sensors have a 90° field of view and an accuracy of ±0.2 °C. The 8–14 µm wavelength band was viewed. They were placed in the center of the canopy at a height of 10 cm above the foliage, where the chamber walls could not be seen. The calibration procedures, the field of view considerations, and the functions used to correct for sensor body temperature for these sensors are described in Bugbee et al. [
29].
Canopy T
Aero, formally defined as the extrapolation of air temperature profile down to an effective height within the canopy at which the vegetation components of sensible and latent heat flux arise [
18], is the mean canopy temperature felt by the air that solves the energy balance equation exactly. T
Aero cannot be measured directly. It can be obtained from H when T
air and g
A are known, but is typically approximated by T
R, the canopy radiometric temperature [
13,
27]. Canopy T
R was derived from T
canopy,IR after correcting for the sky irradiance (e.g., proportional to sky temperature, T
Sky) that is reflected by the canopy and by the chamber walls into the field of view of the infrared sensor [
28]. In the controlled-environment chambers, sky irradiance is emitted by the warm chamber surface areas above the canopy, which were proportionally divided into a 20% chamber wall and an 80% glass water filter. The difference between T
R and T
canopy,IR depends on the canopy emissivity, ε
c (Equation (1)):
where σ = Stefan–Boltzman constant (W m
−2 K
−4), and T
Sky = temperature of the chamber surfaces above the canopy (K). In this paper, it was assumed that T
R ≈ T
canopy,IR because the correction for canopy emissivity is small (≈ 0.2 °C). For example, if T
glass = 30 °C, T
wall = T
air = 23 °C, T
canopy,IR = 24 °C (e.g., 20% wall and 80% glass temperature), and ε
c = 0.97, then the difference between T
R and T
canopy,IR is only 0.14 °C. If the water filter under the lamps is removed, T
R increases by ~0.5 °C, T
glass = 45 °C, and the difference between T
R and T
canopy,IR rises to ~0.5 °C (Equation (1)). These conditions are unique to controlled-environment conditions because such high T
Sky temperatures are never observed in the field.
2.6. Absorbed Radiation
Energy exchange and photosynthesis are proportional to the amount of radiation absorbed by plant canopies, which is determined by the direct beam fraction of incident radiation, the canopy structure, and the optical properties of the plant elements [
34]. Incident PPF
o and shortwave radiation within the growth chamber were measured at canopy height. Shortwave radiation between 0.285 and 2.8 µm was measured with a precision spectral pyranometer (The Eppley Laboratory, Model PSP, Newport, RI, USA). Incident non-photosynthetic, shortwave radiation (NPSW
o) was determined by subtracting PPF
o (converted to energy units assuming 5 µmol m
−2 s
−1 per W m
−2 for HPS lamps) from the total shortwave radiation. The fraction of PPF absorbed by the canopy (PPF
abs) was calculated from the product of radiation capture and PPF
o, as described by Monje and Bugbee [
30]. A diffuse light fraction of 0.7 was measured in the chamber using a shadow band to shield the quantum sensor from direct radiation. The fraction of non-photosynthetic, shortwave radiation absorbed by the canopy (NPSW
abs = (1 − ρ
c) NPSW
o) depends on the canopy reflection coefficient (or surface albedo), ρ
c, in the near-infrared (NIR). ρ
c was estimated using Equation (2) from the single leaf scattering coefficient (σ
S) [
35]:
σ
S varies with the wavelength of the radiation and equals the sum of the fractions of reflected and transmitted light. In the visible spectrum, the ρ
c of the high planting density wheat canopies was 0.055 during vegetative growth [
36], which corresponds to a σ
S of 0.2. Since the NIR ρ
c was not measured directly, it was derived from Equation (2) assuming an NIR σ
S of 0.8. For comparison, the single leaf reflectance (0.43) and transmittance of winter wheat (0.33) in the NIR combine to give an NIR σ
S of 0.76 [
37]. Thus, NPSW
abs was 0.62 × NPSW
o for a ρ
c of 0.38 in the NIR. Although this approximation overestimates ρ
c in sunny conditions (e.g., high direct beam radiation), it predicts it accurately under overcast conditions [
38], similar to the highly diffuse radiation found in these controlled-environment chambers.
2.7. Net Radiation, Evapotranspiration, and Photosynthesis
The net radiation above the canopy, R
net, was assumed proportional to net input of shortwave radiation and incoming longwave radiation (Equation (3)).
where PPF
abs = absorbed photosynthetic radiation (W m
−2), NPSW
abs = absorbed non-photosynthetic shortwave radiation (W m
−2), ↓L
g = longwave radiation emitted by the glass from the water filter and the chamber walls (W m
−2), and ↑L
c = longwave radiation emitted by the canopy (W m
−2). Assuming that the longwave radiation components (↓L
g − ↑L
c = ε
c ↓L
g − ε
c σ T
4 R = ε
c σ T
4Sky − ε
c σ T
4R) nearly canceled each other was acceptable as long as the differences between T
Sky and T
R were also small. For example, if T
glass = 30 °C, T
wall = T
air = 23 °C, and T
R = 24 °C, then T
sky = 28.6 °C, and ↓L
g − ↑L
c = 27 W m
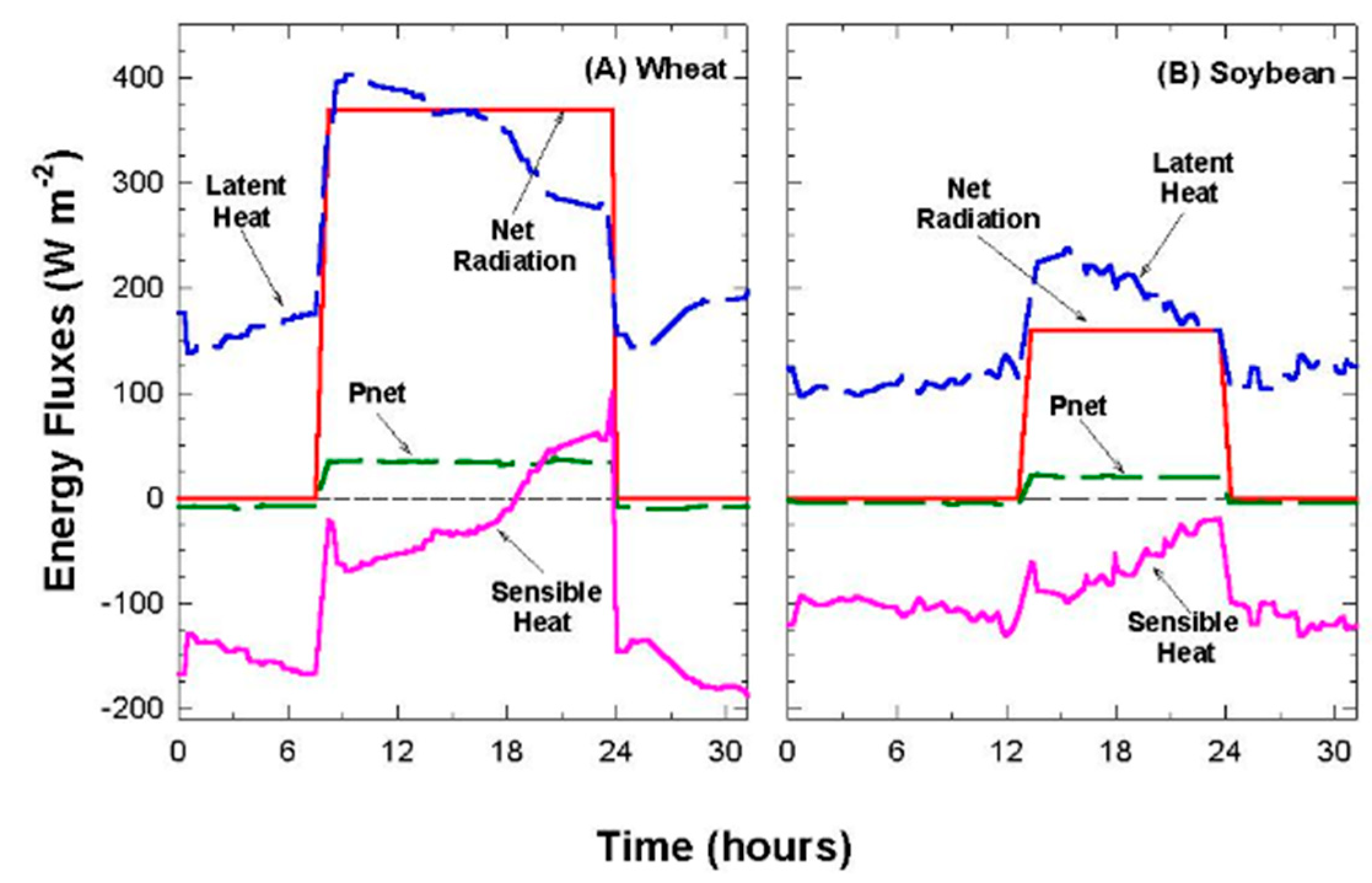
−2. Although Equation (3) ignores changes in longwave radiation within the canopy caused by vertical gradients in temperature, it was a better estimate than direct measurements with a net radiometer. Most net radiometers are calibrated for field operation, where the fraction of longwave radiation is much smaller than in these chambers, and the dimensions of the chambers placed the net radiometer close to the top of the foliage, where self-shading led to significant overestimates of the net radiation flux. Net radiometers are preferred in chambers illuminated by solar radiation, but they are affected during cloudy days with highly diffuse radiation.
Net radiation in the chamber could be varied by either changing PPF
o with neutral density filters (window screen filters) or by draining the water filter under the lamps. Shading with neutral density filters does not alter the spectral composition of the incident radiation. In contrast, the water filter under the lamps reduces the amount of longwave radiation impinging on the canopy, thereby increasing the ratio of PPF
abs to R
net [
39]. Removing the water filter increased ↓L
g compared to ↑L
c and added ~100 W m
−2 to R
net, as the glass temperature measured with a thermocouple reached 45 °C. The PAR
abs to R
net ratio was 83% of R
net in a chamber with a water filter below the lamps, but was only 64% of R
net when the water filter was removed. These changes in surface radiation forcing (R
net) were used to change canopy temperature and H for studying the relation between T
Aero and T
R.
Chamber ET (mmol m
−2 s
−1) consisted of canopy transpiration (E
can) and evaporation (E) from the hydroponic solution through the porous media sustaining the plants (Equation (4)).
Chamber latent heat flux (LE; W m−2) was determined from the product of ET and the heat of vaporization of water (44 kJ mol−1). Evaporation from the hydroponic tubs, covered with lids but without a canopy, was small (~2% of Rnet when expressed in W m−2). This made ET essentially equal to Ecan in this study and ensured that TAero, calculated from the energy balance measurements, was mostly due to the flux of sensible heat between the foliage and the air flowing above the canopy.
In controlled environments, P should be included in the energy balance equation at high light intensities because it becomes a large fraction of R
net. Photosynthesis (P; W m
−2), the conversion of energy in radiation into stored chemical energy, was derived from the product of canopy photosynthesis, P
net [
30], and the enthalpy of combustion for CHO (479 KJ mol
−1) [
40].
2.8. Canopy Sensible Heat Flux
In the steady state, H is the energy exchanged by conduction and convection between the canopy and the chamber air. The canopy energy balance equation was rearranged for calculating H by residual (Equation (5)), where R
net = net radiation, LE = latent heat flux, G = soil heat flux, and P = energy storage in photosynthesis.
LE includes water vapor fluxes mostly due to canopy E
can because evaporation was only 2% of R
net. The soil heat flux, G, is a component of land surface feedbacks that depends on the amount of energy available below the canopy. G was assumed to be zero due to a poor transfer of heat through the dense canopies (high planting densities and leaf area indices > 15) used in this study, but this may not be a valid assumption during early development when the plants are seedlings. P was determined from canopy photosynthesis, which can be as much as 10% of R
net at high light intensities. For example, if P
net = 60 umol m
−2 s
−1 at a PPF
o of 1400 µmol m
−2 s
−1, then P = 29 W m
−2. Equation (5) allows for a comparison of energy fluxes in common energy units (W m
−2) and allows H to be determined by residuals. However, Equation (5) ignores the thermal storage within the canopy, which is small for the short vegetation used in this study, but this storage can be as high as 5–10% of the net radiation in forest canopies [
13].
2.9. Canopy Aerodynamic Conductance
In field settings, the log-wind profile approximation allows canopy g
A to be determined from H provided ΔT
A, the aerodynamic canopy-to-air temperature difference (ΔT
A = T
Aero − T
air), the displacement height, and the roughness length are known [
41]. However, the short fetch (1 m) of the canopies used in this study precludes the use of the log-wind profile approximation for calculating g
A in controlled-environment chambers. Instead, an analog of Ohm’s law (Equation (6)) that relates the surface-to-air temperature difference to the sensible heat loss from the surface was used to describe the energy transfer between the canopy and the chamber air [
8]:
where ρ = density of air (kg m
−3), Cp = heat capacity of air at constant pressure (kJ m
−3 °C
−1), g
A = canopy aerodynamic conductance (mol m
−2 s
−1), and T
R (°C) was approximated by T
canopy,IR. T
air was measured at the reference height above the canopy, and used to determine the radiometric canopy-to-air temperature difference (ΔT
IR = T
R − T
air). Equation (6) assumes that the slope between H and ΔT
IR equals the slope between H and ΔT
A, when T
Aero = T
R. This assumption is valid for fully covered canopies, whereby the contribution to ΔT
IR from the temperature of the surface below the vegetation (e.g., soil or hydroponic tray) is negligible.
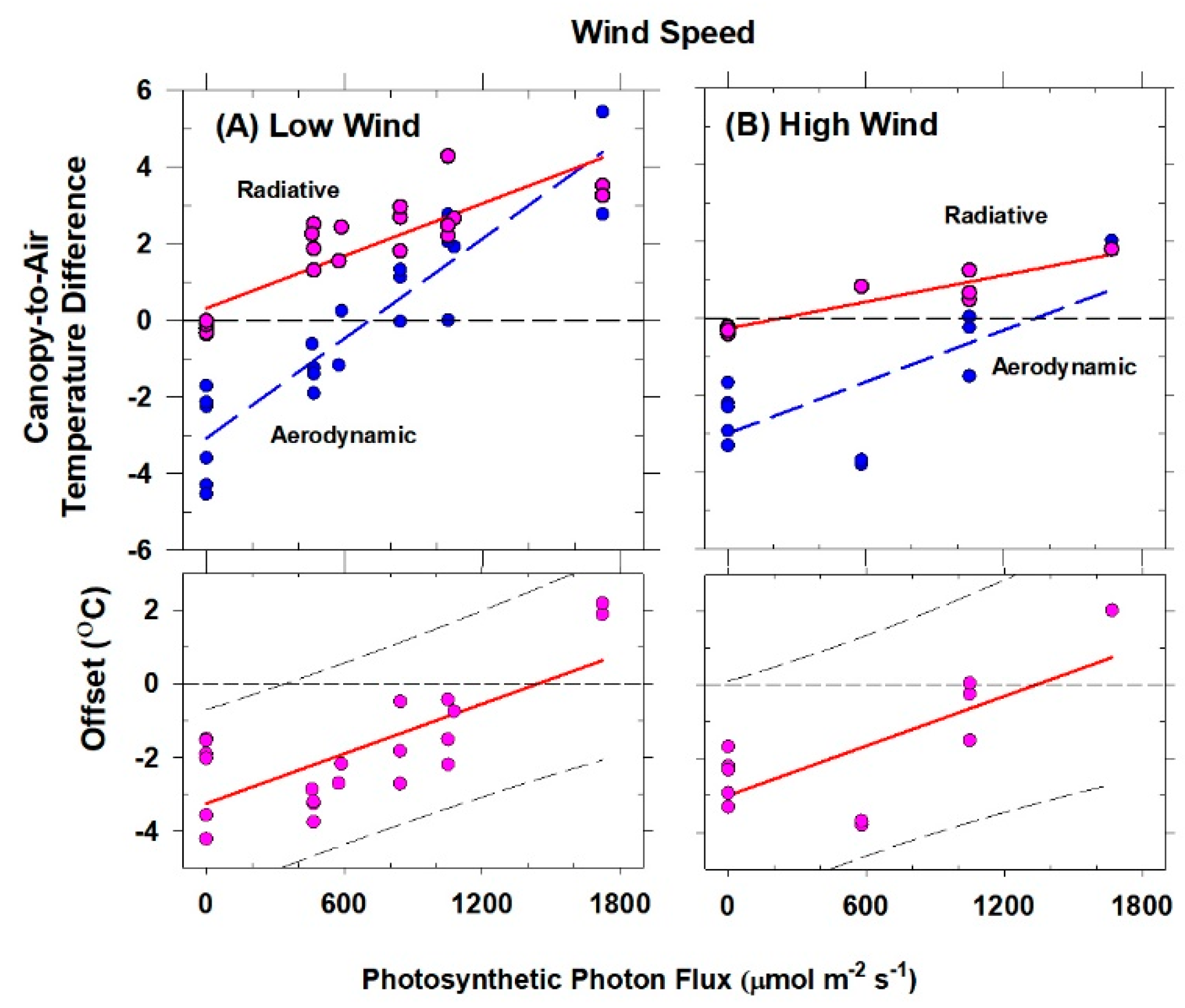
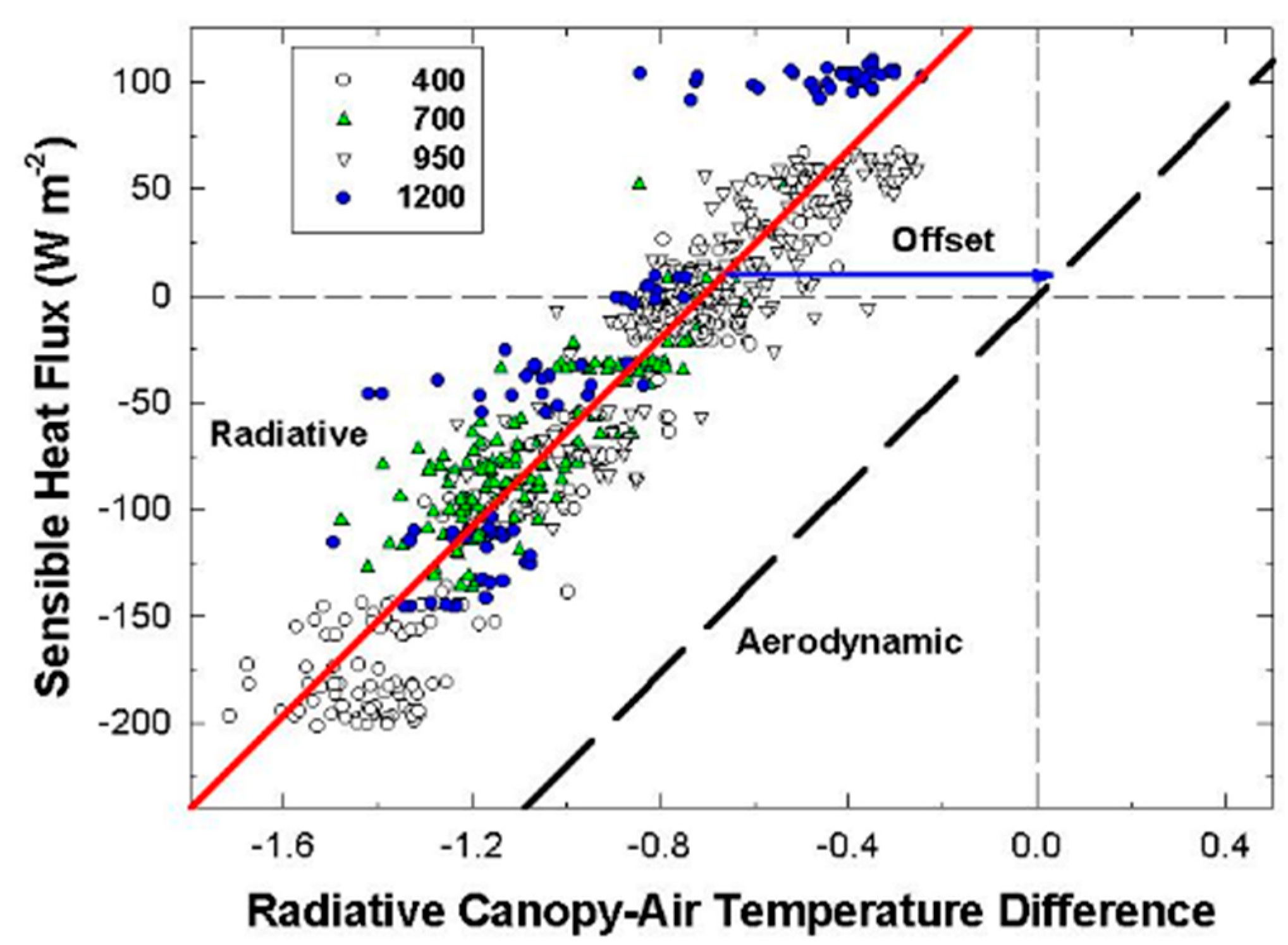
The canopy leaf boundary layer conductance component depends on leaf shape and size, and the turbulent conductance component depends on wind speed and canopy aerodynamic roughness [
8]. Canopy aerodynamic conductances of dense wheat and soybean canopies with distinct canopy architectures were calculated from the slopes of plots of H vs. measured ΔT
IR following Equation (6). Radiometric ΔT
IR and H were varied simultaneously by manipulating chamber CO
2 concentration at constant environmental conditions (wind speed and VPD) over the course of several days. The g
A measured for each species results from the amount of drag generated by the interaction between canopy architecture and the chamber air recirculating at constant wind speed.
Although changes in CO2 affect H and ΔTIR through changes in stomatal conductance, gA remains constant at a fixed chamber wind speed. The highly turbulent conditions in the chamber ensure that free convection effects are negligible compared to forced convection, so changes in light level should not significantly affect canopy gA. Estimates of gA obtained from the slope of a plot of H vs. ΔTIR are also insensitive to systematic errors in H (e.g., offset errors in Rnet) because these do not affect the slope. In this context, the canopy gA obtained by this radiometric method represents the canopy leaf boundary layer conductance, as well as the conductance for turbulent heat transfer between the leaves at TAero and Tair measured at the reference height above the canopy.
The H vs. ΔT
IR plot is also useful for exploring differences between T
Aero and T
R. The offset, defined as the value of ΔT
IR when H and ΔT
A are zero (Equation (7)), quantifies this difference because ΔT
IR and ΔT
A are referenced to a common T
air.
The behavior of Offset was studied by varying the intensity of the radiation incident on the canopy using neutral density filters and by changing the chamber wind speed. These changes effectively alter surface radiation forcing (PPF
o) and surface layer feedbacks (wind speed).
2.10. Canopy GSFC and GS
The measurement of canopy ET in controlled environments makes it possible for calculating a “big-leaf” surface canopy conductance (G
SFC) with a corresponding effective VPD at the “big-leaf” surface (D
S). Surface G
SFC was calculated from the ratio of E
can to D
S (Equation (8)):
where G
SFC = canopy surface conductance, E
can = canopy transpiration measured using the gas exchange system (mmol m
−2 s
−1), and P
Atm = atmospheric pressure. D
Bulk was calculated using T
Air measured at the reference location above the canopy. D
Aero is the VPD of the air within the canopy at T
Aero. When D
S = D
Aero in Equation (8), each leaf surface is at the mean aerodynamic temperature and sees the same saturation deficit at its surface, which treats the canopy as a giant single leaf where the average canopy leaf temperature equals T
Aero.
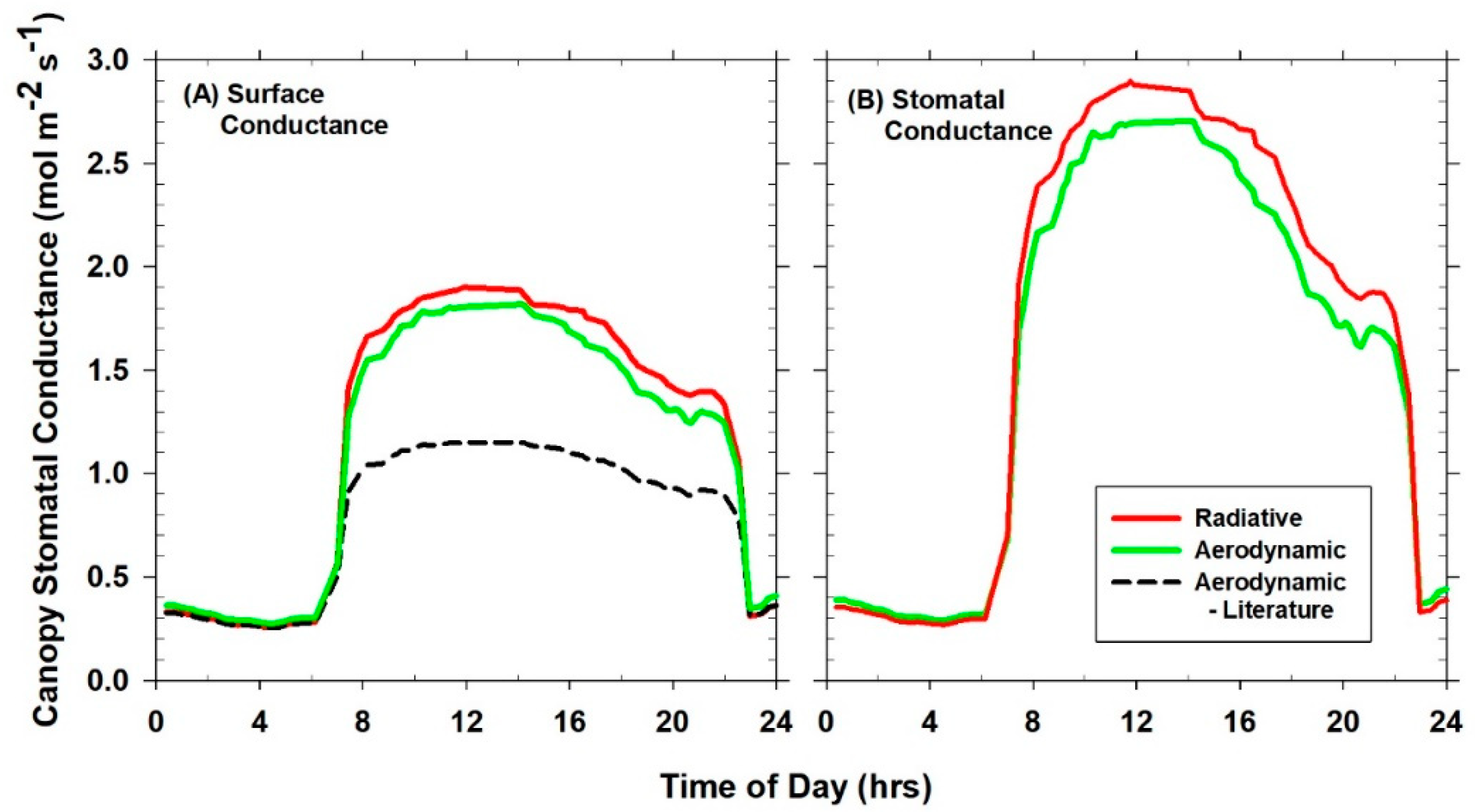
Canopy G
SFC calculated from Equation (8) includes canopy G
S and g
A [
10] because these conductances are additive in series. Canopy G
S was calculated from surface G
SFC and g
A using Equation (9), the resistance subtraction method [
7]. G
S is metabolically controlled canopy stomatal conductance that influences land atmosphere interactions via land surface feedbacks.
2.11. Canopy Decoupling Coefficient
At the canopy level, relative magnitudes of G
S and g
A determine the effect of changes in stomatal conductance on the transport of heat and water vapor from an average leaf surface, through leaf and canopy boundary layers to an effective sink for heat and water vapor above the canopy [
3]. The boundary layer surrounding vegetation allows transpired water vapor to humidify air near the leaf surface (e.g., it lowers D
S compared to D
Bulk), altering the driving force for transpiration; thus, E
can becomes less sensitive to changes in stomatal conductance. This feedback between E
can and D
S is important for diminishing the sensitivity of E
can to proportional changes in G
S [
1,
3,
4].
The dimensionless decoupling coefficient, Ω, quantifies the sensitivity of E
can to changes in stomatal aperture and depends on the influence that G
S and g
A exert on how closely conditions at the leaf surface (e.g., D
S) are linked to D
Bulk of the free air stream. Equation (10) calculates Ω from g
A, G
S, and ε = s/γ, where s = the slope of the saturation vapor pressure versus temperature, and γ = the psychrometric constant [
10].
Equation (10) assumes that the available energy is independent of surface temperature and neglects changes in leaf temperature due to changes in stomatal conductance [
4]. In spite of this simplification, Ω is useful for (1) exploring how differences in canopy architecture (e.g., wheat and soybean) affect canopy transpiration and (2) quantifying the sensitivity of E
can to changes in stomatal conductance. Typical values for g
A, G
S, and Ω for crops and forests are depicted in
Table 1. The magnitude of Ω effectively determines whether Ecan is primarily controlled by stomata or by the supply of energy. Generally, forests are well coupled, and their transpiration rate is accurately predicted by the Priestley–Taylor equation [
3,
4]. The sensitivity of transpiration to stomatal control, dE
can, is determined by the degree of coupling (1 − Ω) between D
S and D
Bulk (Equation (11); [
3,
6,
7]).
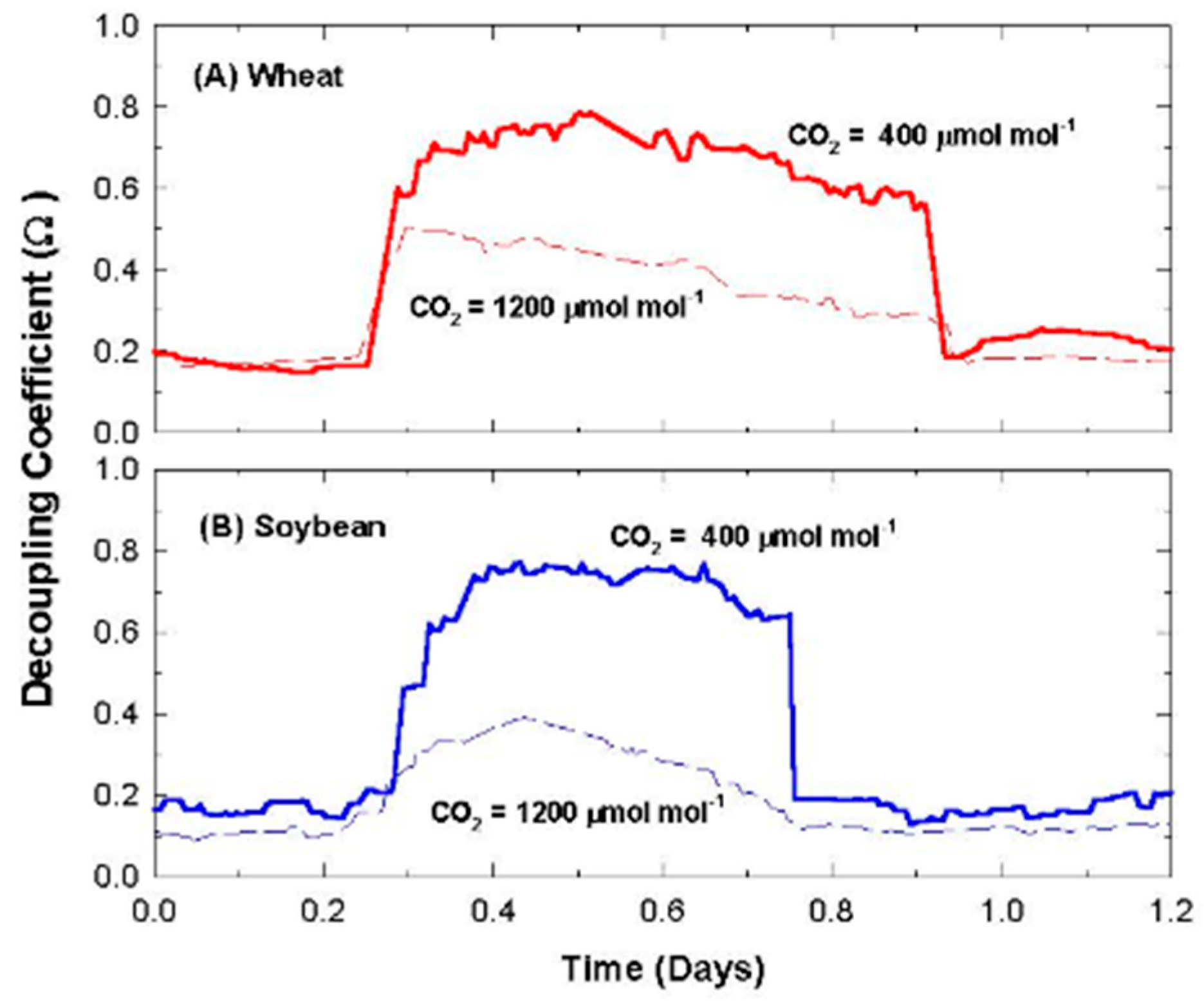
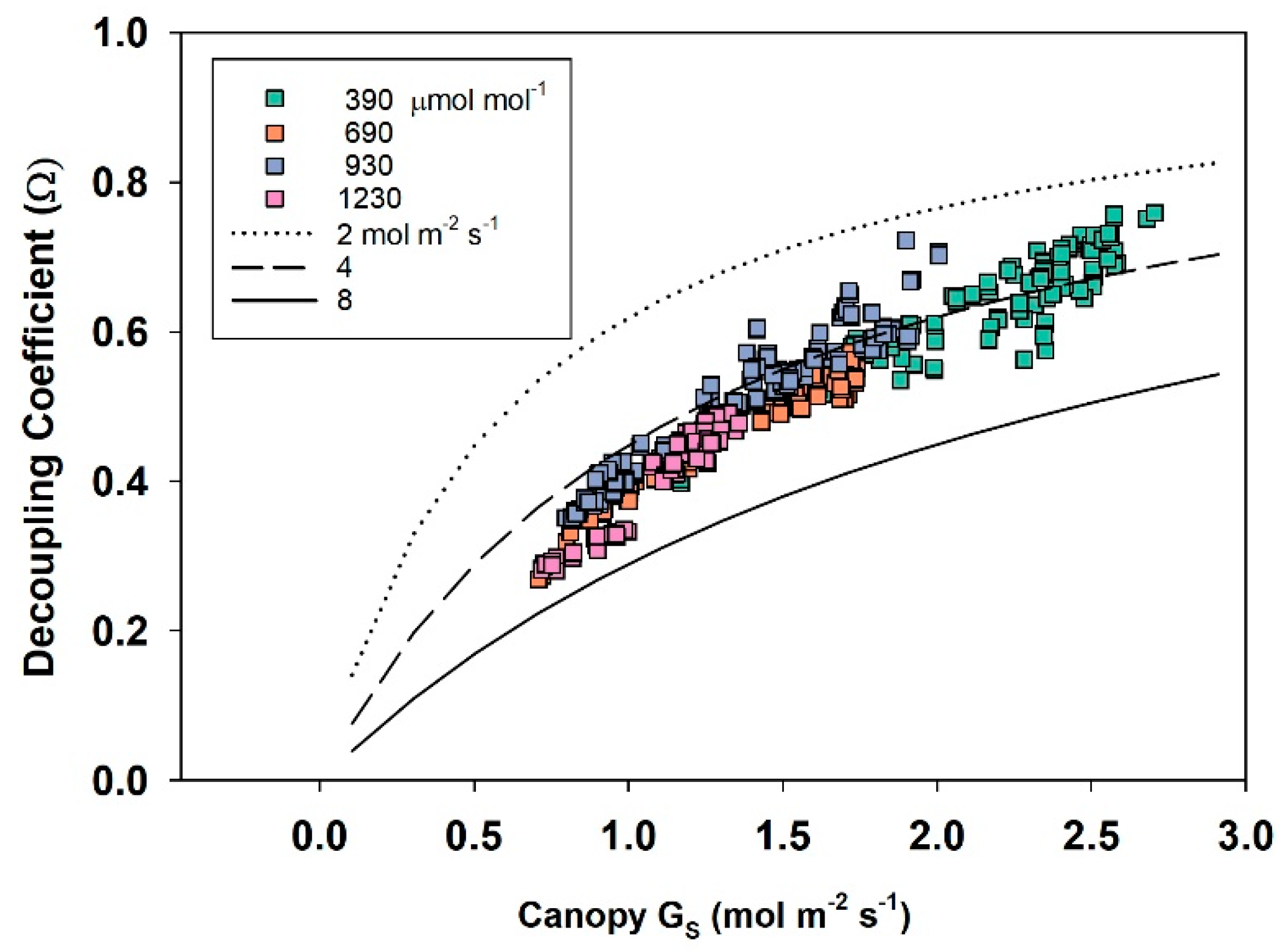
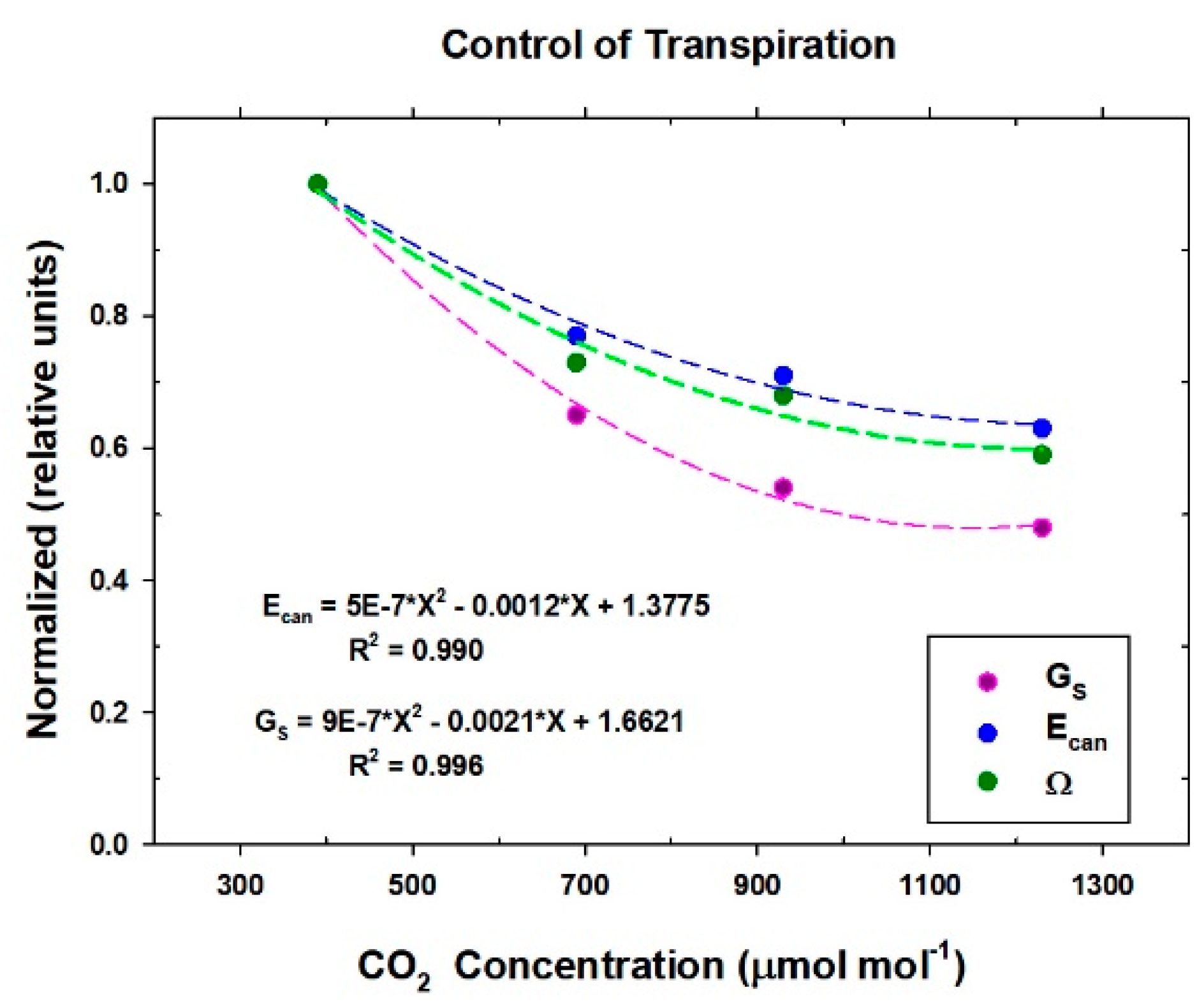
2.12. Responses of Transpiration to Elevated CO2
Responses of transpiration to CO2 concentration were measured at a constant PPFo using the same vegetative wheat canopy over a span of 8 days. During this time, chamber CO2 was increased in a stepwise fashion from 400, to 700, to 950, and to 1200 umol mol−1. Canopy gas exchange fluxes and energy balance components were held at each CO2 concentration for 48 h to allow the incremental buildup of sugar pools in tissues throughout the canopy. These data were used to measure canopy aerodynamic conductance and to determine the response of canopy transpiration to increased CO2 concentration. Daily average values of Ecan, Pnet, LE, H, GS, Ω, and WUE were calculated because GS and Ecan did not remain constant throughout the day due to diurnal changes in stomatal conductance.