Classification of Crop Tolerance to Heat and Drought—A Deep Convolutional Neural Networks Approach
Abstract
1. Introduction
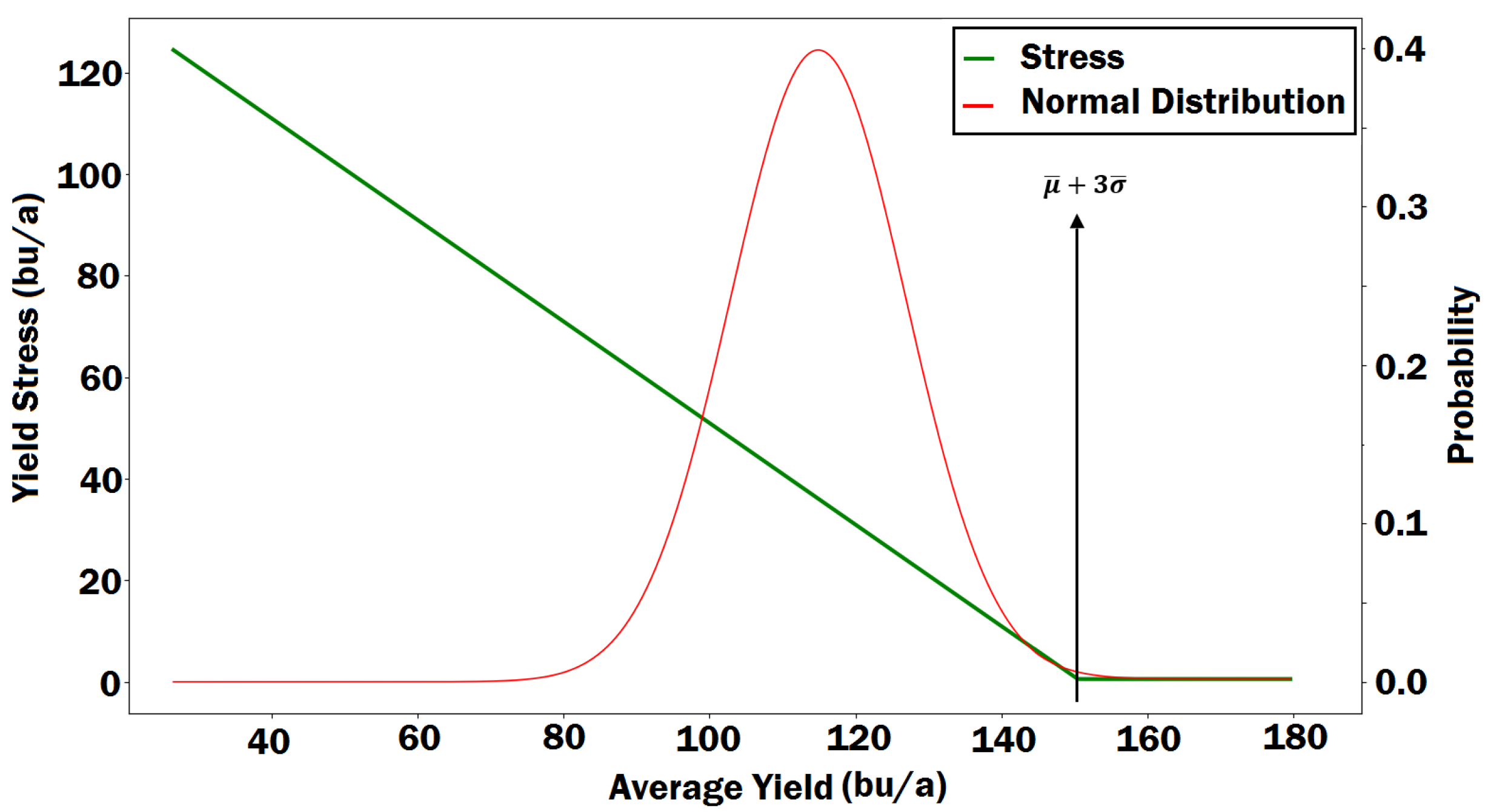
2. Problem Statement
3. Methods and Results
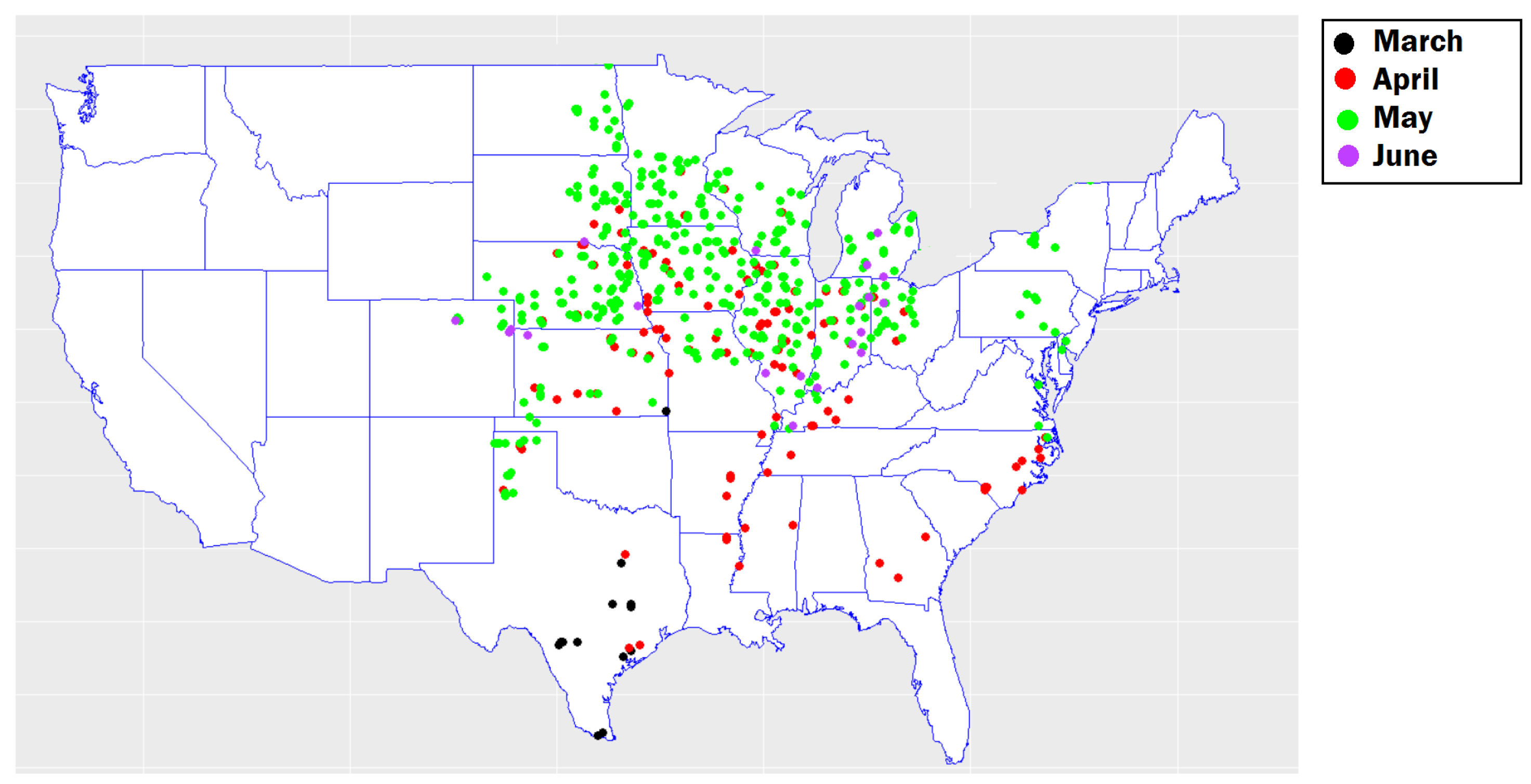
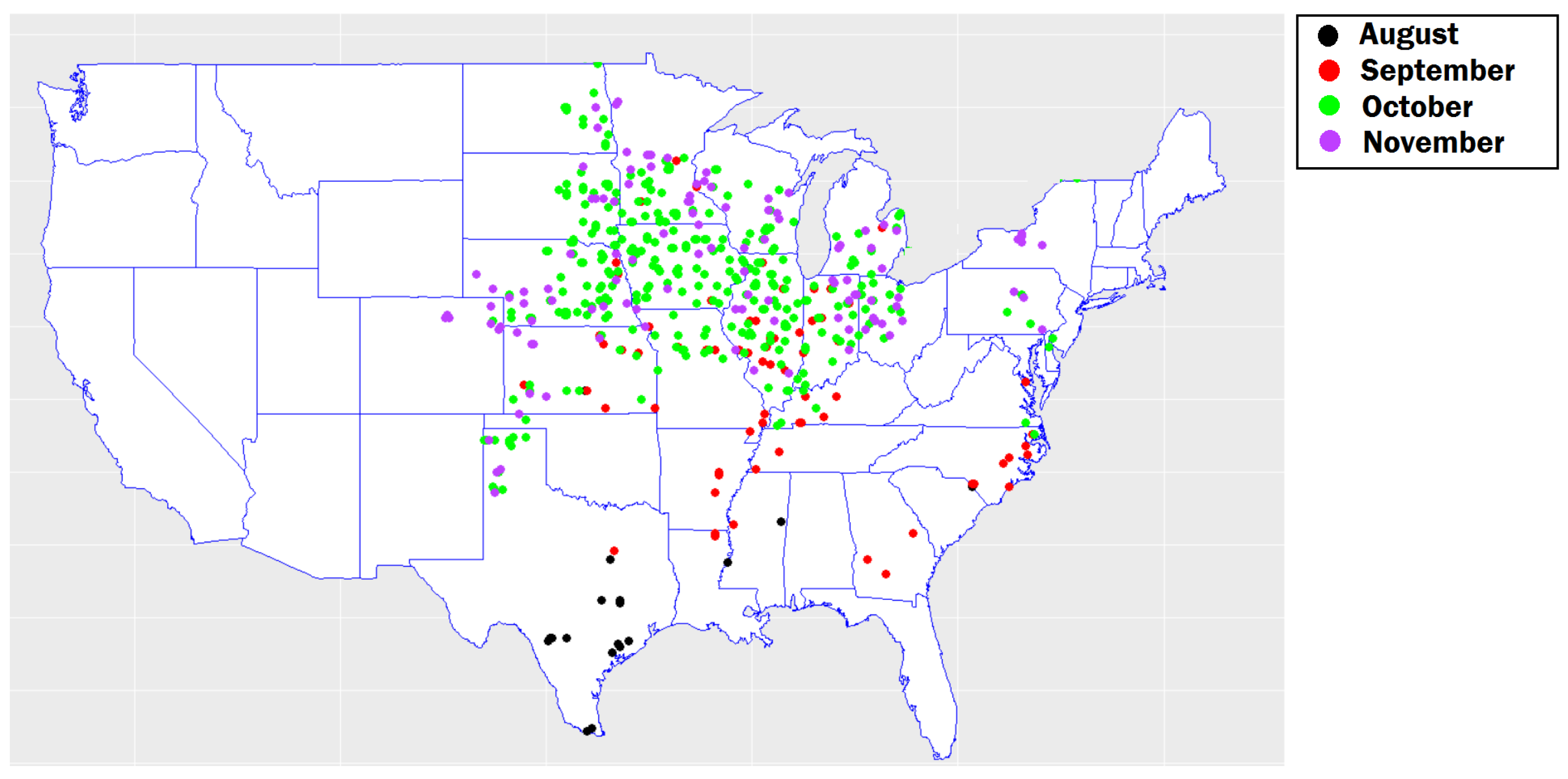
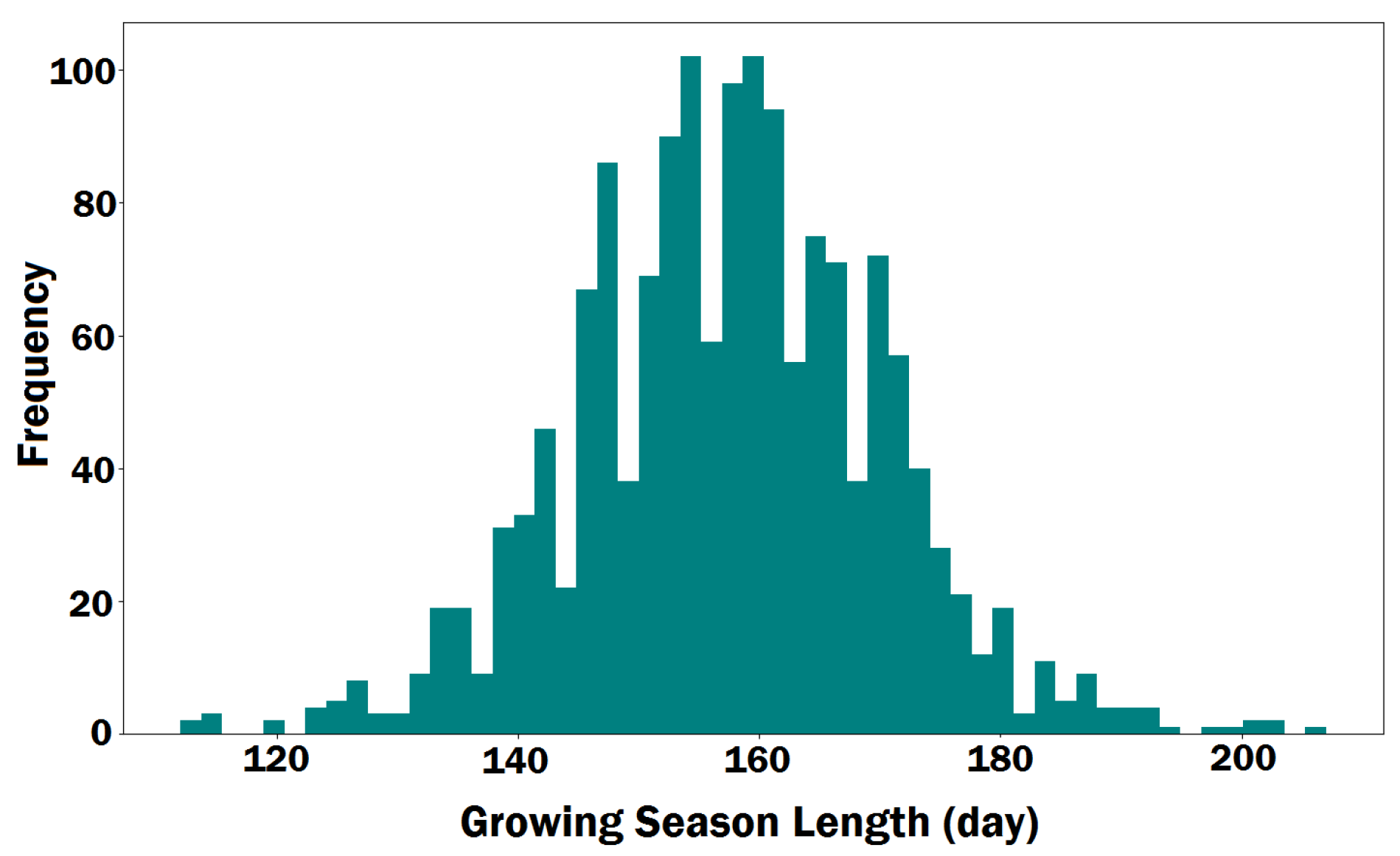
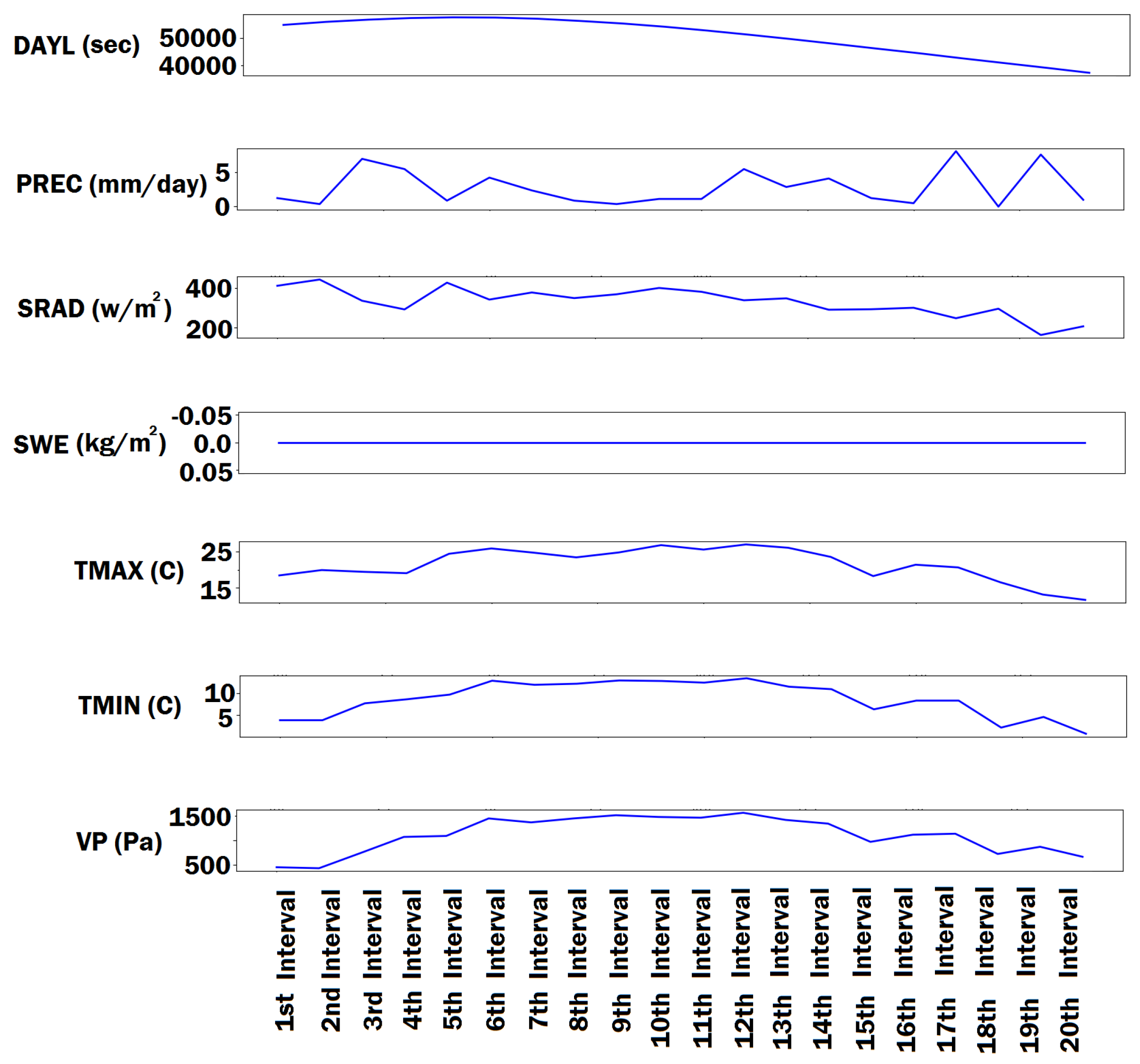
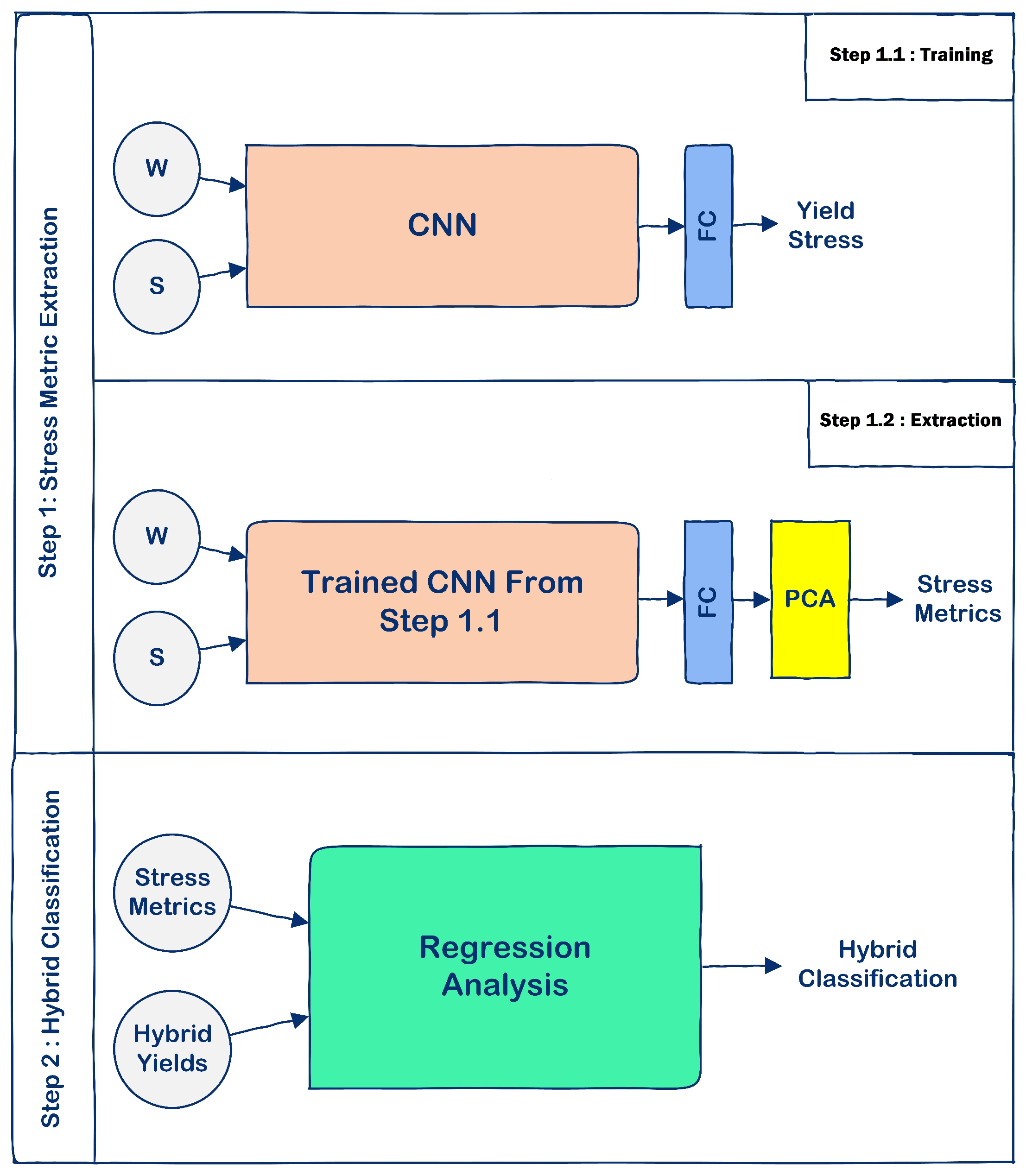
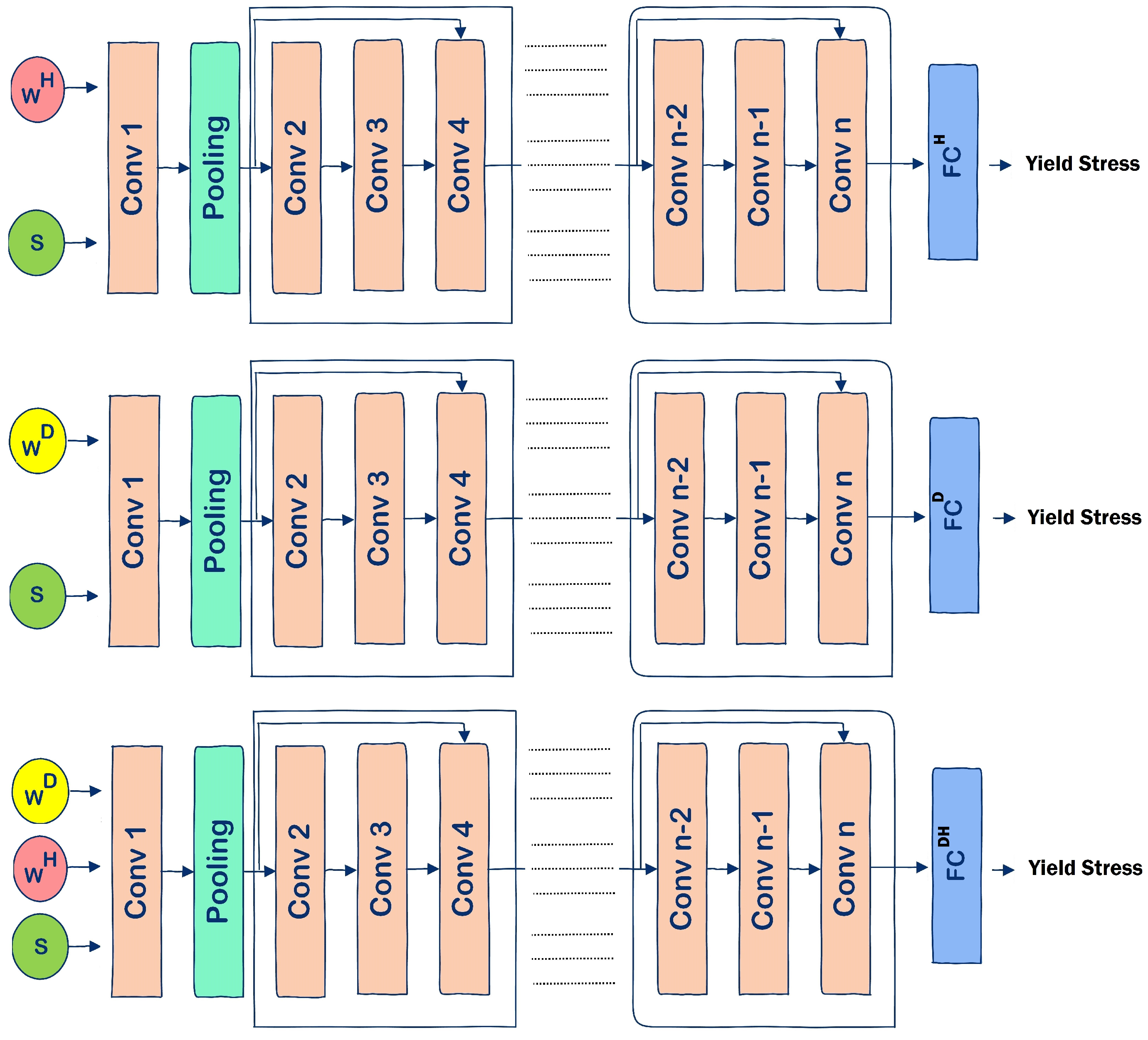
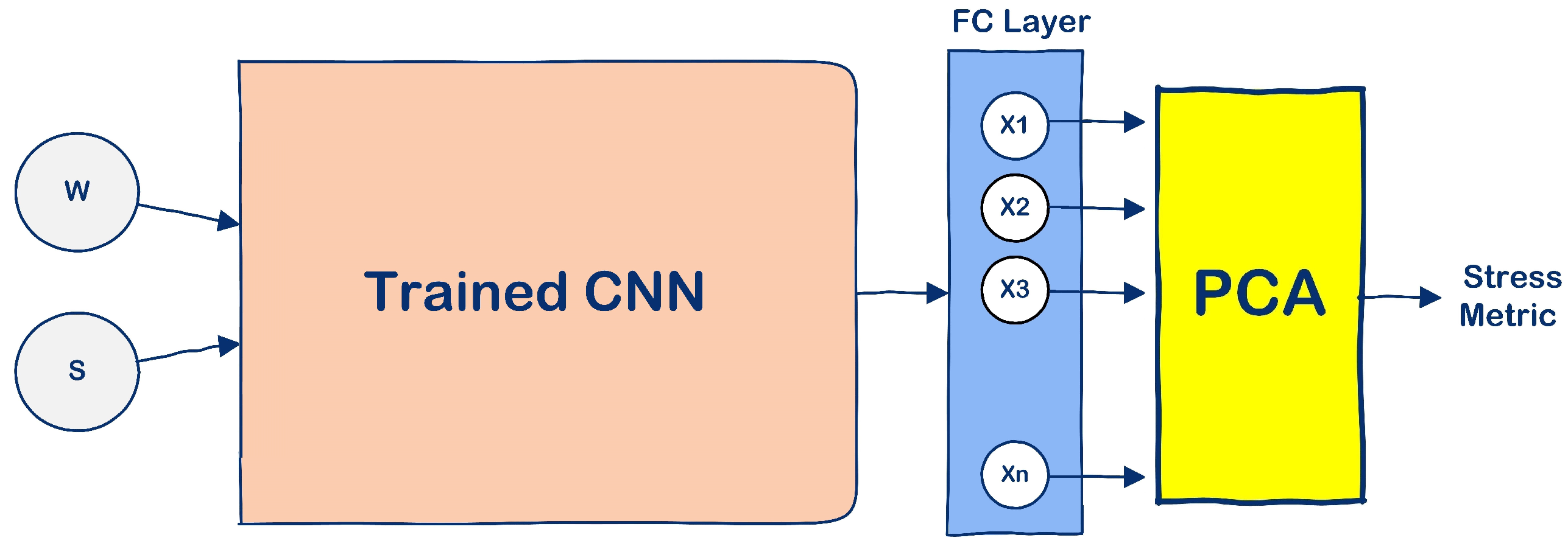
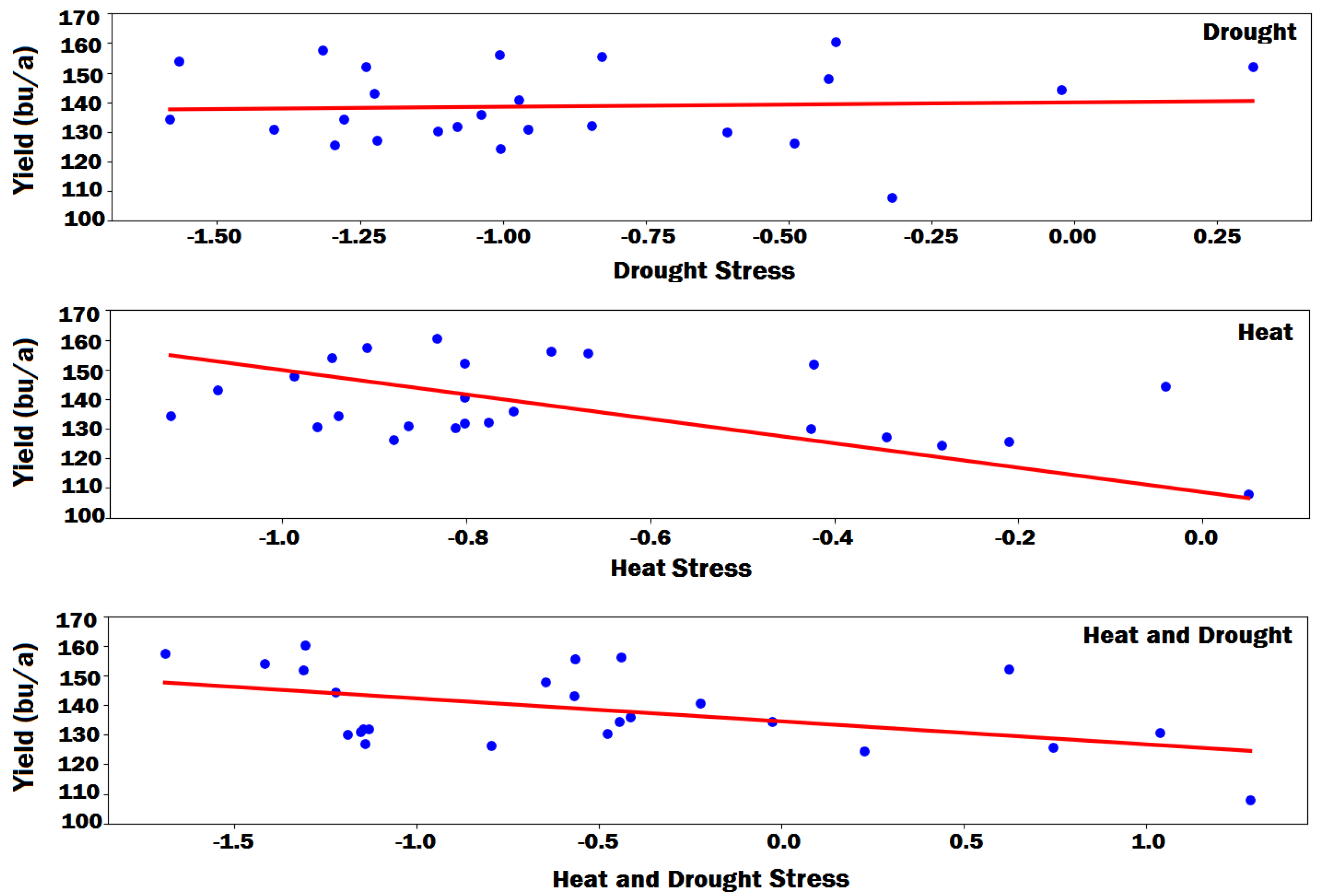
3.1. Stress Metric Extraction Method
3.2. Stress Metric Extraction Results
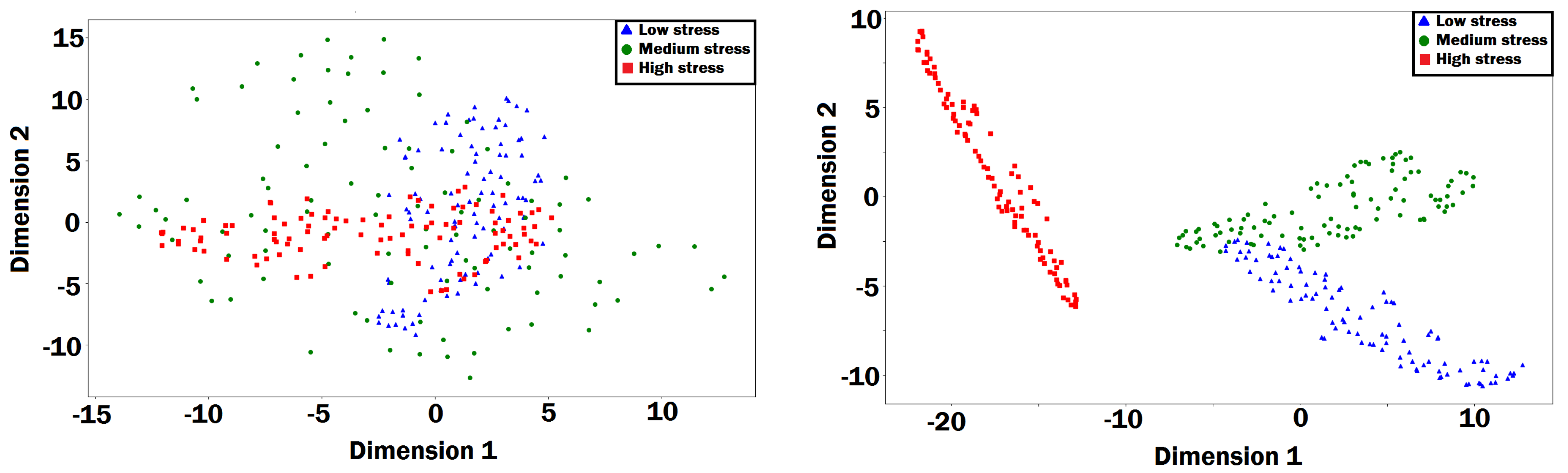
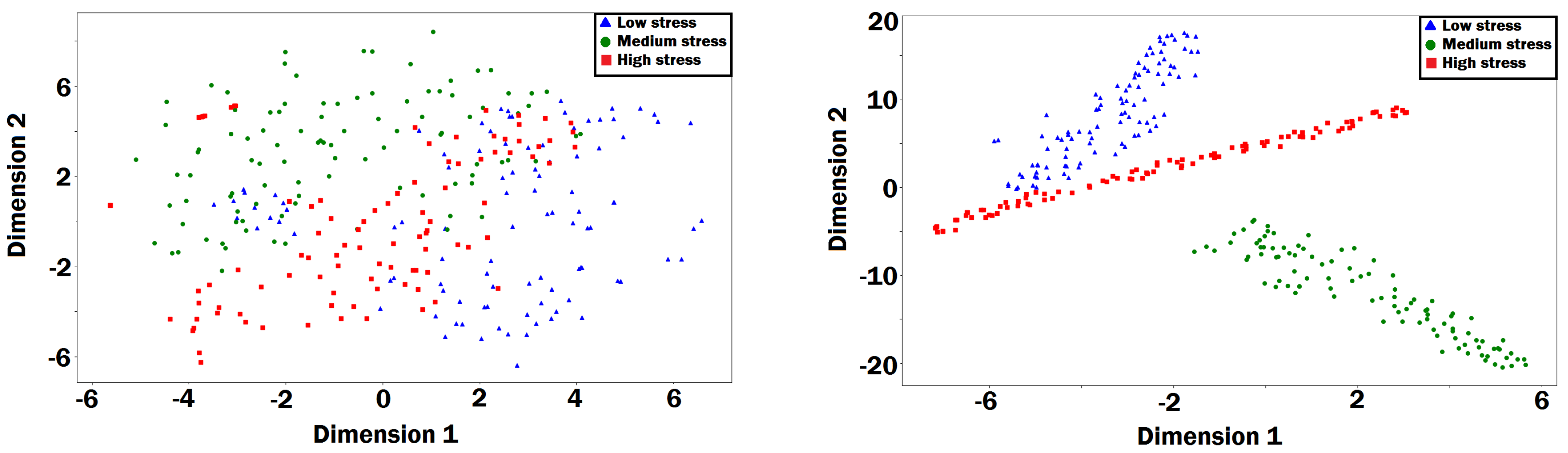
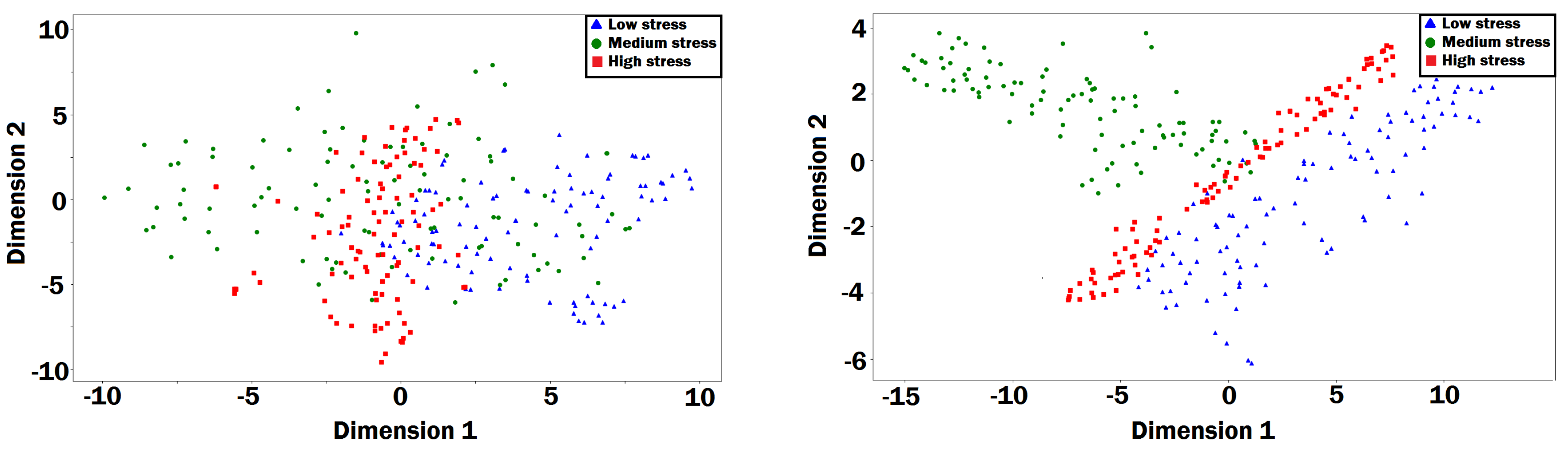
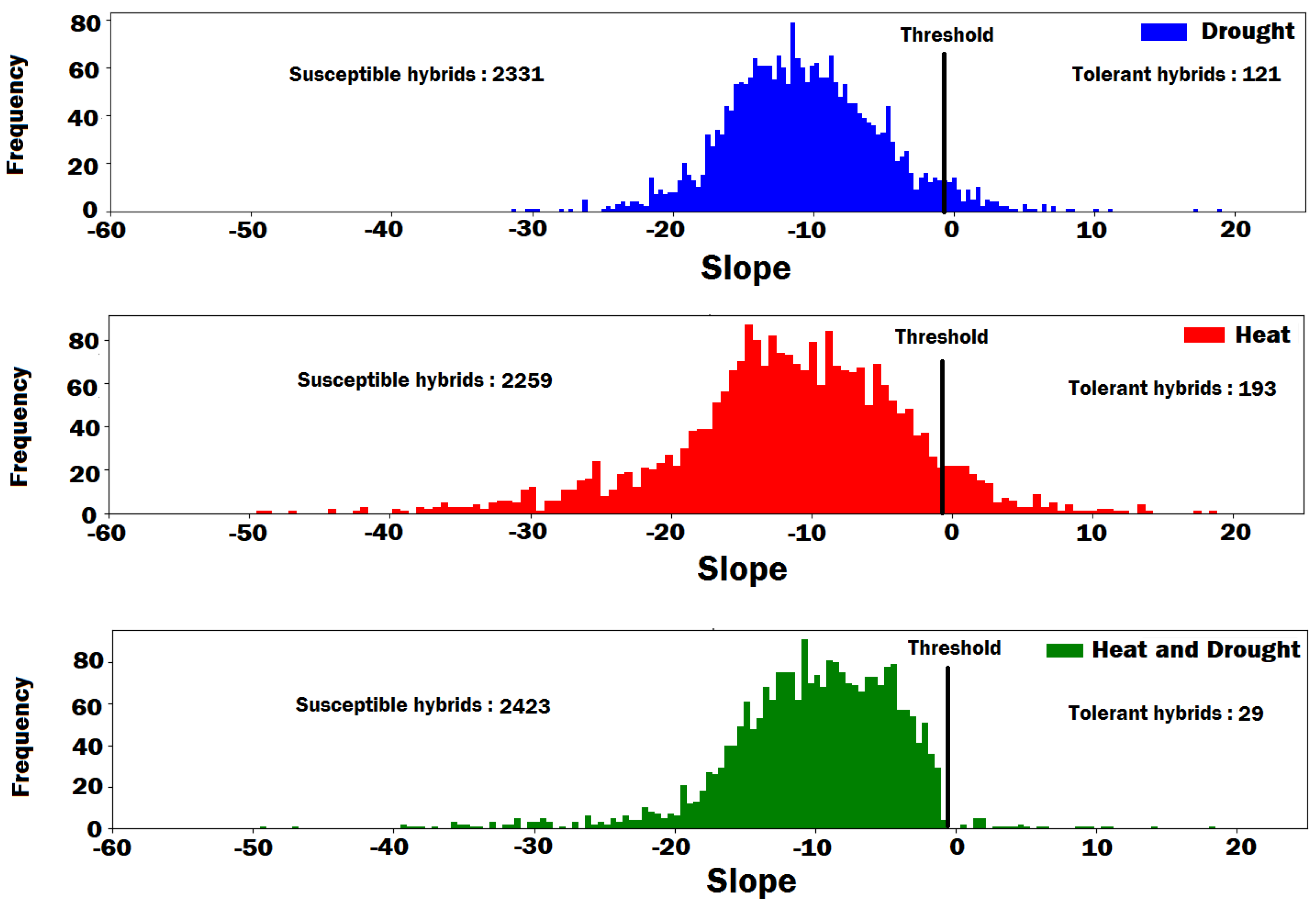
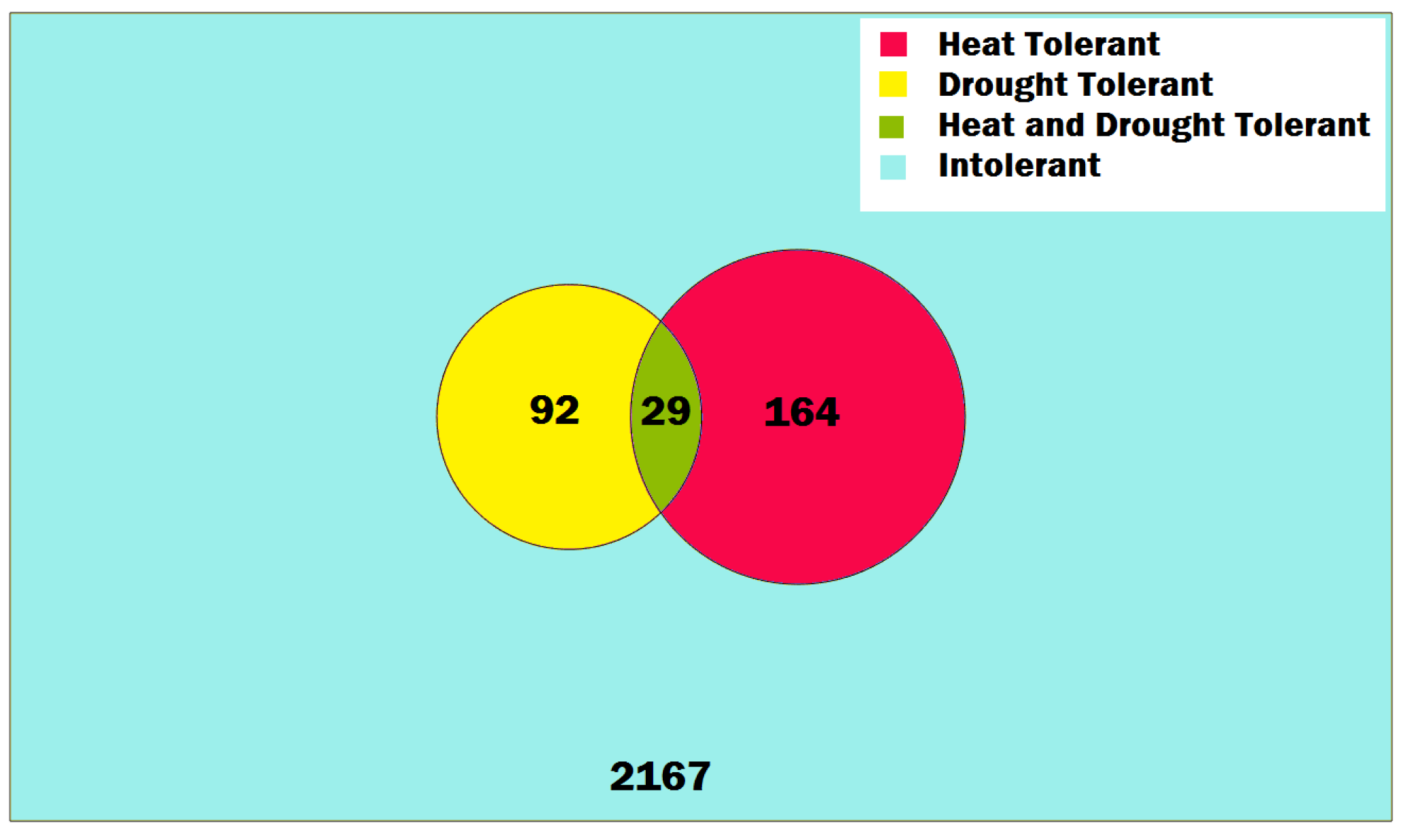
3.3. Hybrid Stress Classification Method
3.4. Hybrid Stress Classification Results
4. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, J.; Xu, W.; Velten, J.; Xin, Z.; Stout, J. Characterization of maize inbred lines for drought and heat tolerance. J. Soil Water Conserv. 2012, 67, 354–364. [Google Scholar] [CrossRef]
- Peng, S.; Huang, J.; Sheehy, J.E.; Laza, R.C.; Visperas, R.M.; Zhong, X.; Centeno, G.S.; Khush, G.S.; Cassman, K.G. Rice yields decline with higher night temperature from global warming. Proc. Natl. Acad. Sci. USA 2004, 101, 9971–9975. [Google Scholar] [CrossRef] [PubMed]
- Boyer, J.; Byrne, P.; Cassman, K.; Cooper, M.; Delmer, D.; Greene, T.; Gruis, F.; Habben, J.; Hausmann, N.; Kenny, N.; et al. The US drought of 2012 in perspective: A call to action. Glob. Food Secur. 2013, 2, 139–143. [Google Scholar] [CrossRef]
- Cayan, D.R.; Das, T.; Pierce, D.W.; Barnett, T.P.; Tyree, M.; Gershunov, A. Future dryness in the southwest US and the hydrology of the early 21st century drought. Proc. Natl. Acad. Sci. USA 2010, 107, 21271–21276. [Google Scholar] [CrossRef] [PubMed]
- Sanderson, M.; Hemming, D.; Betts, R. Regional temperature and precipitation changes under high-end (>4 °C) global warming. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 2011, 369, 85–98. [Google Scholar] [CrossRef]
- Hlavinka, P.; Trnka, M.; Semerádová, D.; Dubrovskỳ, M.; Žalud, Z.; Možnỳ, M. Effect of drought on yield variability of key crops in Czech Republic. Agric. Forest Meteorol. 2009, 149, 431–442. [Google Scholar] [CrossRef]
- Heisey, P.W.; Edmeades, G.O. CIMMYT 1997/98 World Maize Facts and Trends; Maize Production in Drought-Stressed Environments: Technical Options and Research Resource Allocation; Technical Report; CIMMYT: Mexico City, Mexico, 1999. [Google Scholar]
- Shaw, R. Estimates of yield reductions in corn caused by water and temperature stress. In Crop Reactions to Water and Temperature Stresses in Humid, Temperate Climates; Westview Press: Boulder, CO, USA, 1983; pp. 49–66. [Google Scholar]
- Farré, I.; Faci, J.M. Comparative response of maize (Zea mays L.) and sorghum (Sorghum bicolor L. Moench) to deficit irrigation in a Mediterranean environment. Agric. Water Manag. 2006, 83, 135–143. [Google Scholar] [CrossRef]
- Schussler, J.; Westgate, M. Maize kernel set at low water potential: II. Sensitivity to reduced assimilates at pollination. Crop Sci. 1991, 31, 1196–1203. [Google Scholar] [CrossRef]
- Lobell, D.B.; Bänziger, M.; Magorokosho, C.; Vivek, B. Nonlinear heat effects on African maize as evidenced by historical yield trials. Nat. Clim. Chang. 2011, 1, 42. [Google Scholar] [CrossRef]
- Chen, J.; Xu, W.; Burke, J.J.; Xin, Z. Role of phosphatidic acid in high temperature tolerance in maize. Crop Sci. 2010, 50, 2506–2515. [Google Scholar] [CrossRef]
- Lobell, D.B.; Burke, M.B. On the use of statistical models to predict crop yield responses to climate change. Agric. Forest Meteorol. 2010, 150, 1443–1452. [Google Scholar] [CrossRef]
- Badu-Apraku, Á.; Hunter, R.; Tollenaar, M. Effect of temperature during grain filling on whole plant and grain yield in maize (Zea mays L.). Can. J. Plant Sci. 1983, 63, 357–363. [Google Scholar] [CrossRef]
- Cairns, J.E.; Crossa, J.; Zaidi, P.; Grudloyma, P.; Sanchez, C.; Araus, J.L.; Thaitad, S.; Makumbi, D.; Magorokosho, C.; Bänziger, M.; et al. Identification of drought, heat, and combined drought and heat tolerant donors in maize. Crop Sci. 2013, 53, 1335–1346. [Google Scholar] [CrossRef]
- Cantarero, M.; Cirilo, A.; Andrade, F. Night temperature at silking affects set in maize. Crop Sci. 1999, 39, 703–710. [Google Scholar] [CrossRef]
- Cheikh, N.; Jones, R.J. Disruption of maize kernel growth and development by heat stress (role of cytokinin/abscisic acid balance). Plant Physiol. 1994, 106, 45–51. [Google Scholar] [CrossRef]
- Adee, E.; Roozeboom, K.; Balboa, G.R.; Schlegel, A.; Ciampitti, I.A. Drought-Tolerant Corn Hybrids Yield More in Drought-Stressed Environments with No Penalty in Non-stressed Environments. Front. Plant Sci. 2016, 7, 1534. [Google Scholar] [CrossRef]
- Barnabás, B.; Jäger, K.; Fehér, A. The effect of drought and heat stress on reproductive processes in cereals. Plant Cell Environ. 2008, 31, 11–38. [Google Scholar] [CrossRef]
- Rizhsky, L.; Liang, H.; Mittler, R. The combined effect of drought stress and heat shock on gene expression in tobacco. Plant Physiol. 2002, 130, 1143–1151. [Google Scholar] [CrossRef]
- Chapman, S.C. Use of crop models to understand genotype by environment interactions for drought in real-world and simulated plant breeding trials. Euphytica 2008, 161, 195–208. [Google Scholar] [CrossRef]
- Sadras, V.; Reynolds, M.; De la Vega, A.; Petrie, P.; Robinson, R. Phenotypic plasticity of yield and phenology in wheat, sunflower and grapevine. Field Crops Res. 2009, 110, 242–250. [Google Scholar] [CrossRef]
- Bradshaw, A.D. Evolutionary significance of phenotypic plasticity in plants. In Advances in Genetics; Elsevier: Amsterdam, The Netherlands, 1965; Volume 13, pp. 115–155. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press Cambridge: Cambridge, MA, USA, 2016; Volume 1. [Google Scholar]
- Etminan, A.; Pour-Aboughadareh, A.; Mohammadi, R.; Shooshtari, L.; Yousefiazarkhanian, M.; Moradkhani, H. Determining the best drought tolerance indices using Artificial Neural Network (ANN): Insight into application of intelligent agriculture in agronomy and plant breeding. Cereal Res. Commun. 2019, 47, 170–181. [Google Scholar] [CrossRef]
- An, J.; Li, W.; Li, M.; Cui, S.; Yue, H. Identification and Classification of Maize Drought Stress Using Deep Convolutional Neural Network. Symmetry 2019, 11, 256. [Google Scholar] [CrossRef]
- Kamilaris, A.; Prenafeta-Boldú, F.X. Deep learning in agriculture: A survey. Comput. Electron. Agric. 2018, 147, 70–90. [Google Scholar] [CrossRef]
- Khaki, S.; Wang, L.; Archontoulis, S.V. A CNN-RNN Framework for Crop Yield Prediction. arXiv 2019, arXiv:1911.09045. [Google Scholar]
- Kim, N.; Ha, K.J.; Park, N.W.; Cho, J.; Hong, S.; Lee, Y.W. A Comparison Between Major Artificial Intelligence Models for Crop Yield Prediction: Case Study of the Midwestern United States, 2006–2015. ISPRS Int. J. Geo-Inf. 2019, 8, 240. [Google Scholar] [CrossRef]
- Wang, A.X.; Tran, C.; Desai, N.; Lobell, D.; Ermon, S. Deep transfer learning for crop yield prediction with remote sensing data. In Proceedings of the 1st ACM SIGCAS Conference on Computing and Sustainable Societies, San Jose, CA, USA, 20–22 June 2018; p. 50. [Google Scholar]
- Khaki, S.; Wang, L. Crop Yield Prediction Using Deep Neural Networks. Front. Plant Sci. 2019, 10, 621. [Google Scholar] [CrossRef]
- Hilborn, R.; Mangel, M. The Ecological Detective: Confronting Mmodels with Data; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- Bolker, B.M. Ecological Models and Data in R; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Syngenta. Syngenta Crop Challenge in Analytics. 2019. Available online: https://www.ideaconnection.com/syngenta-crop-challenge/challenge.php (accessed on 25 September 2019).
- Nafziger, E.D. Corn planting date and plant population. J. Prod. Agric. 1994, 7, 59–62. [Google Scholar] [CrossRef]
- Borovykh, A.; Bohte, S.; Oosterlee, C.W. Conditional time series forecasting with convolutional neural networks. arXiv 2017, arXiv:1703.04691. [Google Scholar]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A critical review of recurrent neural networks for sequence learning. arXiv 2015, arXiv:1506.00019. [Google Scholar]
- Garcia-Gasulla, D.; Parés, F.; Vilalta, A.; Moreno, J.; Ayguadé, E.; Labarta, J.; Cortés, U.; Suzumura, T. On the behavior of convolutional nets for feature extraction. J. Artif. Intell. Res. 2018, 61, 563–592. [Google Scholar] [CrossRef]
- Sharif Razavian, A.; Azizpour, H.; Sullivan, J.; Carlsson, S. CNN features off-the-shelf: An astounding baseline for recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Columbus, OH, USA, 24–27 June 2014; pp. 806–813. [Google Scholar]
- Azizpour, H.; Razavian, A.S.; Sullivan, J.; Maki, A.; Carlsson, S. Factors of transferability for a generic convnet representation. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 1790–1802. [Google Scholar] [CrossRef] [PubMed]
- Dara, S.; Tumma, P. Feature Extraction by Using Deep Learning: A Survey. In Proceedings of the 2018 Second International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 29–31 March 2018; pp. 1795–1801. [Google Scholar]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Chia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M. TensorFlow: A System for Large Scale Machine Learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI’16), Savannah, GA, USA, 2–4 November 2016; Volume 16, pp. 265–283. [Google Scholar]
- Maaten, L.V.D.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Khaki, S. Source Code. 2019. Available online: https://github.com/saeedkhaki92/Crop-stress-classification (accessed on 25 September 2019).
| Literature | Method | Type | Input Data | Model Output |
|---|---|---|---|---|
| Lobell et al. [11] | linear fixed-effects model | supervised | weather | analysis of yield response to heat and drought stresses |
| Lobell and Burke [13] | panel regression and time-series regression | supervised | weather | analysis of yield response to heat and drought stresses |
| Badu-Apraku et al. [14] | linear regression model | supervised | weather | analysis of yield response to heat stress |
| Adee et al. [18] | segmented regression model | supervised | weather | analysis of yield response to drought stress |
| Chen et al. [1] | general linear model | supervised | weather | analysis of yield response to heat and drought stresses |
| Cairns et al. [15] | linear mixed model | supervised | weather | analysis of yield response to heat and drought stresses |
| Etminan et al. [27] | artificial neural network | supervised | weather | identification of drought-related factors |
| An et al. [28] | CNN | supervised | digital image | classification of crop tolerance to drought |
| Proposed method | CNN and linear regression | unsupervised | weather and soil | (1) classification of crop tolerance to drought, heat and their combination (2) stress metrics extraction |
| CNN Structure | |||||
|---|---|---|---|---|---|
| Block | Layer Name | FS | NF | S | P |
| a | Conv1 | 3 | 8 | 1 | same |
| - | Average pooling 1 | 2 | - | 2 | valid |
| b | Conv2 | 1 | 8 | 1 | valid |
| Conv3 | 3 | 8 | 1 | same | |
| Conv4 | 1 | 8 | 1 | valid | |
| - | Average pooling 2 | 2 | - | 2 | valid |
| c | Conv5 | 1 | 8 | 2 | valid |
| Conv6 | 3 | 8 | 1 | same | |
| Conv7 | 1 | 12 | 1 | valid | |
| - | Average pooling 3 | 2 | - | 2 | valid |
| d | Conv8 | 1 | 10 | 1 | valid |
| Conv9 | 3 | 10 | 1 | same | |
| Conv10 | 1 | 12 | 1 | valid | |
| - | Average pooling 4 | 2 | - | 2 | valid |
| e | Conv11 | 1 | 10 | 1 | valid |
| Conv12 | 3 | 10 | 1 | same | |
| Conv13 | 1 | 12 | 1 | valid | |
| - | Average pooling 5 | 2 | - | 2 | valid |
| Model | Training RMSE | Test RMSE |
|---|---|---|
| CNN using H and S variables | 16.65 | 19.31 |
| CNN using D and S variables | 16.46 | 20.01 |
| CNN using D, H and S variables | 18.38 | 20.69 |
| Stress Type | Slope | Intercept |
|---|---|---|
| Drought | 1.49 | 139.99 |
| Heat | −16.21 | 127.39 |
| Combined Drought and Heat | −7.75 | 134.46 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khaki, S.; Khalilzadeh, Z.; Wang, L. Classification of Crop Tolerance to Heat and Drought—A Deep Convolutional Neural Networks Approach. Agronomy 2019, 9, 833. https://doi.org/10.3390/agronomy9120833
Khaki S, Khalilzadeh Z, Wang L. Classification of Crop Tolerance to Heat and Drought—A Deep Convolutional Neural Networks Approach. Agronomy. 2019; 9(12):833. https://doi.org/10.3390/agronomy9120833
Chicago/Turabian StyleKhaki, Saeed, Zahra Khalilzadeh, and Lizhi Wang. 2019. "Classification of Crop Tolerance to Heat and Drought—A Deep Convolutional Neural Networks Approach" Agronomy 9, no. 12: 833. https://doi.org/10.3390/agronomy9120833
APA StyleKhaki, S., Khalilzadeh, Z., & Wang, L. (2019). Classification of Crop Tolerance to Heat and Drought—A Deep Convolutional Neural Networks Approach. Agronomy, 9(12), 833. https://doi.org/10.3390/agronomy9120833




