A Pipeline for Mushroom Mass Estimation Based on Phenotypic Parameters: A Multiple Oudemansiella raphanipies Model

Abstract

Estimating the mass of Oudemansiella raphanipies quickly and accurately is indispensable in optimizing post-harvest packaging processes. Traditional methods typically involve manual grading followed by weighing with a balance, which is inefficient and labor-intensive. To address the challenges encountered in actual production scenarios, in this work, we developed a novel pipeline for estimating the mass of multiple Oudemansiella raphanipies. To achieve this goal, an enhanced deep learning (DL) algorithm for instance segmentation and a machine learning (ML) model for mass prediction were introduced. On one hand, to segment multiple samples in the same image, a novel instance segmentation network named FinePoint-ORSeg was applied to obtain the finer edges of samples, by integrating an edge attention module to improve the fineness of the edges. On the other hand, for individual samples, a novel cap–stem segmentation approach was applied and 18 phenotypic parameters were obtained. Furthermore, principal component analysis (PCA) was utilized to reduce the redundancy among features. Combining the two aspects mentioned above, the mass was computed by an exponential GPR model with seven principal components. In terms of segmentation performance, our model outperforms the original Mask R-CNN; the $\mathrm{A}\mathrm{P}$, ${\mathrm{A}\mathrm{P}}_{50}$, ${\mathrm{A}\mathrm{P}}_{75}$, and ${\mathrm{A}\mathrm{P}}_{\mathrm{s}}$ are improved by 2%, 0.7%, 1.9%, and 0.3%, respectively. Additionally, our model outperforms other networks such as YOLACT, SOLOV2, and Mask R-CNN with Swin. As for mass estimation, the results show that the average coefficient of variation (CV) of a single sample mass in different attitudes is 6.81%. Moreover, the average mean absolute percentage error (MAPE) for multiple samples is 8.53%. Overall, the experimental results indicate that the proposed method is time-saving, non-destructive, and accurate. This can provide a reference for research on post-harvest packaging technology for Oudemansiella raphanipies.

1. Introduction

Oudemansiella raphanipies is a precious edible mushroom that not only contains essential nutrients such as protein, fat, amino acids, and various vitamins but also contains certain amounts of polyphenols and polysaccharides [1]. Additionally, its unique flavor, rich nutritional value, and excellent antioxidant activity are making it increasingly popular among consumers. Thus, Oudemansiella raphanipies has gained popularity as a cultivated crop among mushroom farmers. However, the surge in Oudemansiella raphanipies production has intensified post-harvest packaging and processing difficulties, attributable to its high water content and absence of epidermal tissue. Post-harvest delays in packaging and storage accelerate quality loss in mushrooms, adversely impacting their marketability and farmer incomes. This is also one of the key factors hindering the rapid development of the Oudemansiella raphanipies industry.

Typically, the packaging of post-harvest agricultural products is based on mass. To improve the weighing efficiency, electronic weighing equipment is used to replace traditional mechanical weighing devices [2]. However, during the operation process, workers may cause physical damage, which further reduces the value of samples. With the rapid development of computer vision technology, non-destructive mass estimation has emerged as the predominant methodology. One method is to determine the mass of the sample by measuring its volume. This approach relies on the principle that the density of a homogeneous material is constant, implying a direct proportional relationship between the volume and mass. Currently, researchers have achieved satisfactory accuracy in the volume measurement of many agricultural products, such as watermelon [3], apple [4], egg [5,6], orange [7], cucumber, and carrot [8]. Another method is to estimate the mass of samples via a regression method based on phenotypic parameters. Similarly, many researchers have successfully developed regression models to estimate the mass of agricultural products, such as apple [9], kiwi fruit [10], tomato [11], and potato [12]. In contrast to other agricultural products, Oudemansiella raphanipies is not symmetrical, and there are undetermined hollowed-out areas at the bottom when they are processed on the conveyor belt. Therefore, it is difficult to measure the volume of Oudemansiella raphanipies directly via image-based methods; thus, the approach of estimating the mass via the volume is not suitable. From another perspective, owing to the distinct morphological characteristics of Oudemansiella raphanipies compared to conventional agricultural commodities, regression models relying exclusively on basic phenotypic parameters (e.g., length and width) exhibit substantial errors in mass estimation. Furthermore, Oudemansiella raphanipies is commonly handled in batches rather than processed individually in practical production due to the small sizes of individual units. Consequently, it is necessary to design a new means to obtain the mass of a batch of Oudemansiella raphanipies in a rapid and accurate manner. For this purpose, the task can be divided into three subtasks, namely the segmentation of multiple samples, the extraction of multiple complex phenotypic parameters, and the selection of appropriate parameters and approaches for mass regression.

The separation of samples is an instance segmentation task in the field of computer vision. With the development of computer hardware and deep learning, various instance segmentation networks have rapidly emerged, such as Mask R-CNN [13], YOLACT [14], SOLOV2 [15], and Mask R-CNN with Swin [16]. These approaches have achieved impressive performance in the agriculture field. For instance, Yang et al. [17] and Li et al. [18] applied Mask R-CNN to segment soybean to calculate its phenotypic parameters, and the experimental results showed that the method is robust in segmenting targets, even under densely cluttered environments. Sapkota et al. [19] compared YOLOv8 and Mask R-CNN with immature green fruit and trunk and branch datasets. The experimental results showed that both of them effectively segmented apple tree canopy images from both the dormant and early growing seasons, and YOLOv8 performed slightly better in different environments. Moreover, to solve the problem whereby rice field detection technology cannot be adapted to the complexity of the real world, Chen et al. [20] considered the rice row detection problem as an instance segmentation problem and successfully implemented a two-pathway-based method. However, the application of these advanced methods in the field of edible mushrooms is scarce, especially for Oudemansiella raphanipies.

For the phenotypic parameters subtask, recent advances in computer vision and deep learning techniques have enabled the application of automatic phenotype extraction in agronomy. Yang et al. [17] applied principal component analysis (PCA) to correct the pod’s direction and then calculate the width and length of the pod. The results showed that the average measurement error for pod length was 1.33 mm, with an average relative error of 2.90%, while the pod width had an average measurement error of 1.19 mm and an average relative error of 13.32%. Except for length and width, He et al. [21] extracted the pod’s area using the minimum circumscribed rectangle method combined with the template calibration method, and the results showed that the accuracy of the pod area was 97.1%. Additionally, Liu et al. [22] proposed a core diameter Ostu method to judge the posture and then obtained the length, surface area and volume, which were calculated by the elliptic long and short axes of the cross section of the silique. The experimental results reported that the errors of all phenotypic parameters were less than 5.0%. To meet the phenotypic information requirements of Flammulina filiformis breeding, Zhu et al. [23] utilized image recognition technology and deep learning models to automatically calculate phenotypic parameters of Flammulina filiformis fruiting bodies, including cap shape, area, growth position, color, stem length, width, and color. Furthermore, some studies apply the extracted phenotypic characteristics to other tasks. Kumar et al. [24] extracted the centroid, main axis length, and perimeter of plant leaves and then combined them with multiple classifiers to achieve classification. The accuracy of this method can reach 95.42%. Moreover, Okinda et al. [25] fitted the egg to an ellipse using the direct least square method and then extracted 2D features of the ellipse, such as area, eccentricity and perimeter, to establish the relationship between these parameters and the product’s volume using thirteen regression models, achieving excellent results in volume estimation of the egg. However, although the previous studies have obtained the basic parameters of Oudemansiella raphanipies like length and width [26,27], these characteristics cannot fully represent the morphology of Oudemansiella raphanipies. Thus, to obtain an accurate mass result, more complex phenotypic parameters of Oudemansiella raphanipies need to be calculated.

For the mass estimation subtask, existing research has primarily focused on mathematical model-based methods and regression-based methods. Due to the irregularity of agricultural products, more and more regression-based methods have been used. For instance, Nyalala et al. [28] directly fed five phenotypic parameters of tomato (area, perimeter, eccentricity, axis-length, and radial distance) into a support vector machine (SVM) with different kernels and an artificial neural network (ANN) with different training algorithms models to predict its mass. The experimental results showed that the Bayesian regularization ANN outperformed other models, with a root mean square error (RMSE) of 1.468 g. Nevertheless, this approach neglected feature redundancy and correlations between predictors and target variables. To make up for this insufficiency, Saikumar et al. [29] calculated a high linear correlation between the mass and the length, width, perimeter, and projection area first with a correlation coefficient of 0.96, 0.92, 0.92, and 0.95, respectively, and built multiple univariate and multivariate regression models for elephant apple (Dillenia indica L.) mass prediction. The results showed that the multivariate rational model performed the best, with an RMSE of 18.196 g. However, this simplistic variation in input combinations did not consider potential redundancy among the input parameters, which could lead to suboptimal model performance. Moreover, the performance of regression models varies depending on the target. Consequently, to accurately predict the mass of Oudemansiella raphanipies, it is essential to explore optimal model selection and feature optimization strategies.

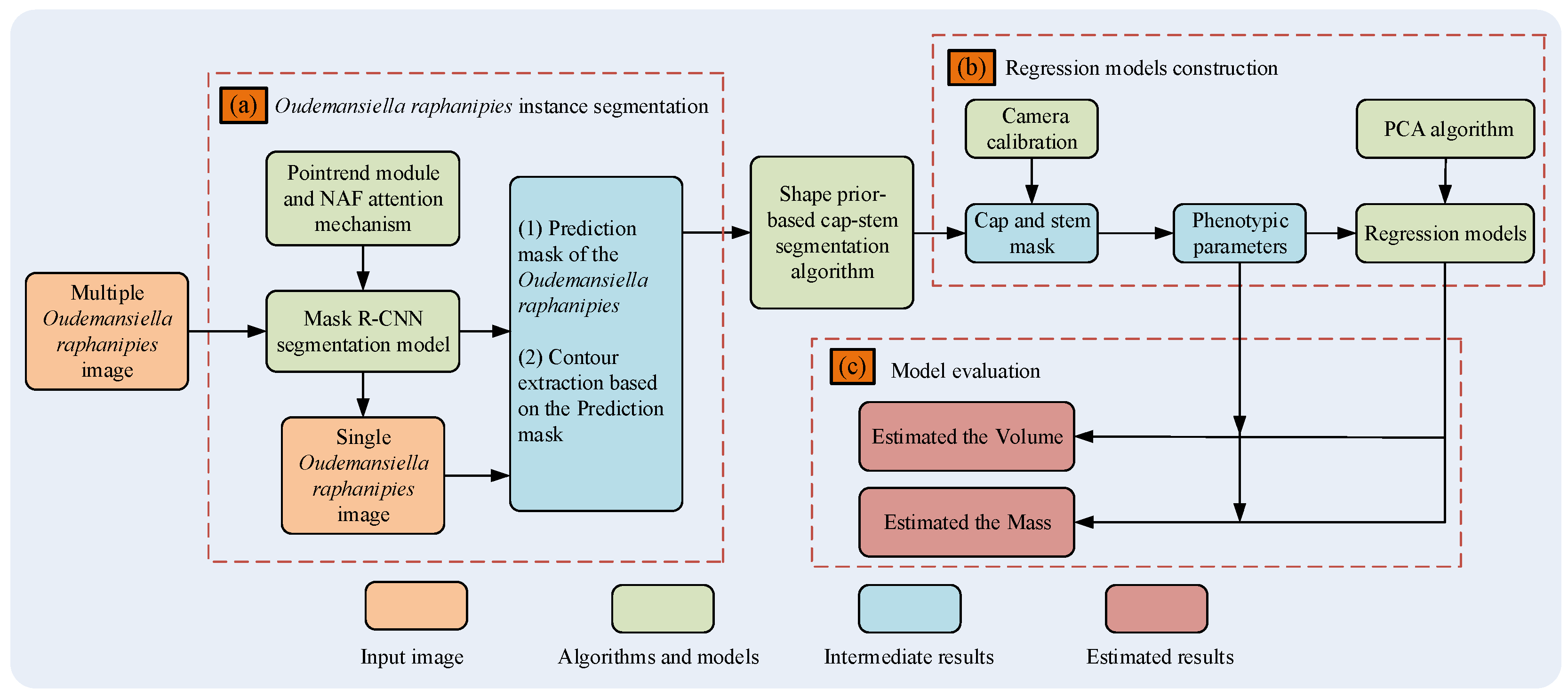
In this study, we implemented a machine learning- and deep learning-based framework for estimating the mass of a batch of Oudemansiella raphanipies. The main contributions are as follows:

(1) A dataset including 1201 images was constructed and a novel instance segmentation network for Oudemansiella raphanipes Segmentation (FinePoint-ORSeg) was applied to obtain the individual sample;

(2) A novel stem–cap-based segmentation method was proposed for extracting phenotypic parameters robustly, and 18 phenotypic parameters were extracted;

(3) We evaluated the performance of various mass regression methods and the best means of calculating the mass of multiple Oudemansiella raphanipies was determined.

2. Materials and Methods

2.1. Materials

2.1.1. Image Acquisition System

The image acquisition system consists of a camera (RealSense SR305, Intel, Santa Clara, CA, USA), a computer (Intel Core i5-7500, 16 GB memory), two LED lights and a camera holder, as shown in Figure 1. Since the proposed method will be applied to the post-harvest packaging assembly line of Oudemansiella raphanipies, the imaging background is set to green to match the conveyor belt. The distance between the camera and the Oudemansiella raphanipies was maintained at 31.5 cm to ensure a sufficient number of samples in the field of view. The RGB images are transferred to the computer via a USB 3.0 data cable and saved in the “PNG” format (640 × 480 pixels).

2.1.2. Dataset

The samples in our work were collected from the School of Biological Science and Engineering, Jiangxi Agricultural University in May 2024 and the edible mushroom factory in Zhangshu City, Jiangxi Province from January to November 2024. Four sub-datasets (Dataset 1, Dataset 2, Dataset 3, Dataset 4) were established as shown in Figure 2.

Dataset 1 contains 1201 labeled images and each image contains several (1–10) Oudemansiella raphanipes. Dataset 2 is used to build the mass regression model, where each sample is shot from different angles seven times at the image center. After removing the blurry images, a total of 1475 images remain. Additionally, we randomly split Dataset 1 and Dataset 2 into a training set and a validation set in an 8:2 ratio, respectively.

On the assembly line, it is easy to fix a camera above the conveyor belt and clearer images can be obtained by controlling the conveyor speed. However, the orientation and position of the Oudemansiella raphanipes in the image cannot be ascertained. Therefore, we additionally set up two datasets, Dataset 3 and Dataset 4, to validate the model’s performance. To explore the robustness of the mass estimation model under different placement states of Oudemansiella raphanipes, Dataset 3 includes 24 Oudemansiella raphanipes and a total of 240 images, where each sample was randomly thrown 10 times, respectively. Dataset 4 contains 30 Oudemansiella raphanipes images, with 10 large (L) samples, 10 medium (M) samples, and 10 small (S) samples, which were classified by experienced farmers and partial examples are shown in Figure 3. For each grade, 10 Oudemansiella raphanipes are grouped together and then randomly thrown on the platform 10 times. This dataset can be used to evaluate the accuracy of the mass estimation method proposed in this paper. Additionally, a high-precision densitometer (MDJ-300S, LICHEN technology, Shanghai, China) was applied to acquire the ground truth of mass and volume of Datasets 2, 3, and 4.

2.2. Methods

The main objective of this study is to predict the overall mass of multiple Oudemansiella raphanipes. To achieve this goal, the pipeline is described as follows: First, an instance segmentation network is trained to segment individual samples, with the specific steps shown in the Oudemansiella raphanipes instance segmentation (Figure 4a). Then, based on the Oudemansiella raphanipes mask, a shape prior-based cap–stem segmentation algorithm is presented for building a mass regression model (Figure 4b). Finally, combining the results of the above step, the overall mass of Oudemansiella raphanipes in one image is obtained (Figure 4c). Since the volume of a solid is closely related to its mass, we also conducted a regression analysis on the volume.

2.2.1. FinePoint-ORSeg Model for Sample Segmentation

Mask R-CNN [13] is a classical deep learning model specifically designed for instance segmentation tasks. As a method based on convolutional neural networks (CNNs), Mask R-CNN relies on convolutional layers to extract features during the segmentation process. However, convolution operations have a local receptive field, which may lead to blurring effects when processing image details, especially at the edges, resulting in less smooth or precise boundaries. For general applications, such as animal or vehicle segmentation, this does not have an adverse effect on the results. Nevertheless, in our task, it may result in inaccurate phenotypic parameters. Therefore, we hope to obtain finer edge shapes by introducing the PointRend module [30]. Additionally, we consider that traditional nonlinear activation functions (such as ReLU, Sigmoid/Tanh) have significant drawbacks in information transmission, which severely damage high-frequency details of the image (such as sharp edges) and result in information loss or distortion, causing blurred results, inaccurate boundaries, and loss of details. Therefore, we have also embedded the Nonlinear Activation Free (NAF) block [31] to improve the model’s performance. The structures of the above two modules are shown in Figure 5.

(1)

PointRend module

PointRend (Point-based Rendering) is an image segmentation refinement module based on adaptive point sampling. Its core goal is to improve the segmentation accuracy of object boundaries and detailed regions through iterative refinement, thereby enabling more precise subsequent extraction of phenotypic parameters. The workflow of this module can be divided into three key stages modules, as shown in Figure 6a. First, the PointRend module uses a mixed strategy of uncertainty sampling and uniform sampling to select a set of candidate points for refinement from the initial coarse-grained segmentation results. For each candidate point, the module extracts corresponding feature vectors from different layers of the backbone network and aligns them to the target point’s spatial coordinates using bilinear interpolation. Then, feature concatenation is performed to merge low-level high-resolution detail information with high-level semantic information, forming a point-level feature vector with rich contextual representation. The fused feature vector is then passed through a small multi-layer perceptron (MLP) to predict the refined segmentation result for each point. The MLP is designed for efficient computation, and its output is the binary classification probability (foreground/background) for each candidate point. Finally, the refined point predictions are interpolated back to the original resolution and merged with the coarse segmentation map to generate a high-precision segmentation mask.

(2)

Nonlinear Activation Free block

Traditional activation functions (such as ReLU) introduce information truncation in nonlinear transformations (e.g., ReLU sets negative values to zero), which may lead to the loss of feature details. In contrast, segmentation tasks rely on pixel-level localization, and NAF may preserve more high-frequency details (such as object edges), improving the boundary accuracy of the mask. The structure of the Nonlinear Activation Free (NAF) block is shown in Figure 6b. Given a feature map $\mathrm{X}$, the gated linear units can be calculated as described in Equation (1):

$$\mathrm{G}\mathrm{a}\mathrm{t}\mathrm{e}\left(\mathrm{X},\mathrm{f},\mathrm{g},\mathsf{\sigma }\right)=\mathrm{f}\left(\mathrm{X}\right)⨀\mathsf{\sigma }\left(\mathrm{g}\left(\mathrm{X}\right)\right)$$

(1)

where the $\mathrm{f}$ and $\mathrm{g}$ are linear transformers, $\mathsf{\sigma }$ is a nonlinear activation function, and the $⨀$ represents element-wise multiplication. However, this operation may increase the intra-block complexity; thus, the authors revisit the activation function as shown in Equation (2):

$$\mathrm{G}\mathrm{E}\mathrm{L}\mathrm{U}\left(\mathrm{X}\right)=\mathrm{x}\mathsf{\Phi }\left(\mathrm{x}\right)$$

(2)

where the $\mathsf{\Phi }$ refers to the cumulative distribution function of the standard normal.

Furthermore, comparing Equations (1) and (2), it can be observed that due to the inherent nonlinearity of the GLU function, the formula still holds even when σ is removed. Therefore, directly splitting the feature map into two parts along the channel dimension and multiplying them can reduce complexity as shown in Equation (3):

$$\mathrm{S}\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{G}\mathrm{a}\mathrm{t}\mathrm{e}\left(\mathrm{F},\mathrm{Y}\right)=\mathrm{X}⨀\mathrm{Y}$$

(3)

where $\mathrm{Y}$ is a feature map of the same size as $\mathrm{X}$.

Additionally, the authors compress spatial information into channel information and utilize a multi-layer perceptron to attend to the channels to capture global information, as demonstrated by the calculation in Equation (4):

$$\mathrm{C}\mathrm{A}\left(\mathrm{X}\right)=\mathrm{X}\ast \mathsf{\sigma }\left({\mathrm{W}}_2\max \left(0,{\mathrm{W}}_1\mathrm{p}\mathrm{o}\mathrm{o}\mathrm{l}\left(\mathrm{X}\right)\right)\right)$$

(4)

where ${\mathrm{W}}_1$ and ${\mathrm{W}}_2$ are fully connected layers and ReLU is adopted between two fully connected layers, $\ast$ is a channelwise product operation.

Further, if we consider the channel-attention calculation as a function noted as $\mathsf{\Psi }$, then Equation (4) can be rewritten as Equation (5):

$$\mathrm{C}\mathrm{A}\left(\mathrm{X}\right)=\mathrm{X}\ast \mathsf{\Psi }\left(\mathrm{X}\right)$$

(5)

Comparing Equation (5) and Equation (2), we find that the two are similar. This inspires us to explore whether we can simplify Equation (5) in a similar manner to Equation (2) by aggregating global information and channel information to retain channel attention. Thus, the Simplified Channel Attention can be represented by Equation (6):

$$\mathrm{S}\mathrm{C}\mathrm{A}\left(\mathrm{X}\right)=\mathrm{X}\ast \mathrm{W}\mathrm{p}\mathrm{o}\mathrm{o}\mathrm{l}\left(\mathrm{X}\right)$$

(6)

2.2.2. Shape Prior-Based Phenotypic Extraction Algorithm

(1)

Cap–Stem segmentation algorithm

Since Oudemansiella raphanipies consists of the cap and stem, it is necessary to segment the stem and cap for the convenience of subsequent phenotypic parameter measurements. Based on the morphological characteristics of the Oudemansiella raphanipies, a novel cap–stem segmentation algorithm is presented in Figure 7. The procedure includes the following steps:

(a) Extract ordering contour point. In the task used to obtain the phenotype parameters, a key step is to calculate the position of the measurement point. Although the function find_contours in the OpenCV library can obtain sorted contours, they are discontinuous. Thus, a new contour-sporting approach needs to be developed. Establish an image coordinate system with the top-left corner as the origin. Traverse the image ${\mathrm{G}}_{\mathrm{x},\mathrm{y}}$ from top to bottom, then left to right. If the pixel value ${\mathrm{G}}_{\mathrm{x},\mathrm{y}}$ at the current position is 255, and there exists at least one neighboring pixel with a value of 0 in the 8-connected neighborhood, the current pixel is considered a contour point. Otherwise, it is considered an interior point, as shown in Equation (7).

$${\mathrm{C}}_{\mathrm{x},\mathrm{y}}=\left\{\left(\mathrm{x},\mathrm{y}\right)|\mathrm{i}\mathrm{f} {\mathrm{G}}_{\mathrm{x},\mathrm{y}}=255 \mathrm{a}\mathrm{n}\mathrm{d} \exists {\mathrm{G}}_{\mathrm{x}-1:\mathrm{x}+1,\mathrm{y}-1:\mathrm{y}+1}=0\right\}$$

(7)

With the contour point ${\mathrm{C}}_{\mathrm{x},\mathrm{y}}$, randomly select a contour point $\mathrm{p}$ ${\mathrm{C}}_{\mathrm{x},\mathrm{y}}$ as the starting point ${\mathrm{C}}^{\prime }({\mathrm{x}}_1,{\mathrm{y}}_1)$ of the ordered contour. As shown in Equation (8), calculate the Euclidean distance between the point ${\mathrm{C}}^{\prime }({\mathrm{x}}_1,{\mathrm{y}}_1)$ and other points ${\mathrm{C}}_{\mathrm{j}}$, which the points in ${\mathrm{C}}_{\mathrm{x},\mathrm{y}}$ but not in ${\mathrm{C}}_{\mathrm{x},\mathrm{y}}^{\prime }$. Then, add the point with the shortest distance as the next point ${\mathrm{C}}^{\prime }({\mathrm{x}}_2,{\mathrm{y}}_2)$ in the ordered contour. Then, calculate the Euclidean distance between point ${\mathrm{C}}^{\prime }({\mathrm{x}}_2,{\mathrm{y}}_2)$ and the remaining points ${\mathrm{C}}_{\mathrm{j}}$, which there are points in ${\mathrm{C}}_{\mathrm{x},\mathrm{y}}$ but not in ${\mathrm{C}}_{\mathrm{x},\mathrm{y}}^{\prime }$, and again add the point with the shortest distance as the next point in the ordered contour in which there are points in ${\mathrm{C}}_{\mathrm{x},\mathrm{y}}$ but not in ${\mathrm{C}}_{\mathrm{x},\mathrm{y}}^{\prime }$. Repeat the above process until all contour points have been traversed and obtain the complete ordered contour ${\mathrm{C}}^{\prime }$.

$${\mathrm{C}}_{\mathrm{x},\mathrm{y}}^{\prime }=\{\{({\mathrm{x}}_1,{\mathrm{y}}_1),({\mathrm{x}}_2,{\mathrm{y}}_2),\cdots ({\mathrm{x}}_{\mathrm{i}},{\mathrm{y}}_{\mathrm{i}})|({\mathrm{x}}_{\mathrm{i}},{\mathrm{y}}_{\mathrm{i}})=\min (\mathrm{E}\mathrm{u}\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{n}(({\mathrm{x}}_{\mathrm{i}},{\mathrm{y}}_{\mathrm{i}}),{\mathrm{C}}_{\mathrm{j}}))\}\}$$

(8)

(b) Extract the segmentation points. After obtaining the ordering contour points ${\mathrm{C}}_{\mathrm{x},\mathrm{y}}^{\prime }$, calculating the vector ${\stackrel{⃑}{{\mathrm{A}}_{\mathrm{n}1}}}_{\mathrm{i}}$ (Equation (9)) from the current point to the previous m points, and the vectors ${\stackrel{⃑}{{\mathrm{A}}_{\mathrm{n}2}}}_{\mathrm{i}}$ (Equation (10)) from the current point to the next m points. Then, compute the angle between vectors ${\stackrel{⃑}{{\mathrm{A}}_{\mathrm{n}1}}}_{\mathrm{i}}$ and ${\stackrel{⃑}{{\mathrm{A}}_{\mathrm{n}2}}}_{\mathrm{i}}$. If the angle is smaller than the threshold $\mathsf{\epsilon }$, the current point is considered as a segmentation point ${\mathrm{S}}_{\mathrm{i}}$ (Equation (11)). Based on multiple experiments and the morphological structure of Oudemansiella raphanipies, the value of m was chosen to be 7 and the $\mathsf{\epsilon }$ was set to 135 degrees.

$${\stackrel{⃑}{{\mathrm{A}}_{\mathrm{n}1}}}_{\mathrm{i}}=({\mathrm{x}}_{\mathrm{i}}-{\mathrm{x}}_{\left(\mathrm{i}-\mathrm{m}\right)},{\mathrm{y}}_{\mathrm{i}}-{\mathrm{y}}_{\left(\mathrm{i}-\mathrm{m}\right)}),\mathrm{i}\in \left[0,\mathrm{n}\right]$$

(9)

$${\stackrel{⃑}{{\mathrm{A}}_{\mathrm{n}2}}}_{\mathrm{i}}=({\mathrm{x}}_{\mathrm{i}}-{\mathrm{x}}_{\left(\mathrm{i}+\mathrm{m}\right)},{\mathrm{y}}_{\mathrm{i}}-{\mathrm{y}}_{\left(\mathrm{i}+\mathrm{m}\right)}),\mathrm{i}\in \left[0,\mathrm{n}\right]$$

(10)

$$\mathrm{S}=\left\{\left\{\left({\mathrm{x}}_1,{\mathrm{y}}_1\right),\cdots ,\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{y}}_{\mathrm{i}}\right),\cdots \right.\left({\mathrm{x}}_{\mathrm{n}},{\mathrm{y}}_{\mathrm{n}}\right)|\mathrm{i}\mathrm{f}\arccos \left({\displaystyle \frac{{\stackrel{⃑}{{\mathrm{A}}_{\mathrm{n}1}}}_{\mathrm{i}}·{\stackrel{⃑}{{\mathrm{A}}_{\mathrm{n}2}}}_{\mathrm{i}}}{\left|{\stackrel{⃑}{{\mathrm{A}}_{\mathrm{n}1}}}_{\mathrm{i}}\right|\times \left|{\stackrel{⃑}{{\mathrm{A}}_{\mathrm{n}2}}}_{\mathrm{i}}\right|}}\right)<\mathsf{\epsilon }\right\},\mathrm{i}\in \left[0,\mathrm{n}\right]$$

(11)

(c) Filter segmentation points. Due to the morphological variations of Oudemansiella raphanipies, neighboring positions around the segmentation points may also meet the threshold set by Equation (12). Therefore, it is necessary to filter the obtained segmentation points and select two points as the final segmentation points. With the segmentation points $\mathrm{S}$, randomly select a segmentation point $({\mathrm{S}}_{\mathrm{x}},{\mathrm{S}}_{\mathrm{y}})$ from $\mathrm{S}$ as the starting point ${\mathrm{S}}^{\prime }({\mathrm{x}}_1,{\mathrm{y}}_1)$ of the filtered segmentation points. Calculate the Euclidean distance between the current point ${\mathrm{S}}^{\prime }({\mathrm{x}}_1,{\mathrm{y}}_1)$ and the other unfiltered points $\mathrm{S}$. If the distance is smaller than the threshold, remove this unfiltered point from $\mathrm{S}$ and recompute the distance to the next unfiltered points $\mathrm{S}$. Repeat the calculation until find a point that the distance is greater than the threshold, and consider this point as another segmentation point ${\mathrm{S}}^{\prime }({\mathrm{x}}_2,{\mathrm{y}}_2)$. Thus, the points ${\mathrm{S}}^{\prime }({\mathrm{x}}_1,{\mathrm{y}}_1)$ and ${\mathrm{S}}^{\prime }({\mathrm{x}}_2,{\mathrm{y}}_2)$ were considered as the final segmentation points.

$${\mathrm{S}}^{\prime }=\left\{\left({\mathrm{x}}_1,{\mathrm{y}}_1\right),\left({\mathrm{x}}_2,{\mathrm{y}}_2\right)|\begin{array}{c}\mathrm{if} \mathrm{Euclidean}\left(\left({\mathrm{x}}_1,{\mathrm{y}}_1\right),{\mathrm{S}}_{\mathrm{i}}\right)>\mathrm{\gamma } \mathrm{and}\\ \mathrm{Euclidean}\left(\left({\mathrm{x}}_2,{\mathrm{y}}_2\right),{\mathrm{S}}_{\mathrm{i}}\right)>\mathrm{\gamma }\end{array}\right\},\mathrm{i}\in \left[0,\mathrm{n}-1\right]$$

(12)

where the ${\mathrm{S}}_{\mathrm{i}}$ refer to the points of the unfiltered segmentation points besides $\left({\mathrm{x}}_1,{\mathrm{y}}_1\right)$ and $\left({\mathrm{x}}_2,{\mathrm{y}}_2\right)$, and the $\mathsf{\gamma }$ was set to 10.

(d) Obtain the cap and stem region. After obtaining the segmentation points of the stem and cap $\left({\mathrm{x}}_1,{\mathrm{y}}_1\right) \mathrm{a}\mathrm{n}\mathrm{d} \left({\mathrm{x}}_2,{\mathrm{y}}_2\right)$, divide the ordered contour ${\mathrm{C}}_{\mathrm{x},\mathrm{y}}^{\prime }$ into two contours, ${\mathrm{C}}_1$ and ${\mathrm{C}}_2$. Then, calculate the centroid $\left({\mathrm{M}}_{\mathrm{x}},{\mathrm{M}}_{\mathrm{y}}\right)$ of the ordered contour obtained in Step (a). If $\left({\mathrm{M}}_{\mathrm{x}},{\mathrm{M}}_{\mathrm{y}}\right)$ lies within the range of ${\mathrm{C}}_1$, then ${\mathrm{C}}_1$ is the stem region and ${\mathrm{C}}_2$ is the cap region; if $\left({\mathrm{M}}_{\mathrm{x}},{\mathrm{M}}_{\mathrm{y}}\right)$ lies within the range of ${\mathrm{C}}_2$, then ${\mathrm{C}}_2$ is the stem region and ${\mathrm{C}}_1$ is the cap region.

(2)

Definition of phenotypic parameters

By the cap–stem segmentation algorithm, the separate masks of the cap and the stem can be obtained. However, the randomly placed sample may cause the Oudemansiella raphanipies to be tilted, making it hard to directly measure the parameters by bounding box, and this introduces systematic error, as shown in Figure 8a. To overcome this drawback, we first used the principal component analysis (PCA) algorithm to acquire the main direction of the cap (stem) as shown in Figure 8b. Then, we rotated the cap (stem) so that the main direction aligned with the image coordinate system, as shown in Figure 8c. Figure 8d illustrates the five primary phenotypic parameters (CD, CH, Angle, SH, SD), and 18 phenotypic parameters are defined in

Table 1. Definition of 18 phenotypic parameters.

ID	Abbreviation	Phenotypic Parameters	Equations	Units
1	CD	Cap Diameter	$\begin{array}{c}\max \left({\mathrm{x}}_{\mathrm{i}}\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left({\mathrm{x}}_{\mathrm{i}}\right)\end{array}$	mm
2	SD	Stem Diameter	$\begin{array}{c}\max \left({\mathrm{x}}_{\mathrm{i}}\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left({\mathrm{x}}_{\mathrm{i}}\right)\end{array}$	mm
3	CH	Cap Height	$\begin{array}{c}\max \left({\mathrm{y}}_{\mathrm{i}}\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left({\mathrm{y}}_{\mathrm{i}}\right)\end{array}$	mm
4	SH	Stem Height	$\begin{array}{c}\max \left({\mathrm{y}}_{\mathrm{i}}\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left({\mathrm{y}}_{\mathrm{i}}\right)\end{array}$	mm
5	${\mathrm{R}\mathrm{D}\mathrm{H}}_{\mathrm{c}\mathrm{a}\mathrm{p}}$	Cap Diameter–Height Ratio	$\begin{array}{c}{\displaystyle \frac{\mathrm{C}\mathrm{D}}{\mathrm{C}\mathrm{H}}}\end{array}$	-
6	${\mathrm{R}\mathrm{D}\mathrm{H}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{m}}$	Stem Diameter–Height Ratio	${\displaystyle \frac{\mathrm{S}\mathrm{D}}{\mathrm{S}\mathrm{H}}}$	-
7	${\mathrm{P}}_{\mathrm{c}\mathrm{a}\mathrm{p}}$	Perimeter of Cap	$\begin{array}{c}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}-1}}\sqrt{{({\mathrm{x}}_{\mathrm{i}+1}-{\mathrm{x}}_{\mathrm{i}})}^2+{({\mathrm{y}}_{\mathrm{i}+1}-{\mathrm{y}}_{\mathrm{i}})}^2}\end{array}$	mm
8	${\mathrm{P}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{m}}$	Perimeter of Stem	$\begin{array}{c}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}-1}}\sqrt{{({\mathrm{x}}_{\mathrm{i}+1}-{\mathrm{x}}_{\mathrm{i}})}^2+{({\mathrm{y}}_{\mathrm{i}+1}-{\mathrm{y}}_{\mathrm{i}})}^2}\end{array}$	mm
9	${\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}}_{\mathrm{c}\mathrm{a}\mathrm{p}}$	Area of cap	$\begin{array}{c}\left|{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}-1}}\left({\mathrm{x}}_{\mathrm{i}}{\mathrm{y}}_{\mathrm{i}+1}-{{\mathrm{y}}_{\mathrm{i}}\mathrm{x}}_{\mathrm{i}+1}\right)+\left({\mathrm{x}}_{\mathrm{n}}{\mathrm{y}}_1-{{\mathrm{y}}_{\mathrm{n}}\mathrm{x}}_1\right)\right|\end{array}$	${\mathrm{m}\mathrm{m}}^2$
10	${\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{m}}$	Area of stem	$\begin{array}{c}\left|{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}-1}}\left({\mathrm{x}}_{\mathrm{i}}{\mathrm{y}}_{\mathrm{i}+1}-{{\mathrm{y}}_{\mathrm{i}}\mathrm{x}}_{\mathrm{i}+1}\right)+\left({\mathrm{x}}_{\mathrm{n}}{\mathrm{y}}_1-{{\mathrm{y}}_{\mathrm{n}}\mathrm{x}}_1\right)\right|\end{array}$	${\mathrm{m}\mathrm{m}}^2$
11	${\mathrm{R}}_{\mathrm{c}\mathrm{a}\mathrm{p}}$	Roughness of Cap	$\begin{array}{c}{\displaystyle \frac{{\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}}_{\mathrm{c}\mathrm{a}\mathrm{p}}}{{\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}\mathrm{e}\mathrm{x}\mathrm{h}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}}_{\mathrm{c}\mathrm{a}\mathrm{p}}}}\end{array}$	-
12	${\mathrm{R}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{m}}$	Roughness of Stem	$\begin{array}{c}{\displaystyle \frac{{\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{m}}}{{\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}\mathrm{e}\mathrm{x}\mathrm{h}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{m}}}}\end{array}$	-
13	${\mathrm{A}\mathrm{R}\mathrm{M}\mathrm{B}}_{\mathrm{c}\mathrm{a}\mathrm{p}}$	Ratio of Cap Area to Bounding Box	$\begin{array}{c}{\displaystyle \frac{\mathrm{C}\mathrm{D}\times \mathrm{C}\mathrm{H}}{{\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}}_{\mathrm{c}\mathrm{a}\mathrm{p}}}}\end{array}$	-
14	${\mathrm{A}\mathrm{R}\mathrm{M}\mathrm{B}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{m}}$	Ratio of Stem Area to Bounding Box	${\displaystyle \frac{\mathrm{S}\mathrm{D}\times \mathrm{S}\mathrm{H}}{{\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{m}}}}$	-
15	$\mathrm{A}\mathrm{n}\mathrm{g}\mathrm{l}\mathrm{e}$	Opening Angle of Cap	$\begin{array}{c}\mathrm{A}\mathrm{n}\mathrm{g}\mathrm{l}\mathrm{e}={\displaystyle \frac{\overrightarrow{{\mathrm{v}}_1}·\overrightarrow{{\mathrm{v}}_2}}{\left|\overrightarrow{{\mathrm{v}}_1}\right|\times \left|\overrightarrow{{\mathrm{v}}_2}\right|}}\end{array}$	-
16	${\mathrm{H}}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}$	Total Height	$\begin{array}{c}\mathrm{C}\mathrm{H}+\mathrm{S}\mathrm{H}\end{array}$	mm
17	${\mathrm{P}}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}$	Total Perimeter	$\begin{array}{c}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}-1}}\sqrt{{({\mathrm{x}}_{\mathrm{i}+1}-{\mathrm{x}}_{\mathrm{i}})}^2+{({\mathrm{y}}_{\mathrm{i}+1}-{\mathrm{y}}_{\mathrm{i}})}^2}\end{array}$	mm
18	${\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}$	Total Area	$\begin{array}{c}\left|{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}-1}}\left({\mathrm{x}}_{\mathrm{i}}{\mathrm{y}}_{\mathrm{i}+1}-{{\mathrm{y}}_{\mathrm{i}}\mathrm{x}}_{\mathrm{i}+1}\right)+\left({\mathrm{x}}_{\mathrm{n}}{\mathrm{y}}_1-{{\mathrm{y}}_{\mathrm{n}}\mathrm{x}}_1\right)\right|\end{array}$	${\mathrm{m}\mathrm{m}}^2$

Note: the coordinate ($x_i, y_i$) represented the cap (stem/fruit body) mask; the Convexhull area was the area of the convex hull of the cap (stem) mask.

.

2.2.3. Mass Estimation Model

To predict the mass of an Oudemansiella raphanipies based on phenotypic parameters, nine regression models were evaluated in this study (

Table 2. The property descriptions of the GPR and SVR kernels.

Models	Kernel Equations
Linear SVM	$\begin{array}{c}{\mathrm{K}}_{\mathrm{L}}\left(\mathrm{x},{\mathrm{x}}^{\prime }\right)={\mathrm{x}}^{\mathrm{T}}{\mathrm{x}}^{\prime }\end{array}$
Fine Gaussian SVM Medium Gaussian SVM Coarse Gaussian SVM	$\begin{array}{c}{\mathrm{K}}_{\mathrm{G}}\left(\mathrm{x},{\mathrm{x}}^{\prime }\right)=\mathrm{e}\mathrm{x}\mathrm{p}{(-{\displaystyle \frac{‖\mathrm{x}-{\mathrm{x}}^{\prime }‖}{2{\mathsf{\sigma }}^2}})}^2\end{array}$
Rational Quadratic GPR	$\begin{array}{c}{\mathrm{K}}_{\mathrm{R}\mathrm{Q}}\left(\mathrm{x},{\mathrm{x}}^{\prime }\right)={(1+{\displaystyle \frac{{\left|\mathrm{x}-{\mathrm{x}}^{\prime }\right|}^2}{2\mathsf{\alpha }{\mathrm{l}}^2}})}^{-\mathsf{\alpha }}\end{array}$
Exponential GPR	$\begin{array}{c}{\mathrm{K}}_{\mathrm{E}}\left(\mathrm{x},{\mathrm{x}}^{\prime }\right)=\mathrm{e}\mathrm{x}\mathrm{p}(-{\displaystyle \frac{\left|\mathrm{x}-{\mathrm{x}}^{\prime }\right|}{\mathrm{l}}})\end{array}$
Bayesian Regularization ANN	n-11-2 layers
Levenberg–Marquardt ANN	n-11-2 layers
Scaled Conjugate Gradient ANN	n-11-2 layers

Note: σ is the dimensional feature-space scale, $\alpha$ is the decay exponent, and $l$ is the length scale.

): support vector machine (SVM) (Linear, Fine Gaussian, Medium Gaussian and Coarse Gaussian), Gaussian Process Regression (GPR) (Rational Quadratic and Exponential), and Artificial Neural Networks (ANNs) (Bayesian Regularization, Levenberg–Marquardt, and Scaled Conjugate Gradient training algorithms).

Support vector machine (SVM) [32] is a powerful supervised learning algorithm primarily used for classification and regression tasks. Further, SVM can be extended into Support Vector Regression (SVR), a regression method that can utilize multiple different kernel functions such as Linear and Gaussian kernel to solve nonlinear problems. For example, Nyalala et al. [28] used SVM with different kernels to predict the volume and mass of tomatoes, and the accuracy was all above 90%.

Gaussian Process Regression (GPR) [33] is a non-parametric regression method based on Bayesian inference, using Gaussian processes (GP) as the prior model for the target function. Similarly to SVM, different types of data require distinct kernel functions to characterize their underlying structure. Consequently, selecting appropriate kernel functions is critical for enhancing both the performance and flexibility of Gaussian Process Regression (GPR) models. Okinda et al. [25] used the Exponential Gaussian Process to predict the volume of a single egg, achieving an excellent result with an RMSE of 1.175 ${\mathrm{c}\mathrm{m}}^3$ and ${\mathrm{R}}^2$ of 0.984. Moreover, Gonzalez et al. [34] estimated the weight of rice based on Exponential kernel and rational quadratic GPR, which obtained an RMSE of 31.081 g and 31.115 g, respectively. This study will explore the performance of two kernel functions, Rational Quadratic and Exponential, in estimating the mass and volume of Oudemansiella raphanipies.

Comparing the SVM and GPR methods, the advantage of Artificial Neural Networks (ANNs) [35] lies in the fact that there is no need to manually design the kernel function and they can automatically capture complex deep structures. During the learning process, the network’s objective is to adjust parameters using optimization algorithms to minimize prediction errors. Depending on the different optimization algorithms, the commonly used ANNs include Bayesian Regularization, Levenberg–Marquardt, and Scaled Conjugate Gradient ANN [36], and they have all been well applied in different scenarios. Kayabaşı et al. [37] obtained five features (length, width, area, perimeter and fullness) of wheat and then applied the Bayesian Regularization ANN to identify the grain type of the wheat. Amraei et al. [38] predicted broiler mass based on different ANN techniques, while Bayesian Regulation ANN was the best network with an ${\mathrm{R}}^2$ value of 0.98. Sofwan et al. [35] utilized the Levenberg–Marquardt ANN to predict the air temperature inside the greenhouse 30 min in the future, which helped to adjust the growing environment of water spinach.

2.2.4. Implementation Details

All DL and ML algorithms were run on the Ubuntu 20.04.6 (GNU/Linux 5.14.0-1051-oem x86_64) operating system (Intel(R) Xeon(R) Silver 4112 CPU @ 2.60 GHz, 64 GB of RAM and NVIDIA GeForce RTX 5000 GPUs), using the PyTorch 1.7.1 framework and Python 3.7. CUDA version 11.7 was used for this experiment. The software used to train the model was PyCharm 2019.

To fine-tune the dataset of the DL model during the training process, we used the pretraining weight trained on the open-source dataset ImageNet. In addition, we used the Adam optimizer with a learning rate of 0.0001, while the learning rate was controlled by the steep descent method with a weight decay of 0.0001 and a batch size of 4.

2.2.5. Evaluation Metrics

For the Oudemansiella raphanipies instance segmentation subtask, the instance segmentation model was evaluated with the average precision ($\mathrm{A}\mathrm{P}$). Depending on the IoU threshold setting, it can be specifically divided into $\mathrm{A}\mathrm{P}$, ${\mathrm{A}\mathrm{P}}_{50}$, ${\mathrm{A}\mathrm{P}}_{75}$. $\mathrm{A}\mathrm{P}$ represents the average of $\mathrm{A}\mathrm{P}$ values calculated at each IoU threshold, with the IoU thresholds ranging from 0.5 to 0.95 in steps of 0.05. ${\mathrm{A}\mathrm{P}}_{50}$ and ${\mathrm{A}\mathrm{P}}_{75}$ are the $\mathrm{A}\mathrm{P}$ values when the IoU threshold is 0.5 and 0.75, respectively. Additionally, depending on the size of the objects, $\mathrm{A}\mathrm{P}$ includes ${\mathrm{A}\mathrm{P}}_{\mathrm{s}}$, ${\mathrm{A}\mathrm{P}}_{\mathrm{m}}$, and ${\mathrm{A}\mathrm{P}}_{\mathrm{l}}$, where ${\mathrm{A}\mathrm{P}}_{\mathrm{s}}$ refers to the average precision calculated for small objects, typically defined as objects with an area smaller than a specific threshold (less than $32\times 32$ pixels). The calculation equations were shown in

Table 3. The calculation equations of evaluation metrics.

Tasks	Evaluation Metrics	Equations
Instance segmentation	The average precision ($\mathrm{A}\mathrm{P}$)	$\begin{array}{c}\mathrm{P}={\displaystyle \frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}}}\end{array}$ $\begin{array}{c}\mathrm{R}={\displaystyle \frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}}\end{array}$ $\begin{array}{c}\mathrm{A}\mathrm{P}={\displaystyle \underset{0}{\overset{1}{\int }}}\mathrm{P}\mathrm{R}\left(\mathrm{r}\right)\mathrm{d}\mathrm{r}\end{array}$
	${\mathrm{A}\mathrm{P}}_{50}$
	${\mathrm{A}\mathrm{P}}_{75}$
	${\mathrm{A}\mathrm{P}}_{\mathrm{s}}$
Phenotypic parameter extraction	Mean absolute error ($\mathrm{M}\mathrm{A}\mathrm{E}$)	$\begin{array}{c}\mathrm{M}\mathrm{A}\mathrm{E}={\displaystyle \frac{1}{\mathrm{n}}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\left|{\mathrm{y}}_{\mathrm{i}}-\widehat{{\mathrm{y}}_{\mathrm{i}}}\right|\end{array}$
	Mean absolute percentage error ($\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}$)	$\begin{array}{c}\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}={\displaystyle \frac{1}{\mathrm{n}}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\left|{\displaystyle \frac{\left({\mathrm{y}}_{\mathrm{i}}-\widehat{{\mathrm{y}}_{\mathrm{i}}}\right)}{{\mathrm{y}}_{\mathrm{i}}}}\right|\times 100\%\end{array}$
Regression model	Adjusted ${\mathrm{R}}^2$ (${\mathrm{R}}_{\mathrm{a}\mathrm{d}\mathrm{j}}^2$)	$\begin{array}{c}{\mathrm{R}}^2=1-{\displaystyle \frac{{\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{n}}}{({\mathrm{y}}_{\mathrm{i}}-\widehat{{\mathrm{y}}_{\mathrm{i}}})}^2}{{\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{n}}}{({\mathrm{y}}_{\mathrm{i}}-\overline{{\mathrm{y}}_{\mathrm{i}}})}^2}}\end{array}$ $\begin{array}{c}{\mathrm{R}}_{\mathrm{a}\mathrm{d}\mathrm{j}}^2=1-\left(1-{\mathrm{R}}^2\right)(\mathrm{n}-1)/(\mathrm{n}-\mathrm{m}-1)\end{array}$
	Mean absolute error ($\mathrm{M}\mathrm{A}\mathrm{E}$)	$\begin{array}{c}\mathrm{M}\mathrm{A}\mathrm{E}={\displaystyle \frac{1}{\mathrm{n}}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\left|{\mathrm{y}}_{\mathrm{i}}-\widehat{{\mathrm{y}}_{\mathrm{i}}}\right|\end{array}$
	Root mean square error ($\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}$)	$\begin{array}{c}\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{{\displaystyle \frac{1}{\mathrm{n}}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}{\left({\mathrm{y}}_{\mathrm{i}}-\widehat{{\mathrm{y}}_{\mathrm{i}}}\right)}^2}\end{array}$
	Ratio of performance to deviation ($\mathrm{R}\mathrm{P}\mathrm{D}$)	$\begin{array}{c}{\mathrm{S}\mathrm{D}}^{\mathrm{r}\mathrm{e}\mathrm{f}}=\sqrt{{\displaystyle \frac{1}{\mathrm{n}}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}{({\mathrm{y}}_{\mathrm{i}}-\overline{{\mathrm{y}}_{\mathrm{i}}})}^2}\end{array}$ $\begin{array}{c}\mathrm{R}\mathrm{P}\mathrm{D}={\mathrm{S}\mathrm{D}}^{\mathrm{r}\mathrm{e}\mathrm{f}}/\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}\end{array}$
Mass evaluation under different conditions	Mean absolute percentage error ($\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}$)	$\begin{array}{c}\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}={\displaystyle \frac{1}{\mathrm{n}}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\left|{\displaystyle \frac{\left({\mathrm{y}}_{\mathrm{i}}-\widehat{{\mathrm{y}}_{\mathrm{i}}}\right)}{{\mathrm{y}}_{\mathrm{i}}}}\right|\times 100\%\end{array}$
	$\mathrm{A}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{y}$	$\begin{array}{c}\mathrm{A}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{y}=1-\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}\end{array}$
	Coefficient of variation ($\mathrm{C}\mathrm{V}$)	$\begin{array}{c}{\mathrm{S}\mathrm{D}}^{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}=\sqrt{{\displaystyle \frac{1}{\mathrm{n}}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}{(\widehat{{\mathrm{y}}_{\mathrm{i}}}-\mathsf{\mu })}^2}\end{array}$ $\begin{array}{c}\mathrm{C}\mathrm{V}={\displaystyle \frac{{\mathrm{S}\mathrm{D}}^{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}}{\mathsf{\mu }}}\times 100\%\end{array}$

Note: $\mathrm{T}\mathrm{P}$ represents a positive sample predicted as positive, $\mathrm{F}\mathrm{P}$ represents a negative sample predicted as positive, $\mathrm{F}\mathrm{N}$ represents a positive sample predicted as negative, $\mathrm{P}$ represents precision and $\mathrm{R}$ represents recall. ${\mathrm{y}}_{\mathrm{i}}$ represents the reference value, $\widehat{{\mathrm{y}}_{\mathrm{i}}}$ represents the predicted value, $\overline{{\mathrm{y}}_{\mathrm{i}}}$ represents the mean value of the reference value, $\mathrm{n}$ represents the number of data, $\mathrm{m}$ represents the number of independent variables, ${\mathrm{S}\mathrm{D}}^{\mathrm{r}\mathrm{e}\mathrm{f}}$ represents the standard deviation of the reference values, ${\mathrm{S}\mathrm{D}}^{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}$ represents the standard deviation of the predicted values, and $\mathsf{\mu }$ represents the average predicted values.

.

Given the positive correlation between volume and mass, we also analyzed the volume regression model. The performance of volume and mass regression models was evaluated with four metrics: adjusted ${\mathrm{R}}^2$ (${\mathrm{R}}_{\mathrm{a}\mathrm{d}\mathrm{j}}^2$) [39,40], mean absolute error ($\mathrm{M}\mathrm{A}\mathrm{E}$), root mean square error ($\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}$) [41] and ratio of performance to deviation ($\mathrm{R}\mathrm{P}\mathrm{D}$) [42]. ${\mathrm{R}}_{\mathrm{a}\mathrm{d}\mathrm{j}}^2$ is the adjusted coefficient of determination, which accounts for the number of independent variables in the model. It adjusts ${\mathrm{R}}^2$ by penalizing the inclusion of unnecessary predictors, providing a more accurate measure of model fit, especially in multiple regression. $\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}$ is the root mean square of the square error between the predicted and reference values. $\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}$ measures the prediction error in the same units as the original data, so it is easier to interpret. $\mathrm{R}\mathrm{P}\mathrm{D}$ is the ratio of the standard deviation (${\mathrm{S}\mathrm{D}}^{\mathrm{r}\mathrm{e}\mathrm{f}}$) to the root mean square error ($\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}$). The performance of the model can be evaluated through $\mathrm{R}\mathrm{P}\mathrm{D}$: $\mathrm{R}\mathrm{P}\mathrm{D}$ > 2.5 shows excellent performance; 2.0 < $\mathrm{R}\mathrm{P}\mathrm{D}$ ≤ 2.5 shows very good performance; 1.8 < $\mathrm{R}\mathrm{P}\mathrm{D}$ ≤ 2.0 signals good performance; 1.0 < $\mathrm{R}\mathrm{P}\mathrm{D}$ ≤ 1.4 is considered to indicate poor performance; and $\mathrm{R}\mathrm{P}\mathrm{D}$ ≤ 1 reflects unsuitability for application. Their definitions are listed in Table 3.

Furthermore, to validate the model’s performance, we also used three metrics: mean absolute percentage error ($\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}$) [43], $\mathrm{A}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{y}$, and coefficient of variation ($\mathrm{C}\mathrm{V}$) [44]. $\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}$ is the mean percentage of the absolute error between the predicted and reference values. $\mathrm{A}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{y}$ is a metric defined in this paper, which was described as the complement of the $\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}$. Specifically, it represents how close the predicted values are to the reference values, with a higher $\mathrm{A}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{y}$ indicating a smaller error between the predictions and the reference values. $\mathrm{C}\mathrm{V}$ shows the volatility between predicted values and average of them. In addition, the smaller $\mathrm{C}\mathrm{V}$ indicates less variability in the predicted values for the same sample across multiple measurements. Their definitions are provided in Table 3.

3. Results

3.1. Overall Performance of Our Method

As shown in Figure 9, the data points are densely distributed near the reference line (y = x), and the slope of the fitting line (red) formula is close to 1 with an extremely small intercept, indicating that the predicted values have a slight systematic overestimation (with an average overestimation of 4%), but also reporting that the estimated values showed a high correlation with the manual measurements, with an ${\mathrm{R}}^2$ of 0.99. Specifically, our methods achieved an $\mathrm{M}\mathrm{A}\mathrm{E}$ of 1.75 g, a $\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}$ of 0.09%, and an $\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}$ of 0.86 g for mass estimation and an $\mathrm{M}\mathrm{A}\mathrm{E}$ of 2.75 ${\mathrm{c}\mathrm{m}}^3$, a $\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}$ of 0.09%, and an $\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}$ of 1.36 ${\mathrm{c}\mathrm{m}}^3$ for volume estimation, respectively. These results confirm that our method provides accurate and reliable estimations of both mass and volume for Oudemansiella raphanipies.

3.2. The Results of Instance Segmentation

3.2.1. Performance of Model

After completing the training, the loss function curves of the training and validation datasets were obtained. As shown in Figure 10, it can be observed that as the number of iterations increases, the training loss gradually decreases from its initial value, indicating that the model is continuously learning the features of the training data through parameter optimization and the fitting ability progressively improves. Additionally, the validation loss rapidly decreases in the early stages of training (the first 6000 iterations), and then the rate of decline slows down and gradually stabilizes, suggesting that the model’s generalization performance on the validation set has reached a stage of convergence. Moreover, partial instance segmentation results are visualized in Figure 11.

3.2.2. Ablation Experiment

Four ablation experiments were conducted to intuitively analyze the effect of each module. As shown in

Table 4. The results of ablation experiment. Bold represents the best result.

ID	PointRend	NAF	$\mathbf{A}\mathbf{P}$	${\mathbf{A}\mathbf{P}}_{50}$	${\mathbf{A}\mathbf{P}}_{75}$	${\mathbf{A}\mathbf{P}}_{\mathbf{s}}$
1	-	-	0.811	0.977	0.911	0.857
2	√	-	0.813	0.975	0.921	0.843
3	-	√	0.814	0.976	0.935	0.855
4	√	√	0.831	0.984	0.930	0.860

, the experimental results in Row 1 represent the original Mask R-CNN without any improvement, achieving an $\mathrm{A}\mathrm{P}$ of 0.811, an ${\mathrm{A}\mathrm{P}}_{50}$ of 0.977, an ${\mathrm{A}\mathrm{P}}_{75}$ of 0.911, and an ${\mathrm{A}\mathrm{P}}_{\mathrm{s}}$ of 0.857. With the addition of the PointRend module (row 2), the ${\mathrm{A}\mathrm{P}}_{50}$ was 0.975 and the ${\mathrm{A}\mathrm{P}}_{\mathrm{s}}$ was 0.843, which were 0.002 and 0.014 lower than those in Row 1, respectively. However, Row 2 showed improvements in both $\mathrm{A}\mathrm{P}$ and ${\mathrm{A}\mathrm{P}}_{75}$, increasing from 0.811 to 0.813 and from 0.911 to 0.921, respectively. Row 3 introduced the NAF module, resulting in a decrease of 0.001 in ${\mathrm{A}\mathrm{P}}_{50}$ and 0.002 in ${\mathrm{A}\mathrm{P}}_{\mathrm{s}}$, while the $\mathrm{A}\mathrm{P}$ increased by 0.003. Additionally, it gained an ${\mathrm{A}\mathrm{P}}_{75}$ of 0.935, which showed a significant increase of 0.024. When both the PointRend and NAF modules were combined, the $\mathrm{A}\mathrm{P}$, the ${\mathrm{A}\mathrm{P}}_{75}$, the ${\mathrm{A}\mathrm{P}}_{50}$, and the ${\mathrm{A}\mathrm{P}}_{\mathrm{s}}$ reached 0.831, 0.930, 0.984 and 0.860, respectively, improving by 2%, 1.9%, 0.7% and 0.3%, respectively. Meanwhile, the $\mathrm{A}\mathrm{P}$, the ${\mathrm{A}\mathrm{P}}_{50}$, and the ${\mathrm{A}\mathrm{P}}_{\mathrm{s}}$ were the highest among the four experiments. The experimental results demonstrated that the PointRend and NAF modules improved the overall performance of the baseline.

3.2.3. Comparison Results of Different Instance Segmentation Models

To further explore the performance of FinePoint-ORSeg model, standard COCO evaluation indicators such as $\mathrm{A}\mathrm{P}$, ${\mathrm{A}\mathrm{P}}_{50}$, ${\mathrm{A}\mathrm{P}}_{75}$ and ${\mathrm{A}\mathrm{P}}_{\mathrm{s}}$ were used for evaluation. We compared the performance of our model with Mask R-CNN, SOLOv2, YOLACT, Mask2former, TensorMask, Mask R-CNN with swin and InstaBoost on Dataset 1, and the evaluation results were shown in

Table 5. Comparison of different instance segmentation networks on Oudemansiella raphanipies.

Method	$\mathbf{A}\mathbf{P}$	${\mathbf{A}\mathbf{P}}_{50}$	${\mathbf{A}\mathbf{P}}_{75}$	${\mathbf{A}\mathbf{P}}_{\mathbf{s}}$
Mask R-CNN	0.811	0.977	0.911	0.857
SOLOv2	0.818	0.973	0.917	0.857
YOLACT	0.655	0.937	0.740	0.730
Mask2former	0.831	0.969	0.908	0.864
TensorMask	0.798	0.966	0.908	0.830
Mask R-CNN with swin	0.829	0.977	0.960	0.857
InstaBoost	0.760	0.965	0.874	0.792
FinePoint-ORSeg	0.831	0.984	0.930	0.860

. The experimental results show that the proposed FinePoint-ORSeg network achieves optimal performance across multiple key metrics: its $\mathrm{A}\mathrm{P}$ value is 0.831, tied for first place with Mask2former; the ${\mathrm{A}\mathrm{P}}_{50}$ is significantly leading at 0.984, improving by 0.7% over the second-best Mask R-CNN and Mask R-CNN with swin (0.977). Notably, traditional methods like YOLACT have a weaker performance ($\mathrm{A}\mathrm{P}$ = 0.655), while Mask2former (Swin Transformer-based) performs excellently in terms of $\mathrm{A}\mathrm{P}$ and ${\mathrm{A}\mathrm{P}}_{\mathrm{s}}$ (small target precision), but slightly lag behind FinePoint-ORSeg at higher thresholds (${\mathrm{A}\mathrm{P}}_{75}$). The FinePoint-ORSeg model reduces unnecessary complex operations in traditional modules by effective channel attention and a simple gating mechanism while maintaining high robustness (${\mathrm{A}\mathrm{P}}_{\mathrm{s}}$ = 0.860), providing a data foundation for the subsequent extraction of Oudemansiella raphanipies phenotypic parameters.

3.3. The Result of Phenotypic Parameters Extraction

To verify the accuracy of the extracted phenotypic parameters, we randomly selected and manually measured the CD, CH, SD, and SH of 10 samples of Dataset 2, while the other phenotypic parameters cannot be directly measured manually.

Table 6. Examples of the extracted phenotypic parameters.

Parameter	Number	${\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{s}\mathbf{u}\mathbf{r}\mathbf{e}}_{\mathbf{r}\mathbf{e}\mathbf{f}\mathbf{e}\mathbf{r}\mathbf{e}\mathbf{n}\mathbf{c}\mathbf{e}}$ (mm)	${\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{s}\mathbf{u}\mathbf{r}\mathbf{e}}_{\mathbf{e}\mathbf{s}\mathbf{t}\mathbf{i}\mathbf{m}\mathbf{a}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n}}$ (mm)	MAE (mm)	MAPE (%)
CD	1	14.9	16.88	1.98	13.26
	2	20.6	21.88	1.28	6.19
	3	19.5	18.75	0.75	3.85
	4	20.9	21.25	0.35	1.68
	5	21.4	21.88	0.48	2.22
	6	22.1	23.75	1.67	7.47
	7	25.3	25.00	0.30	1.29
	8	20.2	22.50	2.30	11.39
	9	23.7	24.38	0.68	2.85
	10	25.9	26.25	0.35	1.35
	Average	21.45	22.25	1.01	5.16
CH	1	12.7	12.50	0.20	1.58
	2	14.6	16.25	1.65	11.30
	3	14.0	13.75	0.25	1.79
	4	15.8	16.88	1.08	6.80
	5	15.5	15.63	0.13	0.80
	6	17.8	19.38	1.58	8.85
	7	15.4	15.63	0.23	1.46
	8	13.1	14.38	1.28	9.73
	9	15.2	15.63	0.43	2.80
	10	12.1	12.50	0.44	3.65
	Average	14.62	15.25	0.73	4.88
SD	1	39.1	39.38	0.28	0.70
	2	30.9	30.63	0.28	0.89
	3	36.5	38.13	1.63	4.45
	4	41.8	43.13	1.33	3.17
	5	58.6	61.88	3.28	5.59
	6	33.7	33.75	0.05	1.48
	7	33.6	30.00	3.60	10.71
	8	33.1	31.25	1.85	5.59
	9	32.7	33.13	0.43	1.30
	10	37.16	36.88	0.29	0.77
	Average	37.72	37.82	1.30	3.47
SH	1	13.1	13.75	0.65	4.96
	2	14.9	15.63	0.725	4.87
	3	18.5	18.75	0.25	1.35
	4	18.8	19.38	0.575	3.06
	5	17.5	18.13	0.625	3.57
	6	17.8	18.75	0.95	5.34
	7	12.1	11.88	0.225	1.86
	8	18.1	18.75	0.65	3.59
	9	15.9	16.25	0.35	2.20
	10	18.0	18.75	0.75	4.17
	Average	16.47	17.00	0.58	3.50

shows the manual measurement (${\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}}_{\mathrm{r}\mathrm{e}\mathrm{f}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}}$), estimated measurement (${\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}}_{\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}$), and the MAE and MAPE of the Oudemansiella raphanipies examples. For CD, CH, SD, and SH, the phenotypic extraction method has an average MAE of 1.10 mm, 0.73 mm, 1.30 mm and 0.58 mm, respectively. In addition, the MAPEs were 5.16%, 4.88%, 3.47%, and 3.50%, respectively.

3.4. Correlation Analysis and Best Regression Model Selection

To explore the relationship between Oudemansiella raphanipies parameters and mass while reducing feature redundancy, we constructed a correlation heatmap, as shown in Figure 12. Furthermore, since volume and mass have a close correlation, the relationship between phenotypic parameters and volume was evaluated as well. From Figure 12, it can be seen that the height, width, perimeter, and area have a high correlation with the mass and volume. However, there is also a high correlation between height, width, perimeter, and area, indicating some redundancy. Therefore, to explore the impact of nine ML models and the number of Principal Component Analysis (PCA) components on model performance, we applied the phenotypic data obtained in Section 3.4 to evaluate the accuracy of the mass and volume estimation, and the results are shown in Figure 13. Whether for mass or volume estimation, as the number of principal components increases, MAE and RMSE all show a downward trend. When the number of principal components reaches 7, the evaluation metrics begin to converge, which indicates a high level of information redundancy among the 18 features.

For mass estimation, the Gaussian kernel in SVM outperforms the linear kernel, especially the Medium Gaussian SVM and Coarse Gaussian SVM, both of which achieved a ${\mathrm{R}}_{\mathrm{a}\mathrm{d}\mathrm{j}}^2$ of 0.92. Additionally, the Medium Gaussian SVM achieved the highest RPD and the lowest RMSE, 3.61 and 0.70 g, respectively, while the Coarse Gaussian SVM achieved the lowest MAE of 0.35 g. In comparison, the Linear SVM had a ${\mathrm{R}}_{\mathrm{a}\mathrm{d}\mathrm{j}}^2$ of 0.91, RMSE of 0.77 g, RPD of 3.30, and MAE of 0.50 g. For GPR models, Rational Quadratic GPR and Exponential GPR both had identical ${\mathrm{R}}_{\mathrm{a}\mathrm{d}\mathrm{j}}^2$, RMSE, RPD, and MAE values of 0.96, 0.53 g, 4.78, and 0.21 g, respectively. However, Exponential GPR demonstrated more stable performance compared to Rational Quadratic GPR. For Artificial Neural Networks (ANNs), the Bayesian Regularization ANN performed the best, with a ${\mathrm{R}}_{\mathrm{a}\mathrm{d}\mathrm{j}}^2$ of 0.97, RMSE of 0.47 g, RPD of 5.43, and MAE of 0.29 g. Among the models, Exponential GPR had the smallest MAE of 0.21 g, while Bayesian Regularization ANN had the highest ${\mathrm{R}}_{\mathrm{a}\mathrm{d}\mathrm{j}}^2$ and RPD, at 0.97 and 5.34, respectively, and the smallest RMSE at 0.47 g. For volume estimation, Exponential GPR performed the best, achieving the highest ${\mathrm{R}}_{\mathrm{a}\mathrm{d}\mathrm{j}}^2$ and RPD of 0.95 and 4.74, and the lowest RMSE and MAE of 0.76 ${\mathrm{c}\mathrm{m}}^3$ and 0.29 ${\mathrm{c}\mathrm{m}}^3$, respectively. Considering both the stability and accuracy of the models for mass and volume estimation, we ultimately select the Exponential GPR with seven principal components as the model for subsequent mass and volume estimation.

3.5. The Results Under Different Conditions

3.5.1. Estimation Results of a Single Sample at Random States

Since the phenotypic parameters of the same Oudemansiella raphanipies vary when viewed from different perspectives, we selected 24 Oudemansiella raphanipies instances (Dataset 3), each with 10 randomly generated states, to validate the impact of placement state on the Exponential GPR model obtained in Section 3.4.

Table 7. The results of the estimated results of single samples at random states. Ref refers to the reference data from manual measurements. APV refers to the average predicted values. STD represents the standard deviation.

ID	Mass					Volume
	Ref (g)	APV (g)	MAE (g)	STD (g)	CV (%)	Ref (cm3)	APV (cm3)	MAE (cm3)	STD (cm3)	CV (%)
1	3.23	3.10	0.19	0.17	5.42	4.28	4.32	0.26	0.32	7.31
2	2.20	2.15	0.14	0.17	7.92	3.04	2.93	0.20	0.22	7.62
3	3.21	3.20	0.22	0.25	7.92	4.25	4.46	0.32	0.30	6.81
4	3.36	3.10	0.29	0.28	9.13	4.29	4.43	0.21	0.23	5.25
5	2.37	2.45	0.17	0.19	7.59	3.55	3.46	0.28	0.28	8.16
6	2.53	2.40	0.23	0.20	8.27	3.34	3.46	0.23	0.25	7.26
7	2.95	2.40	0.55	0.10	4.12	3.96	3.51	0.45	0.11	3.09
8	2.72	2.70	0.08	0.10	3.84	3.45	3.65	0.25	0.26	7.02
9	3.10	2.93	0.40	0.39	13.34	4.38	4.66	0.64	0.58	12.37
10	3.31	3.43	0.15	0.12	3.37	4.35	4.81	0.46	0.11	2.21
11	2.92	2.57	0.35	0.14	5.40	4.20	3.70	0.49	0.15	3.95
12	3.11	2.95	0.27	0.28	9.57	4.25	4.24	0.28	0.37	8.84
13	3.25	2.74	0.51	0.16	5.86	4.25	4.13	0.29	0.29	7.13
14	3.08	3.08	0.14	0.15	5.03	4.24	4.29	0.22	0.29	6.67
15	2.17	2.27	0.21	0.22	9.69	2.98	3.31	0.33	0.26	7.99
16	3.06	2.96	0.15	0.13	4.46	4.51	4.56	0.20	0.24	5.22
17	2.35	2.12	0.19	0.12	5.71	3.37	3.29	0.22	0.23	7.01
18	2.98	2.70	0.19	0.32	11.88	4.01	3.85	0.44	0.51	13.21
19	2.25	2.34	0.19	0.08	3.45	3.16	3.34	0.37	0.33	9.79
20	3.34	3.12	0.32	0.29	9.17	4.25	4.51	0.34	0.30	6.61
21	3.40	2.54	0.86	0.18	6.99	4.70	4.03	0.67	0.20	4.98
22	3.35	3.29	0.10	0.11	3.47	4.72	4.93	0.29	0.24	4.94
23	3.17	3.05	0.16	0.15	4.85	4.64	4.36	0.29	0.22	4.94
24	3.29	3.29	0.21	0.23	6.90	4.46	4.46	0.33	0.36	8.12
Average	2.95	2.79	0.26	0.19	6.81	4.03	4.03	0.34	0.28	6.94

shows the estimated mass and volume results of a single sample at random states. The manual measurements of mass and volume had average values ranging from 2.20 g to 3.40 g and from 3.04 ${\mathrm{c}\mathrm{m}}^3$ to 4.70 ${\mathrm{c}\mathrm{m}}^3$, respectively. Compared with the measured value, the estimated value of mass and volume had an average MAE of 0.26 g and 0.34 ${\mathrm{c}\mathrm{m}}^3$, with an average STD of 0.19 g and 0.28 ${\mathrm{c}\mathrm{m}}^3$, respectively. Moreover, the average CVs of mass and volume were 6.81% and 6.94%, which indicated that the Exponential GPR model had robustness against Oudemansiella raphanipies at different states.

3.5.2. Mass/Volume Estimation of Multiple Samples in a Single Image with Random Orientations

Although our method demonstrates acceptable performance on individual images of Oudemansiella raphanipies, the number of samples is typically multiple and in random states in real-world assembly lines. Therefore, to validate the practicality of the proposed algorithm in real scenarios, Dataset 4 is selected to simulate the orientations of Oudemansiella raphanipies on the assembly line. The estimated mass and volume are shown in Figure 14 and the total error is shown in

Table 8. Average error of the multiple Oudemansiella raphanipies in one image compared with manual measurement.

		Grade			Total
		S	M	L
Number of Images		10	10	10	30
Mass	RMSE ($\mathrm{g}$)	0.590	0.493	1.323	0.802
	MAE (g)	1.454	1.323	2.367	1.714
	MAPE (%)	18.17	4.22	3.21	8.53
Volume	RMSE (${\mathrm{c}\mathrm{m}}^3$)	0.835	0.757	2.327	1.306
	MAE (${\mathrm{c}\mathrm{m}}^3$)	2.140	1.796	4.713	2.703
	MAPE (%)	17.94	3.77	3.66	8.46

.

For S samples, our method achieved an accuracy of over 70% both for mass and volume and an RMSE of 0.590 g and 0.835 ${\mathrm{c}\mathrm{m}}^3$, respectively. Moreover, the average MAPE for the mass and volume of S samples was the largest compared to both M and L samples, with values of 18.17% and 17.94%, respectively. This is because although the MAE for the S sample is only 1.454 g for mass (2.14 ${\mathrm{c}\mathrm{m}}^3$ for volume) higher than that of the M sample, the reference value for the former is much smaller than that of the latter, as the S samples have a smaller reference mass and volume. For M samples, although the MAPE of mass (volume) is 1.01% (1.11%) higher than L samples, the RMSE between reference mass (volume) and estimated mass (volume) is the lowest. The performance on L samples is the best, with an MAPE of 3.21% for mass and 3.66% for volume due to them having the most regular shape, and our extraction method of phenotypic parameters can obtain more accurate data. Despite this, the proposed method showed an MAE of 1.714 g and 2.703 ${\mathrm{c}\mathrm{m}}^3$ for multiple Oudemansiella raphanipies of different grades in one image to estimate the mean mass and volume at single view. The mass and volume estimation were robust at different grades instances. Additionally, as shown in Figure 14c,d, the violin plot visualizes the relative estimation errors of 10 results for 10 Oudemansiella raphanipies samples at different grades. The width of the violin plot represents the distribution of the data, with a wider section indicating that the estimations are more concentrated at that position. The length of the violin plot represents the degree of dispersion, where a longer instrument body signifies greater instability in the measurement results. It can be reported that the relative error of mass might even exceed 4 g, such as the No.5 of S samples and the No.7 of L samples, resulting in low accuracy. Meanwhile, the volume estimation also contains instances with large errors. The large errors imply that these instances will contribute to a greater prediction error for the corresponding images.

3.5.3. Comparison Results of Samples at Different Grades

To further demonstrate the robustness of our method and the consistency of the estimated results, we also statistically analyzed the MAE and CV of the same Oudemansiella raphanipies across different images, as shown in Figure 15 and

Table 9. Average error of the each Oudemansiella raphanipies in different images compared with manual measurement.

		Grade			Total
		S	M	L
Number of Samples		10	10	10	30
Mass	RMSE ($\mathrm{g}$)	0.390	0.494	1.083	0.656
	MAE (g)	0.422	0.421	1.045	0.629
	MAPE (%)	48.62%	12.76%	13.97%	25.12%
Volume	RMSE (${\mathrm{c}\mathrm{m}}^3$)	0.556	0.752	1.884	1.064
	MAE (${\mathrm{c}\mathrm{m}}^3$)	0.601	0.634	1.830	1.022
	MAPE (%)	44.89%	12.76%	15.18%	24.28%

. For S samples, the CV for both mass and volume estimation are within 5%, which implies high robustness.

For L samples, it has an MAE with 1.045 g and 1.830 ${\mathrm{c}\mathrm{m}}^3$ and has higher overall CV than S and M samples both for mass and volume, indicating that the estimated results of L samples have higher volatility. In addition, the MAPE for the S samples obtains an opposite result, with a value of 48.62% for mass and a value of 44.89% for volume, while that of the M and L samples is much lower. This is because the mass and volume variations of the M and L samples are more significant, leading to higher variability in their measurements, resulting in a larger CV. Furthermore, the MAPE is sensitive to the relative impact of errors with respect to the target size. For L samples, it has a larger overall mass and volume, so the same MAE has a smaller relative impact in terms of percentage, leading to a lower MAPE. On the other hand, the shape of the same Oudemansiella raphanipies is not exactly the same on different placement surfaces, leading to variations in the extracted phenotypic parameters, which ultimately affect the estimates of mass and volume.

4. Discussion

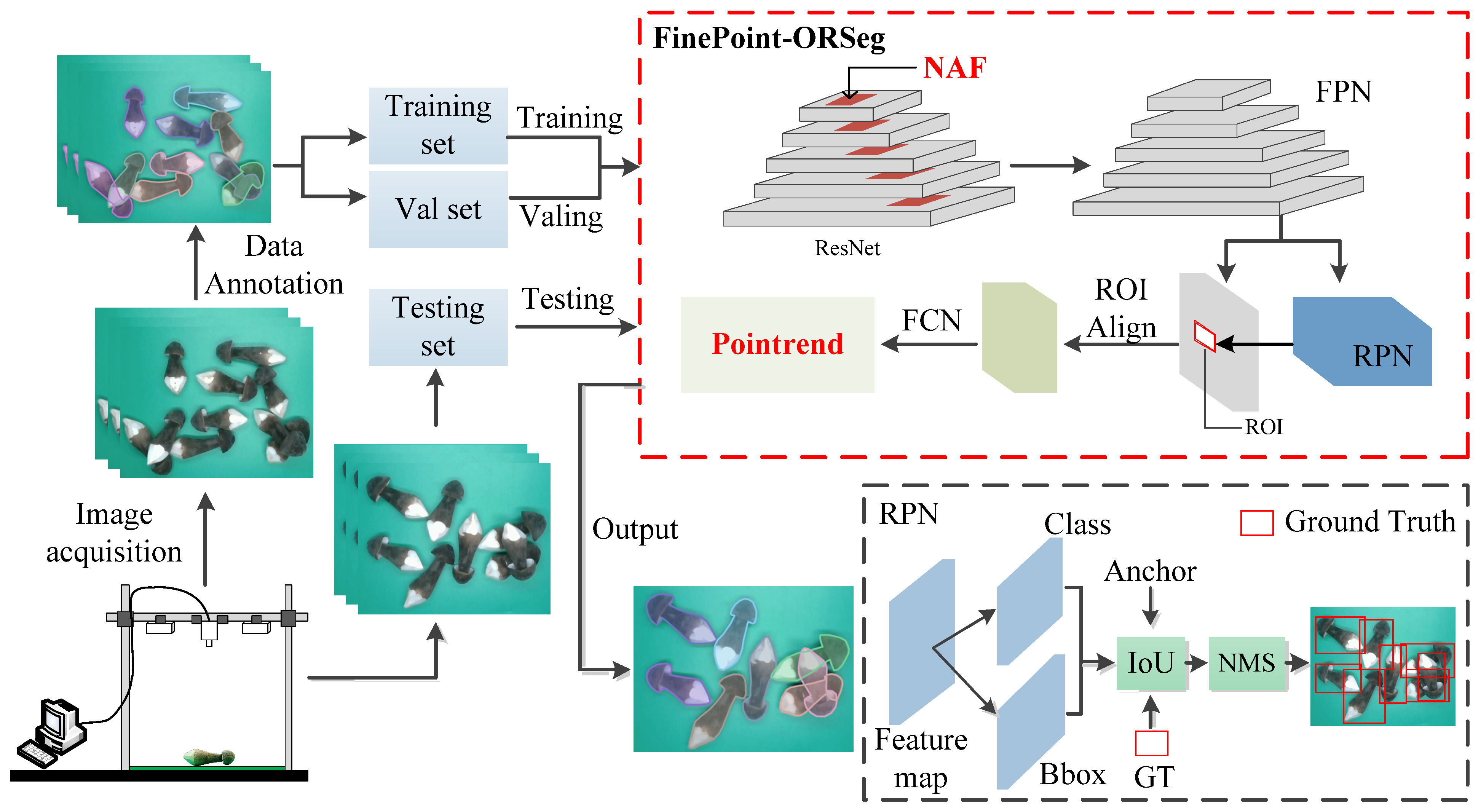
Regarding the Oudemansiella raphanipies instance segmentation task, we integrated the NAF module and the PointRend module into the FinePoint-ORSeg network to improve the segmentation capabilities and address the issue of rough target boundaries during inference. Specifically, NAF helps the network maintain an awareness of the overall morphology and spatial distribution of the targets while extracting local details, while PointRend significantly improves the geometric accuracy of the segmentation masks, which is particularly important for subsequent geometry-based volume estimation, thereby improving the model’s robustness in complex scenarios. Table 4 shows that adding only the NAF or PointRend module could improve the average precision, which demonstrates its contribution to high-precision mask generation. Table 5 shows a similar performance to other state-of-the-art works based on DL which reported an AP result of 0.831.

The main contribution of this work is the phenotypic parameters extraction algorithms and the use of ML to estimate the Oudemansiella raphanipies (mass and volume) even in the presence of multiple targets. The results (Table 6) show that the phenotypic parameters extraction algorithm was able to robustly obtain features such as CD (MAE = 1.01 mm), CH (MAE = 0.73 mm), SD (MAE = 1.30 mm) and SH (MAE = 0.58 mm). Compared with other state-of-the-art results that measure the CD of Oudemansiella raphanipies [26,27], this study achieved MAE values of between 0.35 mm and 2.30 mm and is considered as an accurate and acceptable results and achieved. However, it is notable that the error (Table 6) of the number 1 (MAPE = 13.26%) and 8 (MAPE = 11.39%) of CD, the number 2 (MAPE = 11.30%) of CH and the number 7 (MAPE = 10.71%) of SD were significantly higher than other Oudemansiella raphanipies. The main reasons are as follows: (1) Error introduced by manual measurement. Since the Oudemansiella raphanipies is a non-rigid object, compression may occur during measurement, leading to an underestimation of the reference value. Additionally, the determination of measurement points manually involves a certain degree of subjectivity. (2) Error introduced by the view angle of measurement. Due to the irregular shape of the Oudemansiella raphanipies and the fact that the manual measurement perspective is different from the camera’s perspective, there is a discrepancy between the manual measurement and the system’s measurement results. (3) Error introduced by our extraction approach. Due to the significant influence of external environmental factors on the shape of the Oudemansiella raphanipies, some instances have large caps but narrow stems, while others have small caps but thick stems. As a result, our segmentation method based on the angle between the stem and cap requires different threshold values for the latter case, which would also cause errors in the phenotypic parameters’ extraction.

The correlation analysis results show that RDH, roughness, and ARMB have low correlations with mass and volume. Therefore, the performance of nine machine learning models was compared under different numbers of principal components, and the Exponential GPR was finally selected as the subsequent basic model. Furthermore, the Exponential GPR was applied to evaluate the samples in different states. The experiments show that the CV of instance number 9 and 18 for single samples (Table 6) and the accuracy of image numbers 5 and 9 for multiple samples (Figure 14b) have unsatisfactory results. Figure 16 depicts the CV of 18 phenotypic parameters extracted from the above samples. It can be seen that the Angle and Total Area of the No.9 sample have a relatively larger error of 8.97% and 9.12% compared with other features. Moreover, the opening angle, perimeter and total area also have a relatively larger error. For three samples of different grades, all of the opening angles obtain a CV exceeding 5%. This indicates a relatively large volatility, which might be an important reason for the significant difference in the prediction results of the two images. In addition, Table 8 shows that the MAPE of the large samples is 5.32% and 4.80% lower than average error for mass and volume, respectively, and this means that the economic loss can be reduced by 9.77%.

The phenotypic parameters extracted in this work were obtained with 2D image and calibration at fixed height, which limited the data precision and the number of features. The use of 2.5D or 3D data would provide higher precision for subsequent estimation. However, the Oudemansiella raphanipies is relatively small in size, so higher-precision depth cameras or three-dimensional phenotypic extraction methods need to be adopted. In addition, the phenotypes of Oudemansiella raphanipies of different varieties and in different planting environments vary greatly. Therefore, it is urgent to develop an adaptive phenotypic parameter extraction method with high robustness.

5. Conclusions

In this research, a computer vision-based method was proposed for estimating the mass and volume of Oudemansiella raphanipies and achieved an impressive performance. This study was motivated by the limitations of existing methods, which are not robust to irregular agricultural products. By establishing a fitting model between phenotypic parameters and mass, we can effectively solve the problem of inaccurate mass estimation caused by the irregular shape of the Oudemansiella raphanipies. The improved instance segmentation model directly obtains a finer edge of the segmentation region. In addition, a novel prior-based segmentation method of Oudemansiella raphanipies cap and stem was proposed to extract 18 phenotypic parameters, as validated on the proposed datasets. Additionally, the analysis of Oudemansiella raphanipies of three different grades demonstrated that the mass and volume estimated by our methods could effectively breakthrough the limitation of an irregular shape. However, although the mass and volume estimation approach has achieved excellent results, it still has limitations. For instance, our method divides the work into three subtasks, but each subtask will introduce systematic errors, which increases the accuracy of the result. Future work should consider using a single-stage method to reduce these errors.