Abstract
This study, leveraging near-infrared spectroscopy technology and integrating vegetation index analysis, aims to develop a hyperspectral imaging-based non-destructive inspection technique for swift monitoring of crop chlorophyll content by rapidly predicting leaf SPAD. To this end, a high-precision spectral prediction model was first established under laboratory conditions using ex situ lyophilized Leaf samples. This model provides a core algorithmic foundation for future non-destructive field applications. A systematic study was conducted to develop prediction models for leaf SPAD values of Korla fragrant pear at different growth stages (fruit-setting period, fruit swelling period and Maturity period). This involved comparing various spectral preprocessing algorithms (AirPLS, Savitzky–Golay, Multiplicative Scatter Correction, FD, etc.) and CARS Feature Selection methods for the screening of optimal spectral feature band. Subsequently, models were constructed using BP Neural Network and Support Vector Regression algorithms. The results showed that leaf samples at different growth stages exhibited significant differences in their spectral features within the 5000–7000 cm−1 (effective features for predicting chlorophyll (SPAD)) and 7000–8000 cm−1 (moisture absorption valley) bands. The Savitzky–Golay+FD (Savitzky–Golay smoothing combined with first-order derivative (FD)) preprocessing algorithm performed optimally in feature extraction. Growth period specificity models significantly outperformed whole growth period models, with the optimal models for the fruit-setting period and fruit swelling period being FD-CARS-BP (Coefficient of determination (R2) > 0.86), and the optimal model for the Maturity period being Savitzky–Golay-FD+Savitzky–Golay-CARS-BP (Coefficient_of_determination (R2) = 0.862). Furthermore, joint modeling of characteristic spectra and vegetation indices further improved prediction performance (Coefficient of determination (R2) > 0.85, Root Mean Square Error (RMSE) 2.5). This study presents a reliable method for non-destructive monitoring of chlorophyll content in Korla fragrant pears, offering significant value for nutrient management and stress early warning in precision agriculture.
1. Introduction
Chlorophyll, as the core pigment of plant photosynthesis, is responsible for capturing light energy and converting it into chemical energy. It is the fundamental source of energy and dry matter accumulation essential for fruit tree growth and development, directly influencing fruit quality and yield. Therefore, accurate assessment of chlorophyll content is crucial for monitoring the physiological status, managing the health, and predicting the yield of fruit trees.
A SPAD meter non-destructively measures leaf chlorophyll content by emitting two specific wavelengths of light (red light ≈ 650 nm, infrared light ≈ 940 nm). The higher the leaf chlorophyll content, the greater the absorption rate of red light and the lower the transmittance. The SPAD values provided by this instrument can quickly and non-destructively reflect chlorophyll and nitrogen levels. The Korla fragrant pear from Xinjiang, China, is one of Xinjiang Province’s distinctive economic fruit trees, where achieving high fruit quality and yield are key production goals. Accurate monitoring and prediction of SPAD values in fruit trees is crucial for understanding their physiological development and healthy growth, controlling fruit quality, and forecasting final yields.
Numerous studies have confirmed a significant linear positive correlation between leaf SPAD values and nitrogen (N) content in fruit trees, making it a crucial indicator for assessing N nutritional status. Benati et al. [1] established a quantitative relationship between SPAD values and leaf nitrogen content in peach trees (Coefficient of determination (R2) = 0.652–0.767) and identified the SPAD range corresponding to normal nitrogen levels (39–49). Djumaeva et al. [2] further verified this strong correlation in apple (r2 = 0.89). Since chlorophyll synthesis relies not only on nitrogen but also directly on magnesium (Mg) as a central atom, SPAD values also exhibit a significant positive correlation with magnesium content. However, this correlation is typically weaker than that with nitrogen and shows greater variability among varieties. For instance, Afonso et al. [3] reported a Coefficient of determination (R2) of 0.2–0.68 in apple, and Pinzón-Sandoval et al. [4] drew similar conclusions in blueberry. SPAD values can also effectively indicate the photosynthetic potential of leaves. Tucci et al. [5] observed a significant positive correlation between SPAD values and CO2 assimilation rates in palm (Coefficient of determination (R2) = 0.99), with similar findings reported by Williams et al. [6] in grapes and citrus.
In practical agricultural production, SPAD values have become an important tool for assessing the physiological state of fruit trees and guiding cultivation management. For example, Lantos [7] found that SPAD values were highly significantly correlated with capsaicin content in chili varieties; Roslan [8] demonstrated their effectiveness in assessing the health status of mangoes. Additionally, other research [7] has indicated that apple SPAD values exhibit clear seasonal dynamics, reflecting changes in photosynthetic physiology and assisting in cultivation regulation.
However, traditional SPAD measurement still faces multiple challenges, including inconsistent measurement sites leading to data variability [9,10]; environmental and climatic factors interfering with accuracy [11,12]; the influence of leaf structure [10]; lagging data processing [13]; and insufficient robustness of prediction models [12], among others. Therefore, there is an urgent need to develop new efficient, precise, and non-destructive methods to meet current agricultural demands.
Near-infrared spectroscopy technology (near-infrared spectroscopy, NIRS) is a non-destructive and rapid analytical technique based on molecular vibrational energy level transitions. By detecting the spectral absorption characteristics of samples in the near-infrared region (780–2500 nm), it enables both qualitative and quantitative analysis of substances. NIRS offers several advantages, including fast analysis, simultaneous multi-component detection, and low cost [14].
Although this technology does not directly measure chlorophyll, it can indirectly estimate chlorophyll concentration [15], distribution [16], as well as nitrogen dynamics and photosynthetic efficiency [17], by analyzing the feature band associated with components (such as moisture and nitrogen) that covary with chlorophyll content. This indirect modeling approach, based on the covariation between spectral features and physiological traits, is a key advantage of NIRS for achieving non-destructive prediction in complex biological systems.
Vegetation indices (VIs) are mathematical indicators derived from remote sensing spectral data and are used to quantify vegetation cover, physiological status, and responses to environmental stress. Their core principle lies in leveraging the differences in vegetation reflectance in the visible and near-infrared spectral bands to effectively monitor vegetation growth conditions [18,19]. For example, NDVI values show a positive correlation with chlorophyll concentration and photosynthetic activity [15]. Therefore, vegetation indices serve as a crucial link between spectral information and plant physiological parameters such as the SPAD value.
This study integrates near-infrared spectroscopy with vegetation indices to develop a high-precision prediction model for Korla fragrant pear’s different growth stages leaf SPAD value. Regarding band selection, we focused on two ranges, 5000–7000 cm−1 and 7000–8000 cm−1, for the following reasons:
To address the aforementioned challenges, this study employs nine spectral preprocessing algorithms, including AirPLS, Detrend, and DOSC, to optimize issues such as baseline drift, random noise, scattering interference, and spectral peak overlap present in the original spectrum. AirPLS (adaptive iterative penalized least squares) [20,21,22] effectively estimates and removes low-frequency baseline drift; Detrend (detrending algorithm) [23,24] eliminates linear or quadratic baseline trends; and DOSC (Direct Orthogonal Signal Correction) [23] removes orthogonal signal interference unrelated to the target variable.
Building on this, the CARS (Competitive Adaptive Reweighted Sampling) algorithm [25,26,27] is applied to perform characteristic wavelength screening on the preprocessed spectra. Combined with vegetation index-based collaborative analysis, this approach strengthens the correlation between the spectra and the SPAD value, thereby identifying specific prediction models suitable for the developmental stages of the Korla fragrant pear. Machine learning methods can effectively handle high-dimensional and nonlinear data, automatically uncovering complex relationships between near-infrared spectroscopy, vegetation indices, and SPAD. This significantly enhances prediction accuracy and overcomes the limitations of traditional models [28]. Therefore, SPAD modeling based on near-infrared spectroscopy and vegetation indices has become a major focus of current research.
In recent years, SPAD prediction modeling based on near-infrared spectroscopy and the vegetation index has achieved significant success across various crops, including fruit trees, rice, and maize, with models typically demonstrating high accuracy (Coefficient of determination (R2) > 0.8). For instance, Chetan et al. [29] developed a high-precision prediction model for SPAD and yield in maize after tasseling by integrating sensor data with NDVI, achieving a Coefficient of determination (R2) of 0.98. Guo et al. [30] found that the SVM performed exceptionally well in predicting SPAD across different growing stages (Coefficient of determination (R2) = 0.81). Huang [31] and Xie [32] each developed SPAD prediction models with strong correlations for apple, pear, and lychee (Coefficient of determination (R2) > 0.8). Mao et al. [33] further noted that the observation angle of the vegetation index (e.g., NDVI, GCI) can influence the accuracy of SPAD prediction. However, existing studies still have the following limitations: (1) insufficient consideration of the differences in chlorophyll content among new, mature, and old leaves, making the models vulnerable to environmental disturbances; (2) most models are constructed based on statistical correlation rather than physiological mechanisms, resulting in limited interpretability; (3) most models are developed using data from a single or mixed growth stage, failing to capture the physiological changes in trees across different developmental stages. Fruit trees exhibit significant variations in internal components (such as chlorophyll and soluble sugars) during different growth stages (e.g., flower bud differentiation, fruit development). Therefore, “static” modeling approaches fall short of meeting the dynamic monitoring needs of precision agriculture.
To address these issues, this study focuses on the Korla fragrant pear and proposes a “Growth period specificity” SPAD prediction modeling strategy. The main highlights of this study include (1) for the first time, stage-based models were developed for Korla fragrant pear different growth stages, demonstrating that stage-based modeling outperforms a unified full-period model; (2) the integrated application of nine spectral preprocessing algorithms (including Adaptive iteratively reweighted Penalized Least Squares, Detrend, Direct Orthogonal Signal Correction, etc.), the Competitive Adaptive Reweighted Sampling feature extraction algorithm, and BP Neural Network/Support Vector Regression machine learning methods to build a high-precision prediction model; and (3) the combination of spectral data and vegetation index to improve model performance and robustness.
By developing a growth period-specific model for predicting leaf SPAD using near-infrared spectroscopy integrated with the vegetation index, this study not only enhances the understanding of the chlorophyll–spectral response mechanism but also offers a new approach for the dynamic monitoring of fruit tree physiological status. The modeling strategy is highly adaptable and can be effectively applied in production settings to accurately monitor the growth period of fruit trees, thereby improving both fruit quality and yield.
2. Materials and Methods
2.1. Survey of Test Sites and Materials
This study was conducted in 2024 at the experimental base of Tarim University (40°22′ N, 81°58′ E) in Alar City, Xinjiang, China. Twenty-three-year-old mature Korla fragrant pear trees (grafted onto *Pyrus betulifolia* rootstock) were used as the observation object. The tested fruit trees were planted in a north–south-oriented orchard with a spacing of 2 m × 4 m. To minimize the influence of local micro-environmental variations, the researchers specifically selected sample trees located in the central area of the orchard that exhibited vigorous growth, uniform development, sufficient sunlight, and no shading as the research objects.
The experimental base is situated in a typical warm-temperate extreme continental arid desert climate zone. The region experiences sparse annual precipitation (approximately 50 mm), which is mainly concentrated in summer (June–August), with snowfall predominating in winter. Conversely, the annual potential evaporation is high (>2000 mm), and solar radiation resources are extremely abundant, with an annual sunshine duration of approximately 2900 h. Influenced by the strong continental climate, both the diurnal (typically 10–15 °C) and seasonal temperature ranges are extremely significant. Traditional flood irrigation is employed for water management in the orchard, with irrigation cycles of approximately 15 to 20 days. The annual irrigation volume is maintained at 8000 to 10,000 cubic meters per hectare.
2.2. Sample Collection
To monitor changes in fragrant pear leaf characteristics during key fruit development stages, we collected leaf sample at three time points: the fruit setting stage (23 April 2024), the fruit expansion stage (11 July 2024), and the Maturity period (20 September 2024). At each sampling time, one mature and healthy leaf was selected from each of the 150 designated trees. Leaves were taken from the middle to lower sections of the outer canopy on current-year branches, with one leaf collected from each of the east, south, west, and north sides. (The test process is shown in Figure 1).
Figure 1.
Test flowchart.
After measuring the SPAD value, the leaves were picked. Immediately after collection, the leaves were labeled, placed into Ziplock bag, and promptly stored in a refrigerator at 4 °C to minimize physiological and biochemical changes and preserve their original state at the time of sampling [34,35]. All spectroscopy measurements were completed within 24 h of sample collection. Previous studies have shown that under such short-term refrigerated conditions, the spectroscopy properties of leaf, particularly those related to chlorophyll content, are well preserved and sufficient for developing reliable prediction model [36,37]. These preserved leaf samples will be used for subsequent spectroscopy property measurements.
2.3. Acquisition of Leaf Spectral Data
To ensure that each spectral signal we collect accurately reflects the biochemical properties of the leaf itself, rather than being influenced by environmental interference, we must establish a high-quality and reliable data foundation for constructing the prediction model. Therefore, measurements should be conducted in a relatively stable and standardized environment, such as a laboratory. Additionally, after SPAD measurement, spectral scanning must be performed at exactly the same location on the same leaf to achieve precise one-to-one correspondence without spatial deviation. This level of accuracy is extremely difficult to achieve in the field and is crucial for successful model training. In conclusion, spectral data should be collected in the laboratory.
After being stored in a refrigerator at 4 °C, the sample was equilibrated for 12 h in the spectroscopic measurement room (maintained at a constant temperature of 24 °C) to eliminate thermal effects on the measurements. The Antaris II FT-NIR (Thermo Fisher Scientific, Waltham, MA, USA) (4000–10,000 cm−1) spectrometer system was started simultaneously: after a 30 min warm-up, diffuse reflectance correction was performed using the standard whiteboard as the reference.
For leaf spectral acquisition, using the main vein as a reference, two scan areas were designated at both the proximal and distal ends of the leaf (four marked sites in total). spectral data from different sites were distinguished using color coding. Measurements were conducted using the Antaris II FT-NIR Spectrometer (Thermo Fisher Scientific, Waltham, MA, USA) with the following settings: scan range of 4000–10,000 cm−1, resolution of 8 cm−1, gain of 2×, and 32 scans per accumulation. Each site was scanned four times, resulting in a total of 16 spectral curves per single leaf. After baseline correction, the average of four scans at each measurement point was calculated, followed by the integration of data from four points to obtain the final reflectance (R) of leaf, which was used for chemometric modeling [38]. This method significantly reduced errors caused by environmental temperature fluctuations, instrument instability, and the heterogeneity of leaf through a three-tier quality control process, preprocessing standardization, instrument calibration, and spatial replicate sampling, thereby ensuring high-quality data for model development. In this study, Origin 2024 (OriginLab Corporation, Northampton, MA, USA) and MATLAB 2022b (MathWorks, Natick, MA, USA) were used for plotting.
2.4. Leaf SPAD Value Measurement
The relative chlorophyll content (SPAD value) of pear tree functional leaf was measured using a SPAD-502 handheld chlorophyll meter (Konica Minolta, Inc., Tokyo, Japan). Measurements were taken sequentially on each leaf at 4 fixed measurement points (strictly corresponding to spectral scanning points), with a single-point interval of ≥15 s to eliminate probe thermal drift. Under strong light conditions (>1000 μmol·m−2·s−1), shade cloth was used to shield against ambient light interference. The single-leaf SPAD value was calculated as the arithmetic mean of the 4 points, according to the following formula:
2.5. Spectral Outlier Removal Method
In this study, the Mahalanobis distance (MD) method is employed to detect and remove outliers from the spectral data, thereby improving the robustness of the modeling data [39]. The Mahalanobis distance is calculated as follows:
where xi is the sample vector (column vector) to be calculated; μ is the mean vector of all samples.
In this study, the Mahalanobis distance method was employed for outlier detection on 450 initial samples because it better accommodates the covariance structure characteristics of high-dimensional spectral data compared to Euclidean distance. Following the identification and removal of 14 spectral outlier samples, 436 valid samples were ultimately retained. This preprocessing workflow significantly reduced the interference of data noise on model generalization ability, thereby providing reliable data assurance for constructing a robust chlorophyll content prediction model.
2.6. Spectral Preprocessing Methods
In the acquisition and component quantification of near-infrared spectroscopy, external interferences, such as thermal noise from electronic components, Mie scattering effects, and systematic deviations introduced by operators, can easily lead to baseline drift in absorbance and distortion of characteristic peaks [40]. Spectral preprocessing techniques are employed to suppress non-target signal interference and enhance the separation of the Characteristic Absorption Peak of the components to be measured, thereby laying the foundation for establishing high-precision quantitative models. In this experiment, nine preprocessing algorithm were used, including Adaptive iteratively reweighted Penalized Least Squares (AirPLS), Detrending (Detrend), Direct Orthogonal Signal Correction (DOSC), Multiplicative Scatter Correction (MSC), Savitzky–Golay Smoothing (SG), First Derivative (FD), Second Derivative, SG+FD, and SG+Second Derivative.
Baseline correction relies on AirPLS and Detrend algorithms to eliminate background interference caused by optical path fluctuations and instrument drift. Scattering compensation is achieved through Multiplicative Scatter Correction to address particle scattering effects, while DOSC removes orthogonal signals unrelated to the target component. During feature optimization, SG filtering is employed to suppress random noise and preserve the spectral peak profile. Furthermore, FD/SD differentiation amplifies the second-order features of the absorption band, enhancing spectral resolution. The composite processing of SG+FD/SG+SD, through the synergistic effects of noise reduction and feature enhancement, generates spectral data suitable for quantitative modeling.
(1) The Adaptive iteratively reweighted Penalized Least Squares [23] (Adaptive iteratively reweighted Penalized Least Squares, AirPLS) algorithm is described as follows:
where yi is the original spectrum; zi is the fitted baseline; wi is the iterative weight; is the smoothing penalty parameter, a scalar (λ > 0), where a larger value results in a smoother baseline.
(2) Detrending method [24] (Detrend, Detrend):
where the polynomial fitting function is k of order ( = 2), with λ wavelength as the independent variable, and the vector is represented by .
(3) Direct Orthogonal Signal Correction [23] (Direct Orthogonal Signal Correction, DOSC):
where the original data matrix is denoted by X; t represents the subvector of DOSC; t = Xw and twT stands for the interference signal to be removed.
(4) The formula of multiple scattering correction (MSC) is as follows:
average spectrum of all the sample spectra, let each sample spectrum have P wavelength points, , where is the average of the absorbance of all samples at the i th wavelength point; Xj for the each sample spectrum; bj is the regression coefficient obtained from the linear regression fit; aj is the intercept obtained from the linear regression fit.
(5) Savitzky–Golay Smoothing (Savitzky–Golay Smoothing, SG):
Among them, yi represents the given spectral data sequence for i = 1, 2, … n; is the data point after convolution smoothing with the Savitzky–Golay filter (where j corresponds to the central position within the window); ; m is the window width (m is usually an odd number); and Ci is the weight coefficient related to the polynomial fitting coefficients.
(6) The first-order derivative (FD) and second-order derivative (SD) formulas are as follows:
yi is a discrete sequence of spectral data (i = 1, 2, … n) and Δλ is the wavelength interval.
2.7. Feature Extraction
To enhance model performance and suppress redundant spectral information, the Competitive Adaptive Reweighted Sampling (CARS) algorithm was employed in this study to screen key wavelength features. This algorithm integrates Monte Carlo Sampling with an exponentially decreasing weight strategy for variable importance assessment. The core steps are as follows: (1) The initial weights of each wavelength are calculated based on the t-test statistic of the partial least squares regression (PLS-R) coefficient, and the weight distribution is dynamically updated through an exponential decay function. (2) An adaptive weighted sampling strategy is used to select variable subsets, and their prediction performance is evaluated based on the cross-validation Root Mean Square Error (Root Mean Square Error of CalibrationV) of the PLS-R model. (3) The above process is iteratively executed, gradually eliminating wavelength variables with low contribution until the Root Mean Square Error of CalibrationV reaches its minimum value or begins to increase significantly, finally determining the optimal wavelength subset [41,42].
2.8. Vegetation Index Screening and Calculation
To comprehensively monitor the physiological status of the Korla fragrant pear, this study first selected 20 widely used candidate vegetation index from the literature that are associated with plant water content, nitrogen levels, pigments, and canopy structure (see Supplementary Materials: Vegetation Index Screening).
This study aims to accurately monitor key physiological and biochemical parameters of Korla fragrant pear. The selection of vegetation index was primarily based on two core principles:
(1) Physiological Correlation: Priority was given to indices that show strong correlations with plant water content, nitrogen levels, and fiber components (cellulose/lignin). For instance, the NDWI [43], MSI [44], and NDII [45] series are sensitive to plant water stress and can be used to characterize the equivalent water thickness of leaf [46]; NDNI has been validated as an effective indicator for assessing plant nitrogen content [47,48]; CAI [49] and LI [50] reflect vegetation senescence and lignification levels, respectively [49]. All of these indices are closely linked to the target parameters of this study, including SPAD values (relative chlorophyll content), water content, and nitrogen levels. (2) Technical adaptability: This study employed the Antaris II Fourier Transform Near-Infrared Spectrometer, whose measurement range of 4000–10,000 cm−1 (1000–2500 nm) precisely encompasses the characteristic absorption regions of the aforementioned biochemical components (e.g., around 1200 nm, 1450 nm, 1680 nm, and 2100 nm). Therefore, all indices must be calculable from spectral bands within this range to fully exploit the device’s technical advantages in biochemical quantitative analysis.
Based on this principle, six complementary vegetation index were ultimately selected, including NDWI-L, MSI-L, and NDII-L, which reflect moisture status. Among them, the 1080 nm band serves as a highly reflective and stable reference platform within the Spectral range of this study, while the 1240 nm and 1600 nm bands are highly sensitive to the liquid water content in the leaf [51]. The NDNI, which reflects nitrogen levels, quantitatively assesses nitrogen by directly utilizing its characteristic absorption at 1510 nm and 1680 nm [48,52]. In addition, the CAI and LI indices, which indicate senescence and lignification, are used to capture the unique spectral features of cellulose and lignin in the 2000–2500 nm range [53].
The calculation formula of each index is as follows:
Normalized Difference Water Index—Linearized (NDWI-L) [43]:
Moisture Stress Index—Linearized (MSI-L) [44]:
Normalized Difference Infrared Index—Linearized (NDII-L) [45]:
The formula for calculating the Normalized Difference Nitrogen Index (NDNI) is as follows [43]:
The formula for calculating the Cellulose Absorption Index (CAI) is as follows [49]:
The formula for calculating the Lignin Index (LI) is as follows [50]:
where RX represents the spectroscopy reflectance value at a wavelength of x nm.
2.9. Modeling Algorithms
To enhance the robustness of the Spectral Analysis model, this study employs two algorithms for modeling: Support Vector Regression (SVR) and the BP Neural Network. SVR, grounded in Statistical Learning Theory, seeks to identify the optimal hyperplane that best fits the data relationship. This is achieved by maximizing the margin and employing the ε-insensitive Loss Function to manage fitting error. The algorithm utilizes the Kernel Function to project data into a high-dimensional Feature Space, thereby effectively tackling Nonlinear Regression problems. Its strong Generalization Performance and adaptability to high-dimensional data provide advantages in Spectral Analysis [42,54]. The BP Neural Network, a classic Multi-layer Network Structure, learns intricate data patterns through Nonlinear Transformation. It optimizes weights via the Gradient Descent Method and iteratively refines parameters using the Error Backpropagation mechanism, showcasing robust Nonlinear Fitting capabilities. To address the characteristics of spectral data, the BP Neural Network constructed in this study employs a Single Hidden Layer design and incorporates the ReLU Activation Function and Regularization Technique, with the aim of effectively balancing model complexity and Generalization Performance [55,56].
2.10. Model Evaluation Methods
In this study, four indicators—Coefficient of determination (R2), Root Mean Square Error (RMSE), Residual Prediction Deviation (RPD), and Ratio of Performance to Interquartile Range (RPIQ)—were selected to systematically evaluate model performance. R2 (Formula (17)) is used to evaluate the Goodness of Fit of the model, with values ranging from 0 to 1. A value closer to 1 indicates a better agreement between the predicted value and the measured value [57]. RMSE (Formula (18)) represents the absolute magnitude of the prediction error; a decrease in its value corresponds to an improvement in prediction accuracy [58]. RPD (Formula (19)) measures the model’s prediction capability, and the evaluation criteria are as follows: RPD > 3 (excellent), 2 < RPD ≤ 3 (can be used for preliminary prediction), RPD ≤ 2 (insufficient prediction capability) [59]. RPIQ (Formula (20)) is calculated as the ratio of the interquartile range (IQR) of the dataset to RMSE (i.e., RPIQ = IQR/RMSE). A larger value indicates better model performance, and the evaluation levels are categorized as follows: >3 (excellent), 2–3 (good), 1–2 (average), and ≤1 (poor) [60]. For model evaluation, the Training Set–Test Set partitioning strategy is adopted, and each indicator’s value is calculated separately to comprehensively examine the model’s fitting effect, prediction accuracy, and Generalization Performance [61].
3. Results and Analysis
3.1. Original Spectral Images
In Figure 2, images a, b, and c, respectively, display the near-infrared spectra (4000–10,000 cm−1) of the fruit-setting period, fruit swelling period, and Maturity period leaf, covering the characteristic absorption regions associated with chlorophyll (5000–7000 cm−1) and moisture (7000–8000 cm−1). Image d visually compares the differences in relative chlorophyll content of leaf at different growth stages using a SPAD value box plot.
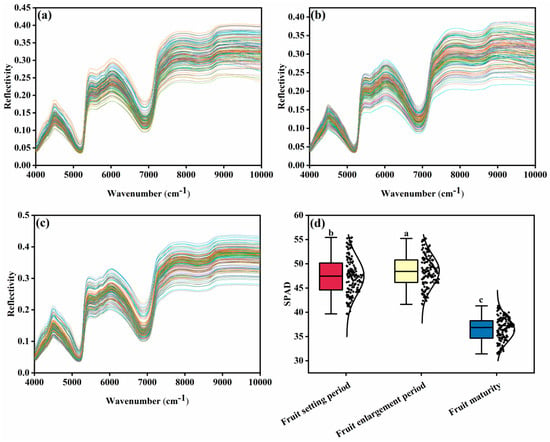
Figure 2.
(a) is the original spectrum of fruit setting period; (b) is the original spectrum of fruit swelling period; (c) is the original spectrum of fruit maturing period; (d) is the content of leaf SPAD in each period (the different letter marks (a–c) in the box plot represent significant differences between groups (p < 0.05)).
During the fruit-setting period, the leaf is in its early developmental stage, and chlorophyll synthesis has just begun. In the 5000–7000 cm−1 range, chlorophyll-related reflection peaks are weak. Meanwhile, due to the high moisture concentration in young leaves, the moisture absorption valleys in the 7000–8000 cm−1 range are deep and narrow, and the spectral dispersion among samples is relatively high. During the fruit expansion period, the leaf grows vigorously, and chlorophyll content reaches its peak (with the highest SPAD value, showing a significant difference from the fruit setting period). Dominated by chlorophyll, the reflection peaks in the 5000–7000 cm−1 range become sharper and more consistent across samples. Meanwhile, the depth of the moisture absorption trough in the 7000–8000 cm−1 range remains similar to that of the fruit setting period, with the overall spectral trends showing a high degree of overlap.
During the Maturity period, the leaf undergoes senescence, with the most prominent change being the rapid degradation of chlorophyll (evidenced by a significant drop in SPAD value), which directly results in the breakdown of the spectral features “framework” it governs. This is reflected in the flattening and collapse of reflection peaks in the 5000–7000 cm−1 range. At the same time, moisture loss is also observed, indicated by a shallower absorption trough in the 7000–8000 cm−1 range. However, the fundamental differentiation in spectral morphology—such as the collapse of reflection peaks rather than a simple overall increase in reflectance—is primarily driven by the loss of the main light-absorbing substance (chlorophyll), with moisture exerting a secondary effect layered upon this primary cause.
In summary, the main driver of spectral evolution across the three growth period stages shown in Figure 2 is the dynamic change in chlorophyll content. As a key light-absorbing pigment, chlorophyll plays a dominant role in shaping and “sharpening” spectral morphology when abundant (during the fruit expansion period); its degradation (during the Maturity period) results in the “collapse” of spectral features, thereby allowing the spectral signals of other factors, such as moisture, to emerge.
In conclusion, chlorophyll is the primary driver of spectral variation, while moisture serves as an important but secondary background signal. This provides a key physiological explanation and spectral features basis for using spectral technology non-destructive to identify the growth period and estimate chlorophyll content.
3.2. Spectral Preprocessing
Figure 3 illustrates how nine spectral preprocessing algorithms optimize original spectra. To address typical errors like baseline drift, random noise, scattering interference, and spectral peak overlap, different strategies are employed for correction and enhancement. Specifically, AirPLS iteratively fits and subtracts the nonlinear baseline (Figure 3), while Detrend eliminates linear/low-order trends. These two methods complement each other to improve baseline flatness and highlight the intrinsic characteristics of absorption peaks (Figure 3b). DOSC constructs an orthogonal subspace to filter out background interference, enhancing the spectral overlap of the sample, though it may compress weak signals (Figure 3c). SG smooths the spectra for noise reduction through sliding window polynomial fitting, retaining the spectral peak profile. Optimizing window parameters is necessary to balance noise reduction and detail retention (Figure 3d). MSC corrects the multiplicative effect of surface scattering, bringing the spectrum closer to the “pure absorption” mode (Figure 3e), whereas SD standardizes the mean and standard deviation to eliminate amplitude differences due to physical heterogeneity, focusing on chemical peak shapes (Figure 3f). FD resolves overlapping peak and accurately locates feature bands using the first derivative, but this amplifies noise (Figure 3g). In contrast, SG+FD, after smoothing and derivation, balances resolution enhancement and noise amplification, resulting in sharper and more continuous derivative spectrum peak shapes, making it suitable for densely packed spectral systems (Figure 3h). SG+SD integrates the advantages of smoothing for noise reduction and normalization, highlighting chemical shape differences and reducing noise interference, which improves sample consistency and makes it suitable for multivariate modeling (Figure 3i).
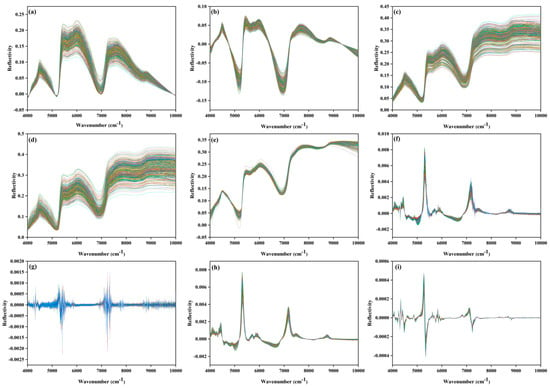
Figure 3.
Spectral images processed by various preprocessing algorithms: (a) is AirPLS; (b) is Detrend; (c) is DOSC; (d) is SG; (e) is MSC; (f) is FD; (g) is SD; (h) is SG+FD; (i) is SG+SD.
These algorithms are complementary in addressing error sources and achieving processing objectives. In practice, spectral visualization and modeling validation (e.g., PLS model R-squared, RMSE) should be combined, focusing on “maximizing chemical information retention and minimizing error interference.” This enables the selection of appropriate strategies for diverse goals, such as wide-peak quantification (e.g., water content) or narrow-peak analysis (e.g., functional groups), ultimately bolstering the reliability of spectral quantitative analysis.
3.3. Preprocessing Correlation
These subgraphs illustrate how different preprocessing algorithm applied to spectral data of Korla fragrant pear leaves alter the correlation between the spectra and SPAD (reflecting chlorophyll content). The horizontal axis is scaled by wavenumber, covering the common Spectral Analysis range. The vertical axis represents the correlation coefficient between the spectrum and SPAD, ranging from −1 to 1, where larger absolute values indicate a stronger linear correlation. As shown in Figure 4a, the correlation ranges only from 0.12 to 0.28 within the 4000–10,000 cm–1 range. In contrast, subgraphs Figure 4b–j correspond to nine types of preprocessing algorithm, including Adaptive iteratively reweighted Penalized Least Squares and Detrend. As a baseline correction algorithm, Adaptive iteratively reweighted Penalized Least Squares maintains the correlation coefficient in the 5000–7000 cm−1 band mostly between 0.6 and 0.8. After correction, the correlation between the spectrum and chlorophyll in this interval is stable, while the coefficient near 10,000 cm−1 drops to 0.3, indicating a decay in correlation at the longwave end.
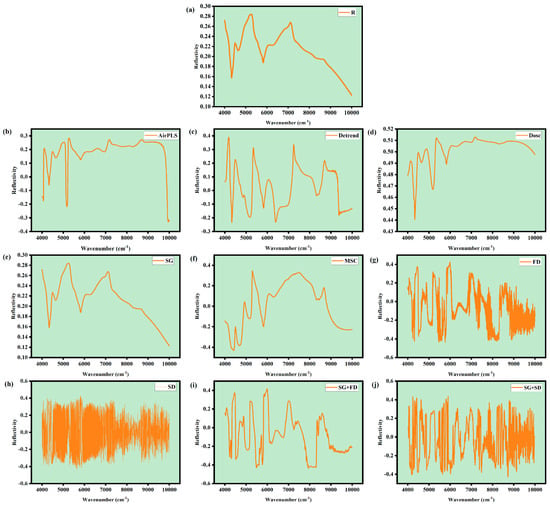
Figure 4.
Correlation between each band and SPAD of Korla pears after processing by different pretreatment algorithms: (a) is AirPLS; (b) is Detrend; (c) is DOSC; (d) is SG; (e) is MSC; (f) is FD; (g) is SD; (h) is SG+FD; (i) is SG+SD; (j) is SG+SD.
Detrending removes spectral drift, with coefficients fluctuating between −0.4 and 0.7 in the 4000–6000 cm−1 range. Consequently, the associated fluctuations at the shortwave end, which are affected by drift, are “flattened.” Coefficients in the 7000–9000 cm−1 range stabilize at 0.5–0.6, and the correlation at the longwave end is improved through correction. Deno focuses on noise reduction, resulting in a smooth processed curve with correlation coefficients mostly in the range of 0.4–0.7. The peak value of the 5000–6000 cm−1 coefficient reaches 0.8, and noise reduction significantly enhances the correlation between the spectrum in this range and SPAD. Savitzky–Golay (Savitzky–Golay smoothing) reduces curve fluctuations, maintaining coefficients at 0.3–0.6, and stabilizes around 0.55 in the 7000–8000 cm−1 range. This smoothing leads to a more consistent longwave end correlation, facilitating the extraction of stable features. MSC (Multiplicative Scatter Correction) increases the 4000–5000 cm−1 coefficient from 0.4 to 0.7, and this scattering correction enhances the shortwave end correlation. The 8000–9000 cm−1 coefficient drops back to 0.5, and the scattering-affected correlation at the longwave end is partially “corrected”.
The first derivative highlights changes in spectral slope, with coefficients in the 5000–7000 cm−1 range fluctuating drastically between −0.3 and 0.8. This derivative amplification of spectral details and their correlation differences with SPAD is beneficial for extracting characteristic peaks and valleys. Standard Deviation curves exhibit strong noise, with coefficients oscillating between −0.2 and 0.7, particularly noticeably in the 4000–6000 cm−1 range. After transformation, spectral fluctuations at the shortwave end show a more complex correlation with SPAD, which can easily introduce redundant information. The combination of Savitzky–Golay + First Derivative leverages the advantages of both smoothing and derivative methods; coefficient peaks reach 0.85 in the 5000–8000 cm−1 range. Details are retained through the derivative, while noise is suppressed with Savitzky–Golay, significantly enhancing the correlation in key intervals and making it suitable for precise feature extraction. Savitzky–Golay + Standard Deviation (smoothing + normal variate transformation) reduces the noise impact of Standard Deviation through smoothing; coefficients stabilize between 0.6 and 0.7 in the 7000–9000 cm−1 range, balancing feature retention and noise suppression. Overall, the 5000–8000 cm−1 region is identified as the high correlation region with SPAD after processing by most algorithms. Savitzky–Golay and Deno are suitable for basic modeling to maintain stability. The First Derivative and Savitzky–Golay + First Derivative methods are beneficial for detail extraction, while Savitzky–Golay + Standard Deviation and Adaptive iteratively reweighted Penalized Least Squares can balance noise and correlation.
3.4. Spectral Feature Extraction
In this study, we applied the Competitive Adaptive Reweighted Sampling algorithm to perform feature wavenumber screening on spectral data processed with different preprocessing methods across various different growth stages. As clearly shown in Figure 5, the number of selected feature wavenumbers differs significantly across the different processing combinations. This variation reflects two key aspects: first, the dominant physiological processes in the crop change across different growth stages; second, different preprocessing methods vary in their ability to enhance specific chemical information.
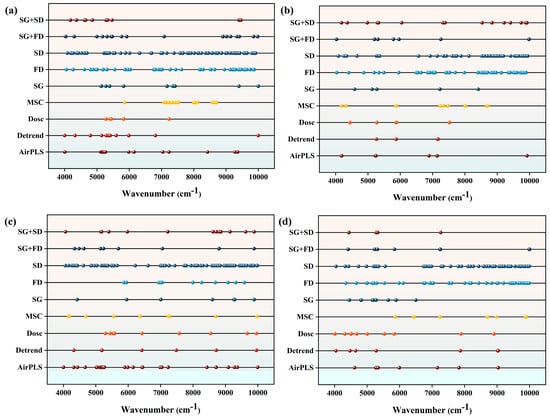
Figure 5.
Feature extraction: (a) is the feature wave position extracted by CARS algorithm for 9 kinds of pretreatment in full growth period; (b) is the feature wave position extracted by CARS algorithm for 9 kinds of pretreatment in fruit setting period; (c) is the feature wave position extracted by CARS algorithm for 9 kinds of pretreatment in fruit enlargement period; (d) is the feature wave position extracted by CARS algorithm under 9 kinds of pretreatment in fruit ripening period.
Regarding changes in the number of feature wavenumbers: during the fruit ripening period, all preprocessing methods yield significantly fewer feature wavenumbers. For instance, the combination of Savitzky–Golay and Second Derivative can extract at least 15 feature wavenumbers at other growth stages, but only four during the ripening stage. The reason is that during the fruit maturation stage, a large amount of chlorophyll in the leaf decomposes, physiological and metabolic activities gradually stabilize, the complexity of spectral information decreases, and fewer effective features can be extracted.
In contrast, during the fruit-setting period and the fruit swelling period, which are stages of vigorous vegetative growth, preprocessing methods such as the Second Derivative and First Derivative can extract more characteristic wavenumbers. For example, during the fruit-setting period, both First Derivative and Second Derivative preprocessing methods can extract 54 features; during the swelling period, the Second Derivative method can extract up to 86 characteristic wavenumbers. This indicates that derivative preprocessing can effectively amplify subtle spectral features associated with the dynamic change in chlorophyll, and these amplified features are precisely captured by the Competitive Adaptive Reweighted Sampling algorithm. In addition, when Multiplicative Scatter Correction is used for preprocessing, the number of characteristic wavenumbers identified at different growth stages remains relatively consistent. This highlights the advantage of Multiplicative Scatter Correction—regardless of the crop’s physiological status, it can reliably extract core spectroscopy information that is directly related to chemical components.
More importantly, the distribution of these selected characteristic wavenumbers exhibits a distinct pattern. Their significance lies in their direct correspondence to the molecular vibrations of key components such as chlorophyll. A detailed analysis shows that the vast majority of these characteristic wavenumbers are concentrated in several key sensitive spectral regions. The first is the 5000–7000 cm−1 range, which primarily corresponds to the fundamental double frequency absorption of O-H bonds and the characteristic absorption of chlorophyll. During the fruit-setting and expansion stages, the characteristic wavenumbers in this range are frequently screening identified. These wavenumbers not only directly capture the characteristic vibrations of the porphyrin ring structure containing magnesium in chlorophyll molecules, but also reflect changes in leaf moisture status. They serve as direct indicators of photosynthetic intensity and are sensitive bands for predicting SPAD values.
The second range, 7000–8000 cm−1, primarily corresponds to the secondary double frequency absorption of N-H bonds and water. The characteristic wavenumbers in this range are closely associated with the nitrogen content in chlorophyll molecules. From a physicochemical standpoint, the molecular vibration signals in this range originate from nitrogen-containing groups involved in chlorophyll synthesis and degradation processes. Therefore, the presence or absence of characteristic wavenumbers in this range can accurately reflect the crop’s nitrogen status and the activity level of chlorophyll metabolism. In summary, the importance of the characteristic wavenumbers selected by the Competitive Adaptive Reweighted Sampling algorithm is reflected in two main aspects. First, in terms of quantity, they align with the physiological changes during the different growth stages—the more active the physiological processes and the more complex the information, the greater the number of characteristic wavenumbers. Second, in terms of position, they directly correspond to the molecular vibrational features of key components such as chlorophyll and moisture, carrying clear physicochemical significance. The differences among various preprocessing methods essentially enhance chemical information in different dimensions, providing a reliable foundation for constructing spectral data.
3.5. Spectral Model Development
Figure 6 illustrates a comparison of the optimal spectral model performance achieved by each modeling algorithm across different growth stages. Specifically, FD-CARS-BP and FD-CARS-SVR represent models developed for the whole growth period based on the BP Neural Network and Support Vector Regression (SVR), respectively. The growth stage specificity models include MSC-CARS-SVR (S1-MSC-CARS-SVR) and SG+FD-CARS-BP (S1-SG+FD-CARS-BP) for the fruit setting stage, FD-CARS-BP (S2-FD-CARS-BP) and SG+FD-CARS-SVR (S2-SG+FD-CARS-SVR) for the fruit expansion stage, and FD-CARS-BP (S3-FD-CARS-BP) and SG+FD-CARS-SVR (S3-SG+FD-CARS-SVR) for the fruit maturation stage. In this study, model performance was comprehensively evaluated based on four metrics: the Coefficient of determination (R-squared), the Root Mean Square Error (Root Mean Square Error), Residual Prediction Deviation (RPD), and the Ratio Of Performance To Interquartile Range value (RPIQ). Figure 6a shows that, within the whole growth period model, the FD-CARS-SVR model performed optimally (Supplementary Materials Table S1), achieving R-squared values of 0.8384 and 0.767 for the Training Set and validation set, respectively. Further analysis indicated that model performance with growth stage specificity was significantly superior to the whole growth period model. Specifically, the optimal model for the fruit setting stage, SG+FD-CARS-BP, exhibited an R-squared as high as 0.8636 (training set) and 0.8559 (validation set) (Supplementary Materials Table S2). For the fruit expansion stage, the optimal model achieved an R-squared of 0.8114 (training set) and 0.8195 (validation set) (Supplementary Materials Table S3). The FD-CARS-BP model demonstrated the best performance during the fruit maturation stage (R-squared = 0.825 and 0.8196), while the model constructed using the SVR algorithm during this stage exhibited overfitting (Supplementary Materials Table S4). The Root Mean Square Error analysis in Figure 6b further confirmed that the prediction error of each growth stage specificity model was significantly lower than that of the whole growth period model (all Root Mean Square Errors < 1.5).
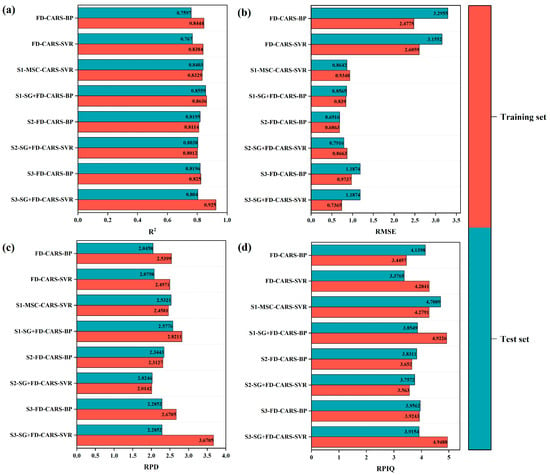
Figure 6.
Comparison of the best spectral model indexes under each modeling algorithm in different periods: (a) is R2 of training set and verification set, (b) is the RMSE of training set and verification set; (c) is the RPD of the training set and verification set; (d) is the RPIQ of the training set and verification set.
Upon comparing the RPD and RPIQ indicators (Figure 6c,d), the S1-SG+FD-CARS-BP model demonstrated the best performance, with RPD values of 2.4581 for the training set and 2.5321 for the validation set, and RPIQ values of 4.9226 for the training set and 3.8549 for the validation set. The S2-FD-CARS-BP model followed, exhibiting RPD values of 2.3127 for the training set and 2.3443 for the validation set, and RPIQ values of 3.652 for the training set and 3.8311 for the validation set. The S3-FD-CARS-BP model displayed good generalization ability (RPD = 2.2852 for the training set, 2.6705 for the validation set; RPIQ = 3.9562 for the training set, 3.9243 for the validation set). Comprehensive evaluation indicated that the growth stage-specific modeling strategy was significantly superior to the full growth stage modeling. The recommended optimal SPAD prediction model for each growth stage is as follows: the S1-SG+FD-CARS-BP model for the fruit setting stage, the S2-FD-CARS-BP model for the fruit expansion stage, and the S3-FD-CARS-BP model for the fruit maturation stage.
3.6. Establishment of Vegetation Index Model
In this study, six vegetation indices (NDWI-L, MSI-L, NDII-L, CAI, NDNI, and LI) were calculated from spectral data to obtain more comprehensive plant physiological information. With respect to the water content sub-indices (Figure 7a–c), NDII-L and MSI-L reflect the internal water content status of plants, while NDWI-L characterizes the overall water content relationship of the vegetation–soil system. Statistical analysis showed a significant positive correlation between MSI-L values and the degree of vegetation drought (p < 0.05), with the S2 stage (fruit expansion stage) exhibiting the highest degree of drought (the largest MSI-L value), followed by the S3 stage (maturity stage). The water content in the S3 stage was significantly higher than that in the S1 and S2 stages (p < 0.05). The nitrogen index NDNI (Figure 7e) indicated that leaf nitrogen content in the S2 stage was significantly higher than that in the S3 stage (p < 0.05). In cellulose/lignin-related indices (Figure 7d,f), CAI and LI reflect the degree of vegetation senescence and lignification, respectively. Vegetation aging characteristics are indicated by CAI > 3 or LI > 1.1, while a fresh state of vegetation is characterized by CAI < 0 or LI < 0.9. Correlation analysis (Figure 7g) confirmed significant correlations between SPAD Value and NDWI-L, MSI-L, NDII-L, NDNI, and LI (p < 0.05). Consequently, the Phenological Period-specific BP Neural Network model that was established exhibited excellent prediction performance (Figure 7h–k): For the fruit setting stage model, the R2 values for the training set and validation set were 0.83 and 0.79, respectively, the RMSE values were 0.6372 and 0.9644, and the RPD values reached 2.4102 and 2.2072; the corresponding indicators for the fruit expansion stage were 0.80/0.75, 0.8765/0.8910, and 2.2583/2.0108, and those for the maturity stage were 0.79/0.75, 0.8703/1.4001, and 2.2101/2.0043. Model evaluation results indicate that the Phenological Period-specific model performs significantly better than the whole growth period model. The BP algorithm demonstrates a greater advantage compared to the SVR algorithm. Furthermore, the selected vegetation index can effectively predict the leaf SPAD value of Korla fragrant pear, offering a reliable basis for nutrient management and stress monitoring in precision agriculture. These findings also provide a foundation for developing multi-index models by integrating with spectral data.
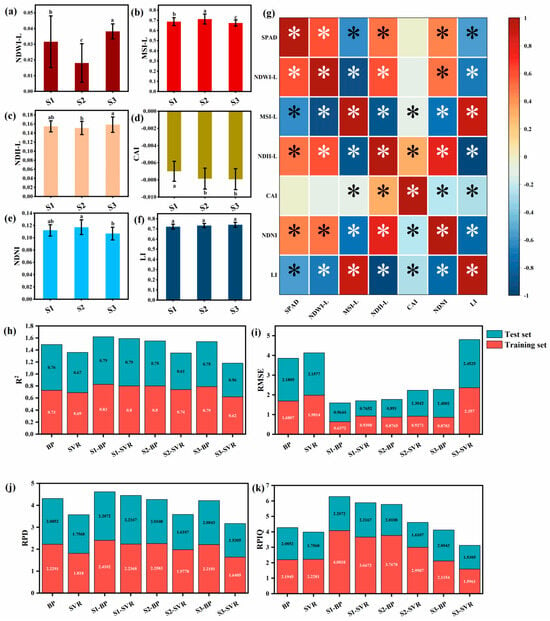
Figure 7.
Vegetation index model; (a) NDWI-L for each period; (b) MSI-L for each period; (c) NDII-L for each period; (d) CAI for each period; (e) NDNI for each period; (f) LI for each period; (g) Correlation analysis between vegetation index and leaf SPAD; (h) R2 of training set vs. validation set in vegetation index model; (i) RMSE of training set vs. validation set in vegetation index model; (j) RPD of training set vs. validation set in vegetation index model; (k) RPIQ of training set vs. validation set in vegetation index model (different letter marks (a–c) in the bar chart indicate significant differences between groups (p < 0.05)). In the correlation heat map, the asterisk was used to indicate that there was a significant difference between different vegetation models and SPAD (relative chlorophyll content) (corresponding p < 0.05).
3.7. Characteristic Spectrum-Vegetation Index Joint Model
Building upon the established spectral model, this study innovatively employs characteristic spectrum and Vegetation Index in joint modeling to significantly improve the Prediction Performance of SPAD Value in Korla fragrant pear leaves. The results demonstrate that the joint model exhibits excellent performance across all evaluation metrics: the coefficient of determination (R-squared) is greater than 0.85, the Root Mean Square Error (RMSE) is less than 1, the Residual Prediction Deviation (RPD) exceeds 2.5, and the Residual Prediction Deviation (RPIQ) is higher than 3.5 (Figure 8a). Compared with the previous single spectral model, significant improvements in all indicators are observed with the joint model (Figure 8b). Specifically, the minimum increase in R-squared is 0.00486 (Training Set) and 0.02297 (Validation Set), with a maximum increase of 0.10224; the maximum decrease in RMSE is 0.07056 (Training Set) and 0.05814 (Validation Set); the minimum increase in Residual Prediction Deviation is 0.0528 (Training Set) and 0.2382 (Validation Set), and the minimum increase in RPIQ is 0.021 (Training Set) and 0.1261 (Validation Set).
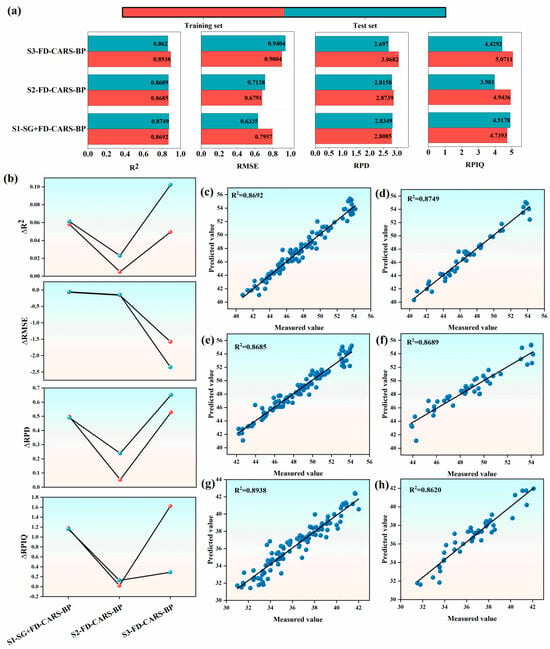
Figure 8.
Characteristic spectral vegetation index model. (a) Evaluation metrics (R2, RMSE, RPD, RPIQ). (b) Differences in metrics between training and validation sets. (c) Linear fitting of the fruit-set model S1-SG+FD-CARS-BP on training set. (d) Linear fitting of the fruit-set model S1-SG+FD-CARS-BP on validation set. (e) Linear fitting of the fruit-ripening set model S2-FD-CARS-BP on training set. (f) Linear fitting of the fruit-ripening set model S2-FD-CARS-BP on validation set. (g) Linear fitting of the fruit-maturing set model S3-FD-CARS-BP on training set. (h) Linear fitting of the fruit-maturing set model S3-FD-CARS-BP on validation set.
These data fully demonstrate the advantages of characteristic spectrum and vegetation index joint modeling in improving prediction accuracy and model stability. Further fitting analysis of predicted value and measured value indicates that each growth stage model exhibits good fitting performance (Figure 8c–h). Specifically, the fruit setting stage FD-CARS-BP model (S1-FD-CARS-BP) achieved R-squared values of 0.8692 and 0.8749 for the training set and validation set, respectively. For the fruit expansion stage FD-CARS-BP model (S2-FD-CARS-BP), the R-squared values were 0.8685 and 0.8689, respectively, and the fruit maturation stage SG-FD+SG-CARS-BP model (S3-SG-FD+SG-CARS-BP) achieved R-squared values of 0.8938 and 0.8620, respectively. Based on the above research results, this study determined that FD-CARS-BP is the optimal prediction model for both the fruit setting stage and the fruit expansion stage, while SG-FD+SG-CARS-BP is the optimal model for the fruit maturation stage.
Through the method of multi-source data fusion, this study not only verified the feasibility of characteristic spectrum and vegetation index joint modeling, but also provides reliable technical support for the precise cultivation management of Korla fragrant pear. The research results are of significant practical guidance value for realizing intelligent monitoring and precise management of the fragrant pear industry.
4. Discussion
This study systematically analyzes the variation patterns of spectral characteristics and vegetation index at different growth stage of Korla fragrant pear. Based on this analysis, a SPAD value prediction model was established, integrating the characteristic spectrum and vegetation index, thus offering a novel approach for the non-destructive monitoring of the physiological status of fragrant pear leaves. The findings not only elucidate the response mechanism between spectral characteristics and leaf physiological state but also provide a theoretical foundation and technical support for nutrient management decision-making within the context of precision agriculture.
4.1. Spectral Characteristics and Response Relationship of Leaf Physiological State
The physiological and biochemical properties of the Korla fragrant pear leaf undergo significant changes throughout the entire growth cycle—from the initiation of chlorophyll synthesis during the fruit-setting stage, to the dominance of chlorophyll during the fruit expansion stage, and finally to chlorophyll degradation and moisture loss during the Maturity period. These transitions reflect a fundamental shift in the dominant internal factors within the leaf.
As a result, the correlation mechanism between spectral features and SPAD value changes significantly. However, the global spectral model is static and cannot capture these dynamic, nonlinear relationships, inevitably leading to errors. Therefore, it is necessary to perform modeling based on growth period specificity.
Original Spectral Analysis indicated significant differences in spectral characteristics of leaves at different growth stage (Figure 2). The chlorophyll Characteristic Absorption Peak of leaves at the fruit setting stage was weak in the range of 5000–7000 cm−1, consistent with the physiological characteristic that chlorophyll synthesis was just beginning at this stage [62,63].
Meanwhile, the deep and narrow Water Absorption Valley at 7000–8000 cm−1 reflected the high water content of young leaves [64,65].
Notably, high spectral dispersion among sample was observed during this period, possibly due to large individual differences in the early development of new leaves [66,67]. Leaves at the fruit expansion stage exhibited typical spectral characteristics: the chlorophyll absorption peak in the range of 5000–7000 cm−1 became sharper, and the consistency among sample increased, consistent with the physiological state of the chlorophyll content reaching its peak (highest SPAD value) during this period [68,69,70]. Of particular note is that although the depth of the Water Absorption Valley during this period is similar to that at the fruit setting stage, the overall spectral trends are highly consistent, suggesting that with sufficient chlorophyll, its dominant role in spectral characteristics may mask the influence of other components. The spectral changes in leaves at the maturity stage are the most significant. Specifically, the chlorophyll absorption peak in the 5000–7000 cm−1 region collapses and becomes flattened, directly reflecting the physiological process of Chlorophyll Degradation [71,72]. Simultaneously, the Water Absorption Valley at 7000–8000 cm−1 becomes significantly shallower, indicating Water Loss in the leaves. These changes are highly consistent with the physiological and biochemical changes observed during leaf senescence. Furthermore, variations in the progression of leaf senescence lead to dramatic differentiation of spectral characteristics during this period, providing an important basis for monitoring leaf senescence status using spectral techniques.
4.2. Impact of Preprocessing Algorithm on Feature Extraction
Spectral preprocessing is a critical step to ensure model reliability and can enhance the robustness of the model [73,74,75]. This study found that different preprocessing algorithm exhibit significant differences in their optimization effect on spectral characteristics (Figure 3).
AirPLS and Detrend algorithms excel in baseline correction, effectively highlighting the intrinsic characteristics of the absorption peak [76]. While the Direct Orthogonal Signal Correction algorithm can enhance the spectral overlap of the sample, it may also compress the weak signal [77]. The SG smoothing algorithm achieves effective denoising while preserving the spectral peak profile [76], and the MSC algorithm successfully corrects the surface scattering effect, bringing the spectrum closer to the “pure absorption” mode [77].
Of particular note is the unique advantage that derivative transformation algorithms [78,79] (FD and SG+FD) exhibit in resolving overlapping peaks. Furthermore, when these preprocessing-treated spectra are combined with the CARS algorithm for feature extraction, key information can be further extracted. The CARS algorithm, based on the principle of Competitive Adaptive Reweighted Sampling, can screen out the most representative characteristic wavelength from massive spectral bands according to the correlation between the bands and the target attribute [80,81,82]. For example, while the FD algorithm can accurately locate the characteristic wavelength, it also amplifies noise; however, screening by the CARS algorithm can eliminate bands with significant noise interference and retain effective features closely related to the analysis target. The SG+FD algorithm performs smoothing followed by differentiation first, maintaining resolution while controlling noise. Subsequently, the CARS algorithm enables a more precise focus on the most valuable feature combinations for model building, allowing the selected characteristic wavelength to play a more effective role in subsequent modeling (such as BP Neural Networks [83] and SVR models [84] and improving the model’s ability to resolve complex spectral data. This observation aligns with the changes in model indicators observed after different preprocessing techniques are combined with feature extraction in subsequent parameter optimization experiments, providing a comprehensive reference from preprocessing to feature selection for processing dense spectral peak system.
4.3. Physiological Basis and Advantages of Growth Period-Specific Modeling
The results of this study indicate that the growth period specificity modeling strategy significantly outperforms the whole growth period modeling approach (Figure 6). This advantage stems from the intrinsic dynamic patterns of leaf physiological metabolism. As discussed in Section 4.1, the core physiological processes of pear leaf vary significantly across different growth stages, resulting in a fundamental shift in the dominant mechanisms underlying its spectral response [85]. A study by Yang et al. reached a similar conclusion: through both overall and population-level modeling analyses of four hardwood species, they found that the overall-level modeling outperformed the population-level approach, further supporting the necessity of modeling based on specific growth periods [86]. Moreover, Mariia et al. found that stage-based management of fruit trees with different Maturity period significantly enhanced economic returns [87], further demonstrating the superiority of specific growth period modeling over the whole-period approach. During the fruit setting stage, the leaf is in the early phase of development, with chloroplast structures not yet fully formed. Although the rate of chlorophyll synthesis is high, its absolute content remains relatively low [88,89,90]. At this stage, the leaf exhibits high moisture content and active cell division; the influence of moisture and cellular structure on spectroscopy is comparable to, or even greater than, that of the chlorophyll signal [91]. Therefore, the SPAD value prediction model during this period must be capable of detecting the subtle chlorophyll features that are partially obscured by moisture signals. The whole growth period model, designed to account for the stronger chlorophyll signals in later stages, struggles to accurately capture these early stage characteristics, leading to reduced accuracy.
During the fruit swelling period, the leaf is fully mature, and the chlorophyll content reaches its peak, becoming the dominant optically active substance in the leaf. Its strong absorption effect masks the spectral variations in other components, such as moisture, resulting in highly uniform spectral features primarily driven by chlorophyll [92]. This period is ideal for constructing high-precision models; however, models built over the entire growth cycle are diluted by the “abnormal” data from the fruit-setting stage and the Maturity period, preventing optimal performance.
During the Maturity period, the leaf initiates the senescence process [93], marked by rapid degradation of chlorophyll and cellular dehydration [94]. At this stage, the spectral signals become complex again: the chlorophyll absorption peak collapses, previously masked moisture absorption valleys become more pronounced, and even the spectral features of cell wall substances—such as cellulose and lignin—begin to emerge [93]. The full growth period model attempts to capture two fundamentally opposing trends using a single equation, which inevitably leads to substantial systematic errors.
The model performance data from this study validate the aforementioned physiological mechanisms. The whole growth period model had the lowest accuracy (test set Coefficient of determination (R2) = 0.767), as it had to reconcile three physiologically distinct stages. Among the stage-specific models, the fruit expansion period model achieved the highest accuracy (R2 = 0.8689), confirming the stability of spectral signals dominated by chlorophyll. The fruit-setting period model followed (R2 = 0.8749), reflecting the challenge of extracting weak signal extraction. The Maturity period model showed the greatest variability in accuracy (R2 = 0.862), consistent with the physiological phenomena of heterogeneous senescence and sharply differentiated spectral features during this stage.
Therefore, the essence of growth period specificity modeling lies in tailoring analytical algorithms to each distinct physiological stage, in accordance with the objective patterns of plant physiological development, thereby enabling more accurate SPAD value surveillance. In terms of model performance metrics, the growth period-specific model exhibited significant advantages across various indicators, including Coefficient of determination (R2), Root Mean Square Error (RMSE), RPD, and RPIQ. For example, the optimal model during the fruit-setting period—Savitzky–Golay + First Derivative—Competitive Adaptive Reweighted Sampling—BP—achieved a test set Coefficient of determination (R2) of 0.8749, an Root Mean Square Error (RMSE) of 0.6335, an RPD of 2.8349, and an RPIQ of 4.9178. These results were significantly better than those of the best model for the whole growth period (test set Coefficient of determination (R2) = 0.767, Root Mean Square Error (RMSE) = 3.1552).
The performance gap was even more pronounced during the fruit ripening period (test set Coefficient of determination (R2) = 0.862, Root Mean Square Error (RMSE) = 0.9404), further confirming the necessity of modeling based on growth period specificity.
This conclusion is supported by other studies. Gao et al., in their research on orchard soil, observed similar trends. Their growth period-specific model (Coefficient of determination (R2) ≥ 0.92; 0.0024 ≤ Root Mean Square Error (RMSE) ≤ 0.0035) clearly outperformed the integrated model for the entire fertilization period (Coefficient of determination (R2) = 0.89; Root Mean Square Error (RMSE) = 0.0041) [95]. Similarly, studies on wheat have demonstrated that growth period specificity modeling (Coefficient of determination (R2) = 0.692, Root Mean Square Error (RMSE) = 0.916, RPD = 1.771, RPIQ = 2.602) can achieve better predictive performance [96].
However, it is worth noting that although growth period specificity modeling techniques have shown promise and have been explored in certain crops (such as wheat) and specific applications (such as soil analysis), their use in the accurate monitoring and modeling of key physiological processes in fruit trees—such as nutrient diagnostics, yield prediction, and stress response—still lacks systematic documentation in the literature. This underscores the importance and urgency of advancing research in this area within the field of fruit tree science.
In this study, the BP Neural Network algorithm generally outperformed the Support Vector Regression algorithm, particularly excelling in modeling nonlinear relationships. This may be because the relationship between leaf SPAD value and spectral features exhibits complex nonlinear characteristics, which are better captured by the BP Neural Network. Wang et al. compared BP and Support Vector Regression and found that BP provides greater flexibility in modeling nonlinear relationships [97].
This study focuses on the parameter optimization of the BP Neural Network (First Derivative—Competitive Adaptive Reweighted Sampling—BP model) and Support Vector Regression (Savitzky–Golay + First Derivative—Competitive Adaptive Reweighted Sampling—Support Vector Regression model), evaluating the optimal configurations using multiple metrics (R2, Root Mean Square Error (RMSE), RPD, and RPIQ).
For the First Derivative—Competitive Adaptive Reweighted Sampling—BP model, when the parameter q = 10, both the training sets and validation set demonstrate excellent performance in terms of fitting accuracy, generalization ability, and discrimination precision. The R2 is high, and the values for Root Mean Square Error (RMSE), RPD, and RPIQ are reasonable, indicating a good balance between fitting and generalization. This configuration represents the optimal parameter setting (Figure 9a).
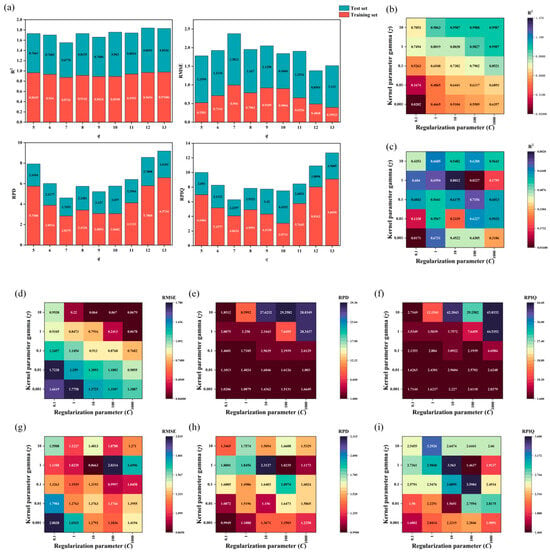
Figure 9.
Parameter optimization of BP Neural Network and SVR: (a) R2, RMSE, RPD, and RPIQ metrics for the FD-CARS-BP model after parameter tuning on training and validation sets; (b,c) R2 values for the SG+FD-CARS-SVR model after parameter adjustment; (d,g) RMSE values for the SG+FD-CARS-SVR model after optimization; (e,h) RPD values for the SG+FD-CARS-SVR model after parameter tuning; (f,i) RPQI values for the SG+FD-CARS-SVR model after parameter refinement.
For the Savitzky–Golay + First Derivative—Competitive Adaptive Reweighted Sampling—Support Vector Regression model, when the kernel parameter γ = 0.1 and the regularization parameter C = 10, R2 approaches 1, Root Mean Square Error (RMSE) is very low, RPD exceeds 2, and the RPIQ value is well aligned. The model achieves excellent training fit and strong generalization on the validation set, making this the optimal parameter configuration for the model (Figure 9b–i).
After optimization, the two types of models achieve a balance between training accuracy and validation generalization, providing high-precision and highly generalizable prediction tools for tasks such as spectral data analysis. Subsequently, actual sample prediction can be carried out using the optimal parameters to verify their practical value in applications such as substance composition detection.
4.4. Research Significance and Application Prospects
The Korla fragrant pear leaf SPAD value prediction model established in this study holds significant theoretical and practical value. Theoretically, the study elucidates the evolutionary patterns of leaf spectral characteristics across different growth stages, along with their underlying physiological mechanisms, thereby offering novel insights into the spectral diagnosis of plant physiological state. In terms of application, the growth stage specificity and multi-source data fusion prediction model developed herein furnish robust technical support for the precision management of the Korla fragrant pear industry. Future research can be further explored in the following areas: (1) Expanding the sample size and variety range to validate the model’s universality. (2) Investigating a wider array of vegetation index combinations to enhance model performance further. (3) Developing portable detection devices to facilitate the on-site application of technological advancements. (4) Integrating other agronomic indicators to establish a comprehensive monitoring system. These efforts will contribute to the intelligentization and precision management of the fragrant pear industry, thereby enhancing its competitiveness.
5. Conclusions
Through a systematic comparison of different modeling methods, this study ultimately determined the optimal SPAD prediction model for each reproductive period. The results indicated that the FD-CARS-BP model yielded the best performance for predicting SPAD value in Korla fragrant pear leaves during both the fruit setting stage and the fruit expansion stage. This model incorporates First Derivative (FD) preprocessing and Competitive Adaptive Reweighted Sampling (CARS) Feature Selection, and is constructed using the BP Neural Network algorithm. During the fruit maturation stage, the SG-FD+SG-CARS-BP model demonstrated the optimal prediction performance. This model innovatively integrates a joint preprocessing method of Savitzky–Golay smoothing (SG) and First Derivative (FD), also relying on CARS Feature Selection and the BP Neural Network algorithm. This growth stage specificity model selection strategy fully accounts for the variations in leaf physiological characteristics across different developmental stages, leading to more accurate SPAD value prediction.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/agronomy15092218/s1; Table S1: Results of the full gestation period model; Table S2: Results of the sitting period model; Table S3: Results of the fruit enlargement model; Table S4: Results of fruit ripening model. References [47,98,99,100,101,102,103,104,105,106,107,108,109,110,111] are cited in Supplementary Files.
Author Contributions
M.Y.: conceptualization, methodology, data curation, writing—original draft, writing—review and editing; W.F.: conceptualization, methodology, data curation, writing—original draft, writing—review and editing; J.Z.: visualization, software; Y.L.: validation, investigation; L.W.: visualization, formal analysis; H.W.: supervision, formal analysis; J.B.: resources, writing—review and editing, project administration, funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This project is supported by the Strong Youth Science and Technology Talent Project of the Corps “Research on nitrogen regulation of pear calyx desiccation/retention fertilization strategy” (project number: 2022CB001-11).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| R2 | Coefficient of Determination |
| RMSE | Root Mean Square Error |
| RPD | Ratio of Performance to Deviation |
| BP | Backpropagation |
| CARS | Competitive Adaptive Reweighted Sampling |
| SPA | Successive Projections Algorithm |
| SG | Savitzky–Golay |
| MSC | Multiplicative Scatter Correction |
| SD | Second Derivative |
| FD | First Derivative |
| AirPLS | Adaptive iteratively reweighted Penalized Least Squares |
| DOSC | Direct Orthogonal Signal Correction |
| RPIQ | Ratio of Performance to Interquartile Range |
| NDWI-L | Normalized Difference Water Index—Linearized |
| NDII-L | Normalized Difference Infrared Index—Linearized |
| NDNI | Normalized Difference Nitrogen Index |
| CAI | Cellulose Absorption Index |
| LI | Lignin Index |
References
- Benati, J.; Nava, G.; Mayer, N.A. Spad index for diagnosis of nitrogen status in ‘Esmeralda’ peach. Rev. Bras. Frutic. 2021, 43, e-093. [Google Scholar] [CrossRef]
- Djumaeva, D.; Lamers, J.P.A.; Martius, C.; Vlek, P.L.G. Chlorophyll meters for monitoring foliar nitrogen in three tree species from arid Central Asia. J. Arid. Environ. 2012, 85, 41–45. [Google Scholar] [CrossRef]
- Afonso, S.; Arrobas, M.; Ferreira, I.Q.; Rodrigues, M.Â. Assessing the potential use of two portable chlorophyll meters in diagnosing the nutritional status of plants. J. Plant Nutr. 2018, 41, 261–271. [Google Scholar] [CrossRef]
- Pinzón-Sandoval, E.H.; Balaguera-López, H.E.; Almanza-Merchán, P.J. Evaluation of SPAD Index for Estimating Nitrogen and Magnesium Contents in Three Blueberry Varieties (Vaccinium corymbosum L.) on the Andean Tropics. Horticulturae 2023, 9, 269. [Google Scholar] [CrossRef]
- Tucci, M.L.S.A.; Modolo, V.A.; Erismann, N.d.M.; Machado, E.C. Gas exchanges in peach palms as a function of the spad chlorophyll meter readings. Rev. Bras. Frutic. 2011, 33, 267–274. [Google Scholar] [CrossRef][Green Version]
- Williams, L.E.; Smith, R.J. Net CO2 Assimilation Rate and Nitrogen Content of Grape Leaves Subsequent to Fruit Harvest. J. Am. Soc. Hortic. Sci. 1985, 110, 846–850. [Google Scholar] [CrossRef]
- Lantos, F.; Makra, L.; Mike, K.; Gyalai, I. SPAD values, as well as sugar- and capsaicin content in different varieties of outdoor peppers. COLUMELLA J. Agric. Environ. Sci. 2022, 9, 5–15. [Google Scholar] [CrossRef]
- Roslan, N.; Aznan, A.A.; Ruslan, R.; Jaafar, M.N.; Azizan, F.A. Growth Monitoring of Harumanis Mango Leaves (Mangifera Indica) at Vegetative Stage Using SPAD Meter and Leaf Area Meter. IOP Conf. Ser. Mater. Sci. Eng. 2019, 557, 012010. [Google Scholar] [CrossRef]
- Singh, S.; Mohanty, S.; Sahu, M.; Bhaskar, N.; Verma, B. Evaluation of SPAD meter values for estimating rice nitrogen status. Int. J. Chem. Stud. 2020, 8, 1–5. [Google Scholar] [CrossRef]
- Liu, Y.; Hatou, K.; Aihara, T.; Kurose, S.; Akiyama, T.; Kohno, Y.; Lu, S.; Omasa, K. A Robust Vegetation Index Based on Different UAV RGB Images to Estimate SPAD Values of Naked Barley Leaves. Remote Sens. 2021, 13, 686. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Q.; Shang, J.; Liu, C.; Zhuang, T.; Ding, J.; Xian, Y.; Zhao, L.; Wang, W.; Zhou, G.; et al. UAV- and Machine Learning-Based Retrieval of Wheat SPAD Values at the Overwintering Stage for Variety Screening. Remote Sens. 2021, 13, 5166. [Google Scholar] [CrossRef]
- Shen, L.; Gao, M.; Yan, J.; Wang, Q.; Shen, H. Winter Wheat SPAD Value Inversion Based on Multiple Pretreatment Methods. Remote Sens. 2022, 14, 4660. [Google Scholar] [CrossRef]
- Liu, N.; Liu, G.; Sun, H. Real-Time Detection on SPAD Value of Potato Plant Using an In-Field Spectral Imaging Sensor System. Sensors 2020, 20, 3430. [Google Scholar] [CrossRef] [PubMed]
- Vasseur, F.; Cornet, D.; Beurier, G.; Messier, J.; Rouan, L.; Bresson, J.; Ecarnot, M.; Stahl, M.; Heumos, S.; Gérard, M.; et al. A Perspective on Plant Phenomics: Coupling Deep Learning and Near-Infrared Spectroscopy. Front. Plant Sci. 2022, 13, 836488. [Google Scholar] [CrossRef] [PubMed]
- Kothari, S.; Hobbie, S.E.; Cavender-Bares, J. Rapid estimates of leaf litter chemistry using reflectance spectroscopy. Can. J. For. Res. 2024, 54, 978–991. [Google Scholar] [CrossRef]
- Manley, M. Near-infrared spectroscopy and hyperspectral imaging: Non-destructive analysis of biological materials. Chem. Soc. Rev. 2014, 43, 8200–8214. [Google Scholar] [CrossRef]
- Awiti, A.O.; Walsh, M.G.; Shepherd, K.D.; Kinyamario, J. Soil condition classification using infrared spectroscopy: A proposition for assessment of soil condition along a tropical forest-cropland chronosequence. Geoderma 2008, 143, 73–84. [Google Scholar] [CrossRef]
- Ayala Izurieta, J.; Marquez, C.O.; Garcia, V.; Recalde, C.; Rodríguez-Llerena, M.; Damián Carrión, D. Land Cover Classification in an Ecuadorian Mountain Geosystem Using a Random Forest Classifier, Spectral Vegetation Indices, and Ancillary Geographic Data. Geosciences 2017, 7, 34. [Google Scholar] [CrossRef]
- Zhang, K. Exploring Hyperspectral and Very High Spatial Resolution Imagery in Vegetation Characterization. Ph.D. Thesis, York University, Toronto, ON, Canada, 2014. [Google Scholar]
- Bush, T.; Papaioannou, N.; Leach, F.; Pope, F.D.; Singh, A.; Thomas, G.N.; Stacey, B.; Bartington, S. Machine learning techniques to improve the field performance of low-cost air quality sensors. Atmos. Meas. Tech. 2022, 15, 3261–3278. [Google Scholar] [CrossRef]
- Chen, Q.; Yang, L.; Yu, H.; He, Y.; Liu, H.; Wang, X. Quantitative Measurements of DP in Cellulose Paper Based on Terahertz Spectroscopy. Polymers 2023, 15, 247. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, X.; Feng, Z.; Chen, J.; Zhou, X.; Luo, J.; Sun, J.; Zhao, Y. Enhanced Wind-Field Detection Using an Adaptive Noise-Reduction Peak-Retrieval (ANRPR) Algorithm for Coherent Doppler Lidar. Atmosphere 2024, 15, 7. [Google Scholar] [CrossRef]
- Bos, T.S. Chemometric tools for automated method-development and data interpretation in liquid chromatography. Anal. Chem. 2022, 94, 16060–16068. [Google Scholar] [CrossRef] [PubMed]
- Song, J.-J.; Wang, Y.-Y.; Tong, W.-C.; Ma, F.-L.; Wang, J.-N.; Yu, Y.-J. A New X-ray Diffraction Spectrum-Based Untargeted Strategy for Accurately Identifying Ancient Painted Pottery from Various Dynasties and Locations in China. Chemosensors 2024, 12, 64. [Google Scholar] [CrossRef]
- Lin, Y.-L.; Ding, N.-D. Competitive gamification in crowdsourcing-based contextual-aware recommender systems. Int. J. Hum. Comput. Stud. 2023, 177, 103083. [Google Scholar] [CrossRef] [PubMed]
- Haruna, K.; Akmar Ismail, M.; Suhendroyono, S.; Damiasih, D.; Pierewan, A.C.; Chiroma, H.; Herawan, T. Context-Aware Recommender System: A Review of Recent Developmental Process and Future Research Direction. Appl. Sci. 2017, 7, 1211. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, K.; Wang, H.; Chen, B. Auto-STGCN: Autonomous Spatial-Temporal Graph Convolutional Network Search. ACM Trans. Knowl. Discov. Data 2023, 17, 73. [Google Scholar] [CrossRef]
- Yoosefzadeh-Najafabadi, M.; Tulpan, D.; Eskandari, M. Using Hybrid Artificial Intelligence and Evolutionary Optimization Algorithms for Estimating Soybean Yield and Fresh Biomass Using Hyperspectral Vegetation Indices. Remote Sens. 2021, 13, 2555. [Google Scholar] [CrossRef]
- Chetan, H.T.; Potdar, M.P. Yield prediction models in maize using SPAD and NDVI. Res. Environ. Life Sci. 2016, 9, 1002–1004. [Google Scholar]
- Guo, Y.; Chen, S.; Li, X.; Cunha, M.; Jayavelu, S.; Cammarano, D.; Fu, Y. Machine Learning-Based Approaches for Predicting SPAD Values of Maize Using Multi-Spectral Images. Remote Sens. 2022, 14, 1337. [Google Scholar] [CrossRef]
- Huang, Y.; Li, D.; Liu, X.; Ren, Z. Monitoring canopy SPAD based on UAV and multispectral imaging over fruit tree growth stages and species. Front. Plant Sci. 2024, 15, 1435613. [Google Scholar] [CrossRef]
- Xie, J.; Wang, J.; Chen, Y.; Gao, P.; Yin, H.; Chen, S.; Sun, D.; Wang, W.; Mo, H.; Shen, J.; et al. Estimating the SPAD of Litchi in the Growth Period and Autumn Shoot Period Based on UAV Multi-Spectrum. Remote Sens. 2023, 15, 5767. [Google Scholar] [CrossRef]
- Mao, Z.-H.; Deng, L.; Duan, F.-Z.; Li, X.-J.; Qiao, D.-Y. Angle effects of vegetation indices and the influence on prediction of SPAD values in soybean and maize. Int. J. Appl. Earth Obs. Geoinf. 2020, 93, 102198. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, H.; Zhang, B.; Bai, X.; Zhou, C. Physiological and molecular changes of detached wheat leaves in responding to various treatments. J. Integr. Plant Biol. 2012, 54, 567–576. [Google Scholar] [CrossRef]
- Serbin, S.P.; Townsend, P.A. Scaling Functional Traits from Leaves to Canopies. In Remote Sensing of Plant Biodiversity; Cavender-Bares, J., Gamon, J.A., Townsend, P.A., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 43–82. [Google Scholar]
- Daughtry, C.S.T.; Ranson, K.J. Measuring and Modeling Biophysical and Optical Properties of Diverse Vegetative Canopies. LARS Tech. Rep. 1986, 41, 2. [Google Scholar]
- Mei, S.; Yu, Z.; Chen, J.; Zheng, P.; Sun, B.; Guo, J.; Liu, S. The Physiology of Postharvest Tea (Camellia sinensis) Leaves, According to Metabolic Phenotypes and Gene Expression Analysis. Molecules 2022, 27, 1708. [Google Scholar] [CrossRef] [PubMed]
- Yu, M.; Bai, X.; Bao, J.; Wang, Z.; Tang, Z.; Zheng, Q.; Zhi, J. The Prediction Model of Total Nitrogen Content in Leaves of Korla Fragrant Pear Was Established Based on Near Infrared Spectroscopy. Agronomy 2024, 14, 1284. [Google Scholar] [CrossRef]
- Su, T.; Wang, C.; Zhao, G.; Fan, S.; Yang, G.; Xu, C.; Su, H. Investigations on Spectra of Terahertz and Raman of L-Alabinose at Fingerprint Region. Spectrosc. Spectr. Anal. 2018, 38, 2713–2719. [Google Scholar]
- Wang, J.J.; Liu, H.; Ren, G.X. Using Fourier Transform Near-Infrared Spectroscopy For the Evaluation and Regional Analysis of Pea (Pisum sativum L.). J. Plant Genet. Resour. 2014, 15, 779–787. [Google Scholar] [CrossRef]
- Yang, H.; Qian, H.; Xu, Y.; Zhai, X.; Zhu, J. A Sensitive SERS Sensor Combined with Intelligent Variable Selection Models for Detecting Chlorpyrifos Residue in Tea. Foods 2024, 13, 2363. [Google Scholar] [CrossRef]
- Li, X.; Fu, X.; Li, H. A CARS-SPA-GA Feature Wavelength Selection Method Based on Hyperspectral Imaging with Potato Leaf Disease Classification. Sensors 2024, 24, 6566. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Lin, H.; He, Y. Data-Driven Methods for the Estimation of Leaf Water and Dry Matter Content: Performances, Potential and Limitations. Sensors 2020, 20, 5394. [Google Scholar] [CrossRef]
- Ihuoma, S.O.; Madramootoo, C.A. Recent advances in crop water stress detection. Comput. Electron. Agric. 2017, 141, 267–275. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, G.; Song, X.; He, Q. Dynamic Characteristics of Canopy and Vegetation Water Content during an Entire Maize Growing Season in Relation to Spectral-Based Indices. Remote Sens. 2022, 14, 584. [Google Scholar] [CrossRef]
- Safdar, M.; Shahid, M.A.; Sarwar, A.; Rasul, F.; Majeed, M.D.; Sabir, R.M. Crop Water Stress Detection Using Remote Sensing Techniques. Environ. Sci. Proc. 2023, 25, 20. [Google Scholar]
- Li, D.; Zhang, P.; Chen, T.; Qin, W. Recent Development and Challenges in Spectroscopy and Machine Vision Technologies for Crop Nitrogen Diagnosis: A Review. Remote Sens. 2020, 12, 2578. [Google Scholar] [CrossRef]
- Çimtay, Y. Estimating Plant Nitrogen by Developing an Accurate Correlation between VNIR-Only Vegetation Indexes and the Normalized Difference Nitrogen Index. Remote Sens. 2023, 15, 3898. [Google Scholar] [CrossRef]
- Flynn, W.R.M.; Owen, H.J.F.; Grieve, S.W.D.; Lines, E.R. Quantifying vegetation indices using terrestrial laser scanning: Methodological complexities and ecological insights from a Mediterranean forest. Biogeosciences 2023, 20, 2769–2784. [Google Scholar] [CrossRef]
- Taylor, G.; Tallis, M.J.; Giardina, C.P.; Percy, K.E.; Miglietta, F.; Gupta, P.S.; Gioli, B.; Calfapietra, C.; Gielen, B.; Kubiske, M.E.; et al. Future atmospheric CO2 leads to delayed autumnal senescence. Glob. Change Biol. 2008, 14, 264–275. [Google Scholar] [CrossRef]
- Zhao, T.; Nakano, A.; Iwaski, Y.; Umeda, H. Application of Hyperspectral Imaging for Assessment of Tomato Leaf Water Status in Plant Factories. Appl. Sci. 2020, 10, 4665. [Google Scholar] [CrossRef]
- Jenal, A.; Bareth, G.; Bolten, A.; Kneer, C.; Weber, I.; Bongartz, J. Development of a VNIR/SWIR Multispectral Imaging System for Vegetation Monitoring with Unmanned Aerial Vehicles. Sensors 2019, 19, 5507. [Google Scholar] [CrossRef]
- Dunne, K.S.; Holden, N.M.; O’Rourke, S.M.; Fenelon, A.; Daly, K. Prediction of phosphorus sorption indices and isotherm parameters in agricultural soils using mid-infrared spectroscopy. Geoderma 2020, 358, 113981. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, Q. A Dynamic Model Updating Method with Thermal Effects Based on Improved Support Vector Regression. Appl. Sci. 2021, 11, 8025. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, R.; Wang, W.; Zhang, T. Construction and optimization of non-parametric analysis model for meter coefficients via back propagation neural network. Sci. Rep. 2024, 14, 11452. [Google Scholar] [CrossRef]
- Gao, J.; Mao, Y.; Xu, Z.; Luo, Q. Quantitative investment decisions based on machine learning and investor attention analysis. Technol. Econ. Dev. Econ. 2023, 30, 527–561. [Google Scholar] [CrossRef]
- Ahmad Yasmin, N.S.; Abdul Wahab, N.; Ismail, F.S.; Musa, M.a.J.; Halim, M.H.A.; Anuar, A.N. Support Vector Regression Modelling of an Aerobic Granular Sludge in Sequential Batch Reactor. Membranes 2021, 11, 554. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Jin, N.; Dogani, A.; Yang, Y.; Zhang, M.; Gu, X. Enhancing LightGBM for Industrial Fault Warning: An Innovative Hybrid Algorithm. Processes 2024, 12, 221. [Google Scholar] [CrossRef]
- Zhou, L.; Yao, J.; Xu, H.; Zhang, Y.; Nie, P. Research on the Effects of Drying Temperature for the Detection of Soil Nitrogen by Near-Infrared Spectroscopy. Molecules 2023, 28, 6507. [Google Scholar] [CrossRef]
- Akter, S.; de Jonge, L.W.; Møldrup, P.; Greve, M.H.; Nørgaard, T.; Weber, P.L.; Hermansen, C.; Mouazen, A.M.; Knadel, M. Visible Near-Infrared Spectroscopy and Pedotransfer Function Well Predict Soil Sorption Coefficient of Glyphosate. Remote Sens. 2023, 15, 1712. [Google Scholar] [CrossRef]
- Chu, C.; Wang, H.; Luo, X.; Wen, P.; Nan, L.; Du, C.; Fan, Y.; Gao, D.; Wang, D.; Yang, Z.; et al. Possible Alternatives: Identifying and Quantifying Adulteration in Buffalo, Goat, and Camel Milk Using Mid-Infrared Spectroscopy Combined with Modern Statistical Machine Learning Methods. Foods 2023, 12, 3856. [Google Scholar] [CrossRef]
- Fouche, J. Increasing Class One Fruit in ‘Granny Smith’ and ‘Cripps’ Pink’ Apple. Master’s Thesis, University of Stellenbosch, Stellenbosch, South Africa, 2009. [Google Scholar]
- Thomas, H.; Ougham, H. The stay-green trait. J. Exp. Bot. 2014, 65, 3889–3900. [Google Scholar] [CrossRef]
- Goncharova, Y.; Bragina, O.; Goncharov, S.; Kharitonov, E. Water content of seedlings of Russian rice varieties. IOP Conf. Ser. Mater. Sci. Eng. 2020, 1001, 012124. [Google Scholar] [CrossRef]
- Losso, A.; Dämon, B.; Hacke, U.; Mayr, S. High potential for foliar water uptake in early stages of leaf development of three woody angiosperms. Physiol. Plant. 2023, 175, e13961. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.; Whang, S. A comparative study of early leaf development in the Viola albida complex. Korean J. Plant Taxon. 2019, 49, 1–7. [Google Scholar] [CrossRef][Green Version]
- Jiang, F.; Cadotte, M.W.; Jin, G. Individual-level leaf trait variation and correlation across biological and spatial scales. Ecol. Evol. 2021, 11, 5344–5354. [Google Scholar] [CrossRef]
- Trong, L.; Phuong, H.; Thinh, B. Changes in the Physiological and Biochemical Parameters of Cucumber (Cucumis sativus L.) during Fruit Development. Bull. Transilv. Univ. Bras. 2023, 16, 143–154. [Google Scholar] [CrossRef]
- Soare, R.; Maria, D.; Apahidean, A.; Soare, M. The evolution of some nutritional parameters of the tomato fruit during the harvesting stages. Hortic. Sci. 2019, 46, 132–137. [Google Scholar] [CrossRef]
- Zhao, W.; Wu, H.; Gao, X.; Cai, H.; Zhang, J.; Zhao, C.; Chen, W.; Qiao, H.; Zhang, J. Unraveling the Genetic Control of Pigment Accumulation in Physalis Fruits. Int. J. Mol. Sci. 2024, 25, 9852. [Google Scholar] [CrossRef] [PubMed]
- Kapoor, L.; Simkin, A.J.; George Priya Doss, C.; Siva, R. Fruit ripening: Dynamics and integrated analysis of carotenoids and anthocyanins. BMC Plant Biology 2022, 22, 27. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Ying, S.; Tang, B.; Yu, C.; Wang, Y.; Wu, M.; Liu, M. The mechanistic insights into fruit ripening: Integrating phytohormones, transcription factors, and epigenetic modification. J. Genet. Genom. 2025. [Google Scholar] [CrossRef] [PubMed]
- Junaedi, E.C.; Lestari, K.; Muchtaridi, M. Infrared spectroscopy technique for quantification of compounds in plant-based medicine and supplement. J. Adv. Pharm. Technol. Res. 2021, 12, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Taghinezhad, E.; Szumny, A.; Figiel, A. The Application of Hyperspectral Imaging Technologies for the Prediction and Measurement of the Moisture Content of Various Agricultural Crops during the Drying Process. Molecules 2023, 28, 2930. [Google Scholar] [CrossRef] [PubMed]
- Rolinger, L.; Rüdt, M.; Hubbuch, J. A critical review of recent trends, and a future perspective of optical spectroscopy as PAT in biopharmaceutical downstream processing. Anal. Bioanal. Chem. 2020, 412, 2047–2064. [Google Scholar] [CrossRef]
- Witteveen, M.; Sterenborg, H.; van Leeuwen, T.G.; Aalders, M.C.G.; Ruers, T.J.M.; Post, A.L. Comparison of preprocessing techniques to reduce nontissue-related variations in hyperspectral reflectance imaging. J. Biomed. Opt. 2022, 27, 106003. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; He, J.M.; Chen, X.; Zhu, X.Q.; Wu, J.J.; He, G.T. A Preprocessing Algorithm of Corn Infrared Spectrum Based on MSC and DOSC. Adv. Mater. Res. 2013, 734–737, 2893–2897. [Google Scholar] [CrossRef]
- Dickens, C. Ridge Regression with Frequent Directions: Statistical and Optimization Perspectives. arXiv 2020, arXiv:2011.03607. [Google Scholar] [CrossRef]
- Bottou, L.; Curtis, F.E.; Nocedal, J. Optimization Methods for Large-Scale Machine Learning. SIAM Rev. 2018, 60, 223–311. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Y.; Chen, X.; Shi, B.; Xu, C.; Xu, C.; Tian, Q.; Xu, C. CARS: Continuous Evolution for Efficient Neural Architecture Search. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1826–1835. [Google Scholar]
- Markou, I.; Papathanasopoulou, V.; Antoniou, C. Dynamic car-following model calibration using spsa and isres algorithms dynamic car-following model calibration using spsa and isres algorithms. Period. Polytech. Transp. Eng. 2018, 47, 146–156. [Google Scholar] [CrossRef]
- He, X.; Zhao, K.; Chu, X. AutoML: A survey of the state-of-the-art. Knowl. Based Syst. 2021, 212, 106622. [Google Scholar] [CrossRef]
- Lin, W.; Chen, J.; Huang, R.; Ding, H. An Effective Dynamic Gradient Calibration Method for Continual Learning. arXiv 2024, arXiv:2407.20956. [Google Scholar] [CrossRef]
- Pan, Y.; Fang, C.; Zhu, X.; Wan, J. Construction of a predictive model based on MIV-SVR for prognosis and length of stay in patients with traumatic brain injury: Retrospective cohort study. Digit. Health 2023, 9, 20552076231217814. [Google Scholar] [CrossRef]
- Goldschmidt, E.E. The Evolution of Fruit Tree Productivity: A Review. Econ. Bot. 2013, 67, 51–62. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.-I.; Green, P.C. Comparison of Data Grouping Strategies on Prediction Accuracy of Tree-Stem Taper for Six Common Species in the Southeastern US. Forests 2022, 13, 156. [Google Scholar] [CrossRef]
- Mariia Belousova, O.D. Game-Theoretic Model of the Species and Varietal Composition of Fruit Plantations. Int. J. Technol. 2021, 12, 291–319. [Google Scholar] [CrossRef]
- Zhao, L.; Xia, Y.; Wu, X.Y.; Schippers, J.H.M.; Jing, H.C. Phenotypic Analysis and Molecular Markers of Leaf Senescence. In Plant Senescence. Methods in Molecular Biology; Humana Press: New York, NY, USA, 2018; Volume 1744, pp. 35–48. [Google Scholar] [CrossRef]
- Teixeira, A.; Noronha, H.; Frusciante, S.; Diretto, G.; Gerós, H. Biosynthesis of Chlorophyll and Other Isoprenoids in the Plastid of Red Grape Berry Skins. J. Agric. Food Chem. 2023, 71, 1873–1885. [Google Scholar] [CrossRef]
- Wang, P.; Richter, A.S.; Kleeberg, J.R.W.; Geimer, S.; Grimm, B. Post-translational coordination of chlorophyll biosynthesis and breakdown by BCMs maintains chlorophyll homeostasis during leaf development. Nat. Commun. 2020, 11, 1254. [Google Scholar] [CrossRef] [PubMed]
- Genesio, L.; Bassi, R.; Miglietta, F. Plants with less chlorophyll: A global change perspective. Glob. Change Biol. 2021, 27, 959–967. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Ren, G.; Zhang, K.; Li, Z.; Miao, Y.; Guo, H. Leaf senescence: Progression, regulation, and application. Mol. Hortic. 2021, 1, 5. [Google Scholar] [CrossRef] [PubMed]
- Mishra, S.; Das, S.; Bhol, R.; Beura, J.; Dash, S.K.; Sarkar, S.; Mohanty, A. Morpho-physiological traits associated with leaf senescence at peak fruiting stage in tomato under water deficit condition. Int. J. Res. Agron. 2024, SP-7, 16–19. [Google Scholar] [CrossRef]
- Gao, Z.; Wang, W.; Wang, H.; Li, R. Selection of Spectral Parameters and Optimization of Estimation Models for Soil Total Nitrogen Content during Fertilization Period in Apple Orchards. Horticulturae 2024, 10, 358. [Google Scholar] [CrossRef]
- Fei, S.; Hassan, M.A.; Xiao, Y.; Su, X.; Chen, Z.; Cheng, Q.; Duan, F.; Chen, R.; Ma, Y. UAV-based multi-sensor data fusion and machine learning algorithm for yield prediction in wheat. Precis. Agric. 2023, 24, 187–212. [Google Scholar] [CrossRef]
- Wang, X. Analysis of Bank Credit Risk Evaluation Model Based on BP Neural Network. Comput. Intell. Neurosci. 2022, 2022, 2724842. [Google Scholar] [CrossRef] [PubMed]
- Olmo, V.; Tordoni, E.; Petruzzellis, F.; Bacaro, G.; Altobelli, A. Use of Sentinel-2 Satellite Data for Windthrows Monitoring and Delimiting: The Case of “Vaia” Storm in Friuli Venezia Giulia Region (North-Eastern Italy). Remote Sens. 2021, 13, 1530. [Google Scholar] [CrossRef]
- Val, A.L.; Duarte, R.M.; Campos, D.; de Almeida-Val, V.M.F. Chapter 5—Environmental stressors in Amazonian riverine systems. In Fish Physiology; Fangue, N.A., Cooke, S.J., Farrell, A.P., Brauner, C.J., Eliason, E.J., Eds.; Academic Press: Cambridge, MA, USA, 2022; Volume 39, pp. 209–271. [Google Scholar]
- Zununjan, Z.; Turghan, M.A.; Sattar, M.; Kasim, N.; Emin, B.; Abliz, A. Combining the fractional order derivative and machine learning for leaf water content estimation of spring wheat using hyper-spectral indices. Plant Methods 2024, 20, 97. [Google Scholar] [CrossRef]
- Wang, Y.-P.; Chen, C.-T.; Tsai, Y.-C.; Shen, Y. A Sentinel-2 Image-Based Irrigation Advisory Service: Cases for Tea Plantations. Water 2021, 13, 1305. [Google Scholar] [CrossRef]
- Sishodia, R.P.; Ray, R.L.; Singh, S.K. Applications of Remote Sensing in Precision Agriculture: A Review. Remote Sens. 2020, 12, 3136. [Google Scholar] [CrossRef]
- Janoušek, J.; Jambor, V.; Marcoň, P.; Dohnal, P.; Synková, H.; Fiala, P. Using UAV-Based Photogrammetry to Obtain Correlation between the Vegetation Indices and Chemical Analysis of Agricultural Crops. Remote Sens. 2021, 13, 1878. [Google Scholar] [CrossRef]
- Padilla, F.M.; Farneselli, M.; Gianquinto, G.; Tei, F.; Thompson, R.B. Monitoring nitrogen status of vegetable crops and soils for optimal nitrogen management. Agric. Water Manag. 2020, 241, 106356. [Google Scholar] [CrossRef]
- Zhang, H.; Li, J.; Liu, Q.; Lin, S.; Huete, A.; Liu, L.; Croft, H.; Clevers, J.G.P.W.; Zeng, Y.; Wang, X.; et al. A novel red-edge spectral index for retrieving the leaf chlorophyll content. Methods Ecol. Evol. 2022, 13, 2771–2787. [Google Scholar] [CrossRef]
- Dillen, S.Y.; de Beeck, M.O.; Hufkens, K.; Buonanduci, M.; Phillips, N.G. Seasonal patterns of foliar reflectance in relation to photosynthetic capacity and color index in two co-occurring tree species, Quercus rubra and Betula papyrifera. Agric. For. Meteorol. 2012, 160, 60–68. [Google Scholar] [CrossRef]
- Hernández-Clemente, R.; Navarro-Cerrillo, R.M.; Zarco-Tejada, P.J. Carotenoid content estimation in a heterogeneous conifer forest using narrow-band indices and PROSPECT+DART simulations. Remote Sens. Environ. 2012, 127, 298–315. [Google Scholar] [CrossRef]
- Lleó, L.; Roger, J.M.; Herrero-Langreo, A.; Diezma-Iglesias, B.; Barreiro, P. Comparison of multispectral indexes extracted from hyperspectral images for the assessment of fruit ripening. J. Food Eng. 2011, 104, 612–620. [Google Scholar] [CrossRef]
- Zou, C.; Zhu, X.; Wang, F.; Wu, J.; Wang, Y.-G. Rapeseed Seed Coat Color Classification Based on the Visibility Graph Algorithm and Hyperspectral Technique. Agronomy 2024, 14, 941. [Google Scholar] [CrossRef]
- Glenn, E.P.; Huete, A.R.; Nagler, P.L.; Nelson, S.G. Relationship Between Remotely-sensed Vegetation Indices, Canopy Attributes and Plant Physiological Processes: What Vegetation Indices Can and Cannot Tell Us About the Landscape. Sensors 2008, 8, 2136–2160. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.; Moskal, L.M. Retrieving Leaf Area Index (LAI) Using Remote Sensing: Theories, Methods and Sensors. Sensors 2009, 9, 2719–2745. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).