Evapotranspiration Differences, Driving Factors, and Numerical Simulation of Typical Irrigated Wheat Fields in Northwest China
Abstract
1. Introduction
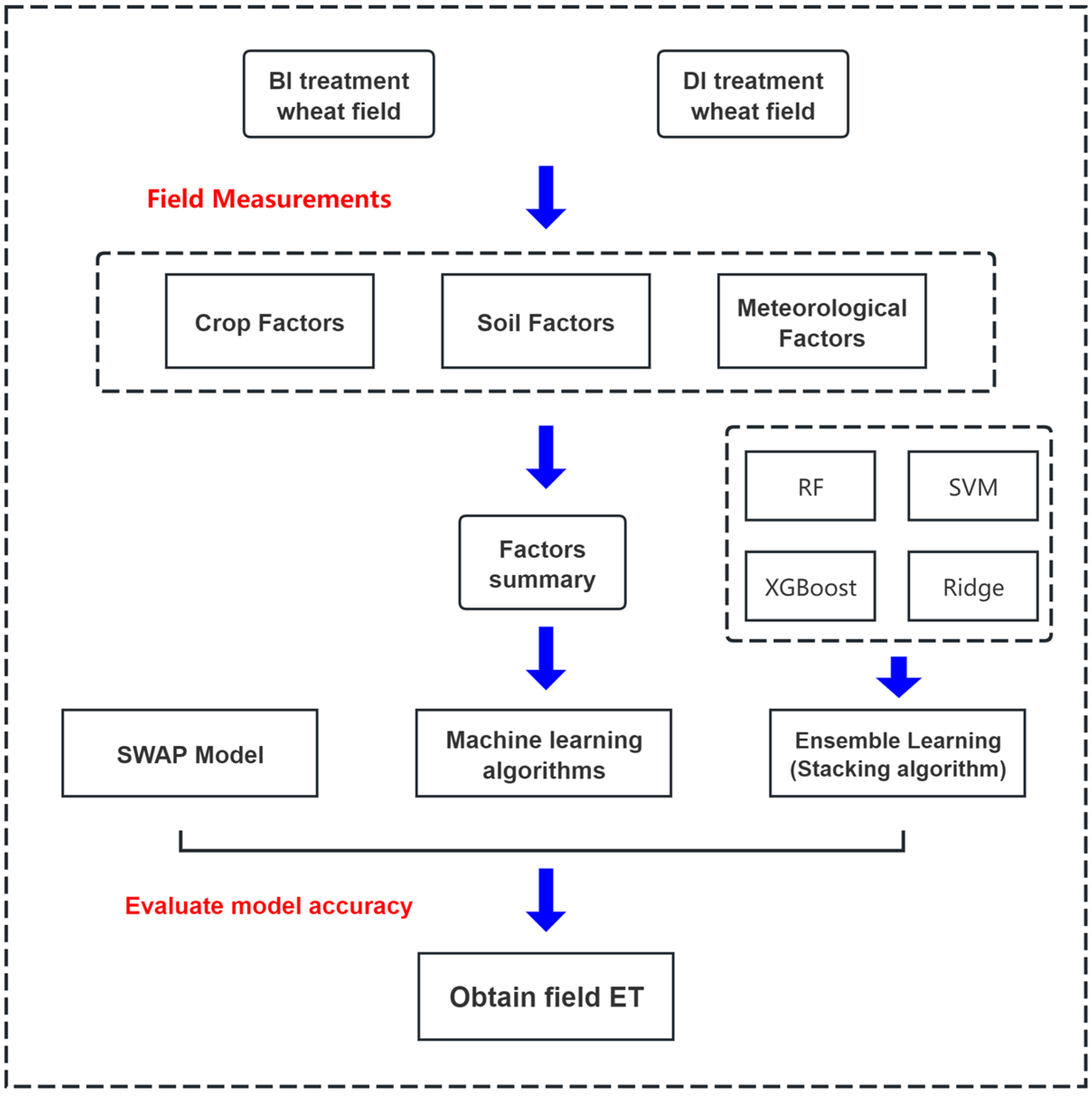
2. Materials and Methods
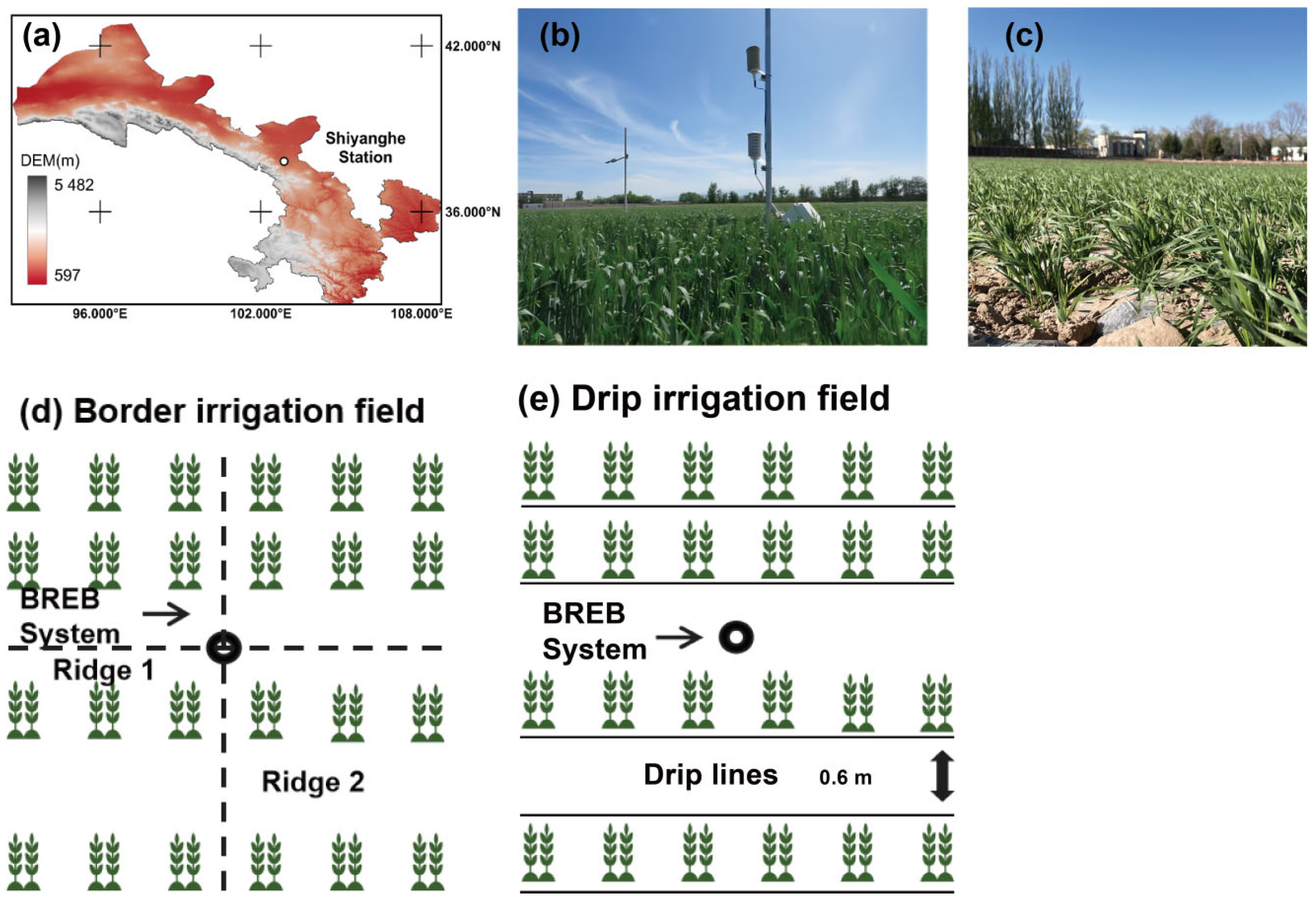
2.1. Overview of the Research Area
2.2. Experimental Design
2.3. Field Observation
2.4. Partial Correlation Analysis
2.5. SWAP Model
2.6. Machine Learning Algorithms
2.6.1. Random Forest
2.6.2. Support Vector Machine
2.6.3. Extreme Gradient Boosting
2.6.4. Ridge Regression
2.6.5. Stacking
2.7. Statistical Analysis
3. Results
3.1. Dynamics of Meteorological Factors
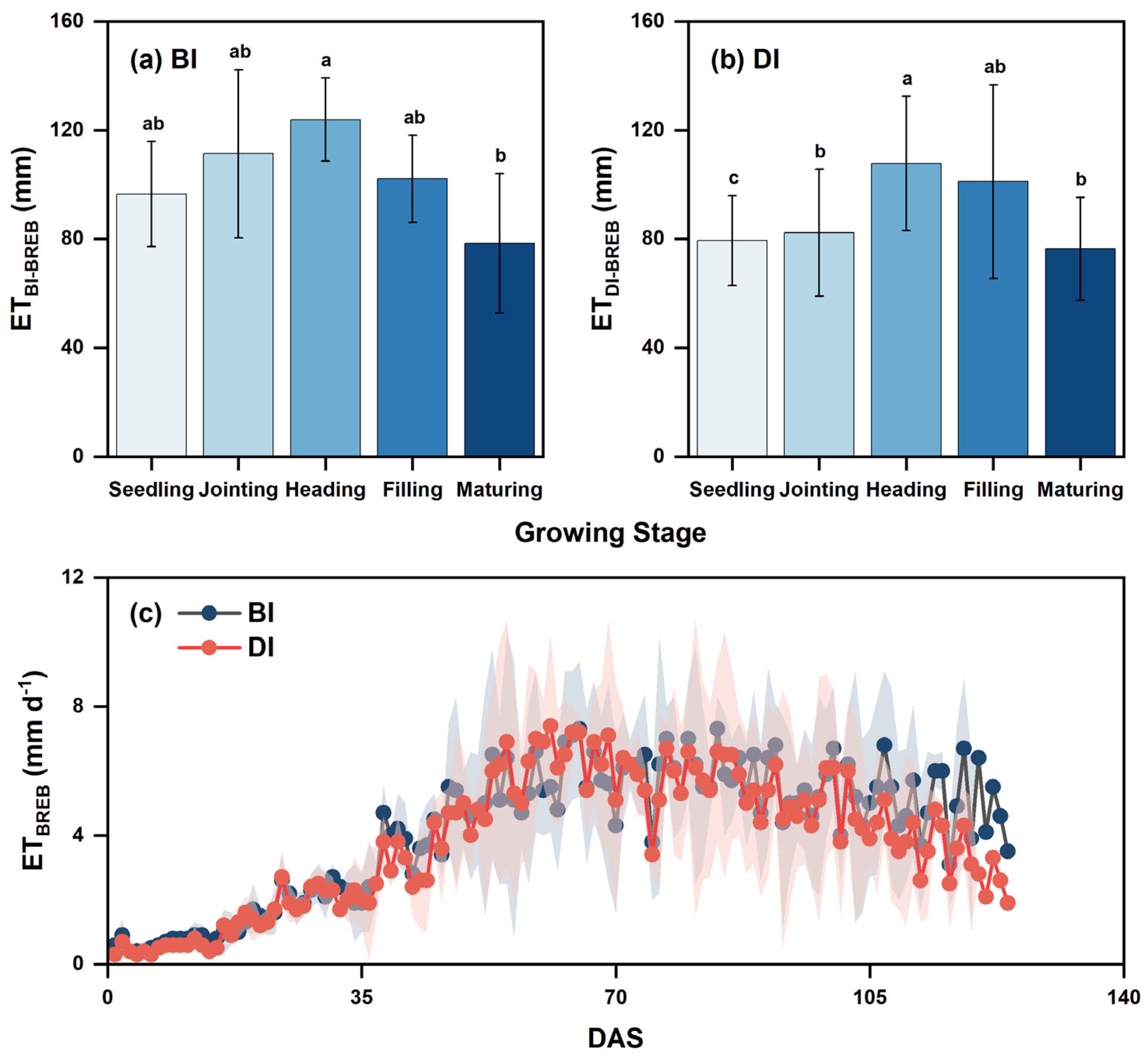
3.2. Changes in ET in Wheat Fields
3.3. Driving Factors of ET in Wheat Fields
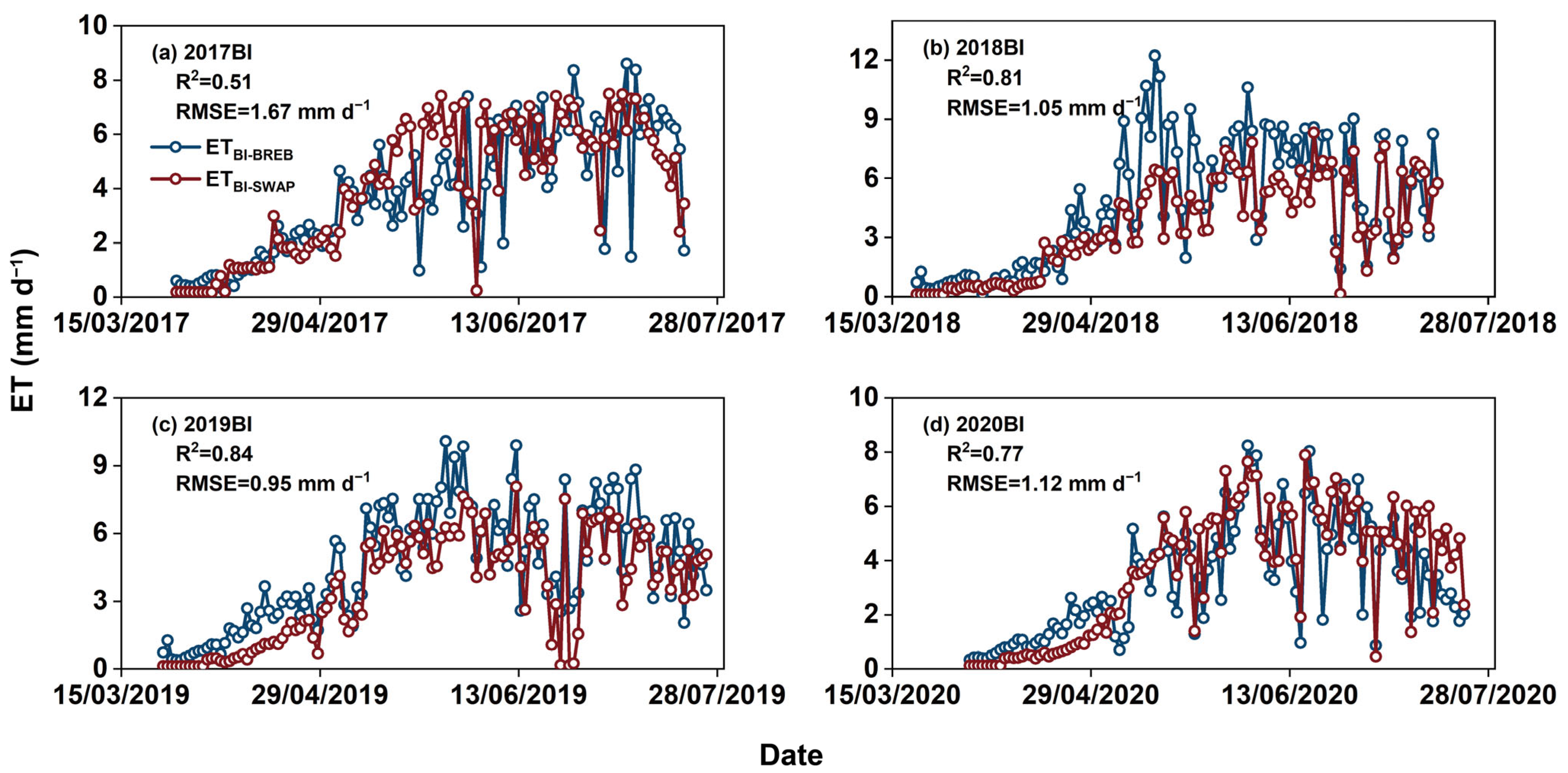
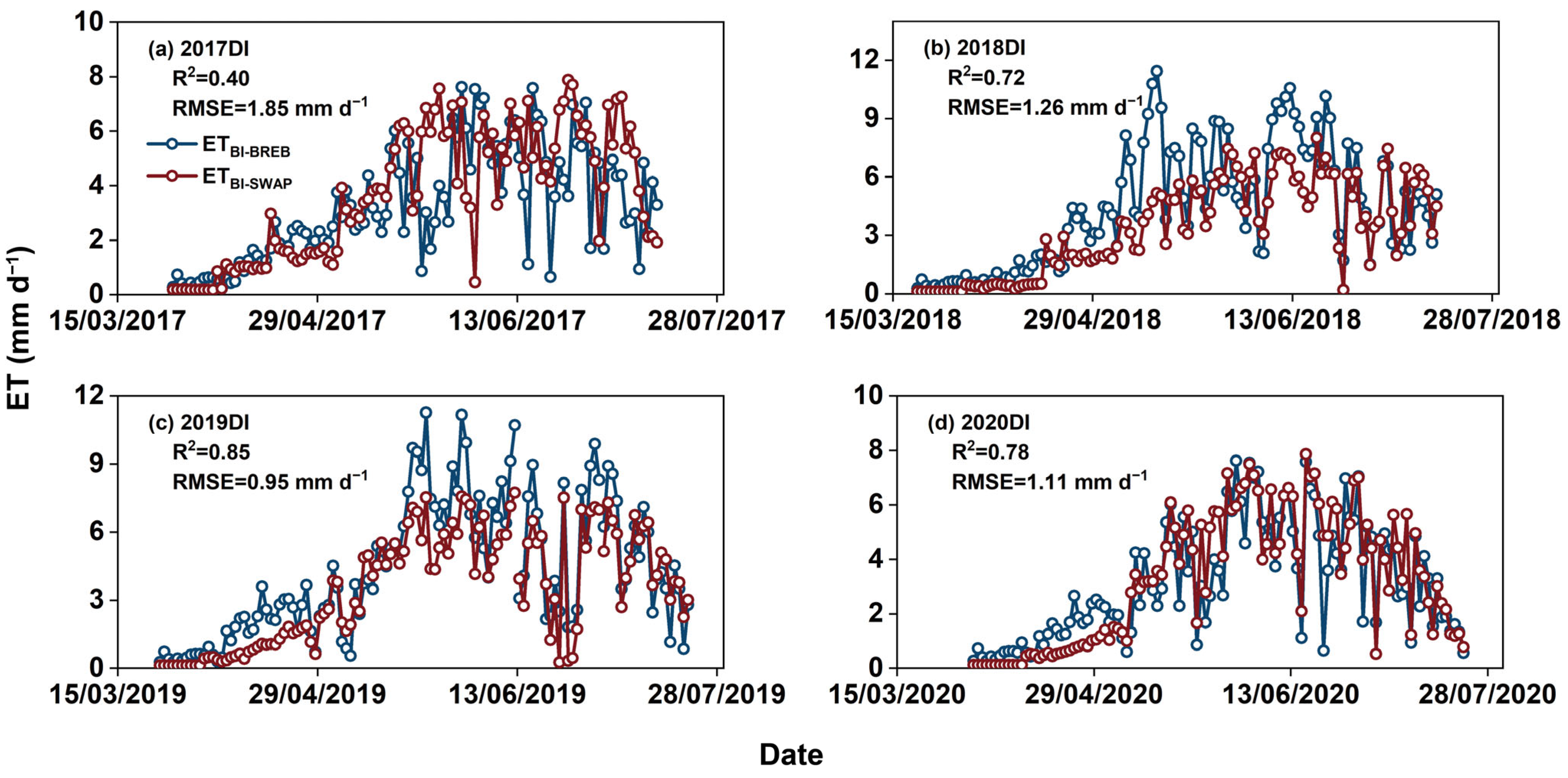
3.4. ET Simulation with the SWAP Model
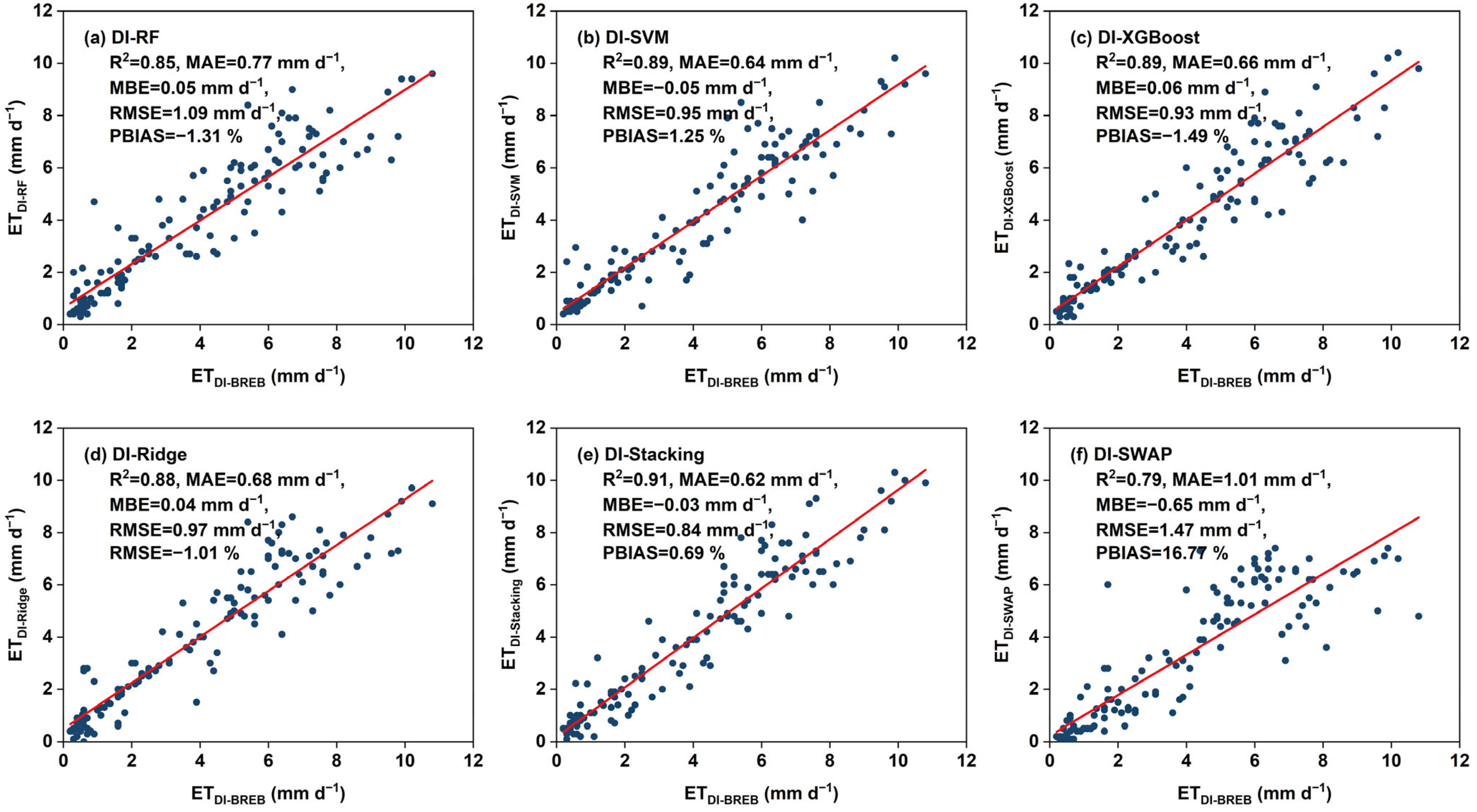
3.5. ET Simulation with Machine Learning Algorithms
4. Discussions
4.1. ET of the Field
4.2. Analysis of Driving Factors for Field ET
4.3. Evaluation of Simulation ET Accuracy in Different Methods
4.4. Advantages and Disadvantages of Different Methods for Obtaining ET
4.5. The Feasibility of Applying ET Simulation with Machine Learning in Practice
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, X.M.; Wang, Y.T.; A, Y.L.; Wang, G.Q.; Zhang, X.J.; Ma, G.W.; Duan, L.M.; Liu, K. Optimizing actual evapotranspiration simulation to identify evapotranspiration partitioning variations: A fusion of physical processes and machine learning techniques. Agric. Water Manag. 2024, 295, 108755. [Google Scholar] [CrossRef]
- Li, M.; Chu, R.H.; Abu, R.M.; Towfiqul, T.; Jiang, Y.L.; Shen, S.H. Estimating daily actual evapotranspiration of a rice-wheat rotation system in typical farmland in the Huai River Basin using a two-step model and two one-step models. J. Integr. Agric. 2021, 20, 274–288. [Google Scholar] [CrossRef]
- Wang, B.; Dam, J.v.; Yang, X.L.; Coen, R.; Du, T.S.; Kang, S.Z. Reducing water productivity gap by optimizing irrigation regime for winter wheat-summer maize system in the North China Plain. Agric. Water Manag. 2023, 280, 108229. [Google Scholar] [CrossRef]
- Xiong, Y.J.; Chen, X.H.; Tang, L.; Wang, H. Comparison of surface renewal and Bowen ratio derived evapotranspiration measurements in an arid vineyard. J. Hydrol. 2022, 613, 128474. [Google Scholar] [CrossRef]
- Bian, J.; Hu, X.L.; Shi, L.S.; Min, L.L.; Zhang, Y.C.; Shen, Y.J.; Zhao, F.H.; Zha, Y.Y.; Lian, X.; Huang, J.S. Improving the evapotranspiration estimation by considering the effect of flux footprint climatology. J. Hydrol. 2024, 631, 130769. [Google Scholar] [CrossRef]
- Li, H.T.; Shao, L.W.; Liu, X.W.; Sun, H.Y.; Chen, S.Y.; Zhang, X.Y. What matters more, biomass accumulation or allocation, in yield and water productivity improvement for winter wheat during the past two decades? Eur. J. Agron. 2023, 149, 126910. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper No.56; FAO: Rome, Italy, 1998. [Google Scholar]
- Li, P.; Ren, L. Evaluating the differences in irrigation methods for winter wheat under limited irrigation quotas in the water-food-economy nexus in the North China Plain. Agric. Water Manag. 2023, 289, 108497. [Google Scholar] [CrossRef]
- Amani, S.; Hossein, S.M. A review of machine learning models and influential factors for estimating evapotranspiration using remote sensing and ground-based data. Agric. Water Manag. 2023, 284, 108324. [Google Scholar] [CrossRef]
- Wang, F.J.; Liang, W.; Fu, B.J.; Jin, Z.; Yan, J.W.; Zhang, W.B.; Fu, S.Y.; Yan, N.N. Changes of cropland evapotranspiration and its driving factors on the loess plateau of China. Sci. Total Environ. 2020, 728, 138582. [Google Scholar] [CrossRef] [PubMed]
- Li, X.L.; Xu, X.F.; Tian, W.; Tian, J.; He, C.S. Contribution of climate change and vegetation restoration to interannual variability of evapotranspiration in the agro-pastoral ecotone in northern China. Ecol. Indic. 2023, 154, 110485. [Google Scholar] [CrossRef]
- Chen, Y.M.; Xue, Y.J.; Hu, Y.M. How multiple factors control evapotranspiration in North America evergreen needleleaf forests. Sci. Total Environ. 2018, 622, 1217–1224. [Google Scholar] [CrossRef]
- Zhang, Z.T.; Sun, S.; Zhang, F.L.; Guo, S.B.; Guo, E.J.; Loi, Z.J.; Zhao, J.; Zhao, C.; Li, T.; Yang, X.G. Using estimated radiation in crop models amplified the negative impacts of climate variability on maize and winter wheat yields in China. Agric. For. Meteorol. 2022, 318, 108914. [Google Scholar] [CrossRef]
- He, Q.S.; Li, S.E.; Hu, D.; Wang, Y.H.; Cong, X. Performance assessment of the AquaCrop model for film-mulched maize with full drip irrigation in Northwest China. Irrig. Sci. 2021, 39, 277–292. [Google Scholar] [CrossRef]
- Yan, Z.Z.; Zhang, X.Y.; Rashid, M.A.; Li, H.J.; Jing, H.C.; Hochman, Z. Assessment of the sustainability of different cropping systems under three irrigation strategies in the North China Plain under climate change. Agric. Syst. 2020, 178, 102745. [Google Scholar] [CrossRef]
- Yang, J.H.; Wu, J.J.; Liu, L.Z.; Zhou, H.K.; Gong, A.D.; Han, X.Y.; Zhao, W.H. Responses of winter wheat yield to drought in the North China Plain: Spatial-temporal patterns and climatic drivers. Water 2020, 12, 3094. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, Y.; Guo, T.K.; Mao, X.M. Enhancing SWAP simulation accuracy via assimilation of leaf area index and soil moisture under different irrigation, film mulching and maize varieties conditions. Comput. Electron. Agric. 2024, 218, 108625. [Google Scholar] [CrossRef]
- Yuan, C.F. Simulation of water-salt transport and balance in cultivated-wasteland system based on SWAP model in Hetao Irrigation District of China. Agric. Water Manag. 2024, 305, 109132. [Google Scholar] [CrossRef]
- Li, X.Q. Simulation of the Suitable Autumn Irrigation Mode under Spring Wheat Planting Condition in the Hetao Irrigation District. Master’s Thesis, Taiyuan University of Technology, Taiyuan, China, 2021. [Google Scholar]
- Ma, Y.; Feng, S.Y.; Song, X.F. Evaluation of optimal irrigation scheduling and groundwater recharge at representative sites in the North China Plain with SWAP model and field experiments. Comput. Electron. Agric. 2015, 116, 125–136. [Google Scholar] [CrossRef]
- Zhang, C.; Brodylo, D.; Rahman, M.; Rahman, M.A.; Douglas, T.A.; Comas, X. Using an object-based machine learning ensemble approach to upscale evapotranspiration measured from eddy covariance towers in a subtropical wetland. Sci. Total Environ. 2022, 831, 154969. [Google Scholar] [CrossRef]
- Liu, M.Z.; Guo, Y.; Zhang, X.L.; Shen, Y.-J.; Zhang, Y.C.; Pei, H.W.; Min, L.L.; Wang, S.Q.; Shen, Y.J. China’s Black Soil Granary is increasingly facing extreme hydrological drought threats. Sci. Bull. 2023, 68, 481–484. [Google Scholar] [CrossRef]
- Bian, L.K.; Qin, X.E.; Zhang, C.L.; Guo, P.; Wu, H. Application, interpretability and prediction of machine learning method combined with LSTM and LightGBM-a case study for runoff simulation in an arid area. J. Hydrol. 2023, 625, 130091. [Google Scholar] [CrossRef]
- Himangshu, S.; Swastik, S.G.; Jayanta, K.G.; Chandra, S.P.O.; Sanjay, K.G. Potential of machine learning algorithms in groundwater level prediction using temporal gravity data. Groundw. Sustain. Dev. 2024, 25, 101114. [Google Scholar] [CrossRef]
- Du, C.M.; Jiang, S.Z.; Chen, C.Q.; Guo, Q.Y.; He, Q.Y.; Zhan, C. Machine learning based estimation of daily cropland evapotranspiration in diverse climate zones. Remote Sens. 2024, 16, 730. [Google Scholar] [CrossRef]
- Antonino, P.; Federico, A.; Matteo, I.; Dario, D.C.; Daniele, C.; Antonio, M.; Giuseppe, P.; Ilenia, T. Machine learning models to predict daily actual evapotranspiration of citrus orchards under regulated deficit irrigation. Ecol. Inform. 2023, 76, 102133. [Google Scholar] [CrossRef]
- Mohammad, A.; Albaji, M.; Mona, G.; Abd, A.N.; Saeid, H. Estimation of sugarcane evapotranspiration from remote sensing and limited meteorological variables using machine learning models. J. Hydrol. 2024, 629, 130605. [Google Scholar] [CrossRef]
- Jia, Y.; Su, Y.J.; Zhang, R.; Zhang, Z.N.; Lu, Y.K.; Shi, D.X.; Xu, C.Q.; Huang, D.F. Optimization of an extreme learning machine model with the sparrow search algorithm to estimate spring maize evapotranspiration with film mulching in the semiarid regions of China. Comput. Electron. Agric. 2022, 201, 107298. [Google Scholar] [CrossRef]
- Wu, Z.J.; Cui, N.B.; Gong, D.Z.; Zhu, F.Y.; Xing, L.W.; Zhu, B.; Chen, X.; We, S.L.; Liu, Q.S. Simulation of daily maize evapotranspiration at different growth stages using four machine learning models in semi-humid regions of northwest China. J. Hydrol. 2023, 617, 128947. [Google Scholar] [CrossRef]
- Yu, H.C.; Li, S.E.; Ding, J.; Yang, T.Y.; Wang, Y.X. Water use efficiency and its drivers of two typical cash crops in an arid area of Northwest China. Agric. Water Manag. 2023, 287, 108433. [Google Scholar] [CrossRef]
- Wang, C.Y.; Li, S.E.; Kang, S.Z.; Du, T.S.; Huang, S.Y.; Yang, H.B.; Wang, X.H.; Cui, Y.K.; Wu, M.S. Evapotranspiration and potential water saving effect evaluation of mulched maize fields in China. J. Hydrol. 2024, 630, 130658. [Google Scholar] [CrossRef]
- Yang, D.N.; Li, S.E.; Kang, S.Z.; Du, T.S.; Guo, P.; Mao, X.M.; Tong, L.; Hao, X.M.; Ding, R.S.; Niu, J. Effect of drip irrigation on wheat evapotranspiration, soil evaporation and transpiration in Northwest China. Agric. Water Manag. 2020, 232, 106001. [Google Scholar] [CrossRef]
- Shen, Q.X.; Niu, J.; Liu, Q.; Liao, D.H.; Du, T.S. A resilience-based approach for water resources management over a typical agricultural region in Northwest China under water-energy-food nexus. Ecol. Indic. 2022, 144, 109562. [Google Scholar] [CrossRef]
- Ding, J.; Li, S.E.; Wang, H.S.; Wang, C.Y.; Zhang, Y.X.; Yang, D.N. Estimation of Evapotranspiration and Crop Coefficient of Chinese Cabbage Using Eddy Covariance in Northwest China. Water 2021, 13, 2781. [Google Scholar] [CrossRef]
- Yang, D.N.; Li, S.E.; Wu, M.S.; Yang, H.B.; Zhang, W.X.; Chen, J.; Wang, C.Y.; Huang, S.Y.; Zhang, R.Q.; Zhang, Y.X. Drip irrigation improves spring wheat water productivity by reducing leaf area while increasing yield. Eur. J. Agron. 2023, 143, 126710. [Google Scholar] [CrossRef]
- Liu, B.Q.; Ba, T.T.; Zhang, J.G.; Zhai, M.Z.; Peng, S.B. Effects of long-term fertilization modes on soil physicochemical properties and economic benefits of walnut orchards in Southern Shaanxi. J. Northwest For. Univ. 2025, 40, 76–84. [Google Scholar]
- Han, W.; Chen, X.Y.; Tao, T.T. Characteristics of soil saturated hydraulic conductivity in typical agricultural small watershed of three gorges reservoir area. Bull. Soil Water Conserv. 2024, 44, 83–91. [Google Scholar] [CrossRef]
- LY/T 1215-1999; Determination of Forest Soil Moisture and Physical Properties. State Forestry Administration of the People’s Republic of China: Beijing, China, 1999.
- Xu, Z.Q.; Wallach, R.; Mao, X.M. Understanding evaporation from salinized soils in Xinjiang: Impact of sodium adsorption ratio, salt type, and concentrations. Soil Sci. Soc. Am. J. 2025, 89, e20796. [Google Scholar] [CrossRef]
- Jiang, J. Experiment and Simulation on the Field Soil Water and Salt Movement Under Deficit Irrigation with Saline Water in the Shiyang River Basin. Ph.D. Thesis, China Agricultural University, Beijing, China, 2011. [Google Scholar]
- Bowen, I.S. The ratio of heat losses by conduction and by evaporation from any water surface. Phys. Rev. 1926, 27, 779–787. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: I. Factors governing measurement accuracy. Agric. Water Manag. 2011, 98, 899–920. [Google Scholar] [CrossRef]
- Allen, R.G. Assessing integrity of weather data for reference evapotranspiration estimation. J. Irrig. Drain. Eng. 1996, 122, 97–106. [Google Scholar] [CrossRef]
- Perez, P.J.; Castellvi, F.; Ibanez, M.; Rosell, J.I. Assessment of reliability of Bowen ratio method for partitioning fluxes. Agric. Forest. Meteorol. 1999, 97, 141–150. [Google Scholar] [CrossRef]
- Zhang, B.Z.; Kang, S.Z.; Li, F.S.; Zhang, L. Comparison of three evapotranspiration models to Bowen ratio-energy balance method for a vineyard in an arid desert region of northwest China. Agric. For. Meteorol. 2008, 148, 1629–1640. [Google Scholar] [CrossRef]
- Zou, Y.F.; Saddique, Q.; Dong, W.J.; Zhao, Y.; Zhang, X.; Liu, J.C.; Ding, D.Y.; Feng, H.; Wendroth, O.; Siddique, K.H.M. Quantifying the compensatory effect of increased soil temperature under plastic film mulching on crop growing degree days in a wheat-maize rotation system. Field Crop Res. 2021, 260, 107993. [Google Scholar] [CrossRef]
- Damir, J.; Vesna, D.J. Investigating relationships between rainfall and karst-spring discharge by higher-order partial correlation functions. J. Hydrol. 2015, 530, 24–36. [Google Scholar] [CrossRef]
- Chen, J.L.; Shao, Z.F.; Deng, X.J.; Huang, X.; Dang, C.Y. Vegetation as the catalyst for water circulation on global terrestrial ecosystem. Sci. Total Environ. 2023, 895, 165071. [Google Scholar] [CrossRef]
- Kroes, J.G.; Wesseling, J.G.; Van Dam, J.C. Integrated modelling of the soil-water-atmosphere–plant system using the model SWAP 2.0, an overview of theory and an application. Hydrol. Process. 2000, 14, 1993–2002. [Google Scholar] [CrossRef]
- Kroes, J.G.; Dam, J.C.V.; Barthoiomeus, R.P.; Groenendijk, P.; Heinen, M.; Hendriks, R.F.A.; Mulder, H.M.; Supit, I.; Walsum, P.E.V. SWAP Version 4: Theory Description and User Manual; Wageningen Environmental Research: Wageningen, The Netherlands, 2017. [Google Scholar]
- Ma, Y.; Duan, S.; Lei, H. SWAP model parameters for typical crops in the arid regions of Northwest China. Trans. CSAE 2025, 41, 73–80, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Sepideh, K.; Jalal, S.; Pau, M. Supplanting missing climatic inputs in classical and random forest models for estimating reference evapotranspiration in humid coastal areas of Iran. Comput. Electron. Agric. 2020, 176, 105633. [Google Scholar] [CrossRef]
- Vapnik, V. Support vector machine. Mach. Learn. 1995, 20, 273–297. [Google Scholar]
- Yao, Y.; Liang, S.; Li, X.; Chen, J.; Liu, S.M.; Jia, K.; Zhang, X.T.; Xiao, Z.Q.; Joshua, B.F.; Mu, Q.Z.; et al. Improving global terrestrial evapotranspiration estimation using support vector machine by integrating three process-based algorithms. Agric. For. Meteorol. 2017, 242, 55–74. [Google Scholar] [CrossRef]
- Majid, N.; Andrea, M.; Bruno, B.; Reza, P.; David, J.; Pranav, D.; Maurizio, R. Applications of XGBoost in water resources engineering: A systematic literature review (Dec 2018–May 2023). Environ. Model. Softw. 2024, 174, 105971. [Google Scholar] [CrossRef]
- Anurag, M.; Mehdi, J.; Mumtaz, A.; Ramendra, P.; Masoud, K.; Zaher, M.Y. Multi-step daily forecasting of reference evapotranspiration for different climates of India: A modern multivariate complementary technique reinforced with ridge regression feature selection. Agric. Water Manag. 2022, 272, 107812. [Google Scholar] [CrossRef]
- Wu, T.A.; Zhang, W.; Jiao, X.Y.; Guo, W.H.; Hamoud, Y.A. Evaluation of stacking and blending ensemble learning methods for estimating daily reference evapotranspiration. Comput. Electron. Agric. 2021, 184, 106039. [Google Scholar] [CrossRef]
- Li, H.R.; Mei, X.R.; Wang, J.D.; Huang, F.; Hao, W.P.; Li, B.G. Drip fertigation significantly increased crop yield, water productivity and nitrogen use efficiency with respect to traditional irrigation and fertilization practices: A meta-analysis in China. Agric. Water Manag. 2021, 244, 106534. [Google Scholar] [CrossRef]
- Wu, Z.Q.; Fan, Y.Q.; Qiu, Y.; Hao, X.M.; Li, S.E.; Kang, S.Z. Response of yield and quality of greenhouse tomatoes to water and salt stresses and biochar addition in Northwest China. Agric. Water Manag. 2022, 270, 107736. [Google Scholar] [CrossRef]
- Umair, M.; Hussain, T.; Jiang, H.B.; Ahmad, A.; Yao, J.W.; Qi, Y.Q.; Zhang, Y.C.; Min, L.L.; Shen, Y.J. Water-Saving Potential of Subsurface Drip Irrigation For Winter Wheat. Sustainability 2019, 11, 2978. [Google Scholar] [CrossRef]
- Guo, H.; Li, S.E.; Kang, S.Z.; Du, T.S.; Liu, W.F.; Tong, L.; Hao, X.M.; Ding, R.S. The controlling factors of ecosystem water use efficiency in maize fields under drip and border irrigation systems in Northwest China. Agric. Water Manag. 2022, 272, 107839. [Google Scholar] [CrossRef]
- Wang, Z.H.; Han, M.Q.; Song, L.B.; Zong, R.; Wen, Y.; Wu, X.D. Effects of aeration on the growth and water use efficiency of cotton under mulched drip irrigation in the dry areas of Northwest China. Trans. Chin. Soc. Agric. Eng. 2022, 38, 108–116. [Google Scholar]
- Zhang, B.Z.; Xu, D.; Liu, Y.; Li, F.S.; Cai, J.B.; Du, L.J. Multi-scale evapotranspiration of summer maize and the controlling meteorological factors in north China. Agric. For. Meteorol. 2016, 216, 1–12. [Google Scholar] [CrossRef]
- Han, X.; Zhang, B.Z.; Liu, T.J.; Wang, J.; Zhou, Q.Y.; Che, Z. The effect of time scales on the distribution of evapotranspiration and driving factors in desert grasslands. Agric. Water Manag. 2023, 284, 108348. [Google Scholar] [CrossRef]
- Fang, B.J.; Lei, H.M.; Zhang, Y.C.; Quan, Q.; Yang, D.W. Spatio-temporal patterns of evapotranspiration based on upscaling eddy covariance measurements in the dryland of the North China Plain. Agric. For. Meteorol. 2020, 281, 107844. [Google Scholar] [CrossRef]
- Qiu, R.J.; Katul, G.G.; Zhang, L.; Qin, S.J.; Jiang, X.L. The effects of changing environments, abiotic stresses, and management practices on cropland evapotranspiration: A review. Rev. Geophys. 2025, 63, e2024RG000858. [Google Scholar] [CrossRef]
- Shan, X.Q.; Cui, N.B.; Cai, H.J.; Hu, X.T.; Zhao, L. Estimation of summer maize evapotranspiration using MARS model in the semi-arid region of northwest China. Comput. Electron. Agric. 2020, 174, 105495. [Google Scholar] [CrossRef]
- Zhao, L.; Qing, S.H.; Bai, J.Y.; Hao, H.H.; Li, H.; Shi, Y.; Xing, X.G.; Yang, R. A hybrid optimized model for predicting evapotranspiration in early and late rice based on a categorical regression tree combination of key influencing factors. Comput. Electron. Agric. 2023, 211, 108031. [Google Scholar] [CrossRef]
- Wang, T.X.; Sun, S.K.; Yin, Y.L.; Zhao, J.F.; Tang, Y.H.; Wang, Y.B.; Gao, F.; Luan, X.B. Status of crop water use efficiency evaluation methods: A review. Agric. For. Meteorol. 2024, 349, 109961. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Chen, S.Y.; Sun, H.Y.; Shao, L.W.; Wang, Y.Z. Changes in evapotranspiration over irrigated winter wheat and maize in North China Plain over three decades. Agric. Water Manag. 2011, 98, 1097–1104. [Google Scholar] [CrossRef]
- Pereira, L.S.; Richard, G.A.; Martin, S.; Dirk, R. Crop evapotranspiration estimation with FAO56: Past and future. Agric. Water Manag. 2015, 147, 4–20. [Google Scholar] [CrossRef]
- Pereira, L.S.; Paredes, P.; Hunsaker, D.J.; Urrea, R.L.; Shad, Z.M. Standard single and basal crop coefficients for field crops. Updates and advances to the FAO56 crop water requirements method. Agric. Water Manag. 2021, 243, 106466. [Google Scholar] [CrossRef]
- Gabriela, P.; Milan, F.; Bram, V.K.; Matej, O.; Petr, H.; Zdenek, Z.; Miroslav, T. Quantifying turbulent energy fluxes and evapotranspiration in agricultural field conditions: A comparison of micrometeorological methods. Agric. Water Manag. 2018, 209, 249–263. [Google Scholar] [CrossRef]
- Sun, Y.B.; Bilige, S.; Geng, B.; Ma, J.Y.; Lin, X.W.; Hao, Z.Z.; Jing, W.J.; Chen, Q.T.; Quan, Z.J. Observation of the winter regional evaporative fraction using a UAV-based eddy covariance system over wetland area. Agric. For. Meteorol. 2021, 310, 108619. [Google Scholar] [CrossRef]
- Soufiane, T.; Andrea, S.; Lamia, E.; Malika, K.; Abdelaziz, M.; Souad, H.; Jamal, C.; Bouabid, E.M. Comparing the ability of different remotely sensed evapotranspiration products in enhancing hydrological model performance and reducing prediction uncertainty. Ecol. Inform. 2023, 78, 102352. [Google Scholar] [CrossRef]
- Srivastava, S.; Kumar, N.; Malakar, A.; Choudhury, S.D.; Ray, C.; Roy, T. A machine learning-based probabilistic approach for irrigation scheduling. Water Resour. Manag. 2024, 38, 1639–1653. [Google Scholar] [CrossRef]
- Asish, S.; Subodh, C.P. Application of machine learning and emerging remote sensing techniques in hydrology: A state-of-the-art review and current research trends. J. Hydrol. 2024, 632, 130907. [Google Scholar] [CrossRef]
- Srinivasulu, A.; Su, Q.; Jasdeep, S.; Sushil, H.; Fan, Y.B.; Blake, S.; Eric, G.; Bala, R.S.; Curtis, A.; Keith, B.; et al. Development and evaluation of a decision support mobile application for cotton irrigation management. Smart Agric. Technol. 2023, 5, 100270. [Google Scholar] [CrossRef]
- Amarendra, G.; Deepak, S.; Shukla, A.K.; Krishna, C.R. An IoT based smart irrigation management system using Machine learning and open source technologies. Comput. Electron. Agric. 2018, 155, 41–49. [Google Scholar] [CrossRef]
- Lisa, U.; Vidya, S. Application of machine learning approaches in supporting irrigation decision making: A review. Agric. Water Manag. 2024, 294, 108710. [Google Scholar] [CrossRef]



| Treatment | Soil Depths (cm) | Bulk Density (g cm−3) | Field Capacity (cm3 cm−3) | Residual Water Content (cm3 cm−3) | Saturated Water Content (cm3 cm−3) | Saturated Hydraulic Conductivity (cm d−1) | pH | Soil Salt Content (g kg−1) |
|---|---|---|---|---|---|---|---|---|
| DI | 0–20 | 1.41 | 0.32 | 0.04 | 0.41 | 35.84 | 8.55 | 1.36 |
| 20–40 | 1.57 | 0.31 | 0.07 | 0.40 | 32.73 | 8.77 | 1.37 | |
| 40–60 | 1.57 | 0.31 | 0.06 | 0.42 | 30.05 | 8.84 | 2.62 | |
| 60–80 | 1.51 | 0.33 | 0.08 | 0.45 | 28.66 | 8.95 | 2.48 | |
| 80–100 | 1.43 | 0.34 | 0.11 | 0.43 | 28.41 | 8.94 | 2.26 | |
| BI | 0–20 | 1.53 | 0.30 | 0.04 | 0.44 | 36.84 | 8.75 | 1.17 |
| 20–40 | 1.56 | 0.30 | 0.04 | 0.44 | 33.65 | 8.87 | 1.10 | |
| 40–60 | 1.49 | 0.32 | 0.06 | 0.45 | 30.77 | 8.91 | 1.73 | |
| 60–80 | 1.44 | 0.34 | 0.08 | 0.45 | 24.97 | 8.76 | 2.61 | |
| 80–100 | 1.45 | 0.35 | 0.09 | 0.44 | 28.41 | 8.84 | 2.25 |
| Irrigation Method | Irrigation Date | Irrigation Amount/mm | Fertilization Amount/kg N ha−1 | Irrigation Method | Irrigation Date | Irrigation Amount/mm | Fertilization Amount/kg N ha−1 |
|---|---|---|---|---|---|---|---|
| DI | 06/05/2017 | 60 | 45 | BI | 05/05/2017 | 120 | 90 |
| 17/05/2017 | 60 | 45 | 26/05/2017 | 117 | 62 | ||
| 27/05/2017 | 60 | 22.5 | 13/06/2017 | 73 | |||
| 12/06/2017 | 57 | 03/07/2017 | 64 | ||||
| 23/06/2017 | 57 | ||||||
| 04/07/2017 | 41 | ||||||
| Sum | 335 | 112.5 | Sum | 374 | 152 | ||
| 05/05/2018 | 100 | 54 | 05/05/2018 | 100 | 82 | ||
| 19/05/2018 | 55 | 41 | 27/05/2018 | 118 | 54 | ||
| 28/05/2018 | 55 | 41 | 16/06/2018 | 108 | |||
| 09/06/2018 | 55 | 04/072018 | 90 | ||||
| 18/06/2018 | 55 | ||||||
| 29/06/2018 | 45 | ||||||
| 05/07/2018 | 45 | ||||||
| Sum | 410 | 136 | Sum | 416 | 136 | ||
| 06/05/2019 | 66 | 68 | 04/05/2019 | 98 | 150 | ||
| 19/05/2019 | 66 | 68 | 25/05/2019 | 98 | |||
| 30/05/2019 | 54 | 13/06/2019 | 84 | ||||
| 09/06/2019 | 45 | 06/07/2019 | 72 | ||||
| 17/06/2019 | 37 | ||||||
| 30/06/2019 | 18 | ||||||
| 09/07/2019 | 30 | ||||||
| Sum | 316 | 136 | Sum | 352 | 150 | ||
| 08/05/2020 | 66 | 68 | 07/052020 | 108 | 150 | ||
| 17/05/2020 | 66 | 68 | 29/05/2020 | 87 | |||
| 29/05/2020 | 50 | 17/062020 | 76 | ||||
| 08/06/2020 | 45 | 07/07/2020 | 76 | ||||
| 17/06/2020 | 35 | ||||||
| 27/06/2020 | 25 | ||||||
| 07/07/2020 | 25 | ||||||
| Sum | 312 | 136 | Sum | 347 | 150 |
| Year | Month | u2 (m s−1) | Tmax (°C) | Tmin (°C) | RHmax (%) | RHmin (%) | P (mm) |
|---|---|---|---|---|---|---|---|
| 2017 | 3 | 1.1 | 14.4 | −0.3 | 73.6 | 25.7 | 4.2 |
| 4 | 1.3 | 18.5 | 3.6 | 71.1 | 26.1 | 22.0 | |
| 5 | 1.1 | 25.0 | 9.4 | 65.8 | 20.1 | 21.4 | |
| 6 | 0.8 | 27.7 | 13.0 | 74.1 | 30.2 | 21.8 | |
| 7 | 0.7 | 32.2 | 16.0 | 73.3 | 30.8 | 7.2 | |
| 2018 | 3 | 1.1 | 21.9 | 2.7 | 46.8 | 13.2 | 0.0 |
| 4 | 1.0 | 17.9 | 3.5 | 69.6 | 26.8 | 21.6 | |
| 5 | 0.8 | 25.3 | 9.4 | 62.7 | 17.6 | 4.6 | |
| 6 | 0.7 | 28.7 | 13.8 | 69.5 | 29.1 | 8.8 | |
| 7 | 0.5 | 29.4 | 14.7 | 84.8 | 39.8 | 6.4 | |
| 2019 | 3 | 0.6 | 16.8 | −1.8 | 45.1 | 11.4 | 0.0 |
| 4 | 0.9 | 22.0 | 5.7 | 61.6 | 20.0 | 7.8 | |
| 5 | 1.0 | 22.5 | 8.5 | 71.2 | 29.3 | 27.0 | |
| 6 | 0.6 | 26.6 | 13.4 | 80.0 | 41.1 | 51.6 | |
| 7 | 0.3 | 29.6 | 13.4 | 84.2 | 37.9 | 23.8 | |
| 2020 | 4 | 1.0 | 19.9 | 3.0 | 43.5 | 13.7 | 0.0 |
| 5 | 1.2 | 23.6 | 9.1 | 63.7 | 24.7 | 23.8 | |
| 6 | 0.8 | 28.3 | 12.9 | 71.1 | 26.7 | 10.8 | |
| 7 | 0.3 | 29.3 | 14.4 | 83.0 | 35.6 | 23.0 |
| Year | Growing Stage | BI | Days | GDD (°C) | DI | Days | GDD (°C) |
|---|---|---|---|---|---|---|---|
| 2017 | Seedling Stage | 28/03/2017−11/05/2017 | 45 | 323.5 | 28/03/2017−11/05/2017 | 45 | 324.9 |
| Jointing Stage | 12/05/2017−30/05/2017 | 19 | 287.1 | 12/05/2017−26/05/2017 | 15 | 186.0 | |
| Heading Stage | 31/05/2017−20/06/2017 | 21 | 293.9 | 27/05/2017−14/06/2017 | 19 | 267.0 | |
| Filling Stage | 21/06/2017−05/07/2017 | 15 | 238.4 | 15/06/2017−29/06/2017 | 15 | 319.4 | |
| Maturing Stage | 06/07/2017−21/07/2017 | 16 | 309.6 | 30/06/2017−15/07/2017 | 16 | 408.1 | |
| Entire crop season | 28/03/2017−21/07/2017 | 116 | 1452.5 | 28/03/2017−15/07/2017 | 110 | 1505.4 | |
| 2018 | Seedling Stage | 21/03/2018−09/05/2018 | 50 | 402.4 | 21/03/2018−09/05/2018 | 50 | 406.5 |
| Jointing Stage | 10/05/2018−27/05/2018 | 18 | 225.3 | 10/05/2018−23/05/2018 | 14 | 176.6 | |
| Heading Stage | 28/05/2018−13/06/2018 | 17 | 241.1 | 24/05/2018−07/06/2018 | 15 | 236.2 | |
| Filling Stage | 14/06/2018−03/07/2018 | 20 | 335.9 | 08/06/2018−26/06/2018 | 19 | 313.9 | |
| Maturing Stage | 04/07/2018−23/07/2018 | 20 | 350.2 | 27/06/2018−16/07/2018 | 20 | 341.7 | |
| Entire crop season | 21/03/2018–23/07/2018 | 125 | 1554.9 | 21/03/2018−16/07/2018 | 118 | 1474.9 | |
| 2019 | Seedling Stage | 25/03/2019−10/05/2019 | 47 | 352.9 | 25/03/2019−10/05/2019 | 47 | 369.2 |
| Jointing Stage | 11/05/2019−28/05/2019 | 18 | 198.5 | 11/05/2019−25/05/2019 | 15 | 172.4 | |
| Heading Stage | 29/05/2019−17/06/2019 | 20 | 293.5 | 26/05/2019−13/06/2019 | 19 | 265.8 | |
| Filling Stage | 18/06/2019−07/07/2019 | 20 | 289.9 | 14/06/2019−02/07/2019 | 19 | 268.1 | |
| Maturing Stage | 08/07/2019−28/07/2019 | 21 | 336.3 | 03/07/2019−22/07/2019 | 20 | 316.8 | |
| Entire crop season | 25/03/2019−28/07/2019 | 126 | 1471.1 | 25/03/2019−22/07/2019 | 120 | 1392.3 | |
| 2020 | Seedling Stage | 02/04/2020−13/05/2020 | 42 | 361.3 | 02/04/2020−13/05/2020 | 42 | 372.5 |
| Jointing Stage | 14/05/2020−30/05/2020 | 17 | 199.3 | 14/05/2020−28/05/2020 | 15 | 204.3 | |
| Heading Stage | 31/05/2020−18/06/2020 | 19 | 279.0 | 29/05/2020−15/06/2020 | 18 | 251.4 | |
| Filling Stage | 19/06/2020−08/07/2020 | 20 | 334.4 | 16/06/2020−04/07/2020 | 19 | 319.3 | |
| Maturing Stage | 09/07/2020−28/07/2020 | 20 | 326.7 | 05/07/2020−23/07/2020 | 19 | 333.6 | |
| Entire crop season | 02/04/2020−28/07/2020 | 118 | 1500.7 | 02/04/2020−23/07/2020 | 113 | 1481.1 |
| Growing Stage | 2017 | 2018 | 2019 | 2020 | Average | |
|---|---|---|---|---|---|---|
| ETBIBREB (mm) | Seedling | 109.0 | 103.9 | 105.2 | 67.7 | 96.5 |
| Jointing | 129.6 | 130.6 | 119.6 | 65.3 | 111.3 | |
| Heading | 133.8 | 123.6 | 135.7 | 102.3 | 123.9 | |
| Filling | 83.5 | 119.5 | 110.2 | 95.1 | 102.1 | |
| Maturing | 91.4 | 74.8 | 103.2 | 44.1 | 78.4 | |
| All growing stages | 547.3 | 552.4 | 573.9 | 374.5 | 512.0 | |
| ETBISWAP (mm) | Seedling | 72.4 | 73.2 | 60.3 | 49.3 | 63.8 |
| Jointing | 106.6 | 84.8 | 97.4 | 78.6 | 91.9 | |
| Heading | 113.5 | 99.0 | 114.3 | 108.2 | 108.8 | |
| Filling | 90.3 | 96.3 | 88.0 | 105.9 | 95.1 | |
| Maturing | 90.5 | 74.0 | 89.3 | 65.2 | 79.8 | |
| All growing stages | 473.3 | 427.3 | 449.3 | 407.2 | 439.3 | |
| ETDIBREB (mm) | Seedling | 73.1 | 100.1 | 83.1 | 61.2 | 79.4 |
| Jointing | 74.0 | 103.3 | 98.8 | 53.2 | 82.3 | |
| Heading | 103.3 | 83.9 | 142.4 | 101.3 | 107.7 | |
| Filling | 66.0 | 149.7 | 102.0 | 86.6 | 101.1 | |
| Maturing | 74.4 | 85.0 | 95.0 | 51.0 | 76.4 | |
| All growing stages | 390.8 | 522.0 | 521.3 | 353.3 | 446.9 | |
| ETDISWAP (mm) | Seedling | 60.5 | 55.7 | 56.5 | 40.0 | 53.2 |
| Jointing | 75.9 | 60.1 | 81.9 | 68.0 | 71.5 | |
| Heading | 100.8 | 82.2 | 113.1 | 104.9 | 100.3 | |
| Filling | 89.6 | 107.9 | 81.6 | 97.8 | 94.2 | |
| Maturing | 73.0 | 91.4 | 94.9 | 54.7 | 78.5 | |
| All growing stages | 399.8 | 397.3 | 428.0 | 365.4 | 397.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, T.; Chen, H.; Yu, H.; Liao, Z.; Yang, D.; Li, S. Evapotranspiration Differences, Driving Factors, and Numerical Simulation of Typical Irrigated Wheat Fields in Northwest China. Agronomy 2025, 15, 1984. https://doi.org/10.3390/agronomy15081984
Yang T, Chen H, Yu H, Liao Z, Yang D, Li S. Evapotranspiration Differences, Driving Factors, and Numerical Simulation of Typical Irrigated Wheat Fields in Northwest China. Agronomy. 2025; 15(8):1984. https://doi.org/10.3390/agronomy15081984
Chicago/Turabian StyleYang, Tianyi, Haochong Chen, Haichao Yu, Zhenqi Liao, Danni Yang, and Sien Li. 2025. "Evapotranspiration Differences, Driving Factors, and Numerical Simulation of Typical Irrigated Wheat Fields in Northwest China" Agronomy 15, no. 8: 1984. https://doi.org/10.3390/agronomy15081984
APA StyleYang, T., Chen, H., Yu, H., Liao, Z., Yang, D., & Li, S. (2025). Evapotranspiration Differences, Driving Factors, and Numerical Simulation of Typical Irrigated Wheat Fields in Northwest China. Agronomy, 15(8), 1984. https://doi.org/10.3390/agronomy15081984





