Quantitative Analysis of Adulteration in Anoectochilus roxburghii Powder Using Hyperspectral Imaging and Multi-Channel Convolutional Neural Network

Abstract

Adulteration detection in medicinal plant powders remains a critical challenge in quality control. In this study, we propose a hyperspectral imaging (HSI)-based method combined with deep learning models to quantitatively analyze adulteration levels in Anoectochilus roxburghii powder. After preprocessing the spectral data using raw, first-order, and second-order Savitzky–Golay derivatives, we systematically evaluated the performance of traditional machine learning models (Random Forest, Support Vector Regression, Partial Least Squares Regression) and deep learning architectures. While traditional models achieved reasonable accuracy (R² up to 0.885), their performance was limited by feature extraction and generalization ability. A single-channel convolutional neural network (CNN) utilizing individual spectral representations improved performance marginally (maximum R² = 0.882), but still failed to fully capture the multi-scale spectral features. To overcome this, we developed a multi-channel CNN that simultaneously integrates raw, SG-1, and SG-2 spectra, effectively leveraging complementary spectral information. This architecture achieved a significantly higher prediction accuracy (R² = 0.964, MSE = 0.005), demonstrating superior robustness and generalization. The findings highlight the potential of multi-channel deep learning models in enhancing quantitative adulteration detection and ensuring the authenticity of herbal products.

1. Introduction

Traditional Chinese medicine (TCM) materials have historically been authenticated based on empirical morphological and sensory characteristics, such as plant shape, color, texture, odor, and taste [1,2,3]. This process relies heavily on the expertise of practitioners to visually identify raw herbs and detect obvious adulterants. However, once the materials are ground into fine powders, most visible and olfactory cues are lost [4]. In powdered form, TCM ingredients appear visually similar regardless of origin, making traditional identification methods unreliable. As a result, adulteration or substitution of powdered TCM products often goes undetected using conventional techniques, highlighting the need for more advanced, high-throughput authentication methods. Anoectochilus roxburghii is an increasingly targeted species for adulteration. Anoectochilus roxburghii, commonly known as Jinxianlian, is a highly esteemed traditional Chinese medicinal herb renowned for its diverse pharmacological properties [5,6,7,8]. It has been traditionally used to treat conditions such as hyperuricemia, type 2 diabetes mellitus, cancers, and inflammatory diseases. Recent studies have identified bioactive compounds like quercetin, kinsenoside, and rhamnazin, which contribute to its anti-inflammatory, antioxidant, and antihyperlipidemic effects [9,10,11,12]. The main active constituent, known as Anoectochilus roxburghii glycoside, has recently received considerable medical attention. In 2023, this glycoside was approved by the Chinese National Medical Products Administration (NMPA) for clinical trials in treating non-alcoholic fatty liver disease, reflecting its demonstrated efficacy in liver-related disorders. This milestone highlights the powerful therapeutic potential of Anoectochilus roxburghii in modern medicine, particularly for protecting the liver and regulating metabolism. Despite its high medicinal value, Anoectochilus roxburghii is visually similar to other orchidaceous plants, especially in powdered form, making it a common target for adulteration in herbal markets [13]. One of the most frequent adulterants is Ludisia discolor (commonly known as the jewel orchid), which resembles A. roxburghii in appearance but lacks its key pharmacologically active compounds, such as kinsenoside and quercetin. The substitution of L. discolor significantly reduces therapeutic efficacy and may delay treatment in conditions like diabetes, liver disorders, or chronic inflammation, where A. roxburghii is commonly used. Although L. discolor is not acutely toxic, its use as a counterfeit undermines consumer safety and trust. This highlights the urgent need for accurate, high-throughput, and non-destructive methods for authenticating powdered herbal products to ensure quality and efficacy.

Traditional spectroscopic techniques such as Fourier-transform infrared (FT-IR), near-infrared (FT-NIR), and Raman spectroscopy have been widely used for adulteration detection in food and herbal products. For instance, FT-NIR has been applied to identify adulterants in nuts, ginger, and coffee by analyzing molecular vibrations in the near-infrared region [14,15,16]. Raman spectroscopy has demonstrated effectiveness in detecting economically motivated adulteration in oil and milk [17,18]. However, these techniques often provide only point-wise or small-area measurements, lacking spatial information about heterogeneous samples. Furthermore, their performance can be affected by sample presentation, particle size, surface homogeneity, and light scattering effects. These limitations make it challenging to detect minor or unevenly distributed adulterants in powdered mixtures. By contrast, hyperspectral imaging (HSI) captures both spatial and spectral information simultaneously across an entire sample surface. This advantage allows for non-destructive, high-throughput analysis and improves the detection of subtle spectral variations associated with adulterants, even in visually indistinguishable powders. Therefore, HSI offers a more robust and scalable solution for the authentication of complex herbal and food products. Hyperspectral imaging (HSI) is an advanced technique that simultaneously acquires spatial and spectral information across an entire sample [19,20]. Each pixel in an HSI image contains a full reflectance spectrum (often spanning visible to near-infrared wavelengths), providing detailed chemical and physical information without destroying the sample [21,22]. This non-destructive approach requires minimal preparation and enables rapid scanning of large sample areas or multiple specimens [23]. As a result, HSI offers high-throughput, accurate analysis of material composition. Key advantages of HSI for authenticating plant materials include: non-destructive imaging with minimal or no sample preparation, rapid acquisition and high-throughput screening of many samples, rich spectral information across many contiguous wavelengths, and combined spatial–spectral data that reveal heterogeneity in powdered mixtures [24,25,26]. These strengths make HSI particularly powerful for detecting adulteration in powdered TCM products and visually similar herb samples. Unlike conventional chemical assays or point-based spectroscopy, HSI can quickly scan batches of herbal powders and map their composition, enabling large-scale, accurate identification of contaminants or substitutes. HSI data are inherently high-dimensional and complex. A typical hyperspectral image contains hundreds of contiguous spectral bands for each spatial pixel, leading to excessive spectral redundancy and multi-collinearity. In addition, hyperspectral measurements often suffer from sensor noise and variability in illumination or sample presentation, which can introduce spurious spectral differences. Together, these issues increase the risk of overfitting and make direct analysis difficult. Key challenges of HSI data include extremely high dimensionality and correlated bands, sensor noise and environmental variability, large data volume, and computational burden. To manage this complexity, dimensionality reduction and robust feature extraction are essential. Techniques such as principal component analysis (PCA), partial least squares (PLS) regression, or band selection are commonly applied to compress the data and discard irrelevant or noisy information [27,28]. By focusing on the most informative spectral features, these methods improve the efficiency and accuracy of subsequent classification or regression models for adulteration detection.

Machine learning algorithms have long been used to analyze hyperspectral data. Conventional methods like support vector machines (SVM), or random forests typically require manual feature selection or preprocessing and often rely on linear assumptions [29]. These methods may perform well under simple conditions, but they can struggle with the complex, nonlinear nature of high-dimensional hyperspectral datasets [30,31]. Deep learning approaches, especially convolutional neural networks (CNNs), offer a powerful alternative [13,32,33]. CNNs can automatically learn hierarchical feature representations directly from raw spectral images, capturing both spectral and spatial patterns without manual intervention. By using convolutional filters and multiple hidden layers, CNNs effectively exploit the spatial structure and local correlations in hyperspectral images. This enables them to model complex, nonlinear relationships and to be more robust to noise and data variability. Key advantages of deep learning for HSI analysis include automated feature extraction without manual selection, powerful nonlinear modeling to capture complex spectral-spatial patterns, utilization of spatial context through convolutional architectures, often higher accuracy and better generalization than traditional models in HSI tasks. Consequently, CNN-based methods have demonstrated superior performance in many hyperspectral imaging applications, motivating their adoption for detecting and quantifying adulteration in Anoectochilus roxburghii powder.

In this study, we propose a hyperspectral imaging-based method combined with a multi-channel CNN to quantitatively detect adulteration in Anoectochilus roxburghii powder. By integrating raw spectra with first- and second-order spectral derivatives, the model is designed to capture both spectral and spatial features associated with adulterant presence. While traditional machine learning methods such as PLSR, SVR, and RF have been widely used for spectral regression tasks, they typically require manual feature extraction and often struggle to capture nonlinear relationships in high-dimensional hyperspectral data [34,35,36]. Moreover, single-channel CNN models, although more automated, are limited in their ability to extract multi-scale spectral features. In contrast, the proposed multi-channel CNN architecture assigns dedicated branches to different spectral inputs, enabling complementary feature learning and enhanced discriminative power. Our approach aims to improve both accuracy and robustness in powdered herbal product authentication, offering a rapid, non-destructive solution for quality control in the medicinal plant industry. To validate the model, we benchmark its performance against conventional methods and single-channel CNNs, demonstrating its superior predictive capability.

2. Materials and Methods

2.1. Sample Preparation

Anoectochilus roxburghii and counterfeit samples (Ludisia discolor) used in this study were provided and taxonomically identified by Professor Hongzhen Wang from the Department of Traditional Chinese Herbal Medicine at Zhejiang A&F University. To ensure complete dehydration, both Anoectochilus roxburghii and Ludisia discolor samples were placed in a drying oven (Jinghong, Shanghai, China) at 70 °C for 20 h. After drying, the samples were finely ground into powder using a laboratory grinder (Anka, Zhongshan, China) to ensure uniformity and consistency. To simulate varying levels of adulteration, powder mixtures were prepared by blending genuine Anoectochilus roxburghii powder with L. discolor powder at six different mass ratios: 0%, 20%, 40%, 60%, 80%, and 100% (where 0% represents pure counterfeit and 100% represents pure genuine sample). Each mixture was thoroughly homogenized to ensure even distribution of the components. After preparation, all samples were stored in sealed, airtight containers to prevent moisture absorption and contamination, thus preserving sample integrity for subsequent hyperspectral imaging and analysis.

2.2. Hyperspectral Image System

The hyperspectral imaging system employed in this study was the GaiaField-N17E system (Dualix Spectral Imaging, Jiangsu, China). Figure 1 provides an overview of the complete experimental workflow, including the imaging system setup, sample preparation, data acquisition, preprocessing, and model analysis. This system covers a spectral range from 900 nm to 1700 nm with a spectral resolution of 5 nm and a spatial resolution of 640 pixels across 512 bands. To ensure consistent and uniform illumination during the scanning process, the setup includes an enclosed testing chamber equipped with four 50 W halogen lamps. The hyperspectral scanner (Dualix Spectral Imaging, Jiangsu, China) utilizes an array-based detector (Dualix Spectral Imaging, Jiangsu, China) that is positioned perpendicular to the sample’s motion direction, allowing for two-dimensional space scanning as the platform moves. The platform speed is set at 0.8 cm/s, ensuring smooth, stable movement of samples through the scanning zone. Exposure settings are automatically adjusted by the system, with the gain factor fixed at 1. The vertical distance between the lens and the sample is consistently maintained at 42 cm throughout the scan. Samples are placed on a black substrate during scanning to optimize image contrast and reduce the influence of background diffuse reflection on the spectral data. To ensure high-quality data, each sample is scanned twice, increasing both reliability and repeatability of the measurements. After scanning, the raw hyperspectral data undergo black-and-white correction to eliminate any image distortion or noise. Spectral data are then extracted from the regions of interest (ROI) of each sample using ENVI 5.3 software. A rectangular region is randomly selected within each sample’s surface area, typically covering a quarter of the total sample. Each pixel within this ROI holds unique spectral information, and the final spectral signature for each sample is determined by averaging the reflectance values from all pixels in the selected region.

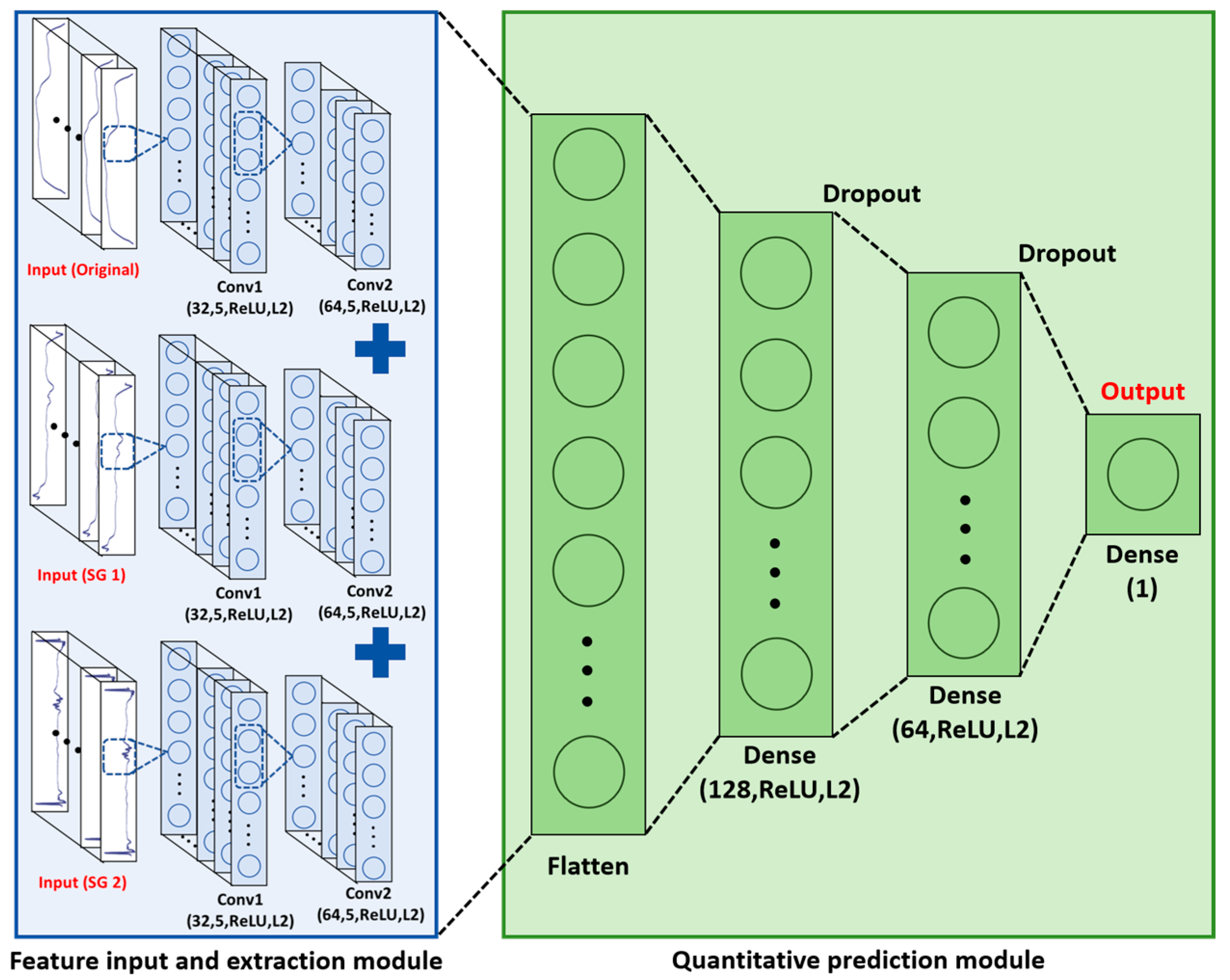
2.3. Spectral Data Analysis Models

A total of 240 powder mixture samples were prepared, covering six adulteration levels (0%, 20%, 40%, 60%, 80%, and 100%), with 40 samples per class. Each hyperspectral image provided hundreds of pixel-level spectral vectors, which were used as the model inputs. The dataset was divided into training and testing sets using an 80/20 stratified split. To enhance robustness and reduce overfitting risk, five-fold cross-validation was performed during model training. Although the number of physical mixture samples was moderate, the pixel-level resolution of hyperspectral imaging substantially expanded the effective dataset size. Combined with regularization techniques and architectural simplification, this allowed deep learning models to learn meaningful patterns without overfitting.

Random Forest (RF) constructs an ensemble of decision trees through bootstrap sampling and randomized feature selection. Predictions for regression tasks are obtained by averaging the outputs of individual trees. RF excels at handling high-dimensional data—such as hyperspectral inputs with hundreds of bands—because it naturally resists overfitting, can accommodate noisy or correlated features without manual feature selection, and supports parallel computation to accelerate training.

Support Vector Regression (SVR) adapts the Support Vector Machine framework for regression by optimizing a loss function to fit an optimal hyperplane that tolerates small errors. SVR is well suited for small-sample, high-dimensional problems, as its kernel functions map data into higher-dimensional spaces to capture complex nonlinear relationships. In hyperspectral analysis—where the number of samples is often limited relative to the number of spectral channels—SVR’s ability to uncover nonlinear patterns via kernel methods is particularly advantageous.

Partial Least Squares Regression (PLSR) is a multivariate technique that iteratively extracts latent variables (components) from both predictors and responses to maximize their covariance. PLSR effectively handles multicollinearity by projecting the original spectra onto a lower-dimensional subspace, preserving the most informative variance. Given that hyperspectral bands are highly correlated and often outnumber samples, PLSR can integrate redundant information while reducing dimensionality, resulting in a stable regression model.

RF, SVR, and PLSR have demonstrated reasonable performance in various hyperspectral applications, including adulteration detection tasks [34,35,36]. While RF and SVR are capable of modeling nonlinear relationships to some extent, their effectiveness can be hindered in high-dimensional spectral spaces due to challenges such as feature redundancy, the curse of dimensionality, and the need for careful hyperparameter tuning. Moreover, these models typically rely on manual feature selection or dimensionality reduction steps, which may limit their ability to fully exploit complex spectral patterns. Each relies on manual preprocessing or dimension reduction and can still be sensitive to noise, baseline drift, and complex spectral interactions. To address these challenges, we introduced a convolutional neural network (CNN) architecture capable of automatic, hierarchical feature learning. The proposed CNN uses a multi-branch input structure (Figure 2), with three parallel channels that separately accept the raw spectral vectors, first-order Savitzky–Golay (SG) derivatives, and second-order SG derivatives. Each branch processes its input through two successive convolutional layers (the first with 32 kernels of size 5 × 1, the second with 64 kernels of size 5 × 1; both employ ReLU activations), followed by flattening into a feature vector. The three flattened feature vectors are then concatenated and passed through two fully connected layers (128 and 64 neurons, respectively, with ReLU activations) to produce a single quantitative prediction. To improve generalization, L₂ regularization (λ = 5 × 10⁻³) was applied to all convolutional and dense layer weights, and a dropout rate of 0.05 was introduced between the two fully connected layers. This multi-channel CNN leverages complementary information from different spectral transformations—preserving intrinsic absorption features, enhancing peak resolution, and capturing subtle curvature changes—thereby providing a more comprehensive and robust solution for hyperspectral adulteration analysis.

3. Results and Discussion

3.1. Data Preprocessing

Hyperspectral data contain rich information that may be distributed across multiple feature levels—such as raw reflectance, first derivatives, and second derivatives—and a single representation often fails to capture all relevant signals. To ensure comprehensive and accurate feature extraction, we processed each spectrum from three perspectives, as illustrated in Figure 3. The raw spectral data preserve the intrinsic absorption characteristics governed by the Beer–Lambert law, making them fundamentally important for quantitative analysis. In Figure 3a, the raw spectra display distinct patterns corresponding to each adulteration level, which serve as the primary inputs for downstream modeling. The first derivative (Savitzky–Golay, order 1) enhances changes in spectral slope, thus sharpening overlapping peaks, especially when the wavelength difference (Δλ) between adjacent peaks is smaller than the full width at half maximum (FWHM). As shown in Figure 3b, the SG-1 spectra exhibit more pronounced peaks and valleys, facilitating clearer discrimination among different sample compositions. The second derivative (Savitzky–Golay, order 2) further accentuates subtle curvature changes, making fine spectral features more visible while simultaneously suppressing baseline drift and scattering artifacts. It should be noted that the spectra presented in Figure 3 are averaged reflectance curves derived from the selected regions of interest (ROIs) for each adulteration level. This averaging process reduces pixel-level noise and reflects the general spectral trend, but it may mask fine-grained differences among individual pixels. While the SG-1 spectra in Figure 3b appear visually similar, the first-order derivatives do enhance subtle variations in slope and curvature that are not always easily visible in 2D plots. These subtle features, although imperceptible to the naked eye, are captured and utilized by machine learning models, especially in the high-dimensional space considered during CNN training. In Figure 3c, the SG-2 spectra reveal even finer details that are barely discernible in the raw data, thereby improving sensitivity to small variations in chemical composition. The spectral similarity between pure Anoectochilus roxburghii and pure Ludisia discolor is expected, as both belong to the Orchidaceae family and share comparable physical properties in the near-infrared range. However, despite this similarity, derivative preprocessing (SG-1 and SG-2) helps to amplify fine differences in peak position and curvature, which, when integrated through advanced models such as multi-channel CNNs, yield reliable quantitative predictions.

By combining these three representations—(1) raw reflectance for absolute absorption information, (2) first derivatives for enhanced peak resolution, and (3) second derivatives for fine-feature sensitivity and baseline correction—this layered preprocessing strategy addresses key challenges in hyperspectral analysis. The complementary patterns observed across Figure 3a–c visually confirm that each representation contributes unique yet related information, validating the rationale for a multi-channel deep learning approach. Notably, the progression from raw to first- and second-derivative spectra demonstrates increasingly clear spectral features, underscoring the effectiveness of derivative transforms in resolving fine details that a single-channel model would otherwise miss.

3.2. Traditional Machine Learning Models

Traditional machine learning methods, such as RF, SVR, and PLSR, have been widely applied in hyperspectral plant species identification. Figure 4 shows the quantitative analysis results of these three traditional models. The R² value is used to assess the goodness of fit in linear regression models. It reflects the extent to which the explanatory variables can account for the variation in the dependent variable. R² is a value between 0 and 1, where values closer to 1 indicate a better fit and greater explanatory power. The Mean Squared Error (MSE) is a commonly used metric to evaluate the accuracy of predictive models. It calculates the average squared difference between predicted and actual values, with smaller values indicating lower prediction error. Figure 4 presents scatter plots that illustrate the relationship between the predicted values and the true values of the test set. In an ideal case, the points should lie along the diagonal (red dashed line), indicating that the model’s predictions are close to the actual values. In the figure, we observe that some points are near the diagonal, indicating that the predictions for these samples are accurate. However, other points deviate significantly from the diagonal, suggesting larger prediction errors for those samples. These deviations may indicate that the model has not effectively captured the features of certain samples, leading to suboptimal predictions. In Figure 4a, the MSE is 0.015 and the R² value is 0.885, in Figure 4b, the MSE is 0.021 and the R² value is 0.843, and in Figure 4c, the MSE is 0.017 and the R² value is 0.873. These results demonstrate that the models perform well overall, though there is still room for improvement.

Next, we applied first-order SG1 derivative preprocessing to enhance peaks and suppress noise (Figure 4d–f). Despite SG1’s ability to highlight subtle spectral changes, the performance of all three models declined: RF, SVR, and PLSR each displayed lower R² and higher MSE compared to their raw data results. Similarly, when using second-order SG2 derivative inputs (Figure 4h–i), which further accentuate curvature changes and correct baseline drift, RF, SVR, and PLSR again exhibited reduced accuracy relative to the raw spectrum case. These observations suggest that although SG1 and SG2 transformations enhance specific spectral features (sharpening overlapping peaks, mitigating baseline drift, and amplifying fine details), the resulting derivative data introduce complex, nonlinear patterns that traditional models struggle to exploit fully. The decline in performance can be attributed to several factors. First, SG1 and SG2 highlight nonlinear spectral variations that exceed the modeling capacity of RF, SVR, and PLSR: while RF can average over ensemble trees, SVR can apply kernel tricks, and PLSR can extract latent variables, none of these methods match the flexibility of deep architectures in capturing intricate, high-order interactions among spectral bands.

Second, although derivative transforms improve feature visibility, they also amplify noise and reduce low-frequency signals; traditional models may therefore underutilize useful information or be misled by amplified noise. Finally, all three algorithms remain susceptible to the “curse of dimensionality” in high-dimensional hyperspectral spaces, where meaningful variance can be masked by redundant or noisy bands. Even with smoothing or dimension reduction steps (such as PCA before PLSR), critical information may be lost. Consequently, while RF, SVR, and PLSR can perform adequately on raw spectra, their robustness and predictive power are limited when handling derivative-transformed inputs and the highly nonlinear relationships inherent in hyperspectral adulteration data.

3.3. Single-Channel Deep Learning Model

To address the limitations observed with traditional machine learning models, we implemented a single-channel CNN to learn complex, nonlinear relationships directly from the spectral data. Figure 5a–c display the training and validation loss curves for each channel—raw spectra, first-order (SG-1) derivative, and second-order (SG-2) derivative—using sparse categorical cross-entropy loss. Across all three channels, the validation loss decreases steadily during the early epochs, indicating that the model is successfully learning from the data and generalizing to unseen samples. Occasional upticks in validation loss suggest slight overfitting in later epochs, but overall, each channel exhibits a consistent downward trend. Figure 5d–f present scatter plots of the true versus predicted adulteration levels on the test set for the three channels. In Figure 5d, which uses raw spectra, the MSE is 0.018 and R² = 0.830; in Figure 5e, using SG-1 data, the MSE is 0.014 and R² = 0.882; and in Figure 5f, using SG-2 data, the MSE is 0.021 and R² = 0.832. These results show that the SG-1 channel achieved the best performance among the three single-channel variants, but none of the channels significantly outperformed the traditional models described in Section 3.2.

Although the single-channel CNN demonstrates the ability to capture nonlinear spectral features—particularly with the SG-1 derivative achieving the highest R²—the model still cannot fully leverage the diverse information present in the raw and derivative spectra. For instance, while the raw spectra channel retains intrinsic absorption characteristics governed by the Beer–Lambert law (essential for direct quantification), it remains highly susceptible to baseline drift, scattering effects, and random noise, which can obscure subtle adulteration signals. Conversely, the SG-1 channel enhances peak resolution and attenuates high-frequency noise, facilitating clearer identification of key spectral features—yet this processing can inadvertently filter out low-frequency information that may also correlate with adulterant concentration. The SG-2 channel excels at highlighting minor curvature changes in the spectrum, enabling the detection of fine-grained spectral variations; however, it also amplifies any residual noise, which can mislead the model when data quality is suboptimal or sample size is limited. As a result, each single-channel representation introduces its own trade-offs, and relying solely on one transformation leaves the CNN vulnerable to missing or misinterpreting relevant features. These channel-specific shortcomings help explain why no single preprocessing step yielded a markedly superior performance over the traditional models: each captures only part of the signal while potentially discarding or distorting other important information. To address this, we propose in Section 3.4 a multi-channel CNN architecture that concurrently ingests raw, SG-1, and SG-2 inputs, allowing the network to learn complementary features across channels and thereby improve overall prediction accuracy.

3.4. Multi-Channel Deep Learning Model

To overcome the limitations of single-channel approaches, we implemented a multi-channel CN that simultaneously processes the raw spectral data, first-order SG derivative, and second-order SG derivative. Figure 6a shows the training and validation loss curves for this three-branch architecture. As the number of epochs increases, the loss steadily decreases and eventually stabilizes, indicating that the model is effectively learning from the combined spectral inputs. Figure 6b plots the corresponding R² values on the training and validation sets, which consistently rise toward 1.0 with minimal fluctuation, further confirming the model’s stability and strong generalization ability. In Figure 6c, the scatter plot of true versus predicted adulteration levels on the test set demonstrates the high accuracy of this multi-channel method, achieving R² = 0.964 and MSE = 0.005.

The superior performance of the multi-channel CNN stems from several synergistic effects. Compared to the best-performing single-channel model (SG-1 input, R² = 0.882), the multi-channel CNN achieved a notably higher accuracy (R² = 0.964), demonstrating that combining raw and derivative spectra provides complementary and discriminative features. This ablation-style comparison confirms that assigning dedicated branches to each input type allows the network to capture richer spectral representations than any individual input alone. Specifically, the raw spectral branch preserves fundamental absorption peaks important for quantification, while the SG-1 branch enhances peak resolution and suppresses high-frequency noise. The SG-2 branch highlights subtle curvature changes that may indicate minor adulterants. By fusing these heterogeneous features—via concatenation of learned feature maps—the model constructs a more informative joint representation. Furthermore, the multi-branch architecture, equipped with convolutional layers, batch normalization, and dropout regularization, enables the extraction of nonlinear inter-channel relationships while preventing overfitting. Simultaneous training of all branches encourages gradient diversity and stabilizes learning. Together, these factors contribute to the model’s superior accuracy and robustness, as evidenced by its performance (R² = 0.964, MSE = 0.005) compared to both traditional methods and single-input CNNs.

The improved performance of the multi-channel CNN can be theoretically attributed to feature complementarity and multi-scale spectral representation. Derivative preprocessing techniques, such as SG-1 and SG-2, have been shown to enhance fine spectral details, improve peak resolution, and reduce baseline noise, thereby improving class separability in spectroscopic analysis [37,38]. In parallel, studies on deep learning for hyperspectral data have demonstrated that multi-branch architectures can effectively decouple hierarchical feature patterns, mitigate redundancy, and promote more robust generalization across complex datasets [39,40]. These findings align with our design, in which parallel branches separately process raw and derivative spectral features before fusion, enabling the network to jointly learn both fundamental absorption patterns and subtle variations indicative of adulteration. Collectively, these structural advantages underpin the strong performance observed in our model.

Traditional chemometric models applied to FT-NIR or HSI data, such as PLSR, SVR, and RF, typically achieve R² values in the range of 0.80–0.90 for adulteration detection in foods and herbal powders [14,16,35]. While these approaches can provide reasonable accuracy, they require extensive manual feature selection and remain vulnerable to high-dimensional redundancy. More recent one-dimensional CNNs applied to FT-NIR spectra of products like coffee have reported R² values exceeding 0.98 in controlled adulteration tasks [15], yet they utilize only a single spectral representation and often depend on data-specific augmentation strategies.

In comparison, our three-branch CNN fuses raw, first-order, and second-order derivative spectra in parallel and achieves R² = 0.964 (MSE = 0.005) on Anoectochilus roxburghii powder mixtures. This performance notably surpasses typical chemometric baselines and outperforms a single-channel CNN (R² ≈ 0.882) on the same dataset. By jointly capturing intrinsic absorption features, sharpened peak transitions, and subtle curvature variations, our multi-scale fusion approach effectively mitigates the curse of dimensionality and extracts nonlinear spectral–spatial interactions that shallow or single-branch networks miss. These findings echo recent reviews on deep-fusion spectroscopic methods, which highlight the advantages of multi-branch architectures for robust feature learning [41,42,43,44].

Despite these promising results, the present study has several limitations that must be acknowledged. First, the dataset was constructed using a single known adulterant (Ludisia discolor) under controlled mixing ratios. In real-world scenarios, adulteration practices may involve multiple counterfeit species, unknown contaminants, and complex physical mixtures that are not replicated in this study. Additionally, all samples were prepared and imaged under controlled laboratory conditions with uniform particle size and consistent illumination, which may not fully reflect the variability encountered in practical applications. These factors necessitate further validation using diverse, market-sourced samples to confirm the model’s robustness and adaptability. Moreover, while the multi-branch CNN architecture demonstrated superior prediction accuracy, its “black-box” nature limits interpretability—a critical consideration for quality control environments where traceability and decision transparency are highly valued. Future work should explore the integration of attention mechanisms or explainable AI techniques to identify and visualize the most diagnostic wavelengths contributing to adulteration detection. This enhancement will not only improve model transparency but also provide domain experts with actionable insights into the spectral signatures of counterfeit materials. Another limitation is the exclusive reliance on spectral data. Although hyperspectral imaging provides rich spectral-spatial information, incorporating complementary modalities—such as microscopic texture analysis, chemical fingerprinting, or laser-induced breakdown spectroscopy (LIBS)—could further enhance detection accuracy, particularly for visually indistinguishable adulterants.

Future research should explore multimodal data fusion strategies to establish a more holistic and robust detection framework. Finally, while the pixel-level richness of hyperspectral images significantly augments the effective dataset size, the number of physical samples in this study remains moderate. Expanding the dataset to include a broader range of adulteration scenarios, multiple counterfeit species, and diverse sample sources will be essential to further validate model generalizability. Additionally, cross-device and cross-site validation studies will be critical to ensure consistent performance across different hardware configurations and acquisition environments.

Despite these challenges, the improved accuracy and robustness of our multi-channel CNN model suggest clear potential for practical deployment in on-site quality control workflows. Embedding this framework within portable or benchtop hyperspectral imaging devices could enable rapid, non-destructive screening of powdered herbal products at production facilities, distribution centers, and marketplaces. Compared with conventional chemical assays, our method offers reagent-free operation, immediate results, and minimal operator intervention—features critical for high-throughput screening applications. To ensure robustness under real-world conditions, future work will focus on addressing environmental variability (e.g., lighting fluctuations, sample heterogeneity, inconsistent particle distribution) through adaptive preprocessing strategies, spectral calibration protocols, and model optimization for edge computing. Techniques such as model pruning, quantization, or deployment via TensorRT and ONNX frameworks may be employed to ensure computational efficiency in portable devices. Additionally, large-scale external validation using market-sourced powders with unknown adulterants and diverse textures will be pivotal in ensuring generalizability. These efforts will lay a solid foundation for transitioning our framework from laboratory research to practical applications in quality assurance systems, enabling reliable, real-time adulteration detection across the herbal medicine supply chain.

4. Conclusions

In this study, we evaluated hyperspectral imaging combined with deep learning for quantifying adulteration in Anoectochilus roxburghii powder. Traditional machine learning models (RF, SVR, and PLSR) achieved moderate performance (R² between 0.843 and 0.885) but proved limited by manual feature engineering, sensitivity to noise, and difficulty handling high-dimensional, nonlinear spectral data. Single-channel CNNs improved prediction accuracy (SG-1 input, R² = 0.882), yet each individual input type sacrificed certain spectral characteristics. To address these shortcomings, we developed a three-branch, multi-channel CNN that simultaneously processes raw spectra, SG-1, and SG-2 inputs. By fusing complementary features—fundamental absorption peaks, enhanced peak resolution, and subtle curvature variations—the multi-channel model achieved superior accuracy (R² = 0.964, MSE = 0.005) and demonstrated robust generalization. These results confirm that integrating multiple spectral transformations within a unified deep learning framework maximizes feature extraction and significantly enhances adulteration detection performance. Future work will extend this approach to the authentication of other traditional Chinese medicinal powders and food products with similar spectral characteristics. Further improvements may involve the integration of attention-based mechanisms and the development of portable or real-time hyperspectral systems for on-site quality control. Validation using larger and multi-source datasets will also be pursued to assess generalizability and practical deployment potential. These efforts are expected to support the transition of our method from controlled experimental settings to practical implementation in quality inspection workflows.