Self-Adjusting Look-Ahead Distance of Precision Path Tracking for High-Clearance Sprayers in Field Navigation
Abstract
1. Introduction
2. Materials and Methods
2.1. The Platform of the High-Clearance Sprayer
2.2. The Mathematical Model for the High-Clearance Sprayers
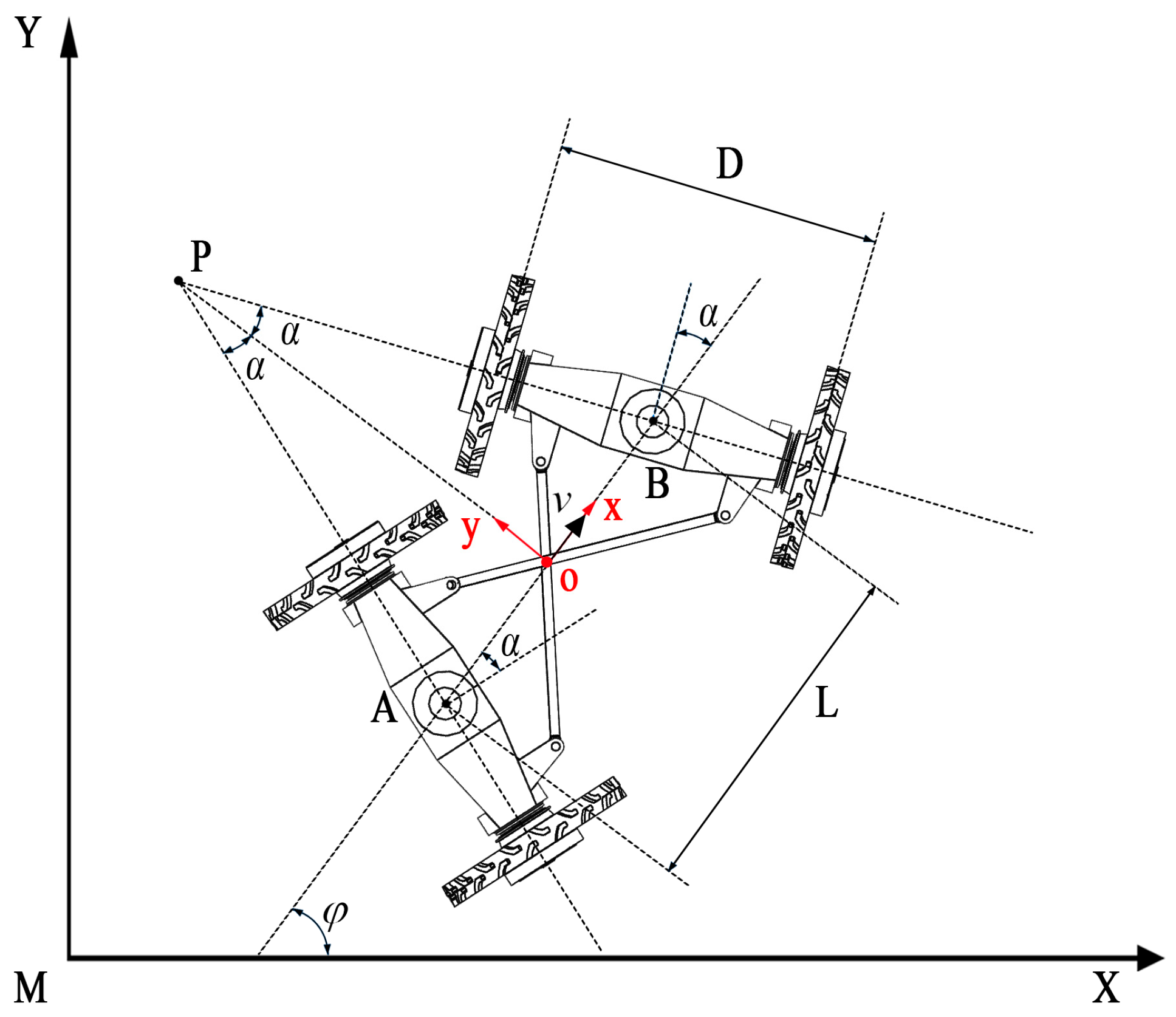
2.2.1. Kinematic Modeling of the Chassis
2.2.2. Pure Pursuit Strategy Applied to the Chassis
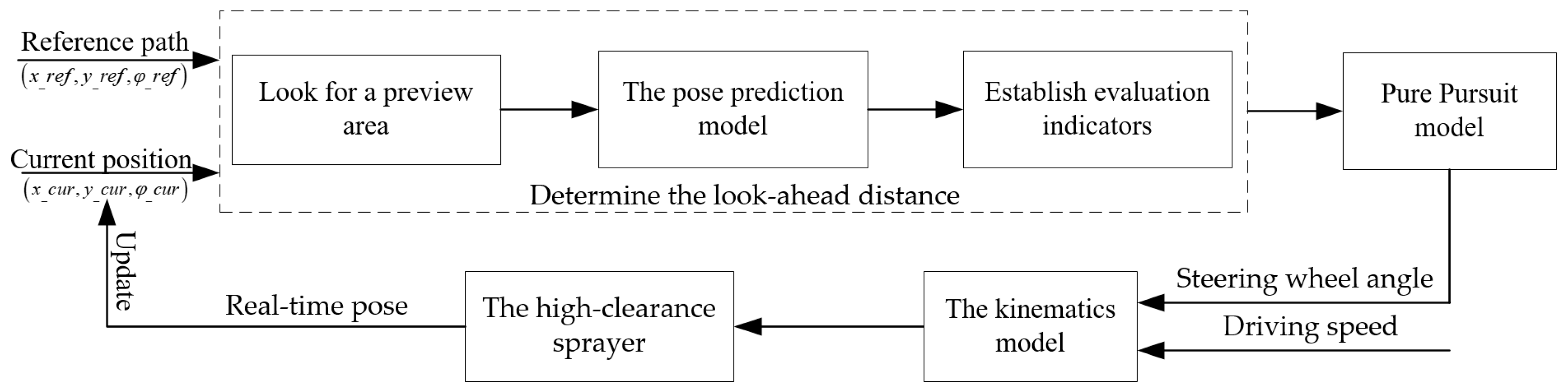
2.3. Path Tracking Strategy Based on Self-Adjusting Look-Ahead Distance
2.3.1. Look for the Preview Area
2.3.2. The Model for Predicting the Pose
2.3.3. Establishment of Error Evaluation
3. Results and Discussion
3.1. Model-Based Simulation Verification
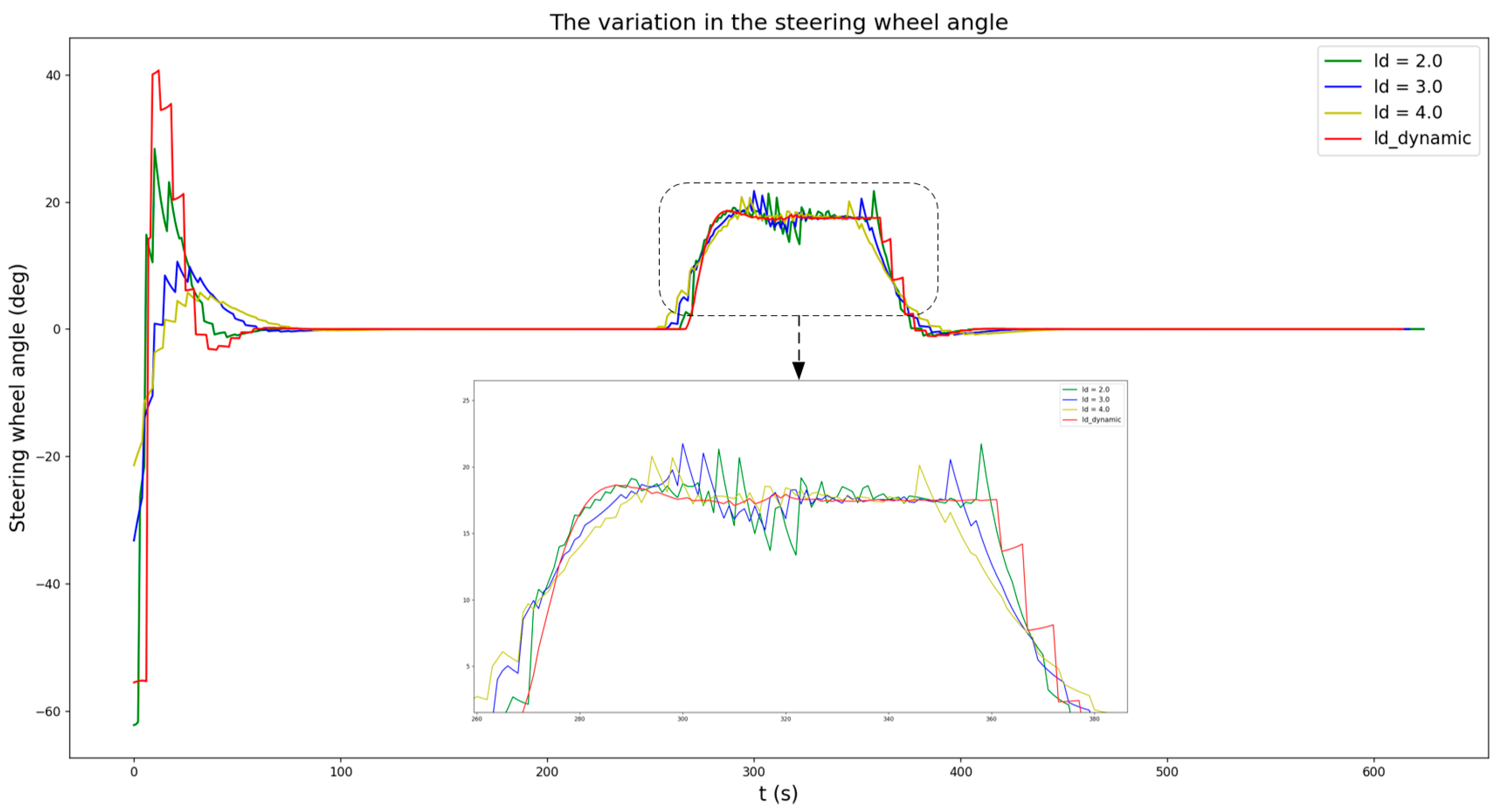
3.1.1. Algorithm Simulation Test
3.1.2. Analysis of the Algorithm Simulation
3.2. Path Tracking Tests in the Field
3.2.1. The Experimental Site of the Field Trials
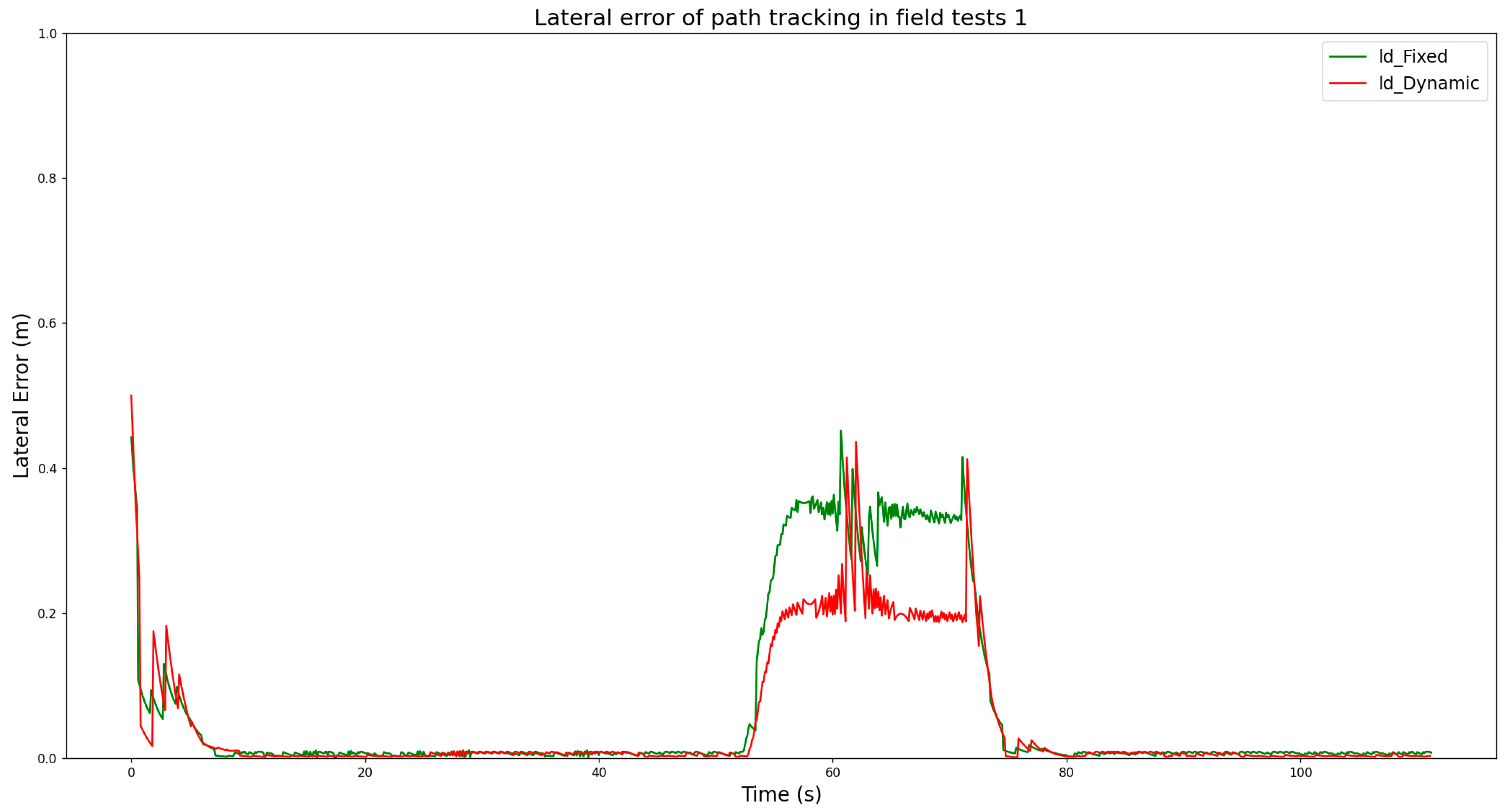
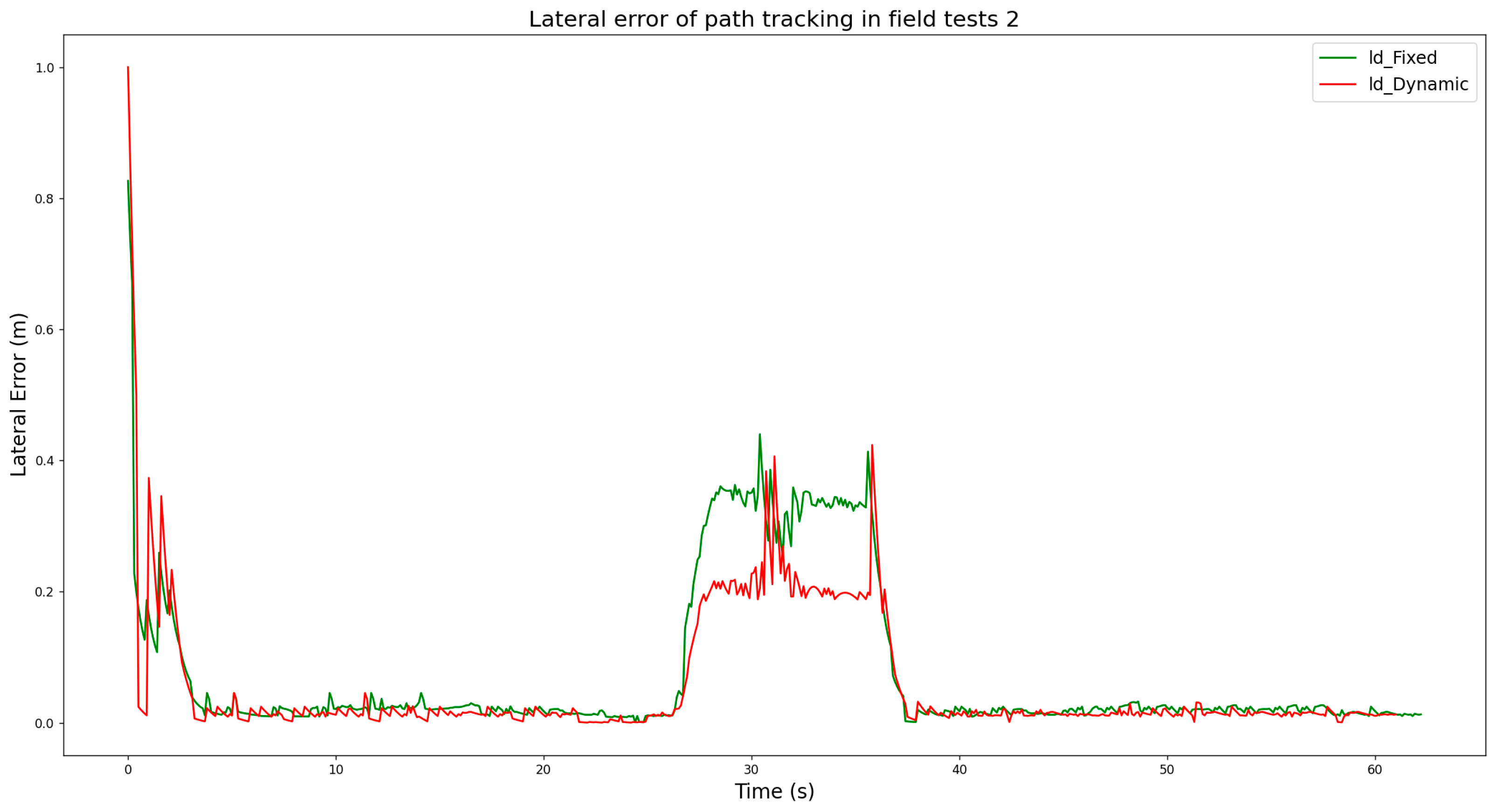
3.2.2. The Analysis and Results of the Field Tests
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shen, Y.; Zhang, Y.; Liu, H. Review of Automatic Control Technology for Agricultural Equipment. Trans. Chin. Soc. Agric. Eng. 2023, 54, 1–18. [Google Scholar]
- Zhang, M.; Ji, Y.; Li, S. Research progress of agricultural machinery navigation technology. Trans. Chinese Soc. Agric. Eng. 2020, 51, 1–18. [Google Scholar]
- Li, H.; Chen, L.; Zhang, Z. A Study on the Utilization Rate and Influencing Factors of Small Agricultural Machinery: Evidence from 10 Hilly and Mountainous Provinces in China. Agriculture 2023, 13, 51. [Google Scholar] [CrossRef]
- Li, C.; Wu, J.; Pan, X.; Dou, H.; Zhao, X.; Yang, S.; Zhai, C. Design and Experiment of a Breakpoint Continuous Spraying System for Automatic-Guidance Boom Sprayers. Agriculture 2023, 27, 13. [Google Scholar] [CrossRef]
- Jin, Y.; Liu, J.; Xu, Z. Development status and trend of agricultural robot technology. Int. J. Agric. Biol. Eng. 2021, 14, 1–19. [Google Scholar] [CrossRef]
- Chao, S. Current Status and Development Trends of Agricultural Plant Protection Mechanization. Agric. Equip. Technol. 2020, 46, 7–8. [Google Scholar]
- Liu, Z.; Zhang, Z.; Luo, X.; Wang, H.; Huang, P. Design of automatic navigation operation system for Lovol ZP9500 high clearance boom sprayer based on GNSS. Trans. Chin. Soc. Agric. Eng. 2018, 34, 15–21. [Google Scholar]
- Jing, L.; Zhang, Y.; Shen, Y.; He, S.; Liu, H. Adaptive Trajectory Tracking Control of 4WID High Clearance Unmanned Sprayer. Trans. Chin. Soc. Agric. Eng. 2021, 52, 408–416. [Google Scholar]
- Zhang, C.; Gao, G.; Zhao, C.; Li, L.; Li, C.; Chen, X. Research on 4WS agricultural machine path tracking algorithm based on fuzzy control pure tracking model. Machines 2022, 10, 597. [Google Scholar] [CrossRef]
- Shen, Y.; He, S.; Liu, H.; Cui, Y. Design and experiment of self-steering electric chassis structure of high clearance sprayer. Trans. Chin. Soc. Agric. Eng. 2020, 51, 385–392, 402. [Google Scholar]
- Cui, B.; Cui, X.; Wei, X.; Zhu, Y.; Ma, Z.; Zhao, Y.; Liu, Y. Design and Testing of a Tractor Automatic Navigation System Based on Dynamic Path Search and a Fuzzy Stanley Model. Agriculture 2024, 14, 2136. [Google Scholar] [CrossRef]
- Chai, X.; Hu, J.; Ma, T.; Liu, P.; Shi, M.; Zhu, L.; Zhang, M.; Xu, L. Construction and Characteristic Analysis of Dynamic Stress Coupling Simulation Models for the Attitude-Adjustable Chassis of a Combine Harvester. Agronomy 2024, 14, 1874. [Google Scholar] [CrossRef]
- Li, J.; Shang, Z.; Li, R.; Cui, B. Adaptive Sliding Mode Path Tracking Control of Unmanned Rice Transplanter. Agriculture 2022, 12, 1225. [Google Scholar] [CrossRef]
- Kong, F.; Qiu, B.; Dong, X.; Yi, K.; Wang, Q.; Jiang, C.; Zhang, X.; Huang, X. Design and Development of a Side Spray Devicefor UAVs to Improve Spray Coverage in Obstacle Neighborhoods. Agronomy 2024, 14, 2002. [Google Scholar] [CrossRef]
- Li, Z.Q.; Chen, L.Q.; Zheng, Q.; Dou, X.Y.; Yang, L. Control of a path-following caterpillar robot based on a sliding mode variable structure algorithm. Biosyst. Eng. 2019, 186, 293–306. [Google Scholar] [CrossRef]
- Wang, H.; Wang, G.; Luo, X.; Zhang, Z.; Gao, Y.; He, J.; Yue, B. Control method of agricultural machinery navigation path tracking based on pre-aiming tracking model. Trans. CSAE 2019, 35, 11–19. [Google Scholar]
- Cui, B.; Sun, Y.; Ji, F.; Wei, X.; Zhu, Y.; Zhang, S. Study on whole field path tracking of agricultural machinery based on fuzzy Stanley model. Trans. CSAM 2022, 53, 43–48, 88. [Google Scholar]
- Heredia, G.; Ollero, A. Stability of autonomous vehicle path tracking with pure delays in the control loop. Adv. Rob. 2007, 21, 23–50. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, J.; Liu, Y.; Zhang, T.; Yan, M.; Chen, J.; Zhou, C.; Hu, J.; Chen, X. An Ultrasonic Ridge-Tracking Method Based on Limiter Sliding Window Filter and Fuzzy Pure Pursuit Control for Ridge Transplanter. Agriculture 2024, 14, 1713. [Google Scholar] [CrossRef]
- Iida, M.; Uchida, T.; Ishibashi, Y.; Saito, K.; Suguri, S.; Masuda, K. Path-following control of a head-feeding combine robot. Eng. Agric. Environ. Food 2013, 6, 61–68. [Google Scholar] [CrossRef]
- Kurita, H.; Iida, M.; Cho, W.; Suguri, M. Rice autonomous harvesting: Operation framework. J. Field Rob. 2017, 34, 1084–1099. [Google Scholar] [CrossRef]
- Lu, E.; Xue, J.; Chen, T.; Jiang, S. Robust Trajectory Tracking Control of an Autonomous Tractor-Trailer Considering Model Parameter Uncertainties and Disturbances. Agriculture 2023, 13, 869. [Google Scholar] [CrossRef]
- Li, G.; Ma, X.; Li, Y. Adaptive sliding mode control based on time-delay estimation for underactuated 7-DOF tower cranes. IEEE Trans. Syst. Man Cybern. Syst. 2025; early access. [Google Scholar]
- Li, G.; Ma, X.; Li, Y. Robust command shaped vibration control for stacker crane subject to parameter uncertainties and external disturbances. IEEE Trans. Ind. Electron. 2024, 71, 14740–14752. [Google Scholar] [CrossRef]
- Huang, Y.; Tian, Z.; Jiang, Q.; Xu, J. Path tracking based on improved pure pursuit model and PID. In Proceedings of the 2020 IEEE 2nd International Conference on Civil Aviation Safety and Information Technology (ICCASIT), Chengdu, China, 14–16 October 2020; pp. 359–364. [Google Scholar]
- Macenski, S.; Singh, S.; Martin, F.; Ginés, J. Regulated pure pursuit for robot path tracking. Auton. Robot. 2023, 47, 685–694. [Google Scholar] [CrossRef]
- Choi, W.Y.; Chung, C.C. Optimizing look-ahead distance for vehicle lateral control: A controller-adaptive approach. IEEE Trans. Intell. Veh. 2024, 4, 1–12. [Google Scholar] [CrossRef]
- Kamal, M.A.S.; Bakibillah, A.S.M.; Hayakawa, T.; Yamada, K. Cooperative look-ahead lane change system for improving driving intelligence of automated vehicles in critical scenarios. IEEE Trans. Intell. Veh. 2024, 9, 5876–5888. [Google Scholar] [CrossRef]
- Zhang, S.; Wei, X.; Liu, C.; Ge, J.; Cui, X.; Wang, F.; Wang, A.; Chen, W.-M. Adaptive path tracking and control system for unmanned crawler harvesters in paddy fields. Comput. Electron. Agric. 2024, 210, 109878. [Google Scholar] [CrossRef]
- Li, G.; Wang, Y.; Guo, L.; Tong, J. Improved pure pursuit algorithm for rice transplanter path tracking. Trans. CSAM 2018, 49, 21–26. [Google Scholar]
- Yang, Y.; Liu, Y.; Wang, Y.; Zhang, G.; Cui, X.; Qiao, Y.; Xie, C. An optimal goal point determination algorithm for automatic navigation of agricultural machinery: Improving the tracking accuracy of the Pure Pursuit algorithm. Comput. Electron. Agric. 2022, 196, 106760. [Google Scholar] [CrossRef]
- Fu, X.; Han, Z.; Han, K.; Feng, X.; Huang, T. Improved pure pursuit algorithm for path tracking of wheeled harvesters based on particle swarm optimization. J. Agric. Eng. Res. 2023, 27, 1–10. [Google Scholar]
- Zhang, H.Q.; Wang, G.D.; Lv, Y.F.; Qi, C.L.; Liu, L.; Gong, J.L. Research on agricultural machinery path tracking algorithm based on improved pure pursuit model. Trans. CSAM 2020, 51, 18–25. [Google Scholar]
- MathWorks. (n.d.). Pure Pursuit Controller—MATLAB & Simulink. MathWorks Documentation. Available online: https://de.mathworks.com/help/robotics/ug/pure-pursuit-controller.html (accessed on 21 May 2025).
- Yang, H.; Huang, J.; Li, P.; Han, Z.H. Driver Model Based on Path Preview. Automob. Technol. 2019, 2, 7–13. [Google Scholar]
- Luo, Y.; Wei, L.; Xu, L.; Zhang, Q. Stereo-vision-based multi-crop harvesting edge detection for precise automatic steering of combine harvester. Biosyst. Eng. 2022, 215, 115–128. [Google Scholar] [CrossRef]
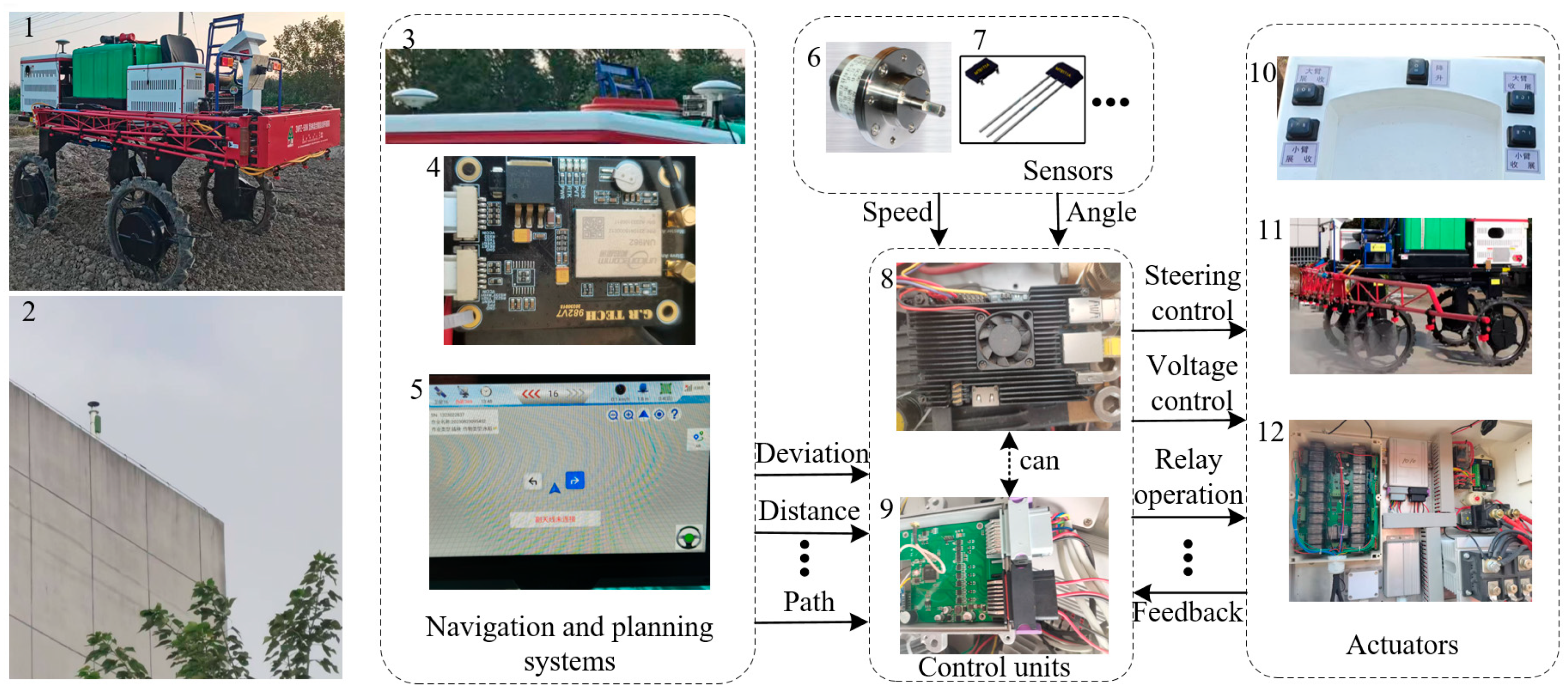




| Parameters | Unit | Value |
|---|---|---|
| Overall size | mm | 3080 × 11,200 × 2400 |
| Weight | kg | 1680 |
| Wheelbase | mm | 1680 |
| Track width | mm | 2200 |
| Ground clearance | m | 1.1 |
| Maximum steering angle | ° | −40~40 |
| Minimum turning radius | m | 1.2 |
| Speed | m/s | 0.4~2 |
| Symbol | Meaning |
|---|---|
| R | Instantaneous steering radius |
| A | Center point of front axle |
| B | Center point of rear axle |
| O | Turning center of the high-clearance sprayer |
| G | Tracking waypoints along the path |
| P | Instantaneous center of rotation |
| L | Wheelbase of the high-clearance sprayer |
| Angle between the direction to the target point | |
| The steering angle of the high-clearance sprayer | |
| Turning curvature of the high-clearance sprayer | |
| Lateral error based on the current position | |
| Heading angle based on the current position | |
| Look-ahead distance |
| Look-Ahead Distance | The Average Value of Lateral Error (m) | Variance (m) |
|---|---|---|
| ld = 2.0 m | 0.075 | 0.033 |
| ld = 3.0 m | 0.150 | 0.076 |
| ld = 4.0 m | 0.256 | 0.214 |
| ld_dynamic | 0.072 | 0.031 |
| Look-Ahead Distance | The Average Value of Lateral Error (m) | The Max Lateral Error (m) |
|---|---|---|
| ld = 2.0 m | 0.211 | 0.419 |
| ld = 3.0 m | 0.476 | 0.945 |
| ld = 4.0 m | 0.847 | 1.599 |
| ld_dynamic | 0.145 | 0.417 |
| Ref Path | Path Tracking Algorithm | Average Value of Lateral Error (m) | Maximum Lateral Error (m) | Variance (m) |
|---|---|---|---|---|
| Curve line | Fixed look-ahead | 0.212 | 0.452 | 0.021 |
| Dynamic look-ahead | 0.143 | 0.436 | 0.011 |
| Ref Path | Path Tracking Algorithm | Average Value of Lateral Error (m) | Maximum Lateral Error (m) | Variance (m) |
|---|---|---|---|---|
| Curve line | Fixed look-ahead | 0.198 | 0.439 | 0.023 |
| Dynamic look-ahead | 0.137 | 0.423 | 0.011 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhang, B.; Du, X.; Chen, H.; Zhu, T.; Wu, C. Self-Adjusting Look-Ahead Distance of Precision Path Tracking for High-Clearance Sprayers in Field Navigation. Agronomy 2025, 15, 1433. https://doi.org/10.3390/agronomy15061433
Wang X, Zhang B, Du X, Chen H, Zhu T, Wu C. Self-Adjusting Look-Ahead Distance of Precision Path Tracking for High-Clearance Sprayers in Field Navigation. Agronomy. 2025; 15(6):1433. https://doi.org/10.3390/agronomy15061433
Chicago/Turabian StyleWang, Xu, Bo Zhang, Xintong Du, Huailin Chen, Tianwen Zhu, and Chundu Wu. 2025. "Self-Adjusting Look-Ahead Distance of Precision Path Tracking for High-Clearance Sprayers in Field Navigation" Agronomy 15, no. 6: 1433. https://doi.org/10.3390/agronomy15061433
APA StyleWang, X., Zhang, B., Du, X., Chen, H., Zhu, T., & Wu, C. (2025). Self-Adjusting Look-Ahead Distance of Precision Path Tracking for High-Clearance Sprayers in Field Navigation. Agronomy, 15(6), 1433. https://doi.org/10.3390/agronomy15061433







