Adaptive SOM-GA Hybrid Algorithm for Grasping Sequence Optimization in Apple Harvesting Robots: Enhancing Efficiency in Open-Field Orchards
Abstract
1. Introduction
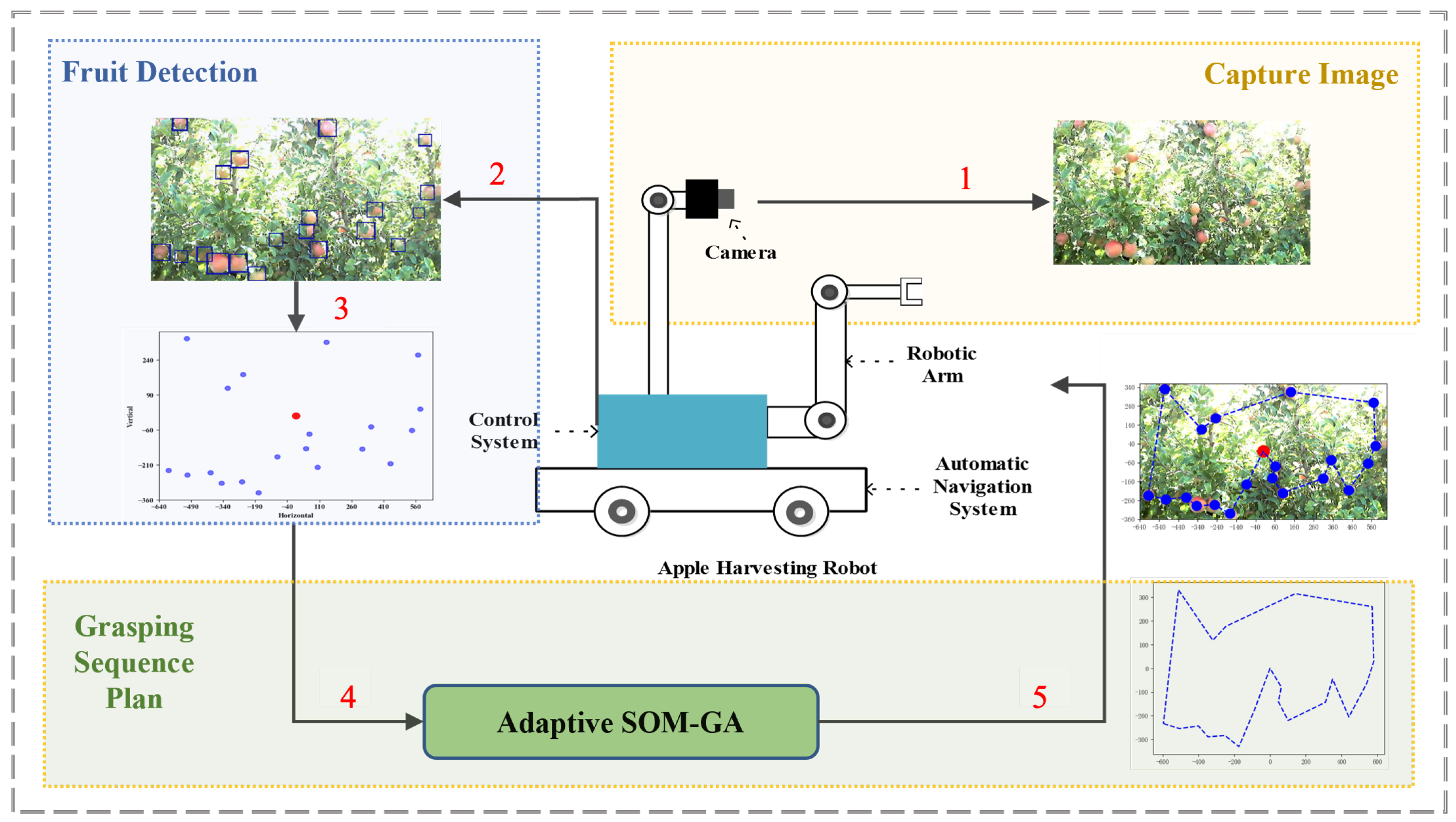
2. Material and Methods
2.1. Formalization and Data Preparation
2.1.1. Problem Statement
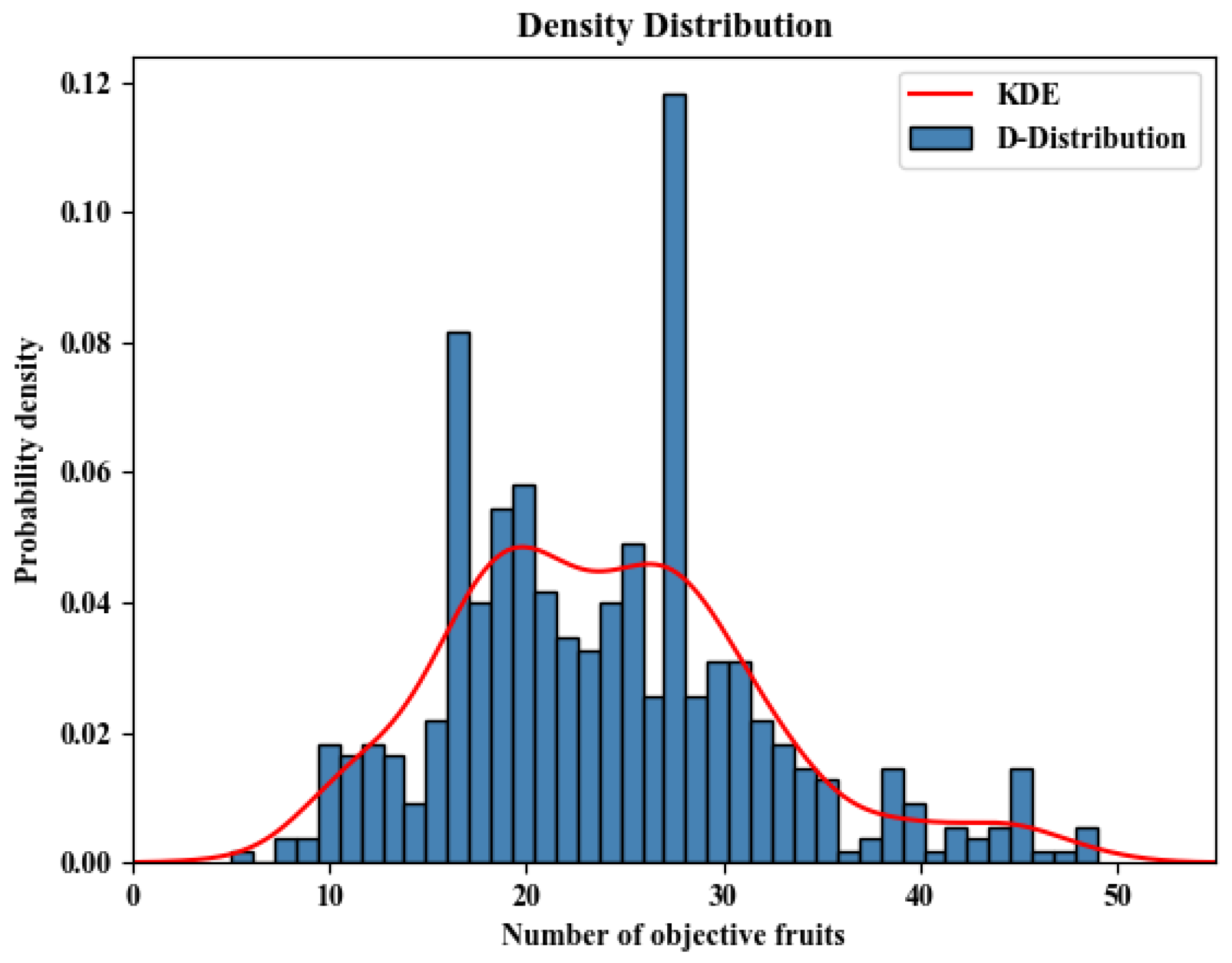
2.1.2. Data Collection and Analysis
- Customized optimization for high-probability fruit density ranges;
- Dynamic adjustment of planning parameters based on empirical distributions;
- Efficient computation through focused analysis of predominant operational scenarios.
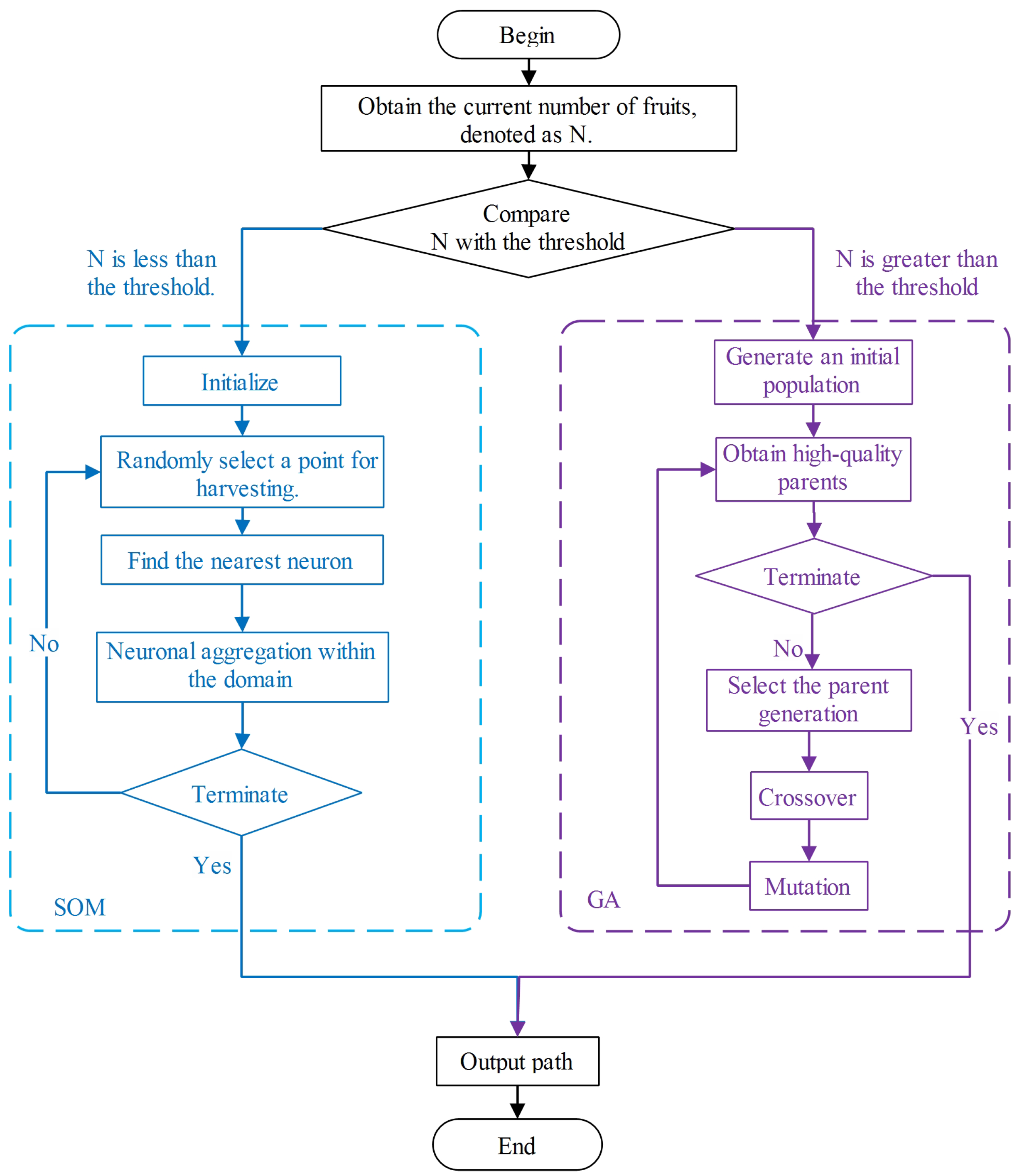
2.2. Adaptive SOM-GA Algorithm
- SOM phase (): initializes neurons with Gaussian neighborhood updates (, ).
- GA phase (): employs roulette-wheel selection, two-point crossover (probability = 0.8), and swap mutation (probability = 0.05) within a population of 200 individuals.
| Algorithm 1 Adaptive SOM-GA Path Planning |
|
2.2.1. Threshold Selection and Setting
2.2.2. SOM Algorithm
- Initialization: begin with numbers to distribute the neurons evenly around the coordinates of the points to be harvested.
- Selection of harvesting point: randomly select a harvesting point, .
- Neuron positioning: identify the neuron closest to the selected harvesting point, . Establish a Gaussian distribution and move towards the selected neuron.
- Iteration check: determine if the iteration count has reached the termination condition. If the termination condition is met, identify the neuron closest to each point to be harvested and output the sequence of harvesting points according to the order of the neurons. If the termination condition is not met, return to step 2.
2.2.3. GA Algorithm Strategy
- Initialization and fitness calculation: define the fitness function , where M is the population size. Calculate the probability of each individual being selected for the next generation defined in Equation (12).
- Cumulative probability calculation: after obtaining the probability of each individual being selected, calculate the corresponding cumulative probability defined in Equation (13).Here, represents the cumulative probability of .
- Random number generation: generate a random number, r, within the interval .
- Selection based on cumulative probability: if , select individual 1; otherwise, select individual k, such that .
- Repetition: repeat steps (3) and (4) M times, applying this operation to the entire population.
- Population initialization: initialize the population with random solutions;
- Fitness calculation: calculate the fitness of each individual; the shorter the distance is, the higher is the fitness;
- Termination check: if the iteration limit is reached, the algorithm ends and outputs the current optimal solution. If not, proceed to generate a new population;
- Parent selection: select high-quality parents using the roulette wheel method;
- Crossover: choose two individuals from the population and perform crossover with a certain probability to obtain a new population;
- Mutation: perform mutation on the results from step 5, which involves randomly selecting two positions to swap and moving one of the elements to the end.
3. Results
3.1. Single-Case Result
3.1.1. Performance Analysis When
3.1.2. Performance Analysis When the Number of Fruits Is Less than the Threshold
3.2. Multiple-Case Results
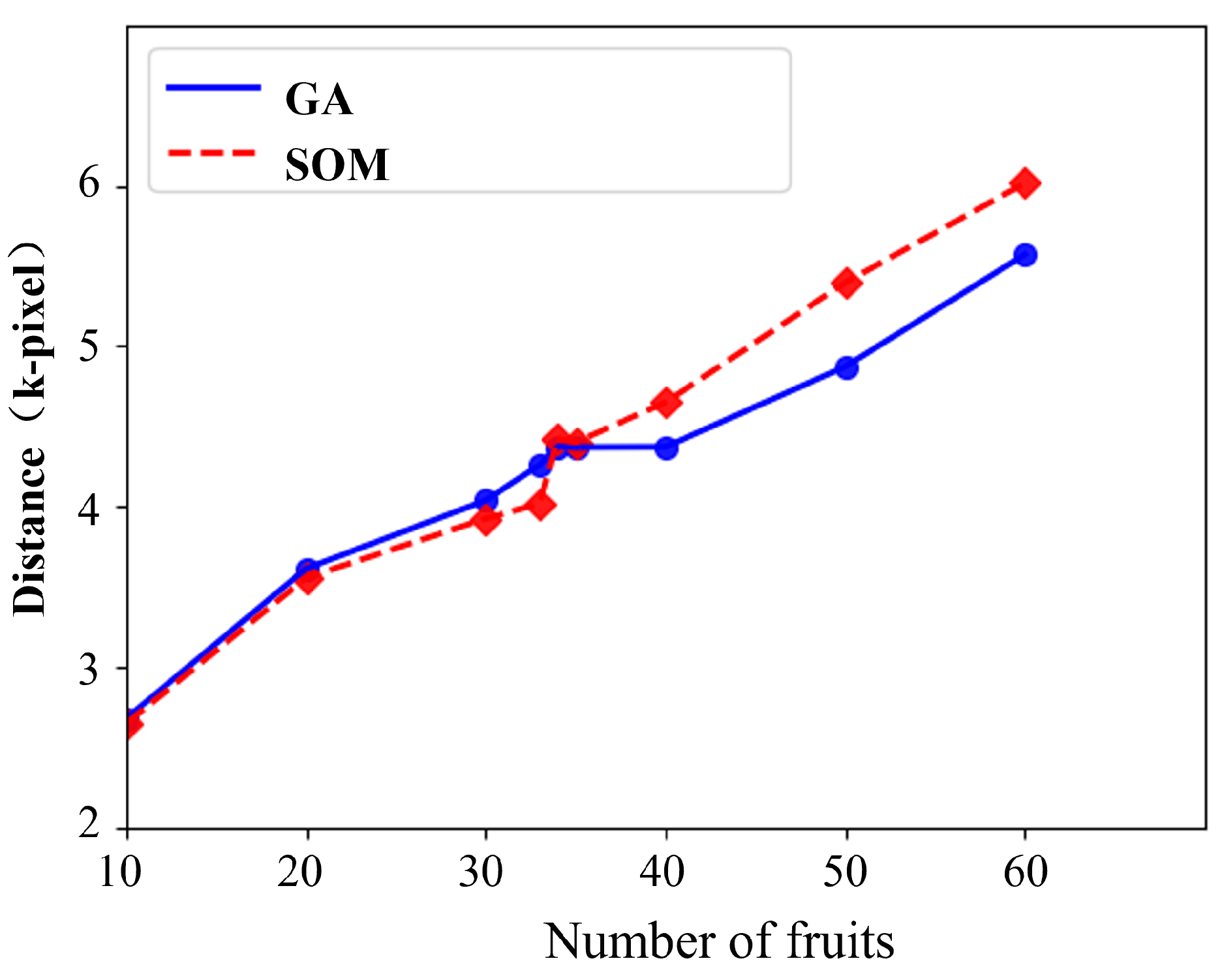
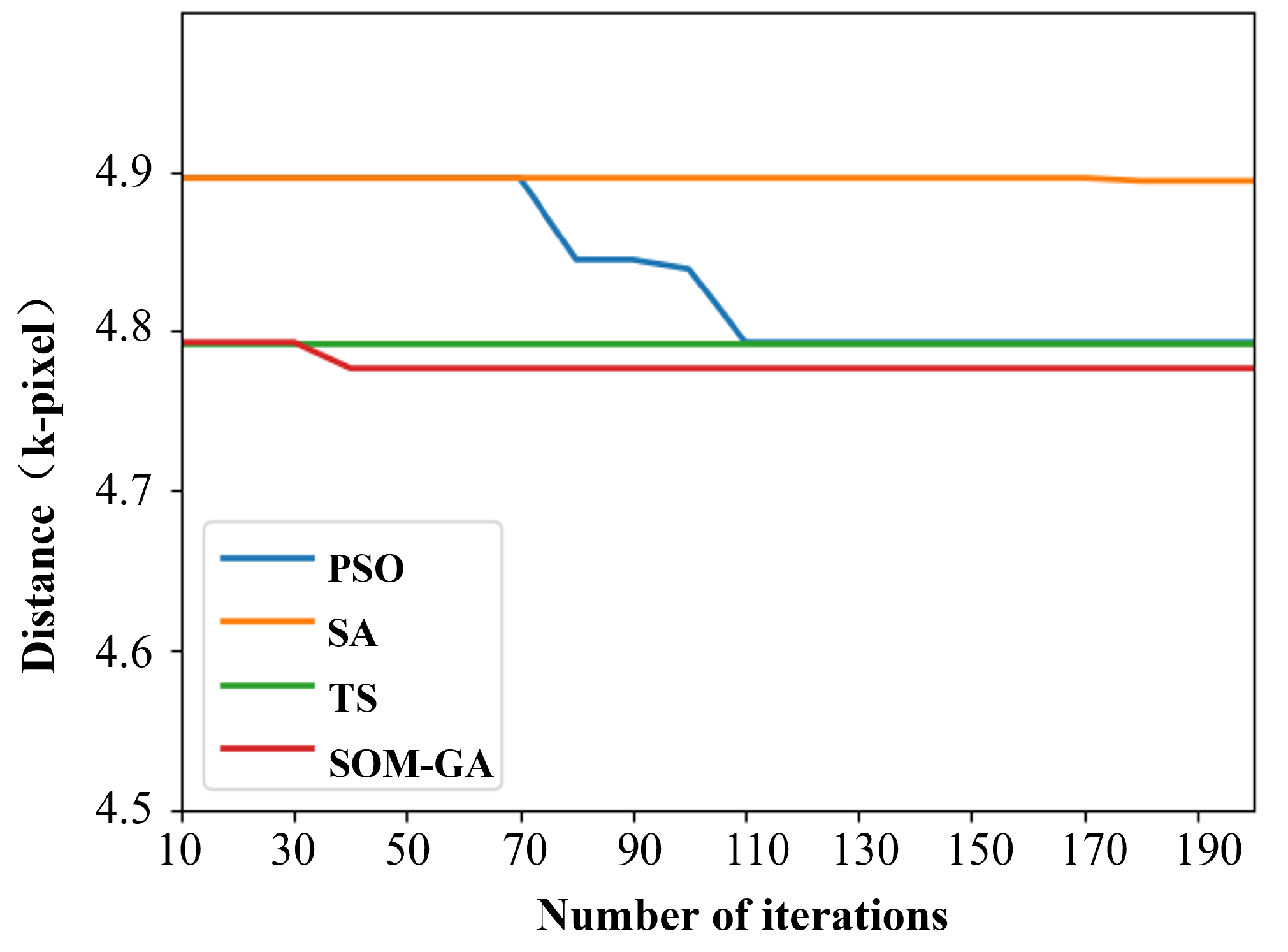
3.3. Convergence Comparison Experiment
3.4. Threshold Sensitivity Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- FAO. Revealing the True Cost of Food to Transform Agrifood Systems; FAO: Rome, Italy, 2023. [Google Scholar]
- Łakomiak, A.; Zhichkin, K.A. Economic aspects of fruit production: A case study in Poland. BIO Web Conf. 2020, 17, 00236. [Google Scholar]
- Bac, C.W.; Van Henten, E.J.; Hemming, J.; Edan, Y. Harvesting robots for high-value crops: State-of-the-art review and challenges ahead. J. Field Robot. 2014, 31, 888–911. [Google Scholar] [CrossRef]
- Hemming, J.; Bac, C.W.; van Tuijl, B.A.; Barth, R.; Bontsema, J.; Pekkeriet, E.; Van Henten, E. A robot for harvesting sweet-pepper in greenhouses. In Proceedings of the International Conference of Agricultural Engineering, Zurich, Switzerland, 6–10 July 2014. [Google Scholar]
- Jia, W.; Zhang, Y.; Lian, J.; Zheng, Y.; Zhao, D.; Li, C. Apple harvesting robot under information technology: A review. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420925310. [Google Scholar] [CrossRef]
- Edan, Y.; Flash, T.; Peiper, U.M.; Shmulevich, I.; Sarig, Y. Near-minimum-time task planning for fruit-picking robots. IEEE Trans. Robot. Autom. 1991, 7, 48–56. [Google Scholar] [CrossRef]
- Mann, M.P.; Zion, B.; Shmulevich, I.; Rubinstein, D.; Linker, R. Combinatorial optimization and performance analysis of a multi-arm cartesian robotic fruit harvester—Extensions of graph coloring. J. Intell. Robot. Syst. 2016, 82, 399–411. [Google Scholar] [CrossRef]
- Zion, B.; Mann, M.; Levin, D.; Shilo, A.; Rubinstein, D.; Shmulevich, I. Harvest-order planning for a multiarm robotic harvester. Comput. Electron. Agric. 2014, 103, 75–81. [Google Scholar] [CrossRef]
- Qu, H.R.; Su, W.H. Deep Learning-Based Weed–Crop Recognition for Smart Agricultural Equipment: A Review. Agronomy 2024, 14, 363. [Google Scholar] [CrossRef]
- Fu, H.; Li, Z.; Zhang, W.; Feng, Y.; Zhu, L.; Fang, X.; Li, J. Research on Path Planning of Agricultural UAV Based on Improved Deep Reinforcement Learning. Agronomy 2024, 14, 2669. [Google Scholar] [CrossRef]
- Hu, M.; Huang, Q.; Cai, J.; Chen, Y.; Li, J.; Shi, L. HPS-RRT*: An Improved Path Planning Algorithm for a Nonholonomic Orchard Robot in Unstructured Environments. Agronomy 2025, 15, 712. [Google Scholar] [CrossRef]
- Wang, J.; Zhai, Z.; Xu, G.; Zhang, R.; Zhang, X.; Hu, R. Optimizing Sampling Points and Path Planning for Soil Monitoring in Agricultural Land. Agronomy 2024, 14, 2947. [Google Scholar] [CrossRef]
- Latombe, J.C.; Lazanas, A.; Shekhar, S. Robot motion planning with uncertainty in control and sensing. Artif. Intell. 1991, 52, 1–47. [Google Scholar] [CrossRef]
- De Giacomo, G.; Iocchi, L.; Nardi, D.; Rosati, R. Planning with sensing for a mobile robot. In Proceedings of the European Conference on Planning, Toulouse, France, 1 September 1997; pp. 156–168. [Google Scholar]
- LaValle, S.M.; Hutchinson, S.A. An objective-based framework for motion planning under sensing and control uncertainties. Int. J. Robot. Res. 1998, 17, 19–42. [Google Scholar] [CrossRef]
- Burns, B.; Brock, O. Sampling-based motion planning with sensing uncertainty. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 3313–3318. [Google Scholar]
- Mann, M.P.; Zion, B.; Rubinstein, D.; Linker, R.; Shmulevich, I. Minimum time kinematic motions of a cartesian mobile manipulator for a fruit harvesting robot. J. Dyn. Syst. Meas. Control. 2014, 136, 051009. [Google Scholar] [CrossRef]
- Duggal, V.; Sukhwani, M.; Bipin, K.; Reddy, G.S.; Krishna, K.M. Plantation monitoring and yield estimation using autonomous quadcopter for precision agriculture. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 5121–5127. [Google Scholar]
- Edan, Y.; Rogozin, D.; Flash, T.; Miles, G.E. Robotic melon harvesting. IEEE Trans. Robot. Autom. 2000, 16, 831–835. [Google Scholar] [CrossRef]
- Van Henten, E.; Van’t Slot, D.; Hol, C.; Van Willigenburg, L. Optimal manipulator design for a cucumber harvesting robot. Comput. Electron. Agric. 2009, 65, 247–257. [Google Scholar] [CrossRef]
- Schuetz, C.; Baur, J.; Pfaff, J.; Buschmann, T.; Ulbrich, H. Evaluation of a direct optimization method for trajectory planning of a 9-DOF redundant fruit-picking manipulator. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2660–2666. [Google Scholar]
- Cruz-Ancona, C.D.; Martínez-Guerra, R.; Pérez-Pinacho, C.A. Generalized multi-synchronization: A leader-following consensus problem of multi-agent systems. Neurocomputing 2017, 233, 52–60. [Google Scholar] [CrossRef]
- Williams, H.; Ting, C.; Nejati, M.; Jones, M.H.; Penhall, N.; Lim, J.; Seabright, M.; Bell, J.; Ahn, H.S.; Scarfe, A.; et al. Improvements to and large-scale evaluation of a robotic kiwifruit harvester. J. Field Robot. 2020, 37, 187–201. [Google Scholar] [CrossRef]
- Somhom, S.; Modares, A.; Enkawa, T. Competition-based neural network for the multiple travelling salesmen problem with minmax objective. Comput. Oper. Res. 1999, 26, 395–407. [Google Scholar] [CrossRef]
- Laporte, G. The traveling salesman problem: An overview of exact and approximate algorithms. Eur. J. Oper. Res. 1992, 59, 231–247. [Google Scholar] [CrossRef]
- Lawler, E.L. The traveling salesman problem: A guided tour of combinatorial optimization. In Wiley-Interscience Series in Discrete Mathematics; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 1985. [Google Scholar]
- Rosenkrantz, D.J.; Stearns, R.E.; Lewis, P.M., II. An analysis of several heuristics for the traveling salesman problem. SIAM J. Comput. 1977, 6, 563–581. [Google Scholar] [CrossRef]
- Papadimitriou, C.H. The Euclidean travelling salesman problem is NP-complete. Theor. Comput. Sci. 1977, 4, 237–244. [Google Scholar] [CrossRef]
- Helsgaun, K. An effective implementation of the Lin–Kernighan traveling salesman heuristic. Eur. J. Oper. Res. 2000, 126, 106–130. [Google Scholar] [CrossRef]
- Kurtser, P.; Edan, Y. Planning the sequence of tasks for harvesting robots. Robot. Auton. Syst. 2020, 131, 103591. [Google Scholar] [CrossRef]
- Cao, H.; Wang, H.; Li, Y.; Hamani, A.K.M.; Zhang, N.; Wang, X.; Gao, Y. Evapotranspiration partition and dual crop coefficients in apple orchard with dwarf stocks and dense planting in arid region, Aksu oasis, southern Xinjiang. Agriculture 2021, 11, 1167. [Google Scholar] [CrossRef]
- Jamar, L.; Mostade, O.; Huyghebaert, B.; Pigeon, O.; Lateur, M. Comparative performance of recycling tunnel and conventional sprayers using standard and drift-mitigating nozzles in dwarf apple orchards. Crop. Prot. 2010, 29, 561–566. [Google Scholar] [CrossRef]
- Weber, M. Optimizing the tree density in apple orchards on dwarf rootstocks. In Proceedings of the VII International Symposium on Orchard and Plantation Systems 557, Nelson, New Zealand, 30 January–5 February 2000; pp. 229–234. [Google Scholar]
- Jia, W.; Mou, S.; Wang, J.; Liu, X.; Zheng, Y.; Lian, J.; Zhao, D. Fruit recognition based on pulse coupled neural network and genetic Elman algorithm application in apple harvesting robot. Int. J. Adv. Robot. Syst. 2020, 17, 1729881419897473. [Google Scholar] [CrossRef]
- Jia, W.; Tian, Y.; Luo, R.; Zhang, Z.; Lian, J.; Zheng, Y. Detection and segmentation of overlapped fruits based on optimized mask R-CNN application in apple harvesting robot. Comput. Electron. Agric. 2020, 172, 105380. [Google Scholar] [CrossRef]
- Kim, M.; Park, J. Learning collaborative policies to solve np-hard routing problems. Adv. Neural Inf. Process. Syst. 2021, 34, 10418–10430. [Google Scholar]
- Christofides, N. Worst-case analysis of a new heuristic for the travelling salesman problem. SIAM J. Comput. 1976, 6, 699–711. [Google Scholar] [CrossRef]
- Arora, S. Polynomial time approximation schemes for Euclidean TSP and other geometric problems. In Proceedings of the 37th Annual Symposium on Foundations of Computer Science (FOCS), Burlington, VT, USA, 14–16 October 1996; pp. 2–11. [Google Scholar]
- Kohonen, T. The self-organizing map. Proc. IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
- Zhu, D.Q.; Qu, Y.; Yang, S.X. Multi-AUV SOM task allocation algorithm considering initial orientation and ocean current environment. Front. Inf. Technol. Electron. Eng. 2019, 20, 330–341. [Google Scholar] [CrossRef]
- Faigl, J. An application of self-organizing map for multirobot multigoal path planning with minmax objective. Comput. Intell. Neurosci. 2016, 2016, 2720630. [Google Scholar] [CrossRef]
- Sampson, J.R. Adaptation in natural and artificial systems (John H. Holland). SIAM Rev. 1976, 18, 2. [Google Scholar] [CrossRef]
- Liu, F.; Zeng, G. Study of genetic algorithm with reinforcement learning to solve the TSP. Expert Syst. Appl. 2009, 36, 6995–7001. [Google Scholar] [CrossRef]
- Gan, Y.; Lan, L.W.; Li, S. Study on parameters configuration for ant colony optimization. Adv. Mater. Res. 2011, 279, 371–376. [Google Scholar] [CrossRef]
- Aicardi, M.; Giglio, D.; Minciardi, R. Determination of optimal control strategies for TSP by dynamic programming. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 2160–2167. [Google Scholar]
- Shi, X.H.; Liang, Y.C.; Lee, H.P.; Lu, C.; Wang, Q. Particle swarm optimization-based algorithms for TSP and generalized TSP. Inf. Process. Lett. 2007, 103, 169–176. [Google Scholar] [CrossRef]
- Puspita, F.; Meitrilova, A.; Yahdin, S. Mathematical modelling of traveling salesman problem (TSP) by implementing simulated annealing and genetic algorithms. J. Phys. Conf. Ser. 2020, 1480, 012029. [Google Scholar] [CrossRef]
- Lin, Y.; Bian, Z.; Liu, X. Developing a dynamic neighborhood structure for an adaptive hybrid simulated annealing–tabu search algorithm to solve the symmetrical traveling salesman problem. Appl. Soft Comput. 2016, 49, 937–952. [Google Scholar] [CrossRef]



| Method | Path Distance (Pixels) | Improvement vs. Ours |
|---|---|---|
| ACO | 7880.88 | 39.4% ↓ |
| DP | 5672.36 | 15.8% ↓ |
| PSO | 4792.90 | 0.34% ↓ |
| SA | 4894.10 | 2.41% ↓ |
| TS | 4792.90 | 0.34% ↓ |
| Ours | 4776.72 | – |
| ID | Planned Harvesting Path Distance | Improvement vs. Ours |
|---|---|---|
| ACO | 2713.80 | 12.2% ↓ |
| DP | 2473.57 | 3.66% ↓ |
| PSO | 2383.05 | 0.00% |
| SA | 2406.71 | 0.98% ↓ |
| TS | 2383.05 | 0.00% |
| Ours | 2383.05 | 0.00% |
| Name | Count | ACO | DP | PSO | SA | TS | Ours |
|---|---|---|---|---|---|---|---|
| 1 | 11 | 2713.80 | 2473.51 | 2383.05 | 2406.72 | 2473.51 | 2383.05 |
| 2 | 13 | 4108.75 | 3392.96 | 3376.42 | 3376.42 | 3376.42 | 3366.91 |
| 3 | 24 | 4725.97 | 3495.99 | 3495.99 | 3495.99 | 3479.70 | 3479.70 |
| 4 | 37 | 7443.85 | 5767.40 | 4577.58 | 4418.10 | 4577.58 | 4288.52 |
| 5 | 47 | 7045.34 | 4667.33 | 4587.63 | 4587.63 | 4667.33 | 4453.26 |
| 6 | 51 | 7789.22 | 5783.23 | 4783.26 | 4783.26 | 4783.26 | 4679.52 |
| 7 | 54 | 7637.24 | 4933.34 | 4933.34 | 4984.28 | 4832.56 | 4832.56 |
| 8 | 16 | 4213.24 | 3412.56 | 3412.56 | 3412.56 | 4213.24 | 3412.56 |
| 9 | 28 | 4756.12 | 3488.26 | 3488.26 | 3597.01 | 3488.26 | 3483.19 |
| 10 | 24 | 4720.19 | 3436.11 | 3483.95 | 3483.95 | 3483.59 | 3436.11 |
| Metric | Threshold Value (n) | ||
|---|---|---|---|
| 25 | 35 | 45 | |
| Mean Deviation (%) | +3.6 ± 0.8 | 0 (Reference) | +3.2 ± 1.1 |
| p-value (vs. n = 35) | 0.003 | – | 0.007 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; He, Z.; Zhu, H.; Wei, Z.; Lu, J.; He, X. Adaptive SOM-GA Hybrid Algorithm for Grasping Sequence Optimization in Apple Harvesting Robots: Enhancing Efficiency in Open-Field Orchards. Agronomy 2025, 15, 1230. https://doi.org/10.3390/agronomy15051230
Zhang L, He Z, Zhu H, Wei Z, Lu J, He X. Adaptive SOM-GA Hybrid Algorithm for Grasping Sequence Optimization in Apple Harvesting Robots: Enhancing Efficiency in Open-Field Orchards. Agronomy. 2025; 15(5):1230. https://doi.org/10.3390/agronomy15051230
Chicago/Turabian StyleZhang, Li, Zhihui He, Haobin Zhu, Zhanhong Wei, Juan Lu, and Xiongkui He. 2025. "Adaptive SOM-GA Hybrid Algorithm for Grasping Sequence Optimization in Apple Harvesting Robots: Enhancing Efficiency in Open-Field Orchards" Agronomy 15, no. 5: 1230. https://doi.org/10.3390/agronomy15051230
APA StyleZhang, L., He, Z., Zhu, H., Wei, Z., Lu, J., & He, X. (2025). Adaptive SOM-GA Hybrid Algorithm for Grasping Sequence Optimization in Apple Harvesting Robots: Enhancing Efficiency in Open-Field Orchards. Agronomy, 15(5), 1230. https://doi.org/10.3390/agronomy15051230






