Abstract
To address practical issues, such as uneven fertilizer distribution and poor particle dispersion, during the operation of a centrifugal double-disc fertilizer spreader, a discrete element method (DEM) simulation was initially performed. In this simulation, the blade inclination angle, fertilizer discharge offset angle, and spreading height were selected as experimental factors. The spreading width and the coefficient of variation (Cv) of fertilizer uniformity served as evaluation indicators. A quadratic orthogonal simulation experiment was designed to evaluate spreading performance. Subsequently, regression equations were established to optimize parameters and determine the optimal design configuration. Experimental results showed optimal performance with a blade inclination angle of −5°, fertilizer discharge offset angle of 45°, spreading height of 1050 mm, and disc rotational speed of 400 rpm. Considering that fertilizer spreaders are susceptible to air resistance and environmental wind during field operations, an EDEM-CFD coupling method was employed to simulate realistic operating conditions. Virtual simulation results demonstrated optimal fertilizer spreading performance at disc rotational speeds ranging from 350 to 400 rpm under tailwind conditions, and from 400 to 500 rpm under headwind conditions. Based on the simulation results, a prototype was built and tested. The experimental results closely matched the simulation predictions, thereby confirming the effectiveness of the simulation model. This study provides valuable insights and serves as a reference for designing and optimizing fertilizer spreader performance under practical operational conditions.
1. Introduction
According to the Food and Agriculture Organization of the United Nations (FAO), global fertilizer usage is approximately 200 million tons annually, contributing to an increase in crop yields ranging from 40–60% [1,2]. However, the extensive application of fertilizers has resulted in serious ecological and environmental issues, including soil compaction, degradation of soil quality, and crop burn [3,4].
EDEM simulations have been instrumental in fertilizer spreader research. Dintwa et al. precisely characterized particle trajectories of disc fertilizer spreaders and developed a dynamic model for fertilizer particles [5]. Antille et al. investigated fertilizer particle trajectories after leaving the spreading disc and proposed a theoretical model to predict individual particle motion [6]. Bivainis, using both EDEM simulations and field experiments, examined the effects of organic granular fertilizers on spreading efficiency. The results showed that particle diameter and length had a significant impact on spreading efficiency, while other physical properties, including density, moisture content, and friction coefficients (static and dynamic), also played key roles [7]. Fulton et al. analyzed the influence of blade shape on fertilizer distribution in double-disc fertilizer spreaders [8]. Through experiments on four blade designs, they concluded that the blade-top structure had a significant impact on fertilizer splashing and distribution. Consequently, they designed a fertilizer spreader with backward-inclined blades, reducing splashing by 13% and inducing reverse particle spin upon contact, thereby enhancing distribution uniformity. Liu Cailing et al. optimized the structure of a disc fertilizer spreader via discrete element method simulations, performing multi-factor tests on disc rotation speed, feed angle, feed quantity, and feeding position angle [9]. Structural parameters were optimized through regression modeling and validated via field trials. The results demonstrated that the optimized spreader reduced the coefficient of variation (Cv) in uniformity to 11.43%.
The discrete element method (DEM) [10,11,12] and computational fluid dynamics [13] (CFD) are widely used in agricultural engineering; however, each approach has inherent limitations when applied independently. The coupled DEM-CFD approach integrates the strengths of both methods, offering a more accurate and comprehensive representation of fluid–solid interactions [14,15,16]. This coupled approach has helped researchers resolve various challenges, providing valuable insights for mechanism design and operational parameter selection. It has been successfully implemented in various agricultural engineering studies.
Meng et al. developed a CFD-DEM coupled simulation system for air-assisted spraying equipment, identifying the optimal combination of operational parameters to establish a theoretical foundation for the design and optimization of air-assisted powder spraying devices [17]. Fei et al. conducted CFD-DEM-based research on the measurement and simulation of the suspension velocity of flax threshing materials, confirming the feasibility of the CFD-DEM coupling approach for velocity prediction [18]. Man et al. employed CFD-DEM coupled simulations to investigate the mixed transport of three-phase particle flows, offering valuable insights into particle transport and flow pattern identification [19]. Ma et al. conducted simulations and experiments on rice cleaning in pneumatic separation equipment using the DEM-CFD coupled method, demonstrating its reliability in analyzing straw and grain separation dynamics in airflow fields [20].
Therefore, this paper analyzes the motion characteristics to identify key structural parameters influencing fertilizer spreader performance. An EDEM-based discrete element model for urea particles was established, and a quadratic orthogonal simulation experiment was designed to analyze particle trajectories and optimize spreader structural parameters. Subsequently, simulations of the optimized spreader’s performance were conducted under operational conditions. Additionally, the motion of fertilizer particles under crosswind conditions was examined. An EDEM-Fluent coupled simulation was conducted. In this research, the urea particle model and spreader motion were defined in EDEM, while Fluent was used to develop a wind field model simulating realistic fertilizer application conditions. Data exchange between the two programs was facilitated through a coupling interface, enabling coupled simulations to examine crosswind effects on spreader performance. These findings contribute to optimizing fertilizer spreader efficiency, improving fertilizer utilization, and mitigating the environmental impacts of excessive fertilization.
2. Materials and Methods
2.1. Simulation and Optimization of Key Structures of the Disc Fertilizer Spreader Based on EDEM
The electrically driven disc fertilizer spreader designed in this study was modeled and simplified using SolidWorks software (version 2021). To emphasize the components directly influencing fertilizer particle motion, only the spreading disc and blade structures were retained. Meanwhile, the fertilizer discharge and drive mechanisms were simplified. The simplified fertilizer spreader simulation model is shown in Figure 1.
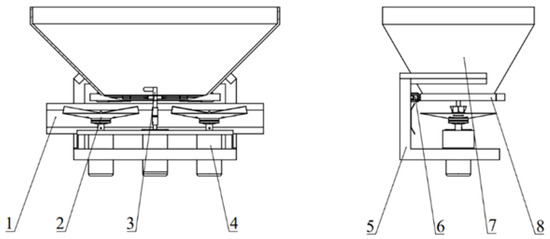
Figure 1.
Fertilizer spreader simulation model. 1. Fertilizer spreading baffle; 2. Fertilizer spreading disc; 3. Stirring dragon; 4. DC motor; 5. Fertilizer spreader bracket; 6. Electric push rod; 7. Fertilizer box; 8. Fertilizer discharge mechanism.
In EDEM (version 2022), a coordinate system was defined with the center of the fertilizer disc as the origin in a top view. A 125-mm-diameter arc trajectory, representing the position of the fertilizer discharge outlet, was created around the origin, with “A” denoting the blade inclination angle and “B” denoting the offset angle (Figure 2). Particle sources were placed in the shaded area of Figure 2, at the fertilizer discharge positions, to dynamically generate fertilizer particles. These sources were positioned above the spreading disc and directly below the discharge outlet. Fertilizer particles were continuously generated to simulate the discharge process.
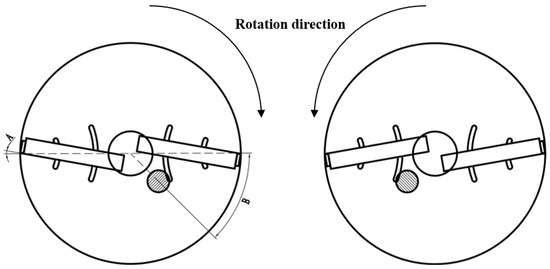
Figure 2.
Fertilizer spreading disc model.
The specific fertilizer parameters used in the EDEM simulation are summarized in Table 1. The fertilizer-related data in Table 1 were acquired from laboratory measurements. Additional parameters were obtained from the Agricultural Machinery Design Handbook [21]. Based on experimental requirements and prior design experience, the spreading disc rotational speed was set to 300–700 rpm. The left and right particle sources each dynamically generated 50 g of fertilizer particles, with a particle release rate of 160 g/s. The simulation time step was set to 2.5 × 10⁻⁶ s, corresponding to approximately 16% of the Rayleigh time step, with a total simulation duration of 2 s.

Table 1.
Physical parameters of fertilizer particles.
The selection of the contact model was based on factors such as particle hardness, elasticity, and surface characteristics. Given that the fertilizer particles in this study are solid, involving neither fragmentation nor moisture-related effects, and drawing on previous research, the basic Hertz–Mindlin (no slip) contact model [22] was adopted for the simulation.
A 16 m × 10 m virtual spreading region was established in EDEM. The region contained 640 fertilizer collection boxes (500 mm × 500 mm × 150 mm each), arranged in a 20-row by 32-column grid, as shown in Figure 3. After each simulation, the vertical accumulation of fertilizer particles in each column of boxes was recorded, resulting in a horizontal distribution across 32 longitudinal units.
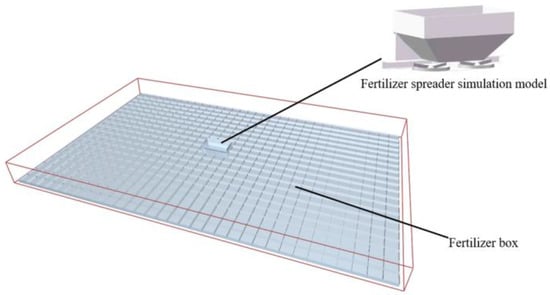
Figure 3.
EDEM virtual fertilizer collection box setting.
The Cv of the horizontal fertilizer distribution serves as a key metric for evaluating fertilizer spreader performance. A higher Cv corresponds to poorer spreading uniformity, whereas a lower Cv indicates better uniformity. The formula for calculating the horizontal distribution Cv is given as follows: (1)–(3).
where: represents the average mass of fertilizer particles per column unit (g); xi is the mass of fertilizer particles in each column unit (g); n is the number of column units; S denotes the standard deviation of particle mass across column units (g); Cv represents the coefficient of variation (%) for horizontal particle distribution.
To optimize the structure of the electrically driven disc fertilizer spreader, three key structural factors were selected: blade inclination angle (A), fertilizer discharge offset angle (B), and spreading height (C) (the distance from the spreading disc to the ground). Cv was selected as the evaluation index. A three-factor, five-level quadratic orthogonal central composite design (CCD) simulation experiment was conducted to assess the effects of structural parameters on fertilizer spreading performance. Experimental parameters were determined based on structural parameters of existing disc fertilizer spreaders, as detailed in Table 2. Spreading height was defined as the vertical distance from the fertilizer spreader to the ground.

Table 2.
Test factor level coding table.
To gain a comprehensive understanding of how individual parameters influence spreader performance and to identify critical factors, a quadratic orthogonal simulation test was conducted. In each analysis, one factor was held at the zero level, while interactions between the remaining two factors were examined to determine their influence on the horizontal distribution Cv. Particle motion simulations were performed using the EDEM to study the lateral distribution pattern of fertilizer particles and analyze the effects of different factors on Cv.
Simulation results were analyzed with Design-Expert software (version 13). Under predefined boundary conditions, structural parameters were further optimized, and performance simulations were conducted on the improved fertilizer spreader model. To accommodate the increased spreading width resulting from higher disc rotational speeds, the fertilizer particle collection area was expanded to 25 m × 15 m. Disc rotational speed was selected as a study variable to analyze its effects on spreading width and uniformity.
Spreading width is a key parameter in evaluating operational performance. In this study, spreading width was defined as follows: it is symmetrically divided into left and right halves along the spreader’s centerline, with each side analyzed separately. The overall proportion (Qa) of fertilizer particles collected in each longitudinal section on each side was calculated separately. Single-side spreading width was determined by the longitudinal collection positions at which the cumulative proportion of fertilizer particles exceeds 95%. The total spreading width is the sum of the left-side and right-side spreading widths. The calculation formulas are provided in Equations (4) and (5):
where: Ta is the cumulative amount of fertilizer particles (left or right) on one side, g; xai is the mass of particles in each column unit of fertilizer particles (left or right) on one side, g; Qai is the overall occupancy rate of each column unit (left or right) on one side, %; na is the number of single-sided column units (left or right); na′ is the calculation column unit.
2.2. Coupled Simulation Based on EDEM-Fluent and Analysis of Fertilizer Particle Motion Under Crosswind Conditions
During actual operations, the left and right fertilizer-spreading discs rotate in opposite directions, causing the fertilizer particles’ trajectories to diverge and disperse toward the left and right sides of the spreader, respectively. Depending on crosswind direction, two scenarios arise: wind blowing from the left side or the right side of the spreader. Accordingly, fertilizer particles experience either tailwind or headwind effects during flight.
Therefore, the following scenarios were analyzed: (1) particle motion in the absence of wind; (2) particle motion under tailwind influence; and (3) particle motion under headwind influence. To clarify particle distribution under crosswind conditions, the spreading discs were defined as follows: the disc dispersing fertilizer particles downwind is termed the tailwind spreading disc, while the disc dispersing particles upwind is termed the headwind spreading disc.
The wind field model was developed in Fluent (version 2021 R1) to encompass the full width and height of the fertilizer spreading area. Additionally, to account for the trajectory deviation of fertilizer particles caused by crosswinds, the wind field model dimensions were adjusted based on discrete element simulation results.
The base dimensions of the wind field model were set to 2500 mm × 1500 mm. To accommodate mid-air particle trajectories, the wind field model was defined as a rectangular volume of 2500 mm × 1500 mm × 1300 mm. A rectangular space was allocated at the model’s center to accommodate the fertilizer spreader. The wind field model was constructed and meshed using SolidWorks software (version 2021).
The coupling between EDEM and Fluent was implemented via two interfaces: one based on the Eulerian model and the other on the dense discrete phase model (DDPM). The key difference between these two approaches lies in Fluent’s treatment of the particle-phase volume fraction.
This study used the DDPM for EDEM-Fluent coupled simulations. EDEM parameters were configured as described in Section 2.1. In Fluent, a transient solver was selected, gravity was activated, and the viscous model was configured as the k-omega (2-equation) SST model. The coupling interface and discrete phase model (DPM) were enabled, with air defined as the fluid material. Boundary conditions were defined as follows: the inlet was specified as a velocity inlet and the outlet was set as a pressure outlet. The turbulence intensity was set to 5%, the turbulence viscosity ratio to 10, and the wall condition was defined as a reflecting surface. After model initialization, the simulation time step was set to 2.0×10⁻⁴ s, with a maximum of 20 iterations per time step and a total of 10,000 time steps for the coupled simulation.
The optimized fertilizer spreader and wind field models were independently imported into EDEM and Fluent, with parameters configured as described above. In the coupled simulations, the spreading disc rotational speed and crosswind conditions were selected as independent variables. Coupled simulations were conducted to analyze fertilizer particle behavior under tailwind and headwind conditions. The simulation procedure adhered to the static disc fertilizer spreader test guidelines specified in ISO 5690 and ASAE S341.2 [23,24]. Accordingly, the maximum wind speed for the experiment was set to 6 m/s.
In EDEM, the fertilizer spreading region was defined as a rectangular area of 25 m × 15 m. Within this region, 1500 fertilizer collection boxes (500 mm × 500 mm × 150 mm each) were arranged in a 50-row by 30-column grid, as shown in Figure 4a. After each trial, vertical columns were summed to generate a horizontal distribution comprising 1 × 50 vertical spreading units. In Fluent, the wind field mesh model was imported and inlet velocity parameters were adjusted to simulate various crosswind conditions as illustrated in Figure 4b.
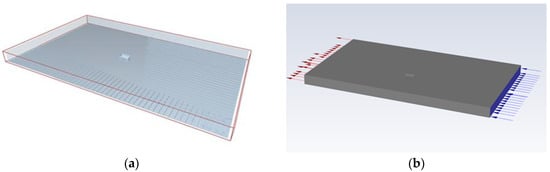
Figure 4.
Models in EDEM and models: (a) The setting of fertilizer collection box in EDEM virtual fertilizer spreading area in coupling simulation; (b) Fluent wind field simulation setting in coupling simulation.
To analyze fertilizer particle behavior under tailwind and headwind conditions, the unilateral spreading width and unilateral coefficient of variation for horizontal distribution (Cva) were evaluated separately for the left and right sides. When calculating Cva, particle distribution data from the opposite side at the optimal rotational speed (400 rpm) were incorporated to generate complete bilateral data and compensate for any data gaps. For example, when computing the left-side Cva, particle distribution data from the right side were integrated and vice versa.
The spreading disc rotational speed and crosswind velocity were selected as variables to investigate their influence on fertilizer particle trajectories under varying wind conditions. During the experiments, particle motion was analyzed under both tailwind and headwind conditions, using the optimal spreading width and uniformity in windless conditions as the benchmark to define the testing range.
Under tailwind conditions, the spreading disc rotational speed was sequentially reduced from 400 rpm to 200 rpm in 50 rpm increments at wind velocities of 0 m/s, 2 m/s, 4 m/s, and 6 m/s. Changes in operational performance at reduced rotational speeds under each wind velocity were recorded. Detailed experimental parameters are provided in Table 3.

Table 3.
Tailwind coupling test factor data.
Under headwind conditions, the spreading disc rotational speed was sequentially increased from 400 rpm to 800 rpm in 100 rpm increments at wind velocities of 0 m/s, 2 m/s, 4 m/s, and 6 m/s. The effect of increased rotational speed on operational performance was measured at each wind velocity. Detailed experimental parameters are provided in Table 4.

Table 4.
Headwind coupling test factor data.
2.3. Field Experiment on Fertilizer Spreader Operational Performance
To validate the accuracy of the EDEM-CFD simulation, a prototype was manufactured based on the optimized simulation results. Key components of the fertilizer spreader were fabricated and assembled into a complete system. A brushed direct current motor was used to control the rotational speed of the fertilizer disc and mounted on the rear of an unmanned, self-propelled, high-clearance wheeled chassis, as shown in Figure 5. The prototype parameters are shown in Table 5.

Figure 5.
Prototype of electric disc fertilizer spreader.

Table 5.
Parameters of the prototype.
The field experiment was conducted in April 2024 at the experimental site of the College of Agricultural Engineering, Jiangsu University, Zhenjiang, China. Natural wind speed during the test ranged from 0 to 4 m/s, and the 280 m2 test area was flat. Tests were conducted under ambient humidity below 50% within a 10 m × 10 m designated test zone.
In this test zone, the Y-axis was defined as the forward direction of machine movement along the ground. The X-axis was defined as the direction perpendicular to the Y-axis on the same ground plane. Fertilizer collection boxes (500 mm × 500 mm × 150 mm each) were arranged in a 10 × 8 grid. Along the X-axis, 10 boxes were placed at 0.5 m intervals. Along the Y-axis, 8 rows were placed at 0.8 m intervals. A schematic diagram of the layout is provided in Figure 6a. Due to experimental constraints, an ideal controlled crosswind environment could not be established; therefore, tests were conducted under natural wind conditions. The layout of the fertilizer spreader performance test area is shown in Figure 6b.

Figure 6.
Experimental layout diagram: (a) Layout diagram of fertilizer collection box in test area: 1. Fertilizer collection box; 2. Test site; 3. Position of fertilizer spreader; (b) fertilizer spreader operation performance test site layout.
During the test, crosswind speed data were measured in real time using an ultrasonic wind speed and direction sensor (RS-FSXCS, Jianda Renke, Jinan, China). Wind data were monitored in real time using a controller, and the maximum and minimum wind speeds during each spreading operation were recorded. The average wind speed was calculated and used as the representative crosswind value for analysis. The fertilizer disc operated at an optimal speed of 400 rpm, and the fertilizer discharge rate was set at 160 g/s. At the end of each spreading operation, the mass of fertilizer collected in each row of boxes was measured. The entire spreading area was effectively converted into a 1-row by 10-column collection region. The test was repeated five times. After each trial, the fertilizer mass collected in each column was recorded, and both the single-sided spreading width and the horizontal distribution Cv were calculated to evaluate the spreader’s operational performance.
3. Results and Discussion
3.1. Influence of Different Factors on the Operational Performance of Fertilizer Spreaders
The experimental results were analyzed with Design-Expert software (version 13) to determine how various test factors affect the operational performance of fertilizer spreaders. Statistical analysis produced a regression equation, from which the optimized structural parameters were derived. Detailed experimental results are summarized in Table 6.

Table 6.
Experimental scheme and results.
Variance analysis results of the quadratic orthogonal experiment are summarized in Table 7. The analysis revealed an R2 value of 0.97, an F-value of 29.31, and a regression term significance of p < 0.0001. These results indicate the reliability and significance of the regression model. The lack-of-fit term had a p-value of 0.0603 (>0.05), indicating no significant lack of fit and thus a good model fit.

Table 7.
Variance analysis.
Based on the p-values of each factor, the blade inclination angle (A) and fertilizer discharge offset angle (B) had a significant affected the evaluation index Cv (p < 0.01). Additionally, the interaction term AB (blade inclination angle × fertilizer discharge offset angle) and the quadratic term A2 (blade inclination angle) had a notable influence on Cv, findings consistent with previous research [25,26]. The relative influence of the remaining factors on Cv was ranked as follows: B, A, AB, A2, B2, C, C2, BC, AC. The regression equation derived from this analysis is provided in Equation (6).
3.2. Response Surface Analysis and Parameter Optimization
To better understand how various parameters influence the operational performance of the fertilizer spreader, we aimed to identify key factors and determine optimal parameters. In this process, one of the three factors was systematically set at the zero level. Response surface plots were then generated to analyze the interaction effects between the remaining two factors on the coefficient of variation (Cv), with visual results presented in Figure 7.
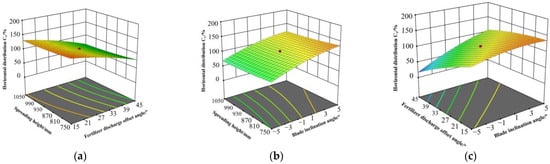
Figure 7.
Factor interaction response surface diagram: (a) Spreading height and fertilizer discharge offset angle; (b) Spreading height and blade inclination angle; (c) Fertilizer discharge offset angle and blade inclination angle.
The analysis revealed that the fertilizer discharge offset angle had a greater impact on the horizontal distribution Cv than spreading height, a finding supported by earlier research [27], which concluded that an inclined disc alters fertilizer distribution uniformity. In this study, the minimum Cv occurred at a spreading height of approximately 1050 mm and a fertilizer discharge offset angle of 45°. When the offset angle was set to 30°, a response surface (Figure 7b) was obtained. The response surface indicated that, with a fixed offset angle, increasing blade inclination and spreading height led to an increase in Cv. However, spreading height had a weaker effect, confirming that blade inclination was the dominant factor affecting Cv. The minimum Cv was observed at a blade inclination angle of −5° and a spreading height of 1050 mm.
When the spreading height was fixed at 900 mm (Figure 7c), the response surface showed that Cv slightly decreased with increasing offset angle and blade inclination. Changes in Cv were more sensitive to the offset angle than to blade inclination, confirming the stronger influence of the offset angle. The minimum Cv occurred at an offset angle of 45° and a blade inclination angle of −5°.
The optimized parameters were determined: blade inclination angle of −5°, fertilizer discharge offset angle of 45°, spreading height of 1050 mm, and a predicted horizontal distribution Cv of 13.372%.
3.3. Simulation Test of Fertilizer Spreader Operational Performance
After optimizing the fertilizer spreader simulation model, EDEM software (version 2022) was used to evaluate its operational performance. The influence of disc rotational speed on fertilizer particle distribution under optimized structural parameters is illustrated in Figure 8.
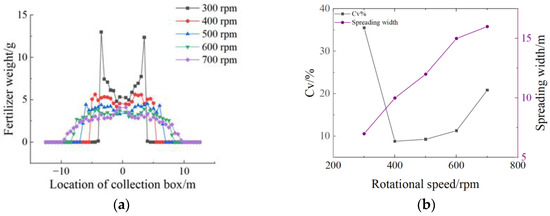
Figure 8.
Results of job performance simulation analysis as: (a) Distribution of fertilizers; (b) Performance of fertilizer spreader operation.
Analysis of Figure 8 reveals that, as the fertilizer spreading disc’s rotational speed increases, the fertilizer particle distribution pattern transitions from an “M” shape to a “W” shape. Results showed that, as the disc rotational speed increased, the fertilizer spreading width initially increased and then decreased, while Cv first decreased and then increased. The optimal disc speed was determined to be 400 rpm, producing a minimum Cv of 8.82% and a spreading width of 10 m.
Further analysis revealed that, at lower rotational speeds, the centrifugal force was insufficient, causing shorter fertilizer particle flight times, higher particle concentration, and increased distribution variation. At higher rotational speeds, the centrifugal force caused excessive fertilizer particle dispersion [28], thereby increasing Cv. Thus, the optimal balance was found at a disc rotational speed of 400 rpm, yielding the lowest variation coefficient (Cv = 8.82%) and an optimal spreading width of 10 m, meeting the relevant agricultural machinery standards.
3.4. Coupled Simulation and Particle Distribution Analysis Under Crosswind Conditions
3.4.1. Fertilizer Particle Distribution Under Windless Conditions
To investigate fertilizer spreader performance under airflow resistance in the absence of wind, simulations were conducted using EDEM-Fluent coupling. EDEM parameters were configured according to Section 3.1, while Fluent parameters were set as previously described. The crosswind speed was set to 0 m/s to simulate particle trajectories without wind but under air resistance, as shown in Figure 9.
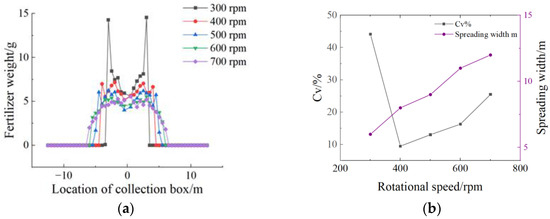
Figure 9.
Results of air resistance under the wide variation of manure as: (a) Distribution of fertilizers; (b) Performance of fertilizer spreader operation.
Results indicated that, compared to ideal conditions without air resistance, the presence of air resistance slightly reduced the spreading width and increased the horizontal distribution Cv. Under these conditions, the optimal rotational speed remained at 400 rpm, with a reduced spreading width of 8 m and an increased Cv of 9.52%. The overall analysis suggests that air resistance significantly effects fertilizer spreading performance even in the absence of crosswinds. These findings are consistent with those reported in [29].
3.4.2. Single-Side Fertilizer Spreading Width Distribution Under Tailwind Conditions
Under tailwind conditions, fertilizer particles on one side of the spreader were selected as the focus of the study. As wind speed varied, the rotational speed of the tailwind spreading disc was adjusted to analyze particle distribution patterns. Simulations were conducted at wind speeds of 0 m/s, 2 m/s, 4 m/s, and 6 m/s, with disc rotational speeds gradually decreasing from 400 rpm to 200 rpm in 50 rpm increments. The simulation results are presented in Figure 10.
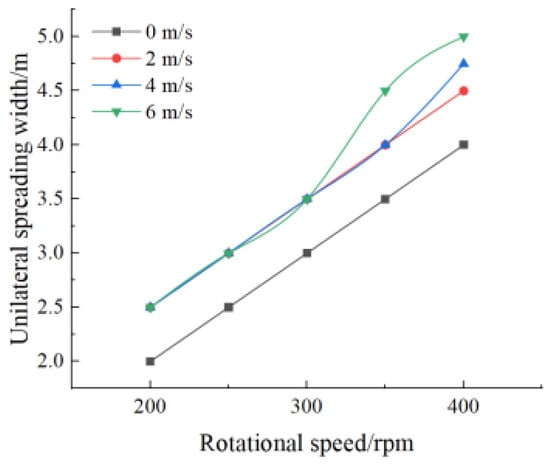
Figure 10.
Unilateral spreading width under tailwind conditions.
Results indicated that the single-sided fertilizer spreading width generally increased under tailwind conditions. At fixed wind speeds, reducing rotational speed gradually decreased single-sided spreading width, although it remained wider than under windless conditions. At wind speeds of 0–2 m/s, reducing the tailwind spreading disc’s rotational speed consistently reduced single-sided spreading width. At wind speeds of 2–6 m/s, decreasing the tailwind spreading disc’s rotational speed also reduced single-sided spreading width but caused fluctuations. Conversely, at a fixed rotational speed, higher wind speeds led to increased spreading width, but this effect diminished as rotational speed decreased. Within the rotational speed range of 200–300 rpm, different wind speeds had similar effects on single-sided spreading width. When rotational speeds ranged from 300–400 rpm, wind speed had a more pronounced effect on single-sided spreading width.
3.4.3. Single-Side Fertilizer Spreading Width Distribution Under Headwind Conditions
A crosswind was applied to one side of the fertilizer spreader, focusing on fertilizer particles subjected to headwind conditions. Under headwind conditions, fertilizer particles flying against the wind were analyzed by adjusting disc rotational speeds from 400 rpm to 800 rpm in 100 rpm increments at crosswind speeds of 0 m/s, 2 m/s, 4 m/s, and 6 m/s. Detailed experimental parameters are shown in Figure 11.
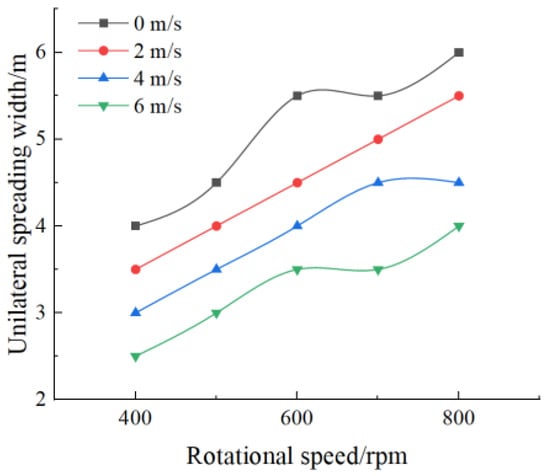
Figure 11.
Unilateral spreading width under headwind conditions.
The results showed that headwinds generally reduced the single-sided spreading width compared to windless conditions. At a constant wind speed, increasing rotational speed gradually widened spreading width, yet resulted in narrower distributions compared to windless conditions.
At wind speeds of 0–2 m/s, increasing the headwind spreading disc’s rotational speed led to a steady increase in single-sided spreading width. At wind speeds of 2–6 m/s, increasing the headwind spreading disc’s rotational speed induced fluctuations in single-sided spreading width. As the headwind spreading disc’s rotational speed increased, the influence of wind speed on single-sided spreading width diminished. At fixed rotational speeds, increasing wind speeds generally reduced spreading width.
Between 400 rpm and 500 rpm, spreading width remained stable, whereas at higher speeds (500 rpm to 800 rpm), fluctuations became more pronounced. Additionally, as rotational speed increased, the effect of wind speed variations on spreading width gradually weakened.
3.4.4. Double-Sided Spreading Width Distribution Under Wind Conditions
Crosswind speeds ranging from 0 m/s to 6 m/s were set to examine how variations in rotational speed affected the single-sided horizontal distribution Cva under different wind conditions. The simulation results are presented in Figure 12.
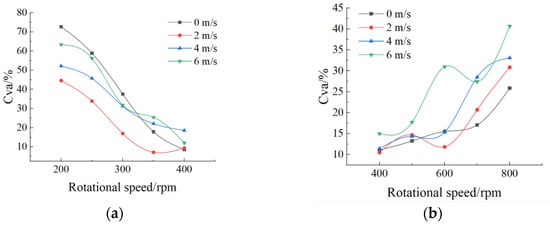
Figure 12.
Unilateral transverse distribution coefficient of variation with: (a) Tailwind; (b) Headwind.
Under tailwind conditions, as rotational speeds decreased from 400 rpm to 200 rpm, the single-sided Cva increased progressively. Specifically, when rotational speeds ranged from 350 rpm to 400 rpm, Cva remained stable; however, at speeds below 350 rpm, significant increases in Cva were observed.
Under headwind conditions, as rotational speeds increased from 400 rpm to 800 rpm, Cva values gradually increased. The variation remained stable between 400 rpm and 500 rpm but became more pronounced at higher speeds. At fixed disc speeds, increasing wind speed generally resulted in higher Cva, indicating reduced distribution uniformity.
Unlike most EDEM-CFD studies on fertilizer spreading, this study specifically focused on a double-disc spreader operating under crosswind conditions, where the left and right discs rotate in opposite directions. Because the discs rotate in contrary orientations, crosswind forces exert varying effects on the fertilizer discharged from each disc. To address this asymmetry, the two discs were configured to run at different rotational speeds, ensuring consistent spreading width and uniformity on both sides of the spreader even under crosswind scenarios. By systematically analyzing multiple wind speeds (0–6 m/s) and a broad range of disc rotational speeds (200–800 rpm) in both headwind and tailwind contexts, our approach significantly advances existing EDEM-CFD research. These findings clarify how wind interacts with disc orientation and rotational speed, offering practical strategies to mitigate uneven fertilizer distribution and improve real-world application.
3.5. Performance of the Fertilizer Spreader Prototype
The prototype system built in this study aims to validate the EDEM-CFD simulation results and was designed for the field experiment specially, thus the main technical parameters such as the disc rotational speed and spreading width were designed according to the commercial production or system. Nevertheless, considering the experimental constraint conditions, some of the technical parameters are smaller than those of a commercial model or production. A comparison table between the prototype and the ZA-XW 503 mounted fertilizer spreader from the company AMAZONE is shown below.
Following five field tests, the results are summarized in Table 8. The analysis reveals that environmental crosswinds noticeably affected spreading width. However, due to experimental limitations, precise positioning of the spreading width could not be achieved, resulting in only minor variations in the measured width. In contrast, crosswinds had a significant impact on the Cv. Excessive wind speeds were shown to negatively affect the operational performance of the fertilizer spreader.

Table 8.
Performance test results of fertilizer spreader.
As shown in Table 8 and Table 9, the spreading width of prototype was optimal (10 m), which was calculated from the EDEM simulation without air resistance. The corresponding spreading width from the EDEM-Fluent simulation is about 8 m under windless conditions. Meanwhile, the experimental spreading width from windy field experiments ranged from approximately 7–8, and these results indicated that the EDEM-Fluent simulation is suitable for fertilizer spreading calculation.

Table 9.
Comparison between prototype and ZA-XW 503.
Overall, the experimental results are generally aligned with the simulation results: under tailwind conditions, the single-sided spreading width increased with increasing wind speed. Under headwind conditions, the single-sided spreading width decreased as wind speed increased.
Compared to previous studies, the wind in our field experiments resulted in higher Cv as wind speed increased. Nonetheless, even under low wind conditions, the double-disc spreader used in this study achieved lower Cv values than those reported by Liu [9] under windless conditions. In comparison with Fulton’s [8] double-disc fertilizer spreader, although our spreading width was smaller, this study obtained a lower Cv at a similar spreading rate per unit area, suggesting a higher fertilizer application density. Furthermore, our system exhibited more stable performance under crosswind conditions.
3.6. Limitations of the Field Experiments and Future Requirements
Although the field test results generally agreed with the simulation results, there were several limitations during the study. Firstly, these experiments were conducted under outdoor environmental conditions, and the speed and direction of the ambient wind are variable and are not identical to the conditions used in simulations. Such variability should be controlled and eliminated using complex and expensive wind tunnel systems in future strict field validation study. Secondly, the size of the test site used in these field experiments constrained the evaluation of particle dispersion at higher disc speeds. Terrain and plant canopy effects were also omitted which can potentially affect the system performance in real-world agricultural operations. Furthermore, there was only one particle size used in the study, which may also have influenced the fertilizer distribution in operations and should be considered in future research.
The future research work should include the large-scale field experiment across diverse crop types and terrains. In order to verify the results of numerical simulation under strict conditions, wind tunnel or controlled wind conditions experiments should be conducted in future for detailed comparison analysis and validation. Various fertilizer types and evaluating long-term operational stability are also necessary for broader applicability of this study.
4. Conclusions
This study employed EDEM simulation modeling to analyze the influence of structural parameters and operational conditions on fertilizer particle distribution in a double-disc fertilizer spreader. Through a quadratic orthogonal experiment with optimized design parameters, the optimal settings were determined as follows: blade inclination angle of −5°, fertilizer discharge offset angle of 45°, and spreading height of 1050 mm. Subsequently, an EDEM-Fluent coupled simulation model was utilized to examine the effects of disc rotational speed on spreading uniformity under both windless and windy conditions. The findings indicate optimal efficiency at disc rotational speeds of 400–500 rpm under headwind conditions and 350–400 rpm under tailwind conditions. Through controlled experiments and systematic analysis, these insights provide valuable guidance for optimizing fertilizer spreader performance under real-world field conditions and provide farmers with actionable strategies to reduce waste, improve efficiency, and adapt to varying environmental wind conditions.
While the optimized fertilizer spreader provides lower Cv and windy condition adaptation in practice, it can achieve a maximum swath width and minimum uneven fertilizer spreading during field operations, thus the optimized fertilizer spreader is estimated to reduce excessive fertilizer overlap, operational path, and time consumed and, ultimately, it is able to enhance the overall operational efficiency and reduce fuel consumption and environmental pollution. Furthermore, if the Cv of the fertilizer in the field operation is decreased by 20% in future, the fertilizer consumption is estimated to decrease by more than 5% according to a previous study [30].
5. Limitations and Future Work
Fertilizer is one of the most important factors in enhancing agricultural productivity and ensuring food security. This study provided a potential approach to enhancing operational performance and reducing fertilizer waste. Nevertheless, the field experiments using the prototype did not provide identical boundary conditions as in stimulations, so stricter validation experiments under controlled wind and other field conditions are still needed in future. The previous research demonstrated that changes in Cv have a significant financial impact on fertilizer operation, the relationship between Cv and the fertilizer cost was exponential, and a summary reported that the economic loss changed from 21.06 $/ha to 3.04 $/ha when the Cv changed from 37% to 20% [30]. The improvement in fertilizer spreading operation can provide huge economic benefits for agricultural production around the world. This study aims to improve the operation efficiency and economic cost of fertilizer spreaders. The simulation results in this article indicated that the Cv decreased from 36.21% to 8.82% under optimal conditions, and the field experiments using the prototype system partly proved the finding. Stricter validations for more detailed analysis are expected in future research which should consider a wind tunnel system, terrain, and plants. Furthermore, advanced fertilizer technology is important for sustainable agricultural production and development which can reduce fertilizer cost and environmental pollution. In particular, how to improve the spreader system’s true performance in windy conditions is one of the challenges in future research.
Author Contributions
M.O.: conceptualization, methodology, writing—review and editing, supervision. G.W.: investigation, formal analysis, writing—original draft. Y.L.: investigation, formal analysis. Z.Z.: investigation, writing—original draft. H.P.: investigation, validation, writing—original draft. W.J.: conceptualization, writing—review and editing. X.D.: investigation. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the High-tech Key Laboratory of Agricultural Equipment and Intelligence of Jiangsu Province, the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD-2023-87).
Data Availability Statement
The data presented in this study are available within the article.
Acknowledgments
The authors thank the Faculty of Agricultural Equipment of Jiangsu University for its facilities and support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Stewart, W.M.; Dibb, D.W.; Johnston, A.E.; Smyth, T.J. The Contribution of Commercial Fertilizer Nutrients to Food Production. Agron. J. 2005, 97, 1–6. [Google Scholar] [CrossRef]
- Randive, K.; Raut, T.; Jawadand, S. An Overview of the Global Fertilizer Trends and India’s Position in 2020. Miner. Econ. 2021, 34, 371–384. [Google Scholar] [CrossRef]
- Guo, J.; Li, C.; Xu, X.; Sun, M.; Zhang, L. Farmland Scale and Chemical Fertilizer Use in Rural China: New Evidence from the Perspective of Nutrient Elements. J. Clean. Prod. 2022, 376, 134278. [Google Scholar] [CrossRef]
- Tyagi, J.; Ahmad, S.; Malik, M. Nitrogenous Fertilizers: Impact on Environment Sustainability, Mitigation Strategies, and Challenges. Int. J. Environ. Sci. Technol. 2022, 19, 11649–11672. [Google Scholar] [CrossRef]
- Dintwa, E.; Liedekerke, P.V.; Olieslagers, R.; Tijskens, E.; Ramon, H. Model for Simulation of Particle Flow on a Centrifugal Fertiliser Spreader. Biosyst. Eng. 2004, 87, 407–415. [Google Scholar] [CrossRef]
- Antille, D.L.; Gallar, L.; Miller, P.C.; Godwin, R.J. An Investigation into the FertilizerParticle Dynamics off-the-Disc. Appl. Eng. Agric. 2015, 30, 49–60. [Google Scholar] [CrossRef][Green Version]
- Bivainis, V.; Jotautienė, E.; Lekavičienė, K.; Mieldažys, R.; Juodišius, G. Theoretical and Experimental Verification of Organic Granular Fertilizer Spreading. Agriculture 2023, 13, 1135. [Google Scholar] [CrossRef]
- Fulton, J.P.; Thaper, R.K.; Virk, S.S.; McDonald, T.; Fasina, O. Effect of Vane Shape on Fertilizer Distribution for a Dual-Disc Spinner Spreader. Appl. Eng. Agric. 2020, 36, 743–751. [Google Scholar] [CrossRef]
- Liu, C.; Li, Y.; Song, J.; Ma, T.; Wang, M.; Wang, X.; Zhang, C. Performance Analysis and Experiment on Fertilizer Spreader with Centrifugal Swing Disk Based on EDEM. Trans. Chin. Soc. Agric. Eng. 2017, 33, 32–39. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, X.; Wu, S.; Chen, C.; Wang, J.; Yuan, S.; Chen, B.; Li, P.; Xu, R. Numerical Simulation of Particle Motion at Cucumber Straw Grinding Process Based on EDEM. Int. J. Agric. Biol. Eng. 2020, 13, 227–235. [Google Scholar] [CrossRef]
- Yuan, H.; Liang, S.; Wang, J.; Lu, Y. Numerical Simulation and Analysis of Vibrating Rice Filling Based on EDEM Software. Agriculture 2022, 12, 2013. [Google Scholar] [CrossRef]
- Xu, L.; Wei, C.; Liang, Z.; Chai, X.; Li, Y.; Liu, Q. Development of Rapeseed Cleaning Loss Monitoring System and Experiments in a Combine Harvester. Biosyst. Eng. 2019, 178, 118–130. [Google Scholar] [CrossRef]
- Liang, Z.; Xu, L.; Baerdemaeker, J.D.; Li, Y.; Saeys, W. Optimisation of a Multi-Duct Cleaning Device for Rice Combine Harvesters Utilising CFD and Experiments. Biosyst. Eng. 2020, 190, 25–40. [Google Scholar] [CrossRef]
- Ding, B.; Liang, Z.; Qi, Y.; Ye, Z.; Zhou, J. Improving Cleaning Performance of Rice Combine Harvesters by DEM–CFD Coupling Technology. Agriculture 2022, 12, 1457. [Google Scholar] [CrossRef]
- El-Emam, M.A.; Zhou, L.; Omara, A.I. Predicting the Performance of Aero-Type Cyclone Separators with Different Spiral Inlets under Macroscopic Bio-Granular Flow Using CFD–DEM Modelling. Biosyst. Eng. 2023, 233, 125–150. [Google Scholar] [CrossRef]
- Fang, W.; Wang, X.; Zhu, C.; Han, D.; Zang, N.; Chen, X. Analysis of Film Unloading Mechanism and Parameter Optimization of Air Suction-Type Cotton Plough Residual Film Recovery Machine Based on CFD—DEM Coupling. Agriculture 2024, 14, 1021. [Google Scholar] [CrossRef]
- Fu, M.; Zhang, H.; Wang, Y.; Fu, W.; Zhang, B.; Fu, Y.; Zeng, T. Parameter Optimization and Experiment of Air-Fed Rubber Tree Pesticide Application Device Based on CFD-DEM Coupling Method. Comput. Electron. Agric. 2024, 225, 109247. [Google Scholar] [CrossRef]
- Dai, F.; Guo, W.; Song, X.; Shi, R.; Qu, J.; Zhao, W. Measurement and Simulation of the Suspension Velocity of Flax Threshing Material Using CFD-DEM. Int. J. Agric. Biol. Eng. 2021, 14, 230–237. [Google Scholar] [CrossRef]
- Ge, M.; Chen, J.; Zhao, L.; Zheng, G. Mixing Transport Mechanism of Three-Phase Particle Flow Based on CFD-DEM Coupling. Processes 2023, 11, 1619. [Google Scholar] [CrossRef]
- Ma, X.; Zhao, L.; Guo, B.; Dang, H. Simulation and Experiment of Rice Cleaning in Air-Separation Device Based on DEM-CFD Coupling Method. Int. J. Agric. Biol. Eng. 2019, 13, 226–233. [Google Scholar] [CrossRef]
- Institute of China Agricultural Science and Technology. Agricultural Machinery Design Manual; China Agricultural Science and Technology Press: Nanjing, China, 2007; Volume 2. [Google Scholar]
- Duan, J.; Liu, D.; Xie, F.; Zhang, Y.; Zheng, P. Breakage Simulations and Experiments of Granular Fertilisers for Optimizing a Device of Side-Deep Fertilisation by Using the Discrete Element Method. Biosyst. Eng. 2024, 238, 105–114. [Google Scholar] [CrossRef]
- ISO 5690-2:1984; Equipment for Distributing Fertilizers—Test Methods. ISO: Geneva, Switzerland, 1984.
- ASAE S341.5; Procedure for Measuring Distribution Uniform and Calibrating Granular Broadcast Spreaders. ASAE Standards: St Joseph, MI, USA, 2018.
- Yildirim, Y. Effect of Side to Side Spreader Angle on Pattern Uniformity in Single- and Twin-Disc Rotary Fertilizer Spreaders. Appl. Eng. Agric. 2008, 24, 173–179. [Google Scholar] [CrossRef]
- Przywara, A. The Impact of Structural and Operational Parameters of the Centrifugal Disc Spreader on the Spatial Distribution of Fertilizer. Agric. Agric. Sci. Procedia 2015, 7, 215–222. [Google Scholar] [CrossRef]
- Bulgakov, V.; Adamchuk, O.; Pascuzzi, S.; Santoro, F.; Olt, J. Experimental Research into Uniformity in Spreading Mineral Fertilizers with Fertilizer Spreader Disc with Tilted Axis. Agron. Res. 2021, 19, 28–41. [Google Scholar] [CrossRef]
- Przywara, A.; Santoro, F.; Kraszkiewicz, A.; Pecyna, A.; Pascuzzi, S. Experimental Study of Disc Fertilizer Spreader Performance. Agriculture 2020, 10, 467. [Google Scholar] [CrossRef]
- Zinkevičienė, R.; Jotautienė, E.; Juostas, A.; Comparetti, A.; Vaiciukevičius, E. Simulation of Granular Organic Fertilizer Application by Centrifugal Spreader. Agronomy 2021, 11, 247. [Google Scholar] [CrossRef]
- Grafton, M.C.E.; Yule, I.J.; Manning, M.J. A review of the economic impact of high levels of variance in fertiliser spreading systems. Proc. New Zealand Grassl. Assoc. 2013, 75, 139–144. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).