Development of Mathematical and Computational Models for Predicting Agricultural Soil–Water Management Properties (ASWMPs) to Optimize Intelligent Irrigation Systems and Enhance Crop Resilience
Abstract
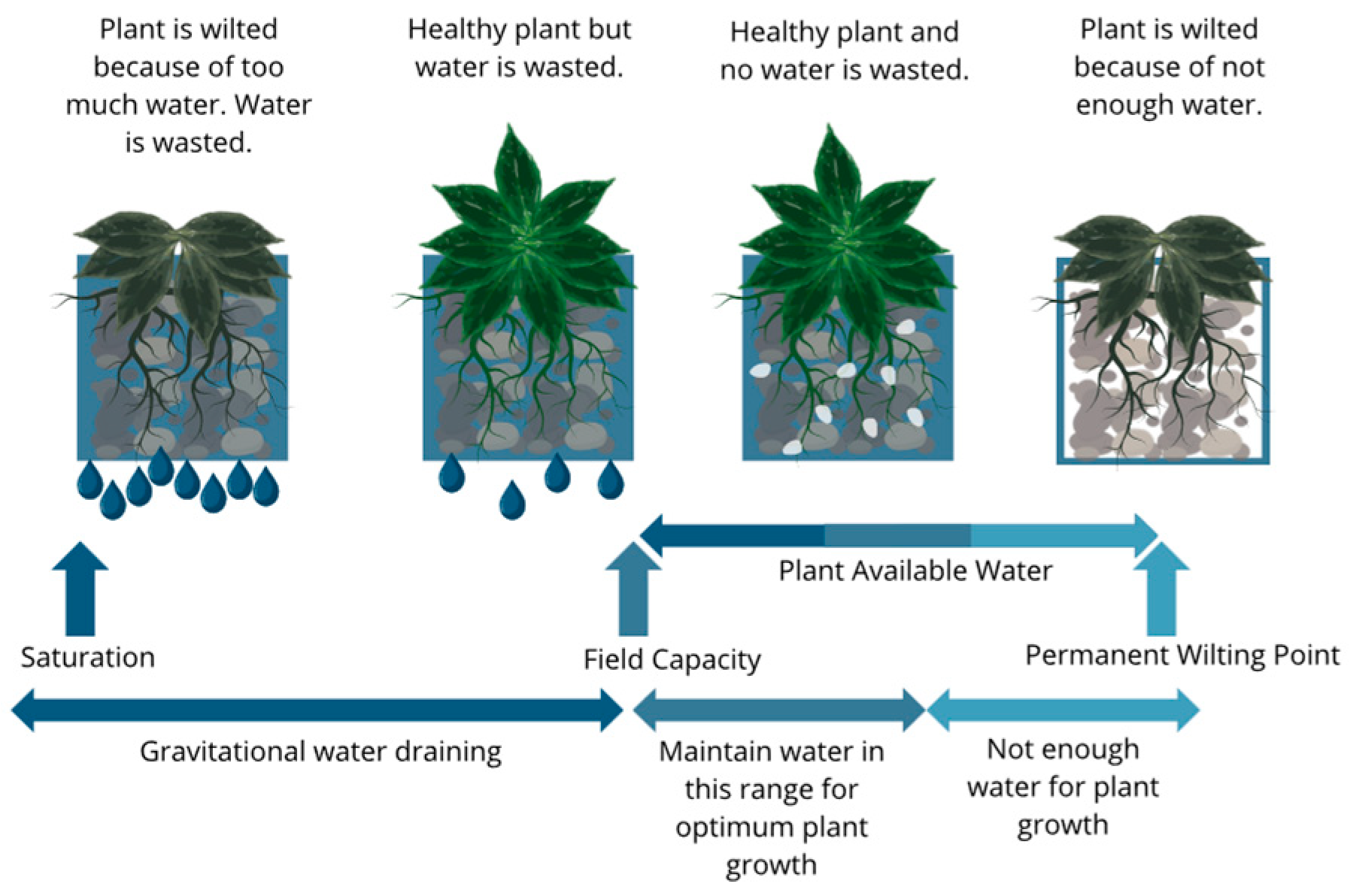
1. Introduction
2. Data Source
3. Methods
3.1. Mathematical Modelling
3.2. Computational Modelling
4. Results
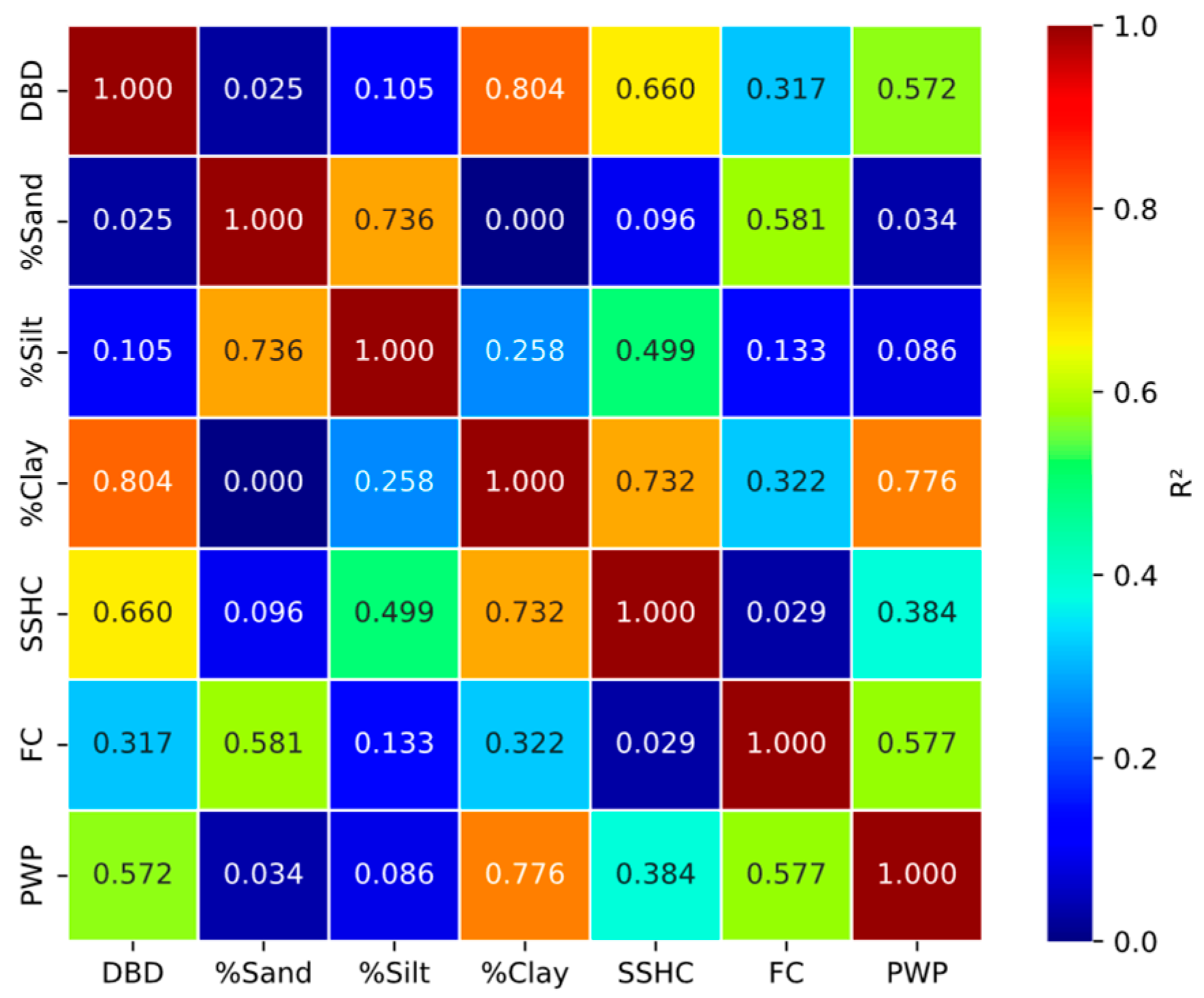
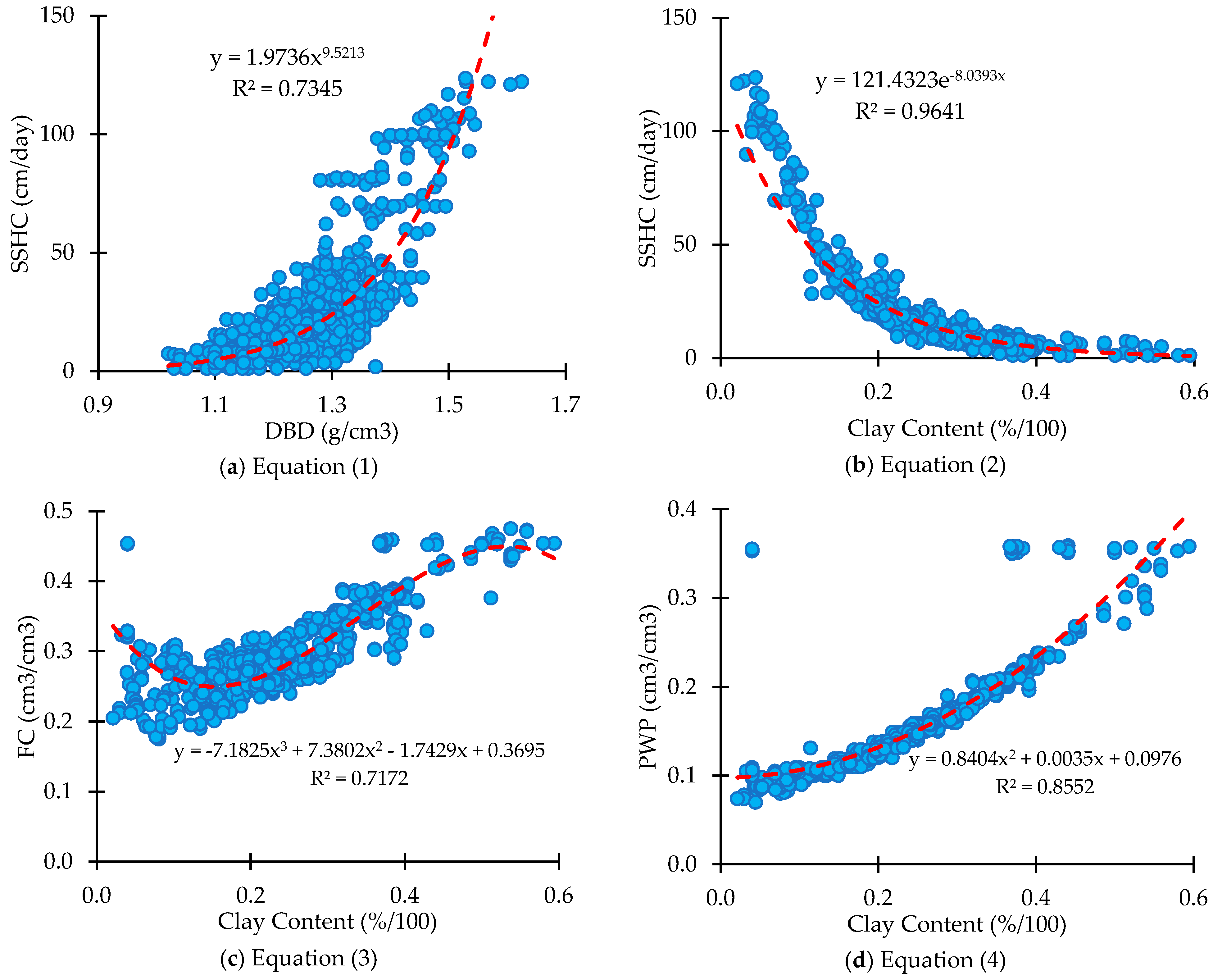
4.1. Statistical Correlations
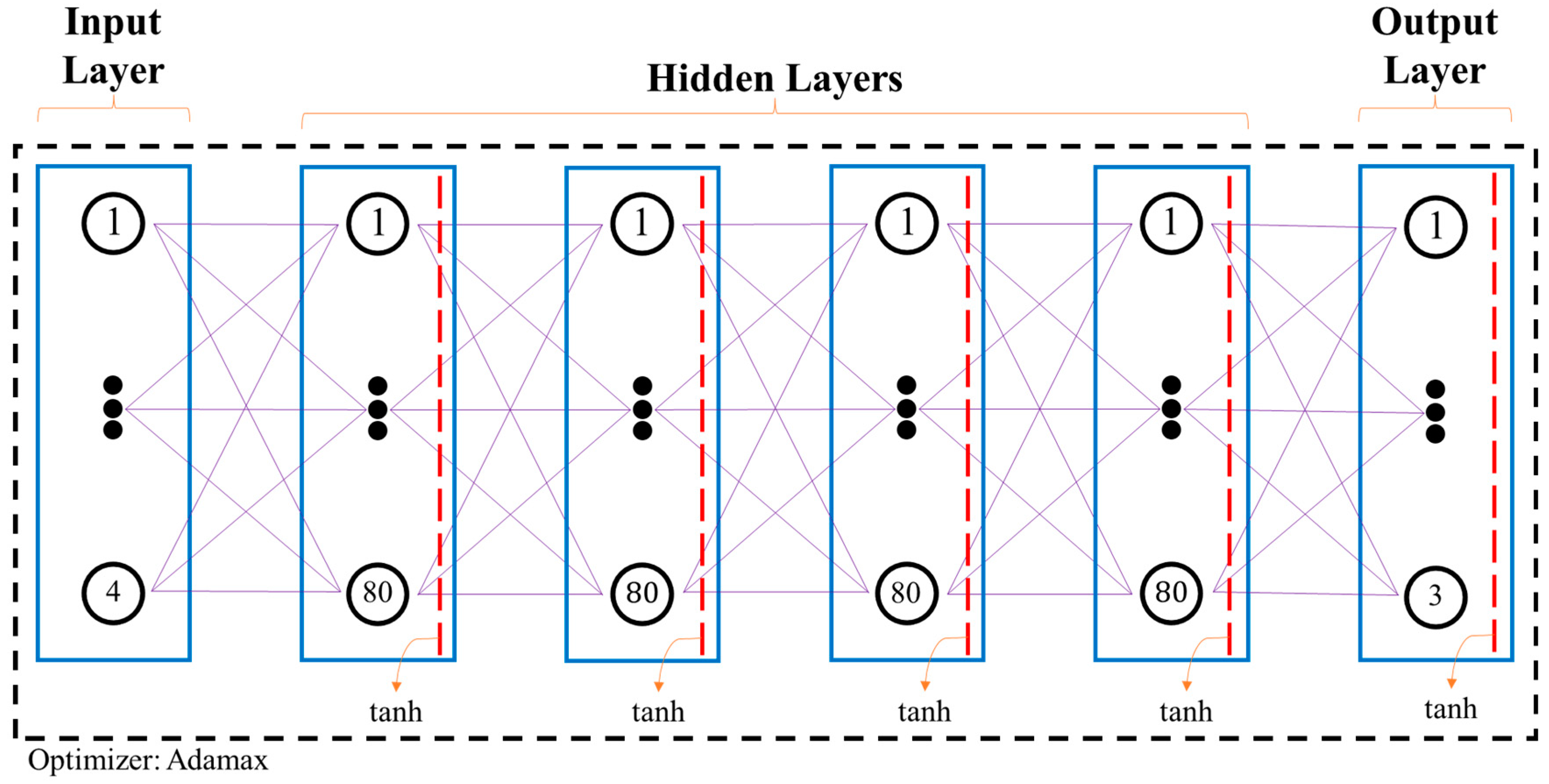
4.2. Artificial Neural Network
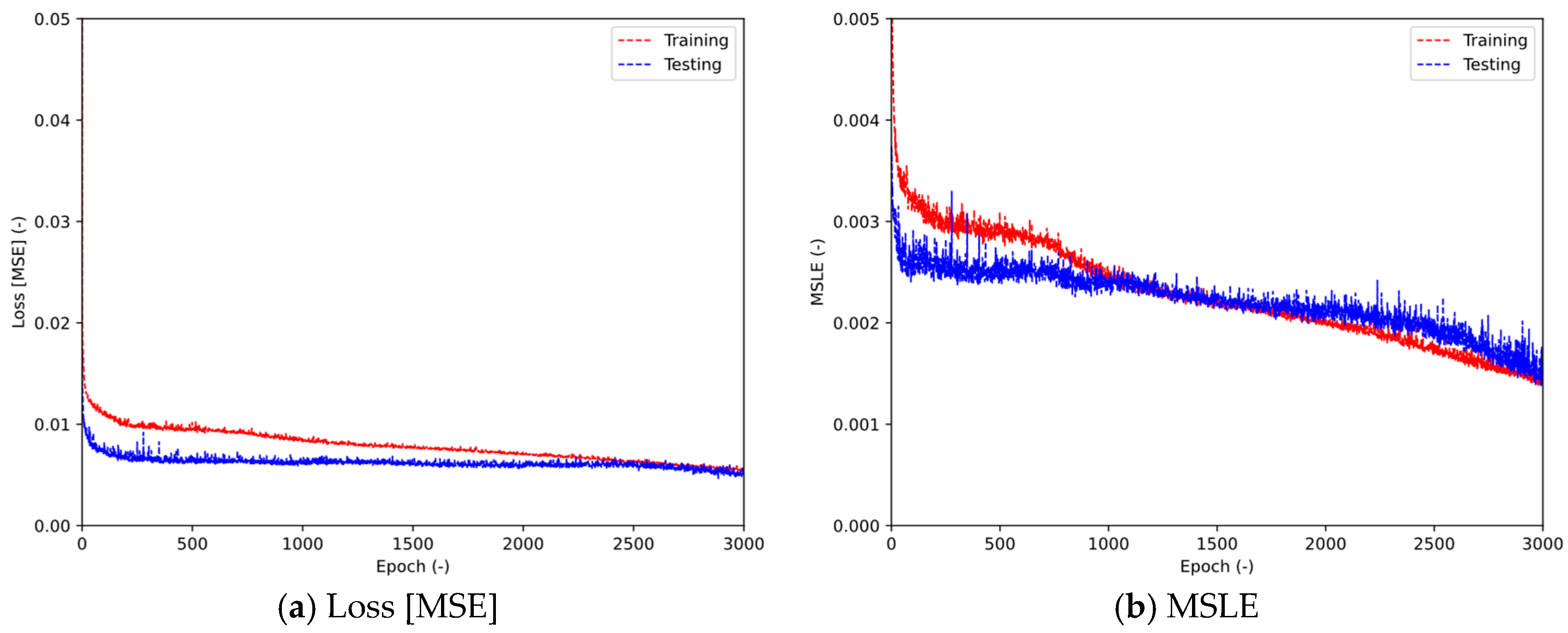
4.2.1. Model’s Precision
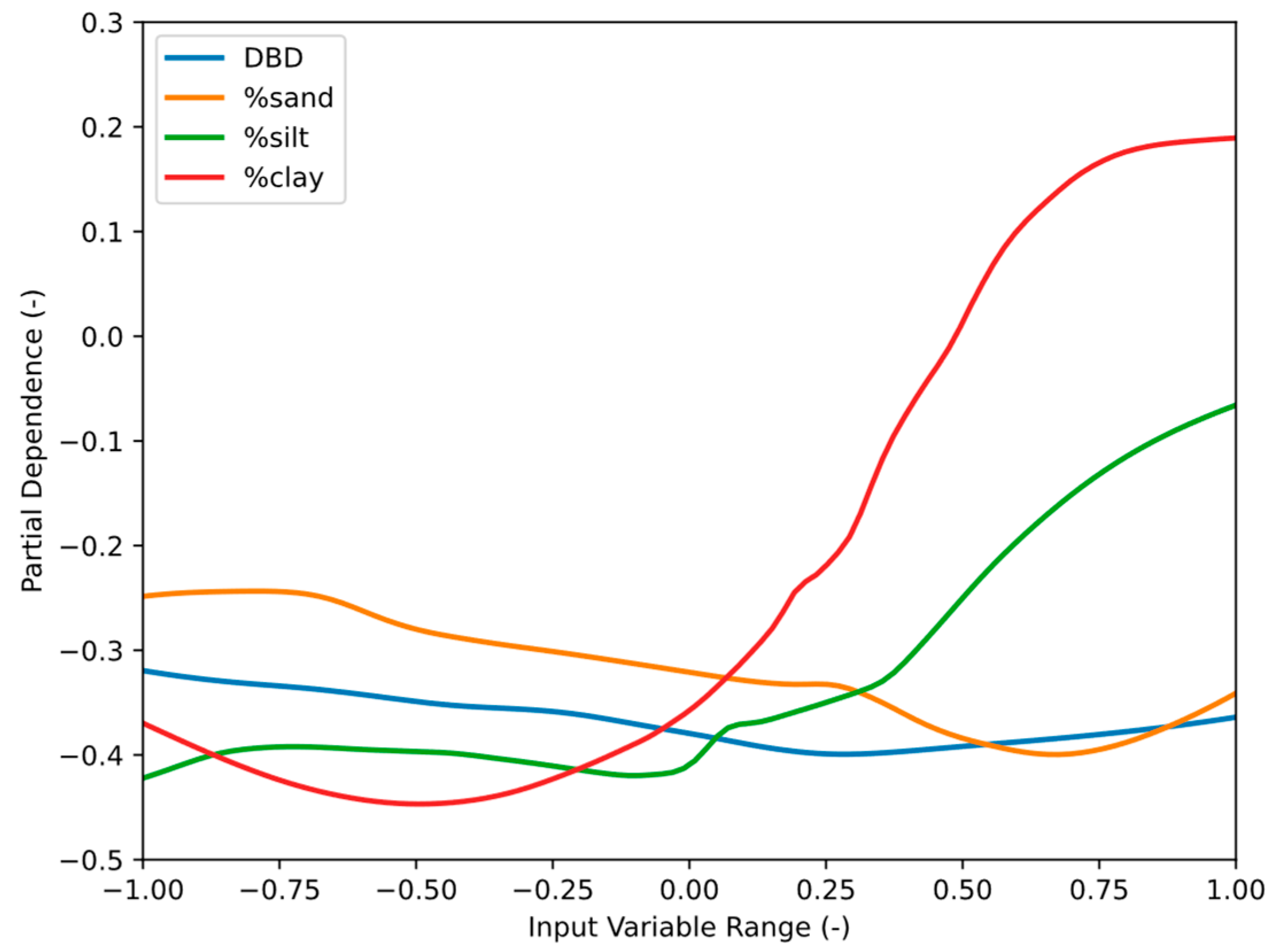
4.2.2. Model’s Explainability
- The clay content has the strongest effect, with a sharp rise, suggesting a strong positive impact on predictions at higher values. The preceding is consistent with the findings discovered in Figure 3, Figure 4 and Figure 5. These graphs showed that clay content is highly correlated with all output variables, and there is a general upward trend between the clay content and two ASWMPs (i.e., FC and PWP).
- The silt content follows a pattern similar to that of clay but with a less pronounced effect. Initially, the silt content shows a decreasing trend, but over time, it begins to rise. This suggests that the model’s output also increases as the silt content augments. Likewise, these results are congruent with Figure 3, where it is clear that there is a general upward trend between the silt content and two ASWMPs (i.e., SSHC and FC).
- The sand content exhibits a mild, oscillating effect, suggesting it moderately influences predictions. The preceding agrees with Figure 4. Regardless, the sand content undergoes a general downward trend, suggesting that the model’s output decreases as the sand content augments. This dependency was previously observed in Figure 3, where two ASWMPs (i.e., FC and PWP) diminished at higher sand content values.
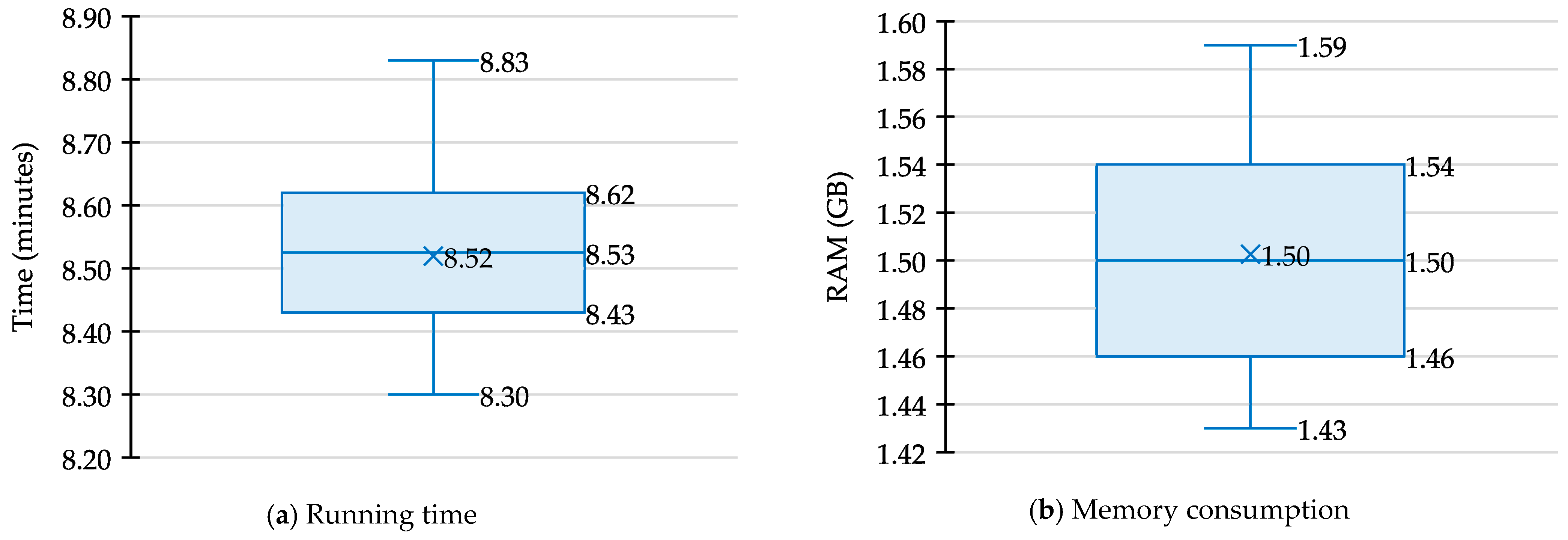
4.2.3. Model’s Efficiency
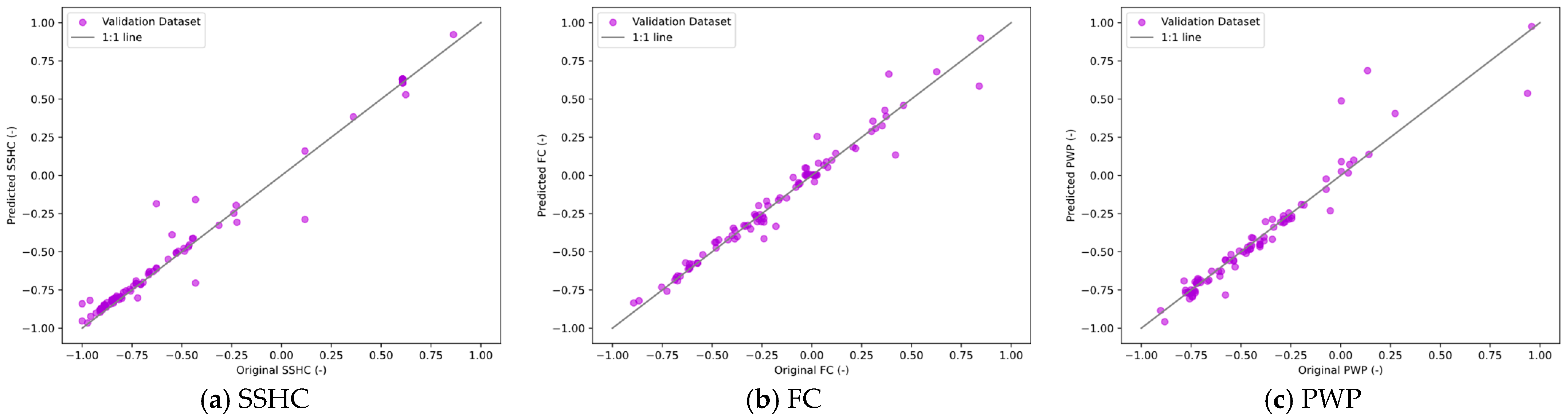
4.2.4. Model’s Generalizability
4.2.5. Comparison Versus Automatic ML-Based Models
5. Discussion
5.1. Comparison of the Proposed Models
5.2. Limitations of the Study
5.3. Real-World Applications
5.4. Future Research Lines
6. Conclusions
- The findings reveal strong correlations between the input variables (i.e., DBD, sand content, silt content, and clay content) and the ASWMPs (i.e., SSHC, FC, and PWP). In addition, mathematical models derived from these correlations demonstrate high accuracy in estimating ASWMPs, making them suitable for preliminary estimations in daily engineering practices.
- DBD correlates significantly with SSHC, confirming that soil density influences its hydraulic conductivity. Meanwhile, clay content strongly correlates with SSHC, FC, and PWP, highlighting its importance in determining these ASWMPs. This underscores the importance of soil texture in water retention and movement.
- This study also highlights the limitations of traditional mathematical models in capturing complex relationships, particularly when compared to advanced computational models such as DNNs. The introduction of a DNN-based model offers a promising approach for improving prediction accuracy and uncovering hidden relationships that may not be evident through traditional statistical methods.
- The developed DNN-based model exhibits exactness between 91.4 and 99.7%, thereby exceeding the accuracy of the proposed statistical correlations (i.e., 71.7–96.4%).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| ASWMPs | Agricultural Soil–Water Management Properties |
| DBD | Dry Bulk Density |
| DNN | Deep Neural Network |
| EDi | Estimated Data Point |
| EDR | Exponential Decay Rate |
| FC | Field Capacity |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MSE | Mean Squared Error |
| MSLE | Mean Squared Logarithm Error |
| ML | Machine Learning |
| ODi | Original/Experimental Data Point |
| PDP | Partial Dependence Plot |
| PWP | Permanent Wilting Point |
| R2 | Coefficient of Determination |
| RAM | Random-Access Memory |
| SHAP | SHapley Additive exPlanations |
| SSHC | Soil Saturated Hydraulic Conductivity |
| tanh | Tangent Hyperbolic |
References
- USDA Practice Code 449: Irrigation Water Management Plan-Small Farms and Gardens; Natural Resources Conservation Service, United States Department of Agriculture: Washington, DC, USA, 2023; pp. 1–8.
- Flores-Saavedra, M.; Plazas, M.; Vilanova, S.; Prohens, J.; Gramazio, P. Induction of Water Stress in Major Solanum Crops: A Review on Methodologies and Their Application for Identifying Drought Tolerant Materials. Sci. Hortic. 2023, 318, 112105. [Google Scholar] [CrossRef]
- Ihuoma, S.O.; Madramootoo, C.A. Recent Advances in Crop Water Stress Detection. Comput. Electron. Agric. 2017, 141, 267–275. [Google Scholar] [CrossRef]
- Silber-Coats, N.; Elias, E.; Fernald, K.; Gagliardi, M. Evaluating Alternative Crops as a Solution to Water Stress in the U.S. Southwest. Agric. Water Manag. 2025, 312, 109439. [Google Scholar] [CrossRef]
- Katsoulas, N.; Elvanidi, A.; Ferentinos, K.P.; Kacira, M.; Bartzanas, T.; Kittas, C. Crop Reflectance Monitoring as a Tool for Water Stress Detection in Greenhouses: A Review. Biosyst. Eng. 2016, 151, 374–398. [Google Scholar] [CrossRef]
- Zhou, Z.; Majeed, Y.; Diverres Naranjo, G.; Gambacorta, E.M.T. Assessment for Crop Water Stress with Infrared Thermal Imagery in Precision Agriculture: A Review and Future Prospects for Deep Learning Applications. Comput. Electron. Agric. 2021, 182, 106019. [Google Scholar] [CrossRef]
- Nasta, P.; Szabó, B.; Romano, N. Evaluation of Pedotransfer Functions for Predicting Soil Hydraulic Properties: A Voyage from Regional to Field Scales across Europe. J. Hydrol. Reg. Stud. 2021, 37, 100903. [Google Scholar] [CrossRef]
- Zhang, Y.; Weihermüller, L.; Toth, B.; Noman, M.; Vereecken, H. Analyzing Dual Porosity in Soil Hydraulic Properties Using Soil Databases for Pedotransfer Function Development. Vadose Zone J. 2022, 21, e20227. [Google Scholar] [CrossRef]
- Kumari, A.; Singh, D.K.; Sarangi, A.; Hasan, M.; Sehgal, V.K. Optimizing Wheat Supplementary Irrigation: Integrating Soil Stress and Crop Water Stress Index for Smart Scheduling. Agric. Water Manag. 2024, 305, 109104. [Google Scholar] [CrossRef]
- Pereira da Silva, A.J.; Rodrigues Pinheiro, E.A.; van Lier, Q. de J. Determination of Soil Hydraulic Properties and Its Implications for Mechanistic Simulations and Irrigation Management. Irrig. Sci. 2020, 38, 223–234. [Google Scholar] [CrossRef]
- Arbat, G.; Masseroni, D. The Use and Management of Agricultural Irrigation Systems and Technologies. Agriculture 2024, 14, 236. [Google Scholar] [CrossRef]
- Kirkham, M.B. Chapter 8: Field Capacity, Wilting Point, Available Water, and the Non-Limiting Water Range. In Principles of Soil and Plant Water Relations; Dana Dreibelbi: New York, NY, USA, 2005; pp. 101–115. [Google Scholar]
- Loiskand, W.; Kammerer, G. Soil Water Management. In Encyclopedia of Agrophysics; Springer: Dordrecht, The Netherlands, 2014; pp. 802–805. [Google Scholar]
- Altchenko, Y.; Villholth, K.G. Mapping Irrigation Potential from Renewable Groundwater in Africa—A Quantitative Hydrological Approach. Hydrol. Earth Syst. Sci. 2015, 19, 1055–1067. [Google Scholar] [CrossRef]
- Weir, P.; Dahlhaus, P. In Search of Pragmatic Soil Moisture Mapping at the Field Scale: A Review. Smart Agric. Technol. 2023, 6, 100330. [Google Scholar] [CrossRef]
- Dinamarca, D.I.; Galleguillos, M.; Seguel, O.; Faúndez Urbina, C. CLSoilMaps: A National Soil Gridded Database of Physical and Hydraulic Soil Properties for Chile. Sci. Data 2023, 10, 630. [Google Scholar] [CrossRef]
- Maynard, J.J.; Yeboah, E.; Owusu, S.; Buenemann, M.; Neff, J.C.; Herrick, J.E. Accuracy of Regional-to-Global Soil Maps for on-Farm Decision-Making: Are Soil Maps “Good Enough”? Soil 2023, 9, 277–300. [Google Scholar] [CrossRef]
- Nenkam, A.M.; Wadoux, A.M.J.C.; Minasny, B.; Silatsa, F.B.T.; Yemefack, M.; Ugbaje, S.U.; Akpa, S.; Van Zijl, G.; Bouasria, A.; Bouslihim, Y.; et al. Applications and Challenges of Digital Soil Mapping in Africa. Geoderma 2024, 449, 117007. [Google Scholar] [CrossRef]
- Marthews, T.R.; Quesada, C.A.; Galbraith, D.R.; Malhi, Y.; Mullins, C.E.; Hodnett, M.G.; Dharssi, I. High-Resolution Hydraulic Parameter Maps for Surface Soils in Tropical South America. Geosci. Model Dev. 2014, 7, 711–723. [Google Scholar] [CrossRef]
- Szabó, B.; Szatmári, G.; Takács, K.; Laborczi, A.; Makó, A.; Rajkai, K.; Pásztor, L. Mapping Soil Hydraulic Properties Using Random-Forest-Based Pedotransfer Functions and Geostatistics. Hydrol. Earth Syst. Sci. 2019, 23, 2615–2635. [Google Scholar] [CrossRef]
- Trejo-Alonso, J.; Fuentes, S.; Morales-Durán, N.; Chávez, C. Evaluation and Development of Pedotransfer Functions and Artificial Neural Networks to Saturation Moisture Content Estimation. Water 2023, 15, 220. [Google Scholar] [CrossRef]
- Keïta, A.; Zorom, M.; Faye, M.D.; Damba, D.D.; Konaté, Y.; Hayde, L.G.; Lidon, B. Achieving Real-World Saturated Hydraulic Conductivity: Practical and Theoretical Findings from Using an Exponential One-Phase Decay Model. Hydrology 2023, 10, 235. [Google Scholar] [CrossRef]
- Picciafuoco, T.; Morbidelli, R.; Flammini, A.; Saltalippi, C.; Corradini, C.; Strauss, P.; Blöschl, G. On the Estimation of Spatially Representative Plot Scale Saturated Hydraulic Conductivity in an Agricultural Setting. J. Hydrol. 2019, 570, 106–117. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Shamshirband, S.; Zare Haghi, D.; Azani, A.; Bonakdari, H.; Ebtehaj, I. Application of Firefly Algorithm-Based Support Vector Machines for Prediction of Field Capacity and Permanent Wilting Point. Soil Tillage Res. 2017, 172, 32–38. [Google Scholar] [CrossRef]
- Chen, S.; Huo, Z.; Xu, X.; Huang, G. A Conceptual Agricultural Water Productivity Model Considering under Field Capacity Soil Water Redistribution Applicable for Arid and Semi-Arid Areas with Deep Groundwater. Agric. Water Manag. 2019, 213, 309–323. [Google Scholar] [CrossRef]
- de Freitas, E.M.; Vital, T.N.B.; Guimarães, G.F.C.; da Silveira, F.A.; Gomes, C.N.; da Cunha, F.F. Determination of the Permanent Wilting Point of Physalis peruviana L. Horticulturae 2023, 9, 873. [Google Scholar] [CrossRef]
- Chagas Torres, L.; Keller, T.; Paiva de Lima, R.; Antônio Tormena, C.; Veras de Lima, H.; Giarola, N.F.B. Impacts of Soil Type and Crop Species on Permanent Wilting of Plants. Geoderma 2021, 384, 114798. [Google Scholar] [CrossRef]
- Zhang, J.; Guan, K.; Peng, B.; Jiang, C.; Zhou, W.; Yang, Y.; Pan, M.; Franz, T.E.; Heeren, D.M.; Rudnick, D.R.; et al. Challenges and Opportunities in Precision Irrigation Decision-Support Systems for Center Pivots. Environ. Res. Lett. 2021, 16, 053003. [Google Scholar] [CrossRef]
- Goyal, A.; Flammini, A.; Morbidelli, R.; Corradini, C.; Govindaraju, R.S. Impact of Observation Thresholds in the Assessment of Field-Scale Soil Saturated Hydraulic Conductivity. J. Hydrol. 2023, 626, 130310. [Google Scholar] [CrossRef]
- Yu, M.; Zhang, J.; Wei, L.; Wang, G.; Dong, W.; Liu, X. Impact of Soil Textures on Agricultural Drought Evolution and Field Capacity Estimation in Humid Regions. J. Hydrol. 2023, 626, 130257. [Google Scholar] [CrossRef]
- Wiecheteck, L.H.; Giarola, N.F.B.; de Lima, R.P.; Tormena, C.A.; Torres, L.C.; de Paula, A.L. Comparing the Classical Permanent Wilting Point Concept of Soil (−15,000 HPa) to Biological Wilting of Wheat and Barley Plants under Contrasting Soil Textures. Agric. Water Manag. 2020, 230, 105965. [Google Scholar] [CrossRef]
- Liu, L.; Ma, X. Prediction of Soil Field Capacity and Permanent Wilting Point Using Accessible Parameters by Machine Learning. AgriEngineering 2024, 6, 2592–2611. [Google Scholar] [CrossRef]
- McCauley, A.; Jones, C.; Jacobsen, J. Soil & Water Management Module I: Basic Soil Properties; Montana State University Extension Services, Montana State University: Bozeman, MT, USA, 2005. [Google Scholar]
- Morales-Durán, N.; Fuentes, S.; Chávez, C. A Soil Database from Queretaro, Mexico for Assessment of Crop and Irrigation Water Requirements. Sci. Data 2023, 10, 429. [Google Scholar] [CrossRef]
- Trejo-Alonso, J.; Fuentes, C.; Chávez, C.; Quevedo, A.; Gutierrez-Lopez, A.; González-Correa, B. Saturated Hydraulic Conductivity Estimation Using Artificial Neural Networks. Water 2021, 13, 705. [Google Scholar] [CrossRef]
- Trejo-Alonso, J.; Quevedo, A.; Fuentes, C.; Chávez, C. Evaluation and Development of Pedotransfer Functions for Predicting Saturated Hydraulic Conductivity for Mexican Soils. Agronomy 2020, 10, 1516. [Google Scholar] [CrossRef]
- Polo-Mendoza, R.; Martinez-Arguelles, G.; Peñabaena-Niebles, R.; Duque, J. Development of a Machine Learning (ML)-Based Computational Model to Estimate the Engineering Properties of Portland Cement Concrete (PCC). Arab. J. Sci. Eng. 2024, 49, 14351–14365. [Google Scholar] [CrossRef]
- Polo-Mendoza, R.; Martinez-Arguelles, G.; Peñabaena-Niebles, R. Environmental Optimization of Warm Mix Asphalt (WMA) Design with Recycled Concrete Aggregates (RCA) Inclusion through Artificial Intelligence (AI) Techniques. Results Eng. 2023, 17, 100984. [Google Scholar] [CrossRef]
- Navarro-Rodríguez, A.; Castro-Artola, O.A.; García-Guerrero, E.E.; Aguirre-Castro, O.A.; Tamayo-Pérez, U.J.; López-Mercado, C.A.; Inzunza-Gonzalez, E. Recent Advances in Early Earthquake Magnitude Estimation by Using Machine Learning Algorithms: A Systematic Review. Appl. Sci. 2025, 15, 3492. [Google Scholar] [CrossRef]
- Wang, T.; Zuo, Y.; Manda, T.; Hwarari, D.; Yang, L. Harnessing Artificial Intelligence, Machine Learning and Deep Learning for Sustainable Forestry Management and Conservation: Transformative Potential and Future Perspectives. Plants 2025, 14, 998. [Google Scholar] [CrossRef]
- Ahsan, M.M.; Mahmud, M.A.P.; Saha, P.K.; Gupta, K.D.; Siddique, Z. Effect of Data Scaling Methods on Machine Learning Algorithms and Model Performance. Technologies 2021, 9, 52. [Google Scholar] [CrossRef]
- Mukhamediev, R.I.; Popova, Y.; Kuchin, Y.; Zaitseva, E.; Kalimoldayev, A.; Symagulov, A.; Levashenko, V.; Abdoldina, F.; Gopejenko, V.; Yakunin, K.; et al. Review of Artificial Intelligence and Machine Learning Technologies: Classification, Restrictions, Opportunities and Challenges. Mathematics 2022, 10, 2552. [Google Scholar] [CrossRef]
- Gombolay, G.Y.; Gopalan, N.; Bernasconi, A.; Nabbout, R.; Megerian, J.T.; Siegel, B.; Hallman-Cooper, J.; Bhalla, S.; Gombolay, M.C. Review of Machine Learning and Artificial Intelligence (ML/AI) for the Pediatric Neurologist. Pediatr. Neurol. 2023, 141, 42–51. [Google Scholar] [CrossRef]
- Tapeh, A.T.G.; Naser, M.Z. Artificial Intelligence, Machine Learning, and Deep Learning in Structural Engineering: A Scientometrics Review of Trends and Best Practices. Arch. Comput. Methods Eng. 2023, 30, 115–159. [Google Scholar] [CrossRef]
- Kujawa, S.; Niedbala, G. Artificial Neural Networks in Agriculture. Agriculture 2021, 11, 497. [Google Scholar] [CrossRef]
- Castillo-Girones, S.; Munera, S.; Martínez-Sober, M.; Blasco, J.; Cubero, S.; Gómez-Sanchis, J. Artificial Neural Networks in Agriculture, the Core of Artificial Intelligence: What, When, and Why. Comput. Electron. Agric. 2025, 230, 109938. [Google Scholar] [CrossRef]
- Attri, I.; Awasthi, L.K.; Sharma, T.P.; Rathee, P. A Review of Deep Learning Techniques Used in Agriculture. Ecol. Inform. 2023, 77, 102217. [Google Scholar] [CrossRef]
- Susanti, R.; Nofendra, R.; Zaini; Suhaimi, M.; Rusydi, M. The Use of Artificial Neural Networks in Agricultural Plants. Andalas J. Electr. Electron. Eng. Technol. 2022, 2, 62–68. [Google Scholar] [CrossRef]
- Basir, M.S.; Chowdhury, M.; Islam, M.N.; Ashik-E-Rabbani, M. Artificial Neural Network Model in Predicting Yield of Mechanically Transplanted Rice from Transplanting Parameters in Bangladesh. J. Agric. Food Res. 2021, 5, 100186. [Google Scholar] [CrossRef]
- Phogat, M.; Kumar, A.; Nandal, D.; Shokhanda, J. A Novel Automating Irrigation Techniques Based on Artificial Neural Network and Fuzzy Logic. J. Phys. Conf. Ser. 2021, 1950, 012088. [Google Scholar] [CrossRef]
- Polo-Mendoza, R.; Martinez-Arguelles, G.; Peñabaena-Niebles, R.; Covilla-Valera, E. Neural Networks Implementation for the Environmental Optimisation of the Recycled Concrete Aggregate Inclusion in Warm Mix Asphalt. Road Mater. Pavement Des. 2024, 25, 941–966. [Google Scholar] [CrossRef]
- de Amorim, L.B.V.; Cavalcanti, G.D.C.; Cruz, R.M.O. The Choice of Scaling Technique Matters for Classification Performance. Appl. Soft Comput. 2023, 133, 109924. [Google Scholar] [CrossRef]
- Sharma, V. A Study on Data Scaling Methods for Machine Learning. Int. J. Glob. Acad. Sci. Res. 2022, 1, 31–42. [Google Scholar] [CrossRef]
- Herwanto, H.W.; Handayani, A.N.; Wibawa, A.P.; Chandrika, K.L.; Arai, K. Comparison of Min-Max, Z-Score and Decimal Scaling Normalization for Zoning Feature Extraction on Javanese Character Recognition. In Proceedings of the 7th International Conference on Electrical, Electronics and Information Engineering (ICEEIE), Malang, Indonesia, 2 October 2021; pp. 457–459. [Google Scholar]
- Sinsomboonthong, S. Performance Comparison of New Adjusted Min-Max with Decimal Scaling and Statistical Column Normalization Methods for Artificial Neural Network Classification. Int. J. Math. Math. Sci. 2022, 2022, 3584406. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Kim, M.K.; Fu, N.; Liu, J.; Wang, J.; Srebric, J. Investigating the Impact of Data Normalization Methods on Predicting Electricity Consumption in a Building Using Different Artificial Neural Network Models. Sustain. Cities Soc. 2024, 118, 105570. [Google Scholar] [CrossRef]
- Shen, S.-L.; Zhang, N.; Zhou, A.; Yin, Z.-Y. Enhancement of Neural Networks with an Alternative Activation Function TanhLU. Expert Syst. Appl. 2022, 199, 117181. [Google Scholar] [CrossRef]
- Fathi, E.; Maleki Shoja, B. Chapter 9: Deep Neural Networks for Natural Language Processing. In Handbook of Statistics; Elsevier: Amsterdam, The Netherlands, 2018; Volume 38, pp. 229–316. [Google Scholar]
- Kandel, I.; Castelli, M.; Popovič, A. Comparative Study of First Order Optimizers for Image Classification Using Convolutional Neural Networks on Histopathology Images. J. Imaging 2020, 6, 92. [Google Scholar] [CrossRef] [PubMed]
- Hassan, E.; Shams, M.Y.; Hikal, N.A.; Elmougy, S. The Effect of Choosing Optimizer Algorithms to Improve Computer Vision Tasks: A Comparative Study. Multimed. Tools Appl. 2023, 82, 16591–16633. [Google Scholar] [CrossRef]
- Yi, D.; Ahn, J.; Ji, S. An Effective Optimization Method for Machine Learning Based on ADAM. Appl. Sci. 2020, 10, 1073. [Google Scholar] [CrossRef]
- Qamar, T.; Bawany, N.Z. Understanding the Black-Box: Towards Interpretable and Reliable Deep Learning Models. PeerJ Comput. Sci. 2023, 9, e1629. [Google Scholar] [CrossRef]
- Hassija, V.; Chamola, V.; Mahapatra, A.; Singal, A.; Goel, D.; Huang, K.; Scardapane, S.; Spinelli, I.; Mahmud, M.; Hussain, A. Interpreting Black-Box Models: A Review on Explainable Artificial Intelligence. Cognit. Comput. 2024, 16, 45–74. [Google Scholar] [CrossRef]
- Taye, M.M. Understanding of Machine Learning with Deep Learning: Architectures, Workflow, Applications and Future Directions. Computers 2023, 12, 91. [Google Scholar] [CrossRef]
- Maier, H.R.; Galelli, S.; Razavi, S.; Castelletti, A.; Rizzoli, A.; Athanasiadis, I.N.; Sanchez-Marre, M.; Acutis, M.; Wu, W.; Humphrey, G.B. Exploding the Myths: An Introduction to Artificial Neural Networks for Prediction and Forecasting. Environ. Model. Softw. 2023, 167, 105776. [Google Scholar] [CrossRef]
- van der Westhuizen, S.; Heuvelink, G.B.M.; Gardner-Lubbe, S.; Clarke, C.E. Biplots for Understanding Machine Learning Predictions in Digital Soil Mapping. Ecol. Inform. 2024, 84, 102892. [Google Scholar] [CrossRef]
- Tatar, A.; Zeinijahromi, A.; Haghighi, M. Explainable Artificial Intelligence in Modelling Hydrogen Gas Solubility in N-Alkanes. Sep. Purif. Technol. 2025, 362, 131741. [Google Scholar] [CrossRef]
- Heger, J.; Min, A.; Zagst, R. Analyzing Credit Spread Changes Using Explainable Artificial Intelligence. Int. Rev. Financ. Anal. 2024, 94, 103315. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, H.; Yao, Y.; Qi, H.; Guo, M.; Su, Y. Factors Affecting Traffic Risks on Bridge Sections of Freeways Based on Partial Dependence Plots. Phys. A Stat. Mech. Its Appl. 2022, 598, 127343. [Google Scholar] [CrossRef]
- Johnson, P.M.; Barbour, W.; Camp, J.V.; Baroud, H. Using Machine Learning to Examine Freight Network Spatial Vulnerabilities to Disasters: A New Take on Partial Dependence Plots. Transp. Res. Interdiscip. Perspect. 2022, 14, 100617. [Google Scholar] [CrossRef]
- Liang, B.; Liu, H.; Cressey, E.L.; Xu, C.; Shi, L.; Wang, L.; Dai, J.; Wang, Z.; Wang, J. Uncertainty of Partial Dependence Relationship between Climate and Vegetation Growth Calculated by Machine Learning Models. Remote Sens. 2023, 15, 2920. [Google Scholar] [CrossRef]
- Alomari, Y.; Andó, M. SHAP-Based Insights for Aerospace PHM: Temporal Feature Importance, Dependencies, Robustness, and Interaction Analysis. Results Eng. 2024, 21, 101834. [Google Scholar] [CrossRef]
- Gunduz, H.I.; Torun, A.T.; Gezgin, C. Post-Fire Burned Area Detection Using Machine Learning and Burn Severity Classification with Spectral Indices in Izmir: A SHAP-Driven XAI Approach. Fire 2025, 8, 121. [Google Scholar] [CrossRef]
- Bilgilioglu, S.S.; Gezgin, C.; Iban, M.C.; Bilgilioglu, H.; Gunduz, H.I.; Arslan, S. Explainable Sinkhole Susceptibility Mapping Using Machine-Learning-Based SHAP: Quantifying and Comparing the Effects of Contributing Factors in Konya, Türkiye. Appl. Sci. 2025, 15, 3139. [Google Scholar] [CrossRef]
- Gong, Y.; Zhang, Q.; Ren, Y.; Liu, Z.; Abu Seman, M.T. Research on Fuzzy Control of Methanol Distillation Based on SHAP (SHapley Additive ExPlanations) Interpretability and Generative Artificial Intelligence. Sensors 2025, 25, 1308. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, M.; Wei, J.; Cen, X.; Du, S.; Wu, Z.; Liu, H.; Wang, W. Interpretable Machine Learning for Multi-Energy Supply Station Revenue Forecasting: A SHAP-Driven Framework to Accelerate Urban Carbon Neutrality. Energies 2025, 18, 1624. [Google Scholar] [CrossRef]
- Guo, Y.; Ma, F.; Li, P.; Guo, L.; Liu, Z.; Huo, C.; Shi, C.; Zhu, L.; Gu, M.; Na, R.; et al. Comprehensive SHAP Values and Single-Cell Sequencing Technology Reveal Key Cell Clusters in Bovine Skeletal Muscle. Int. J. Mol. Sci. 2025, 26, 2054. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, D.; Aldrich, C.; Shao, Q.; O’Connor, L. A Field-Scale Framework for Assessing the Influence of Measure-While-Drilling Variables on Geotechnical Characterization Using a Boruta-SHAP Approach. Mining 2025, 5, 20. [Google Scholar] [CrossRef]
- Lincoln, T.M.; Schlier, B.; Strakeljahn, F.; Gaudiano, B.A.; So, S.H.; Kingston, J.; Morris, E.M.J.; Ellett, L. Taking a Machine Learning Approach to Optimize Prediction of Vaccine Hesitancy in High Income Countries. Sci. Rep. 2022, 12, 2055. [Google Scholar] [CrossRef] [PubMed]
- Choi, H.; Kang, H.J.; Ahn, I.; Gwon, H.; Kim, Y.; Seo, H.; Cho, H.N.; Han, J.Y.; Kim, M.; Kee, G.; et al. Machine Learning Models to Predict the Warfarin Discharge Dosage Using Clinical Information of Inpatients from South Korea. Sci. Rep. 2023, 13, 22461. [Google Scholar] [CrossRef]
- Ghimire, S.; Abdulla, S.; Joseph, L.P.; Prasad, S.; Murphy, A.; Devi, A.; Barua, P.D.; Deo, R.C.; Acharya, R.; Yaseen, Z.M. Explainable Artificial Intelligence-Machine Learning Models to Estimate Overall Scores in Tertiary Preparatory General Science Course. Comput. Educ. Artif. Intell. 2024, 7, 100331. [Google Scholar] [CrossRef]
- Schaub, N.J.; Hotaling, N. Assessing Efficiency in Artificial Neural Networks. Appl. Sci. 2023, 13, 10286. [Google Scholar] [CrossRef]
- Ying, H.; Song, M.; Tang, Y.; Xiao, S.; Xiao, Z. Enhancing Deep Neural Network Training Efficiency and Performance through Linear Prediction. Sci. Rep. 2024, 14, 15197. [Google Scholar] [CrossRef]
- Bielecki, J.; Śmiałek, M. Estimation of Execution Time for Computing Tasks. Clust. Comput. 2023, 26, 3943–3956. [Google Scholar] [CrossRef]
- Wess, M.; Ivanov, M.; Unger, C.; Nookala, A.; Wendt, A.; Jantsch, A. ANNETTE: Accurate Neural Network Execution Time Estimation With Stacked Models. IEEE Access 2021, 9, 3545–3556. [Google Scholar] [CrossRef]
- Chen, W.; Qi, Z.; Akhtar, Z.; Siddique, K. Resistive-RAM-Based In-Memory Computing for Neural Network: A Review. Electronics 2022, 11, 3667. [Google Scholar] [CrossRef]
- Kaur, R.; Asad, A.; Mohammadi, F. A Comprehensive Review of Processing-in-Memory Architectures for Deep Neural Networks. Computers 2024, 13, 174. [Google Scholar] [CrossRef]
- Zeng, Z.; Cui, L.; Qian, M.; Zhang, Z.; Wei, K. A Survey on Sliding Window Sketch for Network Measurement. Comput. Netw. 2023, 226, 109696. [Google Scholar] [CrossRef]
- Pratheeksha, P.; Pranav, B.M.; Nasreen, A. Memory Optimization Techniques in Neural Networks: A Review. Int. J. Eng. Adv. Technol. 2021, 10, 44–48. [Google Scholar] [CrossRef]
- Wieczorek, J.; Guerin, C.; McMahon, T. K-Fold Cross-Validation for Complex Sample Surveys. Stat 2022, 11, 1–10. [Google Scholar] [CrossRef]
- White, J.; Power, S.D. K-Fold Cross-Validation Can Significantly Over-Estimate True Classification Accuracy in Common EEG-Based Passive BCI Experimental Designs: An Empirical Investigation. Sensors 2023, 23, 6077. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Luo, Z.; Su, B.; Song, Z.; Deng, J.; Ji, X. Prediction of Explosion Hazard of Aluminum Powder Two-Phase Mixed System Using Random Forest Based on K-Fold Cross-Validation. J. Loss Prev. Process Ind. 2025, 94, 105574. [Google Scholar] [CrossRef]
- Ait tchakoucht, T.; Elkari, B.; Chaibi, Y.; Kousksou, T. Random Forest with Feature Selection and K-Fold Cross Validation for Predicting the Electrical and Thermal Efficiencies of Air Based Photovoltaic-Thermal Systems. Energy Rep. 2024, 12, 988–999. [Google Scholar] [CrossRef]
- Shebl, A.; Abriha, D.; Dawoud, M.; Ali Hussein Ali, M.; Csámer, Á. PRISMA vs. Landsat 9 in Lithological Mapping—A K-Fold Cross-Validation Implementation with Random Forest. Egypt. J. Remote Sens. Space Sci. 2024, 27, 577–596. [Google Scholar] [CrossRef]
- Ünalan, S.; Günay, O.; Akkurt, I.; Gunoglu, K.; Tekin, H.O. A Comparative Study on Breast Cancer Classification with Stratified Shuffle Split and K-Fold Cross Validation via Ensembled Machine Learning. J. Radiat. Res. Appl. Sci. 2024, 17, 101080. [Google Scholar] [CrossRef]
- H2O.ai H2O AutoML: Automatic Machine Learning. Available online: https://docs.h2o.ai/h2o/latest-stable/h2o-docs/automl.html (accessed on 22 March 2025).
- Matta, A.; Matos, L.M.; Pilastri, A.; Silva, J.M.; Bastos Gomes, M.; Cortez, P. Ahead of Time Prediction of Decorated Particleboard Production Disruptions and Defects Using Single and Multi-Target AutoML. Procedia Comput. Sci. 2024, 246, 2110–2119. [Google Scholar] [CrossRef]
- Papík, M.; Papíková, L. The Possibilities of Using AutoML in Bankruptcy Prediction: Case of Slovakia. Technol. Forecast. Soc. Change 2025, 215, 124098. [Google Scholar] [CrossRef]
- Bagnall, D.K.; Morgan, C.L.S.; Bean, G.M.; Liptzin, D.; Cappellazzi, S.B.; Cope, M.; Greub, K.L.H.; Rieke, E.L.; Norris, C.E.; Tracy, P.W.; et al. Selecting Soil Hydraulic Properties as Indicators of Soil Health: Measurement Response to Management and Site Characteristics. Soil Sci. Soc. Am. J. 2022, 86, 1206–1226. [Google Scholar] [CrossRef]
- Gülser, C.; Candemir, F. Using Soil Moisture Constants and Physical Properties to Predict Saturated Hydraulic Conductivity. Eurasian J. Soil Sci. 2014, 3, 77–81. [Google Scholar] [CrossRef][Green Version]
- Tripathy, K.P.; Mishra, A.K. Deep Learning in Hydrology and Water Resources Disciplines: Concepts, Methods, Applications, and Research Directions. J. Hydrol. 2024, 628, 130458. [Google Scholar] [CrossRef]
- Kay, B.D. Chapter 13: Soil Structure and Organic Carbon: A Review. In Soil Processes and the Carbon Cycle; Taylor Francis Group: Abingdon, UK, 1998; pp. 1–29. [Google Scholar]
- Rawls, W.J.; Pachepsky, Y.A.; Ritchie, J.C.; Sobecki, T.M.; Bloodworth, H. Effect of Soil Organic Carbon on Soil Water Retention. Geoderma 2003, 116, 61–76. [Google Scholar] [CrossRef]
- Panagea, I.S.; Berti, A.; Čermak, P.; Diels, J.; Elsen, A.; Kusá, H.; Piccoli, I.; Poesen, J.; Stoate, C.; Tits, M.; et al. Soil Water Retention as Affected by Management Induced Changes of Soil Organic Carbon: Analysis of Long-Term Experiments in Europe. Land 2021, 10, 1362. [Google Scholar] [CrossRef]
- Bienes, R.; Marques, M.J.; Sastre, B.; García-Díaz, A.; Esparza, I.; Antón, O.; Navarrete, L.; Hernánz, J.L.; Sánchez-Girón, V.; Sánchez del Arco, M.J.; et al. Tracking Changes on Soil Structure and Organic Carbon Sequestration after 30 Years of Different Tillage and Management Practices. Agronomy 2021, 11, 291. [Google Scholar] [CrossRef]
- Younes, A.; Elassad, Z.E.A.; El Meslouhi, O.; Elassad, D.E.A.; Majid, E.-D.A. The Application of Machine Learning Techniques for Smart Irrigation Systems: A Systematic Literature Review. Smart Agric. Technol. 2024, 7, 100425. [Google Scholar] [CrossRef]
- Pathmudi, V.R.; Khatri, N.; Kumar, S.; Abdul-Qawy, A.S.H.; Vyas, A.K. A Systematic Review of IoT Technologies and Their Constituents for Smart and Sustainable Agriculture Applications. Sci. Afr. 2023, 19, e01577. [Google Scholar] [CrossRef]
- Del-Coco, M.; Leo, M.; Carcagnì, P. Machine Learning for Smart Irrigation in Agriculture: How Far along Are We? Information 2024, 15, 306. [Google Scholar] [CrossRef]
- Viana, J.L.; de Souza, J.L.M.; Auler, A.C.; de Oliveira, R.A.; Araújo, R.M.; Hoshide, A.K.; de Abreu, D.C.; da Silva, W.M. Water Dynamics and Hydraulic Functions in Sandy Soils: Limitations to Sugarcane Cultivation in Southern Brazil. Sustainability 2023, 15, 7456. [Google Scholar] [CrossRef]
- Indoria, A.K.; Sharma, K.L.; Reddy, K.S. Chaper 18: Hydraulic Properties of Soil under Warming Climate. In Climate Change and Soil Interactions; Elsevier: Amsterdam, The Netherlands, 2020; pp. 473–508. [Google Scholar]
- Awedat, A.M.; Zhu, Y.; Bennett, J.M.L.; Raine, S.R. The Impact of Clay Dispersion and Migration on Soil Hydraulic Conductivity and Pore Networks. Geoderma 2021, 404, 115297. [Google Scholar] [CrossRef]
- Ahmed, Z.; Gui, D.; Murtaza, G.; Yunfei, L.; Ali, S. An Overview of Smart Irrigation Management for Improving Water Productivity under Climate Change in Drylands. Agronomy 2023, 13, 2113. [Google Scholar] [CrossRef]
- Nam, S.; Kang, S.; Kim, J. Maintaining a Constant Soil Moisture Level Can Enhance the Growth and Phenolic Content of Sweet Basil Better than Fluctuating Irrigation. Agric. Water Manag. 2020, 238, 106203. [Google Scholar] [CrossRef]
- Bwambale, E.; Abagale, F.K.; Anornu, G.K. Smart Irrigation for Climate Change Adaptation and Improved Food Security. In Irrigation and Drainage-Recent Advances; Muhammad, S., Ahmad, F., Eds.; IntechOpen: London, UK, 2022; pp. 1–18. [Google Scholar]
- Li, M.; Zhou, S.; Shen, S.; Wang, J.; Yang, Y.; Wu, Y.; Chen, F.; Lei, Y. Climate-Smart Irrigation Strategy Can Mitigate Agricultural Water Consumption While Ensuring Food Security under a Changing Climate. Agric. Water Manag. 2024, 292, 108663. [Google Scholar] [CrossRef]
- Durmuş, Y.; Arslansoy, G.; Gürbüz, T.K. Impact of Smart Irrigation Systems and Water Management on Climate Change. BIO Web Conf. 2024, 85, 01057. [Google Scholar] [CrossRef]
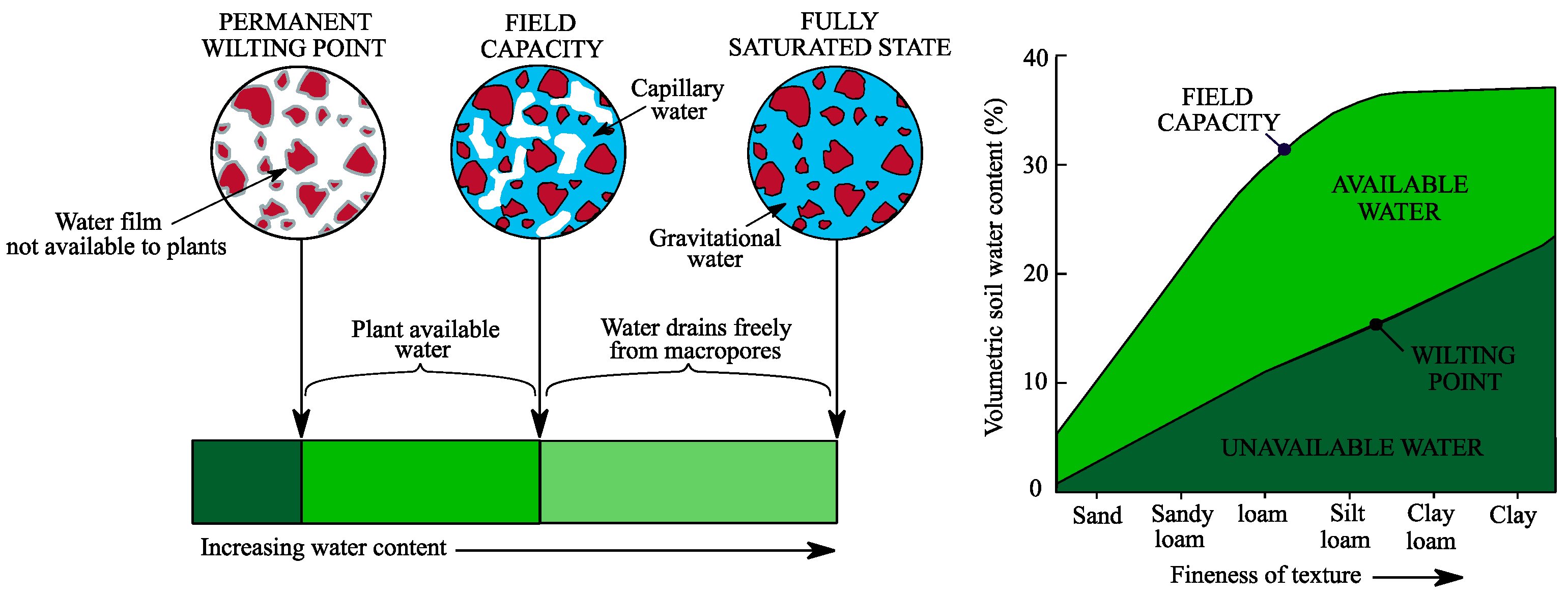
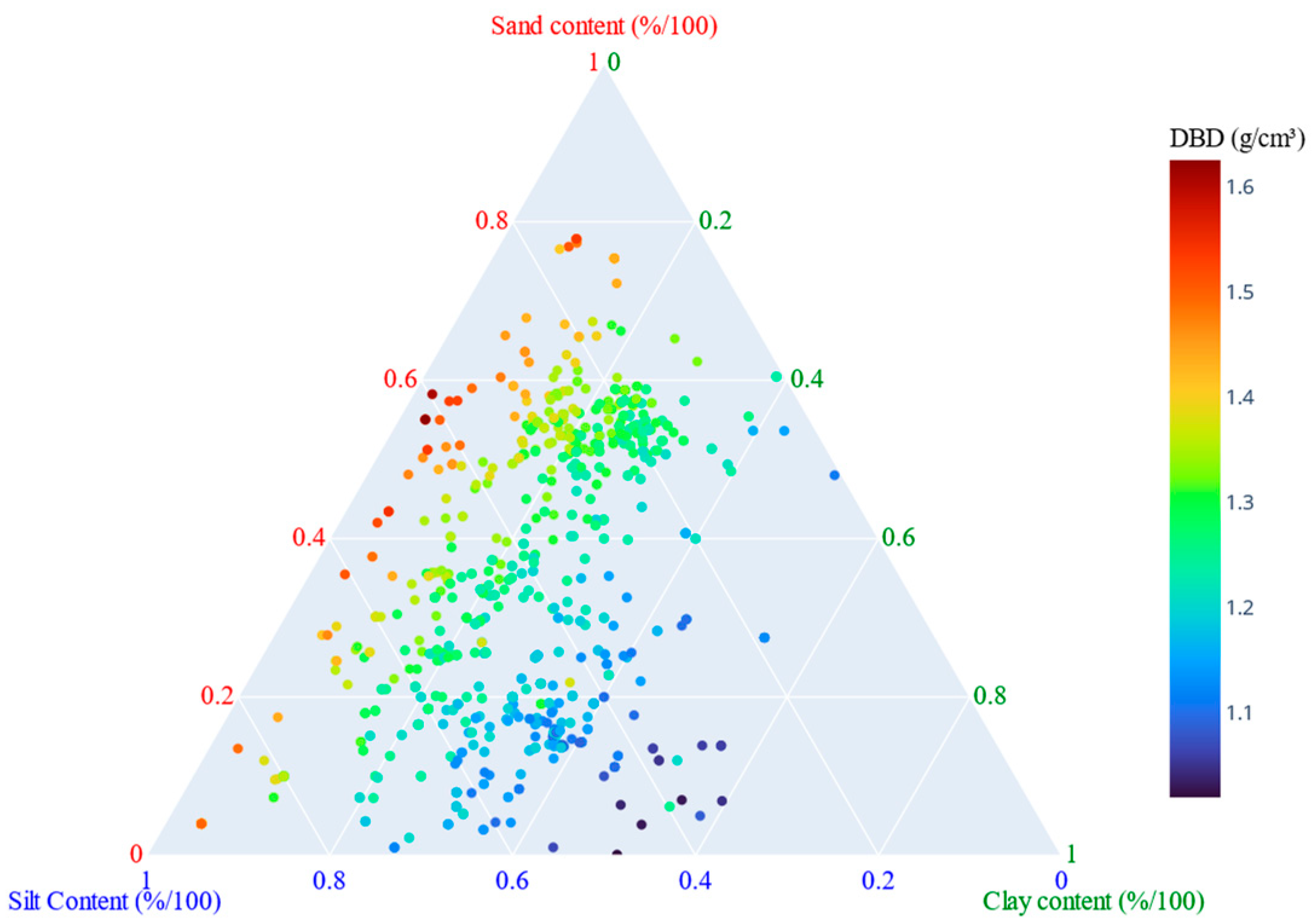
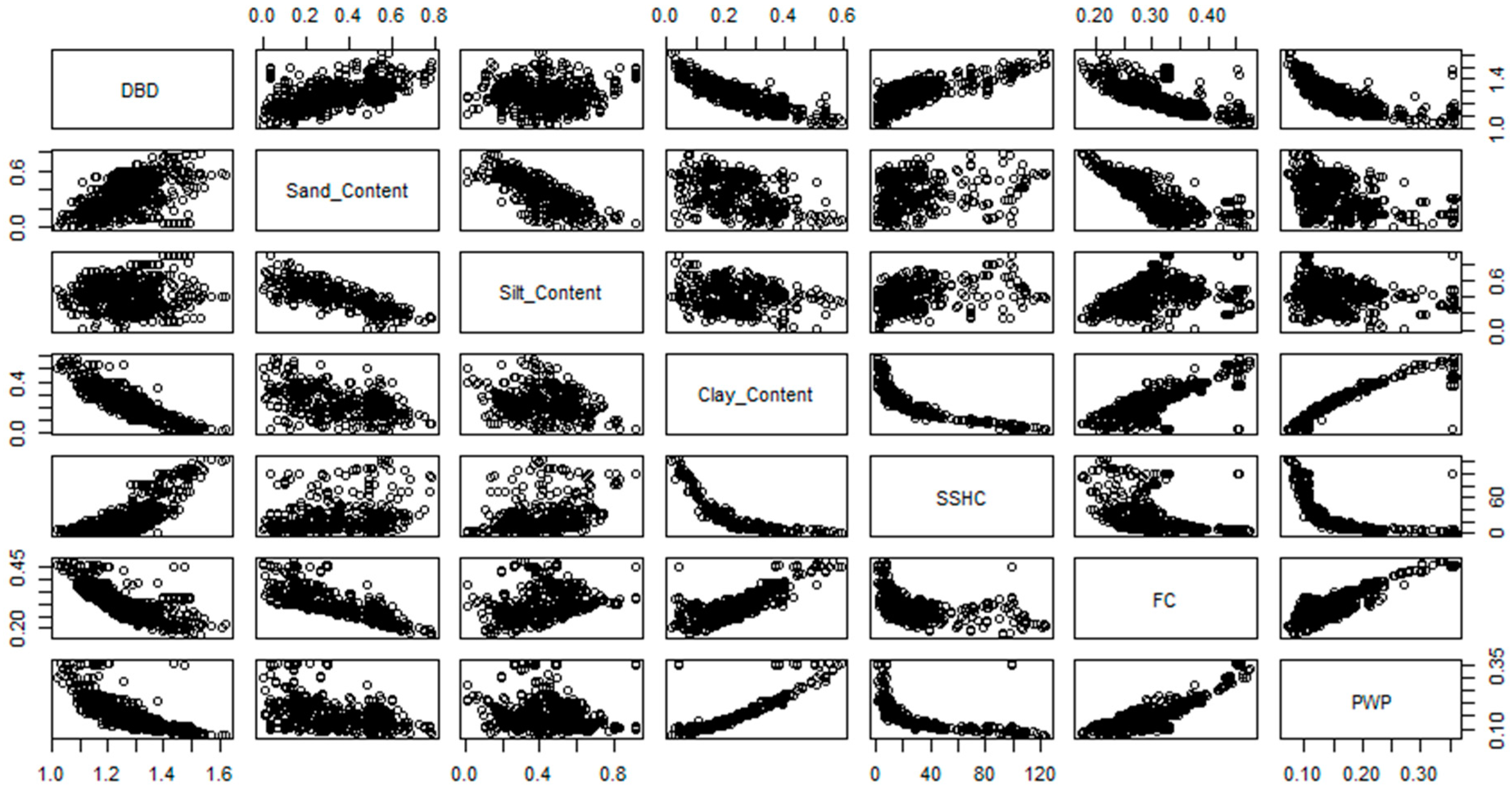



| Soil Textures | Crops | ||
|---|---|---|---|
| Type | No. of Samples (-) | Type | No. of Samples (-) |
| Clay | 30 | Maize (Zea mays L.) | 180 |
| Clay loam | 64 | Alfalfa (Medicago sativa L.) | 135 |
| Loam | 106 | Barley (Hordeum vulgare L.) | 135 |
| Sandy clay | 10 | Oats (Avena sativa L.) | 135 |
| Sandy clay loam | 140 | Sorghum (Sorghum vulgare Pers.) | 135 |
| Sandy loam | 108 | Wheat (Triticum aestivum L.) | 90 |
| Silt | 136 | Beans (Phaseolus vulgaris L.) | 45 |
| Silt loam | 150 | Carrots (Daucus carota L.) | 45 |
| Silty clay | 23 | ||
| Silty clay loam | 133 | ||
| Parameters | Coefficients | 95% Confidence Interval | Statistical Tests | |||||
| Estimate | Std. Error | Lower Limit | Upper Limit | t Value | Pr (>|t|) | F Value | Pr (>F) | |
| Intercept | 0.23512 | 0.04370 | 0.14934 | 0.32089 | 5.380 | 9.53 × 10−8 | ||
| ln (DBD+1) | 0.28034 | 0.03289 | 0.21579 | 0.34488 | 8.524 | <2 ×10−16 | 3344.793 | <2.2 ×10−16 |
| ln (sand+1) | −0.51224 | 0.02604 | −0.56334 | −0.46113 | −19.671 | <2 ×10−16 | 4604.163 | <2.2 ×10−16 |
| ln (silt+1) | −0.23735 | 0.03064 | −0.29749 | −0.17721 | −7.746 | 2.57 ×10−14 | 1126.254 | <2.2 ×10−16 |
| ln (clay+1) | 0.28913 | 0.03195 | 0.22642 | 0.35183 | 9.049 | <2 ×10−16 | 81.893 | <2.2 ×10−16 |
| Model information | ||||||||
| Residual standard error: 0.01726 on 895 degrees of freedom. Multiple R2: 0.911, Adjusted R2: 0.9106. F-statistic: 2289 on 4 and 895 degrees of freedom, p-value: <2.2 ×10−16. | ||||||||
| Variable (Unit) | Minimum | Maximum | Mean | Median | Standard Deviation | Kurtosis | Skewness | |
|---|---|---|---|---|---|---|---|---|
| Input Variables | DBD (g/cm3) | 1.0200 | 1.6250 | 1.2855 | 1.2800 | 0.1127 | −0.5856 | 0.1847 |
| sand (%/100) | 0.0007 | 0.7783 | 0.3114 | 0.2835 | 0.2021 | −1.2870 | 0.1695 | |
| silt (%/100) | 0.0080 | 0.9200 | 0.4691 | 0.4527 | 0.2346 | −0.5320 | 0.5889 | |
| clay (%/100) | 0.0212 | 0.5946 | 0.2195 | 0.2174 | 0.1205 | −0.2931 | 0.2973 | |
| Input Variables | SSHC (cm/day) | 1.2000 | 123.6000 | 34.1541 | 18.7200 | 34.0005 | −0.1770 | 1.1713 |
| FC (cm3/cm3) | 0.1750 | 0.4750 | 0.3013 | 0.2950 | 0.0577 | 0.3122 | 0.6273 | |
| PWP (cm3/cm3) | 0.0700 | 0.3590 | 0.1511 | 0.1380 | 0.0551 | 3.3849 | 1.6833 | |
| Variable (Unit) | Minimum | Maximum | Mean | Median | Standard Deviation | Kurtosis | Skewness | |
|---|---|---|---|---|---|---|---|---|
| Input Variables | DBD (-) | −1.0000 | 1.0000 | −0.1223 | −0.1405 | 0.3725 | −0.5856 | 0.1847 |
| sand (-) | −1.0000 | 1.0000 | −0.2009 | −0.2726 | 0.5198 | −1.2870 | 0.1695 | |
| silt (-) | −1.0000 | 1.0000 | 0.0112 | −0.0248 | 0.5145 | −0.5320 | 0.5889 | |
| clay (-) | −1.0000 | 1.0000 | −0.3083 | −0.3157 | 0.4203 | −0.2931 | 0.2973 | |
| Input Variables | SSHC (-) | −1.0000 | 1.0000 | −0.4615 | −0.7137 | 0.5556 | −0.1770 | 1.1713 |
| FC (-) | −1.0000 | 1.0000 | −0.1577 | −0.2000 | 0.3846 | 0.3122 | 0.6273 | |
| PWP (-) | −1.0000 | 1.0000 | −0.4391 | −0.5294 | 0.3810 | 3.3849 | 1.6833 | |
| Layer | Number of Neurons Received (Nr) | Number of Biases (Nb) | Number of Neurons Contained (Nc) | Number of Parameters [(Nr + Nb) × Nc] |
|---|---|---|---|---|
| First hidden layer | 4 | 1 | 80 | 400 |
| Second hidden layer | 80 | 1 | 80 | 6480 |
| Third hidden layer | 80 | 1 | 80 | 6480 |
| Fourth hidden layer | 80 | 1 | 80 | 6480 |
| Output layer | 80 | 1 | 3 | 243 |
| Total number of trainable parameters | 20,083 | |||
| Working Principle. Adapted from [37,61]. | Adopted Hyperparameter Values | |
|---|---|---|
| Pseudocode | Legend | |
| t, m, u, w = 0, 0, 0, 0 for t = 1 to T do gt = ▽w × w m = β1 × m + (1 − β1) × gt u = max(β2 × u, abs(gt)) lr = lr/(1 − β1^t) w = w − lr × m/(u + ε) end for | t—iteration index m—first moment vector u—exponentially weighted infinity norm w—convergence parameter (weight variable) T—number of iterations to reach the convergence gt—gradient β1—EDR for the first moment estimates β2—EDR for the exponentially weighted infinity norm lr—learning rate ε—small constant for numerical stability | β1 = 0.9 β2 = 0.999 lr = 0.0007 ε = 0.0000001 |
| Output Variable | Goodness-of-Fit Parameter | Dataset | ||
|---|---|---|---|---|
| Training | Testing | Validation | ||
| SSHC | MSE | 0.0011 | 0.0034 | 0.0020 |
| MSLE | 0.1849 | 0.1228 | 0.1266 | |
| MAE | 0.0162 | 0.0252 | 0.0207 | |
| MAPE | 0.1377 | 0.1460 | 0.0453 | |
| R2 | 0.9966 | 0.9873 | 0.9923 | |
| FC | MSE | 0.0033 | 0.0038 | 0.0031 |
| MSLE | 0.0069 | 0.0054 | 0.0035 | |
| MAE | 0.0259 | 0.0342 | 0.0331 | |
| MAPE | 0.1927 | 0.1793 | 0.2495 | |
| R2 | 0.9782 | 0.9736 | 0.9743 | |
| PWP | MSE | 0.0103 | 0.0107 | 0.0070 |
| MSLE | 0.0244 | 0.0138 | 0.0137 | |
| MAE | 0.0341 | 0.0523 | 0.0426 | |
| MAPE | 0.1926 | 0.6112 | 0.9279 | |
| R2 | 0.9325 | 0.9136 | 0.9397 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tóth, B.; Guerrero-Bustamante, O.; Murillo, M.; Duque, J.; Polo-Mendoza, R. Development of Mathematical and Computational Models for Predicting Agricultural Soil–Water Management Properties (ASWMPs) to Optimize Intelligent Irrigation Systems and Enhance Crop Resilience. Agronomy 2025, 15, 942. https://doi.org/10.3390/agronomy15040942
Tóth B, Guerrero-Bustamante O, Murillo M, Duque J, Polo-Mendoza R. Development of Mathematical and Computational Models for Predicting Agricultural Soil–Water Management Properties (ASWMPs) to Optimize Intelligent Irrigation Systems and Enhance Crop Resilience. Agronomy. 2025; 15(4):942. https://doi.org/10.3390/agronomy15040942
Chicago/Turabian StyleTóth, Brigitta, Oswaldo Guerrero-Bustamante, Michel Murillo, Jose Duque, and Rodrigo Polo-Mendoza. 2025. "Development of Mathematical and Computational Models for Predicting Agricultural Soil–Water Management Properties (ASWMPs) to Optimize Intelligent Irrigation Systems and Enhance Crop Resilience" Agronomy 15, no. 4: 942. https://doi.org/10.3390/agronomy15040942
APA StyleTóth, B., Guerrero-Bustamante, O., Murillo, M., Duque, J., & Polo-Mendoza, R. (2025). Development of Mathematical and Computational Models for Predicting Agricultural Soil–Water Management Properties (ASWMPs) to Optimize Intelligent Irrigation Systems and Enhance Crop Resilience. Agronomy, 15(4), 942. https://doi.org/10.3390/agronomy15040942







