Pareto Optimization for Selecting Discriminating Test Locations in Plant Breeding
Abstract
1. Introduction
2. Materials and Methods
2.1. Relative Discriminating Value of Locations
2.2. Precision of Locations
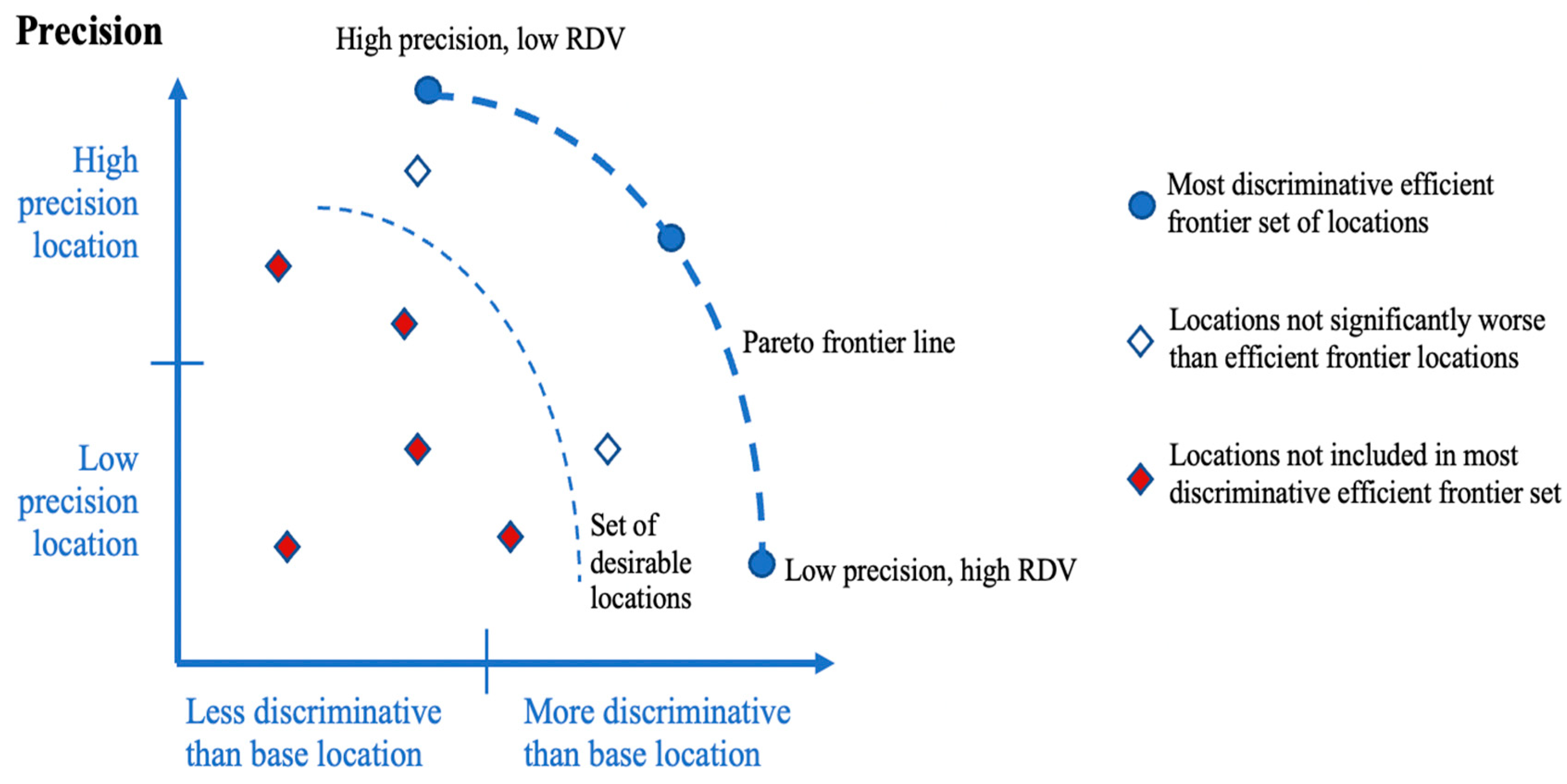
2.3. Pareto Optimization of Precision and RDV
2.4. Data
3. Results
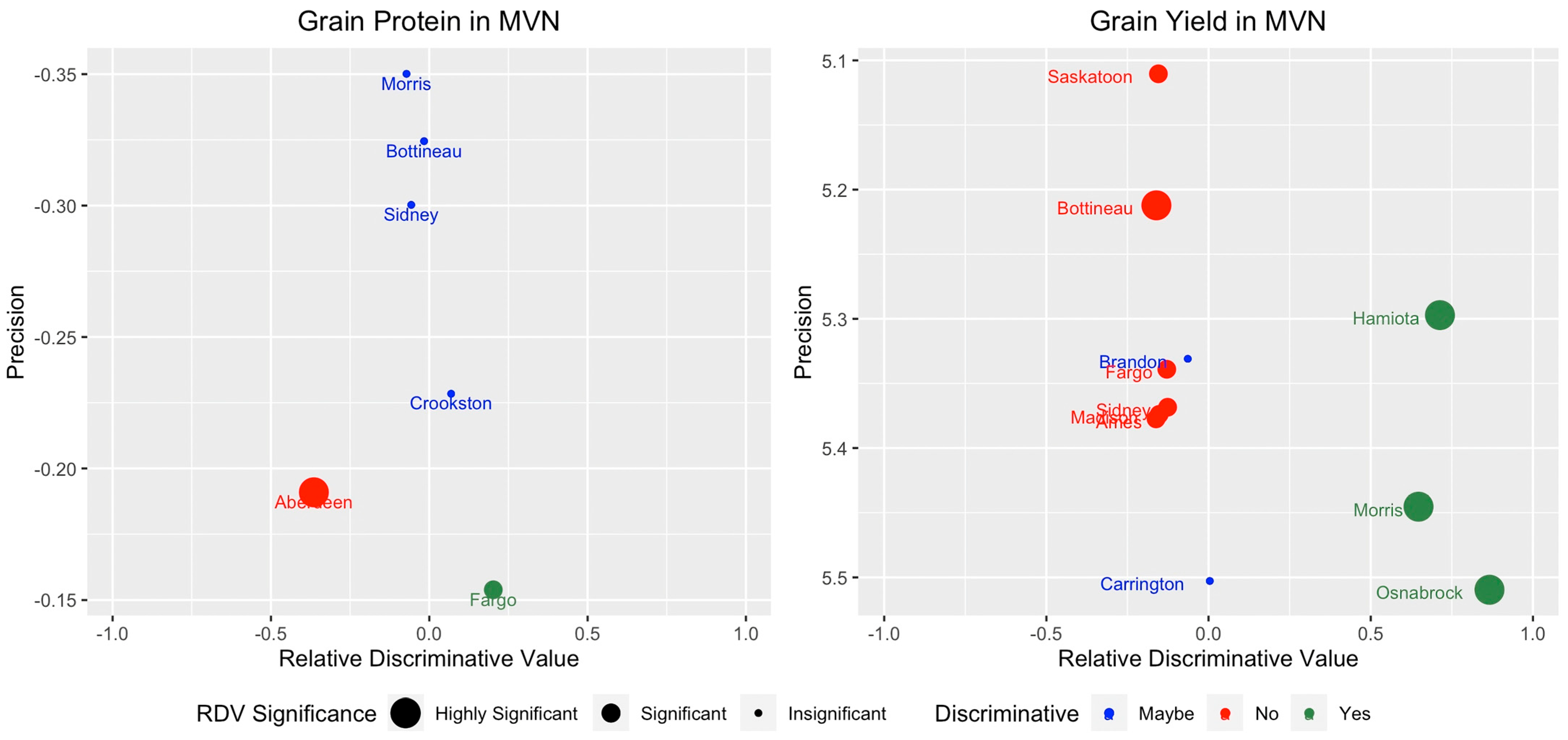
3.1. RDV and Precision Tradeoff for Discriminating Locations
3.2. Pareto Optimality and Discriminative Locations
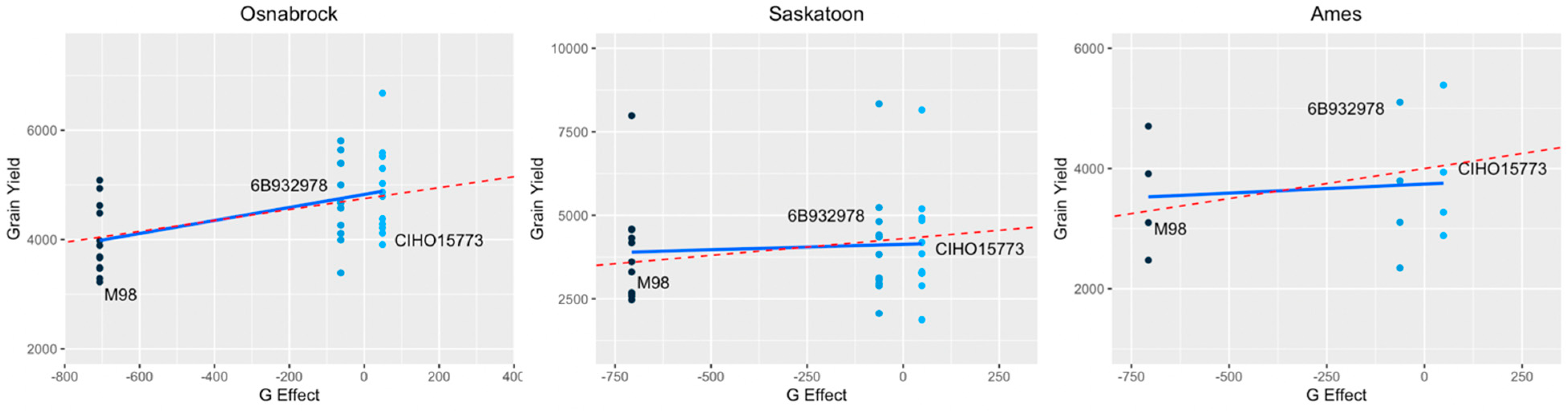
3.3. Insights into Pareto Optimality Tradeoff
4. Conclusions
- A discriminative location should not be defined only in terms of precision or equivalently low variance. Some high-variance locations are discriminative because they are sensitive to the main genotype effect and those will tend to have high variance.
- No location will maximize both precision and the RDV. Instead, there is a tradeoff that can be addressed through a Pareto optimization approach that considers precision and the RDV simultaneously and identifies a set of desirable locations from the perspective of discriminating genotype main effects.
- While there is no ideal location, the Pareto optimization does identify locations that could be excluded from the perspective of discriminating main effects. In our results for grain yield, half of the locations for both regions are found to be less useful.
- The selection of a high RDV versus low variance may depend on the trial stage and the number of observations available. When there is a substantial amount of data, increasing precision may be more important, as in such cases, it is more plausible that sufficient precision can be obtained to discriminate between cultivars with close main effects. Vice versa, when there is a small amount of data available, the biased estimate of the genotype difference that results from using high-RDV locations may be more useful to discriminate between such cultivars.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Locations | B Value (Estimate) | Standard Error | t-Value | p-Value |
|---|---|---|---|---|
| Aberdeen | −0.364 | 0.079 | −4.563 | 10−6 |
| Bottineau | −0.016 | 0.093 | −0.174 | 10−1 |
| Crookston | 0.069 | 0.082 | 0.837 | 10−1 |
| Fargo | 0.202 | 0.087 | 2.311 | 10−2 |
| Morris | −0.071 | 0.084 | −0.847 | 10−1 |
| Sidney | −0.056 | 0.090 | −0.626 | 10−1 |
| Locations | B Value (Estimate) | Standard Error | t-Value | p-Value |
|---|---|---|---|---|
| Ames | −0.161 | 0.075 | −2.154 | 10−2 |
| Bottineau | −0.160 | 0.059 | −2.711 | 10−3 |
| Brandon | −0.064 | 0.070 | −0.903 | 10−1 |
| Carrington | 0.003 | 0.058 | 0.065 | 10−1 |
| Fargo | −0.128 | 0.059 | −2.181 | 10−2 |
| Hamiota | 0.713 | 0.132 | 5.388 | 10−8 |
| Madison | −0.152 | 0.059 | −2.553 | 10−2 |
| Morris | 0.647 | 0.090 | 7.162 | 10−13 |
| Osnabrock | 0.866 | 0.094 | 9.157 | 10−20 |
| Saskatoon | −0.154 | 0.068 | −2.250 | 10−2 |
| Sidney | −0.126 | 0.059 | −2.110 | 10−2 |
| Conrad | −0.194 | 0.088 | −2.189 | 10−2 |
| Fairfield | 0.085 | 0.066 | 1.291 | 10−1 |
| IdahoFalls | −0.298 | 0.061 | −4.813 | 10−6 |
| Pullman | 0.034 | 0.077 | −0.443 | 10−1 |
| Locations | B Value (Estimate) | Standard Error | t-Value | p-Value |
|---|---|---|---|---|
| Aberdeen | 0.271 | 0.071 | 3.810 | 10−4 |
| Conrad | −0.176 | 0.077 | −2.264 | 10−2 |
| Fairfield | 0.157 | 0.072 | 2.180 | 10−2 |
| Fargo | −0.237 | 0.067 | −3.492 | 10−4 |
| Hettinger | 0.060 | 0.072 | 0.835 | 10−1 |
| IdahoFalls | 0.152 | 0.071 | 2.140 | 10−2 |
| KlamathFalls | −0.110 | 0.078 | −1.402 | 10−1 |
| Langdon | −0.270 | 0.080 | −3.364 | 10−4 |
| Logan | 0.247 | 0.072 | 3.423 | 10−4 |
| Manhattan | 0.790 | 0.204 | 3.860 | 10−4 |
| McVille | 0.617 | 0.116 | 5.299 | 10−7 |
| Moscow | 0.653 | 0.249 | 2.622 | 10−3 |
| Potlatch | −0.267 | 0.082 | −3.251 | 10−3 |
| Powell | 0.331 | 0.070 | 4.679 | 10−6 |
| Saskatoon | −0.144 | 0.064 | −2.234 | 10−2 |
| Sterling | −0.194 | 0.077 | −2.499 | 10−2 |
| Tetonia | −0.145 | 0.072 | −1.998 | 10−2 |
| Tulelake | 0.009 | 0.078 | 0.114 | 10−1 |
| Williston | −0.025 | 0.071 | −0.355 | 10−1 |
| Locations in MVN | Locations in WRN | ||||||
|---|---|---|---|---|---|---|---|
| Grain Protein | Precision | Grain Yield | Precision | Grain Protein | Precision | Yield | Precision |
| Aberdeen | −0.190 | Ames | 5.377 | Conrad | −0.355 | Aberdeen | 5.656 |
| Bottineau | −0.324 | Bottineau | 5.212 | Fairfield | −0.133 | Conrad | 5.622 |
| Crookston | −0.228 | Brandon | 5.330 | IdahoFalls | −0.092 | Fairfield | 5.354 |
| Fargo | −0.153 | Carrington | 5.502 | Pullman | −0.149 | Fargo | 5.505 |
| Morris | −0.350 | Fargo | 5.339 | Hettinger | 5.738 | ||
| Sidney | −0.300 | Hamiota | 5.297 | IdahoFalls | 5.765 | ||
| Madison | 5.373 | KlamathFalls | 5.386 | ||||
| Morris | 5.445 | Langdon | 5.796 | ||||
| Osnabrock | 5.509 | Logan | 5.539 | ||||
| Saskatoon | 5.110 | Manhattan | 5.511 | ||||
| Sidney | 5.368 | McVille | 5.562 | ||||
| Moscow | 5.736 | ||||||
| Potlatch | 5.849 | ||||||
| Powell | 5.442 | ||||||
| Saskatoon | 5.316 | ||||||
| Sterling | 5.309 | ||||||
| Tetonia | 5.359 | ||||||
| Tulelake | 5.863 | ||||||
| Williston | 5.365 | ||||||
| Regression Model p Values | ||||
|---|---|---|---|---|
| Base Location | Osnabrock | Morris | Hamiota | Saskatoon |
| Osnabrock | - | 10−2 * | 10−1 | 10−23 ** |
| Morris | 10−2 * | - | 10−1 | 10−16 ** |
| Hamiota | 10−1 | 10−1 | - | 10−10 ** |
| Regression Model p Value | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Base Location | Williston | Sterling | Fargo | Saskatoon | Tetonia | McVille | Manhattan | Moses Lake | Langdon |
| MosesLake | 2.031 10−11 ** | 1.264 10−14 ** | 1.100 10−16 ** | 1.181 10−14 ** | 6.115 10−14 ** | 7.131 10−2 * | 5.827 10−1 | - | 3.565 10−16 ** |
| Manhattan | 6.878 10−5 ** | 2.041 10−6 ** | 4.650 10−7 ** | 4.023 10−6 ** | 5.263 10−6 ** | 4.411 10−1 | - | 5.827 10−1 | 3.562 10−7 ** |
| McVille | 3.691 10−8 ** | 1.921 10−11 ** | 1.011 10−13 ** | 1.521 10−11 ** | 9.591 10−11 ** | - | 4.411 10−1 | 7.131 10−2 * | 4.593 10−13 ** |
| Tetonia | 9.944 10−2 * | 5.427 10−1 | 1.926 10−1 | 9.830 10−1 | - | 9.591 10−11 ** | 5.263 10−6 ** | 6.115 10−14 ** | 1.298 10−1 |
| Saskatoon | 6.624 10−2 * | 4.887 10−1 | 1.305 10−1 | - | 9.830 10−1 | 1.521 10−11 ** | 4.023 10−6 ** | 1.181 10−13 ** | 9.264 10−2 * |
| Fargo | 1.876 10−3 ** | 5.684 10−1 | - | 1.305 10−1 | 1.926 10−1 | 1.011 10−13 ** | 4.650 10−7 ** | 1.100 10−16 ** | 6.684 10−1 |
| Sterling | 3.011 10−2 * | - | 5.684 10−1 | 4.887 10−1 | 5.427 10−1 | 1.921 10−11 ** | 2.041 10−6 ** | 1.264 10−14 ** | 3.790 10−1 |
| Langdon | 2.354 10−3 ** | 3.790 10−1 | 6.684 10−1 | 9.264 10−2 * | 1.298 10−1 | 4.593 10−13 ** | 3.562 10−7 ** | 3.565 10−16 ** | - |
References
- Neyhart, J.L.; Gutierrez, L.; Smith, K.P. Optimizing the choice of test locations for multitrait genotypic evaluation. Crop Sci. 2022, 62, 192–202. [Google Scholar] [CrossRef]
- Yan, W. GGE biplot: A Windows application for graphical analysis of multi environment trial data and other types of two- way data. Agron. J. 2001, 93, 1111–1118. [Google Scholar] [CrossRef]
- Yan, W.; Kang, M.S. GGE Biplot Analysis: A Graphical Tool for Breeders, Geneticist, and Agronomists; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Gauch, H.G., Jr. Statistical Analysis of Yield Trials by AMMI and GGE. Crop Sci. 2006, 46, 1488–1500. [Google Scholar] [CrossRef]
- Gauch, H.G., Jr.; Piepho, H.-P.; Annicchiarico, P. Statistical Analysis of Yield Trials by AMMI and GGE: Further Considerations. Crop Sci. 2008, 48, 866–889. [Google Scholar] [CrossRef]
- Yan, W.; Kang, M.S.; Ma, B.; Woods, S.; Cornelius, P.L. GGE Biplot vs. AMMI Analysis of Genotype-by-Environment Data. Crop Sci. 2007, 47, 643–653. [Google Scholar] [CrossRef]
- Shahriari, Z.; Heidari, B.; Dadkhodale, A. Dissection of genotype × environment interactions for mucilage and seed yield in Plantago species: Application of AMMI and GGE biplot analyses. PLoS ONE 2018, 13, e0196095. [Google Scholar] [CrossRef] [PubMed]
- Hassani, M.; Heidari, B.; Dadkhodale, A.; Stevanato, P. Genotype by environment interaction components underlying variations in root, sugar and white sugar yield in sugar beet (Beta vulgaris L.). Euphytica 2018, 214, 79. [Google Scholar] [CrossRef]
- Bernardo, R. Breeding for Quantitative Traits in Plants, 2nd ed.; Stemma Press: Woodbury, MN, USA, 2010. [Google Scholar]
- Vemireddy, H.; Olafsson, S. A Regression Approach to Identify Discriminating Locations. Crop Sci. 2022, 63, 598–612. [Google Scholar] [CrossRef]
- Clark, S.A.; van der Werf, J. Genomic best linear unbiased prediction (gBLUP) for the estimation of genomic breeding values. Methods Mol. Biol. 2013, 1019, 321–330. [Google Scholar] [CrossRef] [PubMed]
- Piepho, H.P.; Möhring, J.; Melchinger, A.E.; Büchse, A. BLUP for phenotypic selection in plant breeding and variety testing. Euphytica 2008, 161, 209–228. [Google Scholar] [CrossRef]
- Chinchuluun, A.; Pardalos, P.M. A survey of recent developments in multiobjective optimization. Ann. Oper. Res. 2007, 154, 29–50. [Google Scholar] [CrossRef]
- Mattson, C.A.; Messac, A. Pareto frontier based concept selection under uncertainty, with visualization. Optim. Eng. 2005, 6, 85–115. [Google Scholar] [CrossRef]
- Cheng, D.; Yao, Y.; Liu, R.; Li, X.; Guan, B. Precision agriculture management based on a surrogate model assisted multiobjective algorithmic framework. Sci. Rep. 2023, 13, 1142. [Google Scholar] [CrossRef] [PubMed]



| Nursery | Number of Locations | Name of the Locations | ||
|---|---|---|---|---|
| Total | Grain Protein | Grain Yield | ||
| Mississippi Valley Nursery (MVN) | 13 | 7 | 12 | Aberdeen, Ames, Bottineau. Brandon, Carrington, Crookston, Fargo, Hamiota, Madison, Morris, Osnabrock, Saskatoon, Sidney |
| Western Regional Nursery (WRN) | 24 | 5 | 12 | Aberdeen, Bozeman, Conrad, Fairfield, Fargo, Hettinger, Idaho Falls, Klamath Falls, Langdon, Logan, Manhattan, McVille, Minot, Moscow, Moses Lake, Potlatch, Powell, Pullman, Saskatoon, Soda Springs, Sterling, Tetonia, Tulelake, Williston |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiaghadi, M.; Olafsson, S. Pareto Optimization for Selecting Discriminating Test Locations in Plant Breeding. Agronomy 2025, 15, 935. https://doi.org/10.3390/agronomy15040935
Kiaghadi M, Olafsson S. Pareto Optimization for Selecting Discriminating Test Locations in Plant Breeding. Agronomy. 2025; 15(4):935. https://doi.org/10.3390/agronomy15040935
Chicago/Turabian StyleKiaghadi, Mohammadreza, and Sigurdur Olafsson. 2025. "Pareto Optimization for Selecting Discriminating Test Locations in Plant Breeding" Agronomy 15, no. 4: 935. https://doi.org/10.3390/agronomy15040935
APA StyleKiaghadi, M., & Olafsson, S. (2025). Pareto Optimization for Selecting Discriminating Test Locations in Plant Breeding. Agronomy, 15(4), 935. https://doi.org/10.3390/agronomy15040935






