Abstract
This study investigates the collision model of cassava seed stems in precision planters. Utilizing a physical property analyzer and a custom test platform based on collision dynamics principles, we measured and analyzed the forces and recovery coefficients of seed stem collisions. Mixed orthogonal and one-way tests were conducted to identify the main factors affecting the collision recovery coefficient of seed stems, including collision contact material, drop height, seed stem mass, moisture content, drop direction, and seed stem variety. The results from the orthogonal tests indicated that the factors influencing the collision recovery coefficient were ranked as follows: collision contact material > drop height > seed stem mass > moisture content > drop direction > seed stem variety. Notably, the effects of impact contact material, drop height, stem mass, and moisture content were significant, while the effects of drop direction and seed stem variety were relatively insignificant. The one-way test results revealed that the collision recovery coefficients for cassava seed stems with structural steel Q235, rubber sheet, seed stems, and sandy loam soil decreased progressively, with values for SC205 being 0.8172, 0.6975, 0.6649, and 0.6341, respectively, and values for GR4 being 0.7796, 0.7132, 0.6913, and 0.6134, respectively. Furthermore, as drop height increased, the collision recovery coefficient of cassava seed stems decreased; similarly, higher stem mass and moisture content correlated with lower coefficients. To minimize impact during critical stages of cassava planting, transportation, and processing, materials with lower recovery coefficients should be prioritized in equipment design. Incorporating rubber coatings can effectively mitigate collision effects in components such as seed supply and planting mechanisms. These findings provide valuable insights for designing and enhancing key mechanical features in machinery used for planting, transporting, and processing cassava.
1. Introduction
Cassava, a crop renowned for its low cultivation costs and high yields, offers versatile utility across various industries. Its tubers, stems, and leaves find widespread applications in food, medicine, and light industry sectors [1]. The propagation of cassava primarily relies on stem cuttings, typically 10–15 cm long, planted using flat, diagonal, or straight insertion methods. However, the cassava industry faces significant challenges due to scattered planting practices and low mechanization, resulting in stagnant production efficiency, planting area, and yield. This bottleneck in mechanization has become a critical constraint on the development of the cassava industry [2,3,4]. Cassava seed stems are crucial propagation materials in cassava cultivation. Still, their cylindrical and woody characteristics, raised surfaces, and complex physical properties pose significant challenges during mechanized handling processes. Whether in planting, transportation, or processing, these stems often experience collisions and compressions that can lead to damage, impacting the efficiency of mechanization and the integrity of the seed stems [5]. Machines are commonly categorized into real-time seed-cutting and pre-cutting models in planting operations. The former requires manual labor for feeding stalks into cutting mechanisms, which can lead to seed injury and leakage issues [6,7]. On the other hand, pre-cut seed models utilize pre-cut stem sections stored in seed boxes and employ seeding mechanisms for automatic planting. However, the cylindrical nature and complex physical properties of cassava stems pose challenges for existing pre-cut seeders, resulting in poor seed-filling performance and low seed-filling eligibility indices [8]. Additionally, during seeding, cassava seed stems are subjected to varying degrees of damage, primarily through collision and pressure, which significantly impacts crop yield and hinders the advancement of mechanized cassava production [9,10,11,12]. These issues necessitate a deeper understanding of the collision recovery behavior of cassava seed stems to provide theoretical guidance for optimizing mechanized equipment.
During the seed displacement movement, cassava seed stems inevitably experience various forms of collision, crushing, and rolling [13]. These seed stems are composed of shoots, epidermis, bast, xylem, and pith, which exhibit viscoelastic properties. Viscoelastic materials undergo both elastic and plastic deformation processes when subjected to impact [14]. A critical mechanical parameter for cassava seed stems is the collision recovery coefficient, which plays a significant role in understanding their mechanism of action and developing key technologies for seeding components [15]. Furthermore, this coefficient is essential for conducting discrete element simulations [16,17]. At present, extensive research has been conducted on the elasticity characteristics of various crops, including rice, wheat, and oilseed rape [18]. Yang et al. developed a theoretical model and experimental device to study the collision recovery coefficient during the dehulling process of castor capsules, focusing on their interaction with dehulling components [19]. Similarly, Wang et al. investigated the particle collision recovery coefficient of frozen corn kernels by analyzing its dependence on collision velocity. Their research involved experimentally determining the density and three-dimensional model of the kernels, designing a control platform to test collisions, and exploring the effects of factors such as humidity on the recovery coefficient [20]. Feng et al. established a collision mechanics model for potato tubers with soil and potato separating mechanisms and vibrating sieves during impact. They also developed a custom measuring device to determine the recovery coefficient of potato collisions [21]. Yang et al. addressed the limitations of existing experimental equipment in determining the collision recovery coefficient for unstructured agricultural bulk materials (agricultural materials with irregular shapes and composed of numerous discrete particles), focusing on experiments involving different collision angles between fruits [22]. Chen et al. developed a measurement system for evaluating the collision recovery coefficient of half-summer bulbs and analyzed factors influencing this coefficient [23]. Similarly, Liu et al. designed a device simulating a three-dimensional spatial coordinate system to measure the collision recovery coefficient of oil sunflower seeds [24]. However, a comprehensive review of the literature shows that no research has been reported on the determination and analysis of the collision recovery coefficient for cassava seed stems.
This study aims to investigate the collision recovery behavior of cassava seed stems under mechanized planting conditions, with a focus on addressing the key challenge of seed stem damage control in agricultural mechanization. The research has three primary objectives: (1) to determine the main factors influencing the collision recovery coefficient of seed stems; (2) to quantitatively assess the magnitude of their effects on collision recovery behavior; and (3) to establish an empirical dataset for cassava seed stems and analyze collision recovery patterns under single-factor parameter adjustments, thereby filling the critical knowledge gaps highlighted in prior literature. The findings are expected to guide the optimization of material selection and structural design in cassava planting equipment to minimize collision energy transfer. The ultimate goal of this work is to resolve the conflict between mechanical efficiency and seed stem integrity, contributing to the sustainable development of cassava production systems.
2. Analysis of Collision Contact Theory
The collision recovery coefficient is defined, influenced by, and assessed differently [25]. As cassava exhibits elastoplastic material properties [14], the collision process can be theoretically divided into three phases based on elastoplastic collision theory [25]: elastic phase, yield phase, and rebound phase. Figure 1A illustrates the free-fall collision model of cassava seed stems, which assumes that no relative slip occurs during contact between the seed stem and the collision plate. The seed stem is irregular and can be approximately modeled as a spherical convex contact with uniform mass distribution at the point of contact. In Figure 1A, point 1 marks the beginning of the collision between the cassava seed stem and the collision plate. Point 2 signifies the transition from the elastic deformation phase to the plastic deformation phase during the collision between the cassava seed stem and the collision plate. As the seed stem impacts the plate (initiated at point 1), point 2 marks the elastic limit of the stem under compression, beyond which irreversible plastic deformation begins. Point 3 represents the transition from the compression stage to the rebound stage, where the relative velocity is 0 m/s, but the elastic deformation of the seed stem reaches its maximum. Point 4 indicates where the seed stem departs from the collision plate. The segments from points 1 to 3 correspond to the compression stage, while those from points 3 to 4 represent the rebound stage of the seed stem. The biological characteristics of the seed stem can be considered akin to a viscoelastic material, and the collision process between the seed stem and the collision plate is classified as an elastic–plastic collision, as depicted in Figure 1B. In this figure, segments 1 to 3 illustrate the compression stage of the seed stem, during which it and the collision plate are compressed. The deformation of the seed stem in this compression phase consists of an elastic stage (segments 1 to 2) followed by a yield stage (segments 2 to 3). As the deformation of the seed stems increases, the collision contact force F also rises. Due to irreversible plastic deformation during the yielding stage, when the contact force reaches its maximum value, further compression deformation occurs while F begins to decrease. Once maximum compression deformation is achieved, the relative velocity of the seed stem becomes 0 m/s, signaling its entry into the rebound stage (segments 3 to 4). During this stage, it gradually moves away from the collision plate, and both compression deformation and collision contact force F progressively decrease.
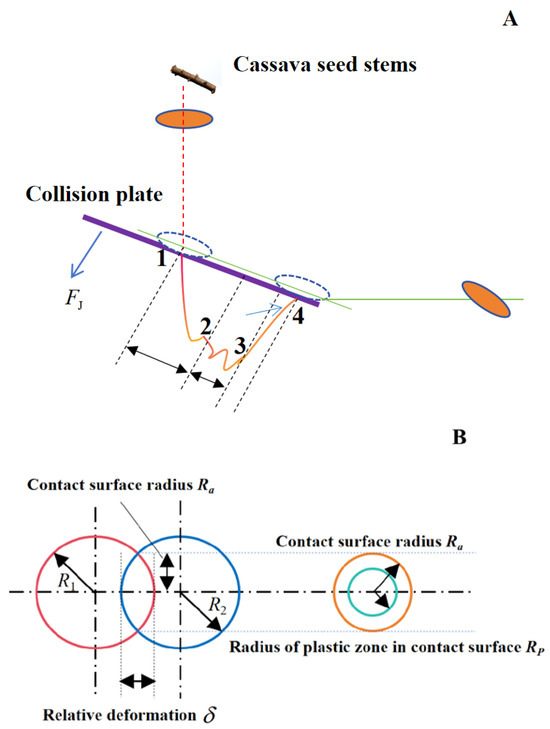
Figure 1.
Theoretical analysis of cassava seed stem collision: (A) theoretical analysis of the collision process of cassava seed stems; (B) collision diagram.
To simplify the calculation, the influence of air resistance and friction on the collision recovery coefficient is not considered. Taking the point of collision at the origin of the coordinates, the deformation at the point of collision of the colliding material is calculated from the impulse at that point [25].
Here, is the deformation at the contact point of the collision material, m; is the density of the collision material, g/mm3; is the modulus of elasticity of the collision material, MPa; is the Poisson’s ratio of the collision material, m/s; is the elastic force of the collision, N; is the time of the collision, s; and is the thickness of the collision material, m.
Let , then Equation (1) is simplified to the following:
where is the deformation at the contact point of the seed stem, m; is the initial velocity of the seed stem collision, m/s; and is the mass of the seed stem, g.
The relative deformation of the seed stem and the collision material in contact with the collision material is expressed as follows:
where is the relative deformation, m.
Joining Equations (2)–(4) and taking the quadratic derivative of , the kinetic system of seed stem collision and the boundary condition are expressed as follows:
During the collision of cassava seed stems, the relationship between the Hertzian contact elastic force and the amount of deformation was analyzed. Equation (5) was utilized to establish the correlation between maximum deformation and collision velocity. Additionally, the coefficient of recovery of the seed stems was associated with the maximum deformation occurring at the point of collision, as well as with the material properties.
2.1. Elastic Deformation Phase
In the elastic collision deformation phase, the relationship between the elastic force and the amount of deformation is approximated by the following:
where is the stiffness coefficient, ; is the equivalent radius of curvature, m; and is the equivalent modulus of elasticity, MPa.
Since the collision material is a flat plate with an infinite radius of curvature, the equivalent radius of curvature is approximately equal to the seed stem equivalent radius. Associated with Equations (5) and (6), the kinetic equations and boundary conditions of the seed stem in the elastic deformation stage are expressed as follows:
where is the elastic deformation end time, s; and is the deformation amount at the end of elastic deformation, m. The seed stem collision recovery coefficient is expressed as follows:
where , and is the coefficient.
2.2. Elastic–Plastic Deformation Stage
With increasing elastic force, the contact region during seed stem collision progressively expands. Under the action of elastic forces, the contact zone evolves from a circular deformation area into an annular configuration, accompanied by the transition from purely elastic to elastoplastic deformation [23]. As illustrated in Figure 1B, the contact surface radius during the elastic stage is expressed as follows:
where , and . Let , and . The above equation can be rewritten as follows:
From Equations (9) and (10) the following two relations can be introduced:
With an expression for the contact force, the equations of motion for the elastic compression phase can be written as follows:
where is the equivalent mass of the two contacting objects, .
According to Hertz contact theory, the distribution of compressive stress in the elastic contact zone is spherical, i.e., the compressive stress can be expressed as follows:
where is the center compressive stress in the contact zone.
Considering Equations (3) and (4), the above equation can be written as follows:
With the increase in contact force, the plastic region in the center part is enlarged gradually, and the elastic contact boundary in the periphery is also enlarged gradually. The contact area can be divided into the inner circular plastic zone and the outer circular elastic zone, with indicating the radius of the plastic zone within the contact surface. In addition, the contact force in the plastic zone is . Assuming that the stress distribution in the elastic ring still adopts the expression of Equation (15), the total contact force F in the elastic ring can be expressed as follows:
Considering Equations (11) and (15), the total contact force in the elastic–plastic compression phase is expressed as follows:
where is the yield stress at the point of collision contact, N. With and , Equation (9) simplifies to the following:
Associated with Equations (5) and (19), the kinetic equations and boundary conditions for the seed stems in the elastic–plastic deformation stage are expressed as follows:
where is the end time of elastic-plastic deformation, s; and is the maximum deformation amount, m.
2.3. Resilient Recovery Phase
At the end of the elastic–plastic deformation of the seed stem, all stored elastic potential energy is converted into the kinetic energy of the seed stem and will make the seed stem rebound with a certain initial velocity. The relationship between elastic force and deformation is expressed as follows:
where is the residual deformation, m.
Associating Equations (5) and (21), the kinetic equations and boundary conditions for the rebound phase of the seed stem collision are expressed as follows:
where is the end time of the recovery phase, s; and is the initial velocity that cassava seed stems have at the end of the recovery phase, m/s.
For the residual deformation , since the elastic force at the end of elastic–plastic deformation is equal to the elastic force at the beginning of rebound, the couplings (19) and (21) can be used. The residual deformation of the cassava seed stems at the time of rebound are expressed as follows:
For the rebound phase [24], then the collision recovery coefficient for the rebound phase of the seed stem is expressed as follows:
where ; ; and , , and are coefficients
Considering that the seed stem collision time is very short, and considering the whole process of seed stem collision rebound [24,25,26], based on the principle of linear superposition, the theoretical model of seed stem collision recovery coefficient is derived as follows:
3. Test Materials and Methods
3.1. Research Framework and Hypotheses
Guided by the theory of collision dynamics and the viscoelastic properties of cassava stems, this study proposes a theoretical framework that, in conjunction with actual cassava production and processing conditions, suggests that the collision recovery coefficient is governed by six candidate parameters: contact material stiffness, cassava variety, seed stem mass, water content, fall direction, and drop height. It was hypothesized that higher contact material stiffness, lower drop height, smaller stem mass, and lower water content would minimize irreversible deformation of cassava and adhesion to the collision plate, with less dissipated energy, thus increasing the collision recovery coefficient. Conversely, softer contact materials, higher drop heights, greater stem mass, and higher water content reduce this coefficient, as these conditions lead to more energy loss through plastic deformation or increased viscosity with the collision plate. Subsequent experimental validation of these hypotheses prioritized orthogonal tests to eliminate interactions between parameters, followed by univariate tests to analyze the individual influence patterns of each dominant factor.
3.2. Test Materials
The research focuses on the cassava seed stems of SC205 (Manihot esculenta Crantz ‘South China 205’) and GR4 (Manihot esculenta Crantz cv. GR No. 4), extensively cultivated in the Guangxi region. These seed stems, provided by the Guangxi Subtropical Crops Research Institute, were pre-cut to lengths of 150 mm following a clearing treatment. The selected stems exhibited a mass ranging from 86.8 to 513.7 g, diameters between 15 and 47 mm, and a water content of 50–80%. Efforts were made to select seed stems of uniform size and good uprightness from various varieties and qualities for the study. The test soil was sourced from the farm test site in the Zhongfeng City North Development Zone, Resource County, Guilin, Guangxi (110°54′ E, 25°48′ N), characterized by parameters including 14.77% water content, 267 kPa soil firmness, and 0.017 MPa soil cohesion. Based on previous research [9,10,27], the study considered common contact materials in seed supply and drop seed movement. The collision objects included structural steel Q235, a rubber plate, seed stems, and soil. Soil specimens were prepared with a height of 20 cm and a diameter of 10 cm, with material properties presented in Table 1 [27,28,29]. Quasi-static uniaxial compression tests were conducted to determine the elastic modulus and Poisson’s ratio of SC205 and GR4 cassava seed stems using a TA-XT2i texture analyzer (load range: 0–50 kg; force accuracy: ±0.0002% FS) within a controlled environment of 25–30 °C. Axial compressive loads were applied to 30 defect-free cylindrical specimens (diameter: 12 mm, length: 20 mm) at a displacement rate of 10 mm/min until fracture. During testing, the equipment automatically recorded axial and calculated the elastic modulus and Poisson’s ratio using real-time strain data. Results from monotonic loading tests were averaged across specimens to ensure reproducibility. Hydrostatic mechanical testing and liquid displacement methods were employed to measure material densities, while peer-reviewed reference tables provided mechanical properties and density values for other materials. Material thickness was measured using vernier calipers with an accuracy of 0.02 mm and a range of 0–150 mm. The technical route for the study is illustrated in Figure 2.

Table 1.
Basic parameters of cassava seed stem specimens and collision materials.
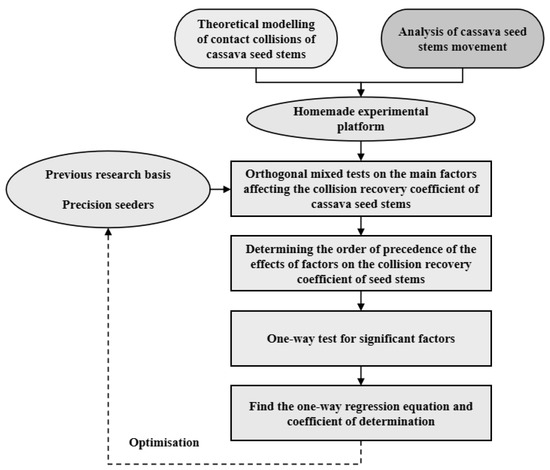
Figure 2.
Methodological framework.
3.3. Test Methods
3.3.1. Mechanical Tests
To ensure the mechanical integrity of cassava seed stems during planting operations, determining their maximum energy absorption capacity prior to impact testing is critical for evaluating their resistance to mechanical damage under dynamic loading conditions. A TA-XT2i texture analyzer (force accuracy: ±0.0002% FS; load range: 0–50 kg) was employed to perform compression tests on seed stems (length: 45 mm) in a controlled ambient temperature environment (25–30 °C). The test configuration is detailed in Figure 3. During the compression test, the seed stems were placed on a flat plate with a loading speed set to 10 mm/min. The test was stopped when the stems were crushed and damaged. The load–displacement data from the compression process were output using post-processing software. The test was repeated 10 times, and the data were imported into Origin 2022 plotting software. The area under the load–displacement curve was calculated, and the average value was taken as the energy absorbed by the cassava stems before failure. Based on the gravitational potential energy formula, the maximum allowable drop height of the cassava seed stems was calculated.
Here, is the vertical distance between the cassava and the collision plate before free fall, m; is the gravitational potential energy of cassava seed stem, J; is the mass of cassava seed stem, g; and is the acceleration of gravity, taken as 9.81 m/s2.

Figure 3.
Mechanical testing apparatus for cassava seed stems: (1) test arm bracket, (2) test arm, (3) sensor probe position, (4) carrier table, and (5) base.
3.3.2. Crash Test
To determine the moisture content of cassava seed stems, the 105 °C drying method is employed using a JC101-3 electric heating blast drying box manufactured by Nantong Jia Cheng Instrument Co., Ltd. (Nantong, China). The process involves cutting the seed stem specimen into three similarly sized blocks and placing them in an aluminum box. After weighing the total mass, the box is placed in the drying oven at 105 °C for 10 continuous hours. Once cooled to room temperature, the box is weighed again to determine the post-drying mass. The difference in weight is used to calculate the water content of the cassava seed stems. The collision recovery coefficient measures the rebound capacity of granular materials and is categorized into tangential, normal, and overall recovery coefficients based on research needs [24,25,26]. This study determined the collision recovery coefficient of seed stems using a mass against fixed surface collision test method [30]. Figure 4B,C show the collision recovery coefficient test setup and seed stem motion analysis. The contact collision plate was mounted on the test bench scale at a 45° inclination to the horizontal plane, and there were screw holes along the edge of the contact collision plate for mounting a guard plate (at the circular position in the center of the collision plate in Figure 4B) in order to place the Q235 steel, rubber, soil block, and seed stem. The collision point is set at the center of the circle in the center of the collision ramp. The seed stems are adjusted to the height of the drop holes by adjusting the nuts. The seed stems are placed in the drop hole position and ensured to be directly above the collision point. The seeds are then made to fall freely to the collision contact plate, collide with the collision material, make a parabolic movement after rebound, and finally fall to the sand plate. Practical steel tape was used to measure the distance of the falling point of the seed stem from the vertical line perpendicular to the ground at the collision point. Finally, the horizontal displacement of the tuber movement falling into the sand tray when there is a support base and the horizontal displacement of the seed stem movement falling into the sand tray when there is no support base were measured. In addition, the steel tape was used to directly measure the vertical distance between the collision point and the falling point, i.e., the vertical displacements and . The relevant formulas in the principle of the test were used to calculate the coefficient of recovery of the collision.
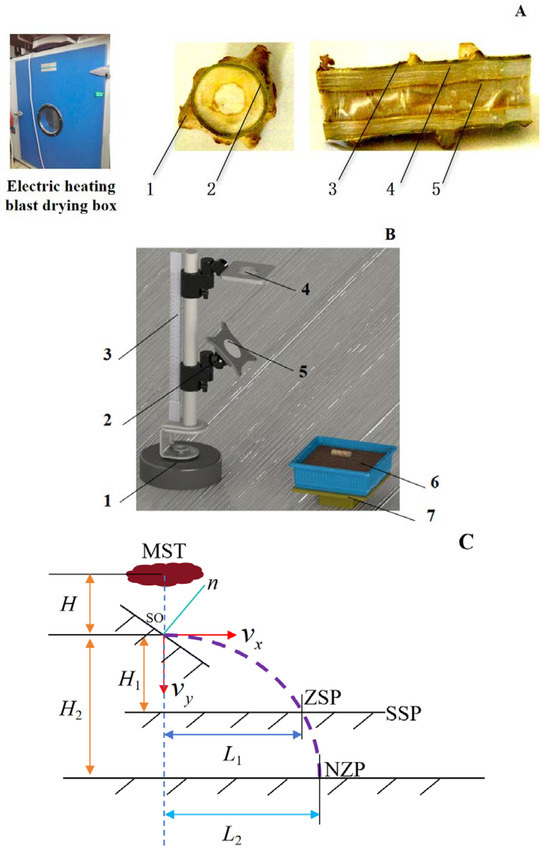
Figure 4.
Test rig and motion analysis for determining the collision recovery coefficient of seed stems: (A) structural diagram of sliced cassava seed stems (1. bud eye, 2. phloem, 3. epidermis, 4. xylem, 5. medulla); (B) test device for determining collision recovery coefficient (1. support base, 2. 45° collision ramp height adjustment screw, 3. Scale bar, 4. drop hole, 5. 45° collision ramp, 6. sand tray, 7. support base); (C) analysis of seed stem contact collision motion.
3.4. Crash Test Device and Test Principle
In Figure 4C, let the position MST be the seed stem dropping place, SPP be the position of the sand plate plane with the support base, SO be the collision contact position, ZSP be the dropping position of the seed stem on the sand plate when there is a support base, and NZP be the dropping position of the seed stem on the sand plate when there is no support base. The height is the displacement of the seed stem during the free-fall process before it collides with the collision ramp with a 45°inclination angle; and and are the horizontal and vertical direction partial velocities of the seed stem at the instant of collision, respectively.
The seed stem falls freely from the height and collides with the collision material on the collision plate. To simplify the analysis, ignoring the effect of air resistance, the kinematics equation can be obtained as follows:
where is the instantaneous velocity of the seed stem before collision, m/s; and is the falling time, s. Using Equation (18), the instantaneous velocity of the seed stem before collision at the SO collision contact location is expressed as follows:
The seed stem and collision material on the collision plate after collision exhibit parabolic motion. The motion is decomposed into horizontal uniform linear motion and vertical motion with constant acceleration, following uniformly variable linear motion.
Here, is the cassava seed stem rebound movement time.
Measure , , , and , and substitute them into Equation (29) to obtain the horizontal and vertical partial velocities of the seed stems at the instant after collision as follows:
Using the theoretical analysis of cassava seed stem collision and the definition of collision recovery coefficient [30,31], it was calculated as shown in Equation (31).
where is the seed stem collision recovery coefficient; is the normal partial velocity of the contact point at the end of the seed stem collision, m/s; and is the normal partial velocity of the contact point at the beginning of the seed stem collision, m/s.
3.5. Experimental Design
3.5.1. Orthogonal Test Factors and Levels Crash Test
The test was divided into two steps. In Step 1, an orthogonal mixed test was conducted to assess the order of influence of various factors on the collision recovery coefficient of seed stems, focusing on the main influencing factors, including collision contact material, drop height, seed stem mass, moisture content, drop direction, and seed stem variety. In Step 2, a one-way test was performed on the significant factors to derive the one-way regression equation and its determination coefficient, Mixed orthogonal test factors and levels as shown in Table 2.

Table 2.
Mixed orthogonal test factors and levels.
3.5.2. One-Way Test Factors and Levels
From the mixed orthogonal test, it was determined that the significant factors influencing the collision recovery coefficient of seed stems include contact material, drop height, seed stem mass, and moisture content. Since the contact material factor could not be quantified, only a one-factor test was conducted. The single-factor levels for drop height were set at 400 mm, 500 mm, 600 mm, 700 mm, 800 mm, and 900 mm. For seed stem mass , the levels were established at 140.82 g, 194.94 g, 287.72 g, 375.56 g, 425.21 g, and 482.91 g. The moisture content levels were 55.44%, 58.84%, 64.77%, 71.57%, and 76.39%. To achieve these moisture content levels, seed stems were baked at 105 °C for durations of 5, 6, 8, 10, and 12 h, after which they were cooled to room temperature and weighed to determine their mass. Additionally, due to gravitational influence, seed stems were more likely to fall axially; therefore, axial fall was selected as the test condition.
4. Test Results and Analysis
4.1. Mixed Orthogonal Test Results and Analysis
In the experimental part, we first conducted a collision test on the seed stems at a preset drop height using the test apparatus shown in Figure 4, calculated the horizontal and vertical velocity components, and calculated the collision recovery coefficient using Equation (31). The results of the mixed orthogonal test are summarized in Table 3, while the analysis of variance (ANOVA) results are detailed in Table 4. To visualize the impact of various factors on the collision recovery coefficient, Figure 5 presents an index relationship graph, with factor levels plotted on the horizontal axis and the collision recovery coefficient on the vertical axis. The findings indicate that the collision recovery coefficient of seed stems decreases as the drop height increases. Similarly, increasing water content correlates with reducing the collision recovery coefficient. A comprehensive analysis reveals that the factors influencing the collision recovery coefficient of seed stock are ranked in the following order: collision contact material > fall height > seed stem mass > water content > fall direction > seed stem variety. The ANOVA results demonstrate that collision contact material, drop height, seed stem mass, and water content significantly affect the collision recovery coefficient. In contrast, drop direction and seed stock variety have relatively insignificant impacts.

Table 3.
Mixed orthogonal test results.

Table 4.
Analysis of variance of mixed orthogonal test results.
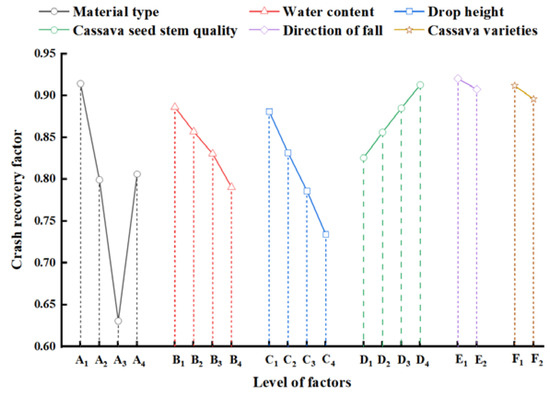
Figure 5.
Indicative relationship between crash recovery coefficient and test factors.
4.2. Results and Analysis of the One-Way Test
4.2.1. Effect of Collision Contact Materials on the Collision Recovery Coefficient of Seed Stems
The orthogonal test results indicate that the type of contact material significantly influences the collision recovery coefficient of seed stems among the various test factors. Conducted with a seed stem drop height of 75 mm, a water content of 76.39%, and a seed stem mass of 287.72 g, a one-factor test was performed and repeated three times to obtain an average value. The findings revealed that the recovery coefficients for the interactions between seed stems and collision materials ranked as follows: structural steel Q235, rubber sheet, seed stems, and sandy loam. Specifically, the coefficients for SC205 were 0.8172, 0.6975, 0.6649, and 0.6341. For GR4, they were 0.7796, 0.7132, 0.6913, and 0.6134, as illustrated in Figure 6. Further analysis indicates that the superior hardness and strength of structural steel Q235 contribute to its higher recovery coefficient (Figure 1A). Collision theory suggests that the small contact area between the seed stem and the collision surface minimizes energy loss during impact and results in limited deformation. In contrast, sandy loam exhibits lower hardness, a larger contact area, and greater deformation variability; thus, it has a lower collision recovery coefficient as it absorbs most of the energy generated during the seed stem’s impact, providing a buffering effect [32].
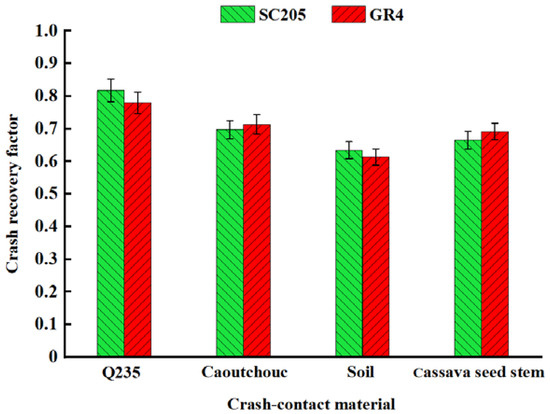
Figure 6.
Results of one-factor testing of crash contact materials.
4.2.2. Effect of Fall Height on the Collision Recovery Coefficient of Seed Stems
The hybrid orthogonal test indicates that the drop height has the second most significant effect on the collision recovery coefficient of seed stems, following the contact collision material. When the contact collision material was Q235, the moisture content was measured at 76.39%, and the mass of the seed stems was 287.72 g. The results (see Table 5 and Table 6) demonstrate that as the drop height increased, the collision recovery coefficient of the seed stems decreased. Additionally, the quadratic regression equations relating drop height to recovery coefficients for SC205 and GR4 were established, with R² values of 0.9985 and 0.9864, respectively, as illustrated in Figure 7.

Table 5.
Effect of fall height on the collision recovery coefficient of cassava seed stems (SC205).

Table 6.
Effect of drop height on the collision recovery coefficient of cassava seed stems (GR4).
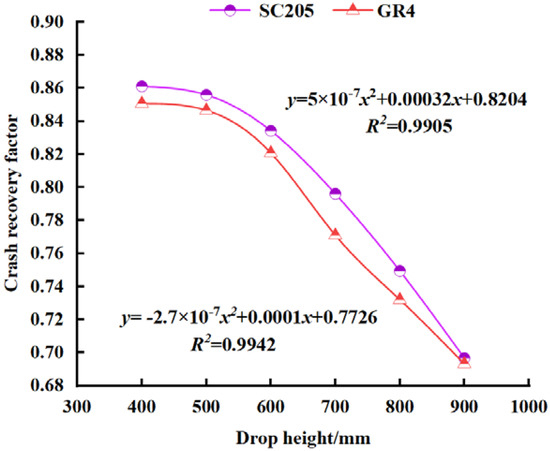
Figure 7.
Effect of fall height and collision recovery coefficient of cassava seed stems.
Further analysis based on the theoretical collision model of seed stems in Figure 1A reveals that as the drop height increases, the potential energy is converted into greater kinetic energy, amplifying the deformation of the seed stem during its collision with the material. Since cassava exhibits elastoplastic material properties, more irreversible deformation occurs during the yield phase, resulting in higher energy loss during collision. This reduces the post-collision rebound velocity and consequently decreases the coefficient of restitution of the seed stems.
4.2.3. Effect of Cassava Seed Stem Mass on the Coefficient of Recovery of Seed Stem Collisions
The mixed orthogonal test indicates that the impact of seed stem mass on the collision recovery coefficient is less significant compared to the effects of the contact collision material and fall height. The findings, detailed in Table 7 and Table 8 and illustrated in Figure 8 and Figure 9, pertain to a fall height of 75 mm, a contact collision material of Q235, and a moisture content of 76.39%. An increase in seed stem mass within a specific range corresponds to a decrease in its collision recovery coefficient, demonstrating an approximate linear decreasing trend. The quadratic regression equations for the mass and recovery coefficient of the SC205 and GR4 seed stems yielded R2 values of 0.9901 and 0.9835, respectively. This phenomenon occurs because, during the drop of the seed stems, the work performed against air drag is negligible; thus, potential energy is gradually converted into kinetic energy. Before the collision with the contact material, potential energy reaches its minimum while kinetic energy peaks. As shown in the seed stem collision theory in Figure 1A, seed stems of varying masses exhibit identical instantaneous velocities when contacting the collision material. However, heavier seed stems possess greater potential energy, which increases the contact force with the colliding plate. This amplifies deformation (particularly irreversible plastic deformation due to the elastoplastic properties of cassava), dissipating more energy during collision. Consequently, the normal rebound velocity decreases, leading to a reduction in the coefficient of restitution.

Table 7.
Effect of cassava seed stem mass on the seed stem collision recovery coefficient (SC205).

Table 8.
Effect of cassava seed stem mass on the seed stem collision recovery coefficient (GR4).
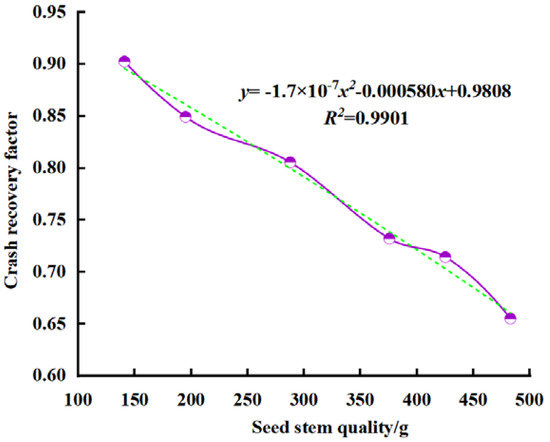
Figure 8.
Effect of seed stem mass on the collision recovery coefficient of cassava seed stem (SC205). Note: The purple curve represents the spline curve of the experimental results of cassava crash recovery factor at different masses, and the green dashed line represents the quadratic function fitting curve of the crash recovery factor at different masses.
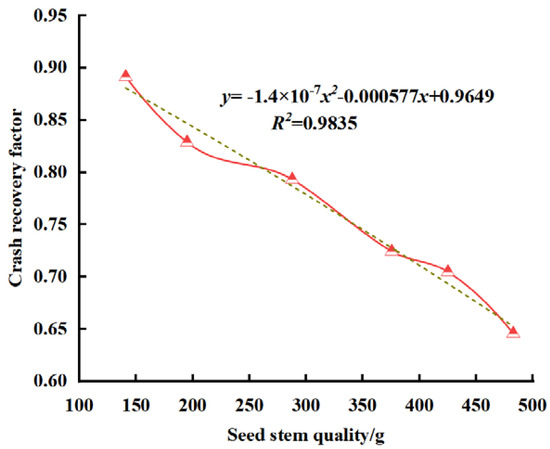
Figure 9.
Effect of seed stem mass on the collision recovery coefficient of cassava seed stem (GR4). Note: The red curve represents the spline curve of the experimental results of cassava crash recovery factor at different masses, and the brown dashed line represents the quadratic function fitting curve of the crash recovery factor at different masses.
4.2.4. Effect of Water Content on the Collision Recovery Coefficient of Seed Stems
The mixed orthogonal test demonstrated that the water content of seed stems had a significantly weaker effect on the collision recovery coefficient compared to factors such as contact collision material, drop height, and cassava seed stem mass. When the drop height of the seed stem was set at 750 mm, and the contact collision material was Q235 structural steel, it was observed that, under identical conditions of collision material and falling height, the collision recovery coefficients of seed stems decreased as water content increased. This trend was clearly illustrated in the test results presented in Table 9 and Table 10. Additionally, quadratic regression equations were derived to describe the relationship between water content and recovery coefficients for SC205 and GR4 seed stems, yielding R2 values of 0.9725 and 0.9791, respectively, as shown in Figure 10 and Figure 11. The analysis indicated that higher water content in seed stems resulted in greater deformation during collisions with the material, increased viscosity upon contact, and higher energy loss during the collision process. This ultimately led to a reduced normal separation velocity of the seed stems after rebounding from the collision material, lowering their recovery coefficients. Consequently, water content should be comprehensively considered during seeding to minimize seed stem damage and scratching.

Table 9.
Effect of water content on the collision recovery coefficients of seed stems (SC205).

Table 10.
Effect of water content on the collision recovery coefficients of seed stems (GR4).
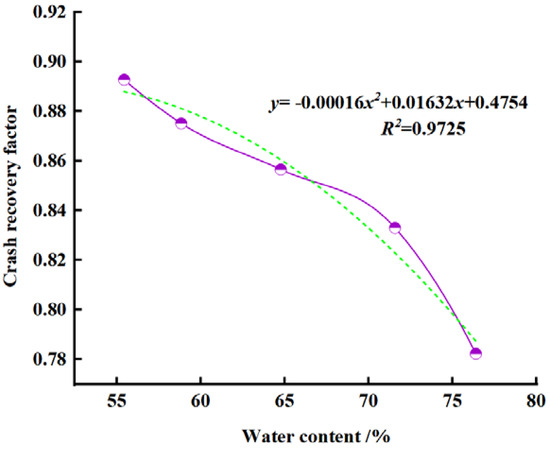
Figure 10.
Effect of water content on the collision recovery coefficient of cassava seed stems (SC205). Note: The purple curve represents the spline curve of the experimental results of cassava crash recovery factor at different water contents, and the green dashed line represents the quadratic function fitting curve of the crash recovery factor at different water contents.
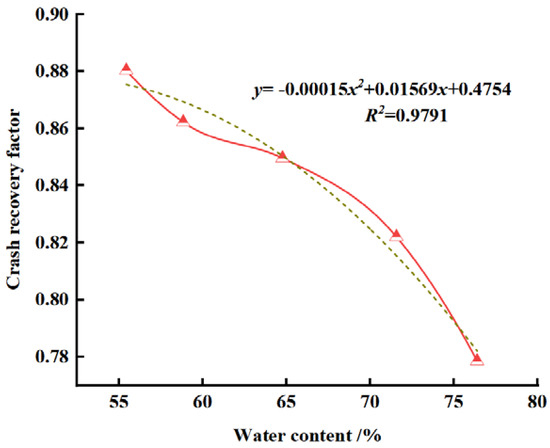
Figure 11.
Effect of water content on the collision recovery coefficient of cassava seed stems (GR4). Note: The red curve represents the spline curve of the experimental results of cassava crash recovery factor at different water contents, and the brown dashed line represents the quadratic function fitting curve of the crash recovery factor at different water contents.
4.2.5. Influence of Seed Stem Fall Direction and Species on Collision Recovery Coefficients
A free-fall test was conducted to simulate the actual movement of seed stems during sowing to determine the collision recovery coefficient of seed stems. The test involved dropping seed stems from two positions—axial and radial. Observations of bruises on the seed stem and the Q235 collision material revealed that, regardless of whether the fall was along the axial or radial direction or even for identical axial falls, the collision points varied due to the irregular shape of the seed stems. This variability arises because different seed stems have distinct centers of gravity, causing them to self-adjust and exhibit rotational movement during free fall. Consequently, the falling direction of the seed stem has an insignificant effect on the collision recovery coefficient due to these uncontrollable shapes and rotational characteristics. Additionally, single-factor tests showed that variations in seed stem mass and water content were controlled, rendering the impact of various factors on the collision recovery coefficient negligible. According to collision theory, energy conservation principles apply when a seed stem transitions from free fall to colliding with a material. The maximum kinetic energy of the seed stem occurs immediately before impacting the collision ramp, during its free-fall phase prior to contact. During a collision, deformation occurs in two forms: elastic deformation and plastic deformation. Elastic deformation during compression is converted into elastic potential energy, while plastic deformation generates internal energy. In the rebound stage, part of the elastic energy is converted back into kinetic energy, while another portion contributes to overcoming gravity and forming potential energy [33].
5. Discussion
Seed-stem-propagated crops necessitate meticulous preservation of seed and stem mass before sowing to enhance germination rates and improve overall crop growth [34,35]. This study identified the factors influencing the collision recovery coefficient of cassava seed stems using a controlled variable method, providing valuable insights for minimizing collision impacts and reducing collision forces. In practical production, cassava seed stems frequently experience epidermal abrasions, leading to water loss, increased vulnerability to bacterial infections, and lower survival rates. Furthermore, internal tissue damage compromises the quality of processed cassava products, while damage incurred during sowing adversely affects seedling emergence rates [36,37]. Therefore, it is essential to thoroughly evaluate the interaction forces exerted by key production equipment components on seed stems during cassava production and processing. In designing automated equipment, minimizing damage to seed stems is crucial for enhancing seeding efficiency and reducing planting losses. The findings of this study offer a significant theoretical foundation for developing optimized mechanical structures tailored to the specific needs of cassava sowing, transportation, and processing.
5.1. Material Type
Collision contact material is a critical factor influencing the collision recovery coefficient of cassava seed stems. This observation is consistent with research on other crops, such as potatoes and castor capsules, which revealed that contact materials’ hardness and elastic modulus significantly affect crop collision damage [19,38]. Similarly, studies on oil sunflower seeds [39] and peanut [40] demonstrated that rigid materials like Q235 steel yield higher recovery coefficients than rubber due to reduced energy absorption. Wheat seed collisions [41] further corroborate this trend, emphasizing material stiffness as a key determinant of damage mitigation. Therefore, in designing cassava planters, it is essential to select contact materials carefully and utilize highly elastic materials at contact points with the stems to optimize damage reduction during processing. Additionally, for vital components of planters, such as seed dispensers and seed guides, it is advisable to prioritize materials with excellent shock-absorbing properties to minimize collision-related damage.
5.2. Water Content
Water content is a critical factor influencing the recovery coefficient of cassava seed stems following impact. Research indicates that high water content softens the internal tissues of the seed stems, resulting in decreased mechanical strength and increased susceptibility to deformation under pressure. The internal structure retains good flexibility and elasticity in this state, leading to a high recovery coefficient. Conversely, at low water content, the cell walls and fibers of the seed stems dry out and become brittle, significantly increasing the hardness of the internal tissues. This condition results in a marked reduction in the recovery coefficient after a collision. Dry cassava seed stems are more prone to breaking during impacts and are less capable of returning to their original shape [42,43]. Similar trends have been observed in agricultural materials such as potato tubers [44], where higher moisture content improved tissue resilience and recovery. In contrast, oil sunflower seeds [40] exhibit reduced recovery coefficients at higher moisture levels due to increased energy dissipation. This discrepancy highlights the influence of crop-specific structural characteristics: cassava’s woody stems may retain elasticity even at elevated moisture, unlike fragile seeds. Consequently, it is essential to consider storage and transportation conditions for cassava seed stems in practical production settings. Implementing appropriate humidity preservation measures post-harvest or controlling environmental humidity during transport can help maintain optimal moisture levels, thereby ensuring the mechanical integrity of the seed stems throughout processing and transport.
5.3. Drop Height
Drop height significantly influences the collision recovery coefficient of cassava seed stems. Experimental results indicate that as the dropping height increases, the recovery coefficient of the seed stems gradually decreases following a collision. This trend suggests that higher dropping heights subject the seed stems to greater impact forces, leading to more severe structural damage. Similar findings have been reported in oil sunflower seeds [40], where recovery coefficients declined with increasing drop height due to amplified energy dissipation. Wheat seed collisions [41] and potato tuber impacts [44] further corroborate this inverse relationship, emphasizing the universal role of kinetic energy in collision outcomes. Consequently, it is essential to minimize the fall height of cassava seed stems during transport and handling. Transport systems should be designed to facilitate loading and unloading in a manner that reduces the likelihood of high falls, which can be accomplished by adjusting conveyor belt heights, installing cushioning devices, or utilizing inclined transport lanes. Furthermore, during the packing and storage phases, appropriate stacking methods can effectively mitigate the risk of falls during transport, ensuring that the seed stems remain intact.
5.4. Seed Stem Mass
The mass of seed stems significantly influences the collision recovery coefficient, with findings indicating that this coefficient tends to decrease as the weight of the seed stem increases. Heavier cassava seed stems generate greater impact forces upon falling, leading to more substantial structural damage during collisions. This aligns with research on peanut [40], where heavier seeds exhibited lower recovery coefficients due to increased kinetic energy during impacts. Consequently, in practical production settings, it is essential to make appropriate adjustments based on the weight of cassava seed stems. Strategies such as reducing drop height or incorporating additional cushioning can be employed for heavier seed stems. Alternatively, selecting and processing seed stems with suitable weight characteristics can minimize collision-related damage. The analysis reveals that four factors—material type, moisture content, drop height, and seed stem mass—significantly affect the collision recovery coefficient. By reasonably adjusting these factors, it is possible to enhance the mechanical properties of cassava seed stems, reduce damage risk, and improve overall production efficiency.
5.5. Limitations of This Study and Directions for Future Studies
This study has several limitations. First, the theoretical model assumes homogeneity in the material properties of seed stems, whereas real-world cassava stems exhibit heterogeneity due to variations in vascular bundles, cellular structures, and voids. This simplification may lead to deviations from actual deformation patterns during collisions. Second, the collision theory in this study primarily relies on Hertz contact theory and elastoplastic theory. While it theoretically divides the collision process of cassava seed stems into elastic, yield, and rebound phases and derives corresponding formulas to describe the mechanical relationships, the current theoretical framework has not been directly validated experimentally due to experimental constraints. The lack of force–deformation curve measurements under collision conditions, as well as experimental verification of boundaries among the elastic, plastic, and rebound phases, constitutes a major limitation of this work. Additionally, while the experimental analysis focuses on specific factors, other variables, such as seed stem length, collision position, and rotational characteristics, may also influence the restitution coefficient.
In terms of theoretical model validation, future research can seek breakthroughs in experimental measurement technologies and explore more advanced measurement methods to obtain accurate data of key parameters during collision processes. Additionally, simulation methods serve as an important approach to validate the effectiveness of theoretical models. On one hand, it is necessary to explore parameter calibration methods for cassava seed stems to determine their physical parameters under different conditions. On the other hand, the calibrated parameters can be applied to simulation software to simulate the collision process of cassava seed stems and study the relationship between force and deformation. Based on this foundation, the boundary times for the elastic phase, yield phase, and rebound phase, as well as residual deformation, can be defined. By rationally designing algorithmic workflows, the Runge–Kutta algorithm can be used to solve the formulas derived theoretically in this study, obtaining theoretical solutions for the restitution coefficient, which will then be compared with experimental data to verify the model’s validity. Regarding the exploration of factors influencing the restitution coefficient, future research can investigate seed stems with different shapes and surface roughness to improve the accuracy of the restitution coefficient, thereby optimizing the processing and transportation techniques for cassava seed stems. This implementation of measures will provide scientific support for the sustainable development of the cassava industry.
6. Conclusions
Based on seed stem collision dynamics principles and kinematic equations, this study measured and analyzed the seed stem collision recovery coefficient using a custom-designed test platform. Orthogonal tests were conducted to evaluate the main factors influencing the collision recovery coefficient of cassava seed stems, including collision contact material, fall height, seed stem mass, moisture content, fall direction, and seed stem variety. The results indicated that the factors affecting the collision recovery coefficient of seed stems were ranked in the following order: collision contact material > drop height > seed stem mass > moisture content > fall direction > seed stem variety. Notably, the impacts of collision contact material, drop height, seed stem mass, and moisture content were significant, while fall direction and seed stem variety had relatively minor effects. The one-way analysis revealed that the collision recovery coefficients between seed stems and structural steel (Q235), rubber sheets, seed stems, and sandy loam soil decreased progressively, with values recorded at 0.8172, 0.6975, 0.6649, and 0.6341, respectively, for SC205 and 0.7796, 0.7132, 0.6913, and 0.6134, respectively, for GR4. As fall height increased, the collision recovery coefficients of the seed stems decreased; similarly, both seed stem mass and moisture content exhibited a decreasing trend with increasing values. The coefficients of determination for the regression equations were all above 0.97. Based on these findings, when designing and manufacturing equipment for seeding and transporting cassava seed stems, selecting materials with lower recovery coefficients is advisable to minimize impact damage. For instance, incorporating rubber cladding on critical components such as seed supply and discharge mechanisms in precision seeders can reduce collision recovery rates. Furthermore, maintaining optimal control over the water content, quality, and drop height of the seed stems is an effective strategy to mitigate losses during handling. This research provides a theoretical foundation for optimizing seeder structures and offers valuable insights for designing equipment tailored to cassava seed stem production and transportation processes.
Author Contributions
Conceptualization, X.M., R.C., L.C. and E.M.A.; Data curation, R.C.; Investigation, Y.L. and M.M.; Methodology, X.M., R.C., L.C., Y.L. and E.M.A.; Resources, R.C. and E.M.A.; Software, E.M.A. and P.Z.; Supervision, L.C. and E.M.A.; Validation, X.M.; Visualization, X.M. and E.M.A.; Writing—original draft, X.M., R.C., L.C., Y.L. and E.M.A.; Writing—review & editing, L.C., E.M.A., M.M., H.J. and P.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by financial support from the Guangxi Natural Science Foundation [NO. 2025GXNSFBA069533], Guilin Major Special Program [No. 20220102-3], the Guangxi Key R&D Program [No. 2021AB38023].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Peng Zhang was employed by Wuhan Huazhong Numerical Control Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be constructed as a potential conflict of interest.
References
- Chen, L.; Chen, R.; Atwa, E.M.; Mabrouk, M.; Jiang, H.; Mou, X.; Ma, X. Nutritional Quality Assessment of Miscellaneous Cassava Tubers Using Principal Component Analysis and Cluster Analysis. Foods 2024, 13, 1861. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.; Lei, K.; Wei, L.; Ma, C.; Xu, C.; Chen, R. Climate suitability analysis and high yield cultivation techniques of cassava in Guangxi. Agric. Technol. 2021, 41, 57–59. [Google Scholar] [CrossRef]
- Cao, S.; Chen, J.; Huang, F.; Yan, H.; Wei, C.; Li, F.; Lu, L.; Qin, X.; Chen, H.; Li, H. Current situation analysis and development suggestions of cassava industry in Guangxi. J. South. Agric. 2021, 52, 1468–1476. [Google Scholar] [CrossRef]
- Lungkapin, J.; Salokhe, V.; Kalsirisilp, R.; Nakashima, H. Development of a stem cutting unit for a cassava planter. Agric. Eng. Int. 2007, 9, 1–16. Available online: https://api.semanticscholar.org/CorpusID:54547530 (accessed on 1 November 2024).
- Chen, L.; Li, K.; Mou, X.; Liu, Z.; Jiang, H.; Mabrouk, M.; Pan, J.; Atwa, E.M. Evaluating the Impact of Moisture Content and Loading Orientation on the Geometrical Characteristics and Mechanical Behavior of Cassava Tubers. Agronomy 2024, 14, 2254. [Google Scholar] [CrossRef]
- Lungkapin, J.; Salokhe, V.; Kalsirisilp, R.; Nakashima, H. Design and development of a cassava planter. Trans. ASABE 2009, 52, 393–399. [Google Scholar] [CrossRef]
- Li, G.; Zhou, S.; Deng, G.; Zheng, S.; He, F.; Cui, Z.; Dai, Y.; Li, L.; Yan, B.; Qin, S.; et al. Research Progress on Mechanization Technology and Equipment for Cassava Field Production. Agriculture 2024, 14, 1926. [Google Scholar] [CrossRef]
- Zeng, B.; Ye, C.; Lu, H. Research and design of 2CMS-2 cassava combine planter. Guangxi Agric. Mech. 2011, 06, 21–22. [Google Scholar] [CrossRef]
- Mou, X.; Chen, L.; Ma, X.; Xue, J.; Xiang, J. Design and Experiment of Spoon Chain Seed Metering Mechanism of Precutting Vibration Seed Feeding Cassava Planter. Trans. Chin. Soc. Agric. Mach. 2023, 54, 20–31. [Google Scholar]
- Chen, L.; Xue, J.; Mou, X.; Ma, X.; Xiang, J. Design and experiments of the stepped vibration seed dispersal mechanism for pre-cut cassava planters. Trans. CSAE 2022, 38, 27–37. [Google Scholar] [CrossRef]
- GB/T 6973-2005; Testing Methods of Single Seed Drills (Precision Drills), the Standardization Administration of the People’s Republic of China. China Standards Press: Beijing, China, 2005.
- Yang, W.; Cai, G.; Yang, J.; Huang, Y. Mechanical and mathematical model analysis of uprooted force on cassava storage root. Trans. CSAE 2011, 27, 95–100. [Google Scholar] [CrossRef]
- China Academy of Agricultural Mechanization. Agricultural Machinery Design Manual; Machinery Industry Press: Beijing, China, 1988. [Google Scholar]
- Yang, W.; Yang, J.; Zheng, X.; Wang, Q.; Jia, F.; Zhao, J. Experiment on mechanical properties of cassava. Trans. CSAE 2011, 27, 50–54. Available online: http://www.tcsae.org/article/id/20111411 (accessed on 5 November 2024).
- Peng, C.; Zhou, T.; Song, S.; Fang, Q.; Zhu, H.; Sun, S. Measurement and Analysis of Restitution Coefficient of Black Soldier Fly Larvae in Collision Models Based on Hertz Contact Theory. Trans. Chin. Soc. Agric. Mach. 2021, 52, 125–134. [Google Scholar] [CrossRef]
- Lv, Z.; Wang, W.; Yang, D.; He, X.; Qu, Z.; Jing, W.; Mei, Y.; Huang, H.; Su, B.; Zhuang, Y. Optimal Design and Tests of a Pulsating Roll-Cleaning Device for Tiger Nuts. Agriculture 2024, 14, 1673. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, X.; Chen, J.; Wang, H.; Cao, Y. Analysis and Optimization of Low-Resistance Animal Bionic Subsoiling Shovel Based on EDEM. Agriculture 2024, 14, 2046. [Google Scholar] [CrossRef]
- Wang, L.; Liu, T.; Feng, X.; Gao, Y.; Wang, B.; Zhang, S. Research progress of the restitution coefficients of collision of particles in agricultural and food fields. Trans. Chin. Soc. Agric. Eng. 2021, 37, 313–322. [Google Scholar] [CrossRef]
- Yang, Y.; Hou, J.; Bai, J.; Yao, E.; He, T.; Li, J. Determination and analysis of collision recovery coefficient of typical castor capsules. J. China Agric. Univ. 2019, 24, 138–148. [Google Scholar] [CrossRef]
- Wang, L.; Wu, B.; Wu, Z.; Li, R.; Feng, X. Experimental determination of the coefficient of restitution of particle-particle collision for frozen maize grains. Powder Technol. 2018, 338, 263–273. [Google Scholar] [CrossRef]
- Feng, B.; Sun, W.; Sun, B.; Zhang, T.; Wu, J.; Shi, L. Determination of restitution coefficient of potato tubers collision in harvest and analysis of its influence factors. Trans. Chin. Soc. Agric. Eng. 2017, 33, 50–57. [Google Scholar] [CrossRef]
- Yang, J.; Liu, G.; Fu, H.; Du, W.; Wu, Z. Experimental platform for determining the recovery coefficient of collision between unstructured agricultural bulk materials. Exp. Technol. Manag. 2022, 39, 109–114. [Google Scholar] [CrossRef]
- Chen, D.; Yang, Z.; La, G.; Yuan, C.; Wang, H.; Wang, C.; Sun, G. Determination of collision recovery coefficient in harvesting of Hibiscus sabdariffa. Agric. Eng. 2021, 11, 82–88. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, X.; Ma, L.; Zong, W.; Li, M.; Tang, C. Determination of three-dimensional collision restitution coefficient of oil sunflower grain by high-speed photography. Trans. Chin. Soc. Agric. Eng. 2020, 36, 44–53. [Google Scholar] [CrossRef]
- Du, Y.; Wang, S. Dissipation modeling of elastic-plastic positive collision of two particles. J. Mech. Eng. 2009, 45, 149–156. [Google Scholar] [CrossRef]
- Chang, B.; Zhu, Y.; Jin, G.; Song, Y.; Li, X.; Lu, C. Impact Motion Analysis and Optimization of Redundant Serial Robot Considering Collision. Trans. Chin. Soc. Agric. Mach. 2019, 50, 413–420. [Google Scholar] [CrossRef]
- Liu, G.; Han, X.; Wang, Z.; Wang, K.; Zhang, Z.; Duan, Z. Viscosity Reduction and Drag Reduction Performance Analysis of Bionic Excavator Buckets Based on Discrete Element Method. Biomimetics 2024, 9, 686. [Google Scholar] [CrossRef]
- Du, X.; Liu, J.; Zhao, Y.; Zhang, C.; Zhang, X.; Wang, Y. Design and Test of Discrete Element-Based Separation Roller Potato–Soil Separation Device. Agriculture 2024, 14, 1053. [Google Scholar] [CrossRef]
- Liu, C.; Wang, C.; Song, J.; Du, X.; Zhang, F. Design and seed-filling test of cell-type precision seed-metering device with vibration technology. Trans. Chin. Soc. Agric. Mach. 2018, 49, 108–115. [Google Scholar] [CrossRef]
- Zheng, Z.; Li, D.; Qiu, X.; Zhu, X.; Ma, P.; Zhang, D. Numerical Analysis of Effect of Impacting Velocity on Diesel Droplet Impacting on Inclined Surface. Trans. Chin. Soc. Agric. Mach. 2016, 47, 317–324. [Google Scholar] [CrossRef]
- Zhang, S.; Fu, J.; Zhang, R.; Zhang, Y.; Yuan, H. Experimental Study on the Mechanical Properties of Friction, Collision and Compression of Tiger Nut Tubers. Agriculture 2022, 12, 65. [Google Scholar] [CrossRef]
- Zhang, B. Principles of Sowing Machinery Design; Machinery Industry Press: Beijing, China, 1982. [Google Scholar]
- Campbell, C.M.; Fulton, J.P.; Mcdonald, T.P.; Wood, C.W.; Zech, W.C.; Srivastava, P. Spinner-disc technology to enhance the application of poultry litter. Appl. Eng. Agric. 2020, 26, 759–767. [Google Scholar] [CrossRef]
- Li, M.; Liu, R.; Zhong, Y.; Li, X. Current progress on the associative nitrogen fixation in sugarcane and its application potentials. Acta Microbiol. Sin. 2021, 61, 564–579. [Google Scholar] [CrossRef]
- Liu, J.; Jing, Y.; Lai, Y.; Shi, J.; Li, M. Discussion on the Unqualified Factors of Pinelliae Rhizoma. J. Chin. Med. Mater. 2019, 42, 1261–1266. [Google Scholar] [CrossRef]
- Cui, Z.; Deng, G.; Li, G.; Liu, Z.; Zheng, S.; Li, L. Design of Cassava Stalk Cutter for Cassava Planting Machine. J. Agric. Mech. Res. 2017, 39, 144–148. [Google Scholar] [CrossRef]
- Roger, C.B. Impact testing of potato harvesting equipment. Am. Potato J. 1993, 70, 243–256. [Google Scholar] [CrossRef]
- Huang, T.; Wu, B.; Li, L.; Zuo, T.; Xie, F. Construction of impact mechanics model and experimental study on impact damage of potato tuber. INMATEH—Agric. Eng. 2022, 66, 139–146. [Google Scholar] [CrossRef]
- Huang, X.; Zha, X.; Pan, M.; Zong, W.; Chen, H. Measurement and analysis of rapeseeds’restitution coefficient in point-to-plate collision model. Trans. Chin. Soc. Agric. Eng. 2014, 30, 22–29. [Google Scholar] [CrossRef]
- Lu, Y.; Wu, N.; Wang, B.; Yu, Z.; Lin, D. Measurement and analysis of peanuts’restitution coefficient inpointto plate collision mode. J. China Agric. Univ. 2016, 21, 111–118. [Google Scholar] [CrossRef]
- Wang, C.; Li, Y.; Ma, L.; Ma, Z. Experimental study on measurement of restitution coefficient of wheat seeds in collision models. Trans. Chin. Soc. Agric. Eng. 2012, 28, 274–279. [Google Scholar] [CrossRef]
- Szwed, G.; Lukaszuk, J. Effect of rapeseed and wheat kernel moisture on impact damage. Int. Agrophys. 2007, 21, 299–304. [Google Scholar] [CrossRef]
- Wojtkowski, M.; Pecen, J.; Horabik, J.; Molenda, M. Rapeseed impact against a flat surface: Physical testing and DEM simulation with two contact models. Powder Technol. 2010, 198, 61–68. [Google Scholar] [CrossRef]
- Meng, J.; Wang, C.; Xie, S.; Deng, W.; Qi, S. Measurement test analysis of potato restitution coefficient. J. China Agric. Univ. 2017, 22, 93–100. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).