Droplet Deposition Behavior on the Surface of Flexible Pepper Leaves

Abstract

In spray application contexts, plant leaves are bent and twisted upon droplet impact, which has a significant impact on the droplet’s impact behavior and its deposition effect on the leaves. This study examines the impact behavior of droplets on flexible pepper leaves and develops a mathematical model for droplet spreading and rebound, integrating the effects of leaf bending and torsion via energy conservation and cantilever beam theory. The energy required for leaf bending and twisting due to droplet impact was estimated in accordance with Hooke’s law. The droplets attained their maximum spreading diameter 4 ms post-impact on flexible pepper leaves, with droplet retraction occurring significantly faster on flexible leaves than on rigid ones, resulting in a return to steady state in half the duration required by rigid leaves. This study aims to establish a scientific foundation for optimizing pesticide application strategies and selecting parameters for spraying equipment in pepper production.

1. Introduction

Enhancing the bioefficacy of pesticides and minimizing environmental contamination are primary aims in the domain of spray application for controlling agricultural and forestry pests and illnesses [1]. Adhesion, fragmentation, rebound, or splash occurs following droplet impact on plant leaves, with rebound and splash generating secondary droplets that may disperse and reach non-target areas [2]. Furthermore, assessing the spray deposition efficacy and leaf retention of droplets depends on expensive field trials [3,4]. The capacity of droplets to deposit and adhere to the leaf surface is not only contingent upon the droplet’s chemistry at the moment of contact but also intricately linked to droplet spreading and leaf movement subsequent to contact with the leaf surface [5]. An extensive examination of droplet dynamics and the mechanical properties of leaf surfaces post-contact is crucial for enhancing pesticide application efficiency, minimizing environmental contamination, and mitigating economic losses [6]. Mathematical models of droplet impact behavior can yield estimates of spray impact behavior and serve as a crucial reference before field trials.

Research has concentrated on the behavior of droplet impacts on fixed rigid surfaces [7,8,9]. Mao et al. [10] formulated a droplet rebound model grounded in energy conservation, utilizing three distinct rigid substrate materials as impact objects, which forecasted rebound tendencies in relation to maximum spread and static contact angle. The prediction of droplet impaction behavior has also been studied in the field of spray application. Liu et al. [11] attached tea tree leaves to a rigid substrate and investigated the impact behavior and impact mechanism when droplets obliquely impacted tea tree leaves, proposed the use of an elliptical spreading area to measure the change in droplet spreading during obliquely impacting, and derived a mathematical prediction model for obliquely impacting droplet spreading and rebound that included leaf inclination and impact angle. Dorr et al. [3] developed a formulation based on scanned leaf images and measured formulation properties to predict spray retention on leaf surfaces, using a combination of ballistic and random wandering methods to simulate the trajectory of spray droplets in air and to calculate whether the droplets impacted the leaf as well as the impact angle and velocity. Delele et al. [12] studied the dynamic impact behavior of water droplets on plant surfaces based on a multiphase flow computational fluid dynamics (CFD) model. Although this study was conducted on plant leaves, it differs from the actual situation of the crop application process, ignoring the fact that plant leaves can bend and twist upon droplet impact [13]. During pesticide application, the bending and twisting of plant leaves by droplet impact can change droplet motion behavior, thus affecting droplet deposition efficiency and the adsorption capacity of the leaf for droplets [14,15].

Researchers recognized that affixing the leaf to a rigid substrate disregarded the flexible properties of the leaf surface, prompting them to concentrate on the bending and torsion of the pliable leaf surface. Gart et al. [16] constructed a cantilever beam model to describe the behavior of droplet-impacted elastic leaves through experimental and theoretical analyses, and verified its applicability under different surface wettability conditions, revealing the effects of surface wettability on leaf bending and energy transfer. Bhosale et al. [17] examined the transformation of energy into bending and torsion modes upon the impact of a raindrop on the leaf of a Lianxiang tree, along with the influence of various parameters on these modes; however, their study did not address droplet impact behavior and spreading dynamics on leaves. In recent years, our group has conducted a study on droplet impact on flexible leaves and developed a mathematical model to predict the maximum spreading factor of droplets at the primary leaf veins of plant leaves [18]. This model simplifies the problem by considering only leaf bending, as droplet impact occurs near the main leaf veins, while neglecting the influence of leaf torsion.

In this study, based on previous theoretical and experimental studies, the influence of blade bending and torsion deformation on droplet impact behavior and spreading is increased, and a mathematical model of energy conservation in the droplet–leaf system is established to quantify the potential energy of bending and torsion obtained from blade impact by droplets, which is used for the prediction of the maximum spreading factor of droplets impacting on a flexible plant blade and the rebound of droplets. Theoretical and experimental studies of droplet impact patterns on flexible leaves were conducted to investigate the effects of blade bending and twisting on droplet maximum diffusion factor and spreading time, with a view to providing a method for investigating the optimal spraying parameters for different plants and different spraying scenarios, and providing a reference for pre-test estimation of spray deposition effects in the field.

2. Materials and Methods

2.1. Mathematical Model for Predicting the Maximum Spreading Diameter of Liquid Droplets

In this experiment, the leaf is regarded as a cantilever beam, and a droplet of particle size D₀ impacts the pepper leaf. The moment of impact between the droplet and the leaf surface is recorded as t_a. At this time, the droplet’s velocity is v_a, the droplet’s falling shape in the air is simplified as a sphere, and the angle between the leaf and the horizontal line is θ₀ (Figure 1a). After the droplet impacts with the leaf, the leaf is deformed by the force and moves downward, while the droplet spreads outward from the center. When the droplet reaches the maximum spread, this moment is recorded as t_b, the shape of the droplet is approximated as a thin disk, and the diameter of the droplet spread is recorded as D_max. At the t_b moment, the droplet’s kinetic energy is zero [11]. The liquid, having diffused outward from the center to its maximum spread, is transformed inward to be contracted not has not yet contracted, and the foliage surface is moved downward to the lowest point. At this time, the horizontal position of the leaf is set to be the point of the system with zero potential energy. When a droplet impacts the leaf surface, the leaf surface bends and twists. Experimental observations showed a large displacement from the impact point’s position to the tip of the leaf, while the displacement between the impact point and the petiole of the leaf is relatively small. In this study, the gravitational potential energy of this part of the leaf from the petiole to the impact point is ignored, considering only the change in gravitational potential energy from the impact point to the tip (Figure 1b). After t_b, the droplet starts to retract. At this time, the retracted droplet may stay on the leaf or may rebound. The moment when the droplet retracts to reach stability or rebounds is recorded as t_c. Because the droplet’s retraction time is too short, it is assumed that at t_c, the pepper leaf remains at zero potential energy. Whether the droplet can rebound depends on the critical instant when it returns to its original spherical shape without touching the surface of the leaf (Figure 1c), at which point its kinetic energy is zero.

The established mathematical model considers the droplet–pepper leaf system in its entirety, neglecting wind resistance and thermal energy in the overall energy conservation analysis [7]. The total energy E_a of the droplet–leaf system encompasses the droplet’s kinetic energy E_K1, the gravitational potential energy E_p1 of the droplet–leaf system (containing the droplet and falling leaf), and the droplet’s surface energy E_S1, as indicated in Equation (1):

$$E_{\mathrm{a}}=E_{K1}+E_{P1}+E_{S1}$$

(1)

The expression for E_K1 is shown in Equation (2):

$$E_{K1}={\displaystyle \frac{1}{12}}\pi \rho v_0^2{D}_0^3$$

(2)

where ρ is the density of the droplet, kg/m³; v₀ is the droplet velocity at the t_a moment, m/s; D₀ is the initial particle size of the droplet, m.

The expression for E_P1 is given in Equation (3):

$$E_{P1}=({\displaystyle \frac{1}{6}}\pi \rho D_0^3) g(h_1+{\displaystyle \frac{D_0}{2}}\cos {\theta }_0)+mgh$$

(3)

where g is the acceleration of gravity, m/s²; h₁ is the falling height of the impact point of the leaf, m; θ₀ is the initial angle between the tangent line of the droplet’s impact point and the horizontal direction, °; m is the mass of the leaf, Kg; h is the vertical falling height of the center of gravity of the leaf, m.

The expression for E_S1 is shown in Equation (4):

$$E_{S1}={\sigma }_{LG}\pi D_0^2$$

(4)

σ_LG is the surface tension between liquid–gas surfaces, mN/m.

The droplet attains its maximum spread at time t_b, at which point its shape is approximated as a thin disk, as shown in Figure 1b. The kinetic energy of the droplet at time ta and the gravitational potential energy of the system are converted into the surface energy at the liquid–gas and solid–liquid interfaces at time t_b, E_S2. Additionally, the energy lost due to viscous dissipation during the droplet spreading on the foliage surface, Diss_a~b, along with the elastic and torsional potential energies of the leaf, E_P2 and E_P3, are represented by the expressions in Equation (5):

$$E_a=E_b+Dis{s}_{a~b}$$

(5)

Because viscous dissipation is mainly related to droplet viscosity and solid surface properties, the effect of leaf inclination on viscous dissipation is negligible. In this study, Diss_a~b is selected from the literature [10] for horizontal leaf surfaces, and its expression is given in Equation (6):

$${\displaystyle \frac{Dis{s}_{a~b}}{\pi D_0^2{\sigma }_{LG}}}=0.35{\displaystyle \frac{We}{\sqrt{\mathrm{Re}}}}{\left({\displaystyle \frac{D_m}{D_0}}\right)}^2$$

(6)

where Diss_a~b is the viscous power dissipation energy from t_a to t_b, J; We is the droplet Weber number; Re is the droplet Reynolds number.

The formula for the energy E_b of the droplet–leaf system at the time t_b is provided in Equation (7):

$$E_b=E_{S2}+E_{P2}+E_{P3}$$

(7)

The surface energy E_S2 is the liquid–gas surface energy and the energy of the new solid–liquid surface, minus the solid–gas surface energy lost in the process, as in Equation (8):

$$E_{S2}={\sigma }_{LG}\left({\displaystyle \frac{\pi }{4}}{D}_m^2+{\displaystyle \frac{2\pi }{3}}{\displaystyle \frac{D_0^3}{D_m}}\right)+{\displaystyle \frac{\pi }{4}}{D}_m^2\left({\sigma }_{SL}-{\sigma }_{SG}\right)$$

(8)

Young’s equation combined with the surface tension between different interfaces is used [19]:

$${\sigma }_{LG}\cos \theta ={\sigma }_{SG}-{\sigma }_{SL}$$

(9)

Substituting Equation (9) into (8) yields Equation (10):

$$E_{S2}=\left({\displaystyle \frac{\pi }{4}}{D}_m^2(1-\cos \theta )+{\displaystyle \frac{2\pi }{3}}{\displaystyle \frac{D_0^3}{D_m}}\right){\sigma }_{LG}$$

(10)

where θ is the static contact angle of the droplet on the surface of the pepper leaf, °; σ_SG is the surface tension between the solid–gas surface, mN/m; σ_SL is the surface tension between the solid–liquid surface, mN/m; and D_m is the maximum spreading diameter of the droplet, m.

The elastic and torsional potential energy equations are Equations (11) and (12), respectively:

$$E_{P2}={\displaystyle \frac{1}{2}}k{h}_1^2$$

(11)

$$E_{P3}={\displaystyle \frac{1}{2}}K{\theta }_1^2$$

(12)

where k is the bending coefficient of the pepper leaf, mN/m; K is the torsion coefficient of the pepper leaf, mN/deg; h₁ is the falling height of the impact point, m; θ₁ is the torsion angle of the leaf on impact, °.

Substituting Equations (2)–(4), (6) and (10)–(12) into Equation (5) to obtain Equation (14) yields a one-variable three-dimensional equation about β that predicts the maximum spreading diameter of a droplet impacting a pepper leaf.

The maximum diffusion factor expression is shown in Equation (13):

$$\beta ={\displaystyle \frac{D_m}{D_0}}$$

(13)

$$\begin{array}{c}[{\displaystyle \frac{1}{4}}\left(1-\cos \theta \right)+0.35{\displaystyle \frac{We}{\sqrt{\mathrm{Re}}}}]{\beta }^3-\\ [{\displaystyle \frac{We}{12}}+1+{\displaystyle \frac{\rho g{D}_0}{6{\sigma }_{LG}}}(h_1+{\displaystyle \frac{D_0}{2}}\cos {\theta }_0)+{\displaystyle \frac{mgh}{\pi D_0^2{\sigma }_{LG}}}-{\displaystyle \frac{k{h}_1^2+K{\theta }_1^2}{2\pi D_0^2{\sigma }_{LG}}})]\beta +{\displaystyle \frac{2}{3}}=0\end{array}$$

(14)

2.2. Mathematical Prediction Model for Droplet Bounce

The droplet energy at the moment of t_c is E_c. The expression for E_c is presented in Equation (15):

$$E_c=E_{S2}-Dis{s}_{b~c}$$

(15)

Diss_b~c in this study is chosen from the literature [10] for a horizontal foliage surface, and its expression is shown in Equation (16):

$${\displaystyle \frac{Dis{s}_{b~c}}{E_{S3}}}=0.12{({\displaystyle \frac{D_m}{D_0}})}^{2.3}{(1-\cos \theta )}^{0.63}$$

(16)

The droplet surface energy that a droplet has at the instant of bouncing is E_S3, expressed as in Equation (17):

$$E_{S3}=\pi D_0^2{\sigma }_{LG}$$

(17)

When E_c > E_S3, the droplet starts to bounce off the leaf surface, as expressed in Equation (18):

$$E_{ERE}^{\ast }={\displaystyle \frac{E_c-E_{S3}}{E_{S3}}}={\displaystyle \frac{E_{S2}-Dis{s}_{b~c}-E_{S3}}{E_{S3}}}>0$$

(18)

where E^∗_ERE is the relative residual energy, J; E_S3 is the surface energy of the droplet during rebound, J.

Substituting Equations (10), (13), (16), and (17) into Equation (18) yields Equation (19) for predicting droplet rebound:

$${\displaystyle \frac{1}{4}}{\beta }^2(1-\cos \theta )+{\displaystyle \frac{2}{3\beta }}-0.12{\beta }^{2.3}{(1-\cos \theta )}^{0.63}-1>0$$

(19)

Equation (19) is an inequality with respect to β and is used to predict droplet rebound.

2.3. Plant Culture

Capsicum annuum L. (Capsicum annuum L., Tianshuai 101) was chosen as the experimental subject. The peppers were cultivated in a greenhouse in Zhenjiang City, Jiangsu Province, China, and after 90 days of meticulous care, they were transferred to pots for an additional 10 days of growth. Ten healthy, pest-free chili plants were selected, and three developed leaves from each plant were designated as experimental materials. The experiment was conducted in the laboratory, where the temperature was regulated at 26 ± 1 °C, and the relative humidity was controlled between 57% and 70% to ensure the leaves were in optimal condition, measures critical for obtaining precise and dependable experimental data.

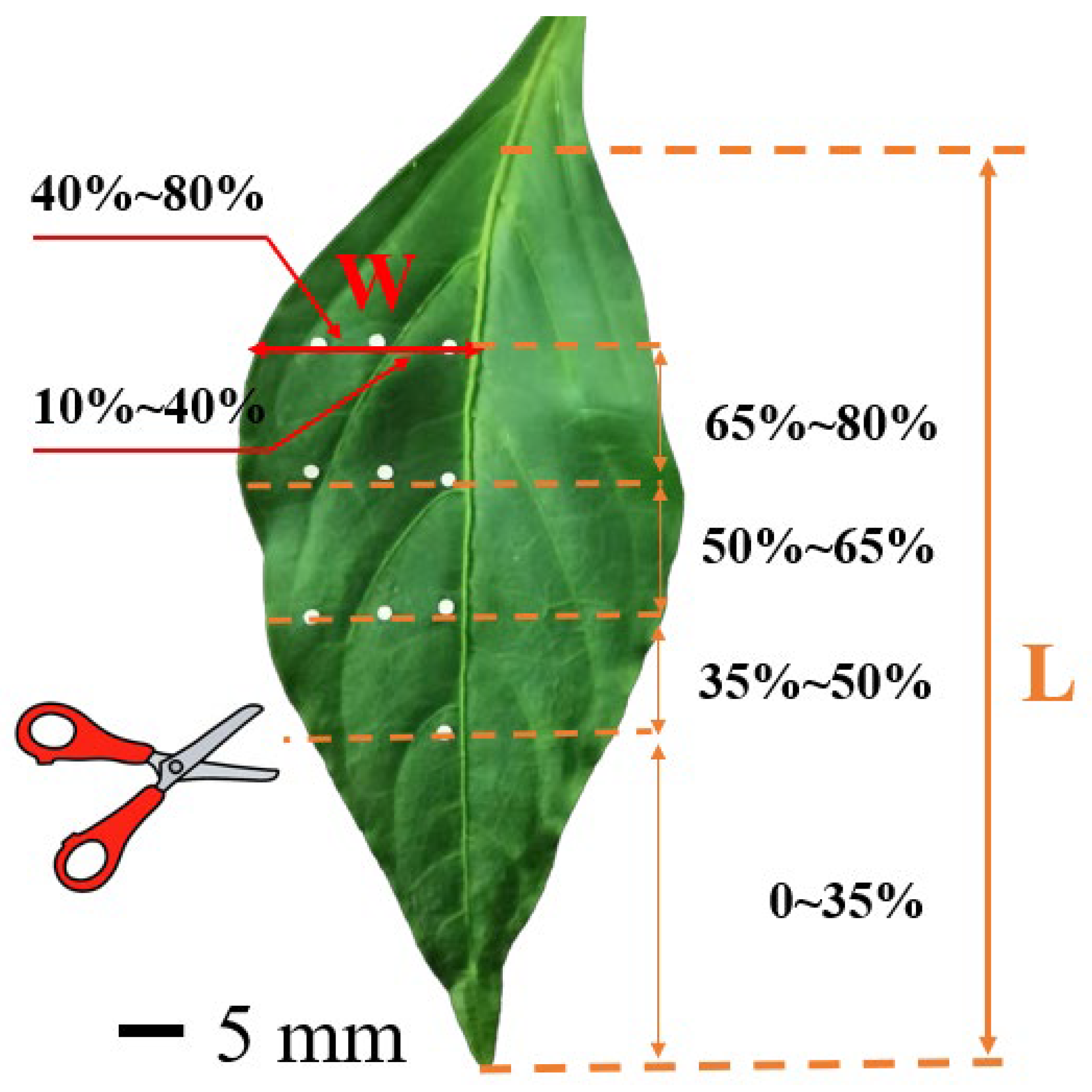
2.4. Leaf Impact Points

To investigate the influence of leaf bending and twisting on droplet impact behavior and spreading, specific impact locations were designated on the leaves for droplet impact studies. Ten loci were chosen on the lateral aspect of the primary leaf vein, corresponding to the white dots seen in Figure 2, owing to the symmetry of pepper leaves. To prevent droplet dispersion from exceeding the leaf’s edge and affecting the maximum droplet spread, three loci were designated in each row. Additionally, to minimize longitudinal data gaps along the leaf, an extra locus was chosen near the leaf tip, resulting in a configuration of four rows and three columns overall. The leaf’s length was L, the left leaf’s width was W, the longitudinal distance from the point of contact to the leaf tip was L_b (see Figure 3a), and the transverse distance to the major leaf vein was L_t (see Figure 3b). The leaf surface was segmented by L_b/L = 35%, 50%, 65%, 80%, and L_t/W = 10%, 40%, 80%, with 10 loci designated as droplet impact sites.

2.5. Measurement of Leaf Mass

Upon completion of the impact test and the measurement of leaf elasticity and torsion coefficients, the leaf was divided transversely (refer to Figure 3). The mass of each segment of the leaf was then measured using a Sartorius electronic balance (model BT125D, with an accuracy of 0.1 mg). This allowed for the determination of the mass distribution at points along the leaf, specifically at 35%, 50%, 65%, and 80% from the tip of the leaf. The pepper leaf was modeled as a structure with a homogeneous mass distribution, disregarding its thickness when determining the position of its center of gravity, thus simplifying each segment of the leaf to a ‘plate’, with the center of mass and center of gravity coinciding. The center of gravity for each component of the leaf was determined using the ‘hanging method’ by suspending various places and capturing images of the leaf’s suspension using a calibrated, stationary camera, aligned with the intersection of the plumb line’s extension lines.

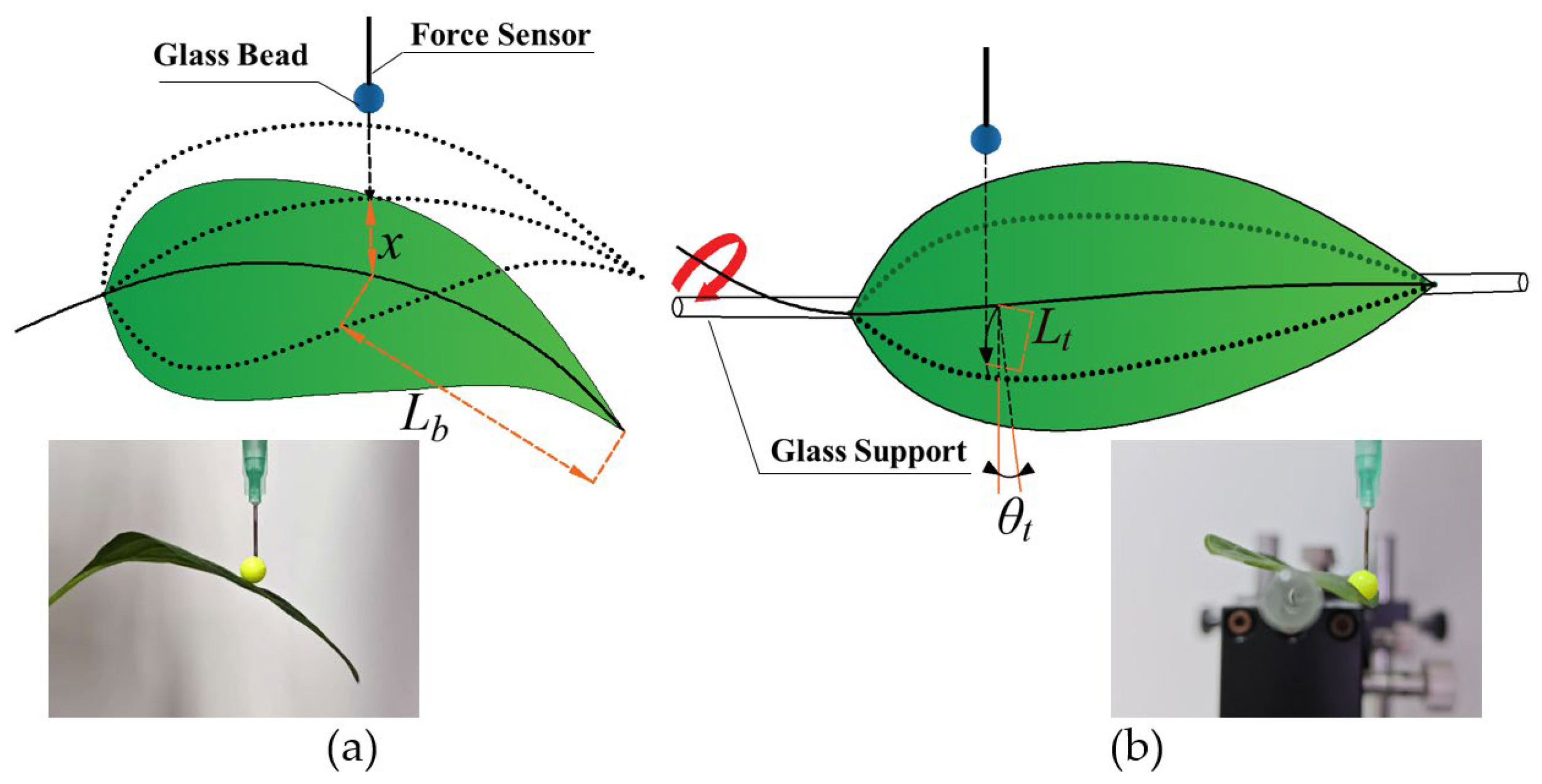
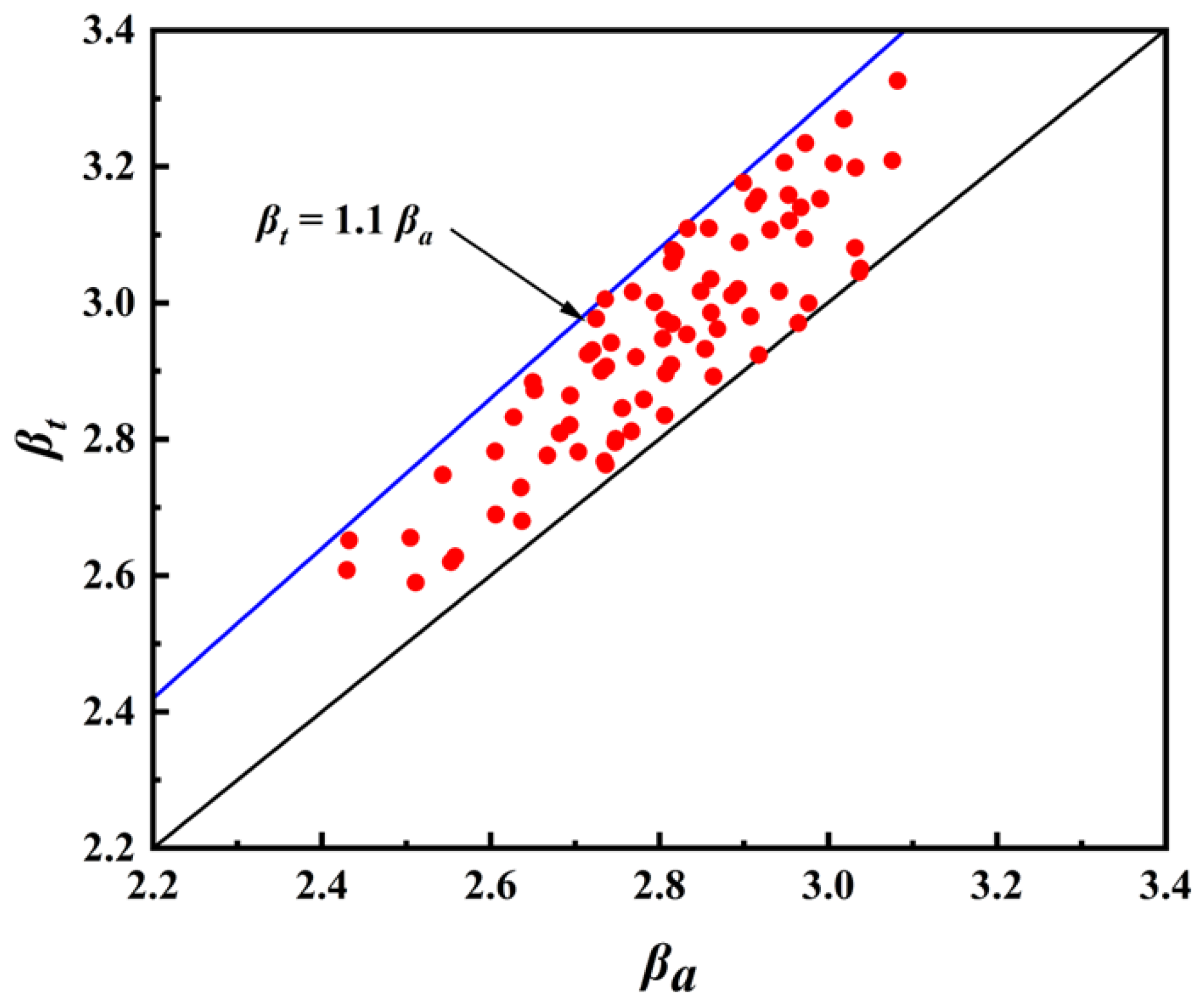
2.6. Measurement of Leaf Bending and Torsion Coefficients

The structural and biomechanical characteristics of pepper leaves significantly influence their behavior during spray application. Moulia et al. [20] assert that the primary leaf veins significantly contribute to the bending deformation of the entire leaf, accounting for over 87% of the leaf’s stiffness. The primary leaf vein, serving as the principal support structure of the leaf, can flex akin to a cantilever beam, while the leaf on either side experiences a similar bending deformation. The petiole resembles a torsion axis, enabling the leaf to revolve around the primary leaf vein when torque is exerted. When downward pressure is exerted away from the primary leaf vein, the leaf will exhibit a simultaneous bending and twisting deformation along the main leaf vein.

Measurement of the bending and torsion coefficients of the part of the pepper leaf at the droplet’s impact location should be carried out immediately after the flexible leaf test to prevent leaf deformation due to environmental changes [21,22,23]. When measuring the bending resistance coefficient (Figure 3a), the pressure transducer was clamped on a linear platform, and the pressure transducer with a 5 mm diameter ball fixed at the end was pressed vertically on the leaf surface at 10 points, respectively, to ensure that only bending movement of the leaf occurred, as shown in Figure 3a, and the drop height of the marked points, x, and the pressure shown by the pressure transducer, F, were recorded.

Hooke’s theorem was used to solve the bending resistance coefficient of the leaf by averaging three measurements for each point. The bending resistance coefficient was calculated by the formula:

$$k={\displaystyle \frac{F}{\mathrm{x}}}$$

(20)

where k is the bending resistance coefficient at the impact site of the pepper leaf, N/m; F is the load force applied at the impact site, N; x is the vertical drop height of the main leaf vein after the load is applied at the impact site, m.

To prevent inaccuracies in the torsion trials caused by leaf bending, the primary veins of the pepper leaves were secured to glass rods (see Figure 3b) during torsion testing, ensuring that the leaves could rotate freely around the primary veins without bending deformation. This form of support was utilized solely during the torsion test, while no support was employed during the test involving droplet impact on the flexible leaf to prevent restricting the leaf. The torsional coefficient was determined similarly to the bending coefficient by recording the force from the pressure transducer, the transverse distance L_t from the site of impact to the major leaf vein, and the leaf twist angle θ_t.

The load was applied to the leaf and averaged for each point of impact, and the torsional coefficient was calculated as follows:

$$K={\displaystyle \frac{F{L}_t}{{\theta }_{\mathrm{t}}}}$$

(21)

where K is the torsional coefficient at the impact site of the pepper leaf, N/θ; F is the load force applied at the impact site, N; L_t is the lateral distance from the impact site to the main leaf vein, m; θ_t is the torsional angle of the leaf after applying the load at the impact site, °.

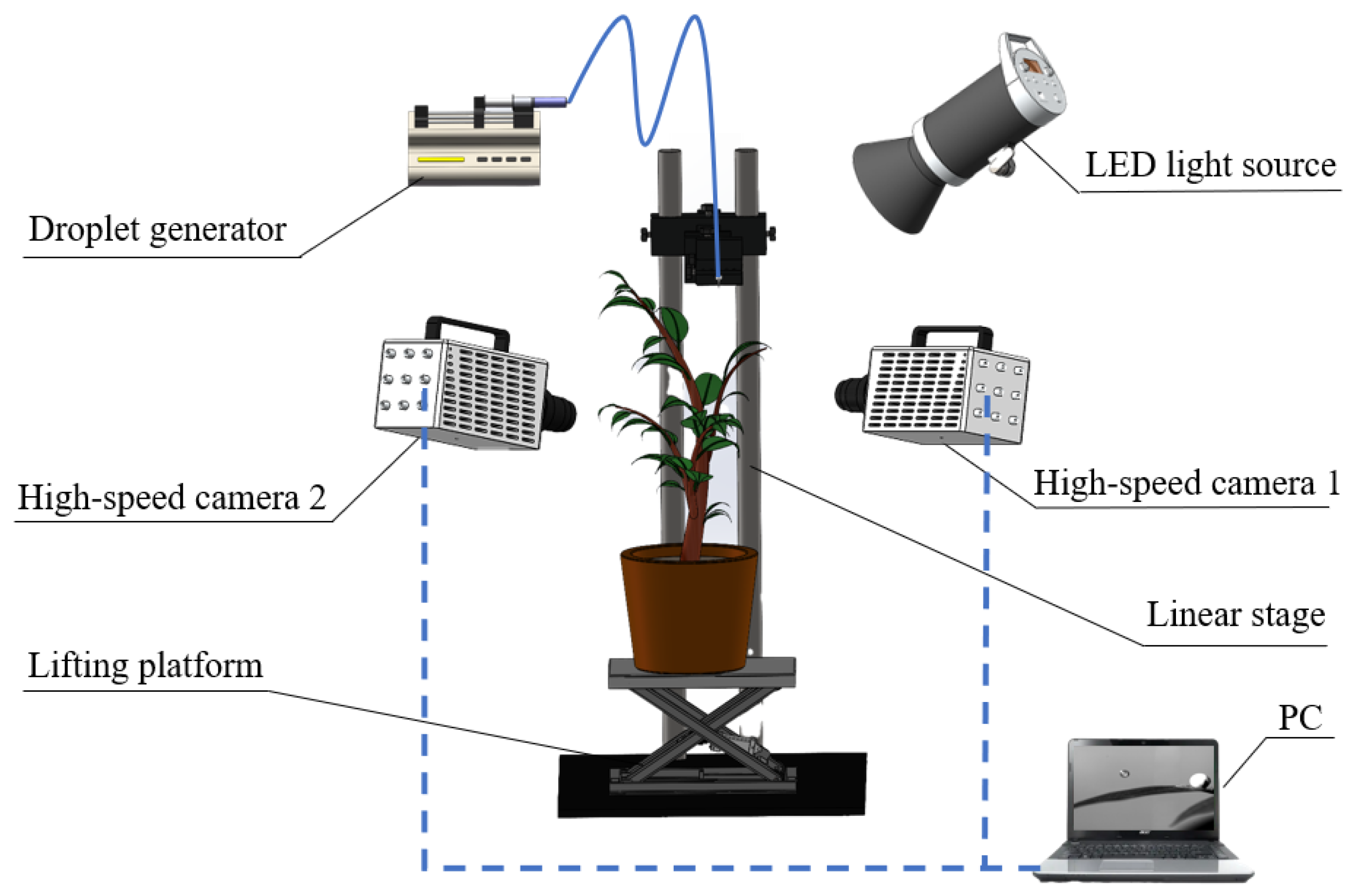
2.7. Behavior of Liquid Droplet Impact on Flexible Pepper Leaves and Rigid Substrate Test

The experimental configuration is depicted in Figure 4, encompassing the droplet-generating apparatus and the image capture system. The droplet-generating apparatus comprises a syringe pump NE-1000 (serial number 269269, New Era Pump Systems, Inc, East Farmingdale, NY, USA), a 20 mL syringe, an injection needle, and a linear platform. The syringe pump delivered the syringe at a rate of 1 mL/s, causing the distilled water to flow from the hose through the injection needle and deposit as droplets on the leaf surface of the pepper plant. The experiment utilized distilled water, characterized by a surface tension of 0.0728 N/m, a viscosity of 1.01 × 10⁻³ Pa-s, and a density of 103 kg/m³ at 20 °C. The injection needle was secured by a fixture on the linear platform. By regulating the motion of the linear platform, the needle was enabled to traverse a limited range inside three-dimensional space. The image acquisition system comprises an OSRAM high-brightness light source, two high-speed digital video cameras, and a computer for recording droplet impacts on the leaf. The OSRAM high-brightness light source operated at a voltage of 230 V and a power of 1000 W. The two high-speed video cameras (OLYMPUS I-Speed 3, manufactured by Navitar, Rochester, NY, USA) were interconnected via synchronous cables and operated in unison to record droplet hits on the leaf. The dual high-speed cameras offer enhanced detail of droplet impact and more precise droplet motion parameters compared to a single-camera imaging system. The lenses of the two high-speed cameras were positioned at the same horizontal elevation and were orthogonal to each other to capture the primary view and the lateral view of the droplet’s impact on the leaf and its subsequent motion behavior, respectively. The cameras were configured to a frame rate of 3000 fps and a resolution of 1024 pixels by 512 pixels. To guarantee test accuracy, a standard ceramic calibration sphere, possessing a genuine roundness of 0.001 mm and a repeatability of 0.0005 to 0.001 mm, was affixed to the leaf surface, and pixel calibration was conducted utilizing the I-speed suite program accompanying the high-speed camera.

To study the effects of droplet particle size, droplet impact velocity, and leaf bending and twisting on droplet spreading, droplets with particle sizes of 2.6 mm, 2.4 mm, and 2.2 mm and velocities of 1.55 m/s, 1.41 m/s, and 1.28 m/s were used to impact the leaf at 10 sites, respectively (Figure 2). Different droplet sizes were obtained by changing the needle model. Under the same propulsion speed of the syringe pump, 9 drops of each droplet produced by 3 types of needles were taken, and the maximum and minimum values of droplet sizes were removed to obtain the average size defined as the droplet size produced by this type of needle, and the droplet impingement velocity was controlled by adjusting the vertical height between the injection needle and the impingement point on the linear platform. The first four frames of the photographs taken by the high-speed camera in which the droplets first contacted the leaf surface were manually selected. Taking the bottom-most position of the droplet as the reference, the actual height H of the droplet falling was calculated from the actual size of the calibration ball in the photographs, and the droplet impact velocity v₀ was calculated by the formula:

$$v_0={\displaystyle \frac{H}{t}}$$

(22)

where t is the time between the 4 frames, s; H is the droplet falling height between the selected 4 frames, m.

The purpose of this study is to study the effect of the elastic coefficient of the leaf on the impact behavior of the droplet, and the selection of a larger droplet can enhance the interaction between the two droplets when the droplet hits the leaf, so that the experimental phenomenon becomes obvious and easy to observe and study. Although the particle size of the droplets selected for the experiment did not conform to the particle size of the actual spray scene, a theoretical model of dynamic similarity without a dimension number was proposed in ref. [24] through fluid mechanics analysis, and the two fluids exhibited similar dynamic characteristics under the condition of satisfying the dynamic similarity of dimensionless numbers.

$$W{e}_m=W{e}_p$$

(23)

where We_m is the Weber number of the model, and We_p is the Weber number corresponding to the prototype.

The material selected for the test was distilled water, and the surface tension of the droplets under this test condition was 71.86 mN/m. However, in the actual spraying scenario, the density of the liquid medicine is approximately unchanged, and the surface tension range of the commonly used pesticides with additives is 20.35~34.34 mN/m [25]. According to the dynamic similarity theory of dimensional analysis, when the Weber number, We_m, of the droplet and the Weber number, We_p, of the pesticide droplet with additives are equal under the test conditions, the particle size selected in this test is consistent with the droplet size in the actual scene under the corresponding test speed. Therefore, the dynamic characteristics of the droplets obtained under the conditions of the droplet size and test speed selected in this study are also in line with the actual scenario.

In order to obtain the droplet spreading diameter after the droplet impacts the leaf, the coordinates of the two endpoints of the droplet spreading, (X₁, Y₁) and (X₂, Y₂), were marked by the i-SPEED Control Software Suite 2.0, and the straight-line distance between the two endpoints was calculated to find out the spreading diameter of the droplet with the formula:

$$D=\sqrt{{(X_1-X_2)}^2+{(Y_1-Y_2)}^2}$$

(24)

where X₁ is the X-axis coordinate of droplet endpoint 1, X₂ is the X-axis coordinate of droplet endpoint 2, Y₁ is the Y-axis coordinate of droplet endpoint 1, and Y₂ is the Y-axis coordinate of droplet endpoint 2.

Droplet impact experiments on inclined stiff leaves were conducted to comparatively assess the influence of torsion and elasticity of the leaves on droplet impact behavior. The angle of inclination was ascertained according to the surface on which the point of impact was situated in its natural growing stage (θ₀ in Figure 1). The leaves were secured to an acrylic sheet with double-sided tape, intended to preserve the integrity of the leaves’ surface qualities. The acrylic sheet with the attached vane was positioned at a tilt angle of θ₀ using a jig. The droplet impact test on a tilted rigid vane was conducted by regulating the droplet particle size, impact velocity, and impact position, similar to the flexible vane test.

The sessile drop technique was employed to quantify the contact angle and acquire contact angle data at various impact locations on the leaf surface. The contact angle measurements were conducted at 10 locations on the pepper leaves, as seen in Figure 2, utilizing an OCA-type video optical contact angle meter (Data Physics Inc., Filderstadt, Germany). Distilled water was introduced into a syringe (SNS-052), and the droplet volume was regulated to 2 μL via a computer. The contact angle of the droplet on the surface of the pepper leaf was determined using the analysis system associated with the contact angle measuring instrument, and the average of three measurements was recorded for each point as the contact angle at that location. The contact angles at ten specific locations on the leaf were consistent in the transverse W direction yet varied in the longitudinal L direction. The contact angles measured from the leaf tip along the primary vein toward the petiole were 84°, 82°, 81°, and 80°, respectively.

3. Results and Discussion

A comparative analysis was conducted to evaluate the accuracy of the mathematical model of droplet impact behavior by comparing theoretical predictions of the maximum diffusion factor with experimental results. The β_t = 1.1 β_a in Figure 5 denotes the threshold at which theoretical predictions exceed actual observations by 10%. The experimental data show that the difference between the maximum diffusion factor predicted by the theoretical model and the experimental measured value is within the error range of 10%. Incorporating the theoretically anticipated maximum diffusion factor into the droplet rebound prediction model yields calculated predictions that align with the observed droplet impact behavior, with none exhibiting rebound. In contrast to the model proposed by Liu et al. [11], this work incorporates the effects of leaf torsion angle and leaf bending on droplet dispersal. The augmentation of the bending and torsion coefficients led to a significant enhancement of the model. Although the factors of leaf bending and torsion are taken into account in this paper, the predictive model of droplet impact behavior is mainly based on the kinetic energy of the droplets themselves, and does not take into account the influence of external energy inputs (e.g., air-fed or electrostatic sprays) on droplet behavior. In addition, the model simplifies the leaf surface structure and does not take into account the complexity of the actual leaf surface, such as the unevenness of the leaf veins, the microstructure of the leaf surface [26], and the droplet escape phenomenon that may occur at the edge of the leaf, as well as the air resistance of the leaf during bending and twisting. These factors, which may significantly affect droplet impact behavior in real applications, are not included in the mathematical model of this paper. Therefore, the model has some limitations in describing droplet behavior on real leaves, and these also need to be improved in the future and should be further integrated into real spray scenarios.

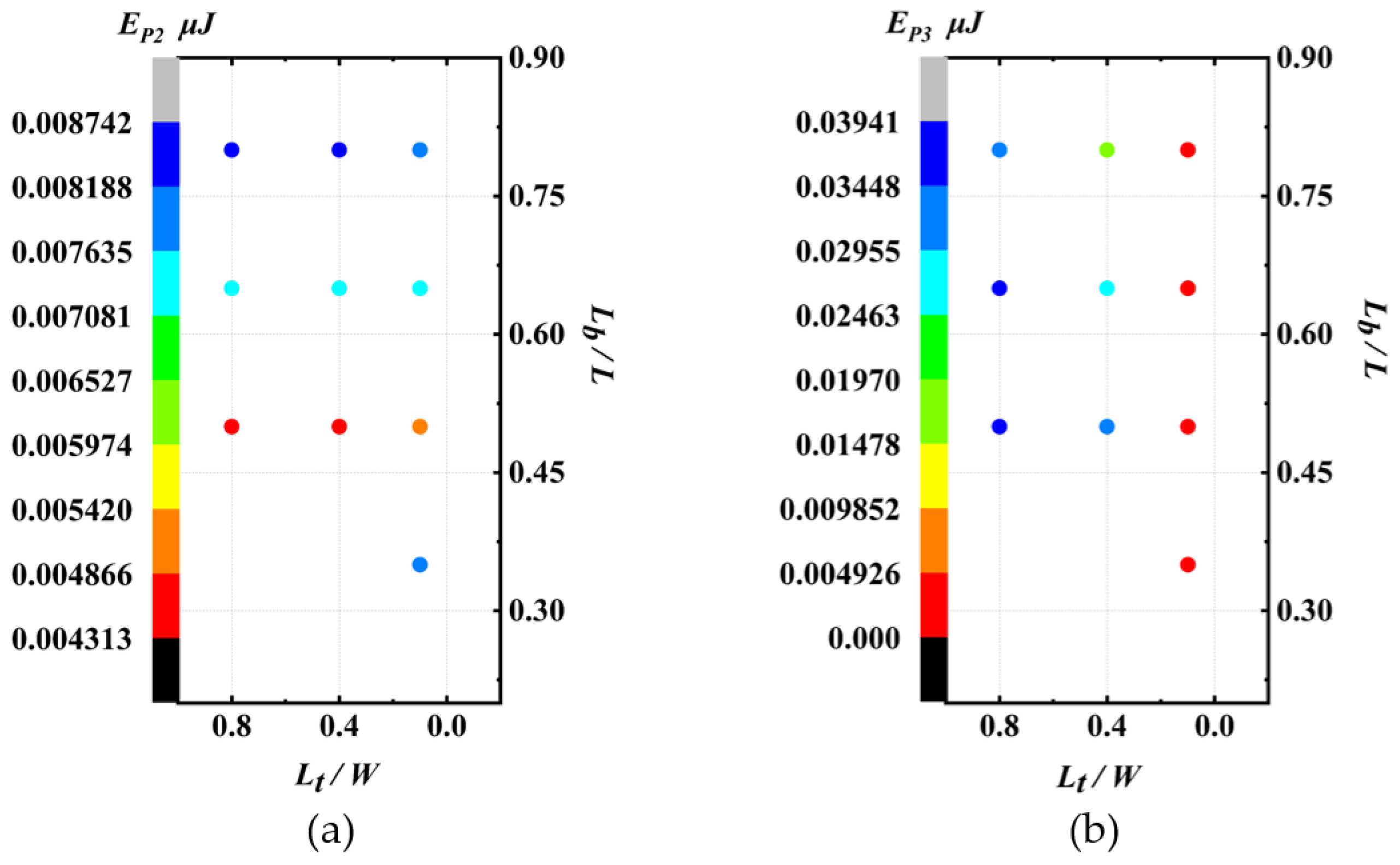
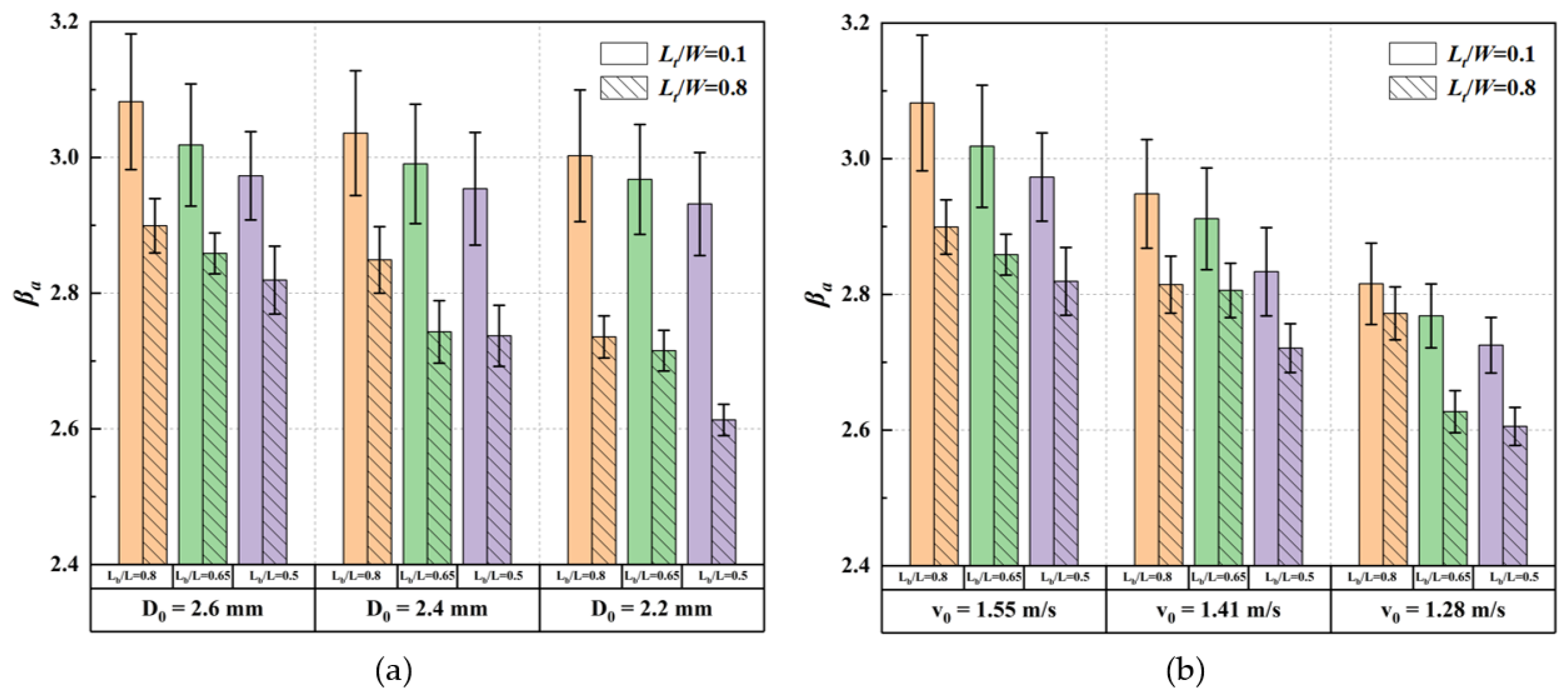
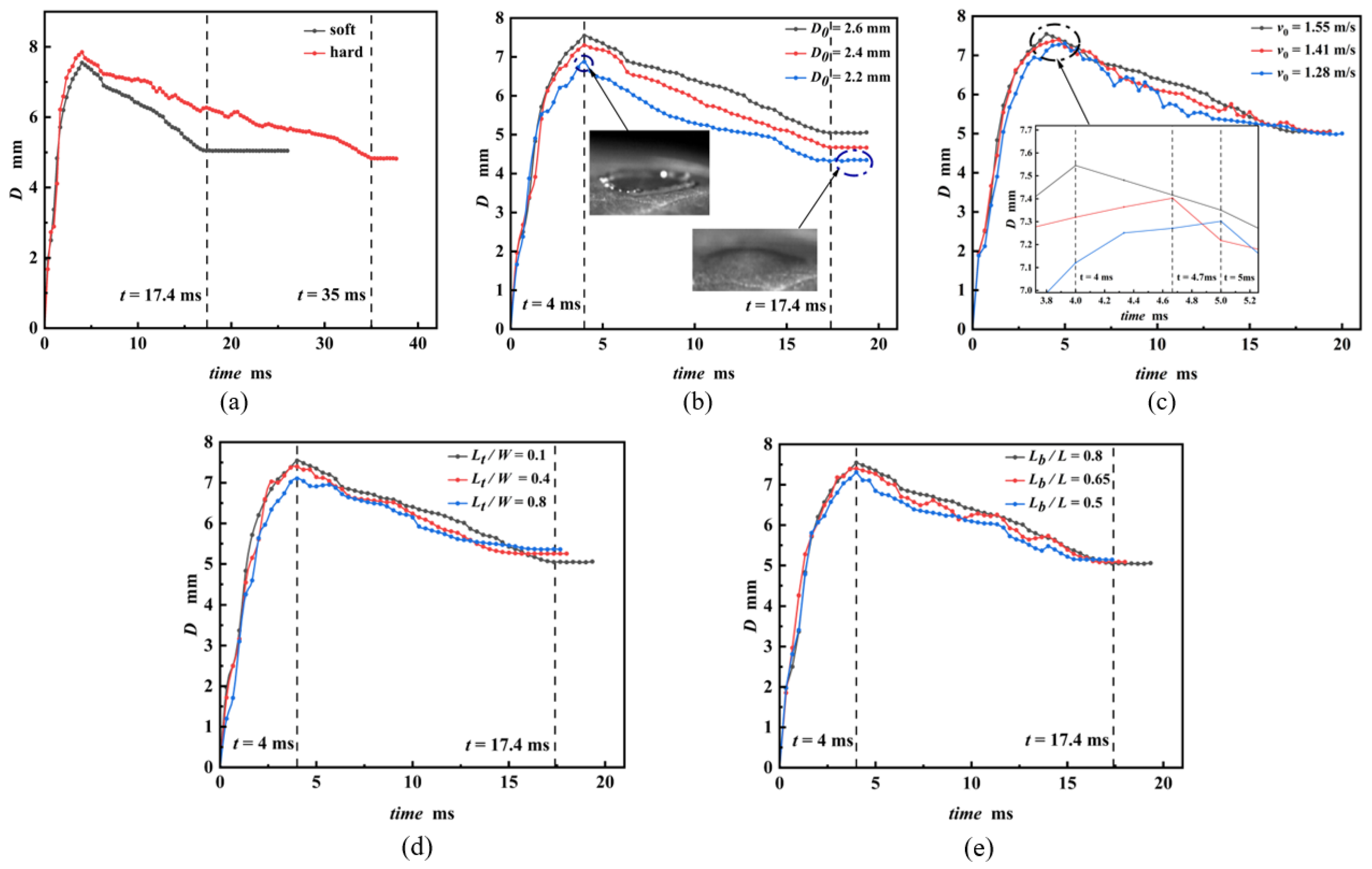
3.1. Effect of Leaf Bending and Twisting on Spreading

The process of a droplet impacting a pepper leaf involves several energy conversions and distributions. The droplet has a certain amount of kinetic energy before it hits the pepper leaf, and the amount of kinetic energy is determined by the mass and speed of the droplet. After the droplet hits the pepper leaf, the droplet is deformed, and the leaf is bent and twisted by the droplet, which can convert part of the initial kinetic energy of the droplet into the surface energy of the droplet, the elasticity of the leaf, and torsional potential energy [23]. In the process of droplet spreading and contraction, part of the initial kinetic energy is converted into energy dissipated to overcome the viscosity.

The elastic and torsional potentials at various locations on the pepper leaf were graphed based on the formulae for elastic potential energy (Equation (11)) and torsional potential energy (Equation (12)) provided by the mathematical model for forecasting the maximum droplet spreading diameter. The analysis of the distribution of elastic and torsional potential energy at various points of droplet impact on pepper leaves revealed that the distribution trends were largely consistent across different particle sizes and velocities. In light of this finding, the current study selected a droplet diameter D₀ of 2.6 mm and a velocity v₀ of 1.55 m/s, and examined the distribution of elastic and torsional potential energy upon the droplet’s impact at various locations on the leaf. The distribution of impact sites indicates that the energy within a row is essentially uniform throughout four rows and three columns, signifying that the elastic potential energy resulting from varying positions within a row is largely equivalent. The elastic potential energy imparted to the leaf upon droplet impact initially decreases and subsequently increases from the leaf tip to the petiole (Figure 6a). This phenomenon may be attributed to two primary factors: firstly, as one moves from the petiole to the tip, the main leaf vein transitions from thick to thin, resulting in a nonlinear alteration in the bending resistance coefficient of the leaf, thereby influencing the elastic potential energy trend [27,28]; secondly, the inherent curvature of the leaf modifies the force direction during droplet impact. Figure 6b illustrates the torsional potential energy generated by various spots on the leaf when the droplet diameter D₀ is 2.6 mm and the velocity v₀ is 1.55 m/s. The torsional potential energy differs from the elastic potential energy. In contrast to elastic potential energy, the torsional potential energy resulting from varying droplet impact locations exhibits greater variability across rows, with notable differences in each column; additionally, the torsional potential energy increases as one approaches the leaf’s edge. The torsional potential energy of the leaf does not exhibit the same trend as the bending potential energy, likely due to the lesser curvature in the width direction (W) compared to the length direction (L), and concurrently, each row remains unaffected by variations in the thickness of the primary leaf veins. The elastic potential energy of the leaf attains a maximum at around 35% from the tip along the primary leaf vein and a minimum at around 50% from the tip along the same vein, influenced by the drooping curvature and edge spillage of the leaf (Figure 6a).

The primary leaf veins of chili pepper exhibit greater roughness than the leaf tissue. To mitigate the effect of the primary leaf veins on droplet impact behavior and spreading, the impact site column ratio L_t/W = 0.1 is approximated as a purely bending deformation of the chili pepper leaf due to impact. Figure 7 illustrates the correlation between E_p2/E_a following the impact of droplets of varying particle sizes into the column with L_t/W = 0.1, under the conditions where the velocities v₀ are 1.55 m/s, 1.41 m/s, and 1.28 m/s, respectively. Figure 8 illustrates the E_p3/E_a correlation following the influence of varying particle sizes on L_b/L = 0.8 within the row at distinct velocities, under the condition of a particle size D₀ of 2.6 mm (Figure 8a), and subsequent to the impact of different particle sizes on L_b/L = 0.8 in the row at various velocities, under the condition of a velocity v₀ of 1.55 m/s (Figure 8b). The particle size and velocity minimally influence the ratio of leaf elastic potential energy to initial energy, yet significantly affect the ratio of leaf torsional potential energy to initial energy, with a decrease in droplet particle size and velocity resulting in an increase in E_p3/E_a. The analyzed data indicate that within the specified droplet size and velocity range, the elastic potential energy of the leaf remained constant despite significant variations in droplet size and speed, with E_p2/E_a ranging from 1.2% to 2.7%. The torsional potential energy of the leaves fluctuated with droplet size and velocity, exhibiting a range of 8.2% to 11.9% for E_p3/E_a in the column of L_t/W = 0.8 at the impact location.

Figure 9 illustrates that, with identical impact speed and particle size, for a droplet impacting a leaf with L_t/W = 0.1, the maximum spreading diameter of the droplet diminishes as it approaches the tip. Currently, the leaf’s pure bending deformation does not account for the energy absorbed by leaf torsion. According to the mathematical model predicting the maximum spreading diameter of the droplet, this diameter should correspond to the variations in the leaf’s elastic potential energy. The ratio of leaf elastic potential energy to the initial energy, measured from the leaf tip to the petiole, exhibited a trend of first decreasing and then increasing (Figure 7). This observation contradicts the actual pattern of maximum droplet spreading diameter, potentially due to the inertia of the leaf. Experimental observations indicate that the droplet’s impact on the pepper leaf results in more pronounced deformation at the tip of the leaf. Additionally, the gravitational potential energy of the droplet–leaf system is considered equivalent to that of the pepper leaf, thereby defining the droplet’s impact at various points on the leaf in relation to the leaf’s mass and the impact location. The mass ratio is defined as the ratio of the mass of the flexible substrate to the mass of the droplet. Ma et al. [29] proposed that an increase in the mass ratio enhances substrate inertia, resulting in a greater maximum diffusion factor of the droplet, as the substrate becomes more resistant to displacement from the droplet’s impacts, exhibiting behavior akin to that of a rigid substrate. Conversely, as the mass ratio diminishes (i.e., the substrate becomes lighter), the impact of the droplet is accentuated, leading to an increased transfer of kinetic energy to the substrate. This diminishes the energy available for droplet spreading and results in a reduction in the maximum diffusion factor. The mass ratio influences energy conversion during droplet contact, since a lighter substrate (lower mass ratio) absorbs a greater portion of the initial kinetic energy, leading to reduced energy availability for droplet spreading and thus impacting the spreading outcomes. The mass ratio may be the primary factor contributing to a reduced maximum spreading diameter as the droplet approaches the tip of the leaf.

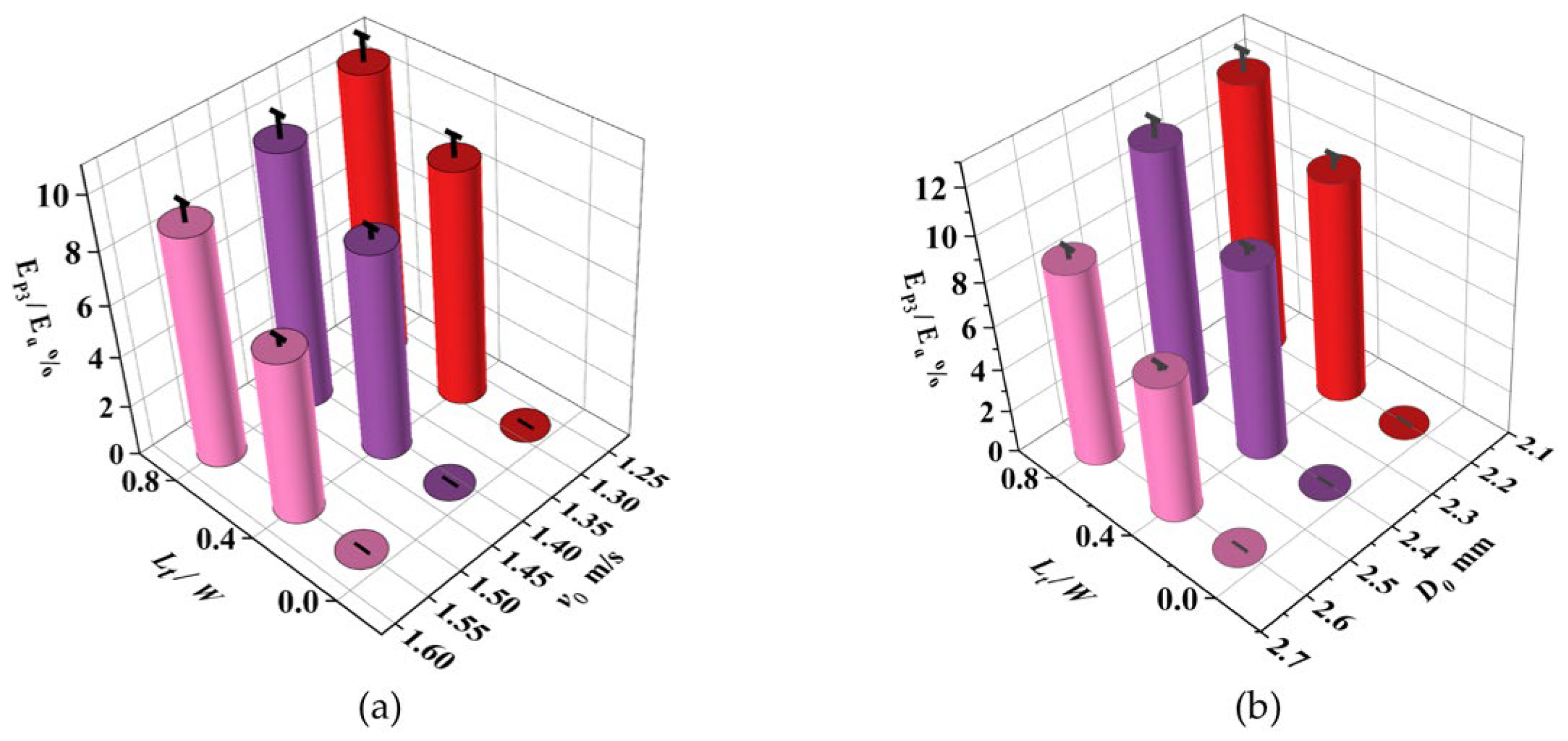
3.2. Effect of Droplet Size, Impact Velocity, and Leaf Bending and Twisting on Droplet Spreading Time on Flexible Pepper Leaves

The duration of droplet dissemination on plant leaves is a crucial determinant of droplet deposition, which directly impacts the distribution and absorption efficacy of pesticides. The duration of droplet dispersion dictates the extent and uniformity of pesticide application on the leaf surface. Li et al. [30] discovered that an extended spreading duration (10 ms to 100 s) facilitates the formation of a more uniform coverage on the leaf surface, hence enhancing the effective contact area of the pesticide and improving its absorption. A brief spreading time (0–10 ms) may lead to uneven droplet distribution, causing droplet rebound and splash, which adversely impacts efficacy.

Figure 10 illustrates the droplet impact spreading curves across various impact surfaces, droplet particle sizes, impact velocities, and impact locations. The horizontal axis is time, and the vertical axis is the spreading diameter of the droplet on the leaf surface. Figure 10a illustrates the droplet spreading curves resulting from droplet impact on both flexible leaves and stiff substrates, whereas Figure 10d and e depict the droplet spreading curves at various impact positions on the flexible leaf. The comparison indicates that leaf flexibility does not significantly influence the duration for the droplet to attain maximum spreading. The spreading time of the droplet impacting the flexible leaf is nearly equivalent to that on the rigid substrate. However, the retraction time of the droplet on the flexible substrate is considerably shorter, resulting in a total duration of droplet spreading and retraction that is merely half of that observed on the rigid substrate. Simultaneously, the droplets exhibited an expanded deposition area on the flexible leaf upon achieving a steady state (Figure 10a). The reduced droplet retraction time may occur from the interplay between the stored energy from leaf deformation and the droplet’s residual energy, leading to a fast return of the droplet to equilibrium [31,32]. The experiments indicate that droplet size does not significantly influence droplet spreading time and retraction time (Figure 10b). At a droplet impact velocity of 1.55 m/s, droplets of varying sizes strike the pepper leaf, achieving maximum spreading at t = 4 ms and attaining a steady state at t = 17.4 ms. The droplet impact velocity influenced both the droplet spreading time and retraction time (Figure 10c), with both parameters decreasing as the impact velocity diminished. S. Mangili et al. [33] noted a comparable phenomenon in their study involving droplets of fresh water with a particle size of D₀ measuring 2.85 mm striking a soft PDMS substrate within a Weber number range of 110 to 520. They determined that the substrate’s softness had a diminished impact on droplet spreading during droplet impingement conditions; however, the retraction rate on the soft substrate was slower, the total oscillation duration was markedly reduced, and the wetting range of the final deposition was greater with a smaller steady-state contact angle, which aligns closely with our experimental findings.

3.3. Influence of Droplet Particle Size, Impact Velocity, and Impact Point Location on the Maximum Diffusion Factor of Droplets Impinging on Flexible Pepper Leaves

The maximum spreading factor of a droplet is influenced by multiple variables, each exerting a different degree of impact on the maximum spreading factor. Experimental variables, including droplet particle size, impact velocity, and the position of the impact point, can substantially influence droplet adhesion and splashing [34,35]. Changes in droplet particle size and impact velocity immediately influence the kinetic energy of the droplets, thereby affecting their spreading behavior upon contact with the surface. The impact point’s location may alter the leaf’s bending and twisting variations, thus influencing the droplet spreading effect.

The experimental data were analyzed by multifactorial ANOVA using SPSS Statistics 29, and the results of the main effect analysis among the multifactors are shown in

Table 1. Analysis of variance of the effects of leaf deformation, impact velocity, and droplet size on the maximum diffusion factor at the point of impact.

Source	Sum of Squares	Degrees of Freedom (df)	Mean Square (MS)	F-Value	Significance (p-Value)	Partial Eta Squared
Corrected Model	5.216	80	0.065	220.537	<0.0001	0.991
Intercept	1907.872	1	1907.872	6,453,836.036	<0.0001	1.000
Particle Size	0.210	2	0.105	354.494	<0.0001	0.814
Impact Velocity	2.462	2	1.231	4164.218	<0.0001	0.981
Leaf Bending	0.562	2	0.281	949.890	<0.0001	0.921
Leaf Torsion	1.520	2	0.760	2571.366	<0.0001	0.969
Error (Residual)	0.048	162	<0.0001
Total	1913.135	243
Corrected Total	5.263	242

. The three test factors of impact location (leaf bending and twisting), impact velocity, and droplet particle size all significantly affected the maximum diffusion factor of adherent droplets (p < 0.05). Partial E_ta squared is the proportion of the contribution of the independent variables to the overall variance, and the values of the bias E_ta squared of the four independent variables were, in descending order, the impact speed (0.981), the percentage of the distance of the impact point from the perpendicular main leaf vein (0.969), the percentage of the distance of the impact point from the tip of the leaf (0.921), and the droplet particle size (0.814), and the four independent variables passed the test of significance. Thus, the contribution of impact velocity to the overall variation was the most significant among the four factors selected for the experiment, followed by impact location and finally droplet size, and all were positively correlated.

4. Conclusions

In this study, the leaf is treated as a cantilever beam model, and the effects of leaf bending and torsion on droplet impact behavior are taken into account, so that a mathematical model predicting the maximum spreading diameter of the droplet and the impact behavior is constructed through energy conservation. The theoretical predictions are verified by practical tests, and the results show good agreement between the predictions and the experimental results.

Leaf bending and twisting had a significant effect on droplet spreading. The bending coefficient of the leaf decreases as the distance from the tip decreases, while the torsion coefficient of the leaf increases as the vertical distance from the main leaf vein increases. The ratio of the elastic potential energy to the total initial energy transferred to the leaf after droplet impact shows a trend of decreasing and then increasing with the increase in the ratio of the distance from the impact point to the tip, and the ratio of the torsional potential energy to the total initial energy transferred to the leaf shows a trend of increasing with the increase in the ratio of the vertical distance to the main vein, and the torsional potential energy transferred by the droplet to the leaf is greater than the bending potential energy at the same impact position in the presence of leaf bending and torsion, and also with the increase in the velocity of impact. The torsional potential energy transferred from the droplet to the leaf was greater than the bending potential energy at the same impact location in the case of leaf bending and twisting, and there was a strong positive correlation with the impact velocity. The four factors of leaf bending and twisting, impact velocity, and droplet size all had a significant effect on the maximum diffusion factor of droplets (p < 0.05) and were positively correlated with each other, and the effects on the maximum diffusion factor of droplets were, in descending order, the impact velocity, leaf twisting, leaf bending, and droplet size.

Among the selected variables, droplet impact velocity had the greatest effect on the time for the droplet to reach maximum spreading: the faster the impact velocity, the shorter the time for the droplet to reach maximum spreading. Compared to impinging on a rigid fixed tilting leaf, the droplet reaches maximum spreading within the same time on both the flexible pepper leaf and the rigid fixed tilting leaf for the same impingement velocity, but the droplet retraction time on the flexible pepper leaf is explicitly shorter, with the total time for the droplet to spread and retract on the flexible pepper leaf being approximately half that of the rigid fixed tilting leaf.