Influence of Sugarcane on Runoff and Sediment Yield in Sloping Laterite Soils During High-Intensity Rainfall
Abstract
1. Introduction
2. Materials and Methods
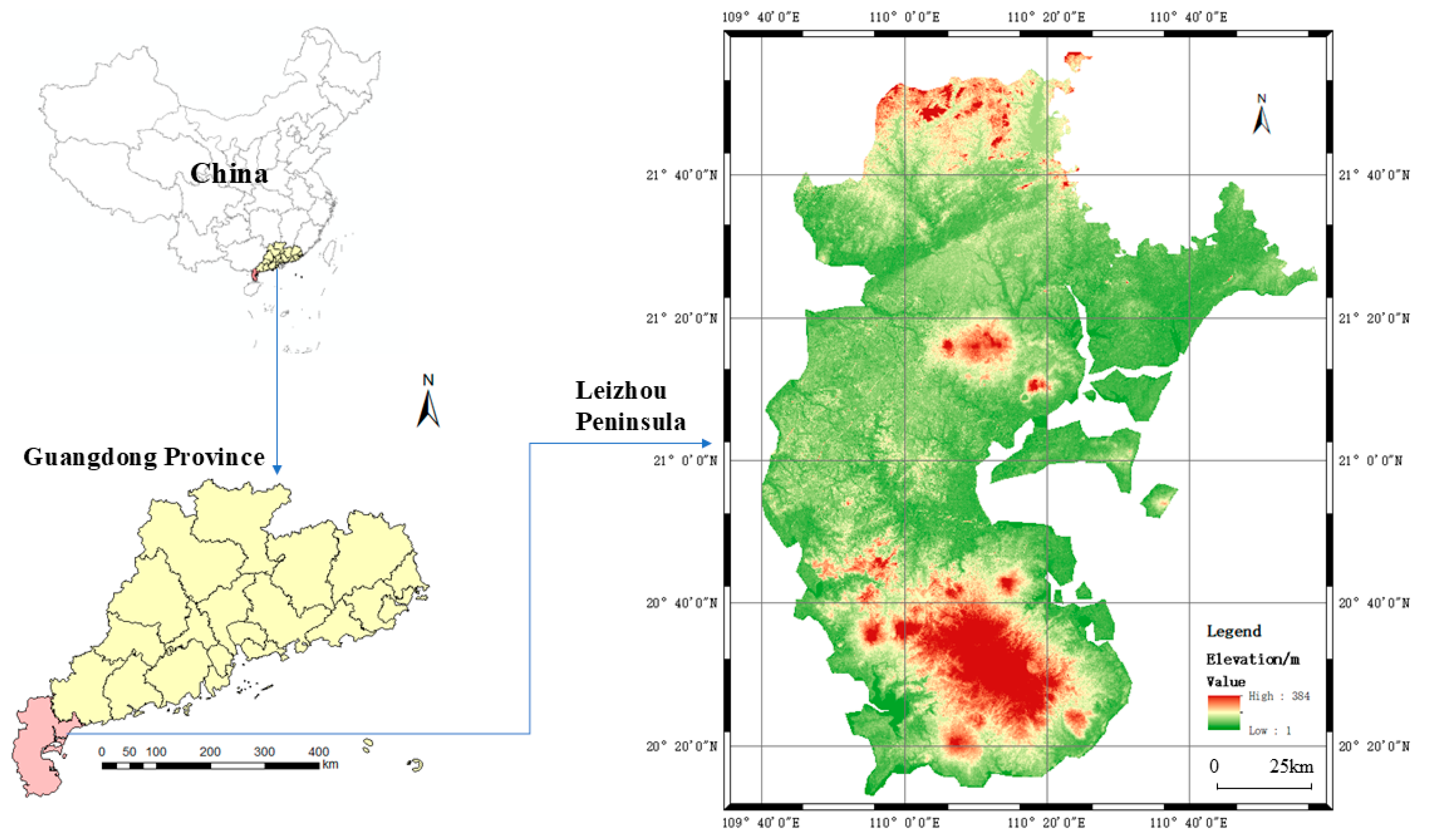
2.1. Research Area
2.2. Laboratory Experiments
2.3. Analysis Methods
3. Results and Discussions
3.1. Effects of Initial Runoff Time
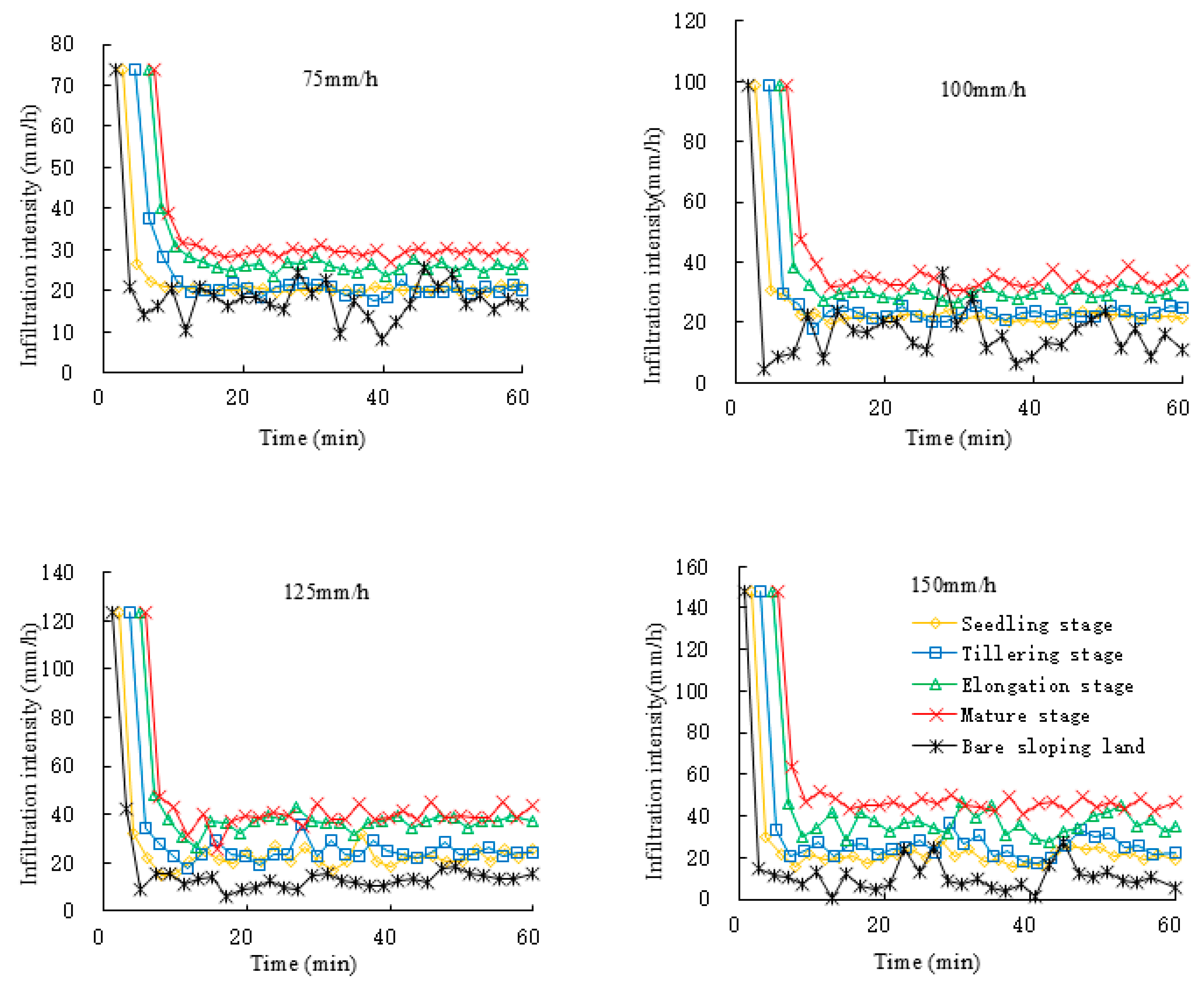
3.2. Infiltration Rate on Sugarcane-Cropped Slope
3.3. Runoff Intensity Variation
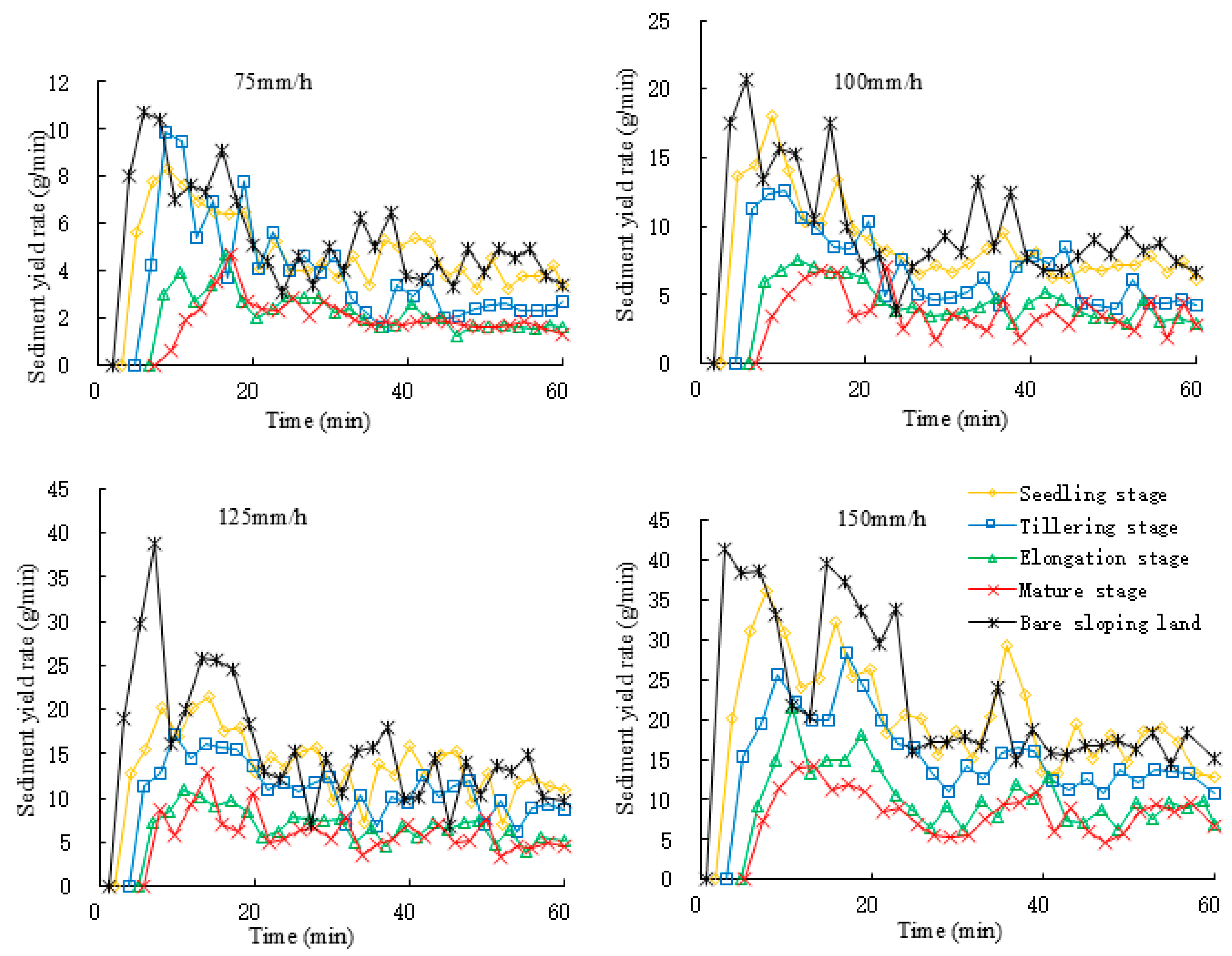
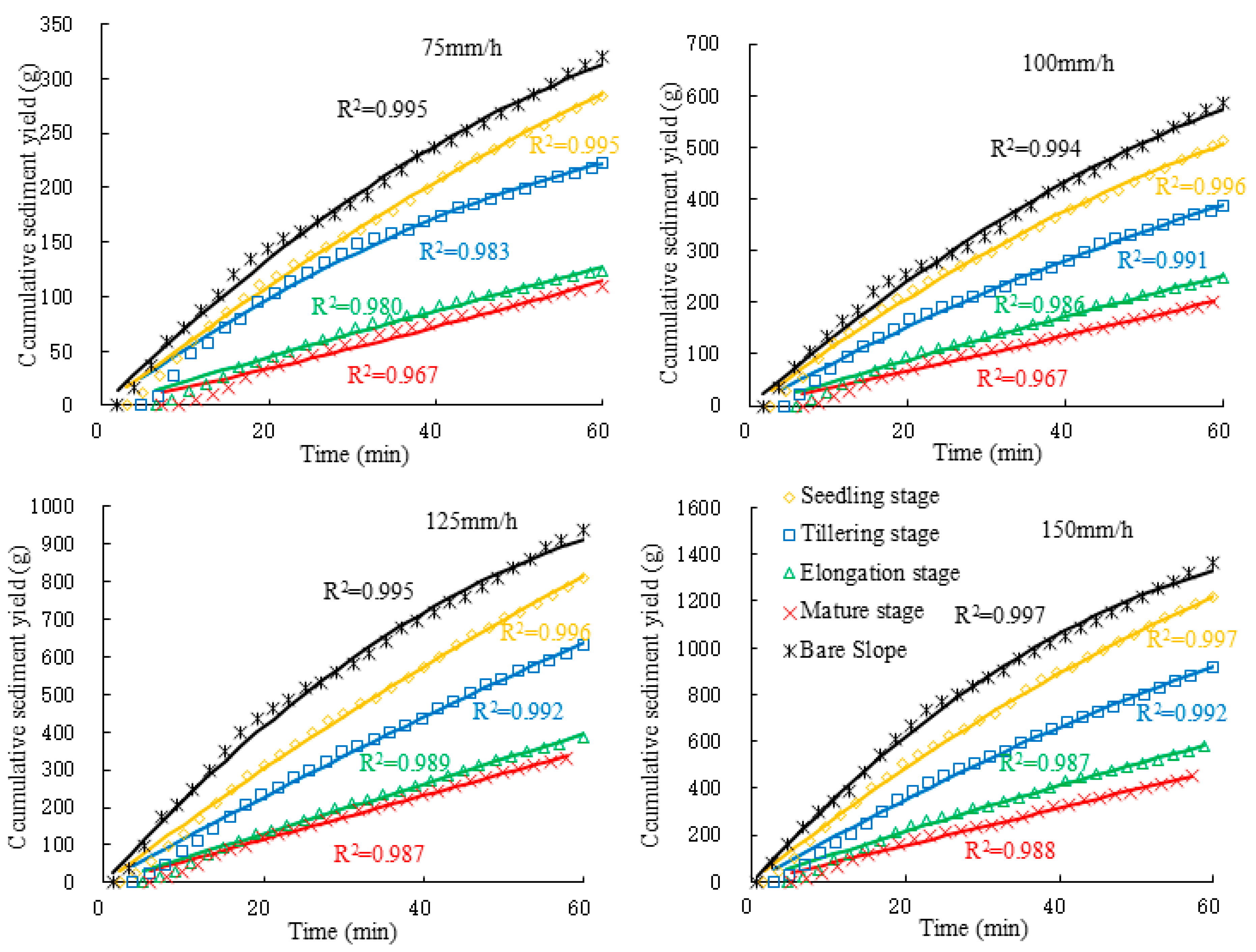
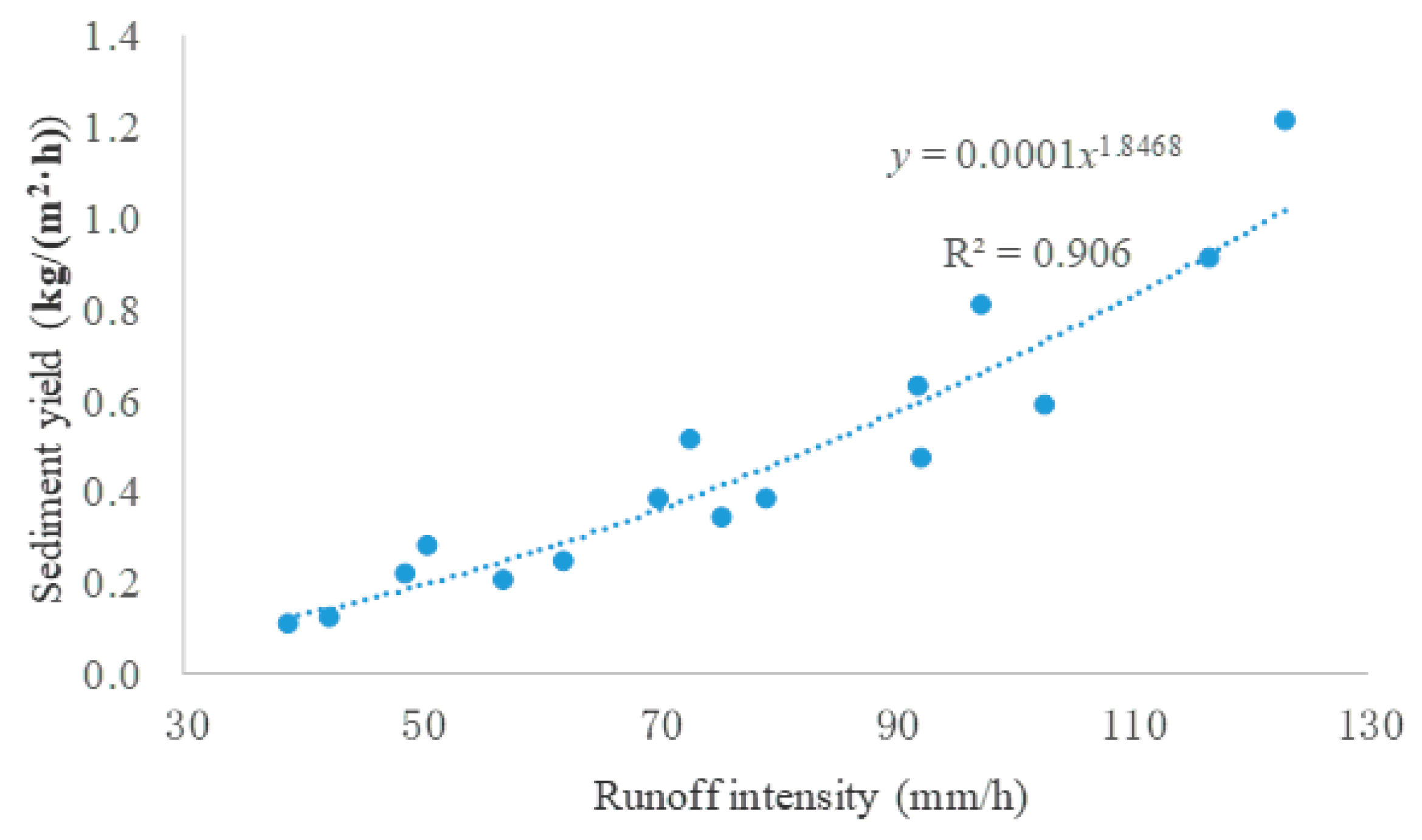
3.4. Sediment Yield
3.5. Development of Mathematical Models
3.5.1. Identification of Significant Independent Variables
3.5.2. Mathematical Models
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khosravi, K.; Rezaie, F.; Cooper, J.R.; Kalantari, Z.; Abolfathi, S.; Hatamiafkoueieh, J. Soil water erosion susceptibility assessment using deep learning algorithms. J. Hydrol. 2023, 618, 129229. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhu, D.; Wu, Z.; Cao, Z. Extreme rainfall erosivity: Research advances and future perspectives. Sci. Total Environ. 2024, 917, 170425. [Google Scholar] [CrossRef]
- Pan, L.D.; Jiang, G.Y.; Shi, D.M.; Wu, J.H.; Liu, J. Effects of Soil Erosion on the Tillage-Layer Quality and Limiting Factors of Sloping Farmland. Ecosyst. Health Sustain. 2024, 10, 0150. [Google Scholar] [CrossRef]
- Wang, S.H.; Xu, X.L.; Huang, L. Spatial and Temporal Variability of Soil Erosion in Northeast China from 2000 to 2020. Remote Sens. 2023, 15, 225. [Google Scholar] [CrossRef]
- Andualem, T.G.; Hewa, G.A.; Myers, B.R.; Peters, S.; Boland, J. Erosion and Sediment Transport Modeling: A Systematic Review. Land 2023, 12, 1396. [Google Scholar] [CrossRef]
- Guo, Z.Q.; Yan, Z.J.; He, R.; Yang, H.; Ci, H.; Wang, R. Impacts of Land Use Conversion on Soil Erosion in the Urban Agglomeration on the Northern Slopes of the Tianshan Mountains. Land 2024, 13, 550. [Google Scholar] [CrossRef]
- Ministry of Water Resources of the People’s Republic of China. 2023 China Soil and Water Conservation Bulletin; Ministry of Water Resources of the People’s Republic of China: Beijing, China, 2024.
- Gil, E.; Kijowska-Strugala, M.; Demczuk, P. Soil erosion dynamics on a cultivated slope in the Western Polish Carpathians based on over 30 years of plot studies. Catena 2021, 207, 105682. [Google Scholar] [CrossRef]
- Wang, D.D.; Yuan, Z.J.; Cai, Y.T.; Jing, D.W.; Liu, F.; Tang, Y.; Song, N.N.; Li, Y.Y.; Zhao, C.Y.; Fu, X.Y. Characterisation of soil erosion and overland flow on vegetation-growing slopes in fragile ecological regions: A review. J. Environ. Manag. 2021, 285, 112165. [Google Scholar] [CrossRef]
- Yao, Z.H.; Zhang, Y.; Xiao, P.Q.; Zhang, L.; Wang, B.; Yang, J.C. Soil Erosion Process Simulation and Factor Analysis of Jihe Basin. Sustainability 2022, 14, 8114. [Google Scholar] [CrossRef]
- Luo, B.L.; Li, J.W.; Gong, C.M.; Zhong, S.Q.; Wei, C.F. Driving forces and their interactions of soil erosion in soil and water conservation regionalization at the county scale with a high cultivation rate. J. Mt. Sci. 2023, 20, 2502–2518. [Google Scholar] [CrossRef]
- Wang, H.; Wang, X.P.; Yang, S.C.; Zhang, Z.; Jiang, F.S.; Zhang, Y.; Huang, Y.H.; Lin, J.S. Water Erosion Response to Rainfall Type on Typical Land Use Slopes in the Red Soil Region of Southern China. Water 2024, 16, 76. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, S.H.; Zhou, Y.; Hou, X.N.; Yang, X.Y. Characteristics of watershed dynamic sediment delivery based on improved RUSLE model. Catena 2022, 219, 106602. [Google Scholar] [CrossRef]
- Guo, Y.R.; Peng, C.H.; Zhu, Q.A.; Wang, M.; Wang, H.; Peng, S.S.; He, H.L. Modelling the impacts of climate and land use changes on soil water erosion: Model applications, limitations and future challenges. J. Environ. Manag. 2019, 250, 109403. [Google Scholar] [CrossRef]
- Fan, C.A.; Luan, D.; Bu, R.W.; Sheng, Z.Q.; Wang, F.Y.; Huang, X.Y. Can heavy rainfall affect the burning and smoke spreading characteristics of fire in tunnels? Int. J. Heat Mass Tran. 2023, 207, 123972. [Google Scholar] [CrossRef]
- Dong, W.H.; Lin, Y.L.; Wright, J.S.; Xie, Y.Y.; Yin, X.G.; Guo, J.P. Precipitable water and CAPE dependence of rainfall intensities in China. Clim. Dynam. 2019, 52, 3357–3368. [Google Scholar] [CrossRef]
- Ma, X.F.; Zhao, C.Y.; Zhu, J.T. Aggravated risk of soil erosion with global warming—A global meta-analysis. Catena 2021, 200, 105129. [Google Scholar] [CrossRef]
- Anagnostopoulou, C.; Tolika, K. Extreme precipitation in Europe: Statistical threshold selection based on climatological criteria. Theor. Appl. Clim. 2012, 107, 479–489. [Google Scholar] [CrossRef]
- Yue, Z.Z.; Xiong, L.H.; Zha, X.N.; Liu, C.K.; Chen, J.; Liu, D.D. Impact of thresholds on nonstationary frequency analyses of peak over threshold extreme rainfall series in Pearl River Basin, China. Atmos. Res. 2022, 276, 106269. [Google Scholar] [CrossRef]
- Sun, L.Y.; Zhou, J.L.; Cai, Q.G.; Liu, S.X.; Xiao, J.A. Comparing surface erosion processes in four soils from the Loess Plateau under extreme rainfall events. Int. Soil. Water Conse 2021, 9, 520–531. [Google Scholar] [CrossRef]
- Thompson, S.E.; Katul, G.G.; Porporato, A. Role of microtopography in rainfall-runoff partitioning: An analysis using idealized geometry. Water Resour. Res. 2010, 46, W07520. [Google Scholar] [CrossRef]
- Wu, L.; Peng, M.L.; Qiao, S.S.; Ma, X.Y. Assessing impacts of rainfall intensity and slope on dissolved and adsorbed nitrogen loss under bare loessial soil by simulated rainfalls. Catena 2018, 170, 51–63. [Google Scholar] [CrossRef]
- Chen, T.; Shu, J.S.; Han, L.; Tian, G.; Yang, G.Y.; Lv, J.X. Modeling the effects of topography and slope gradient of an artificially formed slope on runoff, sediment yield, water and soil loss of sandy soil. Catena 2022, 212, 106060. [Google Scholar] [CrossRef]
- Han, Y.; Zhao, W.W.; Ding, J.Y.; Ferreira, C.S.S. Soil erodibility for water and wind erosion and its relationship to vegetation and soil properties in China’s drylands. Sci. Total Environ. 2023, 903, 166639. [Google Scholar] [CrossRef]
- Wen, F.; Li, X.A.; Yang, W.F.; Li, J.; Zhou, B.Q.; Gao, R.R.; Lei, J.W. Mechanism of loess planar erosion and numerical simulation based on CFD-DEM coupling model. Environ. Earth Sci. 2023, 82, 197. [Google Scholar] [CrossRef]
- Yao, Z.H.; Lian, J.; Zhang, J.; Zhu, M.J. On erosion characteristics of compacted loess during wetting procedure under laboratory conditions. Environ. Earth Sci. 2019, 78, 570. [Google Scholar] [CrossRef]
- Wang, H.; Yang, S.L.; Wang, Y.D.; Gu, Z.Y.; Xiong, S.F.; Huang, X.F.; Sun, M.M.; Zhang, S.H.; Guo, L.C.; Cui, J.Y.; et al. Rates and causes of black soil erosion in Northeast China. Catena 2022, 214, 106250. [Google Scholar] [CrossRef]
- Li, D.D.; Chen, X.Y.; Han, Z.; Gu, X.J.; Li, Y.H. Determination of rill erodibility and critical shear stress of saturated purple soil slopes. Int. Soil. Water Conse 2022, 10, 38–45. [Google Scholar] [CrossRef]
- Liu, M.; Han, G.L. Distribution of soil nutrients and erodibility factor under different soil types in an erosion region of Southeast China. PeerJ 2021, 9, e11630. [Google Scholar] [CrossRef]
- Zhang, J.E.; Feng, L.F.; Ouyang, Y.; Hu, R.R.; Xu, H.Q.; Wang, J.X. Phosphate-solubilizing bacteria and fungi in relation to phosphorus availability under different land uses for some latosols from Guangdong, China. Catena 2020, 195, 104686. [Google Scholar] [CrossRef]
- Liu, Y.S.; Bai, Q.Z.; Nie, Y.F. Properties of bentonite enhanced loess and laterite. Chin. J. Chem. Eng. 2004, 12, 37–41. [Google Scholar]
- Zhang, X.; Yu, G.Q.; Li, Z.B.; Li, P. Experimental Study on Slope Runoff, Erosion and Sediment under Different Vegetation Types. Water Resour. Manag. 2014, 28, 2415–2433. [Google Scholar] [CrossRef]
- Neumann, M.; Kavka, P.; Deváty, J.; Stasek, J.; Strouhal, L.; Tejkl, A.; Kubínová, R.; Rodrigo-Comino, J. Effect of plot size and precipitation magnitudes on the activation of soil erosion processes using simulated rainfall experiments in vineyards. Front. Environ. Sci. 2022, 10, 949774. [Google Scholar] [CrossRef]
- Zhu, R.P.; Yu, Y.; Liu, D.J.; Wang, J.X.; Gao, Z.Q.; Liu, J.; Serrano-Bernardo, F.; Rodrigo-Comino, J. Vegetation pattern and topography determine erosion characteristics in a semi-arid sandstone hillslope-gully system. Eur. J. Soil. Sci. 2024, 75, e13498. [Google Scholar] [CrossRef]
- Zhu, B.B.; Zhou, Z.C.; Li, Z.B. Soil Erosion and Controls in the Slope-Gully System of the Loess Plateau of China: A Review. Front. Environ. Sci. 2021, 9, 657030. [Google Scholar] [CrossRef]
- Zhang, X.; Li, P.; Li, Z.B.; Yu, G.Q.; Li, C. Effects of precipitation and different distributions of grass strips on runoff and sediment in the loess convex hillslope. Catena 2018, 162, 130–140. [Google Scholar] [CrossRef]
- Ding, W.F.; Li, M.A. Effects of grass coverage and distribution patterns on erosion and overland flow hydraulic characteristics. Environ. Earth Sci. 2016, 75, 477. [Google Scholar] [CrossRef]
- Zhou, J.; Fu, B.J.; Yan, D.C.; Lu, Y.H.; Wang, S.; Gao, G.Y. Assessing the integrity of soil erosion in different patch covers in semi-arid environment. J. Hydrol. 2019, 571, 71–86. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, X.P.; Abla, M.; Lü, D.; Yan, R.; Ren, Q.F.; Ren, Z.Y.; Yang, Y.H.; Zhao, W.H.; Lin, P.F.; et al. Effects of vegetation and rainfall types on surface runoff and soil erosion on steep slopes on the Loess Plateau, China. Catena 2018, 170, 141–149. [Google Scholar] [CrossRef]
- Dan, C.X.; Liu, G.; Zhang, Q.; Zhao, Y.G.; Shen, E.S.; Liu, C.; Liu, Y.; Shu, C.B.; Xia, X.L.; Liu, D.D.; et al. The coupling effects of grass and shrub with biological crust on the overland flow hydrodynamic characteristics. Catena 2024, 245, 108281. [Google Scholar] [CrossRef]
- Tao, W.H.; Wang, Q.J.; Guo, L.; Lin, H.R. A new analytical model for predicting soil erosion and nutrient loss during crop growth on the Chinese loess plateau. Soil Till Res. 2020, 199, 104585. [Google Scholar] [CrossRef]
- Ma, B.; Li, C.D.; Li, Z.B.; Wu, F.Q. Effects of Crops on Runoff and Soil Loss on Sloping Farmland Under Simulated Rainfall. Clean-Soil Air Water 2016, 44, 849–857. [Google Scholar] [CrossRef]
- Singh, S.K.; Vishwakarma, D.K.; Abed, S.A.; Al-Ansari, N.; Kashyap, P.S.; Kumar, A.; Kumar, P.; Kumar, R.; Jat, R.; Saraswat, A.; et al. Soil erosion control from trash residues at varying land slopes under simulated rainfall conditions. Math. Biosci. Eng. 2023, 20, 11403–11428. [Google Scholar] [CrossRef]
- Ou, Y.D.; Quiñónez-Barraza, G.; Wang, C.B. Effects of Land-Use Types on Topsoil Physicochemical Properties in a Tropical Coastal Ecologically Fragile Zone of South China. Sustainability 2023, 15, 5484. [Google Scholar] [CrossRef]
- Zhan, L.; Xu, Z.H.; Huang, Z.G. Analysis of regional comparative advantages of China’s sugarcane industry. Chin. J. Trop. Agric. 1–7. Available online: http://kns.cnki.net/kcms/detail/46.1038.S.20240814.1114.002.html (accessed on 25 February 2025).
- Yan, Y.R. Development Status and Countermeasures of Foreign Trade of Sugarcane Industry in Western Guangdong. Eucalypt Sci. Technol. 2019, 36, 6. [Google Scholar] [CrossRef]
- Ting, Z.; Xin, J.; Pan, G.; Song, Y.; Tang, S.; Zhang, Y.; Liang, G. Study on the effects of slope and crop species on soil erosion in red soil slope farmland. Water Sav. Irrig. 2024, 7, 119–124. [Google Scholar] [CrossRef]
- Li, C.J.; Pan, C.Z. The relative importance of different grass components in controlling runoff and erosion on a hillslope under simulated rainfall. J. Hydrol. 2018, 558, 90–103. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Ta, N.; Guo, S.; Chen, Q.; Zhao, L.C.; Li, F.L.; Chang, Q.R. Combining Spectral and Textural Information from UAV RGB Images for Leaf Area Index Monitoring in Kiwifruit Orchard. Remote Sens. 2022, 14, 1063. [Google Scholar] [CrossRef]
- Brandao, Z.N.; Zonta, J.H. Hemispherical photography to estimate biophysical variables of cotton. Rev. Bras. Eng. Agríc. Ambient. 2016, 20, 789–794. [Google Scholar] [CrossRef]
- Rasool, T.; Dar, A.Q.; Wani, M.A. Comparative Evaluation of Infiltration Models under Different Land Covers. Water Resour. 2021, 48, 624–634. [Google Scholar] [CrossRef]
- Wang, J.L.; Song, J.Y.; Lin, H.J.; Peng, L.W.; Li, K.; Wang, Z.X. Comparison of infiltration models to describe infiltration characteristics of bioretention. J. Hydro-Environ. Res. 2021, 38, 35–43. [Google Scholar] [CrossRef]
- Hörnschemeyer, B.; Henrichs, M.; Uhl, M. SWMM-UrbanEVA: A Model for the Evapotranspiration of Urban Vegetation. Water 2021, 13, 243. [Google Scholar] [CrossRef]
- Li, J.M.; Li, L.; Wang, W.L.; Kang, H.L.; Guo, M.M.; Huang, J.Q.; Wang, Y.F.; Lou, Y.B.; Tong, X.X.; Nie, H.Y. Hydrological and erosion responses of steep spoil heaps to taproot and fibrous root grasses under simulated rainfalls. J. Hydrol. 2023, 618, 129169. [Google Scholar] [CrossRef]
- dos Santos, T.E.M.; de Souza, E.R.; Montenegro, A.A.A. Modeling of soil water infiltration with rainfall simulator in different agricultural systems. Rev. Bras. Eng. Agríc. Ambient. 2016, 20, 513–518. [Google Scholar] [CrossRef]
- Allen, S.T.; Brooks, J.R.; Keim, R.F.; Bond, B.J.; McDonnell, J.J. The role of pre- event canopy storage in throughfall and stemflow by using isotopic tracers. Ecohydrology 2014, 7, 858–868. [Google Scholar] [CrossRef]
- Wen, B.J.; Duan, G.H.; Lu, J.X.; Zhou, R.L.; Ren, H.Y.; Wen, Z.M. Response relationship between vegetation structure and runoff-sediment yield in the hilly and gully area of the Loess Plateau, China. Catena 2023, 227, 107107. [Google Scholar] [CrossRef]
- Fang, Y.; Wang, J.J.; Li, F.X.; Zhang, R.R.; Wang, K.Y.; Shangguan, Z. Contribution of root and soil properties on soil infiltration capacity of gramineous and leguminous forages during root decomposition. Catena 2024, 246, 108388. [Google Scholar] [CrossRef]
- Bahddou, S.; Otten, W.; Whalley, W.R.; Shin, H.C.; El Gharous, M.; Rickson, R.J. Changes in soil surface properties under simulated rainfall and the effect of surface roughness on runoff, infiltration and soil loss. Geoderma 2023, 431, 116341. [Google Scholar] [CrossRef]
- Li, J.H.; Tan, Y.; Zhang, Z.B.; Luo, X.W. Experimental study on water movement of latosol under drip irrigation. Trans. CSAE 2005, 21, 36–39. [Google Scholar]
- dos Santos, M.A.D.; Panachuki, E.; Sobrinho, T.A.; de Oliveira, P.T.S.; Rodrigues, D.B.B. Water Infiltration in an Ultisol after Cultivation of Common Bean. Rev. Bras. Cienc. Solo 2014, 38, 1612–1620. [Google Scholar] [CrossRef]
- Klimenko, D.; Ostakhova, A.; Tuneva, A. Experimental Data on Maximum Rainfall Retention on Crowns of Deciduous Tree Species of the Middle Ural (Russia). Forests 2019, 10, 183. [Google Scholar] [CrossRef]
- Tamta, S.; Kumar, A.; Kushwaha, D.P. Potential of roots and shoots of Napier grass for arresting soil erosion and runoff of mollisols soils of Himalayas. Int. Soil Water Conserv. Res. 2023, 11, 538–548. [Google Scholar] [CrossRef]
- Khanal, A.; Fox, G.A. Detachment characteristics of root-permeated soils from laboratory jet erosion tests. Ecol. Eng. 2017, 100, 335–343. [Google Scholar] [CrossRef]
- Friesen, P.; Park, A.; Sarmiento-Serrud, A.A. Comparing rainfall interception in plantation trials of six tropical hardwood trees and wild sugar cane Saccharum spontaneum L. Ecohydrol. 2013, 6, 765–774. [Google Scholar] [CrossRef]



| Mean | Coefficient of Variation | Design Storm Rainfall Intensity (mm/h) | ||||
|---|---|---|---|---|---|---|
| (mm) | 1% | 2% | 5% | 10% | 20% | |
| 60 | 0.4 | 138.6 | 124.8 | 106.5 | 92.1 | 76.9 |
| 70 | 0.4 | 161.7 | 145.6 | 124.3 | 107.5 | 89.7 |
| Rainfall Intensity (mm/h) | Initial Runoff Time on Bare Slope (min) | Initial Runoff Time of Laterite Slope (min) | |||
|---|---|---|---|---|---|
| Grown Stages and LAI | |||||
| Seedling Stage | Tillering Stage | Elongation Stage | Mature Stage | ||
| 0.72 | 1.69 | 3.25 | 4.06 | ||
| 75 | 1.83 ± 0.11 a C | 2.93 ± 0.40 a C | 4.65 ± 0.71 a B | 6.45 ± 0.62 a A | 7.22 ± 0.77 a A |
| 100 | 1.67 ± 0.13 a C | 2.62 ± 0.18 ab C | 4.28 ± 0.42 ab B | 5.78 ± 0.72 ab A | 6.63 ± 0.63 ab A |
| 125 | 1.18 ± 0.11 b C | 2.03 ± 0.17 bc C | 3.70 ± 0.25 ab B | 4.95 ± 0.45 ab A | 5.78 ± 0.75 ab A |
| 150 | 0.75 ± 0.16 c C | 1.73 ± 0.16 c C | 2.98 ± 0.52 b B | 4.70 ± 0.40 b A | 5.22 ± 0.56 b A |
| Growth Stages and LAI | Rainfall Intensity (mm/h) | ifc | β | R2 |
|---|---|---|---|---|
| Bare slope | 75 | 17.448 | 1.448 | 0.862 |
| 100 | 15.630 | 1.996 | 0.819 | |
| 125 | 12.635 | 0.727 | 0.975 | |
| 150 | 10.391 | 1.694 | 0.941 | |
| Seedling stage LAI = 0.72 | 75 | 20.505 | 1.053 | 0.998 |
| 100 | 21.917 | 1.012 | 0.988 | |
| 125 | 21.995 | 1.179 | 0.964 | |
| 150 | 20.762 | 1.313 | 0.984 | |
| Tillering stage LAI = 1.69 | 75 | 20.232 | 0.541 | 0.987 |
| 100 | 22.846 | 1.175 | 0.983 | |
| 125 | 24.623 | 1.137 | 0.968 | |
| 150 | 24.966 | 1.381 | 0.962 | |
| Elongation stage LAI = 3.25 | 75 | 25.875 | 0.592 | 0.986 |
| 100 | 29.543 | 1.020 | 0.984 | |
| 125 | 36.508 | 1.012 | 0.961 | |
| 150 | 36.100 | 1.281 | 0.942 | |
| Mature stage LAI = 4.06 | 75 | 29.429 | 0.765 | 0.989 |
| 100 | 33.904 | 0.761 | 0.970 | |
| 125 | 39.205 | 1.133 | 0.941 | |
| 150 | 45.839 | 0.873 | 0.982 |
| Rainfall Intensity (mm/h) | Infiltration Rate on Bare Slope (mm/h) | Infiltration Rate on the Sugarcane-Cropped Slope (mm/h) | |||
|---|---|---|---|---|---|
| Growth Stages and LAI | |||||
| Seedling Stage | Tillering Stage | Elongation Stage | Mature Stage | ||
| 0.72 | 1.69 | 3.25 | 4.06 | ||
| 75 | 19.28 ± 3.11 a C | 23.35 ± 3.63 a C | 25.30 ± 2.45 a BC | 31.73 ± 3.89 a AB | 35.17 ± 1.80 a A |
| 100 | 17.95 ± 2.35 a D | 25.65 ± 4.20 a CD | 28.50 ± 1.82 a BC | 36.54 ± 1.26 a AB | 41.61 ± 5.09 a A |
| 125 | 15.99 ± 2.52 a C | 25.77 ± 3.99 a BC | 31.07 ± 7.76 a ABC | 44.11 ± 9.77 a AB | 47.63 ± 11.43 a A |
| 150 | 12.16 ± 2.93 a C | 24.75 ± 3.11 a BC | 31.30 ± 3.65 a B | 45.17 ± 6.60 a A | 55.43 ± 8.60 a A |
| Rainfall Intensity (mm/h) | Runoff Intensity on Bare Slope (mm/h) | Runoff Intensity on the Sugarcane-Cropped Slope (mm/h) | |||
|---|---|---|---|---|---|
| Growth Stages and LAI | |||||
| Seedling Stage | Tillering Stage | Elongation Stage | Mature Stage | ||
| 0.72 | 1.69 | 3.25 | 4.06 | ||
| 75 | 54.58 ± 3.11 d A | 50.51 ± 3.63 d A | 48.56 ± 2.45 d AB | 42.13 ± 3.89 c BC | 38.69 ± 1.80 c C |
| 100 | 80.53 ± 2.35 c A | 72.83 ± 4.20 c AB | 69.98 ± 1.82 c BC | 61.94 ± 1.26 b CD | 56.87 ± 5.09 bc D |
| 125 | 107.11 ± 2.52 b A | 97.33 ± 3.99 b AB | 92.03 ± 7.76 b ABC | 78.99 ± 9.77 b BC | 75.47 ± 11.43 ab C |
| 150 | 135.56 ± 2.93 a A | 122.97 ± 3.11 a AB | 116.42 ± 3.65 a B | 102.55 ± 6.60 a C | 92.29 ± 8.60 a C |
| Growth Stages and Leaf Area Index (LAI) | Rainfall Intensity (mm/h) | a | b | R2 |
|---|---|---|---|---|
| Seedling stage LAI = 0.72 | 75 | −0.018 | 5.849 | 0.995 |
| 100 | −0.049 | 11.392 | 0.996 | |
| 125 | −0.038 | 15.881 | 0.996 | |
| 150 | −0.098 | 26.228 | 0.997 | |
| Tillering stage LAI = 1.69 | 75 | −0.030 | 5.502 | 0.983 |
| 100 | −0.029 | 8.215 | 0.991 | |
| 125 | −0.019 | 11.760 | 0.992 | |
| 150 | −0.056 | 18.723 | 0.992 | |
| Elongation stage LAI = 3.25 | 75 | −0.003 | 2.289 | 0.980 |
| 100 | −0.006 | 4.553 | 0.986 | |
| 125 | 0.001 | 6.521 | 0.989 | |
| 150 | −0.021 | 11.140 | 0.987 | |
| Mature stage LAI = 4.06 | 75 | 0.005 | 1.605 | 0.967 |
| 100 | 0.002 | 3.324 | 0.982 | |
| 125 | 0.002 | 5.715 | 0.987 | |
| 150 | 0.002 | 7.815 | 0.988 |
| Rainfall Intensity (mm/h) | Sediment Yield on Bare Slope (kg/(m2·h)) | Sediment Yield on the Sugarcane-Cropped Slope (kg/(m2·h)) | |||
|---|---|---|---|---|---|
| Growth Stages and LAI | |||||
| Seedling Stage | Tillering Stage | Elongation Stage | Mature Stage | ||
| 0.72 | 1.69 | 3.25 | 4.06 | ||
| 75 | 0.320 ± 0.016 d A | 0.284 ± 0.045 d A | 0.222 ± 0.025 c B | 0.124 ± 0.007 d C | 0.109 ± 0.006 d C |
| 100 | 0.587 ± 0.082 c A | 0.513 ± 0.033 c AB | 0.385 ± 0.085 c BC | 0.248 ± 0.052 c CD | 0.204 ± 0.006 c D |
| 125 | 0.939 ± 0.035 b A | 0.810 ± 0.027 b B | 0.629 ± 0.054 b C | 0.383 ± 0.015 b D | 0.340 ± 0.048 b D |
| 150 | 1.368 ± 0.160 a A | 1.218 ± 0.071 a A | 0.916 ± 0.105 a C | 0.588 ± 0.066 a C | 0.473 ± 0.045 a C |
| average | 0.804 | 0.706 | 0.538 | 0.336 | 0.282 |
| Significant Parameters | Mathematical Model | R2 | F |
|---|---|---|---|
| LAI | tps = 1.139LAI + 1.711 | 0.816 | 67.714 |
| I | tps = −0.023I + 7.033 | 0.091 | 2.499 |
| LAI, I | tps = 1.139LAI−0.023I + 4.266 | 0.977 | 320.769 |
| LAI | Iis = 6.109LAI + 19.723 | 0.708 | 37.325 |
| I | Iis = 0.140I + 18.865 | 0.115 | 2.958 |
| LAI, I | Iis = 6.109LAI + 0.140I + 4.02 | 0.887 | 59.609 |
| LAI | IRs = −6.109LAI + 91.067 | 0.036 | 1.567 |
| I | IRs = 0.845I−18.865 | 0.878 | 108.481 |
| LAI, I | IRs = 0.845I−6.109LAI−4.02 | 0.984 | 470.965 |
| LAI | Mss = −0.128LAI + 0.777 | 0.268 | 6.478 |
| I | Mss = 0.008I−0.455 | 0.563 | 20.232 |
| LAI, I | Mss = 0.008I−0.128LAI−0.143 | 0.894 | 64.486 |
| Mathematical Model | t-Test | ||
|---|---|---|---|
| Variable | Standardized Coefficients Beta | t | |
| tps = 1.139LAI − 0.023I + 4.266, R2 = 0.977 | LAI | 0.91 | 23.289 |
| I | −0.389 | −9.957 | |
| Iis = 6.109LAI + 0.140I + 4.02, R2 = 0.887 | LAI | 0.853 | 9.806 |
| I | 0.418 | 4.803 | |
| IRs = −6.109LAI + 0.845I − 4.02, R2 = 0.984 | LAI | −0.317 | −9.806 |
| I | 0.941 | 29.082 | |
| Mss = −0.128LAI + 0.008I − 0.143, R2 = 0.894 | LAI | −0.562 | −6.702 |
| I | 0.769 | 9.168 | |
| Mathematical Model | Training Period | Simulation Period | |
|---|---|---|---|
| NSE | NSE | ||
| initial runoff time | tps = 1.165LAI − 0.024I + 4.315, R2 = 0.973 | 0.978 | 0.973 |
| infiltration rate | Iis = 5.111LAI + 0.165I + 4.101, R2 = 0.925 | 0.939 | 0.767 |
| runoff intensity | IRs = −5.111LAI + 0.82I − 4.101, R2 = 0.986 | 0.989 | 0.768 |
| sediment yield | Mss = −0.097LAI + 0.007I − 0.122, R2 = 0.912 | 0.924 | 0.538 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, C.; Yang, H.; Li, J.; Li, C. Influence of Sugarcane on Runoff and Sediment Yield in Sloping Laterite Soils During High-Intensity Rainfall. Agronomy 2025, 15, 596. https://doi.org/10.3390/agronomy15030596
Yu C, Yang H, Li J, Li C. Influence of Sugarcane on Runoff and Sediment Yield in Sloping Laterite Soils During High-Intensity Rainfall. Agronomy. 2025; 15(3):596. https://doi.org/10.3390/agronomy15030596
Chicago/Turabian StyleYu, Changhong, Haiyan Yang, Jiuhao Li, and Cong Li. 2025. "Influence of Sugarcane on Runoff and Sediment Yield in Sloping Laterite Soils During High-Intensity Rainfall" Agronomy 15, no. 3: 596. https://doi.org/10.3390/agronomy15030596
APA StyleYu, C., Yang, H., Li, J., & Li, C. (2025). Influence of Sugarcane on Runoff and Sediment Yield in Sloping Laterite Soils During High-Intensity Rainfall. Agronomy, 15(3), 596. https://doi.org/10.3390/agronomy15030596





