A Support End-Effector for Banana Bunches Based on Contact Mechanics Constraints

Abstract

Banana harvesting relies heavily on manual labor, which is labor-intensive and prone to fruit damage due to insufficient control of contact forces. This paper presents a systematic methodology for the design and optimization of adaptive flexible end-effectors for banana bunch harvesting, focusing on contact behavior and mechanical constraints. By integrating response surface methodology (RSM) with multi-objective genetic algorithm (MOGA) optimization, the relationships between finger geometry parameters and key performance metrics—contact area, contact stress, and radial stiffness—were quantified, and Pareto-optimal structural configurations were identified. Experimental and simulation results demonstrate that the optimized flexible fingers effectively improve handling performance: contact area increased by 13–28%, contact stress reduced by 45–56%, and radial stiffness enhanced by 193%, while the maximum shear stress on the fruit stalk decreased by 90%, ensuring harvesting stability during dynamic loading. The optimization effectively distributes contact pressure, minimizes fruit damage, and enhances grasping reliability. The proposed contact-behavior-constrained design framework enables passive adaptation to fruit morphology without complex sensors, offering a generalizable solution for soft robotic handling of fragile and irregular agricultural products. This work bridges the gap between bio-inspired gripper design and practical agricultural application, providing both theoretical insights and engineering guidance for automated, low-damage fruit harvesting systems.

1. Introduction

Bananas are among the most widely cultivated and highest-yielding tropical fruits worldwide, predominantly grown across tropical and subtropical regions such as Southeast Asia, South America, and Africa [1]. Due to their high nutritional value and year-round availability, bananas have become a major commodity in the international fruit trade, accounting for over 20% of global fruit production. According to the latest statistics from the Food and Agriculture Organization of the United Nations [2], the global banana cultivation area has reached approximately $5.97\times {10}^6{\mathrm{hm}}^2$, with an annual yield of about $1.39\times {10}^8$ tons.

Despite the large scale of global banana production, plantation management and harvesting operations still depend heavily on manual labor. Conventional harvesting generally requires at least two workers: one to cut the banana stalk and another to support and stabilize the bunch during harvesting and transportation. Since a single banana bunch often weighs more than 30 kg, this process is labor-intensive, inefficient, and physically demanding, placing considerable strain on field workers. The application of robotic arms for banana harvesting has been explored [3]. However, these systems often lead to bulky and heavy machinery, limited maneuverability within orchards, and low harvesting efficiency, which restrict their widespread adoption. To overcome these limitations, our previous research proposed a flexible supporting device designed to replace manual handling and provide adaptive support for banana bunches [4], as illustrated in Figure 1.

During harvesting, mechanical impacts frequently cause localized bruising or internal textural changes in bananas [5]. As a climacteric fruit, bananas do not always exhibit immediate external signs of damage following impact. However, such latent injuries often become visible after a period of storage, leading to quality deterioration and reduced market value [6,7]. Therefore, in post-harvest handling, precise control of the contact force is essential to minimize contact-induced mechanical stress and prevent bruising. Current strategies to mitigate excessive contact stress in flexible end-effectors [8,9] primarily rely on sensor-based feedback [10,11,12], smart materials [13,14], or force-control algorithms [15,16]. While effective to some extent, these approaches are often limited by complex control schemes, delayed response times, and high fabrication costs [17,18]. An alternative approach is to design actuators that utilize the mechanical compliance of flexible structures [19]. Such actuators can achieve self-adaptive deformation and low contact stress through their structural properties, without relying on complex control systems. This approach simplifies the overall system design and improves the robustness of robotic operations in agricultural environments [20,21].

However, designing flexible end-effectors that provide both adaptability and controlled contact stress remains a major challenge [22,23]. One key difficulty is the lack of standardized design frameworks and systematic methods. Most current designs still depend on empirical or experience-based approaches, including bio-inspired [24,25,26], origami-based [27,28], and geometry-driven strategies [29]. These methods have produced many successful prototypes, but they rely heavily on designer intuition and repeated trial-and-error [30]. As a result, their performance and consistency in real agricultural applications are often difficult to guarantee.

Building upon our previous research and experimental validation of a flexible docking device, this study proposes a design methodology for flexible end-effectors that accounts for contact behavior constraints [4]. The methodology is applied to the development of an adaptive banana supporting gripper, which aims to improve harvesting safety and efficiency. By maximizing the contact area between the flexible supporting gripper and the fruit surface, the design effectively distributes contact stress, thereby minimizing mechanical damage during grasping and transportation. Furthermore, the proposed approach provides a generalizable framework for designing soft end-effectors and interaction devices intended for fragile, irregularly shaped, or unstructured agricultural products.

The remainder of this paper is organized as follows. Section 2 presents a response surface optimization framework for a flexible gripper design considering contact behavior constraints, and investigates the influence of key structural parameters on the output responses. Section 3 details the optimization results under contact behavior constraints and evaluates the gripper’s performance through finite element analysis (FEA) and experimental validation. In addition, the operational performance and characteristics of the optimized banana bunch-supporting device are compared and discussed. Finally, Section 4 provides the conclusions and summary of the research findings.

2. Materials and Methods

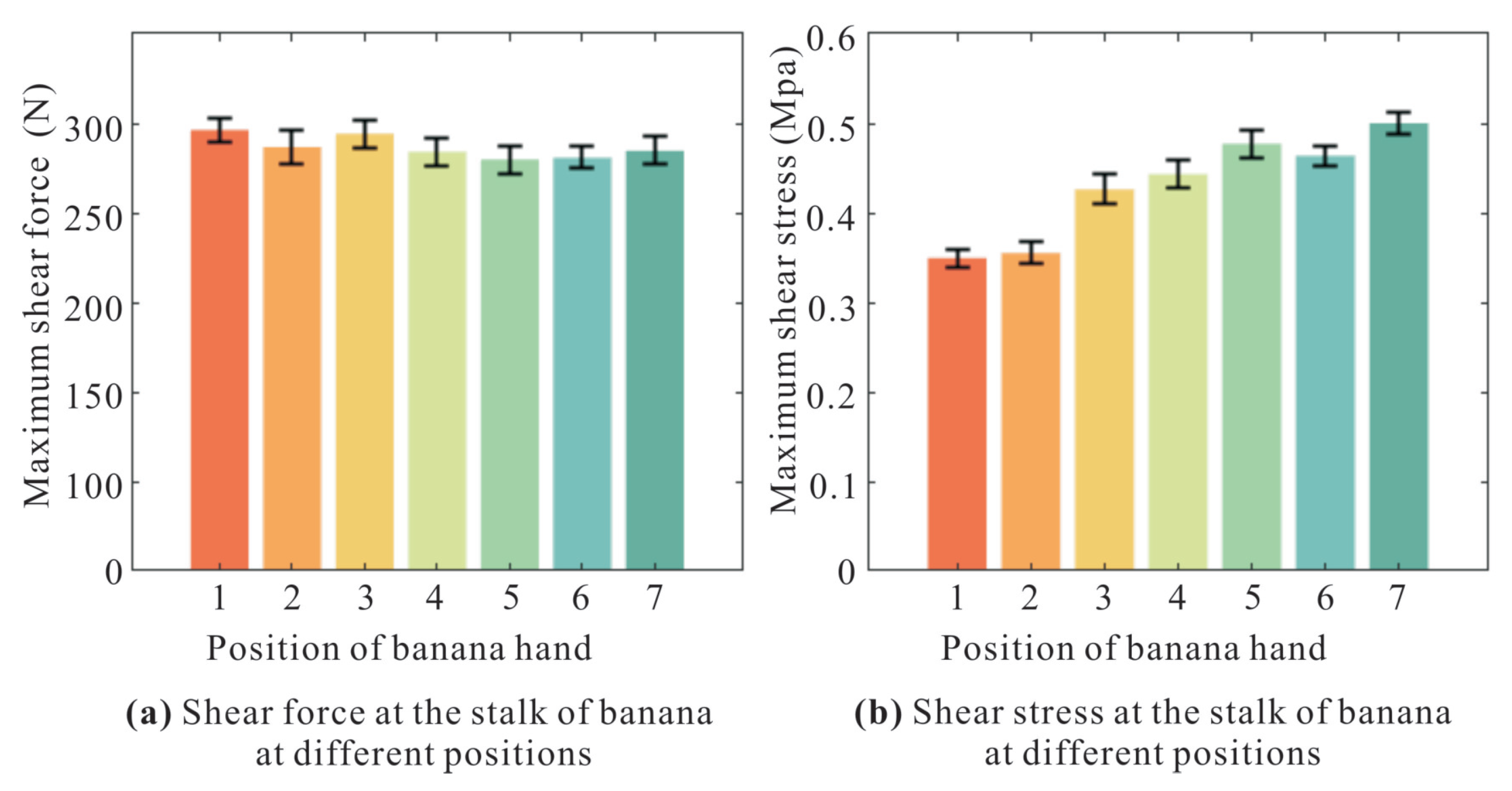
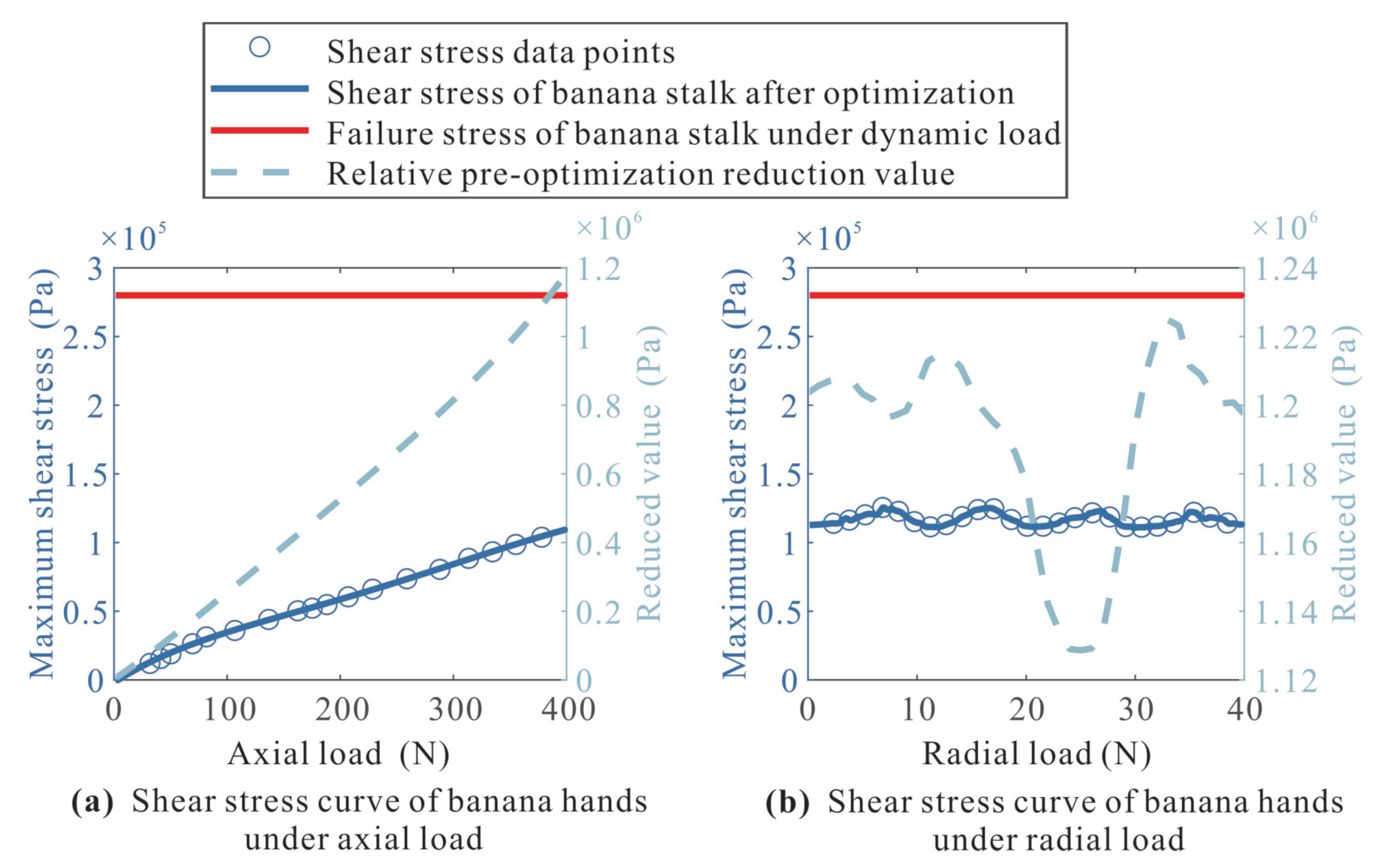
2.1. Response Surface Methodology-Based Optimization for an Adaptive Banana Gripper

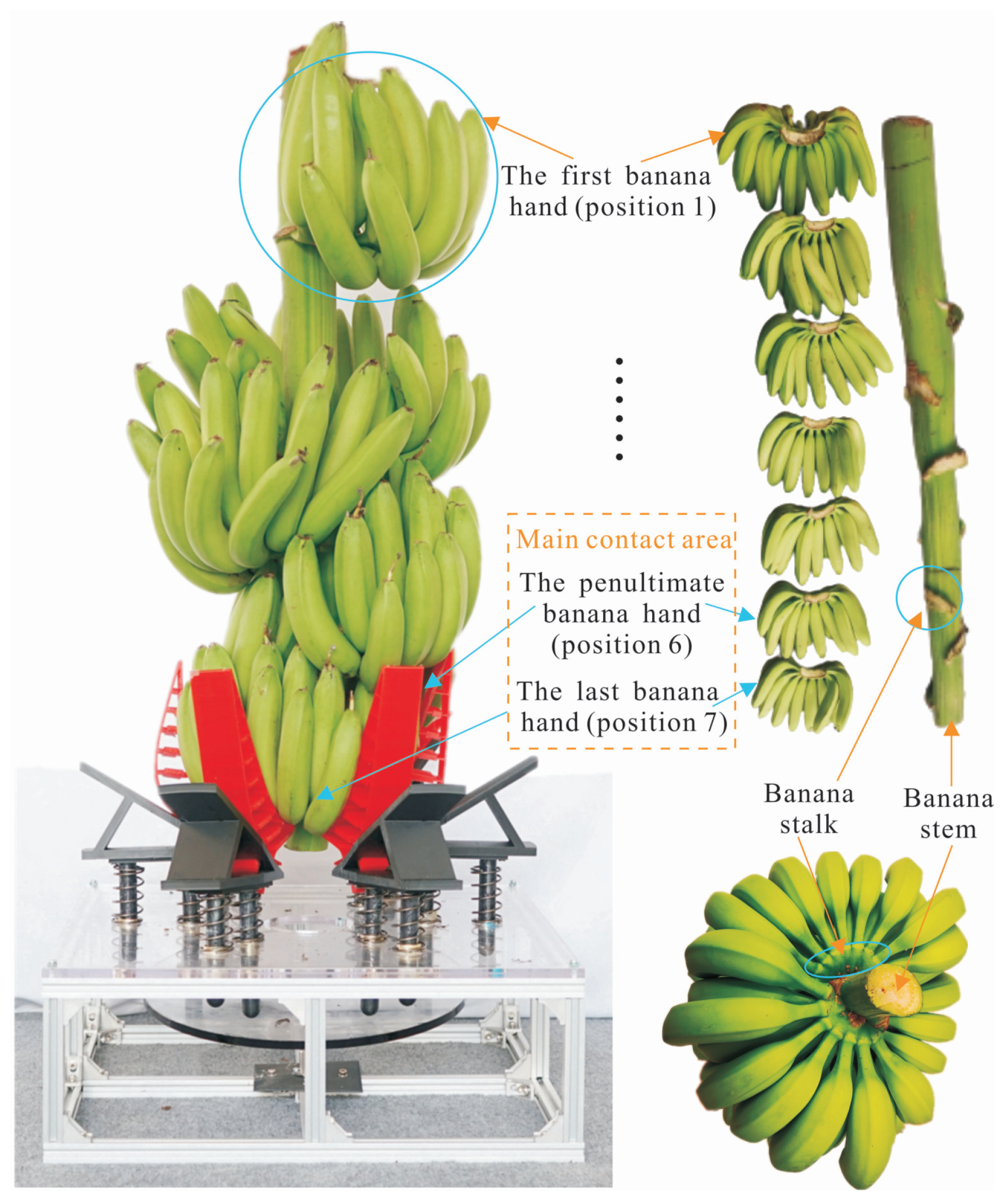
As shown in Figure 1, the device incorporates a banana support mechanism equipped with flexible supporting fingers. These fingers were fabricated from Thermoplastic Polyurethane (TPU) with a Shore hardness of 83A using Fused Deposition Modeling (FDM) 3D printing, with an infill density of 60% (TPU and 3D printer, Tuozhu Technology Co., Ltd., Shenzhen, China). This material configuration was selected to ensure sufficient surface friction for stable grasping while providing the structural compliance necessary for the passive adaptive mechanism. The experimental gripper assembly comprises six flexible fingers arranged circumferentially and integrated into a passive adaptive adjustment mechanism. This configuration enables the device to automatically compensate for irregularities in banana bunch morphology, such as variations in stem curvature and differences in hand height, as confirmed through preliminary continuity and load-bearing tests.

This study applies the Response Surface Methodology (RSM) to optimize the structural parameters of the adaptive gripper. By integrating experimental design, statistical modeling, and response analysis, RSM enables the identification of key factors affecting contact performance and determines their optimal configurations, thereby enhancing the overall grasping stability and supporting capability of the flexible banana harvesting device.

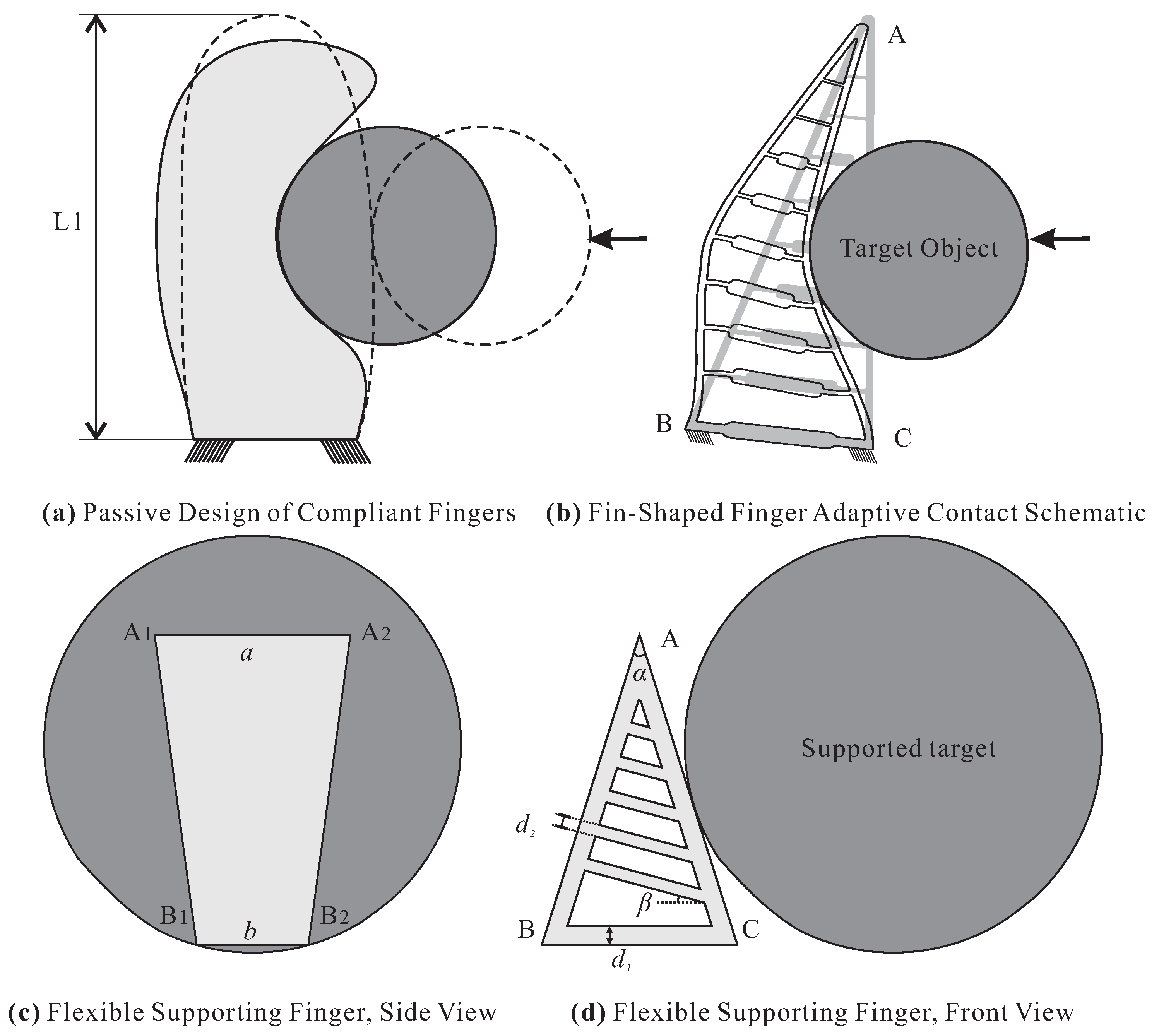
Based on the previous experimental evaluation of the flexible banana support system, a set of contact behavior constraints was introduced to guide the optimization process. The passive adaptive configuration of the supporting fingers is shown in Figure 2. Considering the practical requirements for supporting banana bunches, the finger length $L_1$ was fixed at 260 mm. The key geometric parameters selected for optimization include: the upper base length a and lower base length b of the trapezoidal finger section, the outer beam angle $\alpha$ and thickness $d_1$, the inner beam inclination angle $\beta$ and thickness $d_2$, and the number of inner beams N. The initial design parameters were set as follows: $a=100$ mm, $b=60$ mm, $\alpha ={30}^{\circ }$, $d_1=2$ mm, $\beta =5^{\circ }$, $d_2=2$ mm, and $N=6$. These initial parameters were established based on the geometric envelope of the harvesting robot’s end-effector and the manufacturing constraints of FDM 3D printing. Specifically, the base dimensions ($a,b$) were sized to fit the average curvature of the banana hands, while the thickness values ($d_1,d_2$) were set to the minimum printable wall thickness for TPU to ensure baseline structural integrity before optimization. The optimization objective is to improve the contact interaction between the gripper and the banana bunch during harvesting. By enhancing the gripper’s surface conformity and pressure distribution uniformity, the design aims to ensure reliable grasping while minimizing mechanical damage to the fruit. Accordingly, three performance indicators were defined as optimization objectives: contact area (A), contact stress ($\sigma$), and radial static stiffness ($K_r$). The comprehensive objective function for the supporting finger design is expressed as:

$$\left(A,\sigma ,K_r\right)=f\left(a,b,\alpha ,d_1,\beta ,d_2,N\right)$$

(1)

The range of each optimization parameter of the banana holding finger is shown in

Table 1. Optimized parameter range of banana holding fingers.

Optimization Variable	Symbol	Upper Limit	Lower Limit
Upper sole length (mm)	a	130	60
Bottom length (mm)	b	100	30
Angle of outer beam (°)	$\alpha$	60	10
Thickness of outer beam (mm)	$d_1$	30	1
Inclination angle of inner beam (°)	$\beta$	30	0
Thickness of inner beam (mm)	$d_2$	20	1
Number of inner beams (strips)	N	11	3

.

In the Response Surface Methodology (RSM), selecting an appropriate experimental design is crucial for obtaining reliable and interpretable results. Different design strategies possess distinct advantages and limitations, making each suitable for specific research objectives and experimental constraints. Considering the practical requirements and experimental complexity associated with optimizing the adaptive flexible banana support gripper, a Central Composite Design (CCD) was adopted.

After completing the experimental trials, a surrogate model was constructed to approximate the functional relationship between the input variables and output responses. Within the RSM framework, commonly used fitting models include multivariate quadratic polynomials, Kriging functions, and genetic aggregation models, each offering a trade-off between predictive accuracy and computational efficiency. Among these, the quadratic polynomial model serves as the fundamental regression form in RSM. Through variable substitution, the regression equation can be simplified into a multiple linear regression form, as expressed in Equation (2). The regression coefficients are then obtained via least-squares estimation, yielding the final response surface model, as shown in Equation (3). As a basic surrogate model, the quadratic polynomial offers high computational efficiency compared with more complex regression models. However, the contact behavior of the flexible finger against the irregular banana surface involves complex, non-linear deformations. Its limited capability for error control and nonlinearity representation may result in larger residual deviations in highly nonlinear systems.

$$Y={\beta }_0+{\beta }_1{X}_1+{\beta }_3{X}_2+\dots +{\beta }_k{X}_k+\epsilon$$

(2)

$$\widehat{Y}={\widehat{\beta }}_0+{\widehat{\beta }}_1{X}_1+{\widehat{\beta }}_2{X}_2+\dots +{\widehat{\beta }}_k{X}_k$$

(3)

The Kriging model (Equation (4)) integrates a global polynomial trend function, typically a quadratic polynomial $f\left(x\right)$, with a Gaussian stochastic process $Z\left(x\right)$ characterized by a zero mean and a non-zero covariance structure (Equation (5)). This hybrid formulation enables the model to exactly interpolate all sampled data points while simultaneously providing a quantitative measure of prediction uncertainty at unsampled locations. Consequently, Kriging is particularly effective for modeling complex and nonlinear relationships that cannot be captured by simpler regression methods.

$$y\left(x\right)=f\left(x\right)+Z\left(x\right)$$

(4)

$$\left\{\begin{array}{c}Cov\left[Z\left(x_i\right),Z\left(x_j\right)\right]={\sigma }^{2}R{\left[R\left(x_i,x_j\right)\right]}_{N\times N}\\ R(\Theta )=\prod _{k=1}^{L}exp\left(-{\theta }_k{d}_k^2\right)\\ d_k=x_{ik}-x_{jk}\end{array}\right.$$

(5)

The response estimate of the Kriging model is given by Equation (6), and the variance of the estimate is expressed in Equation (7). These two formulations enable the Kriging model to not only predict the response at any unsampled point but also quantify the uncertainty associated with each prediction. Such dual capability makes it particularly effective for modeling nonlinear and spatially correlated response surfaces, thereby improving the reliability of optimization and design analyses.

$$\left\{\begin{array}{c}\widehat{y}\left(x\right)=\widehat{\beta }+{\mathrm{r}}^T\left(x\right){\mathrm{R}}^{-1}(y-\widehat{\beta }\mathrm{f})\\ \widehat{\beta }=\left({\mathrm{f}}^T{\mathrm{R}}^{-1}\mathrm{f}\right){\mathrm{f}}^T{\mathrm{R}}^{-1}\mathrm{y}\\ {\mathrm{r}}^T\left(x\right)={\left[R\left(x,x_1\right),R\left(x,x_3\right),\dots ,R\left(x,x_N\right)\right]}^T\end{array}\right.$$

(6)

$${\widehat{\sigma }}^2={\displaystyle \frac{{(\mathrm{y}-\widehat{\beta }\mathrm{f})}^T{\mathrm{R}}^{-1}(\mathrm{y}-\widehat{\beta }\mathrm{f})}{N}}$$

(7)

In the modeling process, a key hyperparameter controlling the covariance scale of the Kriging model is determined by Equation (8). During the fitting stage, the global trend of the response surface is represented by a quadratic polynomial, while the local deviations are captured through a Gaussian stochastic process. For improved error control, the model utilizes the local interpolation characteristics of the Gaussian kernel, which allows the adaptive insertion of additional sampling points in regions of high nonlinearity or uncertainty. Although this approach provides better error regulation than a pure quadratic polynomial model, it also increases computational cost due to repeated matrix inversion operations within the stochastic component. Given our 7-variable design space, pure Kriging can suffer from stability issues or excessive computational costs without providing the global generalization needed for the radial stiffness objective.

$$\left\{\begin{array}{c}Max:\Phi (\Theta )={\displaystyle \frac{-\left[Nln\left({\widehat{\sigma }}^2\right)+ln\left|\mathrm{R}\right|\right]}{2}}\\ st.\Theta >0\end{array}\right.$$

(8)

The genetic aggregation response surface model, as defined in Equation (9), integrates multiple surrogate modeling techniques—including a full quadratic polynomial, non-parametric regression, and Kriging functions—to achieve a balance between predictive robustness and computational efficiency. Our optimization needs to balance conflicting objectives: maximizing Contact Area while minimizing Contact Stress and ensuring sufficient Radial Stiffness. The Genetic Aggregation model functions as an ensemble, automatically weighing and combining different algorithms. This allows it to use the global trend capabilities of polynomials for stiffness predictions while leveraging the local adjustment capabilities of Kriging for precise stress peak prediction. In this study, the genetic aggregation model is adopted as the optimization algorithm for the flexible support gripper. By combining the complementary strengths of different surrogate models, it effectively mitigates overfitting and improves generalization performance across diverse design conditions.

$$\left\{\begin{array}{c}\widehat{y}\left(x\right)=\sum _{i=1}^N{w}_i·{\widehat{y}}_i\left(x\right)\\ \mathrm{w}={\displaystyle \frac{C^{-1}I}{I^T{C}^{-1}I}}\\ C_{ij}={\displaystyle \frac{1}{N}}{E}_i^T{E}_j\\ E_i={\displaystyle \frac{1}{K}}\sum _{k=1}^K{\left(y_k-{\widehat{y}}_k\right)}^3\end{array}\right.$$

(9)

The predictive accuracy of the response surface model developed using the above methodology must be quantitatively evaluated to verify its capability to represent the actual physical behavior. The coefficient of determination ($R^2$) is employed as the primary metric to assess the goodness of fit of the model, and it is defined as:

$$R^2={\displaystyle \frac{SSR}{SSY}}=1-{\displaystyle \frac{SSE}{SSY}}$$

(10)

In Equation (10), $SSY$ denotes the total sum of squares, which quantifies the overall deviation of each observed response from the mean value. $SSR$ represents the regression sum of squares, corresponding to the variation explained by the model, whereas $SSE$ denotes the error sum of squares, reflecting the portion of variability not captured by the model. An $R^2$ value approaching 1 indicates that a larger proportion of the total response variability is explained by the regression model. The three statistical terms are calculated as follows:

$$\left\{\begin{array}{c}SSY=\sum _{i=1}^m{\left(y_i-\overline{y}\right)}^2\hfill \\ SSE=\sum _{i=1}^m{\left(y_i-\overline{y_i}\right)}^2\hfill \\ SSR=\sum _{i=1}^m{\left(\overline{y_i}-\overline{y}\right)}^2\hfill \end{array}\right.$$

(11)

And the following relationship is satisfied among the three:

$$SSR=SSY-SSE$$

(12)

The coefficient of determination ($R^2$) ranges from 0 to 1, where values closer to 1 indicate smaller modeling errors and higher fitting accuracy. An $R^2$ value of 1 represents a perfect fit, meaning that the model precisely captures the input–output relationship and all data points lie exactly on the response surface. However, a key limitation of $R^2$ is its tendency to increase with the inclusion of additional predictor variables, even when those variables contribute little or no explanatory power. Such behavior can lead to overfitting, where the model performs well on training data but poorly on unseen data. To mitigate this problem, the adjusted coefficient of determination ($R_{adj}^2$) is introduced. It incorporates a penalty term for the number of predictors, thereby providing a more reliable measure of model performance—particularly when comparing regression models with different numbers of variables. The adjusted $R^2$ is defined as:

$$R_{adj}^2=1-\left({\displaystyle \frac{m-1}{m-k}}\right)\times {\displaystyle \frac{SSE}{SSY}}$$

(13)

where k denotes the number of model parameters. The adjusted coefficient of determination ($R_{\mathrm{adj}}^2$) also ranges between 0 and 1, with values closer to 1 indicating a more accurate representation of the input–output relationship by the response surface model. In general, $R_{\mathrm{adj}}^2$ is slightly lower than $R^2$. A large discrepancy between the two (i.e., $R_{\mathrm{adj}}^2\ll R^2$) suggests the presence of redundant or insignificant terms in the polynomial model, implying that model recalibration or parameter reduction may be necessary.

The optimization of contact behavior and radial stiffness for the adaptive banana gripper constitutes a multi-objective optimization problem (MOOP). Conventional genetic algorithms often face challenges in effectively resolving the trade-offs among competing objectives in such problems. To address this, a Multi-Objective Genetic Algorithm (MOGA) is employed. This algorithm mimics natural selection and genetic operations to evolve a population of candidate designs toward the Pareto front. The optimization variables are classified as continuous or discrete, depending on their nature. Continuous variables can assume any value within a specified range. For these variables, crossover and mutation operations—defined by Equations (14) and (15), respectively—are applied to generate new candidate solutions during the evolutionary process.

$$\left\{\begin{array}{c}\mathrm{Child}1=\alpha \times \mathrm{Parent}1+(1-\alpha )\times \mathrm{Parent}2\hfill \\ \mathrm{Child}2=(1-\alpha )\times \mathrm{Parent}1+\alpha \times \mathrm{Parent}2\hfill \end{array}\right.$$

(14)

$$\mathrm{Child}=\mathrm{Parent}+[\mathrm{UpperBound}-\mathrm{LowerBound}]\times \delta$$

(15)

Based on the optimization objectives for contact behavior and radial stiffness of the adaptive banana supporting finger, a Multi-Objective Genetic Algorithm (MOGA) was employed to optimize its structural parameters. MOGA is particularly suitable for handling mixed variables, including continuous parameters (e.g., geometric dimensions) and discrete parameters (e.g., standard manufacturing specifications), without requiring explicit functional expressions to propagate parameter information to offspring. The algorithm begins with the random generation of an initial population of potential solutions. Through selection, crossover, and mutation operations, parental genetic information is recombined and passed on to offspring. Discrete variables, representing non-continuous parameter values, are processed via recombination and random alteration rather than formula-based computation. During each iteration, individuals satisfying the optimization conditions are selected, elite members are retained, and new offspring are generated to maintain the population size. This cycle of selection and genetic variation continues until the convergence criteria are met. By applying MOGA, the multi-objective optimization of the supporting finger’s contact behavior and radial stiffness was successfully achieved. The resulting design effectively balances competing performance requirements without introducing complex sensing or control systems.

2.2. Multi-Objective Optimization of Flexible Banana Supporting Fingers

To reduce computational complexity while maintaining generality and representativeness, a single flexible finger was selected as the optimization unit, as the supporting device comprises six fingers arranged circumferentially around the central frame. A simplified support target was constructed based on the morphological characteristics of banana bunches, as illustrated in Figure 2a,b.

Using the fundamental principles of a genetic algorithm, the structural parameters influencing contact behavior and radial static stiffness of the flexible finger were optimized to generate a Pareto-optimal solution set. From this set, the best parameter combination was selected to determine the final structural design, thereby enhancing the overall adaptability, force distribution uniformity, and stability of the supporting device. A multiple regression model was fitted to the experimental data using MATLAB R2020b, establishing the relationship between the contact area (A) and key geometric parameters of the trapezoidal section of the flexible finger: the upper base length (a), lower base length (b), outer beam angle ($\alpha$), outer beam thickness ($d_1$), inner beam inclination angle ($\beta$), inner beam thickness ($d_2$), and the number of inner beams (N). 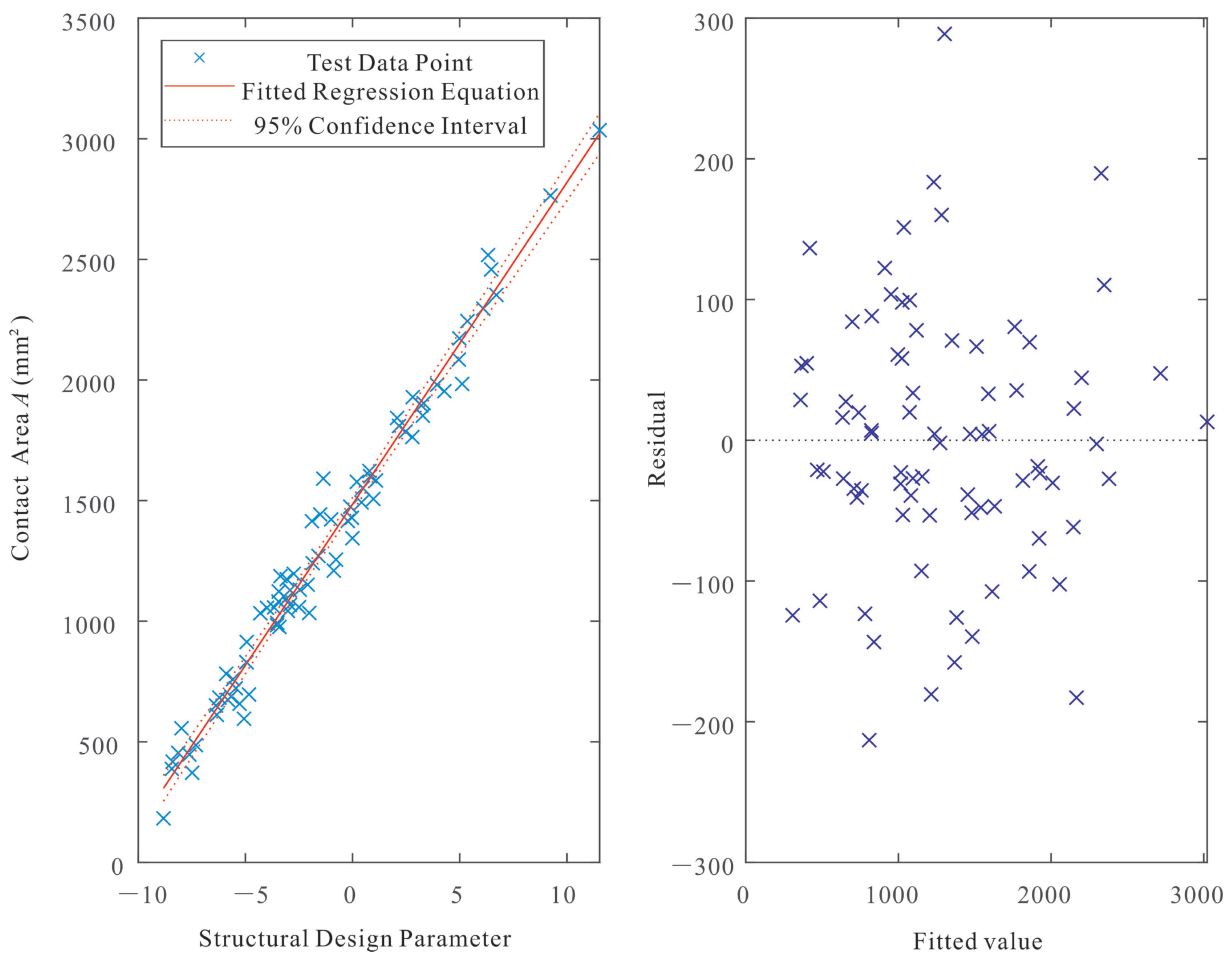This relationship is expressed in Equation (16), and the corresponding fit is visualized in Figure 3.

$$A=\left\{\begin{array}{c}1484.42-4.40a-15.09b-1.52\alpha -65.49d_1+4.20\beta +3.41d_2\\ -114.55N+0.0079ab+0.076a\alpha +0.081b\alpha +0.16a{d}_1+0.44b{d}_1\\ +2.26\alpha d_1+0.051a\beta +0.044b\beta -0.047\alpha \beta -0.32d_1\beta +0.049a{d}_2\\ +0.36b{d}_2+0.028\alpha d_2+0.033d_1{d}_2-0.68\beta d_2+0.052aN+0.63bN\\ +0.015\alpha N+0.42d_{1}N-2.77\beta N+1.54d_{2}N+0.0025a^2+0.046b^2\\ -0.53{\alpha }^2+0.27d_1^2+0.59{\beta }^2+0.41d_2^2+9.84N^2\end{array}\right.$$

(16)

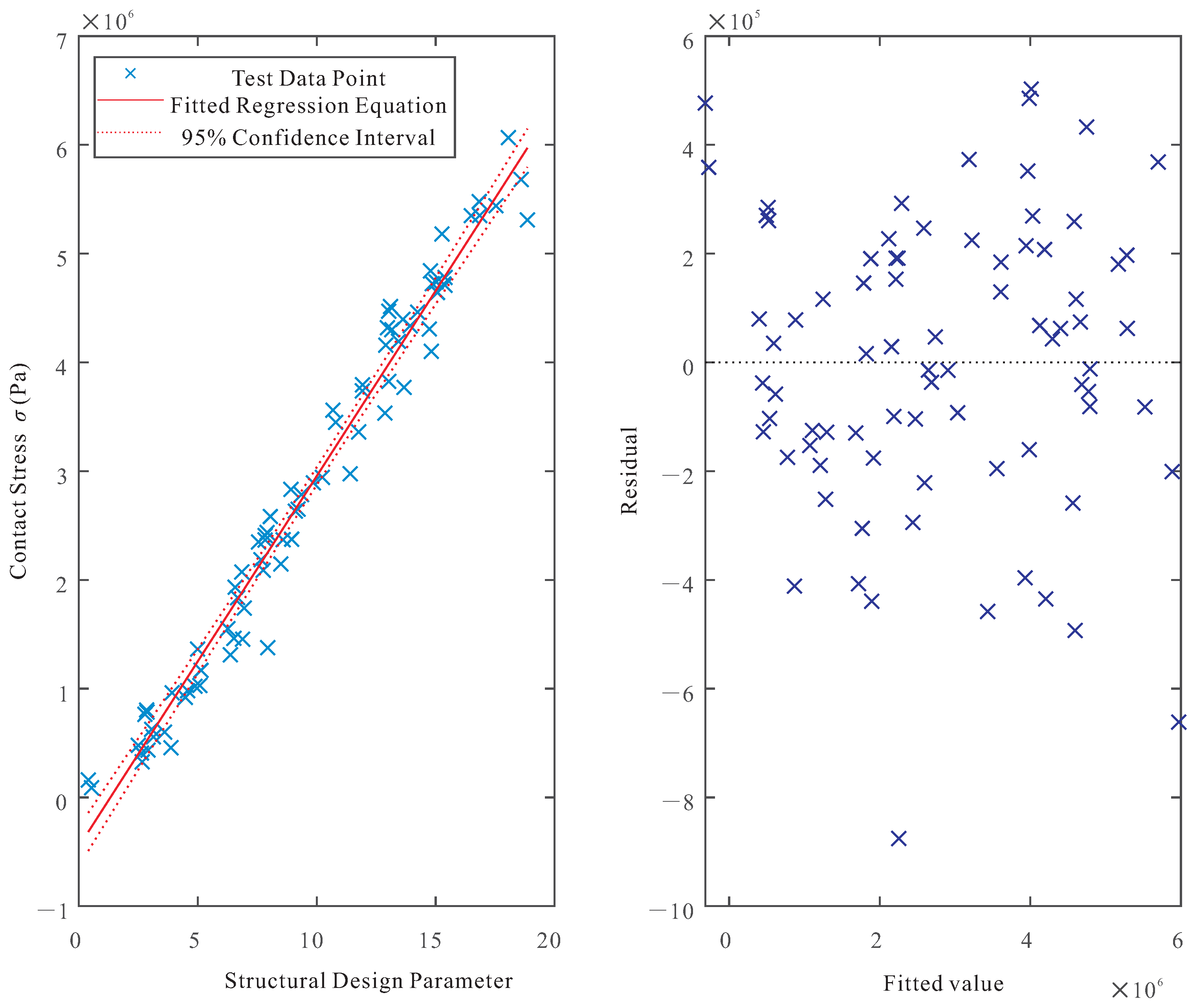
Error analysis performed on all response surface models, using an F-test, indicated that the probability of model unreliability was less than 1%, confirming the model’s ability to accurately represent the underlying input-output statistical relationship. Furthermore, the residual plots presented in Figure 3, Figure 4, Figure 5 and Figure 6 show a random distribution of residuals around the zero line, confirming that the model has no systematic bias and adequately captures the nonlinear behavior across the parameter range. The coefficient of determination ($R^2$) for the contact area model was 0.977, while the adjusted coefficient of determination ($R_{\mathrm{adj}}^2$) was 0.959. These values indicate that approximately 95.9% of the variation in contact area can be attributed to the structural parameters of the flexible finger, demonstrating a well-fitted response model that effectively captures the input-output relationship.

The relationship between contact stress ($\sigma$) and the key geometric parameters of the trapezoidal section of the flexible finger—including the upper base length (a), lower base length (b), outer beam angle ($\alpha$), outer beam thickness ($d_1$), inner beam inclination angle ($\beta$), inner beam thickness ($d_2$), and the number of inner beams (N)—was modeled using a multiple regression equation, as given in Equation (17). The corresponding fit is illustrated in Figure 4.

$$\sigma =\left\{\begin{array}{c}-451386.56+5977.72a-37246.69b-5110.45\alpha +195703.81d_1\\ -36437.55\beta -113097.99d_2+248018.12N-47.32ab-203.03a\alpha \\ -46.41b\alpha -335.47a{d}_1+1327.03b{d}_1-321.59\alpha d_1-225.55a\beta \\ -22.74b\beta -150.01\alpha \beta +1317.73d_1\beta +46.28a{d}_2+1132.99b{d}_2\\ -3399.61\alpha N-13874.84d_{1}N-1639.98\beta N+7553.21d_{2}N\\ +70.03a^2+271.29b^2+679.50{\alpha }^2+3024.20d_1^2+1536.53{\beta }^2\\ +10017.10d_2^2+14573.14N^2\end{array}\right.$$

(17)

The coefficient of determination ($R^2$) for the contact stress model was 0.974, while the adjusted coefficient of determination ($R_{\mathrm{adj}}^2$) was 0.954. These values indicate that approximately 95.4% of the observed variation in contact stress can be attributed to the combined effects of the specified structural parameters, confirming the model’s excellent predictive capability.

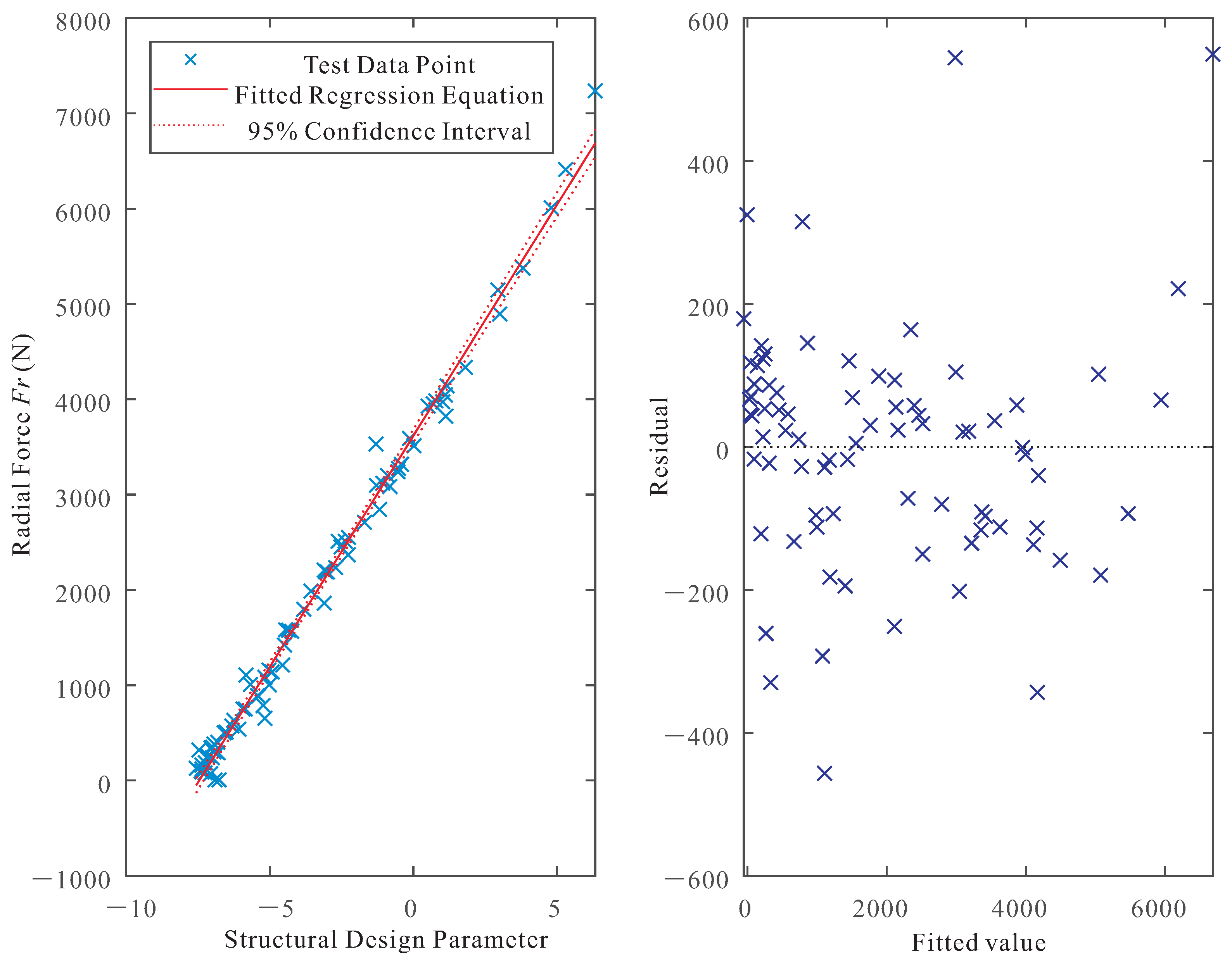
The relationship between radial force ($F_r$) and the key geometric parameters of the trapezoidal section of the flexible finger—including the upper base length (a), lower base length (b), outer beam angle ($\alpha$), outer beam thickness ($d_1$), inner beam inclination angle ($\beta$), inner beam thickness ($d_2$), and the number of inner beams (N)—was modeled using a multiple regression equation, as given in Equation (18). The corresponding fit is illustrated in Figure 5.

The coefficient of determination ($R^2$) for the radial force model was 0.992, while the adjusted coefficient of determination ($R_{\mathrm{adj}}^2$) was 0.984. These values indicate that approximately 98.4% of the observed variation in radial force can be attributed to the combined effects of the specified structural parameters, confirming the model’s excellent predictive capability.

$$F_{\mathrm{r}}=\left\{\begin{array}{c}3616.85-18.75a-51.35b+81.71\alpha -349.01d_1+19.53\beta \\ -227.87d_2-226.32N-0.076ab-0.031a\alpha -0.078b\alpha \\ +0.58a{d}_1+2.59b{d}_1+0.39\alpha d_1+0.033a\beta -0.052b\beta \\ -0.19\alpha \beta -0.36d_1\beta +0.38a{d}_2+1.30b{d}_2-0.95\alpha d_2\\ +3.91d_1{d}_2-0.96\beta d_2+0.23aN+1.24bN-1.72\alpha N\\ -0.051d_{1}N-0.15\beta N+13.43d_{2}N+0.078a^2+0.21b^2\\ -0.92{\alpha }^2+9.53d_1^2+0.014{\beta }^2+5.97d_2^2+12.08N^2\end{array}\right.$$

(18)

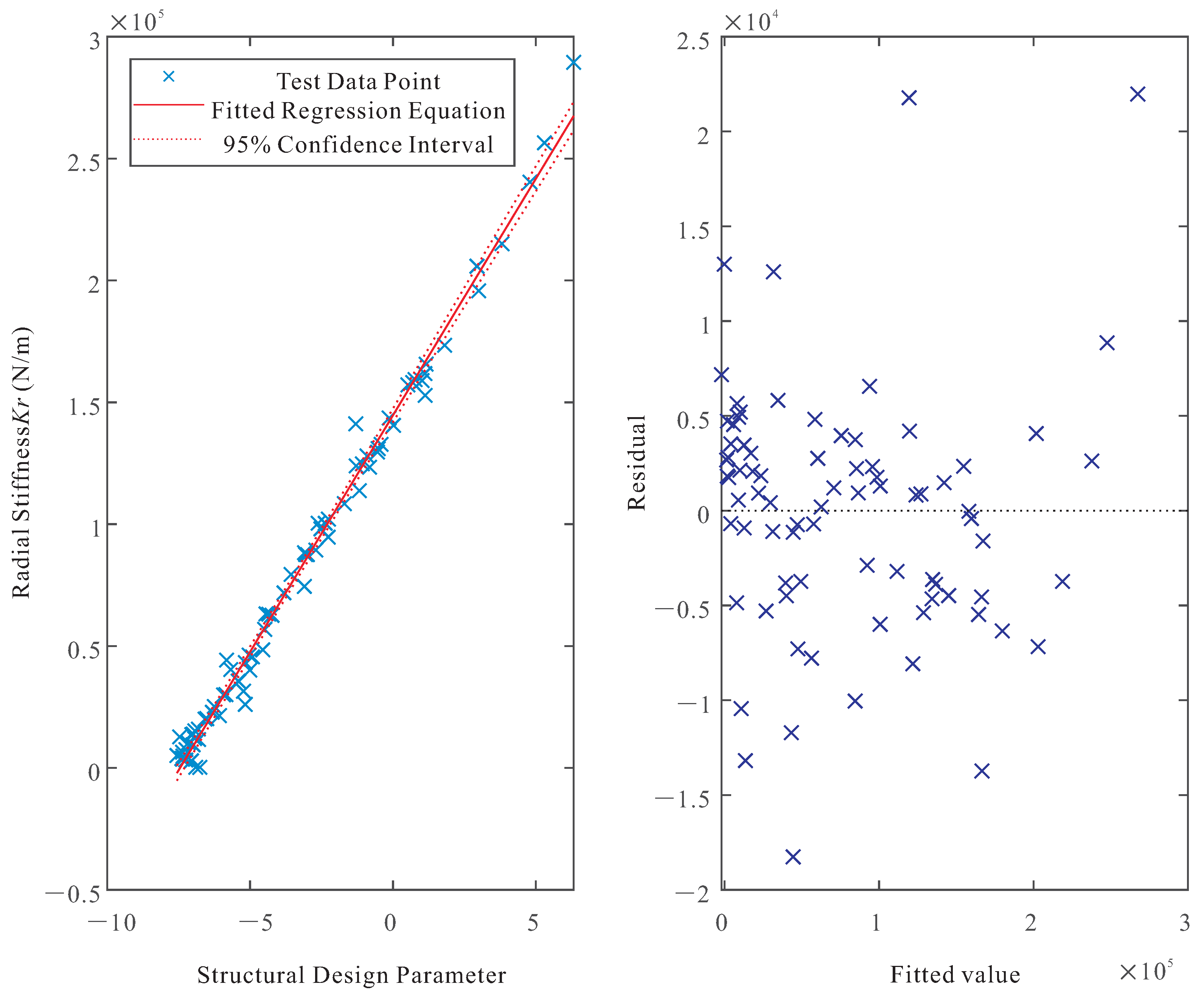
Similarly, the relationship between radial stiffness ($K_r$) and the key geometric parameters of the trapezoidal section was modeled using a multiple regression equation, as given in Equation (19). The corresponding fit is illustrated in Figure 6. The $R^2$ and $R_{\mathrm{adj}}^2$ values for the radial stiffness model were 0.992 and 0.984, respectively, indicating that approximately 98.4% of the observed variation in radial stiffness is explained by the combined effects of the structural parameters. These results confirm that the regression models provide excellent predictive capability for both radial force and stiffness.

By leveraging these regression models, the contact behavior and radial stiffness of the adaptive banana gripper can be effectively optimized. This enables the identification of the optimal combination of structural parameters for the flexible fingers, thereby enhancing grasping performance while minimizing mechanical damage to the fruit.

$$K_{\mathrm{r}}=\left\{\begin{array}{c}144674.51-749.79a-2054.19b+3268.26\alpha -13960.43d_1\\ +781.18\beta -9114.87d_2-9053.05N-3.05ab-1.23a\alpha \\ -3.12b\alpha +23.07a{d}_1+103.80b{d}_1+15.72\alpha d_1+1.34a\beta -2.09b\beta \\ -7.59\alpha \beta -14.55d_1\beta +15.37a{d}_2+52.15b{d}_2-38.15\alpha d_2\\ +156.42d_1{d}_2-38.47\beta d_2+9.37aN+49.51bN-68.61\alpha N\\ -2.04d_{1}N-5.84\beta N+537.01d_{2}N+3.11a^2+8.60b^2-36.65{\alpha }^2\\ +381.21d_1^2+0.57{\beta }^2+238.82d_2^2+483.33N^2\end{array}\right.$$

(19)

2.3. Analysis of Response Surface Results for Flexible Supporting Fingers

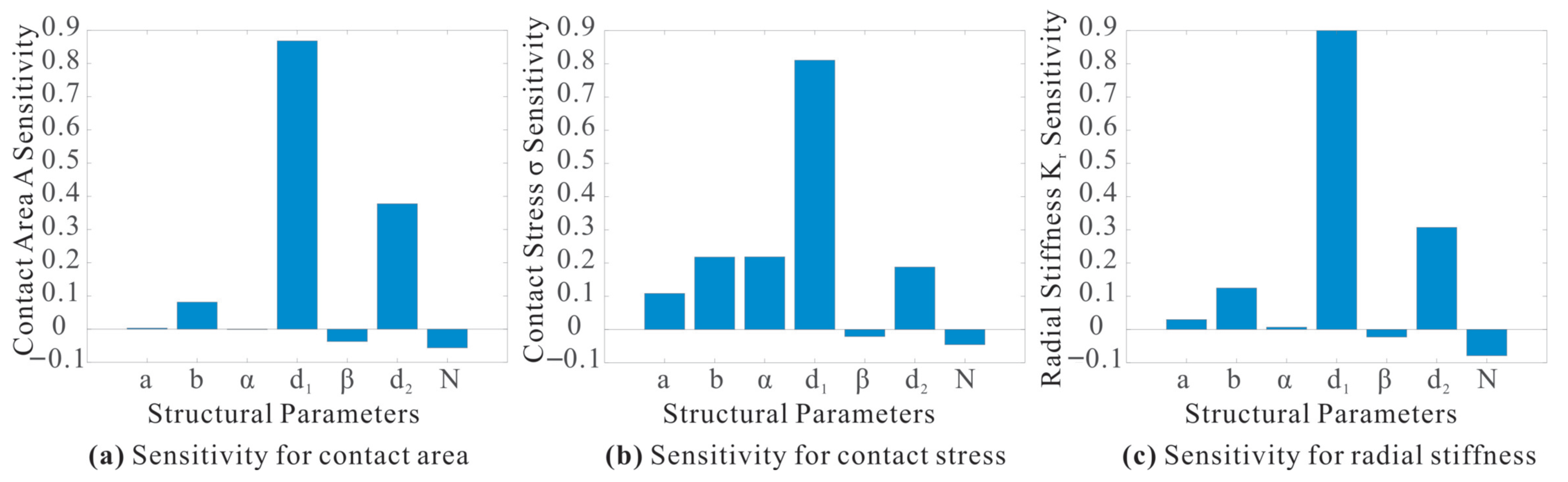
Sensitivity analysis provides a scientific basis for design decisions in the development of pick-up grippers, enabling the identification of key design variables that significantly influence output performance. This approach supports targeted design improvements, leading to more reliable and higher-quality products while optimizing manufacturing costs without compromising performance. A correlation analysis of the experimental data was conducted, and the sensitivity of the trapezoidal structural parameters of the flexible finger to the contact area was quantified, as shown in Figure 7a.

The magnitude of sensitivity reflects the degree to which each input parameter affects the target output. As illustrated in Figure 7a, the sensitivity of each design variable to contact area varies significantly. The trapezoidal base length a and the outer beam angle $\alpha$ exhibit the lowest sensitivity to contact area, indicating that their individual effects on contact area during support operations are minimal. However, as shown in Figure 7b, both parameters demonstrate high sensitivity to contact stress ($\sigma$), and therefore cannot be neglected in the overall optimization process.

By contrast, the outer beam thickness ($d_1$) shows high sensitivity to both contact behavior and radial stiffness ($K_r$), highlighting its critical influence on overall support performance. Furthermore, because the banana initially contacts the region near the base of the flexible finger during operation, the lower base length (b) of the trapezoidal section has a stronger effect on contact performance than the upper base length (a). This observation aligns with the sensitivity patterns presented in Figure 7.

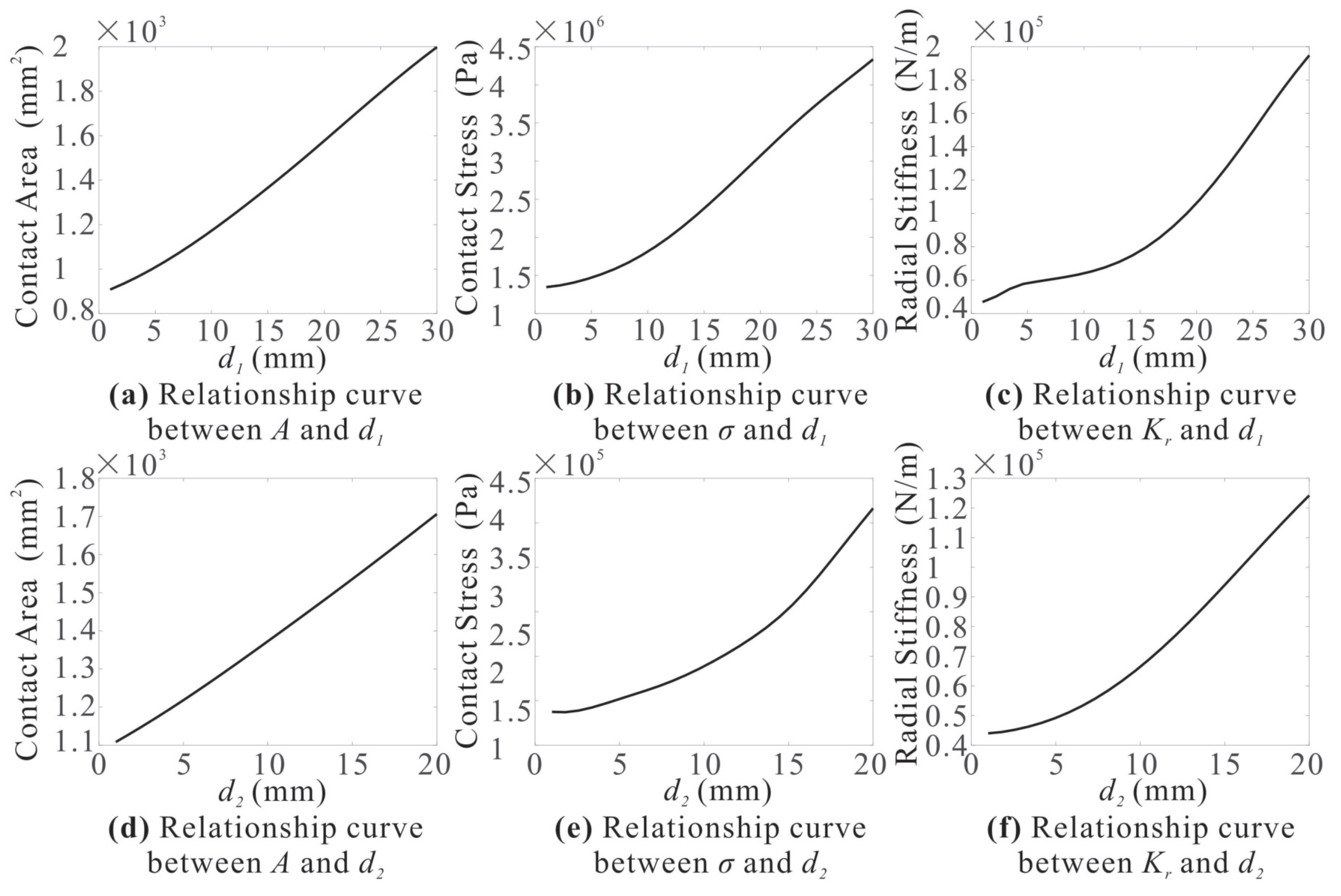
In addition, the relationships between the structural design parameters of the flexible finger and the key performance targets for docking tasks were established. Correlation curves illustrating the influence of the maximum outer beam thickness ($d_1$) and inner beam thickness ($d_2$) on the output responses are presented in Figure 8.

The results indicate that the contact area increases approximately linearly with both outer and inner beam thicknesses.

In contrast, contact stress ($\sigma$) and radial stiffness ($K_r$) exhibit distinct nonlinear growth patterns depending on the parameter range. When the outer beam thickness $d_1$ is below 15 mm, both contact stress and radial stiffness increase nonlinearly, with the rate of change accelerating as $d_1$ increases. Beyond $d_1=15$ mm, the responses transition to an approximately linear growth trend. Similarly, the inner beam thickness $d_2$ shows a nonlinear relationship with contact stress and radial stiffness, with the magnitude of increase becoming more pronounced for larger $d_2$ values.

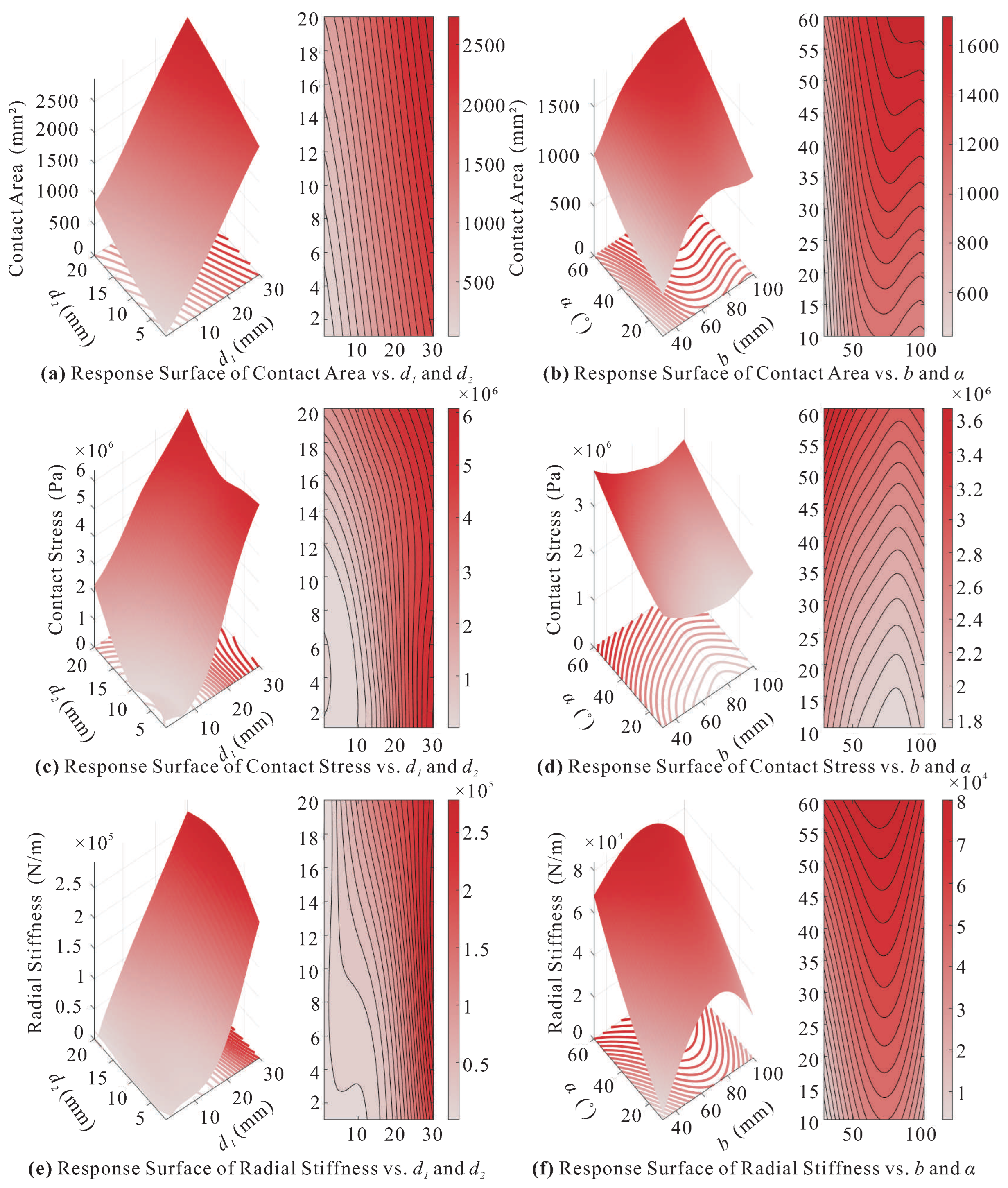
Based on the experimental sample data, response surface models were constructed to characterize the relationships between the key design parameters of the flexible finger structure—including outer beam thickness ($d_1$), inner beam thickness ($d_2$), trapezoidal lower base length (b), and outer beam angle ($\alpha$)—and the corresponding output performance targets. The resulting response surfaces are illustrated in Figure 9.

Analysis of the response surfaces indicates that the interaction between the thickness and dimensional parameters of the inner and outer beams has a substantially greater influence on the output targets than the interaction between the trapezoidal lower base length (b) and the outer beam angle ($\alpha$). The combined effect of beam thickness and size on contact area is approximately linear, whereas its influence on contact stress ($\sigma$) and radial stiffness ($K_r$) exhibits a nonlinear increasing trend.

In contrast, the response surface corresponding to b and $\alpha$ displays distinct peaks and troughs, indicating a more complex interactive behavior. These results suggest that the influence of the lower base length (b) on the output responses is predominantly linear, while the outer beam angle ($\alpha$) follows a pronounced nonlinear relationship. The presence of characteristic peaks and troughs further validates the appropriateness of the selected upper and lower bounds for the optimized design parameters.

3. Results and Discussion

To improve both the contact performance and anti-overturning stability of the flexible supporting fingers during banana harvesting, an optimization model was established. The model considers contact area (A), contact stress ($\sigma$), and radial stiffness ($K_r$) as the objective functions, which can be expressed as:

$$\left\{\begin{array}{c}MaxA=f_1\left(a,b,\alpha ,d_1,\beta ,d_2,N\right)\\ Min\sigma =f_2\left(a,b,\alpha ,d_1,\beta ,d_2,N\right)\\ Max{K}_r=f_3\left(a,b,\alpha ,d_1,\beta ,d_2,N\right)\end{array}\right.$$

(20)

The constraints are:

$$\mathrm{s}.\mathrm{t}.=\left\{\begin{array}{c}60\le a\le 130\\ 30\le b\le 100\\ 10\le \alpha \le 60\\ 1\le d_1\le 30\\ 0\le \beta \le 30\\ 1\le d_2\le 20\\ 3\le N\le 11\\ a\le b\end{array}\right.$$

(21)

A Multi-Objective Genetic Algorithm (MOGA) was employed to optimize the structural parameters of the flexible supporting fingers. The algorithm was configured with seven input parameters and three output objective functions. The initial sample size was set to 100, with a maximum of 20 iterations and 100 samples generated per iteration. The maximum allowable Pareto percentage was set to 70%, and the convergence stability threshold was defined as 2%. The optimization followed the standard MOGA workflow: non-dominated sorting, crowding distance calculation, selection, crossover, and mutation. During the selection phase, tournament selection was applied: when comparing two individuals, the one with the lower non-dominated rank was preferred; if both belonged to the same rank, the individual with the larger crowding distance was selected to promote population diversity.

The optimization process converged after seven iterations. A total of 642 samples were evaluated, yielding a final Pareto percentage of 1% and a convergence stability value of 1.99%. The optimized structural parameters of the flexible supporting finger are summarized in

Table 2. Final optimization comparison results of the banana flexible supporting finger.

	Parameter	Before Optimization	After Optimization	Change Rate
Design variable	Upper sole length (mm)	100	99.97	−0.03%
	Bottom length (mm)	60	77.76	29.60%
	Angle of outer beam (°)	30	26.92	−10.27%
	Thickness of outer beam (mm)	2	2.64	32%
	Inclination angle of inner beam (°)	5	26.65	433%
	Thickness of inner beam (mm)	2	2.79	−39.50%
	Number of internal beams (strips)	6	4	−33.33%
Optimization objective	Contact area (mm2)	182.85	596.87	226.43%
	Contact stress (Pa)	160,230	42,640.23	−73.39%
	Radial static stiffness (N/m)	262.69	772.04	193.90%

. The results indicate that the optimized finger design effectively enhances contact performance with banana bunches. Specifically, the contact area increased by 226.43%, the contact stress decreased by 73.39%, and the radial static stiffness improved by 193.9%. These enhancements collectively demonstrate a more uniform pressure distribution and greater mechanical stability during supporting operations.

The optimized flexible fingers were then integrated into the distributed supporting device described in previous work, replacing the original finger units. A simulation analysis was performed using ANSYS Workbench 2021R1 to evaluate the device’s performance under realistic banana harvesting conditions. The working state of the optimized device is illustrated in Figure 10.

Simulation results indicate that the optimized device exhibits excellent axial stiffness, adaptive height adjustment, and effective radial wrapping capability. To further validate performance, a comparative analysis was conducted between the contact behavior and stress distribution on the banana during operation of the optimized device and the pre-optimization baseline. The analysis confirms that the structural optimization effectively improves contact uniformity and reduces peak stress on the fruit surface, demonstrating the effectiveness of the proposed design methodology in enhancing grasping safety and operational stability.

3.1. Contact Performance Results

Figure 11 compares the contact area curves of bananas supported by the device before and after optimization. The results indicate that, under axial load, the optimized flexible finger exhibits noticeable fluctuations in contact area. This behavior can be attributed to the increased angle between the trapezoidal section and the outer beam in the optimized design.

Initially, when the banana makes tangential contact with the finger section, the finger undergoes minimal deformation, resulting in a gradual increase in contact area. As the axial load increases, substantial finger deformation occurs, causing partial separation from the fruit surface and a rapid decrease in the theoretical contact area. Subsequently, the contact area stabilizes and remains largely unaffected by further variations in axial or radial load. This phenomenon validates the rationality of the optimized design and demonstrates improved stability and adaptability of the fingers during the holding process. Quantitative results show that the optimized flexible gripper achieves a maximum stable contact area of approximately 2600 mm² under axial load, representing a 23.81% increase compared to the pre-optimization value of 2100 mm². Under radial load, the maximum stable contact area reaches approximately 2500 mm², a 25% improvement from the initial 2000 mm². For penultimate banana hand, the maximum stable contact area under axial load is approximately 1800 mm² (a 28.57% increase from 1400 mm²), while under radial load it stabilizes at around 1700 mm² (a 13.33% increase from 1500 mm²). The consistent performance observed across these different fruit positions, which possess varying curvatures and diameters, confirms the robustness of the optimized structural parameters against biological morphological uncertainties.

Figure 12 illustrates the variation in contact stress on the last banana hand after optimization. As shown in Figure 12a, the contact stress on the last banana hand exhibits a nonlinear increasing trend with axial load. However, fluctuations in stress growth are significantly reduced compared to pre-optimization results. This improvement is due to the optimized supporting structure, which distributes the banana’s mass over multiple contact areas. Although the contact force increases more slowly, the contact area continues to expand gradually, resulting in a more uniform rise in contact stress. After optimization, the growth trend of contact stress can be approximated as linear, in contrast to the more variable pre-optimization behavior. This stabilization helps mitigate stress peaks, reducing the risk of mechanical damage to the fruit.

Quantitatively, under axial loading, the optimized structure reduces the maximum contact stress on the last banana hand by 0.076 MPa, corresponding to a 44.71% reduction compared to the pre-optimization level. Under radial loading (Figure 12b), contact stress increases steadily with load but no longer exhibits the fluctuations observed previously. The optimized response demonstrates enhanced stability, reflecting improved support consistency and validating the inclusion of radial stiffness ($K_r$) as a key optimization objective. Under radial load, the maximum contact stress decreases by 0.11 MPa, a 56% reduction relative to the initial design. These results collectively indicate that the optimized flexible supporting finger achieves more predictable and uniform contact stress distribution under both axial and radial loading conditions. The suppression of stress fluctuations and near-linear stress growth contribute to enhanced operational stability and reduced likelihood of banana damage during mechanical harvesting and handling.

Figure 12c,d illustrates contact stress variation for the penultimate banana hand after optimization. Under a 20% axial load, the contact stress curve exhibits a distinct trough, corresponding to the contact area fluctuations previously observed in Figure 11c. After this initial phase, stress stabilizes and subsequently follows an approximately linear growth trend with increasing load. Quantitative analysis shows that the optimized structure reduces maximum contact stress under axial load by approximately 0.067 MPa (a 55.83% reduction) and under radial load by 0.068 MPa (a 56.67% reduction) compared to the pre-optimization design.

3.2. Shear Performance Results

In the dynamic environment typical of banana harvesting and transport—where factors such as the weight of the banana bunch, wind disturbances, and road-induced vibrations are present—maintaining ideal static loading conditions is challenging. Therefore, evaluating the potential for stalk detachment during harvesting and support operations requires analyzing stalk damage under dynamic loading.

In this study, extensive experiments were conducted to systematically investigate the damage characteristics of banana stems at different positions within the same bunch under dynamic loads.

Figure 13 presents the maximum shear force and corresponding shear stress endured by stems at various positions, with the minimum withstandable shear stress measured at approximately 0.28 MPa.

Figure 14 illustrates the variation in maximum shear stress within the stem–stalk transition zone after optimization. As shown in Figure 14a, shear stress increases approximately linearly with axial load, reaching a maximum of about 0.11 MPa—a 91.6% reduction compared to the pre-optimization design. Under radial loading, shear stress remains stable with minor fluctuations, attaining a maximum of approximately 0.13 MPa, corresponding to a 90.3% decrease relative to the initial design.

In both loading scenarios, the maximum shear stress remains well below the experimentally determined critical shear stress of 0.28 MPa for banana stalks under dynamic conditions. This significant difference establishes a safety factor of approximately 2.15, demonstrating the robust fault tolerance of the optimized design. Even in the presence of uncertainties such as minor material property variations or unexpected dynamic disturbances, the generated stress remains far below the damage threshold. This margin confirms that the optimized flexible gripper provides sufficient mechanical stability and robustness during grasping and wrapping operations, effectively minimizing the risk of stalk detachment.

Performance analysis of the optimized flexible supporting claw demonstrates substantial improvements over the pre-optimization design. The optimized device achieves a significant increase in contact area with the banana fruit fingers, accompanied by a notable reduction in contact stress. Additionally, the enhanced radial stiffness contributes to greater stability during support and wrapping, effectively lowering the shear stress applied to the banana fruit stalk and improving operational safety.

To further validate that these theoretical stress reductions translate into practical damage mitigation, validation tests were conducted on 30 banana bunches with an average weight of 28.28 kg. The results indicated a 100% supporting success rate, confirming that the Safety Factor of approximately 2.15 effectively prevents stalk detachment under realistic loads. Furthermore, the average damaged area ratio was limited to 5.44%, and the damaged finger ratio was 5.19%. These values are significantly lower than the typical 20–32% damage rates observed in conventional harvesting operations, providing empirical confirmation that the optimized stress distribution effectively preserves fruit integrity during the support process.

4. Conclusions

This paper presents a systematic methodology for the design and optimization of adaptive flexible end-effectors for banana bunch harvesting, with an emphasis on contact behavior and mechanical constraints. By integrating contact-behavior-constrained response surface modeling (RSM) with multi-objective genetic algorithm (MOGA) optimization, the study identifies the key geometric factors of the flexible supporting fingers and determines their optimal configurations to enhance grasping performance while minimizing mechanical damage. A contact-behavior-constrained design framework was developed to enable precise control of contact stress while maximizing surface conformability, thereby addressing the challenge of designing adaptive, low-contact-stress end-effectors without the need for complex sensors or active control. Sensitivity and interaction analyses further revealed that beam thickness and dimensional parameters have the most significant influence on performance, providing a rigorous basis for targeted optimization. By integrating contact-behavior-constrained optimization with explicit engineering specifications—including material selection and geometry definition informed by agronomic data—the study establishes a complete and reproducible design methodology. This ensures that the proposed solution is not only theoretically robust but also practically viable for low-damage banana harvesting applications.

Multi-objective optimization successfully identified the Pareto-optimal structural parameters, yielding good improvements: under axial loading, the maximum contact area increased by 23.81% and 28.57% for the last banana hand and penultimate banana hand, respectively; under radial loading, the increases were 25% and 13.33%. Contact stress was substantially reduced, with axial-load reductions of 44.71% and 55.83% and radial-load reductions of 56% and 56.67%, respectively. Moreover, the maximum shear stress in the fruit stem–stalk transition zone decreased by approximately 90.3%, ensuring banana bunches’ stability under dynamic loading conditions. Finite element simulations and experimental validation confirmed that the optimized gripper provides uniform contact pressure distribution, predictable stress growth, and enhanced radial stiffness, collectively contributing to a more stable supporting wrap and a reduced risk of mechanical damage.

Overall, this paper presents a novel, generalizable framework for designing adaptive, low-contact-stress end-effectors suitable not only for banana harvesting but also for handling other fragile and irregular agricultural products. By bridging the gap between bio-inspired flexible gripper design and practical agricultural implementation, the study provides both theoretical insights and engineering solutions for the development of advanced robotic harvesting systems, enhancing safety, reliability, and operational efficiency in automated fruit handling.