Orchard Variable-Rate Sprayer Using LiDAR-Based Canopy Volume Measurement
Abstract
1. Introduction
2. Development Plan for the Sprayer
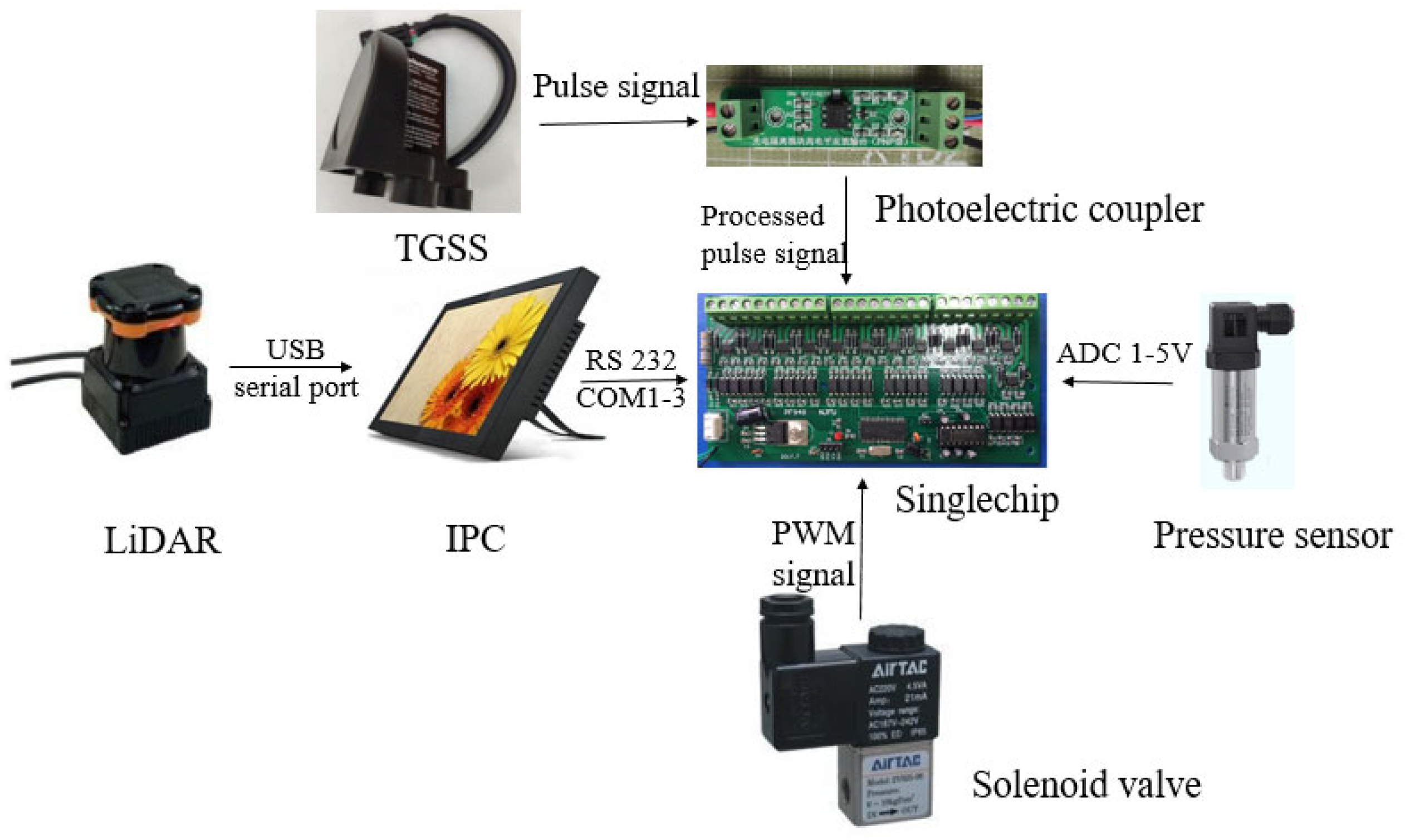
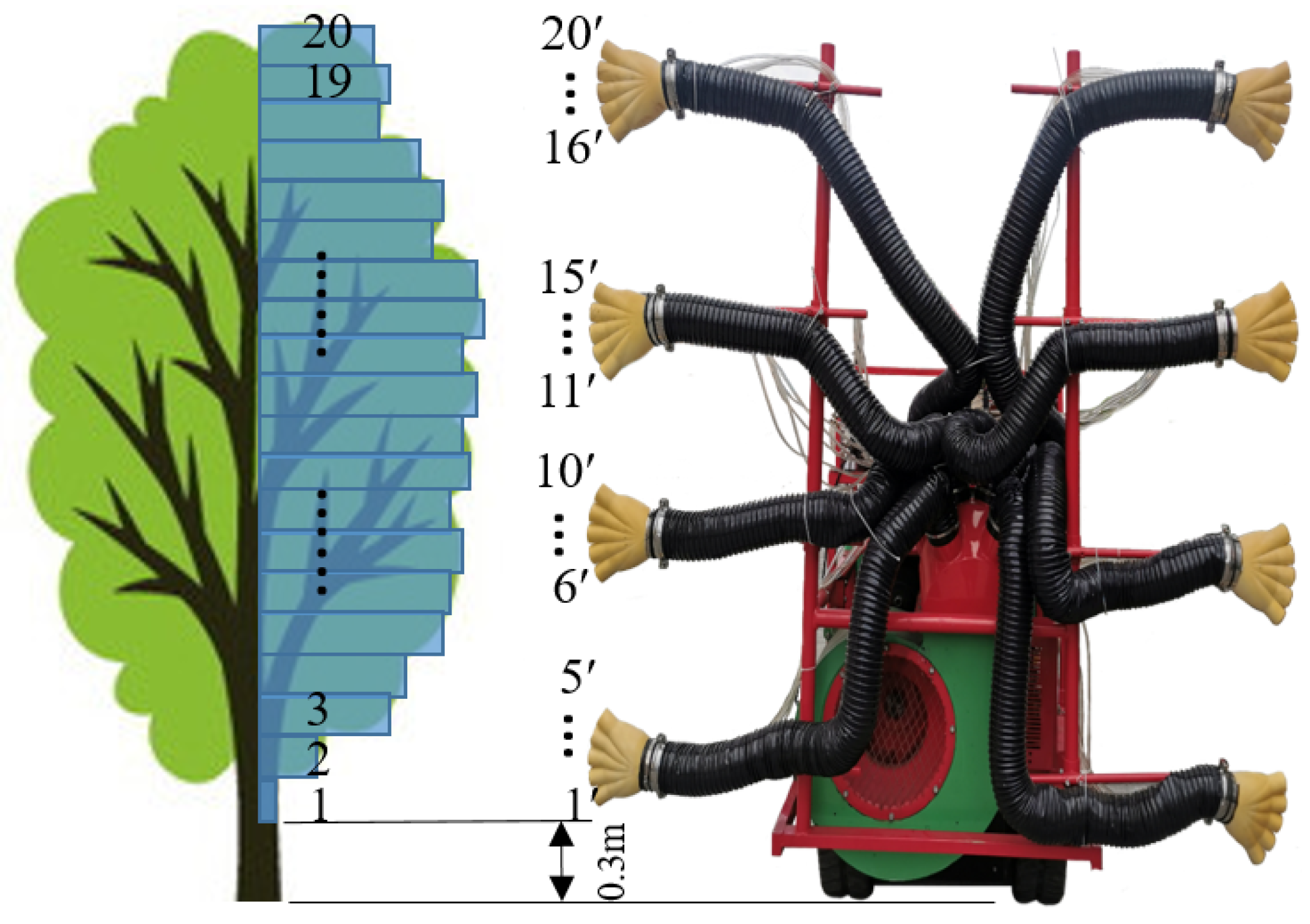
2.1. Test Equipment
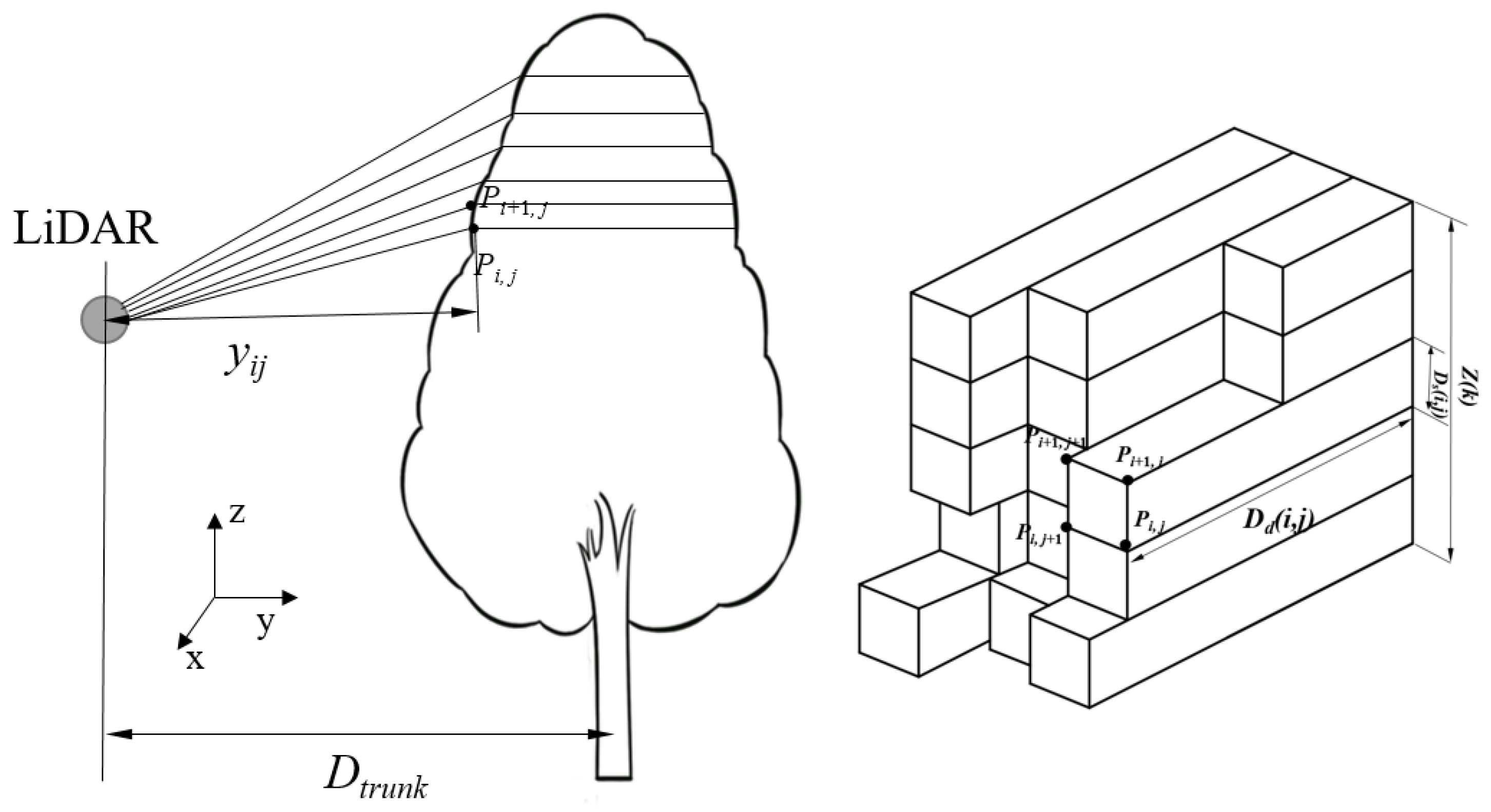
2.2. Canopy Volume Calculate Model
2.3. Variable-Rate Spray Model
2.4. Hardware Design of the Spray System
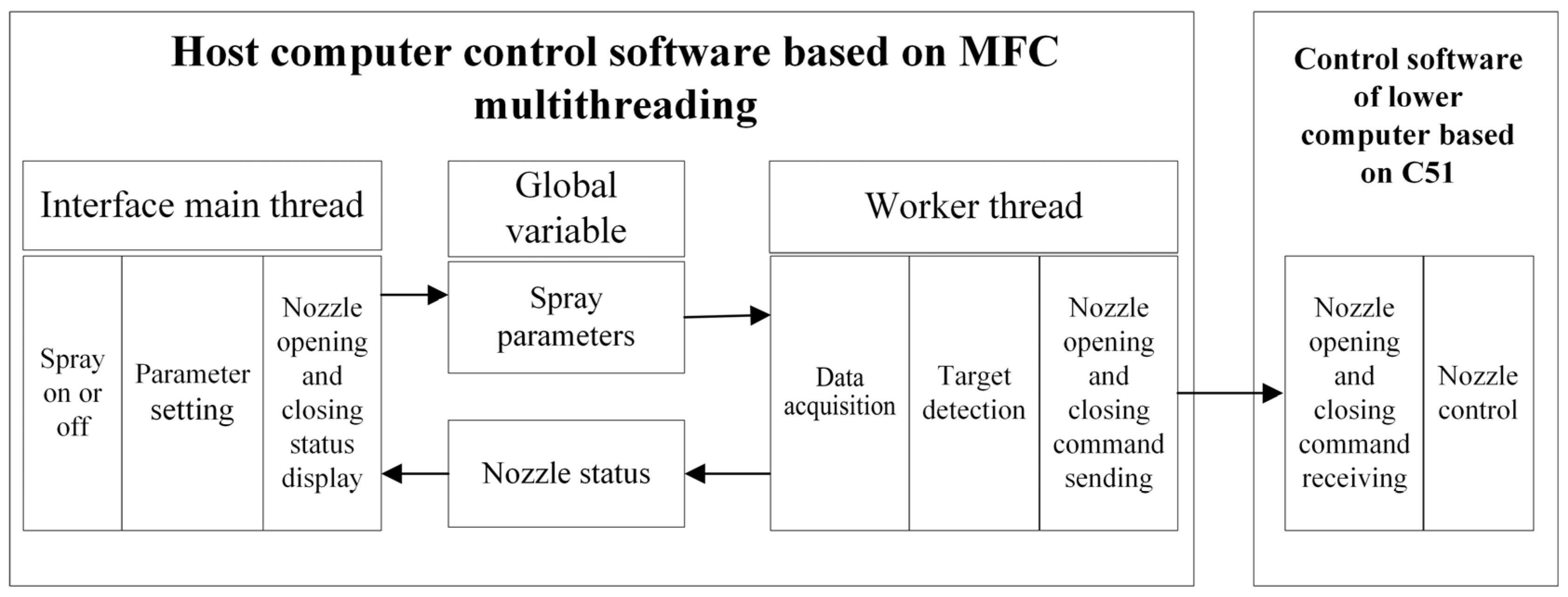
2.5. Sprayer Control System Design
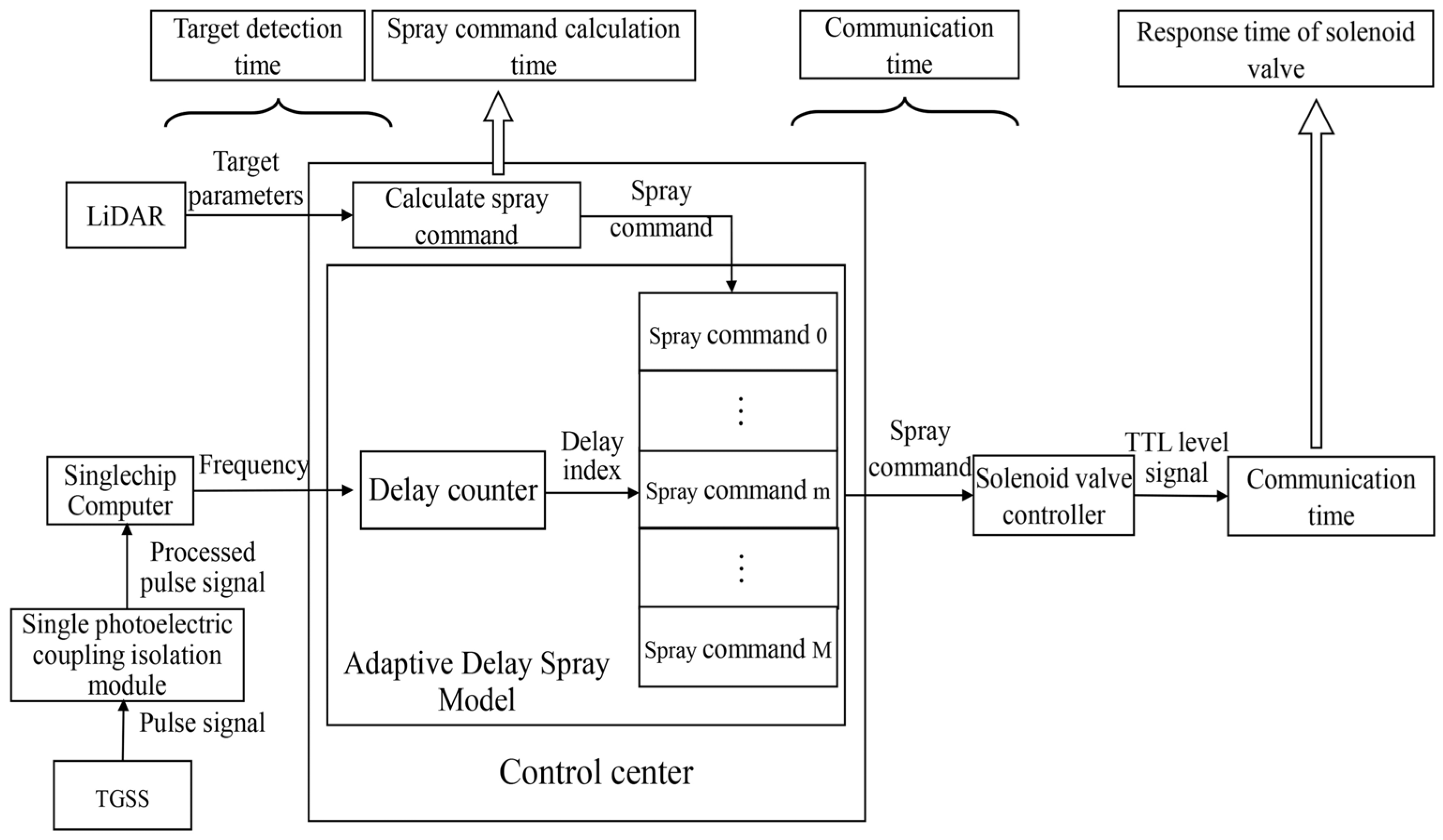
2.6. Adaptive Real-Time Target-Based Spray Control
3. Materials and Methods
3.1. Spray Volume Calculation and Dosage Experiment
3.2. Real-Time Spray Control Test
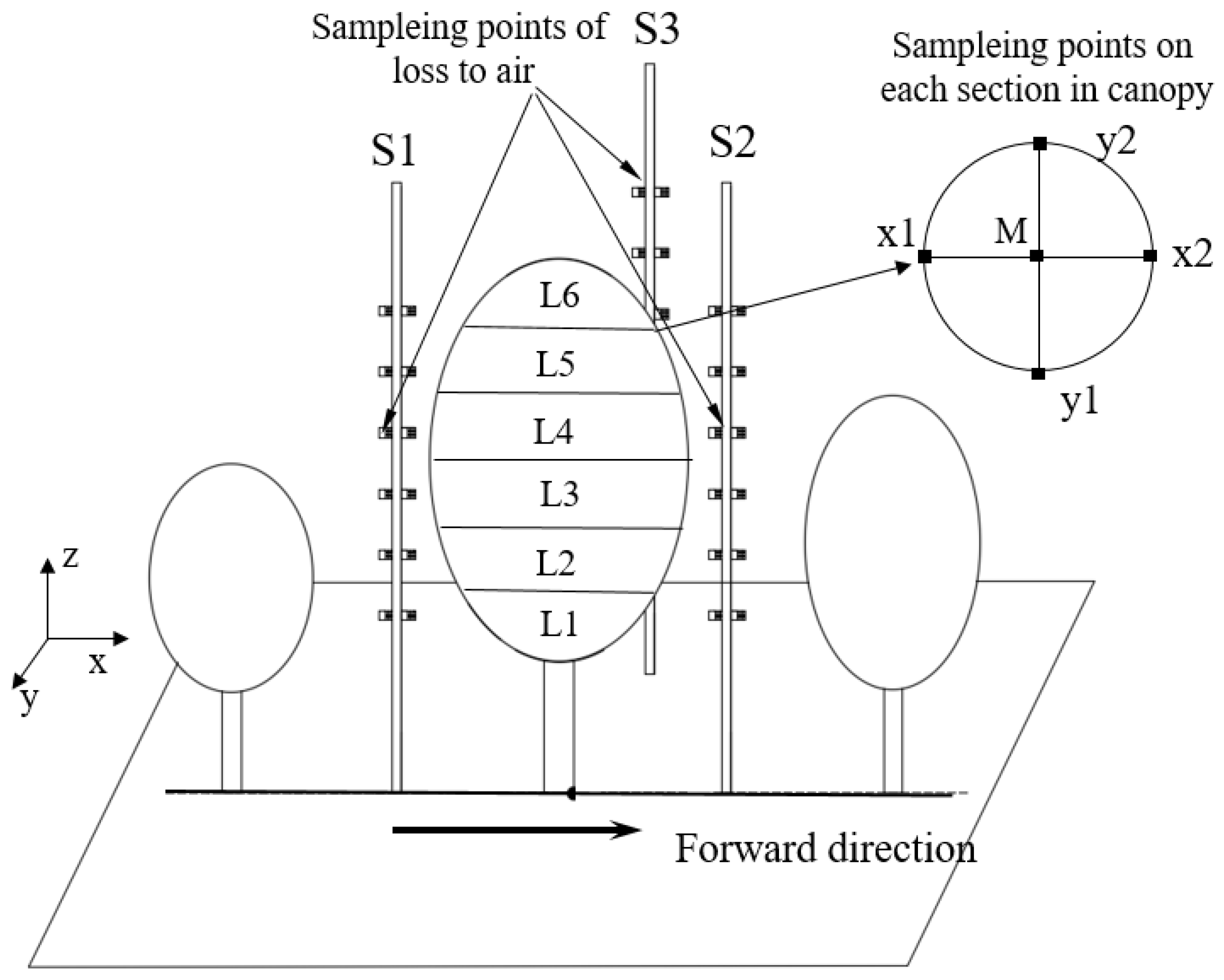
3.3. Spray Deposition Test
4. Results
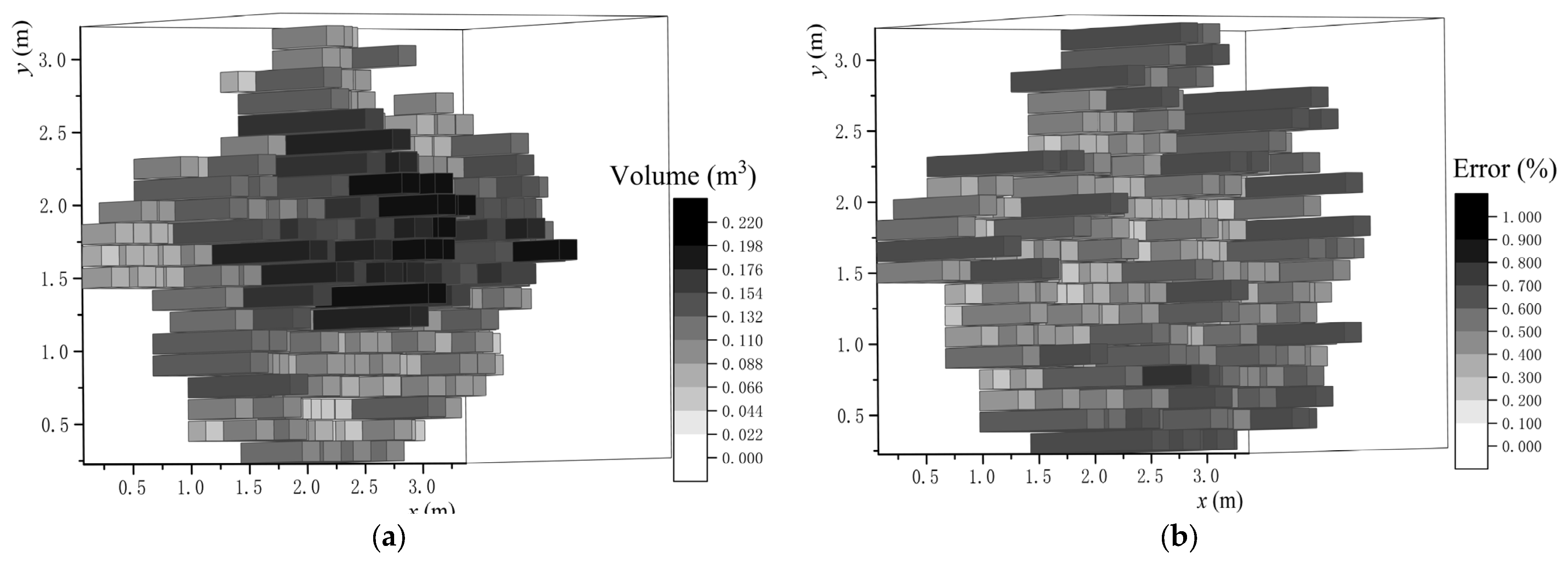
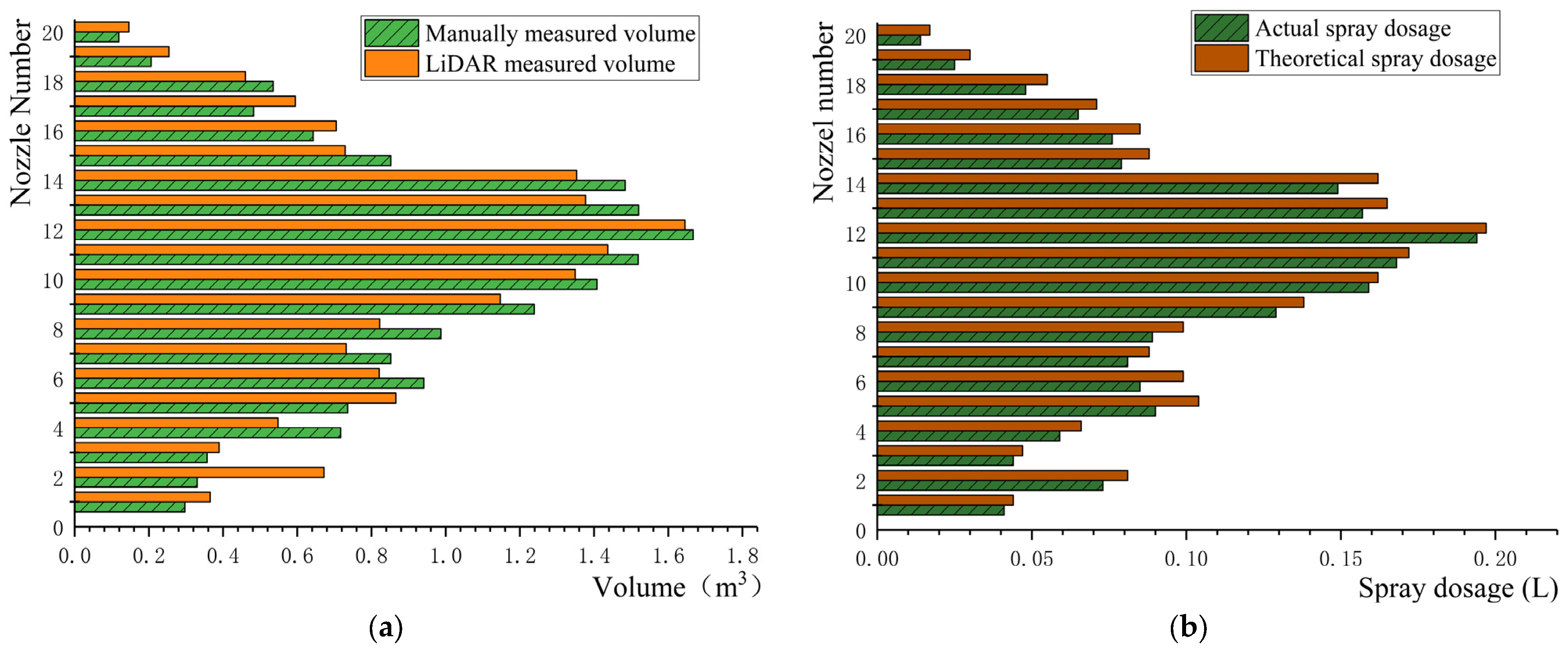
4.1. Canopy Volume and Spray Dosage
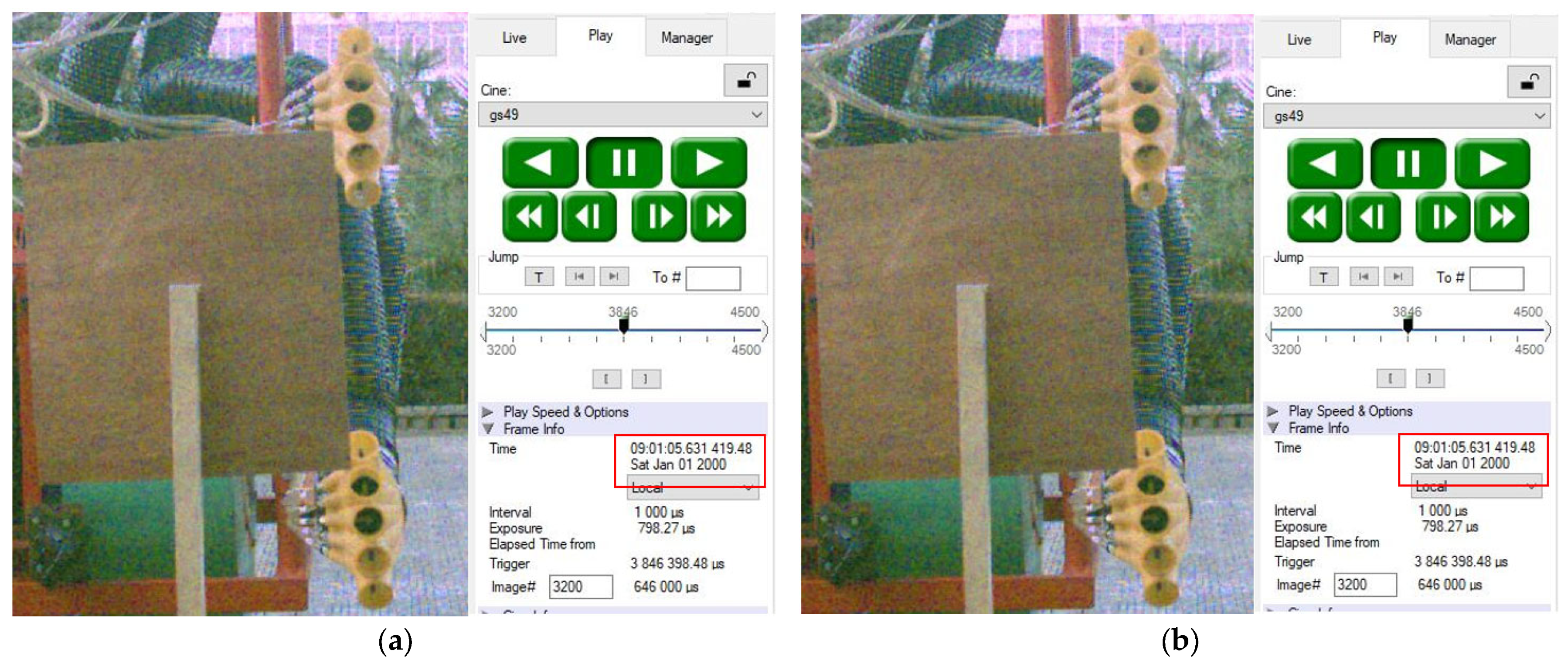
4.2. Spray Response Time and Delay
4.3. Spray Deposition Performance
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LiDAR | Light Detection and Ranging |
| TGSS | True ground speed sensor |
| ADC | Analog-to-digital converter |
| PWM | Pulse-width modulation |
| MFC | Microsoft foundation classes |
| TTL | Transistor–transistor logic |
| FIFO | First-in-first-out |
| Dd | Canopy thickness (m) |
| Ds | Distance in the Z-direction between two detection points in the j-th frame (m) |
| Z(k) | Spray region for the k-th nozzle |
| Tree canopy volume corresponding to the k-th nozzle (m3) | |
| v | Travel speed of sprayer (m·s−1) |
| Spray dosage of k-th nozzle (L) | |
| Spray flow rate (L·min−1) | |
| DCk | Duty cycle (%) |
| Proportional coefficient between spray dosage and canopy volume (-) | |
| tcomp | Compensation time (s) |
| L | Horizontal distance between the lidar and the nozzles (m) |
| tsys | System response time (s) |
| tcal | Spray command computation time (s) |
| tvalve | Solenoid valve response time (s) |
| tcom | Communication time for transmitting spray commands |
| M | Number of delay memory units (-) |
| DT | Target deposition (μL) |
| Ve | Eluent volume (mL) |
| Ae | Absorbance of the eluent |
| Ac | Absorbance of the calibration solution |
| N | Dilution factor of the tartrazine stock solution |
| d | Deposition per unit area (μL·cm−2) |
| S | Area of leaf surface (cm2) |
References
- Salas, B.; Salcedo, R.; Garcia-Ruiz, F.; Gil, E. Design, implementation and validation of a sensor-based precise airblast sprayer to improve pesticide applications in orchards. Precis. Agric. 2024, 25, 865–888. [Google Scholar] [CrossRef]
- Meshram, A.T.; Vanalkar, A.V.; Kalambe, K.B.; Badar, A.M. Pesticide spraying robot for precision agriculture: A categorical literature review and future trends. J. Field Robot. 2022, 39, 153–171. [Google Scholar] [CrossRef]
- Wu, M.; Liu, S.; Li, Z.; Ou, M.; Dai, S.; Dong, X.; Wang, X.; Jiang, L.; Jia, W. A Review of Intelligent Orchard Sprayer Technologies: Perception, Control, and System Integration. Horticulturae 2025, 11, 668. [Google Scholar] [CrossRef]
- Miranda-Fuentes, A.; Llorens, J.; Rodríguez-Lizana, A.; Cuenca, A.; Gil, E.; Blanco-Roldán, G.L.; Gil-Ribes, J.A. Assessing the optimal liquid volume to be sprayed on isolated olive trees according to their canopy volumes. Sci. Total Environ. 2016, 568, 296–305. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Chen, Y.; Gu, C.; Li, Z.; Huang, J.; Lv, X.; Qiu, W. A variable-rate spraying method fusing canopy volume and disease detection to reduce pesticide dosage. Comput. Electron. Agric. 2025, 237 Pt A, 110606. [Google Scholar] [CrossRef]
- Mahmud, M.S.; Zahid, A.; He, L.; Choi, D.; Krawczyk, G.; Zhu, H.; Heinemann, P. Development of a LiDAR-guided section-based tree canopy density measurement system for precision spray applications. Comput. Electron. Agric. 2021, 182, 106053. [Google Scholar] [CrossRef]
- Wang, M.; Dou, H.; Sun, H.; Zhai, C.; Zhang, Y.; Yuan, F. Calculation method of canopy dynamic meshing division volumes for precision pesticide application in orchards based on lidar. Agronomy 2023, 13, 1077. [Google Scholar] [CrossRef]
- Rosell, J.R.; Sanz, R. A review of methods and applications of the geometric characterization of tree crops in agricultural activities. Comput. Electron. Agric. 2012, 81, 124–141. [Google Scholar] [CrossRef]
- Maghsoudi, H.; Minaei, S.; Ghobadian, B.; Masoudi, H. Ultrasonic sensing of pistachio canopy for low-volume precision spraying. Comput. Electron. Agric. 2015, 112, 149–160. [Google Scholar] [CrossRef]
- Gu, C.; Zhao, C.; Zou, W.; Yang, S.; Dou, H.; Zhai, C. Innovative leaf area detection models for orchard tree thick canopy based on LiDAR point cloud data. Agriculture 2022, 12, 1241. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Y.; He, X.; Liu, W. Precision variable-rate spraying robot by using single 3D LIDAR in orchards. Agronomy 2022, 12, 2509. [Google Scholar] [CrossRef]
- Baltazar, A.R.; Dos Santos, F.N.; De Sousa, M.L.; Moreira, A.P.; Cunha, J.B. 2D lidar-based system for canopy sensing in smart spraying applications. IEEE Access 2023, 11, 43583–43591. [Google Scholar] [CrossRef]
- Qiao, B.; Han, L.; Wang, Z.; Li, Y.; Wang, L.; Han, H.; He, X. Design and testing of an intelligent variable-rate spraying system based on LiDAR-guided application. Crop Prot. 2024, 184, 106874. [Google Scholar] [CrossRef]
- Fessler, L.; Fulcher, A.; Lockwood, D.; Wright, W.; Zhu, H. Advancing Sustainability in Tree Crop Pest Management: Refining: Spray Application Rate with a Laser-guided Variable-rate Sprayer in Apple Orchards. HortScience 2020, 55, 1522–1530. [Google Scholar] [CrossRef]
- Polo, J.R.R.; Sanz, R.; Llorens, J.; Arnó, J.; Escola, A.; Ribes-Dasi, M.; Palacin, J. A tractor-mounted scanning LIDAR for the non-destructive measurement of vegetative volume and surface area of tree-row plantations: A comparison with conventional destructive measurements. Biosyst. Eng. 2009, 102, 128–134. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, H.; Ozkan, H.E. Development of LIDAR-guided sprayer to synchronize spray outputs with canopy structures. In Louisville, Kentucky, 7–10 August 2011; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2011. [Google Scholar] [CrossRef]
- Osterman, A.; Godeša, T.; Hočevar, M.; Širok, B.; Stopar, M. Real-time positioning algorithm for variable-geometry air-assisted orchard sprayer. Comput. Electron. Agric. 2013, 98, 175–182. [Google Scholar] [CrossRef]
- Li, L.; He, X.; Song, J.; Wang, X.; Jia, X.; Liu, C. Design and experiment of automatic profiling orchard sprayer based on variable air volume and flow rate. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2017, 33, 70–76, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Li, L.; He, X.; Song, J.; Liu, Y.; Wang, Z.; Li, J.; Liu, Z. Comparative experiment on profile variable rate spray and conventional air assisted spray in orchards. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2017, 33, 56–63, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Furness, G.O.; Magarey, P.A.; Miller, P.M.; Drew, H.J. Fruit tree and vine sprayer calibration based on canopy size and length of row: Unit canopy row method. Crop Prot. 1998, 17, 639–644. [Google Scholar] [CrossRef]
- ISO 225522: 2006; Crop Protection Equipment—Field Measurement of Spray Distribution in Tree and Bush Crops. International Organization for Standardization: Geneva, Switzerland, 2006.
- Li, W.; Luo, Y.; Jiang, P.; Dong, X.; Tang, K.; Liang, Z.; Shi, Y. A sustainable crop protection through integrated technologies: UAV-based detection, real-time pesticide mixing, and adaptive spraying. Sci. Rep. 2025, 15, 35748. [Google Scholar] [CrossRef]
- Bing, Q.; Zhang, R.; Zhang, L.; Li, L.; Chen, L. UAV-SfM Photogrammetry for Canopy Characterization Toward Unmanned Aerial Spraying Systems Precision Pesticide Application in an Orchard. Drones 2025, 9, 151. [Google Scholar] [CrossRef]


| Test Speed (m·s−1) | Theoretical Recognizable Spacing (mm) | Test Recognizable Spacing (mm) | Target Spray Advance Time (s) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 50 | 75 | 100 | 125 | 150 | 175 | ||||
| Low speed | 0.351 (±0.003) | 56.16 | × | ○ | ○ | ○ | ○ | ○ | 40 |
| 0.400 (±0.004) | 64.00 | × | ○ | ○ | ○ | ○ | ○ | 40 | |
| 0.450 (±0.003) | 72.00 | × | × | ○ | ○ | ○ | ○ | 41 | |
| 0.499 (±0.003) | 79.84 | × | × | ○ | ○ | ○ | ○ | 41 | |
| Medium speed | 0.551 (±0.002) | 88.16 | × | × | ○ | ○ | ○ | ○ | 42 |
| 0.602 (±0.003) | 96.32 | × | × | × | ○ | ○ | ○ | 42 | |
| 0.651 (±0.003) | 104.16 | × | × | × | ○ | ○ | ○ | 43 | |
| 0.698 (±0.002) | 111.68 | × | × | × | ○ | ○ | ○ | 44 | |
| 0.752 (±0.003) | 120.32 | × | × | × | × | ○ | ○ | 45 | |
| High speed | 0.802 (±0.002) | 128.32 | × | × | × | × | ○ | ○ | 47 |
| 0.847 (±0.003) | 135.52 | × | × | × | × | ○ | ○ | 48 | |
| 0.898 (±0.004) | 143.68 | × | × | × | × | ○ | ○ | 48 | |
| 0.950 (±0.001) | 152.00 | × | × | × | × | × | ○ | 49 | |
| 0.998 (±0.002) | 159.68 | × | × | × | × | × | ○ | 50 | |
| Sampling Points | Deposition Coverage (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| x1 | M | x2 | y1 | y2 | S1 | S2 | S3 | |
| L6 | 29.13 | 11.60 | 30.61 | 30.73 | 6.77 | 0 | 0 | 1.69 |
| L5 | 32.68 | 21.31 | 37.27 | 43.42 | 5.46 | 1.33 | 1.83 | 0.72 |
| L4 | 27.35 | 16.34 | 32.13 | 47.04 | 4.73 | 1.31 | 2.36 | 0.35 |
| L3 | 36.36 | 17.37 | 29.83 | 50.97 | 4.47 | 2.07 | 2.35 | 0.42 |
| L2 | 31.71 | 21.42 | 26.97 | 32.13 | 6.63 | 0 | 0.22 | 0.93 |
| L1 | 22.47 | 15.10 | 21.57 | 32.16 | 7.88 | 0 | 0 | 1.45 |
| Average value | 29.95 | 17.19 | 29.73 | 39.41 | 5.99 | 0.79 | 1.11 | 0.92 |
| Sample Point | Deposition Rate (μL·cm2) | Coefficient of Variation (%) | ||||
|---|---|---|---|---|---|---|
| x1 | M | x2 | y1 | y2 | ||
| L6 | 1.67 (0.33) | 1.59 (0.17) | 1.74 (0.26) | 2.01 (0.42) | 2.34 (0.36) | 13.4 |
| L5 | 2.68 (0.41) | 2.19 (0.28) | 2.97 (0.43) | 3.42 (0.69) | 3.96 (0.52) | 15.6 |
| L4 | 2.75 (0.37) | 2.32 (0.23) | 2.43 (0.32) | 4.74 (0.30) | 4.33 (0.39) | 16.9 |
| L3 | 2.36 (0.36) | 2.37 (0.41) | 2.93 (0.46) | 3.99 (0.39) | 3.48 (0.24) | 15.7 |
| L2 | 2.71 (0.26) | 1.92 (0.17) | 2.97 (0.30) | 2.33 (0.16) | 2.63 (0.33) | 13.1 |
| L1 | 1.77 (0.29) | 1.60 (0.18) | 1.97 (0.22) | 2.16 (0.29) | 2.58 (0.35) | 15.3 |
| Average value | 2.57 | 2.12 | 2.73 | 3.11 | 3.22 | 13.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Li, Q.; Yuan, P.; Zhou, H. Orchard Variable-Rate Sprayer Using LiDAR-Based Canopy Volume Measurement. Agronomy 2025, 15, 2709. https://doi.org/10.3390/agronomy15122709
Zhang C, Li Q, Yuan P, Zhou H. Orchard Variable-Rate Sprayer Using LiDAR-Based Canopy Volume Measurement. Agronomy. 2025; 15(12):2709. https://doi.org/10.3390/agronomy15122709
Chicago/Turabian StyleZhang, Chao, Qiujie Li, Pengcheng Yuan, and Hongping Zhou. 2025. "Orchard Variable-Rate Sprayer Using LiDAR-Based Canopy Volume Measurement" Agronomy 15, no. 12: 2709. https://doi.org/10.3390/agronomy15122709
APA StyleZhang, C., Li, Q., Yuan, P., & Zhou, H. (2025). Orchard Variable-Rate Sprayer Using LiDAR-Based Canopy Volume Measurement. Agronomy, 15(12), 2709. https://doi.org/10.3390/agronomy15122709






