A New Approach to Sensible Heat Flux via CFD-Surface Renewal Integration
Abstract
1. Introduction
2. Materials and Methods
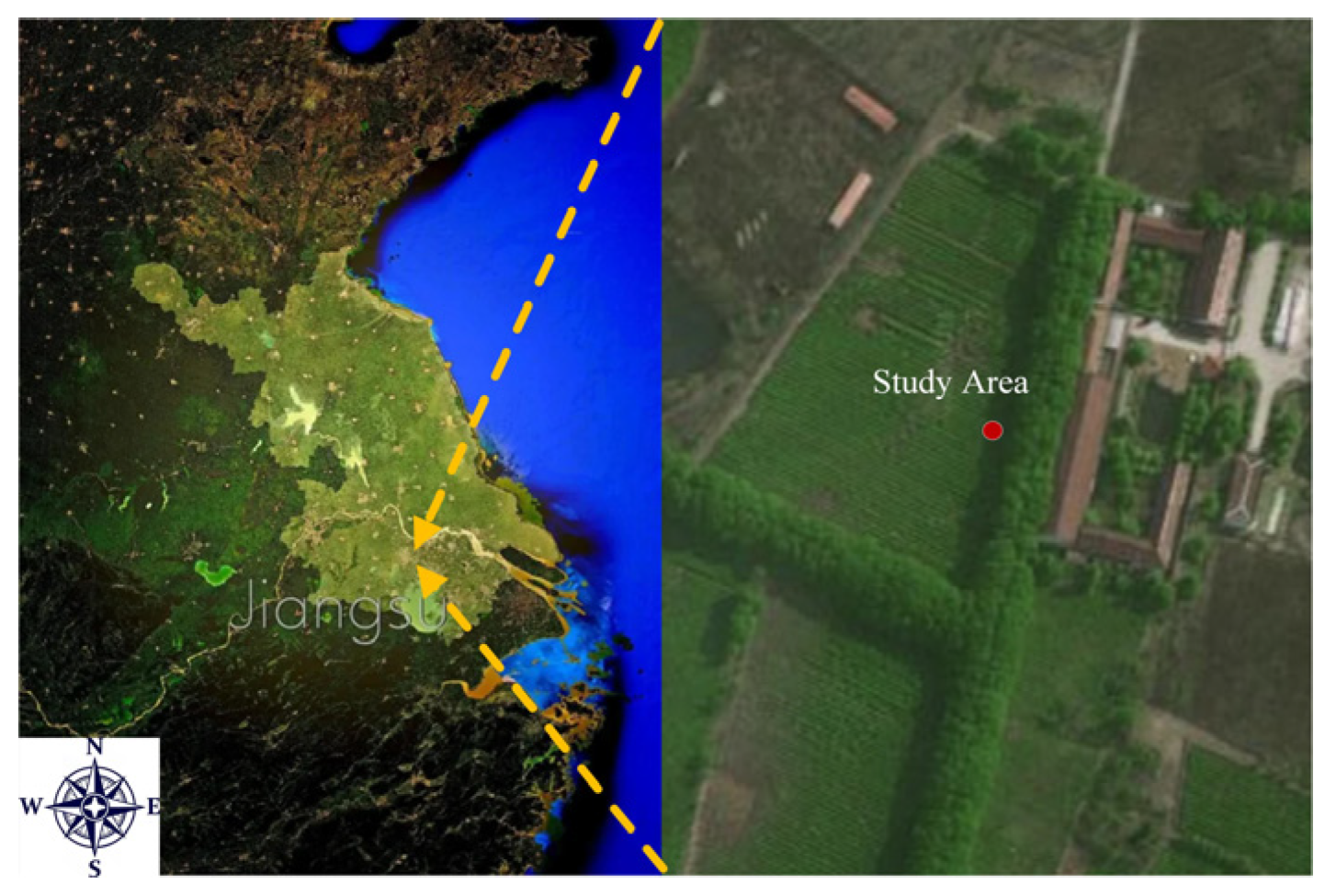
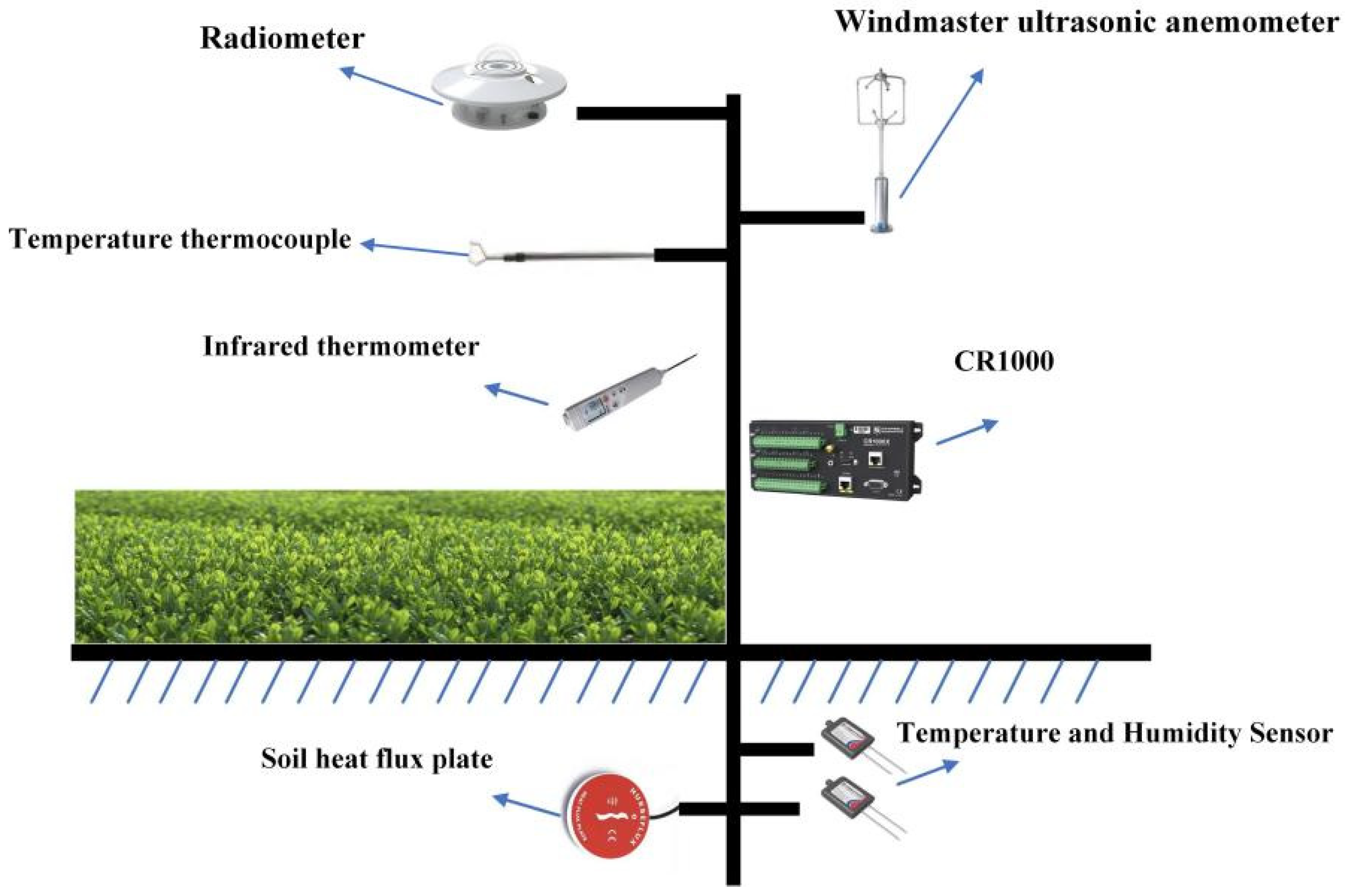
2.1. Test Tea Garden Experiments
2.2. Experimental Design and Data Analysis Methods
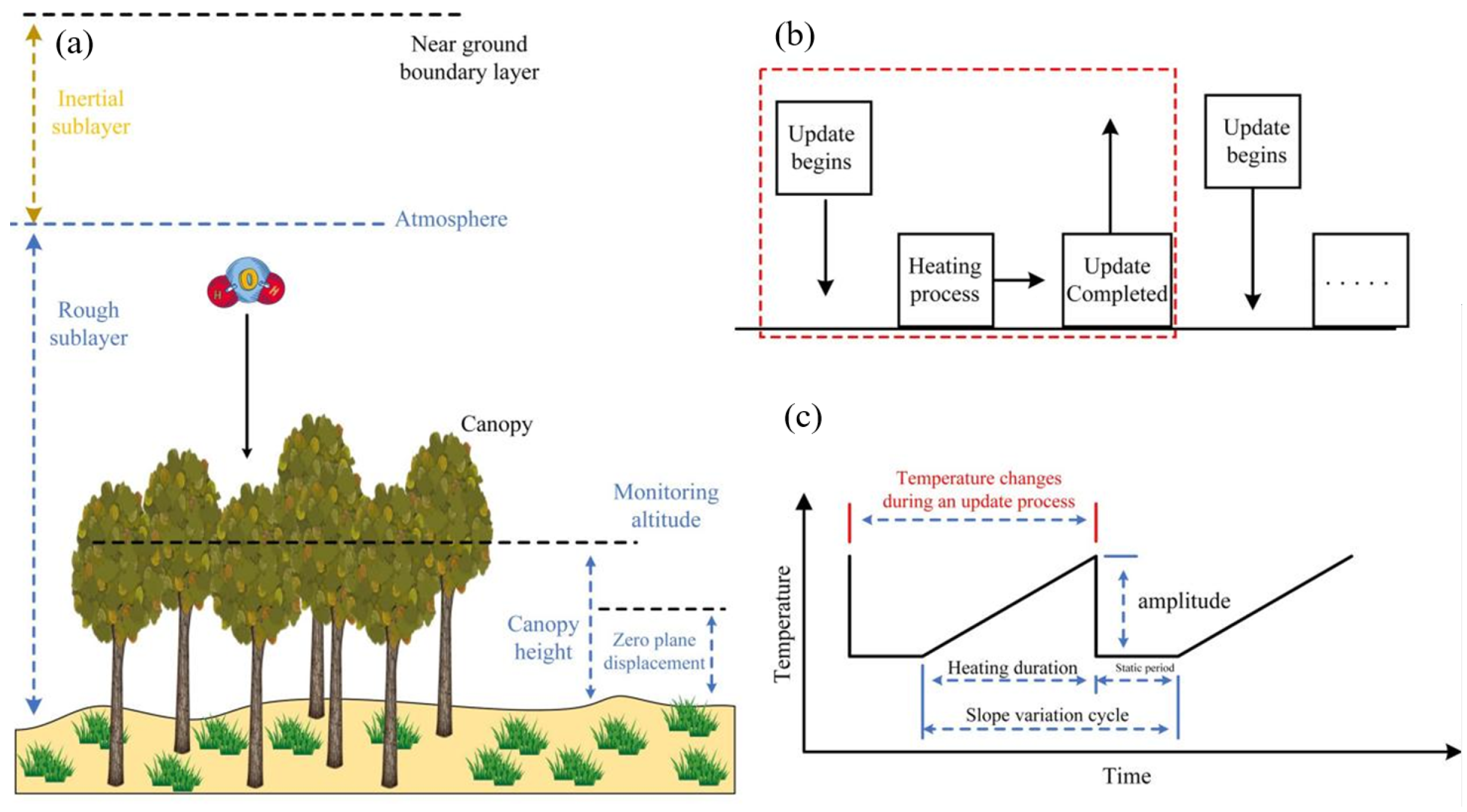
2.3. Estimation of Sensible Heat Flux by the SR Method
2.4. CFD Method for Flow Field Simulation
2.4.1. Model Construction and Mesh Generation
2.4.2. Boundary Condition Setup
2.4.3. Control Equations and Numerical Formats
2.4.4. Verification of Grid Independence
3. Results
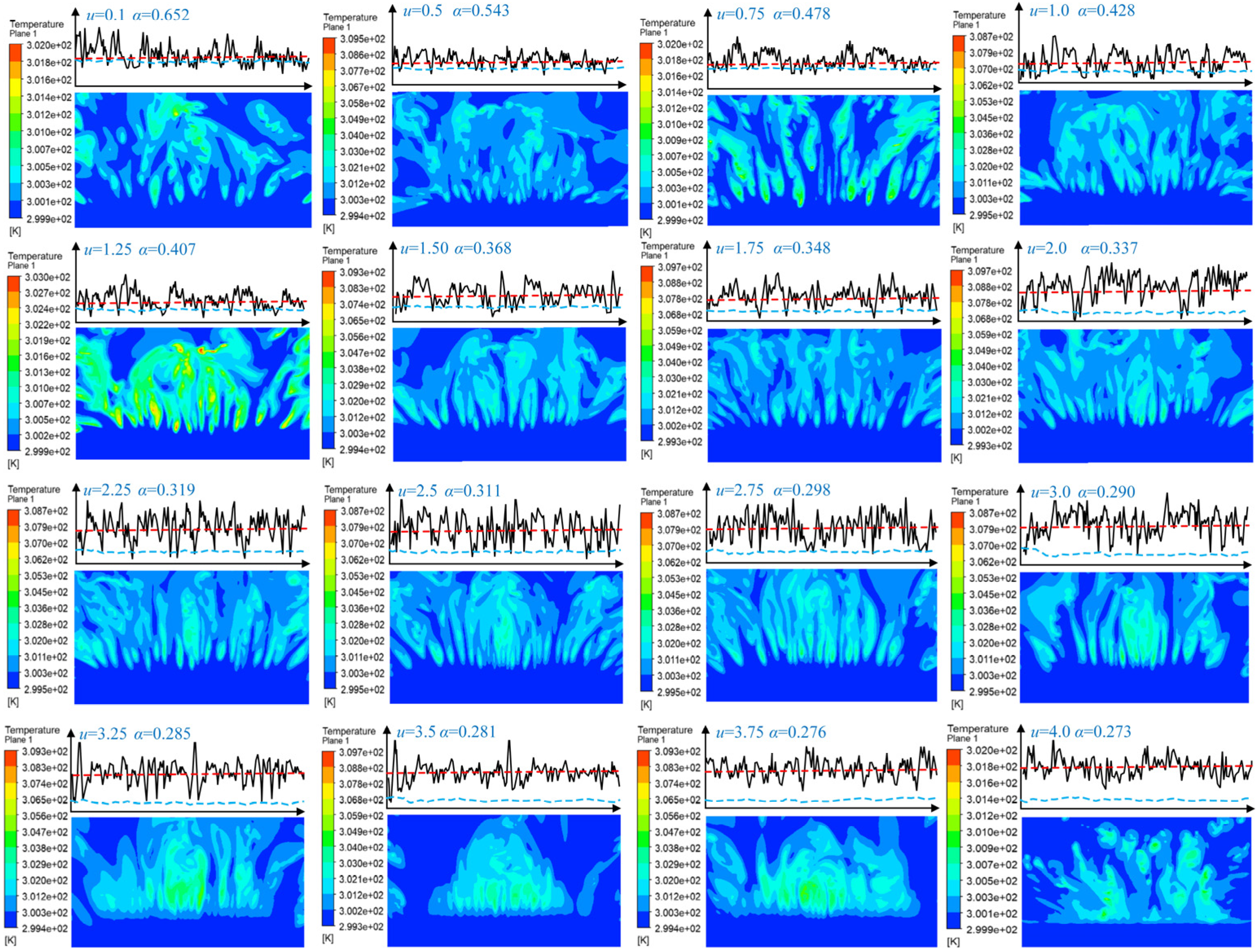
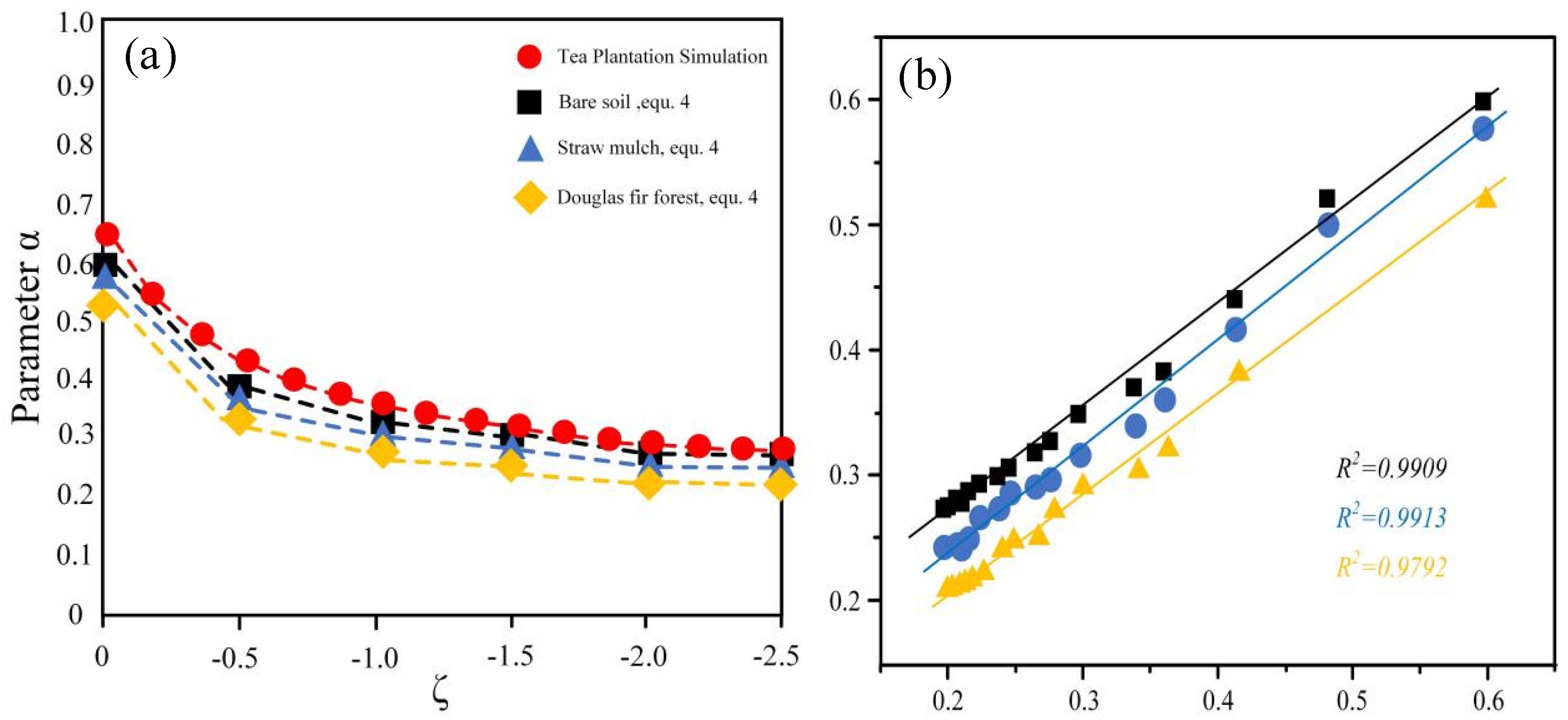
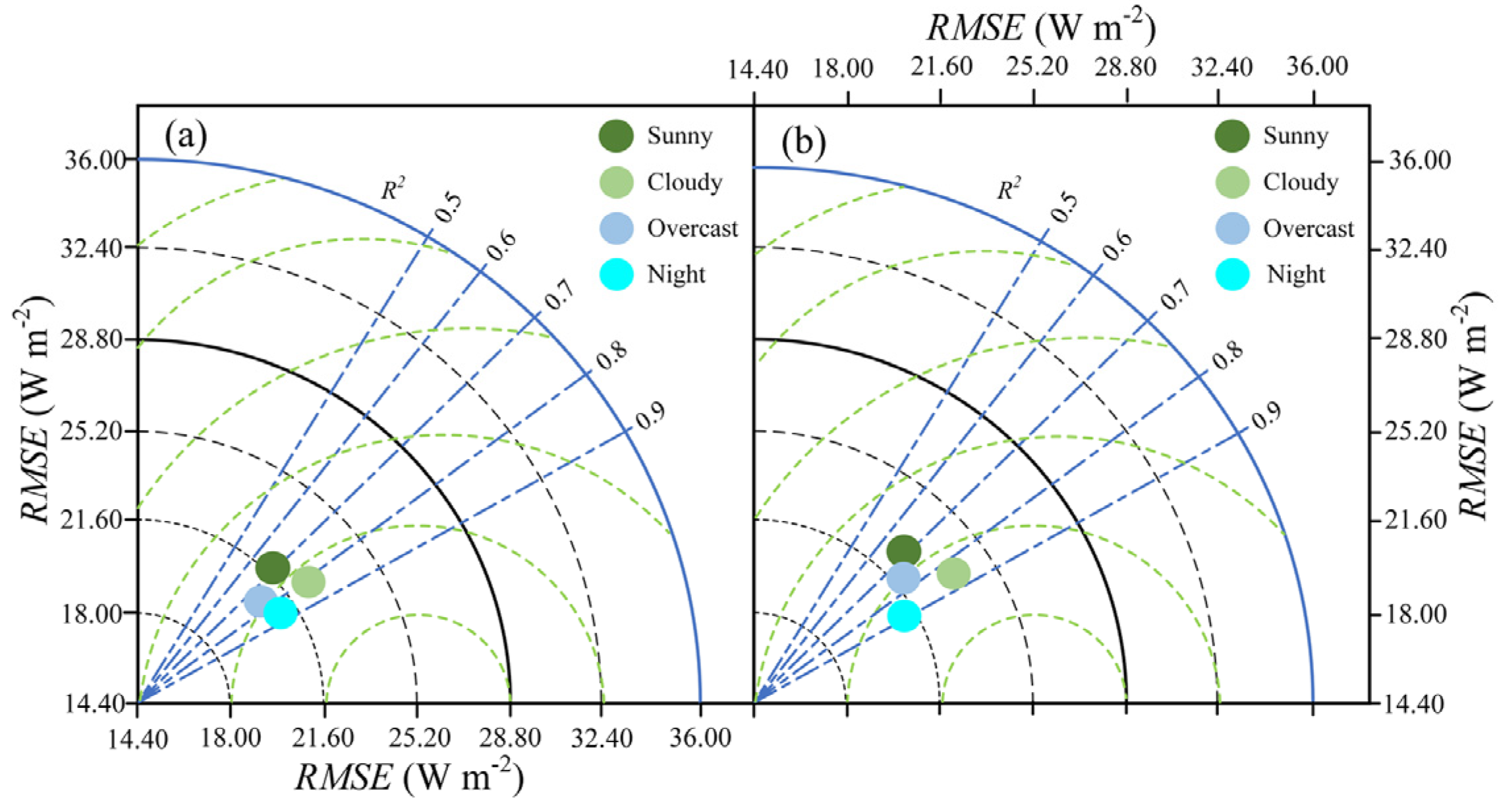
3.1. Extraction and Application of the Flow Field Heat Flux Calibration Coefficient α Based on Large Eddy Simulation
3.2. Study on the Mechanism of the Surface Renewal Theory Based on Large Eddy Simulation
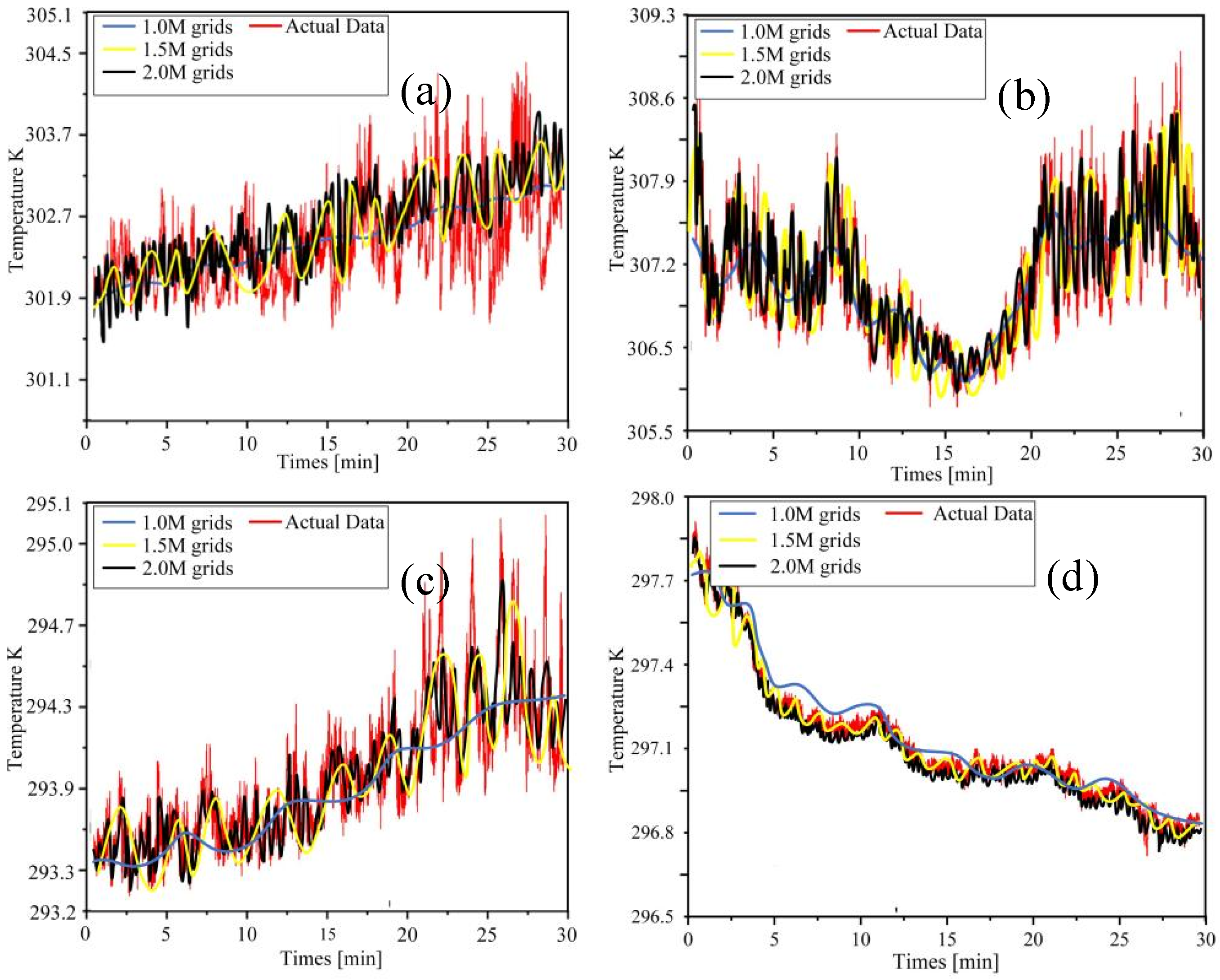
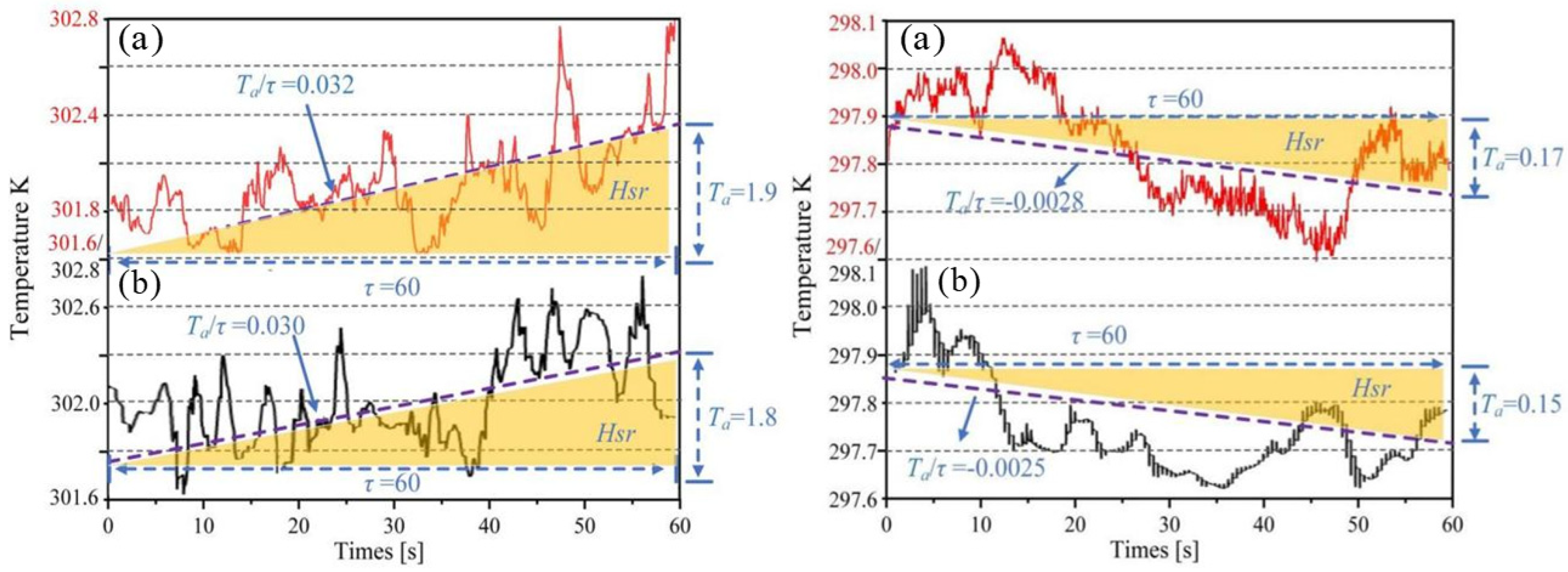
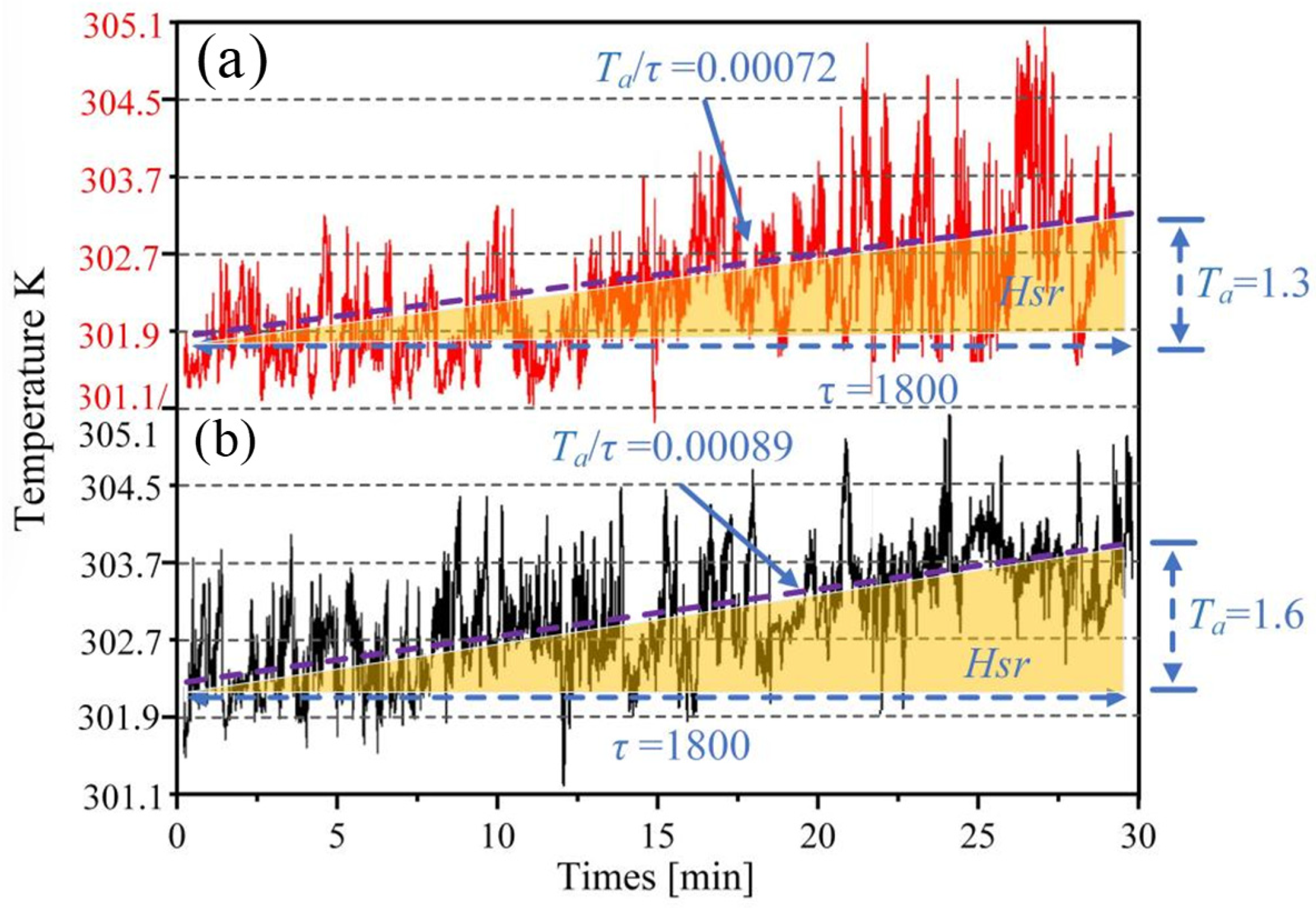
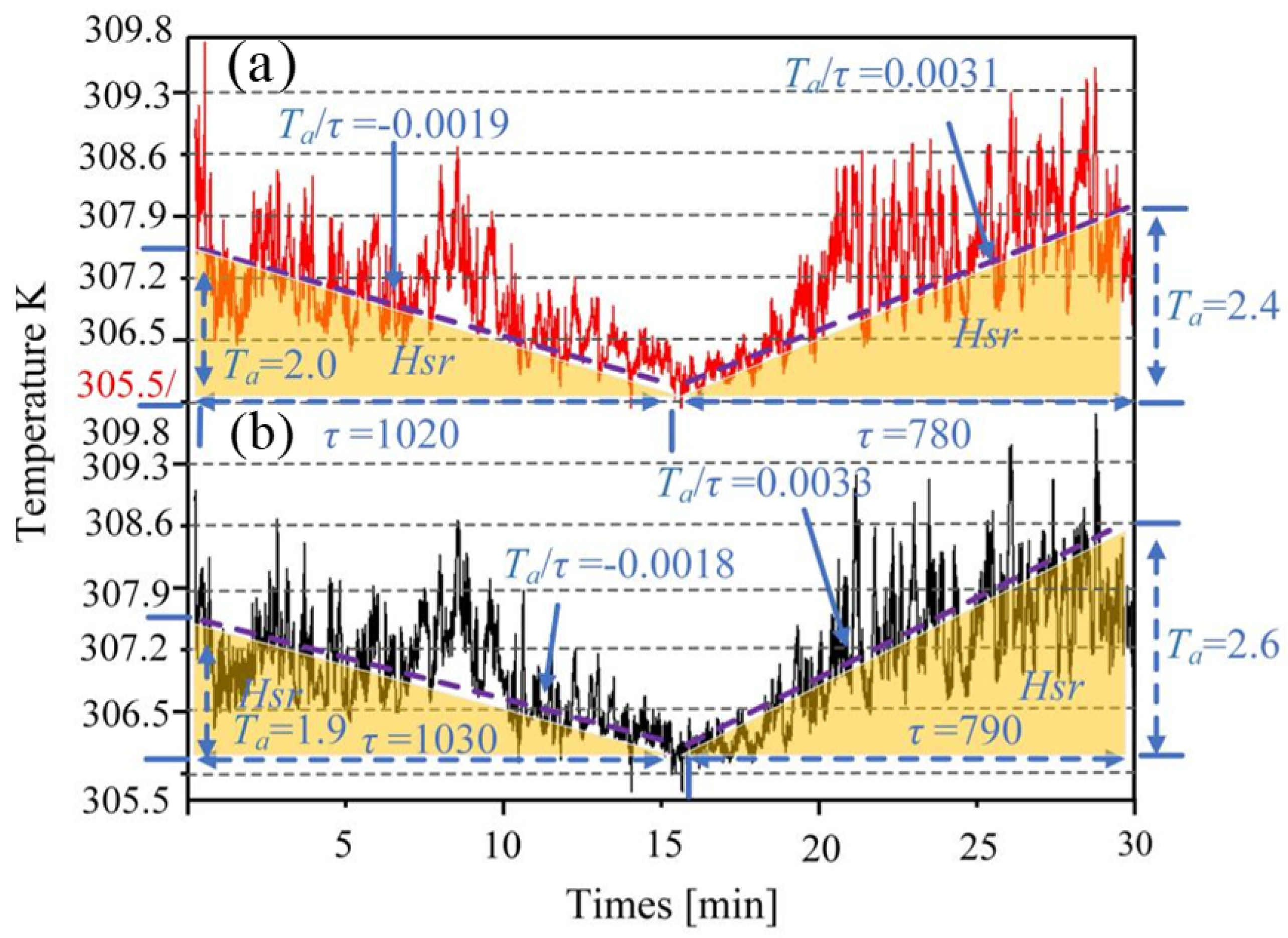
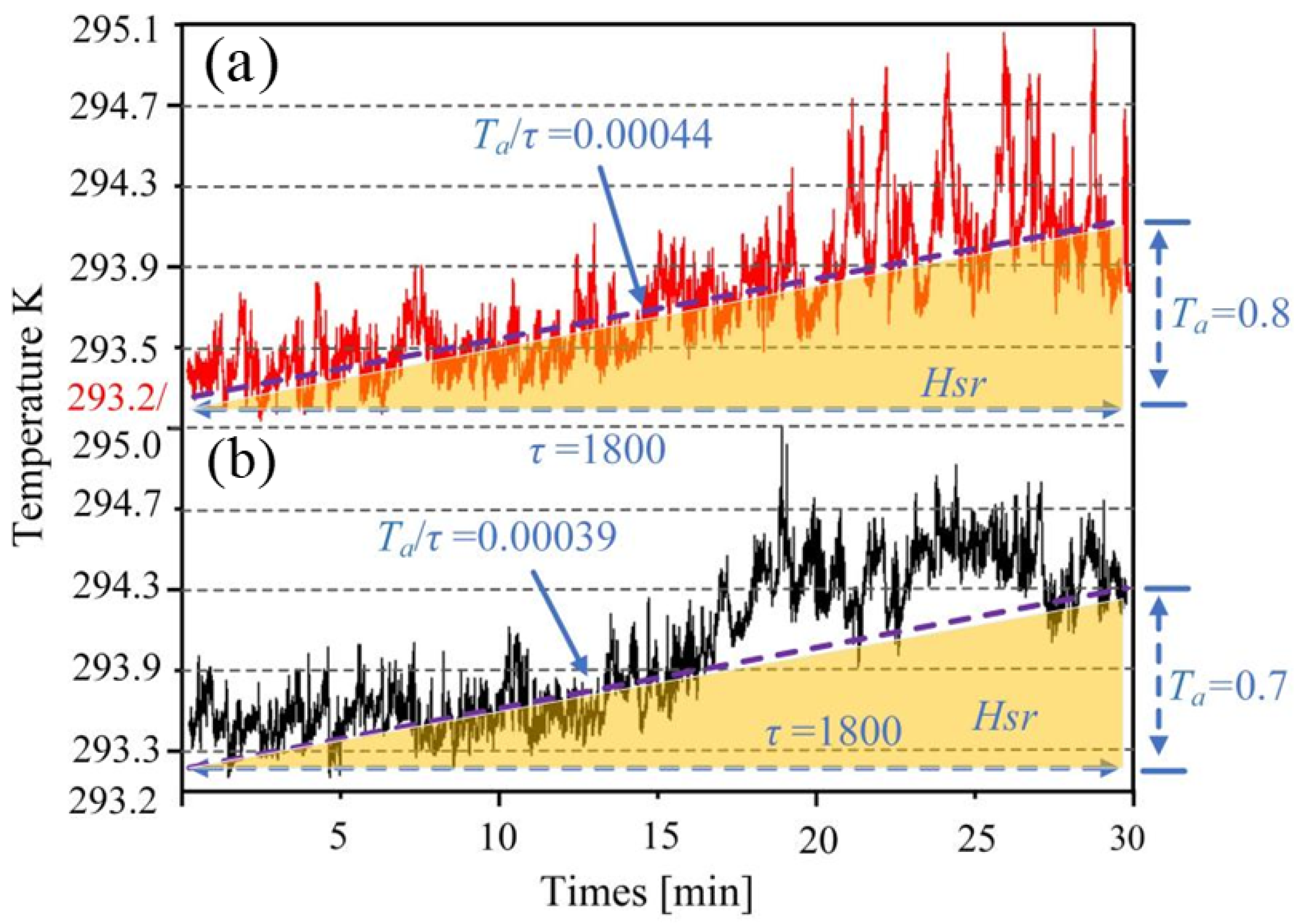
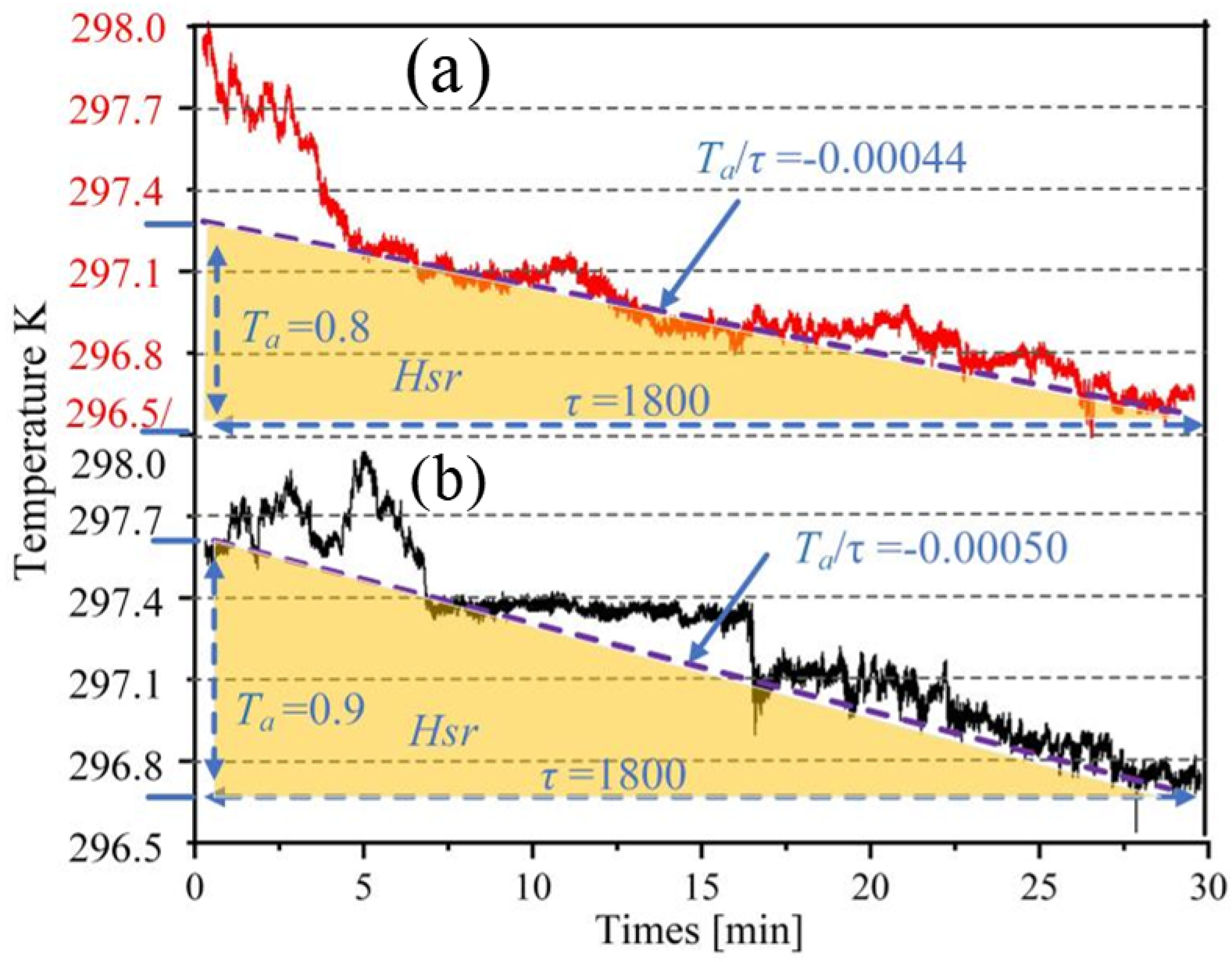
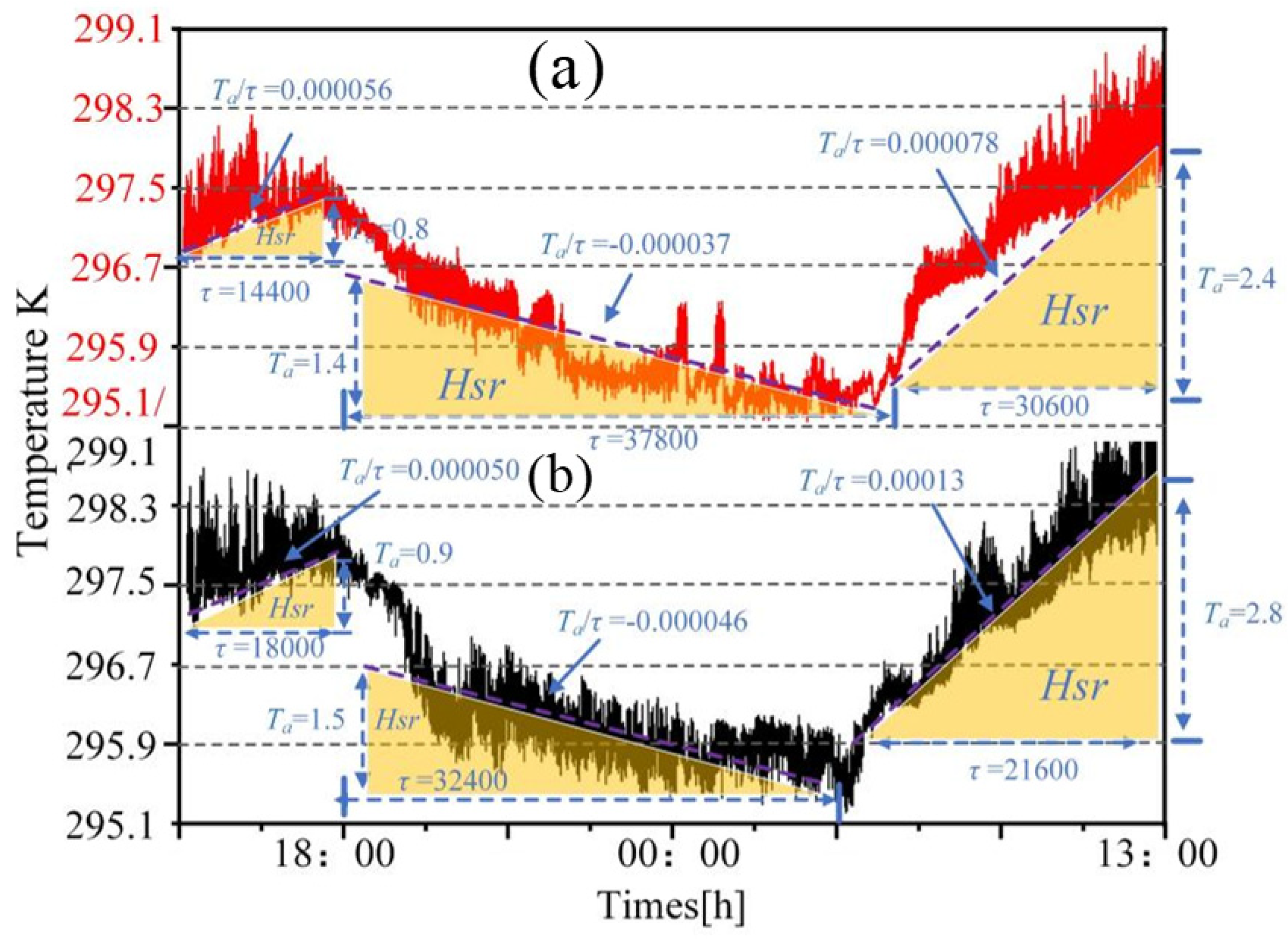
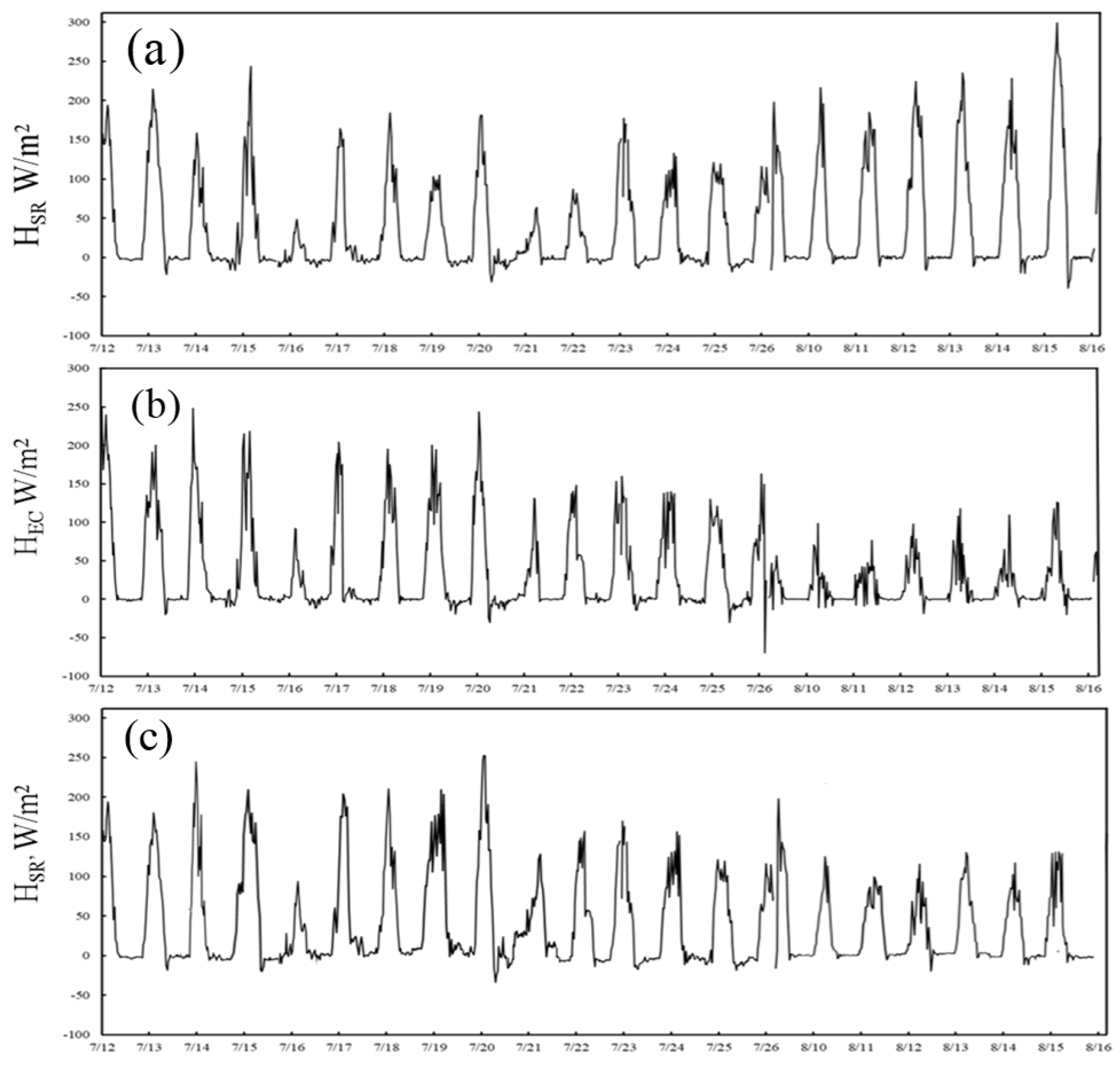
3.3. Analysis of High-Frequency Temperature Results from Actual and Simulated Data at Large Time Scales Under the Large Eddy Simulation
3.4. Analysis of High-Frequency Temperature Results from Actual and Simulated Data at Small and Large Time Scales Under the Large Eddy Simulation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Suvocarev, K.; Castellvi, F.; Reba, M.L. Surface renewal measurements of H, λE and CO2 fluxes over two different agricultural systems. Agric. For. Meteorol. 2019, 279, 107763. [Google Scholar] [CrossRef]
- Maltese, A.; Awada, H.; Capodici, F.; Ciraolo, G.; La Loggia, G.; Rallo, G. On the use of the eddy covariance latent heat flux and sap flow transpiration for the validation of a surface energy balance model. Remote Sens. 2018, 10, 195. [Google Scholar] [CrossRef]
- González-Piqueras, J.; Villodre, J.; Campos, I.; Calera, A.; Balbontín, C. Monitoring the latent and sensible heat fluxes in vineyard by applying the energy balance model METRIC. Rev. Teledetección 2015, 43, 43–54. [Google Scholar] [CrossRef]
- Rajasekaran, E.; Muddu, S.; Bimal, K.; Bhattacharya, S.B. Spatial disaggregation of latent heat flux using contextual models over India. Remote Sens. 2017, 9, 949. [Google Scholar] [CrossRef]
- Paw, U.K.T.; Qiu, J.; Su, H.B.; Watanabe, T. Surface renewal analysis: A new method to obtain scalar fluxes. Agric. For. Meteorol. 1995, 74, 119–137. [Google Scholar] [CrossRef]
- Xiong, Y.J.; Wang, X.; Wu, C.B. Review of surface renewal, a new method for measuring evapotranspiration based on high frequency temperature. Adv. Earth Sci. 2023, 38, 1097–1106. [Google Scholar] [CrossRef]
- Holwerda, F.; Guerrero-Medina, O.; Meesters, A.G.C.A. Evaluating surface renewal models for estimating sensible heat flux above and within a coffee agroforestry system. Agric. For. Meteorol. 2021, 308–309, 108598. [Google Scholar] [CrossRef]
- Castellvi, F.; Gavilan, P.; Gonzalez-Dugo, M.P. Combining the bulk transfer formulation and surface renewal analysis for estimating the sensible heat flux without involving the parameter KB-1. Water Resour. Res. 2014, 50, 8179–8190. [Google Scholar] [CrossRef]
- Parry, C.K.; Shapland, T.M.; Williams, L.E.; Calderon-Orellana, A.; McElrone, A.J. Comparison of a stand-alone surface renewal method to weighing lysimetry and eddy covariance for determining vineyard evapotranspiration and vine water stress. Irrig. Sci. 2019, 37, 737–749. [Google Scholar] [CrossRef]
- Yonatan, M.; Moran, P.; Ori, A.; Josef, T. Application of the surface renewal technique in two types of screenhouses: Sensible heat flux estimates and turbulence characteristics. Agric. For. Meteorol. 2015, 203, 229–242. [Google Scholar] [CrossRef]
- Li, Y.Q.; Shi, C.X.; Shen, R.P.; Li, Y.; Zhang, D.J.; Ge, L.L. Simulation of Near-Surface wind over mentougou with WRF-LES and sensitivity study of planetary boundary layer schemes. Plateau. Meteorol. 2023, 42, 758–770. [Google Scholar] [CrossRef]
- Sun, X.J.; Li, Y.; Zhang, Y.H.; Ning, H.; Tang, J.; Wen, Y.H. Near-surface wind simulation over acrid lakeshore area and sensitivity studies using the WRF-LES. Plateau. Meteorol. 2017, 36, 835–844. [Google Scholar]
- Jonas, W.; Christopher, J.; Marco, G.; Andreas, C.; Dirk, S. Introducing new morphometric parameters to improve urban canopy air flow modeling: A CFD to machine-learning study in real urban environments. Urban Clim. 2024, 58, 102173. [Google Scholar] [CrossRef]
- Zhao, D.; Yin, J.; Pan, X.; Ma, Y.; Ren, X.; Jiang, Y.; Ma, Y.; Gong, C. Large-eddy simulation of the effects of horizontal and vertical adjustments in a wind farm. Front. Energy Res. 2024, 11, 133578. [Google Scholar] [CrossRef]
- Iman, M.D.; Hossein, M.; Smaeyl, H.; Siegfried, R. Large eddy simulation of the combined effect of heat fluxes and wave forcing of summer monsoon on a diurnal ocean mixed layer in the north Arabian Sea. Eur. Phys. J. Plus 2024, 139, 984. [Google Scholar] [CrossRef]
- Santoni, C.; García-Cartagena, E.; Ciri, U.; Iungo, G.; Leonardi, S. Coupling of mesoscale Weather Research and Forecasting model to a high fidelity Large Eddy Simulation. J. Phys. Conf. Ser. 2018, 1037, 062010. [Google Scholar] [CrossRef]
- Castellvi, F. Combining surface renewal analysis and similarity theory: A new approach for estimating sensible heat flux. Water Resour. Res. 2004, 40, 1–20. [Google Scholar] [CrossRef]
- Shapland, T.M.; Snyder, R.L.; Paw, U.K.T.; McElrone, A.J. Thermocouple frequency response compensation leads to convergence of the surface renewal alpha calibration. Agric. For. Meteorol. 2014, 189, 36–47. [Google Scholar] [CrossRef]
- Hu, H.J.; Lu, Y.Z.; Hu, Y.G.; Ding, R.S. Evaluation of two surface renewal methods for calculating the sensible heat flux over a tea field ecosystem in hilly terrain. Agronomy 2023, 13, 1302. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Z.M.; Huang, G.; Xue, X.W. Local wind simulation over complex terrain of Chongli using WRF-LES. Plateau Meteorol. 2023, 42, 197–209. [Google Scholar] [CrossRef]
- Mohammad, B.S. Large eddy simulation of vorticity in compressible turbulent mixing layer concentrating on steam flow in solar system. Prog. Sol. Energy Eng. Syst. 2017, 1, 17–23. [Google Scholar] [CrossRef]
- George, H.B.; Nathan, A.D.; David, S.N.; Richard, R. An eddy injection method for large-eddy simulations of tornado-like vortices. Mon. Weather Rev. 2017, 145, 1937–1961. [Google Scholar] [CrossRef]
- Fang, H.W.; Bai, J.; He, G.J.; Zhao, H.M. Calculations of nonsubmerged groin flow in a shallow open channel by large-eddy simulation. J. Eng. Mech. 2013, 140, 04014016. [Google Scholar] [CrossRef]
- Liu, H.P.; Liu, C.; Zhou, Y.; Zhang, Q.Y.; Desai, A.R.; Ghannam, K.; Huang, J.P.; Katul, G.G. Is there a scalar atmospheric surface layer within a convective boundary layer? Implications for flux measurements. Geophys. Res. Lett. 2025, 52, e2024GL112619. [Google Scholar] [CrossRef]
- Gao, Z.M.; Liu, H.P.; Russel, E.S.; Huang, J.P.; Foken, T.; Oncley, S.P. Large eddies modulating flux convergence and divergence in a disturbed unstable atmospheric surface layer. J. Geophys. Res. Atmos. 2016, 121, 1475–1492. [Google Scholar] [CrossRef]
- Sanemitsu, T.; Wang, W.; Ikegaya, N. Impact of momentum sources on pedestrian-level peak wind predictions of an urban-like array using large-eddy simulations and statistical models. Build. Environ. 2025, 267, 112244. [Google Scholar] [CrossRef]
- Buttar, N.A.; Yongguang, H.; Tanny, J.; Akram, M.W.; Shabbir, A. Fetch effect on flux-variance estimations of sensible and latent heat fluxes of Camellia sinensis. Atmosphere 2019, 10, 299. [Google Scholar] [CrossRef]
- Hassan, M.W.; Al-Asadi, K.A.W.H. Analysis of large-scale correlations on temperatures over Iraq. Arab Gulf J. Sci. Res. 2023, 41, 2–17. [Google Scholar] [CrossRef]
- Hu, Y.G.; Noman, A.B.; Tanny, J.; Snyder, R.L.; Savage, M.J.; Lakhiar, I.A. Surface renewal application for estimating evapotranspiration: A review. Adv. Meteorol. 2018, 13, 1–11. [Google Scholar] [CrossRef]
- Xiong, Y.J.; Chen, X.H.; Tang, L.; Wang, H. Comparison of surface renewal and Bowen ratio derived evapotranspiration measurements in an arid vineyard. J. Hydrol. 2022, 613, 128474. [Google Scholar] [CrossRef]
- Yavuz, V. An analysis of atmospheric stability indices and parameters under air pollution conditions. Environ. Monit. Assess. 2023, 195, 934. [Google Scholar] [CrossRef]
- Bhatia, N.; Pullanagari, R.R.; Cumming, G.S. Propagation of atmospheric condition parameter uncertainty in measurements of landscape heterogeneity. Int. J. Remote Sens. 2021, 42, 8345–8364. [Google Scholar] [CrossRef]
- Carsten, A.; Amber, M.H.; Adam, H.M. A prototype stochastic parameterization of regime behaviour in the stably stratified atmospheric boundary layer. Nonlinear Process. Geophys. 2019, 26, 401–427. [Google Scholar] [CrossRef]
- Fletcher, C.G.; Kravitz, B.; Badawy, B. Quantifying uncertainty from aerosol and atmospheric parameters and their impact on climate sensitivity. Atmos. Chem. Phys. 2018, 18, 17529–17543. [Google Scholar] [CrossRef]
- Zhang, Y.; Yasutake, D.; Hidaka, K.; Kimura, K.; Okayasu, T.; Kitano, M.; Hirota, T. Eco-friendly strategy for CO2 enrichment performance in commercial greenhouses based on the CO2 spatial distribution and photosynthesis. Sci. Rep. 2023, 13, 17277. [Google Scholar] [CrossRef]
- Zhang, L.X.; Jia, J.; Luan, T. Effects of rough strips on surface wind loads and aerodynamic forces on high-rise buildings. J. Aerosp. Eng. 2025, 38, 04025032. [Google Scholar] [CrossRef]
- Muhammad, R.B.S.; Mohammad, H.D.; Wei, B.C.; Zheng, L. Large eddy simulation of wind farm performance in horizontally and vertically staggered layouts. Energy 2025, 322, 135569. [Google Scholar] [CrossRef]
- Zheng, D.; Wu, X.; Zhu, Y.; Ma, W.; Fang, P. Large eddy simulation of flow around twin tower buildings in tandem arrangements with upstream corner modification. Atmosphere 2024, 15, 1540. [Google Scholar] [CrossRef]
- Usman, S.; Jasna, B.J.; Naoki, I.; Knut, E.T.G. Validation of large eddy simulations in urban wind studies using a new overall area metric. Build. Environ. 2025, 267, 112285. [Google Scholar] [CrossRef]
- Kermani, A.; Shen, L. Surface age of surface renewal in turbulent interfacial transport. Geophys. Res. Lett. 2009, 36, 123–156. [Google Scholar] [CrossRef]
- Lu, J.X.; Ning, C.Z.; Wu, F.; Liu, X.B.; Luo, K. Dynamic mode decomposition based investigation of unsteady flow characteristics and pressure pulsations in centrifugal pumps operating under partial load conditions for scientific advancement. Flow Meas. Instrum. 2025, 103, 102850. [Google Scholar] [CrossRef]
- Spano, D.; Snyder, R.L.; Duce, P.; Paw, U.K.T. Estimating sensible and latent heat flux densities from grapevine canopies using surface renewal. Agric. For. Meteorol. 2000, 104, 171–183. [Google Scholar] [CrossRef]
- Shapland, T.M.; McElrone, A.J.; Snyder, R.L.; Paw, U.K.T. Structure function analysis of two-scale scalar ramps. Part I: Theory and modelling. Bound.-Layer Meteorol. 2012, 145, 5–25. [Google Scholar] [CrossRef]
- Parry, C.K.; Kustas, W.P.; Knipper, K.R.; Anderson, M.C.; Alfieri, J.G.; Prueger, J.H.; McElrone, A.J. Comparison of vineyard evapotranspiration estimates from surface renewal using measured and modelled energy balance components in the GRAPEX project. Irrig. Sci. 2019, 37, 333–343. [Google Scholar] [CrossRef]
- Chen, W.J.; Nvak, M.D.; Black, T.A.; Lee, X.H. Coherent eddies and temperature structure functions for three contrasting surfaces. part II: Renewal model for sensible heat flux. Bound.-Layer Meteorol. 1997, 84, 125–147. [Google Scholar] [CrossRef]
| Material | Specific Heat Capacity (J·kg−1·K−1) | Coefficient of Thermal Conductivity (W·m) | Absorption Coefficient | Scattering Coefficient | Emissivity |
|---|---|---|---|---|---|
| Air | 1006.43 | 0.0242 | 0.2 | 0 | - |
| Soil | 2200 | 2 | 0.5 | 1 | 0.9 |
| Plantation | 1465 | 1.12 | 0.48 | 0.8 | 0.9 |
| Water vapor | 1850 | 0.025 | 0.42 | 0.7 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Hu, Y.; Lu, Y.; Fu, Y.; Wang, J. A New Approach to Sensible Heat Flux via CFD-Surface Renewal Integration. Agronomy 2025, 15, 2708. https://doi.org/10.3390/agronomy15122708
Li Y, Hu Y, Lu Y, Fu Y, Wang J. A New Approach to Sensible Heat Flux via CFD-Surface Renewal Integration. Agronomy. 2025; 15(12):2708. https://doi.org/10.3390/agronomy15122708
Chicago/Turabian StyleLi, Yang, Yongguang Hu, Yongzong Lu, Yihui Fu, and Jizhang Wang. 2025. "A New Approach to Sensible Heat Flux via CFD-Surface Renewal Integration" Agronomy 15, no. 12: 2708. https://doi.org/10.3390/agronomy15122708
APA StyleLi, Y., Hu, Y., Lu, Y., Fu, Y., & Wang, J. (2025). A New Approach to Sensible Heat Flux via CFD-Surface Renewal Integration. Agronomy, 15(12), 2708. https://doi.org/10.3390/agronomy15122708










