Disturbance Characteristics of Subsoiling in Paddy Soil Based on Smoothed Particle Hydrodynamics (SPH)
Abstract
1. Introduction
2. Materials and Methods
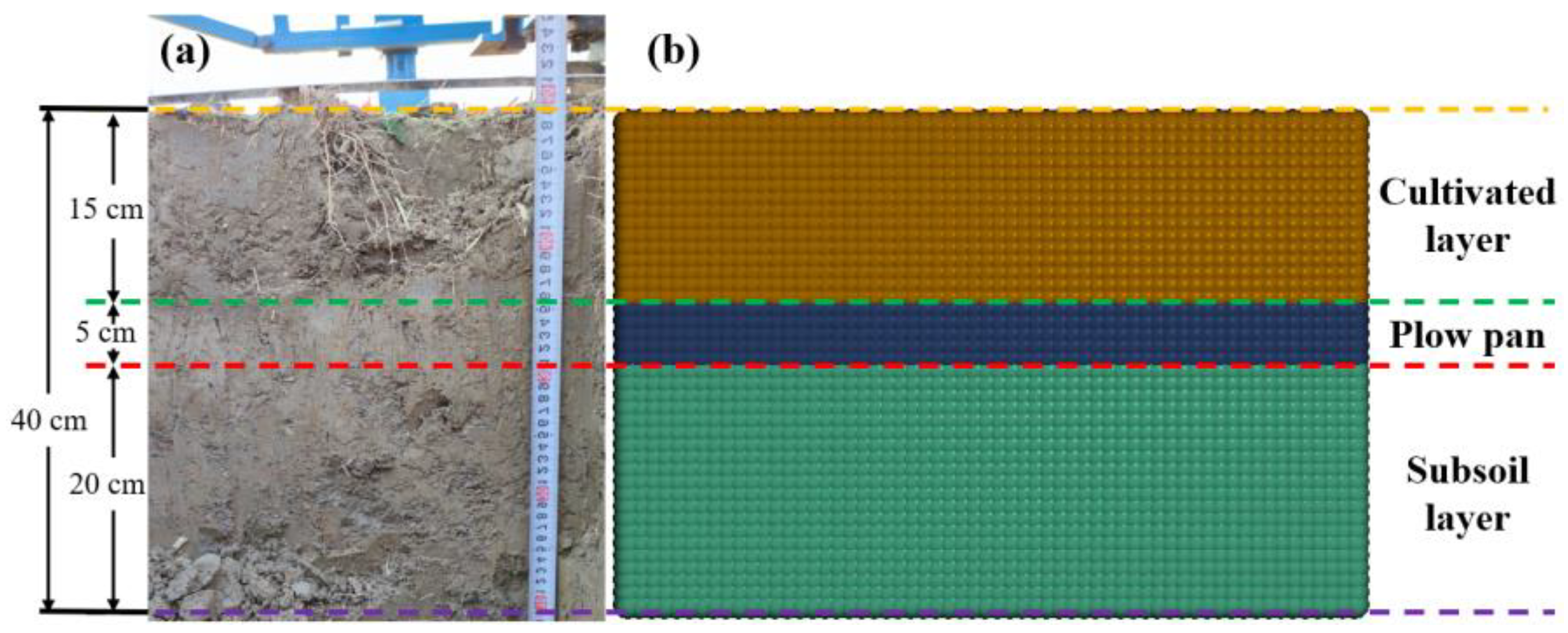
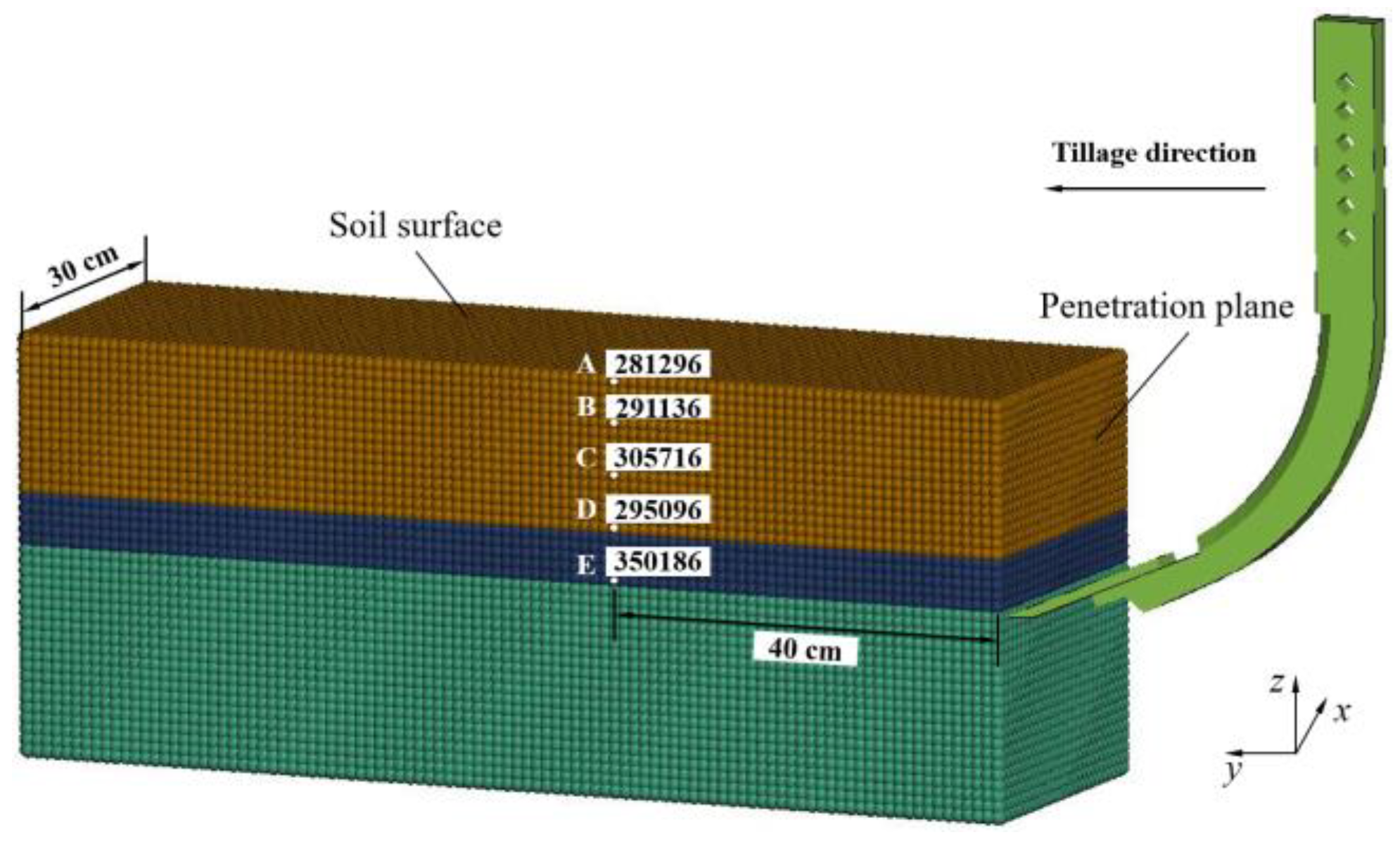
2.1. Experimental Site
2.2. Experimental Method
2.3. Smoothed Particle Hydrodynamics Model
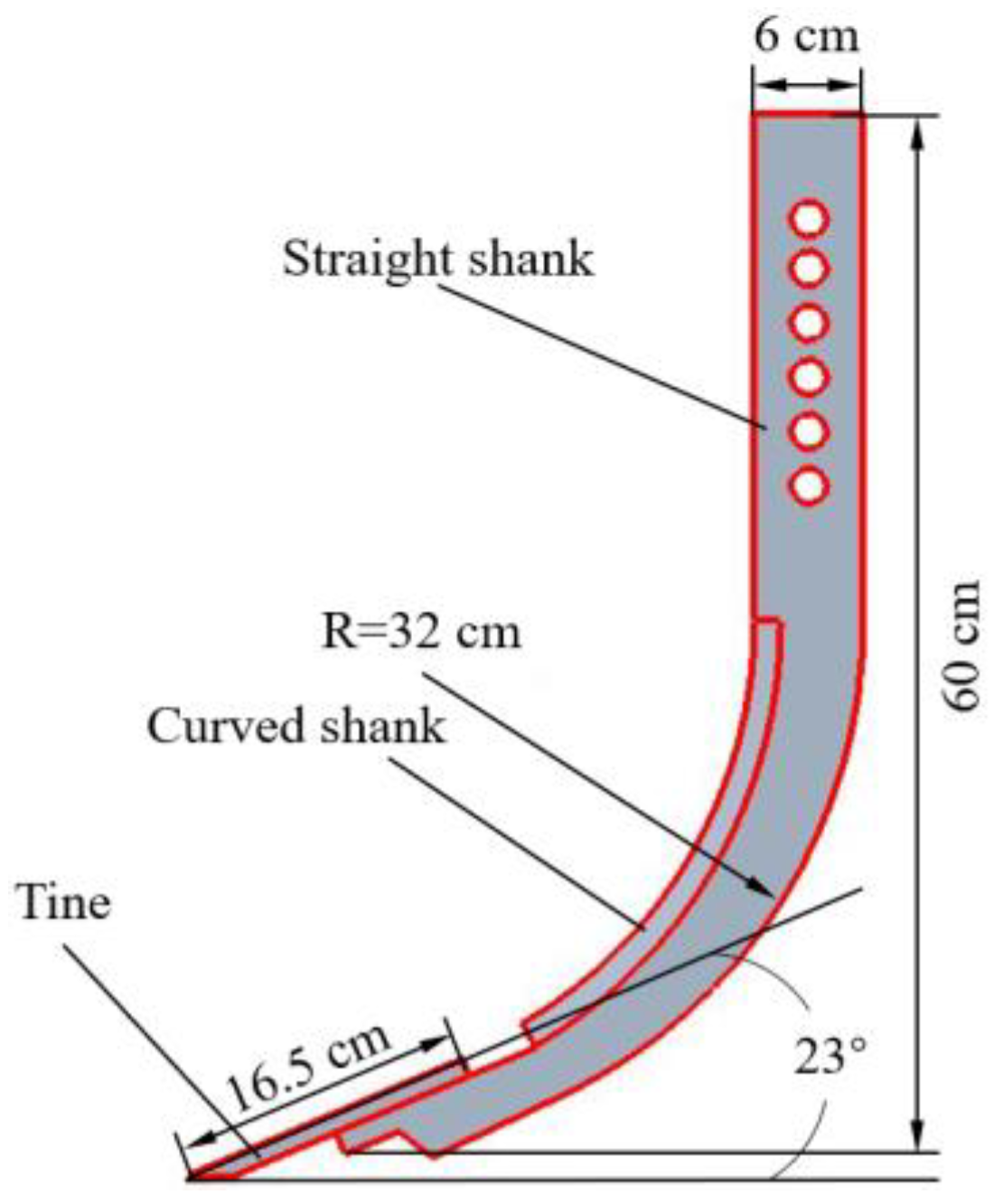
2.3.1. Subsoiler Model
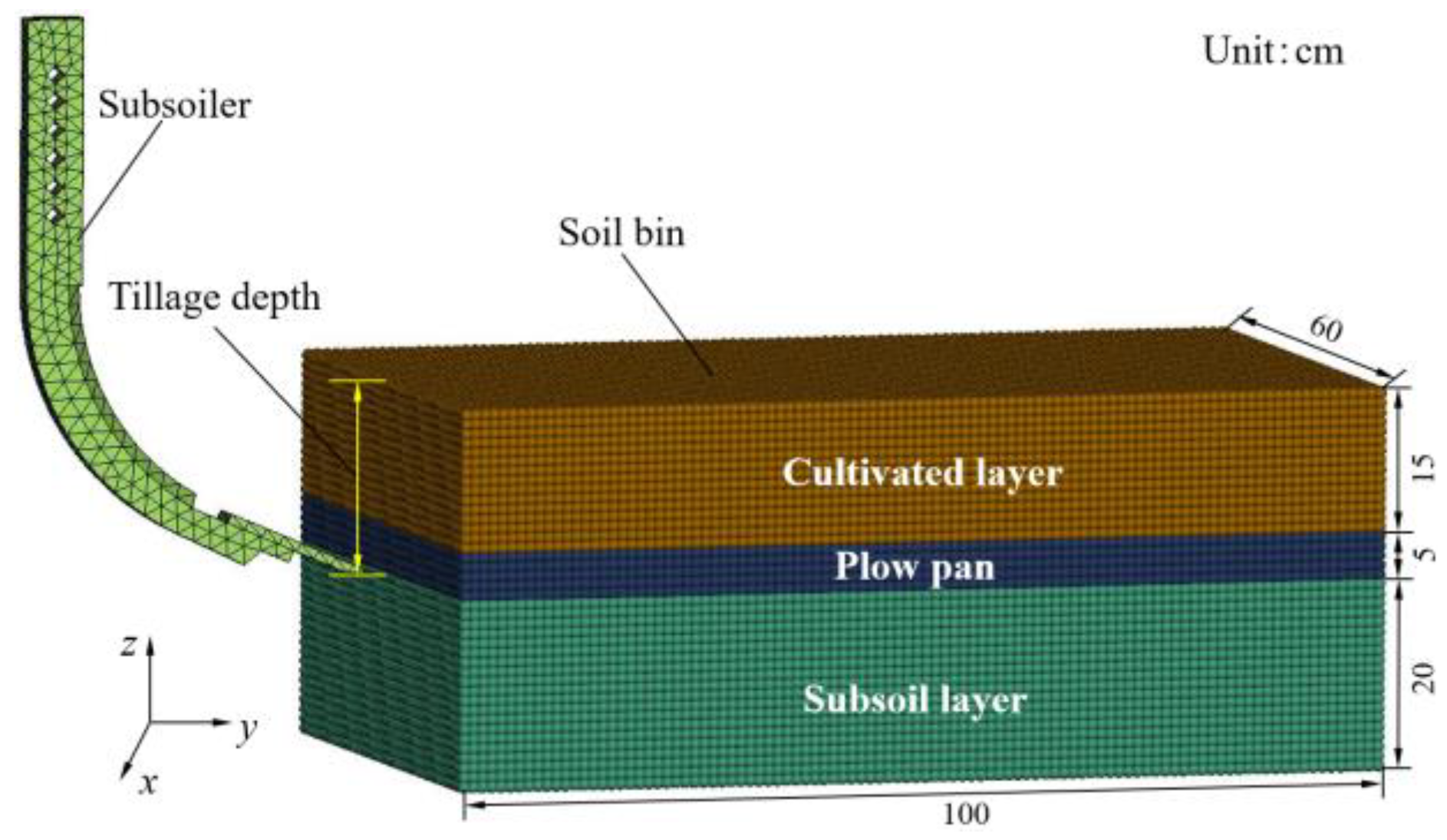
2.3.2. Soil Bin Model
2.3.3. Material Model
2.3.4. Numerical Calculation Model
2.3.5. Data Analysis
3. Results
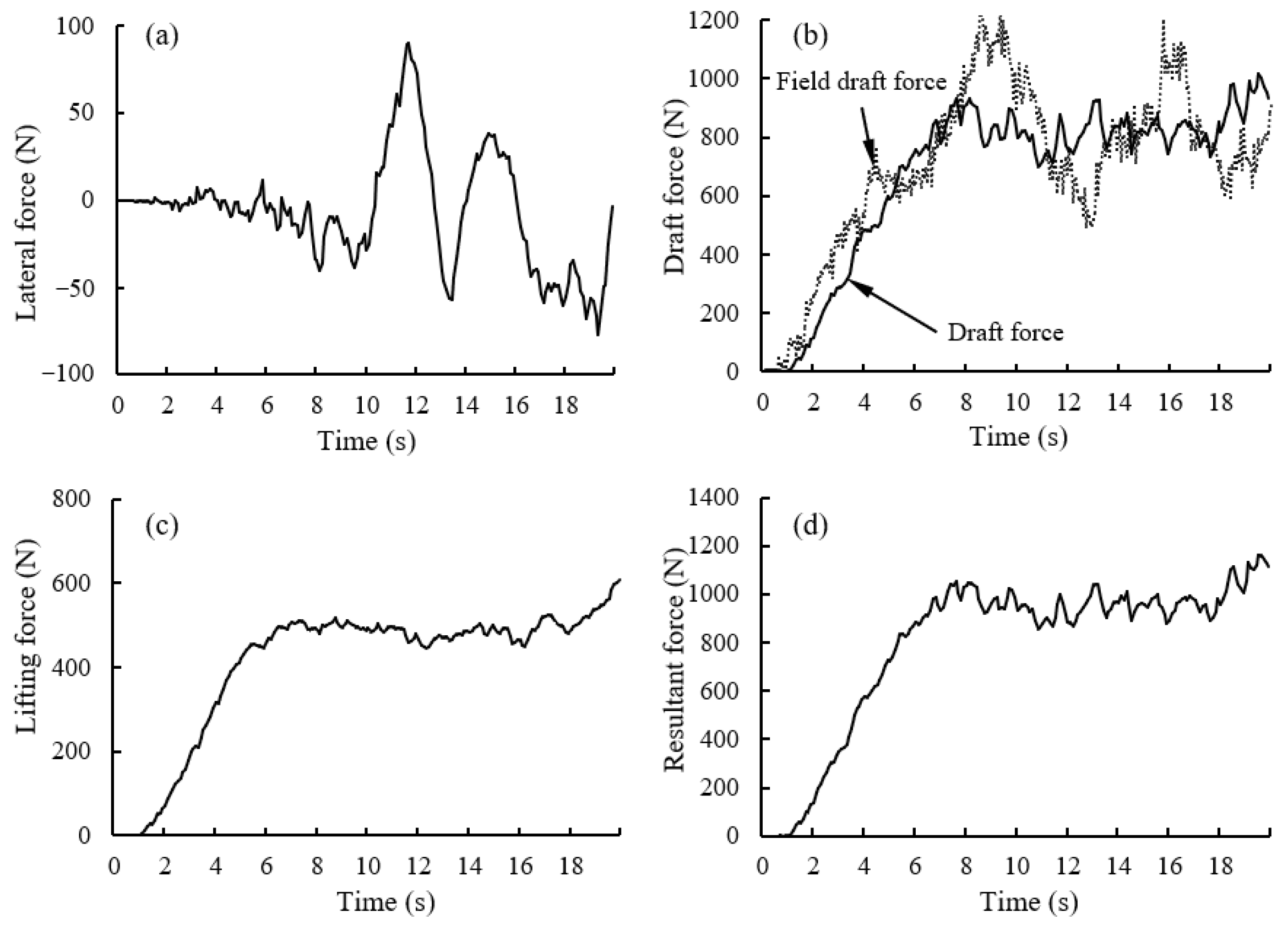
3.1. Draft Force
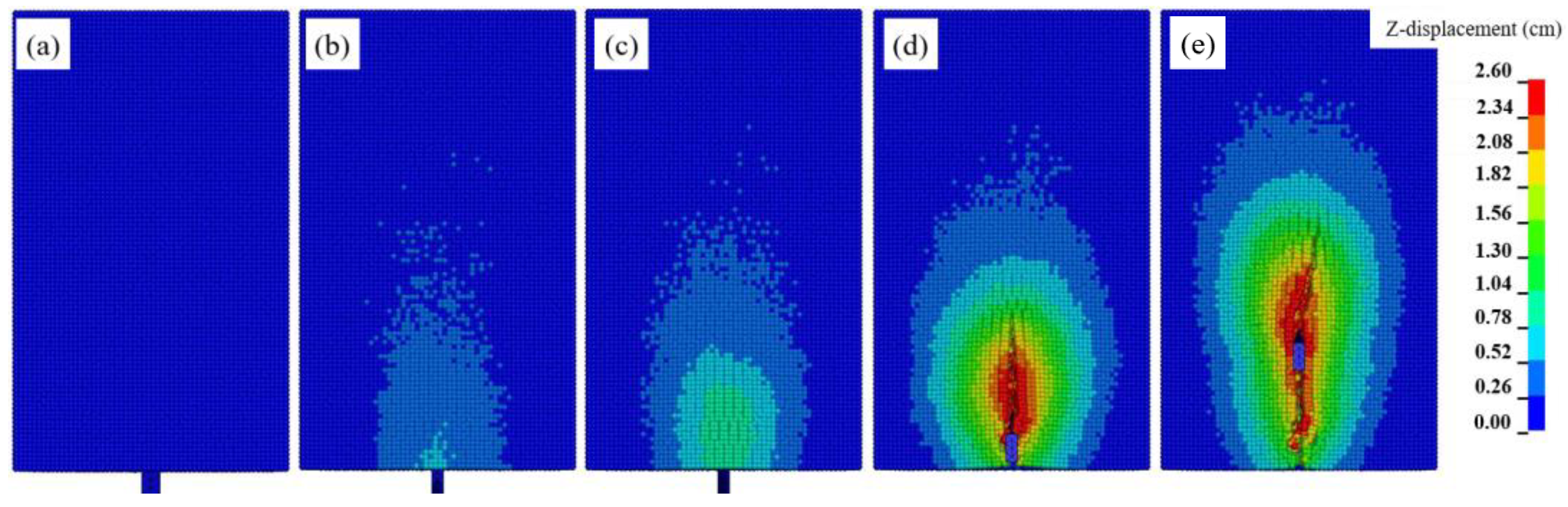
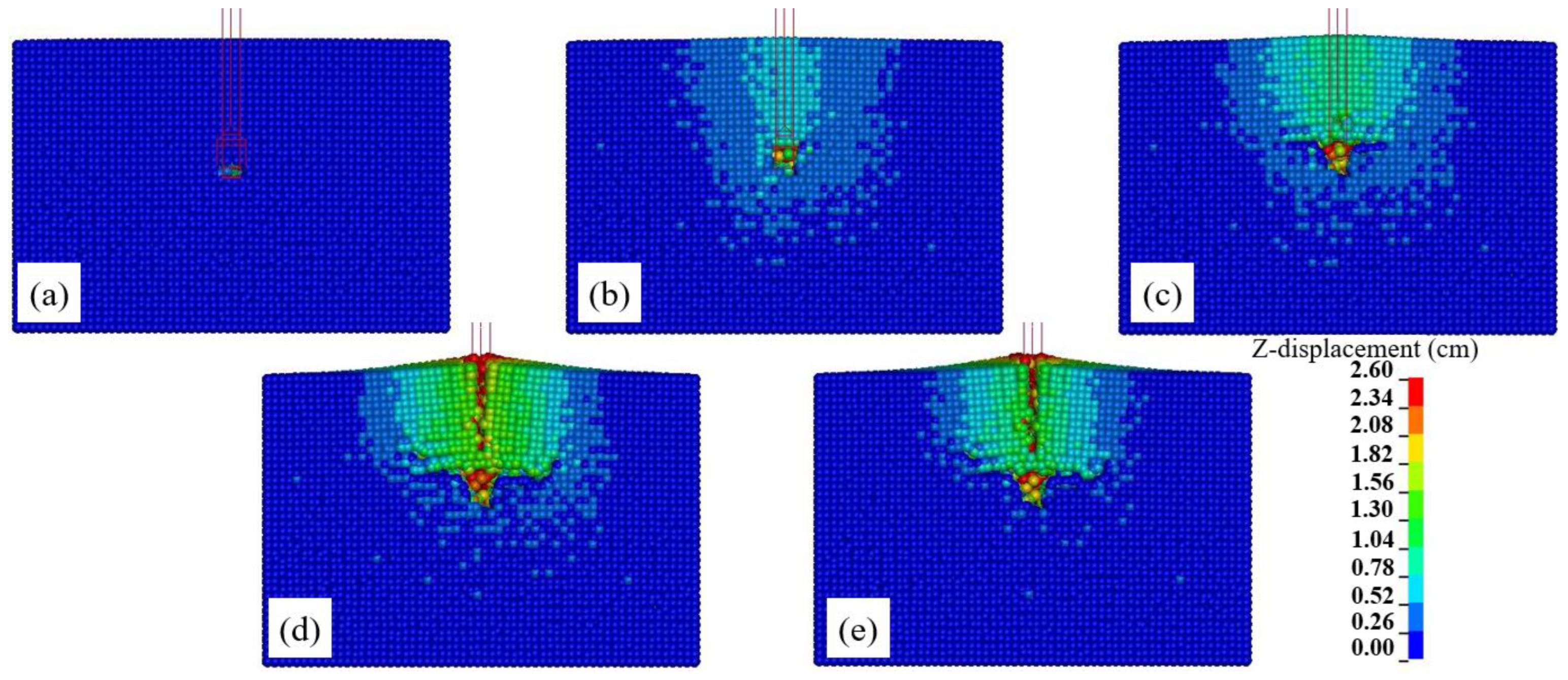
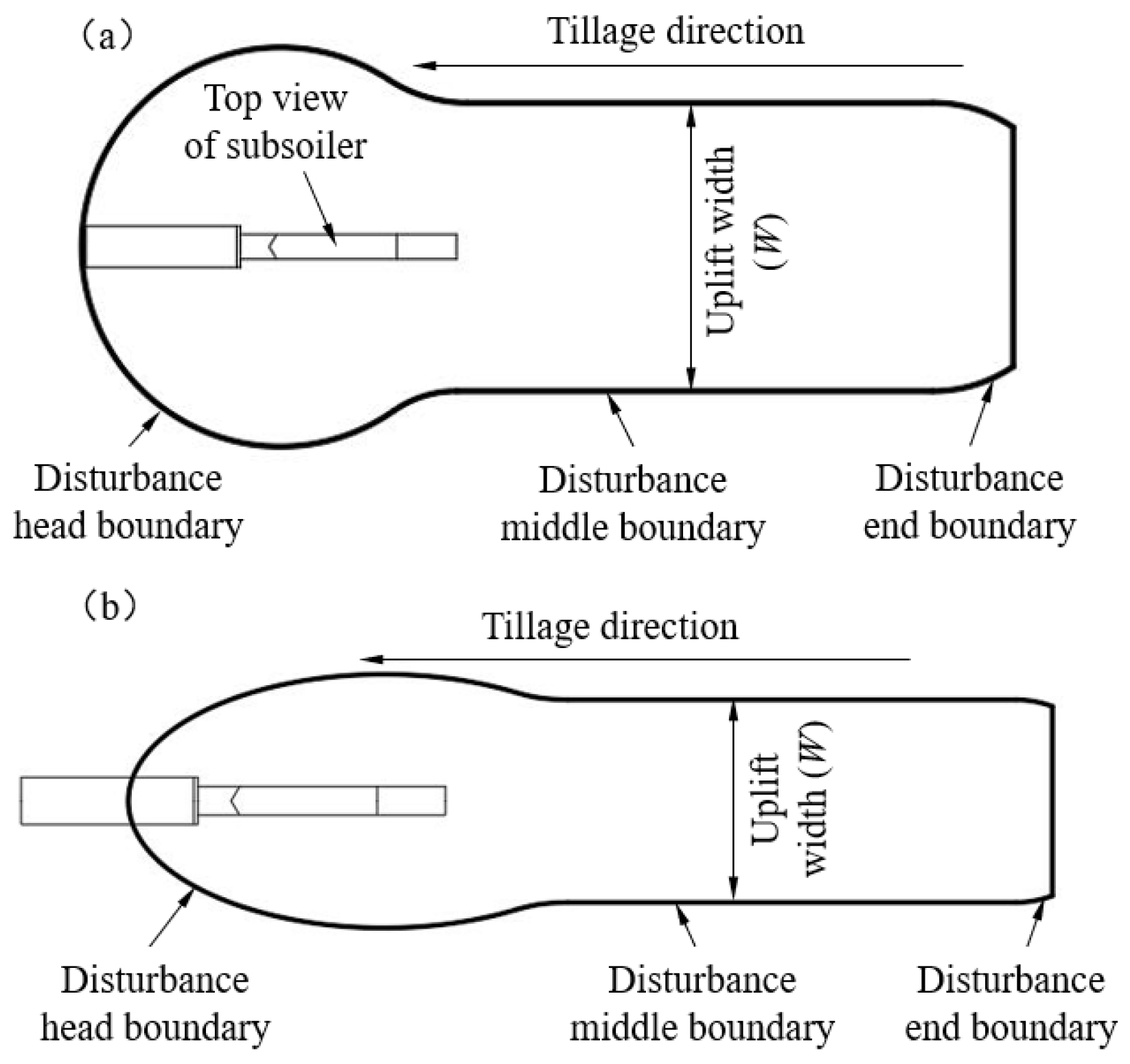
3.2. Soil Disturbance Characteristics
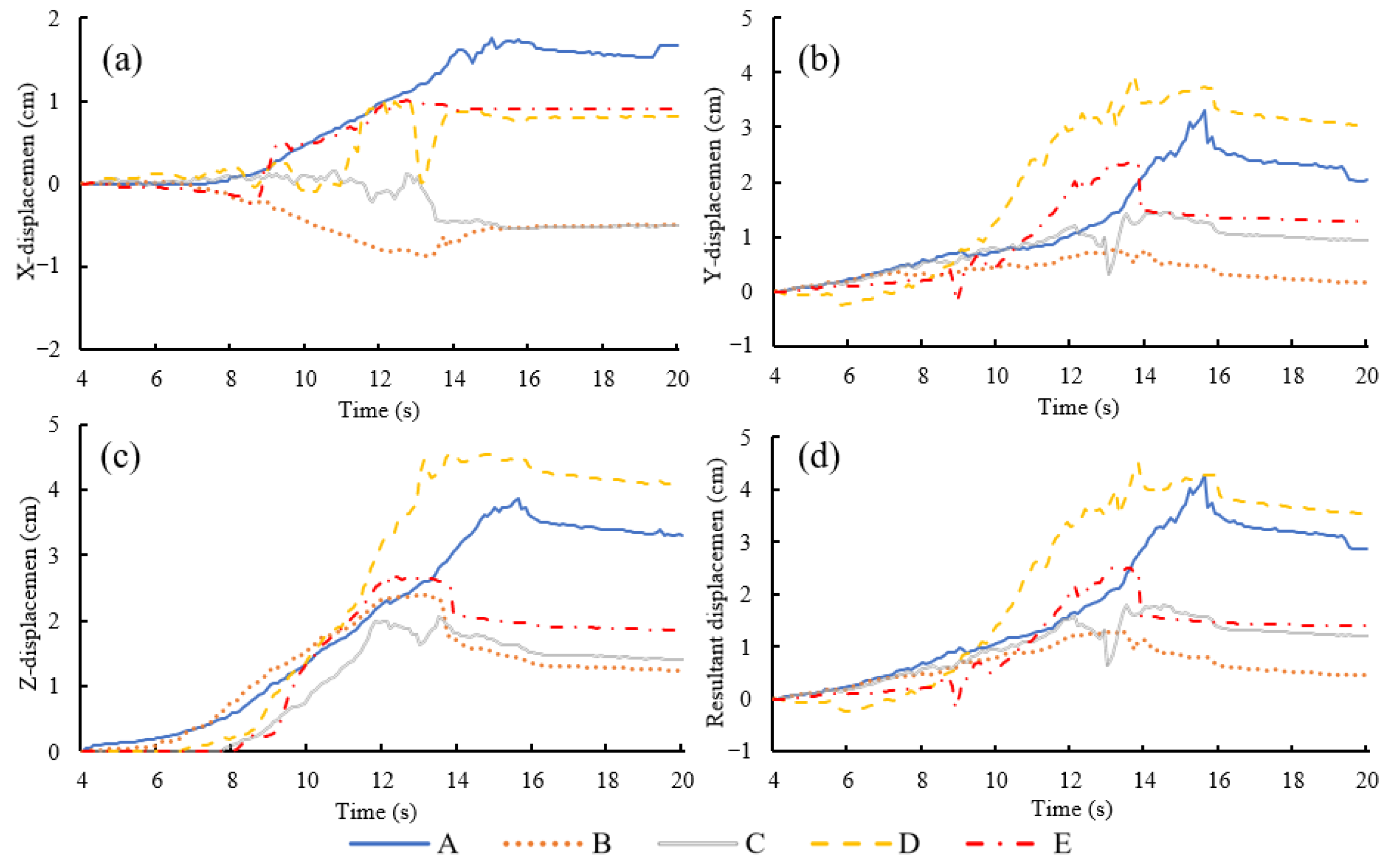
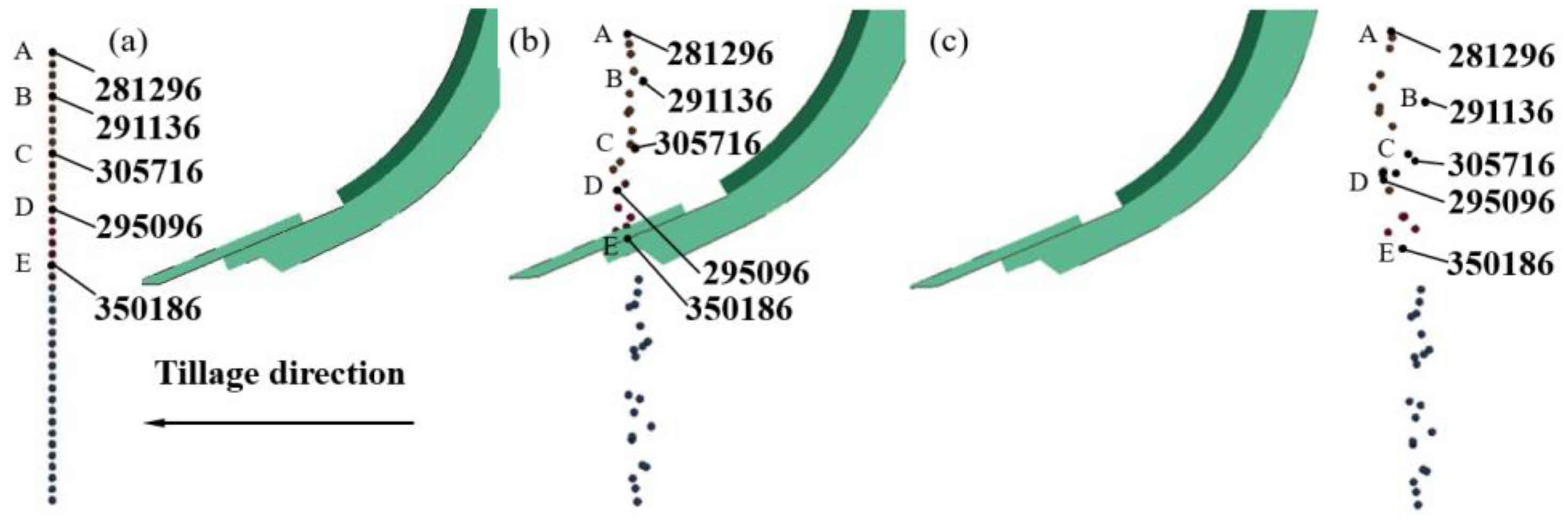
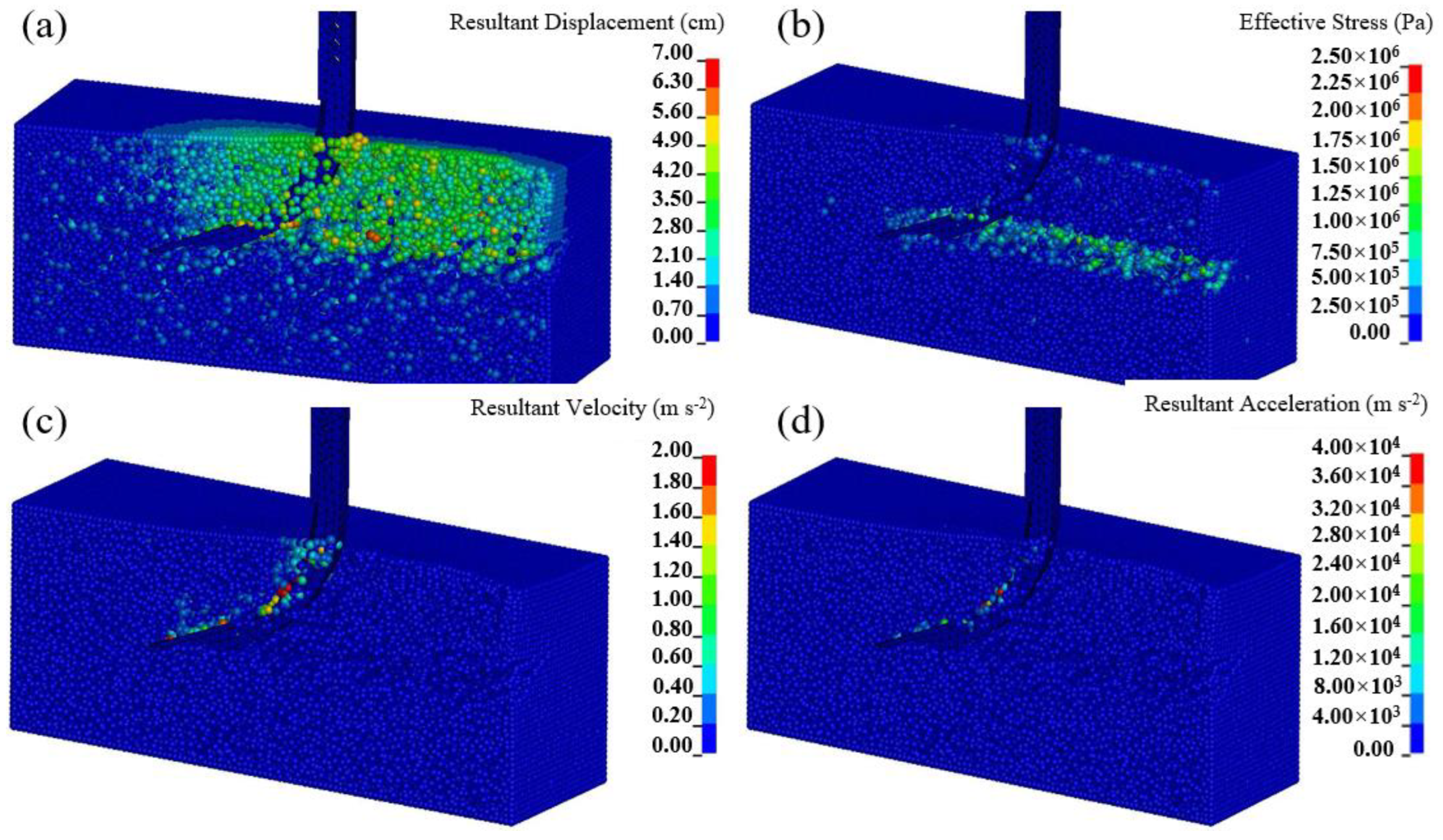
3.3. Soil Particle Displacement
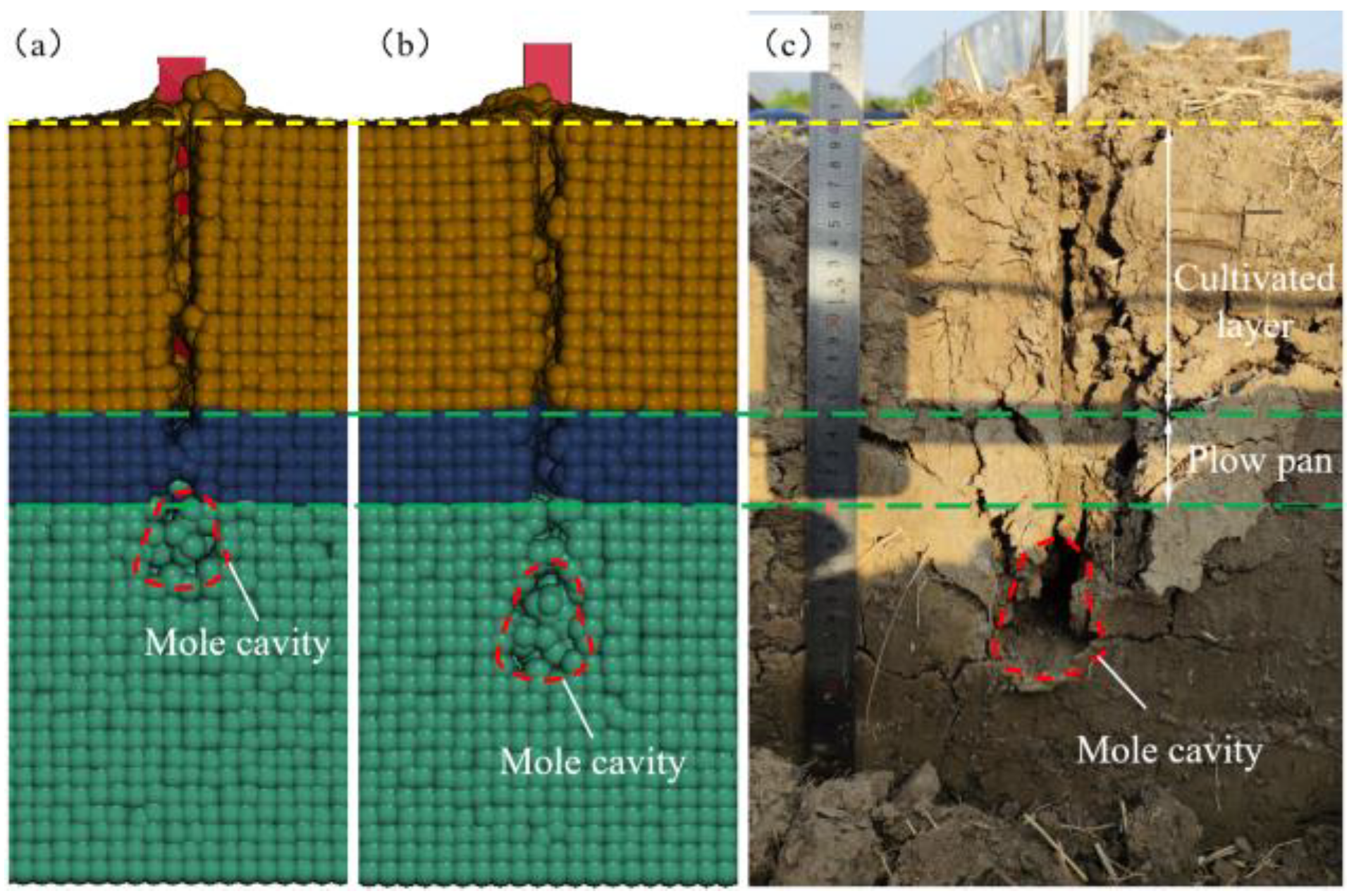
3.4. Soil Particle Distribution in Soil Profile
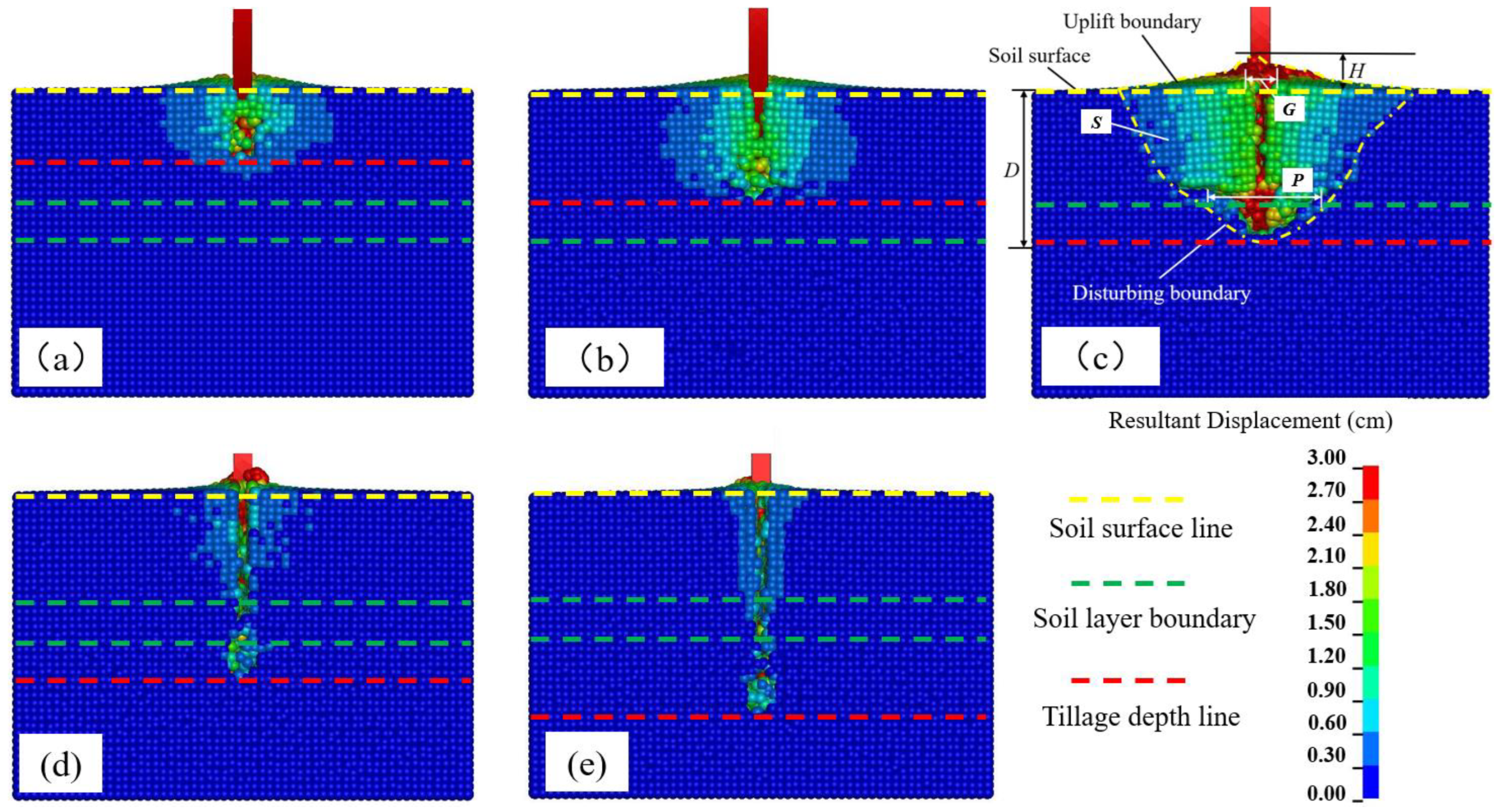
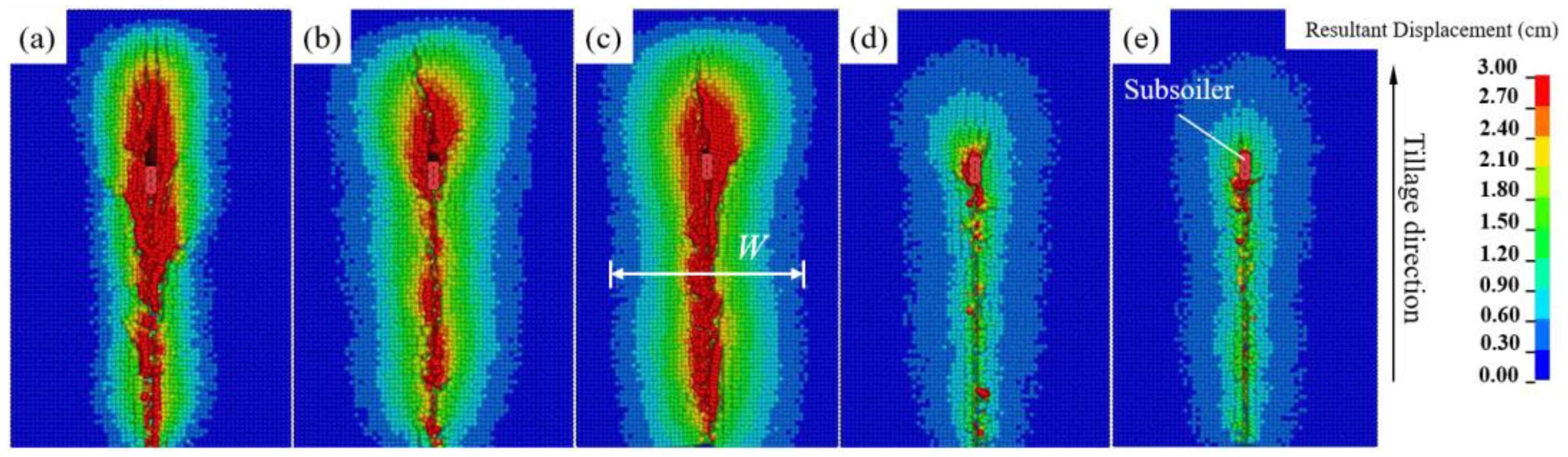
3.5. Soil Disturbance Profile
4. Discussion
4.1. Effect of Subsoiler on Draft Force
4.2. Effect of Subsoiler on Simulated and Field Disturbance
5. Conclusions
- (i)
- Simulation and field experiment showed that draft force increased with increasing tillage depth. However, the simulated soil physical properties were uniform, and the field soil physical properties were variable, resulting in the average draft force in the simulation being consistently lower than in the field and the field draft force fluctuating greatly. The results showed that the simulation was difficult to completely match the real field soil conditions.
- (ii)
- From the movement process of soil particles with shallow to deep arrangement on the soil profile, it can be observed that the soil block above the tine was not lifted up as a big block but broken into many small soil blocks and then lifted up. Theoretically, the soil particles above the tine moved mainly upward and forward during subsoiling. However, this was not the case in practice. Therefore, in future research, the structure of the subsoiler should be optimized to ensure that all soil particles move upward and forward.
- (iii)
- Analysis of the displacement, stress, velocity, and acceleration of the soil particles showed that the particle displacements were concentrated above the tine, the stress was concentrated around the tine, while the velocity and acceleration were closely attached to the subsoiler. Therefore, it is necessary to research a special subsoiler to expand the stress range in the future.
- (iv)
- From the analysis of soil disturbance at different tillage depths, it was found that the “mole cavity” at 25 and 30 cm tillage depths existed at the bottom of the disturbance. The disturbance area and specific draft were maximum and minimum at 20 cm tillage depth, respectively. When multiple subsoilers were working, the optimum spacing between the subsoilers was 15 cm. In the future, when tillage was carried out in the field, breaking the root anchorage of soil in the cultivated layer could reduce the tillage force and thus reduce the energy consumption of subsoiling.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pulido-Moncada, M.; Katuwal, S.; Kristensen, J.B.; Munkholm, L.J. Effects of bio-subsoilers on subsoil pore-system functionality: Case study with intact soil columns. Geoderma 2021, 385, 114897. [Google Scholar] [CrossRef]
- Janbazialamdari, S.; Flippo, D.; Ridder, E.; Brokesh, E. Soil compaction prediction in precision agriculture using cultivator shank vibration and soil moisture data. Agriculture 2025, 15, 1896. [Google Scholar] [CrossRef]
- Song, W.; Jiang, X.; Li, L.; Ren, L.; Tong, J. Increasing the width of disturbance of plough pan with bionic inspired subsoilers. Soil Tillage Res. 2022, 220, 105356. [Google Scholar] [CrossRef]
- Askari, M.; Shahgholi, G.; Abbaspour-Gilandeh, Y. New wings on the interaction between conventional subsoiler and paraplow tines with the soil: Effects on the draft and the properties of soil. Arch. Agron. Soil Sci. 2019, 65, 88–100. [Google Scholar] [CrossRef]
- Huo, L.F.; Liang, L.; Abbas, A.; White, D.; Ding, Q.S.; Wang, X.C.; He, R.Y. Soil disturbance under small harvester traffic in paddy-based smallholder farms in China. Agron. J. 2020, 112, 1441–1451. [Google Scholar] [CrossRef]
- Li, X.; Luo, Z.; Hao, Z.; Zheng, E.; Yao, H.; Zhu, Y.; Wang, X. Investigation on tillage resistance and soil disturbance in wet adhesive soil using discrete element method with three-layer soil-plough coupling model. Powder Technol. 2024, 436, 119463. [Google Scholar] [CrossRef]
- Wang, C.; Yan, Z.; Wang, Z.; Batool, M.; El-Badri, A.M.; Bai, F.; Li, Z.; Wang, B.; Zhou, G.; Kuai, J. Subsoil tillage promotes root and shoot growth of rapeseed in paddy fields and dryland in Yangtze River Basin soils. Eur. J. Agron. 2021, 130, 126351. [Google Scholar] [CrossRef]
- Kong, F.X.; Jiu, A.; Kan, Z.; Zhou, J.; Yang, H.; Li, F.-M. Deep tillage combined with straw biochar return increases rice yield by improving nitrogen availability and root distribution in the subsoil. Field Crops Res. 2024, 315, 109481. [Google Scholar] [CrossRef]
- Hu, M.; Gao, T.; Dong, X.; Tan, Q.; Yi, C.; Wu, F.; Bao, A. Simulation of soil-tool interaction using smoothed particle hydrodynamics (SPH). Soil Tillage Res. 2023, 229, 105671. [Google Scholar] [CrossRef]
- Walunj, A.; Chen, Y.; Tian, Y.; Zeng, Z. Modeling Soil–Plant–Machine Dynamics Using Discrete Element Method: A Review. Agronomy 2023, 13, 1260. [Google Scholar] [CrossRef]
- Tagar, A.A.; Ji, C.Y.; Adamowski, J.; Malard, J.; Chen, S.Q.; Ding, Q.S.; Abbasi, N.A. Finite element simulation of soil failure patterns under soil bin and field testing conditions. Soil Tillage Res. 2015, 145, 157–170. [Google Scholar] [CrossRef]
- Zhu, L.; Cheng, X.; Peng, S.S.; Qi, Y.Y.; Zhang, W.F.; Jiang, R.; Yin, C.L. Three dimensional computational fluid dynamic interaction between soil and plowbreast of horizontally reversal plow. Comput. Electron. Agric. 2016, 123, 1–9. [Google Scholar] [CrossRef]
- Sedara, A.M.; Abdeldayem, M.A.A.; Pratas Glycerio De Freitas, F.; Mehari, T.Z. Optimization of subsoiler design using similitude-based DEM simulation and soil bin testing on cohesive-frictional artificial soil. J. Terramechanics 2025, 117, 101026. [Google Scholar] [CrossRef]
- Aikins, K.A.; Ucgul, M.; Barr, J.B.; Awuah, E.; Antille, D.L.; Jensen, T.A.; Desbiolles, J.M.A. Review of Discrete Element Method Simulations of Soil Tillage and Furrow Opening. Agriculture 2023, 13, 541. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, H.; Ji, J. Effect of Mounting Angle on Bending Subsoiling Tool–Soil Interactions Using DEM Simulations. Agriculture 2022, 12, 1830. [Google Scholar] [CrossRef]
- Tang, Z.; Zeng, Z.; Wu, S.; Fu, D.; He, J.; Cai, Y.; Chen, Y.; Gong, H.; Qi, L. Optimizing soil resistance and disturbance of bionic furrow opener for paddy field based on badger claw using the CFD-DEM method. Comput. Electron. Agric. 2024, 227, 109549. [Google Scholar] [CrossRef]
- Zhang, L.B.; Cai, Z.X.; Liu, H.F. A novel approach for simulation of soil-tool interaction based on an arbitrary Lagrangian–Eulerian description. Soil Tillage Res. 2018, 178, 41–49. [Google Scholar] [CrossRef]
- Wei, L.; Huang, W.; Liu, J.; Li, M.; Zheng, Z.; Wang, S.; Du, D.; Zhang, Y. DEM simulation of subsoiling in tropical sugarcane fields: Effects of opposing subsoiler design and model parameters. Smart Agric. Technol. 2024, 9, 100593. [Google Scholar] [CrossRef]
- Gao, P.; Li, J.; Qi, H.; Liu, X.; Ma, Y. Simulation of Draught Reduction Performance of Subsoiling with Upcutting Belt Motion Using Discrete Element Method. Appl. Sci. 2024, 14, 1313. [Google Scholar] [CrossRef]
- Reese, L.; Qiu, T.; Linzell, D.; Rado, Z. Field-scale testing and numerical investigation of soil-boulder interaction under vehicular impact using FEM and coupled FEM-SPH formulations. Int. J. Prot. Struct. 2016, 7, 77–99. [Google Scholar] [CrossRef]
- Yang, W.; Xiao, X.; Pan, R.; Guo, S.; Yang, J. Numerical Simulation of Spiral Cutter–Soil Interaction in Deep Vertical Rotary Tillage. Agriculture 2023, 13, 1850. [Google Scholar] [CrossRef]
- Liu, M.; Sun, J.; Huang, D.; Qiao, D.; Xiang, M.; Feng, W.; Fu, D.; Wang, J. Mechanism Analysis of Soil Disturbance in Sodic Saline–Alkali Soil Tillage Based on Mathematical Modeling and Discrete Element Simulation. Agriculture 2025, 15, 1885. [Google Scholar] [CrossRef]
- Xu, Z.; Qi, H.; Wang, L.; Wang, S.; Liu, X.; Ma, Y. DEM Study and Field Experiments on Coupling Bionic Subsoilers. Biomimetics 2025, 10, 306. [Google Scholar] [CrossRef]
- Liang, L.; Sun, H.T.; Xu, G.M.; Li, Y.N.; He, R.Y.; Ding, Q.S. Soil infiltration of rice-wheat rotation field under long-term mechanical treatment based on field in situ experiments. Trans. Chin. Soc. Agric. Eng. 2023, 39, 110–118. (In Chinese) [Google Scholar] [CrossRef]
- LSTC. LS-DYNA r8.0 Keyword User’s Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2016. [Google Scholar]
- Ding, Q.S.; Ren, J.; Adam, B.E.; Zhao, J.K.; Ge, S.Y.; Li, Y. DEM analysis of subsoiling process in wet clayey paddy soil. Trans. Chin. Soc. Agric. Mach. 2017, 48, 38–48. (In Chinese) [Google Scholar] [CrossRef]
- Ran, X.; Wang, L.; Xing, J.; Shi, L.; Wang, D.; Guo, W.; Wang, X. A Discrete Element Model for Characterizing Soil-Cotton Seeding Equipment Interactions Using the JKR and Bonding Contact Models. Agriculture 2025, 15, 1693. [Google Scholar] [CrossRef]
- Hoseinian, S.H.; Hemmat, A.; Esehaghbeygi, A.; Shahgoli, G.; Baghbanan, A. Development of a dual sideway-share subsurface tillage implement: Part 1. Modeling tool interaction with soil using DEM. Soil Tillage Res. 2022, 215, 105201. [Google Scholar] [CrossRef]
- Troncone, A.; Pugliese, L.; Parise, A.; Mazzuca, P.; Conte, E. Post-failure stage analysis of flow-type landslides using different numerical techniques. Comput. Geotech. 2025, 182, 107152. [Google Scholar] [CrossRef]
- Yang, W.; Zhao, W.; Liu, Y.; Chen, Y.; Yang, J. Simulation of forces acting on the cutter blade surfaces and root system of sugarcane using FEM and SPH coupled method. Comput. Electron. Agric. 2021, 180, 105893. [Google Scholar] [CrossRef]
- Yang, W.; Li, J.J.; Yang, J.; Wei, L. Numerical simulation of an experienced farmer lifting tubers of cassava for designing a bionic harvester. CMES-Comput. Model. Eng. Sci. 2015, 104, 471–491. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, D.; Yang, L.; Cui, T.; Jing, H.; Zhong, X. Modeling the interaction of soil and a vibrating subsoiler using the discrete element method. Comput. Electron. Agric. 2020, 174, 105518. [Google Scholar] [CrossRef]
- Tong, J.; Jiang, X.H.; Wang, Y.M.; Ma, Y.H.; Li, J.W.; Sun, J.Y. Tillage force and disturbance characteristics of different geometric-shaped subsoilers via DEM. Adv. Manuf. 2020, 8, 392–404. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, H.; Wang, S.; Zhou, H.; Ji, J. Methods for reducing the tillage force of subsoiling tools: A review. Soil Tillage Res. 2023, 229, 105676. [Google Scholar] [CrossRef]
- Mudarisov, S.; Farkhutdinov, I.; Khamaletdinov, R.; Khasanov, E.; Mukhametdinov, A. Evaluation of the significance of the contact model particle parameters in the modelling of wet soils by the discrete element method. Soil Tillage Res. 2022, 215, 105228. [Google Scholar] [CrossRef]
- Gathala, M.K.; Ladha, J.K.; Saharawat, Y.S.; Kumar, V.; Kumar, V.; Sharma, P.K. Effect of tillage and crop establishment methods on physical properties of a medium-textured soil under a seven-year rice−wheat rotation. Soil Sci. Soc. Am. J. 2011, 75, 1851–1862. [Google Scholar] [CrossRef]
- Alhammad, B.A.; Roy, D.K.; Ranjan, S.; Padhan, S.R.; Sow, S.; Nath, D.; Seleiman, M.F.; Gitari, H. Conservation Tillage and Weed Management Influencing Weed Dynamics, Crop Performance, Soil Properties, and Profitability in a Rice–Wheat–Greengram System in the Eastern Indo-Gangetic Plain. Agronomy 2023, 13, 1953. [Google Scholar] [CrossRef]
- Hang, C.; Huang, Y.; Zhu, R. Analysis of the movement behaviour of soil between subsoilers based on the discrete element method. J. Terramechanics 2017, 74, 35–43. [Google Scholar] [CrossRef]
- Hang, C.; Gao, X.; Yuan, M.; Huang, Y.; Zhu, R. Discrete element simulations and experiments of soil disturbance as affected by the tine spacing of subsoiler. Biosyst. Eng. 2018, 168, 73–82. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Y.; Ma, Y.; Tong, J.; Zhang, Z. DEM simulation of bionic subsoilers (tillage depth > 40 cm) with drag reduction and lower soil disturbance characteristics. Adv. Eng. Softw. 2018, 119, 30–37. [Google Scholar] [CrossRef]




| Soil Depth (cm) | Bulk Density (g cm−3) | Water Content (%) | Total Porosity (%) | Soil Penetration Resistance (kPa) |
|---|---|---|---|---|
| 0~5 | 1.25 | 18.05 | 52.83 | 1048.7 |
| 5~10 | 1.26 | 22.62 | 52.45 | 796.9 |
| 10~15 | 1.37 | 23.98 | 48.30 | 2525.5 |
| 15~20 | 1.58 | 20.53 | 40.38 | 1906.5 |
| 20~25 | 1.51 | 23.25 | 43.02 | 1436.7 |
| 25~30 | 1.53 | 24.54 | 42.26 | 1461.5 |
| 30~35 | 1.54 | 24.68 | 41.89 | 1509.9 |
| 35~40 | 1.57 | 24.44 | 40.75 | 1683.1 |
| 40~45 | 1.58 | 23.63 | 40.38 | 1540.7 |
| 45~50 | 1.57 | 23.09 | 40.75 | 1453.7 |
| Soil Depth (cm) | Cohesive (kPa) | Internal Friction Angle (°) |
|---|---|---|
| 0–5 | 33.75 | 23.02 |
| 5–10 | 35.56 | 22.58 |
| 10–15 | 37.36 | 27.26 |
| 15–20 | 98.23 | 19.42 |
| 20–25 | 52.43 | 26.44 |
| 25–30 | 69.30 | 16.14 |
| 30–35 | 69.91 | 15.17 |
| 35–40 | 63.88 | 11.74 |
| Parameters | Cultivated Layer | Plow Pan | Subsoil Layer |
|---|---|---|---|
| Bulk density (kg cm−3) | 1.29 | 1.58 | 1.54 |
| Water density (kg cm−3) | 1000 | 1000 | 1000 |
| Soil particle specific gravity | 2.65 | 2.65 | 2.65 |
| Water content (%) | 21.55 | 20.53 | 24.23 |
| Soil porosity (%) | 51.19 | 40.38 | 41.98 |
| Internal friction angle (rad) | 0.43 | 0.34 | 0.30 |
| Cohesion (Pa) | 35.56 × 103 | 98.23 × 103 | 63.88 × 103 |
| Bulk modulus (Pa) | 23.32 × 105 | 74.31 × 105 | 46.36 × 105 |
| Shear modulus (Pa) | 7.77 × 105 | 24.77 × 105 | 15.45 × 105 |
| Tillage Depth (cm) | Lateral Force (N) | Draft Force (N) | Lifting Force (N) | Resultant Force (N) | Field Draft Force (N) | Error (%) |
|---|---|---|---|---|---|---|
| 10 | 21.89 ± 33.61 | 594.99 ± 31.24 | 319.72 ± 27.64 | 676.44 ± 49.25 | 645.10 ± 114.06 | 7.77 |
| 15 | −1.95 ± 53.07 | 815.98 ± 114.49 | 487.03 ± 46.64 | 951.59 ± 108.61 | 859.29 ± 476.15 | 5.04 |
| 20 | 0.78 ± 54.67 | 1470.40 ± 165.80 | 755.32 ± 95.34 | 1653.49 ± 211.20 | 1518.31 ± 306.83 | 3.16 |
| 25 | 19.96 ± 40.45 | 3247.83 ± 129.47 | 1325.56 ± 58.69 | 3509.24 ± 131.94 | 3888.22 ± 465.77 | 16.47 |
| 30 | −25.51 ± 63.32 | 5411.60 ± 162.66 | 1946.47 ± 60.11 | 5757.09 ± 169.97 | 6657.16 ± 545.05 | 18.71 |
| Tillage Depth (D, cm) | Disturbance Width (W, cm) | Uplift Height (H, cm) | Furrow Width (G, cm) | Disturbance Area (S, cm2) | Specific Draft (kN m−2) | Disturbance Plow Pan Width (P, cm) |
|---|---|---|---|---|---|---|
| 10 | 23.51 d | 2.18 c | 2.73 b | 212.59 c | 27.99 | 0 |
| 15 | 35.67 b | 2.69 c | 2.59 c | 321.80 b | 25.36 | 0 |
| 20 | 46.66 a | 5.15 a | 4.27 a | 597.65 a | 24.60 | 15.31 a |
| 25 | 29.11 c | 3.34 b | 2.55 c | 182.66 d | 177.81 | 1.88 b |
| 30 | 28.71 c | 3.11 bc | 2.92 b | 110.81 e | 488.37 | 2.01 b |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, L.; Ding, Q.; Zhang, H.; Liu, Q. Disturbance Characteristics of Subsoiling in Paddy Soil Based on Smoothed Particle Hydrodynamics (SPH). Agronomy 2025, 15, 2695. https://doi.org/10.3390/agronomy15122695
Liang L, Ding Q, Zhang H, Liu Q. Disturbance Characteristics of Subsoiling in Paddy Soil Based on Smoothed Particle Hydrodynamics (SPH). Agronomy. 2025; 15(12):2695. https://doi.org/10.3390/agronomy15122695
Chicago/Turabian StyleLiang, Lei, Qishuo Ding, Haiyan Zhang, and Qi Liu. 2025. "Disturbance Characteristics of Subsoiling in Paddy Soil Based on Smoothed Particle Hydrodynamics (SPH)" Agronomy 15, no. 12: 2695. https://doi.org/10.3390/agronomy15122695
APA StyleLiang, L., Ding, Q., Zhang, H., & Liu, Q. (2025). Disturbance Characteristics of Subsoiling in Paddy Soil Based on Smoothed Particle Hydrodynamics (SPH). Agronomy, 15(12), 2695. https://doi.org/10.3390/agronomy15122695






