Spectral Index Optimization and Machine Learning for Hyperspectral Inversion of Maize Nitrogen Content
Abstract
1. Introduction
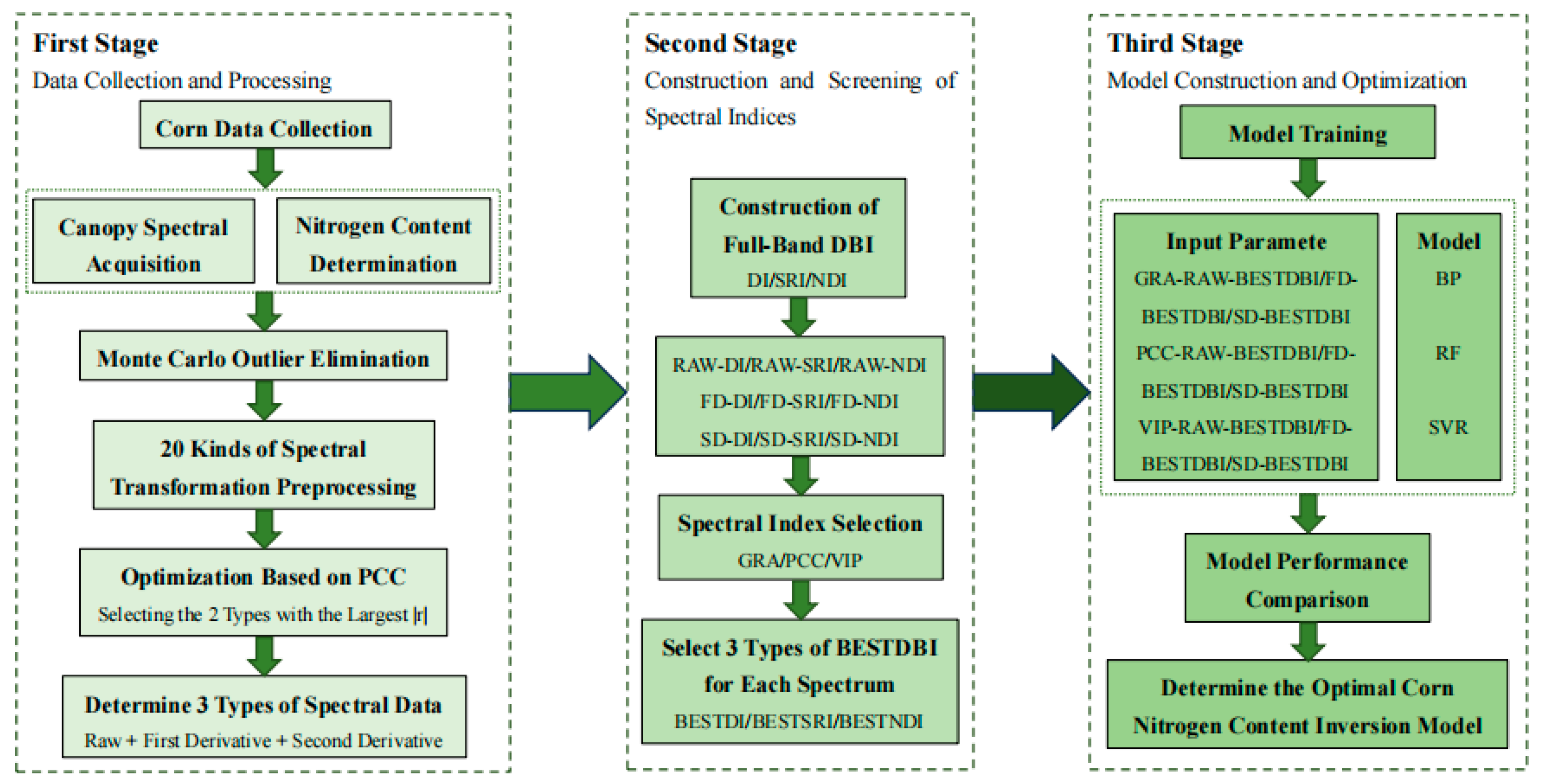
2. Materials and Methods
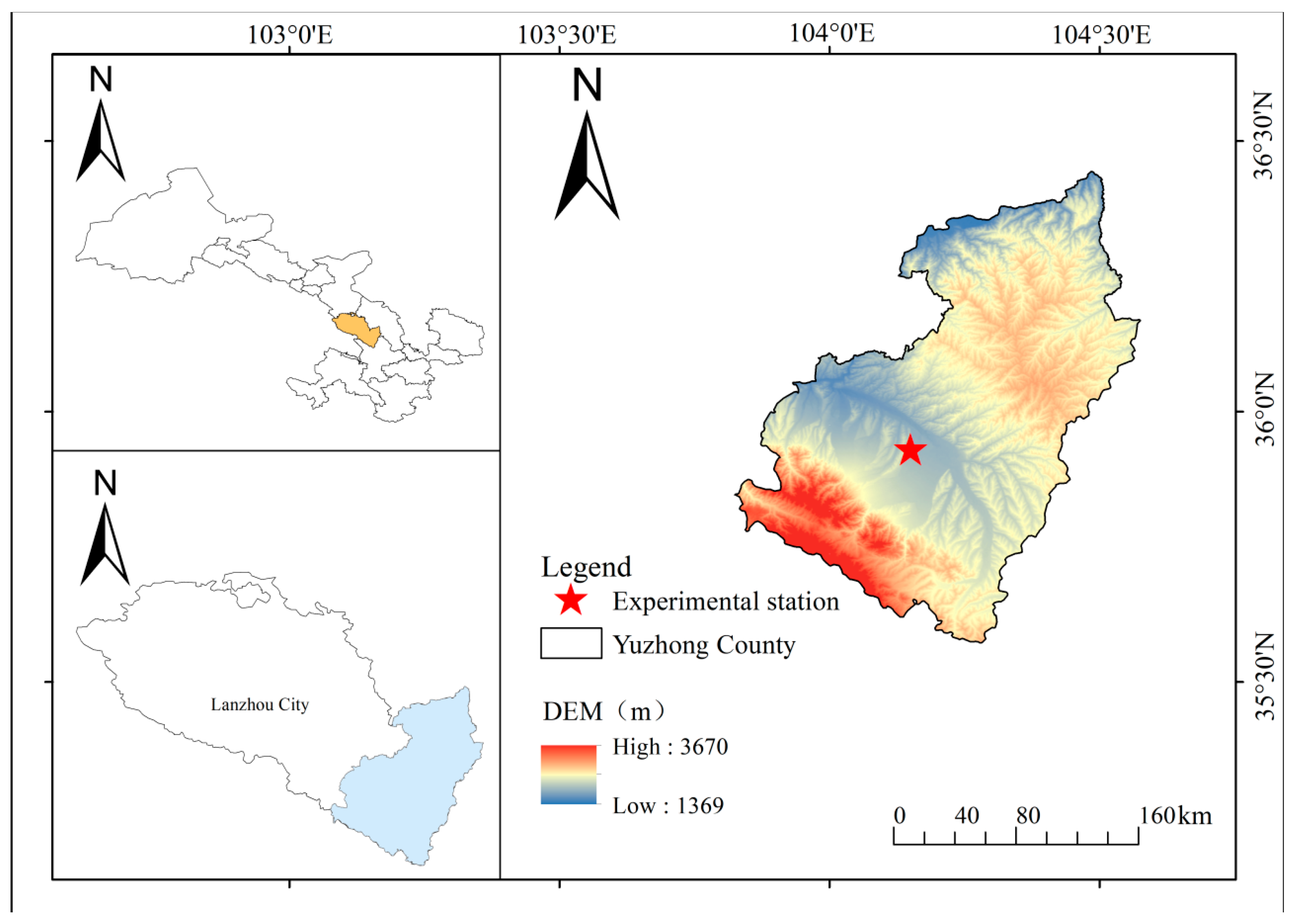
2.1. Study Site and Experimental Design
2.2. Data Collection
2.3. Spectral Data Preprocessing
2.4. Spectral Index Construction and Selection Methods
2.5. Model Construction
3. Results
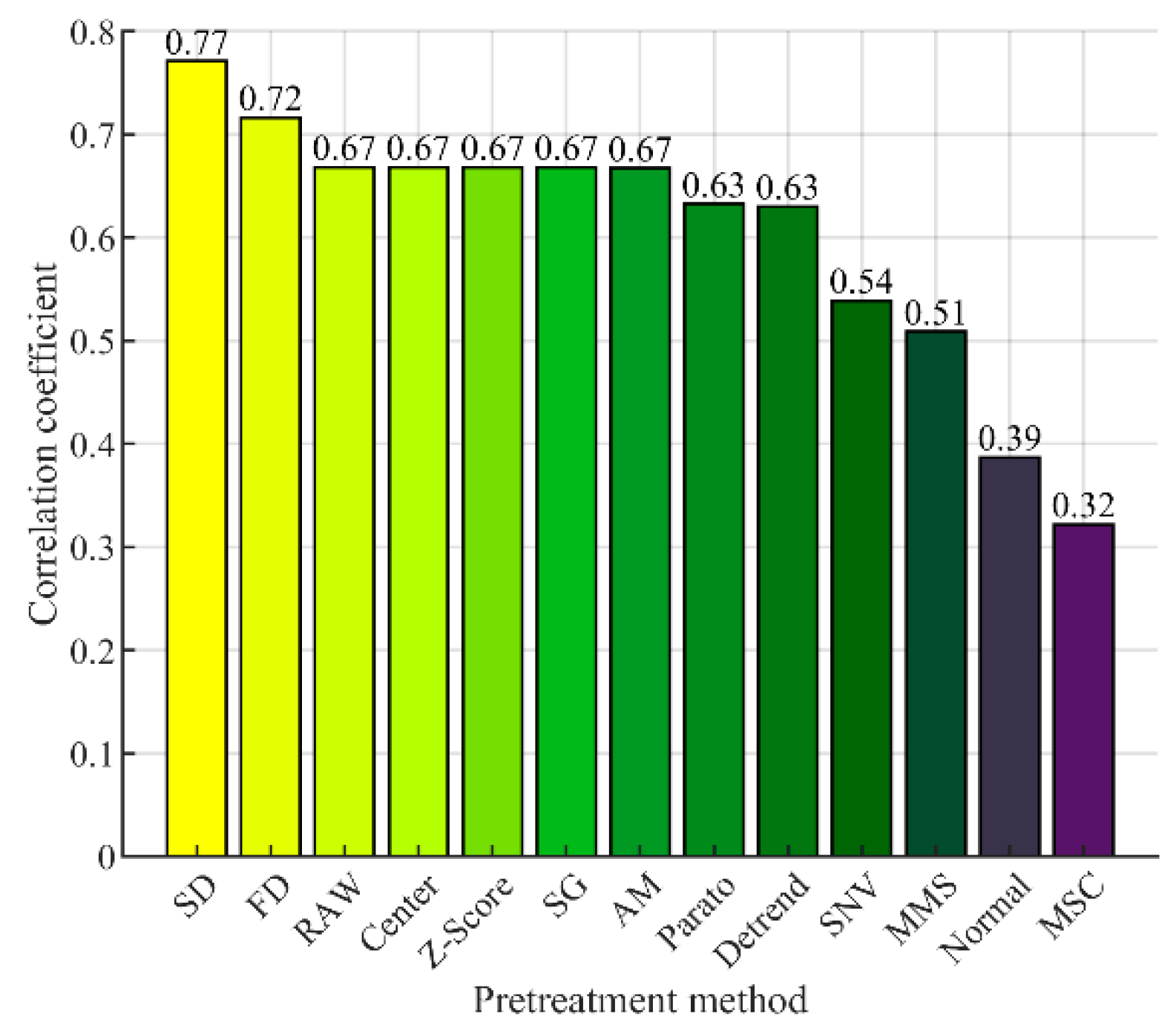
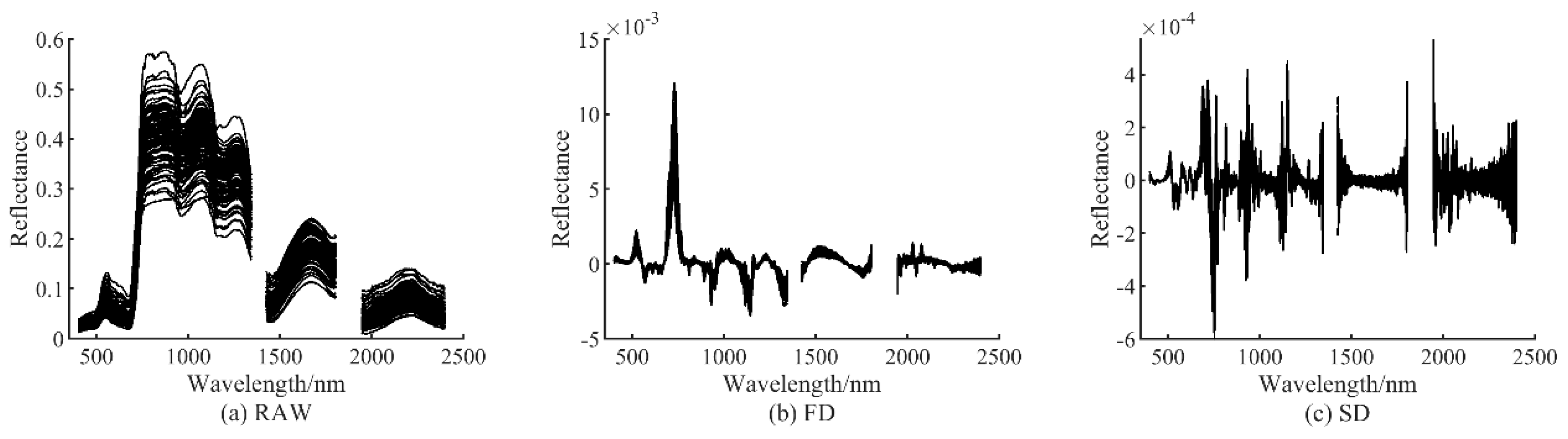
3.1. Spectral Preprocessing
3.2. Results of Spectral Index Construction and Selection
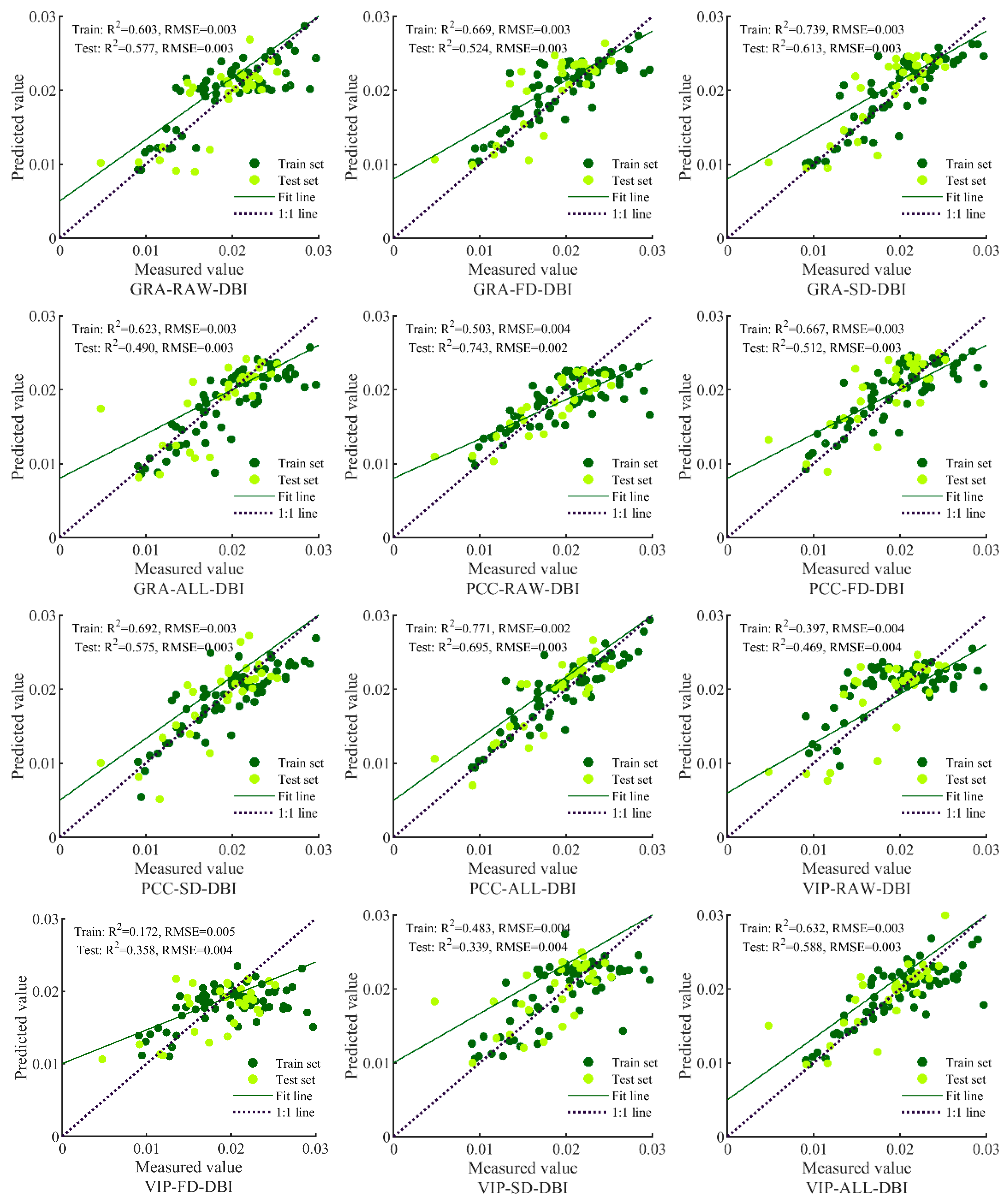
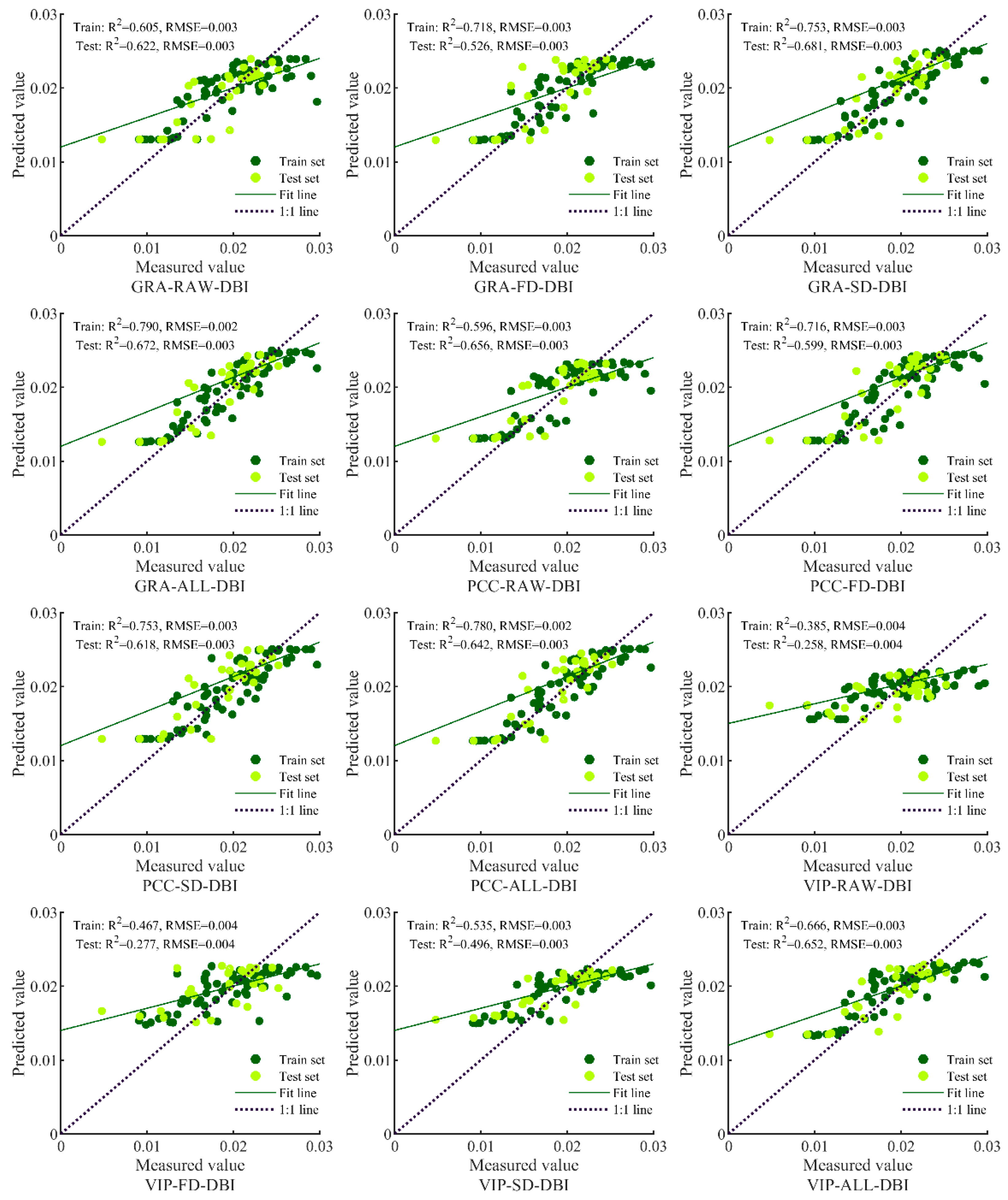
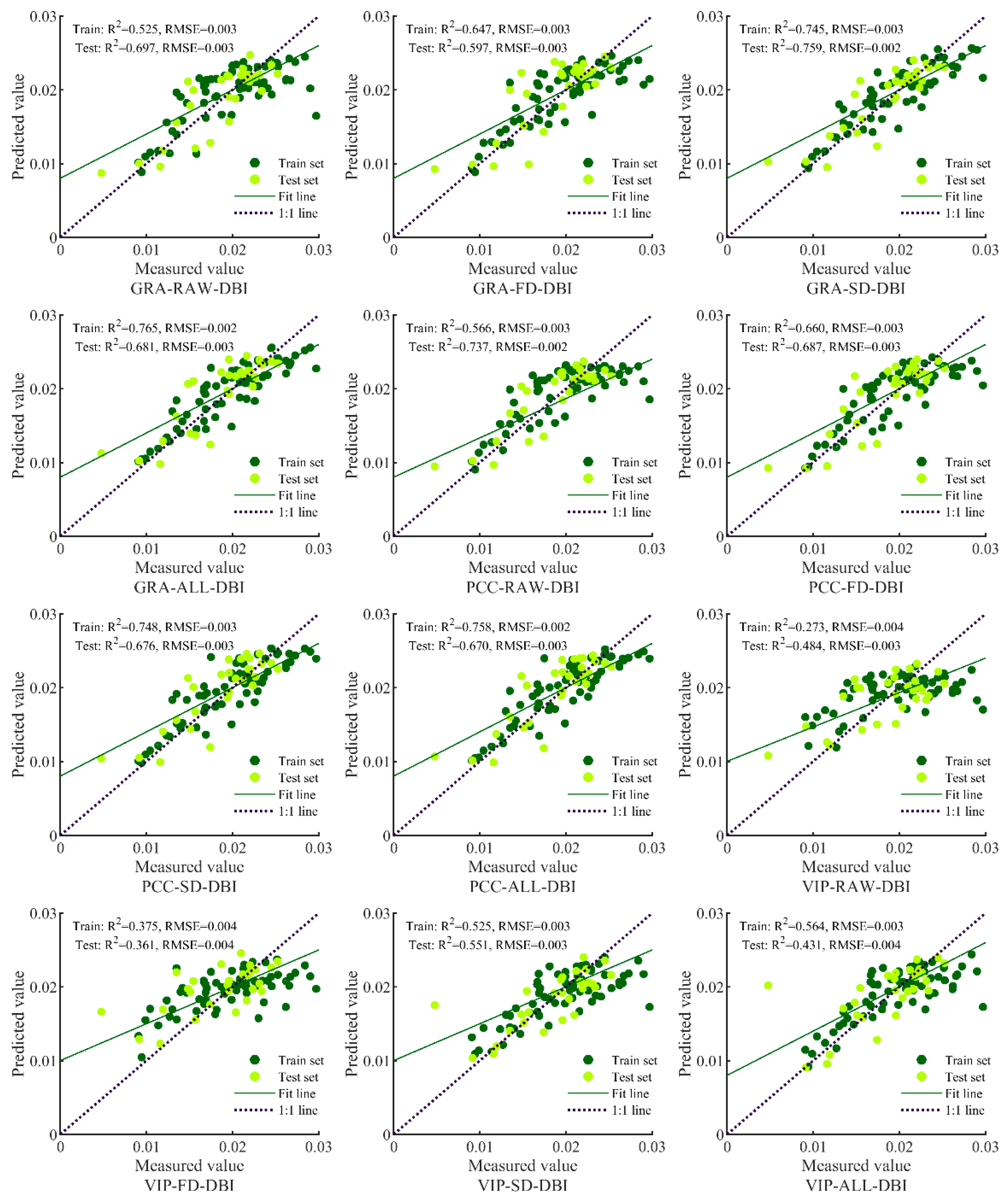
3.3. Model Prediction Results and Analysis
4. Discussion
4.1. Impact of Spectral Index Types and Feature Selection Methods on Inversion Accuracy
4.2. Applicability of Optimal Selection-Modeling Combinations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, B.; Su, Q.; Li, Y.; Chen, R.; Yang, W.; Huang, C. Field rice growth monitoring and fertilization management based on uav spectral and deep image feature fusion. Agronomy 2025, 15, 886. [Google Scholar] [CrossRef]
- Wortman, S.E. Weedy fallow as an alternative strategy for reducing nitrogen loss from annual cropping systems. Agron. Sustain. Dev. 2016, 36, 61. [Google Scholar] [CrossRef]
- Ju, Z.; Liu, K.; Zhao, G.; Ma, X.; Jia, Z. Nitrogen fertilizer and sowing density affect flag leaf photosynthetic characteristics, grain yield, and yield components of oat in a semiarid region of northwest China. Agronomy 2022, 12, 2108. [Google Scholar] [CrossRef]
- Cox, W.E. Water Supply vs. the Environment: Finding the Appropriate Balance. In Critical Transitions in Water and Environmental Resources Management; Scientific Research Publishing Inc.: Salt Lake City, UT, USA, 2004; pp. 1–8. [Google Scholar]
- Chen, J.; Wang, G.; Hamani, A.K.M.; Amin, A.S.; Sun, W.; Zhang, Y.; Liu, Z.; Gao, Y. Optimization of Nitrogen fertilizer application with climate-smart agriculture in the North China Plain. Water 2021, 13, 3415. [Google Scholar] [CrossRef]
- Sandhu, N.; Sethi, M.; Kumar, A.; Dang, D.; Singh, J.; Chhuneja, P. Biochemical and genetic approaches improving nitrogen use efficiency in cereal crops: A review. Front. Plant Sci. 2021, 12, 657629. [Google Scholar] [CrossRef]
- Liu, J.; Feng, Z.; Mannan, A.; Khan, T.U.; Cheng, Z. Comparing non-destructive methods to estimate volume of three tree taxa in Beijing, China. Forests 2019, 10, 92. [Google Scholar] [CrossRef]
- Fu, S.; Meng, W.; Jeon, G.; Chehri, A.; Zhang, R.; Yang, X. Two-path network with feedback connections for pan-sharpening in remote sensing. Remote Sens. 2020, 12, 1674. [Google Scholar] [CrossRef]
- Yu, N.; Ren, B.; Zhao, B.; Liu, P.; Zhang, J. Leaf-nitrogen status affects grain yield formation through modification of spike differentiation in maize. Field Crops Res. 2021, 271, 108238. [Google Scholar] [CrossRef]
- Liu, L.; Huang, W.; Pu, R.; Wang, J. Detection of internal leaf structure deterioration using a new spectral Ratio index in the near-infrared shoulder region. J. Integr. Agr. 2014, 13, 760–769. [Google Scholar] [CrossRef]
- Jung, V.; Albert, C.H.; Violle, C.; Kunstler, G.; Loucougaray, G.; Spiegelberger, T. Intraspecific trait variability mediates the response of subalpine grassland communities to extreme drought events. J. Ecol. 2014, 102, 45–53. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, X. Application of surrogate parameters in characteristic UV–vis absorption bands for rapid analysis of water contaminants. Sens. Actuators B Chem. 2017, 239, 718–726. [Google Scholar] [CrossRef]
- Somers, B.; Delalieux, S.; Verstraeten, W.W.; Eynde, A.V.; Barry, G.H.; Coppin, P. The contribution of the fruit component to the hyperspectral citrus canopy signal. Photogramm. Eng. Remote Sens. 2010, 76, 37–47. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Gitelson, A.A. Using the red-edge bands on Sentinel-2 for retrieving canopy chlorophyll and nitrogen content. In Proceedings of the First Sentinel-2 Preparatory Symposium, Frascati, Italy, 3–27 April 2012; Volume 707, p. 34. [Google Scholar]
- Clevers, J.G.; Gitelson, A.A. Remote estimation of crop and grass chlorophyll and nitrogen content using red-edge bands on Sentinel-2 and-3. Int. J. Appl. Earth. Obs. Geoinf. 2013, 23, 344–351. [Google Scholar] [CrossRef]
- Cao, C.L.; Wang, T.L.; Gao, M.F.; Li, Y.; Li, D.D.; Zhang, H.J. Hyperspectral Inversion of Nitrogen Content in Maize Leaves Based on Different Dimensionality Reduction Algorithms. Comput. Electron. Agric. 2021, 190, 106461. [Google Scholar] [CrossRef]
- Li, W.; Hou, Z.; Zhou, J.; Tao, R. SiamBAG: Band attention grouping-based Siamese object tracking network for hyperspectral videos. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–12. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, D.; Chang, Q.; Zheng, Z.; Fu, X.; Li, K.; Mo, H. Estimation of anthocyanins in leaves of trees with apple mosaic disease based on hyperspectral data. Remote Sens. 2023, 15, 1732. [Google Scholar] [CrossRef]
- Anderson, L.O.; Aragao, L.E.; Shimabukuro, Y.E.; Almeida, S.; Huete, A. Fraction images for monitoring intra-annual phenology of different vegetation physiognomies in Amazonia. Int. J. Remote Sens. 2011, 32, 387–408. [Google Scholar] [CrossRef]
- Chen, C.; Liang, J.; Sun, W.; Yang, G.; Meng, X. An automatically recursive feature elimination method based on threshold decision in random forest classification. Geo-Spat. Inf. Sci. 2025, 28, 1494–1519. [Google Scholar] [CrossRef]
- Koh, J.C.; Banerjee, B.P.; Spangenberg, G.; Kant, S. Automated hyperspectral vegetation index derivation using a hyperparameter optimisation framework for high-throughput plant phenotyping. New Phytol. 2022, 233, 2659–2670. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Remote sensing of chlorophyll concentration in higher plant leaves. Adv. Space Res. 1998, 22, 689–692. [Google Scholar] [CrossRef]
- Xu, W.; Ma, R.; Zhou, Y.; Peng, S.; Hou, Y. Asymptotic properties of Pearson’s rank-variate correlation coefficient in bivariate normal model. Signal Process. 2016, 119, 190–202. [Google Scholar] [CrossRef]
- Han, J.; Guo, J.; Zhang, Z.; Yang, X.; Shi, Y.; Zhou, J. The rapid detection of trash content in seed cotton using near-infrared spectroscopy combined with characteristic wavelength selection. Agriculture 2023, 13, 1928. [Google Scholar] [CrossRef]
- Pei, J.; Xu, L.; Huang, Y.; Jiao, Q.; Yang, M.; Ma, D.; Jiang, S.; Li, H.; Li, Y.; Liu, S.; et al. A two-step simulated annealing algorithm for spectral data feature extraction. Sensors 2023, 23, 893. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, J.; Yan, K.; Lu, X.; Li, W.; Tian, H.; Wang, L.; Deng, J.; Lan, Y. Advances and developments in monitoring and inversion of the biochemical information of crop nutrients based on hyperspectral technology. Agronomy 2023, 13, 2163. [Google Scholar] [CrossRef]
- Hou, Y.; Zhang, A.; Lv, R.; Zhao, S.; Ma, J.; Zhang, H.; Li, Z. A study on water quality parameters estimation for urban rivers based on ground hyperspectral remote sensing technology. Environ. Sci. Pollut. Res. 2022, 29, 63640–63654. [Google Scholar] [CrossRef]
- Morales, G.; Sheppard, J.W.; Logan, R.D.; Shaw, J.A. Hyperspectral dimensionality reduction based on inter-band redundancy analysis and greedy spectral selection. Remote Sens. 2021, 13, 3649. [Google Scholar] [CrossRef]
- Sales, M.H.R.; Souza, C.M.; Kyriakidis, P.C. Fusion of MODIS images using kriging with external drift. IEEE Trans. Geosci. Remote Sens. 2012, 51, 2250–2259. [Google Scholar] [CrossRef]
- Peng, X.; Li, J.; Wang, G.; Wu, Y.; Li, L.; Li, Z.; Bhatti, A.A.; Zhou, C.; Hepburn, D.M.; Reid, A.J.; et al. Random forest based optimal feature selection for partial discharge pattern recognition in HV cables. IEEE Trans. Power Deliv. 2019, 34, 1715–1724. [Google Scholar] [CrossRef]
- Zhang, J.; Dang, Q.; Malik, M. Baseline correction in parallel thorough QT studies. Drug Saf. 2013, 36, 441–453. [Google Scholar] [CrossRef]
- Chen, Y.; Song, Y.; Ma, J.; Zhao, J. Optimization-based scatter estimation using primary modulation for computed tomography. Med. Phys. 2016, 43 Pt 1, 4753–4767. [Google Scholar] [CrossRef]
- Ang, Y.S.; Ang, L.K. Current-temperature scaling for a Schottky interface with nonparabolic energy dispersion. Phys. Rev. Appl. 2016, 6, 034013. [Google Scholar] [CrossRef]
- Steinier, J.; Termonia, Y.; Deltour, J. Smoothing and differentiation of data by simplified least square procedure. Anal. Chem. 1972, 44, 1906–1909. [Google Scholar] [CrossRef]
- Cao, J.; Yang, H. A dynamic normalized difference index for estimating soil organic matter concentration using visible and near-infrared spectroscopy. Ecol. Indic. 2023, 147, 110037. [Google Scholar] [CrossRef]
- Massaoudi, M.; Refaat, S.S.; Abu-Rub, H.; Chihi, I.; Oueslati, F.S. PLS-CNN-BiLSTM: An End-to-End Algorithm-Based Savitzky–Golay Smoothing and Evolution Strategy for Load Forecasting. Energies 2020, 13, 20. [Google Scholar] [CrossRef]
- Rinnan, Å.; Van Den Berg, F.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. Trac-Trend. Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
- Robinson, N.P.; Allred, B.W.; Jones, M.O.; Moreno, A.; Kimball, J.S.; Naugle, D.E.; Erickson, T.A.; Richardson, A.D. A dynamic Landsat derived normalized difference vegetation index (NDVI) product for the conterminous United States. Remote Sens. 2017, 9, 863. [Google Scholar] [CrossRef]
- Fuyan, S.; Jing, L.; Wenjun, C.; Zhijun, T.; Weijing, M.; Suzhen, W.; Yongyong, X. Fatty liver disease index: A simple screening tool to facilitate diagnosis of nonalcoholic fatty liver disease in the Chinese population. Dig. Dis. Sci. 2013, 58, 3326–3334. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, A.R.; Kumbhakar, D.; Sarkar, S. Characterisation of a single mode trapezoidal index fiber by splice loss technique using lateral offset. Optik 2019, 178, 403–410. [Google Scholar] [CrossRef]
- Harrington, J.; Henninger-Voss, E.; Karhadkar, K.; Robinson, E.; Wong, T.W. Sum index and difference index of graphs. Discret. Appl. Math. 2023, 325, 262–283. [Google Scholar] [CrossRef]
- Yang, J.H.; Nie, J.J.; Fan, J.H. Relation of core dominance parameter and extended spectral index for radio sources. J. Astrophys. Astron. 2014, 35, 487–488. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Q.; Zhang, J. The result greyness problem of the grey relational analysis and its solution. J. Intell. Fuzzy Syst. 2023, 44, 6079–6088. [Google Scholar] [CrossRef]
- Feng, W.; Zhu, Q.; Zhuang, J.; Yu, S. An expert recommendation algorithm based on Pearson correlation coefficient and FP-growth. Clust. Comput. 2019, 22 (Suppl. S3), 7401–7412. [Google Scholar] [CrossRef]
- Galindo-Prieto, B.; Trygg, J.; Geladi, P. A new approach for variable influence on projection (VIP) in O2PLS models. Chemometr. Intell. Lab. 2017, 160, 110–124. [Google Scholar] [CrossRef]
- Hu, Z.; Zhao, Q.; Wang, J. The prediction model of cotton yarn quality based on artificial recurrent neural network. In Proceedings of the International Conference on Applications and Techniques in Cyber Security and Intelligence, Huainan, China, 22–24 June 2019; Springer International Publishing: Cham, Switzerland, 2019; pp. 857–866. [Google Scholar]
- Wahjudi, A.; Salamoni, T.D.; Batan, I.M.L.; Harnany, D. Determination of injection molding process parameters using combination of backpropagation neural network and genetic algorithm optimization method. Int. J. Mech. Eng. Sci. 2021, 5, 39–44. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, L.; Yang, J.; Hao, X.; Guan, G.; Gao, Z. An experimental modeling of cyclone separator efficiency with PCA-PSO-SVR algorithm. Powder Technol. 2019, 347, 114–124. [Google Scholar] [CrossRef]
- Marshall, M.; Belgiu, M.; Boschetti, M.; Pepe, M.; Stein, A.; Nelson, A. Field-level crop yield estimation with PRISMA and Sentinel-2. Isprs. J. Photogramm. 2022, 187, 191–210. [Google Scholar] [CrossRef]
- Gao, J.S.; Li, J.M.; Xu, M.G.; Sun, N.; Qin, D.Z. The Effects of longEterm chemical fertilizers on yield of upland crops and paddy rice in red soil. Chin. Agric. Sci. Bull. 2008, 24, 286–292. [Google Scholar]
- Ng, A.; Soo, K. Random forests. In Data Science–Was Ist Das Eigentlich?! Algorithmen Des Maschinellen Lernens Verständlich Erklärt; Springer: Berlin/Heidelberg, Germany, 2018; pp. 117–127. [Google Scholar]
- Nikova, I.; Atanassova, S.; Tanev, S. Normalized indices for minimizing illumination and soil background effects in crop spectral monitoring. Comput. Electron. Agric. 2014, 103, 1–10. [Google Scholar]
- Li, F.; Mistele, B.; Hu, Y.; Chen, X.; Schmidhalter, U. Reflectance estimation of canopy nitrogen content in winter wheat using optimised hyperspectral spectral indices and partial least squares regression. Eur. J. Agron. 2014, 52, 198–209. [Google Scholar] [CrossRef]
- Sun, J.; Yang, J.; Shi, S.; Chen, B.; Du, L.; Gong, W.; Song, S. Estimating rice leaf nitrogen concentration: Influence of regression algorithms based on passive and active leaf reflectance. Remote Sens. 2017, 9, 951. [Google Scholar] [CrossRef]
- Pandey, P.; Ge, Y.; Stoerger, V.; Schnable, J.C. High throughput in vivo analysis of plant leaf chemical properties using hyperspectral imaging. Front. Plant Sci. 2017, 8, 1348. [Google Scholar] [CrossRef]
- Pullanagari, R.R.; Yule, I.J.; Hedley, M.J.; Tuohy, M.P.; Dynes, R.A.; King, W.M. Multi-spectral radiometry to estimate pasture quality components. Precis. Agric. 2012, 13, 442–456. [Google Scholar] [CrossRef]
- Carlier, A.; Dandrifosse, S.; Dumont, B.; Mercatoris, B. Comparing CNNs and PLSr for estimating wheat organs biophysical variables using proximal sensing. Front. Plant Sci. 2023, 14, 1204791. [Google Scholar] [CrossRef] [PubMed]
- Hogan, J.B. Plant-based diets in kidney disease management. Dial. Transplant. 2011, 40, 407–409. [Google Scholar] [CrossRef]
- Tao, L.I.U.; Fengyuan, Y.A.N.G.; Wang, L.I.U.; Dongmei, Y.I.N.; Youzhou, J.I.A.O. Estimation of peanut biomass based on feature selection and particle swarm optimization. Trans. Chin. Soc. Agric. Eng. 2025, 41, 238–247. [Google Scholar]
- Radoglou-Grammatikis, P.; Sarigiannidis, P.; Lagkas, T.; Moscholios, I. A compilation of UAV applications for precision agriculture. Comput. Netw. 2020, 172, 107148. [Google Scholar] [CrossRef]
- Sishodia, R.P.; Ray, R.L.; Singh, S.K. Applications of remote sensing in precision agriculture: A review. Remote Sens. 2020, 12, 3136. [Google Scholar] [CrossRef]
- Wan, Y.; Zhong, Y.; Ma, A.; Hu, X.; Wei, L. Satellite-air-ground integrated multi-source earth observation and machine learning processing brain for tailings reservoir monitoring and rapid emergency response. Land Degrad. Dev. 2023, 34, 1941–1959. [Google Scholar] [CrossRef]
- Vu, A.D.; Nguyen, K.V.; Bui, B.Q.; Kamel, N. A comprehensive survey of super-resolution remote sensing image datasets: Evolution, challenges, and future directions. IEEE Access 2025, 13, 145350–145372. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, L.; Yan, M.; Qi, J.; Fu, T.; Fan, S.; Chen, B. High-resolution mangrove forests classification with machine learning using worldview and UAV hyperspectral data. Remote Sens. 2021, 13, 1529. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Ciganda, V.; Rundquist, D.C.; Arkebauer, T.J. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32, L08403. [Google Scholar] [CrossRef]
- Boerjan, W. Lignin Management: Optimizing Yield and Composition in Lignin-Modified Plants. GCEP (Y1, partial) Report. 2014, pp. 1–20. Available online: https://d1wqtxts1xzle7.cloudfront.net/76564755/2.3.4_Chapple_Sponsor_and_Public_Version-libre.pdf (accessed on 13 August 2025).
- Fu, Y.; Yang, G.; Pu, R.; Li, Z.; Li, H.; Xu, X.; Song, X.; Yang, X.; Zhao, C. An overview of crop nitrogen status assessment using hyperspectral remote sensing: Current status and perspectives. Eur. J. Agron. 2021, 124, 126241. [Google Scholar] [CrossRef]
- Chen, Y.; Shahidehpour, M.; Lin, Y.; Dvorkin, Y.; Peric, V.; Zhao, J.; Ugalde-Loo, C.E.; Ge, L. Guest Editorial: Situational awareness of integrated energy systems. IET Gener. Transm. Dis. 2022, 16, 2761–2765. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Z.; Luo, Y.; Zhang, J.; Chen, Y.; Peng, C.; Ye, K.; Lin, W.; Zhang, J.; Wang, Y.; et al. Quantifying heavy metal concentrations in industrial-transitional zone soils via integrated XRF and VIS-NIR spectroscopy. Environ. Pollut. 2025, 384, 127015. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Feng, X.; Liu, F.; He, Y. Identification of hybrid rice strain based on near-infrared hyperspectral imaging technology. Trans. Chin. Soc. Agric. Eng. 2017, 33, 189–194. [Google Scholar]



| Preprocessing Method [35] | Category | Abbreviation | Main Function |
|---|---|---|---|
| RAW | Raw reflectance | RAW | Original spectral data without any processing |
| Standardization | Min–Max scaling | MMS | Scales values into the range [0, 1] |
| Z-score scaling | Z-Score | Standardizes data to zero mean and unit variance | |
| Normalization | Normalize | Normalizes samples to eliminate scale differences | |
| Smoothing | Moving average | MovingAvg | Reduces noise and smooths spectral curves |
| Savitzky–Golay smoothing [36] | SG | Smooths spectra while preserving curve shape | |
| Scatter correction | Multiplicative scatter correction | MSC | Corrects scattering and particle size effects |
| Standard normal variate | SNV | Reduces variability caused by scatter differences | |
| Derivative transform | First derivative | FD | Enhances slope changes and highlights spectral inflection points |
| Second derivative | SD | Strengthens spectral features and improves resolution | |
| Baseline correction | Detrend | Detrend | Removes baseline drift and background trends |
| Feature Selection Strategies | Processing Method | DI Optimal Wavelength Position (i, j)/nm | Max(ξ/r/Score) | SRI Optimal Wavelength Position (i, j)/nm | Max(ξ/r/Score) | NDI Optimal Wavelength Position (i, j)/nm | Max(ξ/r/Score) |
|---|---|---|---|---|---|---|---|
| GRA | RAW | (718, 1726) | 0.8717 | (702, 1801) | 0.8851 | (700, 1801) | 0.8947 |
| FD | (685, 1507) | 0.8809 | (746, 1126) | 0.8876 | (679, 1639) | 0.9037 | |
| SD | (646, 612) | 0.8923 | (750, 1155) | 0.8939 | (547, 551) | 0.9077 | |
| PCC | RAW | (493, 492) | 0.7510 | (1743, 707) | 0.7797 | (1743, 707) | 0.7771 |
| FD | (1566, 684) | 0.7949 | (1333, 734) | 0.8228 | (1566, 683) | 0.7991 | |
| SD | (646, 612) | 0.8112 | (547,551) | 0.8313 | (551, 547) | 0.8295 | |
| VIP | RAW | (1344, 725) | 1 | (1595, 1596) | 1 | (1595, 1596) | 1 |
| FD | (714, 705) | 1 | (1094, 671) | 1 | (1296, 1071) | 1 | |
| SD | (1153, 721) | 1 | (1778, 2398) | 1 | (2121, 473) | 1 |
| Input Variable | Model Method | Train | Test | ||||
|---|---|---|---|---|---|---|---|
| R2 | 95% CI | RMSE | R2 | 95% CI | RMSE | ||
| GRA-RAW-DBI | BPNN | 0.6034 | [0.4292, 0.7382] | 0.0031 | 0.5774 | [0.2852, 0.7823] | 0.0032 |
| RF | 0.6046 | [0.4306, 0.7391] | 0.0032 | 0.6223 | [0.3409, 0.8087] | 0.0030 | |
| SVR | 0.5250 | [0.3377, 0.6795] | 0.0035 | 0.6972 | [0.4441, 0.8507] | 0.0027 | |
| GRA-FD-DBI | BPNN | 0.6693 | [0.5117, 0.7854] | 0.0029 | 0.5237 | [0.2247, 0.7493] | 0.0034 |
| RF | 0.7178 | [0.5757, 0.8191] | 0.0027 | 0.5257 | [0.2268, 0.7506] | 0.0033 | |
| SVR | 0.6470 | [0.4832, 0.7696] | 0.0030 | 0.5966 | [0.3085, 0.7937] | 0.0031 | |
| GRA-SD-DBI | BPNN | 0.7387 | [0.6041, 0.8333] | 0.0026 | 0.6134 | [0.3295, 0.8036] | 0.0030 |
| RF | 0.7526 | [0.6232, 0.8427] | 0.0025 | 0.6808 | [0.4204, 0.8417] | 0.0027 | |
| SVR | 0.7454 | [0.6133, 0.8378] | 0.0025 | 0.7593 | [0.5397, 0.8838] | 0.0024 | |
| GRA-ALL-DBI | BPNN | 0.6227 | [0.4427, 0.7580] | 0.0031 | 0.4901 | [0.1479, 0.7553] | 0.0035 |
| RF | 0.7900 | [0.6685, 0.8710] | 0.0023 | 0.6716 | [0.3602, 0.8542] | 0.0028 | |
| SVR | 0.7652 | [0.6328, 0.8549] | 0.0024 | 0.6813 | [0.3741, 0.8590] | 0.0027 | |
| PCC-RAW-DBI | BPNN | 0.5031 | [0.3135, 0.6626] | 0.0036 | 0.7432 | [0.5140, 0.8753] | 0.0025 |
| RF | 0.5959 | [0.4201, 0.7327] | 0.0032 | 0.6564 | [0.3863, 0.8281] | 0.0028 | |
| SVR | 0.5661 | [0.3847, 0.7107] | 0.0033 | 0.7366 | [0.5037, 0.8719] | 0.0025 | |
| PCC-FD-DBI | BPNN | 0.6668 | [0.5085, 0.7837] | 0.0029 | 0.5116 | [0.2120, 0.7417] | 0.0034 |
| RF | 0.7156 | [0.5727, 0.8176] | 0.0027 | 0.5991 | [0.3116, 0.7952] | 0.0031 | |
| SVR | 0.6598 | [0.4995, 0.7787] | 0.0029 | 0.6866 | [0.4287, 0.8449] | 0.0027 | |
| PCC-SD-DBI | BPNN | 0.6925 | [0.5420, 0.8016] | 0.0028 | 0.5755 | [0.2830, 0.7812] | 0.0032 |
| RF | 0.7526 | [0.6232, 0.8427] | 0.0025 | 0.6181 | [0.3355, 0.8063] | 0.0030 | |
| SVR | 0.7480 | [0.6169, 0.8396] | 0.0025 | 0.6765 | [0.4143, 0.8393] | 0.0028 | |
| PCC-ALL-DBI | BPNN | 0.7713 | [0.6415, 0.8588] | 0.7713 | 0.6950 | [0.3944, 0.8658] | 0.0027 |
| RF | 0.7798 | [0.6537, 0.8644] | 0.0024 | 0.6422 | [0.3195, 0.8393] | 0.0029 | |
| SVR | 0.7579 | [0.6225, 0.8501] | 0.0025 | 0.6703 | [0.3583, 0.8536] | 0.0028 | |
| VIP-RAW-DBI | BPNN | 0.3971 | [0.2053, 0.5766] | 0.0039 | 0.4694 | [0.1702, 0.7142] | 0.0035 |
| RF | 0.3846 | [0.1936, 0.5660] | 0.0040 | 0.2584 | [0.0253, 0.5543] | 0.0042 | |
| SVR | 0.2727 | [0.0994, 0.4648] | 0.0043 | 0.4844 | [0.1846, 0.7241] | 0.0035 | |
| VIP-FD-DBI | BPNN | 0.1715 | [0.0344, 0.3604] | 0.0046 | 0.3575 | [0.0795, 0.6350] | 0.0039 |
| RF | 0.4672 | [0.2752, 0.6343] | 0.0037 | 0.2771 | [0.0335, 0.5705] | 0.0041 | |
| SVR | 0.3748 | [0.1846, 0.5576] | 0.0040 | 0.3613 | [0.0821, 0.6379] | 0.0039 | |
| VIP-SD-DBI | BPNN | 0.4826 | [0.2914, 0.6465] | 0.0036 | 0.3387 | [0.0672, 0.6206] | 0.0039 |
| RF | 0.5353 | [0.3493, 0.6874] | 0.0034 | 0.4957 | [0.1957, 0.7315] | 0.0034 | |
| SVR | 0.5250 | [0.3377, 0.6795] | 0.0035 | 0.5512 | [0.2549, 0.7664] | 0.0033 | |
| VIP-ALL-DBI | BPNN | 0.6321 | [0.4545, 0.7647] | 0.0027 | 0.5882 | [0.2512, 0.8109] | 0.0031 |
| RF | 0.6665 | [0.4985, 0.7886] | 0.0029 | 0.6519 | [0.3326, 0.8443] | 0.0029 | |
| SVR | 0.5643 | [0.3721, 0.7160] | 0.0033 | 0.4306 | [0.0981, 0.7187] | 0.0037 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Huang, C.; Li, H.; Li, S.; Lu, J. Spectral Index Optimization and Machine Learning for Hyperspectral Inversion of Maize Nitrogen Content. Agronomy 2025, 15, 2485. https://doi.org/10.3390/agronomy15112485
Zhang Y, Huang C, Li H, Li S, Lu J. Spectral Index Optimization and Machine Learning for Hyperspectral Inversion of Maize Nitrogen Content. Agronomy. 2025; 15(11):2485. https://doi.org/10.3390/agronomy15112485
Chicago/Turabian StyleZhang, Yuze, Caixia Huang, Hongyan Li, Shuai Li, and Junsheng Lu. 2025. "Spectral Index Optimization and Machine Learning for Hyperspectral Inversion of Maize Nitrogen Content" Agronomy 15, no. 11: 2485. https://doi.org/10.3390/agronomy15112485
APA StyleZhang, Y., Huang, C., Li, H., Li, S., & Lu, J. (2025). Spectral Index Optimization and Machine Learning for Hyperspectral Inversion of Maize Nitrogen Content. Agronomy, 15(11), 2485. https://doi.org/10.3390/agronomy15112485






