Abstract
In response to water scarcity and low agricultural water-use efficiency in arid regions in Northwest China, this study conducted field experiments in Wuwei, Gansu Province, from 2023 to 2024. It aimed to develop a water stress diagnosis model for spring maize to provide a scientific basis for precision irrigation and water management. In this work, two irrigation methods—plastic film-mulched drip irrigation (FD, where drip lines are laid on the soil surface and covered with film) and plastic film-mulched shallow-buried drip irrigation (MD, where drip lines are buried 3–7 cm below the surface under film)—were tested under five irrigation gradients. Multispectral UAV remote sensing data were collected from key growth stages (i.e., the jointing stage, the tasseling stage, and the grain filling stage). Then, vegetation indices were extracted, and the leaf water content (LWC) was retrieved. LWC inversion models were established using Partial Least Squares Regression (PLSR), Random Forest (RF), and Support Vector Regression (SVR). Different irrigation treatments significantly affected LWC in spring maize, with higher LWC under sufficient water supply. In the correlation analysis, plant height (hc) showed the strongest correlation with LWC under both MD and FD treatments, with R2 values of −0.87 and −0.82, respectively. Among the models tested, the RF model under the MD treatment achieved the highest prediction accuracy (training set: R2 = 0.98, RMSE = 0.01; test set: R2 = 0.88, RMSE = 0.02), which can be attributed to its ability to capture complex nonlinear relationships and reduce multicollinearity. This study can provide theoretical support and practical pathways for precision irrigation and integrated water–fertilizer regulation in smart agriculture, boasting significant potential for broader application of such models.
1. Introduction
Maize is one of the most widely cultivated and high-yield grain and forage crops in China and plays a critical role in national agricultural production and food security [1]. In Gansu Province, it is the leading grain crop, with a planting area of approximately 1.009 million hectares [2]. However, the arid Northwest region is characterized by limited and unevenly distributed precipitation, high evaporation, and seasonal water deficits, so crop productivity there is low and unstable [3,4]. Irrigation remains an essential measure for sustaining and enhancing summer maize yield [5]. Water shortage is a primary yield-limiting factor, often reducing the maize yield by 20–30% or more [6]. Therefore, improving water-use efficiency has become the key to achieving high maize yield in Northwest China.
In typical arid regions in Northwest China, water stress, particularly caused by inadequate rainfall or limited irrigation, has become a key constraint on maize productivity. Soil drought not only affects physiological and developmental processes in maize, but also significantly reduces the yield. Therefore, conducting research on spring maize water stress diagnosis is of practical importance for regional food security, promoting green agricultural transformation, and improving water-use efficiency [7,8,9,10,11,12,13,14,15]. Unmanned Aerial Vehicle (UAV)-based remote sensing enables dynamic monitoring of maize water status and phenotypes [16,17,18,19], thus providing critical technical support for precision irrigation and efficient management in smart agriculture.
Research on maize water monitoring and irrigation efficiency began in the mid-to-late 20th century in China, while foreign studies started earlier. For example, Mazahrih et al. [20] found that subsurface drip irrigation significantly improved water saving and crop yield in alfalfa. Singh et al. [21] reported similar findings for broccoli. In the domain of non-contact imaging technologies, Zhang et al. [22] employed UAV multispectral imaging to construct maize water stress maps. Niu et al. [23] applied various machine learning models to estimate maize vegetation coverage. In addition, Zhou et al. [24] integrated texture and spectral features to improve accuracy of water stress diagnosis. In China, scholars such as Wang Huaiping, Diao Qingyan, and Zhao Xiaoqiang [5,25,26] conducted systematic studies on irrigation methods, maize water stress responses, and remote sensing monitoring, creating valuable theoretical and technical foundations. Among these water-saving techniques, plastic film–mulched drip irrigation (FD), in which drip lines are laid on the soil surface and covered with film, and plastic film–mulched shallow-buried drip irrigation (MD), in which drip lines are buried 3–7 cm below the surface under film, have been widely adopted in arid regions of Northwest China. These two methods effectively reduce soil evaporation, improve irrigation efficiency, and serve as key technologies for sustainable maize production in water-scarce environments.
Despite progress in crop water monitoring and yield prediction, several limitations still exist. Most studies focus on a single growth stage but lack multi-temporal dynamic analysis. For example, Song et al. [27] pointed out that water stress during the seedling stage is often neglected in its impact on maize growth and final yield. Monteleone et al. [28] also noted that many studies focus only on water stress at specific growth stages, lacking a comprehensive analysis across the entire growing season. Chen et al. [29] emphasized the cumulative effects of multi-stage water stress on maize growth, highlighting that water deficits at different stages significantly affect plant development, root morphology, and water use efficiency. Inadequate identification of water-sensitive phenotypic indicators hinders the application of remote sensing indices in drought classification and precision regulation. For instance, Feng et al. [30] highlighted the correlation between phenotypic indicators like leaf area index (LAI) and SPAD values with water stress, supporting the need for better phenotypic identification. Li et al. [31] discussed how multi-modal remote sensing can improve drought tolerance assessment, which is limited by inadequate phenotypic data. Zhang et al. [32] developed a UAV–Sentinel-2 image fusion method that enhances environmental monitoring accuracy, further supporting the application of remote sensing in precision agriculture. Moreover, challenges in multi-source data fusion and high-dimensional modeling have limited UAVs’ spatiotemporal capabilities. Zhu et al. [33] review these challenges, noting that time-space data fusion methods have yet to reach their full potential in improving UAV-based monitoring. Samadzadegan et al. [34] provided a comprehensive review of multi-platform and multi-sensor remote sensing data fusion, analyzing the challenges of improving spatiotemporal capabilities and outlining future development trends. Guo et al. [35] explore the difficulties in high-dimensional modeling, especially in the context of UAV image fusion, which further hinders its application in precision agriculture. Therefore, this study has addressed key issues in dynamic monitoring of water stress and phenotypic inversion for spring maize under precision irrigation in arid areas. By screening water-sensitive phenotypes and constructing water stress diagnosis models with remote sensing indices and inverted phenotypic traits, we have evaluated the performance of SVR, PLSR, and RF models to identify the most suitable one for regional precision irrigation. This research can provide a theoretical foundation and practical solution for smart agriculture in terms of precision water and fertilizer management and present promising application prospects.
2. Materials and Methods
2.1. Overview of the Study Area
This study was conducted from 2023 to 2024 at the National Field Scientific Observation and Research Station for Efficient Water Use in Oasis Agriculture, located in Wuwei, Gansu Province. The experimental site lies in the Hexi Corridor, at 37.52 °N latitude and 102.5 °E longitude, with an elevation of 1580 m, an arid region in Northwest China. It has a typical temperate continental arid climate, with approximately 3000 h of annual sunshine and a frost-free period of around 150 days. Its mean annual temperature is 8 °C, with accumulated temperature above 0 °C exceeding 3550 °C. Its mean annual evaporation is over 2000 mm, while the average annual precipitation is only 164 mm. Its average soil bulk density is 1.56 g/cm3, and the field capacity is 19.23%. In addition, the soil texture there is sandy loam.
2.2. Experimental Design
The crop was spring maize (Xianyu 1225), and was manually sown with hole planting. Its row spacing was 60 cm, plant spacing 21 cm, and planting density 5294 plants per mu (~79,410 plants per hectare). Basal fertilizer (Stanley compound fertilizer, 54% N) was applied before sowing. The fertilization schedule is shown in Table 1. In 2023, sowing was carried out on 5 May and harvesting on 19 September and in 2024, on 25 April and on 14 September, respectively.

Table 1.
Fertilization regime reference table for spring maize in Northwest China.
Two irrigation methods, plastic film-mulched shallow-buried drip irrigation (MD) and plastic film-mulched drip irrigation (FD), were employed. CK denotes the control treatment (conventional irrigation) and corresponds to the suitable irrigation quota per mu (definition and calculation in Equation (1)). Each irrigation method was applied under five water deficit levels: W1 (100% CK), W2 (85% CK), W3 (70% CK), W4 (55% CK), and W5 (40% CK). Each treatment was replicated three times, with each replicate corresponding to a 5.25 m × 6 m plot, totally 30 plots. The drip tape was installed with 0.6 m spacing. The emitter had 0.15 m spacing and a flow rate of 3 L/h. Under drip irrigation, fertilizer was dissolved in a fertigation tank and delivered to the root zone along with irrigation water.
Each treatment had a set lower threshold for soil moisture. The threshold was used to control irrigation from the jointing stage. When soil moisture dropped below the threshold, irrigation was applied. All three replicates under the same water deficit level were irrigated on the same date, while different deficit levels had respective irrigation dates based on their thresholds. Both the lower irrigation thresholds and the planned wetting depth varied across maize growth stages [36]. A “dry sowing, wet emergence” planting strategy was adopted. To ensure uniform germination, a 30 mm emergence irrigation was applied to all treatments after sowing. The irrigation was implemented approximately every 10 days and would be postponed in the event of rainfall. The actual field irrigation amounts under different treatments in 2023 and 2024 are shown in Table 2. The irrigation amount for each treatment was calculated using the following equation:
where CK (m3) represents the suitable irrigation quota per mu, calculated as the product of the planned wetting depth and a crop coefficient; H (m) means the planned wetting depth, which varies with root depth across growth stages (see Table 3); θf (%) signifies the field capacity; θu (%) denotes the lower irrigation threshold, which also varies by growth stage (see Table 1), and γo (t/m3) is the dry soil bulk density.
CK = 666.7 × H × θf × (100% − θu) × γo × 0.75

Table 2.
Field irrigation amounts under different treatments in 2023 and 2024.

Table 3.
Planned wetting depth and lower irrigation limit in different growth stages.
2.3. Observation Items and Methods
2.3.1. Determination of Soil Moisture Content, Bulk Density, and Field Capacity
Beginning at the jointing stage, soil moisture content was measured every 10 days using the gravimetric method with a soil auger. Additional measurements were taken before and after irrigation or rainfall events. One fixed sampling plot was selected for each treatment, with soil samples collected at depths of 0–20 cm, 20–40 cm, 40–60 cm, 60–80 cm, and 80–100 cm.
To determine soil bulk density and field capacity, two representative soil profiles were randomly selected within the experimental area. Soil samples were collected with a cutting ring at the same depth intervals (0–20 cm, 20–40 cm, 40–60 cm, 60–80 cm, and 80–100 cm). For each depth layer, six replicates were collected: three were oven-dried at 105 °C for 24 h (or until a constant weight was reached) to determine dry mass, and the other three were used to determine field capacity. To obtain dry bulk density, three soil samples were dried and then weighed with an electronic balance with 0.01 g precision. The average dry mass for each layer was divided by the volume of the cutting ring to calculate bulk density. To determine field capacity, the other three replicates from each layer were saturated using the cutting ring method. A piece of filter paper was placed at the bottom of the cutting ring and then they placed into a water container where water was 1–2 mm below the ring’s top. After at least 24 h to ensure full saturation, the saturated ring was placed on a layer of air-dried soil (with the filter paper still in place) to simulate drainage. To maintain close contact without disturbing the soil structure, an empty ring was used to apply pressure from above. After an 8 h drainage period, a 20–30 g soil subsample was collected from the ring, placed in an aluminum box, weighed, and oven-dried at 105 °C for 24 h (or until constant weight) to determine the moisture content. The average of the three replicates for each layer was taken as its field capacity.
2.3.2. Determination of Maize Dry Matter and Phenotypic Parameters
In the jointing, tasseling, grain filling, and maturity stages, physiological parameters were measured using whole above-ground maize plant samples. The plants were dried in an oven, initially at 105 °C for 0.5 h to deactivate enzymes, followed by drying at 75 °C until a constant weight. Dry weights were measured using an electronic balance with 0.01 g precision. For phenotypic measurements, three maize plants with uniform growth were selected from each plot. The plant height was measured using a tape measure, the stem diameter with a vernier caliper, and leaf length and width with a tape measure. The leaf area was estimated by a reduction coefficient. SPAD (SPAD refers to the relative chlorophyll content of leaves, measured using a SPAD (Soil Plant Analysis Development) meter) values of the ear leaf (or the third newly emerged leaf if the ear leaf had not yet emerged) were measured using a chlorophyll meter (SPAD-502 Plus, Konica Minolta Sensing, Japan).
where Aa (cm2) represents the total leaf area per plant, n means the number of leaves per plant, Dimax (cm) signifies maximum width of the ith leaf, Li (cm) is length of the ith leaf. The coefficient a = 0.74 for maize.
2.3.3. UAV Multispectral Data Acquisition and Processing
The DJI Matrice 300 RTK drone (manufactured by DJI, Shenzhen, China; DJI refers to Da-Jiang Innovations, the manufacturer of the UAV platform used in this study, and RTK stands for Real-Time Kinematic, a satellite navigation technique that provides centimeter-level positioning accuracy) was employed as the aerial remote sensing platform. It is equipped with six-direction obstacle sensing, and offers an IP45 protection rating, a maximum payload of 2.7 kg, a maximum flight time of 55 min, and a flight ceiling of 7000 m. It can resist a wind speed up to 15 m/s. In addition, it supports triple-channel 1080p video transmission and dual-band communication (2.4/5.8 GHz), and has a maximum transmission distance of 15 km. It can operate under temperatures ranging from −20 °C to 50 °C. Its aircraft and sensor system are designed with redundancy and equipped with binocular vision and infrared sensing for obstacle avoidance. The UAV was equipped with a RedEdge-MX Dual multispectral imaging system manufactured by MicaSense (Seattle, WA, USA). The system consists of two synchronized multispectral cameras: RedEdge-MX and RedEdge-MX Blue. With a total weight of 508.8 g, it provides 10 spectral bands corresponding to wavelengths used by Landsat 8 and Sentinel-2A sensors. The multispectral system delivers images with a spatial resolution of approximately 8 cm per pixel at a flight altitude of 120 m (ground sampling distance), and each camera has a native resolution of 1280 × 960 pixels. This configuration allows for broader spectral information collection in a single flight and can be used in agriculture, forestry, urban planning, and water quality monitoring. Technical specifications of the UAV and the sensor are detailed in Table 4 and Table 5.

Table 4.
Band parameters of the RedEdge-MX sensor.

Table 5.
Band parameters of the RedEdge-MX Blue sensor.
In principle, UAV-based multispectral image acquisition was conducted on the same day when ground-based measurements were performed under clear, windless conditions around solar noon in open fields to ensure optimal lighting. The multispectral camera was mounted in a nadir orientation to capture orthophotos of the crop canopy. The UAV was flown at an altitude of 50 m to minimize the influence of downdraft on the plants and to ensure high image clarity.
The images captured by UAV were processed with Pix4Dmapper software(version 4.4, Pix4D, Lausanne, Switzerland) for stitching, to generate a complete mosaic of the study area. Vector delineation of each maize cultivar plot was performed using GPS control points located between plots. The orthomosaic images were imported into QGIS 3.34.11. Then, the batch extraction of vegetation indices and evapotranspiration data were conducted with the QGIS Raster Calculator and masking tools.
A strict image quality screening process was conducted in the preprocessing stage. To that end, redundant images, including those captured during take-off and landing as well as those with abnormal overlap rates, were discarded, while only images with ideal overlap and clarity were retained. Initial parameter settings were verified in professional aerial photogrammetry software, to ensure the correctness of coordinate systems and sensor parameters. The preliminary outputs were then evaluated through multi-dimensional quality assessments in terms of geometric accuracy (planar and elevation errors within preset thresholds), data completeness (image matching rate >85%), and system compatibility (lens focal length variation within a 5% threshold). Any output failing the required standards underwent iterative parameter optimization to achieve model convergence.
To enhance geospatial accuracy, ground control points (GCPs) with 3D coordinates were embedded into the processing workflow. The integration of 3D spatial registration of GCPs improved accuracy of both horizontal and vertical positions. Each GCP was matched with 7 to 10 neighboring images to ensure spatial error distribution conforms to project specifications.
2.3.4. Vegetation Index Calculation
Based on relevant literatures, vegetation indices highly sensitive to maize water stress were selected to identify and assess the crop’s water status. The selected vegetation indices and their calculation equations are provided in Table 6.

Table 6.
Vegetation indices and their calculation equations.
2.4. Model Overview
2.4.1. Partial Least Squares Regression (PLSR)
Partial least squares regression (PLSR) is a multivariate statistical method designed to address high-dimensional, multicollinear, and small-sample datasets [51]. Its core principle lies in the simultaneous extraction of latent information components from both the independent variable matrix (X) and the dependent variable matrix (Y) through projection transformation and establishing linear regression relationships between such components. Unlike principal component regression (PCR), PLSR maximizes the covariance between X and Y during component extraction, thereby enhancing predictive performance. By reducing dimensionality through latent variables, it effectively mitigates high intercorrelation among predictors, hence enabling stable modeling even when the number of variables (p) exceeds the number of samples (n). Through component selection, irrelevant variable interference is minimized. PLSR’s efficient dimensionality reduction and information co-extraction mechanism makes it a powerful modeling tool for complex high-dimensional systems. It is particularly suitable for multivariate prediction tasks in fields such as agricultural phenotyping and chemometrics.
2.4.2. Support Vector Regression (SVR)
Support vector regression (SVR) is a supervised learning algorithm rooted in the statistical learning theory [52]. Its fundamental goal is to construct an optimal decision boundary to model the data [53]. SVR projects data into a high-dimensional feature space and searches for a hyperplane that best fits the data distribution. To carry out nonlinear regression tasks, kernel functions are employed to transform nonlinear relationships in low-dimensional spaces into linearly separable forms in high-dimensional spaces. Commonly used kernels include the polynomial kernel (for data with explicit polynomial structures), the radial basis function (RBF) kernel (with infinite-dimensional mapping capability), and the sigmoid kernel (mimicking neural network activation functions). SVR relies solely on support vectors (boundary samples) for prediction, thus reducing computational and storage demands. The kernel trick allows implicit high-dimensional mapping, thereby avoiding the curse of dimensionality. In this study, SVR was employed to model the relationships between vegetation indices and leaf water content (LWC) for maize, where the high-dimensional feature space allowed for better handling of complex, nonlinear patterns. However, despite its utility, SVR showed moderate performance compared to Random Forest (RF), particularly in handling the more intricate dependencies inherent in agricultural data.
2.4.3. Random Forest (RF)
Random forest (RF) is a supervised machine learning algorithm based on ensemble learning principles [54]. It constructs multiple decision trees and aggregates their predictions (mean for regression, majority vote for classification), significantly enhancing the generalization ability and predictive accuracy. It is well-suited for high-dimensional data, robust against overfitting, and can be applied in ecological modeling and medical diagnosis [55]. For a new sample, RF predicts by averaging the outputs from all decision trees, which helps reduce variance and improves the overall prediction accuracy. RF’s dual-randomness design, which introduces randomness at both the feature selection and tree construction stages, allows it to outperform single decision trees. Additionally, RF handles missing data and outliers automatically, eliminating the need for data normalization. In this study, RF was chosen for its ability to capture complex, nonlinear relationships between vegetation indices and leaf water content (LWC) in maize, which is critical for accurate water stress monitoring. Its superior performance (R2 = 0.98 on the training set and R2 = 0.88 on the test set) can be attributed to its ability to handle multicollinearity and high-dimensional data, making it ideal for the precision irrigation applications of this study.
2.5. Data Analysis
Microsoft Excel 2013 was used for basic data processing. SPSS 27.0 was employed for correlation analysis, and Duncan’s multiple range test (DMRT) for significance analysis. Origin 2024 introduced for graphical visualization.
Model simulations were conducted using python 3.14.0 with the following key libraries: scikit-learn for model implementation, pandas for data manipulation, and matplotlib for visualizing model outputs. To optimize model performance, hyperparameters were selected based on grid search with 5-fold cross-validation. The Random Forest (RF) model was trained with 100–500 estimators and maximum depth values ranging from 5 to 20 to capture complex nonlinear relationships. The Support Vector Regression (SVR) model was implemented using an RBF kernel with parameter values for C (penalty parameter) ranging from 0.1 to 100, and γ (kernel coefficient) set between 0.01 and 1. For the Partial Least Squares Regression (PLSR) model, 2 principal components (n_components = 2) were selected to reduce the dimension of features and optimize the variance interpretation of the data.
In this study, the input data for the simulation include multispectral UAV remote sensing data, soil moisture content, and phenotypic parameters (such as plant height, leaf area index, and dry matter weight) collected from field experiments conducted in Wuwei, Gansu Province, in 2023 and 2024. These data were gathered during key growth stages of spring maize, including the jointing stage, tasseling stage, and grain filling stage. In addition, irrigation treatments and water deficit levels (W1 to W5) were used as input parameters for the simulation models. The dataset is described in detail within the manuscript, and we have outlined how these data were employed in the calibration and validation of the models, including the sources and processing methods for each variable.
2.6. Model Accuracy Evaluation Metrics
The performance of models was evaluated using the coefficient of determination (R2) and root mean square error (RMSE). A higher R2 value (closer to 1) indicates better model fitting, while a lower RMSE value (closer to 0) reflects higher estimation accuracy. The calculation formulas are as follows:
where yi represents the observed value, signifies the predicted value, denotes the mean of the observed values, and n means the number of samples.
3. Results
3.1. Effects of Different Treatments on Leaf Water Content of Spring Maize
As can be seen from Figure 1, under plastic film-mulched shallow-buried drip irrigation (MD), the leaf water content (LWC) of spring maize exhibited a consistent trend of an initial decline followed by stabilization throughout the growth period. During the early growth stage, LWC decreased rapidly, with the most significant drop observed before 1 July, reaching 18.75% in 2023 and 11.56% in 2024. This sharp decline is likely attributed to intensified competition for assimilates and enhanced transpiration due to rapid growth of the plants in the jointing stage. As maize plants required substantial water and exhibited vigorous physiological activities, the rate of water loss in leaves increased significantly. With the intensification of water stress, LWC continued to decrease and showed a positive correlation with water availability. When water deficit became severe, LWC dropped markedly, showcasing the high sensitivity of maize leaves to water stress.
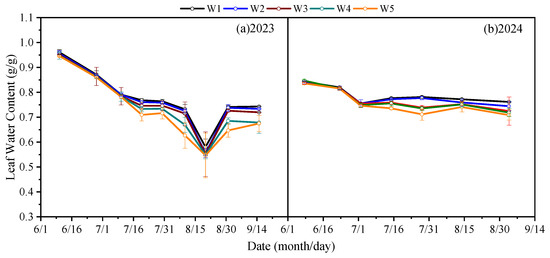
Figure 1.
Changes in spring maize LWC under five water stress levels with MD (plastic film-mulched shallow-buried drip irrigation). Irrigation was applied under five water deficit levels: W1 (100% CK), W2 (85% CK), W3 (70% CK), W4 (55% CK), and W5 (40% CK). CK denotes the control (conventional) irrigation; see Equation (1) for the definition of the suitable irrigation quota per mu. In MD, the drip lines are buried 3–7 cm below the surface under plastic film.
In 2023, the minimum LWC was observed around 20 August, whereas no clear minimum was recorded in 2024. This may be explained by the significant reduction in LWC for lack of irrigation in 2023, while a similar decline was prevented by different irrigation scheduling in 2024. Overall, under MD conditions, LWC of spring maize was highly responsive to water availability and strongly sensitive to drought. Therefore, LWC can serve as a reliable indicator for monitoring maize water status and drought response. These findings provide important guidance for precision irrigation management of maize and offer a scientific basis for optimizing water use and improving water use efficiency in arid and semi-arid regions.
Figure 2 illustrates that in 2023, under plastic film-mulched drip irrigation (FD), LWC of spring maize continuously declined throughout the growth period, presenting a consistent trend across all water treatments. Under severe water stress conditions (W4 and W5), a sharp decrease in LWC occurred around 20 August, accompanied by leaf yellowing, wilting, and in some cases, abscission, indicating that severe water deficit intensified water loss in leaves and possibly impaired physiological functions. Statistical analysis revealed a positive correlation between LWC and water availability, further validating LWC’s sensitivity to water deficit. On 20 August 2023, the lowest LWC was recorded, reflecting the peak impact of water stress on maize. In 2024, under FD conditions, LWC showed a similar overall trend of a sharp decline followed by stabilization across treatments. Before 1 July, LWC decreased most rapidly by 12.62%, which may be related to increased transpiration, accelerated plant growth, and higher water demand in the early developmental stages. After 1 July, fluctuations in LWC were primarily influenced by irrigation events, indicating water regulation capacity to some degree.
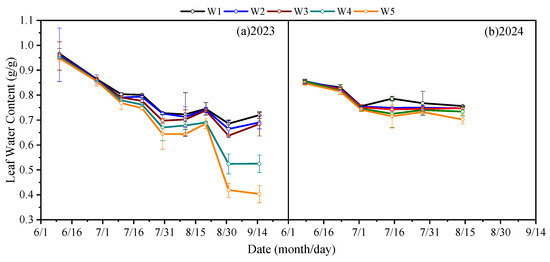
Figure 2.
Changes in spring maize LWC under five water stress levels with FD (plastic film-mulched drip irrigation). Irrigation was applied under five water deficit levels: W1 (100% CK), W2 (85% CK), W3 (70% CK), W4 (55% CK), and W5 (40% CK). CK denotes the control (conventional) irrigation; see Equation (1) for the definition of the suitable irrigation quota per mu.
Although LWC decreased throughout the growing season under all water stress levels, its rate of decline varied by treatment. LWC reduced with increase in water stress, showing significant positive correlation between them. In summary, under FD conditions, LWC was highly sensitive to water supply and effectively reflected the impact of water stress on crop growth. The dynamic changes in LWC can be used as an important water monitoring index to support precision irrigation in spring maize. This approach contributes to optimizing irrigation strategies under limited water resources, improving crop water use efficiency, and minimizing the adverse effects of water deficit on maize yield and quality.
3.2. Optimal Selection of Vegetation Indices Based on Correlation Analysis
Figure 3 and Figure 4 show the Pearson correlation coefficient matrices between vegetation indices, retrieved phenotypic parameters, and LWC under different irrigation regimes. They intuitively demonstrate the strength and direction of the relationships between various indices and LWC. In selection of optimal indices, those with higher correlation coefficients are generally prioritized to improve prediction accuracy. Additionally, indices with low intercorrelation should be chosen to reduce multicollinearity and enhance model stability.
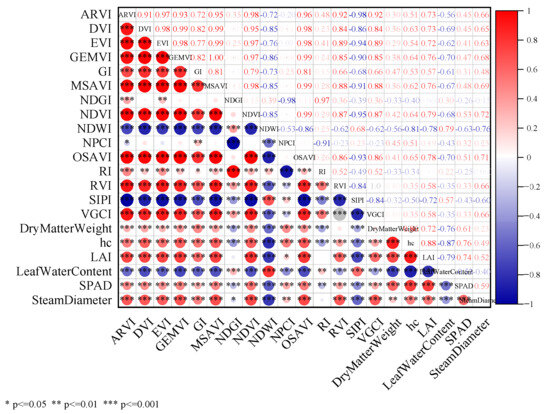
Figure 3.
Correlation matrix between LWC and vegetation indices under MD (plastic film-mulched shallow-buried drip irrigation).
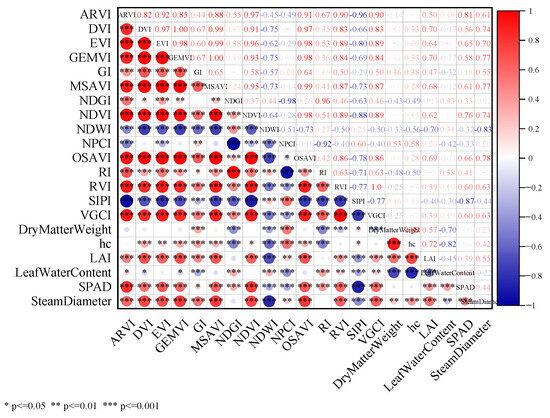
Figure 4.
Correlation matrix between LWC and vegetation indices under FD (plastic film-mulched drip irrigation).
As shown in Figure 3, under MD, many vegetation indices exhibited significant positive correlations with LWC, demonstrating strong potential for water status monitoring. Both the Normalized Difference Water Index (NDWI) and Leaf Area Index (LAI) had a correlation coefficient of 0.79, indicating their strong sensitivity and reliability in detecting water variation. Plant height (hc) showed the highest correlation (−0.87) with LWC, suggesting its strong response to water stress. Dry matter weight (DM) also displayed a good correlation (R2 = −0.76), revealing a close relationship between biomass accumulation and plant water status. Improved vegetation indices such as GEMVI and OSAVI maintained high correlation levels (R2 = −0.7) under complex conditions, showing good adaptability even in arid environments.
Overall, the highly correlated indices above provide a robust foundation for constructing LWC inversion models, enhancing both predictive accuracy and generalization capability. They can offer valuable theoretical support and practical reference for remote sensing-based water status monitoring and precision irrigation decision-making, especially in arid and semi-arid agricultural systems.
In contrast, under FD, as shown in Figure 4, LWC exhibited relatively high negative correlations with plant height (hc) and dry matter (DM), with a correlation coefficient of −0.82 and −0.7, respectively. This suggests that LWC may decrease with increase in plant height and biomass accumulation. This might be related to the water supply conditions and the relationship between biomass partitioning and water distribution during maize development.
Overall, the key vegetation indices affecting LWC differed across irrigation strategies, indicating the necessity of selecting optimal indices based on specific correlation characteristics to improve the accuracy of LWC monitoring and prediction.
As summarized in Table 7, under both MD and FD, plant height (hc), dry matter weight (DM), leaf area index (LAI), Optimized Soil Adjusted Vegetation Index (OSAVI), and Normalized Difference Water Index (NDWI) showed strong correlations with LWC. They consistently reflected plant water status across different irrigation regimes, demonstrating their adaptability and broad application potential. Therefore, they can be used as key input variables in LWC remote sensing inversion models, improving estimation accuracy and supporting dynamic water monitoring and precision irrigation management in spring maize cultivation.

Table 7.
Summary of sensitive vegetation indices and phenotypic parameters under different irrigation regimes.
3.3. Inversion of Leaf Water Content Based on UAV Remote Sensing
In each growth stage, sensitive indices selected through correlation analysis were used as input variables to construct inversion models of spring maize LWC through Partial Least Squares Regression (PLSR), Random Forest (RF), and Support Vector Regression (SVR). Figure 5 and Figure 6 illustrate the predicted and observed LWC values under MD and FD, respectively.
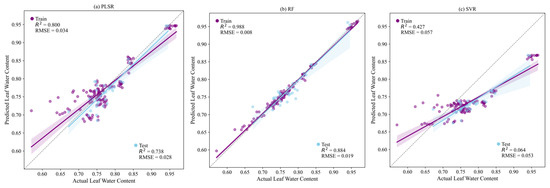
Figure 5.
Comparison of predicted and observed LWC using PLSR, RF, and SVR models under MD (plastic film-mulched shallow-buried drip irrigation).
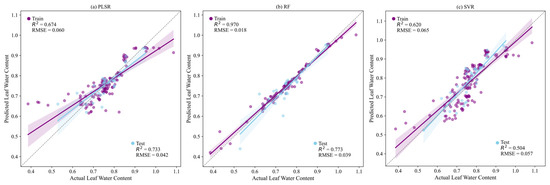
Figure 6.
Comparison of predicted and observed LWC using PLSR, RF, and SVR models under FD (plastic film-mulched drip irrigation).
As shown in Figure 5, under MD, the inversion models constructed exhibited considerable differences in prediction accuracy. Specifically, in the PLSR model, its training had R2 of 0.80 and an RMSE of 0.03, and its test set had R2 of 0.74 with an RMSE of 0.03. This indicates that this model reasonably captured the temporal variation in LWC, demonstrating practical utility. In contrast, the RF model performed best, with its training set having R2 as high as 0.98 and an RMSE of only 0.01 and its test set having R2 of 0.88 and an RMSE of 0.02. This demonstrates that RF not only achieved excellent fitting accuracy and low error, but also displayed stability and robustness, capable of accurately capturing subtle variations in LWC across different irrigation treatments and temporal stages. This can be attributed to its non-parametric ensemble learning characteristics, which effectively handle nonlinear relationships and multicollinearity among variables, making it the optimal choice for LWC prediction tasks. However, the SVR model performed moderately, with its training set having R2 of 0.43 and an RMSE of 0.06, and its test set having R2 of only 0.06 and an RMSE of 0.05. These results indicate that SVR exhibited higher prediction error and lower fitting accuracy than RF and PLSR.
In summary, under MD, the RF algorithm demonstrated the highest predictive performance for LWC inversion. This provides a powerful technical foundation for high-precision remote sensing estimation of LWC and intelligent water management in agriculture. These findings also offer theoretical reference and model guidance for future applications of remote sensing and machine learning-based crop water monitoring across diverse cropping systems and ecological conditions.
As shown in Figure 6, under FD, the LWC inversion models all achieved relatively high prediction capability and good fitting accuracy, adequately reflecting actual variations in LWC. To be precise, the PLSR model yielded intermediate performance, with its training set having R2 of 0.67 and an RMSE of 0.06, and its test set having R2 of 0.73 and an RMSE of 0.04. In comparison, the RF model demonstrated superior predictive performance, with R2 of 0.97 and RMSE of 0.02 for its training set and R2 of 0.77 and an RMSE of 0.04 for its test set. This indicates that this model exhibited strong fitting capability and effectively reflected the actual dynamics of LWC, whereas in the SVR model, its training set had R2 of 0.62 and an RMSE of 0.07, and the two figures for its test set were 0.50 and 0.06, respectively, demonstrating relatively lower prediction accuracy and poorer ability to capture LWC variability than RF and PLSR.
In summary, under FD, the RF algorithm clearly outperformed SVR and exhibited higher model accuracy and reliability and great application potential in LWC inversion for spring maize.
4. Discussions
This study investigated maize leaf water content (LWC) estimation under two drip-irrigation methods using UAV-based multispectral data and multiple machine-learning models. The discussion first addresses the relationships between plant growth indicators and LWC, then compares the performance of different irrigation treatments, and critically analyzes the role of various vegetation indices and model performance metrics in enhancing precision irrigation and drought classification.
In this study, plant height and dry matter weight were found to be strongly and positively correlated with LWC, highlighting the direct impact of water supply on biomass accumulation and morphological development. These relationships highlight the potential of using plant growth indicators, such as plant height and dry matter weight, as reliable proxies for estimating LWC under varying irrigation conditions. The study showed that as an important indicator of the canopy structure, LAI effectively reflected variation in leaf water content (LWC). These findings are consistent with Cohen [56], who reported strong correlations between vegetation indices and leaf water potential in conifer species, suggesting that structural parameters can serve as reliable proxies for crop water status. OSAVI and NDWI, representing soil background interference and improved moisture sensitivity, respectively, also demonstrated good responsiveness to LWC, confirming their robustness in reducing soil background effects and enhancing moisture sensitivity compared with traditional NDVI. The use of vegetation indices can improve the sensitivity of LWC predictions, facilitating more accurate irrigation scheduling.
This study showed that the LWC inversion models constructed under FD generally exhibited lower prediction accuracy than those under MD. This may result from the more heterogeneous soil moisture distribution and complex maize water-use strategies under FD, which increase within-plot variability and reduce model stability. In contrast, MD irrigation, with its more uniform moisture distribution, enabled better performance of the LWC inversion models, indicating that they could provide more reliable theoretical support for water status monitoring and precision irrigation [57,58]. Understanding the varying performances of irrigation methods (FD vs. MD) can inform the selection of the most appropriate irrigation techniques for optimizing water use efficiency and minimizing water stress during critical growth periods.
Among the tested algorithms, the Random Forest (RF) model consistently achieved the highest predictive accuracy, followed by Partial Least Squares Regression (PLSR) and Support Vector Regression (SVR). The superior performance of RF can be attributed to its non-parametric ensemble learning strategy, which effectively handles nonlinear relationships and multicollinearity among vegetation indices [59]. This agrees with previous findings in crop water-status modeling where RF outperformed linear and kernel-based methods.
Despite its strong performance, the RF model exhibited signs of overfitting (training R2 = 0.98 vs. test R2 = 0.88). This suggests that while RF captures complex patterns, careful tuning-such as limiting tree depth, increasing the minimum sample size per leaf node, or applying feature selection-is needed to improve generalization. The highly nonlinear and complex relationship between LWC and vegetation indices also challenges traditional regression approaches such as PLSR and SVR, further highlighting the adaptability of RF for UAV-based crop water monitoring.
5. Conclusions
This study focused on spring maize in field experiments conducted in Wuwei, Gansu Province. Two irrigation methods and five water stress levels were implemented. Throughout the entire growing season, multispectral UAV remote sensing was used to monitor crop water status and generate imagery to construct LWC diagnostic models. The following conclusions have been reached:
(1) Different treatments had significant effects on LWC. Under both irrigation methods, LWC decreased with reduced irrigation. This indicates that water availability directly influenced leaf water status, with higher irrigation volumes maintaining higher LWC.
(2) High-precision inversion models of the leaf water content were established based on multisource remote sensing parameters and phenotypic indicators. By comparing the performance of PLSR, RF, and SVR models under different irrigation strategies, it was found that under MD, the RF model performed best, with its training set having R2 values up to 0.98 and an RMSE of 0.01, and its test set had an R2 of 0.88 and an RMSE of 0.02. The significant differences in model accuracy between irrigation methods provide effective technical pathways for dynamic water monitoring and precision irrigation in spring maize cultivation.
Author Contributions
Conceptualization, J.Z. and P.Z.; validation, H.C.; formal analysis, J.Z.; investigation, J.Z., P.Z. and X.A.; resources, S.L. and W.W.; data curation, J.Z.; writing—original draft preparation, J.Z.; writing—review and editing, J.Z.; visualization, J.Z.; supervision, S.L. and W.W.; project administration, S.L. and W.W.; funding acquisition, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China (2022YFD1900801).
Data Availability Statement
No new data were created or analyzed in this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chen, X. Effect of different planting densities on maize yield. Mod. Agric. Sci. Technol. 2021, 9, 12–13. [Google Scholar]
- Dai, R.; Xu, W. Prediction of maize yield potential in China. Agric. Outlook 2022, 18, 41–49. [Google Scholar]
- Feng, Y.; Hao, W.-P.; Gao, L.-L.; Li, H.; Gong, D.; Cui, N. Comparison of maize water consumption at different scales between mulched and non-mulched croplands. Agric. Water Manag. 2019, 216, 15–324. [Google Scholar] [CrossRef]
- Ibrahim, M.; Khan, A.; Anjum; Ali, W.; Akbar, H. Mulching techniques: An approach for offsetting soil moisture deficit and enhancing manure mineralization during maize cultivation. Soil. Tillage Res. 2020, 200, 104631. [Google Scholar] [CrossRef]
- Wang, H.-P.; Yang, M.-D.; Zhang, S.-Y.; Li, S.; Guan, X.; Wang, T. Effects of different water-saving irrigation methods on growth, yield and water use efficiency of summer maize. Crop J. 2024, 40, 206–212. (In Chinese) [Google Scholar] [CrossRef]
- Mi, N.; Cai, F.; Zhang, Y.-S.; Ji, R.; Fang, Y.; Zhang, S.; Chen, N. Effect of continuous drought during different growth stages on maize and its quantitative relationship with yield loss. Chin. J. Appl. Ecol. 2017, 28, 1563–1570. (In Chinese) [Google Scholar] [CrossRef]
- Jiang, B.; Qu, R.-K.; Li, Y.-D.; Li, C.-L. A review of UAV-based aerial target detection using deep learning. Acta Aeronaut. Sin. 2021, 42, 137–151. (In Chinese) [Google Scholar]
- Guo, Q.-H.; Hu, T.-Y.; Liu, J.; Jin, S.; Xiao, Q.; Yang, G.; Gao, X.; Xu, Q.; Xie, P.; Peng, C.; et al. Advances in small UAV remote sensing and its industrial applications. Prog. Geography. 2021, 40, 1550–1569. (In Chinese) [Google Scholar] [CrossRef]
- Zhou, J.-P.; Gong, J.-H.; Wang, T.; Wang, D.-C.; Yang, L.; Zhao, X.-J.; Hong, Y.; Zhao, Z.-M. Study on UAV Remote Sensing Image Acquiring and Visualization Management System for the Area Affected by 5·12 Wenchuan Earthquake. National Remote Sensing Bulletin. 2008, 877–884. (In Chinese) [Google Scholar]
- Song, Y.; Chen, B.; Wang, Q.; Su, W.; Sun, L.; Zhao, J.; Han, H.; Wang, F. Progress in UAV remote sensing for crop pest and disease monitoring. Cotton Res. 2021, 33, 291–306. (In Chinese) [Google Scholar]
- Li, H.; Zhong, Y.; Feng, Y.-T.; Lin, Z.; Zhu, S.-J. Multi-vegetation index soil moisture inversion model based on UAV remote sensing. Spectrosc. Spectr. Anal. 2024, 44, 207–214. [Google Scholar]
- Hu, J.-B.; Zhang, J. Advances in the application of UAV remote sensing in ecology. Acta Ecol. Sin. 2018, 38, 45. (In Chinese) [Google Scholar]
- Jin, W.; Ge, H.-L.; Du, H.-Q.; Xu, X.-J. A Review on Unmanned Aerial Vehicle Remote Sensing and Its Application. Remote Sens. Inf. 2009, 88–92. (In Chinese) [Google Scholar]
- Yao, H.; Qin, R.; Chen, X. Unmanned aerial vehicle for remote sensing applications—A review. Remote Sens. 2019, 11, 1443. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, L. A review on unmanned aerial vehicle remote sensing: Platforms, sensors, data processing methods, and applications. Drones 2023, 7, 398. [Google Scholar] [CrossRef]
- Yuan, J.; Du, J.-J.; Guo, X.-Y. Research progress on maize phenotyping based on visible light image. Agric. Sci. Technol. 2016, 18, 90–96. (In Chinese) [Google Scholar] [CrossRef]
- Bai, G.; Ge, Y.-F. Review on crop stress perception and plant phenotyping systems. Smart Agric. 2023, 5, 66–81. [Google Scholar] [CrossRef]
- Qiu, R.; Wei, S.; Zhang, M.; Li, H.; Sun, H.; Liu, G.; Li, M. Sensors for measuring plant phenotyping: A review. Int. Agric. Biol. Eng. 2018, 11, 1–17. [Google Scholar] [CrossRef]
- Liu, J.-G.; Zhao, C.-J.; Yang, G.-J.; Yu, H.-Y.; Zhao, X.-Q.; Xu, B.; Niu, Q.-L. Advances in field crop phenotyping information extraction using UAV remote sensing. Trans. CSAE 2016, 32, 98–106. [Google Scholar]
- Mazahrih, N.T.; Albalawneh, A.; Bani Hani, N.; Khadra, R.; Abo Dalo, A.; Al-Omari, Y.; Alomari, B.; Abu Hammad, M.; Martin, I.; Fahd, K.; et al. Impact of reclaimed wastewater on alfalfa production under different irrigation methods. Water Pract. Technol. 2024, 19, 2226–2236. [Google Scholar] [CrossRef]
- Singh, A.; Kumar, S.; Dhaloiya, A.; Kumar, N.; Mor, A.; Kumar, A.; Dhanger, P.; Dagar, H. Soil water dynamics and yield response of broccoli (Brassica oleracea) under drip irrigation with different irrigation frequency. Indian J. Agric. Sci. 2022, 92, 1447–1452. [Google Scholar] [CrossRef]
- Zhang, L.-Y.; Zhang, H.-H.; Niu, Y.-X.; Han, W.-T. Mapping maize water stress based on UAV multispectral remote sensing. Remote Sens. 2019, 11, 605. [Google Scholar] [CrossRef]
- Niu, Y.-X.; Han, W.-T.; Zhang, H.-H.; Zhang, L.-Y.; Chen, H.-P. Estimating fractional vegetation cover of maize under water stress from UAV multispectral imagery using machine learning algorithms. Comput. Electron. Agric. 2021, 189, 106414. [Google Scholar] [CrossRef]
- Zhou, Y.-C.; Lao, C.-C.; Yang, Y.-L.; Zhang, Z.-T.; Chen, H.-Y.; Chen, Y.-W.; Chen, J.-Y.; Ning, J.-F.; Yang, N. Diagnosis of winter-wheat water stress based on UAV-borne multispectral image texture and vegetation indices. Agric. Water Manag. 2021, 256, 107076. [Google Scholar] [CrossRef]
- Diao, Q.-Y. Application of shallow-buried drip irrigation technology for water-saving in wheat and maize. Agric. Dev. Equip. 2025, 3, 232–234. [Google Scholar]
- Zhao, X.-Q.; Lu, Y.-T.; Bai, M.-X.; Xu, M.-X.; Peng, Y.-L.; Ding, Y.-F.; Zhuang, Z.-L.; Chen, F.-Q.; Zhang, D.-Z. Response of different plant-type maize genotypes to drought stress. Acta Prataculturae Sin. 2020, 29, 149–162. (In Chinese) [Google Scholar]
- Song, L.; Jin, J.; He, J. Effects of Severe Water Stress on Maize Growth Processes in the Field. Sustainability 2019, 11, 5086. [Google Scholar] [CrossRef]
- Monteleone, B.; Borzí, I.; Bonaccorso, B.; Martina, M. Developing stage-specific drought vulnerability curves for maize: The case study of the Po River basin. Agric. Water Manag. 2022, 269, 107713. [Google Scholar] [CrossRef]
- Chen, X.; Xing, H.; Liu, B.; Wang, Y.; Cui, N.; Wang, Z.; Zhang, Y. Changes induced by multi-stage water stress on maize growth, water and nitrogen utilization and hormone signaling under different nitrogen supplies. Agric. Water Manag. 2023, 290, 108570. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.; Wang, J.; Zheng, H.; Miao, X.; Sun, X.; Li, P.; Li, Y.; Jia, Y. Relationships Between Oat Phenotypes and UAV Multispectral Imagery Under Different Water Deficit Conditions by Structural Equation Modelling. Agronomy 2025, 15, 1389. [Google Scholar] [CrossRef]
- Li, J.; Schachtman, D.P.; Creech, C.F.; Wang, L.; Ge, Y.; Shi, Y. Evaluation of UAV-derived multimodal remote sensing data for biomass prediction and drought tolerance assessment in bioenergy sorghum. Crop J. 2022, 10, 1363–1375. [Google Scholar] [CrossRef]
- Zhang, F.; Guo, A.; Hu, Z.; Liang, Y. A novel image fusion method based on UAV and Sentinel-2 for environmental monitoring. Sci. Rep. 2025, 15, 27256. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Cai, F.; Tian, J.; Williams, T.K.-A. Spatiotemporal Fusion of Multisource Remote Sensing Data: Literature Survey, Taxonomy, Principles, Applications, and Future Directions. Remote Sens. 2018, 10, 527. [Google Scholar] [CrossRef]
- Samadzadegan, F.; Toosi, A.; Dadrass, J.F. A critical review on multi-sensor and multi-platform remote sensing data fusion approaches: Current status and prospects. Int. J. Remote Sens. 2024, 46, 1327–1402. [Google Scholar] [CrossRef]
- Guo, H.; Ye, D.; Xu, H.; Bruzzone, L. OBSUM: An object-based spatial unmixing model for spatiotemporal fusion of remote sensing images. Remote Sens. Environ. 2024, 304, 114046. [Google Scholar] [CrossRef]
- Zhou, S.-W.; Hu, X.-T.; Wang, W.-E.; Zhang, Y.-J. Yield stability and water-saving effect of controlling soil wetting layer depth in different growth stages of spring maize. Trans. Chin. Soc. Agric. Eng. 2016, 32, 125–132. (In Chinese) [Google Scholar]
- Yang, W.; Kobayashi, H.; Wang, C.; Shen, M.; Chen, J.; Matsushita, B.; Tang, Y.; Kim, Y.; Bret-Harte, M.-S.; Zona, D.; et al. A semi-analytical snow-free vegetation index for improving estimation of plant phenology in tundra and grassland ecosystems. Remote Sens. Environ. 2019, 228, 31–44. [Google Scholar] [CrossRef]
- Penuelas, J.; Baret, F.; Filella, I. Semi-empirical indices to assess carotenoids/chlorophyll a ratio from leaf spectral reflectance. Photosynthetica 1995, 31, 221–230. Available online: https://cdk.lib.cas.cz/client/handle/uuid:0945cc3e-0232-49a4-b687-78524bdd60bf (accessed on 1 August 2025).
- Peñuelas, J.; Gamon, J.-A.; Fredeen, A.-L.; Merino, J.; Field, C.-B. Reflectance indices associated with physiological changes in nitrogen- and water-limited sunflower leaves. Remote Sens. Environ 1994, 48, 135–146. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.-A.; Deering, D.-W. Monitoring vegetation systems in the Great Plains with ERTS. In Proceedings of the NASA Goddard Space Flight Center 3d ERTS-1 Symposium, Washington, DC, USA, 1 January 1974; Volume 1, pp. 309–317. [Google Scholar]
- Madeira, J.; Bedidi, A.; Cervelle, B.; Pouget, M.; Flay, N. Visible spectrometric indices of hematite (Hm) and goethite (Gt) content in lateritic soils: The application of a Thematic Mapper (TM) image for soil-mapping in Brasilia, Brazil. Int. J. Remote Sens. 1997, 18, 2835–2852. [Google Scholar] [CrossRef]
- Pinty, B.; Verstraete, M.-M. GEMI: A non-linear index to monitor global vegetation from satellites. Vegetatio 1992, 101, 15–20. [Google Scholar] [CrossRef]
- Jordan, C.-F. Derivation of leaf-area index from Quality of light on the forest floor. Ecology 1969, 50, 660–663. [Google Scholar] [CrossRef]
- Yuan, B.; Jia, K.; Xia, M.; Zhao, W. Using remote sensing data to evaluate the ecological restoration in Taiyuan from the SDGs perspective. Int. J. Digit. Earth 2023, 16, 4621–4645. [Google Scholar] [CrossRef]
- Gao, B.C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Broge, N.-H.; Mortensen, J.-V. Deriving green crop area index and canopy chlorophyll density of winter wheat from spectral reflectance data. Remote Sens. Environ. 2002, 81, 45–57. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Liu, H.-Q.; Huete, A. A feedback based modification of the NDVI to minimize canopy background and atmospheric noise. T-GRS 1995, 33, 457–465. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanre, D. Atmospherically resistant vegetation index (ARVI) for EOS-MODIS. T-GRS 1992, 30, 261–270. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Ciganda, V.; Rundquist, D.C.; Arkebauer, T.J. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Z.; Li, X.; Zhou, H. Artificial bee colony-based combination approach to forecasting agricultural commodity prices. Int. J. Forecast 2019, 38, 21–34. [Google Scholar] [CrossRef]
- Huang, Q.; Yang, W.-C.; Mao, X.-M. Variations of stem sap flow in spring maize and its upscaling method at field scale in Northeast China. Trans. CSAE 2020, 36, 94–102. [Google Scholar]
- Zhao, J.; Pan, F.-J.; Lan, Y.-B.; Lu, L.-Q.; Cao, D.-L.; Yang, D.-J.; Wen, Y.-T. Extraction of lodging area in wheat based on UAV visible remote sensing and feature fusion. Trans. CSAE 2021, 37, 73–80. [Google Scholar]
- Fei, S.; Hassan, M.-A.; Xiao, Y.; Su, X.; Chen, Z.; Cheng, Q.; Duan, F.-Y.; Chen, R.-Q.; Ma, Y.-T. UAV-based multi-sensor data fusion and machine learning algorithm for yield prediction in wheat. Precis. Agric. 2023, 24, 187–212. [Google Scholar] [CrossRef] [PubMed]
- Cohen, W. Response of vegetation indices to changes in three measures of leaf water stress. PE&RS 1991, 57, 195–202. [Google Scholar]
- Madramootoo, C.A.; Morrison, J. Advances and challenges with micro-irrigation. Irrig. Drain. 2013, 62, 255–261. [Google Scholar] [CrossRef]
- Yang, X.; Chen, J.; Lu, X.; Liu, H.; Liu, Y.; Bai, X.; Qian, L.; Zhang, Z. Advances in UAV Remote Sensing for Monitoring Crop Water and Nutrient Status: Modeling Methods, Influencing Factors, and Challenges. Plants 2025, 14, 2544. [Google Scholar] [CrossRef]
- Wu, Y.; Yuan, S.; Zhu, J.; Tang, Y.; Tang, L. Estimation of Wheat Leaf Water Content Based on UAV Hyper-Spectral Remote Sensing and Machine Learning. Agriculture 2025, 15, 1898. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).